Постройте график функции y x2 4х 5. График функции
«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.
«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).
«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а
«Квадратичная функция и её график» — Решение.у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.
«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения.
Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .
Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .
На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .
Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости). В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.
График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция
Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
Таблица выглядит следующим образом:
Составив такую таблицу, мы можем наметить несколько точек графика функции
y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.
Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:
Соответствующие пять точек показаны на рис. 48.
48.
На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.
Для обоснования своего утверждения рассмотрим функцию
.
Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.
Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.
График функции у = |f(x)|.
Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать
Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х

Пример 2. Построить график функции у = |х|.
Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).
Пример 3 . Построить график функции y = |x 2 — 2x|.
Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x
График функции y = f(x) + g(x)
Рассмотрим задачу построения графика функции y = f(x) + g(x). если заданы графики функций y = f(x) и y = g(x) .
Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).
Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций
 При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)
Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .
При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения
f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.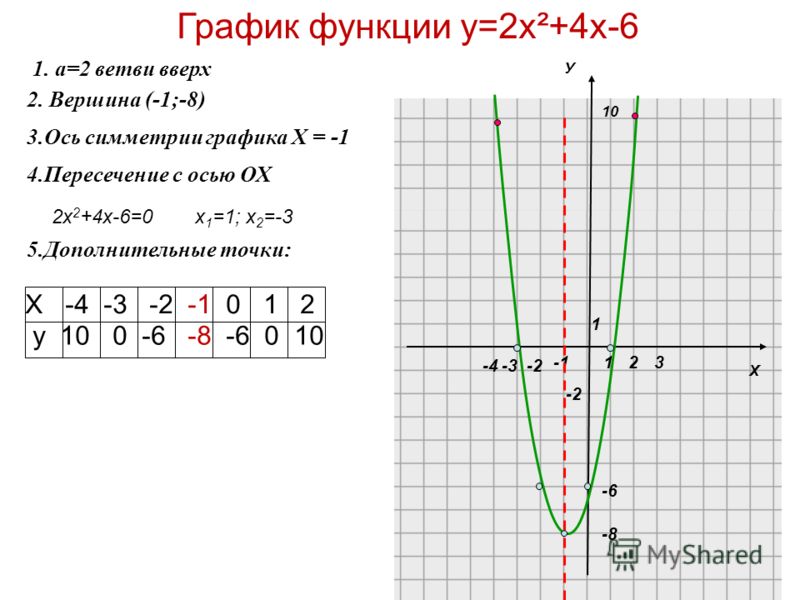
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2 , изображен пунктиром).
2. Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.
(рис. 3) .
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4) .
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Значит, графики таких функций расположены полностью в верхней полуплоскости.
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7) .
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8) .
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.
a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.
2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.
3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.
4) Окончательный график изображен на рисунке (рис. 11) .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Квадратный трехчлен. Квадратичная функция. Вариант 1. Вариант 2. 1.Разложите на множители квадратный трехчлен
100-163-592 Аленушкина Н.Е.Контрольная работа №1
Квадратный трехчлен. Квадратичная функция.
Вариант 1
1.Разложите на множители квадратный трехчлен:
1) х2 – 5х + 6; 2) 5у2 – 3у – 2.
2.Изобразите схематически график функции:
1) у=3х2; 2)у= 14х+22.3.Постройте график функции у=х2 — 4х + 4. С помощью графика найдите:
1)значение у при х= -0,5;
2)значение х при у=2;
3)нули функции;
4)промежутки, в которых у >0 и у
1)у=х2 – 8х; 2)у=5х-2; 3)у=12у2-5у-3.
6.Найдите координаты точки пересечения графиков функций
у=6х2 – 2 и у=11х.
Вариант 2
1.Разложите на множители квадратный трехчлен:
1) х2 + 10х — 11; 2) 3у2 – 4у + 1.

2.Изобразите схематически график функции:
1) у=2х2; 2)у= 14х2+2.3.Постройте график функции у=х2 — 2х + 1. С помощью графика найдите:
1)значение у при х= -0,5;
2)значение х при у= -2;
3)нули функции;
4)промежутки, в которых у >0 и у
1)у=х2 + 9х; 2)у=3х-12; 3)у=15у2-6у+1.
6.Найдите координаты точки пересечения графиков функций
у=2х2 + 2 и у= 5х.
Вариант 3
1.Разложите на множители квадратный трехчлен:
1) х2 – 8х + 7; 2) 5у2 – 8у + 3.
2.Изобразите схематически график функции:
1) у= 12х2; 2)у= х-22.3.Постройте график функции у=х2 — 10х + 25. С помощью графика найдите:
1)значение у при х= 2,5;
2)значение х при у=1;
3)нули функции;
4)промежутки, в которых у >0 и у
1)у=х2 + 12х; 2)у=5-2х; 3)у=13у2-5у+2.
6.Найдите координаты точки пересечения графиков функций
у=6х2 – 1 и у= — х.
Вариант 4
1.Разложите на множители квадратный трехчлен:
1) х2 + 5х + 4; 2) 4у2 – 3у – 7.
2.Изобразите схематически график функции:
1) у= -3х2; 2)у= 14х-32.3.Постройте график функции у=х2 — 4х + 3. С помощью графика найдите:
1)значение у при х= -0,5;
2)значение х при у= — 1;
3)нули функции;
4)промежутки, в которых у >0 и у
1)у=3х2 + 2х; 2)у=5х+4; 3)у=1у2-8у-9.
6.Найдите координаты точки пересечения графиков функций
у=х2 – 3 и у=2х.
Вариант 5
1.Разложите на множители квадратный трехчлен:
1) х2 – 7х + 6; 2) 9у2 + 2у – 7.
2.Изобразите схематически график функции:
1) у= — 2х2; 2)у= 12х-32.3.Постройте график функции у=х2 + 4х — 5. С помощью графика найдите:
1)значение у при х= -0,5;
2)значение х при у=2;
3)нули функции;
4)промежутки, в которых у >0 и у
1)у=х2 + 3х; 2)у=7-2х; 3)у=12у2+5у-7.
6.Найдите координаты точки пересечения графиков функций
у=15 — 2х2 и у=х.
Вариант 6
1.Разложите на множители квадратный трехчлен:
1) х2 – 6х + 8; 2) 6у2 + 2у – 8.

2.Изобразите схематически график функции:
1) у= 5х2; 2)у= 13х+12.3.Постройте график функции у=х2 + 4х + 4. С помощью графика найдите:
1)значение у при х= -0,5;
2)значение х при у=1;
3)нули функции;
4)промежутки, в которых у >0 и у
1)у=х2 – 18х; 2)у=5х+3; 3)у=12у2-5у-3.
6.Найдите координаты точки пересечения графиков функций
у=х2 – 21 и у= -4х.
Как построить график функций? Постройте график функции у 0 5 х2
Сегодня мы внимательно изучим функции, графиком которых является прямая линия.
Запиши в тетрадь тему урока
«Линейная функция и прямая пропорциональность».
Внимательно выполняй все задания и
старайся запомнить новые для тебя определения.
Запомни определение:
Линейной функцией называется функция, которую можно задать формулой вида
у = kx + b, где х — независимая переменная, k и b — некоторые числа.
Например: если k = 0,5 и b = -2, то у = 0,5х — 2.
Задание:
Построить график линейной функции у = 0,5х — 2.
Составь таблицу значений пар (х, у).
Отметь их на координатной плоскости.
Соедини точки линией.
Проверь решение:
Построим график линейной функции у = 0,5х — 2.
Для построения графика у = -х + 3 вычислим координаты двух точек
Отметим их на координатной плоскости две точки и соединим их прямой.
А сможешь ли ты определить:
принадлежит ли точка А(36; 5) графику линейной функции ?
Да
Нет
А теперь сравни эти два графика и увидим, что у линейной функции у = kx + b,
еще до его построения можно «предугадать» расположение прямой линии на координатной плоскости!
Как?
Просто надо внимательно посмотреть на числа k и b…
И они многое нам расскажут!
Попробуй догадаться…
| Функция у = 0,5х — 2 | Функция у = -х + 3 |
Итак, наблюдаем и делаем выводы:
1) Первый пересекает ось ОУ в точке (0; -2), а второй в (0; 3)
!!! у первого b = -2, а у второго b = 3
Вывод: по числу b в формуле y = kx + b мы определим в какой точке прямая пересечет ось ординат.
2) Первый наклонен к положительному направлению оси ОХ под острым углом, а второй — под тупым углом.
!!! у первого k > 0, а у второй функции k
Вывод: если в формуле y = kx + b мы видим, что число k > 0 значит график наклонен к положительному направлению оси абсцисс под острым углом;
если же число k Число k (коэффициент при х) называют за это — угловым коэффициентом.
Запомни это все! Нам такие знания еще не раз пригодятся
Если в формуле y = kx + b, мы возьмем b = 0, то получим формулу y = kx.
Запомни определение:
Функция, которую можно задать формулой y = kx, где k — некоторое число не равное 0, х — переменная, называется прямой пропорциональностью.
Выполни в своей тетради задание:
Придумай несколько формул прямой пропорциональности с разными коэффициентами k и построй их графики в одной координатной плоскости.
Поскольку у прямой пропорциональности b = 0, то график пересечет ось ОУ в точке (0; 0).
На одной координатной плоскости мы можем нарисовать и несколько графиков!
У линейной функции график — прямая линия.
А прямые могут быть параллельными или пересекаться в одной точке…
Интересно, а до построения графиков, только посмотрев (внимательно!) на их формулы, мы может сделать вывод:
Графики этих функций — пересекутся,
графики этих функций — расположены параллельно.
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Урок алгебры в 9 классе по теме «Построение графиков функции, аналитическое выражение которых содержит знак абсолютной величины» был построен на основе компьютерных технологии, применяя исследовательскую деятельность обучения.
Цели урока: Обучающая: Наглядно
продемонстрировать учащимся возможности
использования компьютера при построении
графиков функции с модулями; для самоконтроля,
экономии времени при построении графиков
функций вида у=f |(х)| , у = | f (х)| , у=|f |(х)| |.
Развивающая: Развитие интеллектуальных умений и мыслительных операций — анализ и синтез сравнение, обобщение. Формирование ИКТ компетентности учащихся.
Воспитывающая: Воспитание познавательного интереса к предмету путем введения новейших технологий обучения. Воспитание самостоятельности при решении учебных задач.
Оборудование: Оборудование: компьютерный класс, интерактивная доска, презентация на тему «Построение графиков функции, аналитическое выражение которых содержит знак абсолютной величины», раздаточный материал: карточки для работы с графической моделью функций, листы для фиксирования результатов исследования функций, персональные компьютеры. Лист самоконтроля.
Программное обеспечение: презентация Microsoft PowerPoint «Построение графиков функции, аналитическое выражение которых содержит знак абсолютной величины»
Ход урока
1. Организационный момент
2. Повторение, обобщение и систематизация. Это
этап урока сопровождается компьютерной
презентацией.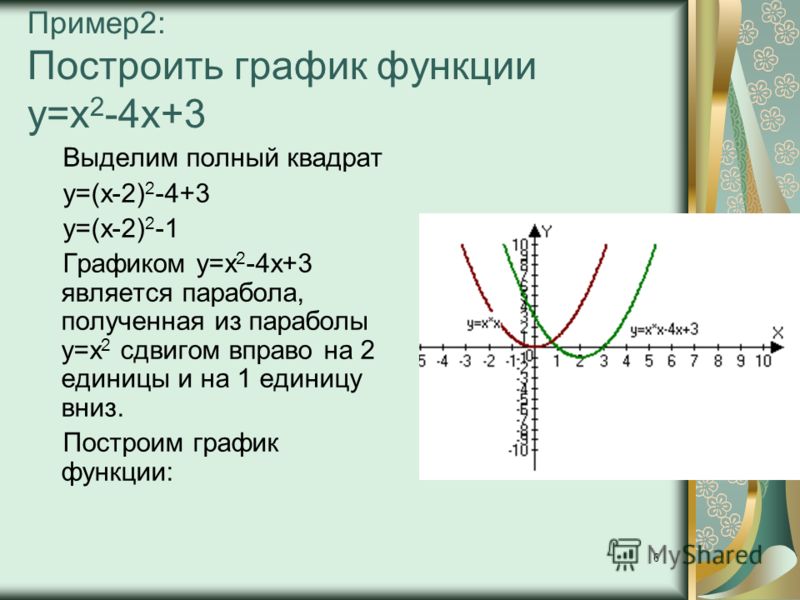
График функции у=f |(х)|
у=f |(х)| — четная функция, т.к. | х | = | -х |, то f |-х| = f | х |
График этой функции симметричен относительно оси координат.
Следовательно, достаточно построить график функции у=f (х) для х>0,а затем достроить его левую часть, симметрично правой относительно оси координат.
Например, пусть графиком функции у=f (х) является кривая, изображенная на рис.1, тогда графиком функции у=f |(х)| будет кривая, изображенная на рис.2.
1. Исследование графика функции у= |х|
Таким образом, искомый график есть ломанная, составленная из двух полупрямых. (Рис.3)
Из сопоставления двух графиков: у=х и у= |х|, учащиеся сделают вывод, что второй получается из первого зеркальным отображением относительно ОХ той части первого графика, которая лежит под осью абсцисс. Это положение вытекает из определения абсолютной величины.
Из сопоставления двух графиков: у = х и у = -х,
сделают вывод: функции у = f(|х|) получается из
графика у = f (x) при х 0 симметричным отображением
относительно оси ОУ.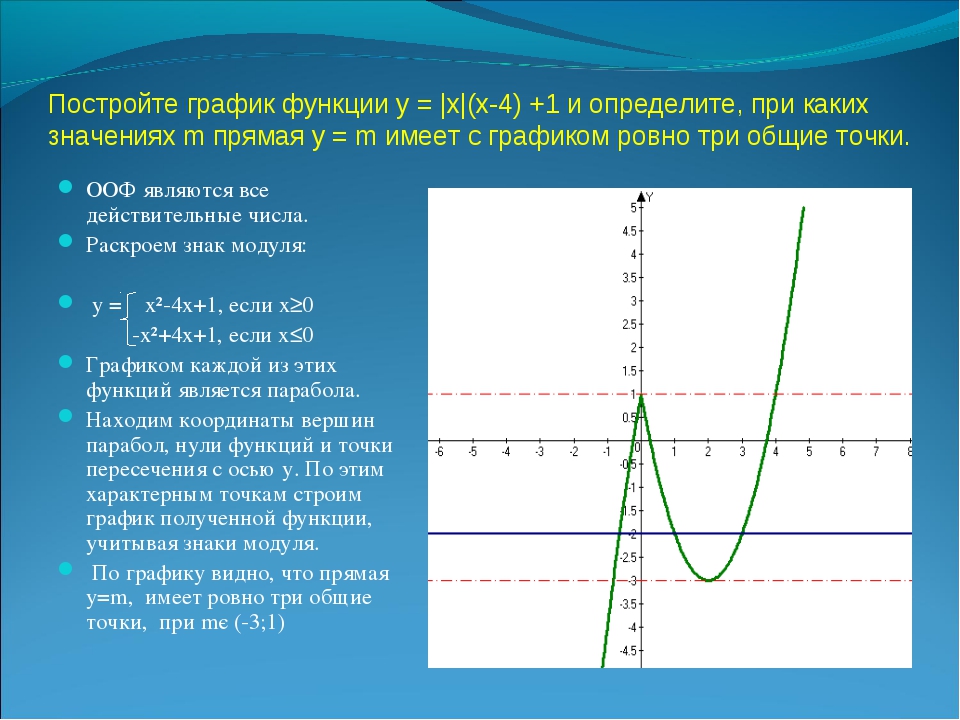
Можно ли применять этот метод построения графиков для любой функции, содержащей абсолютную величину?
Слайд 3 и 4.
1. Построите график функции у=0,5 х 2 — 2|х| — 2,5
1) Поскольку |х| = х при х 0, у=0,5 х 2 — 2х — 2,5 . Если ху=0,5 х 2 + 2х — 2,5 .
2) Если рассмотрим график у=0,5 х 2 -2х — 2,5 при х
Можно ли применять этот метод построения графиков дл квадратичной функции, для графиков обратной пропорциональности, содержащие абсолютную величину?
1) Поскольку |х| = х при х 0, требуемый график совпадает с параболой у=0,25 х 2 — х — 3. Если ху=0,25 х 2 + х — 3.
2) Если рассмотрим график у=0,25 х 2 — х — 3 при х 0 и отобразить его относительно оси ОУ мы получим тот же самый график.
(0; — 3) координаты точки пересечения графика функции с осью ОУ.
у =0, х 2 -х -3 = 0
х 2 -4х -12 = 0
Имеем, х 1 = — 2; х 2 = 6.
(-2; 0) и (6; 0) — координаты точки пересечения
графика функции с осью ОХ.
Если х
Значит, часть требуемого графика, соответствующая значениям х0.
б) Поэтому достраиваю для х
На тетрадях ученики доказывают, что график функции у = f |(х)| совпадает с графиком функции у = f (х) на множестве неотрицательных значений аргумента и симметричен ему относительно оси ОУ на множестве отрицательных значений аргумента.
Доказательство: Если х 0, то f |(х)|= f (х), т.е. на множестве неотрицательных значений аргумента графики функции у = f (х) и у = f |(х)| совпадают. Так как у = f |(х)| — чётная функция, то её график симметричен относительно ОУ.
Таким образом, график функции у = f |(х)| можно получить из графика функции у = f (х) следующим образом:
1. построить график функции у = f(х) для х>0;
2. Для х
Вывод: Для построения графика функции у = f |(х)|
1. построить график функции у = f(х) для х>0;
2. Для х отразить построенную часть
относительно оси ОУ.
Слайд 5
4. Исследовательская работа по построению
графика функции у = | f (х)|
Исследовательская работа по построению
графика функции у = | f (х)|
Построить график функции у = |х 2 — 2х|
Освободимся от знака модуля по определению
Если х 2 — 2х0,
т.е. если х
0 и х2, то |х 2 —
2х|= х 2 — 2х
Если х 2 — 2х
Видим, что на множестве х
0 и х2 графики функции
у = х 2 — 2х и у = |х 2 — 2х|совпадают, а на множестве (0;2)
графики функции у = -х 2 + 2х и у = |х 2 — 2х| совпадают. Построим их.
График функции у = | f (х)| состоит из части графика функции у = f(х) при у?0 и симметрично отражённой части у = f(х) при у
Построить график функции у = |х 2 — х — 6|
1) Если х 2 — х -6 0, т.е. если х
-2 и х3, то |х 2 — х -6|= х 2 — х -6.
Если х 2 — х -6
Построим их.
2) Построим у = х 2 — х -6 . Нижнюю часть графика
симметрично отбражаем относительно ОХ.
Сравнивая 1) и 2), видим что графики одинаковые.
Работа на тетрадях.
Докажем, что график функции у = | f (х)| совпадает с графиком функции у = f (х) для f(х) >0 и симметрично отражённой частью у = f(х) при у
Действительно, поопределению абсолютной величины, можно данную функцию рассмотреть как совокупность двух линий:
у = f(х), если f(х) 0; у = — f(х), если f(х)
Для любой функции у = f(х), если f(х) >0, то
| f (х)| = f(х), значит в этой части график функции
у = | f (х)| совпадает с графиком самой функции
Если же f(х) ) симметричнаточке(х; f (х)) относительно
оси ОХ. Поэтому для получения требуемого графика
отражаем симметрично относительно оси ОХ
«отрицательную» часть графика у = f(х).
Поэтому для получения требуемого графика
отражаем симметрично относительно оси ОХ
«отрицательную» часть графика у = f(х).
Вывод: действительно для построения графика функции у = |f(х) | достаточно:
1.Построить график функции у = f(х) ;
F(х)
Вывод: Для построения графика функции у=|f (х) |
1.Построить график функции у=f (х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где f (х)
Слайды 8-13.
5. Исследовательская работа по построению графиков функции у=|f |(х)| |
Применяя определение абсолютной величины и ранее рассмотренные примеры, построим графиков функции:
у = |2|х| — 3|
у = |х 2 — 5|х||
у = | |х 2 | — 2| и сделал выводы.
Для того чтобы построить график функции у = | f |(х)| надо:
1. Строить график функции у = f(х) для х>0.
2. Строить вторую часть графика, т. е.
построенный график симметрично отражать
относительно ОУ, т. к. данная функция четная.
к. данная функция четная.
3. Участки получившегося графика, расположенные в нижней полуплоскости, преобразовывать на верхнюю полуплоскость симметрично оси ОХ.
Построить график функции у = | 2|х | — 3| (1-й способ по определению модуля)
1. Строим у = 2|х | — 3 , для 2 |х| — 3 > 0 , | х |>1,5 т.е. х1,5
а) у = 2х — 3 , для х>0
б) для х
2. Строим у = —2 |х| + 3 , для 2|х | — 3
а) у = —2х + 3 , для х>0
б) для х
У = | 2|х | — 3|
1) Строим у = 2х-3, для х>0.
2) Строим прямую, симметричную построенной относительно оси ОУ.
3) Участки графика, расположенные в нижней полуплоскости, отображаю симметрично относительно оси ОХ.
Сравнивая оба графика, видим, что они одинаковые.
у = | х 2 — 5|х| |
1. Строим у = х 2 — 5 |х|, для х 2 — 5 |х| > 0 т.е. х >5 и х
а) у = х 2 — 5 х, для х>0
б) для х
2. Строим у = — х 2 + 5 |х| , для х 2 — 5 |х|
Строим у = — х 2 + 5 |х| , для х 2 — 5 |х|
а) у = — х 2 + 5 х, для х>0
б) для х
У = | х 2 — 5|х| |
а) Строим график функции у = х 2 — 5 х для х>0.
Б) Строим часть графика, симметричную построенной относительно оси ОУ
в) Часть графика, расположенные в нижней полуплоскости, преобразовываю на верхнюю полуплоскость симметрично оси ОХ.
Сравнивая оба графика, видим что они одинаковые. (Рис.10)
3. Подведение итогов урока.
14,15 слайды.
у=f |(х)|
1.Построить график функции у=f (х) для х>0;
2.Построить для х
Алгоритм построения графика функции у=|f (х) |
1.Построить график функции у=f (х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где f (х)
Алгоритм построения графика функции у=|f |(х)| |
1. Построить график функции у=f (х) для х>0.
2. Построить кривую графика, симметричную
построенной относительно оси ОУ, т. к. данная
функция четная.
к. данная
функция четная.
3. Участки графика, расположенные в нижней полуплоскости, преобразовывать на верхнюю полуплоскость симметрично оси ОХ.
Здравствуйте, Давид.
График функции представляет собой её геометрический образ. Он показывает, где на координатной плоскости находится точка, координаты которой (Х и У) связаны определенным математическим выражением (функцией).
Перед тем, как приступить к построению графика функций, сначала необходимо начертить оси координат ОХ и ОУ. Лучше всего для этого использовать масштабно — координатную бумагу. Далее следует определить тип функции, потому что у различных функций графики очень сильно отличаются. К примеру, линейная функция, о которой пойдет речь ниже, имеет график в виде прямой линии. После этого нужно определить область определения функций, т.е. ограничения для значений Х и У. К примеру, если Х находиться в знаменателе дроби, то его значение не может быть равным 0. Далее надо найти нули функции, то есть места пересечения графика функции с осями координат.
Приступим к построению графика функции, указанной в пункте а) вашего вопроса.
Функция у= — 6х + 4 , график которой требуется построить в первой задаче вашего вопроса, является линейной функцией, т.к. линейные функции представлены выражением y = kx + m. Областью определения линейной функции считается вся прямая ОХ. Параметр m в линейной функции определяет точку, в которой график линейной функции пересекает ось OY.
Для того, чтобы построить график линейной функции достаточно определить хотя бы две её точки, потому что графиком функции является прямая. Если найти больше точек, то можно построить более точный график. Вообще, при построении графика линейной функции необходимо определить точки, в каких график пересечет оси координат Х, У.
Итак, в вашем случае точки пересечения графика функции с осями координат будут такими:
При Х=0, У= -6*0+4=4 Таким образом, мы получили значение параметра m в линейной функции.
У=0, то есть 0= -6*Х+4, то есть 6х=4, следовательно Х=4/6=0,667
При Х= -1, У=-6*-1+4=10
При Х=1, У= -6*1+4=-2
При Х=2, У= -6*2+4=-8
Получив все вышеуказанные точки, вам остается только отметить их на координатной плоскости, соединить прямой линией, как показано в примере на рисунке, который прикреплен к данной статье.
Теперь построим график функции, указанной в пункте б) вашего вопроса.
Сразу видно, что функция у= 0,5х , из второй задачи, также является линейной функцией. В отличие от первого примера, в данном выражении отсутствует значение m, а это говорит о том, что график функции у= 0,5х проходит через начало осей координат, то есть в их нулевой точке.
При Х=0, У= 0,5*0=0
При Х= 1, У=0,5*1=0,5
При Х=2, У= 0,5*2=1
При Х=3, У=0,5*3=1,5
При Х= -1, У=0,5*-1= -0,5
При Х= -2, У= 0,5*-2= -1
При Х= -3, У=0,5*3= -1,5
Теперь, имея все вышеуказанные значения Х и У вы без труда сможете поставить эти точки на координатной плоскости, соединить их прямой линией при помощи линейки, и у вас получится график линейной функции у=0,5х
Ниже я привела ссылку, перейдя по которой, вы можете найти уроки по математике, алгебре, геометрии и русскому языку. Я бы посоветовала вам прочитать несколько тем, которые касаются построения графиков функций. В данном учебном материале очень наглядно показано, как можно построить графики линейных функций, а в темах, которые расположены далее можно увидеть примеры построения графиков других функций. Все написано достаточно подробно, поэтому это будет понятно не только тем, кто давно закончил школу и имеет представление о том, как можно построить график функции, но и тем, кто только начинает постигать азы науки. Я считаю, что увидев наглядно на конкретных примерах, как строятся графики функций, вы потом без проблем сможете решить любую задачу по построению графика функций.
В данном учебном материале очень наглядно показано, как можно построить графики линейных функций, а в темах, которые расположены далее можно увидеть примеры построения графиков других функций. Все написано достаточно подробно, поэтому это будет понятно не только тем, кто давно закончил школу и имеет представление о том, как можно построить график функции, но и тем, кто только начинает постигать азы науки. Я считаю, что увидев наглядно на конкретных примерах, как строятся графики функций, вы потом без проблем сможете решить любую задачу по построению графика функций.
Контрольная работа 9 класс «Степенная функция» | Материал по алгебре (9 класс):
Контрольная работа № 3 по теме «Степенная функция»
1 вариант
1. Найти область определения функции:
1) у = 2) у =
2. Постройте график функции у = х2 – 4х – 5. Найдите с помощью графика:
а) значение у при х = 3;
б) значения х, при которых у = — 5;
в) нули функции;
г) промежутки, в которых у > 0 и в которых у
д) промежуток, в котором функция возрастает.
3. Исследовать функцию на четность и нечетность:
1) у = 5х8 – 4х2 2) у =
4. В одной системе координат построить графики данных функций и найти точки их пересечения:
у =
у = х2
5. Решить уравнение:
- = х – 1 2)
6. Не строя графики функций, решить систему уравнений:
у = х2 + 3х – 1
у =
7. Найдите наибольшее и наименьшее значения функции y = (x – 2)3 + 4 на отрезке
Контрольная работа № 3 по теме «Степенная функция»
2 вариант
1. 2-2x-3) и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
2-2x-3) и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Функция состоит из трех квадратных трехчленов. разложим их на множители по формуле
ax2 + bx + c = a(x — x1)(x — x2), где х1 и х2 — корни квадратных уравнений.
Все три квадратных уравнения приведенные. Это значит, что можно найти их корни по теореме Виета. Именно поэтому я сразу напишу разложения этих трехчленов на множители. Конечно, решать через дискриминант никто не запрещал и ошибкой это не будет.
Итак, после разложения на множители функция примет такой вид:
Видно невооруженным глазом, что скобки из знаменателя сокращаются со скобками из числителя. Это просто супер-пупер! Но надо обязательно оговориться, что знаменатель не может быть равен нулю, а значит, что x ≠ -1 и x ≠ 3. Эти исключения подразумевают выколотые точки на нашем будущем графике.
После сокращения раскрываем оставшиеся скобки.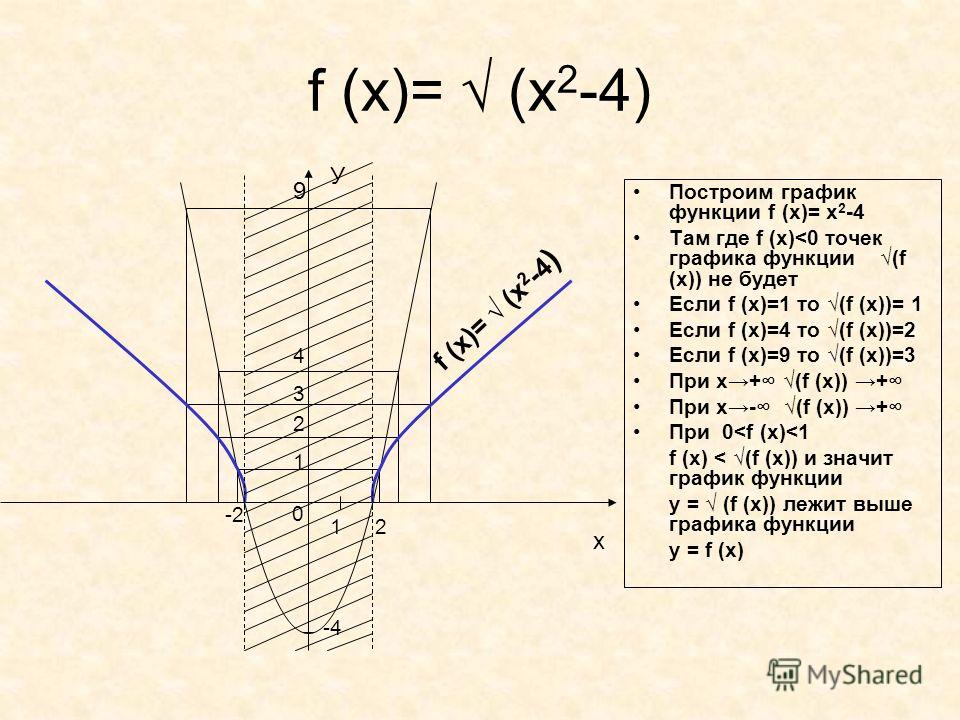
О, чудо! Это квадратичная функция! График — парабола!
Ищем ее вершину О (m; n).
Первая координата m, которую мы будем отмечать на оси Ох, находится по формуле.
А чтобы найти вторую координату надо m подставить в упрощенную ранее функцию и посчитать.
В общем, вершина параболы имеет координаты (-0,5; -2,25).
Чертим координатную плоскость и отмечаем вершину.
Мастера по рисованию парабол могут ее начертить, не прибегая к таблице по нахождению координат других точек. А вот тем, кто не в очень теплых отношениях с параболами, придется ее рисовать.
Поскольку я мастер — обойдусь без таблицы 🙂
Не забываем про выколотые точки!
В условии задачи сказано, что некоторая прямая y = m должна иметь одну общую точку с параболой. Эта прямая будет параллельна оси Ох и одну общую точку она будет иметь в выколотых точках и вершине параболы.
Ответ: 10; -2; -2,25.
P.S. Бывает так, что график нарисован очень криво.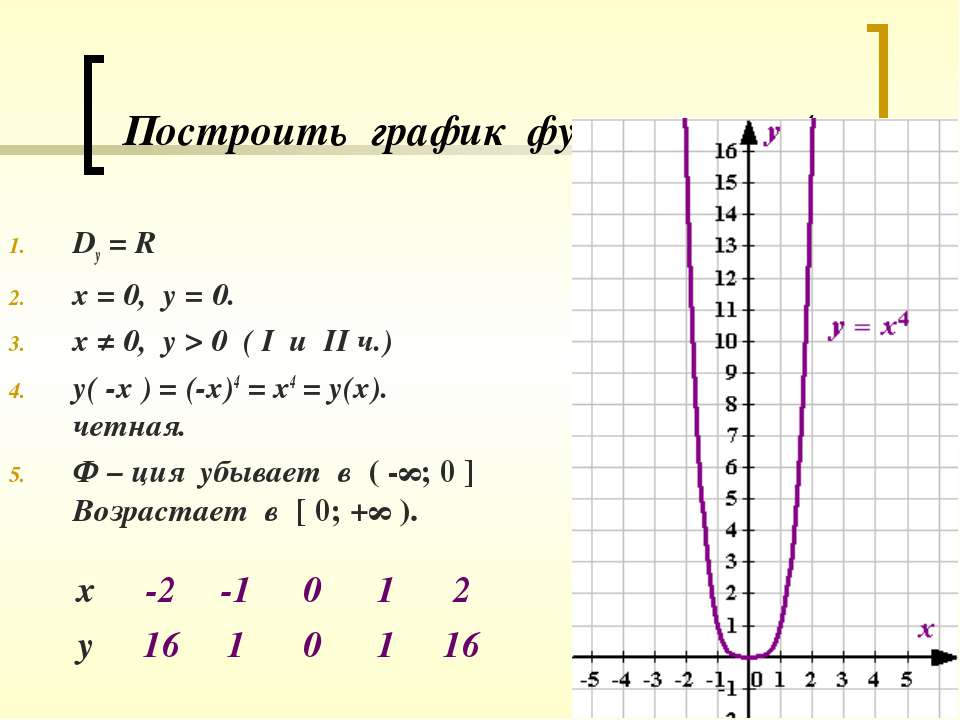 Как не ошибиться в координатах выколотых точек? Очень просто. В нашей задаче x ≠ -1 и x ≠ 3. Подставь эти числа в функцию (упрощенную, разумеется), посчитай и найдешь, чему должны быть не равны координаты по игреку (у ≠ -2 и у ≠ 10).
Как не ошибиться в координатах выколотых точек? Очень просто. В нашей задаче x ≠ -1 и x ≠ 3. Подставь эти числа в функцию (упрощенную, разумеется), посчитай и найдешь, чему должны быть не равны координаты по игреку (у ≠ -2 и у ≠ 10).
РЕШЕНИЕ: 2) Для функции y = x2 — 4x — 5 выполните следующие задачи: a) Представьте функцию в форме y = a (x
РЕШЕНИЕ: 2) Для функции y = x2 — 4x — 5, выполнять следующие задачи: а) Представьте функцию в виде y = a (x — h) 2 + k. Ответ: Показать работы в этой области б) Что такое т Алгебра -> Квадратичные уравнения и параболы -> РЕШЕНИЕ: 2) Для функции y = x2 — 4x — 5 выполните следующие задачи: а) Представьте функцию в виде y = a (x — h) 2 + k.Ответ: Показать работы в этой области б) Что такое т Войти в систему
|
РЕШЕНИЕ: Для функции y = x2 — 4x — 5 выполните следующие задачи: a) Поместите функцию в форму y = a (x
РЕШЕНИЕ: Для функции y = x2 — 4x — 5 выполните следующие задачи : а) Представьте функцию в виде y = a (x — h) 2 + k.Ответ: Показать работы в этой области б) Что такое е Алгебра -> Квадратичные уравнения и параболы -> РЕШЕНИЕ: Для функции y = x2 — 4x — 5 выполните следующие задачи: а) Представьте функцию в виде y = a (x — h) 2 + k. Ответ: Показать работы в этой области б) Что такое е Войти в систему
|
1) Используя квадратное уравнение x2 — 4x
Домашнее задание ответов / архив вопросов / 1) Используя квадратное уравнение x2 — 4x — 5 = 0, выполните следующие задачи: а) Решите факторинг
1) Используя квадратное уравнение x2 — 4x — 5 = 0, выполните следующие задачи: а) Решите факторинг
Математика
Поделиться с
1) Используя квадратное уравнение x2 — 4x — 5 = 0, выполните следующие задачи:
а) Решите факторинг.
б) Решите, завершив квадрат.
c) Решите, используя формулу корней квадратного уравнения.
2) Для функции y = x2 — 4x — 5 выполните следующие задачи:
а) Представьте функцию в виде y = a (x — h) 2 + k.
б) Какое уравнение представляет собой линия симметрии графика этой функции?
c) Постройте график функции, используя уравнение в части a. Объясните, почему нет необходимости наносить точки на график при использовании y = a (x — h) 2 + k.
г) Опишите своими словами, как этот график сравнивается с графиком y = x2?
3) Предположим, что бейсбольный мяч взлетает с земли вертикально вверх с начальной скоростью 32 фута в секунду.Функцию можно создать, выразив расстояние над землей s как функцию времени t. Эта функция имеет вид s = -16t2 + v0t + s0
.
? 16 представляет собой 1 / 2g, гравитационное притяжение, вызванное силой тяжести (измеряется в футах в секунду2).
? v0 — начальная скорость (с какой силой вы бросаете объект, измеряется в футах в секунду).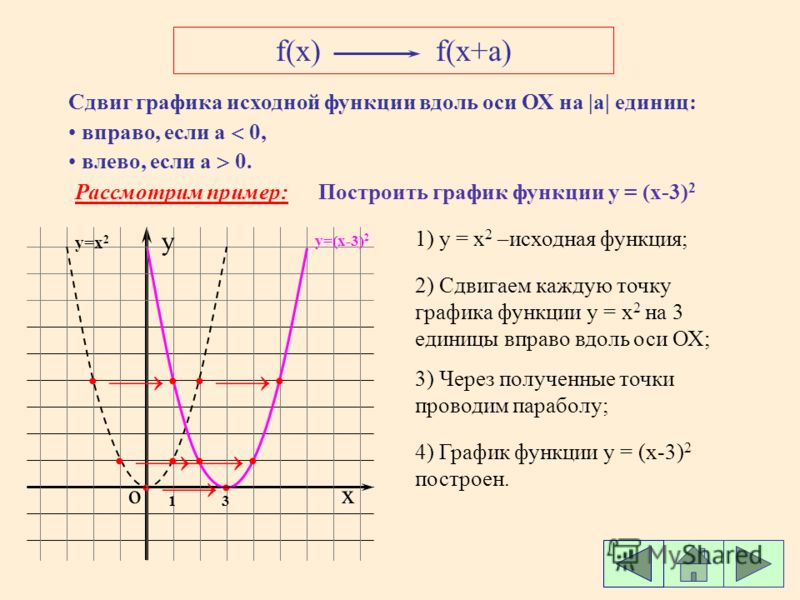
? s0 — начальное расстояние над землей (в футах). Если вы стоите на земле, то s0 = 0.
а) Какая функция описывает эту проблему?
б) Насколько высоко мяч будет над землей через 1 секунду?
в) Сколько времени потребуется, чтобы удариться о землю?
г) Какая максимальная высота мяча? В какое время будет достигнута максимальная высота?
4) У Джона есть 300 футов бруса, чтобы обрамить прямоугольный внутренний дворик (периметр прямоугольника в 2 раза больше длины плюс 2 ширины).2−4x-5 = 0 Tiger Algebra Solver
Пошаговое решение:
Шаг 1:
Попытка разложить на множители путем разделения среднего члена
1.1 Факторинг x 2 -4x-5
Первый член равен , X 2 его коэффициент равен 1.
Средний член, -4x, его коэффициент равен -4.
Последний член, «константа», равен -5
Шаг-1: Умножьте коэффициент первого члена на константу 1 • -5 = -5
Шаг-2: Найдите два множителя -5, сумма которых равен коэффициенту среднего члена, который равен -4.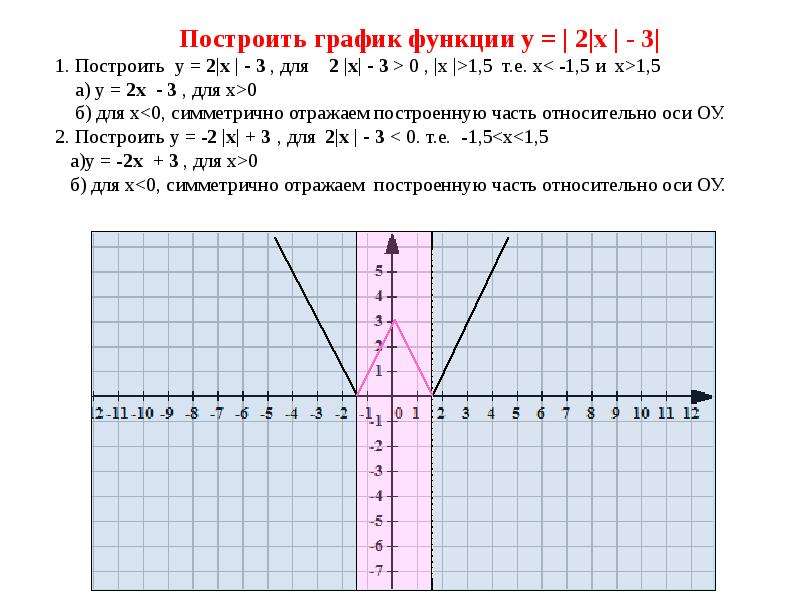
| -5 | + | 1 | = | -4 | Вот и все |
Шаг 3: Перепишите полиномиальное разбиение среднего члена, используя два фактора, найденные в шаг 2 выше, -5 и 1
x 2 — 5x + 1x — 5
Шаг 4: сложите первые 2 члена, вычитая одинаковые множители:
x • (x-5)
Сложите последнее 2 члена, извлекая общие множители:
1 • (x-5)
Шаг 5: сложите четыре члена шага 4:
(x + 1) • (x-5)
Какое желаемое разложение на множители
Уравнение в конце шага 1:
(x + 1) • (x - 5) = 0
Шаг 2:
Теория — Корни продукта:
2.1 Произведение нескольких членов равно нулю.
Если произведение двух или более членов равно нулю, то хотя бы один из членов должен быть равен нулю.
Теперь мы решим каждый член = 0 отдельно
Другими словами, мы собираемся решить столько уравнений, сколько членов есть в произведении.
Любое решение term = 0 также решает product = 0.
Решение уравнения с одной переменной:
2.2 Решение: x + 1 = 0
Вычтите 1 из обеих частей уравнения:
x = -1
Решение уравнения с одной переменной:
2.3 Решите: x-5 = 0
Добавьте 5 к обеим сторонам уравнения:
x = 5
Дополнение: Решение квадратного уравнения напрямую
Решение x 2 -4x-5 = 0 напрямую
Ранее мы факторизовал этот многочлен, разделив средний член. Давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу
Парабола, найдя вершину:
3.1 Найдите вершину y = x 2 -4x-5
Параболы имеют наивысший или наименьший точка называется Вершиной.Наша парабола открывается и, соответственно, имеет самую низкую точку (АКА абсолютный минимум). Мы знаем это даже до того, как нанесли «y», потому что коэффициент первого члена, 1, положительный (больше нуля).
Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы. То есть, если парабола действительно имеет два реальных решения.
Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы. То есть, если парабола действительно имеет два реальных решения.
Параболы могут моделировать множество реальных жизненных ситуаций, например высоту над землей объекта, брошенного вверх через некоторый промежуток времени. Вершина параболы может предоставить нам информацию, например, максимальную высоту, которую может достичь объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
Для любой параболы Ax 2 + Bx + C координата x вершины задается как -B / (2A). В нашем случае координата x равна 2.0000
Подставляя в формулу параболы 2,0000 для x, мы можем вычислить координату y:
y = 1,0 * 2,00 * 2,00 — 4,0 * 2,00 — 5,0
или y = -9,000
Парабола, графическая вершина и пересечение по оси X:
Корневой график для: y = x 2 -4x-5
Ось симметрии (пунктирная линия) {x} = {2,00}
Вершина в точке {x, y} = {2,00, -9,00}
x -Переходы ( Roots):
Корень 1 при {x, y} = {-1. 00, 0.00}
00, 0.00}
Корень 2 при {x, y} = {5.00, 0.00}
Решите квадратное уравнение, заполнив квадрат
3.2 Решение x 2 -4x-5 = 0, заполнив квадрат.
Добавьте 5 к обеим сторонам уравнения:
x 2 -4x = 5
Теперь умный бит: возьмите коэффициент при x, равный 4, разделите его на два, получив 2, и, наконец, возведите его в квадрат, получив 4
Добавьте 4 к обеим частям уравнения:
В правой части мы имеем:
5 + 4 или, (5/1) + (4/1)
Общий знаменатель двух дробей равен 1 Сложение (5 / 1) + (4/1) дает 9/1
Таким образом, прибавляя к обеим сторонам, мы, наконец, получаем:
x 2 -4x + 4 = 9
Добавление 4 завершило левую часть в полный квадрат:
x 2 -4x + 4 =
(x-2) • (x-2) =
(x-2) 2
Вещи, которые равны одному и тому же, также равны друг другу.Так как
x 2 -4x + 4 = 9 и
x 2 -4x + 4 = (x-2) 2
, то согласно закону транзитивности
(x-2) 2 = 9
Мы будем называть это уравнение уравнением. # 3.2.1
# 3.2.1
Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
Обратите внимание, что квадратный корень из
(x-2) 2 равен
(x-2) 2/2 =
(x-2) 1 =
x-2
Теперь, применяя Принцип квадратного корня для уравнения.# 3.2.1 получаем:
x-2 = √ 9
Добавьте 2 к обеим сторонам, чтобы получить:
x = 2 + √ 9
Так как квадратный корень имеет два значения, одно положительное, а другое отрицательное,
x 2 — 4x — 5 = 0
имеет два решения:
x = 2 + √ 9
или
x = 2 — √ 9
Решите квадратное уравнение с помощью квадратичной формулы
3.3 Решение x 2 -4x-5 = 0 по квадратичной формуле.
Согласно квадратичной формуле, x, решение для Ax 2 + Bx + C = 0, где A, B и C — числа, часто называемые коэффициентами, дается как:
— B ± √ B 2 -4AC
x = ————————
2A
В нашем случае A = 1
B = -4
C = -5
Соответственно B 2 — 4AC =
16 — (-20) =
36
Применение квадратичной формулы:
4 ± √ 36
x = —————
2
Можно ли упростить √ 36?
Да! Разложение 36 на простые множители равно
2 • 2 • 3 • 3
Чтобы иметь возможность удалить что-либо из-под корня, должно быть 2 экземпляра этого (поскольку мы берем квадрат i. е. второй корень).
е. второй корень).
√ 36 = √ 2 • 2 • 3 • 3 = 2 • 3 • √ 1 =
± 6 • √ 1 =
± 6
Итак, теперь мы смотрим на:
x = (4 ± 6) / 2
Два реальных решения:
x = (4 + √36) / 2 = 2 + 3 = 5.000
или:
x = (4-√36) / 2 = 2-3 = -1.000
Два были найдены решения:
- x = 5
- x = -1
Графические квадратичные функции: дополнительные примеры
Графики Квадратичные функции: примеры (стр. 4 из 4)
Разделы: Введение, Значение старшего коэффициента / Вершина, Примеры
- Найдите перехваты x и вершина y = x 2 4 x + 2.
Так как это так просто
найти перехват y (и в любом случае это будет точка на моей Т-диаграмме), они всего лишь
просят x -перехватов
этот раз. Чтобы найти перехват x ,
Ставил y равно 0
и решаем:
Чтобы найти перехват x ,
Ставил y равно 0
и решаем:
0 = x 2 4 x + 2
x 2 + 4 x 2 = 0
Для построения графиков
точки перехвата находятся примерно на (4.4,
0) и (0,4,
0). (Когда я пишу
в ответ, я, конечно, буду использовать «точную» форму с
квадратные корни; десятичные приближения моего калькулятора предназначены только для
Помогая мне график.)
Чтобы найти вершину, я посмотрите на коэффициенты: a = 1 и b = 4. Тогда:
Найти k , Подключаю ч = 2 дюйма для x через л = x 2 4 x + 2 и упростить:
Сейчас найду еще точек на графике, чтобы помочь мне заполнить график:
Обратите внимание, что я выбрал значения x которые были сосредоточены вокруг координаты x вершины. Теперь построю параболу:
Теперь построю параболу:
Вершина в (2, 6), и перехваты на следующие точки:
(0, 2),, и
- Найдите перехваты x и вершина y = x 2 + 2 x 4.
Чтобы найти вершину, я посмотрите на коэффициенты: a = 1 и b = 2. Тогда:
Найти k , Подключу ч дюйм для x и упростить:
Вершина находится ниже x — ось,
и, поскольку это отрицательная квадратичная величина, я знаю, что парабола равна
будет перевернутым.Так может ли моя линия пересечь ось x ?
Могут ли быть какие-нибудь перехваты x ?
Конечно, нет! Поэтому я ожидаю получить «нет (настоящего) решения», когда
Я пытаюсь найти x -перехватывания,
но мне все равно нужно показать свою работу. Чтобы найти перехват x ,
Ставил y равно 0
и решаем:
Чтобы найти перехват x ,
Ставил y равно 0
и решаем:
0 = x 2 + 2 x 4
x 2 2 х + 4 = 0
Как только я получаю отрицательный внутри квадратного корня я знаю, что не могу получить наглядное решение.Итак, как и ожидалось, нет никаких перехватов x . Теперь я найду несколько дополнительных точек, чтобы заполнить свой график:
Обратите внимание, что я выбрал значения x которые были сосредоточены вокруг координаты x вершины. Теперь построю параболу: Авторские права Элизабет Стапель 2002-2011 Все права защищены
Вершина
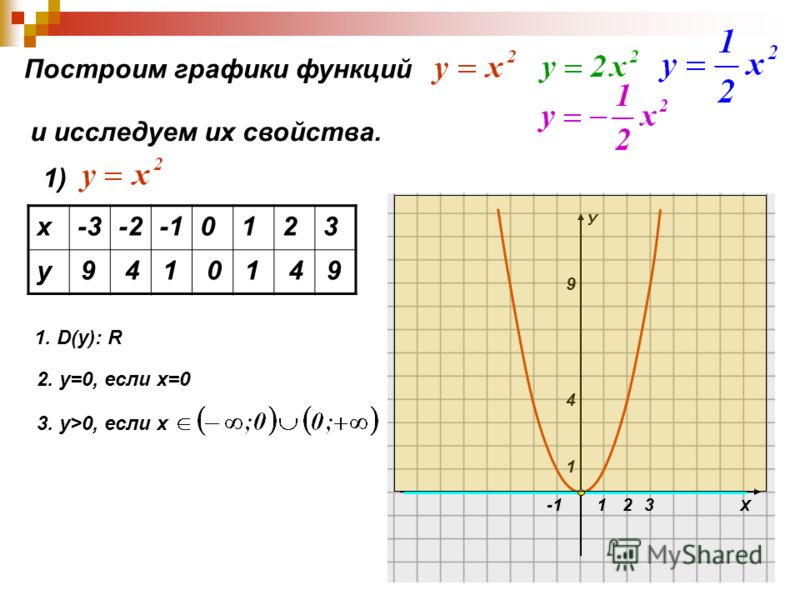
в (1, 3),
и единственный
перехват находится в (0,
4).
Это последнее упражнение иллюстрирует таким образом вы можете немного сократить свою работу. Если вы решите для вершины сначала вы можете легко определить, нужно ли вам продолжить и искать x -перехват, или если вы можете сразу перейти к нанесению некоторых точек и построению графика. Если вершина ниже оси x (то есть, если y -значение отрицательна), а квадратичная отрицательна (поэтому парабола открывается вниз), тогда не будет x -перехватов.Аналогично, если вершина находится выше оси x (то есть, если y -значение положительна), а квадратичная положительна (так что парабола открывается вверх), тогда не будет x -перехватов.
На большинстве графиков
Я сделал (правда, не первый), так уж получилось, что баллы
на Т-диаграмме были симметричны относительно вершины; то есть, что точки
«совпадают» по обе стороны от вершины. Пока парабола
всегда симметрично относительно вертикальной линии, проходящей через вершину (параболы
«ось»), точки Т-диаграммы могут быть несимметричными. Особенно,
точки Т-диаграммы не будут «совпадать», если координата x вершины — это не целое число или половинное число
(например, «3,5»).
Предупреждение: не ожидайте, что сюжетные точки всегда будут «совпадать» на
обе стороны от вершины; в частности, не делайте половину баллов на
ваш T-график, а затем «заполните» остальную часть вашего T-графика,
предполагая симметрию, которая может не существовать.
Пока парабола
всегда симметрично относительно вертикальной линии, проходящей через вершину (параболы
«ось»), точки Т-диаграммы могут быть несимметричными. Особенно,
точки Т-диаграммы не будут «совпадать», если координата x вершины — это не целое число или половинное число
(например, «3,5»).
Предупреждение: не ожидайте, что сюжетные точки всегда будут «совпадать» на
обе стороны от вершины; в частности, не делайте половину баллов на
ваш T-график, а затем «заполните» остальную часть вашего T-графика,
предполагая симметрию, которая может не существовать.
Другие советы по построению графиков:
Если парабола будет «тощей», то ожидайте, что вы
получат очень большие значения на вашем Т-графике. Вы либо закончите
с действительно высоким графиком или довольно коротким T-графиком. Если парабола
будет «толстым», тогда ожидайте, что у вас, вероятно, будет
для построения точек с дробями в качестве координат. В любом случае, когда вы
иди, чтобы соединить точки, чтобы нарисовать параболу, это может оказаться полезным
повернуть бумагу на бок и сначала прорисовать действительно изогнутую часть
вершину, убедившись, что она выглядит красивой и круглой.Затем переверните бумагу
спиной правой стороной вверх и нарисуйте «стороны» параболы.
В любом случае, когда вы
иди, чтобы соединить точки, чтобы нарисовать параболу, это может оказаться полезным
повернуть бумагу на бок и сначала прорисовать действительно изогнутую часть
вершину, убедившись, что она выглядит красивой и круглой.Затем переверните бумагу
спиной правой стороной вверх и нарисуйте «стороны» параболы.
Предупреждение: нарисуйте свои графики достаточно большой, чтобы его хорошо видел ваш инструктор. Если тебе нужно больше чем два или, может быть, три графика на одной стороне стандартного листа бумаги, тогда вы рисуете свои графики слишком маленькими.
<< Предыдущая Вверх | 1 | 2 | 3 | 4 | Вернуться к индексу
Цитируйте эту статью как: | Стапель, Элизабет. |
Квадратичные функции
Квадратичные функцииСодержание : Эта страница соответствует § 3.1 (стр. 244) текста.
Предлагаемые задачи из текста:
с.251 # 1-8, 10, 11, 15, 16, 18, 19, 21, 23, 24, 30, 33, 37, 38, 75
Графики
Стандартная форма
Приложения
Графики
Квадратичная функция представляет собой одну из следующих форм: f (x) = ax 2 + bx + c , где a , b и c — числа, у которых a не равны нулю.
График квадратичной функции — это кривая, называемая параболой .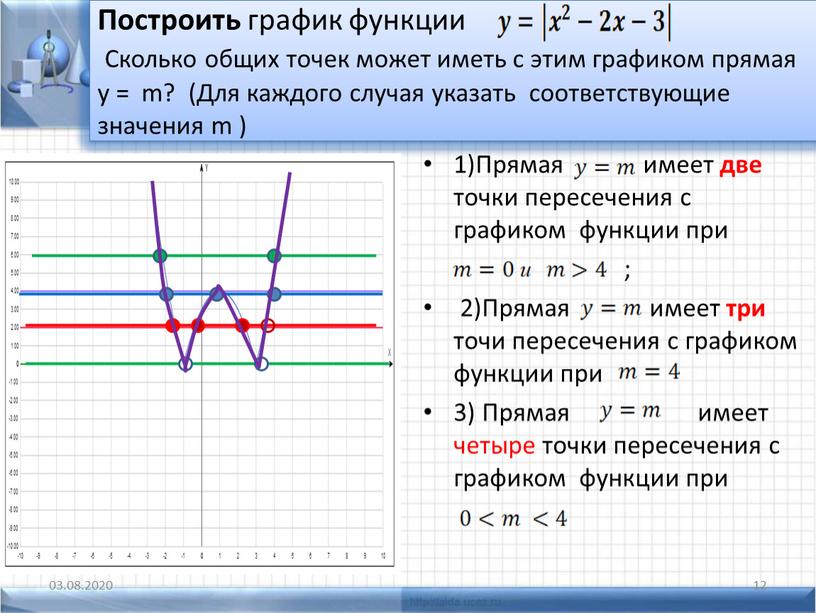 Параболы могут открываться вверх или вниз
и различаются по «ширине» или «крутизне», но все они имеют одинаковую базовую U-образную форму. В
На рисунке ниже показаны три графика, и все они параболы.
Параболы могут открываться вверх или вниз
и различаются по «ширине» или «крутизне», но все они имеют одинаковую базовую U-образную форму. В
На рисунке ниже показаны три графика, и все они параболы.
Все параболы симметричны относительно линии, называемой осью симметрии . Парабола пересекает его ось симметрии находится в точке, называемой вершиной параболы.
Вы знаете, что две точки определяют линию. Это означает, что если вам даны любые две точки на плоскости, то есть одна и только одна линия, содержащая обе точки.Аналогичное утверждение можно сделать относительно точек и квадратичных функции.
Учитывая три точки на плоскости, которые имеют разные первые координаты и не лежат на одной прямой, существует ровно
одна квадратичная функция f, график которой содержит все три точки. Апплет ниже иллюстрирует этот факт. График
содержит три точки и параболу, проходящую через все три. Соответствующая функция показана в тексте
поле под графиком. Если вы перетащите любую из точек, функция и парабола обновятся.
Если вы перетащите любую из точек, функция и парабола обновятся.
Многие квадратичные функции можно легко изобразить вручную, используя методы растяжения / сжатия и сдвига. (перевод) парабола y = x 2 . (См. Раздел о работе с графики.)
Пример 1 .
Нарисуйте график y = x 2 /2. Начиная с графика y = x 2 , мы сокращаемся в раз половины. Это означает, что для каждой точки графика y = x 2 мы рисуем новую точку, равную единице. на половине пути от оси абсцисс до этой точки.2 — 5. Начнем с графика y = x 2 , сдвинем на 4 единицы вправо, затем 5 единиц вниз.
Упражнение 1 :
(a) Нарисуйте график y = (x + 2) 2 — 3. Ответ
(b) Нарисуйте график y = — (x — 5) 2 + 3. Ответ
Вернуться к содержанию
Стандартная форма
Функции в частях (a) и (b) упражнения 1 являются примерами квадратичных функций в стандартной форме . Когда квадратичная функция имеет стандартную форму, ее график легко нарисовать, отражая, сдвигая и
растягивание / сжатие параболы y = x 2 .
Когда квадратичная функция имеет стандартную форму, ее график легко нарисовать, отражая, сдвигая и
растягивание / сжатие параболы y = x 2 .
Квадратичная функция f (x) = a (x — h) 2 + k, не равная нулю, называется стандартной формой . Если а положительно, график открывается вверх, а если отрицательный, то открывается вниз. Линия симметрии — это вертикальная линия x = h, а вершина — это точка (h, k).
Любую квадратичную функцию можно переписать в стандартной форме, добавив , завершив квадрат . (См. Раздел о решая уравнения алгебраически, чтобы просмотреть завершение квадрата.) Шаги, которые мы используем в этом разделе для завершения квадрата, будут выглядеть немного иначе, потому что наш главный цель здесь не в решении уравнения.
Обратите внимание, что когда квадратичная функция имеет стандартную форму, ее нули также легко найти с помощью квадратного корня. принцип.
принцип.
Пример 3 .
Запишите функцию f (x) = x 2 — 6x + 7 в стандартном виде. Нарисуйте график функции f и найдите его нули и вершина.
f (x) = x 2 — 6x + 7.
= (x 2 — 6x) + 7. Сгруппируйте члены x 2 и x и затем заполните квадрат на этих условиях.
= (x 2 — 6x + 9 — 9) + 7.
Нам нужно добавить 9, потому что это квадрат половины коэффициента при x, (-6/2) 2 = 9. Когда мы решая уравнение, мы просто добавляли 9 к обеим частям уравнения. В этой настройке мы добавляем и вычитаем 9 так что мы не меняем функцию.
= (x 2 — 6x + 9) — 9 + 7. Мы видим, что x 2 — 6x + 9 — это полный квадрат, а именно (x — 3) 2 .
f (x) = (x — 3) 2 — 2.Это стандартная форма .
Из этого результата легко найти, что вершина графа f равна (3, -2).
Чтобы найти нули f, мы устанавливаем f равным 0 и решаем относительно x.
(x — 3) 2 — 2 = 0.
(х — 3) 2 = 2.
(x — 3) = ± sqrt (2).
х = 3 ± sqrt (2).
Чтобы нарисовать график f, сдвинем график y = x 2 на три единицы вправо и на две единицы вниз.
Если коэффициент при x 2 не равен 1, то мы должны вынести этот коэффициент из x 2 и x, прежде чем продолжить.
Пример 4 .
Запишите f (x) = -2x 2 + 2x + 3 в стандартном виде и найдите вершину графика f.
f (x) = -2x 2 + 2x + 3.
= (-2x 2 + 2x) + 3.
= -2 (x 2 — x) + 3.
= -2 (x 2 — x + 1/4 — 1/4) + 3.
Мы складываем и вычитаем 1/4, потому что (-1/2) 2 = 1/4, а -1 — коэффициент при x.
= -2 (x 2 — x + 1/4) -2 (-1/4) + 3.
Обратите внимание, что все в круглых скобках умножается на -2, поэтому, когда мы убираем -1/4 из круглых скобок, мы необходимо умножить на -2.
= -2 (x — 1/2) 2 + 1/2 + 3.
= -2 (х — 1/2) 2 + 7/2.
Вершина — это точка (1/2, 7/2). Поскольку граф открывается вниз (-2 <0), вершина является высшей точкой на графике.
Упражнение 2 :
Запишите f (x) = 3x 2 + 12x + 8 в стандартной форме.Нарисуйте график функции f, найдите его вершину и найдите нули f. Ответ
Альтернативный метод поиска вершины
В некоторых случаях завершение квадрата — не самый простой способ найти вершину параболы. Если график
квадратичная функция имеет два пересечения по оси x, тогда линия симметрии — это вертикальная линия, проходящая через среднюю точку
х-перехватчиков.
Х-точки пересечения графика выше находятся в точках -5 и 3.Линия симметрии проходит через -1, что является средним -5 и 3. (-5 + 3) / 2 = -2/2 = -1. Как только мы узнаем, что линия симметрии x = -1, мы узнаем первую координату вершины -1. Вторую координату вершины можно найти, вычислив функцию при x = -1.
Пример 5 .
Найдите вершину графика функции f (x) = (x + 9) (x — 5).
Так как формула для f разложена на множители, легко найти нули: -9 и 5.
Среднее значение нулей (-9 + 5) / 2 = -4/2 = -2. Итак, линия симметрии x = -2 и первая координата вершины -2.
Вторая координата вершины: f (-2) = (-2 + 9) (- 2 — 5) = 7 * (- 7) = -49.
Следовательно, вершина графа f равна (-2, -49).
Вернуться к содержанию
Приложения
Пример 6 .
У владельца ранчо есть 600 метров забора, чтобы ограждать прямоугольный загон с другим забором, разделяющим его посередине.
как на схеме ниже.
Как показано на схеме, каждая из четырех горизонтальных секций забора будет иметь длину х метров, а три каждая вертикальная секция будет иметь длину y метров.
Цель владельца ранчо — использовать весь забор, а оградить как можно большую площадь .
Каждый из двух прямоугольников имеет площадь xy, поэтому мы имеем
Общая площадь: A = 2xy.
Мы мало что можем сделать с величиной A, пока она выражается как произведение двух переменных. Однако, Тот факт, что у нас есть только 1200 метров забора, приводит к уравнению, которому должны удовлетворять x и y.
3г + 4х = 1200.
3y = 1200 — 4x.
y = 400 — 4x / 3.
Теперь у нас есть y, выраженная как функция от x, и мы можем подставить это выражение для y в формулу для общего площадь А.
A = 2xy = 2x (400 -4x / 3).
Нам нужно найти значение x, которое делает A как можно большим.
A — квадратичная функция от x, а график открывается вниз, поэтому наивысшая точка на графике A — вершина. Поскольку A разложено на множители, самый простой способ найти вершина — найти пересечения по оси x и усреднить.
2x (400 -4x / 3) = 0.
2x = 0 или 400 -4x / 3 = 0.
x = 0 или 400 = 4x / 3.
x = 0 или 1200 = 4x.
х = 0 или 300 = х.
Следовательно, линия симметрии графика A равна x = 150, среднему от 0 до 300.
Теперь, когда мы знаем значение x, соответствующее наибольшей площади, мы можем найти значение y, вернувшись назад. к уравнению, связывающему x и y.
y = 400 — 4x / 3 = 400-4 (150) / 3 = 200.
Вернуться к содержанию
% PDF-1.5
%
1905 0 obj>
endobj
xref
1905 306
0000000016 00000 н.
0000016790 00000 н.
0000016927 00000 п.
0000006548 00000 н.
0000017076 00000 п.
0000017208 00000 п. 0000018389 00000 п.
0000018467 00000 п.
0000018519 00000 п.
0000018570 00000 п.
0000018622 00000 п.
0000018672 00000 п.
0000019208 00000 п.
0000019713 00000 п.
0000020342 00000 п.
0000020850 00000 п.
0000021569 00000 п.
0000021911 00000 п.
0000022010 00000 н.
0000022768 00000 п.
0000023179 00000 п.
0000024200 00000 н.
0000024600 00000 п.
0000025182 00000 п.
0000025595 00000 п.
0000025675 00000 п.
0000025989 00000 п.
0000026377 00000 п.
0000031616 00000 п.
0000032173 00000 п.
0000032454 00000 п.
0000032820 00000 н.
0000033337 00000 п.
0000033845 00000 п.
0000034472 00000 п.
0000035083 00000 п.
0000035460 00000 п.
0000035840 00000 п.
0000036571 00000 п.
0000036941 00000 п.
0000037475 00000 п.
0000037556 00000 п.
0000037611 00000 п.
0000038150 00000 п.
0000038774 00000 п.
0000039313 00000 п.
0000039573 00000 п.
0000039983 00000 н.
0000040359 00000 п.
0000040927 00000 п.
0000041085 00000 п.
0000041462 00000 п.
0000048449 00000 н.
0000048925 00000 п.
0000018389 00000 п.
0000018467 00000 п.
0000018519 00000 п.
0000018570 00000 п.
0000018622 00000 п.
0000018672 00000 п.
0000019208 00000 п.
0000019713 00000 п.
0000020342 00000 п.
0000020850 00000 п.
0000021569 00000 п.
0000021911 00000 п.
0000022010 00000 н.
0000022768 00000 п.
0000023179 00000 п.
0000024200 00000 н.
0000024600 00000 п.
0000025182 00000 п.
0000025595 00000 п.
0000025675 00000 п.
0000025989 00000 п.
0000026377 00000 п.
0000031616 00000 п.
0000032173 00000 п.
0000032454 00000 п.
0000032820 00000 н.
0000033337 00000 п.
0000033845 00000 п.
0000034472 00000 п.
0000035083 00000 п.
0000035460 00000 п.
0000035840 00000 п.
0000036571 00000 п.
0000036941 00000 п.
0000037475 00000 п.
0000037556 00000 п.
0000037611 00000 п.
0000038150 00000 п.
0000038774 00000 п.
0000039313 00000 п.
0000039573 00000 п.
0000039983 00000 н.
0000040359 00000 п.
0000040927 00000 п.
0000041085 00000 п.
0000041462 00000 п.
0000048449 00000 н.
0000048925 00000 п. 0000049120 00000 п.
0000050048 00000 н.
0000050962 00000 п.
0000055968 00000 п.
0000060086 00000 п.
0000064818 00000 п.
0000071298 00000 п.
0000071876 00000 п.
0000076506 00000 п.
0000085517 00000 п.
0000085604 00000 п.
0000086493 00000 п.
0000086588 00000 п.
0000087314 00000 п.
0000129245 00000 н.
0000131564 00000 н.
0000135854 00000 п.
0000137237 00000 н.
0000138764 00000 н.
0000158739 00000 н.
0000163661 00000 н.
0000204360 00000 н.
0000220094 00000 н.
0000245504 00000 н.
0000254263 00000 н.
0000262274 00000 н.
0000263000 00000 н.
0000268558 00000 н.
0000270999 00000 н.
0000273254 00000 н.
0000278054 00000 н.
0000281845 00000 н.
0000288388 00000 н.
0000289237 00000 н.
0000289429 00000 н.
00002 00000 н.
0000292482 00000 н.
0000293627 00000 н.
0000294170 00000 н.
0000294568 00000 н.
0000296137 00000 н.
0000296297 00000 н.
0000296478 00000 н.
0000296650 00000 н.
0000296848 00000 н.
0000298436 00000 н.
0000298687 00000 н.
0000302546 00000 н.
0000049120 00000 п.
0000050048 00000 н.
0000050962 00000 п.
0000055968 00000 п.
0000060086 00000 п.
0000064818 00000 п.
0000071298 00000 п.
0000071876 00000 п.
0000076506 00000 п.
0000085517 00000 п.
0000085604 00000 п.
0000086493 00000 п.
0000086588 00000 п.
0000087314 00000 п.
0000129245 00000 н.
0000131564 00000 н.
0000135854 00000 п.
0000137237 00000 н.
0000138764 00000 н.
0000158739 00000 н.
0000163661 00000 н.
0000204360 00000 н.
0000220094 00000 н.
0000245504 00000 н.
0000254263 00000 н.
0000262274 00000 н.
0000263000 00000 н.
0000268558 00000 н.
0000270999 00000 н.
0000273254 00000 н.
0000278054 00000 н.
0000281845 00000 н.
0000288388 00000 н.
0000289237 00000 н.
0000289429 00000 н.
00002 00000 н.
0000292482 00000 н.
0000293627 00000 н.
0000294170 00000 н.
0000294568 00000 н.
0000296137 00000 н.
0000296297 00000 н.
0000296478 00000 н.
0000296650 00000 н.
0000296848 00000 н.
0000298436 00000 н.
0000298687 00000 н.
0000302546 00000 н. 0000306227 00000 п.
0000309939 00000 н.
0000324439 00000 н.
0000324632 00000 н.
0000324838 00000 н.
0000330037 00000 н.
0000330440 00000 н.
0000339930 00000 н.
0000340102 00000 н.
0000340708 00000 н.
0000341560 00000 н.
0000341759 00000 н.
0000342826 00000 н.
0000345728 00000 н.
0000350876 00000 н.
0000350935 00000 н.
0000351114 00000 н.
0000351278 00000 н.
0000351434 00000 н.
0000351479 00000 н.
0000351614 00000 н.
0000351764 00000 н.
0000351891 00000 н.
0000351948 00000 н.
0000352018 00000 н.
0000352182 00000 н.
0000352239 00000 н.
0000352304 00000 н.
0000352430 00000 н.
0000352487 00000 н.
0000352560 00000 н.
0000352689 00000 н.
0000352746 00000 н.
0000352813 00000 н.
0000352962 00000 н.
0000353019 00000 н.
0000353090 00000 н.
0000353198 00000 н.
0000353312 00000 н.
0000353461 00000 н.
0000353569 00000 н.
0000353683 00000 н.
0000353832 00000 н.
0000353940 00000 н.
0000354054 00000 н.
0000354203 00000 н.
0000354311 00000 н.
0000354426 00000 н.
0000306227 00000 п.
0000309939 00000 н.
0000324439 00000 н.
0000324632 00000 н.
0000324838 00000 н.
0000330037 00000 н.
0000330440 00000 н.
0000339930 00000 н.
0000340102 00000 н.
0000340708 00000 н.
0000341560 00000 н.
0000341759 00000 н.
0000342826 00000 н.
0000345728 00000 н.
0000350876 00000 н.
0000350935 00000 н.
0000351114 00000 н.
0000351278 00000 н.
0000351434 00000 н.
0000351479 00000 н.
0000351614 00000 н.
0000351764 00000 н.
0000351891 00000 н.
0000351948 00000 н.
0000352018 00000 н.
0000352182 00000 н.
0000352239 00000 н.
0000352304 00000 н.
0000352430 00000 н.
0000352487 00000 н.
0000352560 00000 н.
0000352689 00000 н.
0000352746 00000 н.
0000352813 00000 н.
0000352962 00000 н.
0000353019 00000 н.
0000353090 00000 н.
0000353198 00000 н.
0000353312 00000 н.
0000353461 00000 н.
0000353569 00000 н.
0000353683 00000 н.
0000353832 00000 н.
0000353940 00000 н.
0000354054 00000 н.
0000354203 00000 н.
0000354311 00000 н.
0000354426 00000 н. 0000354575 00000 п.
0000354683 00000 н.
0000354797 00000 н.
0000354947 00000 н.
0000355055 00000 н.
0000355169 00000 н.
0000355319 00000 п.
0000355427 00000 н.
0000355542 00000 н.
0000355691 00000 п.
0000355799 00000 н.
0000355914 00000 н.
0000356050 00000 н.
0000356107 00000 н.
0000356189 00000 н.
0000356317 00000 п.
0000356374 00000 н.
0000356459 00000 н.
0000356516 00000 н.
0000356596 00000 н.
0000356653 00000 п.
0000356728 00000 н.
0000356863 00000 н.
0000356920 00000 н.
0000357001 00000 н.
0000357128 00000 н.
0000357185 00000 н.
0000357270 00000 н.
0000357327 00000 н.
0000357408 00000 н.
0000357465 00000 н.
0000357539 00000 н.
0000357676 00000 н.
0000357733 00000 н.
0000357817 00000 п.
0000357945 00000 н.
0000358002 00000 н.
0000358088 00000 н.
0000358145 00000 н.
0000358224 00000 н.
0000358281 00000 п.
0000358356 00000 н.
0000358491 00000 п.
0000358548 00000 н.
0000358630 00000 н.
0000358758 00000 н.
0000358815 00000 н.
0000358899 00000 н.
0000354575 00000 п.
0000354683 00000 н.
0000354797 00000 н.
0000354947 00000 н.
0000355055 00000 н.
0000355169 00000 н.
0000355319 00000 п.
0000355427 00000 н.
0000355542 00000 н.
0000355691 00000 п.
0000355799 00000 н.
0000355914 00000 н.
0000356050 00000 н.
0000356107 00000 н.
0000356189 00000 н.
0000356317 00000 п.
0000356374 00000 н.
0000356459 00000 н.
0000356516 00000 н.
0000356596 00000 н.
0000356653 00000 п.
0000356728 00000 н.
0000356863 00000 н.
0000356920 00000 н.
0000357001 00000 н.
0000357128 00000 н.
0000357185 00000 н.
0000357270 00000 н.
0000357327 00000 н.
0000357408 00000 н.
0000357465 00000 н.
0000357539 00000 н.
0000357676 00000 н.
0000357733 00000 н.
0000357817 00000 п.
0000357945 00000 н.
0000358002 00000 н.
0000358088 00000 н.
0000358145 00000 н.
0000358224 00000 н.
0000358281 00000 п.
0000358356 00000 н.
0000358491 00000 п.
0000358548 00000 н.
0000358630 00000 н.
0000358758 00000 н.
0000358815 00000 н.
0000358899 00000 н. 0000358956 00000 н.
0000359035 00000 н.
0000359092 00000 н.
0000359166 00000 н.
0000359301 00000 п.
0000359358 00000 п.
0000359439 00000 н.
0000359566 00000 н.
0000359623 00000 н.
0000359708 00000 н.
0000359765 00000 н.
0000359845 00000 н.
0000359902 00000 н.
0000359976 00000 н.
0000360111 00000 п.
0000360168 00000 н.
0000360248 00000 н.
0000360376 00000 н.
0000360433 00000 н.
0000360517 00000 н.
0000360574 00000 н.
0000360653 00000 н.
0000360710 00000 н.
0000360786 00000 н.
0000360922 00000 н.
0000360979 00000 н.
0000361060 00000 н.
0000361187 00000 н.
0000361244 00000 н.
0000361329 00000 н.
0000361386 00000 н.
0000361465 00000 н.
0000361522 00000 н.
0000361596 00000 н.
0000361731 00000 н.
0000361788 00000 н.
0000361868 00000 н.
0000361995 00000 н.
0000362052 00000 н.
0000362138 00000 п.
0000362195 00000 н.
0000362276 00000 н.
0000362333 00000 п.
0000362407 00000 н.
0000362516 00000 н.
0000362630 00000 н.
0000362765 00000 н.
0000362822 00000 н.
0000358956 00000 н.
0000359035 00000 н.
0000359092 00000 н.
0000359166 00000 н.
0000359301 00000 п.
0000359358 00000 п.
0000359439 00000 н.
0000359566 00000 н.
0000359623 00000 н.
0000359708 00000 н.
0000359765 00000 н.
0000359845 00000 н.
0000359902 00000 н.
0000359976 00000 н.
0000360111 00000 п.
0000360168 00000 н.
0000360248 00000 н.
0000360376 00000 н.
0000360433 00000 н.
0000360517 00000 н.
0000360574 00000 н.
0000360653 00000 н.
0000360710 00000 н.
0000360786 00000 н.
0000360922 00000 н.
0000360979 00000 н.
0000361060 00000 н.
0000361187 00000 н.
0000361244 00000 н.
0000361329 00000 н.
0000361386 00000 н.
0000361465 00000 н.
0000361522 00000 н.
0000361596 00000 н.
0000361731 00000 н.
0000361788 00000 н.
0000361868 00000 н.
0000361995 00000 н.
0000362052 00000 н.
0000362138 00000 п.
0000362195 00000 н.
0000362276 00000 н.
0000362333 00000 п.
0000362407 00000 н.
0000362516 00000 н.
0000362630 00000 н.
0000362765 00000 н.
0000362822 00000 н. 0000362903 00000 н.
0000363030 00000 н.
0000363087 00000 н.
0000363172 00000 н.
0000363229 00000 н.
0000363309 00000 н.
0000363366 00000 н.
0000363440 00000 н.
0000363525 00000 н.
0000363618 00000 н.
0000363663 00000 н.
0000363760 00000 н.
0000363805 00000 н.
0000363922 00000 н.
0000363967 00000 н.
0000364064 00000 н.
0000364109 00000 н.
0000364213 00000 н.
0000364258 00000 н.
0000364359 00000 н.
0000364404 00000 н.
0000364510 00000 н.
0000364555 00000 н.
0000364686 00000 н.
0000364731 00000 н.
0000364842 00000 н.
0000364886 00000 н.
0000364986 00000 н.
0000365030 00000 н.
0000365168 00000 н.
0000365212 00000 н.
0000365350 00000 н.
0000365394 00000 н.
0000365525 00000 н.
0000365569 00000 н.
0000365672 00000 н.
0000365716 00000 н.
0000365844 00000 н.
0000365888 00000 н.
0000365988 00000 н.
0000366032 00000 н.
0000366137 00000 н.
0000366181 00000 н.
0000366303 00000 н.
0000366347 00000 н.
0000366450 00000 н.
0000366494 00000 н.
0000366611 00000 н.
0000362903 00000 н.
0000363030 00000 н.
0000363087 00000 н.
0000363172 00000 н.
0000363229 00000 н.
0000363309 00000 н.
0000363366 00000 н.
0000363440 00000 н.
0000363525 00000 н.
0000363618 00000 н.
0000363663 00000 н.
0000363760 00000 н.
0000363805 00000 н.
0000363922 00000 н.
0000363967 00000 н.
0000364064 00000 н.
0000364109 00000 н.
0000364213 00000 н.
0000364258 00000 н.
0000364359 00000 н.
0000364404 00000 н.
0000364510 00000 н.
0000364555 00000 н.
0000364686 00000 н.
0000364731 00000 н.
0000364842 00000 н.
0000364886 00000 н.
0000364986 00000 н.
0000365030 00000 н.
0000365168 00000 н.
0000365212 00000 н.
0000365350 00000 н.
0000365394 00000 н.
0000365525 00000 н.
0000365569 00000 н.
0000365672 00000 н.
0000365716 00000 н.
0000365844 00000 н.
0000365888 00000 н.
0000365988 00000 н.
0000366032 00000 н.
0000366137 00000 н.
0000366181 00000 н.
0000366303 00000 н.
0000366347 00000 н.
0000366450 00000 н.
0000366494 00000 н.
0000366611 00000 н.
 2
2 
 Объясните, почему нет необходимости наносить точки на график при использовании y = a (x h) 2 + k.
Объясните, почему нет необходимости наносить точки на график при использовании y = a (x h) 2 + k.  «Графические квадратичные функции: примеры». Purplemath .
Доступно по номеру
«Графические квадратичные функции: примеры». Purplemath .
Доступно по номеру 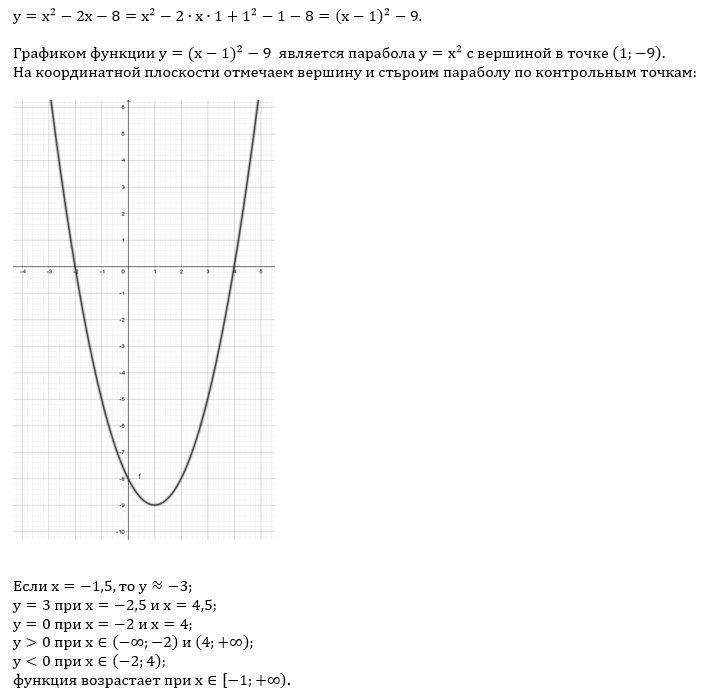

 как на схеме ниже.
как на схеме ниже. A — квадратичная функция от x, а график
открывается вниз, поэтому наивысшая точка на графике A — вершина. Поскольку A разложено на множители, самый простой способ найти
вершина — найти пересечения по оси x и усреднить.
A — квадратичная функция от x, а график
открывается вниз, поэтому наивысшая точка на графике A — вершина. Поскольку A разложено на множители, самый простой способ найти
вершина — найти пересечения по оси x и усреднить.