В\С\В\ боковая грань и сечение АВ\С равновелики. Найдите угол между плоскостью названного сечения и боковым ребром призмы.

39. Плоскость пересекает боковые ребра прямой треуголь­ной призмы АВСА\В\С\ так, что сечением оказался равно­сторонний треугольник КЬМ периметра 36 см. Известно, что АК = 16 см, ВЬ= 11 см, СМ = 5 см. Найдите угол между медианой КВ сечения и плоскостью основания (рис. 59).

40. В правильной четырехугольной призме построены два параллельных сечения: одно через середины двух смежных сторон основания и центр призмы, другое — через диагональ основания (рис. 60). Найдите отношение площадей сечений.

Параллелепипед

41. Сечение призмы плоскостью, пересекающей все боковые ребра — параллелограмм. Докажите, что эта призма — парал­лелепипед.

42. Боковое ребро прямоугольного параллелепипеда I, диагональ его вдвое меньше периметра основания. Определите площадь основания параллелепипеда.

84

43. Докажите, что в прямоугольном параллелепипеде квад­рат площади сечения с вершинами в концах ребер, исходящих из одной вершины, в 8 раз меньше суммы квадратов площадей всех граней параллелепипеда.

44. Докажите, что расстояние между скрещивающимися диагоналями двух смежных граней куба втрое меньше диаго­нали куба.

45. Докажите, что сумма квадратов диагоналей паралле­лепипеда равна сумме квадратов его ребер.

46. Расстояния от центра параллелепипеда до его вершин 18, 15, 11, 10 см. Зная, что длины трех ребер (в сантиметрах) выражаются последовательными целыми числами, определите периметры граней параллелепипеда.

47. Боковое ребро параллелепипеда 10 см, периметр осно­вания 56 см. Расстояния от вершин одного основания до центра другого основания 18, 17, 10, 9 см. Найдите стороны основания.

48. Диагонали параллелепипеда АВСОА \В \С \В\ пересекают­ся в точке О. Периметры треугольников ОАА\, ОАВ и

ОАО рав­ны 36, 37, 29 см, АЛ, == 17 см, АВ = 11 см, АО = 6 см. Найдите диагонали параллелепипеда.

49. Боковое ребро параллелепипеда 3 см, стороны основа­ния 10 и 11 см. Зная, что длины диагоналей (в сантиметрах) выражены последовательными четными числами, найдите пло­щади диагональных сечений.

50. Длины ребер параллелепипеда 9, 13, 14 см, длины его диагоналей (в сантиметрах) выражаются последовательными четными числами. Найдите расстояния от центра параллелепи­педа до вершин.

51. Площадь поверхности прямоугольного параллелепипеда 192 см². Если бы каждое измерение его было на 1 см больше, площадь поверхности равнялась бы 274 см². Определите длину диагонали параллелепипеда.

52. Докажите, что сечение параллелепипеда плоскостью не может быть правильным пятиугольником.

53. Какую наибольшую площадь поверхности может иметь прямоугольный параллелепипед, у которого длина диаго­нали и?

54. Какую наибольшую площадь поверхности может иметь параллелепипед, у которого сумма длин всех ребер 48 см?

Пирамиды

55. Могут ли середины всех высот треугольной пирамиды находиться в одной плоскости?

56. Сумма плоских углов при всех вершинах пятиугольной призмы равна сумме плоских углов при всех вершинах пира­миды. Определите число ребер этой пирамиды.

57. Плоские углы при каждой вершине пирамиды равны между собой. Определите форму основания пирамиды.

58. Какова бы ни была треугольная пирамида, можно по­строить треугольник, стороны которого равны суммам скре­щивающихся ребер этой пирамиды. Докажите.

59. Докажите, что отрезки, соединяющие середины скре­щивающихся ребер треугольной пирамиды, пересекаются в одной точке.

60. Докажите, что сумма квадратов отрезков, которые сое­диняют середины скрещивающихся ребер треугольной пира­миды, в 4 раза меньше суммы квадратов ребер этой пирамиды.

61. Могут ли все грани пирамиды оказаться прямоуголь­ными треугольниками?

62. Плоские углы при вершине пирамиды — прямые. Дока­жите, что сумма квадратов площадей боковых граней равна квадрату площади основания пирамиды.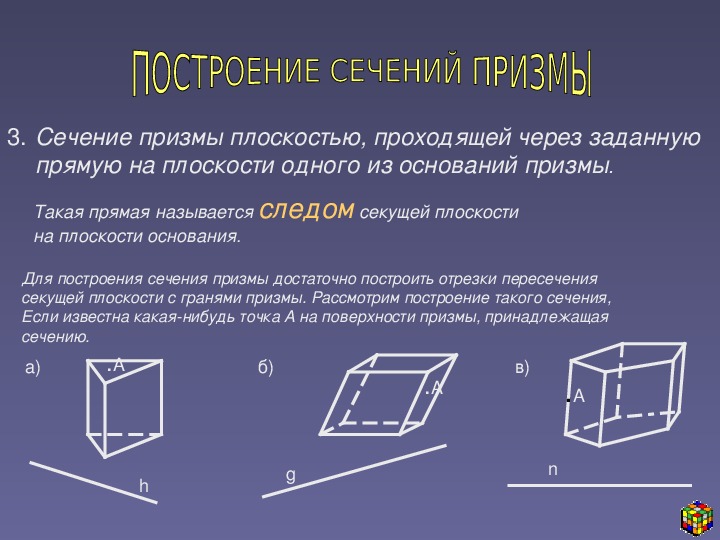

63. Основание пирамиды — параллелограмм, стороны кото­рого 16 и 22 см. Расстояние от вершины пирамиды до центра основания 4 см. Зная, что длины боковых ребер (в сантиметрах) выражаются последовательными нечетными числами, найдите длины боковых ребер пирамиды.

64. Два боковых ребра пирамиды 13 и 14 см, угол между ними 60°, а между их проекциями 120°. Найдите высоту пирамида.

65. Основание пирамиды — параллелограмм, периметр ко­торого 48 см. Центр основания удален от вершины пирамиды на 7,5 см, боковые ребра пирамиды 9, 11, 12, 13 см. Найдите стороны основания.

66. Может ли развертка полной поверхности пирамиды ока­заться: а) равносторонним треугольником; б) квадратом;

в) правильным пятиугольником; г) правильным шестиуголь­ником; д) трапецией?

6Т. Докажите, что центры всех граней правильной призмы являются вершинами двух равных правильных пирамид с общим основанием.

6в. Докажите, что только при п == 3 развертка полной по­верхности

п-угольной пирамиды может оказаться выпуклым многоугольником.

©9. Если плоские углы при вершине пирамиды — прямые, то высота пирамиды проходит через точку пересечения высот основания. Докажите.

Т®. Основание пирамиды — квадрат. Двугранные углы при основании пирамиды относятся, как 1:2:5:2. Найдите вели­чины этих углов.

71. Боковое ребро правильной треугольной пирамиды МАВС имеет длину I и образует со стороной основания, которую пересекает, угол в 75°. Паук начал ползти из вершины А и, по­бывав на всех боковых гранях пирамиды, вернулся в ту же точ­ку (рис. 61). Определите наименьшую возможную длину пути паука.

72. Сторона основания правильной шестиугольной пира­миды МАВСВЕР равна а, угол между боковым ребром и стороной основания, которую оно пересекает, 80°. Паук начал ползти по поверхности пирамиды из точки А и, побывав на всех боковых гранях, вернулся в точку А. Определите наименьшую возможную длину пути паука. МN.

74. Если боковые ребра треугольной пирамиды попарно взаимно перпендикулярны и имеют длины а, Ъ, с, то высота пирамиды Н связана с ними соотношением: Н ² + с~². Докажите.

75. Если суммы квадратов скрещивающихся ребер треуголь­ной пирамиды равны, то высоты пирамиды пересекаются в од­ной точке Г Докажите

.

Построение сечений призмы — презентация онлайн

Учитель математики
МАОУ лицей №3
г. Кропоткин Краснодарского
края
Зозуля Елена Алексеевна

Цель урока: повторить
основные методы сечения многогранников,
определенного тремя точками пространства;
формулы для вычисления площадей плоских
многоугольников;
Оборудование: интерактивная доска

3. Вопросы к классу:

— Что значит построить сечение
многогранника плоскостью?
— Как могут располагаться относительно
друг друга многогранник и плоскость?
— Как задается плоскость?
— Когда задача на построение сечения
многогранника плоскостью считается
решенной?
Постройте сечение четырехугольной призмы плоскостью, проходящей
через три точки на боковых ребрах призмы.
1. Соединим точки M и K (т.к. они лежат в одной
плоскости)
2. Соединим точки M и N (т.к. они лежат в одной
плоскости)
3. Продлим прямую CD до пересечения с прямой
MN (CD MN = L)
4. Продлим прямую CB до пересечения с прямой
MK (CB MK = P)
5. Соединим точки L и P (LP
= F)
AD = E; LP AB =
6. Соединим точки B и F (т.к. они лежат в одной
плоскости)
7. Соединим точки E и N (т.к. они лежат в одной
плоскости)
8. (KMNEF) – искомая плоскость (сечение)
Постройте сечение четырехугольной призмы плоскостью, проходящей
через три точки на боковых ребрах призмы.
1. Соединим точки M и K (т.к. они лежат в одной
плоскости)
2. Соединим точки M и N (т.к. они лежат в одной
плоскости)
3. Продлим прямую CB до пересечения с прямой
MK (CB MK = P)
4. Продлим прямую CD до пересечения с прямой
MN (CD MN = L)
5. Соединим точки L и P
6. Продлим прямую AB до пересечения с прямой
LP (AB LP = F)
7. Проведем прямую KF (KF AA1 = E)
8. Соединим точки E и N (т.к. они лежат в одной
плоскости)
9. (KEMN) – искомая плоскость (сечение)
На ребре AB куба ABCDA1B1C1D1 взята точка P — середина этого
ребра, а на ребре DD1 — точка Q1 такая, что DQ1 : Q1D1 = 1 : 2.
Построить сечение куба плоскостью C1Q1P. Найти его площадь,
считая ребро куба равным a.
1. Соединим точки С и Q1 (т.к. они лежат в одной
плоскости)
2. Продлим прямую CD до пересечения с прямой
CQ1 (CD CQ1 = O)
3. Проведем прямую PO (PO
AD = M)
4. Соединим точки P и Q1 (т.к. они лежат в одной
плоскости)
5. Продлим прямую CB до пересечения с прямой
OP (CB OP =L)
6. Проведем прямую C1L (C1L
BB1 = N)
7. Соединим точки P и N(т.к. они лежат в одной
плоскости)
8. (C1Q1MPN) – искомая плоскость (сечение)

32. Задача 3 (для самостоятельного решения).

Построить сечение куба ABCDA1B1C1D1 со
стороной а плоскостью, проходящей через точки B,
M и N, где Ь – середина ребра АА1, а N – середина
ребра СС1.
Решение.
Сечение строим методом следов.
Площадь сечения находим с помощью
теоремы о площади ортогональной
проекции многоугольника.
Ответ: S = 1/2 · a2 .

Даны две коробки правильной четырехугольной призмы. Правильная четырехугольная призма

Задание:

В правильной четырёхугольной призме ABCDA 1 B 1 C 1 D 1 на ребре СС 1 взята точка К так, что СК: КС 1 = 1: 2.

а) Постройте сечение призмы плоскостью, проходящей через точки D и К параллельно диагонали основания АС.

б) Найдите угол между плоскостью сечения и плоскостью основания, если CC 1 = 4,5√ 2, АВ = 3.

Решение:

а) Так как призма ABCDA 1 B 1 C 1 D 1 правильная, то ABCD — квадрат и боковые грани — равные прямоугольники.

Построим сечение призмы плоскостью, проходящей через точки D и K параллельно AC. Линия пересечения плоскости сечения и плоскости AA 1 C 1 проходит через точку K и параллельна AC.

В плоскости ACC 1 через точку K проведём отрезок KF параллельно диагонали AC.

Так как грани A 1 ADD 1 и B 1 BCC 1 призмы параллельны, то по свойству параллельных плоскостей линии пересечения плоскости сечения и этих граней параллельны. Проведём PK || FD. Четырёхугольник FPKD — искомое сечение.

б) Найдём угол между плоскостью сечения и плоскостью основания. Пусть плоскость сечения пересекает плоскость основания по некоторой прямой p, проходящей через точку D. AC || FK, следовательно, AC || p (если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна этой прямой). Так как диагонали квадрата взаимно перпендикулярны, то BD ⊥ AC, а значит,
BD ⊥ p. BD — проекция PD на плоскость ABC, поэтому PD ⊥ p по теореме о трёх перпендикулярах. Следовательно, ∠PDB — линейный угол двугранного угла между плоскостью сечения и плоскостью основания.

FK || p, значит, FK ⊥ PD. В четырёхугольнике FPKD имеем FD || PK и KD || FP, значит, FPKD — параллелограмм, а так как прямоугольные треугольники FAD и KCD равны по двум катетам (AD = DC как стороны квадрата, FA = KC как расстояния между параллельными прямыми AC и F K), то FPKD — ромб. Отсюда PD = 2OD.

По условию CK: KC 1 = 1: 2, тогда KC = 1/3*CC 1 = 4,5√2 / 3 = 1,5√2.

В ΔDKC по теореме Пифагора KD 2 = DC 2 + KC 2 , KD = =
√13,5.

AC = 3√2 как диагональ квадрата, OK = EC = 1/2*AC, OK = 1,5√2.

В ΔKOD по теореме Пифагора OD 2 = KD 2 − OK 2 ,

OD = = 3. PD = 2OD = 6.

В прямоугольном треугольнике PDB cos ∠PDB = BD / PD = 3√2 / 6 = √2 / 2 , следовательно, ∠PDB = 45◦ .

Ответ: 45◦ .

Определение .

Это шестигранник, основаниями которого являются два равных квадрата, а боковые грани представляют собой равные прямоугольники

Боковое ребро — это общая сторона двух смежных боковых граней

Высота призмы — это отрезок, перпендикулярный основаниям призмы

Диагональ призмы — отрезок, соединяющий две вершины оснований, которые не принадлежат к одной грани

Диагональная плоскость — плоскость, которая проходит через диагональ призмы и ее боковые ребра

Диагональное сечение — границы пересечения призмы и диагональной плоскости. Диагональное сечение правильной четырехугольной призмы представляет собой прямоугольник

Перпендикулярное сечение (ортогональное сечение) — это пересечение призмы и плоскости, проведенной перпендикулярно ее боковым ребрам

Элементы правильной четырехугольной призмы

На рисунке изображены две правильные четырехугольные призмы, у которых обозначены соответствующими буквами:

• Основания ABCD и A 1 B 1 C 1 D 1 равны и параллельны друг другу
• Боковые грани AA 1 D 1 D, AA 1 B 1 B, BB 1 C 1 C и CC 1 D 1 D, каждая из которых является прямоугольником
• Боковая поверхность — сумма площадей всех боковых граней призмы
• Полная поверхность — сумма площадей всех оснований и боковых граней (сумма площади боковой поверхности и оснований)
• Боковые ребра AA 1 , BB 1 , CC 1 и DD 1 .
• Диагональ B 1 D
• Диагональ основания BD
• Диагональное сечение BB 1 D 1 D
• Перпендикулярное сечение A 2 B 2 C 2 D 2 .

Свойства правильной четырехугольной призмы

• Основаниями являются два равных квадрата
• Основания параллельны друг другу
• Боковыми гранями являются прямоугольники
• Боковые грани равны между собой
• Боковые грани перпендикулярны основаниям
• Боковые ребра параллельны между собой и равны
• Перпендикулярное сечение перпендикулярно всем боковым ребрам и параллельно основаниям
• Углы перпендикулярного сечения — прямые
• Диагональное сечение правильной четырехугольной призмы представляет собой прямоугольник
• Перпендикулярное (ортогональное сечение) параллельно основаниям

Формулы для правильной четырехугольной призмы

Указания к решению задач

При решении задач на тему «правильная четырехугольная призма » подразумевается, что:

Правильная призма — призма в основании которой лежит правильный многоугольник, а боковые ребра перпендикулярны плоскостям основания. То есть правильная четырехугольная призма содержит в своем основании квадрат . (см. выше свойства правильной четырехугольной призмы) Примечание . Это часть урока с задачами по геометрии (раздел стереометрия — призма). Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме . Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ .

Задача.

В правильной четырёхугольной призме площадь основания 144 см 2 , а высота 14 см. Найти диагональ призмы и площадь полной поверхности.

Решение .
Правильный четырехугольник — это квадрат.
Соответственно, сторона основания будет равна

√144 = 12 см.
Откуда диагональ основания правильной прямоугольной призмы будет равна
√(12 2 + 12 2 ) = √288 = 12√2

Диагональ правильной призмы образует с диагональю основания и высотой призмы прямоугольный треугольник. Соответственно, по теореме Пифагора диагональ заданной правильной четырехугольной призмы будет равна:
√((12√2) 2 + 14 2 ) = 22 см

Ответ : 22 см

Задача

Определите полную поверхность правильной четырехугольной призмы, если ее диагональ равна 5 см, а диагональ боковой грани равна 4 см.

Решение .
Поскольку в основании правильной четырехугольной призмы лежит квадрат, то сторону основания (обозначим как a) найдем по теореме Пифагора:

A 2 + a 2 = 5 2
2a 2 = 25
a = √12,5

Высота боковой грани (обозначим как h) тогда будет равна:

H 2 + 12,5 = 4 2
h 2 + 12,5 = 16
h 2 = 3,5
h = √3,5

Площадь полной поверхности будет равна сумме площади боковой поверхности и удвоенной площади основания

S = 2a 2 + 4ah
S = 25 + 4√12,5 * √3,5
S = 25 + 4√43,75
S = 25 + 4√(175/4)
S = 25 + 4√(7*25/4)
S = 25 + 10√7 ≈ 51,46 см 2 .

Ответ : 25 + 10√7 ≈ 51,46 см 2 .

Как выглядит правильная четырехугольная призма? и получил лучший ответ

Ответ от Edit Piaf[гуру]
Призма – это многогранник, две грани которой (основания призмы) – равные многоугольники с соответственно параллельными сторонами, а остальные грани — параллелограммы, плоскости которых параллельны прямой. Параллелограммы AabB, BbcC и т. д. называются боковыми гранями; рёбра Aa, Bb, Cc и т. д. называются боковыми рёбрами. Высота призмы – это любой перпендикуляр, опущенный из любой точки основания на плоскость другого основания. В зависимости от формы многоугольника, лежащего в основании, призма может быть соответственно: треугольной, четырёхугольной, пятиугольной, шестиугольной и т. д. Если боковые рёбра призмы перпендикулярны к плоскости основания, то такая призма называется прямой; в противном случае – это наклонная призма. Если в основании прямой призмы лежит правильный многоугольник, то такая призма также называется правильной.
Правильной призмой называется прямая призма, основанием которой является правильный многоугольник, то есть в данном случае — квадрат.
Я нарисовала прямую призму, но она может быть и наклонной

Ответ от Happy End [гуру]
кубик

Ответ от 3 ответа [гуру]

Привет! Вот подборка тем с ответами на Ваш вопрос: Как выглядит правильная четырехугольная призма?

Тип задания: 8
Тема: Призма

Условие

В правильной треугольной призме ABCA_1B_1C_1 стороны основания равны 4 , а боковые рёбра равны 10 . Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер AB, AC, A_1B_1 и A_1C_1.

Показать решение

Решение

Рассмотрим следующий рисунок.

Отрезок MN является средней линией треугольника A_1B_1C_1, поэтому MN = \frac12 B_1C_1=2. Аналогично, KL=\frac12BC=2. Кроме того, MK = NL = 10. Отсюда следует, что четырёхугольник MNLK является параллелограммом. Так как MK\parallel AA_1, то MK\perp ABC и MK\perp KL. Следовательно, четырёхугольник MNLK является прямоугольником. S_{MNLK} = MK\cdot KL = 10\cdot 2 = 20.

Ответ

Тип задания: 8
Тема: Призма

Условие

Объём правильной четырёхугольной призмы ABCDA_1B_1C_1D_1 равен 24 . Точка K — середина ребра CC_1 . Найдите объём пирамиды KBCD .

Показать решение

Решение

Согласно условию, KC является высотой пирамиды KBCD . 2=12+4=16,

AE_1=4.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Тип задания: 8
Тема: Призма

Условие

Найдите площадь боковой поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 4\sqrt5 и 8 , и боковым ребром, равным 5 .

Показать решение

Решение

Площадь боковой поверхности прямой призмы находим по формуле S бок. = P осн. · h = 4a\cdot h, где P осн. и h соответственно периметр основания и высота призмы, равная 5 , и a — сторона ромба. Найдём сторону ромба, пользуясь тем, что диагонали ромба ABCD взаимно перпендикулярны и точкой пересечения делятся пополам.

Сборник для подготовки к ЕГЭ (базовый уровень)

Прототип задания № 13

1.

2. Диаметр основания конуса равен 108, а длина образующей — 90. Найдите высоту конуса.

3. В сосуд, имеющий форму правильной треугольной призмы, налили 2700 см 3 воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 20 см до отметки 33 см. Найдите объем детали. Ответ выразите в см 3 .

4. В бак, имеющий форму цилиндра, налито 10 л воды. После полного погружения в воду детали, уровень воды в баке поднялся в 1,6 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.

5. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

6. От деревянной правильной пятиугольной призмы отпилили все её вершины (см. рисунок). Сколько граней у получившегося многогранника (невидимые рёбра на рисунке не изображены)?

7. Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 40 раз?

8. , , , прямоугольного параллелепипеда , у которого , , .

9. Найдите расстояние между вершинами и

10. Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.

11. Высота конуса равна 5, а диаметр основания – 24. Найдите образующую конуса.

12. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в 4 раза?

13. Площадь боковой поверхности цилиндра равна а диаметр основания равен 5. Найдите высоту цилиндра.

14. ABCDA 1 B 1 C 1 D 1 известны длины рёбер AB = 8, AD = 6, AA 1 = 21. Найдите синус угла между прямыми CD и A 1 C 1 .

15. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.

16. В кубе найдите угол между прямыми и . Ответ дайте в градусах.

17. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?

18. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 23,5. Найдите объем исходной призмы.

19. Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.

20. и многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

21. На рисунке изображён многогранник (все двугранные углы прямые). Сколько вершин у этого многогранника?

22. Даны две кружки цилиндрической формы. Первая кружка вдвое выше второй, а вторая в четыре раза шире первой. Во сколько раз объём второй кружки больше объёма первой?

23. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

24. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.

25. высоты. Объём жидкости равен 810 мл. Сколько миллилитров жидкости нужно долить, чтобы наполнить сосуд доверху?

26.

27. В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём жидкости равен 90 мл. Сколько миллилитров жидкости нужно долить, чтобы наполнить сосуд доверху?

28. Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

29. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?

30. h = 100 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у первого? Ответ дайте в сантиметрах.

31. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

32. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.

33. Вода в сосуде цилиндрической формы находится на уровне h = 80 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания в четыре раза больше, чем у данного? Ответ дайте в сантиметрах.

34. Найдите тангенс угла многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

35. Объем правильной четырехугольной пирамиды SABCD равен 116. Точка E — середина ребра SB . Найдите объем треугольной пирамиды EABC .

36. Найдите угол многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

37.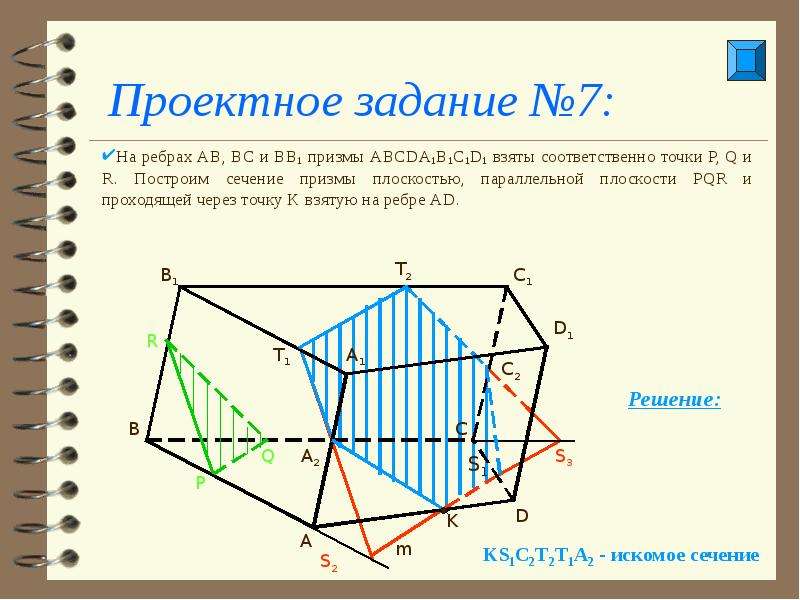 Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 2. Найдите объём куба.

38. В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ выразите в см.

39. В прямоугольном параллелепипеде известно, что Найдите длину ребра .

40. В бак, имеющий форму прямой призмы, налито 12 л воды. После полного погружения в воду детали, уровень воды в баке поднялся в 1,5 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.

41. Даны две кружки цилиндрической формы. Первая кружка в четыре раза ниже второй, а вторая в полтора раза шире первой. Во сколько раз объём первой кружки меньше объёма второй?

42. В правильной треугольной призме , все ребра которой равны 3, найдите угол между прямыми и Ответ дайте в градусах.

43. Высота конуса равна 72, а длина образующей — 90. Найдите диаметр основания конуса.

44. Найдите квадрат расстояния между вершинами и многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

45. Найдите объем многогранника, вершинами которого являются точки , , , правильной шестиугольной призмы , площадь основания которой равна 6, а боковое ребро равно 3.

46. От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

47. Объем первого цилиндра равен 12 м 3 . У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.

48. Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Цифры на рисунке обозначают длины рёбер в сантиметрах. Найдите площадь поверхности этой детали. Ответ дайте в квадратных сантиметрах.

49. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

50. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ: 3

Ответ: 13

Ответ: 64

Ответ: 8

Ответ: 0,6

Ответ: 8

Ответ: 60

Ответ: 27

Ответ: 94

Ответ: 0,25

Ответ: 61

Ответ: 16

Ответ: 8

Ответ: 80

Ответ: 5

Ответ: 21060

Ответ: 58

Ответ: 630

Ответ: 39

Ответ: 4

Ответ: 25

Ответ: 94

Ответ: 10

Ответ: 5

Ответ: 2

Ответ: 29

Ответ: 60

Ответ: 16

Ответ: 4

Ответ: 5

Ответ: 6000

Ответ: 9

Ответ: 45

Ответ: 108

Ответ: 6

Ответ: 1

Ответ: 3

Ответ: 9

Ответ: 146

Ответ: 2

Ответ: 25

Обучение с МК

Пример: модели МК в электронном учебнике

Сечения многогранников

ТЕОРИЯ

В этом разделе мы рассмотрим методы построения сечений многогранников. Плоскость сечения, как правило, будет задаваться тремя точками – K, L, M. Сложность такой задачи во многом определяется расположением точек, задающих плоскость сечения.

Пример 1

Самый простой случай – когда точки лежат на трёх смежных рёбрах пирамиды – не нуждается в разборе.

Модель 1

Основной метод, который используется при построении сечений, называется методом следов.

Следом называется прямая, по которой плоскость сечения пересекает плоскость любой из граней многогранника. Если такой след найден, то точки его пересечения с соответствующими рёбрами многогранника и будут вершинами искомого сечения.

Пример 2

Пусть теперь точки K и M лежат на боковых рёбрах пирамиды, а точка L – на стороне основания.

Модель 2

1. Проведём в плоскости SAC прямую KL – след сечения в этой плоскости.
2. Отметим точку P пересечения KL с SC.
3. Проведём прямую PM – след сечения в плоскости SBC, – и отметим точку пересечения PM и BC.
4. Все четыре вершины сечения получены – строим сечение.

Пример 3

Несколько труднее случай, когда одна из точек лежит на ребре, а две другие — на гранях пирамиды.

Модель 3

Теперь сразу построить след плоскости сечения в какой-то из граней нельзя.

1. Рассмотрим вспомогательную плоскость SKM, которая пересекает рёбра AC и BC в точках E и F соответственно.
2. Построим в этой плоскости прямую KM – след плоскости сечения – и отметим точку P пересечения KM с EF.
3. Точка P лежит в плоскости сечения и в плоскости ABC. Но в этой же плоскости лежит и точка L. Проведём прямую PL – след сечения в плоскости ABC – и отметим точку пересечения PL с BC.
4. Строим след сечения в плоскости SBC и отмечаем точку его пересечения с SC.
5. Строим след сечения в плоскости SAC и отмечаем точку его пересечения с SA.
6. Все четыре вершины сечения получены – строим сечение.

Использованный на первом шаге построения приём часто называют методом вспомогательных плоскостей. Рассмотрим ещё один пример, где он используется.

Пример 4

Рассмотрим теперь самый общий случай, когда все три точки K, L и M лежат на гранях пирамиды.

Модель 4

1. Как и в предыдущем случае проведём вспомогательную плоскость CKM, которая пересекает рёбра SA и SB в точках E и F соответственно.
2. Построим в этой плоскости прямую KM — след плоскости сечения – и отметим точку P пересечения KM с EF.
3. Точка P, как и L, лежит в плоскости SAB, поэтому прямая PL будет следом сечения в плоскости SAB, а её точки пересечения с SA и SB – вершинами сечения.
4. Теперь можно построить следы сечения в плоскостях SAC и SBC и отметить их точки пересечения с рёбрами AC и BC.
5. Все четыре вершины сечения получены – строим сечение.

С помощью метода вспомогательных плоскостей можно строить сечения, «не выходя» за пределы многогранника. Вернёмся в связи с этим к примеру 2.

Пример 2’

Точки K и M лежат на боковых рёбрах пирамиды, а точка L – на стороне основания. Построим сечение, «не выходя» за пределы многогранника.

Модель 5

1. Проведём вспомогательную плоскость SLB и в ней отрезок LM, который принадлежит плоскости сечения.
2. Проведём ещё одну вспомогательную плоскость BCK и построим точку пересечения SL и CK – точку E. Эта точка принадлежит обеим вспомогательным плоскостям.
3. Отметим точку пересечения отрезков LM и EB – точку F. Точка F лежит в плоскости сечения и в плоскости BCK.
4. Проведём прямую KF и отметим точку пересечения этой прямой c BC – точку N. Эта точка будет недостающей четвёртой вершиной сечения.
5. Все четыре вершины сечения получены – построим сечение.

Можно использовать ту же самую идею иначе. Проведём в начале анализ построенного сечения – т.е. начнём с конца. Допустим, что по точкам K, L и M построено сечение KLMN.

Модель 6

Анализ

Обозначим через F точку пересечения диагоналей четырёхугольника KLMN. Проведём прямую CF и обозначим через F₁ точку её пересечения с гранью SAB. С другой стороны, точка F₁ совпадает с точкой пересечения прямых KB и MA, исходя из чего её и можно построить.

Построение

1. Проведём прямые KB и MA и отметим точку их пересечения F₁.
2. Проведём прямые CF₁ и LM и отметим точку их пересечения F.
3. Проведём прямую KF и отметим точку её пересечения с ребром CB – точку N. Эта точка будет недостающей четвёртой вершиной сечения.
4. Все четыре вершины сечения получены – построим сечение.

Использованный в этом решении приём называют методом внутреннего проектирования. Построим с его помощью сечение из примера 4, когда все три точки лежат на гранях пирамиды.

Пример 3’

Точки K, L и M лежат на гранях пирамиды. Построим сечение, «не выходя» за пределы многогранника.

Допустим, что сечение уже построено.

Модель 7

Анализ

Пусть плоскость сечения пересекает ребро CB в точке P. Обозначим через F точку пересечения KM и LP. Построим центральные проекции точек K, F и M из точки C на плоскость SAB и обозначим их K₁, F₁ и M₁. Точки K₁ и M₁ легко находятся, а точку F₁ можно получить как точку пересечения K₁M₁ и LB.

Построение

1. Построим центральные проекции точек K и M из точки C на плоскость SAB и обозначим их K₁ и M₁.
2. Проведём прямые K₁M₁ и LB и отметим точку их пересечения F₁.
3. Проведём прямые CF₁ и KM и отметим точку их пересечения F.
4. Проведём прямую LF и отметим точку её пересечения с ребром CB – точку P. Это первая вершина искомого сечения.
5. Проведём прямую PM и отметим точку её пересечения с ребром SB. Это вторая вершина сечения.
6. Из второй вершины проведём прямую через точку L и найдём третью вершину сечения.
7. Из третьей вершины проведём прямую через точку K и найдём четвёртую вершину сечения.
8. Все четыре вершины сечения получены – построим сечение.

УПРАЖНЕНИЯ

Более сложные упражнения помечены звёздочкой.

1. Постройте сечение треугольной пирамиды плоскостью, проходящей через точки K, L и M (см. модели).

2. Постройте сечение куба плоскостью, проходящей через точки K, L и M (см. модели).

3. На рёбрах пирамиды SABC отмечены точки K, L и M. Постройте:

4*. На рёбрах пирамиды SABC отмечены точки K, L, M, P, N и Q. Постройте:

5*. На ребре AB треугольной пирамиды SABC отмечена точка K. Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной BC и SA.

Модель

6*. На рёбрах AB и CS треугольной пирамиды SABC отмечены точки K и M. Постройте сечение пирамиды плоскостью, проходящей через точки K и M и параллельной AS.

Модель

7*. Постройте сечение треугольной пирамиды плоскостью, проходящей через точки K, L и M, лежащих в плоскостях её боковых граней (но не на самих гранях!).

Модель

8*. На плоскости проведены три луча с общим началом – a, b и с – и отмечены три точки – A, B и C. Постройте треугольник, вершины которого лежат на этих лучах, а стороны проходят через точки A, B и C.

Модель

МЕТОДЫ РЕШЕНИЯ ПОЗИЦИОННЫХ ЗАДАЧ В КУРСЕ СТЕРЕОМЕТРИИ

Номер: 11-1

Год: 2016

Страницы: 35-41

Журнал: Актуальные проблемы гуманитарных и естественных наук

Ключевые слова

сечение, позиционная задача, метод внутреннего проектирования, метод следов, метод параллельного переноса прямых и плоскостей , section, positional task, internal design method, method of tracks, method of parallel traces lines and planes

Аннотация к статье

Тема «Позиционные задачи» является одной из основных тем при изучении многогранников и круглых тел. В данной статье представлены различные методы построения сечений многогранников и круглых тел плоскостями. Эта тема исследования является важной составляющей ЕГЭ по математике.

Текст научной статьи

Введение Тема «Позиционные задачи» является очень важной при изучении многогранников и круглых тел в стереометрии. Это связано, в частности, с построением точек пересечения геометрического тела и прямой, с построением сечения многогранника или круглого тела плоскостью и определением площади сечения. В данной работе дано понятие полного изображения пространственной фигуры и позиционной задачи, указаны способы построения сечения многогранников плоскостями. Работа даёт анализ способов построения сечений призм и пирамид плоскостями, приводятся различные примеры с решениями, решение нескольких задач даётся с рисунками. Общие понятия Напомним основные понятия главы «Методы изображений» курса геометрии, связанные с позиционными задачами. Под аффинным репером мы понимаем любую упорядоченную четвёрку точек общего положения. ОПРЕДЕЛЕНИЕ 1. На плоскости изображений изображение F некоторой фигуры называется полным, если к нему можно присоединить изображение аффинного репера так, что все точки, прямые и плоскости фигуры являются заданными. Точка считается заданной, если известна её аксонометрическая и одна из вторичных проекций. Прямая задаётся с помощью двух точек или аксонометрической и одной из вторичных проекций этой прямой, плоскость — с помощью трёх точек или точки и прямой или двух прямых. Зададим в пространстве фигуры и , а на плоскости изображений — их изображения и . ОПРЕДЕЛЕНИЕ 2. Позиционной задачей называется задача о построении изображения точек пересечения данных фигур и , если известны их изображения и . Если изображения полные, то позиционная задача имеет определённое решение. Наиболее часто в качестве одной из данных фигур выступает прямая l¢ или плоскость П¢, и тогда позиционная задача рассматривается как построение изображения сечения фигуры прямой или плоскостью. Изображения пространственных фигур в школьном курсе математики, как правило, являются полными, поэтому решение позиционной задачи, то есть, например, построение сечения многогранника или круглого тела плоскостью, носит вполне определённый характер. При построении сечения многогранника плоскостью обычно используют следующие методы: — метод внутреннего проектирования, — применение следа секущей плоскости на плоскости основания геометрического тела (метод следов), — метод параллельного переноса прямых и плоскостей, — метод дополнения n-угольной призмы (пирамиды) до треугольной призмы (пирамиды), — метод разбиения n-угольной призмы (пирамиды) на треугольные призмы (пирамиды). Метод внутреннего проектирования Сечение многогранника плоскостью — многоугольник, представляющий собой множество всех точек пространства, принадлежащих одновременно данному многограннику и плоскости, плоскость при этом называется секущей плоскостью. Секущая плоскость может быть задана различными способами, например: а) тремя точками, которые не лежат на одной прямой; б) прямой и точкой, не лежащей на ней; в) двумя пересекающимися прямыми; г) некоторыми из указанных выше геометрических элементов в совокупности с различными зависимостями между ними и элементами (гранями, ребрами, диагоналями и т. д.) многогранника. Построение плоских сечений многогранников выполняется на основе соответствующих пространственных аксиом и теорем. Построить сечение многогранника плоскостью — это значит построить многоугольник все вершины и стороны, которого — соответственно следы секущей плоскости на ребрах и гранях многогранника. Метод внутреннего проектирования как раз и основан на использовании взаимного расположения точек, прямых и плоскостей в пространстве. В частности, использовании параллельности прямых и плоскостей, поскольку параллельность сохраняется при параллельном проектировании. Пример 1. Дано изображение четырехугольной призмы ABCDA1B1C1D1 и трёх точек ÎАА1, ÎBB1,ÎCC1 , лежащих по одной на её боковых ребрах. Построить сечение призмы плоскостью, проходящей через эти точки. Рис. 1 Построение. (См. рис. 1) Найдём точку пересечения секущей плоскости с ребром DD1. Пусть А1С1ÇB1D1=O1. Проведём OO1 || АА1, OÎ, тогда точка =OÇDD1 — искомая точка. Действительно, ÎÌ, отсюда Î. Сечение является искомым. Пример 2. Построить изображение сечения четырёхугольной призмы ABCDA1B1C1D1 плоскостью, заданной тремя точками KÎАА1B1B, LÎBB1C1C, MÎCC1D1D, лежащими по одной на боковых гранях призмы. Решение. 1) Пусть K1 , L1 , M1 — проекции точек K, L, M на нижнее основание (вторичные проекции этих точек). 2) Найдём точку пересечения секущей плоскости с ребром AA1. Пусть А1L1ÇK1M1=Р1. Проведём РР1||АА1, РÎKM, тогда точка X=LPÇAA1 — искомая точка. Действительно, XÎPLÌKLM, отсюда XÎKLM. 3) Построим Y=XKÇBB1, Z=YLÇCC1, T=ZMÇDD1 , тогда сечение XKYLZMT является искомым. Пример 3. На ребре SC пирамиды SABCD задана точка P, а в гранях SAB и SAD заданы соответственно точки R и Q. Построить сечение плоскостью PQR. Рис. 2 Построение. (См. рис. 2) 1) Пусть R0 =SRÇAB , Q0 =SQÇBC. 2) Найдём точку пересечения D1 секущей плоскости с ребром SD. Для этого строим точки CQ0 ∩ R0D = O0 , PQ ∩ SO0 = O, RO ∩ SD = D1. 3) Пусть A1 =SAÇQD1, B1 =SBÇRA1, тогда A1RB1PD1Q — искомое сечение. Пример 4. Построить изображение сечения четырёхугольной пирамиды SABCD плоскостью α, заданной тремя точками KÎSА, LÎSB, MÎSC, лежащими по одной на боковых рёбрах пирамиды. Решение. Найдём точку пересечения секущей плоскости с ребром SD. Пусть АСÇBD=Р, SРÇKM=T, тогда точка N=LTÇSD — искомая точка. Действительно, NÎTLÌKLM, отсюда NÎKLM. Сечение KLMN является искомым. Метод следов (применение следа секущей плоскости на плоскости основания геометрического тела) Следом плоскости α на плоскости b называют прямую, по которой плоскость α пересекает плоскость b. Следом прямой l на плоскости α называют точку пересечения прямой с плоскостью α. При использовании этого метода сначала строится след секущей плоскости на плоскости одной из граней многогранника (либо на диагональной плоскости или плоскости симметрии), а также следы на прямых, содержащих стороны этой грани.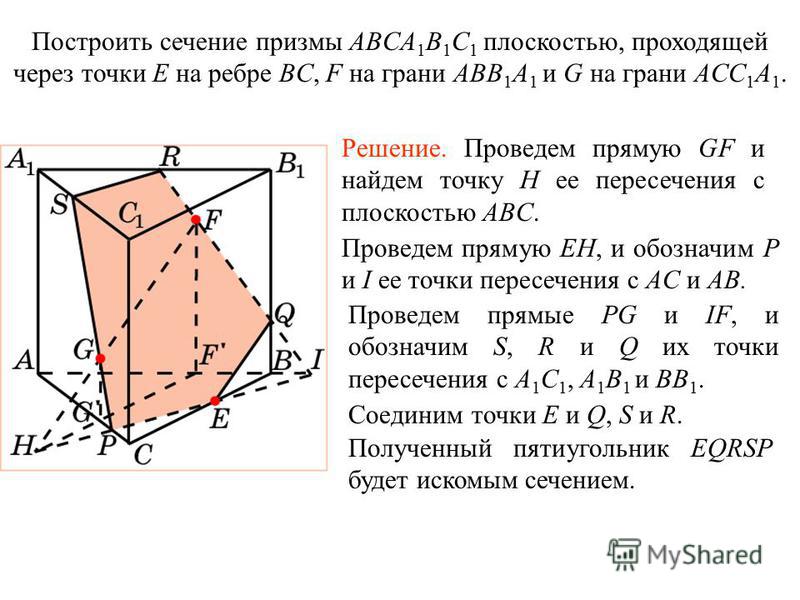 Далее строятся следы секущей плоскости на других гранях при наличии двух следов на прямых, содержащих стороны соответствующей грани. Пример 5. Дана призма ABCDEA1B1C1D1 и три точки M, N, P принадлежащие соответственно рёбрам AA1, BB1, CC1. Построить сечение призмы плоскостью MNP. Рис.3 Построение. (См. рис. 3) 1) NM ∩ A1B1 = X, NP ∩ B1C1 = Y, тогда XY — след секущей плоскости. 2) XY ∩ A1E1 = O, XY ∩ C1D1 = Q. 3) NMOQP — искомое сечение. Пример 6. Построить изображение сечения четырёхугольной призмы ABCDA1B1C1D1 плоскостью, заданной тремя точками KÎАА1, LÎBB1, MÎCC1, лежащими по одной на боковых рёбрах призмы. Решение. 1) Найдём след секущей плоскости, то есть линию пересечения секущей плоскости с плоскостью нижнего основания A1B1C1D1 данной призмы. Пусть MLÇB1C1=S, KMÇA1C1=T, тогда прямая ST — след секущей плоскости. 2) Найдём точку пересечения секущей плоскости с ребром DD1. Пусть A1D1 Ç ST =R, тогда точка N=KRÇDD1 — искомая точка. Действительно, NÎKRÌKLM, отсюда NÎKLM. Сечение KLMN является искомым. Пример 7. Дана пирамида SABCDE, точки A1 AS, B1 BS, C1 CS. Построить сечение, проходящее через эти точки. Рис.4 Построение. (См. рис. 4) 1) A1B1 ∩ AB = X, B1C1 ∩ BC = Y, прямая XY — след секущей плоскости. 2) DC ∩ XY = Z, ZC1 ∩ DS = D1, EA ∩ XY = M, MA1 ∩ SE = E1. 3) A1B1C1D1E1 — искомое сечение. Пример 8. Построить изображение сечения четырёхугольной пирамиды SABCD плоскостью, заданной тремя точками KÎSА, LÎSB, MÎSC, лежащими по одной на боковых рёбрах пирамиды. Решение. 1) Найдём след секущей плоскости, то есть линию пересечения секущей плоскости с плоскостью основания ABCD данной пирамиды. Пусть MLÇBC=S, KMÇAC=T, тогда прямая ST — след секущей плоскости. 2) Найдём точку пересечения секущей плоскости с ребром SD. Пусть AD Ç ST =R, тогда точка N=KRÇSD — искомая точка, а KLMN является искомым сечением. Метод параллельного переноса прямых и плоскостей Метод параллельного переноса прямых и плоскостей применяется в тех случаях, когда секущая плоскость a задана как плоскость, проходящая через данную точку М параллельно двум скрещивающимся прямым а и b, или проходящая через данную прямую а параллельно скрещивающейся с ней прямой b, или проходящая через данную точку М параллельно данной плоскости β. Суть метода параллельного переноса прямых заключается в том, что в секущей плоскости проводят прямую, параллельную данной прямой. При этом очень часто приходится проводить вспомогательную плоскость, параллельную той, в которой находится данная прямая. Суть метода параллельного переноса плоскостей состоит в том, что вместо секущей плоскости строится параллельная ей вспомогательная плоскость, которая пересекает все грани некоторого трехгранного (или многогранного в общем случае) угла данного многогранника. Далее путем параллельного переноса строятся некоторые линейные элементы искомого сечения, соответствующие легко строящимся элементам вспомогательной плоскости. При построении используются известные свойства параллельных прямых и плоскостей: 1) Если а || a, то в плоскости a существует прямая b, параллельная а. 2) Через точку пространства можно провести единственную плоскость, параллельную данной плоскости. 3) Если две параллельные плоскости пересекаются третьей, то линии их пересечения параллельны. 4) Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны. 5) Если плоскость β проходит через прямую а, параллельную плоскости a, и пересекает ее по прямой b, то a || b. 6) Каковы бы ни были скрещивающиеся прямые а и b, существует единственная пара параллельных плоскостей a и β, в которой они соответственно лежат. 7) Признаки параллельности прямых и плоскостей. Пример 9. Даны параллелепипед ABCDA1B1C1D1 и точки MAA1, NB1C1, K AD. Провести сечение плоскостью проходящей через точку N параллельно прямым MB1 и CK. Рис. 5 Построение. (См. рис. 5) 1) Построим плоскость MB1NP , в которой MP ║ B1N, MB1║ NP. 2) Проведем прямую TN параллельную прямой KC. 3) Прямая TP пересекает ребро DD1 в точке E. 4) (NR) параллельно (TE), RÎ(CC1). Тогда TNRE — искомое сечение. Пример 10. Даны точки M, N и P, лежащие соответственно на боковых ребрах SA, SD и SB четырехугольной пирамиды SABCD. Построить сечение пирамиды плоскостью MNP. Решение. Проводим через вершину D прямую, параллельную MN , до пересечения с ребром SA. Через полученную точку K1 параллельно MP проводим прямую до пересечения с ребром AB в точке K2. Плоскость треугольника DK1K2 параллельна плоскости MNP. Плоскость ASC пересекает их по параллельным прямым. Прямая пересечения плоскостей ASC и DK1K2 — прямая K1K3 , где K3 — точка пересечения диагонали AC четырехугольника ABCD и отрезка DK2. Через точку M проводим прямую, параллельную K1K3, до пересечения с ребром SC. Получаем точку Q. Сечение MPQN является искомым. Метод дополнения n-угольной призмы (пирамиды) до треугольной призмы (пирамиды) Если данную призму (пирамиду) достроить до треугольной призмы (пирамиды), затем построить сечение полученной треугольной призмы (пирамиды), то искомое сечение получается как часть сечения треугольной призмы (пирамиды). Пример 11. Построить сечение пирамиды DAEGHF плоскостью AMN, где точки M и N лежат на ребрах DE и DF соответственно. Решение. 1) Достраиваем данную пятиугольную пирамиду до треугольной. Для этого получим точки AE Ç HG = C и AF Ç GH = B, и затем проведем отрезки DC и DB. 2) Строим сечение полученной треугольной пирамиды ABCD плоскостью AMN. Для этого последовательно получаем точки AM Ç DC = P и AN Ç DB = Q, и соединяем точки P и Q. Треугольник APQ — есть сечение пирамиды ABCD плоскостью AMN. 3) Осталось получить точки PQ Ç DG = R и PQ Ç DH = S. Тогда пятиугольник AMRSN — искомое сечение данной пятиугольной пирамиды. Метод разбиения n-угольной призмы (пирамиды) на треугольные призмы (пирамиды) Из данной n-угольной призмы (пирамиды) выделяют основную треугольную призму (пирамиду), на боковых ребрах которой лежат точки, определяющие искомое сечение. Строят сечение этой треугольной призмы (пирамиды), затем строят сечения тех треугольных призм (пирамид), которые имеют общие части с основной призмой (пирамидой). Пример 12. Построить сечение четырехугольной призмы ABCDA1B1C1D1 плоскостью PQR, где точки P и Q лежат на ребрах AA1 и DD1 соответственно, точка R принадлежит плоскости AA1B1B. Решение. 1) Точка R лежит на отрезке EE1, где E Î AB, E1 Î A1B1 , EE1 Î AA1. Треугольник PQR является сечением треугольной призмы ADEA1D1E1. Призмы ADCA1D1C1 и ABCA1B1C1 имеют общую часть с призмой ADEA1D1E1. 2) Получим точки AС Ç DE = M, A1С1 Ç D1E1 = M2. Плоскости ACС1 и EDD1 пересекаются по прямой ММ2. Прямые ММ2 и QR пересекаются в точке М1. 3) Точки Р и М1 принадлежат плоскости ACС1, поэтому прямые PМ1 и CC1 пересекаются в точке T, принадлежащей секущей плоскости PQR. 4) Имеем точку PR Ç BB = K1. Прямые PR и PQ лежат в одной плоскости PQR, поэтому точка K принадлежит плоскости PQR. 5) Точки Q и T лежат в плоскости сечения, значит, прямая QT принадлежит секущей плоскости. Четырехугольник PKTQ — искомое сечение.

Учебник_Погорелов_1995 (Ответы ко всем упражнениям Погорелова по геометрии от седьмого до одиннадцатого класса (Погорелов)), страница 46

// класс 26. Сколько плоскостей симметрии у прямоугольного параллелепипеда? 27. Что такое пирамида (основание пирамиды, боковые грани, ребра, высота)? 28. Что представляют собой сечения пирамиды плоскостями, проходящими через ее вершину? 29. Что такое диагональное сечение пирамиды? 30. Как построить сечение пирамиды плоскостью, проходящей через данную прямую в плоскости основания пирамиды и заданную точку на одной из боковых граней? 31. Докажите, что плоскость, пересекающая пирамиду и параллельная ее основанию, отсекает подобную пирамиду.

32. Объясните, что такое усеченная пирамида. 33. Какая пирамида называется правильной? Что такое ось правильной пирамиды? 34. Что такое апофема правильной пирамиды? 35. Докажите, что боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему, 36. Какой многогранник называется правильным? 37. Перечислите пять типов правильных многогранников и опишите их. ЗАДАЧИ П 1. Нз точек А и В, лежащих в гранях двугранного угла, опущены перпендикуляры АА ~ и ВВ~ на ребро угла.

Найдите: 1) отрезок АВ, если АА~ =а„ВВ~ — — Ь, А~В~=с и двугранный угол равен и; 2) двугранный угол а, если АА~ =3. ВВ| = 4, А В| =6, АВ=?. П 2. У трехгранного угла (аЬс) двугранный угол при ребре 167 с прямой, двугранный угол при ребре Ь равен ср, а плоский угол (Ьс) равен? ~~„?( — . Найдите два дру- 2 / гих плоских угла: сс= Л.(аЬ), р= а.(ас). 3. У трехгранного угла один плоский угол равен?, а прилежащие к нему двугранные углы равны ~( ср ~ — ‘1 . Найди- 2/ те два других плоских угла а и угол р, который образует плоскость угла ? с противолежащим ребром. 4*.

У трехгранного угла два плоских угла острые и равны а, а третий угол равен у. Найдите двугранные углы ср, противолежащие плоским углам я, и угол () между плоскостью? и противолежащим ребром. П 5. Докажите, что сечение призмы, параллельное основаниям, равно основаниям. 6.

Сколько диагоналей имеет л-угольная призма? з1з 1 29. Многогранники 70 7. Постройте сечение четырехугольной призмы плоско- П стью, проходящей через сторону основания и одну из вершин другого основания. 8. Постройте сечение четырехугольной призмы плоскостью, проходящей через три точки на боковых ребрах призмы. И’ 9. У призмы одно боковое ребро перпендикулярно плос- кости основания. Докажите, что остальные боковые ребра тоже перпендикулярны плоскости основания.

10. В прямой треугольной призме стороны основания равны 10 см, 17 см и 21 см, а высота призмы 18 см. Найдите площадь сечения, проведенного через боковое ребро и меньшую высоту основания. 11. Боковое ребро наклонной призмы равно 15 см и наклонено к’плоскости основания под углом 30′. Найдите высоту призмы. 12*. В наклонной треугольной призме расстояния между боковыми ребрами равны 37 см, 13 см и 40 см.

Найдите расстояние между большей боковой гранью и противолежащим боковым ребром. 13. Основанием призмы является правильный шестиугольник со стороной а, боковые грани — квадраты. Найдите диагонали призмы и площади ее диагональных сечений. 14и. В правильной шестиугольной призме, у которой боковые грани — квадраты, проведите плоскость через сторону нижнего основания и противолежащую ей сторону верхнего основания. Сторона основания равна а. Найдите площадь построенного сечения (рис.

427). 15. Через сторону нижнего основания правильной треугольной призмы проведена плоскость, пересекающая боковые грани по отрезкам, угол между которыми ее. Найдите угол наклона втой плоскости к основанию призмы (рис. 428). 16. В правильной четырехугольной призме через середины двух смежных сторон основания проведеиа плоскость„ пересекающая три боковых ребра и наклоненная к плоско- Ег А л Рне. 427 Рне. 428 314 11 класс сти основания под углом а. Сторона основания равна а. Найдите площадь полученного сечения.

17. В правильной четырехугольной призме площадь основания 144 ем~, а высота 14 см. Найдите диагональ призмы. 18. В правильной четырехугольной призме площадь боковой грани равна Я. Найдите площадь диагонального сечения. 19*. Сторона основания правильной четырехугольной призмы равна 15, высота равна 20. Найдите кратчайшее расстояние от стороны основания до не пересекающей ее диагонали призмы (рис. 429). 20. В прямой треугольной призме все ребра равны. Боковая поверхность равна 12 м~.

Найдите высоту. 21. Боковая поверхность правильной четырехугольной призмы 32 м’, а полная поверхность 40 м’. Найдите высоту. 22а. В наклонной призме проведено сечение, перпендикулярное боковым ребрам и пересекающее все боковые ребра. Найдите боковую поверхность призмы, если периметр сечения равен р, а боковые ребра равны ). 23. Расстояния между параллельными прямыми, содержащими боковые ребра наклонной треугольной призмы, равны 2 см, 3 см и 4 см, а боковые ребра 5 см. Найдите боковую поверхность призмы.

24. По стороне основания а и боковому ребру ‘Ь найдите полную поверхность правильной призмы: 1) треугольной; 2) четырехугольной; 3) шестиугольной. 25. Плоскость, проходящая через сторону основания правильной треугольной призмы и середину противолежащего ребра, образует с основанием угол 45’. Сторона основания й Найдите боковую поверхность призмы. И 26.

У параллелепипеда три грани имеют площади 1 м~, 2-м’ и 3 м’. Чему равна полная поверхность параллелепипеда? 27. Известны углы, образуемые ребрами параллелепипеда, сходящимися в одной вершине. Как найти углы между ребрами, сходящимися в любой другой вершине? 26. Докажите, что отрезок, соединяющий центры оснований параллелепипеда, параллелен боковым ребрам. 29. В прямом параллелепипеде стороны основания 6 м и 8 м образуют угол 30′, боковое ребро равно 5 м. Найдите полную поверхность этого параллелепипеда.

30. В прямом параллелепипеде стороны основания 3 см и 8 см, угол между ними 60′. Боковая поверхность равна 220 см-. Найдите полную поверхность. 31. В прямом параллелепипеде стороны основания 3 см и 5 см, а одна из диагоналей основания 4 см. Найдите ббльшую диагональ параллелепипеда, зная, что меньшая диагональ образует с плоскостью основания угол 60′. Ф 19. Многограннини 32. Найдите диагонали прямого параллелепипеда, у которого каждое ребро равно а, а угол основания равен 60 . 33*. Боковое ребро прямого параллелепипеда 5 м, стороны основания 6 м и 8 м, а одна из диагоналей основания 12 м. Найдите диагонали параллелепипеда. 34.

В прямом параллелепипеде боковое ребро 1 м, стороны основания 23 дм и 11 дм, а диагонали основания относятоя как 2:3. Найдите площади диагональных сечений. И 174 36. Найдите диагонали прямоугольного параллелепи- педа по трем его измерениям: 1) 1, 2, 2; 2) 2, 3, 6; 31 6, 6, 7. 36*. Ребро куба равно а. Найдите расстояние от вершины куба до его диагонали, соединяющей две другие вершины.

37. В прямоугольном параллелепипеде стороны основания 7 дм и 24 дм, а выеота параллелепипеда 8 дм. Найдите площадь диагонального сечения. 38. Найдите поверхность прямоугольного параллелепипеда по трем его измерениям: 10 см, 22 см, 16 см. 39. Найдите боковую поверхность прямоугольного параллелепипеда, если его высота Ь, площадь основания ге, а площадь диагонального сечения М. 40. Диагонали трех граней прямоугольного параллелепипеда, сходящиеся в одной вершине, равны а, Ь, с. Найдите линейные размеры параллелепипеда (рие. 430). И 41.

Оенование пирамиды — равнобедренный треуголь- ник, у которого основание равно 12 см, а боковая сторона 10 см. Боковые грани образуют с оенованием равные двугранные углы, содержащие по 45′. Найдите высоту пирамиды. Рис. 429 Рис. 430 Зтв п з агг 42. Основание пирамиды — прямоугольник со сторонами 6 см и 8 см. Каждое боковое ребро пирамиды равно 13 см.

Вычислите высоту пирамиды. 43. Основанием пирамиды является правильный треугольник; одна из боковых граней перпендикулярна основанию, а две другие наклонены к нему под углом а, Как наклонены к плоскости основания боковые ребра? 44. В основании пирамиды лежит прямоугольный треугольник с гипотенузой а. Каждое боковое ребро образует с плоскостью основания угол 3. Найдите ее высоту. 45. Основание пирамиды — прямоугольный треугольник с катетами 6 см и 8 см. Все двугранные углы при основании пирамиды равны 60′. Найдите высоту пирамиды.

46. Основание пирамиды — параллелограмм, у которого стороны 3 см и Ч см, а одна нз диагоналей 6 см; высота пирамиды проходит через точку пересечения диагоналей, она равна 4 см. Найдите боковое ребро пирамиды. 47*. Основание пирамиды — ромб с диагоналями 6 м и 8 м; высота пирамиды проходит через точку пересечения диагоналей ромба и равна 1 м. Найдите боковую поверхность пирамиды. 48. Основание пирамиды — равнобедренный треугольник со сторонами 40 см, 25 см и 25 см.

Как рисовать прямоугольные тела и шестиугольные плоскости с помощью этих уроков и руководств по рисованию

[Текст вверху сохраняется как изображения, если вам нужно скопировать текст, он внизу]

ЧЕРТЕЖ ПРЯМОУГОЛЬНЫХ ТЕЛ.

Кубики для рисования

Куб может рассматриваться как тип для прямоугольных тел всех видов.

Куб — это твердое тело, ограниченное шестью квадратными гранями. Ограничивающие линии лица — это края куба. Соседние грани куба перпендикулярны друг другу.

Соседние грани перпендикулярны друг другу. Противоположные края параллельны друг друга. Противоположные грани параллельны друг другу.

Эксперименты с кубом спереди, сверху, снизу, слева и справа от глаза, аналогичные описанным для прямой палки и квадратной плоскости, должны показать учащемуся следующее: —

Принципы рисования прямоугольных тел.

1. Если у любого прямоугольного твердого тела одна грань перпендикулярна линии направления, оно будет выглядеть как плоскость.

2. Когда правая и левая грани вертикального куба имеют одинаковую ширину или когда такие грани прямоугольного твердого тела образуют одинаковый угол с линией направления, очевидный наклон отступающих линий, влево и вправо, будет то же самое.

3. Когда правая и левая грани куба кажутся разной ширины, горизонтальные края более широкой грани будут казаться менее наклонными и сходящимися менее быстро, чем грани более узкой грани, если только отступающие линии не окажутся внутри. самолет, проходящий через глаз.

4. Когда видны три грани прямоугольного твердого тела, три прямых угла, которые образуют ближайший телесный угол, всегда будут казаться тупыми, углы каждой видимой грани, противоположные этому телесному углу, будут казаться более тупыми, а все остальные видимые углы будут казаться острыми.

5. Когда видны три грани прямоугольного твердого тела, три видимых параллельных ребра любых двух смежных граней будут казаться сходящимися в направлении, противоположном третьей видимой грани.

Рисование продолговатых квадратных призм.

Прямоугольная призма — это твердое тело, ограниченное двумя квадратными концами и четырьмя продолговатыми прямоугольными гранями. Его ребра и грани связаны друг с другом так же, как и у куба. Ось представляет собой воображаемую линию, проходящую через центр твердого тела и соединяющую центры его концов или оснований. Прямоугольная призма имеет ось, расположенную под прямым углом к ​​ее концам, а ее грани — прямоугольники.

Чертеж квадратных плинтусов.

Квадратный постамент — это низкая или плоская квадратная призма, и его можно определить теми же словами, что и для продолговатой квадратной призмы.

Практика рисования прямоугольных тел приведет к принятию следующего:

Шаги для рисования прямоугольных тел, когда они опираются на горизонтальные плоскости.

1. Проведите вертикальную прямую линию, чтобы обозначить ближайший вертикальный край.Затем эта линия должна быть принята за единицу измерения, с которой сравниваются все остальные линии.

2. Определите и нарисуйте кажущийся наклон двух видимых краев внизу, два видимы.

3. Определите и нарисуйте кажущийся уклон двух ближайших видимых краев вверху.

4. Определите видимую ширину (измеренную по горизонтали и по сравнению с ближайшим вертикальным краем) левой и правой граней и обрежьте их вертикальными прямыми линиями.

5. Определите и нарисуйте кажущийся уклон двух самых дальних видимых краев вверху.

6. Если прямоугольное тело стоит прямо перед зрителем и ниже уровня глаз, сначала нарисуйте вертикальные и горизонтальные линии для изображения лицевой стороны, а затем такие линии, которые необходимы для завершения вершины.

Рисование прямоугольных пирамид.

Прямоугольная пирамида — это твердое тело, ограниченное квадратным основанием и четырьмя треугольными гранями, которые встречаются в точке, называемой вершиной пирамиды.У правой пирамиды ось расположена под прямым углом к ​​основанию, причем ось представляет собой воображаемую прямую линию, проходящую через середину твердого тела от вершины к центру основания.

Шаги для рисования прямоугольной пирамиды.

1. Когда пирамида стоит на основании, зафиксируйте точку для ближайшего угла основания.

2. Определите и нарисуйте видимый наклон видимых краев у основания и определите их сравнительную длину.

3. Завершите представление всей базы, как если бы она была видимой, и нарисуйте диагонали, чтобы найти центр

4. Постройте вертикальную линию в центре, представляющую ось пирамиды, и определите ее кажущуюся длину по сравнению с некоторой частью основания.

5. От вершины, которая является верхним концом оси, проведите прямые линии до видимых углов основания.

6. Когда пирамида лежит на одной из своих треугольных граней, определите и нарисуйте кажущийся наклон и сравнительную длину видимых краев на полу, а затем ребер, соединенных с ними, до тех пор, пока все не будет завершено.

Чертеж равносторонних треугольных призм.

Равносторонняя треугольная призма — это твердое тело, ограниченное двумя равносторонними треугольными концами и тремя прямоугольными гранями.Ось — это линия, соединяющая центры двух концов. У правой призмы ось расположена под прямым углом к ​​ее концам, а грани — прямоугольники. Когда треугольная призма опирается одной прямоугольной гранью на горизонтальную плоскость, высота представляет собой перпендикулярную линию от наивысшей точки одного конца до его основания.

Шаги для рисования равносторонней треугольной призмы.

1. Когда призма опирается одной прямоугольной гранью на горизонтальную плоскость, определите и нарисуйте кажущийся наклон и предполагаемую длину нижнего края видимого конца и поместите точку немного ближе к дальнему концу линии, чем к его ближайший конец.

2. В этой точке проведите вертикальную линию высоты треугольного конца и определите его относительную высоту.

3. Присоедините верхний конец высоты к двум концам базовой линии.

4. Определите и нарисуйте кажущийся наклон и сравнительную длину оставшихся линий для сторон и невидимого конца.

5. Когда призма стоит на одном треугольном конце, сначала нарисуйте видимый конец, затем соединенные с ним вертикальные линии и, наконец, линии для невидимого конца.

Правильная шестиугольная плоскость.

Правильный шестиугольник — это плоская фигура, ограниченная шестью равными прямыми краями или линиями и имеющая шесть равных углов. Он может иметь три диагонали, проходящие через его центр, разделяющие шестиугольник на шесть равносторонних треугольников, как на рис. F, и шесть других диагоналей, не проходящих через центр, как на рис. G, но образующих два пересекающихся равносторонних треугольника или шесть -конечная звезда с центральным шестиугольником.

Прежде чем рисовать правильную шестиугольную плоскость, если смотреть под углом, ученик должен познакомиться со следующими принципами, которые можно понять, нарисовав правильный шестиугольник с его различными диагоналями, как показано на прилагаемых рисунках: —

Принципы построения правильной шестиугольной плоскости.

1. Опустив любые два противоположных угла, оставшиеся четыре угла можно соединить так, чтобы образовать прямоугольник, как 6 — 7 — 8 — 9 на рис. H, или 1-7-2-8 на рис. I, или
7-9-2-6

2. Любая линия, соединяющая два противоположных угла, делится на четыре равные части центр и длинные стороны прямоугольника, образованного другими четырьмя углами, как 1-2 в точках 3, 4 и 5 на рис. H, или 6-9 в точках 3, до и 11 на рис. I , или 7-8 в точках 3, 12 и 13 на рис. y.

3. Любая линия, соединяющая два противоположных угла, будет параллельна концам прямоугольника, образованного оставшимися четырьмя углами, и, следовательно, если смотреть под углом, она будет сходиться с ними.

4. Если плоскость вертикальна и опирается одним краем на горизонтальную плоскость, длинные стороны прямоугольника, образованного соединением двух нижних и двух верхних углов, всегда будут вертикальными.

шагов для рисования правильной шестиугольной плоскости.

1. Если плоскость вертикальна и опирается одним краем на горизонтальную плоскость, нарисуйте прямоугольник с вертикальными длинными сторонами и найдите его центр, нарисовав его диагонали, как показано на рис.К.

2. Проведите через центр линию, сходящуюся с верхом и низом прямоугольника, и такой длины, чтобы центр и длинные стороны прямоугольника делили его на четыре части, почти равные, но очень немного уменьшающиеся от ближайшая к самой дальней части, как показано на рис. L.

3. Соедините концы этой линии с ближайшими углами прямоугольника, образуя шестиугольную плоскость, как показано на рис.Al

4. Если плоскость горизонтальная или наклонная, нарисуйте один из трех возможных прямоугольников, найдите его центр и продолжайте, как прежде. См. Рис. N.

Правильная правильная шестиугольная призма.

Правая правильная шестиугольная призма — это твердое тело, ограниченное двумя шестиугольными плоскостями или концами и шестью прямоугольными гранями. Ось представляет собой воображаемую линию, соединяющую центры двух концов.

Не существует принципов для рисования шестиугольной призмы, специально отличающихся от принципов рисования шестиугольной плоскости или от тех, которые уже объяснялись для параллельных линий, мы можем сразу заявить следующее:

Шаги для рисования правильной шестигранной призмы.

1. Когда призма лежит одной прямоугольной гранью на горизонтальной плоскости, нарисуйте видимый конец призмы, как указано в «Шагах по рисованию правильной шестиугольной плоскости».

2. Определите и нарисуйте кажущийся уклон и сравнительную длину оставшихся линий для длинных краев и невидимого конца.

3. Когда призма стоит одним шестиугольным концом на горизонтальной плоскости, сначала нарисуйте видимый конец, затем соединенные с ним вертикальные линии и, наконец, линии невидимого конца.

Рисование правильных шестиугольных пирамид.

Правильная правильная шестиугольная пирамида — это твердое тело, ограниченное правильным шестиугольником в основании и шестью равнобедренными треугольниками, пересекающимися в точке, называемой вершиной. Ось — это воображаемая линия, соединяющая вершину с центром основания.

Шаги для рисования правильной шестиугольной пирамиды.

1. Когда ось вертикальна, сначала нарисуйте основание в направлении шестиугольной плоскости и найдите его центр, проведя две диагонали, каждая через противоположные углы.

2. В центре основания нарисуйте ось соответствующей сравнительной длины и присоедините вершину к видимым углам основания.

3. Когда пирамида опирается на одну треугольную грань и видна плоскость основания, нарисуйте ее, как указано ранее, а затем соедините линии.

4. Если плоскость основания не видна, начните с видимых краев пола, следуя линиям, соединенным с ними, пока все не будет завершено.

Использование круга при рисовании отступающих самолетов.

Отступающие самолеты — это самолеты, у которых некоторые края или углы ближе к глазу зрителя, чем другие.

Предположим, мы должны нарисовать крышку ящика частично приподнятую, много или мало; открытая книга с листами в одной или нескольких позициях; или дверь более или менее открыта. Крышка, створки и дверь, закрепленные с одной стороны и вращающиеся вокруг нее, будут во многих положениях отступать плоскостями.Любая точка на краях или углах, которые не закреплены, будет описывать круги или части кругов, когда они повернуты вокруг фиксированного края. Эти круги или их части, если смотреть под углом, будут выглядеть как эллипсы или части эллипсов. Способ использования этих кругов и эллипсов проиллюстрирован рис. X.

Пересечение правильных тел — геометрический рисунок

Когда два твердых тела проникают друг в друга, образуется линия пересечения. H иногда необходимо знать точную форму этой линии, обычно для того, чтобы можно было нарисовать точную развертку одного или обоих твердых тел.В этой главе показаны линии пересечения, образующиеся, когда некоторые из более простых геометрических тел проникают друг в друга

Два непохожих друг на друга равных элемента встречаются под прямым углом (Рис. 12/1)

E E. показывает, где углы 1 и 3 встречаются с большей призмой, и они проецируются поперек F.E. На плане показано, где углы 2 и 4 встречаются с концом большей призмы, это проецируется до F.E.

Две одинаковые квадратные призмы, встречающиеся под углом

F.E. показывает, где углы 1 и конец 3 встречаются с большей призмой.На плане показано, где углы 2 и 4 встречаются с большей pdsm, и это спроектировано до F. E.

.

3R0 УГОЛ ВЫПУСК 2

ПРОЕКЦИЯ 1-Й УГОЛ

ПРОЕКЦИЯ УГЛА 3R0 2

ПРОЕКЦИЯ 1-ГО УГЛА

ВЫДЕЛЕНИЕ УГЛА 3-ГО УГЛА Шестиугольная призма с квадратной призмой справа

ПРОЕКЦИЯ НА ТРЕТИЙ УГОЛ Шестиугольная призма с квадратной призмой справа

Две разные шестиугольные призмы, встречающиеся под углом (F »g. 12/4)

Ф.E показывает, где углы 3 и 6 встречаются с большой призмой. На плане показано, где углы 1, 2, 4 и 5 встречаются с большой призмой, и они проецируются до F E.

12/4

УГЛОВОЕ ПРОЕКЦИЯ

12/4

УГОЛ ПРОЕКЦИИ

Шестиугольная призма, встречающаяся с восьмиугольной призмой под углом, их центр «не находится в общей вертикальной плоскости (Rg. 12/6).

F.E. показывает, где концы 6 углов 3 пересекаются с восьмиугольной призмой. На плане показано, где углы 1, 2. 4 и 5 встречаются с восьмиугольной призмой, и они спроектированы вниз до

форинтов.

Стороны шестиугольной призмы между углами 3-4 и концом 5-6 встречаются с двумя сторонами восьмиугольной призмы.Изменение формы происходит в точках а и б. Положение a и b на F.E. (а затем поперек E.E.) определяется путем проецирования вниз на F.E. через конец шестиугольной призмы (следуйте стрелкам). После этого можно будет завершить перекресток на F.E.

Прямоугольная призма, образующая квадратную пирамиду под прямым углом (Рис. 12/6)

Tha E.E. показывает, где углы 1 и 3 пересекаются с пирамидой. Они проецируются на F.E.

.

Углы 2 и 4 не так очевидны.На графическом изображении показано, как эти углы встречаются с пирамидой, если пирамида была разрезана поперек X-X. полученное сечение пирамиды будет квадратным, а точки 2 и 4 будут лежать на этом квадрате. Нет необходимости делать полный закрашенный участок на вашем чертеже, но необходимо нарисовать квадрат на плане. Поскольку точки 2 и 4 лежат на этом квадрате, их точное положение легко найти. EE на план. Точки, где эти проекторы встречаются с квадратом, являются точными положениями пересечения углов 2 и 4 с пирамидой.

Квадратная пирамида и • шестиугольная призма с

F.E. показывает место пересечения углов 1 и конца 4 с пиримидой.

Углы 2 и A лежат в одной плоскости X-X Если эта плоскость очерчена на виде сверху пирамиды (следуйте стрелкам), то получится линия X-X-X Углы 2 и 8 лежат на этой плоскости; их точное положение показано на рисунке

Углы 3 и конец 5 лежат в одной плоскости Y-Y. На виде сверху эта плоскость видна как выступ Y-Y-Y (следуйте стрелкам) На этой плоскости лежат выступы 3 и 5; их руководящие должности показаны на рисунке.

Два одинаковых цилиндра «встречаются под прямым углом» (Рис. 12/8)

Меньший цилиндр разделен на 12 равных секторов на F E. и на плане (E.E. показывает, как они расположены вокруг цилиндра).

На плане показано, где три сектора встречаются с цилиндром лергера, и эти пересечения спроектированы вниз до конечной точки, чтобы встретиться с их соответствующим сектором в 12 «. 3 ‘и т. Д.

ПРОЕКЦИЯ ТРЕТИЙ УГОЛ

Два разнородных цилиндра «встречаются под углом» (Рис. 12/9)

Метод такой же, как и в последней задаче.Меньший цилиндр разделен на 12 равных секторов на F.E. и на плане

.

На плане показано, где эти секторы встречаются с большим цилиндром, и эти пересечения проецируются до F.E., чтобы встретиться с соответствующими им секторами в точке 1 *. 2 ‘. 3 \ и т. Д.

Два разных цилиндра «встречаются под углом, их центры» не находятся в одной вертикальной плоскости (Рис. 12/10)

Onca, опять же, метод идентичен предыдущему примеру. Меньший цилиндр разделен на 12 равных секторов на F.E и на плане

На плане показано, где «сектора встречаются с большим цилиндром, и эти пересечения проецируются вниз до F.E, чтобы встретиться с соответствующими секторами в точке 1 ‘. 2 ‘, 3’. и т. д.

Цилиндр, пересекающий квадратную пирамиду под прямым углом

F.E. показывает, где точки 1 и 7 пересекаются с пирамидой, и они проецируются вниз по плану.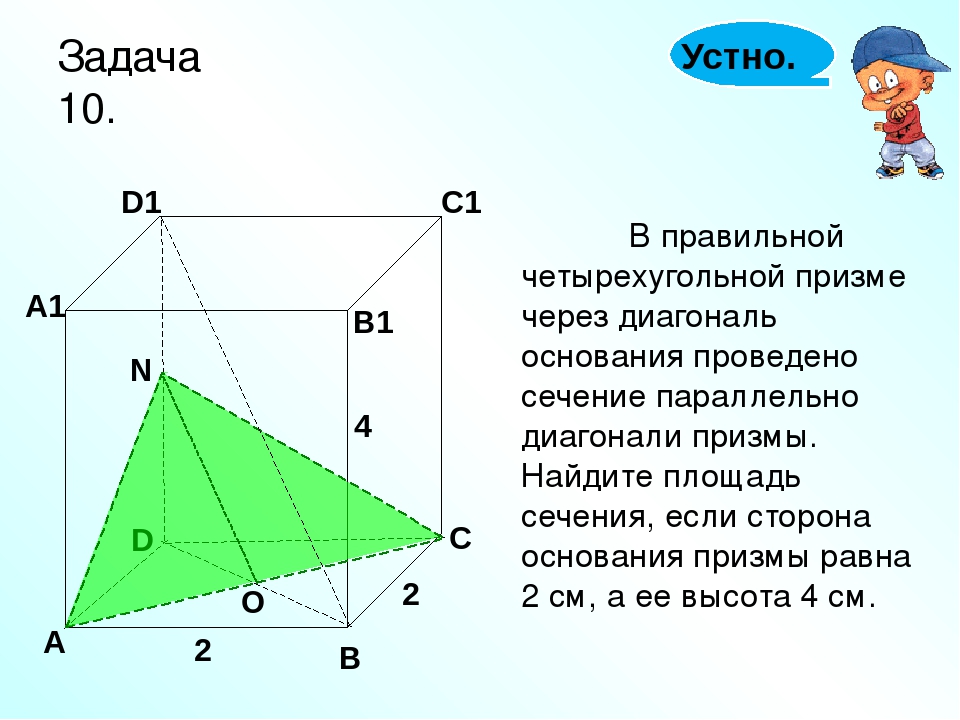

Рассмотрим положение точки 2. Поскольку цилиндр и пирамида проникают друг в друга, точка 2 лежит как на цилиндре, так и на пирамиде.Его положение на цилиндре видно довольно легко. На F.E. он лежит на линии, обозначенной 2.12, а на плане — на линии, обозначенной 2.6. Его положение на пирамиде не так очевидно. Представьте, что на F.E. часть пирамиды, которая находится над линией 2.12, была удалена. Сечение, полученное поперек пирамиды, будет квадратом, а точка 2 будет лежать где-то по периметру этого квадрата. Нет необходимости строить полное заштрихованное сечение поперек пирамиды на линии 2.12, но квадрат, который образовался бы в результате такого сечения, построен на плане. На рис. 12/11 это обозначено как «SQ 2.12». Поскольку точка 2 лежит где-то вдоль линии 2.6 (в плане), то ее точное положение находится на пересечении квадрата и прямой. На плане это обозначено как 2 ‘.

Точка 12 ‘- пересечение того же квадрата и линии 8.12 (в плане).

Процесс Thia повторяется для каждой точки по очереди. Когда пересечение будет завершено на плане, несложно спроецировать точки на F.E. конец нарисуйте пересечение.

ПРОЕКЦИЯ НА 1-Й УГОЛ

Рис. 12/11

ПРОЕКЦИЯ НА 1-Й УГОЛ

Цилиндр, пересекающий квадратную пирамиду под углом (Рис. 12/12)

F.E. показывает, где точки 1 и 7 пересекаются с пирамидой, и они проецируются вниз по плану.

Рассмотрим положение точки 2. На F.E она лежит где-то вдоль линии, обозначенной 2.12, тогда как в плане она лежит на линии, обозначенной 6.2. Если та часть пирамиды над чертой.2.12 в F.E. убрали, точка 2 лежала бы по периметру получившегося сечения. Этот периметр можно нарисовать на плане и. на рис. 12/12 он показан как линия, обозначенная «РАЗДЕЛ 2.12». Точка 2 должна лежать на этой линии: она также должна находиться на линии, обозначенной 6.2, и ее точное положение совпадает с пересечением этих двух линий.

Точка 12 ‘является пересечением той же линии сечения и линии, обозначенной 8.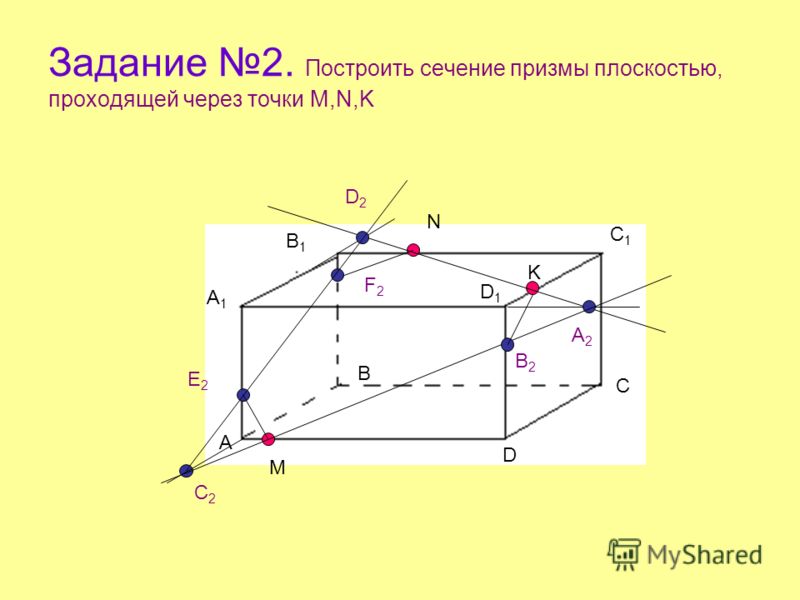 12.

Этот процесс повторяется по очереди для каждой точки. Когда план завершен, перекресток можно спроецировать на два других вида.Для ясности эти проекции не показаны.

1-Й УГОЛ

Цилиндр встречает шестиугольную пирамиду под углом

Онка снова показывает линии на плане, которые представляют периметры секций, взятых на F.E. на линиях 1; 2. 12; 3. 11. и т. Д. Все линии построения на рис. 12/13 служат для определения периметров этих сечений.

Линия mterpe net пайков. Первое, что нарисовано на плане, это пересечение линии 1.7 с участком 1. Линия 2.6 с ответом 2.12 (дает балл 2 *). строка 3.5 с разделом 3.11 (дает пункт 3 *), строка 4 с разделом 4.10. пр.

Когда пересечение завершено на плане, его можно спроецировать на два других фасада. Эти выступы не показаны.

Цилиндр встречается с конусом, конус охватывает цилиндр (рис. 12/14)

Цилиндр разделен на 12 равных секторов »на Ф.Е. и на плане.

Рассмотрим пункт 2. О F.E.Он находится где-то на линии, обозначенной 2.12, а на плане — на линии, обозначенной 2.6. Если. на F.E .. часть конуса над линией 2.12 была удалена, точка 2 будет лежать где-то по периметру полученного участка. В этом случае сечение конуса представляет собой круг, и радиус этого круга легко проецируется на план. На рис. 12/14 разрез отмечен на плане как «РАЗДЕЛ 2.12», а точное положение точки 2 — это пересечение этого разреза и линии, обозначенной цифрой 2.6. Точка 12 ‘является пересечением того же участка и линии, обозначенной 12,8

Этот процесс повторяется для каждой точки по очереди. Когда план завершен, точки могут быть спроецированы на F.E .; это не показано для cianty.

Цилиндр и конус. ни один из других

Конструкции точно такие же, как в предыдущем примере, с одним добавлением tmail.

E.E. показывает точку касания между цилиндром и конусом Эта точка проецируется на F.E. и op в плане, как показано на рисунке

Цилиндр и конус, th «цилиндр, охватывающий конус» (Рис. 12/16)

Требуемая конструкция является модифицированной версией двух предыдущих. Вместо того, чтобы разделить цилиндр на 12 равных секторов, некоторые из которых не будут использоваться, на E E выбрано несколько точек. Они отмечены в верхней части цилиндра как a. b и c, в то время как нижний поддон отмечен 1.2.3 конец 4.

Как и раньше, сечения конуса через каждую из этих точек проецируются до плана от F.E. Затем каждая точка защищается от E E., чтобы соответствовать ее соответствующему участку на плане в точках a ‘, b’. c *. 1 ‘. 2 ‘, 3 «и 4 \

Эти точки затем защищены до F.E. Для ясности это не показано.

I 1-Й УГОЛ

ПРОЕКЦИЯ

I ПЕРВЫЙ УГОЛ

Фиг.12/17

ПРОЕКТ

Цилиндр встречает полусферу (Рис. 12/18) Цилиндр разделен на 12 равных секторов на конце F.E. на плане.

Разрезы спроецированы на план с проспекта Ф.E. Плоскости сечения находятся на уровне линий 1; 2,12; 3.11; 4.10. и т. д., и эти участки отображаются на плане в виде кружков.

На плане секторы цилиндров проецируются поперек, чтобы соответствовать их соответствующему сечению в точке 1 2 ‘. 3 *. 4 ‘и т. Д.

Когда интерпетрация на плане завершена, ее можно спроецировать до F.E. Для ясности эта конструкция не показана.

Фиг.12/18

Цилиндр встречается с конусом, центры которых не находятся в одной вертикальной плоскости (рис.12/17) Разделите цилиндр на 12 равных секторов на F.E и на плане

Разрезы проецируются от ВО на план, плоскости разрезов находятся на уровне линии 1; 2,12; 3.11; 4.10. и т. д. Эти участки отображаются на плане в виде кружков. На плане секторы от цилиндра защищены поперек, чтобы соответствовать их соответствующему сечению в точках 1 ‘. 2 *. 3 ‘. и т. д. Полное взаимопроникновение можно затем спроецировать на F.E. Ради кланти. эта конструкция не показана.

ПРОЕКЦИЯ 1-Й УГОЛ

Рис.17.12.

Цилиндр, встречающийся с полусферой (рис. 12/19) Решение точно такое же, как и в предыдущем примере, за исключением того, что секции проецируются на восточно-восточную, а не на план.

КРИВЫЕ ФИЛЕ Внезапное изменение формы любого несущего компонента создает центр напряжения, то есть. область, которая подвергается большему напряжению, чем остальная часть компонента, и поэтому более подвержена разрушению под нагрузкой. Чтобы избежать этих острых углов, используются радиусы наполнителя. Эти радиусы позволяют равномерно распределять напряжение, делая компонент более прочным.

ПРОЕКЦИЯ 1-Й УГОЛ

РАДИУС ФИЛЕ

ПРОЕКЦИЯ 1-Й УГОЛ

РАДИУС ФИЛЕ

Рис.12/20

Иногда части радиусов скругления удаляются, и получается кривая пересечения. Рис. 12/20 показывает пример этого.

Секции обозначены текеном на F.E. Они отображаются на плане в виде кругов. Точки, в которых эти участки выходят за пределы плана, можно легко увидеть (в 1. 2. 3 и 4), и они проецируются до F.E., чтобы соответствовать своим соответствующим участкам

.

ПРОЕКЦИЯ ТРЕТИЙ УГОЛ

На рис. 12/21 показано, как можно использовать радиус скругления на конце накидного ключа

.

Сделаны разрезы на F.E. конец спроектирован по плану (для наглядности линии проекции разрезов не показаны). Точки, где эти участки выходят за пределы плана, легко увидеть, и эти точки (1. 2. 3. 4 и т. Д.) Спроецированы вниз до F.E, чтобы соответствовать их уважаемым участкам в 12 ‘. 3 «. А ‘и др.

ПРОЕКЦИЯ ТРЕТИЙ УГОЛ

Рис. 12/21

Чтобы найти истинную длину линии e, которая не параллельна ни одной из главных плоскостей, и найти угол, который линия образует с F.В.П. (Рис. 13/2) Линия AB. На F.V.P. он обозначен буквой ab и на H Pas a, 6 ,.

Один конец линии A остается неподвижным, в то время как B поворачивается, так что AB параллельна H P. Теперь B находится в точке B ‘и на F.V.P. b теперь находится на b ‘. Поскольку линия параллельна H.P. он будет проецировать свою истинную длину на H.P. Это отображается как axbt. Обратите внимание, что b и b находятся на одинаковом расстоянии от линии XY.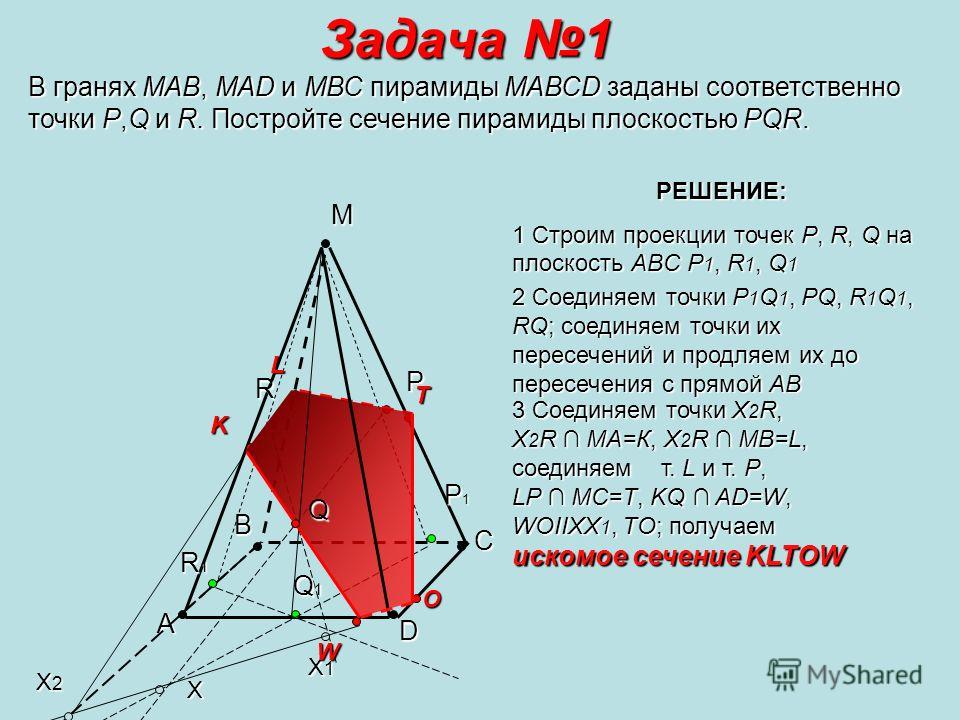

Поскольку AB ‘(и ab’) параллельны H P., угол, который AB образует с F.В.П. можно измерить Это показано как 0.

НАЧАЛЬНЫЕ УСЛОВИЯ (ABIS НЕ ПАРАЛЛЕЛЬНО ЛИБО ПЛОСКОЙ)

ENO A ПОДДЕРЖИВАЕТСЯ СТАЦИОНАРНЫМ, И B КАЧАЕТСЯ КРУГЛЫМ, ТАК, ЧТО AB ПАРАЛЛЕЛЬНО HR

ЛИНИЯ

ПРОЕКТИРУЕТСЯ ИЗ НОВОГО ПОЛОЖЕНИЯ, ЧТОБЫ ПОКАЗАТЬ ИСТИННУЮ ДЛИНУ НА KP И УГОЛ, КОТОРЫЙ ДАЕТ ЛИНИЯ С F.V.P

Чтобы узнать истинную длину линии, которая не параллельна! ®! к любой из основных плоскостей и найти угол, который соответствует линии mekei с H.P. (Рис. 13/3) Линия AB. На Ф.В.П. ¡T обозначается буквой ab, а на H.P. в виде*./»,.

Один конец линии B остается неподвижным, в то время как A поворачивается так, чтобы AB была параллельна F.V.P. А теперь находится в А ‘и. на H.P .. a теперь на # ‘. Поскольку колено теперь параллельно F.V.P. он будет проецировать свою истинную длину на F.V.P. Это показано как «¿r. Обратите внимание, что a и o находятся на одинаковом расстоянии от линии XY.

Поскольку BA- (и b, a ‘) параллельны F.V.P., англа, которую AB делает с H.P. можно замочить.Это показано как

1-Й ПРОЕКЦИЯ КОЖИ

ДЛИНА AE

ИСТИННАЯ ДЛИНА ИСТИННАЯ ДЛИНА

Рис. 13/4 представляет собой пример применения теории, показанной выше. Это показывает, насколько просто применить эту теорию.

Пилон поддерживается тремя тросами. Учитывая план и высоту хеверов. найдите их истинную длину и угол, который они образуют с землей.

В плане каждый трос поворачивается до тех пор, пока он не станет параллельным F.В.П. Новые положения концов тросов проецируются до конца F.E., присоединенного к пилону на конце A, что дает истинные длины и углы.

ИСТИННАЯ ДЛИНА ИСТИННАЯ ДЛИНА

ДЛИНА AE

Чтобы найти следы прямой по плану и высоте этой линии (Рис. 13/6) Линия AB. Если линия произведена, она пройдет через обе плоскости, оставляя следы T. и Tn.

»b производится для соответствия линии XY. Этот перекресток спроектирован вниз до точки a, b, полученной в T *.

»b производится для соответствия линии XY. Этот перекресток спроектирован вниз до точки a, b, полученной в T *.

Чтобы нарисовать алаватлон и план Una AB с учетом его * истинной длины end, расстояния между концами линии от основных плоскостей, в данном случае a, и

1. Зафиксируйте точки a и a на заданных расстояниях av и a »от линии XY. Они измеряются на общем перпендикуляре к XY.

2. Проведите линию, параллельную XY, на расстоянии b от XY.

3.С центром а. радиус равен истинной длине AB. d’aw a arc, чтобы разрезать линию, проведенную параллельно XY в C.

4. Из точки a проведите линию, параллельную XY, чтобы пересечь линию из точки C, перпендикулярную XY в 0.

5. Проведите линию, параллельную XY. расстояние b »от XY.

6. Используя центр * „радиус a.D, нарисуйте дугу, чтобы разрезать линию, проведенную параллельно XY в b ,.

7. Проведите линию от b „перпендикулярно XY до пересечения с линией, проведенной параллельно XY через точку C. b sb ​​- отметка l, линия a J> — это план линии.

Для построения плана линии AB с учетом отклонения одного конца линии от линии XY на плане (a «), истинной длины линии и отметки (Рис. 13/7)

1. Из точки b проведите линию, параллельную линии XY

2. С центром a, редиус равняется истинной длине линии AB. нарисуйте руку, чтобы разрезать параллельную линию в C.

3. Из a (данного) проведите линию, параллельную линии XY, чтобы пересечь линию, проведенную из C перпендикулярно XY в D

.

4.«’- ■ J

1 Дж

ВЫПУСК ТРЕТЬЕГО УГЛА

ПРОЕКЦИЯ ТРЕТЬЕГО УГЛА

ПРОЕКЦИЯ НА 1-Й УГОЛ

ПРОЕКЦИЯ УГЛА 3R0

ПРОЕКЦИЯ 1-Й УГОЛ

GIVEN

УГОЛ Рис. 13/9

Фиг.13/10

АЛЬТЕРНАТИВНОЕ РЕШЕНИЕ

СЛЕДЫ ПЛОСКОСТИ Y

ПРОЕКЦИЯ НА 1-Й УГОЛ

Для построения фасада линии AB по плану талины и угла, которые линия образует с горизонтальной плоскостью (рис. 13/9)

1. Нарисуйте план, а из него удалите перпендикуляр

2. С другого конца плана проведите линию под углом, заданным для пересечения перпендикуляра в C.

3. Fromb, проведите линию, перпендикулярную XY, чтобы пересечь XY в b. 4 От точки a проведите линию, перпендикулярную XY, и отметьте

XYto * равно a.c ab ia требуемому элевагону. Признак Решение, которое указано.

УГОЛ Рис.13/9

3R0 УГЛОВОЕ ПРОЕКЦИЯ

ДАННЫЙ

Рис.13/10

АЛЬТЕРНАТИВНОЕ РЕШЕНИЕ

Чтобы нарисовать всю длину линии AB с учетом выдвижения линии и угла, который линия образует с плоскостью вершины Icel (Рис. 13/10).

Эта конструкция очень похожа на предыдущую, и ее можно проследить из инструкций, приведенных для этого примера.

СЛЕДЫ САМОЛЕТА Y

НАКЛОННАЯ ПЛОСКОСТЬ

Определение

Наклонная плоскость наклонена к двум основным плоскостям и перпендикулярна третьей.

На рис. 13/11 показана прямоугольная плоскость, обращенная к H.P. конец E.V.P. конец перпендикулярен F.V.P. Поскольку он перпендикулярен F.V.P .., истинный угол между наклонной плоскостью и H P. может быть измерен на F.V.P. Это угол 4-

ПРОЕКЦИЯ САМОЛЕТА Рис. 13/11

ПРОЕКЦИЯ САМОЛЕТА

На верхнем рисунке показаны следы самолета после рабатмента. На нижнем рисунке показана полная проекция самолета. Должно быть очевидно, как получается полная проекция, если вам даны трассы и скажут, что плоскость прямоугольная

Рис.13/12 показано треугольное пианино, наклоненное к F.V.P. и E.V.P .. и перпендикулярно H.P. Поскольку он перпендикулярен H.P .. истинный угол между наклонной плоскостью и F.V.P. можно измерить на H P. Этот угол равен $.

ПРОЕКЦИЯ НА ТРЕТИЙ УГОЛ

Еще раз, должно быть очевидно, как полная проекция наклонной плоскости получилась, если вам дали трассы и сказали, что плоскость треугольная.

СЛЕДЫ САМОЛЕТА м *

Рис 13/12

ПРОЕКЦИЯ САМОЛЕТА

Определение истинной формы наклонной пленки Если наклонная плоскость повернута так, что она параллельна одной из базовых плоскостей, истинная форма может быть защищена на Рис. 13/13.план самолета. HT переключается на HT. Истинную форму самолета затем можно нарисовать на F V.P.

ПРОЕКЦИЯ ТРЕТИЙ УГОЛ

СЛЕДЫ САМОЛЕТА

Рис. 13/15

Фиг.13/14

УГЛОВОЕ ПРОЕКЦИЯ 3RO

СТОРОНА A

Рис 13/15

ПРОЕКЦИЯ САМОЛЕТА

ПОВОРОТНЫЙ САМОЛЕТ

Определение

Косая плоскость — это плоскость, которая наклонена ко всем основным плоскостям

Рис.13/15 показана четырехугольная плоскость, наклоненная ко всем основным плоскостям.

ПРОЕКЦИЯ ТРЕТИЙ УГОЛ

Фиг.13/14

На Рис. 13/14 показан пример. На его основании стоит косая усеченная прямоугольная пирамида. Задача состоит в том, чтобы найти истинную форму сторон A и B

В F.E сторона A повернута вертикально, и ее вертикальная высота проецируется поперек E E., откуда можно нарисовать истинную форму стороны A.

На восточной стороне сторона B повернута вертикально и проецируется на F.E. где нарисована истинная форма

СЛЕДЫ САМОЛЕТА

УГЛОВОЕ ПРОЕКЦИЯ 3RO

СТОРОНА A

3. На фиг. 3 показана высота линии AB, истинная длина которой составляет 100 мм. Конец B линии находится на 12 мм впереди V P; конец A также находится перед V P. Нарисуйте план и высоту этой линии, определите и укажите ее V.T и H.T. Измерьте, укажите и укажите угол наклона линии к H P. Совместная регистрационная доска

Рис 3

Рис 3

РАЗМЕРЫ В ММ

РАЗМЕРЫ В ММ

4.Линия AB истинной длины 88 мм лежит во вспомогательной вертикальной плоскости, которая составляет угол 30 ° с вертикальной плоскостью. Линия наклонена под углом 45 ° к горизонтали, точка B является самой низкой на расстоянии 12 мм от горизонтальной плоскости и 12 мм перед вертикальной плоскостью. Нарисуйте план и отметку AB и четко обозначьте Их на чертеже. Ассоциированная экзаменационная комиссия

7. Проекции треугольника RST показаны на рис. 6. Определите истинную форму треугольника. Ассоциированная экзаменационная комиссия

:. План и высота двух прямых показаны на рис. 7. Найдите истинные длины линий, истинный угол между ними и расстояние между A и C

.

Объединенный совет Южных университетов

5. План линии длиной 82 мм показан на рис. 4. Отметка одного конца — на b ‘. Завершите подъем и измерьте наклоны bne к H P. и V P.

Экзамены Лондонского университета

я
ф			Рис 4 РАЗМЕРЫ Н мм 6.На рис. 5 показан план конца A линии AB. Конец A находится в плоскости H.T.V. Конец B находится в H P. Линия AB перпендикулярна плоскости H.T.V. Нарисуйте план и отметку AB. Объединенная доска регистрации (H.V.T. = горизонтальные концевые вертикальные следы) I На рис. 8 показан вид в плане и в вертикальной плоскости треугольной пластинки. Нарисуйте эти два вида и. определив истинную длину каждой стороны, нарисуйте истинную форму пластинки. Измерьте и укажите три угла с точностью до градуса. Экзаменационная комиссия школ Оксфорда и Кембриджа Рис 8 Рис 8 РАЗМЕРЫ В ММ РАЗМЕРЫ В ММ 10.На рис. 9 показаны высота и план треугольника ABC. Определите истинную форму и размер треугольника Университет Лон-Донской школы Экзамены 11. На рис. 10 показаны два вида наклонной треугольной пирамиды, стоящей на ее основании. Нарисуйте данный вид вместе с дополнительным видом, смотрящим в направлении стрелки A, которая перпендикулярна BC. Также нарисуйте истинные формы сторон пирамиды. пирамида. Примечание. Не указывайте размеры, но показывайте скрытые детали на всех видах. Масштаб: полный. Оксфордские местные экзамены (информацию не в главе 13 см. В главе 10) Рис 10 Рис 10

Читать дальше: События

Была ли эта статья полезной?

Трехмерные фигуры

Трехмерные фигуры Вернуться к содержанию

Обзор базовой геометрии — Урок 9

Обзор урока

Плоскости: параллельные, перпендикулярные и прочие

Точка, линия и плоскость — неопределенные термины.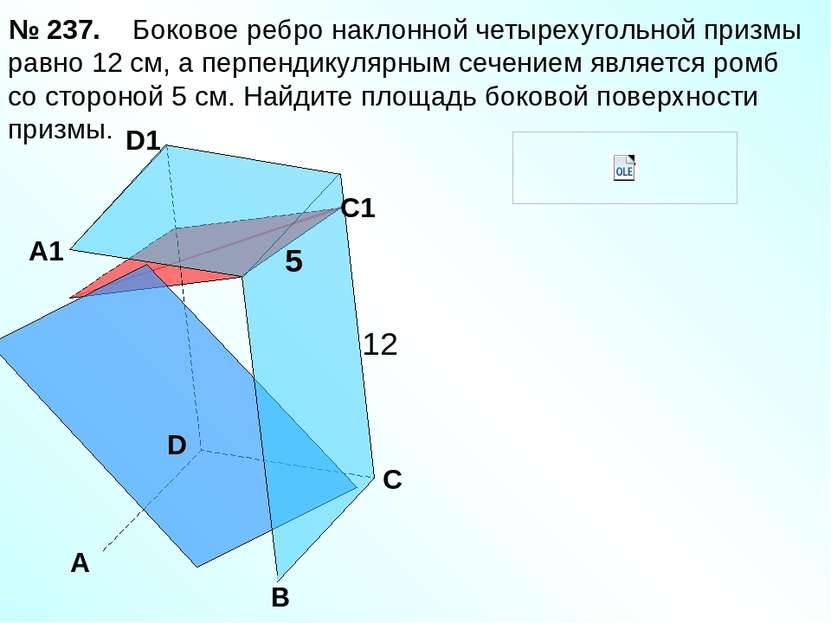 Несколько предположений были сделаны о них через постулат точка-линия-плоскость в уроке 1. Для самолетов мы должны добавить еще три предположения ниже.

Допущение плоской плоскости: Если две точки лежат на плоскости, линия, содержащая их, лежит в плоскости. Допущение уникальной плоскости: Через три неколлинеарных точки, есть ровно один самолет. Пересекающиеся плоскости Допущение: Если две разные плоскости имеют общую точку, то их пересечение является линией.

Самолеты не имеют неровностей и вечны, как линии. Три (неколлинеарные) точки определяют плоскость. Также определяют три точки: треугольник; линия и точка не на линии; и две пересекающиеся линии. Ровно один самолет содержит их. Таким образом, стул на трех ножках стабилен, но большее количество ножек может вызвать стул качаться. Поскольку линии не имеют толщины, плоскости также не имеют толщины. Линия, не лежащая на плоскости, может пересекать плоскость не более чем в одной точке.

Мера наименьшего из всех возможных углов определяет угловая мера между линией и плоскостью.

Если линия l пересекает плоскость X в точке P , то линия l перпендикулярна плоскости X ( л X ) тогда и только тогда, когда l перпендикулярно каждой линии в X , которая содержит П .

Теорема о прямом и плоскости перпендикуляра: Если линия перпендикулярна двум разным линиям в их точке пересечения, то он перпендикулярен плоскости, содержащей эти прямые.

Две плоскости равны параллельным плоскостям тогда и только тогда, когда у них нет точек общие или они идентичны. Опять же, это всеобъемлющее определение не используется повсеместно. Расстояние между параллельными плоскостями — это длина сегмента перпендикулярно плоскостям с концами в каждой плоскости.Измеряется расстояние между плоскостью и точкой не на ней. по перпендикулярному отрезку от точки к плоскости.

При пересечении двух плоскостей образуются четыре двугранных угла . Меру этих углов можно указать, построив лучей, перпендикулярных линии пересечения, и измеряя те углы образовались. Косые линии — это некомпланарные линии, которые не пересекаются.

Так же, как есть разница между многоугольником и многоугольной областью, мы различаем поверхность трехмерной фигуры и пространство он включает.С этого мы начинаем твердую геометрию . Коробка , поверхность прямоугольного твердого тела , или параллелепипед — одна из важнейших трехмерных фигур. Коробка имеет шесть граней , каждая из которых представляет собой прямоугольную область. Противоположные грани лежат в параллельных плоскостях. Куб — это прямоугольник с квадратными областями всех граней. Края — это линейные сегменты, где грани пересекаются. Концами ребер являются вершины .Коробка имеет 12 ребер и 8 вершин. На рисунке справа показано типичное двухмерное изображение. а также Тессерак или гиперкуб — четырехмерный аналог куба. На рисунке слева показано двухмерное представление этого четырехмерного объекта. Более подробную информацию о них можно найти видел и нашел. Многие люди с трудом верят, что такое может существовать, поэтому такие книги, как Плоская земля (Эбботт, 1884 г.), Sphereland (Бюргерс, 1983), и Флаттерленд (Стюарт, 2001) были написано.

Цилиндрические твердые тела / поверхности: призмы и цилиндры

Цилиндрическое тело — это набор точек между областью и его переводное изображение в пространстве, включая регион и его изображение. Цилиндрическая поверхность является границей цилиндрического твердого тела. Цилиндр — это поверхность цилиндрического твердого тела с круглым основанием. Призма представляет собой поверхность цилиндрического твердого тела с многоугольным основанием.

Цилиндрические твердые тела имеют два основания , которые конгруэнтны и параллельны плоскостям. Поверхность, исключая основания, известна как боковая поверхность . Высота или высота — это расстояние между плоскостями. баз. Если вектор трансляции перпендикулярен плоскостям основания, цилиндрическое тело представляет собой правый цилиндр или правую призму , в противном случае это косой .Призмы названы по форме их база. Неосновные грани призмы известны как боковые грани , которые встречаются у боковых кромок . Правая призма, основание которой — правильный многоугольник представляет собой обычную призму .

Конические тела / поверхности: пирамиды и конусы

Коническое тело — это набор точек на любом сегменте между областью (основание ) и точка (вершина ) не в плоскости база. Коническая поверхность является границей конического твердого тела. Пирамида — это поверхность конического твердого тела с многоугольным основанием. Конус — это поверхность конического твердого тела с круглым основанием.

Конические тела имеют только одно основание . Пирамиды имеют боковых ребра, соединяющих вершины основания. многоугольник с вершиной . В конусе боковой кромкой является любой отрезок. конечными точками которого являются вершина и точка на основной окружности.Треугольные, неосновные грани пирамиды — это боковые грани . Пирамиды и конусы также могут быть правыми или наклонными . Правая пирамида с правильным многоугольным основанием тоже правильная . Конус также имеет ось , которая является линия (не сегмент) через вершину и центр основания. Высота коники — это расстояние между вершиной и вершиной. самолет, содержащий базу. В правильной пирамиде наклонной высоты высота любой боковой грани (треугольника).Только в правом конусе она равна длине бокового края. Конус или пирамида могут быть усеченными — многие стаканы усеченные конусы. Усеченный конус тоже известен как усеченная пирамида .

Сферы и прочие предметы круглые

Сфера — это набор точек в пространстве на определенное расстояние ( радиус ) от точки ( центр ).

Сферы имеют нулевых основания .Сферу можно рассматривать как трехмерный аналог круга. Дважды радиус составляет , диаметр . Hypersphere или 4-ball — это четырехмерный аналог сферы. (Аналог намеренно пишется по-другому, но здесь тоже правильно.) Шар (круг, сфера, гиперсфера) размером n называется шаром n .

Плоское сечение трехмерной фигуры — это пересечение этой фигуры с плоскостью.

Сфера и плоскость могут пересекаться очень немногими способами. Во-первых, самолет мог касайтесь сферы только в точке. Эта плоскость должна быть касательной в этой точке. таким образом линия, содержащая центр сферы и точку пересечение будет нормальным (перпендикулярным) к плоскости. Во-вторых, плоскость пересекается более чем в одной точке, и в этом случае пересечение это круг. Это пересечение называется маленьким кругом . если плоскость не содержит центр круга, в этом случае он известен как большой круг .Большие круги делят сферы на полушария , буквально полусферы. Маршруты большого круга очень важны в навигации, потому что они содержат кратчайшее расстояние между двумя точками на поверхности. Геодезическая — это общий термин для кратчайшего расстояния между двумя точками. Метрика — это термин из общей теории относительности. Так мы измеряем пространство-время. В терминах дифференциального исчисления это: dx ² + dy ² + dz ² — c ² dt ² . Antipode с точностью до наоборот или наоборот; также точки сферы, такие как земля, которые диаметрально противоположны (противоположные концы диаметра).

Земля представляет собой сплюснутый сфероид (в форме M & M, т.е. сплюснутый на полюсах). и из трех взаимно перпендикулярных радиусов повторяется тем длиннее). Вытянутый сфероид больше похож на футбольный мяч или сигару (из трех взаимно перпендикулярных радиусов повторяется тем короче).В эллипсоиде три взаимно перпендикулярных радиуса имеют разную длину. Посмотреть этот сайт для некоторых диаграмм и определений, в том числе тор или пончик.

Гипотеза Кеплера

К 1606 году Кеплер начал работу над тем, что стало известно как Гипотеза Кеплера после получения письма от Харриота которые работали над проблемой не менее 15 лет. Сэр Уолтер Рэли фактически предложил это своему помощнику Харриоту.Проблема заключается в наиболее эффективном расположении упаковки. для пушечных ядер или, в конечном счете, атомов в кристалле, хотя тогда о строении атома было мало что известно. В конце концов Кеплер предположил, что гранецентрированная кубическая (FCC) [и эквивалентно гексагональная плотная упаковка (HCP)] оба дали оптимальную плотность упаковки сфер. В конце концов, эта проблема стала частью C проблемы 18 Гильберта. Знаменитый список из 23, созданный в 1900 году. До 1990-х годов это оставалось одним из последних нерешенные проблемы дискретной геометрии. В 1990 г. У-И Сян разослал препринты, а в 1992 г. представил для публикации 100-страничное доказательство, которое осталось неприемлемым в математическом сообществе из-за его нечеткость и отсутствие логической прогрессии. Хотя он был опубликован в International Journal of Mathematics , у некоторых есть «сомнения в серьезности судейства» поскольку « Journal редактируется коллегами Сяна из Беркли». Это «нельзя считать доказательством».» ( Гипотеза Кеплера , Джордж Спиро, 2003, стр. 150.) Примерно в 1996 году Хейлз начал противоречивое доказательство, которое следует вычислительный подход. 9 августа 1998 г. Сэм Хейлз объявил доступность статей и препринтов, доказывающих гипотезу Кеплера. В январе 1999 г. недельный семинар, посвященный исключительно гипотезе Кеплера. был проведен в Институте перспективных исследований в Принстоне, где эксперты чистил его со всех сторон. Они требовали публикации в Анналы математики .В конечном итоге он был (будет?) Опубликован, но с беспрецедентным отказом от ответственности, что судьи не могут проверить доказательство.

Конические секции

Nappes является множественным числом от Nappe . Конус называется двойным, если мы говорим о полном конусе. который больше похож на песочные часы или на две «круговые пирамиды» соединились в их вершинах. Одиночная «пирамида с круговым основанием» — это то, что большинство студентов подумают как конус.

Выше показано пересечение плоскости с конусом — двойным ворсанный конус. Эти локуса (наборы точек) представляют собой конические секции. Loci имеет множественное число для , локус (набор точек). Эти конические сечения ( круг , эллипс , парабола , и гипербола ) будут изучены более подробно в алгебре II. См. Эту веб-страницу для получения более подробной информации.

Платоновы тела

Платоново тело — это выпуклые многогранники с все грани одинаковые многоугольники. Как показано ниже, их ровно пять.

Платоновы тела также известны как правильные многогранники. Тетраэдр также известен как треугольная пирамида . Шестигранник также известен как куб . Дуалы особенно важны в кристаллографии, где рассеянное излучение (электроны, нейтроны, рентгеновские лучи) лучше всего изучать в обратном пространстве. Глядя на приведенную выше таблицу, подумайте о формуле Эйлера который связывает количество граней, вершин и ребер любых многогранников: F + V = E + 2.

Нетрудно показать, что правильных многогранников всего пять. (выпуклый и грани все тот же правильный многоугольник). Подумайте, сколько одинаковых правильных многоугольников может сойтись в одной вершине. Нам всегда нужно больше двух, если мы собираемся сложить его и оградить любое пространство. Для треугольников (с углом 60 °) шесть составят мозаику плоскости. Следовательно, необходимо учитывать три, четыре и пять, и результаты могут быть рассматриваемый выше как тетраэдр, октаэдр и икосаэдр.Для квадратов (с углом 90 °) четыре будут разбивать плоскость мозаикой. Следовательно, нужно рассматривать только три, и куб является результатом. Для пятиугольника (с углом 108 °) четыре превышают 360 °. Следовательно, нужно рассматривать только три, и в результате получается додекаэдр. Три шестиугольника (с углом 120 °) образуют мозаику на плоскости. Таким образом, мы исчерпали все возможности, в результате чего получилось пять правильные многогранники или платоновы тела.

Эта ссылка ведет на страницу с описанием пяти платоновых тел с цветные фигурки.Этот сайт есть твердые тела, которые можно вращать. Этот сайт ссылки на многие другие хорошие сайты. Древние связывали пять платоновых тел с огнем (4), землей (6), воздух (8), вода (20) и космос (12).

Твердые тела Архимеда

В твердом теле Архимеда твердое тело выпуклое, все вершины идентичны, все грани — правильные многоугольники, но не все одинаковые.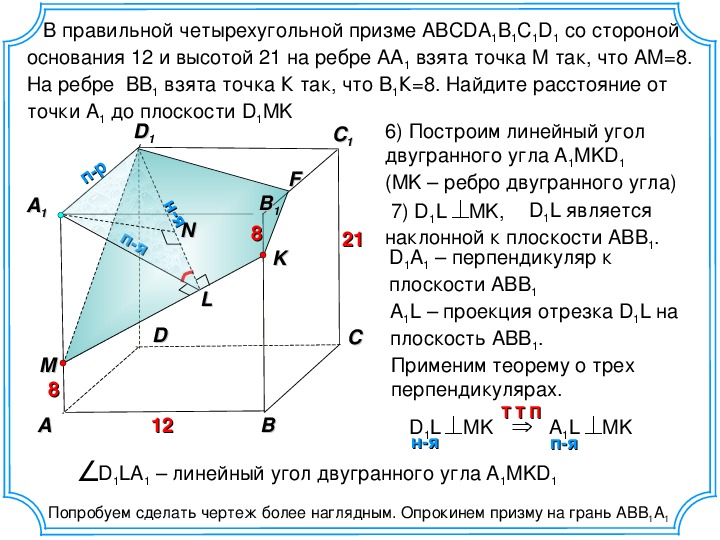

Твердые тела Архимеда можно классифицировать по набору чисел, который указывает количество сторон многоугольников в каждой вершине.Таким образом, {3,6,6} будет обозначать один треугольник и два шестиугольника в каждой вершине. Остальные двенадцать: {3,8,8}; {4,6,6}; {3,10,10}; {5,6,6}; {3,3,4,4}; {3,3,5,5}; {3,4,4,4}; {4,6,8}; {3,4,4,5}; {4,6,10}; {3,3,3,3,4}; и {3,3,3,3,5}. Эта (неработающая) ссылка ведет на страницу с описанием тринадцати архимедовых или полурегулярных тел, в комплекте с цветными фигурами.

C ₆₀ — высокосимметричная молекула чистого углерода. Форма такая же, как у футбольного мяча или Archimedian Solid усеченный икосаэдр: {5,6,6}.C ₆₀ часто обозначается как Buckyballs. Технически это твердое тело Архимеда представляет собой усеченный изокаэдр . Это имя происходит от имени Ричарда Бакминстера Фуллера, известен своими геодезическими куполами. Степан центр в Нотр-Дам является местным примером. C ₆₀ является одним из класса известных соединений как фуллерены также называют в честь американского архитектора выше. Молекула C ₆₀ была открыта в 1985 году, когда группа пытался понять спектры поглощения межзвездной пыли.Их работа принесла им Нобелевскую премию по химии 1996 года. Изначально производился в очень малых количествах или извлекался из сажи. теперь доступен и является центром множества разнообразных исследований. Длинные углеродные трубки называются нанотрубки также были произведены. C ₆₀ представляет собой новую, неожиданную кристаллическую форму твердого углерод. Другие формы: тетраэдрическая углеродная связь в алмазе. и соединение листового типа в графите имеет гораздо более долгую историю.Видеть На этой странице представлена ​​краткая, хорошо задокументированная история C ₆₀ .

Пентамино

Пентамино.

Мои исследовательские интересы связаны с утроением пентамино из подмножество 9 из 12. Можете ли вы утроить все 9 в наборе или даже все 12? Можете ли вы втрое повторить данное пентамино со всеми 220 подмножествами?

Симметрия, виды и сети

Отражения меняют ориентацию, таким образом, как двумерные фигуры, трехмерные фигуры могут также быть прямо конгруэнтным или противоположно конгруэнтным .Это особенно важно в органической химии, где ориентация из четырех связей вокруг углерода (тетраэдр) имеет решающее значение для жизни. Посмотри это ссылка для получения дополнительной информации (загрузить плагин звонка). Я думал, что в последние годы была распространена диетическая добавка с обоими изомерами, и много людей погибло, но триптофан похоже, в конечном итоге возникла другая (димерная) проблема.

Архитекторы часто рисуют в масштабе вида или планы зданий.Некоторые могут назвать эти отметками . Этот сайт есть сети для многих твердых тел и другие лакомые кусочки.

Сетка — это двухмерная фигура, которую можно сложить на сегменты или изогнутый на своих границах в трехмерную поверхность.

Раскраска карты

http://www.ams.org/notices/199807/thomas.pdf Сколько цветов необходимо и сколько цветов достаточно, чтобы раскрасить любую карту на плоскости? На сфере (4)? На ленте Мебиуса (6)? На торе (7)? Карты с границами, состоящими только из прямых или окружностей может понадобиться еще меньше цветов! (Смотрите рисунок справа.) За исключением плоскости / сферы, эти вопросы были легко ответить.

Как и сеть, карта представляет собой двумерное приближение для трехмерной фигуры. Когда это карта земли, часто встречаются различные искажения. Если вы взяли глобус и разрезали его примерно через каждые 15 ° долготы, Полученные клинья (см. рисунок слева) могут быть уложены плашмя. Это было бы довольно точно, но довольно неудобно — разные части одна и та же страна будет на разных глубинах и фактической форме этих стран трудно увидеть. Исторически сложилось так, что проекция Меркатора , созданная обычно используется фламандский картограф 1569 года. Особенно искажены участки земли у полюсов, что приводит к Африка (11 миллионов миль ² ) размером с Гренландию (менее 1 миллиона миль ² ). Это происходит потому, что проекция Меркатора на самом деле является чистой для цилиндра, а не для сферы. Преобразование может быть сгенерировано расширением лучи из центра Земли на боковую грань цилиндра.Как указано выше, это преобразование не является изометрией. Однако он сохраняет промежуточность и коллинеарность, по линиям долготы и широты. Таким образом, четыре направления (север, юг, восток и запад) находятся на перпендикулярных линиях.

Изучив карты, Фрэнсис Гатри в 1852 году предположил, что любой карту на сфере или плоскости можно выделить / раскрасить всего четыре цвета. Нетрудно заметить, что необходимы четыре цвета (см. Справа).Однако доказательство достаточности части было завершено только в 1976 году. Даже тогда доказательство, предоставленное Хакеном и Аппелем , было спорным. на протяжении многих лет. Споры возникли из-за того, что они использовали компьютер чтобы доказать, что нужны были только четыре цвета для каждого из 1952 типов возможных карт. Проблема была встроена в теория графов перед этим анализом.

Теорема о четырех цветах . Предположим, что области, имеющие общую границу некоторой длины, должны иметь разные цвета.Тогда любая карта регионов на плоскости или сфере может быть раскрашенным таким образом, чтобы потребовалось всего четыре цвета. Предположено Гутри в 1852 году; доказано Хакеном и Аппелем в 1976 г.

Ниже представлен раздаточный материал для домашнего задания 9.8 №26. (Где-то добавить угол наклона / угол наклона и график для двугранных углов.)

Назовите различные формы плоскости, необходимые для рисования математики класса 8 CBSE

Подсказка: Здесь мы используем концепцию плоских форм, которые представляют собой просто двухмерные фигуры, которые могут быть составлены из прямых линий или кривых или как прямых линий, так и кривой.
Некоторые основные плоские формы: Треугольник, Квадрат, Круг и т. Д.

Полный пошаговый ответ:
(i) Треугольная призма
Мы знаем, что треугольная призма выглядит вот так

Мы ясно видим, что оба слева и правая грань треугольной призмы имеют форму треугольника, которые обозначены треугольниками \ [\ vartriangle ABC, \ vartriangle DEF \]
Кроме того, основание и две другие стороны в форме прямоугольника участвуют в создании призмы, как это это площадь между двумя треугольниками.
Итак, прямоугольники \ [ACFD, ABED, BCEF \] — это три прямоугольника.
Следовательно, плоские формы, используемые для построения сети треугольной призмы, — это Треугольник и Прямоугольник.

(ii) Конус
Мы знаем, что конус выглядит так.

Мы можем ясно видеть, что основание конуса имеет круглую форму с диаметром \ [AB \].
Кроме того, криволинейная поверхность наверху образована сектором \ [ACB \], который сложен таким образом, чтобы концы сторон пересекались друг с другом.
Следовательно, плоские формы, используемые для рисования сети конуса, — это Круг и Сектор.
(iii) Квадратная призма
Мы знаем, что квадратная призма выглядит так

Мы ясно видим, что и верхняя, и нижняя грани квадратной призмы имеют квадратную форму, которая обозначена квадратами \ [ABCD, EFGH \]
Также четыре стороны сферической призмы имеют форму прямоугольника.

Итак, прямоугольники \ [ABGH, ADEH, DEFC, BCFG \] — это четыре прямоугольника.
Следовательно, плоские формы, используемые для рисования сетки квадратной призмы, — это квадрат и прямоугольник.

Примечание: Ученики много раз делают ошибки при нахождении плоских форм в конусах и пишут треугольники вместо секторов, что неправильно, потому что коническая часть изогнута, и если мы изогнем треугольник, он не образует конуса.

6.2: Определение объемов путем нарезки

В предыдущем разделе мы использовали определенные интегралы, чтобы найти площадь между двумя кривыми. В этом разделе мы используем определенные интегралы для определения объемов трехмерных тел. Мы рассматриваем три подхода — нарезку, диски и шайбы — для нахождения этих объемов в зависимости от характеристик твердого тела.2ч \]

\ [V_ {pyramid} = \ dfrac {1} {3} Ah \]

также были представлены. Хотя некоторые из этих формул были получены с использованием только геометрии, все эти формулы можно получить с помощью интегрирования.

Мы также можем рассчитать объем цилиндра. Хотя большинство из нас думает, что цилиндр имеет круглое основание, такое как консервная банка или металлический стержень, в математике слово цилиндр имеет более общее значение. Чтобы обсудить цилиндры в этом более общем контексте, нам сначала нужно определить некоторый словарь.

Мы определяем поперечного сечения твердого тела как пересечение плоскости с твердым телом. Цилиндр определяется как любое твердое тело, которое может быть создано путем перемещения плоской области вдоль линии, перпендикулярной области, называемой осью цилиндра. Таким образом, все поперечные сечения, перпендикулярные оси цилиндра, идентичны. Твердое тело, показанное на рисунке \ (\ PageIndex {1} \), является примером цилиндра с некруглым основанием. Чтобы вычислить объем цилиндра, мы просто умножаем площадь поперечного сечения на высоту цилиндра: \ (V = A⋅h.2ч. \)

Рисунок \ (\ PageIndex {1} \) : Каждое поперечное сечение одного цилиндра идентично другим.

Если твердое тело не имеет постоянного поперечного сечения (и не является одним из других основных твердых тел), у нас может не быть формулы для его объема. В этом случае мы можем использовать определенный интеграл для вычисления объема твердого тела. Мы делаем это, разрезая твердое тело на части, оценивая объем каждого фрагмента, а затем складывая эти предполагаемые объемы вместе. Срезы должны быть параллельны друг другу, и когда мы сложим все кусочки вместе, мы должны получить цельное тело. Рассмотрим, например, твердое тело S, показанное на рисунке \ (\ PageIndex {2} \), продолжающееся вдоль оси \ (x \) .

Рисунок \ (\ PageIndex {2} \): твердое тело с переменным поперечным сечением.

Мы хотим разделить \ (S \) на срезы, перпендикулярные оси \ (x \) . Как мы увидим позже в этой главе, могут быть моменты, когда мы хотим разрезать твердое тело в каком-то другом направлении, например, срезами, перпендикулярными оси \ (y \). Решение о том, как разрезать твердое тело, очень важно.Если мы сделаем неправильный выбор, вычисления могут стать довольно запутанными. Позже в этой главе мы подробно рассмотрим некоторые из этих ситуаций и посмотрим, как решить, каким образом разрезать твердое тело. Однако для целей этого раздела мы используем срезы, перпендикулярные оси \ (x \) .

Поскольку площадь поперечного сечения непостоянна, мы позволяем \ (A (x) \) представлять площадь поперечного сечения в точке x. Пусть теперь \ (P = {x_0, x_1…, X_n} \) — регулярное разбиение \ ([a, b] \), и для \ (i = 1,2,… n \) пусть \ (S_i \) представляют собой срез \ (S \), простирающийся от \ (x_ {i − 1} \) до \ (x_i \).б А (х) \, dx. \]

Техника, которую мы только что описали, называется методом нарезки. Чтобы применить его, мы используем следующую стратегию.

Стратегия решения проблем: поиск объемов методом нарезки

1. Изучите твердое тело и определите форму поперечного сечения твердого тела. Часто бывает полезно нарисовать рисунок, если он не предоставлен.
2. Определите формулу площади поперечного сечения.
3. Интегрируйте формулу площади по соответствующему интервалу, чтобы получить объем.

Напомним, что в этом разделе мы предполагаем, что срезы перпендикулярны оси \ (x \) . Следовательно, формула площади выражается через x, а пределы интегрирования лежат на оси \ (x \) . Однако показанная здесь стратегия решения проблем действительна независимо от того, как мы решаем разрезать твердое тело. 2−4x + 5, x = 1 \) и \ (x = 4, \) и вращается вокруг оси \ (x \).

Решение

Используя стратегию решения проблем, мы сначала нарисуем график квадратичной функции на интервале \ ([1,4] \), как показано на следующем рисунке.

Рисунок \ (\ PageIndex {6} \): область, используемая для создания тела вращения.

Затем поверните область вокруг оси \ (x \), как показано на следующем рисунке.

Рисунок \ (\ PageIndex {7} \): два вида (a) и (b) тела вращения, полученного путем вращения области на рисунке \ (\ PageIndex {6} \) относительно \ (x \) — ось.3. \)

Упражнение \ (\ PageIndex {2} \)

Используйте метод нарезки, чтобы найти объем тела вращения, образованного вращением области между графиком функции \ (f (x) = 1 / x \) и осью \ (x \) над интервал \ ([1,2] \) вокруг оси \ (x \) . См. Следующий рисунок.

Подсказка

Используйте стратегию решения проблем, представленную ранее, и следуйте примеру \ (\ PageIndex {2} \), чтобы помочь с шагом 2.2 + 1 \) и ось \ (x \) на интервале \ ([- 1,3] \) вокруг оси \ (x \) . График функции и типичный диск показаны на рис. \ (\ PageIndex {8} \) (a) и (b). Область вращения и получившееся твердое тело показаны на рис. \ (\ PageIndex {8} \) (c) и (d).

Рисунок \ (\ PageIndex {8} \): (a) Тонкий прямоугольник для аппроксимации площади под кривой. (b) Типичный диск, образованный вращением прямоугольника вокруг оси \ (x \) .б А (х) \, dx. \ nonumber \]

Единственное отличие от дискового метода состоит в том, что мы заранее знаем формулу площади поперечного сечения; это площадь круга. Это дает следующее правило.

Дисковый метод

Пусть \ (f (x) \) непрерывно и неотрицательно. Определим \ (R \) как область, ограниченную сверху графиком \ (f (x) \), снизу — осью \ (x \) , слева — линией \ (x = a \) , а справа — прямой \ (x = b \). 3 \)

До сих пор в наших примерах все рассматриваемые области вращались вокруг оси \ (x \) -оси , но мы можем создать тело вращения, вращая плоскую область вокруг любой горизонтальной или вертикальной линии.В следующем примере мы смотрим на твердое тело вращения, которое было создано путем вращения области вокруг оси \ (y \) . Механика дискового метода почти такая же, как когда \ (x \) — ось является осью вращения, но мы выражаем функцию через \ (y \) и интегрируем по y. . Это резюмируется в следующем правиле.

Правило: дисковый метод для тел вращения вокруг оси \ (y \)

Пусть \ (g (y) \) непрерывно и неотрицательно.2 \, дн \]

Следующий пример показывает, как это правило работает на практике.

Пример \ (\ PageIndex {4} \): использование дискового метода для определения объема твердого тела вращения 2

Пусть \ (R \) будет областью, ограниченной графиком \ (g (y) = \ sqrt {4 − y} \) и осью \ (y \) над \ (y \) -ось интервал \ ([0,4] \). Используйте дисковый метод, чтобы найти объем тела вращения, созданного вращением \ (R \) вокруг оси \ (y \) .

Решение

Рисунок \ (\ PageIndex {10} \) показывает функцию и типичный диск, который можно использовать для оценки объема.Обратите внимание, что, поскольку мы вращаем функцию вокруг оси \ (y \) , , диски расположены горизонтально, а не вертикально.

Рисунок \ (\ PageIndex {10} \): (a) Показан тонкий прямоугольник между кривой функции \ (g (y) = \ sqrt {4 − y} \) и \ (y \) — ось. (b) Прямоугольник образует типичный диск после вращения вокруг оси \ (y \) .

Поворачиваемая область и полное тело вращения показаны на следующем рисунке.

Рисунок \ (\ PageIndex {11} \): (a) Область слева от функции \ (g (y) = \ sqrt {4 − y} \) на интервале оси \ (y \) \ ( [0,4] \). 3 \)

Метод промывки

Некоторые тела вращения имеют в середине полости; они не прочны на всем протяжении оси вращения.Иногда это просто результат того, как область вращения формируется относительно оси вращения. В других случаях полости возникают, когда область вращения определяется как область между графиками двух функций. Третий способ — выбрать ось вращения, отличную от оси вращения \ (x \) — или \ (y \) — оси .

Когда твердое тело вращения имеет полость посередине, срезы, используемые для аппроксимации объема, являются не дисками, а шайбами ​​(дисками с отверстиями в центре).Например, рассмотрим область, ограниченную сверху графиком функции \ (f (x) = \ sqrt {x} \), а снизу графиком функции \ (g (x) = 1 \) на интервале \ ([1,4] \). Когда эта область вращается вокруг оси \ (x \) , в результате получается твердое тело с полостью посередине, а срезы — шайбы. График функции и типичная шайба показаны на рис. \ (\ PageIndex {12} \) (a) и (b). Область вращения и получившееся твердое тело показаны на рис. \ (\ PageIndex {12} \) (c) и (d).

Рисунок \ (\ PageIndex {12} \): (a) Тонкий прямоугольник в области между двумя кривыми. (b) Типичный диск, образованный вращением прямоугольника вокруг оси \ (x \) . (c) Область между кривыми на заданном интервале. (d) Получающаяся в результате революция.

Рисунок \ (\ PageIndex {12} \): (e) Динамическая версия этого твердого тела вращения, созданная с помощью CalcPlot3D.

Таким образом, площадь поперечного сечения — это площадь внешнего круга за вычетом площади внутреннего круга.3. \]

Обобщение этого процесса дает метод шайбы .

Правило: метод промывки

Предположим, что \ (f (x) \) и \ (g (x) \) — непрерывные неотрицательные функции такие, что \ (f (x) ≥g (x) \) над \ ([a, b] \). Обозначим через \ (R \) область, ограниченную сверху графиком \ (f (x) \), снизу графиком \ (g (x) \), слева прямой \ (x = a \ ), а справа — прямой \ (x = b \). 2 \ right] \, dx.\]

Пример \ (\ PageIndex {5} \): использование метода промывки

Найдите объем тела вращения, образованного вращением области, ограниченной сверху графиком \ (f (x) = x \) и снизу графиком \ (g (x) = 1 / x \) над интервал \ ([1,4] \) вокруг оси \ (x \) .

Решение

Графики функций и тела вращения показаны на следующем рисунке.

Рисунок \ (\ PageIndex {13} \): (a) Область между графиками функций \ (f (x) = x \) и \ (g (x) = 1 / x \) на интервале \ ( [1,4] \).3. \ end {align *} \]

Рисунок \ (\ PageIndex {13} \): (c) Динамическая версия этого твердого тела вращения, созданная с помощью CalcPlot3D.

Упражнение \ (\ PageIndex {5} \)

Найдите объем тела вращения, образованного вращением области, ограниченной графиками \ (f (x) = \ sqrt {x} \) и \ (g (x) = 1 / x \) на интервале \ ([1,3] \) вокруг оси \ (x \).

Подсказка

Изобразите функции, чтобы определить, какой график формирует верхнюю границу, а какой — нижнюю, затем используйте процедуру из примера \ (\ PageIndex {5} \).3 \)

Как и в случае с дисковым методом, мы можем также применить метод шайбы к телам вращения, которые возникают в результате вращения области вокруг оси \ (y \). В этом случае действует следующее правило.

Правило: метод шайбы для тел вращения вокруг оси \ (y \)

Предположим, что \ (u (y) \) и \ (v (y) \) — непрерывные неотрицательные функции такие, что \ (v (y) ≤u (y) \) для \ (y∈ [c, d] \ ). Обозначим через \ (Q \) область, ограниченную справа графиком \ (u (y) \), слева графиком \ (v (y) \), внизу прямой \ (y = c \), а выше — прямой \ (y = d \).2 \ right] \, dy. \]

Вместо того, чтобы смотреть на пример метода шайбы с \ (y \) -осью в качестве оси вращения, мы теперь рассмотрим пример, в котором ось вращения представляет собой линию, отличную от одной из двух осей координат. . Применяется тот же общий метод, но вам, возможно, придется визуализировать, как описать площадь поперечного сечения объема.

Пример \ (\ PageIndex {6} \):

Найдите объем тела вращения, образованного вращением области, ограниченной сверху \ (f (x) = 4 − x \), а снизу — осью \ (x \) на интервале \ ([0, 4] \) вокруг прямой \ (y = −2.\)

Решение

График области и тела вращения показаны на следующем рисунке.

Рисунок \ (\ PageIndex {14} \): (a) Область между графиком функции \ (f (x) = 4 − x \) и осью \ (x \) на интервале \ ([0,4] \). (b) При вращении области вокруг линии \ (y = −2 \) образуется тело вращения с цилиндрическим отверстием в середине.

Мы не можем применить формулу объема к этой задаче напрямую, потому что ось вращения не является одной из осей координат.3. \ end {align *} \]

Рисунок \ (\ PageIndex {14} \): (c) Динамическая версия этого твердого тела вращения, созданного с помощью CalcPlot3D.

Упражнение \ (\ PageIndex {6} \)

Найдите объем тела вращения, образованного вращением области, ограниченной сверху графиком \ (f (x) = x + 2 \) и ниже осью \ (x \) -оси на интервале \ ( [0,3] \) вокруг прямой \ (y = −1. \)

Подсказка

Используйте процедуру из примера \ (\ PageIndex {6} \).

Ответ

\ (60π \) ед. ³

Пирамиды, призмы, цилиндры и конусы (предалгебра, площадь и объем) — Mathplanet

Площадь поверхности — это область, которая описывает материал, который будет использоваться для покрытия геометрического тела. Когда мы определяем площади поверхности геометрического твердого тела, мы берем сумму площадей для каждой геометрической формы внутри твердого тела.

Объем — это мера того, сколько может вместить фигура, и измеряется в кубических единицах.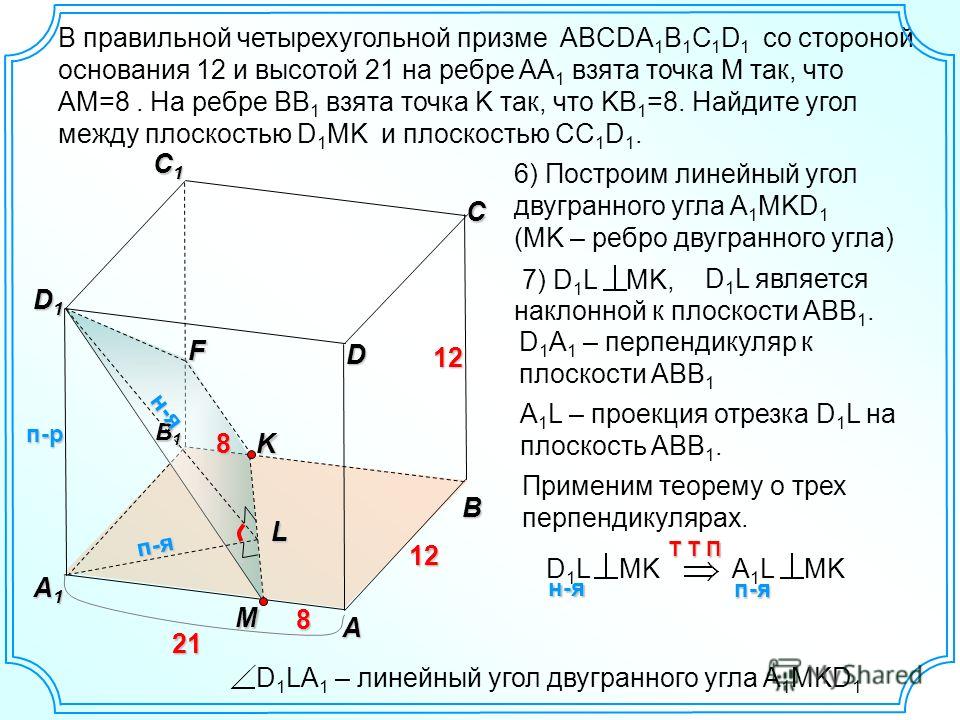 {2} & & A_ {LS} = \ pi \ cdot 3 \ cdot 9 \\ A_ {base} \ приблизительно 28.{3} $$

---

Видеоуроки

Найдите объем конуса высотой 5 и радиусом 3.

---

Найти площадь поверхности цилиндра радиусом 4 и высотой 8

Глоссарий по измерению

	А твердое тело, имеющее 12 плоских граней.
	А сплошная фигура, имеющая двенадцать граней-ромбов.
	А замкнутая плоская кривая, образованная точкой, движущейся таким образом, что суммы расстояния от двух фиксированных точек постоянна: плоское сечение правый круговой конус, представляющий собой замкнутую кривую.
	The часть правильного твердого тела, оставшаяся после срезания верхней части рубанком параллельно основанию; или часть, перехваченная между двумя плоскостями, либо параллельны или наклонены друг к другу.
	А плоская фигура, имеющая шесть сторон и шесть углов.
	А твердое тело, имеющее 6 восьмиугольных граней и 8 треугольных граней.
	А призма, имеющая шесть прямоугольных сторон, 2 шестиугольные грани.
	А плоская кривая, образованная точкой, движущейся так, что разница расстояний из двух фиксированных точек является константой: кривая, образованная пересечением двойного правого кругового конуса плоскостью, разрезающей обе половины конус.
	А многогранник с 20 гранями.
	Кому рисовать внутри фигуры так, чтобы касаться как можно большего количества мест, т.е. правильный многоугольник, вписанный в круг.
	1: Акт обмера: ИЗМЕРЕНИЕ 2: Геометрия, применяемая для вычисления длин, площадей или объемов из данные размеры или углы.
	дюйм наклонное или косое направление или положение; с отклонением от прямой линейный или прямой курс; по диагонали.
	А плоская фигура, имеющая восемь углов и восемь сторон.
	А твердое тело, ограниченное восемью плоскими гранями.
	А сплошная фигура, имеющая 8 шестиугольных граней и 6 квадратных граней.
	А плоская кривая, образованная точкой, движущейся так, что ее расстояние от фиксированной точка равна ее расстоянию от фиксированной линии: пересечение правый круговой конус с плоскостью, параллельной элементу конуса.
	Лежащий или расположенные рядом друг с другом и всегда на одинаковом расстоянии друг от друга; непрерывно равноудаленные: говорят о двух или более линиях, поверхностях или бетоне вещи.
	А четырехгранная прямолинейная фигура, противоположные стороны которой параллельны; иногда спец. применяется к прямоугольнику.
	А сплошная призма, имеющая 6 прямоугольных граней, 2 из которых — длинные и широкие, 2 — длинные и тонкие, и 2 короткие и тонкие.
	А фигура, обычно плоская прямолинейная фигура, имеющая пять углов и пять стороны.
	Расположен под прямым углом к ​​плоскости горизонта или прямо вверх или вниз; вертикальный.
	А сплошная фигура, два конца которой подобны, равны и параллельны прямолинейной фигуры и стороны.
	в форме как четырехугольник (фигура, имеющая четыре угла и, следовательно, четыре стороны) имеющий четыре угла; четырехугольной основы или секции.
	Четырехсторонний; имеющий четырехстороннее основание или секцию.
	Или похожий на ромб, — это фигура, противоположные стороны которой равны, а противоположные углы также равны, но у него нет ни равных сторон, ни прямых углов. Фигура с 2-мя ромбами и 4-мя продолговатыми ромбами, образующая удлиненный твердый.
	А шестигранная призма с тремя ромбами на каждом конце (ромб — плоская фигура имеющий четыре равные стороны и равные противоположные углы, две из которых являются острыми и два тупых).
	А многогранник, имеющий четыре грани Гексаэдр — куб.
	А сплошная фигура, имеющая 4 шестиугольные грани и 4 треугольные грани. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт