Как решать квадратные уравнения? Формулы и Примеры
Понятие квадратного уравнения
Уравнение — это равенство, содержащее переменную, значение которой нужно найти.
Например, х + 8 = 12 — это уравнение, которое содержит переменную х.
Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.
Например, если х = 5, то при подстановке в уравнение мы получим 5 + 8 = 12. 13 = 12 — противоречие. Значит, х = 5 не является корнем уравнения.
А вот если х = 4, то при подстановке в уравнение мы получим 4 + 8 = 12. 12 = 12 — верное равенство. Значит, х = 4 является корнем уравнения.
Решить уравнение — значит найти все его корни или доказать, что их не существует.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.
Квадратные уравнения могут иметь два корня, один корень или не иметь корней.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b2 − 4ac. А вот свойства дискриминанта:
- если D < 0, корней нет;
- если D = 0, есть один корень;
- если D > 0, есть два различных корня.
С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.
Разобраться в теме еще быстрее с помощью опытного преподавателя можно на курсах по математике в онлайн-школе Skysmart.
Приведенные и неприведенные квадратные уравнения
Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.
Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.
Неприведенным называют квадратное уравнение, где старший коэффициент отличается от единицы.
Давайте-ка на примерах — вот у нас есть два уравнения:
- x2 — 2x + 6 = 0
- x2 — x — 1/4 = 0
В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x2 ), а значит уравнение называется приведенным.
- 2x2 − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.
Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.
Запоминаем!
У преобразованного уравнения те же корни, что и у первоначального. Ну или вообще нет корней.
Пример 1. Превратим неприведенное уравнение: 8x
Для этого разделим обе части исходного уравнения на старший коэффициент 8:
Ответ: равносильное данному приведенное уравнение x2 + 2,5x — 1,125 = 0.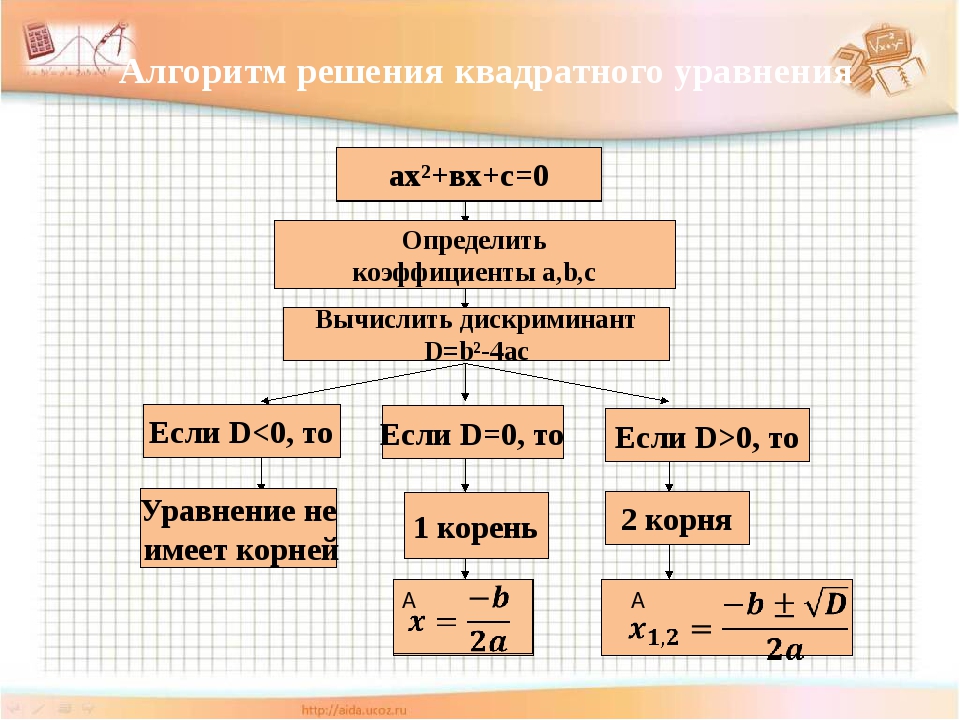
Полные и неполные квадратные уравнения
В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.
Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято называть неполным.
Неполное квадратное уравнение —— это квадратное уравнение вида ax2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.
Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.
| Для самых любопытных объясняем откуда появились такие названия: |
|---|
Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения. |
Решение неполных квадратных уравнений
Как мы уже знаем, есть три вида неполных квадратных уравнений:
- ax2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
- ax2 + c = 0, при b = 0;
- ax2 + bx = 0, при c = 0.
Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.
Как решить уравнение ax
2 = 0Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax2 = 0.
Уравнение ax2 = 0 равносильно x2 = 0.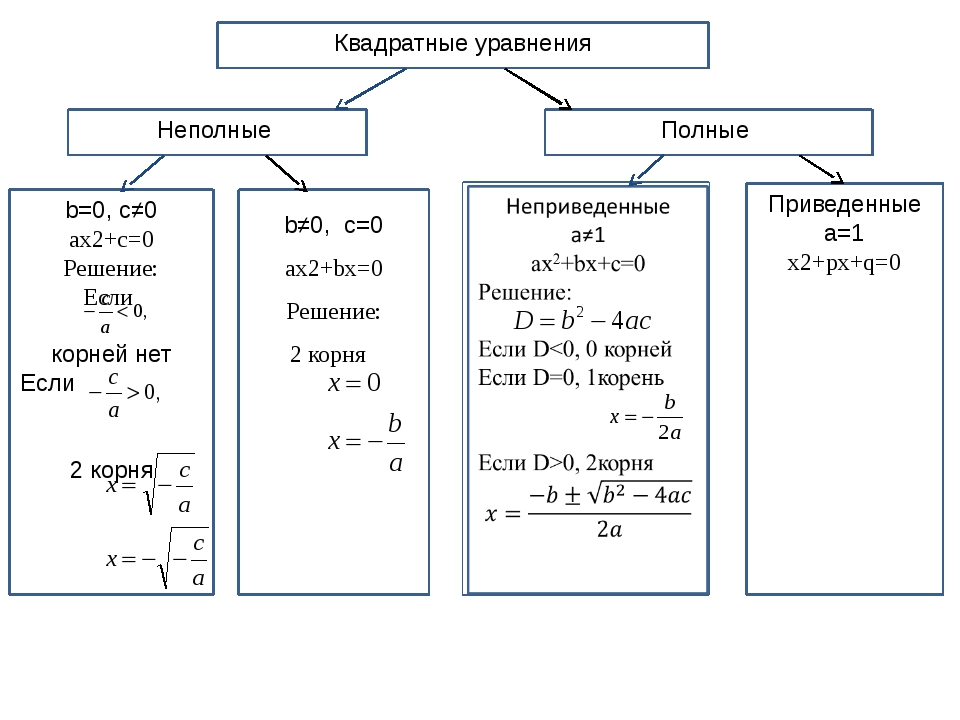 Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x2 = 0 является нуль, так как 02 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.
Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x2 = 0 является нуль, так как 02 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.
Таким образом, неполное квадратное уравнение ax2 = 0 имеет единственный корень x = 0.
Пример 1. Решить −6x2 = 0.
Как решаем:
- Замечаем, что данному уравнению равносильно x 2 = 0, значит исходное уравнение имеет единственный корень — нуль.
- По шагам решение выглядит так:
−6x2 = 0
x2 = 0
x = √0
x = 0
Ответ: 0.
Как решить уравнение ax
2 + с = 0Обратим внимание на неполные квадратные уравнения вида ax2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.
Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.
Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax2 + c = 0:
- перенесем
- разделим обе части на a: x2 = — c/а.
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.
Если — c/а < 0, то уравнение x2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а < 0 ни для какого числа p равенство р2 = — c/а не является верным.
Если — c/а > 0, то корни уравнения x2 = — c/а будут другими.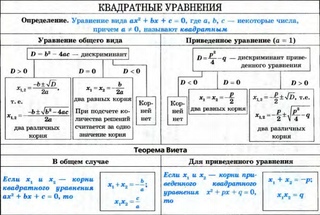 Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)2 = — c/а. Ура, больше у этого уравнения нет корней.
Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)2 = — c/а. Ура, больше у этого уравнения нет корней.
| В двух словах |
|---|
Неполное квадратное уравнение ax2 + c = 0 равносильно уравнению х2= -c/a, которое:
|
Пример 1. Найти решение уравнения 8x2 + 5 = 0.
Как решать:
- Перенесем свободный член в правую часть:
8x2 = — 5
- Разделим обе части на 8:
x2 = — 5/8
- В правой части осталось число со знаком минус, значит у данного уравнения нет корней.
Ответ: уравнение 8x2 + 5 = 0 не имеет корней.
Как решить уравнение ax
2 + bx = 0Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.
Неполное квадратное уравнение ax2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:
Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.
Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.
Таким образом, неполное квадратное уравнение ax2 + bx = 0 имеет два корня:
Пример 1. Решить уравнение 0,5x2 + 0,125x = 0
Как решать:
- Вынести х за скобки
х(0,5x + 0,125) = 0
- Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.
- Решить линейное уравнение:
0,5x = 0,125,
х = 0,125/0,5 - Разделить:
х = 0,25
- Значит корни исходного уравнения — 0 и 0,25.

Ответ: х = 0 и х = 0,25.
Как разложить квадратное уравнение
С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:
Формула разложения квадратного трехчлена Если x1 и x2 — корни квадратного трехчлена ax2 + bx + c, то справедливо равенство ax2 + bx + c = a (x − x1) (x − x2). |
Дискриминант: формула корней квадратного уравнения
Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:
где D = b2 − 4ac — дискриминант квадратного уравнения.
Эта запись означает:
, .
Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.
Алгоритм решения квадратных уравнений по формулам корней
Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.
В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.
Алгоритм решения квадратного уравнения ax2 + bx + c = 0:
- вычислить его значение дискриминанта по формуле D = b2−4ac;
- если дискриминант отрицательный, зафиксировать, что действительных корней нет;
- если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
- если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!
Примеры решения квадратных уравнений
Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.
Пример 1. Решить уравнение −4x2 + 28x — 49 = 0.
Как решаем:
- Найдем дискриминант: D = 282 — 4(-4)(-49) = 784 — 784 = 0
- Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
- Найдем корень
х = — 28/2(-4)
х = 3,5
Ответ: единственный корень 3,5.
Пример 2. Решить уравнение 54 — 6x2 = 0.
Как решаем:
- Произведем равносильные преобразования. Умножим обе части на −1
54 — 6x2 = 0 | *(-1)
6x2 — 54 = 0
- Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую
6x2 = 54
х2 = 9
х = ±√9
х1 = 3, х2 = — 3
Ответ: два корня 3 и — 3.
Пример 3. Решить уравнение x2— х = 0.
Как решаем:
- Преобразуем уравнение так, чтобы появились множители
х(х — 1) = 0
х₁ = 0, х₂ = 1
Ответ: два корня 0 и 1.
Пример 4. Решить уравнение x2— 10 = 39.
Как решаем:
- Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую
x2— 10 = 39
x2= 39 + 10
x2= 49
х = ±√49
х₁ = 7, х₂ = −7
Ответ: два корня 7 и −7.
Пример 5. Решить уравнение 3x2— 4x+94 = 0.
Как решаем:
- Найдем дискриминант по формуле
D = (-4)2 — 4 * 3 * 94 = 16 — 1128 = −1112
- Дискриминант отрицательный, поэтому корней нет.
Ответ: корней нет.
В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.
Формула корней для четных вторых коэффициентов
Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b2 — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.
Рассмотрим, как появилась эта формула.
Например, нам нужно решить квадратное уравнение ax2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n)2— 4ac = 4n2 — 4ac = 4(n2— ac) и подставим в формулу корней:
Для удобства вычислений обозначим выражение n2 -ac как D1. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:
где D1 = n2— ac.
Самые внимательные уже заметили, что D = 4D1, или D1= D/4. Проще говоря, D1 — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.
Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:
- вычислить D1= n2— ac;
- если D1< 0, значит действительных корней нет;
- если D1= 0, значит можно вычислить единственный корень уравнения по формуле x = -n/a;
- если же D1> 0, значит можно найти два действительных корня по формуле
Формула Виета
youtube.com/embed/LKGtbQZzBuo»/>
Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:
Теорема Виета Сумма корней x2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену. |
Если дано x2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:
Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.
Рассмотрим теорему Виета на примере: x2 + 4x + 3 = 0.
Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:
Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:
В данном случае свободным членом является число три. Значит:
Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
Результат проделанных вычислений в том, что мы убедились в справедливости выражения:
Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:
Обратная теорема Виета Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x2 + bx + c = 0. |
Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x1 и x2 равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.
Пример 1. Решить при помощи теоремы Пифагора: x2 − 6x + 8 = 0.
Как решаем:
- Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.
- Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.
Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.
Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x1 + x2 = 6.
 А значения 4 и 2 подходят обоим равенствам:
А значения 4 и 2 подходят обоим равенствам: - Значит числа 4 и 2 — корни уравнения x2 − 6x + 8 = 0. p>
Упрощаем вид квадратных уравнений
Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.
Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x2 — 4 x — 6 = 0, чем 1100x2 — 400x — 600 = 0.
Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x2 — 400x — 600 = 0, просто разделив обе части на 100.
Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.
Покажем, как это работает на примере 12x2— 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x2 — 7x + 8 = 0. Вот так просто.
А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения
умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x2 + 4x — 18 = 0.
Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x2— 3x + 7 = 0 перейти к решению 2x2 + 3x — 7 = 0.
Связь между корнями и коэффициентами
Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:
Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.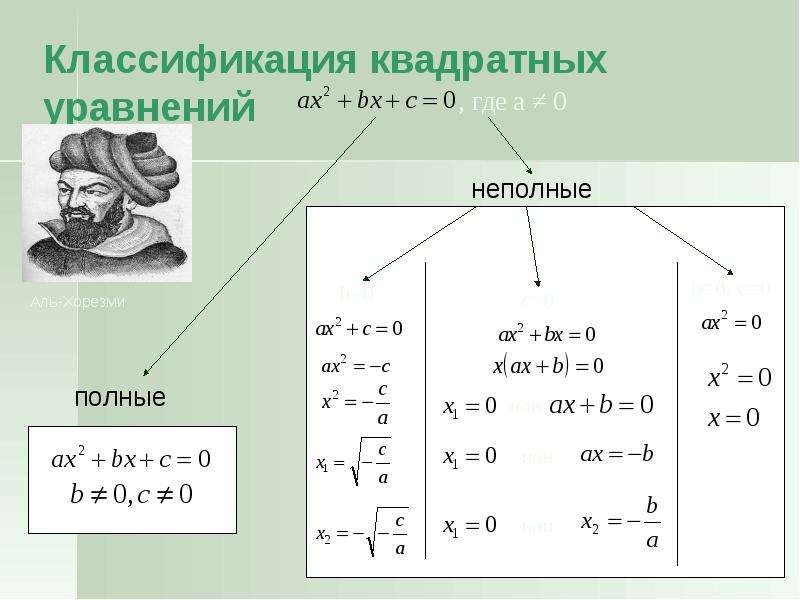
Например, можно применить формулы из теоремы Виета:
- x₁ + x₂ = — b/a,
- x₁* x₂ = c/a.
Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x2— 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.
Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:
Квадратное уравнение
Предварительные навыкиЧто такое квадратное уравнение и как его решать?
Мы помним, что уравнение это равенство, содержащее в себе переменную, значение которой нужно найти.
Если переменная, входящая в уравнение, возведенá во вторую степень (в квадрат), то такое уравнение называют уравнением второй степени или квадратным уравнением.
Например, следующие уравнения являются квадратными:
Решим первое из этих уравнений, а именно x2 − 4 = 0.
Все тождественные преобразования, которые мы применяли при решении обычных линейных уравнений, можно применять и при решении квадратных.
Итак, в уравнении x2 − 4 = 0 перенесем член −4 из левой части в правую часть, изменив знак:
Получили уравнение x2 = 4. Ранее мы говорили, что уравнение считается решённым, если в одной части переменная записана в первой степени и её коэффициент равен единице, а другая часть равна какому-нибудь числу. То есть чтобы решить уравнение, его следует привести к виду x = a, где a — корень уравнения.
У нас переменная x всё ещё во второй степени, поэтому решение необходимо продолжить.
Чтобы решить уравнение x2 = 4, нужно ответить на вопрос при каком значении x левая часть станет равна 4. Очевидно, что при значениях 2 и −2. Чтобы вывести эти значения воспользуемся определением квадратного корня.
Очевидно, что при значениях 2 и −2. Чтобы вывести эти значения воспользуемся определением квадратного корня.
Число b называется квадратным корнем из числа a, если b2 = a и обозначается как
У нас сейчас похожая ситуация. Ведь, что такое x2 = 4? Переменная x в данном случае это квадратный корень из числа 4, поскольку вторая степень x прирáвнена к 4.
Тогда можно записать, что . Вычисление правой части позвóлит узнать чему равно x. Квадратный корень имеет два значения: положительное и отрицательное. Тогда получаем x = 2 и x = −2.
Обычно записывают так: перед квадратным корнем ставят знак «плюс-минус», затем находят арифметическое значение квадратного корня. В нашем случае на этапе когда записано выражение , перед следует поставить знак ±
Затем найти арифметическое значение квадратного корня
Выражение x = ± 2 означает, что x = 2 и x = −2. То есть корнями уравнения x2 − 4 = 0 являются числа 2 и −2. Запишем полностью решение данного уравнения:
То есть корнями уравнения x2 − 4 = 0 являются числа 2 и −2. Запишем полностью решение данного уравнения:
Выполним проверку. Подставим корни 2 и −2 в исходное уравнение и выполним соответствующие вычисления. Если при значениях 2 и −2 левая часть равна нулю, то это будет означать, что уравнение решено верно:
В обоих случаях левая часть равна нулю. Значит уравнение решено верно.
Решим ещё одно уравнение. Пусть требуется решить квадратное уравнение (x + 2)2 = 25
Для начала проанализируем данное уравнение. Левая часть возведенá в квадрат и она равна 25. Какое число в квадрате равно 25? Очевидно, что числа 5 и −5
То есть наша задача найти x, при которых выражение x + 2 будет равно числам 5 и −5. Запишем эти два уравнения:
Решим оба уравнения. Это обычные линейные уравнения, которые решаются легко:
Значит корнями уравнения (x + 2)2 = 25 являются числа 3 и −7.
В данном примере как и в прошлом можно использовать определение квадратного корня. Так, в уравнения (x + 2)2 = 25 выражение (x + 2) представляет собой квадратный корень из числа 25. Поэтому можно cначала записать, что .
Тогда правая часть станет равна ±5. Полýчится два уравнения: x + 2 = 5 и x + 2 = −5. Решив по отдельности каждое из этих уравнений мы придём к корням 3 и −7.
Запишем полностью решение уравнения (x + 2)2 = 25
Из рассмотренных примеров видно, что квадратное уравнение имеет два корня. Чтобы не забыть о найденных корнях, переменную x можно подписывать нижними индексами. Так, корень 3 можно обозначить через x1, а корень −7 через x2
В предыдущем примере тоже можно было сделать так. Уравнение x2 − 4 = 0 имело корни 2 и −2. Эти корни можно было обозначить как x1 = 2 и x2 = −2.
Бывает и так, что квадратное уравнение имеет только один корень или вовсе не имеет корней. Такие уравнения мы рассмотрим позже.
Сделаем проверку для уравнения (x + 2)2 = 25. Подставим в него корни 3 и −7. Если при значениях 3 и −7 левая часть равна 25, то это будет означать, что уравнение решено верно:
В обоих случаях левая часть равна 25. Значит уравнение решено верно.
Квадратное уравнение бывает дано в разном виде. Наиболее его распространенная форма выглядит так:
ax2 + bx + c = 0,
где a, b, c — некоторые числа, x — неизвестное.
Это так называемый общий вид квадратного уравнения. В таком уравнении все члены собраны в общем месте (в одной части), а другая часть равна нулю. По другому такой вид уравнения называют нормальным видом квадратного уравнения.
Пусть дано уравнение 3x2 + 2x = 16. В нём переменная x возведенá во вторую степень, значит уравнение является квадратным. Приведём данное уравнение к общему виду.
Приведём данное уравнение к общему виду.
Итак, нам нужно получить уравнение, которое будет похоже на уравнение ax2 + bx + c = 0. Для этого в уравнении 3x2 + 2x = 16 перенесем 16 из правой части в левую часть, изменив знак:
3x2 + 2x − 16 = 0
Получили уравнение 3x2 + 2x − 16 = 0. В этом уравнении a = 3, b = 2, c = −16.
В квадратном уравнении вида ax2 + bx + c = 0 числа a, b и c имеют собственные названия. Так, число a называют первым или старшим коэффициентом; число b называют вторым коэффициентом; число c называют свободным членом.
В нашем случае для уравнения 3x2 + 2x − 16 = 0 первым или старшим коэффициентом является 3; вторым коэффициентом является число 2; свободным членом является число −16. Есть ещё другое общее название для чисел a, b и c — параметры.
Есть ещё другое общее название для чисел a, b и c — параметры.
Так, в уравнении 3x2 + 2x − 16 = 0 параметрами являются числа 3, 2 и −16.
В квадратном уравнении желательно упорядочивать члены так, чтобы они располагались в таком же порядке как у нормального вида квадратного уравнения.
Например, если дано уравнение −5 + 4x2 + x = 0, то его желательно записать в нормальном виде, то есть в виде ax2+ bx + c = 0.
В уравнении −5 + 4x2 + x = 0 видно, что свободным членом является −5, он должен располагаться в конце левой части. Член 4x2 содержит старший коэффициент, он должен располагаться первым. Член x соответственно будет располагаться вторым:
Квадратное уравнение в зависимости от случая может принимать различный вид. Всё зависит от того, чему равны значения a, b и с.
Если коэффициенты a, b и c не равны нулю, то квадратное уравнение называют полным. Например, полным является квадратное уравнение 2x2 + 6x − 8 = 0.
Если какой-то из коэффициентов равен нулю (то есть отсутствует), то уравнение значительно уменьшается и принимает более простой вид. Такое квадратное уравнение называют неполным. Например, неполным является квадратное уравнение 2x2 + 6x = 0, в нём имеются коэффициенты a и b (числа 2 и 6), но отсутствует свободный член c.
Рассмотрим каждый из этих видов уравнений, и для каждого из этих видов определим свой способ решения.
Пусть дано квадратное уравнение 2x2 + 6x − 8 = 0. В этом уравнении a = 2, b = 6, c = −8. Если b сделать равным нулю, то уравнение примет вид:
Получилось уравнение 2x2 − 8 = 0. Чтобы его решить перенесем −8 в правую часть, изменив знак:
Чтобы его решить перенесем −8 в правую часть, изменив знак:
2x2 = 8
Для дальнейшего упрощения уравнения воспользуемся ранее изученными тождественными преобразованиями. В данном случае можно разделить обе части на 2
У нас получилось уравнение, которое мы решали в начале данного урока. Чтобы решить уравнение x2 = 4, следует воспользоваться определением квадратного корня. Если x2 = 4, то . Отсюда x = 2 и x = −2.
Значит корнями уравнения 2x2 − 8 = 0 являются числа 2 и −2. Запишем полностью решение данного уравнения:
Выполним проверку. Подставим корни 2 и −2 в исходное уравнение и выполним соответствующие вычисления. Если при значениях 2 и −2 левая часть равна нулю, то это будет означать, что уравнение решено верно:
В обоих случаях левая часть равна нулю, значит уравнение решено верно.
Уравнение, которое мы сейчас решили, является неполным квадратным уравнением. Название говорит само за себя. Если полное квадратное уравнение выглядит как ax2 + bx + c = 0, то сделав коэффициент b нулём получится неполное квадратное уравнение ax2 + c = 0.
Название говорит само за себя. Если полное квадратное уравнение выглядит как ax2 + bx + c = 0, то сделав коэффициент b нулём получится неполное квадратное уравнение ax2 + c = 0.
У нас тоже сначала было полное квадратное уравнение 2x2 + 6x − 4 = 0. Но мы сделали коэффициент b нулем, то есть вместо числа 6 поставили 0. В результате уравнение обратилось в неполное квадратное уравнение 2x2 − 4 = 0.
В начале данного урока мы решили квадратное уравнение x2 − 4 = 0. Оно тоже является уравнением вида ax2 + c = 0, то есть неполным. В нем a = 1, b = 0, с = −4.
Также, неполным будет квадратное уравнение, если коэффициент c равен нулю.
Рассмотрим полное квадратное уравнение 2x2 + 6x − 4 = 0. Сделаем коэффициент c нулём.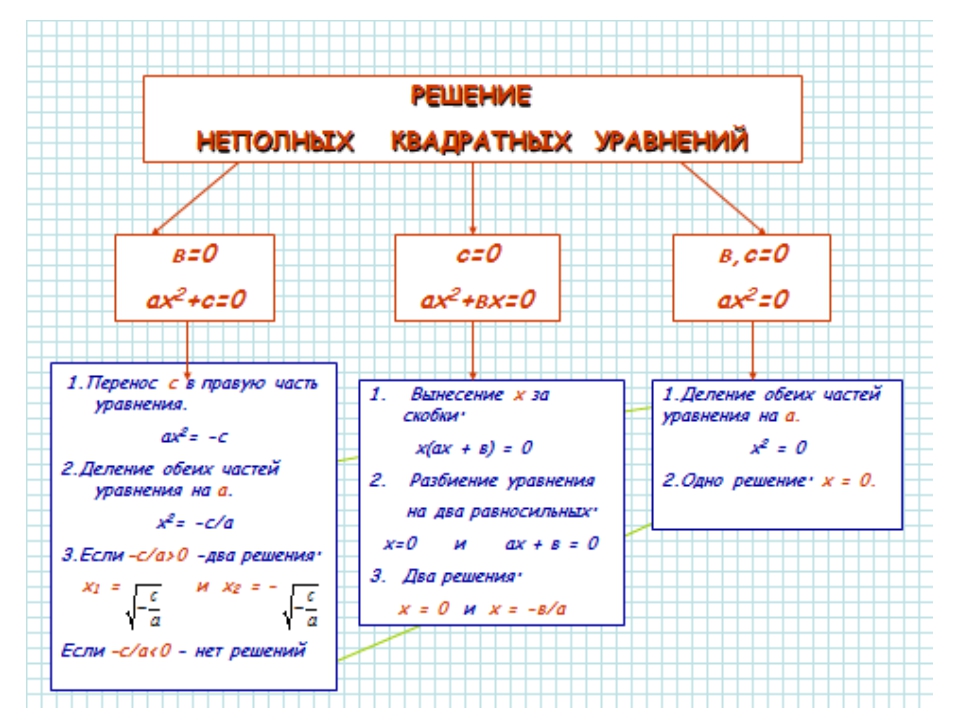 То есть вместо числа 4 поставим 0
То есть вместо числа 4 поставим 0
Получили квадратное уравнение 2x2 + 6x=0, которое является неполным. Чтобы решить такое уравнение, переменную x выносят за скобки:
Получилось уравнение x(2x + 6) = 0 в котором нужно найти x, при котором левая часть станет равна нулю. Заметим, что в этом уравнении выражения x и (2x + 6) являются сомножителями. Одно из свойств умножения говорит, что произведение равно нулю, если хотя бы один из сомножителей равен нулю (или первый сомножитель или второй).
В нашем случае равенство будет достигаться, если x будет равно нулю или (2x + 6) будет равно нулю. Так и запишем для начала:
Получилось два уравнения: x = 0 и 2x + 6 = 0. Первое уравнение решать не нужно — оно уже решено. То есть первый корень равен нулю.
Чтобы найти второй корень, решим уравнение 2x + 6 = 0. Это обычное линейное уравнение, которое решается легко:
Видим, что второй корень равен −3.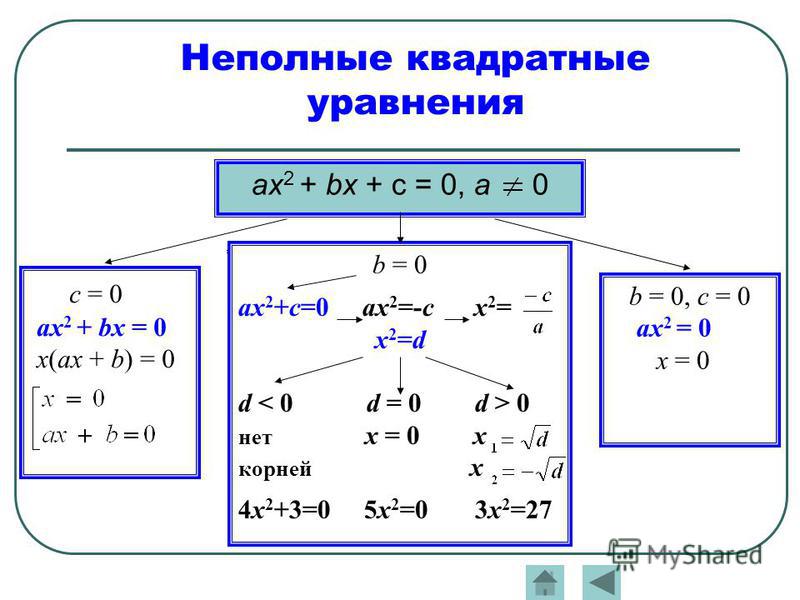
Значит корнями уравнения 2x2 + 6x = 0 являются числа 0 и −3. Запишем полностью решение данного уравнения:
Выполним проверку. Подставим корни 0 и −3 в исходное уравнение и выполним соответствующие вычисления. Если при значениях 0 и −3 левая часть равна нулю, то это будет означать, что уравнение решено верно:
Следующий случай это когда числа b и с равны нулю. Рассмотрим полное квадратное уравнение 2x2 + 6x − 4 = 0. Сделаем коэффициенты b и c нулями. Тогда уравнение примет вид:
Получили уравнение 2x2 = 0. Левая часть является произведением, а правая часть равна нулю. Произведение равно нулю, если хотя бы один из сомножителей равен нулю. Очевидно, что x = 0. Действительно, 2 × 02 = 0. Отсюда, 0 = 0. При других значениях x равенства достигаться не будет.
Проще говоря, если в квадратном уравнении вида ax2 + bx + c = 0 числа b и с равны нулю, то корень такого уравнения равен нулю.
Отметим, что когда употребляются словосочетания «b равно нулю» или «с равно нулю«, то подразумевается, что параметры b или c вовсе отсутствуют в уравнении.
Например, если дано уравнение 2x2 − 32 = 0, то мы говорим, что b = 0. Потому что если сравнить с полным уравнением ax2 + bx + c = 0, то можно заметить, что в уравнении 2x2 − 32 = 0 присутствует старший коэффициент a, равный 2; присутствует свободный член −32; но отсутствует коэффициент b.
Наконец, рассмотрим полное квадратное уравнение ax2 + bx + c = 0. В качестве примера решим квадратное уравнение x2 − 2x + 1 = 0.
Итак, требуется найти x, при котором левая часть станет равна нулю. Воспользуемся изученными ранее тождественными преобразованиями.
Прежде всего заметим, что левая часть уравнения представляет собой квадрат разности двух выражений. Если мы вспомним как раскладывать многочлен на множители, то получим в левой части (x − 1)2.
Если мы вспомним как раскладывать многочлен на множители, то получим в левой части (x − 1)2.
Рассуждаем дальше. Левая часть возведенá в квадрат и она равна нулю. Какое число в квадрате равно нулю? Очевидно, что только 0. Поэтому наша задача найти x, при котором выражение x − 1 равно нулю. Решив простейшее уравнение x − 1 = 0, можно узнать чему равно x
Этот же результат можно получить, если воспользоваться квадратным корнем. В уравнении (x − 1)2 = 0 выражение (x − 1) представляет собой квадратный корень из нуля. Тогда можно записать, что . В этом примере записывать перед корнем знак ± не нужно, поскольку корень из нуля имеет только одно значение — ноль. Тогда получается x − 1 = 0. Отсюда x = 1.
Значит корнем уравнения x2 − 2x + 1 = 0 является единица. Других корней у данного уравнения нет. В данном случае мы решили квадратное уравнение, имеющее только один корень. Такое тоже бывает.
Такое тоже бывает.
Не всегда бывают даны простые уравнения. Рассмотрим например уравнение x2 + 2x − 3 = 0.
В данном случае левая часть уже не является квадратом суммы или разности. Поэтому нужно искать другие пути решения.
Заметим, что левая часть уравнения представляет собой квадратный трехчлен. Тогда можно попробовать выделить полный квадрат из этого трёхчлена и посмотреть что это нам даст.
Выделим полный квадрат из квадратного трёхчлена, располагающего в левой части уравнения:
В получившемся уравнении перенесем −4 в правую часть, изменив знак:
Теперь воспользуемся квадратным корнем. В уравнении (x + 1)2 = 4 выражение (x + 1) представляет собой квадратный корень из числа 4. Тогда можно записать, что . Вычисление правой части даст выражение x + 1 = ±2. Отсюда полýчится два уравнения: x + 1 = 2 и x + 1 = −2, корнями которых являются числа 1 и −3
Значит корнями уравнения x2 + 2x − 3 = 0 являются числа 1 и −3.
Выполним проверку:
Пример 3. Решить уравнение x2 − 6x + 9 = 0, выделив полный квадрат.
Выделим полный квадрат из левой части:
Далее воспользуемся квадратным корнем и узнáем чему равно x
Значит корнем уравнения x2 − 6x + 9 = 0 является 3. Выполним проверку:
Пример 4. Решить квадратное уравнение 4x2 + 28x − 72 = 0, выделив полный квадрат:
Выделим полный квадрат из левой части:
Перенесём −121 из левой части в правую часть, изменив знак:
Воспользуемся квадратным корнем:
Получили два простых уравнения: 2x + 7 = 11 и 2x + 7 = −11. Решим их:
Пример 5. Решить уравнение 2x2 + 3x − 27 = 0
Это уравнение немного посложнее. Когда мы выделяем полный квадрат, первый член квадратного трёхчлена мы представляем в виде квадрата какого-нибудь выражения.
Так, в прошлом примере первым членом уравнения был 4x2. Его можно было представить в виде квадрата выражения 2x, то есть (2x)2 = 22x2 = 4x2. Чтобы убедиться что это правильно, можно извлечь квадратный корень из выражения 4x2. Это квадратный корень из произведения — он равен произведению корней:
В уравнении 2x2 + 3x − 27 = 0 первый член это 2x2. Его нельзя представить в виде квадрата какого-нибудь выражения. Потому что нет числá, квадрат которого равен 2. Если бы такое число было, то этим числом был бы квадратный корень из числа 2. Но квадратный корень из числа 2 извлекается только приближённо. А приближённое значение не годится для представления числá 2 в виде квадрата.
Если обе части исходного уравнения умножить или разделить на одно и то же число, то полýчится уравнение равносильное исходному. Это правило сохраняется и для квадратного уравнения.
Это правило сохраняется и для квадратного уравнения.
Тогда можно разделить обе части нашего уравнения на 2. Это позвóлит избавиться от двойки перед x2 что впоследствии даст нам возможность выделить полный квадрат:
Перепишем левую часть в виде трёх дробей со знаменателем 2
Сократим первую дробь на 2. Остальные члены левой части перепишем без изменений. Правая часть по-прежнему станет равна нулю:
Выделим полный квадрат.
При представлении члена в виде удвоенного произведения, появление множителя 2 привело бы к тому, что этот множитель и знаменатель дроби сократились бы. Чтобы этого не произошло, удвоенное произведение было домножено на . При выделении полного квадрата всегда нужно стараться сделать так, чтобы значение изначального выражения не изменилось.
Свернём полученный полный квадрат:
Приведём подобные члены:
Перенесём дробь в правую часть, изменив знак:
Воспользуемся квадратным корнем. Выражение представляет собой квадратный корень из числа
Выражение представляет собой квадратный корень из числа
Для вычисления правой части воспользуемся правилом извлечения квадратного корня из дроби:
Тогда наше уравнение примет вид:
Полýчим два уравнения:
Решим их:
Значит корнями уравнения 2x2 + 3x − 27 = 0 являются числа 3 и .
Корень удобнее оставить в таком виде, не выполняя деления числителя на знаменатель. Так проще будет выполнять проверку.
Выполним проверку. Подставим найденные корни в исходное уравнение:
В обоих случаях левая часть равна нулю, значит уравнение 2x2 + 3x − 27 = 0 решено верно.
Решая уравнение 2x2 + 3x − 27 = 0, в самом начале мы разделили обе его части на 2. В результате получили квадратное уравнение, в котором коэффициент перед x2 равен единице:
Такой вид квадратного уравнения называют приведённым квадратным уравнением.
Любое квадратное уравнение вида ax2 + bx + c = 0 можно сделать приведённым. Для этого нужно разделить обе его части на коэффициент, который располагается перед x². В данном случае обе части уравнения ax2 + bx + c = 0 нужно разделить на a
Пример 6. Решить квадратное уравнение 2x2 + x + 2 = 0
Сделаем данное уравнение приведённым:
Выделим полный квадрат:
Получили уравнение , в котором квадрат выражения равен отрицательному числу . Такого быть не может, поскольку квадрат любого числа или выражения всегда положителен.
Следовательно, нет такого значения x, при котором левая часть стала бы равна . Значит уравнение не имеет корней.
А поскольку уравнение равносильно исходному уравнению 2x2 + x + 2 = 0, то и оно (исходное уравнение) не имеет корней.
Формулы корней квадратного уравнения
Выделять полный квадрат для каждого решаемого квадратного уравнения не очень удобно.
Можно ли создать универсальные формулы для решения квадратных уравнений? Оказывается можно. Сейчас мы этим и займёмся.
Взяв за основу буквенное уравнение ax2 + bx + c = 0, и выполнив некоторые тождественные преобразования, мы сможем получить формулы для вывода корней квадратного уравнения ax2 + bx + c = 0. В эти формулы можно будет подставлять коэффициенты a, b, с и получать готовые решения.
Итак, выделим полный квадрат из левой части уравнения ax2 + bx + c = 0. Сначала сделаем данное уравнение приведённым. Разделим обе его части на a
Теперь в получившемся уравнении выделим полный квадрат:
Перенесем члены и в правую часть, изменив знак:
Приведём правую часть к общему знаменателю. Дроби, состоящие из букв, привóдят к общему знаменателю методом «крест-нáкрест». То есть знаменатель первой дроби станóвится дополнительным множителем второй дроби, а знаменатель второй дроби станóвится дополнительным множителем первой дроби:
Дроби, состоящие из букв, привóдят к общему знаменателю методом «крест-нáкрест». То есть знаменатель первой дроби станóвится дополнительным множителем второй дроби, а знаменатель второй дроби станóвится дополнительным множителем первой дроби:
В числителе правой части вынесем за скобки a
Сократим правую часть на a
Поскольку все преобразования были тождественными, то получившееся уравнение имеет те же корни, что и исходное уравнение ax2 + bx + c = 0.
Уравнение будет иметь корни только тогда, если правая часть больше нуля или равна нулю. Это потому что в левой части выполнено возведéние в квадрат, а квадрат любого числа положителен или равен нулю (если в этот квадрат возвóдится ноль). А чему будет равна правая часть зависит от того, что будет подставлено вместо переменных a, b и c.
Поскольку при любом a не рáвным нулю, знаменатель правой части уравнения всегда будет положительным, то знак дроби будет зависеть от знака её числителя, то есть от выражения b2 − 4ac.
Выражение b2 − 4ac называют дискриминантом квадратного уравнения. Дискриминант это латинское слово, означающее различитель. Дискриминант квадратного уравнения обозначается через букву D
D = b2 − 4ac
Дискриминант позволяет заранее узнать имеет ли уравнение корни или нет. Так, в предыдущем задании мы долго решали уравнение 2x2 + x + 2 = 0 и оказалось, что оно не имеет корней. Дискриминант же позволил бы нам заранее узнать, что корней нет. В уравнении 2x2 + x + 2 = 0 коэффициенты a, b и c равны 2, 1 и 2 соответственно. Подставим их в формулу D = b2−4ac
D = b2 − 4ac = 12 − 4 × 2 × 2 = 1 − 16 = −15.
Видим, что D (оно же b2 − 4ac) является отрицательным числом.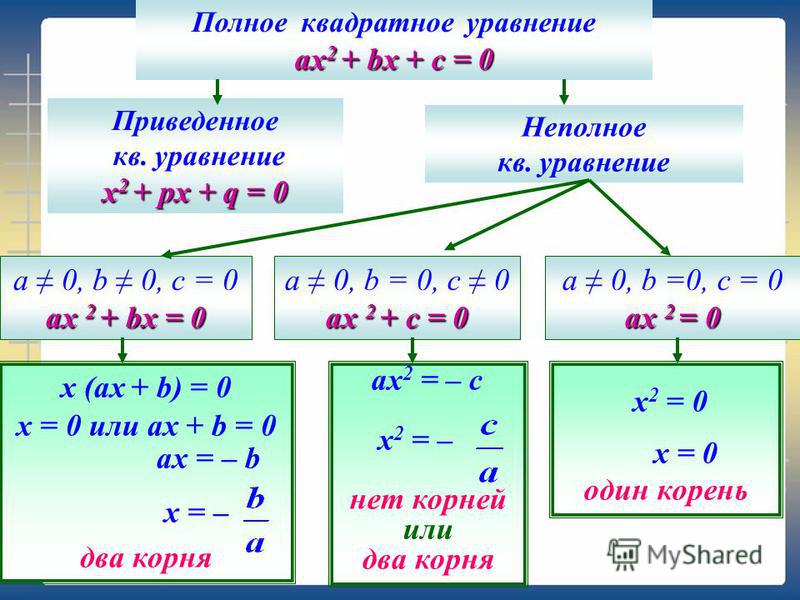 Тогда нет смысла решать уравнение 2x2 + x + 2 = 0, выделяя в нём полный квадрат, потому что когда мы дойдем до уравнения вида , окажется что правая часть станет меньше нуля (из-за отрицательного дискриминанта). А квадрат числа не может быть отрицательным. Следовательно, корней у данного уравнения не будет.
Тогда нет смысла решать уравнение 2x2 + x + 2 = 0, выделяя в нём полный квадрат, потому что когда мы дойдем до уравнения вида , окажется что правая часть станет меньше нуля (из-за отрицательного дискриминанта). А квадрат числа не может быть отрицательным. Следовательно, корней у данного уравнения не будет.
Станóвится понятно почему древние люди считали выражение b2 − 4ac различителем. Это выражение подобно индикатору позволяет различить уравнение имеющего корни от уравнения, не имеющего корней.
Итак, D равно b2 − 4ac. Подставим в уравнении вместо выражения b2 − 4ac букву D
Если дискриминант исходного уравнения окажется меньше нуля (D < 0), то уравнение примет вид:
В этом случае говорят, что у исходного уравнения корней нет, поскольку квадрат любого числа не должен быть отрицательным.
Если дискриминант исходного уравнения окажется больше нуля (D > 0), то уравнение примет вид:
В этом случае уравнение будет иметь два корня. Для их вывода воспользуемся квадратным корнем:
Для их вывода воспользуемся квадратным корнем:
Получили уравнение . Из него полýчится два уравнения: и . Выразим x в каждом из уравнений:
Получившиеся два равенства это и есть универсальные формулы для решения квадратного уравнения ax2 + bx + c = 0. Их называют формулами корней квадратного уравнения.
Чаще всего эти формулы обозначаются как x1 и x2. То есть для вычисления первого корня используется формула c индексом 1; для вывода второго корня — формула с индексом 2. Обозначим свои формулы так же:
Очерёдность применения формул не важнá.
Решим например квадратное уравнение x2 + 2x − 8 = 0 с помощью формул корней квадратного уравнения. Коэффициенты данного квадратного уравнения это числа 1, 2 и −8. То есть, a = 1, b = 2, c = −8.
Прежде чем использовать формулы корней квадратного уравнения, нужно найти дискриминант этого уравнения.
Найдём дискриминант квадратного уравнения. Для этого воспользуемся формулой D = b2 − 4ac. Вместо переменных a, b и c у нас будут коэффициенты уравнения x2 + 2x − 8 = 0
D = b2 − 4ac = 22− 4 × 1 × (−8) = 4 + 32 = 36
Дискриминант больше нуля. Значит уравнение имеет два корня. Теперь можно воспользоваться формулами корней квадратного уравнения:
Значит корнями уравнения x2 + 2x − 8 = 0 являются числа 2 и −4. Проверкой убеждаемся, что корни найдены верно:
Наконец, рассмотрим случай когда дискриминант квадратного уравнения равен нулю. Вернёмся к уравнению . Если дискриминант равен нулю, то правая часть уравнения примет вид:
И в этом случае квадратное уравнение будет иметь только один корень. Воспользуемся квадратным корнем:
Далее выражаем x
Это ещё одна формула для вывода корня квадратного корня. Рассмотрим её применение. Ранее мы решили уравнение x2 − 6x + 9 = 0, имеющее один корень 3. Решили мы его методом выделения полного квадрата. Теперь попробуем решить с помощью формул.
Рассмотрим её применение. Ранее мы решили уравнение x2 − 6x + 9 = 0, имеющее один корень 3. Решили мы его методом выделения полного квадрата. Теперь попробуем решить с помощью формул.
Найдём дискриминант квадратного уравнения. В этом уравнении a = 1, b = −6, c = 9. Тогда по формуле дискриминанта имеем:
D = b2 − 4ac = (−6)2 − 4 × 1 × 9 = 36 − 36 = 0
Дискриминант равен нулю (D = 0). Это означает, что уравнение имеет только один корень, и вычисляется он по формуле
Значит корнем уравнения x2 − 6x + 9 = 0 является число 3.
Для квадратного уравнения, имеющего один корень также применимы формулы и . Но применение каждой из них будет давать один и тот же результат.
Применим эти две формулы для предыдущего уравнения. В обоих случаях получим один и тот же ответ 3
Если квадратное уравнение имеет только один корень, то желательно применять формулу , а не формулы и . Это позволяет сэкономить время и место.
Это позволяет сэкономить время и место.
Пример 3. Решить уравнение 5x2 − 6x + 1 = 0
Найдём дискриминант квадратного уравнения:
Дискриминант больше нуля. Значит уравнение имеет два корня. Воспользуемся формулами корней квадратного уравнения:
Значит корнями уравнения 5x2 − 6x + 1 = 0 являются числа 1 и .
Ответ: 1; .
Пример 4. Решить уравнение x2 + 4x + 4 = 0
Найдём дискриминант квадратного уравнения:
Дискриминант равен нулю. Значит уравнение имеет только один корень. Он вычисляется по формуле
Значит корнем уравнения x2 + 4x + 4 = 0 является число −2.
Ответ: −2.
Пример 5. Решить уравнение 3x2 + 2x + 4 = 0
Найдём дискриминант квадратного уравнения:
Дискриминант меньше нуля. Значит корней у данного уравнения нет.
Значит корней у данного уравнения нет.
Ответ: корней нет.
Пример 6. Решить уравнение (x + 4)2 = 3x + 40
Приведём данное уравнение к нормальному виду. В левой части располагается квадрата суммы двух выражений. Раскрóем его:
Перенесём все члены из правой части в левую часть, изменив их знаки. В правой части останется ноль:
Приведём подобные члены в левой части:
В получившемся уравнении найдём дискриминант:
Дискриминант больше нуля. Значит уравнение имеет два корня. Воспользуемся формулами корней квадратного уравнения:
Значит корнями уравнения (x + 4)2 = 3x + 40 являются числа 3 и −8.
Ответ: 3; −8.
Пример 7. Решить уравнение
Умнóжим обе части данного уравнения на 2. Это позвóлит нам избавиться от дроби в левой части:
В получившемся уравнении перенесём 22 из правой части в левую часть, изменив знак. В правой части останется 0
В правой части останется 0
Приведём подобные члены в левой части:
В получившемся уравнении найдём дискриминант:
Дискриминант больше нуля. Значит уравнение имеет два корня. Воспользуемся формулами корней квадратного уравнения:
Значит корнями уравнения являются числа 23 и −1.
Ответ: 23; −1.
Пример 8. Решить уравнение
Умнóжим обе части на наименьшее общее кратное знаменателей обеих дробей. Это позвóлит избавиться от дробей в обеих частях. Наименьшее общее кратное чисел 2 и 3 это число 6. Тогда получим:
В получившемся уравнении раскроем скобки в обеих частях:
Теперь перенесём все члены из правой части в левую часть, изменив у них знаки. В правой части останется 0
Приведём подобные члены в левой части:
В получившемся уравнении найдём дискриминант:
Дискриминант больше нуля. Значит уравнение имеет два корня. Воспользуемся формулами корней квадратного уравнения:
Воспользуемся формулами корней квадратного уравнения:
Значит корнями уравнения являются числа и 2.
Примеры решения квадратных уравнений
Пример 1. Решить уравнение x2 = 81
Это простейшее квадратное уравнение, в котором надо определить число, квадрат которого равен 81. Таковыми являются числа 9 и −9. Воспользуемся квадратным корнем для их вывода:
Ответ: 9, −9.
Пример 2. Решить уравнение x2 − 9 = 0
Это неполное квадратное уравнение. Для его решения нужно перенести член −9 в правую часть, изменив знак. Тогда получим:
Ответ: 3, −3.
Пример 3. Решить уравнение x2 − 9x = 0
Это неполное квадратное уравнение. Для его решения сначала нужно вынести x за скобки:
Левая часть уравнения является произведением. Произведение равно нулю, если хотя один из сомножителей равен нулю.
Левая часть станет равна нулю, если отдельно x равно нулю, или если выражение x − 9 равно нулю. Получится два уравнения, одно из которых уже решено:
Ответ: 0, 9.
Пример 4. Решить уравнение x2 + 4x − 5 = 0
Это полное квадратное уравнение. Его можно решить методом выделения полного квадрата или с помощью формул корней квадратного уравнения.
Решим данное уравнение с помощью формул. Сначала найдём дискриминант:
D = b2 − 4ac = 42 − 4 × 1 × (−5) = 16 + 20 = 36
Дискриминант больше нуля. Значит уравнение имеет два корня. Вычислим их:
Ответ: 1, −5.
Пример 5. Решить уравнение
Умнóжим обе части на наименьшее общее кратное чисел 5, 3 и 6. Это позвóлит избавиться от дробей в обеих частях:
В получившемся уравнении перенесём все члены из правой части в левую часть, изменив знак. В правой части останется ноль:
В правой части останется ноль:
Приведём подобные члены:
Решим получившееся уравнение с помощью формул:
Ответ: 5, .
Пример 6. Решить уравнение x2 = 6
В данном примере как и в первом нужно воспользоваться квадратным корнем:
Однако, квадратный корень из числа 6 не извлекается. Он извлекается только приближённо. Корень можно извлечь с определённой точностью. Извлечём его с точностью до сотых:
Но чаще всего корень оставляют в виде радикала:
Ответ:
Пример 7. Решить уравнение (2x + 3)2 + (x − 2)2 = 13
Раскроем скобки в левой части уравнения:
В получившемся уравнении перенесём 13 из правой части в левую часть, изменив знак. Затем приведём подобные члены:
Получили неполное квадратное уравнение. Решим его:
Ответ: 0, −1,6.
Пример 8. Решить уравнение (5 + 7x)(4 − 3x) = 0
Данное уравнение можно решить двумя способами. Рассмотрим каждый из них.
Первый способ. Раскрыть скобки и получить нормальный вид квадратного уравнения.
Раскроем скобки:
Приведём подобные члены:
Перепишем получившееся уравнение так, чтобы член со старшим коэффициентом располагался первым, член со вторым коэффициентом — вторым, а свободный член располагался третьим:
Чтобы старший член стал положительным, умнóжим обе части уравнения на −1. Тогда все члены уравнения поменяют свои знаки на противоположные:
Решим получившееся уравнение с помощью формул корней квадратного уравнения:
Второй способ. Найти значения x, при которых сомножители левой части уравнения равны нулю. Этот способ удобнее и намного короче.
Произведение равно нулю, если хотя бы один из сомножителей равен нулю. В данном случае равенство в уравнении (5 + 7x)(4 − 3x) = 0 будет достигаться, если выражение (5 + 7x) равно нулю, или же выражение (4 − 3x) равно нулю. Наша задача выяснить при каких x это происходит:
В данном случае равенство в уравнении (5 + 7x)(4 − 3x) = 0 будет достигаться, если выражение (5 + 7x) равно нулю, или же выражение (4 − 3x) равно нулю. Наша задача выяснить при каких x это происходит:
Примеры решения задач
Предстáвим, что возникла необходимость построить небольшую комнату, площадь которой 8 м2. При этом длина комнаты должна быть в два раза больше её ширины. Как определить длину и ширину такой комнаты?
Сделаем примерный рисунок этой комнаты, который иллюстрирует вид сверху:
Обозначим ширину комнаты через x. А длину комнаты через 2x, потому что по условию задачи длина должна быть в два раза больше ширины. Множитель 2 и выполнит это требование:
Поверхность комнаты (её пол) является прямоугольником. Для вычисления площади прямоугольника, нужно длину данного прямоугольника умножить на его ширину. Сделаем это:
2x × x
По условию задачи площадь должна быть 8 м2. Значит выражение 2x × x следует приравнять к 8
Значит выражение 2x × x следует приравнять к 8
2x × x = 8
Получилось уравнение. Если решить его, то можно найти длину и ширину комнаты.
Первое что можно сделать это выполнить умножение в левой части уравнения:
2x2 = 8
В результате этого преобразования переменная x перешла во вторую степень. А мы говорили, что если переменная, входящая в уравнение, возведенá во вторую степень (в квадрат), то такое уравнение является уравнением второй степени или квадратным уравнением.
Для решения нашего квадратного уравнения воспользуемся изученными ранее тождественными преобразованиями. В данном случае можно разделить обе части на 2
Теперь воспользуемся квадратным корнем. Если x2 = 4, то . Отсюда x = 2 и x = −2.
Через x была обозначена ширина комнаты. Ширина не должна быть отрицательной, поэтому в расчёт берём только значение 2. Такое часто бывает при решении задачи, в которых применяется квадратное уравнение. В ответе получаются два корня, но условию задачи удовлетворяет только один из них.
В ответе получаются два корня, но условию задачи удовлетворяет только один из них.
А длина была обозначена через 2x. Значение x теперь известно, подставим его в выражение 2x и вычислим длину:
2x = 2 × 2 = 4
Значит длина равна 4 м, а ширина 2 м. Это решение удовлетворяет условию задачи, поскольку площадь комнаты равна 8 м2
4 × 2 = 8 м2
Ответ: длина комнаты составляет 4 м, а ширина 2 м.
Пример 2. Огородный участок, имеющий форму прямоугольника, одна сторона которого на 10 м больше другой, требуется обнести изгородью. Определить длину изгороди, если известно, что площадь участка равна 1200 м2
Решение
Длина прямоугольника, как правило, больше его ширины. Пусть ширина участка x метров, а длина (x + 10) метров. Площадь участка составляет 1200 м2. Умножим длину участка на его ширину и приравняем к 1200, получим уравнение:
x(x + 10) = 1200
Решим данное уравнение. Для начала раскроем скобки в левой части:
Для начала раскроем скобки в левой части:
Перенесём 1200 из правой части в левую часть, изменив знак. В правой части останется 0
Решим получившееся уравнение с помощью формул:
Несмотря на то, что квадратное уравнение имеет два корня, в расчёт берём только значение 30. Потому что ширина не может выражаться отрицательным числом.
Итак, через x была обозначена ширина участка. Она равна тридцати метрам. А длина была обозначена через выражение x + 10. Подставим в него найденное значение x и вычислим длину:
x + 10 = 30 + 10 = 40 м
Значит длина участка составляет сорок метров, а ширина тридцать метров. Эти значения удовлетворяют условию задачи, поскольку если перемножить длину и ширину (числа 40 и 30) получится 1200 м2
40 × 30 = 1200 м2
Теперь ответим на вопрос задачи. Какова длина изгороди? Чтобы её вычислить нужно найти периметр участка.
Периметр прямоугольника это сумма всех его сторон. Тогда:
Тогда:
P = 2(a + b) = 2 × (40 + 30) = 2 × 70 = 140 м.
Ответ: длина изгороди огородного участка составляет 140 м.
Задания для самостоятельного решения
Задание 1. Решить уравнение:
Решение:
Ответ: 2; −2.
Задание 2. Решить уравнение:
Решение:
Ответ: корней нет.
Задание 3. Решить уравнение:
Решение:
Ответ: 3; −3.
Задание 4. Решить уравнение, используя выделение полного квадрата:
Решение:
Ответ: 3; −13.
Задание 5. Решить уравнение, используя выделение полного квадрата:
Решение:
Ответ: 12; 4.
Задание 6. Решить уравнение, используя выделение полного квадрата:
Решение:
Ответ: 7; 5.
Задание 7. Решить уравнение:
Решение:
Ответ: 0; 1.
Задание 8. Решить уравнение:
Решение:
Ответ: 0; −3.
Задание 9. Решить уравнение:
Решение:
Ответ: 7; −7.
Задание 10. Решить уравнение:
Решение:
Ответ:Задание 11. Решить уравнение:
Решение:
Ответ: 5; −5.
Задание 12. Решить уравнение:
Решение:
Ответ: 7; 2
Задание 13. Решить уравнение:
Решение:
Ответ: корней нет.
Задание 14. Решить уравнение:
Решение:
Ответ:Задание 15. Решить уравнение:
Решение:
Ответ: 1; −5.
Задание 16. Решить уравнение:
Решение:
Ответ: 5; −9.
Задание 17. Решить уравнение:
Решение:
Ответ: −3; −4.
Задание 18. Решить уравнение:
Решение:
Ответ: .
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Свойства коэффициентов квадратного уравнения — Квадратные уравнения
Этот способ решения помогает не только сэкономить время, но и развить внимание.
Свойство 1
Дано
квадратное уравнение ax2 + bx + c = 0. Если a + b + c = 0 (сумма коэффициентов), то
x1 = 1, x2 = c/a
Свойство 2
Дано квадратное уравнение ax2 + bx + c = 0.
Если a - b + c = 0 (сумма коэффициентов), когда b взято с противоположным знаком или a + c = b, то
x1 = -1, x2 = -c/a
Пример:
341x2 + 290x — 51 = 0
Решение:
Здесь, a = 341, b = 290, c = -51.
Проверим удовлетворяют ли коэффициенты условию
свойства 2
341 — 51 = 290. Получим а + с = b. Следовательно, мы
можем воспользоваться свойством 2.
x1 = -1 и х2 = 51/341
Ответ: -1; 51/341.
Свойство 3
Если в квадратном уравнении ax2 + bx + c = 0. Коэффициент b представлен в виде 2k, т. е. является четным числом, то формулу корней уравнения можно переписать в более простом виде
е. является четным числом, то формулу корней уравнения можно переписать в более простом виде
D = (b/2)2 + a*c
Пример:
3x2 + 2,2x — 0,16 = 0
Решение:
Коэффициент b = 2,2
D = 1,12 + 3 * (-0,16) = 1,69
x1,2 = (-1,1 ± 1,3)/3
Правила решения квадратных уравнений | Партизанская математика
Мало просто научиться применять эффективные способы решений квадратных уравнений. Необходимо соблюдать ещё некоторые правила, чтобы знать все тонкости применения этих приёмов и не совершать случайных ошибок. Мы собрали такие правила в отдельный список.
☝ Сокращайте.Самое простое правило, которое большинство учеников соблюдает. Если у коэффициентов квадратного уравнения есть общий множитель, то на него нужно сократить:
В противном случае можно глубоко закопаться при решении первоначального уравнения.
Иногда старшеклассники получают после преобразований полное квадратное уравнение, но при этом одночлены расположены не в порядке убывания их степени. Например, вот так:
Дальше ученик, понадеявшись на свой могучий ум, решает это уравнение. Рассуждает он так: «Чему равны коэффициенты a, b, и c и так видно без перестановки. Я лучше не буду тратить время на переписывание и сразу посчитаю дискриминант». Интересно, что памяти обычно хватает, чтобы нормально посчитать дискриминант. Но когда дело доходит до корней, ученик забывает, что трёхчлен слева у него не переставлен, и стабильно путает коэффициенты. Это приводит к неправильному решению.
Чтобы этого не происходило, достаточно сделать перестановку:
В таком виде уже можно решать любым удобным способом.
☝ Домножьте на минус один.
Получив квадратное уравнение в таком виде:
ученики резво начинают его решать через дискриминант. В принципе, при последовательном применении алгоритма ошибок не должно быть. Однако, довольно часто вмешивается человеческий фактор. При отрицательном первом коэффициенте ученики часто забывают про знак «минус» и получают ошибочные корни. Чтобы перестраховаться, достаточно домножить уравнение на –1, и получить положительный коэффициент при x²:
Вот такое уравнение гораздо приятнее решать.
☝ Используйте целочисленные коэффициенты.Рассмотрим уравнение:
Не стоит бросаться в решение с головой и сразу начинать считать дискриминант. Наверняка, в конечном счёте у вас всё получится, но всё же стоит упростить себе задачу. Дробные коэффициенты очень неудобны, поэтому от них надо постараться избавится. Для этого нужно домножить уравнение на подходящее число. В примере выше нужно домножить на 5. Но судя по нашему опыту, ученики не сразу это делают. Чаще всего они домножают на 10, а потом, заметив, что все коэффициенты чётные, сокращают на 2 (см. первое правило).
В примере выше нужно домножить на 5. Но судя по нашему опыту, ученики не сразу это делают. Чаще всего они домножают на 10, а потом, заметив, что все коэффициенты чётные, сокращают на 2 (см. первое правило).
Получается вот такое удобное уравнение:
☝ Применяйте эффективные способы решения.В прошлой статье мы рассмотрели несколько способов решения квадратного уравнения. Однако, несмотря на их высокую эффективность, большинство учеников их не применяет, даже когда о них знает. Эти приёмы остаются лишь забавными фокусами, которыми можно удивить друзей.
Чтобы реально овладеть этими методами, мало про них просто прочитать. Их нужно многократно использовать. Вместо этого даже вне стрессовой ситуации (например, во время подготовки к экзаменам) ученики решают неэффективными, но хорошо им знакомыми приёмами. Происходит закрепление неэффективных шаблонов. Из такой петли слабых решений необходимо вырываться через практику. После изучения новых методов, старайтесь сразу пробовать их применять.
После изучения новых методов, старайтесь сразу пробовать их применять.
Отметим, что это правило действует только во время подготовки, то есть когда вы только учитесь новым приёмам. На самом же экзамене нужно выбирать самый эффективный способ лишь из тех, которые вы освоили. Там уже опасно применять новомодные приёмы решения, если не выработали навык их использования.
☝ За 10 секунд не решили устно — считайте письменно.Часто ученики «подвисают», пытаясь решить какое-нибудь уравнение сразу в уме. Это похвально, но если вы ищете корень больше 10 секунд, это значит одно из двух. Либо вы пока не до конца освоили этот метод, чтобы решать его в уме, и лучше пока записывать вычисления. Либо вы недооценили задачу и нужно использовать другой метод. Например, второе бывает, когда ученик пытается подобрать корни через теорему Виета в уравнении, у которого иррациональные корни.
☝ Не спешите перемножать числа в дискриминанте.
Даже решение очень страшного уравнения можно упростить, не кидаясь сразу вычислять значение дискриминанта. Нас ведь интересует не он сам, а квадратный корень из него. Рассмотрим пример:
Обычно его начинают решать так:
Мало того, что при расчётах появились неприятные четырёхзначные числа, так дальше нам ещё нужно извлечь корень из полученного числа! Всё это довольно трудоёмко.
Проще решать задачу иначе. Не перемножать, а постепенно вычленять из дискриминанта множители-полные квадраты:
Можно было бы и из последней скобки вычленить полный квадрат, но уже и так понятно, что 196 — это полный квадрат.
☝ Используйте теорему Виета для проверки корней.Обычно теорему Виета используют для подбора корней. Но на самом деле у неё есть ещё одно полезное применение. Как только вы каким-либо способом получили корни их всегда можно дополнительно легко проверить. По теореме Виета, если корни верные, то их произведение будет равно свободному члену, делённому на первый коэффициент, т.е. c/a.
По теореме Виета, если корни верные, то их произведение будет равно свободному члену, делённому на первый коэффициент, т.е. c/a.
В подавляющем большинстве примеров квадратные уравнения имеют целочисленные коэффициенты. Если они дробные, то их всегда можно (и нужно!) привести к целым. Однако, при вычислениях может получиться, что какой-то из коэффициентов нерациональный. Если такое случается, то скорее всего при обратной замене переменной. И это подозрительно. Нужно ещё раз перепроверить предыдущие вычисления. В очень редких случаях (если экзамены высокого уровня) бывает, что так и было задумано. Но в реальности скорее всего до этого была сделана ошибка.
Решение полных квадратных уравнений
Покажем, как вывести эти формулы:Последнюю формулу можно существенно упростить в случае, если b делится на 2, то есть b = 2k. Тогда формула для корней квадратного уравнения будет иметь вид
,
где k =

Полученную формулу для корней квадратного уравнения в случае четного коэффициента b можно переписать и без использования буквы k:
или , где D1 = (
)2 — ac.Очевидно, полученные формулы для корней полных квадратных уравнений можно использовать и для решения неполных уравнений, хотя проще использовать способы решения неполных квадратных уравнений.
Пример 1. Решить квадратное уравнение 4x2 -28x + 49 = 0.
Решение.
Вычислим дискриминант квадратного трехчлена. У нас a = 4, b = -28, c = 49.
Так как b = -28 — четное число, то вычислим дискриминант D1 :
D1 = (
)2 — ac = (-14)2 — 4*49 = 196 — 196 = 0, следовательно, уравнение имеет единственный кореньx = .
Это уравнение также можно решить без вычисления дискриминанта, преобразовав квадратный трехчлен по формуле сокращенного умножения:
4x2 -28x + 49 = 0 (2x — 7)2 = 0 2x = 7 x =
.
Ответ:
.Пример 2. Решить уравнение .
Решение.
Приведем к общему знаменателю левую часть уравнения:
Умножив обе части уравнения на -6, получим x2 + 3x = 0. Это неполное квадратное уравнение решим способом разложения на множители:
.
Ответ: -3,0.
Пример 3. Решить уравнение .
Решение.
Приведем к общему знаменателю левую часть и правую части уравнения:
.
Умножив обе части уравнения на 15, получим:
6x2 + 3x = 20x-10 6x2 + 3x — 20x + 10 = 0 6x2 — 17x + 10 = 0.
Вычислим дискриминант квадратного трехчлена: a = 6, b = -17, c = 10,
D = b2 — 4ac = (-17)2 — 4*6*10 = 289 — 240 = 49 > 0, следовательно, уравнение имеет два действительных корня.
Ответ:
, 2.Пример 4. Решить уравнение .
Решение.
Вычислим дискриминант квадратного трехчлена. У нас a = 1, b = 2√2, c = 1.
Так как b = 2√2, то есть b делится на 2 (
= √2), вычислим дискриминант D1:D1 = (
)2 — ac = (√2)2 — 1*1 = 1 > 0. 2-4·3·2=1-24=-23\)
2-4·3·2=1-24=-23\)
Найдем корни уравнения по формулам \(x_1=\frac{-b + \sqrt{D}}{2a}\) и \(x_1=\frac{-b — \sqrt{D}}{2a}\).
\(x_1=\frac{-1 + \sqrt{-23}}{2·3}\)
\(x_2=\frac{-1- \sqrt{-23}}{2·3}\)
Оба корня невычислимы, так как арифметический квадратный корень из отрицательного числа не извлекается.
Ответ: нет корней.
Обратите внимание, в первом уравнении у нас два корня, во втором – один, а в третьем – вообще нет корней. Это связано со знаком дискриминанта (подробнее смотри тут).
Также многие квадратные уравнения могут быть решены с помощью обратной теоремы Виета. Это быстрее, но требует определенного навыка.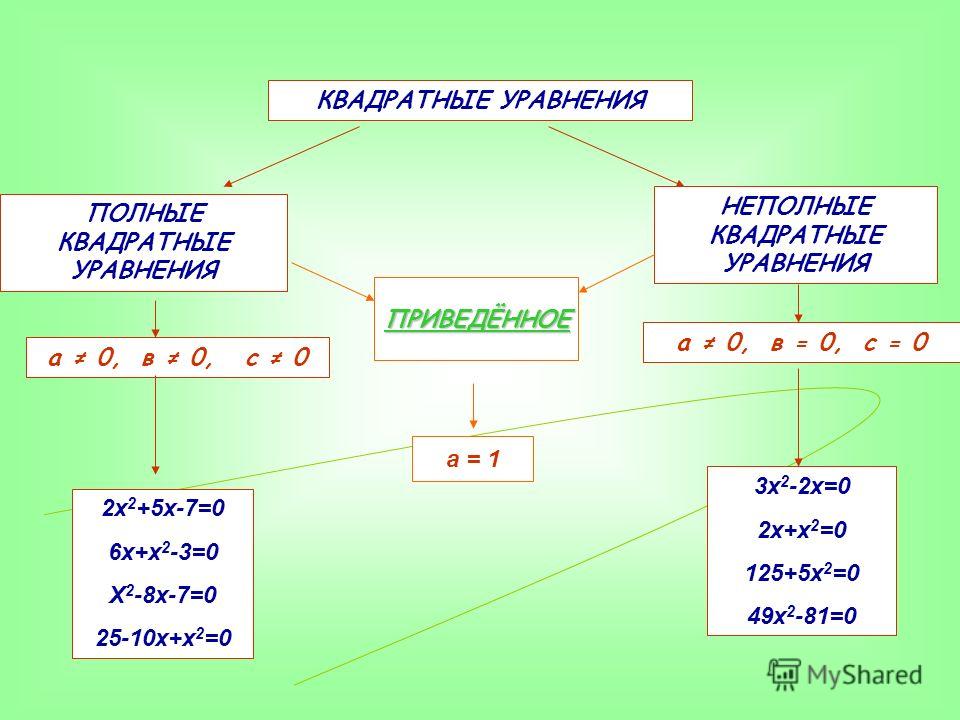 2-7x+6=0\).
2-7x+6=0\).
Решение: Согласно обратной теореме Виета, корнями уравнения будут такие числа, которые в произведении дадут \(6\), а в сумме \(7\). Простым подбором получаем, что эти числа: \(1\) и \(6\). Это и есть наши корни (можете проверить решением через дискриминант).
Ответ: \(x_1=1\), \(x_2=6\).
Данную теорему удобно использовать с приведенными квадратными уравнениями, имеющими целые коэффициенты \(b\) и \(c\).
Примеры решения полных, неполных и приведенных квадратных уравнений
Смотрите также:
Квадратные уравнения (шпаргалка)
Из истории возникновения квадратных уравнений
Из истории возникновения квадратных уравнений
Алгебра возникла в связи с
решением разнообразных задач при помощи
уравнений. Обычно в задачах требуется
найти одну или несколько неизвестных,
зная при этом результаты некоторых
действий, произведенных над искомыми
и данными величинами. Такие задачи
сводятся к решению одного или системы
нескольких уравнений, к нахождению
искомых с помощью алгебраических
действий над данными величинами. В
алгебре изучаются общие свойства
действий над величинами.
Такие задачи
сводятся к решению одного или системы
нескольких уравнений, к нахождению
искомых с помощью алгебраических
действий над данными величинами. В
алгебре изучаются общие свойства
действий над величинами.
Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне.
Квадратные уравнения в Древнем Вавилоне
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
Правило решения этих уравнений,
изложенное в вавилонских текстах,
совпадает по существу с современным,
однако неизвестно, каким образом дошли
вавилоняне до этого правила. Почти все
найденные до сих пор клинописные тексты
приводят только задачи с решениями,
изложенными в виде рецептов, без указаний
относительно того, каким образом они
были найдены. Несмотря на высокий уровень
развития алгебры в Вавилоне, в клинописных
текстах отсутствуют понятие отрицательного
числа и общие методы решения квадратных
уравнений.
Почти все
найденные до сих пор клинописные тексты
приводят только задачи с решениями,
изложенными в виде рецептов, без указаний
относительно того, каким образом они
были найдены. Несмотря на высокий уровень
развития алгебры в Вавилоне, в клинописных
текстах отсутствуют понятие отрицательного
числа и общие методы решения квадратных
уравнений.
В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.
Вот, к примеру, одна из его задач.
Задача 2. «Найти два числа, зная, что их сумма равна 20, а произведение — 96».
Диофант рассуждает следующим
образом: из условия задачи вытекает,
что искомые числа не равны, так как если
бы они были равны, то их произведение
равнялось бы не 96,
а 100.
Таким образом, одно из них будет больше
половины их суммы, т. е.
10 + х. Другое же меньше,
т. е. 10 —
х. Разность между ними 2х. Отсюда уравнение:
е.
10 + х. Другое же меньше,
т. е. 10 —
х. Разность между ними 2х. Отсюда уравнение:
(10+x)(10—x) =96,
или же
100 —x2 = 96.
x2 — 4 = 0
Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = — 2 для Диофанта не существует, так как греческая математика знала только положительные числа.
Если решить эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то можно прийти к решению уравнения:
y (20-y)=96
y2 — 20y+96=0
Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения.
Квадратные уравнения в Индии
Задачи на квадратные уравнения встречаются уже в астрономическом трактате «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:
ax2 + bх
= с, а>
0. (1)
(1)
В уравнении (1) коэффициенты, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары.
Задача 3.
«Обезьянок резвых стая | А двенадцать по лианам |
Всласть поевши, развлекалась | Стали прыгать, повисая |
Их в квадрате часть восьмая | Сколько ж было обезьянок, |
На поляне забавлялась | Ты скажи мне, в этой стае?» |
Решение Бхаскары свидетельствует
о том, что автор знал о двузначности
корней квадратных уравнений.
Соответствующее задаче 3 уравнение:
,
Бхаскара пишет под видом:
x2 — 64x = — 768
и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 322, получая затем:
x2 — б4х + 322 = -768 + 1024,
(х — 32)2 = 256,
х — 32= ±16,
x1 = 16, x2 = 48.
Квадратные уравнения у Аль-Хорезми
В алгебраическом трактате Аль-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
«Квадраты равны корням», т. е. ах2 = bх.
«Квадраты равны числу», т. е. ах2 = с.
«Корни равны числу», т. е. ах = с.
«Квадраты и числа равны корням», т. е. ах2 + с = bх.
«Квадраты и корни равны числу», т. е. ах2 + bх =с.

«Корни и числа равны квадратам», т. е. bх + с == ах2.
Для Аль-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида Аль-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений Аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.
Приведем пример.
Задача 4.
«Квадрат и число 21
равны 10
корням. Найти корень» (подразумевается
корень уравнения х2 + 21 = 10х).
Решение: раздели пополам число корней, получишь 5, умножь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от 5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.
Трактат Аль-Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.[3,75]
Квадратные уравнения в Европе XII—XVII в.
Формы решения квадратных уравнений по образцу Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202г. итальянским математиком Леонардом Фибоначчи. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел.
Эта книга способствовала
распространению алгебраических знаний
не только в Италии, но и в Германии,
Франции и других странах Европы. Многие
задачи из этой книги переходили почти
во все европейские учебники XIV-XVII
вв. Общее правило решения квадратных
уравнений, приведенных к единому
каноническому виду x2 + bх
= с при всевозможных
комбинациях знаков и коэффициентов b,
c,
было сформулировано в Европе в 1544 г.
М.Штифелем.
Многие
задачи из этой книги переходили почти
во все европейские учебники XIV-XVII
вв. Общее правило решения квадратных
уравнений, приведенных к единому
каноническому виду x2 + bх
= с при всевозможных
комбинациях знаков и коэффициентов b,
c,
было сформулировано в Европе в 1544 г.
М.Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.[5,12].
Истоки алгебраических методов
решения практических задач связаны с
наукой древнего мира. Как известно из
истории математики, значительная часть
задач математического характера,
решаемых египетскими, шумерскими,
вавилонскими писцами-вычислителями
(XX—VI вв. до н. э.), имела
расчетный характер. Однако уже тогда
время от времени возникали задачи, в
которых искомое значение величины
задавалось некоторыми косвенными
условиями, требующими, с нашей современной
точки зрения, составления уравнения
или системы уравнений. Первоначально
для решения таких задач применялись
арифметические методы. В дальнейшем
начали формироваться начатки алгебраических
представлений. Например, вавилонские
вычислители умели решать задачи,
сводящиеся с точки зрения современной
классификации к уравнениям второй
степени. Был создан метод решения
текстовых задач, послуживший в дальнейшем
основой для выделения алгебраического
компонента и его независимого изучения.
Однако уже тогда
время от времени возникали задачи, в
которых искомое значение величины
задавалось некоторыми косвенными
условиями, требующими, с нашей современной
точки зрения, составления уравнения
или системы уравнений. Первоначально
для решения таких задач применялись
арифметические методы. В дальнейшем
начали формироваться начатки алгебраических
представлений. Например, вавилонские
вычислители умели решать задачи,
сводящиеся с точки зрения современной
классификации к уравнениям второй
степени. Был создан метод решения
текстовых задач, послуживший в дальнейшем
основой для выделения алгебраического
компонента и его независимого изучения.
Это изучение осуществлялось уже
в другую эпоху сначала арабскими
математиками (VI—Х
вв. н. э.), выделившими характерные
действия, посредством которых уравнения
приводились к стандартному виду
приведение подобных членов, перенос
членов из одной части уравнения в другую
с переменой знака. А затем европейскими
математиками Возрождения, в итоге
длительного поиска создавшими язык
современной алгебры, использование
букв, введение символов арифметических
операций, скобок и т. д. На рубеже
XVI—XVII вв. алгебра как
специфическая часть математики,
обладающая своим предметом, методом,
областями приложения, была уже
сформирована. Дальнейшее ее развитие,
вплоть до нашего времени, состояло в
совершенствовании методов, расширении
области приложений, уточнении понятий
и связей их с понятиями других разделов
математики.
д. На рубеже
XVI—XVII вв. алгебра как
специфическая часть математики,
обладающая своим предметом, методом,
областями приложения, была уже
сформирована. Дальнейшее ее развитие,
вплоть до нашего времени, состояло в
совершенствовании методов, расширении
области приложений, уточнении понятий
и связей их с понятиями других разделов
математики.
Итак, ввиду важности и обширности материала, связанного с понятием уравнения, его изучение в современной методике математики связано с тремя главными областями своего возникновения и функционирования.
Для того чтобы решить любое квадратное уравнение, надо знать:
формулу нахождения дискриминанта;
формулу нахождения корней квадратного уравнения;
алгоритмы решения уравнений данного вида.
уметь:
решать полные квадратные уравнения;
решать приведенные квадратные уравнения;
находить ошибки в решенных уравнениях и исправлять их;
делать проверку.

Решение каждого уравнения складывается из двух основных частей:
Обобщение способов деятельности учащихся при решении квадратных уравнений происходит постепенно. Можно выделить следующие этапы при изучении темы «Квадратные уравнения»:
I этап – «Решение неполных квадратных уравнений».
II этап – «Решение полных квадратных уравнений».
III этап – «Решение приведенных квадратных уравнений».
На первом этапе рассматриваются неполные квадратные уравнения. Так как сначала математики научились решать неполные квадратные уравнения, поскольку для этого не пришлось, как говорится, ничего изобретать. Это уравнения вида: ах2 = 0, ах2 + с = 0, где с≠ 0, ах2 + bх = 0, где b ≠ 0. Рассмотрим решение несколько таких уравнений:
1. Если ах2 = 0. Уравнения такого вида решаются по алгоритму:
1) найти х2;
2) найти х.
Например, 5х2 = 0 . Разделив обе части уравнения на 5
получается: х2 = 0, откуда х = 0.
2. Если ах2 + с = 0, с≠ 0 Уравнения данного вида решаются по алгоритму:
1) перенести слагаемые в правую часть;
2) найти все числа, квадраты которых равны числу с.
Например, х2 — 5 = 0,Это уравнение равносильно уравнению х2 = 5. Следовательно, надо найти все числа, квадраты которых равны числу 5. Таких чисел только два и — . Таким образом, уравнение х2 — 5 = 0 имеет два корня: x1 = , x2 = — и других корней не имеет.
3. Если ах2 + bх = 0, b ≠ 0. Уравнения такого вида решаются по алгоритму:
1) перенести общий множитель за скобки;
2) найти x1, x2.
Например, х2 —
3х = 0. Перепишем уравнение х2 – 3х = 0 в виде х ( х – 3 ) =
0. Это уравнение имеет, очевидно, корни
x1 = 0, x2 = 3. Других корней оно не имеет, ибо если
в него подставить вместо х любое число,
отличное от нуля и 3, то в левой части
уравнения х ( х – 3 ) = 0 получится число,
не равное нулю.
Итак, данные примеры показывают, как решаются неполные квадратные уравнения:
1) если уравнение имеет вид ах2 = 0, то оно имеет один корень х = 0;
2) если уравнение имеет вид ах2 + bх = 0, то используется метод разложения на множители: х (ах +b) = 0; значит, либо х = 0, либо ах + b = 0. В итоге получается два корня: x1 = 0; x2 = — ;
3) если уравнение имеет вид ах2 + с = 0, то его преобразуют к виду ах2 = — с и далее х2.= — В случае, когда — < 0, уравнение х2 = — не имеет корней (значит, не имеет корней и исходное уравнение ах2 + с = 0). В случае, когда — > 0, т.е. — = m , где m>0, уравнение х2 = m имеет два корня
= , = -, (в этом случае допускается более короткая запись = .
Таким образом, неполное квадратное уравнение может иметь два корня, один корень, ни одного корня.
На втором этапе осуществляется
переход к решению полного квадратного
уравнения.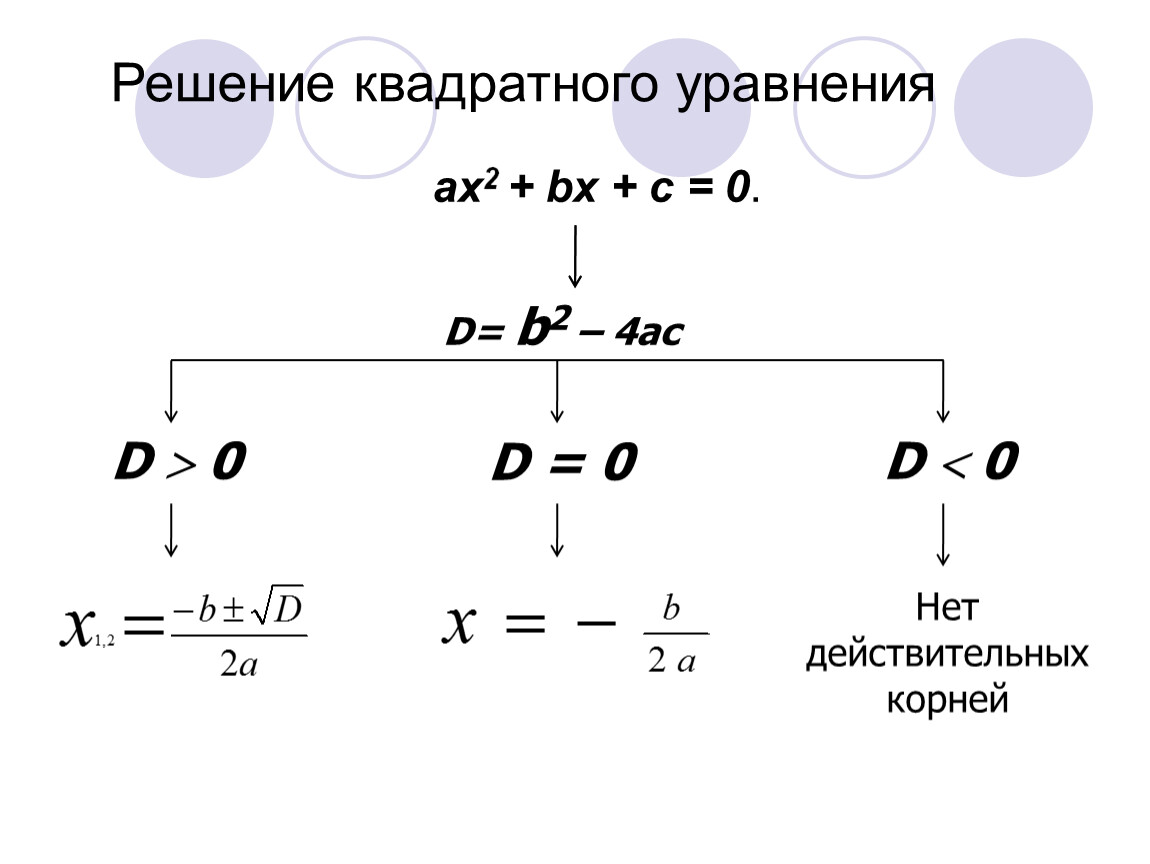 Это уравнения вида ах2 +
bx
+ c
= 0, где a,b,c
– заданные числа, а ≠ 0, х – неизвестное.
Это уравнения вида ах2 +
bx
+ c
= 0, где a,b,c
– заданные числа, а ≠ 0, х – неизвестное.
Любое полное квадратное уравнение можно преобразовать к виду , для того, чтобы определять число корней квадратного уравнения и находить эти корни. Рассмотриваются следующие случаи решения полных квадратных уравнений: D < 0, D = 0, D > 0.
1. Если D < 0, то квадратное уравнение ах2 + bx + c = 0 не имеет действительных корней.
Например, 2х2 + 4х + 7 = 0. Решение: здесь а = 2, b = 4, с = 7.
D = b2 – 4ас = 42 – 4*2*7 = 16 – 56 = — 40.
Так как D < 0, то данное квадратное уравнение не имеет корней.
2. Если D = 0, то квадратное уравнение ах2 + bx + c = 0 имеет один корень, который находится по формуле .
Например, 4х – 20х + 25 = 0. Решение: а = 4, b = — 20, с = 25.
D = b2 – 4ас = (-20) 2 – 4*4*25 = 400 – 400 = 0.
Так как D
= 0, то данное уравнение имеет один корень. Этот корень находится по формуле
.
Значит,
Этот корень находится по формуле
.
Значит,
3. Если D > 0, то квадратное уравнение ах2 + bx + c = 0 имеет два корня, которые находятся по формулам: ; (1)
Например, 3х2 +8х – 11 = 0. Решение: а = 3, b = 8, с = -11. D = b2 – 4ас = 82 – 4*3*(-11) = 64 + 132 = 196.
Так как D > 0, то данное квадратное уравнение имеет два корня. Эти корни находятся по формулам:
.
Составляется алгоритм решения уравнения вида ах2 + bx + c = 0.
Вычислить дискриминант D по формуле D = b2 – 4ас.
2. Если D < 0, то квадратное уравнение ах2 + bx + c = 0 не имеет корней.
3. Если D = 0, то квадратное уравнение имеет один корень, который находится по формуле
4. Если D > 0, то квадратное уравнение ах2 + bx + c = 0 имеет два корня: ; .
Это алгоритм универсален, он
применим как к неполным, так и к полным
квадратным уравнениям. Однако неполные
квадратные уравнения обычно по этому
алгоритму не решают.
Однако неполные
квадратные уравнения обычно по этому
алгоритму не решают.
Математики – люди практичные, экономные, поэтому пользуются формулой: . (2)
Итак, можно сделать вывод, что квадратные уравнения можно решать подробно, используя сформулированное выше правило; можно – записать сразу формулу (2) и с ее помощью делать необходимые выводы. [1,98].
На третьем этапе рассматриваются приведенные квадратные уравнения, которые имеют вид х2 +px + q = 0 (3), где p и q – данные числа. Число p – коэффициент при х, а q – свободный член. Дискриминант уравнения равен: D = p2 – 4q. Рассматривают 3 случая:
1. D > 0, тогда уравнение (3) имеет два корня, вычисляемые по формуле . (4)
2. D = 0, тогда уравнение (3) имеет единственный корень, или, как горят, два совпадающих корня:
3. D
< 0, то уравнение не имеет корней. Обычно
в случае приведенного квадратного
уравнения (3) вместо D
рассматривается выражение
,
имеющее тот же знак, что и D. При этом формулу корней приведенного
квадратного уравнения (4) записывают
так:
При этом формулу корней приведенного
квадратного уравнения (4) записывают
так:
Отсюда следует, что:
если то уравнение (3) имеет два корня;
если то уравнение имеет два совпадающих корня;
если то уравнение не имеет корней.
Важным моментом в изучении квадратных уравнений является рассмотрение теоремы Виета, которая утверждает наличие зависимости между корнями и коэффициентами приведенного квадратного уравнения.
Теорема Виета. Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Иначе говоря, если x1 и x2 — корни уравнения х2 +px + q = 0, то
x1 + x2 = — p,
x1 x2 = q. (5)
Данные формулы называют формулами
Виета в честь французского математика
Ф. Виета (1540-1603), который ввел систему
алгебраических символов, разработал
основы элементарной алгебры. Он был
одним из первых, кто числа стал обозначать
буквами, что существенно развило теорию
уравнений.
Виета (1540-1603), который ввел систему
алгебраических символов, разработал
основы элементарной алгебры. Он был
одним из первых, кто числа стал обозначать
буквами, что существенно развило теорию
уравнений.
Например, приведенное уравнение х2 — 7х +10 = 0 имеет корни 2 и 5. Сумма корней равна 7, а произведение равно 10. Видно, что сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Справедлива также теорема, обратная теореме Виета.
Теорема, обратная теореме Виета. Если для чисел x1, x2, p, q справедливы формулы (5), то x1 и x2 — корни уравнения х2 +px + q = 0 [2,49].
Теорема Виета и теорема, обратная ей, часто применяются при решении различных задач.
Например. Напишем приведенное квадратное уравнение, корнями которого являются числа 1 и -3.
По формулам Виета
– p = x1 + x2 = — 2,
q = x1 x2 = -3.
Следовательно, искомое уравнение имеет вид х2 + 2х – 3 = 0.
Сложность освоения теоремы Виета связана с несколькими обстоятельствами. Прежде всего, требуется учитывать различие прямой и обратной теоремы. В прямой теореме Виета даны квадратное уравнение и его корни; в обратной — только два числа, а квадратное уравнение появляется в заключении теоремы. Учащиеся часто совершают ошибку, обосновывая свои рассуждения неверной ссылкой на прямую или обратную теорему Виета.
Например, при нахождении корней квадратного уравнения подбором ссылаться нужно на обратную теорему Виета, а не на прямую, как часто делают учащиеся. Для того чтобы распространить теоремы Виета на случай нулевого дискриминанта, приходится условиться, что в этом случае квадратное уравнение имеет два равных корня. Удобство такого соглашения проявляется при разложении квадратного трехчлена на множители.
Квадратное уравнение — Формула, примеры
Квадратные уравнения представляют собой алгебраические выражения второй степени и имеют форму ax 2 + bx + c = 0. Слово « Quadratic » происходит от слова « Quad », что означает квадрат. Другими словами, квадратное уравнение — это «уравнение степени 2 ». Есть много сценариев, в которых используется квадратное уравнение. Знаете ли вы, что при запуске ракеты ее путь описывается квадратным уравнением? Кроме того, квадратное уравнение находит множество приложений в физике, технике и астрономии.
Слово « Quadratic » происходит от слова « Quad », что означает квадрат. Другими словами, квадратное уравнение — это «уравнение степени 2 ». Есть много сценариев, в которых используется квадратное уравнение. Знаете ли вы, что при запуске ракеты ее путь описывается квадратным уравнением? Кроме того, квадратное уравнение находит множество приложений в физике, технике и астрономии.
Квадратные уравнения — это уравнения второй степени относительно x, которые имеют два ответа на x. Эти два ответа для x также называются корнями квадратных уравнений и обозначаются как (α, β). Мы узнаем больше о корнях квадратного уравнения в нижеследующем содержании.
Что такое квадратное уравнение?
Квадратное уравнение — это алгебраическое выражение второй степени по x. Квадратное уравнение в его стандартной форме имеет вид ax 2 + bx + c = 0, где a, b — коэффициенты, x — переменная, а c — постоянный член. Первым условием того, что уравнение является квадратным уравнением, является коэффициент при x 2 является ненулевым членом (a 0). Для записи квадратного уравнения в стандартной форме сначала записывается член x 2 , затем член x и, наконец, постоянный член. Числовые значения a, b, c обычно не записываются как дроби или десятичные дроби, а записываются как целые значения.
Первым условием того, что уравнение является квадратным уравнением, является коэффициент при x 2 является ненулевым членом (a 0). Для записи квадратного уравнения в стандартной форме сначала записывается член x 2 , затем член x и, наконец, постоянный член. Числовые значения a, b, c обычно не записываются как дроби или десятичные дроби, а записываются как целые значения.
Далее в реальных математических задачах квадратные уравнения представлены в различных формах: (x — 1) (x + 2) = 0, -x 2 = -3x + 1, 5x (x + 3) = 12x, x 3 = х (х 2 + х — 3).Все эти уравнения необходимо преобразовать в стандартную форму квадратного уравнения перед выполнением дальнейших операций.
Формула квадратного уравнения
Квадратичная формула — это простейший способ найти корни квадратного уравнения. Существуют определенные квадратные уравнения, которые нелегко разложить на множители, и здесь мы можем удобно использовать эту квадратную формулу, чтобы найти корни как можно быстрее.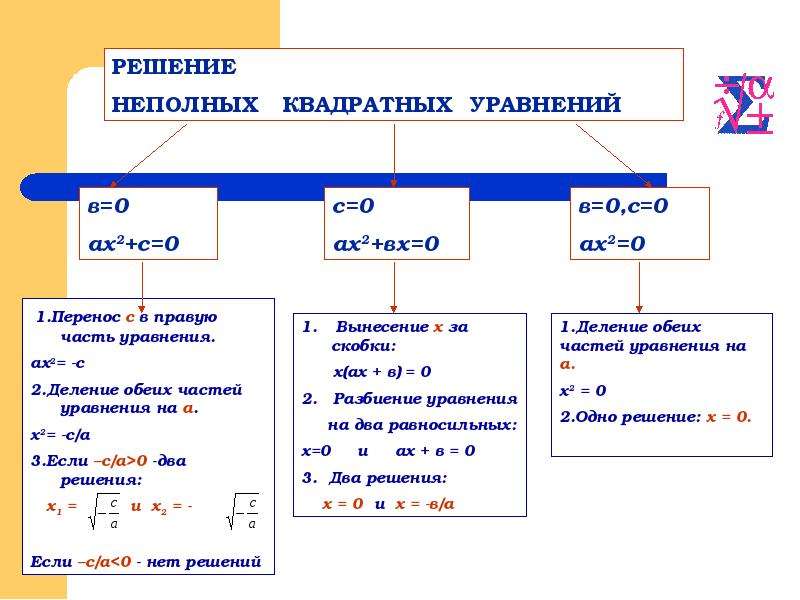 Корни квадратного уравнения также помогают найти сумму корней и произведение корней квадратного уравнения.Два корня в формуле корней квадратного уравнения представлены как одно выражение. В качестве альтернативы можно использовать положительный знак и отрицательный знак для получения двух различных корней уравнения.
Корни квадратного уравнения также помогают найти сумму корней и произведение корней квадратного уравнения.Два корня в формуле корней квадратного уравнения представлены как одно выражение. В качестве альтернативы можно использовать положительный знак и отрицательный знак для получения двух различных корней уравнения.
Квадратичная формула = [-b ± √ (b² — 4ac)] / 2a
Важные формулы для решения квадратных уравнений
Следующий список важных формул полезен при решении квадратных уравнений.
- Квадратное уравнение в его стандартной форме: ax 2 + bx + c = 0
- Дискриминант квадратного уравнения D = b 2 — 4ac
- Для D> 0 корни действительны и различны.2 \).
- Для положительных значений a (a> 0) квадратичное выражение f (x) = ax 2 + bx + c имеет минимальное значение при x = -b / 2a.
- Для отрицательного значения a (a <0) квадратичное выражение f (x) = ax 2 + bx + c имеет максимальное значение при x = -b / 2a.

- Для a> 0 диапазон квадратного уравнения ax 2 + bx + c = 0 равен [b 2 — 4ac / 4a, ∞)
- Для a <0 диапазон квадратного уравнения ax 2 + bx + c = 0 равен: (∞, — (b 2 — 4ac) / 4a]
Доказательство квадратичной формулы
Рассмотрим произвольное квадратное уравнение: ax 2 + bx + c = 0, a ≠ 0
Чтобы определить корни этого уравнения, действуем следующим образом:
ax 2 + bx = -c ⇒ x 2 + bx / a = -c / a
Теперь представим левую часть в виде полного квадрата, введя новый член (b / 2a) 2 с обеих сторон:
x 2 + bx / a + (b / 2a) 2 = -c / a + (b / 2a) 2
Левая часть теперь представляет собой идеальный квадрат:
(x + b / 2a) 2 = -c / a + b 2 / 4a 2 ⇒ (x + b / 2a) 2 = (b 2 — 4ac) / 4a 2
Это хорошо для нас, потому что теперь мы можем извлекать квадратные корни, чтобы получить:
x + b / 2a = ± √ (b 2 — 4ac) / 2a
x = (-b ± √ (b 2 — 4ac)) / 2a
Таким образом, завершив квадраты, мы смогли выделить x и получить два корня уравнения.
Корни квадратного уравнения
Корнями квадратного уравнения являются два значения x, которые получаются путем решения квадратного уравнения. Корни квадратного уравнения обозначаются символами alpha (α) и beta (β). Эти корни квадратного уравнения также называются нулями уравнения. Здесь мы узнаем больше о том, как определить природу корней квадратного уравнения без фактического нахождения корней уравнения.А также проверьте формулы, чтобы найти сумму и произведение корней уравнения.
Природа корней квадратного уравнения
Природу корней квадратного уравнения можно узнать, фактически не находя корни (α, β) уравнения. Это возможно, если взять значение дискриминанта, которое является частью формулы для решения квадратного уравнения. Величина b 2 — 4ac называется дискриминантом квадратного уравнения и обозначается буквой «D».На основе значения дискриминанта можно предсказать природу корней квадратного уравнения.
Дискриминант: D = b
2 — 4ac- D> 0, корни реальные и разные
- D = 0, корни действительные и равные.

- D <0, корни не существуют или корни мнимые.
Связь между коэффициентами и корнями квадратного уравнения
Коэффициент при x 2 , член x и постоянный член квадратного уравнения ax 2 + bx + c = 0 полезны для более подробного изучения свойств корней квадратного уравнения.Сумму и произведение корней квадратного уравнения можно вычислить непосредственно из уравнения, фактически не находя корни квадратного уравнения. Сумма корней квадратного уравнения равна отрицательному значению коэффициента при x, деленного на коэффициент при x 2 . Произведение корня уравнения равно постоянному члену, деленному на коэффициент при x 2 . Для квадратного уравнения ax 2 + bx + c = 0 сумма и произведение корней выглядят следующим образом.
- Сумма корней: α + β = -b / a = — Коэффициент x / Коэффициент x 2
- Произведение корней: αβ = c / a = Постоянный член / Коэффициент x 2
Квадратное уравнение также может быть составлено для заданных корней уравнения. Если α, β, являются корнями квадратного уравнения, то квадратное уравнение выглядит следующим образом.
Если α, β, являются корнями квадратного уравнения, то квадратное уравнение выглядит следующим образом.
x 2 — (α + β) x + αβ = 0
Методы решения квадратных уравнений
Квадратное уравнение можно решить, чтобы получить два значения x или два корня уравнения.Существует четыре различных метода нахождения корней квадратного уравнения. Четыре метода решения квадратных уравнений заключаются в следующем.
- Факторизация квадратного уравнения
- Формульный метод поиска корней
- Способ заполнения квадрата
- Графический метод поиска корней
Давайте подробно рассмотрим каждый из вышеперечисленных методов, чтобы понять, как использовать эти методы, их приложения и способы их использования.
Факторизация квадратного уравнения
Факторизация квадратного уравнения выполняется в несколько шагов. Для общей формы квадратного уравнения ax 2 + bx + c = 0 нам нужно сначала разделить средний член на два члена так, чтобы произведение членов было равно постоянному члену. Далее, мы можем взять общие термины из доступного термина, чтобы окончательно получить требуемые коэффициенты. Для понимания факторизации общий вид квадратного уравнения может быть представлен следующим образом.
Далее, мы можем взять общие термины из доступного термина, чтобы окончательно получить требуемые коэффициенты. Для понимания факторизации общий вид квадратного уравнения может быть представлен следующим образом.
- x 2 + (a + b) x + ab = 0
- x 2 + ax + bx + ab = 0
- х (х + а) + Ь (х + а)
- (х + а) (х + b) = 0
Давайте разберемся с факторизацией на примере ниже.
- x 2 + 5x + 6 = 0
- x 2 + 2x + 3x + 6 = 0
- х (х + 2) + 3 (х + 2) = 0
- (х + 2) (х + 3) = 0
Таким образом, два полученных фактора квадратного уравнения — это (x + 2) и (x + 3).
Квадратичная формула для поиска корней
Квадратные уравнения, которые нельзя решить методом факторизации, можно решить с помощью формулы. В формуле решения квадратного уравнения используются члены стандартной формы квадратного уравнения. С помощью приведенной ниже формулы мы можем получить два корня x, сначала используя положительный знак в формуле, а затем используя отрицательный знак. С помощью этой формулы можно решить любое квадратное уравнение.
С помощью этой формулы можно решить любое квадратное уравнение.
Помимо вышеупомянутых двух методов решения квадратных уравнений, существует еще один важный метод решения квадратного уравнения.Метод завершения квадрата квадратного уравнения также полезен для нахождения корней уравнения. Этот метод включает в себя многочисленные алгебраические вычисления и поэтому был объяснен как отдельная тема.
Способ заполнения квадрата
Метод завершения квадрата квадратного уравнения заключается в алгебраическом возведении в квадрат и упрощении, чтобы получить требуемые корни уравнения. Рассмотрим квадратное уравнение ax 2 + bx + c = 0, a ≠ 0. Чтобы определить корни этого уравнения, мы упростим его следующим образом:
- топор 2 + bx + c = 0
- топор 2 + bx = -c
- x 2 + bx / a = -c / a
Теперь представим левую часть в виде идеального квадрата, введя новый член (b / 2a) 2 с обеих сторон:
- x 2 + bx / a + (b / 2a) 2 = -c / a + (b / 2a) 2
- (x + b / 2a) 2 = -c / a + b 2 / 4a 2
- (x + b / 2a) 2 = (b 2 — 4ac) / 4a 2
- x + b / 2a = + √ (b 2 — 4ac) / 2a
Теперь, используя этот метод завершения квадрата, мы можем консолидировать значения корней уравнения. После упрощения и извлечения квадратного корня два возможных корня квадратного уравнения равны x = (-b + √ (b 2 — 4ac)) / 2a. Здесь знак «+» дает один корень, а знак «-» — другой корень квадратного уравнения. Как правило, этого подробного метода избегают, и для получения требуемых корней используется только формула.
После упрощения и извлечения квадратного корня два возможных корня квадратного уравнения равны x = (-b + √ (b 2 — 4ac)) / 2a. Здесь знак «+» дает один корень, а знак «-» — другой корень квадратного уравнения. Как правило, этого подробного метода избегают, и для получения требуемых корней используется только формула.
Построение квадратного уравнения
График квадратного уравнения ax 2 + bx + c = 0 может быть получен путем представления квадратного уравнения в виде функции y = ax 2 + bx + c.Далее, решая и подставляя значения для x, мы можем получить значения y, мы можем получить множество точек. Эти точки могут быть представлены на оси координат, чтобы получить график в форме параболы для квадратного уравнения.
Точка, где график пересекает горизонтальную ось x, является решением квадратного уравнения. Эти точки также можно получить алгебраически, приравняв значение y к 0 в функции y = ax 2 + bx + c и решив относительно x.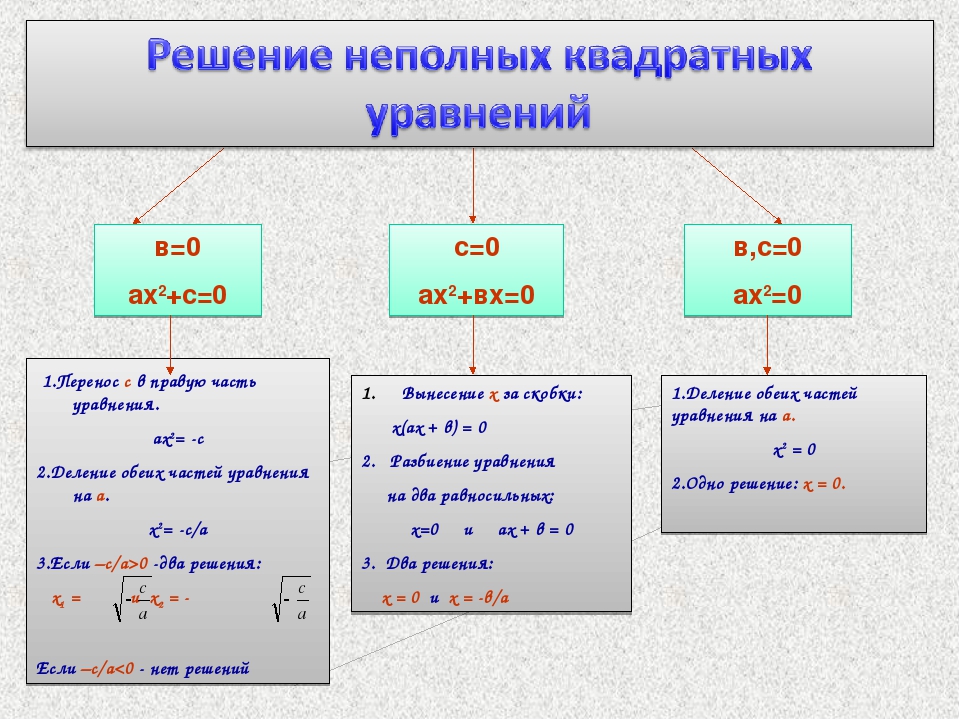 2 + b_2x + c_2 = 0 \).2 \)
2 + b_2x + c_2 = 0 \).2 \)
Максимальное и минимальное значение квадратичного выражения
Максимальное и минимальное значение квадратного уравнения ax 2 + bx + c = 0 можно увидеть на графиках ниже. Для положительных значений a (a> 0) квадратичное выражение имеет минимальное значение при x = -b / 2a, а для отрицательного значения a (a <0) квадратичное выражение имеет максимальное значение при x = -b / 2а.
Максимальное и минимальное значения квадратичных выражений дополнительно помогают найти диапазон квадратичного выражения: диапазон квадратичных выражений также зависит от значения a.Для положительных значений a (a> 0) диапазон равен [f (-b / 2a), ∞), а для отрицательных значений a (a <0) диапазон равен (-∞, f (-b / 2а)].
- Для a> 0, диапазон: [f (-b / 2a), ∞)
- Для a <0, диапазон: (-∞, f (-b / 2a)]
Решение квадратного уравнения — Советы и хитрости
Некоторые из приведенных ниже советов и приемов по квадратным уравнениям помогают упростить решение квадратных уравнений.
- Квадратные уравнения обычно решаются путем факторизации.Но в тех случаях, когда она не может быть решена путем факторизации, используется формула.
- Корни квадратного уравнения также называют нулями уравнения.
- Для квадратных уравнений, имеющих отрицательные значения дискриминанта, корни представлены с помощью комплексных чисел.
- Сумма и произведение корней квадратного уравнения могут использоваться для нахождения высших алгебраических выражений, включающих эти корни.
Связанные темы
Часто задаваемые вопросы о квадратном уравнении
Что такое квадратное уравнение?
Квадратное уравнение в математике — это уравнение второй степени вида ax² + bx + c = 0.Здесь a, b — коэффициенты, c — постоянный член, а x — переменная. Поскольку переменная x имеет вторую степень, у этого квадратного уравнения есть два корня или ответ. Корни квадратного уравнения могут быть найдены либо путем факторизации, либо с помощью формулы.
Что такое квадратичная формула?
Квадратичная формула для решения квадратного уравнения ax² + bx + c = 0: x = [-b ± √ (b² — 4ac)] / 2a. Здесь мы получаем два значения x, применяя в этой формуле символы плюс и минус.Следовательно, два возможных значения x: [-b + √ (b² — 4ac)] / 2a и [-b — √ (b² — 4ac)] / 2a.
Как применить квадратичную формулу?
Значения a, b и c применяются к квадратной формуле x = [-b ± √ (b² — 4ac)] / 2a, чтобы получить два корня квадратного уравнения.
Что является определяющим в квадратной формуле?
Величина b² — 4ac называется определителем и обозначается как D. Определитель является частью формулы корней квадратного уравнения. Определители помогают нам определить природу корней квадратного уравнения, фактически не находя корни квадратного уравнения.
Каковы реальные применения квадратных уравнений
Квадратные уравнения используются для нахождения нулей параболы и ее оси симметрии. Есть много реальных приложений квадратных уравнений. Например, его можно использовать в задачах на время бега, чтобы оценить скорость, расстояние или время во время путешествия на машине, поезде или самолете. Квадратные уравнения описывают взаимосвязь между количеством и ценой товара. Точно так же расчеты спроса и затрат также считаются задачами квадратных уравнений.Также можно отметить, что спутниковая тарелка или телескоп-рефлектор имеет форму, которая определяется квадратным уравнением.
Есть много реальных приложений квадратных уравнений. Например, его можно использовать в задачах на время бега, чтобы оценить скорость, расстояние или время во время путешествия на машине, поезде или самолете. Квадратные уравнения описывают взаимосвязь между количеством и ценой товара. Точно так же расчеты спроса и затрат также считаются задачами квадратных уравнений.Также можно отметить, что спутниковая тарелка или телескоп-рефлектор имеет форму, которая определяется квадратным уравнением.
Чем квадратные уравнения отличаются от линейных?
Линейная степень — это уравнение с одной степенью и одной переменной, а квадратное уравнение — это уравнение с двумя степенями и одной переменной. Линейное уравнение имеет вид ax + b = 0, а квадратное уравнение имеет форму ax² + bx + c = 0. Линейное уравнение имеет один корень, а квадратное уравнение имеет два корня или два ответа.Кроме того, квадратное уравнение является продуктом двух линейных уравнений.
Как упростить квадратное уравнение?
Первым шагом в процессе упрощения квадратного уравнения является преобразование его в стандартную форму ax² + bx + c = 0. Кроме того, его можно упростить, найдя его множители в процессе факторизации. Также для уравнения, которое трудно разложить на множители, оно решается с помощью формулы. Кроме того, есть несколько других способов упростить квадратное уравнение.
Кроме того, его можно упростить, найдя его множители в процессе факторизации. Также для уравнения, которое трудно разложить на множители, оно решается с помощью формулы. Кроме того, есть несколько других способов упростить квадратное уравнение.
Каковы четыре способа решения квадратного уравнения?
Четыре способа решения квадратного уравнения заключаются в следующем.
- Метод факторизации
- Метод формул
- Метод заполнения квадратов
- Метод построения графика
Как решить квадратное уравнение с помощью факторинга?
Квадратное уравнение может быть решено путем факторизации с помощью последовательности из трех шагов. Сначала разделите средний член таким образом, чтобы произведение разделенных членов было равно произведению первого и последнего членов.Предположим, квадратное уравнение имеет вид x² + (a + b) x + ab = 0, и его можно разделить как x² + ax + bx + ab = 0. В качестве второго шага возьмите общий член из первые два и последние два срока. x (x + a) + b (x + a) = 0, (x + a) (x + b) = 0. Наконец, приравняйте каждый из множителей к нулю и получите значения x. x + a = 0 и x + b = 0, и, следовательно, мы можем получить x = -a и x = -b
x (x + a) + b (x + a) = 0, (x + a) (x + b) = 0. Наконец, приравняйте каждый из множителей к нулю и получите значения x. x + a = 0 и x + b = 0, и, следовательно, мы можем получить x = -a и x = -b
Как решить квадратное уравнение, заполнив квадрат?
Квадратное уравнение, решаемое методом завершения квадрата по формуле (a + b) ² = a²
Как найти значение дискриминанта?
Значение дискриминанта в квадратном уравнении может быть найдено из переменных и постоянных членов стандартной формы квадратного уравнения ax² + bx + c = 0.Значение дискриминанта составляет D = b² — 4ac, и он помогает предсказать природу корней квадратного уравнения без фактического нахождения корней уравнения.
Как решить квадратные уравнения с помощью графиков?
Квадратное уравнение решается аналогично линейному уравнению с помощью построения графиков. Возьмем квадратное уравнение ax² + bx + c = 0 как y = ax² + bx + c. Здесь мы берем набор значений x и y и строим график. Эти две точки, где этот график пересекает ось x, являются возможными решениями этого квадратного уравнения.
Эти две точки, где этот график пересекает ось x, являются возможными решениями этого квадратного уравнения.
Как узнать природу корней квадратного уравнения?
Дискриминант помогает предсказать природу корней квадратного уравнения. Определитель квадратного уравнения ax² + bx + c = 0 равен b² — 4ac. Дискриминант обозначается как D = b² — 4ac. Если D> 0, корни действительны и различны, при D = 0 корни равны, а при D <0 корни являются мнимыми комплексными числами.
Насколько важен дискриминант в определении природы корней квадратного уравнения?
Дискриминант очень нужен, чтобы легко определить природу корней квадратного уравнения.Без дискриминанта определение природы корней уравнения — долгий процесс, поскольку нам сначала нужно решить уравнение, чтобы найти оба корня. Следовательно, дискриминант является важной и необходимой величиной, которая помогает легко определить природу корней квадратного уравнения.
Когда квадратные уравнения имеют равные корни?
У данного квадратного уравнения равные корни, если дискриминант равен нулю. Для квадратного уравнения вида ax² + bx + c = 0 дискриминант равен D = b² — 4ac = 0.Здесь оба корня равны и каждый имеет значение x = -b / 2a.
Для квадратного уравнения вида ax² + bx + c = 0 дискриминант равен D = b² — 4ac = 0.Здесь оба корня равны и каждый имеет значение x = -b / 2a.
Каковы значения детерминантов в формуле квадратов?
Определитель (D = b² — 4ac) полезен для предсказания природы корней квадратного уравнения. Для D> 0 корни действительные и различные, для D = 0 корни действительные и равные, а для D <0 корни не существуют или корни являются мнимыми комплексными числами. С помощью этого определителя и с наименьшими вычислениями мы можем выяснить природу корней квадратного уравнения.
Сколько корней имеет квадратное уравнение?
Это уравнение второй степени относительно x, отсюда получается два корня. Мы можем получить эти корни квадратного уравнения, используя формулу корней квадратного уравнения. Один корень можно получить, используя положительный знак, и мы можем получить другой корень, применив отрицательный знак в формуле.
Как решить квадратное уравнение, не используя квадратичную формулу?
Есть два метода, альтернативных квадратичной формуле. Один метод — решить квадратное уравнение путем факторизации, а другой — путем заполнения квадратов. Всего существует три метода нахождения корней квадратного уравнения.
Один метод — решить квадратное уравнение путем факторизации, а другой — путем заполнения квадратов. Всего существует три метода нахождения корней квадратного уравнения.
Как квадратная формула используется для решения квадратного уравнения?
Формула алгебры (a + b) ² = a² + 2ab + b² используется для решения квадратного уравнения и вывода квадратной формулы. Эта алгебраическая формула используется для управления квадратным уравнением и вывода квадратной формулы для нахождения корней уравнения.
Квадратные уравнения
Пример квадратного уравнения :
Функция создает красивые кривые, подобные этой:
Имя
Название Quadratic происходит от «quad», что означает квадрат, потому что переменная возводится в квадрат (например, x 2 ).
Его также называют «уравнением степени 2» (из-за «2» на x ).
Стандартная форма
Стандартная форма квадратного уравнения выглядит так:
- a , b и c — известные значения.
 a не может быть 0.
a не может быть 0.
- « x » — это переменная или неизвестно (мы еще этого не знаем).
Вот несколько примеров:
| 2x 2 + 5x + 3 = 0 | В этом a = 2 , b = 5 и c = 3 | |
| x 2 — 3x = 0 | Это немного сложнее:
| |
| 5x — 3 = 0 | Ой! Это , а не квадратное уравнение: оно отсутствует x 2 (другими словами, a = 0 , что означает, что оно не может быть квадратичным) |
Поиграйте с ним
Поиграйте с «Проводником квадратного уравнения», чтобы увидеть:
- график функции и
- решений (называемых «корнями»).

Скрытые квадратные уравнения!
Как мы видели ранее, Стандартная форма квадратного уравнения — это
Но иногда квадратное уравнение так не выглядит!
Например:
| Скрытый | в стандартной форме | a, b и c | |
|---|---|---|---|
| x 2 = 3x — 1 | Переместить все термины в левую часть | x 2 — 3x + 1 = 0 | a = 1, b = −3, c = 1 |
| 2 (w 2 — 2w) = 5 | Развернуть (снять скобки), и переместить 5 влево | 2 Вт 2 — 4 Вт — 5 = 0 | а = 2, b = −4, c = −5 |
| z (z − 1) = 3 | Разверните и переместите 3 влево | z 2 — z — 3 = 0 | а = 1, b = −1, c = −3 |
Как их решить?
« решений » квадратного уравнения — это где равно нулю .
Их еще называют « корней », а иногда « нулей »
Обычно существует 2 решения (как показано на этом графике).
И есть несколько разных способов найти решения:
Или мы можем использовать специальную квадратичную формулу :Просто введите значения a, b и c и выполняйте вычисления.
Сейчас мы рассмотрим этот метод более подробно.
О квадратичной формуле
Плюс / Минус
Прежде всего, что это за плюс / минус, который выглядит как ±?
± означает ДВА ответа:
x = −b + √ (b 2 — 4ac) 2a
x = −b — √ (b 2 — 4ac) 2a
Вот пример с двумя ответами:
Но не всегда так получается!
- Представьте, что кривая «просто касается» оси x.

- Или представьте, что кривая настолько высока , что даже не пересекает ось x!
Вот тут-то нам и помогает «Дискриминант» …
Дискриминант
Вы видите b 2 — 4ac в приведенной выше формуле? Его называют дискриминантом , потому что он может «различать» возможные типы ответов:
- когда b 2 — 4ac положительный, мы получаем два Реальных решения
- , когда он равен нулю, мы получаем только ОДНО реальное решение (оба ответа одинаковы)
- при отрицательном значении получаем пару Комплексных решений
Комплексные решения? Давайте поговорим о них после того, как мы увидим, как использовать формулу.
Использование квадратичной формулы
Просто введите значения a, b и c в квадратную формулу и произведите вычисления.
Пример: Решить 5x
2 + 6x + 1 = 0Коэффициенты: a = 5, b = 6, c = 1
Квадратичная формула: x = −b ± √ (b 2 — 4ac) 2a
Вставьте a, b и c: x = −6 ± √ (6 2 — 4 × 5 × 1) 2 × 5
Решить: x = −6 ± √ (36−20) 10
х = −6 ± √ (16) 10
х = −6 ± 4 10
х = -0. 2 или -1
2 или -1
Ответ: x = −0,2 или x = −1
И мы их видим на этом графике.
| Чек -0,2 : | 5 × ( −0,2 ) 2 + 6 × ( −0,2 ) + 1 = 5 × (0,04) + 6 × (−0,2) + 1 = 0,2 — 1,2 + 1 = 0 | |
| Чек -1 : | 5 × ( −1 ) 2 + 6 × ( −1 ) + 1 = 5 × (1) + 6 × (−1) + 1 = 5-6 + 1 = 0 |
Вспоминая формулу
Добрый читатель предложил спеть это к «Pop Goes the Weasel»:
| ♫ | «x равно минус b | ♫ | «Вокруг тутового куста | |
| плюс или минус квадратный корень | Обезьяна погналась за лаской | |||
| из квадрата b минус четыре a c | Обезьяна думала, что все было весело | |||
| ВСЕ по двум a « | Поп! идет ласка » |
Попробуйте спеть несколько раз, и она застрянет у вас в голове!
Или вы можете вспомнить эту историю:
х = −b ± √ (b 2 — 4ac) 2a
«Негативный мальчик думал, да или нет, о том, чтобы пойти на вечеринку,
на вечеринке он разговаривал с квадратным мальчиком, но не с четырьмя классными цыпочками.
В 2 часа ночи все было кончено. «
Комплексные решения?
Когда Дискриминант (значение b 2 — 4ac ) отрицателен, мы получаем пару Комплексных решений … что это означает?
Это означает, что наш ответ будет включать в себя мнимые числа. Вау!
Пример: Решить 5x
2 + 2x + 1 = 0Коэффициенты равны : a = 5, b = 2, c = 1
Обратите внимание, что дискриминант отрицательный: b 2 — 4ac = 2 2 — 4 × 5 × 1
= −16
Используйте квадратичную формулу : x = −2 ± √ (−16) 10
√ (−16) = 4 i
(где i — мнимое число √ − 1)
Итак: x = −2 ± 4 i 10
Ответ: x = −0.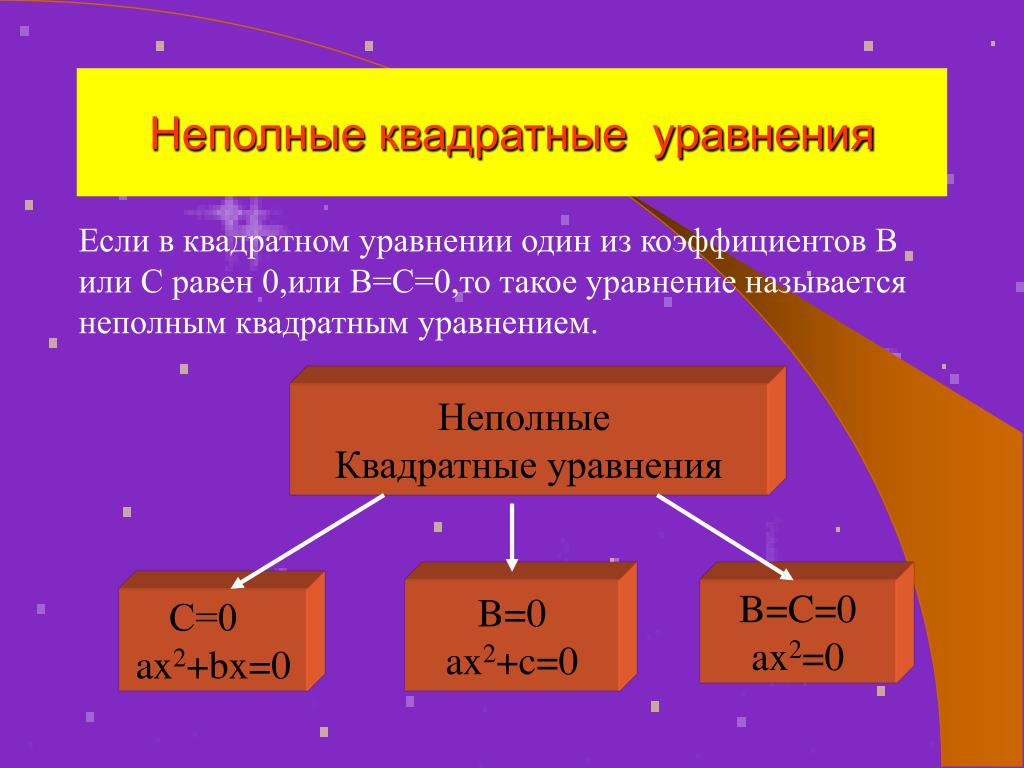 2 ± 0,4 и
2 ± 0,4 и
График не пересекает ось абсцисс. Вот почему мы пришли к комплексным числам.
В некотором смысле это проще: нам не нужно больше вычислений, оставим -0,2 ± 0,4 i .
Пример: Решить x
2 — 4x + 6,25 = 0Коэффициенты равны : a = 1, b = −4, c = 6,25
Обратите внимание, что дискриминант отрицательный: b 2 — 4ac = (−4) 2 — 4 × 1 × 6.25
= −9
Используйте квадратичную формулу : x = — (- 4) ± √ (−9) 2
√ (−9) = 3 i
(где i — мнимое число √ − 1)
Итак: x = 4 ± 3 i 2
Ответ: x = 2 ± 1,5 i
График не пересекает ось абсцисс. Вот почему мы пришли к комплексным числам.
Вот почему мы пришли к комплексным числам.
НО перевернутое зеркальное отображение нашего уравнения действительно пересекает ось x на уровне 2 ± 1,5 (примечание: отсутствует i ).
Просто интересный факт для вас!
Сводка
- Квадратное уравнение в стандартной форме: ax 2 + bx + c = 0
- Квадратные уравнения могут быть разложены на множители
- Квадратичная формула: x = −b ± √ (b 2 — 4ac) 2a
- Когда дискриминант ( b 2 −4ac ) равен:
- положительный, есть 2 реальных решения
- ноль, есть одно реальное решение
- негатив, есть 2 комплексных решения
360, 361, 1201, 1202, 2333, 2334, 3894, 3895, 2335, 2336
Решатель квадратных уравнений
Мы можем помочь вам решить уравнение вида « ax 2 + bx + c = 0 »
Просто введите
значения a, b и c ниже :
алгебра / изображений / квадратичный решатель. js
js
Это квадратичный?
Только если его можно записать в виде ax 2 + bx + c = 0 , а a — это не ноль .
Название происходит от «quad», что означает квадрат, поскольку переменная возведена в квадрат (другими словами, x 2 ).
Это все замаскированные квадратные уравнения:
| Скрытый | В стандартной форме | a, b и c |
|---|---|---|
| x 2 = 3x -1 | x 2 — 3x + 1 = 0 | a = 1, b = -3, c = 1 |
| 2 (x 2 — 2x) = 5 | 2x 2 — 4x — 5 = 0 | a = 2, b = -4, c = -5 |
| x (x-1) = 3 | x 2 — x — 3 = 0 | a = 1, b = -1, c = -3 |
| 5 + 1 / x — 1 / x 2 = 0 | 5x 2 + x — 1 = 0 | a = 5, b = 1, c = -1 |
Как это работает?
Решение квадратного уравнения может быть вычислено с помощью Квадратичной формулы :
«±» означает, что нам нужно сделать плюс И минус, так что обычно есть ДВА решения!
Синяя часть ( b 2 — 4ac ) называется «дискриминантом», потому что она может «различать» возможные типы ответов:
- при положительном результате получаем два реальных решения,
- , когда он равен нулю, мы получаем только ОДНО решение,
- при отрицательном значении получаем комплексных решения.

Подробнее см. Квадратные уравнения
Примечание: вы все еще можете получить доступ к старой версии здесь.
Факторинговая квадратичная система
«Факторинг» (или «Факторинг» в Великобритании) квадратичный:
найти, что умножить, чтобы получить квадратичный
Это называется «факторинг», потому что мы находим коэффициенты (коэффициент — это то, на что мы умножаем).
Пример:
Умножение (x + 4) и (x − 1) вместе (так называемое Расширение) дает x 2 + 3x — 4 :
Таким образом, (x + 4) и (x − 1) являются множителями x 2 + 3x — 4
На всякий случай проверим:
(х + 4) (x − 1) = x (x − 1) + 4 (x − 1)
= х 2 — х + 4х — 4
= х 2 + 3х — 4Да, (x + 4) и (x − 1) определенно являются множителями x 2 + 3x — 4
Вы видели, что расширение и факторинг — противоположности?
Расширение обычно легко, но факторинг часто может быть затруднительным .
Это все равно, что пытаться найти, какие ингредиенты
пошли на торт, чтобы сделать его таким восхитительным.
Это может быть сложно понять!
Итак, давайте попробуем пример, где мы еще не знаем факторов:
Общий коэффициент
Сначала проверьте, есть ли общие факторы.
Пример: каковы множители 6x
2 — 2x = 0?6 и 2 имеют общий множитель 2 :
2 (3x 2 — x) = 0
И x 2 и x имеют общий множитель x :
2x (3x — 1) = 0
И мы это сделали! Множители: 2x и 3x — 1 ,
Теперь мы также можем найти корней (где он равен нулю):
- 2x равно 0, когда x = 0
- 3x — 1 равно нулю, когда x = 1 3
А это график (посмотрите, как он равен нулю при x = 0 и x = 1 3 ):
Но это не всегда так просто. ..
..
Угадай и проверь
Может быть, ответ угадать?
Пример: каковы множители 2x
2 + 7x + 3?Нет общих факторов.
Давайте попробуем угадать ответ, а затем проверим, правы ли мы … нам может повезти!
Мы могли угадать (2x + 3) (x + 1):
(2x + 3) (x + 1) = 2x 2 + 2x + 3x + 3
= 2x 2 + 5x + 3 (НЕПРАВИЛЬНО)
Как насчет (2x + 7) (x − 1):
(2x + 7) (x − 1) = 2x 2 — 2x + 7x — 7
= 2x 2 + 5x — 7 (СНОВА НЕПРАВИЛЬНО)
Хорошо, как насчет (2x + 9) (x − 1):
(2x + 9) (x − 1) = 2x 2 — 2x + 9x — 9
= 2x 2 + 7x — 9 (СНОВА НЕПРАВИЛЬНО)
О нет! Мы могли долго гадать, прежде чем нам повезет.
Это не очень хороший метод. Так что давайте попробуем что-нибудь еще.
Так что давайте попробуем что-нибудь еще.
Метод для простых случаев
К счастью, есть метод, который работает в простых случаях.
С квадратным уравнением в этой форме:
Шаг 1 : Найдите два числа, которые умножаются, чтобы получить ac (другими словами, a, умноженное на c), и сложить, чтобы получить b.
Пример: 2x 2 + 7x + 3
ac равно 2 × 3 = 6 , а b равно 7
Итак, мы хотим, чтобы два числа, которые умножались вместе, давали 6 и в сумме давали 7
Фактически это делают 6 и 1 (6 × 1 = 6 и 6 + 1 = 7)
Как найти 6 и 1?
Это помогает перечислить множители ac = 6 , а затем попытаться добавить некоторые, чтобы получить b = 7 .
Факторы 6 включают 1, 2, 3 и 6.
Ага! 1 и 6 складываются с 7 и 6 × 1 = 6.
Шаг 2 : Перепишите середину с этими числами:
Перепишите 7x с помощью 6 x и 1 x:
2x 2 + 6x + x + 3
Шаг 3 : Разложите на множители первые два и последние два термина отдельно:
Первые два члена 2x 2 + 6x разложить на 2x (x + 3)
Последние два члена x + 3 в данном случае фактически не меняются
Получаем:
2x (x + 3) + (x + 3)
Шаг 4 : Если мы сделали это правильно, два наших новых члена должны иметь четко видимый общий множитель.
В этом случае мы видим, что (x + 3) является общим для обоих терминов, поэтому мы можем пойти:
Начать с: 2x (x + 3) + (x + 3)
Это: 2x (x + 3) + 1 (x + 3)
А так: (2x + 1) (x + 3)
Готово!
Проверить: (2x + 1) (x + 3) = 2x 2 + 6x + x + 3 = 2x 2 + 7x + 3 (Да)
Намного лучше, чем гадать!
Давайте снова посмотрим шаги с 1 по 4 за один раз :
| 2x 2 + 7x + 3 |
| 2x 2 + 6x + x + 3 |
| 2x (x + 3) + (x + 3) |
| 2x (x + 3) + 1 (x + 3) |
| (2x + 1) (x + 3) |
Хорошо, давайте попробуем другой пример:
Пример: 6x
2 + 5x — 6Шаг 1 : ac равно 6 × (−6) = −36 , а b равно 5
Перечислите положительные множители ac = −36 : 1, 2, 3, 4, 6, 9, 12, 18, 36
Одно из чисел должно быть отрицательным, чтобы получилось −36, поэтому, играя с несколькими разными числами, я обнаружил, что −4 и 9 работают хорошо:
−4 × 9 = −36 и −4 + 9 = 5
Шаг 2 : перепишите 5x с −4x и 9x:
6x 2 — 4x + 9x — 6
Шаг 3 : Разложите на множители первые два и последние два:
2x (3x — 2) + 3 (3x — 2)
Шаг 4 : Общий множитель (3x — 2):
(2x + 3) (3x — 2)
Проверка: (2x + 3) (3x — 2) = 6x 2 — 4x + 9x — 6 = 6x 2 + 5x — 6 (Да)
В поисках чисел
Самая сложная часть — найти два числа, которые умножаются, чтобы получить ac, и складывать, чтобы получить b.
Это отчасти предположение, и помогает перечислить все факторы .
Вот еще один пример, который может вам помочь:
Пример: ac = −120 и b = 7
Какие два числа умножают на −120 и добавляют к 7 ?
Множитель 120 составляет (плюс и минус):
1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 и 120
Мы можем попробовать пары множителей (начнем с середины!) И посмотреть, прибавят ли они к 7:
- −10 x 12 = −120 и −10 + 12 = 2 (нет)
- −8 x 15 = −120 и −8 + 15 = 7 (ДА!)
Попрактикуйтесь
Почему фактор?
Ну, одно из больших преимуществ факторизации состоит в том, что мы можем найти корней квадратного уравнения (где уравнение равно нулю).
Все, что нам нужно сделать (после факторизации), это найти, где каждый из двух множителей обращается в ноль
Пример: каковы корни (нули) числа 6x
2 + 5x — 6?Мы уже знаем (сверху) множители
(2x + 3) (3x — 2)
И мы можем выяснить, что
(2x + 3) равно нулю, когда x = −3/2
и
(3x — 2) равно нулю, когда x = 2/3
Итак, корни 6x 2 + 5x — 6 равны:
−3/2 и 2/3
Вот график 6x 2 + 5x — 6, вы видите, где он равен нулю?
И мы также можем проверить это с помощью небольшой арифметики:
При x = -3/2: 6 (-3/2) 2 + 5 (-3/2) — 6 = 6 × (9/4) — 15/2 — 6 = 54/4 — 15 / 2-6 = 6-6 = 0
При x = 2/3: 6 (2/3) 2 + 5 (2/3) — 6 = 6 × (4/9) + 10/3 — 6 = 24/9 + 10/3 — 6 = 6-6 = 0
Графики
Мы также можем попробовать построить квадратное уравнение. Увидев, где оно равно нулю, мы можем понять.
Увидев, где оно равно нулю, мы можем понять.
Пример: (продолжение)
Начиная с 6x 2 + 5x — 6 и только этот участок:
Корни равны около x = −1,5 и x = +0,67, поэтому мы можем предположить, что корни равны:
−3/2 и 2/3
Что может помочь нам вычислить коэффициенты 2x + 3 и 3x — 2
Всегда проверяйте! На графике значение +0.67 может и не быть 2/3
Общее решение
Существует также общее решение (полезно, когда описанный выше метод не работает), в котором используется формула корней квадратного уравнения:
Используйте эту формулу, чтобы получить два ответа x + и x — (один для случая «+», а другой для случая «-» в «±»), и мы получим это факторинг :
а (х — х + ) (х — х — )
Давайте воспользуемся предыдущим примером, чтобы увидеть, как это работает:
Пример: каковы корни у 6x
2 + 5x — 6?Подставляем a = 6, b = 5 и c = −6 в формулу:
x = −b ± √ (b 2 — 4ac) 2a
= −5 ± √ (5 2 — 4 × 6 × (−6)) 2 × 6
= −5 ± √ (25 + 144) 12
= −5 ± √169 12
= −5 ± 13 12
Итак, два корня:
х + = (-5 + 13) / 12 = 8/12 = 2/3,
x — = (−5-13) / 12 = −18/12 = −3/2
(Обратите внимание, что мы получаем тот же ответ, что и при факторинге ранее. )
)
Теперь поместите эти значения в (x — x + ) (x — x — ):
6 (х — 2/3) (х + 3/2)
Мы можем немного изменить это, чтобы упростить:
3 (x — 2/3) × 2 (x + 3/2) = (3x — 2) (2x + 3)
И мы получаем те же факторы, что и раньше.
362, 1203, 2262, 363, 1204, 2263, 2100, 2101, 2102, 2103, 2264, 2265
(Спасибо «mathsyperson» за части этой статьи)
Объяснение квадратичной формулы | Purplemath
Purplemath
Когда мне следует использовать квадратичную формулу?
Вы можете использовать квадратную формулу в любое время, когда пытаетесь решить квадратное уравнение — при условии, что это уравнение имеет форму «(квадратное выражение), которое установлено равным нулю».
Часто самый простой способ решить « ax 2 + bx + c = 0» для значения x — это разложить квадратичный коэффициент на множители, установить каждый множитель равным нулю и затем решить каждый фактор. Но иногда квадратичность слишком беспорядочная, или она вообще не учитывается, или, черт возьми, может быть, вам просто не хочется множить на множители. Хотя факторинг не всегда бывает успешным, квадратичная формула всегда может найти ответы за вас.
MathHelp.com
Квадратичная формула использует « a », « b » и « c » из « ax 2 + bx + c », где « a », » b «и» c «- это просто числа; они представляют собой «числовые коэффициенты» квадратного уравнения, которые они дали вам решить.
Квадратичная формула получена из процесса завершения квадрата и официально записана как:
Что такое квадратная формула?
Квадратичная формула — это правило, которое гласит, что в любом уравнении вида ax 2 + bx + c = 0, решение x -значения уравнения даются как:
Как пользоваться квадратной формулой?
Чтобы использовать квадратичную формулу, необходимо:
Запишите уравнение в виде «(квадратичный) = 0».
Расположите члены в (уравнении) в порядке убывания (сначала возведите в квадрат член, затем член x и, наконец, линейный член).
Вытяните числовые части каждого из этих терминов, а именно « a », « b » и « c » формулы.

Подставьте эти числа в формулу.
Упростите, чтобы получить ответы.
Рекомендации: «2 a » в знаменателе Формулы находится под всем, что указано выше, а не только под квадратным корнем. И внизу это «2 a «, а не просто «2». Убедитесь, что вы осторожны, чтобы не уронить квадратный корень или «плюс / минус» в середине ваших вычислений, иначе я могу гарантировать, что вы забудете «вставить их обратно» в свой тест, и вы запутаетесь себя вверх. Помните, что « b 2 » означает «квадрат ВСЕГО из b , включая его знак», поэтому не оставляйте b 2 отрицательным, даже если b отрицательное, потому что квадрат негатива — это позитив.
Другими словами, не будьте небрежны и не пытайтесь сокращать путь, потому что это только навредит вам в долгосрочной перспективе. Поверьте мне в этом!
Какой пример использования квадратичной формулы?
Это квадратичный коэффициент, который я могу использовать для подтверждения того, что я получаю из квадратичной формулы. Формула должна дать мне те же ответы.
Формула должна дать мне те же ответы.
x 2 + 3 x — 4 = ( x + 4) ( x — 1) = 0
… поэтому я уже знаю, что решения: x = –4 и x = 1.
Итак, как бы мое решение выглядело в квадратичной формуле? Используя a = 1, b = 3 и c = –4, мой процесс решения выглядит следующим образом:
Итак, как и ожидалось, решение: x = –4, x = 1.
Для этого конкретного квадратного уравнения факторинг, вероятно, был бы более быстрым методом. Но квадратичная формула — это метод «plug-n-chug», который всегда будет работать . У вас «замораживание мозгов» на тесте, и неужели ничего не стоит? Используйте формулу plug-n-chug; он всегда позаботится о тебе!
Как квадратная формула соотносится с пересечениями по оси x?
Решения квадратного уравнения, представленные квадратной формулой, представляют собой точки пересечения x соответствующей графической параболы.
Как? Что ж, когда y = 0, вы находитесь на оси x . Перемычки x на графике — это места, где парабола пересекает ось x . Вы применяете квадратичную формулу к уравнению ax 2 + bx + c = y , где y устанавливается равным нулю.
Рассматривая приведенный выше пример, можно увидеть два решения уравнения x 2 + 3 x — 4 = 0.Это говорит нам о том, что на графике должны быть две точки пересечения x . Построив график, мы получим кривую ниже:
Как вы можете видеть, точки пересечения x (красные точки выше) совпадают с решениями, пересекая ось x на x = –4 и x = 1. Это показывает связь между построением графиков и решением: когда вы решаете «(квадратичный) = 0», вы находите пересечение графика x . Это может быть полезно, если у вас есть графический калькулятор, потому что вы можете использовать квадратичную формулу (при необходимости) для решения квадратичной, а затем использовать свой графический калькулятор, чтобы убедиться, что отображаемые интервалы x имеют те же десятичные значения, что и делать решения, предоставляемые квадратной формулой.
Это может быть полезно, если у вас есть графический калькулятор, потому что вы можете использовать квадратичную формулу (при необходимости) для решения квадратичной, а затем использовать свой графический калькулятор, чтобы убедиться, что отображаемые интервалы x имеют те же десятичные значения, что и делать решения, предоставляемые квадратной формулой.
Обратите внимание, однако, что отображение графика калькулятором, вероятно, будет иметь некоторую ошибку округления, связанную с пикселями, поэтому вы должны проверить, были ли вычисленные и нанесенные на график значения достаточно близкими; не ждите точного совпадения.
Решите 2
x 2 — 4 x — 3 = 0. При необходимости округлите ответ до двух десятичных знаков.
Нет множителей при (2) (- 3) = –6, которые в сумме дают –4, поэтому я знаю, что эту квадратичную нельзя разложить на множители. Я буду применять квадратичную формулу. В данном случае a = 2, b = –4 и c = –3:
Я буду применять квадратичную формулу. В данном случае a = 2, b = –4 и c = –3:
Тогда ответ будет x = –0.58, x = 2,58 с округлением до двух десятичных знаков.
Могу ли я округлить ответы на квадратную формулу?
В общем нет, не надо; «решение», или «корни», или «нули» квадратичной функции обычно должны быть в «точной» форме ответа. Вы можете использовать в округленной форме при построении графиков (при необходимости), но «ответ (-ы)» из квадратичной формулы следует записывать в (часто беспорядочной) «точной» форме.
В приведенном выше примере точная форма — это квадратный корень из десяти. Если вы хотите построить график перехватов x или вам нужно упростить окончательный ответ в текстовой задаче, чтобы он имел практическую («реальную») форму, тогда вы можете использовать аппроксимацию калькулятора. Но если у вас нет веских причин полагать, что ответ должен быть округленным, всегда используйте точную форму.
Но если у вас нет веских причин полагать, что ответ должен быть округленным, всегда используйте точную форму.
Подтверждение концепции: сравните решения, которые мы нашли выше для уравнения 2 x 2 — 4 x — 3 = 0 с интерцепциями x на графике:
Как и в предыдущем примере, перехваты x совпадают с нулями из квадратичной формулы.Это всегда правда. «Решения» уравнения — это также точки пересечения x соответствующего графика.
URL: https://www.purplemath.com/modules/quadform.htm
Графические квадратные уравнения с использованием преобразований
Квадратное уравнение это многочлен уравнение степень 2 .Стандартная форма квадратного уравнения:
0 знак равно а Икс 2 + б Икс + c
где
а
,
б
и
c
все реальные числа и
а
≠
0
.
Если мы заменим 0 с участием у , то получаем квадратичная функция
у знак равно а Икс 2 + б Икс + c
чей граф будет парабола .
Иногда, глядя на квадратичную функцию, можно увидеть, как она была преобразована из простой функции
у
знак равно
Икс
2
. Затем вы можете построить уравнение, соответствующим образом преобразовав «родительский график». Например, для положительного числа
c
, график
у
знак равно
Икс
2
+
c
такой же как график
у
знак равно
Икс
2
сдвинутый
c
единиц вверх. Аналогично график
у
знак равно
а
Икс
2
растягивает график по вертикали в раз
а
.(Отрицательные значения
а
переверните параболу вверх дном. )
)
Мы можем увидеть некоторые другие преобразования в следующих примерах.
Пример 1:
Постройте график функции у знак равно 2 Икс 2 — 5 .
Если мы начнем с у знак равно Икс 2 и умножьте правую часть на 2 , он растягивает график по вертикали в раз 2 .
Тогда, если мы вычтем 5 из правой части уравнения сдвигает график вниз 5 единицы.
Пример 2:
Постройте график функции у знак равно — 1 2 ( Икс — 3 ) 2 + 2 .
Если мы начнем с
у
знак равно
Икс
2
и заменить
Икс
с участием
Икс
—
3
, это приводит к смещению графика
3
единиц вправо.
Тогда, если мы умножим правую часть на — 1 2 , он переворачивает параболу вверх ногами и дает ей вертикальное сжатие (или «сжатие») с коэффициентом 2 .
Наконец, если мы добавим 2 вправо сдвигает график 2 единиц вверх.
квадратичных последовательностей — разностный метод
Формула для n-го члена
Квадратичные последовательности чисел характеризуются тем, что разница между терминами всегда изменяется на одинаковую величину .
Следовательно, «разница между различиями между терминами последовательности всегда одинакова» . Мы говорим, что разница в секунд является постоянной .
Вот что мы имеем в виду, рассмотрим последовательность : \ [6,11,18,27,38,51 \ точек \] глядя на первое и «второе отличие» этой последовательности, будет выглядеть так:
Глядя на это, мы видим, что разница в секунд является постоянной и не равна нулю, это означает, что это квадратичная последовательность . {\ text {nd}} \ \ text {разница} \\
3а + Ь = и_2 — и_1 \\
а + б + с = и_1
\ end {case} \] Где:
{\ text {nd}} \ \ text {разница} \\
3а + Ь = и_2 — и_1 \\
а + б + с = и_1
\ end {case} \] Где:
- \ (u_2-u_1 \): разница в между первыми двумя членами последовательности .
- \ (u_1 \): это первый член последовательности .
Пример
На следующем рисунке показаны все различий , на которые мы ссылаемся в этих уравнениях, для квадратичной последовательности : \ (6,11,18,27,38,51 \ dots \)
Глядя на это и на формулу , которую мы видели выше, каждое из уравнений выглядит следующим образом: \ [\ begin {case} 2а = 2 \\ 3а + Ь = 5 \\ а + б + с = 6 \ end {case} \] Мы видим, что значения, которые мы используем, те, которые мы поместили в рамку на иллюстрации, всегда являются первыми в каждой строке.{\ text {th}} \) член каждой из следующих последовательностей :
- Последовательность, первые несколько членов которой: \ [- 3,0,5,12,21,32, \ точки \]
- Последовательность, первые несколько членов которой: \ [- 4,2,12,26,44,66,92, \ точки \]
- Последовательность, первые несколько членов которой: \ [2,6,12,20,30,42,56, \ точки \]
- Последовательность, первые несколько членов которой: \ [1,0, -3, -8, -15, -24, -35, \ точки \]
- Последовательность, первые несколько членов которой: \ [3,7,13,21,31,43,57, \ точки \]
Ответы без работы
- \ (и_n = п ^ 2-4 \)
- \ (u_n = 2n ^ 2 — 6 \)
- \ (и_n = п ^ 2 + п \)
- \ (u_n = -n ^ 2 + 2n \)
- \ (и_n = п ^ 2 + п + 1 \)
Выберите номер вопроса, для которого вы хотели бы видеть работу:
Qu.
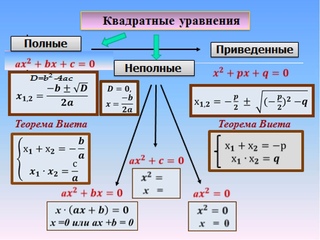


 А значения 4 и 2 подходят обоим равенствам:
А значения 4 и 2 подходят обоим равенствам:



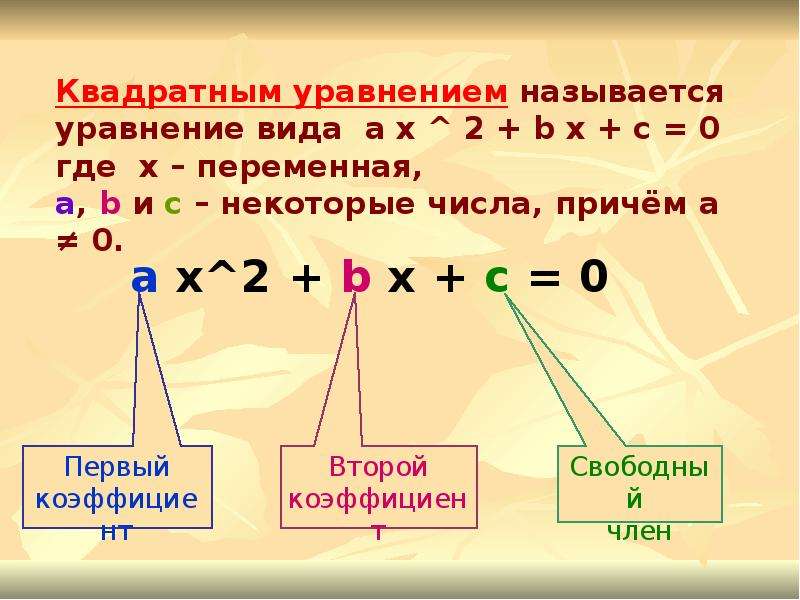 a не может быть 0.
a не может быть 0.


