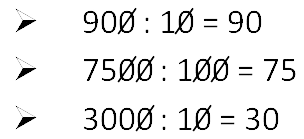Признак делимости — это… Что такое Признак делимости?

При́знак дели́мости — правило, позволяющее сравнительно быстро определить, является ли число кратным заранее заданному без необходимости выполнять фактическое деление. Как правило, основано на действиях с частью цифр из записи числа в позиционной системе счисления (обычно десятичной).

Существуют несколько простых правил, позволяющих найти малые делители числа в десятичной системе счисления:

Признак делимости на 2

Число делится на 2 тогда и только тогда, когда его последняя цифра делится на 2, то есть является чётной.

Признак делимости на 3

Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3 (так как все числа вида 10ⁿ при делении на 3 дают в остатке единицу).

Признак делимости на 4

Число делится на 4 тогда и только тогда, когда число из двух последних его цифр (оно может быть двузначным, однозначным или нулём) делится на 4.

Признак делимости на 5

Число делится на 5 тогда и только тогда, когда последняя цифра делится на 5 (то есть равна 0 или 5).

Признак делимости на 6

Число делится на 6 тогда и только тогда, когда оно делится и на 2, и на 3.

Признак делимости на 7

Число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7 (например, 364 делится на 7, так как 36 — (2 × 4) = 28 делится на 7).

Либо использовать модификацию признака деления на 1001=10³+1, которое само делится на 7:
Для того, чтобы натуральное число делилось на 7 необходимо и достаточно, чтобы алгебраическая сумма чисел, образующих нечётные группы по три цифры (начиная с единиц) взятых со знаком «+» и чётных со знаком «-» делилась на семь.

Ещё один признак — берём первую цифру, умножаем на 3, прибавляем следующую (здесь можно взять остаток от деления на 7 от получившегося числа). И далее — сначала: умножаем на 3, прибавляем следующую… Для 364: 3 * 3 + 6 = 15. Остаток — 1. Далее 1 * 3 + 4 = 7.

Признак делимости на 8

Число делится на 8 тогда и только тогда, когда три его последние цифры — нули или образуют число, которое делится на 8.

Признак делимости на 9

Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.

Признак делимости на 10

Число делится на 10 тогда и только тогда, когда оно оканчивается на ноль.

Признак делимости на 11

Число делится на 11 тогда и только тогда, когда сумма цифр с чередующимися знаками равна 0 или делится на 11 (то есть 182 919 делится на 11, так как 1 — 8 + 2 — 9 + 1 — 9 = −22 делится на 11) — следствие факта, что все числа вида 10ⁿ при делении на 11 дают в остатке (-1)ⁿ.

Признак делимости на 12

Число делится на 12 тогда и только тогда, когда оно делится на 3 и на 4.

Признак делимости на 13

Число делится на 13 тогда и только тогда, когда число его десятков, сложенное с учетверённым числом единиц, кратно 13 (например, 845 делится на 13, так как 84 + (4 × 5) = 104 делится на 13).

Признак делимости на 14

Число делится на 14 тогда и только тогда, когда оно делится на 2 и на 7.

Признак делимости на 15

Число делится на 15 тогда и только тогда, когда оно делится на 3 и на 5.

Признак делимости на 17

Число делится на 17 тогда и только тогда, когда число его десятков, сложенное с увеличенным в 12 раз числом единиц, кратно 17 (например, 29053→2905+36=2941→294+12=306→30+72=102→10+24=34. Поскольку 34 делится на 17, то и 29053 делится на 17). Признак не всегда удобен, но имеет определенное значение в математике. Есть способ немного проще — число делится на 17 тогда и только тогда, когда разность между числом его десятков и упятерённым числом единиц кратна 17 (например, 32952→3295-10=3285→328-25=303→30-15=15; поскольку 15 не делится на 17, то и 32952 не делится на 17)

Признак делимости на 19

Число делится на 19 тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, кратно 19 (например, 646 делится на 19, так как 64 + (6 × 2) = 76 делится на 19).

Признак делимости на 23

Число делится на 23 тогда и только тогда, когда число его сотен, сложенное с утроенным числом десятков и единиц, кратно 23 (например, 28842 делится на 23, так как 288 + (3 * 42) = 414; продолжаем: 4 + (3 * 14) = 46 — очевидно, делится на 23).

Признак делимости на 25

Число делится на 25 тогда и только тогда, когда две его последние цифры делятся на 25 (то есть образуют 00, 25, 50 или 75).

Признак делимости на 99

Разобьем число на группы по 2 цифры справа налево (в самой левой группе может быть одна цифра) и найдем сумму этих групп, считая их двузначными числами. Эта сумма делится на 99 тогда и только тогда, когда само число делится на 99.

Признак делимости на 101

Разобьем число на группы по 2 цифры справа налево (в самой левой группе может быть одна цифра) и найдем сумму этих групп с переменными знаками, считая их двузначными числами. Эта сумма делится на 101 тогда и только тогда, когда само число делится на 101. Например, 590547 делится на 101, так как 59-05+47=101 делится на 101).

Признак делимости на 2ⁿ

Число делится на n-ю степень двойки тогда и только тогда, когда число, образованное его последними n цифрами, делится на ту же степень.

Признак делимости на 5ⁿ

Число делится на n-ю степень пятёрки тогда и только тогда, когда число, образованное его последними n цифрами, делится на ту же степень.

Признак делимости на 10ⁿ − 1

Разобьем число на группы по n цифр справа налево (в самой левой группе может быть от 1 до n цифр) и найдем сумму этих групп, считая их n-значными числами. Эта сумма делится на 10ⁿ − 1 тогда и только тогда, когда само число делится на 10ⁿ − 1.

Признак делимости на 10ⁿ

Число делится на n-ю степень десятки тогда и только тогда, когда n его последних цифр — нули.

Признак делимости на 10ⁿ + 1

Разобьем число на группы по n цифр справа налево (в самой левой группе может быть от 1 до n цифр) и найдем сумму этих групп с переменными знаками, считая их n-числами. Эта сумма делится на 10ⁿ + 1 тогда и только тогда, когда само число делится на 10ⁿ + 1.

См. также

• Признак Паскаля — универсальный признак делимости, позволяющий для любых целых a и b определить, делится ли a на b. Точнее, он позволяет вывести почти все из выше приведённых признаков.

Ссылки

Wikimedia Foundation. 2010.

dic.academic.ru

Признаки делимости на 11,12,13,14,15. Примеры решения задач.

Признак делимости на \(11\)

Число делится на \(11\), если разность всех цифр в нечетных местах и цифр в четных местах, делится на \(11\).

Задача 1. Проверить делимость чисел на \(11\): \(2547039\), \(13165648\) .

Решение.  Найдем сумму цифр в четных и нечетных местах у числа \(2547039\).

1. \((9+0+4+2)-(3+7+5)=15-15=0-\)  делится на 11.
2. \((8+6+6+3)-(4+5+1+1)=23-11=12-\) не делится на 11

Признак делимости на \(12\)

Число делится на 12, если оно кратно \(3\) и \(4.\)

Задача 2. Проверить делимость чисел на \(12\): \(9012\) и \(23988\).

1.   Сумма цифр ​\(9012\) ​делится на \(3:\)  \(9+0+1+2=\frac{12}{3}=4\) и последние две цифры делятся на \(4:\frac{12}{4}=3\).
2.   \(23988\)  сумма цифр делится на \(3:2+3+9+8+8=\frac{30}{3}=10\) и последние две цифры делятся на \(4:\frac{88}{4}=22.\). Вывод: числа \(9012\) и \(23988\)делятся на 12.

Признак делимости на ​\(13\)​
 

Число делится на \(13\), если число его десятков умножить на \(4\) и сложить с оставшимися цифрами, кратно \(13\).

Задача 3. Проверить делимость чисел на \(13\): \(845\) и \(676\).

1. \(84+(4*5)=104 -\)делится на \(13\).
2. \(67+(4*6)=67+24=91-\) делится на 13.

Ответ: числа \(845,676\) делятся на 13.

Признак делимости на \(14\)

 

Число делится на \(14\) тогда и только тогда, когда оно делится на \(2\) и на \(7\).

Рассмотрим число \(994:\) запись числа заканчивается чётной цифрой, следовательно признак делимости на \(2\) выполнен.

Проверяем делимость на \(7:\) \(99-2*4=99-8=91.\)

Повторяем действия:  \(9-2*1=7-\) делится на \(7\). \(994\) делится \(14\).

 

---

Признак делимости на \(15\)

 

Число делится на \(15\), если оно делится на \(3\) и на \(5\).

Рассмотрим число \(6375.\) Число \(6375\) делится на \(3\) так как  сумма его цифр  кратна \(3\). Также данное число делится на \(5\), потому что на последнем месте стоит пятерка. Число \(6375\) делится на \(15\).

Признак делимости на \(17\)

Число делится на \(17\), если число его десятков умножить на \(12\)  и сложить с оставшимися цифрами, кратно \(17\).

Задача 4. Определить кратно ли семнадцати число \(29053\) .

Решение.

\(2905+36=2941\)→\(294+12=306\)→\(30+72=102\)→\(10+24=34\).

\(29053\) делится на \(17\).

---

Признак делимости на \(19\)

Число делится на \(19\), если удвоенное число его десятков сложить с оставшимися цифрами, кратно \(19.\)

Пример: \(646\) делится на \(19\), так как \(64+(6*2)=76\) делится на \(19\).

---

Признак делимости на \(23\)

Число делится на \(23\), если утроенное число его сотен сложить с оставшимися цифрами, кратно \(23\).

Пример: \(28842-288+(3*42)=414\).Повторяем действия: \(4+(3*14)=46\), \(46\) делится на \(23\), значит и \(28842\) кратно \(23\).

 

---

Признак делимости на \(25\)

Число делится на \(25\), если две его последние цифры делятся на \(25\),то есть если его последние цифры оканчиваются на \(00,25,50\) или \(75\) или число кратно \(5\).

Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.
 

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

myalfaschool.ru

Таблица по теме «Признаки делимости»

Признаки	Запомни	Пример
Признак делимости на 2	Число делится на 2, если его последняя цифра делится на 2 или является нулём.	52 делится на 2. Последняя цифра 2 делится на 2 нацело (2 : 2 = 1). 300 делится на 2. Последняя цифра 0. 11 не делится на 2. Последняя цифра 1 не делится на 2.
Признак делимости на 4	Число делится на 4, если две его последние цифры нули или образуют число, делящееся на 4.	548 делится на 4. Две последние цифры 48 делятся на 4 нацело (48 : 4 = 12). 600 делится на 4. Две последние цифры нули. 755 не делится на 4. Две последние цифры 55 не делятся на 4.
Признак делимости на 8	Число делится на 8, если три последние его цифры нули или образуют число, делящееся на 8.	1128 делится на 8. Три последние цифры 128 делятся на 8 нацело (128 : 8 = 16). 7000 делится на 8. Три последние цифры нули. 6755 не делится на 4. Три последние цифры 755 не делятся на 8.
Признак делимости на 3	Число делится на 3, если сумма всех его цифр делится на 3.	153 делится на 3. Сумма всех его цифр: 1 + 5 + 3 = 9 делится на 3 (9 : 3 = 3). 300 делится на 3. Сумма всех его цифр: 3 + 0 + 0 = 3 делится на 3 (3 : 3 = 1). 11 не делится на 3. Сумма всех его цифр: 1 + 1 = 2 не делится на 3.
Признак делимости на 6	Число делится на 6, если оно делится одновременно на 2 и на 3.	126 делится на 6. По признаку делимости на 2 оно делится на 2 (последняя цифра 6 делится на 2). По признаку делимости на 3 оно также делится на 3 (сумма цифр числа 1 + 2 + 6 = 9 делится на три). Это означает, что 126 делится на 6. 801 не делится на 6. По признаку делимости на 2 оно не делится на 2. 757 не делится на 6. По признаку делимости на 3 оно не делится на 3.
Признак делимости на 9	Число делится на 9, если сумма всех его цифр делится на 9.	486 делится на 9. Сумма всех его цифр: 4 + 8 + 6 = 18 делится на 9 (18 : 9 = 2). 9198 делится на 9. Сумма всех его цифр: 9 + 1 + 9 + 8 = 27 делится на 9 (27 : 9 = 3). 55 не делится на 9. Сумма всех его цифр: 5 + 5 = 10 не делится на 9.
Признак делимости на 5	Число делится на 5, если его последняя цифра 5 или 0.	155 делится на 5. Последняя цифра 5. 800 делится на 5. Последняя цифра 0. 61 не делится на 5. Последняя цифра 1.
Признак делимости на 25	Число делится на 25, если его две последние цифры нули или образуют число, которое делится на 25.	675 делится на 25. Две последние цифры образуют число 75, которое делится на 25. (75 : 25 = 3) Это означает, что 675 делится на 25. 3900 делится на 25. Две последние цифры нули. 345 не делится на 25. Две последние цифры образуют число 45, которое не делится на 25.
Признак делимости на 10,100 и 1000.	10 делятся нацело только те числа, последняя цифра которых нуль. На 100 делятся нацело только те числа, две последние цифры которых нули. На 1000 делятся нацело только те числа, три последние цифры нули.	Чтобы было проще делить на 10, 100 и 1000, просто зачеркивайте одинаковое количество нулей в обоих числах.
Признак делимости на 11	Число делится на 11, если сумма цифр, которые стоят на четных местах равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на 11.	Итак, цифры которые стоят на нечетных местах — это 6 (стоит на первом месте) и 1 (стоит на третьим месте). Цифра, которая стоит на четном месте это 7 (стоит на втором месте). 6 + 1 = 7. Сумма цифр стоящих на нечетном месте равна сумме цифр на четном месте, значит 671 делится на 11. Цифры которые стоят на нечетных местах — это 3 (стоит на первом месте) и 0 (стоит на третьим месте). Цифры, которые стоят на четном месте это 9 (стоит на втором месте) и 5 (стоит на четвертом месте) 3 + 0 ≠ 9 + 5 → 3 ≠ 14 Сумма цифр, стоящих на нечетном месте, не равна сумме цифр на четном месте, но суммы цифр отличаются ровно на 11. 14 − 3 = 11. Значит 3905 делится на 11.

infourok.ru