Занимательная математика: правило Гаусса

Цикл «Занимательная математика» посвящен деткам увлекающимся математикой и родителям, которые уделяют время развитию своих детей, «подкидывая» им интересные и занимательные задачки, головоломки.

Первая статья из этого цикла посвящена правилу Гаусса.

Немного истории

Известный немецкий математик Карл Фридрих Гаусс (1777-1855) с раннего детства отличался от своих сверстников. Несмотря на то, что он был из небогатой семьи, он достаточно рано научился читать, писать, считать. В его биографии есть даже упоминание того, что в возрасте 4-5 лет он смог скорректировать ошибку в неверных подсчетах отца, просто наблюдая за ним.

Одно из первых его открытий было сделано в возрасте 6 лет на уроке математики. Учителю было необходимо увлечь детей на продолжительное время и он предложил следующую задачку:

Найти сумму всех натуральных чисел от 1 до 100.

Юный Гаусс справился с этим заданием достаточно быстро, найдя интересную закономерность, которая получила большое распространение и применяется по сей день при устном счете.

Давайте попробуем решить эту задачку устно. Но для начала возьмем числа от 1 до 10:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10

Посмотрите внимательно на эту сумму и попробуйте догадаться, что же необычного смог разглядеть Гаусс? Для ответа необходимо хорошо представлять себе состав чисел.

Гаусс сгруппировал числа следующим образом:

(1+10) + (2+9) + (3+8) + (4+7) + (5+6)

Таким образом маленький Карл получил 5 пар чисел, каждая из которых в отдельности в сумме дает 11. Тогда, чтобы вычислить сумму натуральных чисел от 1 до 10 необходимо

5 * 11 = 55

Вернемся к первоначальной задаче. Гаусс заметил, что перед суммированием необходимо группировать числа в пары и тем самым изобрел алгоритм, благодаря которому можно быстро сложить числа от 1 до100:

1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100

1. Находим количество пар в ряде натуральных чисел. В данном случае их 50.

2. Суммируем первое и последнее числа данного ряда. В нашем примере — это 1 и 100. Получаем 101.

3. Умножаем полученную сумму первого и последнего члена ряда на количество пар этого ряда. Получаем 101 * 50 = 5050

Следовательно, сумма натуральных чисел от 1 до 100 равна 5050.

Задачи на использование правила Гаусса

А сейчас вашему вниманию предлагаются задачи, в которых в той или иной степени используется правило Гаусса. Эти задачки вполне способен понять и решить четвероклассник.

Можно дать возможность ребенку порассуждать самому, чтобы он сам «изобрел» это правило. А можно разобрать вместе и посмотреть как он сможет его применить. Среди ниже приведенных задач есть примеры, в которых нужно понять как модифицировать правило Гаусса, чтобы его применить к данной последовательности.

В любом случае, чтобы ребенок мог оперировать этим в своих вычислениях необходимо понимание алгоритма Гаусса, то есть умение разбить правильно по парам и посчитать.

Важно! Если будет заучена формула без понимания, то это очень быстро будет забыто.

Задача 1

Найти сумму чисел:

• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10;
• 1 + 2 + 3 + … + 14 + 15 + 16;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9;
• 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100.

Решение.

Вначале можно дать возможность ребенку самому решить первый пример и предложить найти способ, при котором это сделать легко в уме. Далее разобрать этот пример вместе с ребенком и показать как это сделал Гаусс. Лучше всего для наглядности записать ряд и соединить линиями пары чисел, дающие в сумме одинаковое число. Важно, чтобы ребенок понял как образуются пары — берем самое маленькое и самое большое из оставшихся чисел при условии, что количество чисел в ряду четно.

• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = (1 + 10) + (2 + 9) + (3 + 8) + (4 + 7) + (5 + 6) = (1 + 10) * 5;
• 1 + 2 + 3 + … + 14 + 15 + 16 = (1 + 16) + (2 + 15) + (3 + 14) + (4 + 13) + (5 + 12) + (6 + 11) + (7 + 10) + (8 + 9) = (1 + 16) * 8 = 136;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 8) + (2 + 7) + (3 + 6) + (4 + 5) + 9 = (1+ 8) * 4 + 9 = 45;
• 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100 = (1 + 100) * 50 = 5050

Задача 2

Имеется 9 гирь весом 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г. Можно ли разложить эти гири на три кучки с равным весом?

Решение.

С помощью правила Гаусса находим сумму всех весов:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 8) * 4 + 9 = 45 (г)

Далее смотрим, можно ли этот вес разбить на три равных веса:

45 : 3 = 15 (г)

Значит, если мы сможем сгруппировать гири так, чтобы в каждой кучке были гири суммарным весом 15г, то задача решена.

Один из вариантов:

• 9г, 6г
• 8г, 7г
• 5г, 4г, 3г, 2г, 1г

Другие возможные варианты найдите сами с ребенком.

Обратите внимание ребенка на то, что когда решаются подобные задачи лучше всегда начинать группировать с большего веса (числа).

Задача 3

Можно ли разделить циферблат часов прямой линией на две части так, чтобы суммы чисел в каждой части были равны?

Решение.

Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим, делится ли она на 2:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = (1 + 12) * 6 = 78

Значит разделить можно. Теперь посмотрим как.

По правилу Гаусса у нас получается 6 пар чисел, каждая из которых в сумме дает 13:

1 и 12, 2 и 11, 3 и 10, 4 и 9, 5 и 8, 6 и 7.

Следовательно, надо провести линию на циферблате так, чтобы 3 пары попали в одну половину, а три в другую.

Ответ: линия пройдет между числами 3 и 4, а затем между числами 9 и 10.

Задача 4

Можно ли провести на циферблате часов две прямые линией так, чтобы в каждой части сумма чисел была одинаковой?

Решение.

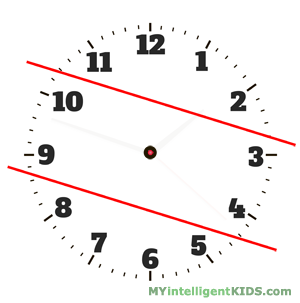
Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим делиться ли она на 3:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = (1 + 12) * 6 = 78

78 делиться на 3 без остатка, значит разделить можно. Теперь посмотрим как.

По правилу Гаусса у нас получается 6 пар чисел, каждая из которых в сумме дает 13:

1 и 12, 2 и 11, 3 и 10, 4 и 9, 5 и 8, 6 и 7.

Следовательно, надо провести линии на циферблате так, чтобы в каждую часть попали по 2 пары.

Ответ: первая линия пройдет между числами 2 и 3, а затем между числами 10 и 11; вторая линия — между числами 4 и 5, а затем между 8 и 9.

Задача 5

Летит стая птиц. Впереди одна птица (вожак), за ней две, потом три, четыре и т. д. Сколько птиц в стае, если в последнем ряду их 20?

Решение.

Получаем, что нам необходимо сложить числа от 1 до 20. А к вычислению такой суммы можно применить правило Гаусса:

1 + 2 + 3 + 4 + 5 + … + 15 + 16 + 17 + 18 + 19 + 20 = (20 + 1) * 10 = 210.

Задача 6

Как рассадить 45 кроликов в 9 клеток так, чтобы во всех клетках было разное количество кроликов?

Решение.

Если ребенок решил и с пониманием разобрал примеры из задания 1, то тут же вспоминается, что 45 это сумма чисел от 1 до 9. Следовательно, сажаем кроликов так:

• первая клетка — 1,
• вторая — 2,
• третья — 3,
• …
• восьмая — 8,
• девятая — 9.

Но если ребенок сразу не может сообразить, то попробуйте натолкнуть его на мысль о том, что подобные задачи можно решить перебором и надо начинать с минимального числа.

Задача 7

Вычислить сумму, используя прием Гаусса:

• 31 + 32 + 33 + … + 40;
• 5 + 10 + 15 + 20 + … + 100;
• 91 + 81 + … + 21 + 11 + 1;
• 1 + 2 + 3 + 4 + … + 18 + 19 + 20;
• 1 + 2 + 3 + 4 + 5 + 6;
• 4 + 6 + 8 + 10 + 12 + 14;
• 4 + 6 + 8 + 10 + 12;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11.

Решение.

• 31 + 32 + 33 + … + 40 = (31 + 40) * 5 = 355;
• 5 + 10 + 15 + 20 + … + 100 = (5 + 100) * 10 = 1050;
• 91 + 81 + … + 21 + 11 + 1 = (91 + 1) * 5 = 460;
• 1 + 2 + 3 + 4 + … + 18 + 19 + 20 = (1 + 20) * 10 =210;
• 1 + 2 + 3 + 4 + 5 + 6 = (1 + 6) * 3 = 21;
• 4 + 6 + 8 + 10 + 12 + 14 = (4 + 14) * 3 = 54;
• 4 + 6 + 8 + 10 + 12 = (4 + 10) * 2 + 12 = 40;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 = (1 + 10) * 5 + 11 = 66.

Задача 8

Имеется набор из 12 гирек массой 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г, 10г, 11г, 12г. Из набора убрали 4 гирьки, общая масса которых равна трети общей массы всего набора гирек. Можно ли оставшиеся гирьки расположить на двух чашках весов по 4 штуки на каждой чашке так, чтобы они оказались в равновесии?

Решение.

Применяем правило Гаусса, чтобы найти общую массу гирек:

1 + 2 + 3 + … + 10 + 11 + 12 = (1 + 12) * 6 = 78 (г)

Вычисляем массу гирек, которые убрали:

78 : 3 = 26 (г)

Следовательно, оставшиеся гирьки (общей массой 78-26 = 52г) надо расположить по 26 г на каждую чашу весов, чтобы они оказались в равновесии.

Нам не известно какие гирьки были убраны, значит мы должны рассмотреть все возможные варианты.

Применяя правило Гаусса можно разбить гирьки на 6 пар с равным весом (по 13г):

1г и 12г, 2г и 11г, 3г и 10, 4г и 9г, 5г и 8г, 6г и 7г.

Тогда лучший вариант, когда при убирании 4 гирек уберутся две пары из приведенных выше. В этом случае у нас останутся 4 пары: 2 пары на одну чашу весов и 2 пары на другую.

Худший вариант — это когда 4 убранные гирьки разобьют 4 пары. У нас останутся 2 неразбитые пары общим весом 26г, значит их помещаем на одну чашу весов, а оставшиеся гирьки можно поместить на другую чашу весов и они тоже будут 26г.

Удачи в развитии Ваших детей.

Метод Гаусса (численное интегрирование) — Википедия

Материал из Википедии — свободной энциклопедии

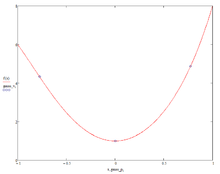Численное интегрирование функции x5+6×2+1{\displaystyle x^{5}+6x^{2}+1} методом гаусса-3

Метод Гаусса — метод численного интегрирования, позволяющий повысить алгебраический порядок точности методов на основе интерполяционных формул путём специального выбора узлов интегрирования без увеличения числа используемых значений подынтегральной функции. Метод Гаусса позволяет достичь максимальной для данного числа узлов интегрирования алгебраической точности.

Например, для двух узлов можно получить метод 3-го порядка точности

I≈b−a2(f(a+b2−b−a23)+f(a+b2+b−a23)),{\displaystyle I\approx {\frac {b-a}{2}}\left(f\left({\frac {a+b}{2}}-{\frac {b-a}{2{\sqrt {3}}}}\right)+f\left({\frac {a+b}{2}}+{\frac {b-a}{2{\sqrt {3}}}}\right)\right)\,,}

тогда как для равноотстоящих узлов метода выше 2-го порядка получить невозможно. В общем случае, используя n{\displaystyle n} точек, можно получить метод с порядком точности 2n−1{\displaystyle 2n-1}. Значения узлов метода Гаусса по n{\displaystyle n} точкам являются корнями полинома Лежандра степени n{\displaystyle n}. Значения весов вычисляются по формуле ai=2(1−xi2)[Pn′(xi)]2{\displaystyle a_{i}={\frac {2}{(1-x_{i}^{2})\,[P_{n}'(x_{i})]^{2}}}}, где Pn′{\displaystyle P_{n}’} — первая производная полинома Лежандра.

Для n=3{\displaystyle n=3} узлы и веса имеют следующие значения : x1,3=±0.6,x2=0,{\displaystyle x_{1,3}=\pm {\sqrt {0.6}},x_{2}=0,} веса : a1,3=59,a2=89{\displaystyle a_{1,3}={\frac {5}{9}},a_{2}={\frac {8}{9}}}.

(Полином определен на отрезке [−1,1]{\displaystyle [-1,1]}).

Наиболее известен метод Гаусса по пяти точкам.

Недостаток метода Гаусса состоит в том, что он не имеет лёгкого (с вычислительной точки зрения) пути оценки погрешности полученного значения интеграла. Использование правила Рунге при дроблении отрезка интегрирования требует вычисления подынтегральной функции примерно в таком же числе точек, не давая при этом практически никакого выигрыша в точности, в отличие от простых методов, где точность увеличивается в несколько раз при каждом новом разбиении. Кронродом был предложен следующий метод оценки значения интеграла

I≈∑i=1naif(xi)+∑i=1n+1bif(yi){\displaystyle I\approx \sum _{i=1}^{n}a_{i}\,f(x_{i})+\sum _{i=1}^{n+1}b_{i}\,f(y_{i})},

где xi{\displaystyle x_{i}} — узлы метода Гаусса по n{\displaystyle n} точкам, а 3n+2{\displaystyle 3n+2} параметров ai{\displaystyle a_{i}}, bi{\displaystyle b_{i}}, yi{\displaystyle y_{i}} подобраны таким образом, чтобы порядок точности метода был равен 3n+1{\displaystyle 3n+1}. Тогда для оценки погрешности можно использовать эмпирическую формулу:

Δ=(200|I−IG|)1.5{\displaystyle \Delta =\left(200|I-I_{G}|\right)^{1.5}},

где IG{\displaystyle I_{G}} — приближённое значение интеграла, полученное методом Гаусса по n{\displaystyle n} точкам. Библиотеки gsl и SLATEC для вычисления определённых интегралов содержат подпрограммы, использующие метод Гаусса — Кронрода по 15, 21, 31, 41, 51 и 61 точкам.

1. Болтачев Г.Ш. Численные методы в теплофизике. Курс лекций Лекция 3: Численное интегрирование

Нормальное распределение — Википедия

Норма́льное распределе́ние^[1][2], также называемое распределением Гаусса или Гаусса — Лапласа^[3] — распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей с функцией Гаусса:

f(x)=1σ2πe−(x−μ)22σ2,{\displaystyle f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}\;e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}},}

где параметр μ{\displaystyle \mu } — математическое ожидание (среднее значение), медиана и мода распределения, а параметр σ{\displaystyle \sigma } — среднеквадратическое отклонение (σ2{\displaystyle \sigma ^{2}} — дисперсия) распределения.

Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений, которое принадлежит экспоненциальному классу распределений.^[4] Многомерный случай описан в статье «Многомерное нормальное распределение».

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием μ=0{\displaystyle \mu =0} и стандартным отклонением σ=1{\displaystyle \sigma =1}.

Если величина является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то центрированное и нормированное распределение такой величины при достаточно большом числе слагаемых стремится к нормальному распределению.

Это следует из центральной предельной теоремы теории вероятностей. В окружающем нас мире часто встречаются величины, значение которых определяется совокупностью многих независимых факторов. Этот факт, а также то, что распределение считалось типичным, обычным, привели к тому, что в конце 19 века стал использоваться термин «нормальное распределение». Нормальное распределение играет заметную роль во многих областях науки, например в математической статистике и статистической физике.

Случайная величина, имеющая нормальное распределение, называется нормальной, или гауссовской, случайной величиной.

Стандартное нормальное распределение[править | править код]

Наиболее простой случай нормального распределения — стандартное нормальное распределение — частный случай, когда μ=0{\displaystyle \mu =0} и σ=1{\displaystyle \sigma =1}. Его плотность вероятности равна

φ(x)=12πe−12×2{\displaystyle \varphi (x)={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}x^{2}}}

Множитель 12π{\displaystyle {\frac {1}{\sqrt {2\pi }}}} в выражении обеспечивает условие нормировки интеграла ∫−∞+∞φ(x)dx{\displaystyle \int \limits _{-\infty }^{+\infty }\varphi (x)\,dx}.^[5] Поскольку множитель 12{\displaystyle {\frac {1}{2}}} в экспоненте обеспечивает единичную дисперсию (то есть дисперсия равна единице), то и стандартное отклонение равно 1. Функция симметрична в точке x=0{\displaystyle x=0}, её значение в ней максимально и равно 12π{\displaystyle {\frac {1}{\sqrt {2\pi }}}}. Точки перегиба функции — x=+1{\displaystyle x=+1} и x=−1{\displaystyle x=-1}.

Гаусс называл стандартным нормальным распределение с σ2=1/2{\displaystyle \sigma ^{2}=1/2}, то есть

φ(x)=e−x2π.{\displaystyle \varphi (x)={\frac {e^{-x^{2}}}{\sqrt {\pi }}}.}

Нормальное распределение с параметрами μ,σ{\displaystyle \mu ,\sigma }[править | править код]

Каждое нормальное распределение — это вариант стандартного нормального распределения, область значений которого растягивается множителем σ{\displaystyle \sigma } (стандартное отклонение) и переносится на μ{\displaystyle \mu } (математическое ожидание):

f(x∣μ,σ2)=1σφ(x−μσ).{\displaystyle f(x\mid \mu ,\sigma ^{2})={\frac {1}{\sigma }}\varphi \left({\frac {x-\mu }{\sigma }}\right).}

μ,σ{\displaystyle \mu ,\sigma } являются параметрами нормального распределения. Плотность вероятности должна нормироваться 1σ{\displaystyle {\frac {1}{\sigma }}}, так что интеграл равен 1.

Если Z{\displaystyle Z} — стандартная нормальная случайная величина, то величина X=σZ+μ{\displaystyle X=\sigma Z+\mu } будет иметь нормальное распределение с математическим ожиданием μ{\displaystyle \mu } и стандартным отклонением σ{\displaystyle \sigma }. Наоборот, если X{\displaystyle X} — нормальная величина с параметрами μ{\displaystyle \mu } и σ2{\displaystyle \sigma ^{2}}, то Z=X−μσ{\displaystyle Z={\frac {X-\mu }{\sigma }}} будет иметь стандартное нормальное распределение.

Каждое нормальное распределение представляет собой экспоненту квадратичной функции:

f(x)=eax2+bx+c{\displaystyle f(x)=e^{ax^{2}+bx+c}}

где a<0{\displaystyle a<0} и c=b2/(4a)+ln⁡(−a/π)/2{\displaystyle c=b^{2}/(4a)+\ln(-a/\pi )/2}. В таком виде среднее значение μ=−b/(2a){\displaystyle \mu =-b/(2a)}, а дисперсия σ2=−1/(2a){\displaystyle \sigma ^{2}=-1/(2a)}. Для стандартного нормального распределения a=−1/2{\displaystyle a=-1/2}, b=0{\displaystyle b=0} и c=−ln⁡(2π)/2{\displaystyle c=-\ln(2\pi )/2}.

Обозначение[править | править код]

Плотность вероятности стандартного нормального распределения (с нулевым средним и единичной дисперсией) часто обозначается греческой буквой ϕ{\displaystyle \phi } (фи).^[6] Также достаточно часто используется альтернативная формы греческой буквы фи φ{\displaystyle \varphi }.

Нормальное распределение часто обозначается N(μ,σ2){\displaystyle N(\mu ,\sigma ^{2})}, или N(μ,σ2){\displaystyle {\mathcal {N}}(\mu ,\sigma ^{2})}.^[7] Если случайная величина X{\displaystyle X} распределена по нормальному закону со средним μ{\displaystyle \mu } и вариацией σ2{\displaystyle \sigma ^{2}}, то пишут

X∼N(μ,σ2).{\displaystyle X\sim {\mathcal {N}}(\mu ,\sigma ^{2}).}

Функция распределения[править | править код]

Функция распределения стандартного нормального распределения обычно обозначается заглавной греческой буквой Φ{\displaystyle \Phi } (фи) и представляет собой интеграл

Φ(x)=12π∫−∞xe−t2/2dt{\displaystyle \Phi (x)={\frac {1}{\sqrt {2\pi }}}\int \limits _{-\infty }^{x}e^{-t^{2}/2}\,dt}

С ней связана функция ошибок (интеграл вероятности) erf⁡(x){\displaystyle \operatorname {erf} (x)}, дающий вероятность того, что нормальная случайная величина со средним 0 и вариацией 1/2 попадёт в отрезок [−x,x]{\displaystyle [-x,x]}:

erf⁡(x)=2π∫0xe−t2dt{\displaystyle \operatorname {erf} (x)={\frac {2}{\sqrt {\pi }}}\int \limits _{0}^{x}e^{-t^{2}}\,dt}

Эти интегралы неберущиеся в элементарных функциях и называются специальными фунциями. Многие их численные приближения известны. См. ниже.

Функции связаны, в частности соотношением

Φ(x)=12[1+erf⁡(x2)]{\displaystyle \Phi (x)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)\right]}

Нормальное распределение с плотностью f{\displaystyle f}, средним μ{\displaystyle \mu } и отклонением σ{\displaystyle \sigma } имеет следующую функцию распределения:

F(x)=Φ(x−μσ)=12[1+erf⁡(x−μσ2)]{\displaystyle F(x)=\Phi \left({\frac {x-\mu }{\sigma }}\right)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right]}

Можно использовать функцию Q(x)=1−Φ(x){\displaystyle Q(x)=1-\Phi (x)} — она даст вероятность того, что значение стандартной нормальной случайной величины X{\displaystyle X} превысит x{\displaystyle x}: P(X>x){\displaystyle P(X>x)}.

График стандартной нормальной функции распределения Φ{\displaystyle \Phi } имеет 2-кратную вращательную симметрию относительно точки (0,1/2), то есть Φ(−x)=1−Φ(x){\displaystyle \Phi (-x)=1-\Phi (x)}. Её неопределенный интеграл равен

∫Φ(x)dx=xΦ(x)+φ(x)+C.{\displaystyle \int \Phi (x)\,dx=x\Phi (x)+\varphi (x)+C.}

Функция распределения стандартной нормальной случайной величины может быть разложена с помощью интегрирования по частям в ряд:

Φ(x)=12+12π⋅e−x2/2[x+x33+x53⋅5+⋯+x2n+1(2n+1)!!+⋯]{\displaystyle \Phi (x)={\frac {1}{2}}+{\frac {1}{\sqrt {2\pi }}}\cdot e^{-x^{2}/2}\left[x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{3\cdot 5}}+\cdots +{\frac {x^{2n+1}}{(2n+1)!!}}+\cdots \right]}

где знак !!{\displaystyle !!} означает двойной факториал.

Асимптотическое разложение функции распределения для больших x{\displaystyle x} может быть также произведено интегрированием по частям.

Стандартное отклонение[править | править код]

Для нормального распределения значения, отличающиеся от среднего на число, меньшее чем одно стандартное отклонение, составляют 68,27 % популяции. В то же время значения, отличающиеся от среднего на два стандартных отклонения, составляют 95,45 %, а на три стандартных отклонения — 99,73 %.

Около 68 % значений из нормального распределения находятся на расстоянии не более одного стандартного отклонения σ от среднего; около 95 % значений лежат расстоянии не более двух стандартных отклонений; и 99,7 % не более трёх. Этот факт является частным случаем правила 3 сигм для нормальной выборки.

Более точно, вероятность получить нормальное число в интервале между μ−nσ{\displaystyle \mu -n\sigma } и μ+nσ{\displaystyle \mu +n\sigma } равна

F(μ+nσ)−F(μ−nσ)=Φ(n)−Φ(−n)=erf⁡(n2).{\displaystyle F(\mu +n\sigma )-F(\mu -n\sigma )=\Phi (n)-\Phi (-n)=\operatorname {erf} \left({\frac {n}{\sqrt {2}}}\right).}

Если рассматривать 12 значимых символов, значения для n=1,2,…,6{\displaystyle n=1,2,\ldots ,6} равны:^[8]

n{\displaystyle n}	p=F(μ+nσ)−F(μ−nσ){\displaystyle p=F(\mu +n\sigma )-F(\mu -n\sigma )}	1−p{\displaystyle 1-p}	11−p{\displaystyle {\frac {1}{1-p}}}	OEIS
1	0.682689492137	0.317310507863		A178647
2	0.954499736104	0.045500263896		A110894
3	0.997300203937	0.002699796063		A270712
4	0.999936657516	0.000063342484
5	0.999999426697	0.000000573303
6	0.999999998027	0.000000001973

Моменты[править | править код]

Моментами и абсолютными моментами случайной величины X{\displaystyle X} называются математические ожидания случайных величин Xp{\displaystyle X^{p}} и |X|p{\displaystyle \left|X\right|^{p}}, соответственно. Если математическое ожидание случайной величины μ=0{\displaystyle \mu =0}, то эти параметры называются центральными моментами. В большинстве случаев представляют интерес моменты для целых p{\displaystyle p}.

Если X{\displaystyle X} имеет нормальное распределение, то для неё существуют (конечные) моменты при всех p{\displaystyle p} с действительной частью больше −1. Для неотрицательных целых p{\displaystyle p}, центральные моменты таковы:

E[Xp]={0p=2n+1,σp(p−1)!!p=2n.{\displaystyle \mathrm {E} \left[X^{p}\right]={\begin{cases}0&p=2n+1,\\\sigma ^{p}\,\left(p-1\right)!!&p=2n.\end{cases}}}

Здесь n{\displaystyle n} — натуральное число, а запись (p−1)!!{\displaystyle (p-1)!!} означает двойной факториал числа p−1{\displaystyle p-1}, то есть (поскольку p−1{\displaystyle p-1} в данном случае нечётно) произведение всех нечётных чисел от 1 до p−1{\displaystyle p-1}.

Центральные абсолютные моменты для неотрицательных целых p{\displaystyle p} таковы:

E⁡[|X|p]=σp(p−1)!!⋅{2πp=2n+1,1p=2n.}=σp⋅2p2Γ(p+12)

Обсуждение:Метод Гаусса — Википедия

Материал из Википедии — свободной энциклопедии

Метод Гаусса — это более общее понятие, чем метод решения СЛАУ. Например, существуют метод Гаусса вычисления определителя, метод Гаусса вычисления ранга матрицы. В общем случае метод Гаусса таков: 1) Выделить тип матрицы, для которой задача решается достаточно просто 2) Выделить тип преобразований, которые либо не меняют решения задачи, либо меняют его контролируемым образом 3) Произвольная матрица выделенными преобразованиями приводится к выделенному виду, тем самым задача сводится к более простой. — Эта реплика добавлена участником Goryachev (о • в)

А разве когда говорят о методе Гаусса в 1) бывает что-то кроме ступенчатого вида матрицы, а в 2) — что-то кроме элементарных преобразований строк (или столбцов, как непопулярный вариант)? Я думаю нет, поэтому давайте сделаем чуть попроще чем вы предлагаете — предподнесём метод Гаусса как в первую очередь метод приведения матрицы к ступенчатому виду с помощью элементарных преобразований. А дальше приведём приложения: ступенчатая форма может быть использована для решения СЛАУ (процедурой обратной подстановки), для нахождения детерминанта (если дополнительно считать число перестановок строк), ранга (= число ненулевых строк), LU-разложения (элементы матрицы L — это числа, на которые домножаются строки перед добавлением к другой строке, или что-то подобное). — X7q 18:33, 31 декабря 2009 (UTC)

1) Ну во-первых бывает(для вычисления определителя — треугольная матрица). Во-вторых, метод Гаусса — это выше изложенные общие принципы, конкретная реализация зависит от задачи. 2) Метод Гаусса — это элементарные преобразования? Смеетесь? Нет, давайте не будем его преподносить, как то, чем он не является. Метод приведения матрицы к ступенчатому виду — это теорема об основном процессе, только теоретическая база для одного пункта метода Гаусса, точнее, реализаций метода Гаусса для конкретных задач. И кстати, допустимые преобразования различны для разных задач. Goryachev 21:34, 1 января 2010 (UTC)

Треугольная матрица — частный вид ступенчатой. — X7q 21:51, 1 января 2010 (UTC)

Скорее, ступенчатая — частный вид треугольной, т.к. множество ступенчатых матриц — есть подмножество треугольных, но не наоборот.

Про «выше изложенные общие принципы» — вы можете привести авторитетный источник в котором были бы изложены эти общие принципы? Википедия — не место для оригинальных исследований, и если эти принципы нигде больше не упоминаются, то в ВП им тоже не место. — X7q 21:51, 1 января 2010 (UTC)

Конечно могу. Все тот же учебник по линейной алгебре Г. Д. Ким. Все, что я говорю, я прочитал в учебниках, и от себя ничего не добавляю. Goryachev 14:47, 2 января 2010 (UTC)

Мне кажется, что статью либо нужно переименовать в «Метод Гаусса(СЛАУ)», либо переписать, чтобы в ней содержались эти общие принципы и основные примеры(решение СЛАУ, вычисление определителя, вычисление ранга). — Эта реплика добавлена участником Goryachev (о • в)

А еще примеры есть? — X7q 18:33, 31 декабря 2009 (UTC)

Я не сталкивался с другими применениями. Goryachev 21:34, 1 января 2010 (UTC)

Про определитель и ранг можно просто сделать по одному подразделу. Про определитель сказать, на что он умножается после каждого элементарного преобразования (вследствие свойств определителей). Про ранг — сказать/доказать, что row space матрицы не меняется от элементарных преобразования строк, а размерность row space матрицы в ступенчатой форме (почти) очевидно равна числу ненулевых строк. — X7q 18:33, 31 декабря 2009 (UTC)

Вычисления определителя, ранга, решение СЛАУ — равноправные применения метода Гаусса, и нельзя выделять один над другими(как это в статье). При вычислении ранга допустимы не только преобразования строк, но и столбцов. Вообще, при вычислении ранга — наибольшая свобода с преобразованиями. Что за row space? И не размерность матрицы, а ранг 🙂 Goryachev 21:34, 1 января 2010 (UTC)

Про равноправные не согласен. Всё же, он наиболее известен именно как метод решения СЛАУ. — X7q 21:51, 1 января 2010 (UTC)

Ну это он Вам наиболее известен, как метод решения СЛАУ. Goryachev 14:47, 2 января 2010 (UTC)

Row space — пространство всех линейных комбинаций строк матрицы. Ранг матрицы (а точнее row rank, но он равен column rank ввиду какой-то теоремы, поэтому просто ранг) = размерность row space. — X7q 21:51, 1 января 2010 (UTC)

Понятно. Ввиду теоремы о базисном миноре. Goryachev 14:47, 2 января 2010 (UTC)

Пожалуйста проверьте в секции «Описание метода» индексы переменных. Мне кажется, что там должен быть вид a1j{\displaystyle a_{1j}} и xj{\displaystyle x_{j}}, а не a1j1{\displaystyle a_{1j_{1}}} и xj1{\displaystyle x_{j_{1}}} LeX 18:04, 3 января 2010 (UTC)

Изначально автор, видимо, предполагал все-таки трапецевидную форму основной матрицы, а для этого необходима перестановка столбцов, т.е. перенумерация переменных. Так что там все правильно. Вообще статья написана очень скверно, с ошибками. Ее бы переписать. Goryachev 10:57, 4 января 2010 (UTC)

ошибка у вас в статье а примере.. пересчитайте пожалуйста — Эта реплика добавлена с IP 89.23.18.112 (о)

исходя из примера, написанного в статье 2Х*1 + 3Х = о. Перепишите 78.128.195.83 22:02, 9 ноября 2010 (UTC)

Всё правильно в примере. Матлабом даже пересчитал. Единственное замечание — по-моему выбрана нестандартная последовательность элементарных операций. Обычно делается так: к строчке, в которой обнуляется коэффициент при старшем члене, прибавляется строчка, с помощью которой мы обнуляем, умноженная на что-то там. — X7q 22:38, 9 ноября 2010 (UTC)

Исправил. — X7q 22:53, 9 ноября 2010 (UTC)

спасибо, все сошлось 78.128.195.83 20:14, 13 ноября 2010 (UTC)

Рисунок изображающий алгоритм решения не совсем корректен. В конце, вместо строки x[i] -= a[i][c+1] * x[c+1] / a[i][i], должен быть цикл по c (c=i; c<n-1; c=c+1) и уже внутри цикла — вышеприведенная строка. К сожалению я не обладаю необходимой квалификацией, чтобы исправить данную ошибку самостоятельно. Прошу исправить более опытных товарищей.

Автор сообщения: YaYauhen 06:45, 22 октября 2013 (UTC)

К обсуждению это надо перерисовывать рисунок, так что суть лучше будет на странице обсуждения. MPI3 11:25, 23 октября 2013 (UTC)

Может, тогда стоит вообще убрать картинку, пока её не исправят? Чтобы не смущать никого. 62.76.92.6 11:30, 21 мая 2014 (UTC)

Теорема Гаусса — Википедия

Теорема Гаусса (закон Гаусса) — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность произвольной формы и алгебраической суммой зарядов, расположенных внутри объёма, ограниченного этой поверхностью. Применяется отдельно для вычисления электростатических полей.

Аналогичная теорема, также входящая в число уравнений Максвелла, существует и для магнитного поля (см. ниже).

Также теорема Гаусса верна для любых полей, для которых верен закон Кулона или его аналог (например, для ньютоновской гравитации). При этом она является, как принято считать, более фундаментальной, так как позволяет в частности вывести степень расстояния^[1] в законе Кулона «из первых принципов», а не постулировать её (или не находить эмпирически).

В этом можно видеть фундаментальное значение теоремы Гаусса (закона Гаусса) в теоретической физике.

Существуют аналоги (обобщения) теоремы Гаусса и для более сложных полевых теорий, чем электродинамика.

Теорема Гаусса для напряжённости электрического поля в вакууме[править | править код]

Общая формулировка: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.

СГС	СИ
ΦE=4πQ,{\displaystyle \Phi _{\mathbf {E} }=4\pi Q,}	ΦE=Qε0,{\displaystyle \Phi _{\mathbf {E} }={\frac {Q}{\varepsilon _{0}}},}

где

Данное выражение представляет собой теорему Гаусса в интегральной форме.

• Замечание: поток вектора напряжённости через поверхность не зависит от распределения заряда (расположения зарядов) внутри поверхности.

В дифференциальной форме теорема Гаусса выражается следующим образом:

СГС	СИ
divE≡∇⋅E=4πρ,{\displaystyle \mathrm {div} \,\mathbf {E} \equiv \nabla \cdot \mathbf {E} =4\pi \rho ,}	divE≡∇⋅E=ρε0.{\displaystyle \mathrm {div} \,\mathbf {E} \equiv \nabla \cdot \mathbf {E} ={\frac {\rho }{\varepsilon _{0}}}.}

Здесь ρ{\displaystyle \rho } — объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а ∇{\displaystyle \nabla } — оператор набла.

• Теорема Гаусса может быть доказана как теорема в электростатике исходя из закона Кулона (см. ниже). Формула, однако, также верна в электродинамике, хотя в ней она чаще всего не выступает в качестве доказываемой теоремы, а выступает в качестве постулируемого уравнения (в этом смысле и контексте её логичнее называть законом Гаусса^[2]).

Теорема Гаусса для электрической индукции (электрического смещения)[править | править код]

Для поля в диэлектрической среде электростатическая теорема Гаусса может быть записана ещё и иначе (альтернативным образом) — через поток вектора электрического смещения (электрической индукции). При этом формулировка теоремы выглядит следующим образом: поток вектора электрического смещения через замкнутую поверхность пропорционален заключённому внутри этой поверхности свободному электрическому заряду:

СГС	СИ
ΦD≡∮S⁡DdS=4πQ,{\displaystyle \Phi _{\mathbf {D} }\equiv \oint \limits _{S}\mathbf {D} \,\mathrm {d} \mathbf {S} =4\pi Q,}	ΦD≡∮S⁡DdS=Q,{\displaystyle \Phi _{\mathbf {D} }\equiv \oint \limits _{S}\mathbf {D} \,\mathrm {d} \mathbf {S} =Q,}

Важный комментарий

Важно заметить, что Q в правой части этого уравнения обозначено не то же самое, что в фундаментальной формулировке ΦE≡∮S⁡EdS=4πQ,{\displaystyle \Phi _{\mathbf {E} }\equiv \oint \limits _{S}\mathbf {E} \,\mathrm {d} \mathbf {S} =4\pi Q,} приведенной выше^[3], в начале статьи. Последняя часто называется «формулировкой для вакуума», однако это название чисто условное, она равно применимо и к случаю диэлектрической среды, только под Q здесь необходимо понимать сумму свободного заряда, находящегося внутри поверхности и поляризационного (индуцированного, связанного) заряда диэлектрика, то есть в уравнении для E надо было бы писать в правой части другую букву:

QΣ=Q+Qb,{\displaystyle Q_{\Sigma }=Q+Q_{b},}

где

• Qb=∮S⁡PdS{\displaystyle Q_{b}=\oint \limits _{S}\mathbf {P} \,\mathrm {d} \mathbf {S} } — связанный заряд внутри поверхности^[4],
• P{\displaystyle \mathbf {P} } — вектор поляризации диэлектрика.

Мы же здесь применили одну и ту же букву в правой части просто потому, что такая запись встречается чаще всего, а поскольку та и другая форма уравнения редко используются совместно, так что путаницы не возникает.

Для случая вакуума (отсутствия диэлектрической среды) то и другое уравнения просто совпадают, поскольку тогда Q_b=0, в то время как D=E (в системе единиц СИ — пропорциональны.

В дифференциальной форме:

СГС	СИ
divD≡∇⋅D=4πρ,{\displaystyle \mathrm {div} \,\mathbf {D} \equiv \nabla \cdot \mathbf {D} =4\pi \rho ,}	divD≡∇⋅D=ρ.{\displaystyle \mathrm {div} \,\mathbf {D} \equiv \nabla \cdot \mathbf {D} =\rho .}

Важный комментарий

• Важно понимать, что Q и ρ в этом параграфе обозначены другие величины, чем в предыдущем: величина свободных зарядов и плотность свободных зарядов, то есть зарядов за исключением индуцируемых при поляризации диэлектрической среды (тогда как в предыдущем параграфе имелись в виду полный заряд и полная плотность заряда (подробнее — см. комментрарий в этом параграфе чуть выше). Совпадают эти величины только для случая вакуума (отсутствия диэлектрической среды), когда и сами уравнения этого параграфа переходят по сути в уравнения предыдущего параграфа.

Теорема Гаусса для магнитной индукции[править | править код]

Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:

ΦB≡∮S⁡B⋅dS=0,{\displaystyle \Phi _{\mathbf {B} }\equiv \oint \limits _{S}\mathbf {B} \cdot \mathrm {d} \mathbf {S} =0,}

или в дифференциальной форме

∇⋅B=0.{\displaystyle \nabla \cdot \mathbf {B} =0.}

Это эквивалентно тому, что в природе не существует «магнитных зарядов» (монополей), которые создавали бы магнитное поле, как электрические заряды создают электрическое поле^[5]. Иными словами, теорема Гаусса для магнитной индукции показывает, что магнитное поле является (полностью) вихревым.

Теорема Гаусса для ньютоновской гравитации[править | править код]

Для напряжённости поля ньютоновской гравитации (ускорения свободного падения) теорема Гаусса практически совпадает с таковой в электростатике, за исключением только констант (впрочем, всё равно зависящих от произвольного выбора системы единиц) и, главное, знака^[6]:

Φg≡∮S⁡g⋅dS=−4πGM,{\displaystyle \Phi _{\mathbf {g} }\equiv \oint \limits _{S}\mathbf {g} \cdot \mathrm {d} \mathbf {S} =-4\pi GM,}

∇⋅g=−4πGρ,{\displaystyle \nabla \cdot \mathbf {g} =-4\pi G\rho ,}

где g — напряжённость гравитационного поля, M — гравитационный заряд (то есть масса) внутри поверхности S, ρ — плотность массы, G — ньютоновская константа.

В терминах силовых линий[править | править код]

Теорема Гаусса может быть интерпретирована в терминах силовых линий^[7] поля так:

1. Поток поля через поверхность есть^[8] количество силовых линий, пронизывающих эту поверхность. При этом учитывается направление — силовые линии, пронизывающие поверхность в обратном направлении считаются со знаком минус.
2. Силовые линии начинаются или кончаются только на зарядах (начинаются на положительных, кончаются на отрицательных), или могут ещё уходить на бесконечность. Количество силовых линий, исходящих из заряда (начинающихся в нём) равно^[9] величине этого заряда (это определение заряда в данной модели). Для отрицательных зарядов всё так же, только заряд равен минус количеству входящих в него (кончающихся на нём) линий.
3. Исходя из этих двух положений, теорема Гаусса представляется очевидной в формулировке: количество линий, исходящих из замкнутой поверхности равно суммарному количеству зарядов внутри неё — то есть количеству линий, появившихся внутри неё. Конечно же, подразумевается учёт знаков, в частности, линия, начавшаяся внутри поверхности на положительном заряде может закончиться на отрицательном заряде также внутри неё (если такой там есть), тогда она не даст вклада в поток через эту поверхность, так как или вообще до неё не дойдёт, или выйдет, а потом войдёт обратно (или, вообще говоря, пересечёт поверхность чётное количество раз поровну в прямом и противоположном направлении), что при суммировании с учётом знака даст вклад в поток ноль. То же можно сказать о линиях, начавшихся и закончившихся вне данной поверхности — по той же причине они также дадут нулевой вклад в поток через неё.

В терминах течения несжимаемой жидкости[править | править код]

Теорема Гаусса верна для поля скоростей несжимаемой жидкости. Этот факт позволяет использовать течение несжимаемой жидкости в качестве аналогии (формальной модели), позволяющей прояснить её смысл и наглядно представить её математическое содержание.^[10]

Полезно здесь заметить, что даже сама терминология векторного анализа, используемая в электродинамике (и в частности при формулировке теоремы Гаусса) сформировалась почти целиком под влиянием этой аналогии. Достаточно указать на такие термины, как источник поля (применительно к заряду) или поток через поверхность, которые полностью и точно соответствуют в рассматриваемой аналогии понятиям:

• источник жидкости (в смысле места, где жидкость возникает и количественной меры её возникновения — объём, возникающий в единицу времени),
• поток (в смысле количества жидкости, проходящей через поверхность в единицу времени).

В терминах течения несжимаемой жидкости теорема Гаусса формулируется так: Поток жидкости, исходящий из замкнутой поверхности, равен сумме источников, находящихся внутри этой поверхности. Или, более формально: Поток вектора скорости жидкости через замкнутую поверхность равен сумме источников, находящихся внутри этой поверхности. (В сущности, это интегральный вариант уравнения непрерывности для несжимаемой жидкости, выражающего сохранение массы жидкости с учётом постоянства её плотности).

В этой формальной аналогии напряжённость поля заменяется на скорость течения жидкости, а заряд — на источник жидкости (отрицательный заряд — на «отрицательный источник» — «сток»).

Теорема Гаусса как определение заряда[править | править код]

Теорема Гаусса^[11] может рассматриваться как определение (величины) заряда.

Так, для точечного заряда очевидно, что поток напряжённости поля через любую поверхность равен потоку через маленькую (бесконечно маленькую) сферу, окружающую этот заряд. Тогда последний (с точностью, быть может, до постоянного коэффициента, в зависимости от нашего произвольного выбора единиц измерения) может быть выбран в качестве определения величины этого заряда.

Вблизи заряда (бесконечно близко к нему) его собственное поле, очевидно, даёт подавляющий вклад в поток через бесконечно маленькую сферу (поскольку поле безгранично растёт с уменьшением расстояния). Значит, остальными полями (порождаемыми другими зарядами) можно пренебречь. Тогда можно увидеть, что данное определение согласуется с обычным (через закон Кулона).

В современной физике обычно принято считать, что определение через закон Гаусса более фундаментально (как и сам закон Гаусса по сравнению с законом Кулона — см. ниже), хотя с определённой точки зрения они просто эквивалентны.

Теорема Гаусса и закон Кулона тесно связаны, как формально, так и по физическому содержанию. В некотором смысле можно утверждать, что теорема Гаусса является интегральной формулировкой закона Кулона или наоборот, что закон Кулона является следствием теоремы (закона) Гаусса.

Что из них считать постулатом, а что следствием — зависит от того, какую аксиоматизацию для электродинамики (или электростатики, если ограничиваться ею) мы выбираем; формально тот или другой выбор практически^[12] равноправны, а в случае электростатики это полностью так. Таким образом, выбор того или другого в качестве основания построения теории — вопрос нашего произвольного выбора.

Впрочем, аксиоматизация через закон Гаусса имеет то преимущество, что в законе Гаусса не содержится никаких произвольных параметров (таких, как степень расстояния −2 в законе Кулона), степень расстояния в законе Кулона возникает при этом автоматически из размерности пространства.

Однако, следует сделать оговорку. Если наивно считать, что закон Кулона и теорема Гаусса эквивалентны, то можно рассуждать так: из теоремы Гаусса следует закон Кулона, из закона Кулона следуют уравнения Максвелла для случая электростатики, т.о. второе уравнение Максвелла (о равенстве нулю ротора электрического поля) следует из теоремы Гаусса и является излишним. На самом деле, при выводе закона Кулона из теоремы Гаусса (см. ниже) мы дополнительно используем сферическую симметрию поля точечного заряда, а также нам необходимо ввести принцип суперпозиции, в то время как уравнения Максвелла являются самодостаточными.

Исторически первым был эмпирически открыт закон Кулона. В этом (историческом) смысле теорема Гаусса является его следствием. Именно в связи с этим она называется теоремой, так как первоначально появилась как теорема.

Непосредственно ниже показано, как закон Кулона и закон Гаусса могут быть получены в рамках электростатики^[13] друг из друга.

Закон Кулона как следствие закона Гаусса[править | править код]

Исходим из теоремы Гаусса, записав её в единицах системы СИ^[14], «Поток ΦE,S{\displaystyle \Phi _{E,S}} вектора напряжённости E{\displaystyle E} через поверхность S{\displaystyle S} пропорционален заряду, заключённому в эту поверхность»:

ΦE,S=Qε0.{\displaystyle \Phi _{E,S}={\frac {Q}{\varepsilon _{0}}}.}

Для вывода Закона Кулона, будем рассматривать единственный точечный заряд в пределах замкнутой поверхности S, таким образом Q здесь будет величиной этого заряда.

Рассчитаем тот же поток прямым интегрированием по поверхности. Замечаем, что задача имеет сферическую симметрию относительно положения заряда. Из этого делаем вывод, что электрическое поле будет направлено прямо от заряда, а его величина будет одинакова для любых точек, расположенных на одинаковом расстоянии от заряда. Из этого следует, что суммарный поток будет проще всего сосчитать, если в качестве поверхности S выбрать сферу с центром в заряде. Действительно, напряжённость поля E тогда будет всюду ортогональна dS, а абсолютная величина вектора E (будем обозначать её E) будет одинакова везде на этой сфере, и её можно будет вынести за знак интеграла. Итак:

ΦE,S=∮S⁡E⋅dS=∮S⁡EdS=E∮S⁡dS=ES.{\displaystyle \Phi _{E,S}=\oint \limits _{S}\mathbf {E} \cdot \mathbf {dS} =\oint \limits _{S}EdS=E\oint \limits _{S}dS=ES.}

Имеем:

{ΦE,S=Qε0ΦE,S=ES{\displaystyle {\begin{cases}\Phi _{E,S}={\frac {Q}{\varepsilon _{0}}}\\\Phi _{E,S}=ES\end{cases}}}

Отсюда:

ES=Qε0.{\displaystyle ES={\frac {Q}{\varepsilon _{0}}}.}

Осталось подставить сюда для площади сферы S=4πr2{\displaystyle S=4\pi r^{2}} и разрешить уравнение относительно E.

Тогда получаем:

E=14πε0Qr2,{\displaystyle E={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r^{2}}},}

то есть — закон Кулона.

Теорема Гаусса как следствие закона Кулона[править | править код]

Элементарное доказательство[править | править код]

Элементарное доказательство строится на двух шагах: доказательстве теоремы для случая одного точечного заряда с использованием геометрических соображений, а затем применении принципа суперпозиции, вследствие которого теорема оказывается доказана для произвольного количества точечных зарядов (а значит и в общем случае).

Исходим из закона Кулона:

E(r)=qr2er{\displaystyle \mathbf {E} (\mathbf {r} )={\frac {q}{r^{2}}}\mathbf {e} _{r}},

где er{\displaystyle \mathbf {e} _{r}} — единичный вектор в направлении радиус-вектора r{\displaystyle \mathbf {r} }, проведённого из заряда (куда мы поместили начало координат) в точку, где измеряется напряжённость поля E(r){\displaystyle \mathbf {E} (\mathbf {r} )}, r — модуль вектора r, то есть расстояние от заряда до этой точки. (В этом параграфе будем пользоваться только системой СГС, то есть кулоновская константа равна единице. Для перехода в систему СИ достаточно просто добавить множитель. Так же и переход к любой другой системе единиц будет отличаться только кулоновской константой.)

Для одного точечного заряда внутри поверхности[править | править код]

Обозначим поверхность, через которую надо вычислить поток E, буквой S. Полагаем, что наш заряд q находится внутри этой поверхности.

Окружим заряд ещё одной поверхностью — сферой S₀ с центром в заряде и радиусом R₀ столь малым, что она целиком находится внутри поверхности S. Вычислим поток через S₀:

ΦS0=4πR02E.{\displaystyle \Phi _{S_{0}}=4\pi R_{0}^{2}E.}

Выберем малый (бесконечно малый, малый не только по величине, но и «компактно», то есть так, чтобы он, скажем, мог быть покрыт круговым конусом также малого телесного угла), телесный угол ω{\displaystyle \omega } с вершиной в заряде.

Докажем, что поток ΦS,ω {\displaystyle \Phi _{S,\omega }\ } через площадку поверхности S, вырезаемую этим телесным углом ω{\displaystyle \omega }, равен потоку ΦS0,ω{\displaystyle \Phi _{S_{0},\omega }} через площадку S0,ω{\displaystyle S_{0,\omega }}, вырезаемую им же из сферы S₀. Для этого покажем, что

1. ΦS,ω =ΦS⊥,ω {\displaystyle \Phi _{S,\omega }\ =\Phi _{S_{\perp ,\omega }}\ } — поток через площадку Sω{\displaystyle S_{\omega }}, вырезаемую телесным углом ω{\displaystyle \omega } из поверхности S, равен потоку через площадку S⊥,ω,{\displaystyle S{\perp ,\omega },} вырезаемую телесным углом ω{\displaystyle \omega } из любой плоскости, перпендикулярной лучам, лежащим внутри ω{\displaystyle \omega }, которые при бесконечно малом телесном угле почти параллельны, отличаясь по направлению бесконечно мало, значит площадка будет одновременно перпендикулярна (говоря строже — почти перпендикулярна) всем им одновременно.

2. ΦS⊥,ω=ΦS0,ω.{\displaystyle \Phi _{S\perp ,\omega }=\Phi _{S_{0},\omega }.} — в пределах телесного угла ω{\displaystyle \omega }, поток через площадку, перпендикулярную лучам, равен потоку через площадку сферы S0{\displaystyle S_{0}}.

Первое доказывается замечанием о том, что поток dΦ=E⋅dS{\displaystyle d\Phi =\mathbf {E} \cdot \mathbf {dS} } через малую площадку dS может быть представлен как dΦ=E(dS)⊥{\displaystyle d\Phi =E(dS)_{\perp }}, где (dS)⊥{\displaystyle (dS)_{\perp }} — проекция вектора dS на направление вектора E, то есть площадь проекции данной площадки на плоскость, перпендикулярную E. А применительно к нашему случаю это и означает равенство ΦS⊥,ω{\displaystyle \Phi _{S\perp ,\omega }} и ΦS,ω{\displaystyle \Phi _{S,\omega }}.

Второе видно из соображений подобия и закона Кулона (обозначив r расстояние от заряда до пересечения ω{\displaystyle \omega } c S, видим, что отношение площадей S⊥,ω{\displaystyle S{\perp ,\omega }} и S0,ω{\displaystyle S_{0,\omega }} равно r2/R02{\displaystyle r^{2}/R_{0}^{2}}, в то время как E(r)/E(R0)=R02/r2{\displaystyle E(r)/E(R_{0})=R_{0}^{2}/r^{2}}, то есть обратному числу, в результате чего их произведения одинаковы, а это и есть потоки ΦS⊥,ω{\displaystyle \Phi _{S\perp ,\omega }} и ΦS0,ω{\displaystyle \Phi _{S_{0},\omega }}, равенство которых надо было доказать.

В случае, если ω{\displaystyle \omega } пересекает S неоднократно (что возможно, если последняя достаточно сложна), все эти рассуждения, если говорить коротко, повторяются столько раз, сколько пересечений имеется, и доказывается равенство по абсолютной величине потока через каждый такой элемент поверхности S. А учитывая знаки при сложении (они, очевидно, чередуются; всего же количество пересечений должно оказаться нечётным), итоговый ответ оказывается тем же, что и для случая единственного пересечения.

А поскольку равенство этих потоков выполняется для любого малого ω{\displaystyle \omega }, то есть для каждого соответственного элемента S и S₀, между которыми устанавливается однозначное соответствие, причём таким образом можно разбить всю сферу S₀ без остатка на такие элементы, то равенство верно и для потоков через полные поверхности (которые суть просто суммы потоков через описанные элементы поверхностей S и S₀). (Поскольку поверхность S замкнутая, каждому элементу на сфере находится соответствующий элемент на S — или нечётное количество элементов, как было описано выше, которые можно объединить, так как учтён поток через их все).

Итак, доказали, что для одного заряда q внутри замкнутой поверхности S поток через неё

ΦS=ΦS0=4πR02E.{\displaystyle \Phi _{S}=\Phi _{S_{0}}=4\pi R_{0}^{2}E.}

Для одного точечного заряда вне поверхности[править | править код]

Совершенно аналогичные рассуждения, проведённые для случая, когда q находится вне области, ограничиваемой поверхностью S, с учётом знака при подсчёте потока через каждую площадку, дают в результате поток ноль. (малый телесный угол теперь пересечёт S чётное число раз, потоки будут равны по абсолютной величине, но противоположны по знаку)^[15].

Суммирование элементарных потоков производится также аналогично сделанному в пункте 1, как и их вычисление.

Итак, для одного заряда вне замкнутой поверхности поток через неё нуль.

Для любого количества зарядов[править |

Обсуждение:Метод Гаусса — Жордана — Википедия

Материал из Википедии — свободной энциклопедии

От AlexxxMksv очень понятно разжовано, но уменя остался вопрос -как будет выглядеть решение системы из двух уравнений и и 3-х неизвестных. Пример Решим следующую систему уравнений:

{a−b+2c=0−3a+2b−c=1{\displaystyle \left\{{\begin{array}{ccccccl}a&-&b&+&2c&=&0\\-3a&+&2b&-&c&=&1\end{array}}\right.}

у меня получилось

(1−12|00−15|1){\displaystyle {\begin{pmatrix}1&-1&2&|&0\\0&-1&5&|&1\end{pmatrix}}}

(10−3|−101−5|−1){\displaystyle {\begin{pmatrix}1&0&-3&|&-1\\0&1&-5&|&-1\end{pmatrix}}}

дальше как? единственного решения нет

-Дальше — все. Так его у данной СЛУ и нет. Как я понимаю, метод используется только для квадратных систем. Или переносихь С в левую часть и решаешь при фиксированном С Nikto 22:48, 20 февраля 2009 (UTC)

Ошибка изложения метода[править код]

Отличие метода Гаусса от его модификации Гаусса-Жордана состоит в том, что в процессе сразу получается еденичная матрица — никаких верхнетреугольных не образуется (в нули обращаются элементы и над диагональю), соответственно требуется изменить содержимое статьи (алгоритм и пример (это чистый Гаусс)), что собственно я ещё не умею.

Полезно добавить информацию по части программирования о модификации связанной с перестановкой строчек с наибольшыми элементами, а также отсечение получаемых значений «возле нуля». Olv33 21:10, 22 ноября 2009 (UTC)

Не указаны уравнения(в дано и ответе), пропущены переменные в тексте, из-за чего теперь нельзя понять какие операции происходят с уравнением.

Автор сообщения: Гекк 109.194.193.25 09:13, 22 сентября 2013 (UTC)

Да, правда — почему-то почти все формулы в статье были в виде картинок, которые из-за отсутствия лицензии были удалены. Теперь этот раздел надо вообще переписать. Поставил пока плашку. Будет время — займусь. MPI3 11:49, 22 сентября 2013 (UTC)

К обсуждению. Sealle 05:05, 26 сентября 2013 (UTC)

Метод Гаусса-Жордана предназначен для решения не только квадратных систем алгебраических уравнений[править код]

В определении указано, что это метод, который используется для решения квадратных систем линейных алгебраических уравнений.

Написано:

5. Далее проводят такую же процедуру с матрицей, получающейся из исходной матрицы после вычёркивания первой строки и первого столбца.

— Из этого можно сделать вывод, что вычеркнутые строки и столбцы не участвуют в пп.2-4. На самом деле это не так, участвуют строки и столбцы целиком.

Написано:

8. Повторяют предыдущий шаг для последующих строк. В итоге получают единичную матрицу и решение на месте свободного вектора (с ним необходимо проводить все те же преобразования).

— Что именно повторяют, вычитание из из предпоследней строки последней? Непонятность тут.

93.123.160.206 09:24, 21 августа 2018 (UTC)ds

Закон Гаусса для магнитного и электрического поля, определение

В статье расскажем про определение потока электрического поля, подробно узнаете про закон Гаусса, его отличия от закона Кулона, а так же рассмотрим на примерах применение закона Гаусса для расчета электрического поля. В дополнении к этому, рассмотрим линии и потоки магнитного поля, закон Гаусса для поля B.

Определение потока электрического поля

Если электрическое поле однородно и когда плоскость с площадью A установлена ​​перпендикулярно линии этого поля E , то поток электрического поля Φ_E,пронизывающий эту поверхность, равен:

Если теперь эта поверхность отклонена на угол φ от предыдущей позиции, поток изменит свое значение и будет:

Поскольку поток имеет скалярный размер, это соотношение для однородного поля можно записать как произведение скалярного вектора поля E и вектора поверхности A:

Φ_E = Е * А

В общем случае, когда поле неоднородно, а поверхность не плоская, приближенное выражение для поля E через участок изогнутой поверхности получается путем деления этого куска на количество из n небольших плоских панелей, каждая из которых имеет небольшую, но конечную поверхность ΔA _i . Электрическое поле, проходящее через поверхность ΔA _i, имеет приблизительно постоянное значение E _i, а приблизительное значение поля E потока получается суммированием потоков через отдельные плоские лепестки.

Поток Е (гомогенная или гетерогенный) через бесконечно малый элемент поверхности d А называются скалярное произведение:

Поток поля E, проходящий через участок области A, будет получен после замены суммы путем интегрирования по всей плоскости A:

Поток поля E, проходящий через замкнутую поверхность A, описывается интегралом (целочисленный символ с кружком)

Вектор dА мы выбираем так , что он обращен к наружной поверхности:

Поток векторного поля может быть проиллюстрирован графически с использованием силовых линий этого поля:

Общее количество силовых линий в телесном угле при 2R такое же, как и на расстоянии R. Напряженность поля обратно пропорциональна R² , но площадь A прямо пропорциональна R² . Таким образом, произведение этих двух величин, 1 / R² × R² , не зависит от R.

Если внутри замкнутой поверхности на чертеже , обозначенном A₁, разместить положительный заряд +Q, поток электронов через поверхность будет положительным. После того, как внутри другой замкнутой поверхности А₂ будет размещать груз с тем же значением, но с противоположным знаком, -Q, поток будет отрицательным (линии поля входят внутрь), но абсолютное значение потока через поверхность A₂ будет таким же, как для поверхности A₁.

Значение потока не зависит от формы замкнутой поверхности, а зависит только от величины нагрузки, заключенной внутри этой поверхности. Следовательно, поток поля, исходящий из электрического диполя внутри любой замкнутой поверхности, будет равен нулю (поскольку алгебраическая сумма +Q и -Q равна нулю).

Если бы заряды не были одинаковыми, поток поля не мог быть нулевым. Если, например, отрицательный заряд больше положительного, поток поля через закрытую поверхность является отрицательным, как на рисунке:

Закон Гаусса для электрического поля

Закон Гаусса, один из важнейших в электродинамике, определяет, что поток электрического поля E через замкнутую поверхность   определяется только алгебраической суммой всех электрических зарядов Q, содержащихся в этой поверхности. Неважно, как эти нагрузки распределяются внутри этой поверхности.

Символ Q является алгебраической суммой зарядов внутри замкнутой поверхности A, после чего мы интегрируем поток; g₀ — электрическая проницаемость вакуума.

 Не имеет значения, как распределяются заряды внутри поверхности A. В то же время на величину общего потока электрического поля не влияют никакие заряды, которые находятся за пределами поверхности А, даже те, которые прилипли к ее внешней стороне.

Закон Гаусса для электрического поля представляет собой обобщенную формулировку взаимосвязи между зарядами и электрическими полями и является одним из четырех уравнений Максвелла, описывающих все электрические и магнитные явления.

Применение закона Гаусса для расчета электрического поля

Имея данное распределение заряда, мы можем использовать закон Гаусса для электрического поля, чтобы вычислить значение электрического поля в конкретной точке или области. Ключевое действие — окружить соответствующую зону нагрузки подходящим образом выбранной закрытой поверхностью. Хотя закон Гаусса выполняется для каждой замкнутой грани А, выбор этой поверхности должен быть таким, чтобы его интегрирование было наиболее простым. В приведенных примерах предлагаемая поверхность Гаусса отмечена красным контуром на рисунке.

1. Закон Кулона содержится в законе Гаусса, но он сам является экспериментальной зависимостью, которую мы использовали для получения закона Гаусса.

Таким образом, закон Гаусса является более общим, чем закон Кулона: закон Гаусса не может быть выведен из закона Кулона, но закон Кулона легко получается из закона Гаусса. Достаточно найти силу F = q * E , действующую на точечный заряд q, расположенный на расстоянии r от другого точечного заряда Q. Чтобы определить F, нам нужно знать только E. Поместим нагрузку Q в центр сферы с радиусом r, как на рисунке:

Поле Е от заряда Q на поверхности сферы имеют то же значение, всюду на поверхности вектора E параллельно вектору dА. После применения закона Гаусса мы получаем:

или

Поскольку вектор E направлен вдоль радиуса r , то:

Согласно определению поля E, сила, действующая на нагрузку q, равна:

Поэтому мы получили закон Кулона от закона Гаусса:

2. Поле заряженной проводящей сферы с радиусом r (внутри сферы нет зарядов):

В соответствии с законом Гаусса, поле вне сферы на расстоянии R от центра , или:

Внутри поля сферы (Q = 0): E = 0.

3. Поле однородно заряженной диэлектрической сферы. Общая нагрузка, содержащаяся в шаре, составляет Q.

При расчете поля E на расстоянии x от центра сферы обозначим через q заряд, содержащийся в сфере с радиусом x. От прямой линии мы получаем:

На основании закона Гаусса искали поле Е внутри шара. Таким образом, поле внутри сферы линейно растет с увеличением x. Вне сферы поле уменьшается с увеличением расстояния от центра:

4. Линейное зарядное поле и заряженный проводящий цилиндр с плотностью заряда 8 [С / м]:

На участке L имеется нагрузка Q = 8 L, поэтому мы получаем закон Гаусса . Отсюда мы находим искомую область:

5. Поле заряженного бесконечного плоского слоя.

Поле является однородным и простирается в обоих направлениях перпендикулярно поверхности пластины (проходит только через основание цилиндра). Мы получаем закон Гаусса:

6. Поле заряженной бесконечной плоской проводящей пластины.

Нагрузка на проводящую пластину распределяется на обе поверхности. Поскольку у нас есть два слоя нагрузки с плотностью заряда σ каждый, то напряженность поля будет в два раза выше в зависимости от результата предыдущего примера.

7. Поле между противоположно заряженными параллельными проводящими пластинами:

В качестве гауссовой поверхности мы выбираем прямоугольную призму с одним основанием, погруженным в металлическую пластину, где нет ни заряда, ни поля E. Поле проникает только в основание прямоугольной призмы, которое находится в пространстве между пластинами. Из закона Гаусса мы получаем:

Снаружи пластин поле равно нулю.

Линии магнитного поля

Магнитные силовые линии , как правило, кривые, иллюстрирующие направления магнитного поля B. Это означает, что в каждой точке линии поля имеется вектор B, касательный к этой линии. В однородном поле B линии поля образуют пучок параллельных прямых. Линий поля B бесконечно много, потому что одна линия проходит через каждую точку поля.

  Из предыдущей статьи мы знаем, что источниками поля B являются движущиеся электрические заряды (электрический ток). Другими широко известными источниками магнитного поля являются постоянные магниты, часто сделанные в форме подковы или стержня. Каждый магнит имеет два полюса, обычно называемых северным и южным (в соответствии с их ориентацией к полюсам Земли). Эти полюса нельзя отделить друг от друга. Стержневой магнит, разрезанный на две части, даст два стержневых магнита, каждый из которых будет иметь собственный набор полюсов N и S. Такие умножающие магниты можно продолжать без надежды на отделение полюсов друг от друга. Каждый магнит, полученный таким образом, будет биполярной системой ( магнитный диполь). Хотя ни один закон природы не запрещает магнитным полюсам появляться отдельно в качестве магнитных монополей, ни в природе, ни в экспериментальных исследованиях магнитных монополей пока не найдено. Поиски продолжаются.

Как мы видели ранее, линии электрического поля генерируются на отдельных зарядах или в системах нагрузки и могут легко исчезать. В случае поля B линии поля образуют замкнутые петли. Такие линии, идущие от одного полюса, могут проникать через различные объекты в непосредственной близости от магнита, но они обязательно должны возвращаться к другому полюсу.

Изображение распределения поля B вокруг стержневого магнита показано на фотографии стеклянной пластины, обсыпанной ферромагнитным порошком и помещенной на магнит. Порошковый слой уплотняется в областях, где поле B сильнее. В непосредственной близости от полюсов, где поле является самым сильным, ферромагнитный порошок энергично натягивается на полюса магнита, заставляя слой истончаться на стекле.

Поскольку линии поля B образуют замкнутые петли, такие линии, пересекающие замкнутую поверхность, обязательно должны давать нулевую сумму — число линий, покидающих эту область, точно равно числу обратных линий.

Отличным местом для всех, кто интересуется природой и экспериментальными исследованиями, является Exploratorium в Сан-Франциско, расположенный во дворце рядом со знаменитым мостом Золотые Ворота и островом тюрьмы Алькатрас (ныне музей). Из более чем ста исследовательских стендов, особенно осажденных детьми, есть станция с магнитом, покрытым ферромагнитными зернами (называемым там «песком»). Магнитное поле, проникая через тело, строит свои структуры в пространстве, вызывая, среди прочего, выращивание ферромагнитных деревьев на поверхности ладони, как показано на фотографиях.

Поток магнитного поля

Поток B определяется аналогично вектору потока любого размера, и, в частности , потока электрического поля Е. Элементарный поток поля В , проходящих через бесконечно малый элемент поверхности d А определяются как скалярное произведение между этими двумя значениями:

Таким образом, поток поля B, проходящий через макроскопический поверхностный слой A:

Единица магнитного потока в системе СИ составляет 1 Вебер (1 Вб) = 1 Н · м · А ^-1 . Таким образом, магнитное поле B иногда называют плотностью потока и 1T = 1 Вт · м ^-2 .

Закон Гаусса для магнитного поля

Закон Гаусса для поля B определяет, что поток магнитного поля через закрытую поверхность равен нулю, т.е. :

Обратите внимание на очень важный символ интеграла с кружком, который говорит, что интеграция должна происходить на замкнутой поверхности. В случае электрического поля плотность электрического заряда находится справа от аналогичного уравнения. Поскольку в природе нет магнитных монополей, полюса N и S должны быть в одном и том же числе, что дает алгебраически ноль. По этой причине справа от уравнения, описывающего закон Гаусса для B , ноль. Закон Гаусса для магнитного поля является одним из четырех уравнений Максвелла (в интегральной форме), описывающих совокупность электрических и магнитных явлений в природе.