Элементы комбинаторики. Правило суммы и произведения

Комбинаторика — это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов, принадлежащих данному множеству.

Решение многих комбинаторных задач основывается на двух фундаментальных правилах, называемых правилом суммы иправилом произведения.

Правило суммы

Если некоторый объект А может быть выбран из совокупности объектов nспособами, а другой объект В может быть выбранmспособами, то выбрать либо объект А, либо объект В можноспособами.

Правило произведения

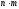Если объект А может быть выбран из совокупности объектов nспособами и посла каждого такого выбора объект В может быть выбранmспособами, то пара объектов (А,В) в указанном порядке может быть выбранаспособами.

Примеры.

7. В первом ящике 8 шаров, во втором -10 шаров. Сколькими способами можно выбрать один шар из двух ящиков?

► Событие А – выбор шара из первого ящика, он может быть осуществлен 8-ю способами, событие В – выбор шара из второго ящика, он может быть осуществлен 10-ю способами, т.е. n=8,m=10. Событие А+В – выбор одного шара либо из первого ящика, либо из второго. По правилу суммы находим:=8+10=18.

8. Сколько можно составить пятизначных чисел так, чтобы любые две соседние цифры были различны?

► Первую цифру можно выбрать 9-ю способами, вторую – 9-ю способами и т.д., следовательно, всего цифр можно составить способами (правило произведения).

1.5. Основные формулы комбинаторики

Пусть дано конечное множество X, состоящее изn элементов.

Размещением изnэлементов поmмножестваXназывают любые наборы, которые отличаются либо составом элементов, либо их порядком:

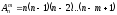. (4)

Частный случай размещения – перестановки: наборы, состоящие изnодних и тех же элементов, отличающиеся только порядком их расположения.

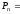n!. (5)

Сочетаниемизnэлементов поmмножестваXназывают любые неупорядоченные наборы, которые отличаются хотя бы одним элементом:

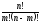. (6)

Отсюда может быть выведена формула размещения, более удобная для счета:

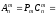
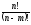. (7)

Перестановки с повторениями– это различные конечные наборы изnэлементов, в которых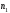элементов принадлежат одному виду,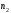элементов – другому виду и т.д. и.

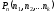=. (8)

Примеры.

9. Сколько различных двузначных чисел можно составить из чисел 1,2,3,4?

►.

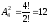10. Сколько различных четырехзначных чисел можно составить из чисел 1,2,3,4?

►.

11. Сколькими способами можно выбрать две детали из ящика с десятью деталями?

►

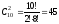
12. Сколько различных шестизначных чисел можно составить из трех единиц, одной двойки и двух троек?

►

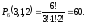
Сочетания с повторениями

Сочетанием из nэлементов множестваXпоmс повторениями называют любые неупорядоченные наборы, состоящие изmэлементов, каждый из которых принадлежит к одному изnвидов.

(9)

Например, из трех различных элементов 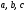можно составить следующие сочетания с повторениями:.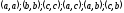

►.

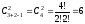Размещения с повторениями

Пусть

X– множество изnэлементов. Достаем один элемент, фиксируем, кладем элемент обратно. Выборку производимтраз. Число таких наборов из nэлементов множестваXпоmравно

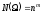. (10)

Пример 13. Сколько существует трехзначных телефонных номеров?

►.

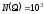studfile.net

Комбинаторика 1. Правило суммы 2. Правило произведения

Комбинаторика 1. Правило суммы 2. Правило произведения 3. Комбинаторные соединения 4. Перестановки 5. Размещения 6. Сочетания

Комбинаторика — один из разделов дискретной математики, который приобрел важное значение в связи с использованием его в информационных технологиях, кибернетике и многих других науках.

ПРАВИЛО СУММЫ Комбинаторные задачи бывают самых разных видов. Однако, большинство задач решается с помощью двух основных правил — правила суммы и правила произведения. Если некоторый объект A можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор «либо А, либо В» можно осуществить (m+n) способами. При использовании правила суммы надо следить, чтобы ни один из способов выбора объекта А не совпадал с каким-либо способом выбора объекта В. Если такие совпадения есть, правило суммы утрачивает силу, и мы получаем лишь (m + n — k) способов выбора, где k—число совпадений.

ПРАВИЛО СУММЫ Пример 1 На одной тарелке 3 груши, на другой – 2 яблока. Сколько есть способов выбрать один фрукт? Пример 2 На полке стоит 2 книги по алгебре, 3 по геометрии, 1 по комбинаторике и 4 по литературе. Сколько есть способов выбрать книгу по математике?

ПРАВИЛО ПРОИЗВЕДЕНИЯ Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать n способами, то выбор пары (А, В) в указанном порядке можно осуществить mn способами. При этом число способов выбора второго элемента не зависит от того, как именно выбран первый элемент.

ПРАВИЛО ПРОИЗВЕДЕНИЯ Пример 3 Имеется 5 видов конвертов без марок и 3 вида марок. Сколькими способами можно получить конверт с маркой? Пример 4 Сколькими способами можно выбрать гласную и согласную из слова «буран» ? Пример 5 Сколько существует пятизначных чисел, делящихся без остатка на 10?

Комбинаторные соединения — это комбинации из каких-либо элементов. Типы соединений: • Перестановки • Размещения • Сочетания Существуют две схемы выбора элементов: • Без повторений • С повторениями

Комбинаторные соединения В комбинаторных соединениях может играть существенную роль или порядок элементов или их состав, или и порядок и состав. В зависимости от этого комбинаторные соединения имеют определённое название.

Перестановки без повторений — комбинаторные соединения, которые могут отличаться друг от друга лишь порядком входящих в них элементов. Pn= n!

Факториал числа — это произведение всех натуральных чисел до этого числа включительно. Обозначается с восклицательным знаком в конце. n! = 1 · 2 · 3 · 4 · … · (n-2) · (n-1) · n Случай 0! определен и имеет значение 0!=1, соответствующее комбинаторной интерпретации комбинации нуля объектов, другими словами, есть единственная комбинация нуля элементов, а именно: пустое множество.

Факториал числа Свойство факториала: (n + 1)! = (n + 1) · n! Пример 6! = (5+1)!=(5+1)*5!=6*(1*2*3*4*5)=720

Перестановки с повторениями — комбинаторные соединения, в которых среди образующих элементов имеются одинаковые.

Примеры Пример 6. На полку нужно поставить 3 разные книги. Сколько есть способов это сделать? P 3=3!=6 Пример 7. Сколько различных «слов» можно составить из слова «март» ?

Примеры Пример 8. Сколькими способами можно переставить буквы слова «ананас» ? Букв «а» – 3, букв «н» – 2, букв «с» – 1.

Размещения без повторений — комбинаторные соединения, составленные из n элементов по m. При этом два соединения считаются различными, если они либо отличаются друг от друга хотя бы одним элементом, либо состоят из одних и тех же элементов, но расположенных в разном порядке.

Размещения без повторений Пример 9. В правление Банка избрано 9 человек. Сколькими способами можно выбрать из них Председателя, Заместителя Председателя и Секретаря?

Размещения без повторений Пример 10. Сколько словарей нужно издать для непосредственного перевода с русского, английского, немецкого и французского языков на любой из этих языков?

Размещения с повторениями — комбинаторные соединения, составленные из n элементов по m. При этом каждый из n элементов может содержаться сколько угодно раз или вообще отсутствовать.

Размещения с повторениями Пример 11. Сколько трехпозиционных комбинаций можно образовать из двоичных цифр? Пример 12. Есть кодовый замок с четырьмя дисками, на каждом из которых цифры от 0 до 9. Сколько существует вариантов кода?

Сочетания без повторений — комбинаторные соединения из n элементов по m, составленные из этих элементов и отличающиеся друг от друга только составом.

Сочетания без повторений Пример 13. В магазине есть краски 5 различных цветов. Вы хотите для оформления комнаты использовать 3 цвета. Сколько есть способов это сделать?

Сочетания с повторениями — комбинаторные соединения из n элементов по m, составленные из этих элементов без учета порядка с возможностью многократного повторения элементов.

Сочетания с повторениями Пример 14. В киоске продается 3 вида открыток сколькими способами можно купить 5 открыток?

present5.com

Access to the site is allowed only for human.

Вы используете прокси или другую странную штуку.
Подтвердите что вы человек.
_{Отвечать нужно быстро}

You are using a proxy or other strange thing.
Confirm that you are a person.

intellect.icu

27. Элементы комбинаторики: правила суммы и произведения.

ПРАВИЛО СУММЫ

Если объект А может быть выбран m способами , а объект В – другими n способами, причем А и В несовместны, то выбор либо А либо В осуществляется m+n способами.

ПРАВИЛО ПРОИЗВЕДЕНИЯ

Если объект А может быть выбран m способами и после каждого из этих выборов объект В может быть выбран n способами, то выбор упорядоченной пары (А;В) может быть осуществлен m*n способами.

28. Алгебра событий: сумма, произведение событий. Противоположные события. Примеры.

О. Суммой двух событий А и В называется событие, заключающееся в наступлении или А или В или обоих событий вместе. Обозначение: А+В.

(иначе А+В – наступление хотя бы одного из событий)

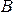Пример. Два стрелка делают по одному выстрелу в мишень. Событие — попадание 1-го стрелка в мишень и событие— попадание 2-го стрелка в мишень. Сумма событий– это попадание в мишень хотя бы одного из этих стрелков.

О. Произведением А и В называется событие, заключающееся в совместном наступлении А и В. Обозначение: А*В

Пример 1. Если А —деталь годная, В — деталь окрашенная, то — деталь А*В годна и окрашена.

Пример 2. Например, если   А;В;С появление «герба» соответственно в первом, втором и третьем бросаниях монеты, то  — выпадение «герба» во всех трех испытаниях.

О. Пусть А – некоторое событие. Под событием , противоположным ему, понимается событие, состоящее в том, что А не наступило. Обозначение: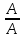

Пример 1. Попадание и промах при выстреле по цели — противоположные события. Если А — попадание, то противоположное событие — промах.

Пример 2. Из ящика наудачу взята деталь. События «появилась стандартная деталь» и «появилась нестандартная деталь» — противоположные.

29. Теорема сложения вероятностей для несовместных событий.

Если события А и В несоместны, то вероятность того, что осуществляется одно из этих событий, равна сумме их вероятностей. Р(А+В) = Р(А) – Р(В)

Следствие: Сумма вероятностей событий , образующих полную группу равна 1

Р(А₁) + Р(А₂)+….+Р(А_n) = 1

В частности : Р(А) +Р(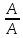) = 1

30. Зависимые и независимые события. Условная вероятность.

О. Два события называются независимыми, если появление одного из них не изменяет вероятность появления другого.

Пример 1. Монета брошена два раза. Вероятность появления «герба» в первом испытании (событие A) не зависит от появления или не появления «герба» во втором испытании (событие B). В свою очередь, вероятность появления «герба» во втором испытании не зависит от результата первого испытания. Таким образом, события A и B независимые.

О. События называются зависимыми, если одно из них влияет на вероятность появления другого.

О. Условной вероятностью 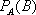называют вероятность событияВ, вычисленную в предположении, что событие А уже наступило.

Пример 1. В урне находятся 3 белых шара и 2 черных. Из урны вынимается один шар, а затем второй. Событие В – появление белого шара при первом вынимании. Событие А – появление белого шара при втором вынимании.

Пример 2. Из колоды в 36 карт последовательно извлекаются 2 карты. Найти вероятность того, что вторая карта окажется червой, если до этого:а) была извлечена черва;б) была извлечена карта другой масти.

studfile.net

Основные понятия комбинаторики

Цель работы: приобретение практических навыков в решении задач пересчета для основных видов комбинаторных соединений.

Теоретическая справка

Правила суммы и произведения

Важную роль при решении многих комбинаторных задач играют правила суммы и произведения.

Сформулируем эти правила с точки зрения теории множеств и комбинаторики.

Правило суммы

Теоретико-множественная формулировка правила суммы

Пусть AиB–конечные множества, |A| =m; |B| =n;AB=. Тогда объединение множеств:ABсодержитm+nэлементов.

В общем случае.

Пусть | M₁ | =m₁, |M₂ | =m₂ , … , |M_k| =m_kиM_iM_j=,

 i,j=1.. k, i  j. Тогда, | M | = | M₁  M₂  …  M_k | = m₁ + m₂ +…+ m_k.

Комбинаторная формулировка правила суммы

Если объект aможет быть выбранmспособами, а объектb–nдругими способами, то выбор «aилиb» может быть осуществленm+nспособами. Выборaиb– взаимоисключающий: выборaисключает выборb; выборaне совпадает с каким-либо способом выбораb.

В общем случае.

Если объект a₁ может быть выбранm₁ способами;a₂–m₂cпособами; … ;a_k–m_kспособами. Выбор «a₁илиa₂…илиa_k» может быть осуществленm₁ +m₂ + … +m_kспособами.

Например:

Из Киева в Донецк в течение суток отправляется 3 поезда, 1 самолет и 2 автобуса. Сколько существует способов выехать из Киева в Донецк?

Решение:

По правилу суммы имеем N= 3+1+2 = 6 способов.

Правило произведения Теоретико – множественная формулировка правила произведения

Если AиB– конечные множества и |A| =m, |B| =n, то мощность множестваABравнаmn.

В общем случае.

Если | M₁ | =m₁, |M₂ | =m₂, … , |M_k|=m_k, то |M₁ M₂ …M_k | = m₁m₂…m_k.

Комбинаторная формулировка правила произведения

Если объект aможет быть выбранmспособами, и после этого объектbможет быть выбранnспособами, то выбор пары (a,b) может осуществлятьсяmnспособами (выборaиbнезависимы).

В общем случае.

Пусть объект a₁может быть выбранm₁способом, объектa₂–m₂способами; объектa_k–m_kспособами, причем выборa₁не влияет на число способов выбораa₂, … ,a_k, выборa₂на число способов выбораa₃, … ,a_kи т.д_. Тогда, выбор упорядоченного множества объектов (a₁,a₂ …a_k) – в указанном порядке можно осуществитьm₁m₂_…m_kспособами.

Например:

Сколько различных танцующих пар можно составить из 3-х девушек и 2-х юношей?

Решение:

Число способов выбрать одну девушку из трех равно 3, при каждом способе выбора девушки число способов выбрать юношу постоянно и равно 2.По правилу произведения имеем N= 32 = 6 пар.

Сложный выбор объектов

Часто в комбинаторных задачах выбор объектов происходит в несколько ступеней, на некоторых работает правило суммы, на других – правило произведения. При сложном выборе объектов важно обеспечить полный перебор всех возможных случаев.

Например:

Имеется три различных флага. На флагштоке поднимается сигнал, состоящий не менее, чем из 2-х флагов. Сколько различных сигналов можно поднять на флагштоке, если порядок сигналов учитывается?

Решение:

Сигнал может состоять либо из 2-х флагов, либо из 3-х. Одновременное выполнение 2-х действий невозможно. Пусть N– общее число способов поднять сигнал, состоящий не менее, чем из 2 флагов;N₂ – число способов поднять сигнал, состоящий ровно из 2 флагов;N₃ – ровно из 3 флагов.

По правилу суммы имеем: N=N₂+N₃. ДалееN₂ иN₃ находим по правилу произведения:

N₂=32=6;

N₃=321=6.

В итоге имеем: N=12.

studfile.net

4. Правила суммы и произведения.

Правило суммы позволяет найти число элементов в объединении двух конечных множеств, а правило произведения – число элементов их декартова произведения.

Обозначим число элементов конечного множества Х через n(X), множество, состоящее из n элементов, назовем n—множеством. Например, если Х={а, б, в, г, д}, то n(Х)=4, т.е. Х является 4-множеством.

Правило суммы: Если множество Х содержит m элементов, а множество У – n элементов, причем эти множества не пересекаются, то множество ХУ содержит m+n элементов, т.е. из ХУ=Ø n(ХУ)=n(Х)+n(У).

Пример. Х={а, б, в, г,}, У={с, е, д}. Найти n(ХУ).

n(X)=4, n(У)=3. Т.к. ХУ=Ø , то (ХУ)=n(Х)+n(У)=4+3=7.

Если пересечение множеств не пусто, т.е. ХУ≠Ø, например: Х={а, б, в, г, д, е}, У={с, е, д}, то ХУ={а, б, в, г, д, е, с},т.е. n(ХУ)=7,несмотря на то, что n(X)=6, а n(У)=3 (из суммы нужно вычесть число элементов пересечения множеств Х и У ).

Правило суммы в общем виде: Для любых двух множеств Х и У справедливо равенство: n(ХУ)=n(Х)+n(У)-n(ХУ),т.е. число элементов объединения двух множеств равно сумме чисел элементов в каждом из них, уменьшенной на число элементов пересечения этих множеств.

Задача. Сколько пар вида (х_k;y_l) можно составить из элементов множеств

Х={х₁; х₂; …,х_m} и У={у₁, у₂,…,у_n}?

Запишем эти пары в виде таблицы:

(х₁;y₁), (х₁;y₂),…,(х₁;y_n)

(х₂;y₁), (х₂;y₂),…,(х₂;y_n)

………………………..

(х_m;y₁), (х_m;y₂),…,(х_m;y_n).

Видно, что она состоит из m строк, в каждой из которых n элементов число пар равноm^.n.

Т.о. число упорядоченных пар, которые можно составить из элементов m-множества Х и n-множества У равно m^.n, т.е. произведению числа элементов множества Х на число элементов множества У. Но множество упорядоченных пар, составленных из элементов множеств Х и У называют декартовым произведением.

Правило произведения: n(Х×У)=n(Х)^.n(У).

Его можно сформулировать и так: если элемент х можно выбрать m способами, а элемент у можно выбрать n способами, то упорядоченную пару (х;у) можно выбрать m^.n способами.

Правило произведения в общем виде:

n(Х₁×Х₂×_…×Х_n)=n(Х₁)^.n(Х₂)^. … ^.n(Х_n).

Пример. Из деревни А в деревню В ведут три дороги, а из В в С ведут две дороги. Сколькими способами можно пройти из деревни А в С через В?

Обозначим дороги из А в В цифрами 1, 2, 3, а из В в С буквамиа, в. Тогда каждый вариант пути из А в С задается парой, состоящей из цифры и буквы. Число таких пар по правилу произведения равно 3^.2=6.

(1;а), (2;а), (3;а), (1;в), (2;в), (3;в).

5. Размещения с повторениями.

Кортеж длины k, составленный из элементов m—множества Х, называют размещением с повторениями из m элементов по k, а число таких кортежей обозначают .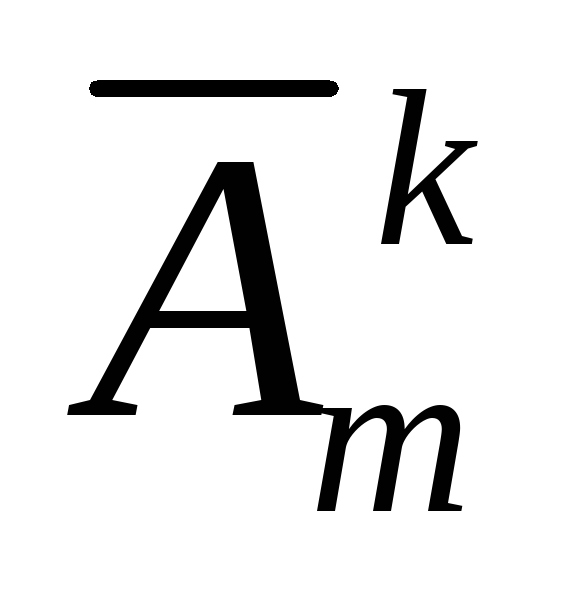

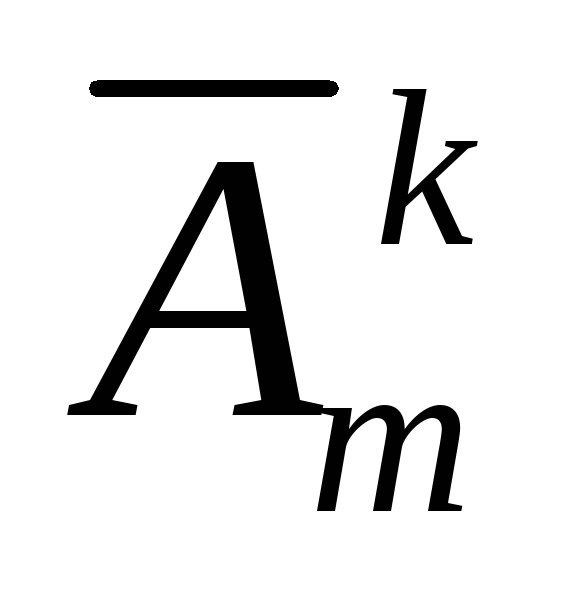=m^k (1)

Например, из 4-множества Х={a, b, c, d} можно составить 16 кортежей длины 2:

(a,a), (a,b), (a,c), (a,d),

(b,a), (b,b), (b,c), (b,d),

(c,a), (c,b), (c,c), (c,d),

(d,a), (d,b), (d,c), (d,d), т.е. 2⁴=16.

Задача. Найти число подмножеств m-множества Х.

Решение. Перенумеруем это множество: Х={х₁; х₂; …,х_m}. Каждое подмножество можно „зашифровать” с помощью кортежа длиныm из нулей и единиц (если элемент с данным номером входит в подмножество, пишем 1, если нет, пишем 0). Например, 5-множество Х={х₁; х₂; х₃, х₄, х₅}. Тогда кортеж (0; 1; 1; 0; 1) шифрует подмножество

{х₂; х₃, х₅}, кортеж (0; 0; 0; 0; 0) шифрует пустое подмножество, (1; 1; 1; 1; 1) – все множество Х. Потому найти число подмножеств m-множества Х – это все равно, что найти число кортежей длины m, составленных из элементов 2-множества {0;1}. По формуле (1) оно равно 2^m.

Число подмножеств m-множества Х равно 2^m.

Например, множество Х={а, в, с} имеет 2³=8 подмножеств: Ø, {а}, {в}, {с}, {а, в}, {а, с}, {в, с}, {а, в, с}.

studfile.net

Элементы комбинаторики

Комбинаторика с (лат. соединение, сочетание) — раздел математики изучающий приёмы вычислений числа различных комбинаций.

Какие задачи называют комбинаторными? Те, где спрашивается каким числом можно осуществить требуемое.

1. Принципы в подсчёте числа комбинации или правила суммы и произведения.

Большинство задач решается с помощью этих двух принципов.

Принцип суммы. «Если некоторый объект А можно выбрать т способами, а другой объект В можно выбрать n способами, то выбор «либо А, либо В» можно осуществить (т +n) способами».

Применяется в том случае, когда изучаемые комбинации удаётся разбить на несколько классов, причём каждая комбинация входит в один, и только в один класс.

Пример 1……

Принцип произведения. «Если объект А можно выбрать т способами, и если после каждого такого выбора объект В можно выбрать n способами, то выбор пары «А и В» в указанном порядке можно осуществить (т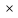n) способами».

Пример 2……

2. Комбинации по типу перестановок, размещений и сочетаний. Такие комбинации встречаются чаще обычного. Рассмотрим их.

2.1. Перестановки. Пусть имеется множество из n элементов. Установленный в некотором множестве порядок называют перестановкой его элементов.

Примеры перестановок: распределение n различных должностей среди n человек или расположение n различных предметов в одном ряду.

Зададимся вопросом: «Сколько различных перестановок можно образовать в множестве из n элементов!» Число перестановок обозначается Р_n (читается «Р из n«).

Чтобы вывести формулу числа перестановок, представим себе n ячеек, пронумерованных числами 1,2,…,n. Все перестановки будем образовывать, располагая элементы множества в этих ячейках. В первую ячейку можно занести любой из n элементов (иначе: первую ячейку можно заполнить n различными способами). Заполнив первую ячейку, можно найти (n-1) вариантов заполнения второй ячейки. Таким образом, существует n(n-1) вариантов заполнения двух первых ячеек. При заполнении первых двух ячеек можно найти (n-2) варианта заполнения третьей ячейки, откуда получается, что три ячейки можно заполнить n(n-1)(n-2) способами. Продолжая этот процесс, получим, что число способов заполнения n ячеек равно n(n—1)(n-2)·…· 3·2 ·1. Отсюда

Р_n = n(n—1)(n-2)·…· 3·2 ·1.

Число n (n-2)·…· 3·2 ·1, то есть произведение всех натуральных чисел от 1 до n, называется «n—факториал» и обозначается n! Отсюда P_n=n!

По определению считается: 1!=1. Но чему равен 0!=?. Для любого n>1 справедливо n!=n(n-1)! Положим n=1, тогда 1!=1·0!, следовательно, 0!=1.

Пример 3. Сколько существует вариантов замещения пяти различных вакантных должностей между пятью кандидатами?

N=5!=5·4·3·2·1=120.

2.2. Размещения. Размещениями из n элементов по т элементов будем называть упорядоченные подмножества, состоящие из т элементов множества, состоящего из n элементов. Число размещений из n элементов по т элементов обозначается 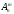(читается «А из n по т «).

Зададимся вопросом: «Сколько упорядоченных подмножеств по т элементов в каждом можно получить из заданного множества в n элементов?»

Одно размещение из n элементов по т элементов может отличаться от другого как набором элементов, так и порядком их расположения.

Примеры задач, приводящих к необходимости подсчета числа размещений. Сколькими способами можно выбрать из пятнадцати человек пять кандидатов и назначить их на пять различных должностей? Сколькими способами можно из двадцати книг отобрать двенадцать и расставить их в ряд на полке?

В задачах о размещениях полагается т < п. В случае если т=n, то легко получить 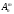= Р_n =n!

Для вычисления используем тот же метод, что использовался для подсчетаР_n только здесь выберем лишь т ячеек. Первую ячейку можно заполнить n способами, вторую, при заполненной первой, можно заполнить (n-1) способами. Таким образом, существует n(n— 1) вариантов заполнения первых двух ячеек. Можно продолжать этот процесс до заполнения последней т -й ячейки. Эту ячейку при заполненных первых (m – 1) ячейках можно заполнить n – (m – 1) = n – m +1 способами. Таким образом, все т ячеек заполняются числом способов, равным

n(n – 1)(n – 2)… (n – m + 2)(n – m + 1) =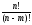

Отсюда получаем:

Пример 4. Сколько существует различных вариантов выбора четырёх кандидатур из девяти специалистов для поездки в четыре страны?

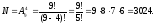
2.3. Сочетания. Сочетаниями из n элементов по т элементов называются подмножества, состоящие из т элементов множества, состоящего из n элементов.

Одно сочетание от другого отличается только составом выбранных элементов, но не порядком их расположения, как у размещений.

Число сочетаний из n элементов по т элементов обозначается (читается «С из n по т «).

Примеры задач, приводящих к подсчету числа сочетаний. Сколько существует вариантов выбора шести человек из пятнадцати кандидатов для назначения на работу в одинаковых должностях? Сколькими способами можно из двадцати книг отобрать двенадцать книг?

Выведем формулу для подсчета числа сочетаний. Пусть имеется множество из n элементов. Образуем подмножество, содержащее т элементов, т.е. сочетание. Известно число упорядоченных подмножеств из т элементов всего множества из n элементов, т.е. размещений из n по т : 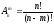. Количество неупорядоченных подмножеств будет вm! раз меньше. Т.е. во столько раз сколькими способами можно установить порядок во множестве из т элементов. Следовательно, .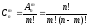

Пример 5. Шесть человек из пятнадцати можно выбрать числом способов, равным

Несложно понять, что осуществить выбор подмножества из т элементов множества, насчитывающего n элементов, можно, выбрав (n — т) элементов, которые не войдут в интересующее нас подмножество. Отсюда следует свойство числа сочетаний

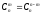
Эту формулу можно легко доказать, используя формулу для числа сочетаний.

studfile.net