4. Представление смешанного числа в виде неправильной дроби и наоборот
\(4\) детей
\(5\) апельсинов
Разделить поровну \(5\) одинаковых апельсинов между четырьмя детьми можно двумя способами.
Первый способ. Разделить между детьми поровну каждый апельсин.
Тогда каждый ребёнок получит по \(5\) частей, и каждая из этих частей равна 14 целого апельсина.
Следовательно, каждый ребёнок получит 54 апельсина.
Второй способ. Сначала дать каждому из детей по целому апельсину, а оставшийся апельсин разделить между ними поровну.
Тогда каждый из детей получит 1+14=114 апельсина.
Получили два равных числа: 54=114.
Чтобы перейти от записи 54 к записи 114, надо разделить \(5\) на \(4\).
Получим неполное частное и остаток. Неполное частное даёт целую часть, а остаток — числитель дробной части.
Чтобы из неправильной дроби выделить целую часть или представить в виде смешанного числа, надо:
1) разделить с остатком числитель на знаменатель;
2) неполное частное будет целой частью;
3) остаток даёт числитель, а делитель — знаменатель дробной части.
Пример:
выделим целую часть из неправильной дроби 197.
Делим \(19\) на \(7\). Неполное частное равно \(2\), а остаток — \(5\).
Значит, 197=257.
1) умножить его целую часть на знаменатель дробной части;
2) к полученному произведению прибавить числитель дробной части;
Пример:
представим в виде неправильной дроби число 1023.
Умножим его целую часть на знаменатель дробной части \(10·3=30\).
К полученному произведению прибавим числитель дробной части \(30+2=32\).
Запишем полученную сумму \(32\) числителем дроби, а знаменатель дробной
части оставим без изменения, т. е. \(3\):
1023=10⋅3+23=323.
www.yaklass.ru
5.4.3. Смешанное число математика-повторение
- Число, состоящее из целой части и дробной части, называется смешанным числом.
- Чтобы неправильную дробь представить в виде смешанного числа, надо разделить числитель дроби на знаменатель, тогда неполное частное будет целой частью смешанного числа, остаток – числителем дробной части, а знаменатель останется тот же.
- Чтобы представить смешанное число в виде неправильной дроби, нужно умножить целую часть смешанного числа на знаменатель, к полученному результату прибавить числитель дробной части и записать в числителе неправильной дроби, а знаменатель оставить тот же.
Примеры.
Представить неправильную дробь в виде смешанного числа:
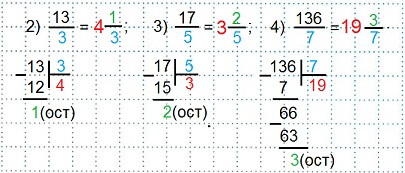Дробная часть означает знак деления. В столбик разделим числитель 9 на знаменатель 2. Частное 4 будет целой частью смешанного числа, остаток 1 станет числителем дробной части, а знаменатель 2 останется тот же.
Еще такие примеры.
Записать смешанное число в виде неправильной дроби:
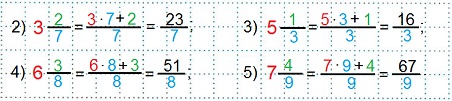
Еще такие примеры.
Запись имеет метки: обыкновенные дроби
www.mathematics-repetition.com
§29. Смешанные числа — Ответы (ГДЗ) рабочая тетрадь (Мерзляк Полонский Якир) 5 класс часть 2
365. Заполните пропуски.
1) Число 3 4/9 называют смешанным числом, в этом числе число 3 называют целой частью смешанного числа, а дробь 4/9 его дробной частью.
2) Дробная часть смешанного числа – это правильная дробь.
3) Любую неправильную дробь, у которой числитель нацело не делится на знаменатель, можно представить в виде смешанного числа.
4) Чтобы неправильную дробь, числитель которого нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток как числитель его дробной части.
5) Чтобы смешанное число преобразовать в неправильную дробь, надо целую часть умножить на знаменатель дробной части и к улучшенному произведению прибавить числитель; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
6) Чтобы сложить два смешанных числа, надо отдельно сложить их целые и дробные части.
7)Чтобы найти разность двух смешанных чисел, надо из целой и дробной частей уменьшаемого вычесть соответственно целую и дробную часть вычитаемого.
366. Заполните таблицу.
367. Проверьте, верно ли выделены целая и дробная части числа. Если задание выполнено неверно, приведите справа верное решение.
1) 9/5=1 4/5
2) 17/4= 3 ¼
3) 31/7=3 4/7
4) 42/10=3 12/10
5) 36/9=3 9/9
6) 69/24 = 2 21/24
368. Запишите число в виде неправильной дроби.
369. Выполните действия.
370. Заполните пропуска.
1) 3/7+4/7 = 1
2) 16/39 + 23/39 = 1
3) 19/9 – 10/9 = 1
4) 17/3 – 14/3 = 1
371. Представьте натуральное число в виде дробного числа по образцу:
372. Представьте смешанное число по образцу :
373. Расшифруйте название геометрической фигуры.
374. Заполните цепочку вычислений.
375. Решите уравнение.
376. Какое наибольшее натуральное значение m удовлетворяет неравенству m<74/9?
377. Какое наименьшее натуральное значение m удовлетворяет неравенству m>58/11?
378. Найдите все натуральные значения х, при которых верно двойное неравенство.
379. Решите уравнение.
380. Четверо друзей собрались есть торт. Один хотел взять 6/25 торта, второй – 7/25, третий – 8/25. а четвертый – 9/25. Могли ли они так поделить торт?
381. Найдите все натуральные значения а , при которых верно неравенство.
382. Впишите в квадратики цифры так, чтобы получились верные неравенства.
matem-gdz.ru