Тригонометричні рівняння | Математика, логіка, інтелект

Рівняння називається тригонометричним, якщо невідома величина знаходиться під знаком тригонометричних функцій.

Найпростіші тригонометричні рівняння

Найпростішими тригонометричними рівняннями називаються рівняння \(\sin x = a\), \(\cos x = a\), \(\operatorname{tg} x = a\), \(\operatorname{ctg} x = a\).

Розв’язати найпростіше тригонометричне рівняння — означає знайти множину всіх кутів, що мають дане значення тригонометричної функції. Якщо тригонометричне рівняння не є найпростішим, то за допомогою тотожних перетворень його треба звести до одного або кількох найпростіших, розв’язання яких визначається стандартними формулами.

1. Розв’язання рівняння \(\sin x = a\)

Всі розв’язки рівняння

\[\sin x = a, |a| \leq 1\]

записуються у вигляді

\[x = {(-1)}^{k} \arcsin a + \pi k, k \in Z.\]

Окремі випадки:

\[\sin x = 0 \Rightarrow x = \pi k, ~k \in Z.\]

\[\sin x = \pm 1 \Rightarrow x = \pm \frac{\pi}{2} + 2\pi k, ~k \in Z.\]

2. Розв’язання рівняння \(\cos x = a\)

Всі розв’язки рівняння

\[\cos x = a, |a| \leq 1\]

записуються у вигляді

\[x = \pm \arccos a + 2 \pi k, ~k \in Z.\]

Окремі випадки:

\[\cos x = 0 \Rightarrow x = \frac{\pi}{2} + \pi k, ~k \in Z.\]

\[\cos x = 1 \Rightarrow x = 2 \pi k, ~k \in Z.\]

\[\cos x = — 1 \Rightarrow x = \pi + 2 \pi k, ~k \in Z.\]

3. Розв’язання рівняння \(\operatorname{tg} x = a\)

Всі розв’язки рівняння

\[\operatorname{tg} x = a\]

записуються у вигляді

\[x = \operatorname{arctg} a + \pi k, ~k \in Z.\]

Окремий випадок:

\[\operatorname{tg} x = 0 \Rightarrow x = \pi k, ~k \in Z.\]

4. Розв’язання рівняння \(\operatorname{ctg} x = a\)

Всі розв’язки рівняння

\[\operatorname{ctg} x = a\]

записуються у вигляді

\[x = \operatorname{arcctg} a + \pi k, ~k \in Z.\]

Окремий випадок:

\[\operatorname{ctg} x = 0 \Rightarrow x = \frac{\pi}{2} + \pi k, ~k \in Z.\]

Розв’язування найпростіших тригонометричних рівнянь

Тригонометричні рівняння | Тригонометрія

Багато тригонометричних рівнянь, права частина яких дорівнює 0, розв’язуються розкладанням їхньої лівої частини на множники.

Приклад 1. Розв’яжіть рівняння 1 + cos x — 2 cos  = 0.

Врахувавши, що 1 + cos х = 2 cos , матимемо:

2cos²

– 2cos= 0,   2cos= 0.

 

Добуток дорівнює нулю, якщо хоча б один із множників до­рівнює нулю. Тому:

1) cos  = 0;  = +πn, n

Z; х = π + 2πп, п Z;

2) cos  = 1;  = 2πn, п Z; х = 4πn, п  Z.

 

Відповідь: π + 2πп, 4πn, п

 Z.

 

Приклад 2. Розв’яжіть рівняння sin 2х — sin х = 0.

Розв’язання

sin 2х — sin х = 0;   2 sin cos = 0;   2 sincos = 0.

1) sin  = 0; 

 = πn, х = 2πn, п Z.  

2) cos = 0, = +πn, х = +, п 

 Z.

      Відповідь: 2πп і +, п  Z.

Методи розв»язування тригонометричних рівнянь рівнянь

Методи розв’язування тригонометричних рівнянь

Відео https://www.youtube.com/watch?v=rZWAGF4MZhs

Відео https://www.youtube.com/watch?v=bCkpX0ceO7s

1.Зведення тригонометричних рівнянь до алгебраїчних

Деякі тригонометричні рівняння можна привести шляхом тотожних перетворень до рівнянь з однією тригонометричною функцією, потім зробити заміну і привести рівняння до алгебрагічного.

 Приклад 1. Розв’яжіть рівняння .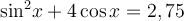

Розв’язування

Замінивши  на 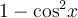, маємо:

,

;

.

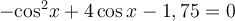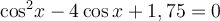     Нехай cos x=t, тоді .

Звідси .

     Оскільки 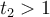, то 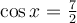 — розв’язків немає.

     Оскільки 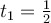, то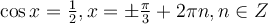 

.

     Відповідь: .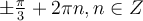

     Приклад 2. Розв’яжіть рівняння tg x+3ctg x=4.

Розв’язання

.

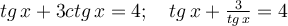Нехай tg x=t, тоді .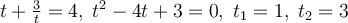

     Маємо:

1) ;

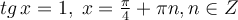2)  .

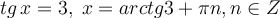 Відповідь: .

2.Зведення тригонометричних рівнянь до рівнянь виду f(x)g(x)=0

Багато тригонометричних рівнянь, права частина яких дорівнює 0, розв’язуються розкладанням їхньої лівої частини на множники.

     Розглянемо приклади.

 Приклад 3. Розв’яжіть рівняння 

.

Розв’язання

 Урахувавши, що 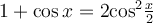, маємо

.

Добуток дорівнює нулю, якщо хоча б один з множників дорівнює нулю. Тому:

1) ;

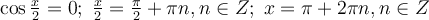2).

     Відповідь: .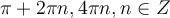

Приклад 4. Розв’яжіть рівняння sin 2x-sin x=0.

Розв’язання

.

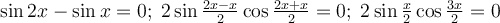1);

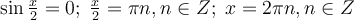2).

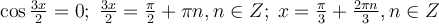     Відповідь:  і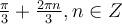 

 .

3. Однорідні тригонометричні рівняння

 Розглянемо рівняння виду asin x+bcos x=0 (однорідне рівняння 1-го степеня), де а і b не дорівнюють нулю.

Значення х  при cos x дорівнює нулю, не задовольняє даному рівнянню, бо тоді й sin x теж дорівнював би нулю, а cos x і sin x не можуть одночасно дорівнювати нулю. Тому можна розділити обидві частини рівняння почленно на cos x.

     Маємо:

.

 Рівняння виду 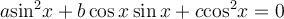 називається однорідним рівнянням 2-го степеня.

 Якщо числа а, b, с не дорівнюють нулю, то розділимо дане рівняння на  (або на 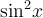). (У даному рівнянні , бо у протилежному випадку 

 теж дорівнював би нулю, а cos x і sin x не можуть одночасно дорівнювати нулю.) Тоді

.

     Розв’язавши отримане рівняння, одержимо корені даного рівняння.

     Рівняння виду

  

називається однорідним рівнянням n-го степеня відносно синуса і косинуса.

     Якщо жоден із коефіцієнтів 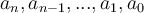 не дорівнює нулю, то розділивши обидві частини рівняння почленно на , одержимо рівняння n-го степеня  відносно tg x.

     Якщо хоча б один із коефіцієнтів  дорівнює нулю, то перш ніж виконувати ділення на , слід довести, що , тобто .

     Приклад 5. Розв’яжіть рівняння .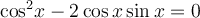

Розв’язання

     Ділити обидві частини на 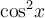 не можна, бо  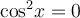є розв’язком даного рівняння. Це рівняння можна розв’язати у такі способи.

     І спосіб (винесення множника)

.

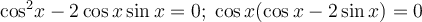     Звідси cos x=0 або cos x-2sin x=0

1) ;

2) ,

.

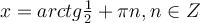     Відповідь: .

     ІІ спосіб. Розділимо обидві частини на 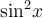, оскільки  у даному рівнянні, бо у протилежному випадку , що неможливо.

.

     Звідси ctg x=0 або ctg x-2=0.

1) ;

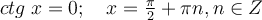2) .

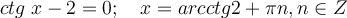     Відповідь: .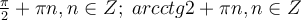

4 Розв’язування найпростіших тригонометричних нерівностей

Відео https://www.youtube.com/watch?v=b3uj-Sq0BCI —7 способів розв’язування тригонометричних рівнянь

Корисні посилання:

sinX = t — http://youtu.be/OJnwFywGsSc

cosX = t — http://youtu.be/X5B5R_ApnA4

tgX = t — http://youtu.be/yem9jzaQxaE

Корисні формули і властивості — http://youtu.be/yVAgerp8OcQ

Детально про тригонометричні функції — http://youtu.be/uRY813gg8XM

Відео «Тригонометричні рівняння. Практичне заняття» https://www.youtube.com/watch?v=-zlov3VuhRw

Складні тригонометричні рівняння

Переходимо до пояснення розв’язків складних тригонометричних рівнянь. Тут маємо приклади де аргумент в тригонометричній функції знаходиться під коренем або в квадраті, також рівняння де аргумент або сама функція містяться під модулем. Кожен з прикладів вимагає іншого підходу при зведенні рівнянь до найпростішого типу. Водночас на подібних прикладах Ви швидко навчитеся розписувати складні завдання та знатимете яку зі схем застосовувати.
При підготовці до зовнішнього незалежного оцінювання наведені далі приклади часто мало кому вдалося вирішити правильно, тож для абітурієнтів наведені відповіді також стануть в нагоді при вступі до ВУЗ-ів.
Для перевірки правильності обчислень можете скористатися графічним методом та програмами, описаними на попередніх уроках.

Приклад 18.13 Розв’язати рівняння cos²(x)+5cos(x)-6=0.

Розв’язання: З вигляду тригонометричного рівняння робимо висновок, що через заміну змінних його слід звести до квадратного рівняння.
Зробимо заміну cos(x)=t, причому змінна має відповідати області визначення косинуса -1≤t≤1.
В такий спосіб прийдемо до квадратного рівняння t²+5t-6=0.
За теоремою Вієта знаходимо: t1=1 і t2=-6<-1 (не задовольняє умові).
Отже, отримали cos(x)=1, звідси корінь рівний

Відповідь: Д.

 

Приклад 18.14 Розв’язати рівняння sin(x)+cos(x)=-√2.

Розв’язання: Подамо вираз sin(x)+cos(x) у вигляді добутку:

Отже, отримали рівняння

звідси
Але якщо , то отримаємо
(Оскільки ).
Відповідь: В.

 

Приклад 18.15 Розв’язати рівняння sin(x²)=0.

Розв’язання: Аргумент під синусом міститься в другому степені, тому з правої частини потрібно буде знаходити корінь квадратний.
Запишемо розв’язок рівняння

звідси , а також 0, оскільки раніше номер пробігав множину цілих чисел (тепер натуральних).
Остаточно отримаємо множину коренів

Відповідь: Д.

 

Приклад 18.16 Розв’язати рівняння tg(√x)=-1.

Розв’язання: Тангенс розкриваємо за допомогою оберненої тригонометричної функції – арктангенса

Тут навмисне відкинули від’ємні номери серед цілих, оскільки корінь від’ємним бути не може.
Далі переходимо до кутів

та підносимо до квадрата обидві частини

Відповідь: В.

 

Приклад 18.17 У якому вигляді можна подати розв’язок рівняння cos(Pi•x)=x2-4x+5?

Розв’язання: Почнемо з аналізу ОДЗ:

Тригонометричні рівняння з параметром

Тригонометричні рівняння з параметром одні з важчих в курсі тригонометрії. При розкритті таких рівнянь потрібно враховувати область допустимих значень тригонометричних функцій, а також застосовувати весь багаж формул, щоб перетворити рівняння до простого типу.
Прикладі, що далі наведені входять в збірники з підготовки до зовнішнього незалежного оцінювання.

Приклад 18.21 За якого найменшого значення параметра a рівняння 2cos(4x)=a-5 має корені?

Розв’язання: Рівняння з параметрами одні з найважчих, і це стосується не тільки курсу тригонометрії.
Тому їх слід розписувати уважно та враховувати всі можливі обмеження.
Запишемо р-ня 2cos(4x)=a-5 у вигляді cos(4x)=(a-5)/2.
Згідно з обмеженнями на область допустимих значень функції косинус, задане тригонометричне рівняння матиме корені, якщо параметр лежатиме в інтервалі

Розв’яжемо отриману систему нерівностей:

Отже, при a[min]=3 рівняння 2cos(4x)=a-5 має корені.
Відповідь: В.

 

Приклад 18.22 Знайти всі значення параметра a, за яких рівняння (a+2)sin(x)=a^2-4 має корені.

Розв’язання: Розпишемо праву частину рівняння з параметром за формулою різниці квадратів

Очевидно, що при a=-2 рівняння матиме безліч коренів, оскільки маємо тотожність 0=0.
Розглянемо випадок:
sin(x)=a-2.
З обмежень на область допустимих значень функції синус виписуємо умову, що параметр повинен знаходитися в межах -1≤a-2≤1.
Спрощуємо систему нерівностей:

Отримали, що при тригонометричне рівняння (a+2)sin(x)=a^2-4 має корені.
Відповідь: Г.

 

Приклад 18.48 За яких значень параметра a рівняння sin⁴x+cos⁴x=a має розв’язки?
У відповідь записати суму найбільшого та найменшого значень a.
Розв’язання: Маємо тригонометричне рівняння четвертого порядку з параметром.
Щоб понизити степінь в кожному з доданків квадрат синуса та косинуса замінимо, використавши основну тригонометричну тотожність.
Далі ще кілька спрощень і прийдемо до синуса подвійного кута в лівій частині від знаку рівності та кореня квадратного від параметричної функції в пр

ЗНО математика. Тригонометричні рівняння

Шановні школярі, випускники, абітурієнти, цей розділ допоможе підготуватися до зовнішнього оцінювання 2017 року. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень, систематизувати та підвищити накопичений рівень знань з математики.

Розділ II. Рівняння і нерівності

Завдання 2.16 Розв’яжіть тригонометричне рівняння

Розв’язання: Маємо тригонометричне рівняння. Перетворимо праву сторону, врахувавши, що тангенс 45 градусів рівний одиниці.


Розв’язком такого рівняння є значення Pi/2, і не забуваємо про період косинуса.

Відповіддю до тестів буде варіант В.
Відповідь: В.

 

Завдання 2.17 (Т-07, 36) Розв’яжіть рівняння

Розв’язання: Оскільки тангенс це відношення синуса до косинуса, то тригонометричне рівняння можна записати у вигляді двох.

причому синус і косинус повинні одночасно приймати або додатні значення, або від’ємні. Це означає, що розв’язок на одиничному колі лежить симетрично відносно початку координат. А це твердження відповідає за період Pi розв’язку рівняння.

Враховуючи, що ми під тангенсом маємо половину змінної, то знайдене значення множимо на 2, періоду це також стосується.

Звідси варіант Г є правильною відповіддю.
Відповідь: Г.

 

Завдання 2.18 Розв’яжіть рівняння

Розв’язання: Все що потрібно знати при розв’язуванні подібних прикладів на тангенс це те, що в нього як і в котангенса період рівний 180 градусів. Корінь знаходимо застосуванням оберненої функції (арктангенса) до обидвох сторін рівняння

Розв’язок прикладу відповідає варіанту Б тестів.
Відповідь: Б.

Завдання 2.19 Розв’яжіть тригонометричне рівняння

Розв’язання: За означенням права сторона тригонометричного рівняння відповідає косинусу подвійного кута

косинус має період 360 градусів, а змінна рівна половині коли кут рівний 60, -60 градусів. Розв’язок можна записати наступним рядком

В тестах до ЗНО відповіді досить подібні, але тільки варіант В є правильним.
Відповідь: В.

Залишайтеся з нами і підготовка до ЗНО 2015 з математики залишиться для Вас приємним спогадом та зекономить багато часу та грошей на репетиторів.

Відповіді до ЗНО тестів

Тригонометричні нерівності | Тригонометрія

1. Розв’яжіть нерівність sint.

Будуємо одиничне коло (рис. 126)та пряму         у =, яка перетинає одиничне коло в точках А і В. Знаходимона одиничному колі точки, значенняординат яких не менші .

Цими точками є то

чки дуги АСВ, де А = , В = . Отже, розв’язком нерівності будуть усі значення t із проміжку . Враховуючи, що період функції sin tдорівнює 2π, маємо розв’язок даної нерівності

.

Відповідь: 

  

 2. Розв’язати нерівність sin t  – .

Детальніше… Додати коментар Категорія: Тригонометричні нерівності Перегляди: 1506