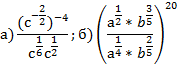правила вычисления степеней с разными основаниями или натуральными показателями по математике и порядок этого

Одной из главных характеристик в алгебре, да и во всей математике является степень. Конечно, в 21 веке все расчеты можно проводить на онлайн-калькуляторе, но лучше для развития мозгов научиться делать это самому.

В данной статье рассмотрим самые важные вопросы, касающиеся этого определения. А именно, поймем что это вообще такое и каковы основные его функции, какие имеются свойства в математике.

Степень, свойства и действия со степенями, сложение, умножение, деление отрицательных степеней, степень с натуральным показателем, правила и формулы

Рассмотрим на примерах то, как выглядит расчет, каковы основные формулы. Разберем основные виды величины и то, чем они отличаются от других функций.

Поймем, как решать с помощью этой величины различные задачи. Покажем на примерах, как возводить в нулевую степень, иррациональную, отрицательную и др.

Что такое степень числа

Что же подразумевают под выражением «возвести число в степень»?

Степенью n числа а является произведение множителей величиной а n-раз подряд.

Математически это выглядит следующим образом: an = a * a * a * …an.

Причем, левая часть уравнения будет читаться, как a в степ. n.

Например:

• 23 = 2 в третьей степ. = 2 * 2 * 2 = 8,
• 42 = 4 в степ. два = 4 * 4 = 16,
• 54 = 5 в степ. четыре = 5 * 5 * 5 * 5 = 625,
• 105 = 10 в 5 степ. = 10 * 10 * 10 * 10 * 10 = 100000,
• 104 = 10 в 4 степ. = 10 * 10 * 10 * 10 = 10000.

Ниже будет представлена таблица квадратов и кубов от 1 до 10.

Таблица степеней от 1 до 10

Ниже будут приведены результаты возведения натуральных чисел в положительные степени – «от 1 до 100».

Ч-ло	2-ая ст-нь	3-я ст-нь
1	1	1
2	4	8
3	9	27
4	16	64
5	25	125
6	36	216
7	49	343
8	64	512
9	81	279
10	100	1000

Свойства степеней

Что же характерно для такой математической функции? Рассмотрим базовые свойства.

Учеными установлено следующие признаки, характерные для всех степеней:

• an * am = (a)(n+m),
• an : am = (a)(n-m),
• (ab ) m=(a)(b*m).

Проверим на примерах:

• 23 * 22 = 8 * 4 = 32. С другой стороны 25 = 2 * 2 * 2 * 2 * 2 =32.

Аналогично:

• 23 : 22 = 8 / 4 =2. Иначе 23-2 = 21 =2.
• (23)2 = 82 = 64. А если по-другому? 26 = 2 * 2 * 2 * 2 * 2 * 2 = 32 * 2 = 64.

Как видим, правила работают.

А как же быть со сложением и вычитанием? Всё просто. Выполняется сначала возведение в степень, а уж потом сложение и вычитание.

Посмотрим на примерах:

• 33 + 24 = 27 + 16 = 43,
• 52 – 32 = 25 – 9 = 16. Обратите внимание: правило не будет выполняться, если сначала произвести вычитание: (5 3)2 = 22 = 4.
• А вот в этом случае надо вычислять сначала сложение, поскольку присутствуют действия в скобках: (5 + 3)3 = 83 = 512.

Как производить вычисления в более сложных случаях? Порядок тот же:

• при наличии скобок – начинать нужно с них,
• затем возведение в степень,
• потом выполнять действия умножения, деления,
• после сложение, вычитание.

Есть специфические свойства, характерные не для всех степеней:

1. Корень n-ой степени из числа a в степени m запишется в виде: am/n.
2. При возведении дроби в степень: этой процедуре подвержены как числитель, так и ее знаменатель.
3. При возведении произведения разных чисел в степень, выражение будет соответствовать произведению этих чисел в заданной степени. То есть: (a * b)n = an * bn.
4. При возведении числа в отрицательную степ., нужно разделить 1 на число в той же ст-ни, но со знаком «+».
5. Если знаменатель дроби находится в отрицательной степени, то это выражение будет равно произведению числителя на знаменатель в положительной степени.
6. Любое число в степени 0 = 1, а в степ. 1 = самому себе.

Степень с отрицательным показателем

Что делать при минусовой степени, т. е. когда показатель отрицательный?

Исходя из свойств 4 и 5

(смотри пункт выше), получается:

• A(-n) = 1 / An, 5(-2) = 1 / 52 = 1 / 25.

И наоборот:

• 1 / A(-n) = An, 1 / 2(-3) = 23 = 8.

А если дробь?

• (A / B)(-n) = (B / A)n, (3 / 5)(-2) = (5 / 3)2 = 25 / 9.

Степень с натуральным показателем

Под ней понимают степень с показателями, равными целым числам.

Что нужно запомнить:

• A0 = 1, 10 = 1, 20 = 1, 3.150 = 1, (-4)0 = 1… и т. д.
• A1 = A, 11 = 1, 21 = 2, 31 = 3 … и т. д.

Кроме того, если (-a)2n+2, n=0, 1, 2…то результат будет со знаком «+». Если отрицательное число возводится в нечетную степень, то наоборот. Общие свойства, да и все специфические признаки, описанные выше, также характерны для них.

Дробная степень

Этот вид можно записать схемой: Am/n. Читается как: корень n-ой степени из числа A в степени m.

С дробным показателем можно делать, что угодно: сокращать, раскладывать на части, возводить в другую степень и т. д.

Степень с иррациональным показателем

Пусть α – иррациональное число, а А ˃ 0.

Чтобы понять суть степени с таким показателем, рассмотрим разные возможные случаи:

• А = 1. Результат будет равен 1. Поскольку существует аксиома – 1 во всех степенях равна единице,
• А˃1.
• Аr1 ˂ Аα ˂ Аr2, r1 ˂ r2 – рациональные числа.

В этом случае наоборот: Аr2 ˂ Аα ˂ Аr1 при тех же условиях, что и во втором пункте.

Например, показатель степени число π. Оно рациональное.

1. r1 – в этом случае равно 3,
2. r2 – будет равно 4.
3. Тогда, при А = 1, 1π = 1.
4. А = 2, то 23 ˂ 2π ˂ 24, 8 ˂ 2π ˂ 16.
5. А = 1/2, то (½)4 ˂ (½)π ˂ (½)3, 1/16 ˂ (½)π ˂ 1/8.

Для таких степеней характерны все математические операции и специфические свойства, описанные выше.

Заключение

Подведём итоги для чего же нужны эти величины, в чем преимущество таких функций? Конечно, в первую очередь они упрощают жизнь математиков и программистов при решении примеров, поскольку позволяют минимизировать расчеты, сократить алгоритмы, систематизировать данные и многое другое.

Где еще могут пригодиться эти знания? В любой рабочей специальности: медицине, фармакологии, стоматологии, строительстве, технике, инженерии, конструировании и т. д.

Источник: https://tvercult.ru/nauka/stepen-svoystva-pravila-deystviya-i-formulyi

Степенные выражения (выражения со степенями) и их преобразование

Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.

Что представляют собой степенные выражения?

В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.

Степенное выражение – это выражение, которое содержит степени.

Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.

• Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 32, 75+1, (2+1)5, (−0,1)4, 2233, 3·a2−a+a2, x3−1, (a2)3.
• А также степени с нулевым показателем: 50, (a+1)0, 3+52−3,20. И степени с целыми отрицательными степенями: (0,5)2+(0,5)-22.
• Чуть сложнее работать со степенью, имеющей рациональный  и иррациональный показатели: 26414-3·3·312, 23,5·2-22-1,5, 1a14·a12-2·a-16·b12, xπ·x1-π, 233+5.
• В качестве показателя может выступать переменная 3x-54-7·3x-58 или логарифм x2·lgx−5·xlgx.

С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.

Основные виды преобразований степенных выражений

В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.

Вычислите значение степенного выражения 23·(42−12).

Решение

Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 23·(42−12)=23·(16−12)=23·4.

Нам остается заменить степень 23 ее значением 8 и вычислить произведение 8·4=32. Вот наш ответ.

Ответ: 23·(42−12)=32.

Упростите выражение со степенями 3·a4·b−7−1+2·a4·b−7.

Решение

Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.

Ответ:

3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.

Источник: https://Zaochnik.com/spravochnik/matematika/vyrazhenija/stepennye-vyrazhenija/

Возведение в степень

Возведение в степень — это арифметическая операция повторяющегося умножения. Если требуется перемножить число n-ное количество раз, то достаточно возвести его в n-ную степень.

Основные действия со степенями

В первую очередь степень — это повторяющееся умножение. Число 134 — это 13 × 13 × 13 × 13, где перемножаются четыре одинаковых сомножителя. Если умножить 134 на 132, то мы получим (13 × 13 × 13 × 13) × (13 × 13), что логично превращается в 136.

Это и есть первое правило возведения в степень, которое гласит: при умножении чисел, возведенных в степень, их показатели суммируются. Математически это записывается как:

Если разделить 134 на 132, то нам потребуется вычислить дробь вида:

• (13 × 13 × 13 × 13) / (13 × 13).

Мы можем просто сократить числа в числителе и знаменателе, и в результате останется 13 × 13 = 132. Очевидно, деление чисел, возведенных в степень, соответствует вычитанию их показателей. Второе правило действий со степенями математически выглядит так: am / an = a(m – n).

Теперь давайте возведем 114 в куб, то есть в третью степень. Для этого нам потребуется вычислить выражение (11 × 11 × 11 × 11) × (11 × 11 × 11 × 11) × (11 × 11 × 11 × 11). Получилось 12 сомножителей, следовательно, при возведении в n-ную степень числа в степени m, показатели перемножаются. Третье правило записывается так: (am)n = a(m × n).

Это основные правила работы со степенными выражениями. Однако число можно возвести в отрицательную степень, дробную и нулевую. Какой результат даст выражение 150? Давайте воспользуемся вторым правилом действий степенями и попробуем разделить 154 на 154, что запишется как дробь: 154 / 154.

Очевидно, что в числителе и знаменателе стоят одни и те же числа, а когда число делится само на себя, оно превращается в единицу. Но согласно правилу действий со степенными числами это будет эквивалентно 150.

Следовательно: 154 / 154 = 150 = 1.

Таким образом, четвертое правило гласит, что любое положительное число в нулевой степени равняется единице. Выглядит это правило так: a0 = 1.

При помощи второго правила легко объяснить и работу с отрицательными степенями. К примеру, давайте разделим 82 на 84 и запишем выражение в виде дроби.

(8 × 8) / (8 × 8 × 8 × 8).

Мы можем сократить две восьмерки в числителе и знаменателе и преобразовать дробь в 1 / (8 × 8). Но согласно правилу в ответе мы должны получить 8-2. В знаменателе у нас как раз стоит восьмерка в квадрате. Таким образом:

При этом для значения -1 правило трансформируется в элегантную формулу:

И последнее правило, которое пригодится вам при работе со степенными функциями, гласит о дробных степенях. Что мы можем сделать с выражением 7(1/2). Очевидно, что возвести его в квадрат, и тогда по третьему правилу в результате у нас останется только семерка.

Степень 1/2 — это извлечение квадратного корня, так как при возведении его в квадрат мы получаем целое число. Степень 1/3 соответствует извлечению кубического корня, но как быть с показателем 2/3? Логично, что это кубический корень из числа, возведенного в квадрат.

Последнее правило гласит, что знаменатель дробного показателя означает извлечение корня, а числитель — возведение в степень. Математически это выглядит как: a(m/n) есть корень n-ной степени из am. Теперь вы знаете, как проводить любые арифметические операции со степенными выражениями.

Вы можете использовать наш калькулятор для вычисления степенных функций. Программа позволяет определить основание, показатель и результат операции. Кроме того, калькулятор сопровождается иллюстрацией графика функций: параболы, кубической параболы и параболы в n-ной степени. Рассмотрим пару примеров.

Примеры из реальной жизни

Депозит в банке

Если мы положим на банковский депозит $1 000 под годовую ставку в размере 9% годовых, то сколько денег на счету будет через 20 лет? Рост с течением времени рассчитываются по экспоненциальной формуле вида:

Рост = a × e(kt),

• где a – начальное значение,
•  e – константа, равная 2,718;
• k – коэффициент роста;
• t – время.

Для решения банковской задачи нам потребуется возвести 2,718 в степень, равную 20 × 0,09 = 1,8. Воспользуемся нашим калькулятором и введем в ячейку «Число, x =» значение 2,718, а в ячейку «Степень, n =» значение 1,8. Мы получим ответ, равный 6,049. Теперь, для подсчета суммы на банковском счету нам необходимо умножить начальное значение $1 000 на прирост в размере 6,049. В итоге, через 20 лет на депозите будет $6 049.

Школьная задача

Пусть в школьной задаче требуется построить график функции y = x2,5. Это алгебраическая задача, для решения которой требуется задаться тремя значениями «x» и вычислить соответствующие ему значения «y». После чего по найденным точкам построить график функции.

Введите в ячейку «Степень, n =» значение 2,5. После этого последовательно рассчитайте значения «y», вводя в «Число, x =» аргументы 1, 2, 3. Вы получите соответствующие значения функции 1; 5,657; 15,588. Вам останется только нарисовать кривую по найденным точкам.

Источник: https://BBF.ru/calculators/73/

Степень с рациональным показателем. Простейшие задачи. Видеоурок. Алгебра 11 Класс

На данном уроке мы рассмотрим основные свойства степени с рациональным показателем и решим простейшие типовые задачи.

Напомним, что такое множество рациональных чисел.

 – рациональные числа.

Каждая дробь может быть представлена в десятичном виде, например :

 

Итак, рациональное число может быть представлено как бесконечная десятичная дробь с периодом.

Напомним определение: для  выполняется равенство:

Например: ; ;  (нужно перевести бесконечную периодическую дробь в обыкновенную).

Рассмотрим свойства степени с рациональным показателем, они аналогичны свойствам степени с натуральным показателем, здесь s и r – рациональные числа:

1. .

Для того чтобы умножить степени с одинаковым основанием, нужно сложить их показатели, основание оставить без изменений.

2. .

Можно разделить степени с одинаковым основанием, для этого их показатели нужно вычесть, а основание оставить без изменений.

3. .

Для того чтобы степень возвести в степень, нужно перемножить показатели степени, основание оставить без изменений.

4. .

При умножении степеней с одинаковым показателем, нужно перемножить основания и возвести результат в исходную степень.

5. .

Чтобы разделить степени с одинаковыми показателями, нужно разделить основания и возвести результат в исходную степень.

Вышеперечисленные свойства справедливы для любых рациональных показателей. Докажем первое свойство:

Доказательство:

s и r – рациональные числа, , ,  

.

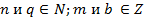
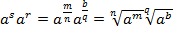Приведем корни к одинаковому показателю:

.

Преобразуем полученное выражение согласно свойствам корня:

.

По определению степени с рациональным показателем:

.

Согласно свойствам степени:

.

Итак, получили:

.

Докажем третье свойство:

Доказательство:

s и r – рациональные числа, , , .

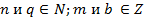Схема доказательства стандартная: от степеней перейти к корням, выполнить преобразования с корнями и вернуться к степеням.

Остальные свойства доказываются аналогично.

Перейдем к решению типовых задач.

Пример 1 – имеет ли смысл выражение:

а)

Ответ: нет.

б)

Ответ: да ().

в)

Ответ: да, т. к. -4 – целое число ().

г)

Ответ: нет.

Пример 2 – вычислить:

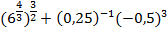
Рассмотрим слагаемые отдельно:

.

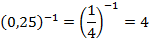
Получаем:

.

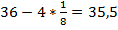Пример 3 – упростить выражение:

Упростим знаменатель:

.

Получаем:

.

Отметим, что обязательно в данном случае .

Пример 4 – упростить выражение:

Возводим в квадрат двучлен:

.

Получили выражение:

.

В данной задаче могут быть поставлены дополнительные вопросы, например, допустимы ли отрицательные значения с. Ответ: нет, т. к. с имеет рациональный показатель степени и по определению является неотрицательным.

Пример 5 – упростить выражение:

Комментарий: ограничение на х наложено в связи с тем, что он имеет отрицательный рациональный показатель степени.

Итак, мы рассмотрели свойства степеней с рациональным показателем. В дальнейшем мы перейдем к решению более сложных задач со степенями и радикалами.

 

Список литературы

1. Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
2. Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа. 
3. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.

 

Домашнее задание

1. Алгебра и начала анализа, 10–11 класс (А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын) 1990, № 432-435.
2. Вычислить:
   
3. Упростить выражение:
   

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал Nado5.ru (Источник).
2. Интернет-портал Terver.ru (Источник).

Материал для подготовки к ЕГЭ (ГИА) по алгебре (10, 11 класс) на тему: действия со степенями 10-11 класс

Действия со степенями

1. Задание 2 № 26738

Найдите значение выражения .

2. Задание 2 № 62113

Найдите значение выражения .

3. Задание 2 № 62429

Найдите значение выражения .

4. Задание 2 № 71883

Найдите значение выражения .

5. Задание 2 № 508383

Найдите значение выражения 

6. Задание 2 № 508403

Найдите значение выражения 

7. Задание 2 № 509209

Найдите значение выражения 

8. Задание 2 № 509587

Найдите значение выражения 

9. Задание 2 № 509607

Найдите значение выражения 

10. Задание 2 № 509627

Найдите значение выражения 

11. Задание 2 № 509647

Найдите значение выражения 4 · 72 + 6 · 72.

12. Задание 2 № 509667

Найдите значение выражения 4 · 10-3 + 8 · 10-2 + 5 · 10-1.

13. Задание 2 № 509687

Найдите значение выражения 7,9 · 10-2 + 4,5 · 10-1.

14. Задание 2 № 509707

Найдите значение выражения (0,01)2 · 105 : 4−2

15. Задание 2 № 509727

Найдите значение выражения 

16. Задание 2 № 509747

Найдите значение выражения 

17. Задание 2 № 509767

Найдите значение выражения 3,4 · 102 + 1,8 · 103.

18. Задание 2 № 509787

Найдите значение выражения: 

 

 

Найдите значение выражения 

19. Задание 2 № 510193

Найдите значение выражения 

20. Задание 2 № 510213

Найдите значение выражения 

21. Задание 2 № 510233

Найдите значение выражения 

22. Задание 2 № 510253

Найдите значение выражения 

23. Задание 2 № 26739

Найдите значение выражения .

24. Задание 2 № 26740

Найдите значение выражения .

25. Задание 2 № 26741

Найдите значение выражения .

26. Задание 2 № 26742

Найдите значение выражения .

27. Задание 2 № 26747

Найдите значение выражения .

28. Задание 2 № 26748

Найдите значение выражения .

29. Задание 2 № 26749

Найдите значение выражения .

30. Задание 2 № 26754

Найдите значение выражения .

31. Задание 2 № 26897

Найдите значение выражения .

32. Задание 2 № 26899

Найдите значение выражения .

33. Задание 2 № 77394

Найдите значение выражения .

34. Задание 2 № 77398

Найдите значение выражения .

35. Задание 2 № 77406

Найдите значение выражения .

36. Задание 2 № 77407

Найдите значение выражения .

37. Задание 2 № 77408

Найдите значение выражения .

38. Задание 2 № 77410

Найдите значение выражения .

39. Задание 2 № 506425

Найдите сумму чисел  и 

40. Задание 2 № 506246

Найдите значение выражения 

41. Задание 2 № 506274

Найдите частное от деления 1,6 · 102 на 4 · 10−2.

42. Задание 2 № 506857

Найдите значение выражения .

43. Задание 2 № 506465

Найдите произведение чисел  и .

44. Задание 2 № 506405

Найдите значение выражения .

45. Задание 2 № 506670

Найдите значение выражения .

46. Задание 2 № 506995

Найдите значение выражения 

47. Задание 2 № 506755

Найдите сумму чисел  и .

48. Задание 2 № 510678

Найдите значение выражения 

49. Задание 2 № 510698

Найдите значение выражения 

50. Задание 2 № 510718

Найдите значение выражения 

51. Задание 2 № 510738

Найдите значение выражения 

52. Задание 2 № 510955

Найдите значение выражения 

53. Задание 2 № 510975

Найдите значение выражения 

54. Задание 2 № 510998

Найдите значение выражения 

55. Задание 2 № 511412

Найдите значение выражения 

Материал по математике на тему «Действия со степенями»

Действия со степенями

1. Най­ди­те зна­че­ние вы­ра­же­ния .

2.

Най­ди­те зна­че­ние вы­ра­же­ния .

3. Най­ди­те зна­че­ние вы­ра­же­ния .

4.

Най­ди­те зна­че­ние вы­ра­же­ния .

5. Най­ди­те зна­че­ние вы­ра­же­ния

6. Най­ди­те зна­че­ние вы­ра­же­ния

7. Най­ди­те зна­че­ние вы­ра­же­ния

8. Най­ди­те зна­че­ние вы­ра­же­ния

9. Най­ди­те зна­че­ние вы­ра­же­ния

10. Най­ди­те зна­че­ние вы­ра­же­ния

11. Най­ди­те зна­че­ние вы­ра­же­ния 4 · 7² + 6 · 7².

12. Най­ди­те зна­че­ние вы­ра­же­ния 4 · 10^-3 + 8 · 10^-2 + 5 · 10^-1.

13. Най­ди­те зна­че­ние вы­ра­же­ния 7,9 · 10^-2 + 4,5 · 10^-1.

14. Най­ди­те зна­че­ние вы­ра­же­ния (0,01)² · 10⁵ : 4⁻²

15. Най­ди­те зна­че­ние вы­ра­же­ния

16. Най­ди­те зна­че­ние вы­ра­же­ния

17. Най­ди­те зна­че­ние вы­ра­же­ния 3,4 · 10² + 1,8 · 10³.

18. Най­ди­те зна­че­ние вы­ра­же­ния .

19. Най­ди­те зна­че­ние вы­ра­же­ния .

20. Най­ди­те зна­че­ние вы­ра­же­ния .

21. Най­ди­те зна­че­ние вы­ра­же­ния .

22. Най­ди­те зна­че­ние вы­ра­же­ния .

23. Най­ди­те зна­че­ние вы­ра­же­ния .

24. Най­ди­те зна­че­ние вы­ра­же­ния .

25. Най­ди­те зна­че­ние вы­ра­же­ния .

26. Най­ди­те зна­че­ние вы­ра­же­ния .

27. Най­ди­те зна­че­ние вы­ра­же­ния .

28. Най­ди­те зна­че­ние вы­ра­же­ния .

29. Най­ди­те зна­че­ние вы­ра­же­ния .

30. Най­ди­те зна­че­ние вы­ра­же­ния .

31. Най­ди­те зна­че­ние вы­ра­же­ния .

32. Най­ди­те зна­че­ние вы­ра­же­ния .

33. Най­ди­те зна­че­ние вы­ра­же­ния .

34. Най­ди­те сумму чисел и

35. Най­ди­те зна­че­ние вы­ра­же­ния

36. Най­ди­те част­ное от де­ле­ния 1,6 · 10² на 4 · 10⁻².

37.Най­ди­те зна­че­ние вы­ра­же­ния .

38. Най­ди­те про­из­ве­де­ние чисел и .

39. Най­ди­те зна­че­ние вы­ра­же­ния .

40. Най­ди­те зна­че­ние вы­ра­же­ния .

41. Най­ди­те зна­че­ние вы­ра­же­ния

42. Най­ди­те сумму чисел и .