Алгебраические выражения ℹ️ определение, виды, формулы, математические действия, смысл значений, примеры преобразований и упрощений
Математические термины
Алгебра — это наука, изучающая действия над числовыми и буквенными величинами. Кроме того, она занимается решениями уравнений и связанными с ними действиями. Под буквенными величинами обычно понимают конкретные или переменные числовые значения. Входящие в состав записи буквы могут иметь различные числовые величины. Например, в формуле S * 4 + 12 символом S может быть заменена известная или неизвестная величина или даже целое выражение.
Математики под алгебраическим выражением понимают запись, составленную со смыслом, состоящую из букв и цифр, обозначающих числа. При этом она может содержать скобки и знаки арифметических действий. Исходя из этого простейшего определения можно утверждать, что формулы 2 * k — s, 4 * (y — 3/2), 0,89 * a — g * (9a + 4b), a
Если же значение переменной известно и его можно подставить на место буквенного обозначения, то результат, полученный после выполнения указанных в уравнении действий, называется ответом алгебраического выражения. Но если число, подставляемое вместо буквы, приводит к бессмысленности записи, то оно считается недопустимым. Из этого можно сделать вывод, что одна и та же алгебраическая запись при различных величинах букв может иметь отличные значения.
На практике приходится сталкиваться с довольно сложными и громоздкими алгебраическими выражениями, поэтому над ними приходится выполнять ряд действий, правил, законов или использовать свойства для упрощения записи.
Кроме определений здесь применяется понятие «тождественность». Под ним понимают два выражения, для которых при любых значениях переменных, входящих в их состав, будет справедливо их равенство, например, 56* (x+с) = 56 * x + 56 * с.
Эти два выражения можно заменить друг другом или, выражаясь математическим языком, — «выполнить тождественное преобразование».
Виды выражений
В школе на уроках алгебры приходится сталкиваться с различными видами выражений. Обычно они состоят из нескольких членов. В математике существует группирование, объединяющее сходные элементы. Обучение понятиям начинают в седьмом классе с того, что приводят следующие определения:

- Одночленом называют числа или переменные, а также степени, имеющие натуральные показатели. Таким образом, одночленами могут быть просто числа или составленные из них произведения, например, 3, 5 * x, 5b / (6 * b).
- Многочленом считается запись, состоящая из суммы одночленов, например, 2x+4, 16b / 23 + b.
Многочлен всегда подразумевает выполнение действий. При описании понятия используют и такие термины, как коэффициент, член, степень. Во время работы с одночленами применяют тождественное их приведение к стандартному виду.
В нём выражение представляют как произведение числового множителя и натуральной степени разных переменных, например, 2 * a, −x * 3.
Выражения в алгебре могут быть следующих видов:
- Рациональные (алгебраические) дроби. Это запись, в которой числитель и знаменатель представляют в виде многочлена. Следует понимать, что любая обыкновенная дробь будет алгебраической.
- Целые рациональные. Математические записи, в которых не содержится деление на уравнения с переменными или выражения с отрицательной степенью.
- Степенные. Формулы, в состав которых входит одночлен или многочлен, возводимый в степень.
- Иррациональные с корнями. Записи уравнений, содержащие подкоренные члены.
- Тригонометрические. К ним относят уравнения, связанные с прямыми и обратными тригонометрическими функциями.
- Логарифмические выражения. Формулы, которые содержат логарифмы.
Все указанные виды относят к простым, но с 7 класса алгебраические выражения будут усложняться. Сложный вид записи обычно состоит из многочлена, включающего в себя извлечение корня, логарифмы и возведение в степень, например, ln (x
Вычисление сложных выражений подразумевает выполнение преобразований, которые позволят проще решить задание и найти правильный ответ.
Алгебраические действия
Решая задачу, приходится выполнять те или иные преобразования. Чаще всего сложность задания определяется громоздкостью и объёмом соответствующих преобразований, поэтому в школе на уроках элементарной математики часто попадаются задачи на упрощения.

Основу всех алгебраических действий составляют три закона. Это правила, касающиеся сложения и умножения: переставное, соединительное и распределительное. Но наряду с ними применяют и формулы сокращённого умножения.
На начальном этапе обучения рекомендуется даже записать данные правила отдельно на листик и пользоваться им, пока применение законов не дойдёт до автоматизма. Вот некоторые практические рекомендации, решаться с которыми примеры будут намного легче:

- Выполнять вычисления и преобразования нужно последовательно, шаг за шагом, на каждом этапе максимально упрощая полученный результат.
- Важным элементом преобразований, необходимым для решения различных задач с любых разделов, является умение раскладывать на множители те или иные одночлены или многочлены. Как правило, результат достигается благодаря удачной группировке слагаемых.
- При возможности всегда нужно использовать правило замены переменных, то есть вводить условные равенства. Переход к новым обозначениям и заменам — это нужный приём, с помощью которого решают не только различные задачи элементарной, но и высшей математики.
- Сильно упростить выражение позволяет приведение подобных членов. Если слагаемые имеют одинаковые буквенные части, то их числовые коэффициенты прилагаются, а буквенная часть сохраняется: 9* a2b — 3 * a2b — 4a2b = (9 — 3 — 4) * a2b = 2 * a2b.
- Используя правила распределительного закона, можно осуществить вынесение множителя за скобки и их раскрытие. В этом также помогают теоремы действий со степенями: 4ax2y + 3 * а2bxy2 — 2 * abx2 = ax * (4 * xy + 3 * aby2 — 2 * bx2).
- Во время преобразований нужно помнить о знаках. Так, если множитель перед скобками имеет отрицательный знак, то при их раскрытии знак изменится у всех слагаемых на противоположный.
Не стоит забывать и о такой операции, как деление многочлена. Для этого используют метод столбика. Заключается он в размещении слагаемых многочлена в порядке убывания степени переменной и разделения первого слагаемого числителя многочлена на первое слагаемое знаменателя.
Затем результат умножают на делитель и отнимают ответ от делимого.
Применение преобразований
Алгебраические выражения, показывающие, что одна величина больше другой или равна ей, называют уравнениями и равенствами. При этом их используют для составления формул, то есть для записи, выражающей зависимость между двумя или несколькими переменными. Это удобно, так как преобразования позволяют привести формулу к простому для запоминания виду.

При решении примеров важно знать все существующие методы. Какой из них применять, конкретно указать нельзя, всё зависит от личных предпочтений и опыта решения подобных заданий. Например, пусть нужно упростить сложное выражение (a3 (b — c) + b3 (c — a) + c3 (a — b)) / (a2 (b — c) + b2 (c — a) + c2 (a — b)).
Сначала можно попробовать разложить на множители делитель и делимое. Один из вариантов преобразования числителя следующий:
a3 (b — c) + b3 (c — a) + c3 (a — b) = a3b — b3c — a3c + b3c + c3(a — b) = ab (a2 — b2
) = ab (a2 — b2) — c (a3 — b3) + c3(a — b) = (a — b) (ab (a + b) — c (a2 + ab + b2) + c3 = (a — b) (a2b — a2c + ab2 — abc + c3 — cb2) = (a — b) (a2 (b — c) + ab (b — c) — c (b2 — c2) = (a — b) (b — c) (a2 — c2 + ab — cb) = (a — b) (b — c) (a — c) (a + b + c).По аналогии раскладывая знаменатель, можно прийти к результату: (a — b) (b — c) (a — c). В итоге получится равенство (a3 (b — c) + b3 (c — a) + c3 (a — b)) / (a2 (b — c) + b2 (c — a) + c2 (a — b)) = ((a — b) (b — c) (a — c) (a + b + c)) / ((a — b)(b — c)(a — c)) = a + b + c.
В числителе возможно выделить множитель (a — b) на том основании, что делимое равно нулю, когда a совпадает с b. Обычно в двух взаимно обратных операциях выполнение одной сложнее, чем другой. Это касается, в частности, выполнения умножения алгебраических выражений и разложения на множители или возведения в степень с извлечением корня. Например, легко увидеть, что (5 + 3 √2)
Следует помнить, что когда при решении задачи встречается выражение подкоренного вида √с + n * √k или √a + b√k, то необходимо попытаться добыть соответствующий корень. Если же это невозможно, то нужно воспользоваться подбором.
Если нужно упростить выражение √11 + 6 √ 2, то его можно представить как c + b √2. Следовательно, справедливо будет следующее равенство: 11 + 6 √2 = с2 + 2b2 + 2 cb √2. Поиск целых (рациональных) c и b приведёт к решению системы: a2 + 2b2 = 11, ab = 3.
При этом подобрать нужную пару целых легко: a = 3, b = 1, то есть можно записать равенство как √11 + 6√ 2 = 3 + √2.
Алгебраическое число — Википедия
Материал из Википедии — свободной энциклопедии
Алгебраи́ческое число́ над полем F{\displaystyle \mathbb {F} } — элемент алгебраического замыкания поля F{\displaystyle \mathbb {F} }, то есть корень многочлена (не равного тождественно нулю) с коэффициентами из F{\displaystyle \mathbb {F} }.
Если поле не указывается, то предполагается поле рациональных чисел, то есть F=Q{\displaystyle \mathbb {F} =\mathbb {Q} }, в этом случае поле алгебраических чисел обычно обозначается A{\displaystyle \mathbb {A} }. Данная статья посвящена именно этим «рациональным алгебраическим числам». Поле A{\displaystyle \mathbb {A} } является подполем поля комплексных чисел.
- Вещественное число или Комплексное число, не являющееся алгебраическим, называется трансцендентным.
- Целыми алгебраическими числами называются корни многочленов с целыми коэффициентами и со старшим коэффициентом, равным единице.
- Если α{\displaystyle \alpha } — алгебраическое число, то среди всех многочленов с рациональными коэффициентами, имеющих α{\displaystyle \alpha } своим корнем, существует единственный многочлен наименьшей степени со старшим коэффициентом, равным единице. Такой многочлен называется минимальным, или каноническим многочленом алгебраического числа α{\displaystyle \alpha } (иногда каноническим называют многочлен, получающийся из минимального домножением на наименьшее общее кратное знаменателей его коэффициентов, то есть многочлен с целыми коэффициентами).
- Множество алгебраических чисел счётно, а следовательно, его мера равна нулю.
- Множество алгебраических чисел плотно на комплексной плоскости.
- Сумма, разность, произведение и частное[1] двух алгебраических чисел — алгебраические числа, то есть множество всех алгебраических чисел образует поле.
- Корень многочлена с алгебраическими коэффициентами есть алгебраическое число, то есть поле алгебраических чисел алгебраически замкнуто.
- Для всякого алгебраического числа α{\displaystyle \alpha } существует такое натуральное N{\displaystyle N}, что Nα{\displaystyle N\alpha } — целое алгебраическое число.
- Алгебраическое число α{\displaystyle \alpha } степени n{\displaystyle n} имеет n{\displaystyle n} различных сопряжённых чисел (включая себя).
- α{\displaystyle \alpha } и β{\displaystyle \beta } сопряжены тогда и только тогда, когда существует автоморфизм поля A{\displaystyle \mathbb {A} }, переводящий α{\displaystyle \alpha } в β{\displaystyle \beta }.
- Любое алгебраическое число вычислимо, а следовательно, арифметично.
- Порядок на множестве действительных алгебраических чисел изоморфен порядку на множестве рациональных чисел.[прояснить]
Числа, записанные при помощи радикалов[править | править код]
Любое число, которое можно получить из целых чисел при помощи четырёх действий арифметики (сложения, вычитания, умножения, деления), а также извлечением корня целой степени, является алгебраическим. Так, например, алгебраическим будет число 19989819−8198{\displaystyle {\sqrt {\frac {1998}{{\sqrt[{19}]{98}}-{\sqrt[{198}]{8}}}}}}, а также числа вида Q1Q2+Q3Q4+…+QnQn+1{\displaystyle Q_{1}^{Q_{2}}+Q_{3}^{Q_{4}}+\ldots +Q_{n}^{Q_{n+1}}}, где Q1,Q2,Q3,Q4…Qn+1{\displaystyle Q_{1},Q_{2},Q_{3},Q_{4}\dots Q_{n+1}}— рациональные числа.
Однако не все алгебраические числа можно записать при помощи радикалов. Так, например, согласно теореме Абеля — Руффини существуют многочлены пятой степени с целыми коэффициентами, которые не разрешимы в радикалах. Корни такого многочлена являются алгебраическими числами, которые невозможно построить из целых четырьмя арифметическими действиями и извлечением корней[2].
Название алгебраические и трансцендентные числа предложил Эйлер в 1775 году. В то время ещё не было известно ни одного трансцендентного числа[2]. Алгебраические поля, отличные от рационального, стал рассматривать Гаусс. При обосновании теории биквадратичных вычетов он развил арифметику целых гауссовых чисел, то есть чисел вида a+bi{\displaystyle a+bi}, где a{\displaystyle a} и b{\displaystyle b} — целые числа. Продолжение исследований Гаусса привело во второй половине XIX века к построению общей теории алгебраических чисел[3]. Далее, изучая теорию кубических вычетов, Якоби и Эйзенштейн создали арифметику чисел вида a+bρ{\displaystyle a+b\rho }, где ρ=(−1+i3)/2{\displaystyle \rho =(-1+i{\sqrt {3}})/2} — кубический корень из единицы, а a{\displaystyle a} и b{\displaystyle b} — целые числа. В 1844 году Лиувилль доказал теорему о невозможности слишком хорошего приближения корней многочленов с рациональными коэффициентами рациональными дробями, и, как следствие, ввёл формальные понятия алгебраических и трансцендентных (то есть всех прочих вещественных) чисел. Попытки доказать великую теорему Ферма привели Куммера к изучению полей деления круга, введению понятия идеала и созданию элементов теории алгебраических чисел. В работах Дирихле, Кронекера, Гильберта и других теория алгебраических чисел получила своё дальнейшее развитие. Большой вклад в неё внесли русские математики Золотарев (теория идеалов), Вороной (кубические иррациональности, единицы кубических полей), Марков (кубическое поле), Сохоцкий (теория идеалов) и другие.
§4. Алгебраические операции. Основные типы алгебраических структур
Алгебра − наука об алгебраических операциях. Свойства множеств с алгебраическими операциями изучаются в этом параграфе.
1°. Алгебраические операции.
Пусть X − произвольное множество.
Определение 1. 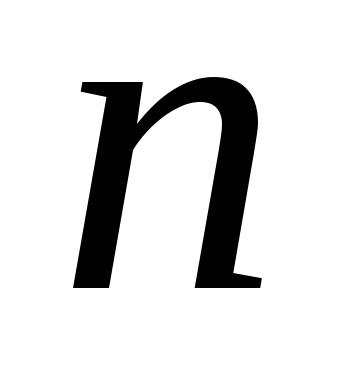 -арной
алгебраической операцией на X называется отображение
-арной
алгебраической операцией на X называется отображение  .
То есть
.
То есть
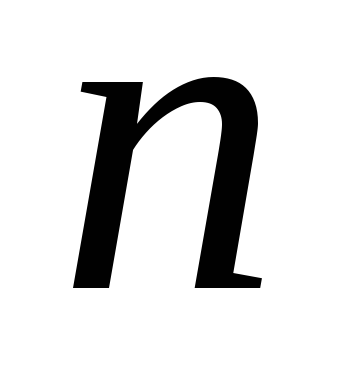 –
компонентному
элементу
–
компонентному
элементу 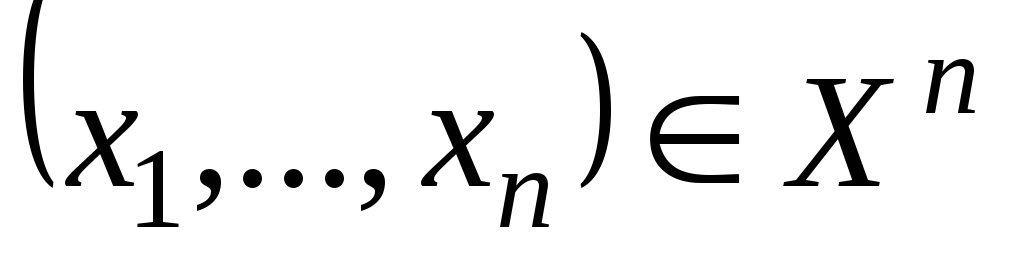 однозначно ставится в соответствие
элемент
однозначно ставится в соответствие
элемент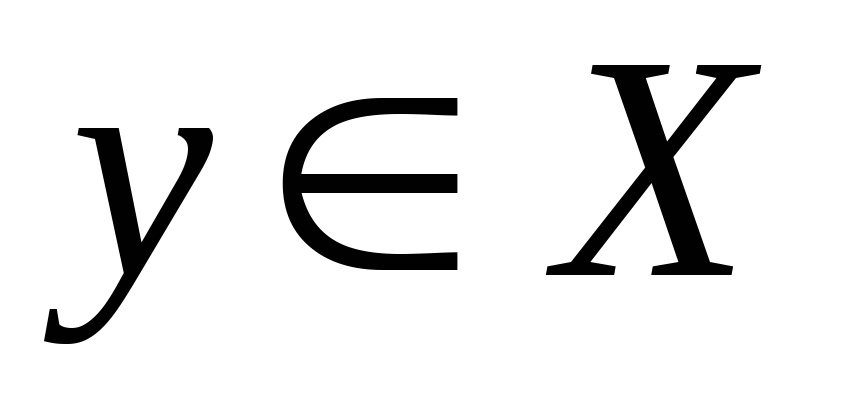 .
.
Задача. Пусть  .
Сколько
.
Сколько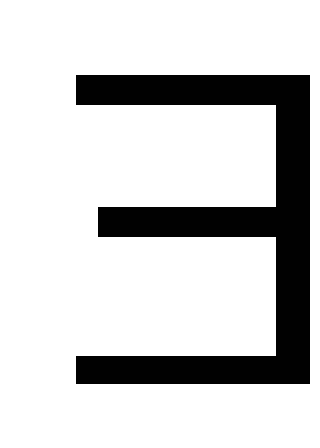 n–арных
алгебраических операций на
n–арных
алгебраических операций на 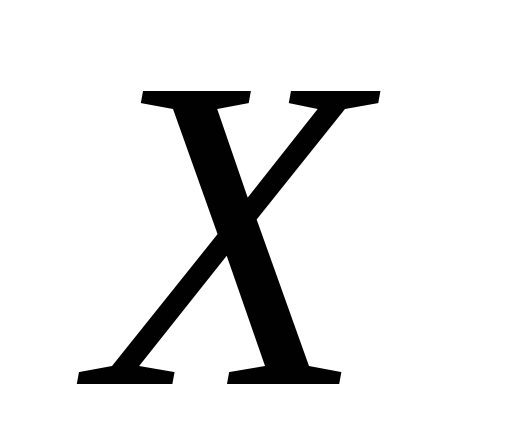 ?Ответ. Таких
операций
?Ответ. Таких
операций 
Алгебраические
операции при  называютсяунарными,
при
называютсяунарными,
при 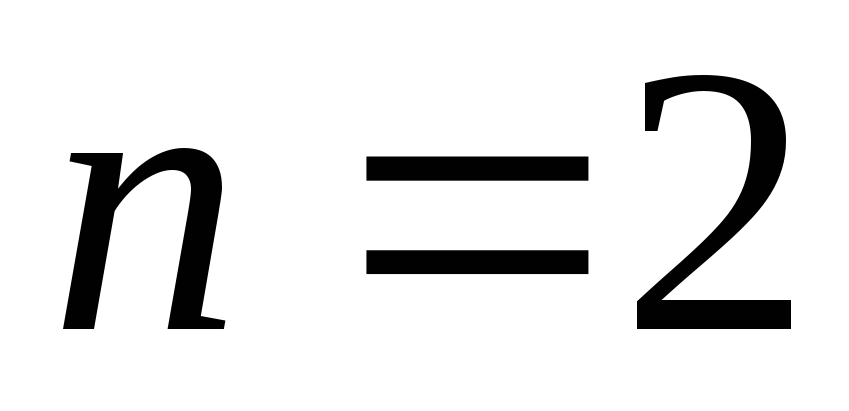 –бинарными,
–бинарными, 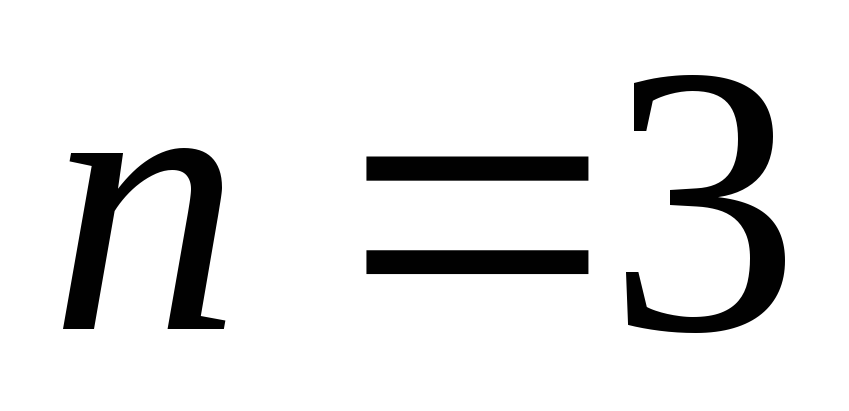 –тернарными.
Далее, как правило, будут рассматриваться
бинарные операции.
–тернарными.
Далее, как правило, будут рассматриваться
бинарные операции.
Если 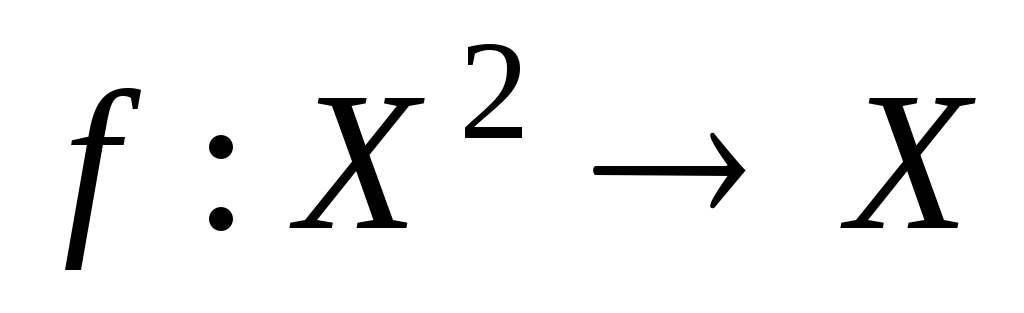 ,
то пишут
,
то пишут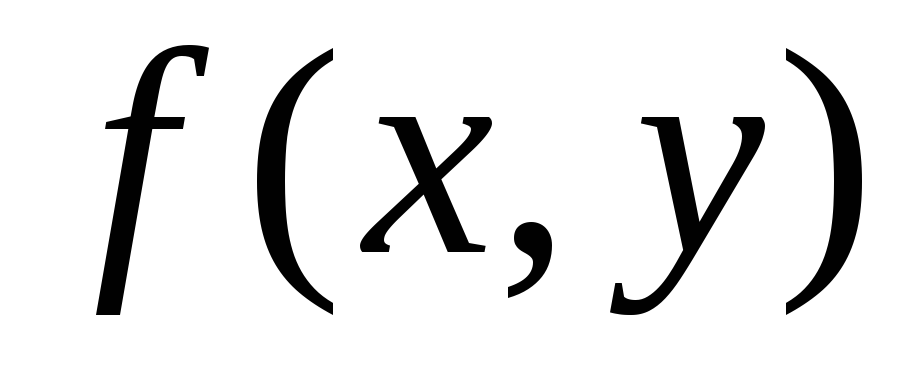 или.
Операции наX обозначают символами
или.
Операции наX обозначают символами 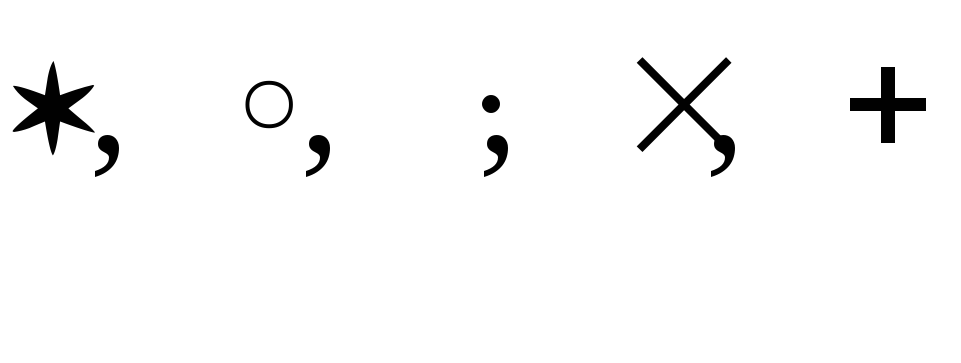 .
Последний символ используется для
операции сложения, остальные − для
операции умножения.
.
Последний символ используется для
операции сложения, остальные − для
операции умножения.
Определение 2. Множество X с конкретной алгебраической операцией называется алгебраической структурой.
На одном и том же множестве X могут быть заданы различные алгебраические структуры.
Примеры (алгебраических операций и алгебраических структур).
1. (R,
+) − алгебраическая структура, и 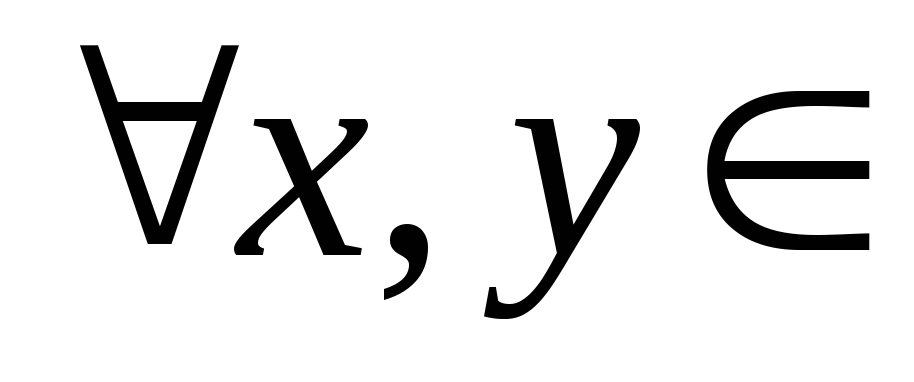 R имеем
R имеем 
2. (R, -) − алгебраическая структура.
3. (R,  )
− алгебраическая структура.
)
− алгебраическая структура.
4. Деление не
является алгебраической операцией на R,
так как не определено деление на нуль.
Однако оно является алгебраической
операцией на (R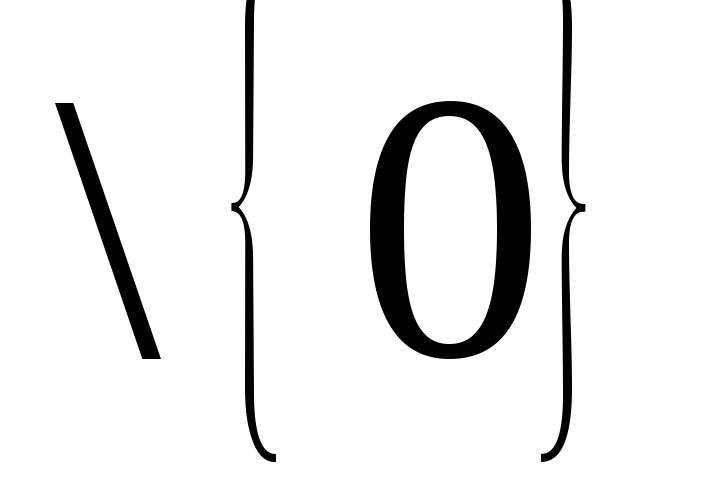 ).
).
5–8. То же самое для С.
9. (Rn, +) − алгебраическая структура.
10. Скалярное произведение не является алгебраической операцией на множестве векторов, так как результатом операции является число.
11. 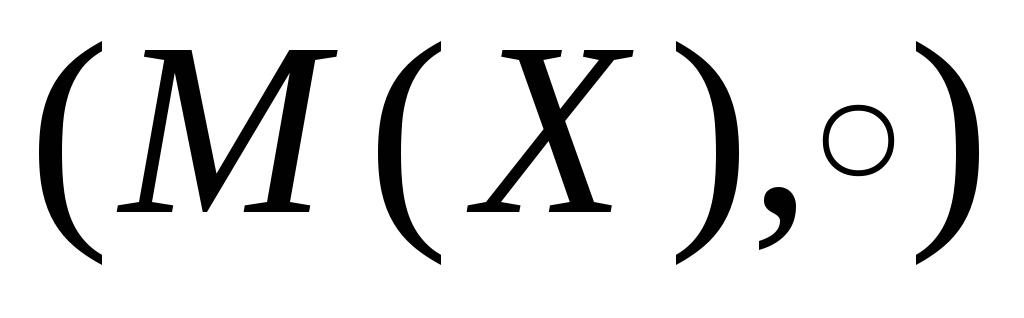 – множество всех отображений
– множество всех отображений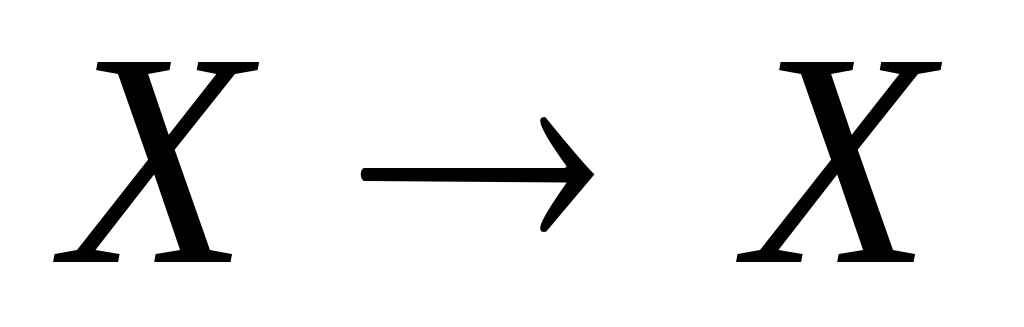 относительно операции композиции
относительно операции композиции является алгебраической структурой.
является алгебраической структурой.
12. Как правило,
алгебраическая операция на конечном
множестве может быть задана с помощью
таблицы Кэли, которая описывает результат
операции на любой паре элементов
множества. Рассмотрим множество,
состоящее из 3-х элементов: {Доска, Окно,
Тряпка} (кратко {Д, О, Т}). Введем следующую
операцию, обозначаемую  (символ операции). Соответствующую
таблицу Кэли можно выбрать в виде
(символ операции). Соответствующую
таблицу Кэли можно выбрать в виде
1 | Д | О | Т |
Д | Д | О | Д |
О | О | Д | Т |
Т | Т | Т | Д |
13. Примерами
тернарных операций на R3 R
R  R
R  R являются:
R являются:
 .
. .
. .
.
Обычно рассматривают операции со специальными свойствами.
Определение 3. Бинарная операция  наX называется коммутативной,
если
наX называется коммутативной,
если 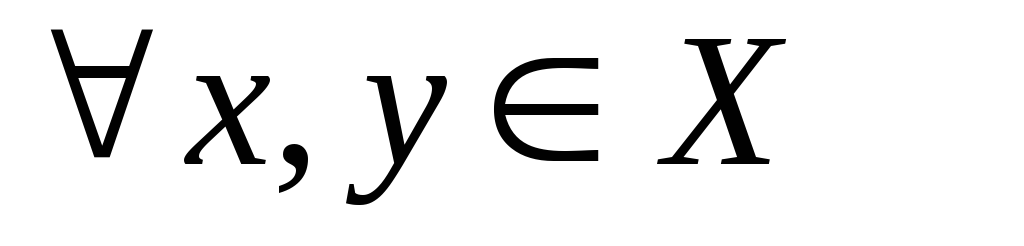 выполняется
выполняется ; ассоциативной,
если
; ассоциативной,
если 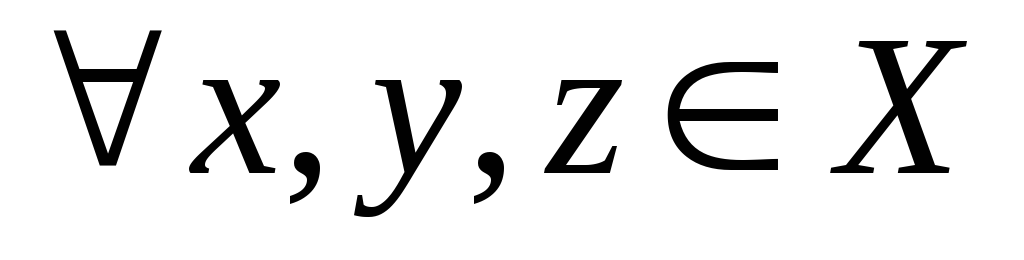 выполняется
выполняется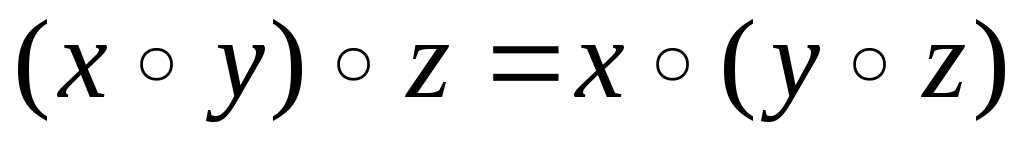 .
.
Замечание. Если 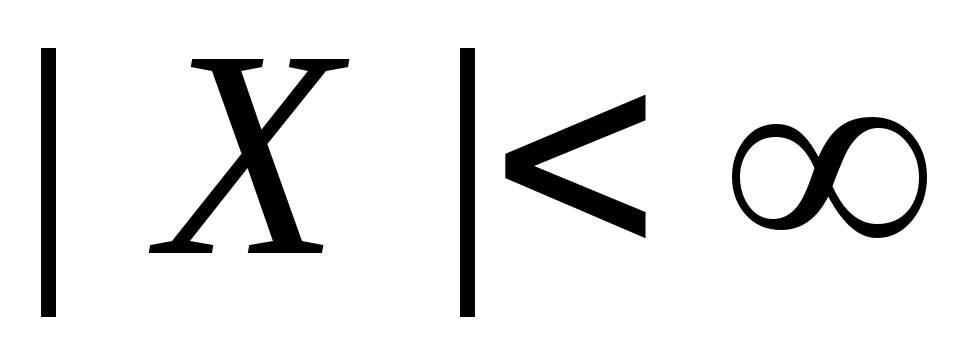 (то есть множество
(то есть множество – конечное) и
– конечное) и − коммутативная операция, то таблица
Кэли симметрична относительно диагонали.
− коммутативная операция, то таблица
Кэли симметрична относительно диагонали.
Задача. Пусть  .
Сколько
.
Сколько коммутативных бинарных операций наX? Ответ.
Таких операций
коммутативных бинарных операций наX? Ответ.
Таких операций 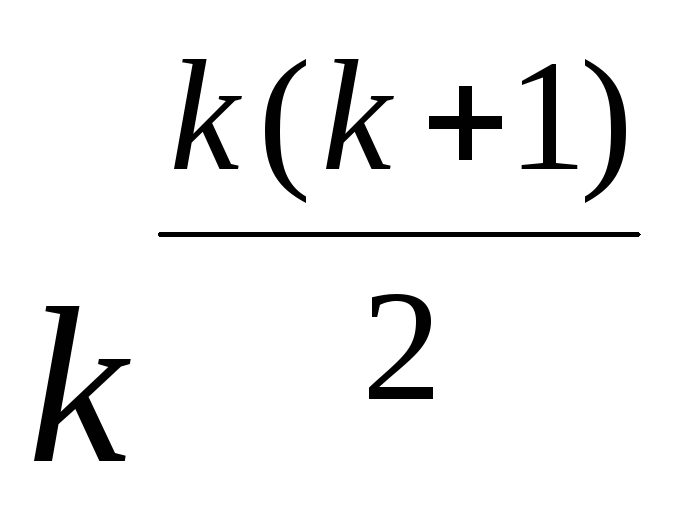 .
.
Примеры.
В (R, +) операция сложения коммутативна и ассоциативна.
В (R, -) операция вычитания не коммутативна и не ассоциативна. Например,
 ,
, .
.(R,
 ),
где
),
где
 ,
такая операция
,
такая операция коммутативна, но не ассоциативна.
Действительно:
коммутативна, но не ассоциативна.
Действительно:
 .
.Умножение матриц является ассоциативной, но не коммутативной операцией.
Теорема 1 (обобщённая
ассоциативность). Если операция  ассоциативна,
то в выражении
ассоциативна,
то в выражении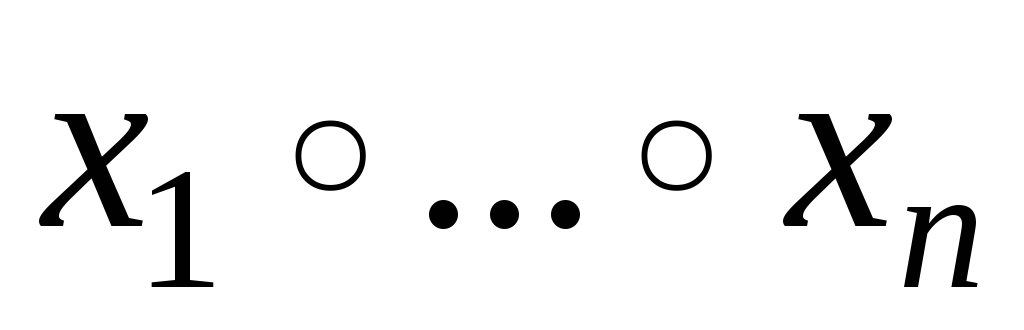 скобки можно расставлять в любых местах.
скобки можно расставлять в любых местах.
Доказательство. Проводится методом математической
индукции. Для 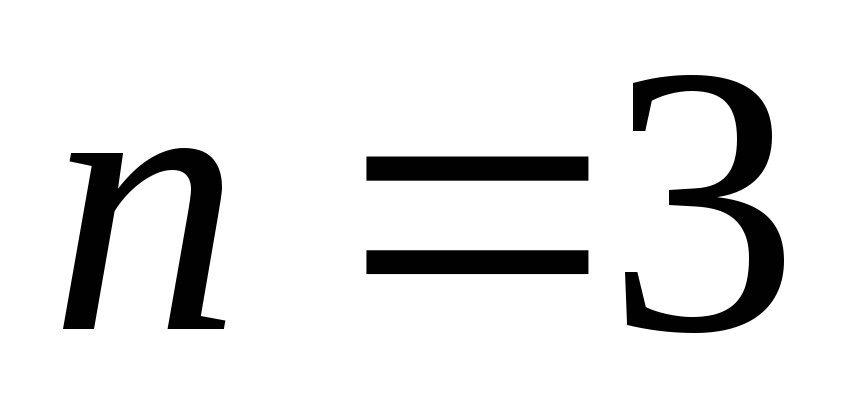 утверждение повторяет определение
ассоциативности. Пусть
утверждение повторяет определение
ассоциативности. Пусть  .
Рассмотрим выражения
.
Рассмотрим выражения
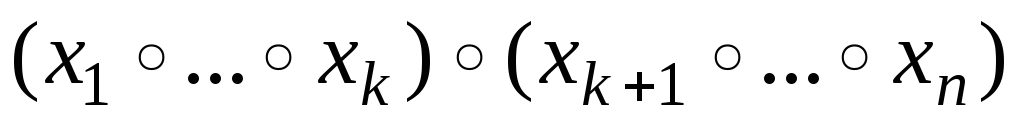 и
и 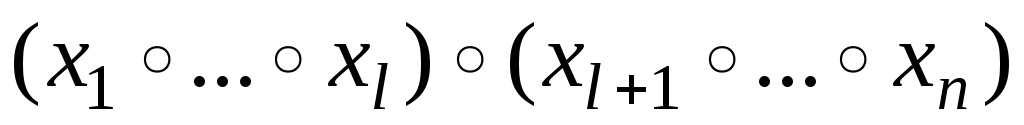 ,
,
в которых выписаны
лишь внешние скобки. Пусть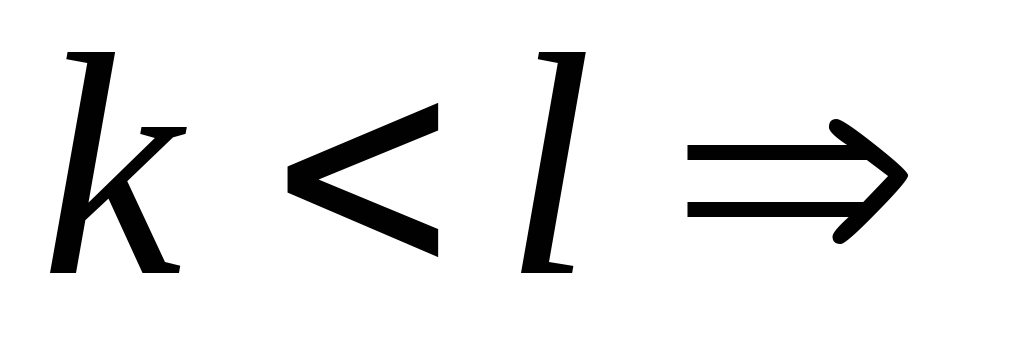 в силу предположения индукции эти
выражения можно переписать в виде
в силу предположения индукции эти
выражения можно переписать в виде
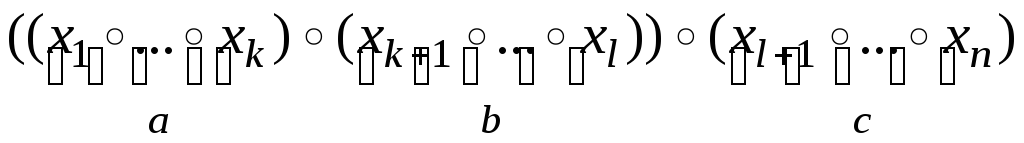
и
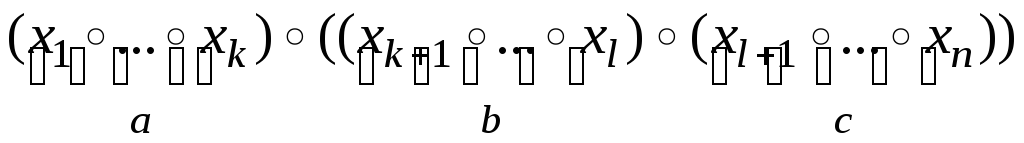 ,
,
или
 и
и 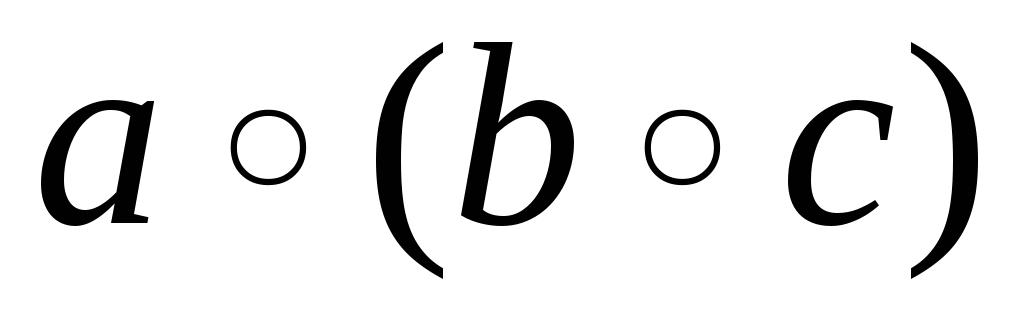
которые равны в силу определения ассоциативности. ■
Определение 4. Элемент 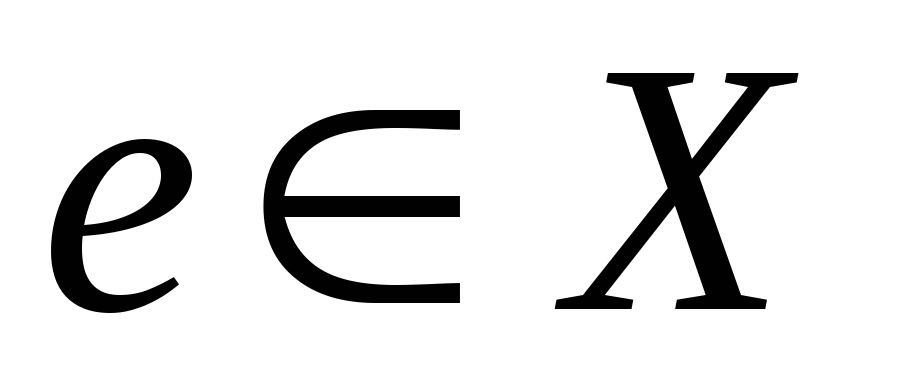 называетсянейтральным относительно алгебраической операции
называетсянейтральным относительно алгебраической операции  ,
если
,
если
. | (1) |
Теорема 2. Нейтральный элемент единственен.
Доказательство.  (от противного). Пусть
(от противного). Пусть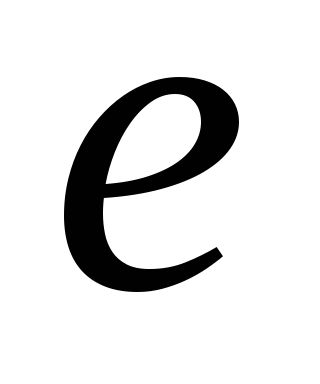 и
и −
два нейтральных элемента
−
два нейтральных элемента
 (по условию
нейтральности
(по условию
нейтральности  )
и
)
и
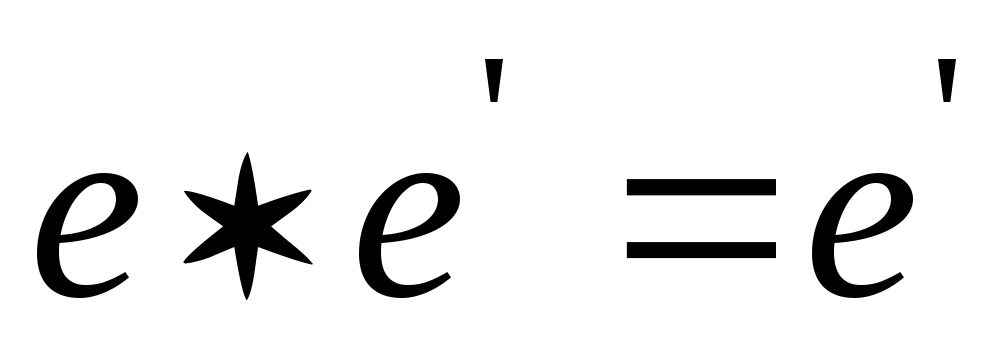 (по условию нейтральности
(по условию нейтральности 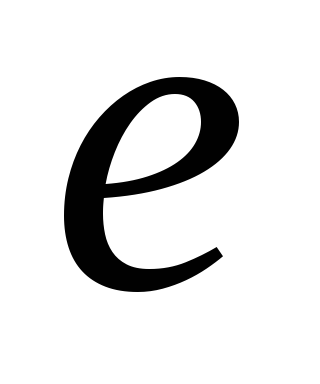 )
)

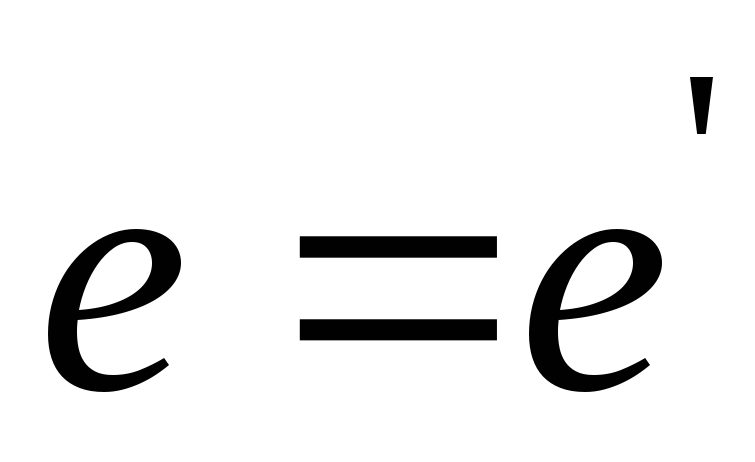 .■
.■
Определение 5. Множество 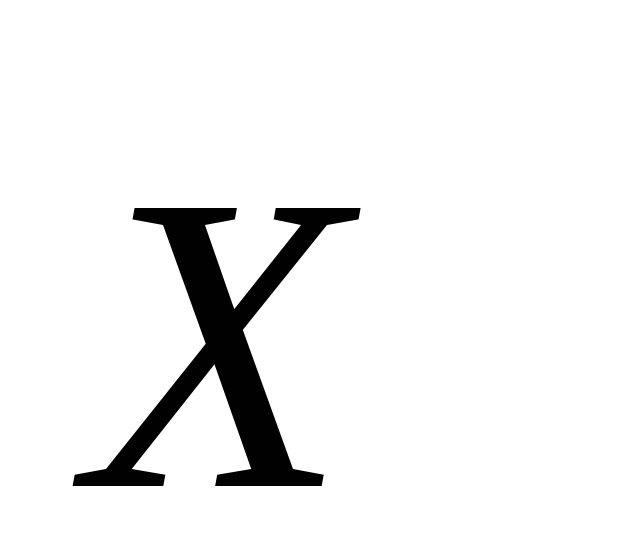 с
заданной на нем бинарной ассоциативной
операцией называетсяполугруппой.
Полугруппа с нейтральным элементом
называется моноидом или полугруппой
с единицей.
с
заданной на нем бинарной ассоциативной
операцией называетсяполугруппой.
Полугруппа с нейтральным элементом
называется моноидом или полугруппой
с единицей.
Определение 6. Элемент  моноида
моноида называетсясимметричным к элементу
называетсясимметричным к элементу 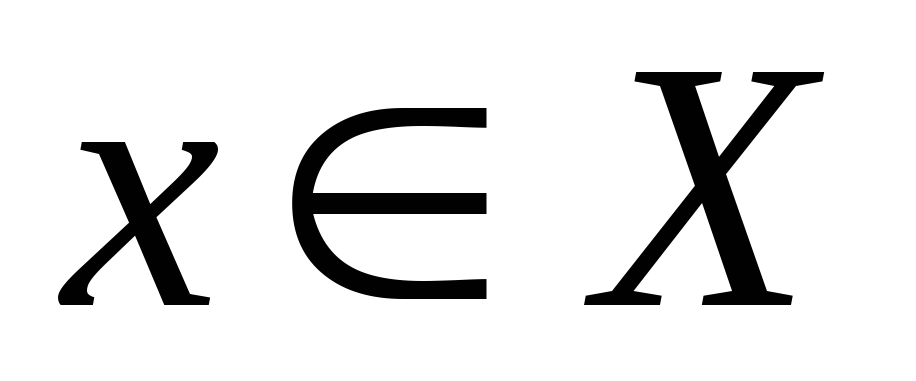 ,
если
,
если
| (2) |
Теорема 3. Если в моноиде для 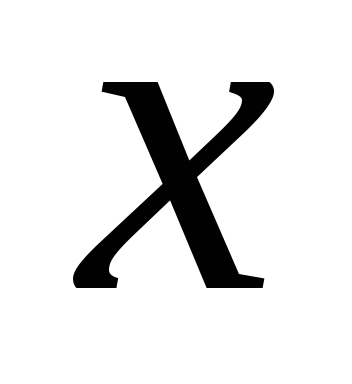 есть
симметричный элемент, то такой элемент
единственен.
есть
симметричный элемент, то такой элемент
единственен.
Доказательство. Пусть для данного 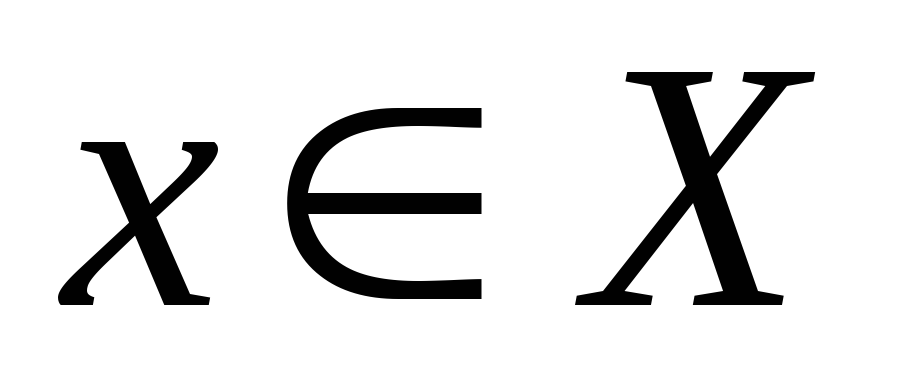
 два симметричных элемента
два симметричных элемента 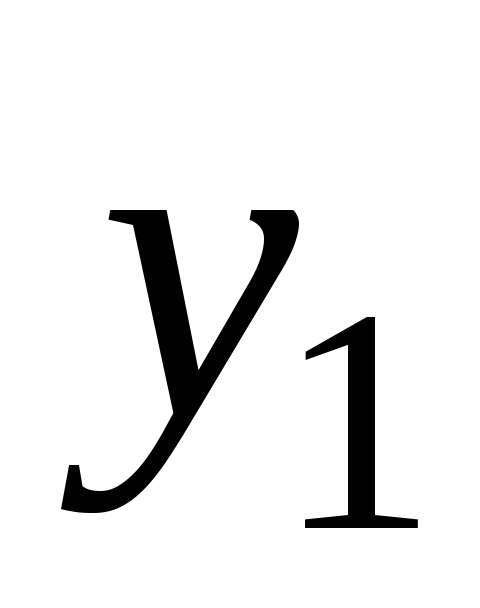 и
и 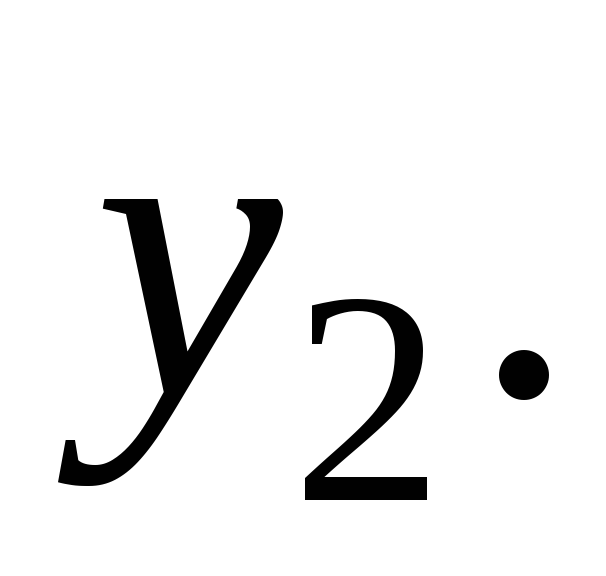 Тогда в силу (1) и (2) имеем:
Тогда в силу (1) и (2) имеем:
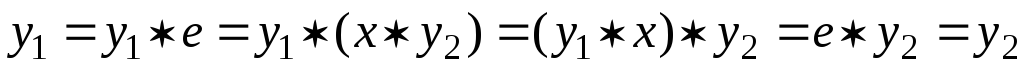 .■
.■
Обычно умножение
называют мультипликативной операцией, сложение – аддитивной.
В случае мультипликативной операции
результат операции  называютпроизведением,
нейтральный элемент – единицей (обозначают 1), симметричный элемент к
называютпроизведением,
нейтральный элемент – единицей (обозначают 1), симметричный элемент к 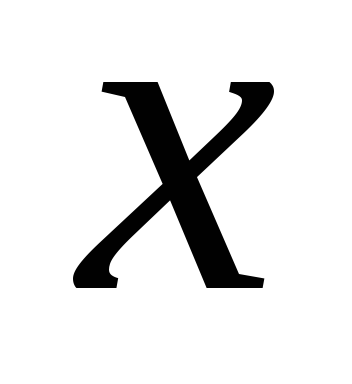 –обратным (пишут
–обратным (пишут  ).
В случае аддитивной операции результат
операции
).
В случае аддитивной операции результат
операции называютсуммой (),
нейтральный – нулём (обозначают 0), симметричный – противоположным (обозначают
называютсуммой (),
нейтральный – нулём (обозначают 0), симметричный – противоположным (обозначают 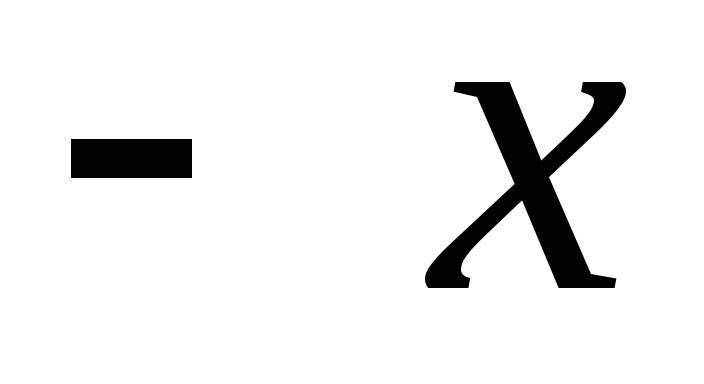 ).
).
Теорема 4. Если в моноиде  для
элементов
для
элементов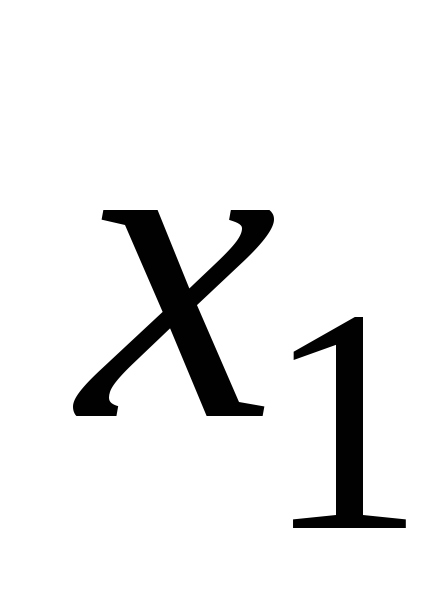 и
и есть симметричные элементы
есть симметричные элементы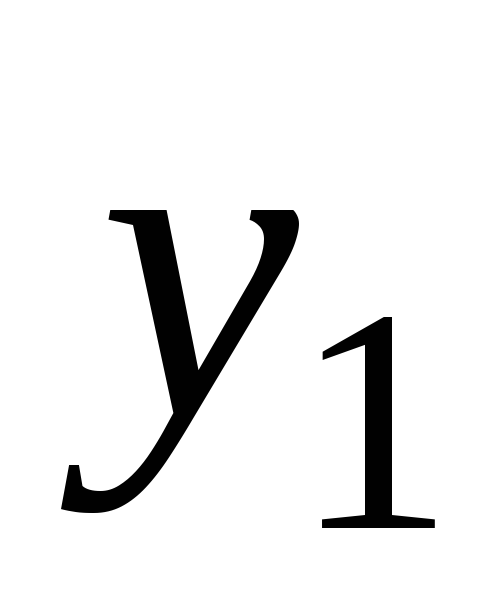 и
и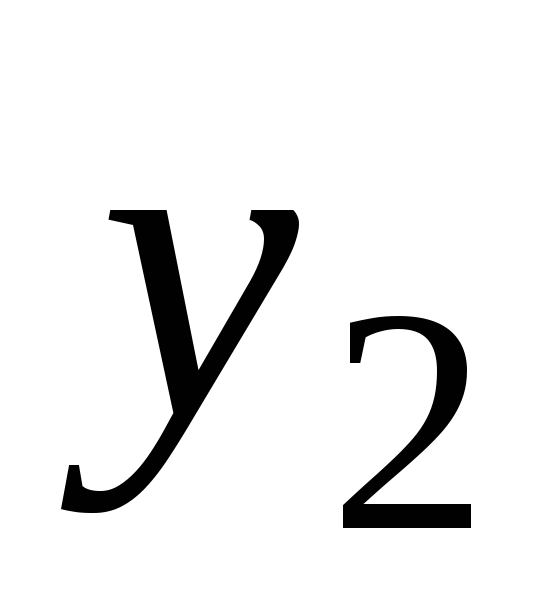 соответственно, то для элемента
соответственно, то для элемента также
существует симметричный элемент, равный
также
существует симметричный элемент, равный
Доказательство. Для
доказательства теоремы необходимо
проверить условия (2): 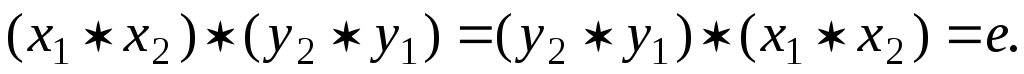 Проверим первое из этих равенств. Имеем:
Проверим первое из этих равенств. Имеем:
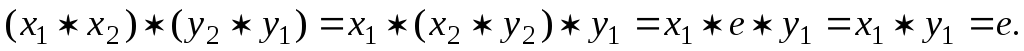
Аналогично проверяется второе условие из (2).■
Алгебраическая сумма и её свойства
Вычитание можно заменить сложением, если взять вычитаемое с противоположным знаком. Это свойство суммы можно выразить в виде общей формулы:
a — b = a + (-b)
Эта формула показывает, что любую разность можно заменить суммой, поэтому в алгебре любое выражение, содержащее действия вычитания и сложения, можно рассматривать как сумму:
2x — y2 = 2x + (-y2)
-21 + n — m = — 21 + n + (-m)
Такие выражения называются алгебраическими суммами.
Алгебраическая сумма — это выражение, которое можно представить в виде суммы положительных и отрицательных чисел.
Обратите внимание, что запись алгебраической суммы обычно упрощают: положительные числа записываются без предшествующего знака +
, а отрицательные числа, стоящие в начале выражения, записываются без скобок:
(-5) + (+7) = -5 + 7
Также в алгебраических суммах на первом месте принято записывать слагаемое со знаком +
(если такое имеется). Например, алгебраическую сумму:
-2x — y + 3z
заменяют на выражение:
3z — 2x — y
Свойства алгебраической суммы
В любой сумме слагаемые можно менять местами и произвольным образом объединять в группы, то есть использовать свойства сложения (переместительное и сочетательное):
a + b = b + a
a + b + c = (a + b) + c = a + (b + c) = (a + c) + b
Пример 1:
10 + (-7) = -7 + 10 = 3
Пример 2:
-7 + 28 + (- 13) + 12 = (-7 + (- 13)) + (28 + 12) = -20 + 40 = 20
Алгебраические дроби. Сокращение алгебраических дробей
Алгебраическая дробь – это дробь, числитель и знаменатель которой являются многочленами. Другими словами, алгебраическая дробь – это деление двух многочленов, записанное с помощью дробной черты.
Любую алгебраическую дробь можно представить в виде выражения:
где a и b – это многочлены и b≠0.
Дробная черта в записи алгебраической дроби заменяет собой скобки, которые должны были бы присутствовать, если частное было бы записано не в виде дроби:
| (a + 3) : (a2 + 9) = | a + 3 |
| a2 + 9 |
Примеры алгебраических дробей:
| a + 3 | ; | 7 | ; | 1 |
| a2 + 9 | x | 2 |
Обратите внимание на последний пример: обыкновенные дроби являются одновременно и алгебраическими, так как любое число можно считать многочленом, состоящим из одного члена.
Любой многочлен можно записать в виде алгебраической дроби, знаменатель которой равен единице:
| a2 + 9 = | a2 + 9 | ; 15 = | 15 | ; x2 + 2xy + y2 = | x2 + 2xy + y2 |
| 1 | 1 | 1 |
Сокращение алгебраических дробей
Основное свойство алгебраической дроби:
Если числитель и знаменатель алгебраической дроби умножить или разделить на один и тот же многочлен, то получится дробь, равная данной.
В виде буквенной формулы основное свойство алгебраической дроби можно записать так:
| a | = | a · c | и | a | = | a : c | |
| b | b · c | b | b : c | , |
где c≠0.
Используя основное свойство алгебраических дробей, выполняют их сокращение. Сокращение алгебраических дробей – это деление числителя и знаменателя дроби на их общий множитель.
Чтобы сократить алгебраическую дробь, надо числитель и знаменатель разложить на множители. Если числитель и знаменатель имеют общие множители, то дробь можно сократить. Если у числителя и знаменателя общих множителей нет, то дробь является несократимой.
Пример 1. Сократить дробь:
Решение: Разложим числитель и знаменатель на множители, выделим их общий множитель и сократим дробь на него:
| ab2 + bc | = | b(ab + с) | = | ab + с |
| ab2 | b · ab | ab |
Пример 2. Упростить дробь:
Решение: Сначала мы можем сократить дробь на общий множитель x в первой степени:
| 3x(a + b) | = | 3(a + b) |
| x2(b — a) | x(b — a) |
Теперь стоит внимательно посмотреть на многочлены, заключённые в скобки:
a + b и b — a
Чтобы многочлен из знаменателя привести к тому же виду, что и у многочлена в числителе, надо поменять у многочлена b — a знак на противоположный и переставить члены местами:
b — a = -(-b + a) = -(a — b)
Теперь и в числителе и в знаменателе у нас есть общий множитель, который можно сократить:
| 3(a + b) | = | 3(a + b) | = — | 3 |
| x(b — a) | —x(a + b) | x |
Пример 3. Сократите дробь:
Решение: числитель и знаменатель дроби являются одночленами. Каждый одночлен – это произведение, состоящее из множителей, значит, можно сразу переходит к сокращению:
- Начинаем с числового множителя. Числовые множители можно сократить на их наибольший общий делитель. Для чисел 24 и 16 – это число 8. После сокращения от 24 останется 3, а от 16 – 2.
- Буквенные множители сокращаем на степень с наименьшим встречающимся показателем:
- a и a5 сокращаем на a. Единицу в числитель не пишем, а в знаменателе остаётся a4.
- b3 и b3 сокращаем на b3, единицы в результат не записываем.
- c5 и c сокращаем на c, в числитель пишем c4, в знаменатель не пишем ничего.
Следовательно:
| 24ab3c5 | = | 3c4 |
| 16a5b3c | 2a4 |
Алгебраический тип данных — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 апреля 2016; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 апреля 2016; проверки требуют 2 правки.Алгебраи́ческий тип да́нных — в информатике наиболее общий составной тип, представляющий собой тип-сумму из типов-произведений. Алгебраический тип имеет набор конструкторов, каждый из которых принимает на вход значения определённых типов и возвращает значение конструируемого типа. Конструктор представляет собой функцию, которая строит значение своего типа на основе входных значений. Для последующего извлечения этих значений из алгебраического типа используется сопоставление с образцом.
Простым примером алгебраического типа данных является список. Действительно, список имеет два конструктора — конструктор пустого списка и конструктор пары, первым элементом которой является значение определённого типа, а вторым — список. Пример определения списка на языке Haskell:
data List a = Nil
| Cons a (List a)
Так что видно, что алгебраические типы данных являются контейнерными типами — они содержат внутри себя значения других типов (или того же самого типа). То, что у списка первый конструктор не принимает на вход каких-либо параметров, не должно вводить в сомнение. Такая форма конструктора является необходимой для создания значений, которые внутри себя не содержат ничего, но являются «единичными» элементами алгебраических типов данных.
Специальными разновидностями алгебраических типов данных являются декартовы типы (они имеют только один конструктор) и перечисления (у них все конструкторы аргументов не имеют вовсе, хотя самих конструкторов может быть несколько). Так простейшим, но очень широко используемым перечислением является логический тип. Код на Haskell:
Также алгебраический тип данных может быть абстрактным, если такой тип определён в некотором модуле, из которого не экспортируются конструкторы соответствующего типа, а доступ к значениям внутри алгебраического типа данных осуществляется при помощи специальных методов — селекторов. Особо стоит отметить так называемые «обобщённые алгебраические типы данных», которые реализованы в языках Haskell и ML.
Остаётся отметить, что с точки зрения синтаксически-ориентированного конструирования данных алгебраическим типом данных является размеченное объединение декартовых произведений типов. Каждое слагаемое в размеченном объединении соответствует одному конструктору, а каждый конструктор в свою очередь определяет декартово произведение типов, соответствующих параметрам конструктора. Конструкторы без параметров являются пустыми произведениями. Если алгебраический тип данных является рекурсивным, всё размеченное объединение обёртывается рекурсивным типом, и каждый конструктор возвращает рекурсивный тип.
Язык Haskell[править | править код]
В языке Haskell любой тип данных, который не является примитивным, является алгебраическим. Все возможные виды значений (перечисления, объекты, структуры и т. д.) строятся при помощи конструкторов алгебраических типов данных. Поэтому рассматриваемая тема является чрезвычайно важной для понимания системы типизации языка Haskell.
Язык Nemerle[править | править код]
В языке Nemerle существует ключевое слово «variant», с помощью которого можно описать алгебраический тип данных. Все созданные таким путём варианты могут быть сопоставлены с образцом через ключевое слово «match».
Язык Haxe[править | править код]
В языке Haxe алгебраический тип данных реализуется при помощи анонимных типов и перечислений. В языке предусмотрено сопоставление с образцом, которое так же можно применить для работы с алгебраическим типом данных.
Алгебраическая система — Википедия
Материал из Википедии — свободной энциклопедии
Алгебраическая система в универсальной алгебре — множество G{\displaystyle G} (носитель) с заданным на нём набором операций и отношений (сигнатурой). Алгебраическая система с пустым множеством отношений называется алгеброй, а система с пустым множеством операций — моделью.
n{\displaystyle n}-арная операция на G{\displaystyle G} — это отображение прямого произведения n{\displaystyle n} экземпляров множества в само множество Gn→G{\displaystyle G^{n}\to G}. По определению, нульарная операция — это просто выделенный элемент множества. Чаще всего рассматриваются унарные и бинарные операции, поскольку с ними легче работать, но в связи с нуждами топологии, алгебры, комбинаторики постепенно накапливается техника работы с операциями большей арности, здесь в качестве примера можно привести теорию операд (клонов полилинейных операций) и алгебр над ними (мультиоператорных алгебр).
Понятие возникло из наблюдений за общностью конструкций, характерных для различных общеалгебраических структур, таких как группы, кольца, решётки; в частности, таковы конструкции подсистемы (обобщающей понятия подгруппы, подкольца, подрешётки соответственно), гомоморфизма, изоморфизма, факторсистемы (обобщающей соответственно конструкции фактогруппы, факторкольца, факторешётки). Эта общность изучается в самостоятельном разделе общей алгебры — универсальной алгебре, при этом получен ряд содержательных результатов, характерных для любых алгебраических систем, например, такова теорема о гомоморфзиме, которая в случае алгебраической системы без заданных отношений — алгебры, уточняется до теорем об изоморфизме, известных ранее из теории групп и теории колец.
В математике с той или иной степенью строгости также используется понятие «алгебраической структуры», в частности, у Бурбаки оно формализовано как множество, наделённое операциями, при этом множество, наделённое отношениями (наличие которых возможно для алгебраической системы) уже рассматривается как математическая структура другого рода — структура порядка. Однако и не все алгебраические структуры описываются алгебраическими системами без дополнительных конструкций, в качестве примера таковых можно упомянуть коалгебры, биалгебры, алгебры Хопфа и комодули над ними; кроме того, даже для определения таких классических структур, как модуля над кольцом или алгебры над полем, в универсальной алгебре используются такие искусственные конструкции, как определение для каждого элемента кольца (поля) унарной операции умножения на этот элемент.
Основные классы алгебраических систем[править | править код]
- Множество можно считать вырожденной алгебраической системой с пустым набором операций и отношений[1].
Группоиды, полугруппы, группы[править | править код]
- Группоид — множество с одной бинарной операцией ⋅:G×G→G{\displaystyle \cdot :G\times G\to G}, обычно называемой умножением.
- Правая квазигруппа — группоид, в котором возможно правое деление, то есть уравнение x⋅a=b{\displaystyle x\cdot a=b} имеет единственное решение для любых a{\displaystyle a} и b{\displaystyle b}.
- Квазигруппа — одновременно правая и левая квазигруппа.
- Лупа — квазигруппа с нейтральным элементом e∈G{\displaystyle e\in G}, таким, что a⋅e=e⋅a=a{\displaystyle a\cdot e=e\cdot a=a}.
- Полугруппа — группоид, в котором умножение ассоциативно: a⋅(b⋅c)=(a⋅b)⋅c{\displaystyle a\cdot (b\cdot c)=(a\cdot b)\cdot c}.
- Моноид — полугруппа с нейтральным элементом.
- Группа — моноид, в котором для каждого элемента a группы можно определить обратный элемент a−1, такой, что a⋅a−1=a−1⋅a=e{\displaystyle a\cdot a^{-1}=a^{-1}\cdot a=e}.
- Абелева группа — группа, в которой операция коммутативна, то есть, a⋅b=b⋅a{\displaystyle a\cdot b=b\cdot a}. Операцию в абелевой группе часто называют сложением (‘+’).
Кольца[править | править код]
- Кольцо — структура с двумя бинарными операциями (абелева группа по сложению с заданной второй ассоциативной бинарной операцией — умножением), в которой выполняется закон дистрибутивности: a⋅(b+c)=a⋅b+a⋅c,(a+b)⋅c=a⋅c+b⋅c{\displaystyle a\cdot (b+c)=a\cdot b+a\cdot c,\quad (a+b)\cdot c=a\cdot c+b\cdot c}.
- Коммутативное кольцо — кольцо с коммутативным умножением.
- Целостное кольцо — кольцо, в котором произведение двух ненулевых элементов не равно нулю.
- Тело — кольцо, в котором ненулевые элементы образуют группу по умножению.
- Поле — коммутативное кольцо, являющееся телом.
- Полукольцо — похоже на кольцо, но без обратимости сложения.
- Почтикольцо — также обобщение кольца, отличающееся от обычного кольца отсутствием требования коммутативности сложения и отсутствием требования дистрибутивности умножения по сложению (левой или правой)
Алгебры[править | править код]
- Алгебра — линейное пространство с билинейной дистрибутивной операцией умножения, иначе говоря, кольцо с согласованной структурой линейного пространства
- Ассоциативная алгебра — алгебра с ассоциативным умножением
- Алгебра термов
- Коммутативная алгебра
- Градуированная алгебра
- Алгебра Ли — алгебра с антикоммутативным умножением (обычно обозначаемым [a,b]{\displaystyle [a,b]}), удовлетворяющим тождеству Якоби [a,[b,c]]+[b,[c,a]]+[c,[a,b]]=0{\displaystyle [a,[b,c]]+[b,[c,a]]+[c,[a,b]]=0}
- Алгебра Лейбница — алгебра с умножением (обычно обозначаемым [a,b]{\displaystyle [a,b]}), удовлетворяющим тождеству Якоби [a,[b,c]]+[b,[c,a]]+[c,[a,b]]=0{\displaystyle [a,[b,c]]+[b,[c,a]]+[c,[a,b]]=0}
- Алгебра Йордана — коммутативная алгебра с тождеством слабой ассоциативности: x2(yx)=(x2y)x{\displaystyle x^{2}(yx)=(x^{2}y)x}
- Алгебра некоммутативная йорданова — некоммутативная алгебра с тождеством слабой ассоциативности: x2(yx)=(x2y)x{\displaystyle x^{2}(yx)=(x^{2}y)x} и тождеством эластичности: x(yx)=(xy)x{\displaystyle x(yx)=(xy)x}
- Альтернативная алгебра — алгебра с тождествами x2y=x(xy),yx2=(yx)x{\displaystyle x^{2}y=x(xy),\quad yx^{2}=(yx)x}
- Алгебра Мальцева — антикоммутативная алгебра с тождеством:
- (xy)(xz)+(y(xz))x+((xz)x)y=((xy)z)x+((yz)x)x+((zx)y)x{\displaystyle (xy)(xz)+(y(xz))x+((xz)x)y=((xy)z)x+((yz)x)x+((zx)y)x}
- Коммутантно-ассоциативная алгебра
- Алгебра над операдой — один из наиболее общих видов алгебраических систем. Здесь сама операда играет роль сигнатуры алгебры.
Решётки[править | править код]
- ↑ Курош А. Г. Общая алгебра. — М.: Наука, 1974. С.15
 2
2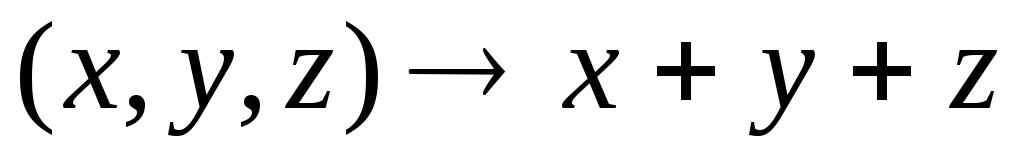 .
. .
.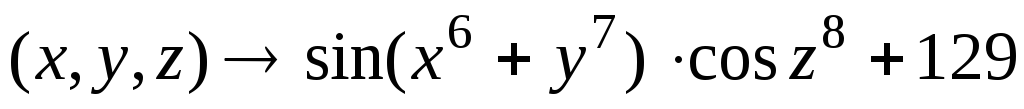 .
.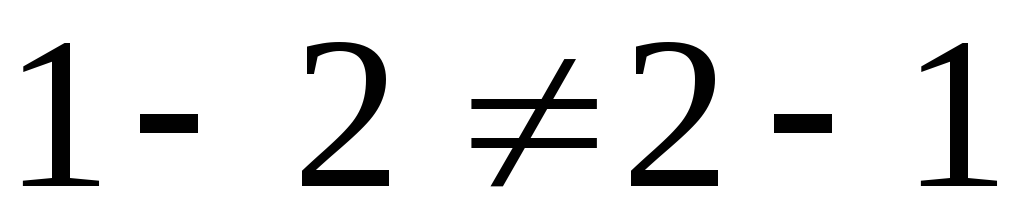 ,
, .
. ),
где
),
где
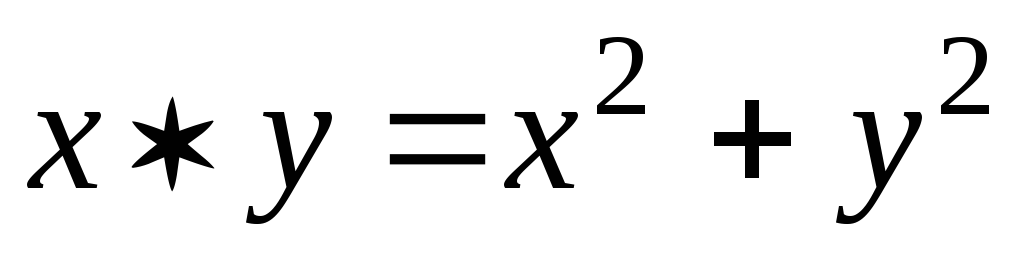 ,
такая операция
,
такая операция коммутативна, но не ассоциативна.
Действительно:
коммутативна, но не ассоциативна.
Действительно:
 .
.