примеры, значение, числовое равенство, правила

 

Запись, которая состоит из чисел, знаков и скобок, а также имеет смысл, называется числовым выражением.

Например, следующие записи:

• (100-32)/17,
• 2*4+7,
• 13,
• 4*0.7 -3/5,
• 1/3 +5/7

будут являться числовыми выражениями. Следует понимать, что одно число тоже будет являться числовым выражением. В нашем примере, это число 13.

А, например,  следующие записи

не будут являться числовыми выражениями, так как они лишены смысла и являются просто набором чисел и знаков.

Значение числового выражения

Так как в качестве знаков в числовых выражениях входят знаки арифметических действий, то мы можем посчитать значение числового выражения. Для этого необходимо выполнить указанные действия.

Например, 

(100-32)/17 = 4, то есть для выражения (100-32)/17 значением этого числового выражения будет являться число 4.

 2*4+7=15, число 15 будет являться значением числового выражения 2*4+7.

Часто для краткости записи не пишут полностью значение числового выражения, а пишут просто «значение выражения», опуская при этом слово «числового».

Числовое равенство

Если два числовых выражения записаны через знак равно, то эти выражения образуют числовое равенство. Например,  выражение 2*4+7=15 является числовым равенством.

Как уже отмечалось выше, в числовых выражениях могут использоваться скобки. Как уже известно скобки влияют на порядок действий.

Вообще, все действия разделены на несколько ступеней.

• Действия первой ступени: сложение и вычитание.
• Действия второй ступени: умножение и деление.
• Действия третей ступени – возведение в квадрат и возведение в куб.

Правила при вычислении значений числовых выражений

При вычислении значений числовых выражений следуют руководствоваться следующими правилами.

• 1. Если выражение не имеет скобок, то надо выполнять действия начиная с высших ступеней: третья ступень, вторая ступень и первая ступень. Если имеется несколько действий одной ступени, то их выполняют в порядке в котором они записаны, то есть слева на право.
• 2. Если в выражении присутствуют скобки, то сначала выполняются действия в скобках, а лишь затем все стальные действия в обычном порядке. При выполнении действий в скобках, если их там несколько, следует пользоваться порядком описанным в пункте 1.
• 3. Если выражение представляет собой дробь, то сначала вычисляются значении в числителе и знаменателе, а потом числитель делится на знаменатель.
• 4. Если в выражении присутствуют вложенные скобки, то выполнять действия следует с внутренних скобок.

Нужна помощь в учебе?

Предыдущая тема: Наименьшее общее кратное (НОК): определение, как найти, общая схема
Следующая тема:&nbsp&nbsp&nbspВыражения с переменными: разбираем пример с фокусом

Все неприличные комментарии будут удаляться.

Числовые выражения

Вопросы занятия:

·  повторить основные действия, которые можно выполнять над рациональными числами;

·  ввести понятия «числовое выражение» и «значение числового выражения»;

·  привести примеры нахождения значений числовых выражений;

·  решить задачу.

Материал урока

Ранее вы уже изучали различные действия над рациональными числами. Это действие сложение, вычитание, умножение и деление.

Действия сложение, вычитание и умножение можно выполнять для любых чисел, а вот деление – нет.

Определение.

Арифметикой (что с греческого означает «число») называется раздел математики, изучающий числа, их отношения и свойства.

Давайте решим следующую задачу.

На сколько шагов больше сделает ребёнок, чем взрослый, на расстоянии 240 м, если длина шага у ребёнка равна 0,3 м, а у взрослого – 0,8 м?

Решение.

Чтобы найти количество шагов, которые сделал ребёнок, нужно 240 м разделить на длину шага ребёнка – 0,3 м, а чтобы найти количество шагов, которые сделал взрослый, нужно 240 м разделить на длину шага взрослого – нуль 0,8 м.

240 : 0,3 = 800

240 : 0,8 = 300

А тогда, чтобы ответить на вопрос задачи, мы от количества шагов ребёнка отнимем количество шагов взрослого, то есть:

800 – 300 = 500 шагов.

То есть ребёнок сделал на 500 шагов больше взрослого.

Решая задачу, мы получили числовое выражение, выполнив действия которого, нашли значение этого выражения.

Таким образом, сформулируем следующие определения.

Числовым выражением называется запись, составленная из чисел, знаков арифметических действий и скобок, указывающих на порядок выполнения действий.

Значением числового выражения называется число, которое получается при выполнении всех действий числового выражения.

Пример.

Найти значение выражения.

Найдём значение следующего выражения.

Пример.

Давайте найдём значение следующего числового выражения.

Пример.

Пример.

Числовые и буквенные выражения. Значение выражения

Числовые выражения

Числовое выражение – это запись, составленная со смыслом, в которой числа обозначены цифрами (в неё также могут входить знаки арифметических действий и скобки). Числовые выражения так же называются

арифметическими выражениями.

7 – числовое выражение

2 + 2 — 1 – числовое выражение

7 — 2 · + : 1 – бессмысленный набор символов

Вычислить значение выражения – это значит выполнить все арифметические действия, указанные в выражении. Действия выполняются в определённом порядке, в зависимости от самих действий и присутствия в выражении скобок. Про порядок выполнения действий можно прочитать тут:

Значение числового выражения – это число, получившееся после выполнения всех вычислений.

Пример 1. Найдите значение числового выражения 4 + 3

Решение:

4 + 3 = 7

Ответ: 7.

Пример 2. Найдите значение числового выражения 4 · 3

Решение:

4 · 3 = 12

Ответ: 12.

Буквенные выражения

Буквенное выражение – это числовое выражение, в котором числа могут быть обозначены и цифрами и буквами. Буквенные выражения так же называются алгебраическими выражениями.

При обозначении чисел буквами обычно используют строчные (маленькие) буквы латинского алфавита:

7 · a – буквенное выражение

a – (b + c) – буквенное выражение

Чаще всего в буквенных выражениях разные числа обозначены разными буквами, но например в выражении:

a = b

подразумевается что a и b являются одним и тем же числом.

Значение буквенного выражения – это число, получившееся после выполнения всех вычислений. Действия в буквенных выражениях выполняются после подстановки вместо букв их численных значений.

Пример. Найдите значение буквенного выражения 2 · a + 3 при a = 7.

Решение:

2 · 7 + 3 = 14 + 3 = 17

Ответ: 17.

В буквенных выражениях знак умножения между числом и буквой, а так же между буквами, не пишут, поэтому считается, что:

7 · a = 7a    и    x · y = xy

Если в записи выражения одна и та же буква, например a, употребляется несколько раз, то под значением этой буквы во всех случаях мы должны иметь ввиду одно и тоже число.

Пример. Найдите значение буквенного выражения 5x — 2x при x = 4.

Решение:

5 · 4 — 2 · 4 = 20 — 8 = 12

Ответ: 12.

В арифметике буквенные обозначения употребляют, когда необходимо выразить, что некоторое свойство (или правило) принадлежит не каким-нибудь отдельным числам, а является общим для любых чисел. Например:

a + b = b + a

Данное равенство показывает нам, что, как бы мы не переставляли слагаемые, сумма от этого не изменится. Подставив вместо букв любые числа, мы можем в этом убедиться сами:

1 + 2 = 2 + 1

Числовые и буквенные выражения. Формула

              Числовые и буквенные выражения.

Формула

Сложение, вычитание, умножение, деление — арифметические действия (или арифметические операции). Этим арифметическим действиям соответствуют знаки арифметических действий:

+ (читаем «плюс«)          —   знак операции сложения,

— (читаем «минус«)         —  знак операции вычитания,

∙ (читаем «умножить«)    —  знак операции умножения,

: (читаем «разделить«)   —  знак операции деления.

Запись, состоящая из чисел, связанных между собой знаками арифметических действий, называется

числовым выражением. В числовом выражении могут присутствовать также скобки Например, запись 1290 : 2 – (3 + 20 ∙ 15) является числовым выражением.

Результат выполнения действий над числами в числовом выражении называется значением числового выражения. Выполнение этих действий называется вычислением значения числового выражения. Перед записью значения числового выражения ставят знак равенства «=». В таблице 1 приведены примеры числовых выражений и их значений.

Запись, состоящая из чисел и малых букв латинского алфавита, связанных между собой знаками арифметических действий называется буквенным выражением. В этой записи могут присутствовать скобки.  Например, запись a + b –  3 ∙ c является буквенным выражением. Вместо букв  в буквенное выражение можно подставлять различные числа. При этом значение букв может изменяться, поэтому буквы в буквенном выражении называют еще

переменными.

Подставив в буквенное выражение числа  вместо букв   и  вычислив значение получившегося числового выражения, находят значение буквенного выражения при данных значениях букв (при данных значениях переменных). В таблице 2 приведены примеры буквенных выражений.

Буквенное выражение может не иметь значения,  если при подстановке   значений букв получается  числовое выражение, значение которого для натуральных чисел не может быть найдено.  Такое числовое выражение называется некорректным для натуральных чисел. Говорят также, что значение такого выражения «не определено» для натуральных чисел, а само выражение «не имеет смысла». Например, буквенное выражение a –  b  не имеет значения  при a = 10 и b = 17. Действительно, для натуральных чисел, уменьшаемое не может быть меньше вычитаемого. Например, имея  всего 10 яблок (a = 10),  нельзя отдать из них 17  (b = 17)! 

В таблице 2 (колонка 2) приведён пример буквенного выражения. По аналогии заполните таблицу полностью.

Для натуральных чисел выражение 10 -17 некорректно (не имеет смысла), т.е. разность 10 -17 не может быть выражена натуральным числом. Другой пример: на ноль делить нельзя, поэтому для  любого натурального  числа b, частное b : 0 не определено.

 Математические законы, свойства, некоторые правила и соотношения часто записывают в буквенном виде (т.е. в виде буквенного выражения). В этих случаях буквенное выражение называют формулой. Например, если стороны семиугольника равны  a, b, c, d, e, f, g,  то формула (буквенное выражение) для вычисления его периметра p имеет вид:                           

                                                       
         

p =

a + b + c + d + e + f + g

При  a = 1, b = 2, c = 4, d = 5, e = 5, f = 7, g = 9, периметр семиугольника p = a + b + c + d + e + f + g = 1 + 2 + 4 + 5 +5 + 7 + 9 = 33.

При  a = 12, b = 5, c = 20, d = 35, e = 4, f = 40, g = 18, периметр другого  семиугольника  p = a + b + c + d + e + f + g = 12 + 5 + 20 + 35 + 4 + 40 + 18 = 134.

 

 

Блок 1. Словарь

Составьте словарь новых терминов и определений из параграфа.  Для этого в пустые клетки впишите  слова из списка терминов, приведенного ниже. В таблице (в конце блока) укажите номера терминов в соответствии с номерами рамок. Рекомендуется перед заполнением  клеток словаря еще раз внимательно просмотреть параграф.

1. Операции: сложение, вычитание, умножение, деление.

     

      2.Знаки «+» (плюс), «-» (минус), «∙» (умножить,  «:» (разделить).

    

      3.Запись, состоящая из чисел, которые связанны между собой знаками арифметических действий и в которой могут присутствовать также скобки.   

   

       4.Результат выполнения действий над числами в числовом выражении.

    

       5. Знак, стоящий перед  значением числового выражения.

    

      6. Запись, состоящая из чисел и малых букв латинского алфавита, связанных между собой знаками арифметических действий (могут присутствовать также скобки).

    

      7. Общее название букв в буквенном выражении.

    

      8. Значение числового выражения, которое получается при подстановке переменных.в буквенное выражение.

   

     9.Числовое выражение, значение которого для натуральных чисел не может быть найдено.

    

     10. Числовое выражение, значение которого для натуральных чисел может быть найдено.

 

     11. Математические законы, свойства, некоторые правила и соотношения, записанные в буквенном виде.

  

     12. Алфавит, малые буквы которого используются для записи буквенных выражений.

   

 

 

 

Блок 2. Установите соответствие

Установите соответствие между заданием  в левой колонке и решением в правой. Ответ запишите в виде:   1а,   2г,    3б…

 

Блок 3. Фасетный тест. Числовые и буквенные выражения

 Фасетные тесты заменяют сборники задач по математике, но выгодно отличаются от них тем, что  их можно решать на компьютере, проверять решения и  сразу узнавать результат работы. В этом тесте содержится 70 задач. Но  решать задачи можно по выбору, для этого есть оценочная таблица, где указаны простые задачи и посложнее. Ниже приведён тест.

16. Дан треугольник со сторонами c, d, m, выраженными в см
17. Дан четырехугольник со сторонами b, c, d, m, выраженными в м
18. Скорость автомобиля в км/ч равна b, время движения в часах равно d
19. Расстояние, которое преодолел турист за m часов, составляет с км
20. Расстояние, которое преодолел турист, двигаясь со скоростью m км/ч, составляет b км
21. Сумма двух чисел больше второго числа на 15
22. Разность меньше уменьшаемого на 7
23. Пассажирский лайнер имеет две палубы с одинаковым количеством пассажирских мест. В каждом  из рядов  палубы m мест, рядов на палубе  на n больше, чем мест в ряду
24. Пете m лет Маше n лет, а Кате на k лет меньше, чем Пете и Маше вместе
25. m = 8,  n = 10,   k = 5
26. m = 6, n = 8,     k = 15
27.  t = 121,  x = 1458

    

 

ТО:

30. Значение данного выражения
31. Буквенное выражение для периметра имеет вид
32. Периметр, выраженный в сантиметрах
33. Формула пути s, пройденного автомобилем
34. Формула скорости v, движения туриста
35. Формула времени t, движения туриста
36. Путь, пройденный автомобилем в километрах
37. Скорость туриста в километрах в час
38. Время движения туриста в часах
39. Первое число равно…
40. Вычитаемое равно….
41. Выражение для наибольшего количества пассажиров, которое может перевезти лайнер за k рейсов
42. Наибольшее количество пассажиров, которое может перевезти лайнер за k рейсов
43. Буквенное выражение для возраста Кати
44. Возраст Кати
45. Координата точки В, если координата точки С равна t
46. Координата точки D, если координата точки С равна t
47. Координата точки А, если координата точки С равна t
48. Длина отрезка BD на числовом луче
49. Длина отрезка CА на числовом луче
50. Длина отрезка DА на числовом луче

Ответы (равно, имеет вид, не определено):

а)1;  б) s=b ∙d;  в) 9;   г) 40;   д) b + c + d + m;  е) 7;   ж) выражение не имеет смысла (некорректно) для натуральных чисел;   з) 2 ∙ m (m + n) ∙ k;   и) (m + n) – k;   к) 6;   л) 15;       м) 3760;   н) t –  3;  о) фигура не может быть  треугольником;   п) 22;    р) t – 3 ∙ 7;   с) 0;   т) 32;   у) 59600;   ф) 6019;   х) 2880;  ц) 10378;  ч)1440;   ш) на ноль делить нельзя;  щ) 13;   ы) 1800;  э) 496;  ю) 2;   я) 12;   аа) 14;   бб) 5;   вв) 35;    дд)  79200;   ее) 1900;   жж) 118;     зз) 18;   ии) 12800;  кк) 98;   лл) 1458;   мм) v = c : m;   нн) 100;   оо) 19900;   пп) t = b : m; рр) 2520;   сс) c + d + m;   тт) x;   уу) 1579;   фф) t + 2;   хх) 10206;   цц) 135;   чч) t + 2 ∙ 7; шш) 7 ∙ x;   щщ) x – 2;   ыы) 7 ∙ x – 2 ∙ 7;   ээ)  t + x ∙ 7;   юю) 10192;   яя) t + x;   ааа) 123;       ббб) 1456;   ввв) 10327.

 

ПОКАЗАТЕЛИ ТЕСТА. Число задач 70,  время выполнения 2 – 3  часа,  сумма баллов: 1 ∙ 22 + 2 ∙ 24 + 3 ∙ 24 = 142. Для фасетного теста можно использовать  следующую шкалу оценок.

Блок 4. Давайте поиграем

 Блок 5. Обучающая игра «Уроки кота Леопольда»

 

 

Для учителя приводим ответы к блокам параграфа 6

Ответы к игре «Уроки Леопольда»

Западня 1 : 1/2, 1/3, 2/3, 7/8.  Западня 2. 12, 2, 13 5. Западня 3.  6

Западня 4. 15.              Западня 5. 396

 

 Блок 1.  Словарь

 

Блок 2. Установите соответствие.

Вариант 1: 1и, 2з, 3е, 4б, 5м, 6л, 7а, 8ж, 9в, 10д, 11г, 12к, 13т, 14н, 15ф, 16о, 17у, 18с, 19р, 20п

Вариант 2: 1д, 2е, 3к, 4а, 5г, 6з, 7и, 8б, 9ж, 10в

 

Блок 3. Фасетный тест. Числовые и буквенные выражения (ответы под заданиями)

Ответы к игре «Сокровища»

Деревянный – 10250. Оловянный – 21640. Медный – 50400. Серебряный – 191000. Золотой – 289800.

Урок 14. числовые выражения. порядок действий в числовых выражениях. скобки. сравнение числовых выражений — Математика — 2 класс

Математика, 2 класс

Урок № 14. Числовые выражения. Порядок действий в числовых выражениях. Скобки. Сравнение числовых выражений

Перечень вопросов, рассматриваемых в теме:

— Что такое числовые выражения?

— Как правильно читать и записывать числовые выражения?

— Как выполнять порядок действий, если есть скобки?

— Как сравнить два выражения?

Глоссарий по теме:

Числовое выражение – это запись, состоящая из чисел и знаков действий между ними.

Значение выражения – это результат выполненных действий.

Сравнить числовые выражения – найти значение каждого из выражений и их сравнить.

Скобки — парные знаки ( )

Порядок выполнения действий – это последовательность проводимых вычислений в данном выражении.

Основная и дополнительная литература по теме:

1. Моро М. И., Бантова М. А., Бельтюкова Г. В.и др. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1. –8-е изд. – М.: Просвещение, 2017. – с.38-40

2. Волкова А. Д. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций. М.: Просвещение, 2017, с. 22-27

3. Глаголева Ю. И., Волкова А. Д. Математика. КИМы. 2 кл: учебное пособие для общеобразовательных организаций. М.: Просвещение, Учлит, 2017, с.16

Теоретический материал для самостоятельного изучения

Маша и Миша решали пример: из числа 12 вычесть сумму чисел 7 и 3. Они записали его по-разному и получили разные ответы. Маша сначала из 12 вычла 7 и получила 5, потом прибавила 3, получила 8.

Маша: 12 – 7 + 3 = 8

Миша обвёл овалом сумму чисел 7 и 3 и сначала посчитал сумму, получил 10. Затем от 12 отнял 10, получил 2.

Миша: 12 — 7 + 3 = 2

Кто из них вычислил верно? Решил верно, Миша.

В математике для обозначения действий, которые должны выполняться первыми используют специальный знак ( ) — скобки.

Запишем пример, который решали дети правильно:

12 — (7 + 3) =2

Вычислим. 7 + 3 равно 10, из 12 вычесть 10, получится 2. Запомните: действия, записанные в скобках, выполняются первыми.

Посмотрим на запись.

9 – (6 + 2) = 1

Запись, в которой разные числа (однозначные и двузначные) соединены знаками «+» и «–» в различных сочетаниях, называется числовым выражением и читается так: «из числа 9 вычесть сумму чисел 6 и 2».

Найти значение выражения – это значит, нужно выполнить все указанные действия в выражении. Значение данного выражения 1.

Теперь мы будем называть примеры числовыми выражениями, а ответы значениями числовых выражений.

9 – (6 + 2) = 1

числовое значение

выражение числового

выражения

Прочитаем выражение: 10 + (8 — 3) =

К числу 10 прибавить разность чисел 8 и 3.

Как найти значение выражения? Нужно выполнить необходимые действия. Но с какого действия нужно начинать? С того, которое записано в скобках. Находим разность чисел 8 и 3, будет 5, к 10 прибавить 5, получится 15.

10+(8-3)=15

Давайте сравним значения двух выражений:

11 — 4 и 16 — 7.

Сначала найдем значение каждого из выражений и их сравним.

11 — 4 = 7

16 — 7 = 9

7 < 9, значит, 11-4 < 16-7

Выводы: Итак, оказывается, порядок должен быть и в действиях, он так и называется «Порядок выполнения действий». Если в числовом выражении стоят скобки, это означает, что действие, которое в них записано, должно быть выполнено первым, а все остальные действия выполняют по порядку. 

Тренировочные задания.

1.Выберите правильный ответ. Как правильно прочитать данное числовое выражение: 13 – (7 + 3)?

Вариант ответов:

1. К 13 прибавить сумму чисел 7 и 3

2. Из 13 вычесть 7 плюс 3

3. Из 13 вычесть сумму чисел 7 и 3

4. Разность чисел 13 и 7 плюс 3

Правильный ответ:

3. Из 13 вычесть сумму чисел 7 и 3

2. Соотнесите числовые выражения с их значениями

3+ (16-6) 15

10-4+9 16

13-(6+4) 13

9+ (13-6) 3

Правильный ответ:

3+ (16 – 6) 13

10 – 4 + 9 15

13 – (6 + 4) 3

9 + (13 – 6) 16

Числовые и буквенные выражения. Формулы

Как найти периметр прямоугольника, стороны которого равны 3 см и 5 см (рис. 67)?

Отвечая на этот вопрос, вы можете сделать такую запись: 2 * 3 + 2 * 5.

Такая запись представляет собой числовое выражение.

Приведем еще несколько примеров числовых выражений: 12 : 4 − 1, (5 + 17) + 11, (19 − 7) * 3. Эти выражения составлены из чисел, знаков арифметических действия и скобок.

Заметим, что не всякая запись, составленная из чисел, знаков арифметических действия и скобок является числовым выражением. Например, запись +) +3 − (2 представляет собой бессмысленный набор символов.

Завершив решение задачи о периметре прямоугольника, получим ответ 16 см. В таких случаях говорят, что число 16 является значением выражения  2 * 3 + 2 * 5.

А чему равен периметр прямоугольника, стороны которого равны 3 см и a см? Ответом будет выражение 2 * 3 + 2 * a.

Запись 2 * 3 + 2 * a представляет собой буквенное выражение.

Приведем еще несколько примеров буквенных выражений: (a + b) + 11, 5 + 3 * x, n : 2 − k * 5. Эти выражения составлены из чисел, букв, знаков арифметических действий и скобок.

Как правило, в буквенных выражениях знак умножения пишут только между числами. В остальных случаях его опускают. Например, вместо 5 * y, m * n, 2 * (a + b) соответственно пишут 5y, mn, 2(a + b).

Пусть стороны прямоугольника равны a см и b см. В этом случае буквенное выражение для нахождения его периметра выглядит так: 2a + 2b.

Подставим в это выражение вместо букв a и b соответственно числа 3 и 5. Получим числовое выражение 2 * 3 + 2 * 5, которое мы уже записывали для нахождения периметра прямоугольника. Если же вместо a и b подставить, например, числа 4 и 9, то получим числовое выражение 2 * 4 + 2 * 9. Вообще, из одного буквенного выражения можно получить бесконечно много числовых выражений.

Обозначим периметр прямоугольника буквой P. Тогда равенство

P = 2a + 2b

можно использовать для нахождения периметра любого прямоугольника. Такие равенства называют формулами.

Например, если сторона квадрата равна a, то его периметр вычисляется по формуле:

P = 4a

Равенство

s = vt

где s − пройденный путь, v − скорость движения, а t − время, за которое пройден путь s, называют формулой пути.

Пример 1. Собранные в саду яблоки фермер разложил в пять ящиков по a кг и в b ящиков по 20 кг. Скоько килограммов яблок собрал фермер? Вычислите значение полученного выражения при a = 18, b = 9.

Решение.

В пяти ящиках содержится 5a кг яблок, а в b ящиках − 20b кг. Всего фермер собрал (5a + 20b) кг яблок.

Если a = 18, b = 9, то получаем: 5 * 18 + 20 * 9 = 90 + 180 = 270 (кг).

Ответ: (5a + 20b) кг, 270 кг.

Пример 2. Найдите, ползуясь формулой пути, скорость, с которой поезд прошел 324 км за 6 ч.

Решение.

Поскольку s = vt, то v = s : t. Тогда можно записать v = 324 : 6 = 54 (км/ч).

Ответ: 54 км/ч.

Пример 3. Буратино купил m булочек по 2 сольдо и торт за 5 сольдо. Составим формулу для вычисления стоимости покупки и найдите эту стоимость, если:

1) m = 4;

2) m = 12.

Решение.

За m булочек Буратино заплатил 2m сольдо.

Обозначив стоимость покупки буквой k, получаем формулу k = 2m + 5.

1) Если m = 4, то k = 2 * 4 + 5 = 13;

2) если m = 12, то k = 2 * 12 + 5 = 29.

Ответ: k = 2m + 5, 13 сольдо, 29 сольдо.

Числовые выражения. Выражения с переменными. Примеры упрощения выражений

Числовое выражение – это совокупность одного или нескольких чисел и функций, соединенных знаками арифметических операций и скобками.

Примеры числовых выражений: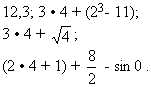

Значением числового выражения является число.

Операции в числовом выражении выполняются в следующей последовательности:

1. Действия в скобках.

2. Вычисление функций.

3. Возведение в степень

4. Умножение и деление.

5. Сложение и вычитание.

6. Однотипные операции выполняются слева на право.

Так значением первого выражения будет само число 12,3

Для того чтобы вычислить значение второго выражения, действия будем выполнять в следующей последовательности:

1. Выполним действия в скобках  в следующей последовательности — сначала 2 возведем в третью степень, затем от полученного числа отнимем 11:

3 • 4 + (2^3 — 11) = 3 • 4 + (8 — 11) = 3 • 4 + (-3)

2. Умножим 3 на 4:

3 • 4 + (-3) = 12 + (-3)

3. Выполним последовательно операции слева направо:

12 + (-3) = 9.

Выражение с переменными – это совокупность одного или нескольких чисел, переменных и функций, соединенных знаками арифметических операций и скобками. Значения выражений с переменными зависят от значений, входящих в него переменных. Последовательность выполнения операций здесь та же, что и для числовых выражений. Выражения с переменными иногда бывает полезно упрощать, выполняя различные действия – вынесение за скобки, раскрытие скобок, группировки, сокращение дробей, приведение подобных и т.д. Так же для упрощения выражений часто используют различные формулы, например, формулы сокращенного умножения, свойства различных функций и т. д.

Пример: Упростить выражение 3 • (x – 4 • y + 11) + 12 • y – 30

1. Раскроем скобки:

3 • (x – 4 • y + 11) + 12 • y – 30 = 3 • x – 12 • y + 33 + 12 • y – 30;

2. Приведем подобные:

3 • x — 12 • y + 33 + 12 • y – 30 = 3 • x + 3;

3. Теперь можно оставить выражение в таком виде, а можно вынести 3 за скобки:

3 • x + 3 = 3 • (x + 1).