примеры решений. Как решать квадратные уравнения через дискриминант

Квадратные уравнения часто появляются во время решения различных задач физики и математики. В данной статье мы рассмотрим, как решать эти равенства универсальным способом «через дискриминант». Примеры использования полученных знаний также даются в статье.

О каких уравнениях пойдет речь?

На рисунке ниже изображена формула, в которой x — неизвестная переменная, а латинские символы a, b, c представляют собой некоторые известные числа.

Каждый из этих символов называется коэффициентом. Как можно заметить, число «a» стоит перед переменной x, возведенной в квадрат. Это максимальная степень представленного выражения, поэтому оно называется квадратным уравнением. Часто используют другое его название: уравнение второго порядка. Само значение a — это квадратный коэффициент (стоящий при переменной в квадрате), b — это линейный коэффициент (он находится рядом с переменной, возведенной в первую степень), наконец, число c — свободный член.

Отметим, что вид уравнения, который изображен на рисунке выше, является общим классическим квадратным выражением. Помимо него существуют другие уравнения второго порядка, в которых коэффициенты b, c могут быть нулевыми.

Когда ставят задачу решить рассматриваемое равенство, то это означает, что такие значения переменной x нужно найти, которые бы ему удовлетворяли. Здесь первым делом нужно запомнить следующую вещь: поскольку максимальная степень икса — это 2, то данный тип выражений не может иметь больше, чем 2 решения. Это означает, что если при решении уравнения были найдены 2 значения x, которые ему удовлетворяют, то можно быть уверенным, что не существует никакого 3-го числа, подставляя которое вместо x, равенство также бы являлось истиной. Решения уравнения в математике называют его корнями.

Способы решения уравнений второго порядка

Решения уравнений этого типа требует знания некоторой теории о них. В школьном курсе алгебры рассматривают 4 различных метода решения. Перечислим их:

• с помощью факторизации;
• используя формулу для полного квадрата;
• применяя график соответствующей квадратичной функции;
• используя уравнение дискриминанта.

Плюс первого метода заключается в его простоте, однако, он не для всех уравнений может применяться. Второй способ является универсальным, однако несколько громоздким. Третий метод отличается своей наглядностью, но он не всегда удобен и применим. И, наконец, использование уравнения дискриминанта — это универсальный и достаточно простой способ нахождения корней абсолютно любого уравнения второго порядка. Поэтому в статье рассмотрим только его.

Формула для получения корней уравнения

Обратимся к общему виду квадратного уравнения. Запишем его: a*x²+ b*x + c =0. Перед тем как пользоваться способом его решения «через дискриминант», следует приводить равенство всегда к записанному виду. То есть оно должно состоять из трех слагаемых (или меньше, если b или c равен 0).

Например, если имеется выражение: x²-9*x+8 = -5*x+7*x², то сначала следует перенести все его члены в одну сторону равенства и сложить слагаемые, содержащие переменную x в одинаковых степенях.

В данном случае эта операция приведет к следующему выражению: -6*x²-4*x+8=0, которое эквивалентно уравнению 6*x²+4*x-8=0 (здесь левую и правую части равенства мы умножили на -1).

Как только усвоен описанный выше шаг, далее, следует научиться различать коэффициенты. Здесь все просто: при x² всегда стоит a, при x1 находится b, свободный член c представляет собой не связанное с x число.

В примере выше a = 6, b=4, c=-8. Заметим, что все члены рассматриваемого равенства всегда суммируются между собой, поэтому если появляется знак «-«, то это означает, что отрицательным является соответствующий коэффициент, как число c в данном случае.

Разобрав этот момент, перейдем теперь к самой формуле, которая дает возможность получения корней квадратного уравнения. Она имеет вид, который представлен на фото ниже.

Как видно из этого выражения, оно позволяет получать два корня (следует обратить внимание на знак «±»). Для этого в него достаточно подставить коэффициенты b, c, и a.

Понятие о дискриминанте

В предыдущем пункте была приведена формула, которая позволяет быстро решить любое уравнение второго порядка. В ней подкоренное выражение называют дискриминантом, то есть D = b²-4*a*c.

Почему эту часть формулы выделяют, и она даже имеет собственное название? Дело в том, что дискриминант связывает в единое выражение все три коэффициента уравнения. Последний факт означает, что он полностью несет информацию о корнях, которую можно выразить следующим списком:

1. D>0: равенство имеет 2 различных решения, причем оба они представляют собой действительные числа.
2. D
3. D=0: у уравнения всего один корень, и он является действительным числом.

Далее в статье приведены примеры с дискриминантом квадратных уравнений и дано их решение.

Задача на определение дискриминанта

Приведем простой пример, как найти дискриминант. Пусть дано такое равенство: 2*x² — 4+5*x-9*x² = 3*x-5*x²+7.

Приведем его к стандартному виду, получаем: (2*x²-9*x²+5*x²) + (5*x-3*x) + (- 4-7) = 0, откуда приходим к равенству: -2*x²+2*x-11 = 0. Здесь a=-2, b=2, c=-11.

Теперь можно воспользоваться названной формулой для дискриминанта: D = 2² — 4*(-2)*(-11) = -84. Полученное число является ответом на поставленную задачу. Поскольку в примере дискриминант меньше нуля, то можно сказать, что данное квадратное уравнение не имеет действительных корней. Его решением будут только числа комплексного типа.

Пример неравенства через дискриминант

Решим задачи несколько иного типа: дано равенство -3*x²-6*x+c = 0. Необходимо найти такие значения c, для которых D>0.

В данном случае известно лишь 2 из 3 коэффициентов, поэтому рассчитать точное значение дискриминанта не получится, однако известно, что он является положительным. Последний факт используем при составлении неравенства: D= (-6)²-4*(-3)*c>0 => 36+12*c>0. Решение полученного неравенства приводит к результату: c>-3.

Проверим полученное число. Для этого вычислим D для 2 случаев: c=-2 и c=-4. Число -2 удовлетворяет полученному результату (-2>-3), соответствующий дискриминант будет иметь значение: D = 12>0. В свою очередь, число -4 не удовлетворяет неравенству (-4

Таким образом, любые числа c, которые больше -3, будут удовлетворять условию.

Пример решения уравнения

Приведем задачу, которая заключается не только в нахождении дискриминанта, но и в решении уравнения. Необходимо найти корни для равенства -2*x²+7-9*x = 0.

В этом примере дискриминант равен следующему значению: D = 81-4*(-2)*7= 137. Тогда корни уравнения определятся так: x = (9±√137)/(-4). Это точные значения корней, если вычислить приближенно корень, тогда получатся числа: x = -5,176 и x = 0,676.

Геометрическая задача

Решим задачу, которая потребует не только умения вычислять дискриминант, но и применения навыков абстрактного мышления и знания, как составлять квадратные уравнения.

У Боба было пуховое одеяло размером 5 x 4 метра. Мальчик захотел пришить к нему по всему периметру сплошную полосу из красивой ткани. Какой толщины будет эта полоса, если известно, что у Боба имеется 10 м² ткани.

Пусть полоса будет иметь толщину x м, тогда площадь ткани по длинной стороне одеяла составит (5+2*x)*x, а поскольку длинных сторон 2, то имеем: 2*x*(5+2*x). По короткой стороне площадь пришитой ткани составит 4*x, так как этих сторон 2, то получаем значение 8*x. Отметим, что к длинной стороне было добавлено значение 2*x, поскольку длина одеяла увеличилась на это число. Общая пришитая к одеялу площадь ткани равна 10 м². Поэтому получаем равенство: 2*x*(5+2*x) + 8*x = 10 => 4*x²+18*x-10 = 0.

Для этого примера дискриминант равен: D = 18²-4*4*(-10) = 484. Его корень равен 22. Воспользовавшись формулой, находим искомые корни: x = (-18±22)/(2*4) = (-5; 0,5). Очевидно, что из двух корней подходит по условию задачи только число 0,5.

Таким образом, полоса из ткани, которую пришьет Боб к своему одеялу, будет иметь ширину 50 см.

www.nastroy.net

Как решать квадратные уравнения? Дискриминант. — МегаЛекции

 

Поработаем с квадратными уравнениями. Это очень популярные уравнения! В самом общем виде квадратное уравнение выглядит так:

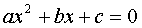
Например:

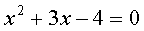
Здесь а =1; b = 3; c = -4

Или:

Здесь а =2; b = -0,5; c = 2,2

Или:

Здесь а =-3; b = 6; c = -18

Ну, вы поняли…

Как решать квадратные уравнения? Если перед вами квадратное уравнение именно в таком виде, дальше уже всё просто. Вспоминаем волшебное слово дискриминант. Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении. Итак, формула для нахождения корней квадратного уравнения выглядит так:

Выражение под знаком корня – и есть тот самый дискриминант. Как видим, для нахождения икса, мы используем только a, b и с. Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в это формулу и считаем. Подставляем со своими знаками! Например, для первого уравнения а =1; b = 3; c = -4. Вот и записываем:

Пример практически решён:

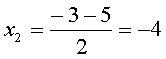
Вот и всё.

Какие случаи возможны при использовании этой формулы? Всего три случая.

1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.

2. Дискриминант равен нулю. Тогда у вас одно решение. Строго говоря, это не один корень, а два одинаковых. Но это играет роль в неравенствах, там мы поподробнее вопрос изучим.

3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.

Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…
Самые распространённые ошибки – путаница со знаками значений a, b и с. Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями,

так и делайте!

Предположим, надо вот такой примерчик решить:

Здесь a = -6; b = -5; c = -1

Допустим, вы знаете, что ответы у вас редко с первого раза получаются.

Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится. Вот и пишем подробно, со всеми скобочками и знаками:

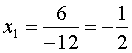
Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!

Итак, как решать квадратные уравнения через дискриминант мы вспомнили. Или научились, что тоже неплохо. Умеете правильно определять a, b и с. Умеете внимательно подставлять их в формулу корней и внимательно считать результат. Вы поняли, что ключевое слово здесь – внимательно?

Однако частенько квадратные уравнения выглядят слегка иначе. Например, вот так:

Или так:

Это

неполные квадратные уравнения. Их тоже можно решать через дискриминант. Надо только правильно сообразить, чему здесь равняются a, b и с.

Сообразили? В первом примере a = 1; b = -4; а c? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с, а b !

Но неполные квадратные уравнения можно решать гораздо проще. Безо всякого дискриминанта. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.

И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!

Не получается? То-то…
Следовательно, можно уверенно записать: х = 0, или х = 4

Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем через дискриминант.

Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:

Остаётся корень извлечь из 9, и всё. Получится:

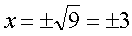
Тоже два корня. х = +3 и х = -3.

Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…

А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности.… За которые потом бывает больно и обидно…

Приём первый. Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:

Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:

И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:

А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.

Приём второй. Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1, проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком. Если не получилось – значит уже где-то накосячили. Ищите ошибку. Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент

b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b, который перед иксом, равен -1. Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1. Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.

Приём третий. Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в предыдущем разделе. При работе с дробями ошибки, почему-то так и лезут…

Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.

Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:

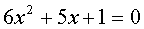
Вот и всё! Решать – одно удовольствие!

Итак, подытожим тему.

Практические советы:

1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно.

2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.

3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.

4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!

Дробные уравнения. ОДЗ.

 

Продолжаем осваивать уравнения. Мы уже в курсе, как работать с линейными уравнениями и квадратными. Остался последний вид – дробные уравнения. Или их ещё называют гораздо солиднее – дробные рациональные уравнения. Это одно и то же.

 

Дробные уравнения.

Как ясно из названия, в этих уравнениях обязательно присутствуют дроби. Но не просто дроби, а дроби, у которых есть неизвестное в знаменателе. Хотя бы в одном. Например:

Или:

Напомню, если в знаменателях только числа, это линейные уравнения.

Как решать дробные уравнения? Прежде всего – избавиться от дробей! После этого уравнение, чаще всего, превращается в линейное или квадратное. А дальше мы знаем, что делать… В некоторых случаях оно может превратиться в тождество, типа 5=5 или неверное выражение, типа 7=2. Но это редко случается. Ниже я про это упомяну.

Но как избавиться от дробей!? Очень просто. Применяя всё те же тождественные преобразования.

Нам надо умножить всё уравнение на одно и то же выражение. Так, чтобы все знаменатели посокращались! Всё сразу станет проще. Поясняю на примере. Пусть нам требуется решить уравнение:

Как учили в младших классах? Переносим все в одну сторону, приводим к общему знаменателю и т.д. Забудьте, как страшный сон! Так нужно делать, когда вы складываете или вычитаете дробные выражения. Или работаете с неравенствами. А в уравнениях мы сразу умножаем обе части на выражение, которое даст нам возможность сократить все знаменатели (т.е., в сущности, на общий знаменатель). И какое же это выражение?

В левой части для сокращения знаменателя требуется умножение на х+2 . А в правой требуется умножение на 2. Значит, уравнение надо умножать на 2(х+2). Умножаем:

Это обычное умножение дробей, но распишу подробно:

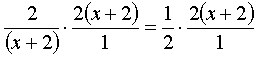
Обратите внимание, я пока не раскрываю скобку (х + 2)! Так, целиком, её и пишу:

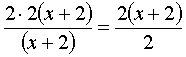
В левой части сокращается целиком (х+2), а в правой 2. Что и требовалось! После сокращения получаем линейное уравнение:

А это уравнение уже решит всякий! х = 2.

Решим ещё один пример, чуть посложнее:

Если вспомнить, что 3 = 3/1, а 2х = 2х/1, можно записать:

И опять избавляемся от того, что нам не очень нравится – от дробей.

Видим, что для сокращения знаменателя с иксом, надо умножить дробь на (х – 2). А единицы нам не помеха. Ну и умножаем. Всю левую часть и всю правую часть:

Опять скобки (х – 2) я не раскрываю. Работаю со скобкой в целом, как будто это одно число! Так надо делать всегда, иначе ничего не сократится.

С чувством глубокого удовлетворения сокращаем (х – 2) и получаем уравнение безо всяких дробей, в линеечку!

А вот теперь уже раскрываем скобки:

Приводим подобные, переносим всё в левую часть и получаем:

Классическое квадратное уравнение. Но минус впереди – нехорош. От него можно всегда избавиться, умножением или делением на -1. Но если присмотреться к примеру, можно заметить, что лучше всего это уравнение разделить на -2! Одним махом и минус исчезнет, и коэффициенты посимпатичнее станут! Делим на -2. В левой части – почленно, а в правой – просто ноль делим на -2, ноль и получим:

Решаем через дискриминант и проверяем по теореме Виета. Получаем х = 1 и х = 3. Два корня.

Как видим, в первом случае уравнение после преобразования стало линейным, а здесь – квадратным. Бывает так, что после избавления от дробей, все иксы сокращаются. Остаётся что-нибудь, типа 5=5. Это означает, что икс может быть любым. Каким бы он не был, всё равно сократится. И получится чистая правда, 5=5. Но, после избавления от дробей, может получиться и совсем неправда, типа 2=7. А это означает, что решений нет! При любом иксе получается неправда.

Осознали главный способ решения дробных уравнений? Он прост и логичен. Мы меняем исходное выражение так, чтобы исчезло всё то, что нам не нравится. Или мешает. В данном случае это – дроби. Точно так же мы будем поступать и со всякими сложными примерами с логарифмами, синусами и прочими ужасами. Мы всегда будем от всего этого избавляться.

Однако менять исходное выражение в нужную нам сторону надо по правилам, да… Освоение которых и есть подготовка к ЕГЭ по математике. Вот и осваиваем.

Сейчас мы с вами научимся обходить одну из главных засад на ЕГЭ! Но для начала посмотрим, попадаете вы в неё, или нет?

Разберём простой пример:

Дело уже знакомое, умножаем обе части на (х – 2), получаем:

Напоминаю, со скобками (х – 2) работаем как с одним, цельным выражением!

Здесь я уже не писал единичку в знаменателях, несолидно… И скобки в знаменателях рисовать не стал, там кроме х – 2 ничего нет, можно и не рисовать. Сокращаем:

Раскрываем скобки, переносим всё влево, приводим подобные:

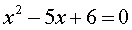
Решаем, проверяем, получаем два корня. х = 2 и х = 3. Отлично.

Предположим в задании сказано записать корень, или их сумму, если корней больше одного. Что писать будем?

Если решите, что ответ 5, – вы попали в засаду. И задание вам не засчитают. Зря трудились… Правильный ответ 3.

В чём дело?! А вы попробуйте проверку сделать. Подставить значения неизвестного в исходный пример. И если при х = 3 у нас всё чудненько срастётся, получим 9 = 9, то при х = 2 получится деление на ноль! Чего делать нельзя категорически. Значит х = 2 решением не является, и в ответе никак не учитывается. Это так называемый посторонний или лишний корень. Мы его просто отбрасываем. Окончательный корень один. х = 3.

Как так?! – слышу возмущённые возгласы. Нас учили, что уравнение можно умножать на выражение! Это тождественное преобразование!

Да, тождественное. При маленьком условии – выражение, на которое умножаем (делим) – отлично от нуля. А х – 2 при х = 2 равно нулю! Так что всё честно.

И что теперь делать?! Не умножать на выражение? Каждый раз проверку делать? Опять непонятно!

Спокойно! Без паники!

В этой тяжелой ситуации нас спасут три магических буквы. Я знаю, о чем вы подумали. Правильно! Это ОДЗ. Область Допустимых Значений.

 

---

Рекомендуемые страницы:

Воспользуйтесь поиском по сайту:

megalektsii.ru

Дискриминант — это… Что такое Дискриминант?

Дискримина́нт многочлена , есть произведение

, где  — все корни (с учётом кратностей) в некотором расширении основного поля, в котором они существуют.

Свойства

• Дискриминант равен нулю тогда и только тогда, когда многочлен имеет кратные корни.
• Дискриминант является симметрическим многочленом относительно корней многочлена и поэтому является многочленом от его коэффициентов; более того, коэффициенты этого многочлена целые независимо от расширения, в котором берутся корни.
• , где  — результант многочлена и его производной .
  • В частности, дискриминант многочлена

равен, с точностью до знака, определителю следующей -матрицы:

Примеры

• В частности, дискриминант многочлена (корни которого вычисляются по формуле Кардано) равен .

История

Термин образован от лат. discrimino — «разбираю», «различаю». Понятие «дискриминант квадратичной формы» использовалось в работах Гаусса, Дедекинда, Кронекера, Вебера и др. Термин ввёл Сильвестр^[1].

Примечания

partners.academic.ru

Открытый урок по теме «Квадратные уравнения»

 

Квадратные уравнения. Дискриминант. Решение, примеры.

Виды квадратных уравнений

Что такое квадратное уравнение? Как оно выглядит? В термине квадратное уравнение ключевым словом является «квадратное». Оно означает, что в уравнении обязательно должен присутствовать икс в квадрате. Кроме него, в уравнении могут быть (а могут и не быть!) просто икс (в первой степени) и просто число (свободный член). И не должно быть иксов в степени, больше двойки.

Говоря математическим языком, квадратное уравнение — это уравнение вида:

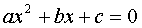
Здесь a, b и с – какие-то числа. b и c – совсем любые, а а – любое, кроме нуля. Например:

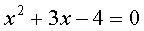
Здесь  а =1; b = 3; c = -4

Или:

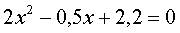
Здесь  а =2; b = -0,5; c = 2,2

Или:

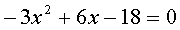
Здесь а =-3; b = 6; c = -18

Ну, вы поняли…

В этих квадратных уравнениях слева присутствует полный набор членов. Икс в квадрате с коэффициентом а, икс в первой степени с коэффициентом b и свободный член с.

Такие квадратные уравнения называются полными.

А если b = 0, что у нас получится? У нас пропадёт икс в первой степени. От умножения на ноль такое случается.) Получается, например:

5х²-25 = 0,

Или:

х²+4 = 0

И так далее. Если же c = 0, получим уравнение без свободного члена:

2х²-6х=0,

Или:

-х²+4х=0

И т.п. А если уж оба коэффицента, b и c равны нулю, то всё ещё проще:

2х²=0,

Или:

-0,3х²=0

Такие уравнения, где чего-то не хватает, называются неполными квадратными уравнениями. Что вполне логично.) Прошу заметить, что икс в квадрате присутствует во всех уравнениях.

Кстати, почему а не может быть равно нулю? А вы подставьте вместо а нолик.) У нас исчезнет икс в квадрате! Уравнение станет линейным. И решается уже совсем иначе…

Вот и все главные виды квадратных уравнений. Полные и неполные.

 

Решение квадратных уравнений.

 

Решение полных квадратных уравнений.

Квадратные уравнения решаются просто. По формулам и чётким несложным правилам. На первом этапе надо заданное уравнение привести к стандартному виду, т.е. к виду:

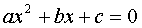
Если уравнение вам дано уже в таком виде — первый этап делать не нужно.) Главное — правильно определить все коэффициенты, а, b и c.

Формула для нахождения корней квадратного уравнения выглядит так:

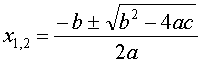
Выражение под знаком корня называется дискриминант. Но о нём — ниже. Как видим, для нахождения икса, мы используем только a, b и с. Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в эту формулу и считаем. Подставляем со своими знаками! Например, в уравнении:

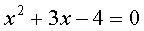
а =1; b = 3; c = -4. Вот и записываем:

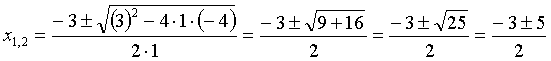
Пример практически решён:

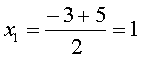
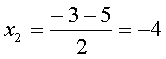
Это ответ.

 

Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…

Самые распространённые ошибки – путаница со знаками  значений  a, b и с.  Вернее, не с их знаками (где там путаться?),  а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте!

Предположим, надо вот такой примерчик решить:

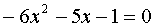
Здесь a = -6; b = -5; c = -1

Допустим, вы знаете, что ответы у вас редко с первого раза получаются.

Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится. Вот и пишем подробно, со всеми скобочками и знаками:

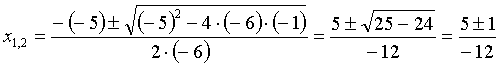
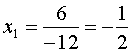
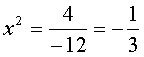
Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!

 

Но, частенько, квадратные уравнения выглядят слегка иначе. Например, вот так:

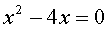
Или так:

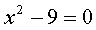
Узнали?) Да! Это неполные квадратные уравнения.

 

Решение неполных квадратных уравнений.

Их тоже можно решать по общей формуле. Надо только правильно сообразить, чему здесь равняются a, b и с.

Сообразили? В первом примере  a = 1; b = -4; а c? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с, а b !

Но неполные квадратные уравнения можно решать гораздо проще. Безо всяких формул. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.

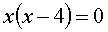
И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать: х₁ = 0, х₂ = 4.

Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем по общей формуле. Замечу, кстати, какой икс будет первым, а какой вторым — абсолютно безразлично. Удобно записывать по порядочку, х₁ — то, что меньше, а х₂ — то, что больше.

Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:

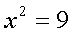
Остаётся корень извлечь из 9, и всё. Получится:

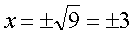
Тоже два корня. х₁ = -3, х₂ = 3.

Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…

 

Дискриминант. Формула дискриминанта.

Волшебное слово дискриминант! Редкий старшеклассник не слышал этого слова! Фраза  «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении.) Напоминаю самую общую формулу для решения любых квадратных уравнений:

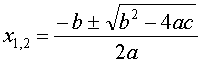
Выражение под знаком корня называется дискриминантом. Обычно дискриминант обозначается буквой D. Формула дискриминанта:

D = b² — 4ac

И чем же примечательно это выражение? Почему оно заслужило специальное название? В чём смысл дискриминанта? Ведь -b, или 2a в этой формуле специально никак не называют… Буквы и буквы.

Дело вот в чём. При решении квадратного уравнения по этой формуле, возможны всего три случая.

1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.

2. Дискриминант равен нулю. Тогда у вас получится одно решение. Так как от прибавления-вычитания нуля в числителе ничего не меняется. Строго говоря, это не один корень, а два одинаковых. Но, в упрощённом варианте, принято говорить об одном решении.

3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.

Честно говоря, при простом решении квадратных уравнений, понятие дискриминанта не особо-то и требуется. Подставляем в формулу значения коэффициентов, да считаем. Там всё само собой получается, и два корня, и один, и ни одного. Однако, при решении более сложных заданий, без знания смысла и формулы дискриминанта не обойтись. Особенно — в уравнениях с параметрами. Такие уравнения — высший пилотаж на ГИА и ЕГЭ!)

Итак, как решать  квадратные уравнения через дискриминант вы вспомнили. Или научились, что тоже неплохо.) Умеете правильно определять a, b и с. Умеете внимательно подставлять их в формулу корней и внимательно считать результат. Вы поняли, что ключевое слово здесь – внимательно?

 

А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности.…  За которые потом бывает больно и обидно…

Приём первый. Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:

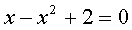
Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:

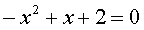
И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:

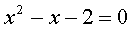
А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.

Приём второй. Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1, проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком. Если не получилось – значит уже где-то накосячили. Ищите ошибку.

Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b, который перед иксом,  равен -1. Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1. Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.

Приём третий. Если в вашем уравнении есть дробные коэффициенты,  —  избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в уроке «Как решать уравнения? Тождественные преобразования». При работе с дробями ошибки, почему-то так и лезут…

Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.

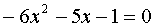
Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:

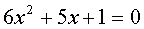
Вот и всё! Решать – одно удовольствие!

Итак, подытожим тему.

Практические советы:

1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно.

2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.

3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.

4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!

 

Теперь можно и порешать.)

Решить уравнения:

8х² — 6x + 1 = 0

х² + 3x + 8 = 0

х² — 4x + 4 = 0

(х+1)² + x + 1 = (x+1)(x+2)

 

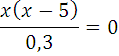
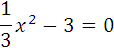
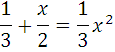
Ответы (в беспорядке):

х₁= 0
х₂= 5

х_1,2= 2

х₁= 2
х₂= -0,5

х — любое число

х₁= -3
х₂= 3

решений нет

х₁= 0,25
х₂= 0,5

infourok.ru

Дискриминант — это… Что такое Дискриминант?

Дискримина́нт многочлена , есть произведение

, где  — все корни (с учётом кратностей) в некотором расширении основного поля, в котором они существуют.

Свойства

• Дискриминант равен нулю тогда и только тогда, когда многочлен имеет кратные корни.
• Дискриминант является симметрическим многочленом относительно корней многочлена и поэтому является многочленом от его коэффициентов; более того, коэффициенты этого многочлена целые независимо от расширения, в котором берутся корни.
• , где  — результант многочлена и его производной .
  • В частности, дискриминант многочлена

равен, с точностью до знака, определителю следующей -матрицы:

Примеры

• В частности, дискриминант многочлена (корни которого вычисляются по формуле Кардано) равен .

История

Термин образован от лат. discrimino — «разбираю», «различаю». Понятие «дискриминант квадратичной формы» использовалось в работах Гаусса, Дедекинда, Кронекера, Вебера и др. Термин ввёл Сильвестр^[1].

Примечания

dikc.academic.ru