Четные и нечетные функции
Четные функции
Определение 1
Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть четной, если для всех точек из множества $X$ будет выполняться
\[f\left(x\right)=f(-x)\]Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будет совпадать, то график этих функции будет подчиняться закону осевой симметрии по отношению к оси ординат (рис. 1).

Рисунок 1.
Для исследования функции на четность необходимо в его аналитической записи заменить переменную $x$ на переменную $-x$, произвести, при необходимости элементарные преобразования, и проверить условие определения 1.
Нечетные функции
Определение 2
Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть нечетной, если для всех точек из множества $X$ будет выполняться
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будут также совпадать по модулю и отрицательны по знакам, то график этих функции будет подчиняться закону центральной симметрии по отношению к началу координат (рис. 2).

Рисунок 2.
Для исследования функции на нечетность необходимо в его аналитической записи заменить переменную $x$ на переменную $-x$, произвести, при необходимости элементарные преобразования, и проверить условие определения 2.
Функция общего вида
Определение 3
Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть функцией общего вида, если она не будет ни четной, ни нечетной.
Для того чтобы понять, что данная функция является функцией общего вида, необходимо в его аналитической записи заменить переменную $x$ на переменную $—x$, произвести, при необходимости элементарные преобразования, и проверить невыполнение условий определений 1 и 2.
Функция общего вида никогда не будет симметрична оси ординат и началу координат. Пример функции общего вида изображен на рисунке 3.

Рисунок 3.
Пример задачи
Пример 1
Исследовать функцию на четность и нечетность и построить их графики.
а) $f(x)=x^2+3$
б) $f(x)=\frac{x^2+4}{x}$
в) $f\left(x\right)=sinx+cosx$
Решение.
а) $f(x)=x^2+3$
$f\left(-x\right)={(-x)}^2+3=x^2+3=f(x)$\textit{ }следовательно, $f(x)$ — четная функция.
Изобразим её на графике:

Рисунок 4.
б) $f(x)=\frac{x^2+4}{x}$
$f\left(-x\right)=\frac{{\left(-x\right)}^2+4}{-x}=-\frac{x^2+4}{x}$ следовательно, $f(x)$ — нечетная функция.
Изобразим её на графике:

Рисунок 5.
в) $f\left(x\right)=sinx+cosx$
$f\left(-x\right)={\sin \left(-x\right)\ }+{\cos \left(-x\right)\ }=cosx-sinx$ следовательно, $f\left(x\right)$ — функция общего вида.
Изобразим её на графике:

Рисунок 6.
spravochnick.ru
Исследование функции
Исследование функции.
1) D(y) – Область опрделения: множество всех тех значений переменной х. при которых алгебраические выражения f(x) и g(x) имеют смысл.
Если функция задана формулой, то область определения состоит из всех значений независимой переменной, при которых формула имеет смысл.
2) Свойства функции: четность/нечетность, периодичность:
Нечётными и чётными называются функции, графики которых обладают симметрией относительно изменения знака аргумента.
Нечётная функция — функция, меняющая значение на противоположное при изменении знака независимой переменной (симметричная относительно центра координат).
Чётная функция — функция, не изменяющая своего значения при изменении знака независимой переменной (симметричная относительно оси ординат).
Ни чётная ни нечётная функция (функция общего вида) — функция, не обладающая симметрией. В эту категорию относят функции, не подпадающие под предыдущие 2 категории.


Функции, не принадлежащие ни одной из категорий выше, называются ни чётными ни нечётными (или функциями общего вида).
Нечётные функции
Нечётная степень 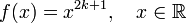 где
где  —
произвольное целое
число.
—
произвольное целое
число.
Синус
 .
.Тангенс
 .
.
Чётные функции
Чётная
степень  где
где 
Периоди́ческая фу́нкция ― функция, повторяющая свои значения через некоторый регулярный интервал аргумента, то есть не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа (пери́ода функции) на всей области определения.
Говоря более формально, функция называется периодической, если существует такое число T≠0 (период), что на всей области определения функции выполняется равенство
 .
.Исходя из определения, для периодической функции справедливо также равенство
 ,
где
,
где  —
любое целое число.
—
любое целое число.Все тригонометрические функции являются периодическими.
3) Нули (корни) функции — точки, где она обращается в ноль.
Нахождение точки пересечения графика с осью Oy. Для этого нужно вычислить значение f(0). Найти также точки пересечения графика с осью Ox, для чего найти корни уравнения f(x) = 0 (или убедиться в отсутствии корней).
Точки, в
которых график  пересекает
ось
пересекает
ось  ,
называют нулями
функции.
Чтобы найти нули функции нужно решить
уравнение
,
называют нулями
функции.
Чтобы найти нули функции нужно решить
уравнение  ,
то есть найти те
значения «икс»,
при которых функция обращается в ноль.
,
то есть найти те
значения «икс»,
при которых функция обращается в ноль.
4) Промежутки постоянства знаков, знаки в них.
Промежутки, где функция f(x) сохраняет знак.
Интервал знакопостоянства – это интервал,
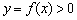 ВЫШЕ
оси абсцисс.
ВЫШЕ
оси абсцисс.
 НИЖЕ
оси
НИЖЕ
оси  .
.
5) Непрерывность (точки разрыва, характер разрыва, ассимптоты).
Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Устранимые точки разрыва
Если предел функции существует, но функция не определена в этой точке, либо предел не совпадает со значением функции в данной точке:
 ,
,
то
точка 
 (в комплексном
анализе —устранимая
особая точка).
(в комплексном
анализе —устранимая
особая точка). Если
«поправить» функцию  в
точке устранимого разрыва и положить
в
точке устранимого разрыва и положить  ,
то получится функция, непрерывная в
данной точке. Такая операция над функцией
называется доопределением
функции до непрерывной или доопределением
функции по непрерывности,
что и обосновывает название точки, как
точки устранимого разрыва.
,
то получится функция, непрерывная в
данной точке. Такая операция над функцией
называется доопределением
функции до непрерывной или доопределением
функции по непрерывности,
что и обосновывает название точки, как
точки устранимого разрыва.
Точки разрыва первого и второго рода
Если функция имеет разрыв в данной точке (то есть предел функции в данной точке отсутствует или не совпадает со значением функции в данной точке), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций
если оба односторонних предела существуют и конечны, то такую точку называют точкой разрыва первого рода. Точки устранимого разрыва являются точками разрыва первого рода;
если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.
Аси́мпто́та — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви вбесконечность.
Вертикальная
Вертикальная
асимптота — прямая вида  при
условии существования предела
при
условии существования предела 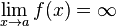 .
.
Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:
Горизонтальная
Горизонтальная
асимптота — прямая вида  при
условии существования предела
при
условии существования предела
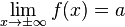 .
.
Наклонная
Наклонная
асимптота — прямая вида  при
условии существования пределов
при
условии существования пределов
Замечание: функция может иметь не более двух наклонных (горизонтальных) асимптот.
Замечание:
если хотя бы один из двух упомянутых
выше пределов не существует (или равен  ),
то наклонной асимптоты при
),
то наклонной асимптоты при  (или
(или 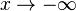 )
не существует.
)
не существует.
если  в
п. 2.), то
в
п. 2.), то  ,
и предел
,
и предел 
 .
. 6) Нахождение
промежутков монотонности. Найти
интервалы монотонности функции f(x)(то
есть интервалы возрастания и убывания).
Это делается с помощью исследования
знака производной f (x).
Для этого находят производную f
(x).
Для этого находят производную f (x) и
решают неравенство f
(x) и
решают неравенство f (x)
(x) 0.
На промежутках, где это неравенство
выполнено, функция f(x)возрастает.
Там, где выполнено обратное неравенство f
0.
На промежутках, где это неравенство
выполнено, функция f(x)возрастает.
Там, где выполнено обратное неравенство f
 0,
функция f(x)убывает.
0,
функция f(x)убывает.Нахождение локального экстремума. Найдя интервалы монотонности, мы можем сразу определить точки локального экстремума там, где возрастание сменяется убыванием, располагаются локальные максимумы, а там, где убывание сменяется возрастанием — локальные минимумы. Вычислить значение функции в этих точках. Если функция имеет критические точки, не являющиеся точками локального экстремума, то полезно вычислить значение функции и в этих точках.
Нахождение наибольшего и наименьшего значений функции y = f(x) на отрезке [a; b](продолжение)
1. Найти
производную функции: f 2. Найти
точки, в которых производная равна
нулю: f 3. Определить
принадлежность точек х1, х2, …отрезку
[a; b]:
пусть x1 4. Найти значения функции в выбранных точках и на концах отрезка:f(x1), f(x2),…, f(xa),f(xb), 5. Выбор наибольшего и наименьшего значений функции из найденных. Замечание. Если на отрезке [a; b] имеются точки разрыва, то необходимо в них вычислить односторонние пределы, а затем их значения учесть в выборе наибольшего и наименьшего значений функции. |
7) Нахождение
интервалов выпуклости и вогнутости.
Это делается с помощью исследования
знака второй производной f
 (x).
Найти точки перегиба на стыках интервалов
выпуклости и вогнутости. Вычислить
значение функции в точках перегиба.
Если функция имеет другие точки
непрерывности (кроме точек перегиба),
в которых вторая производная равна 0
либо не существует, то в этих точках
также полезно вычислить значение
функции. Найдя f
(x).
Найти точки перегиба на стыках интервалов
выпуклости и вогнутости. Вычислить
значение функции в точках перегиба.
Если функция имеет другие точки
непрерывности (кроме точек перегиба),
в которых вторая производная равна 0
либо не существует, то в этих точках
также полезно вычислить значение
функции. Найдя f
 (x) ,
мы решаем неравенство f
(x) ,
мы решаем неравенство f
 (x)
(x)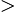 0.
На каждом из интервалов решения функция
будет выпуклой вниз. Решая обратное
неравенство f
0.
На каждом из интервалов решения функция
будет выпуклой вниз. Решая обратное
неравенство f
 (x)
(x)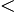 0,
мы находим интервалы, на которых функция
выпукла вверх (то есть вогнута). Определяем
точки перегиба как те точки, в которых
функция меняет направление выпуклости
(и непрерывна).
0,
мы находим интервалы, на которых функция
выпукла вверх (то есть вогнута). Определяем
точки перегиба как те точки, в которых
функция меняет направление выпуклости
(и непрерывна).
Точка перегиба функции — это точка, в которой функция непрерывна и при переходе через которую функция меняет направление выпуклости.
Условия существования
Необходимое
условие существования точки перегиба: если
функция  дважды
дифференцируемая в некоторой выколотой
окрестности точки
дважды
дифференцируемая в некоторой выколотой
окрестности точки  ,
то
,
то  или
или  .
.
studfile.net
Четные и нечетные функции
Определение.
Функция  называетсячетной, если она не
изменяет своего значения при изменении
знака аргумента, т.е.
называетсячетной, если она не
изменяет своего значения при изменении
знака аргумента, т.е. .
.
Например,  ;
; ;
;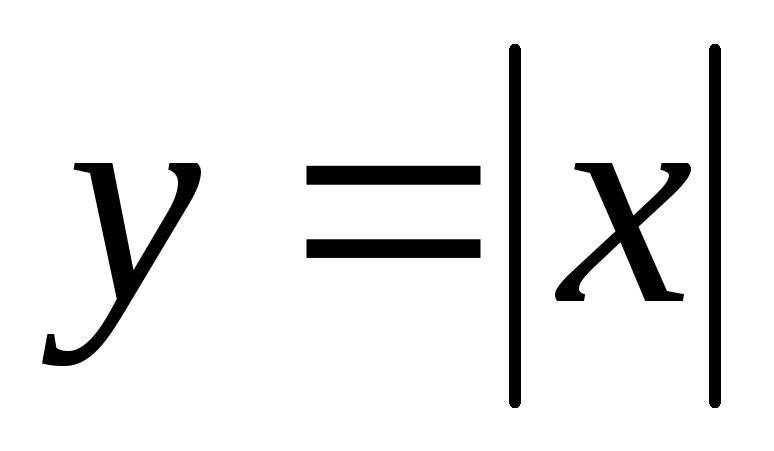 – четные функции.
– четные функции.
График четной
функции расположен симметрично
относительно оси  (рис.1.4).
(рис.1.4).
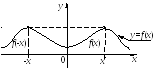
Рис. 1.4
Определение.
Функция
называетсянечетной, если при
изменении знака аргумента знак функции
меняется на противоположный, а числовое
значение её сохраняется, т.е. .
.
Например,  ;
; – нечетные функции.
– нечетные функции.
График нечетной функции расположен симметрично относительно начала координат (рис.1.5).

Рис. 1.5
Функция может быть ни четной. ни нечетной, и в этом случае её называют функцией общего вида.
Например,  ;
;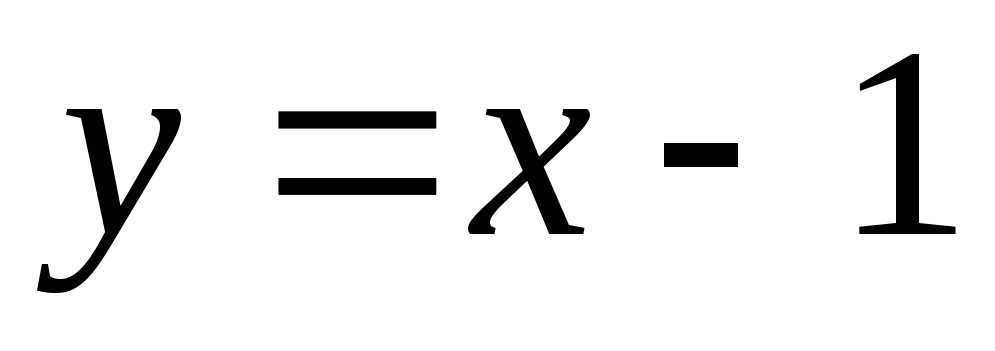 ;
; .
.
Графики таких
функций не симметричны ни относительно
оси  ,
ни относительно начала координат.
,
ни относительно начала координат.
Периодические функции
Определение.
Функция  называется периодической, если существует
такое положительное число
называется периодической, если существует
такое положительное число ,
что
,
что в
области определения функции.
в
области определения функции.
Наименьшее из
положительных чисел Т, удовлетворяющих
условию определения, называетсяпериодомфункции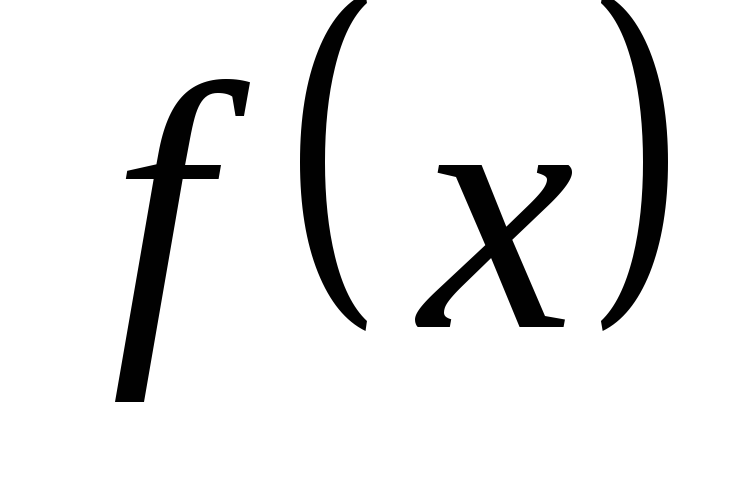 .
.
Например, функции  ,
, являются периодическими с периодом
являются периодическими с периодом .
.
Нули функции
Определение.
Значение аргумента,
при котором функция обращается в нуль,  ,
называетсянулем функции.
,
называетсянулем функции.
Например, нулями
функции  являются значения
являются значения и
и .
.
Монотонные функции
Определение.
Функция называется возрастающей(убывающей) в некоторой области изменения аргумента, еслибольшемузначению аргумента соответствуетбольшее(меньшее) значение функции (рис.1.6, 1.7).

Рис. 1.6 Рис. 1.7
Определение.
Если функция в некоторой области изменения аргумента является только возрастающей или только убывающей, то функция называется монотонной.
Ограниченные функции
Определение.
Функция  называетсяограниченнойна множествеХ, если существует такое число
называетсяограниченнойна множествеХ, если существует такое число ,
что для всех
,
что для всех выполняется неравенство
выполняется неравенство .
.
Например, функции 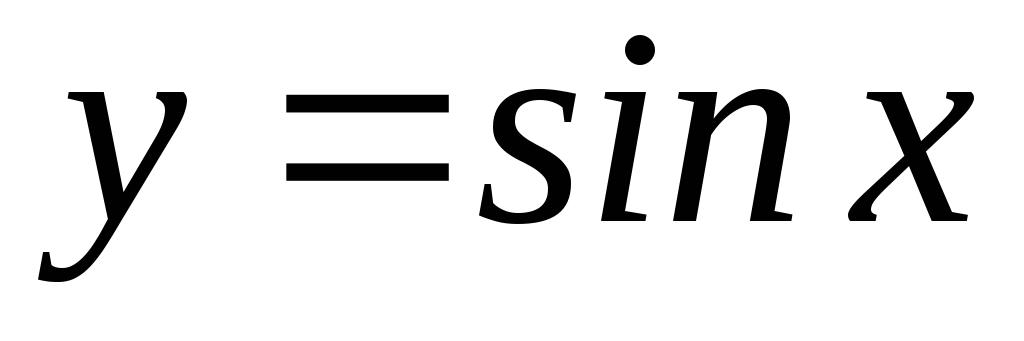 и
и – ограниченные функции, т.к.
– ограниченные функции, т.к. и
и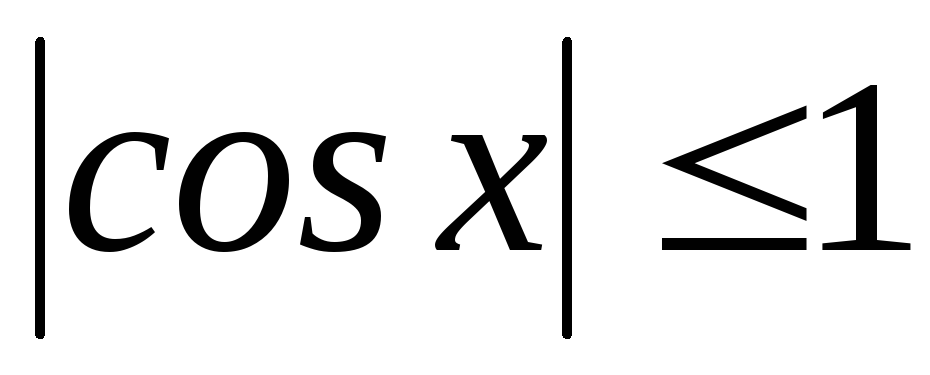 для
для .
.
График ограниченной
функции лежит между прямыми  и
и (рис.1.8).
(рис.1.8).
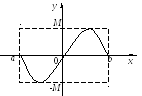
Рис. 1.8
УПРАЖНЕНИЯ
Найти область определения следующих функций:
1) 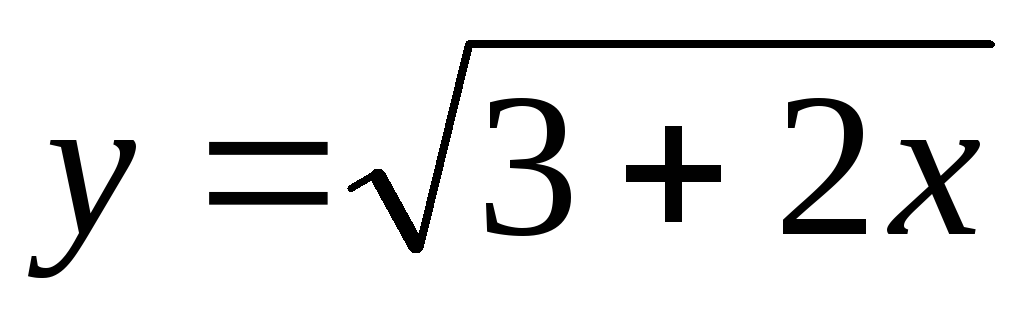 ; Ответ:
; Ответ: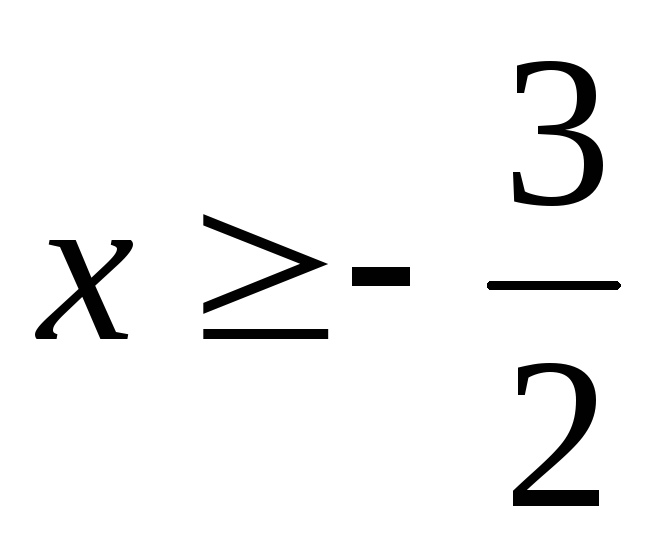 ;
;
2)  ; Ответ:
; Ответ: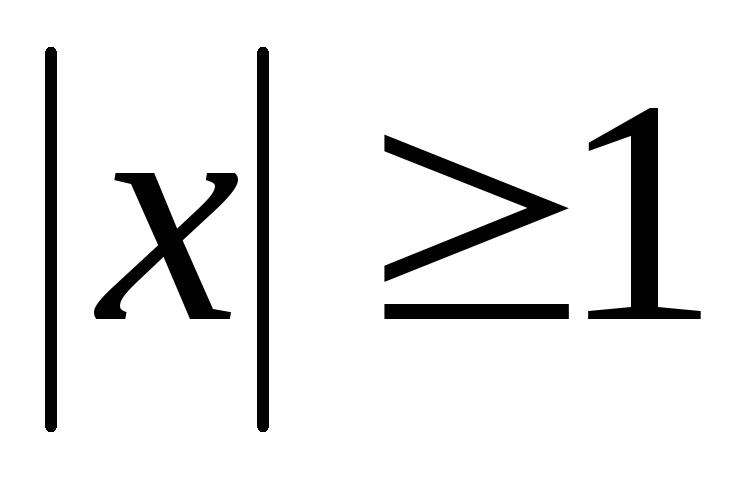 ;
;
3)  ; Ответ:
; Ответ: ;
;
4)  ; Ответ:
; Ответ: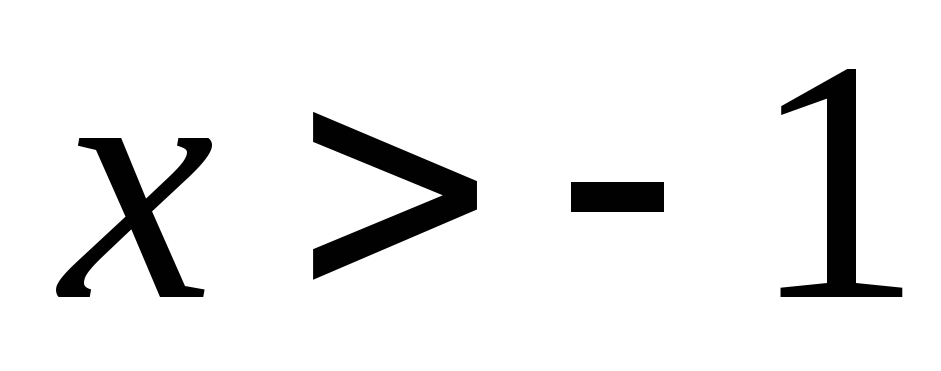 .
.
Найти множество значений функции:
1)  ; Ответ:
; Ответ: ;
;
2) 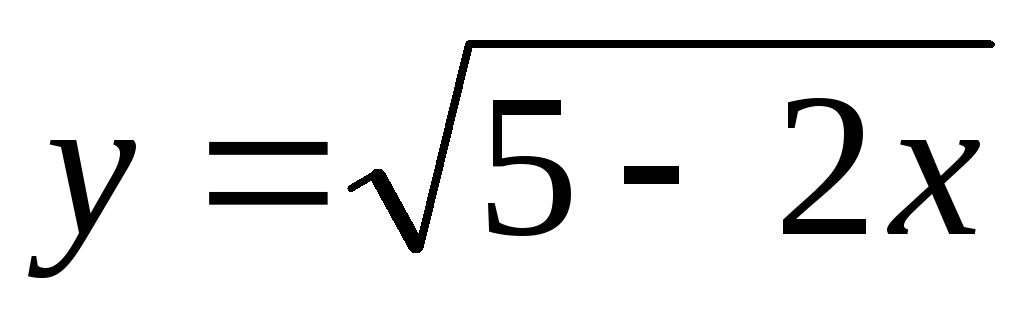 ; Ответ:
; Ответ: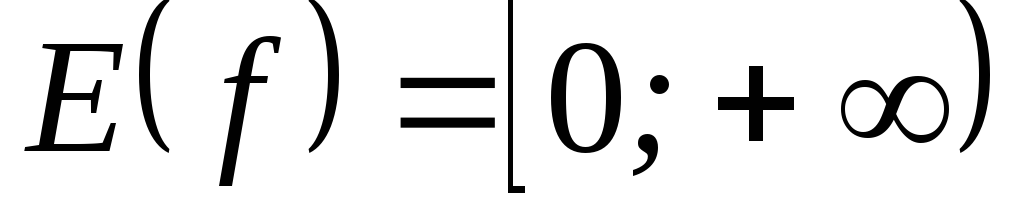 ;
;
3)  ; Ответ:
; Ответ: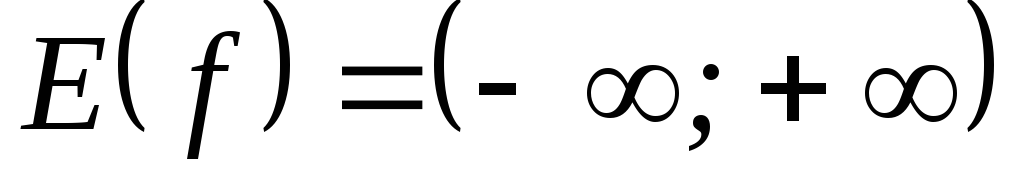 .
.
Найти
 ,
, ,
, ,
, ,
если
,
если .
.
Ответ:  ;
; ;;
;;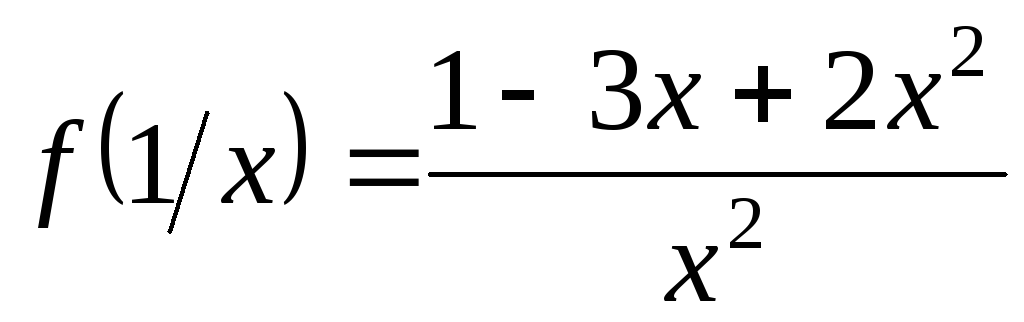 .
.
Пусть
 и
и .
Найти
.
Найти и
и .
.
Ответ: 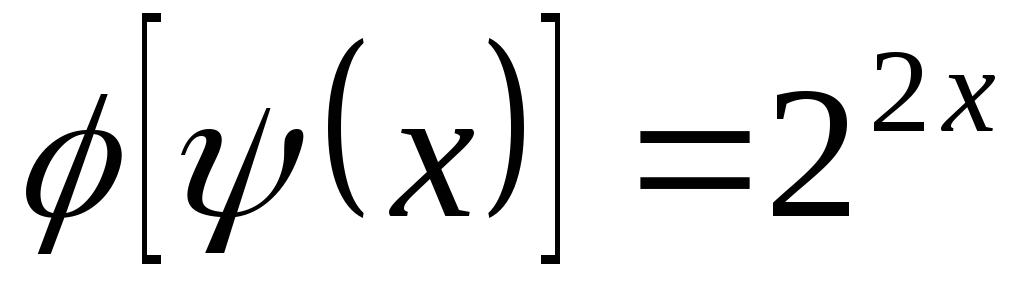 ;
; .
.
Установить чётность или нечётность функции:
1)  ; Ответ:
чётная;
; Ответ:
чётная;
2)  ; Ответ:
чётная;
; Ответ:
чётная;
3)  ; Ответ:
общего вида;
; Ответ:
общего вида;
4)  ; Ответ:
нечётная.
; Ответ:
нечётная.
Найти основные периоды функций:
1)  ; Ответ:
; Ответ: ;
;
2)  ; Ответ:
; Ответ: ;
;
3) 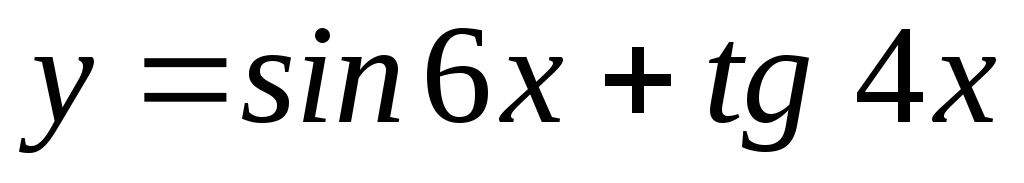 ; Ответ:
; Ответ: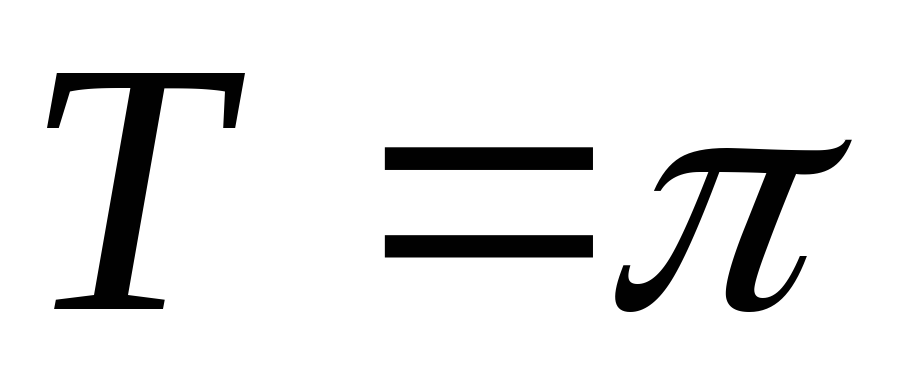 .
.
Введя промежуточные аргументы, представить данную функцию, как суперпозицию других функций:
1)  ; Ответ:
; Ответ: ;
; ;
; ;
;
2) 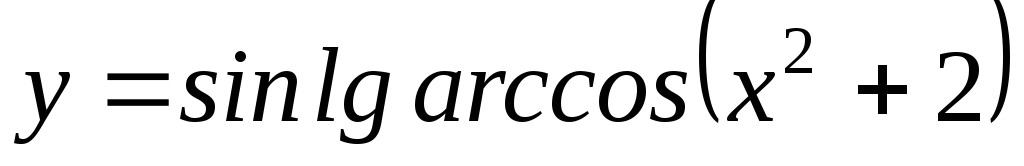 ;
Ответ:
;
Ответ: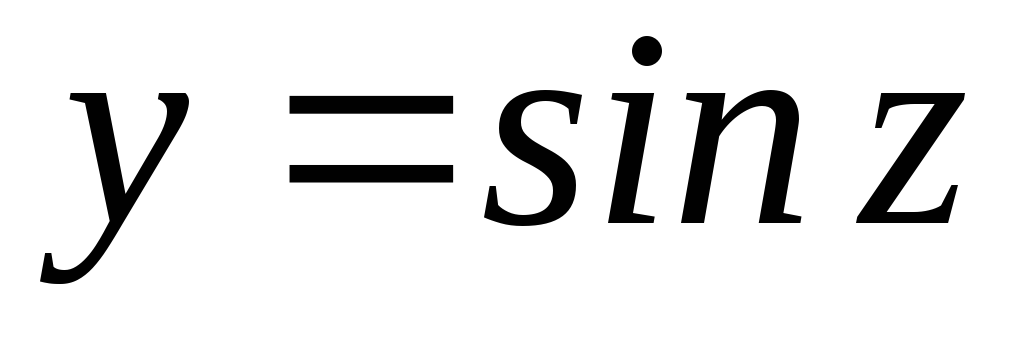 ;
; ;
; ;
; ;
; .
.
Для данных функций найти явные обратные:
1)  ; Ответ:
; Ответ: ;
;
2)  ; Ответ:
; Ответ: ;
;
3) 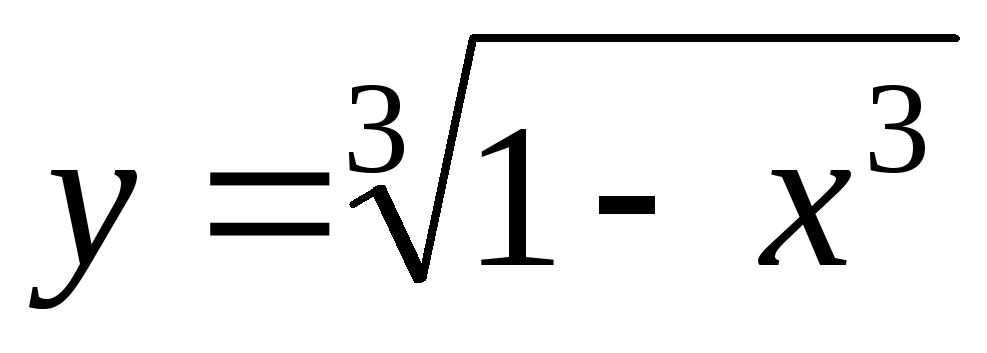 ; Ответ:
; Ответ: .
.
studfile.net
Чётные и нечётные функции. Видеоурок. Алгебра 9 Класс
Данный видеоурок посвящен теме «Чётные и нечётные функции». Рассматривается определение и условия существования четной и нечетной функции. Строятся графики этих функций и описываются их свойства. Объясняется отличие четной функции от нечетной, а также ее отличие от функции общего вида.
Алгебра_ 9 класс
Итоговое повторение курса алгебры 9-го класса
Четные и нечетные функции
1.1. Конспект.
Какую функцию называют четной? А какую нечетной? Что такое функция общего вида? Как определить вид функции? Развернутый ответ на эти вопросы иллюстрируется исследованием на четность (нечетность) различных функций. Особое внимание уделено степенной функции 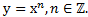
1. Какую функцию называют четной? Определение и свойство графика четной функции.
Функцию 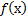 называют четной, если выполнены два условия:
называют четной, если выполнены два условия:
1) Область определения симметрична относительно  .
.
2) Для любого  справедливо
справедливо 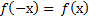 .
.

Разберем данное определение.
1) Первое условие означает: если отрезок 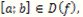 то и отрезок
то и отрезок  .
.
Заметим, что если  не симметрична, то функция является функцией общего вида.
не симметрична, то функция является функцией общего вида.

2) Второе условие означает: если точка с координатами  принадлежит графику функции, то и точка с координатами
принадлежит графику функции, то и точка с координатами  тоже принадлежит графику функции.
тоже принадлежит графику функции.
Заметим, что точки 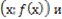
 симметричны относительно оси Оу.
симметричны относительно оси Оу.

Следствие: График четной функции симметричен относительно оси Оу.
Обратно: Если график функции не симметричен относительно оси Оу, то это график функции, которая не обладает свойством четности.
2. Какую функцию называют нечетной? Определение и свойство графика нечетной функции.
Функцию
interneturok.ru
Нечетная функция — это… Что такое Нечетная функция?
- Нечетная функция
-

f(x) = x — пример нечётной функции.

f(x) = x2 — пример чётной функции.

f(x) = x3, нечётная

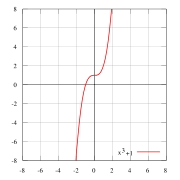
f(x) = x3 + 1 ни чётная, ни нечётная
Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.
Или по-другому
Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.
Определения
- Функция
![f:[-X,X] \subset \mathbb{R} \to \mathbb{R}](//xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) называется нечётной, если справедливо равенство
называется нечётной, если справедливо равенство
- Функция f называется чётной, если справедливо равенство
- Если не выполняется ни одно из этих равенств, то функция называется функцией общего вида.
Свойства
- График нечётной функции симметричен относительно начала координат O.
- График чётной функции симметричен относительно оси ординат Oy.
- Произвольная функция
![f:[-X,X] \subset \mathbb{R} \to \mathbb{R}](//xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) может быть представлена в виде суммы нечётной и чётной функций:
может быть представлена в виде суммы нечётной и чётной функций:
- f(x) = g(x) + h(x),
где
- Функция
 — единственная функция, одновременно являющаяся нечётной и чётной.
— единственная функция, одновременно являющаяся нечётной и чётной. - Сумма, разность и вообще любая линейная комбинация чётных функций чётна, а нечётных — нечётна.
- Произведение или дробь двух нечётных функций чётно.
- Произведение или дробь двух чётных функций чётно.
- Произведение или дробь нечётной и чётной функций нечётно.
- Композиция двух нечётных функция нечётна.
- Композиция двух чётных функций чётна.
- Композиция чётной функции с нечётной чётна.
- Композиция любой функции с чётной чётна (но не наоборот).
- Функция, обратная чётной, чётна, а нечётной — нечётна.
- Производная чётной функции нечётна, а нечётной — чётна.
- То же верно про производную третьего, пятого и вообще любого нечётного порядка.
- Производная чётного порядка сохраняет чётность.
Примеры
Нечётные функции
Чётные функции
Вариации и обобщения
- Функция
Wikimedia Foundation. 2010.
- Нечеткие множества
- Нечетное число
Смотреть что такое «Нечетная функция» в других словарях:
НЕЧЕТНАЯ ФУНКЦИЯ — функция, удовлетворяющая равенству f( x) = f(x) при всех х … Большой Энциклопедический словарь
нечетная функция — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN odd function … Справочник технического переводчика
НЕЧЕТНАЯ ФУНКЦИЯ — функция, меняющая знак при изменении знака независимого переменного, т. е. функция, удовлетворяющая условию . График Н. ф. симметричен относительно начала координат … Математическая энциклопедия
нечётная функция — функция, удовлетворяющая равенству f(–х) = f(х) при всех х. * * * НЕЧЕТНАЯ ФУНКЦИЯ НЕЧЕТНАЯ ФУНКЦИЯ, функция, удовлетворяющая равенству f( x) = f(x) при всех х … Энциклопедический словарь
Единичная функция Хевисайда — Функция Хевисайда, единичная ступенчатая функция, ступенька положения специальная математическая функция, чьё значение равно нулю для отрицательных аргументов и единице для положительных аргументов … Википедия
Единичная Хевисайда — Единичная функция Хевисайда Функция Хевисайда, единичная ступенчатая функция, ступенька положения специальная математическая функция, чьё значение равно нулю для отрицательных аргументов и единице для положительных аргументов … Википедия
Многочлены Лежандра — Многочлен Лежандра многочлен, который в наименьшей степени отклоняется от нуля в смысле среднего квадратического. Образует ортогональную систему многочленов, на отрезке по мере Лебега. Многочлены Лежандра могут быть получены из многочленов… … Википедия
ОБРАТНОЕ ОТОБРАЖЕНИЕ — (обратный оператор) к однозначному отображению (оператору) однозначное отображение gтакое, что где нек рые множества. Если gудовлетворяет лишь условию (1), то оно наз. правым обратным отображением к f, если лишь (2) левым обратным отображением к… … Математическая энциклопедия
ЯКОБИ ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ — эллиптические функции, возникшие при непосредственном обращении эллиптических интегралов в нормальной форме Лежандра. Эта задача обращения была решена в 1827 независимо К. Якоби (С. Jacobi) и, в несколько иной форме, Н. Абелем (N. Abel).… … Математическая энциклопедия
ВЕИЕРШТРАССА ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ — ф>тнкции, положенные К. Вейерштрассом в основу его общей теории эллиптических функций, излагавшейся им с 1862 на лекциях в Берлинском университете (см. [1], [2]). В отличие от более раннего построения теории эллиптич. функций, связанного с… … Математическая энциклопедия
dic.academic.ru
Чётная функция — это… Что такое Чётная функция?
- Чётная функция
-

f(x) = x — пример нечётной функции.

f(x) = x2 — пример чётной функции.

f(x) = x3, нечётная

f(x) = x3 + 1 ни чётная, ни нечётная
Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.
Или по-другому
Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.
Определения
- Функция
![f:[-X,X] \subset \mathbb{R} \to \mathbb{R}](//xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) называется нечётной, если справедливо равенство
называется нечётной, если справедливо равенство
- Функция f называется чётной, если справедливо равенство
- Если не выполняется ни одно из этих равенств, то функция называется функцией общего вида.
Свойства
- График нечётной функции симметричен относительно начала координат O.
- График чётной функции симметричен относительно оси ординат Oy.
- Произвольная функция
![f:[-X,X] \subset \mathbb{R} \to \mathbb{R}](//xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) может быть представлена в виде суммы нечётной и чётной функций:
может быть представлена в виде суммы нечётной и чётной функций:
- f(x) = g(x) + h(x),
где
- Функция
 — единственная функция, одновременно являющаяся нечётной и чётной.
— единственная функция, одновременно являющаяся нечётной и чётной. - Сумма, разность и вообще любая линейная комбинация чётных функций чётна, а нечётных — нечётна.
- Произведение или дробь двух нечётных функций чётно.
- Произведение или дробь двух чётных функций чётно.
- Произведение или дробь нечётной и чётной функций нечётно.
- Композиция двух нечётных функция нечётна.
- Композиция двух чётных функций чётна.
- Композиция чётной функции с нечётной чётна.
- Композиция любой функции с чётной чётна (но не наоборот).
- Функция, обратная чётной, чётна, а нечётной — нечётна.
- Производная чётной функции нечётна, а нечётной — чётна.
- То же верно про производную третьего, пятого и вообще любого нечётного порядка.
- Производная чётного порядка сохраняет чётность.
Примеры
Нечётные функции
Чётные функции
Вариации и обобщения
- Функция
Wikimedia Foundation. 2010.
- Чётное число
- Чётность (математика)
Смотреть что такое «Чётная функция» в других словарях:
Нечётная функция — f(x) = x пример нечётной функции. f(x) = x2 пример чётной функции. f(x) = x3 … Википедия
чётная функция — lyginė funkcija statusas T sritis fizika atitikmenys: angl. even function vok. gerade Funktion, f rus. чётная функция, f pranc. fonction paire, f … Fizikos terminų žodynas
нечётная функция — nelyginė funkcija statusas T sritis fizika atitikmenys: angl. odd function vok. ungerade Funktion, f rus. нечётная функция, f pranc. fonction impaire, f … Fizikos terminų žodynas
нечётная функция — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN odd function … Справочник технического переводчика
Нечётная функция — функция, удовлетворяющая равенству f ( x) = f (x). См. Чётные и нечётные функции … Большая советская энциклопедия
НЕЧЁТНАЯ ФУНКЦИЯ — функция, удовлетворяющая равенству f( x) = f(x) при всех х … Естествознание. Энциклопедический словарь
нечётная функция — функция, удовлетворяющая равенству f(–х) = f(х) при всех х. * * * НЕЧЕТНАЯ ФУНКЦИЯ НЕЧЕТНАЯ ФУНКЦИЯ, функция, удовлетворяющая равенству f( x) = f(x) при всех х … Энциклопедический словарь
чётная функция — функция, удовлетворяющая равенству f( х) = f(х) при всех х. * * * ЧЕТНАЯ ФУНКЦИЯ ЧЕТНАЯ ФУНКЦИЯ, функция, удовлетворяющая равенству f( x) = f(x) при всех x … Энциклопедический словарь
Функция Доусона — вблизи начала координат … Википедия
Функция Хевисайда — Единичная функция Хевисайда Функция Хевисайда (единичная ступенчатая функция, функция единичного скачка, включенная единица) кусочно постоянная функция, равная нулю для отрицательных значений аргумента и единице для пол … Википедия
dic.academic.ru
Исследование функций на четность. Видеоурок. Алгебра 9 Класс
Функция  называется четной, если для любого
называется четной, если для любого 

График четной функции симметричен относительно оси y. Верно и обратное – если график функции симметричен относительно оси y, то функция четная.
Функция  называется нечетной, если для любого
называется нечетной, если для любого 

График нечетной функции симметричен относительно начала координат. Верно и обратное – если график функции симметричен относительно начала координат, то функция нечетна.
Приведенные факты сформулируем более кратко и проиллюстрируем на графике.

1. (рис
(рис ).
).
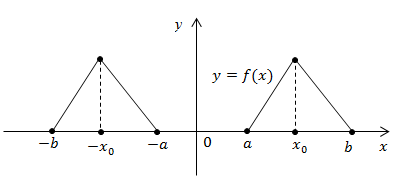
Рис. 1
2.  (рис. 2).
(рис. 2).

Рис. 2
Этими опорными фактами мы будем пользоваться при определении четности функции.
Из приведенных определений и свойств вытекает
Алгоритм исследования функции  на четность.
на четность.
- Исследовать
 на симметричность относительно нуля
на симметричность относительно нуля Если
Если  не симметрична относительно нуля, это функция общего вида.
не симметрична относительно нуля, это функция общего вида. - Найти

- Сравнить

- если
 то функция четная;
то функция четная; - если
interneturok.ru
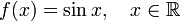 .
. .
. .
.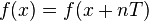 ,
где
,
где  —
любое целое число.
—
любое целое число.

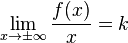

 (x).
(x). (x)=0
(x)=0 x1, x2,…
x1, x2,…
 a;b
a;b ,
а x2
,
а x2

 a;b
a;b .
. ,
, ,
, ,
, ,
если
,
если .
.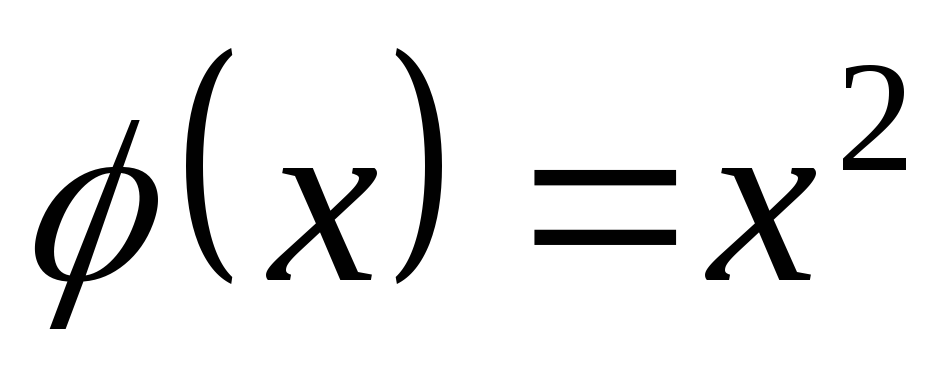 и
и .
Найти
.
Найти и
и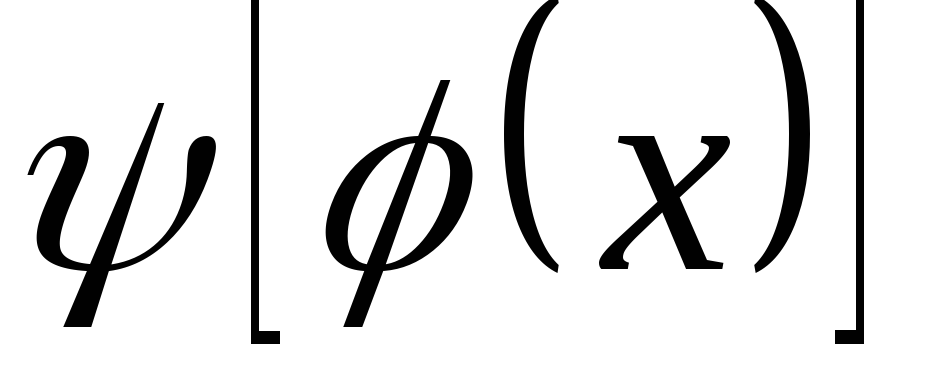 .
.


![f:[-X,X] \subset \mathbb{R} \to \mathbb{R}](/800/600/https/dic.academic.ru/pictures/wiki/files/101/ed5743482e96ed8c5bee8117ee026844.png) называется нечётной, если справедливо равенство
называется нечётной, если справедливо равенство![f(-x)=-f(x), \quad \forall x \in [-X,X].](/800/600/https/dic.academic.ru/pictures/wiki/files/102/f6ab611fbaf32ad9e732deb96e3fb9ca.png)
![f(-x) = f(x),\quad \forall x \in [-X,X].](/800/600/https/dic.academic.ru/pictures/wiki/files/55/712740b91f011d49b277240b725bef17.png)
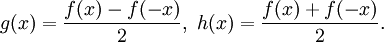
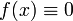 — единственная функция, одновременно являющаяся нечётной и чётной.
— единственная функция, одновременно являющаяся нечётной и чётной. на симметричность относительно нуля
на симметричность относительно нуля Если
Если 

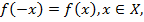 то функция четная;
то функция четная;