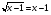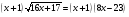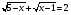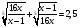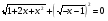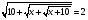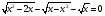Иррациональные уравнения на примерах

Иррациональными называют уравнения в которых неизвестная величина находится под знаком корня определенного степени. Простейшие иррациональные уравнения решаются или подъемом в степень или заменой . Сложные иррациональные уравнения сводятся к предыдущим некоторыми искусственными методами . Например, такое на первый взгляд сложное уравнение

сводится к квадратному заменой

Зачастую при раскрытии иррациональности используют формулу сложного радикала

Стоит отметить, что при решении иррациональных уравнений необходимо определять область допустимых значений. Кроме того следует производить проверку, подставляя найденные значения неизвестных в исходное уравнение, поскольку при возведении в степень мы увеличиваем степень уравнения что может привести к появлению посторонних корней.

Перейдем к вычислениям.

Пример 1. Найти решение уравнения

Решение:

Находим область допустимых значений

Подносим обе части уравнения в квадрат и решаем

Получили решение x=3.

————————-

Пример 2. Найти решение уравнения

Решение:

ОДЗ для уравнения

Раскрываем иррациональность уравнения и находим

Он принадлежит области допустимых значений , то есть — является решением.

————————-

Пример 3. Решить уравнение

Решение:

Находим область допустимых значений

ОДЗ:

По описанной схеме подносим обе части в квадрат чтобы избавиться иррациональности

Переносим все слагаемые кроме корней в правую часть и упрощаем

Для раскрытия иррациональности снова выполняем возведения в квадрат и упрощение

Получили квадратное уравнение, корни которого находим с помощью дискриминанта

Второй корень не принадлежит области допустимых значений . Эту проверку следует выполнять всегда , иначе получите больше корней чем нужно, причем они не удовлетворяют исходное уравнение .

Итак решением будет значение x=4.

————————-

Пример 4. Решить уравнение

Решение:
Область допустимых значений для данного уравнения в простой способ найти не удастся , поэтому выполним решение после чего проверим подстановкой полученные корни.

Подносим обе части уравнения в квадрат

Данное выражение большинство из Вас упростило бы на x и подносило к квадрату. Но это было бы неправильно.
На x делить можно когда он принимает ненулевое значение. В данном случае x=0 будет решением уравнения , в чем легко убедится

После того, как мы это учли можно продолжать вычисления

Выполняем проверку

Получили два корня уравнения x=0, x=6.

————————-

Пример 5. Найти решение уравнения

Решение:
Преподносить к квадрату обе стороны в подобных уравнениях не нужно. Для упрощения делаем замену

Уравнение превратится в следующее

Умножаем на y и переписываем в виде квадратного уравнения

Теорема Виета дает нам два одинаковые корни

Иррациональные уравнения | Формулы с примерами

Определение
Иррациональные уравнения — это такие уравнения, которые содержат переменную под знаком корня.

Решаются с помощью перехода к рациональным уравнениям или системам.

Примеры решения иррациональных уравнений 10, 11 класс

1. Возведение обеих частей уравнения в степень.

Формула
Правило
! При возведении в четную степень возможно появление посторонних корней. Поэтому обязательно нужно выполнить проверку, подставляя полученные корни в исходное уравнение.

! Проверка часто упрощается, если найти ОДЗ уравнения. Посторонними будут корни, не принадлежащие ОДЗ.

Примеры решения
1)  ? x³ — x3 = x + 1 x³ — x = (x + 1) ³ 3x² + 4x + 1 = 0 x₁ = — 13, x = -1.

Ответ: {- 13; -1}

2)  ? x = x — 2 => x = (x — 2)². x² — 5x + 4 = 0 x₁ = 4, x₂ = 1.

Проверка: x₁ = 4, ? 4 = 4 — 2 — верно

x₂ = 1, ? 1 = 1 — 2 — ложно,

Значит x = 1 — посторонний корень.

2. Введение одной или нескольких новых переменных.

Пример решения
2? x²3 + ? x3 = 3

Пусть y = ? x3.   Тогда 2y² + y — 3 = 0 y₁ = 1, y₂ = — 32.

Значит ? x3 = 1 или ? x3 = — 32 x = 1 или x = — 278.

Ответ: {1; — 278}

3. Предварительный анализ ОДЗ и вида уравнения.

Пример решения
? 5 — x + ? 25 — x² = 0

? 5 — x ? 0 и ? 25 — x² ? 0 (как арифметические корни).

Значит из сумма равна нулю, только если:

	? 5 — x = 0			x = 5	x = 5.   Ответ: 5.
	? 25 — x2 = 0			x = ±5

Методическая разработка на тему «Иррациональные уравнения»

Шибанова Татьяна Павловна

Методы решения иррациональных уравнений.

Цели:

• Образовательная –познакомить учащихся с нестандартными методами решения иррациональных уравнений; систематизировать знания учащихся о методах решения иррациональных уравнений, способствовать формированию умений классифицировать иррациональные уравнения по методам решений, научить применять эти методы, выбирать рациональный путь решения.

• Развивающая –способствовать развитию математического кругозора, логического мышления.

• Воспитательная – содействовать воспитанию интереса к иррациональным уравнениям, воспитывать чувство коллективизма, самоконтроля, ответственности.

Задачи урока:

1. Повторить определение и основные методы решения иррациональных уравнений;

2. Продемонстрировать нестандартные методы решения иррациональных уравнений; формировать умение выбирать рациональные пути решения;

3. Освоение всеми учащимися алгоритмов решения иррациональных уравнений, закрепление теоретических знаний при решении конкретных примеров;

4. Развитие у учащихся логического мышления в процессе поиска рациональных методов и алгоритмов решения;

5. Развитие культуры научных и учебных взаимоотношений между учениками и между учениками и учителем; воспитание навыков совместного решения задач.

Методы обучения:

• Информационно- иллюстративный;

• репродуктивный;

• проблемный диалог;

• частично-поисковый;

• системные обобщения.

Формы организации учебной деятельности:

• Фронтальная,

• групповая,

• самопроверка,

• взаимопроверка,

• коллективные способы обучения.

Оборудование урока: компьютер, проектор, карточки с заданием, лист учета знаний.

Продолжительность занятия: 2 урока по 45 минут.

План урока:

1. Организационный момент. Постановка цели, мотивация.

2. Актуализация опорных знаний, проверка домашней работы.

3. Изучение нового материала.

4. Закрепление изученного материала на данном уроке и ранее пройденного, связанного с новым.

5. Подведение итогов и результатов урока. Рефлексия.

6. Задание на дом.

Конспект урока.

1. Организационный момент. Постановка цели, мотивация.

2. Актуализация опорных знаний проводится в форме беседы по лекционному материалу по данной теме с использованием компьютерной презентации. Проверка домашнего задания.

Уравнение, содержащее переменные под знаком корня или дробной степени, называется иррациональным.

Назовите иррациональные уравнения:

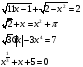
Это значит найти все такие значения переменной, при которых уравнение превращается в верное равенство, либо доказать, что таких значений не существует.

1. Уединение радикала. Возведение в степень.

a) При решении иррационального уравнения с радикалом четной степени возможны два пути:

1. использование равносильных преобразований

для уравнения вида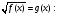

для уравнения вида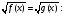

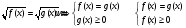
2. после возведения в степень выполнение проверки, так как возможно появление посторонних корней

b) При решении иррационального уравнения с радикалом нечетной степени возведение в нечетную степень правой и левой части уравнения всегда приводит к равносильному уравнению и потеря корней или их приобретения происходить не может.

Пример 1:

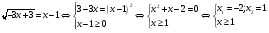
Ответ: x=1

Пример 2: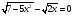

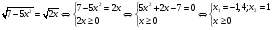
Ответ: x=1

Пример 3:

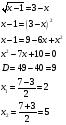Проверка: x=2 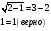x=5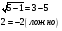

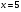— посторонний корень

Ответ: x=2

Если радикалов несколько, то уравнение возводить в степень приходится возводить неоднократно.

Пример 4: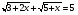

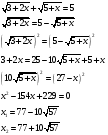
Проверка показывает, что оба корня подходят.

Ответ: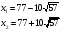

2. Метод введения вспомогательного неизвестного или “метод замены

Пример 5:

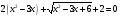
Сделаем замену 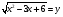причём 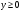тогда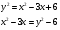

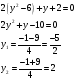не удовлетворяет условию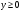

Возвращаемся к замене:

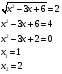Проверка показывает, что оба корня подходят.

Ответ:1;2

Иногда удобно ввести не одну, а несколько переменных.

Пример 6: .

Заметим, что знаки х под радикалом различные. Введем обозначение

, .

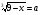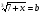Тогда,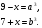

Выполним почленное сложение обеих частей уравнения .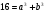

Имеем систему уравнений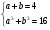

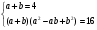
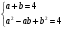
Т.к. а + в = 4, то

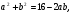
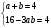
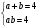
Значит: 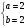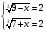9 – x = 8 , х = 1.

Ответ : х = 1

1. 1. 1. 1. 3. Метод разложения на множители или расщепления.

• Произведение равно нулю тогда и только тогда, когда хотя бы один из входящих в него сомножителей равен нулю, а остальные при этом имеют смысл.

Пример 7: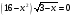

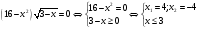
Ответ: -4;3

2. Изучение нового материала.

Нестандартные методы решения иррациональных уравнений.

4. Умножение на сопряжённое выражение.

5. Переход к модулю.

6. Использование свойств функции:

• • • Область определения функции (ОДЗ)

    • Область значения функции

    • Свойство ограниченности функции (метод оценок)

    • Свойство монотонности

    • Использование суперпозиций функций

Воспользуемся формулой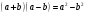

Пример 8: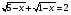

Умножим обе части уравнения на сопряжённое выражение: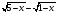

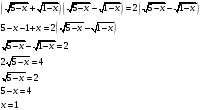
Проверка показывает, что число является корнем.

Ответ: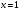

Для этого метода воспользуемся тождеством: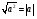

Пример 9: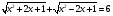

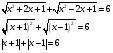
Рассмотрим случаи:

тогда

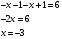
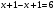
2=6( ложно)

Ответ: -3;3

Иногда нахождение области определения функций, входящих в уравнение, существенно облегчает его решение.

Пример 10: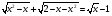

ОДЗ: 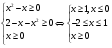ОДЗ: x=0 и x=1

Проверка показывает, что только x=1 является корнем.

Ответ: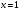

Пример 11: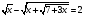

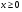, тогда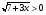

Тогда 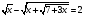невозможно.

Ответ: корней нет.

Пример 12: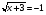

Данное уравнение не имеет решений, так как его левая часть- функция 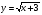может принимать только неотрицательные значения.

Ответ: корней нет

Пример 13: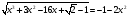

Учитывая то, что левая часть уравнения – функция 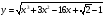может принимать только неотрицательные значения, решим неравенство: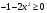

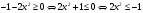неравенство решений не имеет, тогда и исходное уравнение тоже.

Ответ: корней нет

Пример 14:

Заметим, что 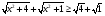, т.е. 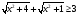, а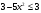

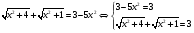
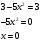Проверка показывает, что это значение является и корнем второго уравнения.

Ответ: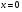

Пример 15: .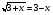

Рассмотрим функци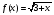и и .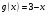

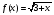монотонно возрастает, а 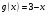— убывает, следовательно, уравнение имеет не более одного корня.

Значение корня легко найти подбором: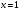

Ответ: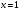

Пример 16: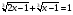

Функция 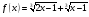возрастает на своей области определения, как сумма двух возрастающих функций, следовательно, уравнение имеет не более одного корня. Так как 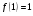, то 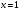— единственный корень .

Ответ: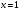

Пример 17: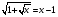

Запишем уравнение в виде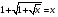

Рассмотрим функцию 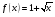— монотонно возрастающую, тогда уравнение имеет вид 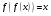. Оно равносильно уравнению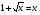

Сделаем замену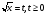

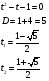не удовлетворяет условию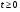

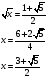
Ответ: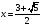

4. Закрепление изученного материала на данном уроке и ранее пройденного, связанного с новым.

Решение уравнений в группах по 6 человек.

Ребята получают карточку с заданием. Решение уравнений обсуждают вместе, записывают его.

После выполнения группами заданий проводится взаимопроверка. Группы меняются заданиями с решениями по кругу:

1 6 5

2 3 4

Учащиеся групп обсуждают решение, исправляют ошибки и выставляют оценки.

Потом работы с выставленными оценками возвращаются в группы для обсуждения вклада каждого в решение проблемы.

Выставляются каждому оценки с занесением в оценочную таблицу. Учитель контролирует и вносит, если нужно, свои коррективы.

4. Подведение итогов и результатов урока. Рефлексия.

5. Задание на дом:

Решить уравнения:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. *

Используемая литература.

1. Чулков П.В. Материалы курса «Уравнения и неравенства в школьном курсе математики»: Лекции 1-8. – М.: Педагогический университет «Первое сентября», 2006.

2. Дьячков А.К., Иконникова Н.И., Казак В.М., Морозова Е.В. Единый государственный экзамен. Математика. – Челябинск: Взгляд, 2006 –Ч.1,2

3. Шарыгин И. Ф. Факультативный курс по математике: Решение задач. – М.: Просвещение, 1989

4. Черкасов О.Ю., Якушев А.Г. Математика: интенсивный курс подготовки к экзамену. – М.: Айрис-пресс, 2004.

5. Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по алгебре и началам анализа для 10-11 классов. – М.: Илекса, 2006.

Задания для работы в группах:

Вариант 1(1,3,5 группы).

Решите уравнения,

используя подсказку:

1. Возведи обе части в квадрат:

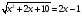
2. Выполни замену:

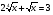
3. Найди ОДЗ:

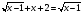
4. Умножай на сопряжённое выражение:

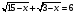
5. Переходи к модулю:

6. Используй свойства функций:

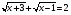
7. Реши любым способом:

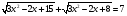
Вариант 2( 2,4,6 группы)

Решите уравнения,

используя подсказку:

1. Возведи обе части в квадрат:

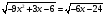
2. Выполни замену:

3. Найди ОДЗ:

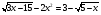
4. Умножай на сопряжённое выражение:

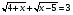
5. Переходи к модулю:

6. Используй свойства функций:

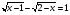
7. Реши любым способом:

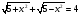
Проверочная работа по теме: «Методы

Вариант 1

Решите уравнения,

используя подсказку:

1. Возведи обе части в квадрат:

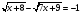
2. Выполни замену:

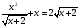
3. Найди ОДЗ:

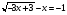
4. Разложи на множители:

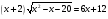
5. Умножай на сопряжённое выражение:

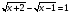
6. Переходи к модулю:

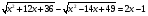
7. Используй свойства функций:

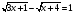
8. Реши любым способом:

решения иррациональных уравнений»

Вариант 2

Решите уравнения,

используя подсказку:

1. Возведи обе части в квадрат:

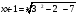
2. Выполни замену:

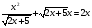
3. Найди ОДЗ:

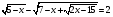
4. Разложи на множители:

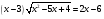
5. Умножай на сопряжённое выражение:

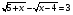
6. Переходи к модулю:

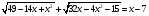
7. Используй свойства функций:

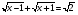
8. Реши любым способом:

Иррациональные уравнения — Мегаобучалка

Иррациональные уравнения и неравенства довольно часто встречаются в материалах вступительных экзаменов различных высших учебных заведений. Разделы Единого государственного экзамена по математике также включают данную тематику как в простых случаях (части А и В), так и в более сложных (часть С). Некоторые правила и особенности решения таких уравнений и неравенств изложены в настоящем разделе.

Уравнение, содержащее неизвестное под знаком радикала, называется иррациональным. Решение иррациональных уравнений сводится к переходу от иррационального к рациональному уравнению путем возведения в степень обеих частей уравнения или замены переменной. При возведении обеих частей уравнения в четную степень возможно появление посторонних корней, поэтому следует проверять корни подстановкой в исходное уравнение.

При решении уравнений необходимо учитывать следующее:

1) если показатель радикала – четное число, то подкоренное выражение должно быть неотрицательно, при этом значение радикала также является неотрицательным;

2) если показатель радикала – нечетное число, то подкоренное выражение может быть любым действительным числом, в этом случае знак радикала совпадает со знаком подкоренного выражения.

 

Пример 1. Решить уравнение:

Решение. Найдем область допустимых значений переменной. Поскольку корни четной степени, то подкоренные выражения должны быть неотрицательны:

Решение данной системы неравенств есть область допустимых значений переменной (или область определения уравнения).

Возведем обе части уравнения в квадрат:

2

или

Значение не входит в область допустимых значений, поэтому является посторонним корнем для исходного уравнения.

Проверим, удовлетворяет ли х = 4 уравнению, для этого подставим х = 4 в уравнение:

4 = 4, поэтому х = 4 – корень исходного уравнения.

Ответ: х = 4.

Пример 2. Решить уравнение:

 

Решение. Допустимые значения переменной должны удовлетворять системе неравенств:

Областью допустимых значений являются _. Возведем левую и правую части уравнения в квадрат:

Вновь возведем левую и правую части уравнения в квадрат:

Корни могут быть найдены по теореме Виета:

откуда

Корень не входит в область допустимых значений, т. е. является посторонним корнем для исходного уравнения. Проверим корень _, подставив его в уравнение:

Ответ:

Замечание:

Получив выражение можно было заметить, что должно выполняться неравенство или Совмещая эти значения с областью допустимых значений, где получаем единственно возможный корень который и надо было проверить.

Пример 3. Решить уравнение:

Решение. При решении этого уравнения можно сразу ввести замену переменной, обозначив один корень за у, а другой за . Можно идти и традиционным путем, начиная с области допустимых значений.

Областью допустимых значений является решение системы неравенств:

 

Поскольку то уравнение может быть записано в виде:

тогда область допустимых значений удовлетворяет системе,

 

Решим неравенство методом интервалов (рис. 7.1).

 

Рис. 7.1.Метод интервала.

Область допустимых значений

Обозначим где тогда

 

Пусть тогда

Пусть тогда

Оба корня х = 0 и х = – 5 принадлежат области допустимых значений. Выполним проверку.

Если х = 0, тогда

 

Если х = – 5, тогда

Ответ: х = 0, х = – 5.

Пример 4. Решить уравнение:

Решение. Допустимыми значениями переменной являются Обозначим где .

Уравнение примет вид

По теореме Виета где посторонний корень, не удовлетворяющий ограничению .

Если у = 2, тогда

Полученное биквадратное уравнение сведем к квадратному уравнению заменой , где ,

По теореме Виета Поскольку , то – посторонний корень. Если то откуда Но не входит в область допустимых значений, поэтому .

Сделаем проверку:

Ответ: х = 1.

Пример 5. Решить уравнение:

Решение. Допустимые значения неизвестного удовлетворяют условиям,

Второе неравенство справедливо для , при этих же значениях переменной левая и правая часть третьего неравенства неотрицательны, поэтому его можно решить возведением в квадрат:

Неравенство выполняется для любых действительных значений переменной. Таким образом, областью допустимых значений переменной являются . Возведем в квадрат левую и правую часть уравнения:

2

2

Если то

По теореме Виета х₁ = 5, х₂= 1.

Условию удовлетворяет только значение .

Если , то

По теореме Виета , Первое из значений не удовлетворяет условию второе значение не принадлежит области допустимых значений, поэтому оба значения и не являются корнями уравнения. Выполним проверку для :

Ответ:

Замечание. Возможен другой вариант решения: в исходном уравнении подкоренные выражения являются полными квадратами; обозначив получим

и уравнение примет вид :

или

Если то

– оба значения не удовлетворяют условию

Если то

Условию удовлетворяет значение

откуда

Остается лишь выполнить проверку.

В некоторых случаях решение может быть получено дополнением уравнения до формул сокращенного умножения (разности квадратов и кубов, суммы кубов). При этом используется известное правило, что уравнение не изменится, если левую и правую его часть умножить на одно и то же отличное от нуля выражение.

 

Пример 6. Решить уравнение:

Решение. Областью допустимых значений являются все действительные значения переменной. Запишем уравнение в виде и домножим левую и правую часть на неполный квадрат разности так, чтобы в левой части получить формулу суммы кубов:

Заметим, что для любых действительных значений a и b, следовательно, обе части уравнения умножены на одно и то же положительное выражение:

Произведение сомножителей равно нулю тогда и только тогда, когда хотя бы один из сомножителей равен нулю. Второй из сомножителей не может обращаться в ноль, так как

для любых действительных значений х, поэтому:

Сделаем проверку:

Ответ:

Иррациональное уравнение — Википедия. Что такое Иррациональное уравнение

Иррациональное уравнение — это уравнение, содержащее неизвестное под знаком корня √{\displaystyle \surd } или возведённое в степень, которую нельзя свести к целому числу. Простейшим примером иррационального уравнения является уравнениеx=2{\displaystyle {\sqrt {x}}=2} или x3=−3{\displaystyle {\sqrt[{3}]{x}}=-3}. Иногда корни могут обозначать в виде рациональных степеней неизвестной, то есть вместо xn{\displaystyle {\sqrt[{n}]{x}}} пишут x1n{\displaystyle x^{\frac {1}{n}}}.

Рассмотрим некоторые уравнения и попытаемся классифицировать их:

Короче сформулировать правило отнесения уравнений к той или иной категории можно так:

• если все степени неизвестной\ых в уравнении принадлежат множеству натуральных чисел N{\displaystyle \mathbb {N} }, то такое уравнение считается алгебраическим.
• если все степени неизвестной\ых в уравнении принадлежат множеству целых чисел Z{\displaystyle \mathbb {Z} }, то такое уравнение называется рациональным.
• если все степени неизвестной\ых в уравнении принадлежат множеству рациональных чисел Q{\displaystyle \mathbb {Q} }, то такое уравнение называется иррациональным.

Образцами более сложных иррациональных уравнений могут послужить такие примеры:

x+4+x+9=5{\displaystyle {\sqrt {x+4}}+{\sqrt {x+9}}=5},

72×2+63−3×23=11{\displaystyle 7{\sqrt[{3}]{2x^{2}+6}}-3{\sqrt[{3}]{x^{2}}}=11},

x2+x−1=10x+x−211+1{\displaystyle x^{2}+{\sqrt {x-1}}=10x+{\sqrt[{11}]{x-2}}+1}

Связь с алгебраическими уравнениями

Всякое иррациональное уравнение с помощью элементарных алгебраических операций (умножение, деление, возведение в целую степень обеих частей уравнения) может быть сведено к рациональному алгебраическому уравнению. Например, уравнение x2+x=2{\displaystyle {\sqrt {x^{2}+x}}=2} возведением во вторую степень можно преобразовать к виду x2+x=4{\displaystyle x^{2}+x=4}, что уже не иррациональное уравнение, но алгебраическое.

При этом следует иметь в виду, что полученное рациональное алгебраическое уравнение может оказаться неэквивалентным исходному иррациональному уравнению, а именно может содержать «лишние» корни, которые не будут корнями исходного иррационального уравнения. Поэтому, найдя корни полученного рационального алгебраического уравнения, необходимо проверить, а будут ли все корни рационального уравнения корнями иррационального уравнения.

Подходы к решению

В общем случае трудно указать какой-либо универсальный метод решения любого иррационального уравнения, так как желательно, чтобы в результате преобразований исходного иррационального уравнения получилось не просто какое-то рациональное алгебраическое уравнение, среди корней которого будут и корни данного иррационального уравнения, а рациональное алгебраическое уравнение образованное из многочленов как можно меньшей степени. Желание получить рациональное алгебраическое уравнение, образованное из многочленов как можно меньшей степени, вполне естественно, так как нахождение всех корней рационального алгебраического уравнения само по себе может оказаться довольно трудной задачей, решить которую полностью мы можем лишь в весьма ограниченном числе случаев.

Возведение в степень

Если обе части иррационального уравнения возвести в одну и ту же нечетную степень и освободиться от радикалов, то получится уравнение, равносильное исходному уравнению.

При возведении уравнения в чётную степень получают уравнение, являющееся следствием исходного. Поэтому возможно появление посторонних решений уравнения. Причина приобретения корней состоит в том, что при возведении в четную степень чисел, равных по абсолютной величине, но разных по знаку, получается один и тот же результат.

Заметим, что потеря корней при возведении уравнения в четную степень невозможна, но могут появиться посторонние корни. Рассмотрим пример:

Решим уравнение x2+4x−5=4x−8{\displaystyle {\sqrt {x^{2}+4x-5}}=4x-8}

Возведём обе части уравнения во вторую степень

(x2+4x−5)2=(4x−8)2{\displaystyle ({\sqrt {x^{2}+4x-5}})^{2}=(4x-8)^{2}}

так как мы возводим в чётную степень, то возможно появление посторонних корней, ибо самим процессом возведения мы расширяем область допустимых значений (ОДЗ) для подкоренных выражений.

Так, когда 4x−8{\displaystyle 4x-8} был приравнен к заведомо положительному числу (так как x2+4x−5⩾0{\displaystyle {\sqrt {x^{2}+4x-5}}\geqslant 0} в силу определения арифметического корня), переменная x{\displaystyle x} не могла принимать значения, которые бы обратили 4x−8{\displaystyle 4x-8} в отрицательные числа, значит 4x−8⩾0{\displaystyle 4x-8\geqslant 0} или x⩾2{\displaystyle x\geqslant 2}.

Другими словами в месте с постановкой задачи нам дали ещё и ограничения на значения переменной (ОДЗ) в виде x⩾2{\displaystyle x\geqslant 2}. Но, после возведения обеих частей в квадрат, мы получаем уравнение

x2+4x−5=16×2−64x+64{\displaystyle x^{2}+4x-5=16x^{2}-64x+64},

уже в котором область допустимых значений (ОДЗ) переменой x{\displaystyle x} совершенна другая (теперь x{\displaystyle x} может принимать совершенно любые значения, то есть ОДЗ расширилось относительно первоначального уравнения).

Очевидно, что вероятность появления посторонних корней резко выросла просто по факту того, что теперь корнем может стать гораздо больше чисел, а не только те, что x⩾2{\displaystyle x\geqslant 2}.

Продолжая решать и упрощать x2+4x−5=16×2−64x+64{\displaystyle x^{2}+4x-5=16x^{2}-64x+64} мы получим квадратное уравнение:

15×2−68x+69=0{\displaystyle 15x^{2}-68x+69=0}, корнями которого являются

x=3{\displaystyle x=3} и x=2315{\displaystyle x={\frac {23}{15}}}

Следует заметить, что x=3{\displaystyle x=3} и x=2315{\displaystyle x={\frac {23}{15}}} точно являются корнями уравнения 15×2−68x+69=0{\displaystyle 15x^{2}-68x+69=0}, но ещё не известно являются ли они корнями первоначального x2+4x−5=4x−8{\displaystyle {\sqrt {x^{2}+4x-5}}=4x-8} уравнения!!!

Так мы знаем, что корни первоначального уравнения не могут быть меньше 2, а меж тем корень x=2315≈1.533333…{\displaystyle x={\frac {23}{15}}\approx 1.533333…} меньше двух, значит он не может быть корнем первоначального уравнения.

Ответ: x∈{3}{\displaystyle x\in \{3\}}

Замена системой условий

Использование свойств корней

Введение новых переменных

Введение вспомогательной переменной в ряде случаев приводит к упрощению уравнения. Чаще всего в качестве новой переменной используют входящий в уравнение корень (радикал). При этом уравнение становится рациональным относительно новой переменной.

Пример 1^[1]: Решить уравнение 2×2+3x+2×2+3x+9=33,x∈R{\displaystyle 2x^{2}+3x+{\sqrt {2x^{2}+3x+9}}=33,x\in \mathbb {R} }

Сделаем замену y=2×2+3x+9{\displaystyle y={\sqrt {2x^{2}+3x+9}}}, ясно что при этом мы наложили ограничения на новую переменную в виде y⩾0{\displaystyle y\geqslant {0}}, так как арифметический корень не может быть отрицательным числом.

После возведения y{\displaystyle y} во вторую степень мы избавимся от знака корня и получим выражение y2=2×2+3x+9{\displaystyle y^{2}=2x^{2}+3x+9}. Далее, после подстановки y{\displaystyle y} в исходное уравнение, мы получим такое уравнение:

y2+y−42=0{\displaystyle y^{2}+y-42=0},

корни которого y=6{\displaystyle y=6} и y=−7{\displaystyle y=-7}. Но y{\displaystyle y} не может быть отрицательным числом ввиду того как мы определили y{\displaystyle y} через нашу подстановку, поэтому корнем будем считать лишь y=6{\displaystyle y=6}. Далее, решая уравнение 2×2+3x+9=6{\displaystyle {\sqrt {2x^{2}+3x+9}}=6}, мы получаем корни x=3{\displaystyle x=3} и x=−4.5{\displaystyle x=-4.5}.

Ответ: x∈{3;−4.5}{\displaystyle x\in \{3;-4.5\}}

Пример 2^[2]: Решить уравнение x+283+x−93=1{\displaystyle {\sqrt[{3}]{x+28}}+{\sqrt[{3}]{x-9}}=1}

Сделаем две замены: u=x+283{\displaystyle u={\sqrt[{3}]{x+28}}} и v=x−93{\displaystyle v={\sqrt[{3}]{x-9}}}, после их возведения в третью степень получим u3=x+28{\displaystyle u^{3}=x+28} и v3=x−9{\displaystyle v^{3}=x-9}. Далее, решив каждое новое уравнение относительно x{\displaystyle x}

x=u3−28{\displaystyle x=u^{3}-28} и x=v3+9{\displaystyle x=v^{3}+9}, и после уравнивания этих уравнений, мы получаем уравнение u3−28=v3+9{\displaystyle u^{3}-28=v^{3}+9}, но ввиду того, как мы вводили u{\displaystyle u} и v{\displaystyle v}, мы так же имеем уравнение u+v=1{\displaystyle u+v=1}, значит у нас появилась система из уравнений:

{u+v=1u3−v3=37{\displaystyle {\begin{cases}u+v=1\\u^{3}-v^{3}=37\end{cases}}}

Решив систему, мы получаем значения v1=3{\displaystyle v_{1}=3} и v2=−4{\displaystyle v_{2}=-4}, это значит нам надо решить ещё два уравнения:

x−93=3{\displaystyle {\sqrt[{3}]{x-9}}=3} и x−93=−4{\displaystyle {\sqrt[{3}]{x-9}}=-4}, решения которых x=36{\displaystyle x=36} и x=−55{\displaystyle x=-55}.

Ответ: x∈{36;−55}{\displaystyle x\in \{36;-55\}}

Использование области определения

Использование области значений

Тождественное преобразования

Использование производной

Использование мажоранты

Термин «мажоранта» происходит от французского слова «majorante», от «majorer» — объявлять большим.

Мажорантой данной функции f(x){\displaystyle f(x)} на заданном промежутке называется такое число A, что либо f(x)⩽A{\displaystyle f(x)\leqslant {A}} для всех x из данного промежутка, либо f(x)⩾A{\displaystyle f(x)\geqslant {A}} для всех x из данного промежутка. Основная идея метода состоит в использовании следующих теорем для решения иррациональных уравнений:

Теорема № 1.

Пусть f(x){\displaystyle f(x)} и g(x){\displaystyle g(x)} — некоторые функции, определённые на множестве D{\displaystyle D}. Пусть f(x){\displaystyle f(x)} ограничена на этом множестве числом А сверху, а g(x){\displaystyle g(x)} ограничена на этом множестве тем же числом А, но снизу.

Тогда уравнение f(x)=g(x){\displaystyle f(x)=g(x)} равносильно системе:

{f(x)=Ag(x)=A{\displaystyle {\begin{cases}f(x)=A\\g(x)=A\end{cases}}}

Теорема № 2.

Пусть f(x){\displaystyle f(x)} и g(x){\displaystyle g(x)} — некоторые функции, определённые на множестве D{\displaystyle D}. Пусть f(x){\displaystyle f(x)} и g(x){\displaystyle g(x)} ограничены на этом множестве снизу (сверху) числами А и В соответственно. Тогда уравнение f(x)+g(x)=A+B{\displaystyle f(x)+g(x)=A+B} равносильно системе уравнений:

{f(x)=Ag(x)=B{\displaystyle {\begin{cases}f(x)=A\\g(x)=B\end{cases}}}

Теорема № 3.

Пусть f(x){\displaystyle f(x)} и g(x){\displaystyle g(x)} — некоторые неотрицательные функции, определённые на множестве D{\displaystyle D}. Пусть f(x){\displaystyle f(x)} ограничена сверху (или снизу) числами А и В соответственно. Тогда уравнение f(x)g(x)=AB{\displaystyle f(x)g(x)=AB} равносильно системе уравнений (при условии, что A>0{\displaystyle A>0} и B>0{\displaystyle B>0}):

{f(x)=Ag(x)=B{\displaystyle {\begin{cases}f(x)=A\\g(x)=B\end{cases}}}

В этом утверждении особенно важно условие неотрицательности функций f(x){\displaystyle f(x)} и g(x){\displaystyle g(x)}, а также условие положительности А и В.

Пример:

Решить уравнение (x−2y+1)2+1+(3x−y−2)2+25=6{\displaystyle {\sqrt {(x-2y+1)^{2}+1}}+{\sqrt {(3x-y-2)^{2}+25}}=6}

Введём более короткие обозначения: f(x,y)=(x−2y+1)2+1{\displaystyle f(x,y)={\sqrt {(x-2y+1)^{2}+1}}} и g(x,y)=(3x−y−2)2+25{\displaystyle g(x,y)={\sqrt {(3x-y-2)^{2}+25}}}.

Значения f(x,y){\displaystyle f(x,y)} больше или равны 1, так как подкоренное выражение (x−2y+1)2+1{\displaystyle (x-2y+1)^{2}+1} очевидно ⩾1{\displaystyle \geqslant {1}}. Причём f(x,y)=1{\displaystyle f(x,y)=1}, только если (x−2y+1)2=0{\displaystyle (x-2y+1)^{2}=0}. Аналогично, значения g(x,y){\displaystyle g(x,y)} не меньше 5. Значит можно записать f(x,y)+g(x,y)=1+5{\displaystyle f(x,y)+g(x,y)=1+5}. Следовательно, используя Теорему № 2:

{f(x,y)=1g(x,y)=5{\displaystyle {\begin{cases}f(x,y)=1\\g(x,y)=5\end{cases}}} или {(x−2y+1)2+1=1(3x−y−2)2+25=5{\displaystyle {\begin{cases}{\sqrt {(x-2y+1)^{2}+1}}=1\\{\sqrt {(3x-y-2)^{2}+25}}=5\end{cases}}}

Возведя оба уравнения в квадрат, получим

{(x−2y+1)2=0(3x−y−2)2=0{\displaystyle {\begin{cases}(x-2y+1)^{2}=0\\(3x-y-2)^{2}=0\end{cases}}}, упрощая далее {x−2y+1=03x−y−2=0{\displaystyle {\begin{cases}x-2y+1=0\\3x-y-2=0\end{cases}}}

Единственное решение этой системы (1;1){\displaystyle (1;1)}

Ответ: (1;1){\displaystyle (1;1)}

Функциональный подход

Графический подход

Примечания

Иррациональным уравнением Называется уравнение, содержащее неизвестную под знаком корня или под дробным показателем. (В этом параграфе термин «корень» будет соответствовать операции извлечения корня с определенным показателем, в отличие от термина «решение»).

Основной метод решения таких уравнений – возведение обеих частей уравнения в одну и ту же степень, чтобы корни исчезли. Иногда приходится возводить в степень несколько раз. При этом следует анализировать, какие корни надо оставлять в левой части уравнения, а какие корни перенести в правую часть (если корней несколько). От этого часто зависит рациональность решения.

Поскольку корни нечетной степени определены для любых по знаку подкоренных выражений и принимают любые по знаку значения, то возведение уравнения в нечетную степень является равносильным преобразованием (т. е. мы не теряем решений и не получаем посторонних).

Корни с четным показателем определены для F(X) ³ 0. Возведение уравнения, содержащего такие корни, в четную степень может изменить ОДЗ уравнения и привести к посторонним решениям. В таком случае итоговым моментом в решении уравнения является проверка полученных решений подстановкой в заданное уравнение. Проверка решения по ОДЗ такого уравнения недостаточна.

ОДЗ иррационального уравнения следует находить в том случае, если предполагается, что она состоит только из нескольких чисел или может быть пустым множеством. Если ОДЗ состоит из одного, двух и т. д. чисел, то уравнение можно не решать, а эти числа проверять (являются ли они решением) подстановкой в заданное уравнение.

Если ОДЗ есть пустое множество, то уравнение не имеет решений.

При решении иррациональных уравнений используют также метод замены переменной и другие методы.

Если имеется уравнение вида где С < 0, то оно не имеет решений, так как корни с четным показателем понимаем в арифметическом смысле, т. е. как неотрицательные.

Некоторые типы иррациональных уравнений

Пусть далее – некоторые выражения с неизвестной Х,

I тип: Уравнение вида

(5.1)

Возведение в -ю степень приводит к равносильному уравнению

Уравнение

(5.2)

После возведения в -ю степень сводится к равносильному уравнению

Уравнение

(5.3)

После возведения в степень 2N приводит к уравнению-следствию

(5.4)

Найденные корни уравнения (5.4) проверяют подстановкой в уравнение (5.3) и отбирают те из них, которые удовлетворяют уравнению (5.3).

Уравнение

(5.5)

После возведения в степень 2N сводится к уравнению-следствию

(5.6)

Корни уравнения (5.6) необходимо проверить подстановкой в уравнение (5.5).

II тип: Уравнение вида

(5.7)

Где

1-й способ. Необходимо возвести уравнение (5.7) в квадрат. В определенных случаях следует один из корней перенести в правую часть уравнения. После упрощения полученное уравнение возводят в квадрат еще раз.

2-й способ. Умножение уравнения (5.7) на сопряженное выражение

Отдельно проверяют, имеет ли решение уравнение H(X) = 0. Затем для H(X) ¹ 0 рассматривают систему

Сложение уравнений этой системы приводит к уравнению вида (5.3).

3-й способ. Замена переменных

И переход к системе уравнений относительно U, V.

Уравнение

(5.8)

Где A, B Î R, возведением в куб обеих частей сводится к уравнению

(5.9)

Выражение в скобках (в левой части уравнения (5.9)) заменяют на используя заданное уравнение. В итоге заданное уравнение (5.8) приводится к уравнению-следствию, которое снова возводят в куб.

Полученные таким образом решения необходимо проверить подстановкой в уравнение (5.8).

III тип: Уравнения, решаемые заменой переменной.

В результате замены может уменьшиться степень выражений, стоящих под корнями, что приведет к уменьшению степени рационального уравнения после избавления от корней.

Если уравнение имеет вид

(5.10)

Где F – Некоторое алгебраическое выражение относительно то заменой оно сводится к уравнению

(5.11)

После решения уравнения (5.11) возвращаются к старой переменной и находят решения уравнения (5.10).

IV тип: уравнения, решаемые исходя из арифметического смысла корней с четными показателями. В частности, решение уравнения

(5.12)

Где A > 0, B > 0, сводится к решению системы

V тип: Уравнения, решаемые функциональными методами и методами, основанными на ограниченности входящих в уравнение функций.

Решение уравнений основывается на следующих утверждениях.

1. Если и для всех , то на множестве X уравнение F(X) = G(X) Равносильно системе уравнений

2. Если функции F(X) и G(X) непрерывны и F(X) возрастает, а G(X) убывает для X Î X, то уравнение F(X) = G(X) имеет не больше одного решения на промежутке X. Если один корень подобрать, то других корней нет.

3. Если F(X) – возрастающая функция, то уравнение равносильно уравнению

4. Если F(X) – возрастающая (убывающая) функция, то уравнение равносильно уравнению

Пример 1. Решить уравнение

Решение. Возведем обе части уравнения в квадрат:

Приводим подобные. При этом в левой части уравнения записываем корень, остальные слагаемые – в правой части:

Возводим полученное уравнение в квадрат еще раз:

Решая последнее квадратное уравнение, находим корни которые теперь необходимо проверить. Делаем проверку корней подстановкой в исходное уравнение. Первый корень не подходит.

Приходим к ответу:

Пример 2. Решить уравнение

Решение. Возведем обе части уравнения в куб:

Воспользовавшись исходным уравнением, заменим выражение выражением Получаем:

Решаем совокупность уравнений

В результате замены выражения могут появиться посторонние корни, так как такое преобразование не является равносильным. Поэтому необходимо произвести проверку. Подставляем найденные значения и убеждаемся, что они являются корнями исходного уравнения.

Приходим к ответу:

Пример 3. Решить уравнение

Решение. Возведение уравнения в квадрат приводит к уравнению четвертой степени и громоздкому решению.

Нетрудно заметить, что в данном уравнении можно произвести замену. Но перед этим преобразуем уравнение следующим образом:

Заменив получаем квадратное уравнение

Решая его, находим корни

Возвращаемся к исходной неизвестной:

Первое уравнение решений не имеет, так как его левая часть неотрицательна, а правая – отрицательна. Второе уравнение возводим в квадрат. Получаем:

т. е.

Его корни С помощью проверки убеждаемся, что оба корня подходят, т. е. приходим к ответу:

Пример 4. Решить уравнение

Решение. 1-й способ. Перенесем второй корень вправо:

Возводим обе части в квадрат:

Еще раз возводим в квадрат и получаем квадратное уравнение, решая которое и получаем корни Делаем проверку корней подстановкой в исходное уравнение. Оба корня подходят.

2-й способ. Введем замену тогда Таким образом получили более простое уравнение

т. е.

Возведем его в квадрат:

Возвращаемся к исходной неизвестной:

Возводим обе части уравнения в квадрат:

откуда

При помощи проверки убеждаемся, что оба корня подходят.

3-й способ. Домножим обе части уравнения на выражение, сопряженное левой части исходного уравнения. Получим:

Сложим последнее уравнение с исходным. Получим:

т. е.

Последнее уравнение возводим в квадрат. Получаем квадратное уравнение

Решая его, находим корни

Приходим к ответу:

Пример 5. Решить уравнение

Решение. Пусть Тогда и по условию.

Получили систему

Решаем ее методом подстановки:

Второе уравнение решим отдельно

Получаем корни:

Возвращаемся к системе:

Получаем:

Переходим к заданным неизвестным:

Решая последнюю совокупность, находим корни и С помощью проверки убеждаемся, что оба корня подходят.

Получили ответ:

При решении иррациональных уравнений, как правило, нахождение ОДЗ является бесполезным, так как проверка решений по ОДЗ недостаточна. Но существует ряд примеров, в которых нахождение ОДЗ является тем методом, который приводит к успеху. Покажем это на следующем примере.

Пример 6. Решить уравнение

Решение. Найдем ОДЗ данного уравнения:

Решаем последнюю систему неравенств графически (рис. 5.10).

Рис. 5.10

Получили, что ОДЗ состоит из единственной точки

Остается подставить значение в уравнение и выяснить, является ли оно решением:

Получили, что – решение.

Пример 7. Решить уравнение

Решение. Используем графический способ. Строим графики функций (рис. 5.11).

Рис. 5.11

Из рисунка видно, что графики пересекаются в единственной точке X = 7. Следовательно, уравнение имеет единственное решение. Проверяем X = 7 подстановкой в заданное уравнение и убеждаемся, что это точное значение решения уравнения.

Получили ответ: X = 7.

< Предыдущая		Следующая >