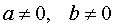Вычисление определенного интеграла
Здравствуйте. Меня зовут Андрей Зварыч. Я онлайн-репетитор сайта Tutoronline по высшей математике. Очень часто ко мне обращаются студенты с просьбой помочь разобраться с вычислением определенных интегралов. Сегодня я покажу несколько примеров решения. Надеюсь, моя статья будет полезной.
Итак, если F(x) – одна из первообразных непрерывной функции f(x) на [a,b], то справедлива формула Ньютона-Лейбница
Если функция f(x) непрерывна на отрезке [a,b], а функция x = φ(t) непрерывно дифференцирована на отрезке [t1,t2], причем a = φ(t1), b = φ(t2), то имеет место формула
Если функции u(x), v(x) и их производные u'(
Пример 1. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (1) имеем:
Пример 2. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (1) имеем:
Пример 3. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (1) имеем:
Пример 4 Вычислить интеграл
Решение.
На основании формулы произведения синусов, таблицы основных интегралов и формулы (1) имеем:
Пример 5. Вычислить интеграл
Решение.
Разложим подынтегральную функцию на сумму простых дробей,
Решив систему
Получим
Тогда на основании таблицы основных интегралов и формулы (1) имеем
Пример 6. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (2) имеем:
Сделаем замену ex + 4 = t2, тогда ex= t2– 4, ex dx = 2t dt,
Если x= ln5, то t = 3; если x= ln12, то t = 4. Тогда
Пример 7. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (2) имеем:
Пример 8.
Решение.
На основании таблицы основных интегралов и формулы (2) имеем:
Сделаем подстановку t = cosx
Если x = 0, то t = cos 0 = 1, если
Следовательно
Пример 9. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (2) имеем:
Найдем пределы по t:
Находим
Следовательно,
Пример 10. Вычислить интеграл
Решение.
Хороший метод решения интегралов, это метод занесения под дифференциал, его плюс состоит в том, что не требуется менять пределы интегрирования
Пример 11. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (3) имеем (интегрируем по частям)Если у Вас остались вопросы или Вам нужна помощь в решении «ваших интегралов», записывайтесь на мои занятия. Буду рад Вам помочь!
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Определенный интеграл, примеры решений
Определенный интеграл от функции на промежутке обозначается и равен разности двух значений первообразной функции, вычисленных при и (формула Ньютона-Лейбница):
Геометрический смысл определенного интеграла. Определенный интеграл есть площадь криволинейной трапеции ограниченной графиком функции , осью и прямыми и (рис. 1), то есть
Для вычисления определенных интегралов подходят все методы, которые используются для нахождения неопределенных интегралов.
Примеры
ПРИМЕР 1| Задание | Вычислить интеграл
|
| Решение | Преобразуем подынтегральное выражение
Разобьем интеграл от суммы на сумму интегралов и вынесем за знак интеграла константы:
Полученные интегралы являются табличными, вычислим их:
|
| Ответ |
| Задание | Вычислить интеграл
|
| Решение | Вынесем константу за знак интеграла и вычислим полученный табличный интеграл:
|
| Ответ |
| Задание | Вычислить интеграл
|
| Решение | Сделаем замену , при этом пределы интегрирования изменятся: и . Подставляя все это в исходный интеграл, получим:
|
| Ответ |
| Задание | Вычислить интеграл
|
| Решение | Внесем под знак дифференциала, тогда
Подставляя все в исходный интеграл, получим:
|
| Ответ |
| Задание | Вычислить площадь криволинейной трапеции ограниченной функцией , осью и прямыми и . |
| Решение | Сделаем рисунок (рис. 2).
По геометрическому смыслу определенного интеграла нахождение площади заданной криволинейной трапеции сводится к вычислению интеграла
Вычислим этот интеграл: (кв. ед.) |
| Ответ |
ru.solverbook.com
Определённый интеграл и методы его вычисления
Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где 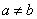 ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись
) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись
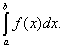
Как видно на графиках внизу (приращение первообразной функции обозначено 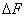 ), определённый
интеграл может быть как положительным, так и отрицательным числом (Вычисляется
как разность между значением первообразной в верхнем пределе и её же значением в
нижнем пределе, т. е. как F(b) — F(a)).
), определённый
интеграл может быть как положительным, так и отрицательным числом (Вычисляется
как разность между значением первообразной в верхнем пределе и её же значением в
нижнем пределе, т. е. как F(b) — F(a)).
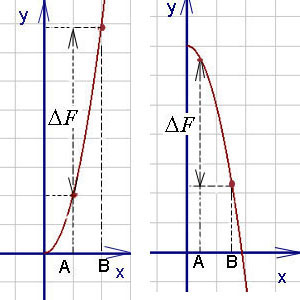
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.
Таким образом, если F(x) – какая-нибудь первообразная функция для f(x), то, согласно определению,
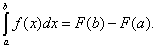
Равенство (38) называется формулой Ньютона-Лейбница. Разность F(b) – F(a) кратко записывают так:
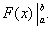
Поэтому формулу Ньютона-Лейбница будем записывать и так:
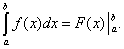 (39)
(39)
Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F(x) и Ф(х) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х) = F(x) + C. Поэтому

Тем самым установлено, что на отрезке [a, b] приращения всех первообразных функции f(x) совпадают.
Таким образом, для вычисления определённого интеграла необходимо найти любую первообразную подынтегральной функции, т.е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница: в первообразную функцию подставляется значение верхнего предела b, далее — значение нижнего предела a и вычисляется разность F(b) — F(a). Полученное число и будет определённым интегралом..
При a = b по определению принимается


Решение. Сначала найдём неопределённый интеграл:

Применяя формулу Ньютона-Лейбница к первообразной
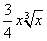
(при С = 0), получим
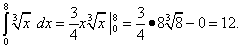
Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39).
Пример 2. Вычислить определённый интеграл
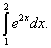
Решение. Используя формулу
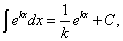
получим

Теорема 1. Определённый интеграл с одинаковыми пределами интегрирования равен нулю, т.е.
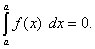
Это свойство содержится в самом определении определённого интеграла. Однако его можно получить и по формуле Ньютона-Лейбница: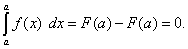
Теорема 2. Величина определённого интеграла не зависит от обозначения переменной интегрирования, т.е.
 (40)
(40)
Пусть F(x) – первообразная для f(x). Для f(t) первообразной служит та же функция F(t), в которой лишь иначе обозначена независимая переменная. Следовательно,
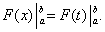
На основании формулы (39) последнее равенство означает равенство интегралов
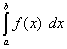
и
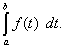
Теорема 3. Постоянный множитель можно выносить за знак определённого интеграла, т.е.
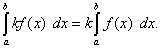 (41)
(41)
Теорема 4. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций, т.е.
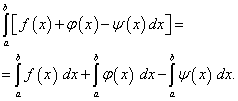 (42)
(42)
Теорема 5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям, т.е. если
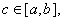
то
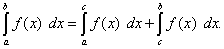 (43)
(43)
Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак, т.е.
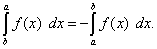 (44)
(44)
Теорема 7 (теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке 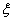 внутри его, т.е.
внутри его, т.е.
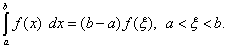 (45)
(45)
Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если

Теорема 9. Если верхний предел интегрирования больше нижнего и функции 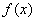 и
и  непрерывны, то неравенство
непрерывны, то неравенство
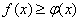
можно почленно интегрировать, т.е.
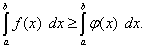 (46)
(46)
Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов.
Пример 5. Вычислить определённый интеграл
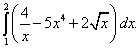
Используя теоремы 4 и 3, а при нахождении первообразных – табличные интегралы (7) и (6), получим
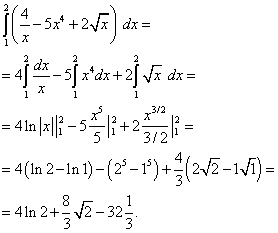
Пусть f(x) – непрерывная на отрезке [a, b] функция, а F(x) – её первообразная. Рассмотрим определённый интеграл
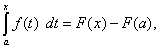 (47)
(47)
где
 ,
,
а через t обозначена переменная интегрирования, чтобы не путать её с верхней границей. При изменении х меняется и опредёленный интеграл (47), т.е. он является функцией верхнего предела интегрирования х, которую обозначим через Ф(х), т.е.
 (48)
(48)
Докажем, что функция Ф(х) является первообразной для f(x) = f(t). Действительно, дифференцируя Ф(х), получим
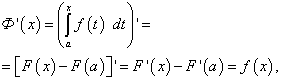
так как F(x) – первообразная для f(x), а F(a) – постояная величина.
Функция Ф(х) – одна из бесконечного множества первообразных для f(x), а именно та, которая при x = aобращается в нуль. Это утверждение получается, если в равенстве (48) положить x = aи воспользоваться теоремой 1 предыдущего параграфа.
При выводе формулы интегрирования по частям было получено равенство u dv = d (uv) – v du. Проинтегрировав его в пределах от a до b и учитывая теорему 4 параграфа этой статьи о свойствах определённого интеграла, получим
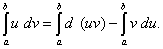
Как это следует из теоремы 2 параграфа о свойствах неопределённого интеграла, первый член в правой части равен разности значений произведения uv при верхнем и нижнем пределах интегрирования. Записав эту разность кратко в виде
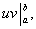
получаем формулу интегрирования по частям для вычисления определенного интеграла:
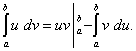 (49)
(49)
Пример 6. Вычислить определённый интеграл
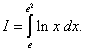
Решение. Интегрируем по частям, полагая u = ln x, dv = dx; тогда du = (1/x)dx, v = x. По формуле (49) находим

Найти определённый интеграл по частям самостоятельно, а затем посмотреть решение
Перейдём к вычислению определённого интеграла методом замены переменной. Пусть
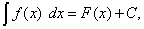
где, по определению, F(x) – первообразная для f(x). Если в подынтегральном выражении произвести замену переменной
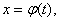
то в соответствии с формулой (16) можно записать
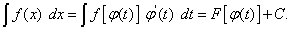
В этом выражении
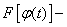
первообразная функция для

В самом деле, её производная, согласно правилу дифференцирования сложной функции, равна

Пусть α и β – значения переменной t , при которых функция
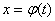
принимает соответственно значения aи b, т.е.
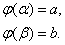
Тогда
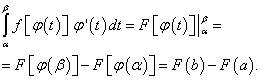
Но, согласно формуле Ньютона-Лейбница, разность F(b) – F(a) есть
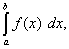
поскольку F(x) – первообразная для f(x).
Итак,
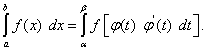 (50)
(50)
Это и есть формула перехода к новой переменной под знаком определённого интеграла. С её помощью определённый интеграл
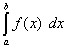
после замены переменной
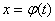
преобразуется в определённый интеграл относительно новой переменной t. При этом старые пределы интегрирования a и b заменяются новыми пределами 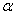 и
и 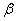 . Чтобы найти новые пределы, нужно в уравнение
. Чтобы найти новые пределы, нужно в уравнение
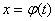
поставить значения x = aи x = b, т.е. решить уравнения

и
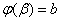
относительно 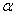 и
и  . После нахождения новых пределов интегрирования вычисление определённого интеграла сводится к применению формулы Ньютона-Лейбница к интегралу от новой переменной t. В первообразной функции, которая получается в результате нахождения интеграла, возвращаться к старой переменной нет необходимости.
. После нахождения новых пределов интегрирования вычисление определённого интеграла сводится к применению формулы Ньютона-Лейбница к интегралу от новой переменной t. В первообразной функции, которая получается в результате нахождения интеграла, возвращаться к старой переменной нет необходимости.
При вычислении определённого интеграла методом замены переменной часто бывает удобно выражать не старую переменную как функцию новой, а, наоборот, новую – как функцию старой.
Пример 9. Вычислить определённый интеграл
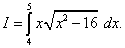
Решение. Произведём замену переменной, полагая

Тогда dt = 2x dx, откуда x dx = (1/2) dt, и подынтегральное выражение преобразуется так:
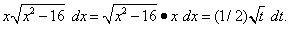
Найдём новые пределы интегрирования. Подстановка значений x = 4 и x = 5 в уравнение

даёт
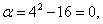
а
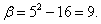
Используя теперь формулу (50), получим

После замены переменной мы не возвращались к старой переменной, а применили формулу Ньютона-Лейбница к полученной первообразной.
Найти определённый интеграл заменой переменной самостоятельно, а затем посмотреть решение

Начало темы «Интеграл»
Продолжение темы «Интеграл»
Поделиться с друзьями
function-x.ru
Определенный интеграл, теория и примеры
Например.
Детальный разбор понятия «Определенный интеграл»
Рассмотрим функцию , определенную и непрерывную на некотором отрезке . Выполним разбиение заданного отрезка с помощью точек на частичных отрезков , ,…, . На каждом частичном отрезке выберем произвольную точку и вычислим значение заданной функции в ней. Умножим полученное значение на длину соответствующего частичного отрезка: . Составим сумму всех таких произведений:
Такая сумма называется интегральной суммой функции на отрезке .
Пусть – длина наибольшего частичного отрезка: . Если предел интегральной суммы , когда максимальный диаметр разбиения , не зависит ни от способа разбиения отрезка на частичные отрезки, ни от выбора точек в них, то число называется определенным интегралом от заданной функции на отрезке и обозначается , то есть
Здесь числа и называются соответственно верхним и нижним пределами интегрирования; – подынтегральная функция; – подынтегральное выражение; – переменная интегрирования; – область или отрезок интегрирования.
Примеры решения задач
Функция называется интегрируемой на отрезке , если для нее на этом отрезке существует определенный интеграл .
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Определенный интеграл. Примеры решений — Мегаобучалка
Для того, чтобы научиться решать определенные интегралы необходимо:
1) Уметь находить соответствующие неопределенные интегралы.
2) Уметь вычислить определенный интеграл.
Как видите, для того, чтобы освоить определенный интеграл, нужно достаточно хорошо ориентироваться в «обыкновенных» неопределенных интегралах. Поэтому, если вы только-только начинаете погружаться в интегральное исчисление, и чайник еще не совсем закипел, то лучше начать с урока Неопределенный интеграл. Примеры решений.
В общем виде определенный интеграл записывается так:
Что прибавилось по сравнению с неопределенным интегралом?
Прибавились пределы интегрирования.
Нижний предел интегрирования стандартно обозначается буквой a.
Верхний предел интегрирования стандартно обозначается буквой b.
Отрезок [a; b] включает граничные точки и называется отрезком интегрирования.
Что такое определенный интеграл? Можно посмотреть в учебниках про диаметр разбиения отрезка, предел интегральных сумм и т. д., но урок носит практический характер. Поэтому скажем, что определенный интеграл – это, прежде всего, самое что ни на есть обычное ЧИСЛО.
Есть ли у определенного интеграла геометрический смысл?Есть. И очень хороший. Самая популярная задача вычисления определённого интеграла – вычисление площади с помощью определенного интеграла.
Что значит решить определенный интеграл?Решить определенный интеграл – это значит, найти число, равное приращению первообразной функции на отрезке [a; b].
Как решить определенный интеграл?С помощью знакомой со школы формулы Ньютона-Лейбница:
.
Формулу лучше переписать на отдельный листочек, она должна быть перед глазами на протяжении всего урока.
Этапы решения определенного интеграла следующие:
1) Сначала находим первообразную функцию F(X) (неопределенный интеграл). Обратите внимание, что константа C в определенном интеграле никогда не добавляется.
Обозначение является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись
?
Это подготовка для применения формулы Ньютона-Лейбница.
2) Подставляем значение верхнего предела в первообразную функцию: F(b).
3) Подставляем значение нижнего предела в первообразную функцию: F(a).
4) Рассчитываем (без ошибок!) разность F(b)-F(a), то есть, находим число, равное приращению первообразной (от подынтегральной) функции на отрезке [a; b].
Готово.
Всегда ли существует определенный интеграл? Нет, не всегда существует всё, что мы напишем в виде определённого интеграла. Например, интеграла
не существует, поскольку отрезок интегрирования не входит в область определения подынтегральной функции и значения под квадратным корнем не могут быть отрицательными. А вот менее очевидный пример:
.
Такого интеграла тоже не существует на всём отрезке [-2; 3], так как в точках
,
этого отрезка подынтегральная функция f(x) = tg(x) не существует.
Для того, чтобы определенный интеграл существовал на данном отрезке, необходимо, чтобы подынтегральная функция была непрерывной на отрезке интегрирования.
Из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования. Бывает так, что подолгу мучаешься с нахождением трудной первообразной, а когда наконец-то ее находишь, то ещё и ломаешь голову над вопросом: «что за ерунда получилась?». Например, если получилось примерно так:
???!!!
то нельзя подставлять отрицательные числа под корень! Если для решения в контрольной работе, на зачете или экзамене Вам предложен несуществующий интеграл вроде
,
то нужно дать ответ, что интеграла не существует и обосновать – почему.
Может ли определенный интеграл быть равен отрицательному числу?Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл, коим отведена отдельная лекция.
Может ли нижний предел интегрирования быть больше верхнего предела интегрирования?Может, и такая ситуация реально встречается на практике. Интеграл
преспокойно вычисляется по формуле Ньютона-Лейбница.
Без чего не обходится высшая математика? Конечно же, без всевозможных свойств. Поэтому рассмотрим некоторые свойства определенного интеграла.
В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак:
Например, в определенном интеграле перед интегрированием
целесообразно поменять пределы интегрирования на «привычный» порядок:
.
В таком виде интегрировать значительно удобнее.
Как и для неопределенного интеграла, для определенного интеграла справедливы свойства линейности:
Это справедливо не только для двух, но и для любого количества функций.
В определенном интеграле можно проводить замену переменной интегрирования, правда, по сравнению с неопределенным интегралом тут есть своя специфика, о которой мы еще поговорим.
Для определенного интеграла справедлива формула интегрирования по частям: .
Пример 1
Вычислить определенный интеграл
.
Решение:
(1) Выносим константу за знак интеграла.
(2) Интегрируем по таблице с помощью самой популярной формулы
.
(3) Используем формулу Ньютона-Лейбница
.
Сначала подставляем в x3 верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.
Пример 2
Вычислить определенный интеграл
.
Это пример для самостоятельно решения, решение и ответ в конце урока.
Пример 3
Вычислить определенный интеграл
.
Решение:
.
(1) Используем свойства линейности определенного интеграла.
(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.
(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница.
СЛАБОЕ ЗВЕНО в определенном интеграле – это ошибки вычислений и часто встречающаяся ПУТАНИЦА В ЗНАКАХ. Будьте внимательны! Особое внимание заостряем на третьем слагаемом:
,
т. к. очень часто машинально пишут
.
Следует заметить, что рассмотренный способ решения определенного интеграла – не единственный. При определенном опыте, решение можно значительно сократить. Например, так:
.
Здесь устно использованы правила линейности, устно проинтегрированы табличные интегралы. Получилась всего одна скобка с отчёркиванием пределов:
(в отличие от трёх скобок в первом способе). И в «целиковую» первообразную функцию мы сначала подставили 4, затем –2, опять же выполнив все действия в уме.
При втором способе существует повышенный риск допустить ошибку в вычислениях, поэтому студенту-чайнику лучше использовать первый способ, чтобы не терять знаки.
Несомненными преимуществами второго способа является быстрота решения, компактность записи и тот факт, что первообразная.
находится в одной скобке.
megaobuchalka.ru
Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа

Первообразная
Определение 1. Функцию F (x) , определенную на интервале (a, b), называют первообразной функции f (x) , определенной на интервале (a, b), если для каждого 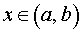 выполнено равенство
выполнено равенство
F’ (x) = f (x) .
Например, из справедливости равенства
(sin 2x)’ = 2 cos 2x
вытекает, что функция F (x) = sin 2x является первообразной функции f (x) = 2 cos 2x .
Замечание. Функция F (x) = sin 2x не является единственной первообразной функции f (x) = 2 cos 2x , поскольку функция F (x) = sin 2x + 10 , или функция F (x) = sin 2x – 3 , или функции вида F (x) = sin 2x + c , где c – любое число, также являются первообразными функции f (x) = 2 cos 2x .
Справедлива следующая теорема, доказательство которой выходит за рамки школьного курса математики.
Теорема 1. Если функция F (x) является первообразной функции f (x) на интервале (a, b) , то любая другая первообразная функции f (x) на интервале (a, b) имеет вид
F (x) + с ,
где c – некоторое число.
Неопределенный интеграл
Определение 2. Множество всех первообразных функции f (x) называют неопределенным интегралом от функции f (x) и обозначают
 | (1) |
Обозначение (1) читается так: «Неопределенный интеграл от функции f (x) по dx» .
Если F (x) является первообразной f (x) , то в силу теоремы 1 смысл формулы (1) заключается в следующем:
 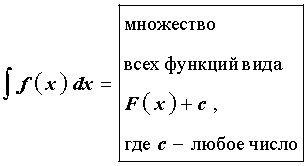 | (2) |
Однако для упрощения формулу (2) принято записывать в виде
 | (3) |
подразумевая, но не указывая специально, что c – любое число.
В формуле (3) функцию f (x) называют подынтегральной функцией, выражение f (x) dx нызывают подынтегральным выражением, а число c называют постоянной интегрирования.
Операцию вычисления (взятия) интеграла по известной подынтегральной функции называют интегрированием функции.
Правила интегрирования. Замена переменной в неопределенном интеграле
Вычисление интегралов (интегрирование) основано на применении следующих правил, которые непосредственно вытекают из правил вычисления производных.
Правило 1 (интеграл от произведения числа на функцию). Справедливо равенство
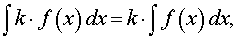
где k – любое число.
Другими словами, интеграл от произведения числа на функцию равен произведению этого числа на интеграл от функции.
Правило 2 (интеграл от суммы функций). Интеграл от суммы функций вычисляется по формуле

то есть интеграл от суммы функций равен сумме интегралов от этих функций.
Правило 3 (интеграл от разности функций). Интеграл от разности функций вычисляется по формуле

то есть интеграл от разности функций равен разности интегралов от этих функций.
Правило 4 (интегрирование при помощи замены переменной). Из справедливости формулы

вытекает, что
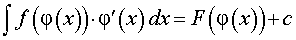 | (4) |
если все входящие в формулу (4) функции f (φ (x)), φ’ (x), F (φ (x)) определены.
Доказательство правила 4. Воспользовавшись формулой для производной сложной функции, вычислим производную от правой части формулы (4):
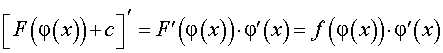
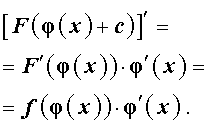
Мы получили подынтегральную функцию из левой части формулы (4), что и требовалось.
Замечание. Рассмотрим частный случай формулы (4), когда функция φ (x) является линейной функцией, то есть
φ (x) = kx + b ,
что k и b – произвольные числа, 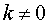 .
.
В этом случае
φ’ (x) = k ,
и формула (4) принимает вид
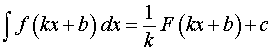 | (5) |
Формула (5) часто используется при решении задач.
Таблица интегралов
Следующая таблица неопределенных интегралов составлена на основе таблицы производных часто встречающихся функций, а также на основе таблицы производных сложных функций
| Основная формула | Обобщения |
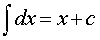 |
|
где n – любое число, не равное – 1 |
где n, k, b – любые числа, |
где n – любое число, | |
|
где k, b – любые числа, |
где φ (x) > 0 | |
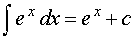 |
где k, b – любые числа, |
 | |
где a – любое положительное число, не равное 1 |
где a – любое положительное число, не равное 1, k, b – любые числа, |
где a – любое положительное число, не равное 1 | |
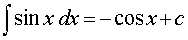 |
где k, b – любые числа, |
 | |
 |
где k, b – любые числа, |
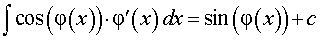 | |
|
где k, b – любые числа, |
| |
|
где k, b – любые числа, |
| |
|
где k, b – любые числа, |
| φ (x) | < 1 | |
где a, b – любые числа, | |
 |
где k, b – любые числа, |
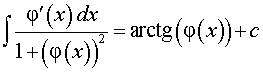 | |
где a, b – любые числа, |
Основная формула:
Обобщения:
|
Основная формула:
где n – любое число, не равное – 1 . Обобщения:
где n, k, b – любые числа, _____
где n – любое число, |
Основная формула:
Обобщения:
где k, b – любые числа, _____
где φ (x) > 0 |
Основная формула:
Обобщения:
где k, b – любые числа, _____
|
Основная формула:
где a – любое положительное число, не равное 1 . Обобщения:
где a – любое положительное число, не равное 1, k, b – любые числа, _____
где a – любое положительное число, не равное 1 |
Основная формула:
Обобщения:
где k, b – любые числа, _____
|
Основная формула:
Обобщения:
где k, b – любые числа, _____
|
Основная формула:
где Обобщения:
где k, b – любые числа, _____
где |
Основная формула:
где Обобщения:
где k, b – любые числа, _____
|
Основная формула:
Обобщения:
где k, b – любые числа, _____
где | φ (x) | < 1 _____
где a, b – любые числа, |
Основная формула:
Обобщения:
где k, b – любые числа, _____
_____
где a, b – любые числа, |
Примеры решения задач
Пример 1. Вычислить интеграл
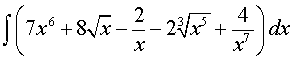
Решение. Воспользовавшись свойствами степеней, а затем правилами интегрирования и формулами из таблицы неопределенных интегралов формулами из таблицы неопределенных интегралов, получаем

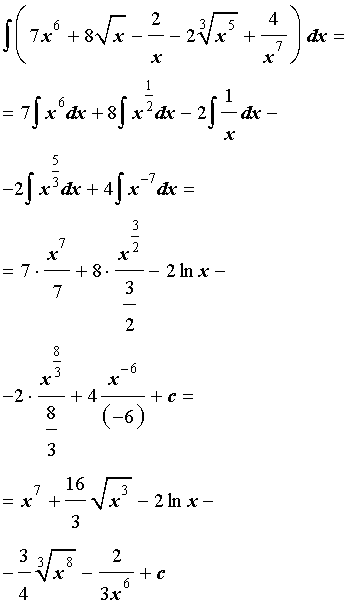
Ответ.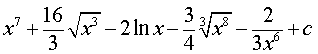
Пример 2. Значение первообразной F (x) функции f (x) = – 4 sin x в точке x = 0 равно 9. Найти 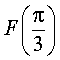 .
.
Решение. Поскольку Поскольку

то
Подставляя в формулу (6) значение x = 0 , находим значение постоянной интегрирования c:
F (0) = 4 cos 0 + c = 9,
4 + c = 9, c = 5.
Следовательно,
F (x) = 4 cos x + 5
Поэтому
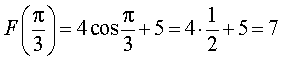
Ответ. 7
Пример 3. Найти первообразную F (x) функции
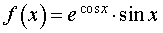
если F (2π) = 2e + 3.
Решение. Воспользовавшись формулой из таблицы неопределенных интегралов формулой из таблицы неопределенных интегралов

для функции φ (x) = cos x , получаем
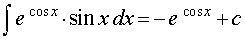
Следовательно,
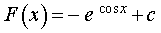 | (7) |
Подставляя в формулу (7) значение x = 2π, находим значение постоянной интегрирования c:

Итак,
c = 3e +3 .
Ответ. 
Пример 4. Вычислить интеграл
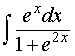
Решение. Воспользовавшись формулой из таблицы неопределенных интегралов формулой из таблицы неопределенных интегралов
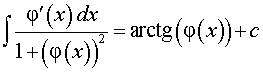
для функции φ (x) = ex, получаем
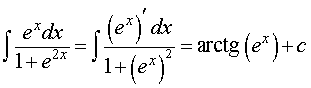
Ответ. 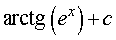

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
www.resolventa.ru
Решение интегралов. Рассказываем, как решать интегралы.
Интегралы и их решение многих пугает. Давайте избавимся от страхов и узнаем, что это такое и как решать интегралы!
Интеграл – расширенное математическое понятие суммы. Решение интегралов или их нахождение называется интегрированием. Пользуясь интегралом можно найти такие величины, как площадь, объем, массу и другое.
Решение интегралов (интегрирование) есть операция обратная диференциированию.
Чтобы лучше представлять, что есть интеграл, представим его в следующей форме. Представьте. У нас есть тело, но пока не можем описать его, мы только знаем какие у него элементарные частицы и как они расположены. Для того, чтобы собрать тело в единое целое необходимо проинтегрировать его элементарные частички – слить части в единую систему.
В геометрическом виде для функции y=f(x), интеграл представляет собой площадь фигуры ограниченной кривой, осью х, и 2-мя вертикальными линиями х=а и х=b .
Так вот площадь закрашенной области, есть интеграл от функции в пределах от a до b.
Не верится? Проверим на любой функции. Возьмем простейшую у=3. Ограничим функцию значениями а=1 и b=2. Построим:
Итак ограниченная фигура прямоугольник. Площадь прямоугольника равна произведению длины на ширину. В наше случае длина 3, ширина 1, площадь 3*1=3.
Попробуем решить тоже самое не прибегая к построению, используя интегрирование:
Как видите ответ получился тот же. Решение интегралов – это собирание во едино каких-либо элементарных частей. В случае с площадью суммируются полоски бесконечно малой ширины. Интегралы могут быть определенными и неопределенными.
Решить определенный интеграл значит найти значение функции в заданных границах. Решение неопределенного интеграла сводиться к нахождению первообразной.
F(x) – первообразная. Дифференцируя первообразую, мы получим исходное подинтегральное выражение. Чтобы проверить правильно ли мы решили интеграл, мы дифференциируем полученный ответ и сравниваем с исходным выражением.
Основные функции и первообразные для них приведены в таблице:
Таблица первообразных для решения интегралов
Основные приемы решения интегралов:
Решить интеграл, значит проинтегрировать функцию по переменной. Если интеграл имеет табличный вид, то можно сказать, что вопрос, как решить интеграл, решен. Если же нет, то основной задачей при решении интеграла становиться сведение его к табличному виду.
Сначала следует запомнить основные свойства интегралов:
Знание только этих основ позволит решать простые интегралы. Но следует понимать, что большинство интегралов сложные и для их решения необходимо прибегнуть к использованию дополнительных приемов. Ниже мы рассмотрим основные приемы решения интегралов. Данные приемы охватывают большую часть заданий по теме нахождения интегралов.
Также мы рассмотрим несколько базовых примеров решения интегралов на базе этих приемов. Важно понимать, что за 5 минут прочтения статьи решать все сложные интегралы вы не научитесь, но правильно сформированный каркас понимания, позволит сэкономить часы времени на обучение и выработку навыков по решению интегралов.
Основные приемы решения интегралов
1. Замена переменной.
Для выполнения данного приема потребуется хороший навык нахождения производных.
2. Интегрирование по частям. Пользуются следующей формулой.
Применения этой формулы позволяет казалось бы нерешаемые интегралы привести к решению.
3. Интегрирование дробно-рациональных функций.
— разложить дробь на простейшие
— выделить полный квадрат.
— создать в числителе дифференциал знаменателя.
4. Интегрирование дробно-иррациональных функций.
— выделить под корнем полный квадрат
— создать в числителе дифференциал подкоренного выважения.
5. Интегрирование тригонометрических функций.
При интегрировании выражений вида
применяет формулы разложения для произведения.
Для выражений
m-нечетное, n –любое, создаем d(cosx). Используем тождество sin2+cos2=1
m,n – четные, sin2x=(1-cos2x)/2 и cos2x=(1+cos2x)/2
Для выражений вида:
— Применяем свойство tg2x=1/cos2x — 1
С базовыми приемами на этой всё. Теперь выведем своего рода алгоритм:
Алгоритм обучения решению интегралов:
1. Разобраться в сути интегралов. Необходимо понять базовую сущность интеграла и его решения. Интеграл по сути есть сумма элементарных частей объекта интегрирования. Если речь идет об интегрирование функции, то интеграл есть площадь фигуры между графиком функции, осью х и границами интегрирования. Если интеграл неопределенный, то есть границы интегрирования не указаны, то решение сводиться к нахождению первобразной. Если интеграл определенный, то необходимо подставить значения границ в найденную функцию.
2. Отработать использование таблицы первообразных и основным свойства интегралов. Необходимо научиться пользоваться таблицей первообразных. По множеству функций первообразные найдены и занесены в таблицу. Если мы имеем интеграл, которые есть в таблице, можно сказать, что он решен.
3. Разобраться в приемах и наработать навыки решения интегралов.Если интеграла не табличного вида, то его решение сводиться к приведению его к виду одного из табличных интегралов. Для этого мы используем основные свойства и приемы решения. В случае, если на каких то этапах применения приемов у вас возникают трудности и непонимания, то вы более подробно разбираетесь именно по этому приему, смотрите примеры подобного плана, спрашиваете у преподавателя.
Дополнительно после решения интеграла на первых этапах рекомендуется сверять решение. Для этого мы дифференциируем полученное выражение и сравниваем с исходным интегралом.
Отработаем основные моменты на нескольких примерах:
Примеры решения интегралов
Пример 1:
Решить интеграл: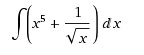
Интеграл неопределенный. Находим первообразную.
Для этого интеграл суммы разложим на сумму интегралов.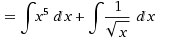
Каждый из интегралов табличного вида. Смотрим первообразные по таблице.
Решение интеграла: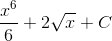
Проверим решение(найдем производную):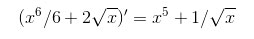
Пример 2. Решаем интеграл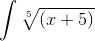
Интеграл неопределенный. Находим первообразную.
Сравниваем с таблицей. В таблице нет.
Разложить, пользуясь свойствами, нельзя.
Смотрим приемы. Наиболее подходит замена переменной.
Заменяем х+5 на t5. t5 = x+5 . Получаем.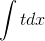
Но dx нужно тоже заменить на t. x= t5 — 5, dx = (t5 — 5)’ = 5t4. Подставляем: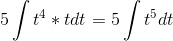
Интеграл из таблицы. Считаем: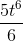
Подставляем в ответ вместо t ,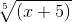
Решение интеграла: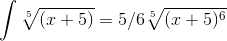
Пример 3. Решение интеграла: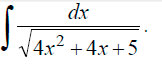
Для решения в этом случае необходимо выделить полный квадрат. Выделяем: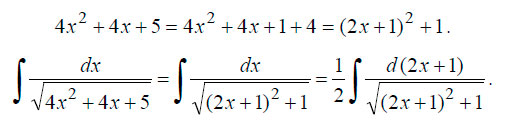
В данном случае коэфециент ? перед интегралом получился в результате замены dx на ?*d(2x+1). Если вы найдете производные x’ = 1 и ?*(2x+1)’= 1, то поймете почему так.
В результате мы привели интеграл к табличному виду.
Находим первообразную.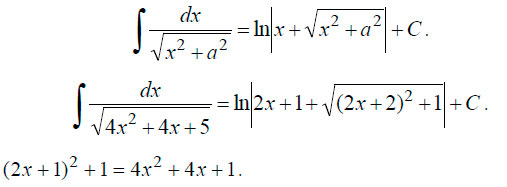
В итоге получаем: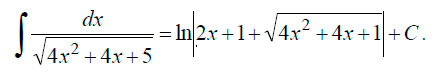
Для закрепления темы интегралов рекомендуем также посмотреть видео.
В нем мы на примере физики показываем практическое применение интегрирования, а также решаем еще несколько задач.
Надеюсь вопрос, как решать интегралы для вас прояснился. Мы дорабатываем статью по мере поступления предложений. Поэтому если у вас появились какие то предложения или вопросы по теме решения интегралов, пишите в комментариях.
Рекламная заметка: Для особо пытливых умов советуем Видео-лекции по математическому программированию. Программирование одна из дочек математики!
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
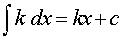 , где k – любое число
, где k – любое число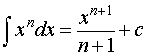
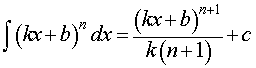 ,
,
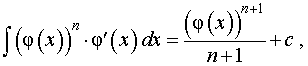
 , x > 0
, x > 0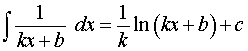 ,
,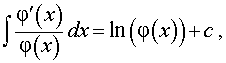
 ,
,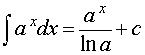
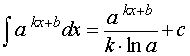 ,
,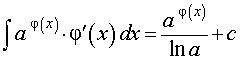 ,
, ,
,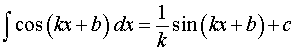 ,
,
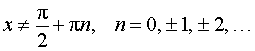
 ,
,
 ,
,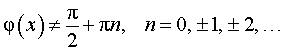
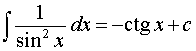
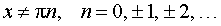
 ,
,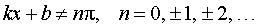
 ,
,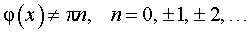
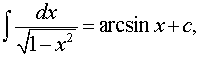 | x | < 1
| x | < 1
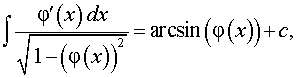

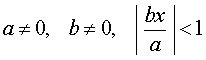
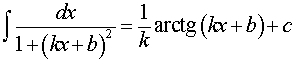 ,
,