Практическое занятие «Исследование функции с помощью производной» (для студентов СПО)
Практическая работа №16 (естественно-научный профиль)
Тема: «Исследование функций с помощью производной»
Цели: научиться проводить исследование функции с помощью производной и .строить графики функций; закрепить основные признаки возрастания (убывания ) функции, условия существования точек экстремума; проводить исследование функции по графику производной.
Краткая теоретическая справка

1. Находим область определения D(f) функции y = f(x).
2. Проверяем функцию на четность.
Если f(-x) = f(x), то функция
Если f(-x) = — f(x), то функция нечетная, график нечетной функции симметричен относительно начала координат.
В противном случае функция является ни четной, ни нечетной.
3. Если функция периодическая, то находим период функции.
4. Находим точки пересечения графика с осями координат.
Находим нули функции — это точки пересечения графика функции с осью абсцисс (Ox).
Для этого мы решаем уравнение f(x) = 0.
Находим точку пересечения графика функции с осью ординат (Oy). Для этого ищем значение функции при x=0.
5. Находим промежутки знакопостоянства функции, то есть промежутки, на которых функция сохраняет знак. Это нам потребуется для контроля правильности построения графика.
Чтобы найти промежутки знакопостоянства функции, нам нужно решить неравенства  f(x) >0 и f(x) <0
f(x) >0 и f(x) <0  .
.
6. Исследуем функцию с помощью производной: находим промежутки возрастания и убывания функции, а также точки максимума и минимума.
Для этого мы следуем привычному алгоритму.
а) Находим производную
б) Приравниваем производную к нулю и находим корни уравнения
— это стационарные точки.
в) Находим промежутки знакопостоянства производной. Промежутки, на которых
Промежутки, на которых производная отрицательна, являются промежутками убывания функции.
Точки, в которых производная меняет знак с плюса на минус, являются точками максимума.
Точки, в которых производная меняет знак с минуса на плюс, являются точками минимума.
7. Найти значения функции в точках экстремума.
8. По данным исследования построить график функции.
Пример 1. Исследовать функцию и по результатам исследования построить график.

Решение.
1) D(f): R
2) Проверим функцию на чётность/нечётность: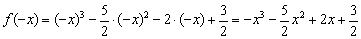
 , значит, данная функция не является чётной или нечётной.
, значит, данная функция не является чётной или нечётной.
3) Функция непериодическая.
4) Нули функции.
С осью Оy:
Чтобы найти точки пересечения с осью Ox (нули функции) требуется решить уравнение f(x) = 0: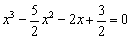
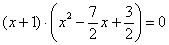
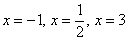

5) Таким образом, на интервалах график расположен ниже оси абсцисс f(x)<0, а на интервалах – выше данной оси f(x) >0.
6) Возрастание, убывание.
Найдём критические точки: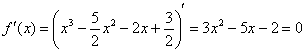
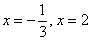
Отложим их на числовой прямой и определим знаки производной:
1
Следовательно, функция возрастает на и убывает на .
точка максимума, так как при переходе через нее производная меняет знак с «+» на «-»
.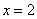 точка минимума, так как при переходе через нее производная меняет знак с «-» на «+».
точка минимума, так как при переходе через нее производная меняет знак с «-» на «+».
8). 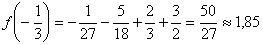
: 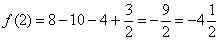 .
.
9) Строим график функции.
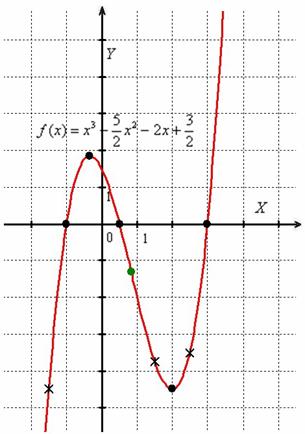
Пример 2. На рисунке изображен график производной функции 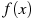
 . В какой точке отрезка
. В какой точке отрезка 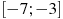
 принимает наибольшее значение.
принимает наибольшее значение.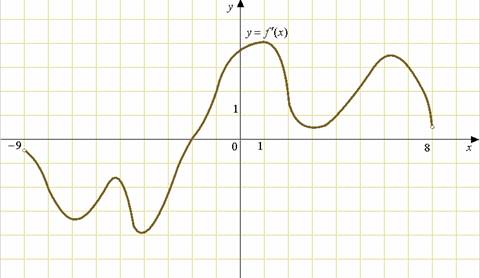
Решение. На отрезке [-7;-3] график производной расположен ниже оси Ох, это означает, что , то есть сама функция на данном отрезке монотонно убывает. Таким образом, убывающая функция принимает наибольшего значения на левом конце промежутка, то есть в точке x=-7.
Ответ. -7.
Алгоритм нахождения наибольшего или наименьшего значения функции на отрезке:
Найти производную функции.
Определить критические точки (те точки, в которых производная функции обращается в ноль или не существует).
Выбрать из найденных точек те, которые принадлежат данному отрезку.
Вычислить значения функции (не производной!) в этих точках и на концах отрезка.
Среди полученных значений выбрать наибольшее или наименьшее, оно и будет искомым.
Пример 3. Найдите наименьшее значение функции y = x3 – 18x2 + 81x + 23 на отрезке [8; 13].
Решение: действуем по алгоритму нахождения наименьшего значения функции на отрезке:
y’ = 3x2 – 36x + 81 = 0
x2 – 12x + 27 = 0,
x = 3 и x = 9
x = 9 [8; 13].
y = x3 – 18x2 + 81x + 23 = x(x-9)2+23:
y(8) = 8 · (8-9)2+23 = 31;
y(9) = 9 · (9-9)2+23 = 23;
y(13) = 13 · (13-9)2+23 = 231.
Ответ. ;
Порядок выполнения работы.
Внимательно изучите теоретическую справку по теме.
Решите следующие задания по учебнику №9.40А(2в, 2г), №9.41Б(1в) , № 9.44А(2), №9.43А(6)
Выполните разбор примеров 3-7.
Пример 4. На рисунке изображен график производной функции  , определенной на интервале
, определенной на интервале 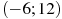 . Найдите промежутки возрастания функции
. Найдите промежутки возрастания функции 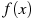 . В ответе укажите длину наибольшего из них.
. В ответе укажите длину наибольшего из них.

Пример 5. На рисунке изображен график производной функции 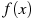
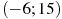 . Найдите количество точек экстремума функции
. Найдите количество точек экстремума функции 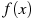 на отрезке
на отрезке 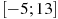 .
.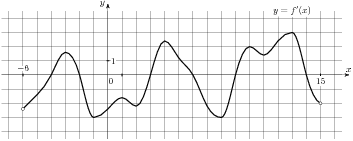
Пример 6. На рисунке изображен график производной функции 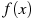 , определенной на интервале
, определенной на интервале 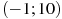 . Найдите промежутки возрастания функции
. Найдите промежутки возрастания функции 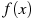 . В ответе укажите сумму целых точек, входящих в эти промежутки.
. В ответе укажите сумму целых точек, входящих в эти промежутки.

Пример 7. На рисунке изображен график функции 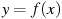 , определенной на интервале
, определенной на интервале 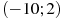 . Определите количество целых точек, в которых производная функции отрицательна.
. Определите количество целых точек, в которых производная функции отрицательна.

Пример 8. На рисунке изображен график производной функции 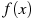 , определенной на интервале
, определенной на интервале 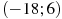 . Найдите количество точек максимума функции
. Найдите количество точек максимума функции 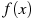 на отрезке
на отрезке 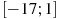 .
.
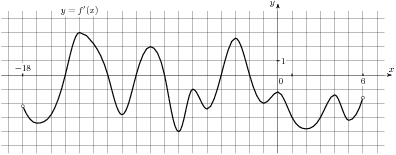
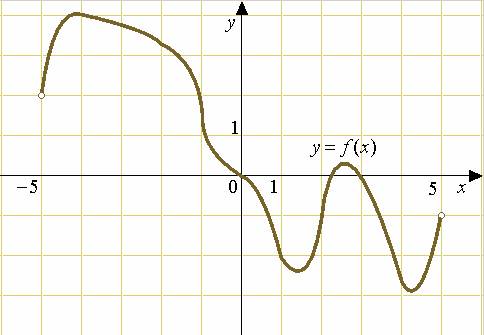
Пример 9. На рисунке изображен график функции 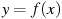 , определенной на интервале
, определенной на интервале 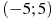 . Определите количество целых точек, в которых производная функции
. Определите количество целых точек, в которых производная функции 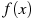 положительна.
положительна.
Задание на дом:
№9.40А(2а,2б), №9.44А(1) №9.41Б(1а,1б) , № 9.44А(2)
№9.43А(1-5), №9.44А(3) №9.45А(1-4) №9.44А(9)
Выполните самостоятельно по вариантам.
Самостоятельная работа.
Задание №1. Исследуйте функцию с помощью производной и постройте ее график1
11
2
12
3
13
4
14
5
15
6
16
7
17
8
18
9
19
10
20
Задание №2. Найдите наибольшее и наименьшее значение функции на отрезке
1
 ,
, 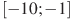
11
 ,
, 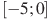
2
 ,
, 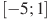
12
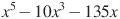 ,
, 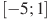
3
 ,
, 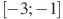
13
 ,
, 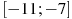
4
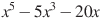 ,
, 
14
 ,
, 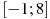
5
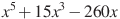 ,
, 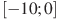
15
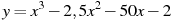 ,
, 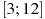
6
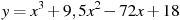 ,
, 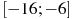
16
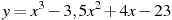 ,
, 
7
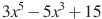 ,
, 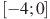
17
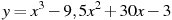 ,
, 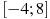
8
 ,
,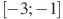
18
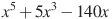 ,
, 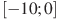
9
 ,
,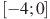
19
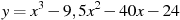 ,
, 
10
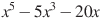 ,
, 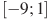
20
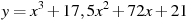 ,
, 
Урок-зачет по теме «Исследование функции с помощью производной»
Цель урока: проверка умений и навыков исследования функций и построения графиков с помощью производной.
Теоретическая часть зачета.
Вопросы
Определение точки минимума и точки максимума.
Теоретическая часть зачета
Ответы
1) Определение точки минимума.
Если функция определена в некоторой окрестности точки Х0 , то точка Х0 называется точкой минимума функции f(х), если существует такая окрестность точки Х0 ,что для всех хх0 из этой окрестности выполняется неравенство f(х)>f(х0).
Определение точки максимума.
Если функция определена в некоторой окрестности точки Х0 , то точка Х0 называется точкой максимума функции f(х),если существует такая окрестность точки Х0 , что для всех х?х0 из этой окрестности выполняется неравенство f(х)<f(х0).
2) Определение критических точек.
Критические точки – это внутренние точки области определения функции в которых производная не существует или равна нулю.
3) Необходимое условие, чтобы Х0 была точкой экстремума: эта точка должна быть критической.
4) Алгоритм нахождения критических точек.
1. Найти область определения функции.
2. Найти производную функции.
3. Найти область определения производной данной функции.(Чтобы определить есть ли точки в которых производная не существует. Если такие точки есть, то проверить являются ли они внутренними точками области определения функции.
4. Найти точки, в которых производная равна нулю, решив уравнение: f ‘(х)=0.
Проверить являются ли найденные точки внутренними точками области определения функции.
5) Стационарные точки — точки, в которых производная функции равна нулю.
6) Теорема Ферма. (Необходимое условие экстремума функции.)
у=f(х)-функция, которая определена в некоторой окрестности точки Х0, и имеет производную в этой точке.
Теорема: если Х0-точка экстремума дифференцируемой функции f(х), то f ‘(х)=0.
7) Достаточные условия существования экстремума функции в точке.
y=f(х) определена на (а;в). Х0-критическая точка.
Если функция f непрерывна в точке Х0, а f '(х)>0 на интервале (а;х0) и f ‘(х)<0 на интервале (х0;в), то точка х0 является точкой максимума функции f.
(Упрощенная формулировка: если в точке Х0 производная меняет знак с “+” на “ _”, то Х0есть точка максимума.)
Если функция f непрерывна в точке Х0, а f '(х)<0 на интервале (а;X0) и f ‘(х)>0 на интервале (X0;в), то точка х0 является точкой минимума функции f.
(Упрощенная формулировка: если в точке Х0 производная меняет знак с “_” на “+”, то Х0 есть точка минимума.)
8) Достаточный признак возрастания, убывания функции.
Если f ‘(х)>0 для всех х из промежутка (а; в), то функция возрастает на промежутке (а; в).
Если f ‘(х)<0 для всех х из промежутка (а; в), то функция убывает на промежутке (а; в).
(Если функция непрерывна на конце промежутка, то его можно присоединить к промежутку возрастания (убывания) функции.)
9) Точки экстремума, экстремум функции.
Х0 — точка максимума, Х0 –точка минимума называются точками экстремума.
f(х0) — максимум функции,
f(х0) — минимум функции называются экстремумами функции.
10) Алгоритм нахождения экстремумов функции.
1. Находим область определения функции.
2. Находим производную функции.
3. Находим критические точки.
4. Определим знак производной на каждом из интервалов, на которые критические точки разбивают область определения.
5. Найдем точки экстремума, учитывая характер изменения знака производной.
6. Найдем экстремумы функций.
11) Алгоритм нахождения наибольшего и наименьшего значений функции на отрезке.
1. Найти значения функции на концах отрезка [а; в].
2. Найти значения функции в тех критических точках, которые принадлежат интервалу (а; в).
3. Из найденных значений выбрать наибольшее и наименьшее.
Практическая часть зачета
“Исследование функций с помощью производной.
Наибольшее и наименьшее значения функций на отрезке”
Найти:
а) критические точки функций,
б) экстремумы функций
в) наибольшее и наименьшее значения функций на указанном промежутке
г) построить график.
| 1. у=(х-3)2(х-2). | [1;4] | 11. у=2х4-х. | [-1;1] |
| 2. у=1/3х3+х2 | [-4;1] | 12. у=х2-2/х. | [-3;-0,5] |
| 3. у=1/3х3-х2-3х | [-2;6] | 13. у=1/(х2+1). | [-1;2] |
| 4. у=-1/4х4+2х2+1. | [-3;3] | 14. у=3х-х3. | [-1,5;1,5] |
| 5. у=х4-8х2-9. | [-3;3] | 15. у=2х2-х4. | [-2;1,5] |
| 6. у=(х-2)(х+1)2. | [-1,5;1,5] | 16. у=3х2/3-х2. | [-8;8] |
| 7. у=-2/3х3+2х-4/3. | [-1,5;1,5] | 17. у=3х1/3-х. | [-8;8] |
| 8. у=3х5-5х4+4. | [-1;1] | 18. у=х3-1,5х2-6х+4. | [-2;3] |
| 9. у=9х2-9х3. | [-0,5;1] | 19. у=(1-х)/(х2+3). | [-2;5] |
| 10. у=1/3х3-4х. | [-3;3] | 20. у= -х4+2х2+3. | [-0,5;2] |
Ответы к практической части зачета (Приложение1)
Исследование функции и построение ее графика
1) Найдем область определения функции. Функция представляет собой рациональную дробь, поэтому нужно исключить значения обнуляющие знаменатель.
таким образом, область определения функции:
2) Точки пересечения графика функции с осями координат:
с осью ;
с осью .
Таким образом, функция проходит через начало координат — точку .
3) Функция не периодическая. Исследуем функции на четность:
Ни одно из равенств или не выполняется, поэтому функция не является ни четной, ни нечетной. График функции не будет иметь никакой симметрии.
4) Найдем асимптоты графика функции.
В точке функция разрывная. Определим, как ведет себя точка в окрестности этой точки
Таким образом, — уравнение вертикальной асимптоты.
Найдем наклонные асимптоты , где
Получаем уравнение наклонной асимптоты .
5) Найдем экстремум функции и интервалы возрастания и убывания. Для этого вычислим первую производную, используя правило дифференцирования частного:
Найдем критические точки: при
не существует при , но эта точка не принадлежит области определения. Находим знак производной в каждом из интервалов и результаты занесем в таблицу
То есть точка — точка максимума.
6) Найдем точки перегиба, интервалы выпуклости и вогнутости. Для этого находим вторую производную
Найдем критические точки: при не существует при , но эта точка не принадлежит области определения. Находим знак второй производной в каждом из интервалов и результат занесем в таблицу:
Значение функции в точке перегиба . Точка — точка перегиба.
7) Используя полученные данные, строим пунктиром асимптоты и жирным график функции.
«Исследование функции при помощи производной»
Дисциплина – «Математика»
Курс -2
Семестр -3
Практическая работа № 6
Тема: «Исследование функции при помощи производной»
Цель: формирование умений исследовать функции при помощи производной, применять производную при решении задач на максимум и минимум.
Методические указания для практической работы
Теоретические сведения
Возрастание и убывание функции
Функция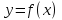 называется возрастающей в промежутке
называется возрастающей в промежутке 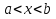 , если для любых
, если для любых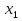 и
и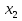 , принадлежащих этому промежутку и таких, что
, принадлежащих этому промежутку и таких, что 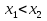 , имеет место неравенство
, имеет место неравенство 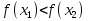 .
.
Функция 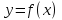 называется убывающей в промежутке
называется убывающей в промежутке 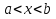 , если для любых
, если для любых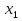 и
и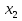 , принадлежащих этому промежутку и таких, что
, принадлежащих этому промежутку и таких, что 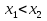 , имеет место неравенство
, имеет место неравенство 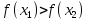 .
.
Как возрастающие , так и убывающие функции называются монотонными, а промежутки, в которых функция возрастает или убывает, — промежутками монотонности.
Возрастание и убывание функции 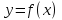 характеризуется знаком ее производной:
характеризуется знаком ее производной:
если в некотором промежутке 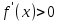 , то функция возрастает в этом промежутке;
, то функция возрастает в этом промежутке;
если в некотором промежутке 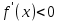 , то функция убывает в этом промежутке.
, то функция убывает в этом промежутке.
Пример 1. Найти промежутки монотонности следующих функций:
а)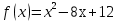 б)
б)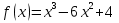
а) Находим производную: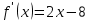 , имеем
, имеем 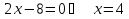 .
.
Последующие рассуждения представим в таблице:
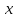
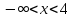
4
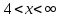

—
0
+
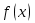
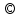

Таким образом, данная функция в промежутке 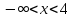 убывает,
убывает,
а в промежутке 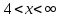 возрастает.
возрастает.
б)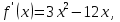
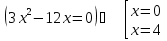
Составим таблицу:
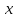
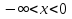
0
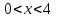
4
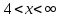

+
0
—
0
+
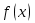


Итак, в промежутках 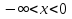 и
и 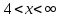 функция возрастает, а в промежутке
функция возрастает, а в промежутке 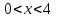 — убывает.
— убывает.
Исследование функции на экстремум
с помощью первой производной
Точка 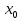 из области определения функции
из области определения функции 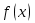 называется точкой минимума этой функции, если существует такая
называется точкой минимума этой функции, если существует такая 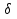 – окрестность
– окрестность
 точки
точки 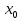 , что для всех
, что для всех 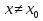 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 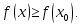
Точка 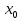 из области определения функции
из области определения функции 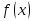 называется точкой максимума этой функции, если существует такая
называется точкой максимума этой функции, если существует такая 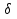 – окрестность
– окрестность
 точки
точки 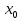 , что для всех
, что для всех 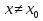 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 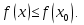
Точки минимума и максимума функции называются точками экстремума данной функции, а значения функции в этих точках – минимумом и максимумом (или экстремумами) функции.
Точками экстремумами могут служить только критические точки, т.е. точки, принадлежащие области определения функции, в которых производная  обращается в нуль или терпит разрыв.
обращается в нуль или терпит разрыв.
Если при переходе через критическую точку 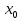 производная
производная  меняет знак, то функция
меняет знак, то функция 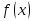 имеет в точке
имеет в точке 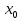 экстремум: минимум в том случае, когда производная меняет знак с минуса на плюс, и максимум – когда с плюса на минус. Если же при переходе через критическую точку
экстремум: минимум в том случае, когда производная меняет знак с минуса на плюс, и максимум – когда с плюса на минус. Если же при переходе через критическую точку 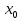 производная
производная  не меняет знака, то функция
не меняет знака, то функция 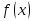 в точке
в точке 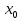 не имеет экстремума.
не имеет экстремума.
Правило нахождения экстремумов функции

с помощью первой производной
Найти производную
 .
.Найти критические точки функции
 , т.е. точки в которых
, т.е. точки в которых  обращается в нуль или терпит разрыв.
обращается в нуль или терпит разрыв.Исследовать знак производной
 в промежутках, на которые найденные критические точки делят область определения функции
в промежутках, на которые найденные критические точки делят область определения функции  . При этом критическая точка
. При этом критическая точка  есть точка минимума, если она отделяет промежуток, в котором
есть точка минимума, если она отделяет промежуток, в котором  , от промежутка, в котором
, от промежутка, в котором  , и точка максимума – в противном случае. Если же в соседних промежутках, разделенных критической точкой
, и точка максимума – в противном случае. Если же в соседних промежутках, разделенных критической точкой  , знак производной не меняется, то в точке
, знак производной не меняется, то в точке  функция экстремума не имеет.
функция экстремума не имеет.Вычислить значения функции в точках экстремума.
Пример 2. Исследовать на экстремум следующие функции:
а)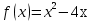 б)
б) 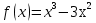
а) Находим 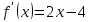 , приравняем производную к нулю, имеем
, приравняем производную к нулю, имеем 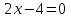 . Получим единственную критическую точку
. Получим единственную критическую точку 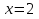 .
.
Последующие рассуждения представим в таблице:
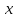
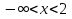
2
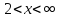

—
0
+
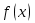
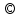
Минимум
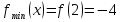

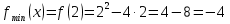
График функции 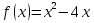 есть парабола. Точка минимума (2;-4) является вершиной параболы.
есть парабола. Точка минимума (2;-4) является вершиной параболы.
б) Находим 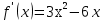 , приравняем производную к нулю, имеем
, приравняем производную к нулю, имеем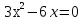 . Получим две критические точки
. Получим две критические точки 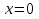 и
и 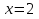 .
.
Последующие рассуждения представим в таблице:
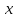
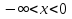
0

2
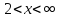

+
0
—
0
+
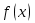

Максимум

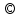
Минимум
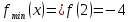

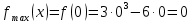
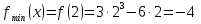
Наименьшее и наибольшее значения функции
Для нахождения наименьшего и наибольшего значений функции, непрерывной в некотором промежутке, необходимо:
Найти критические точки, принадлежащие заданному промежутку, и вычислить значения функции в этих точках;
Найти значения функции на концах промежутка;
Сравнить полученные значения; тогда наименьшее и наибольшее из них являются соответственно наименьшим и наибольшим значениями функции в рассматриваемом промежутке.
Пример 3. Найти наименьшее и наибольшее значение функции 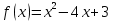 в промежутке
в промежутке 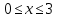 .
.
Имеем 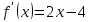 ; 2
; 2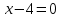 , т.е.
, т.е. 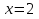 — критическая точка. Находим
— критическая точка. Находим 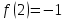 ; далее, вычисляем значения функции на концах промежутка:
; далее, вычисляем значения функции на концах промежутка: 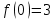 ,
, 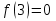 .
.
Итак, наименьшее значение функции равно — 1 и достигается ею во внутренней точке промежутка, а наибольшее значение равно 3 и достигается на левом конце промежутка.
Построение графиков функций
Общая схема построения графиков функций
Найти область определения функции.
Выяснить, не является ли функция четной, нечетной или периодической.
Найти точки пересечения графика с осями координат (если это не вызывает затруднений).
Найти асимптоты графика функции.
Найти промежутки монотонности функции и ее экстремумы.
Найти промежутки выпуклости графика функции и точки перегиба.
Построить график, используя полученные результаты исследования.
Пример 4 . Построить график функции 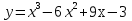 .
.
Функция определена на всей числовой прямой, т.е.
 .
.Данная функция не является ни четной, ни нечетной; кроме того, она не является периодической.
Найдем точку пересечения графика с осью
 : полагая
: полагая  , получим
, получим  . Точки пересечения графика с осью
. Точки пересечения графика с осью  в данном случае найти затруднительно.
в данном случае найти затруднительно.Очевидно, что график функции не имеет асимптот.
Найдем производную:
 . Далее, имеем
. Далее, имеем  .
.
Точки 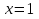 и
и 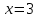 делят область определения функции на три промежутка:
делят область определения функции на три промежутка: 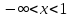 ,
, 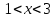 ,
, 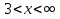 . В промежутках
. В промежутках 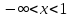 и
и 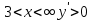 , то есть функция возрастает, а в промежутке
, то есть функция возрастает, а в промежутке 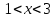
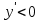 , то есть функция убывает. При переходе через точку
, то есть функция убывает. При переходе через точку 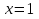 производная меняет знак с плюса на минус, а при переходе через точку
производная меняет знак с плюса на минус, а при переходе через точку 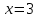 — с минуса на плюс. Значит,
— с минуса на плюс. Значит, 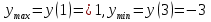 .
.
Найдем вторую производную:
 . Точка
. Точка  делит область определения функции на два промежутка
делит область определения функции на два промежутка  и
и  . В первом из них
. В первом из них  , а во втором
, а во втором
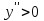 , то есть в промежутке
, то есть в промежутке 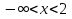 кривая выпукла вверх, а в промежутке
кривая выпукла вверх, а в промежутке 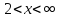 выпукла вниз. Таким образом, получим точку перегиба (2;-1).
выпукла вниз. Таким образом, получим точку перегиба (2;-1).
Используя полученные данные, строим искомый график.
Дисциплина – «Математика»
Курс -2
Семестр -3
Практическая работа № 6
Тема: «Исследование функции при помощи производной»
Цель: формирование умений исследовать функции при помощи производной, применять производную при решении задач на максимум и минимум.
Вариант 1.
Найдите промежутки монотонности функции
 .
.Найдите наименьшее и наибольшее значение функции:
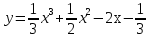 на отрезке
на отрезке 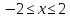 .
.
Найдите промежутки выпуклости и точки перегиба кривых:
 ; б)
; б)  .
.
Дан закон прямолинейного движения точки

(t — в секундах, s — в метрах). Найдите максимальную скорость движения этой точки.
Исследуйте функцию и постройте ее график:
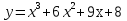 .
.
Вариант 2.
Найдите промежутки монотонности функции
 .
.Найдите наименьшее и наибольшее значение функции
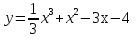 на отрезке
на отрезке 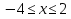 .
.
Найдите промежутки выпуклости и точки перегиба кривых:
 ; б)
; б)  .
.
Дан закон прямолинейного движения точки
 (t — в секундах, s — в метрах). Найдите максимальную скорость движения этой точки.
(t — в секундах, s — в метрах). Найдите максимальную скорость движения этой точки.Исследуйте функцию и постройте ее график:
 .
.
Лекция 19. Исследование функций с помощью производной. Возрастание и убывание функций.
12
Теорема. 1) Если функция f(x) имеет производную на отрезке [a, b] и возрастает на этом отрезке, то ее производная на этом отрезке неотрицательна, т.е. f(x) 0.
2) Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на промежутке (а, b), причем f(x) > 0 для a < x < b, то эта функция возрастает на отрезке [a, b].
Доказательство.
Если функция f(x) возрастает, то f(x + x) > f(x) при x>0 и f(x + x) < f(x) при х<0, тогда:
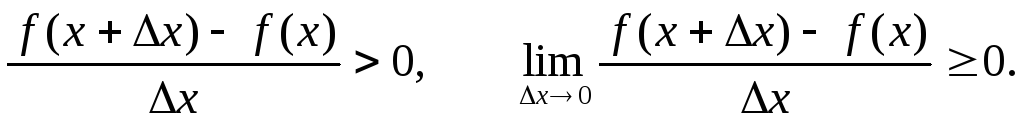
2) Пусть f(x)>0 для любых точек х1 и х2, принадлежащих отрезку [a, b], причем x1<x2.
Тогда по теореме Лагранжа: f(x2) – f(x1) = f()(x2 – x1), x1 < < x2
По условию f()>0, следовательно, f(x2) – f(x1) >0, т.е. функция f(x) возрастает.
Теорема доказана.
Аналогично можно сделать вывод о том, что если функция f(x) убывает на отрезке [a, b], то f(x)0 на этом отрезке. Если f(x)<0 в промежутке (a, b), то f(x) убывает на отрезке [a, b].
Конечно, данное утверждение справедливо, если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (a, b).
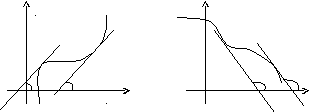 Доказанную
выше теорему можно проиллюстрировать
геометрически:
Доказанную
выше теорему можно проиллюстрировать
геометрически:
y y
x x
Точки экстремума.
Определение. Точка х0 называется точкой локального максимума функции f(x) если для любого x из ε окрестности точки х0 (х0 — ε <x< х0 + ε) f(х0)≥f(x), локального минимума, если f(х0)≤f(x). Точки максимума и минимума называются точками экстремума.
Очевидно, что функция, определенная на отрезке может иметь максимум и минимум только в точках, находящихся внутри этого отрезка. Нельзя также путать максимум и минимум функции с ее наибольшим и наименьшим значением на отрезке – это понятия принципиально различные.
Теорема. (необходимое условие существования экстремума) Если функция f(x) дифференцируема в точке х = х1 и точка х1 является точкой экстремума, то производная функции обращается в нуль в этой точке f’(х1)=0.
Доказательство. Предположим, что функция f(x) имеет в точке х = х1 максимум.
Тогда при достаточно малых положительных х>0 верно неравенство:
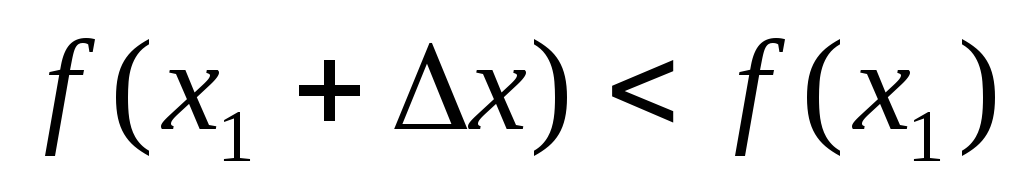 ,
т.е.
,
т.е.
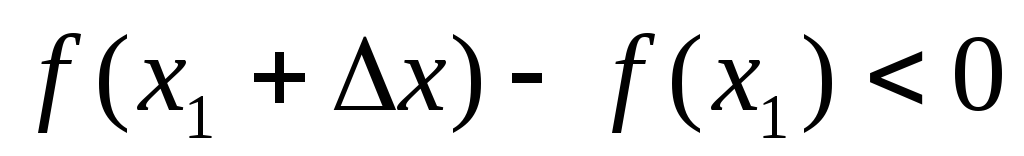
Тогда
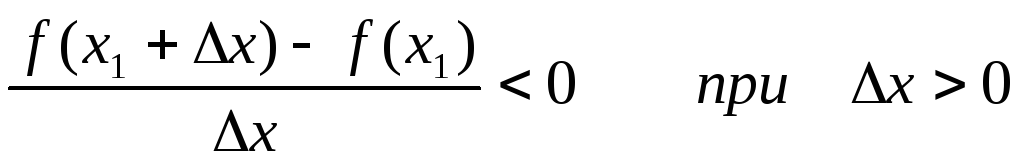
По определению:
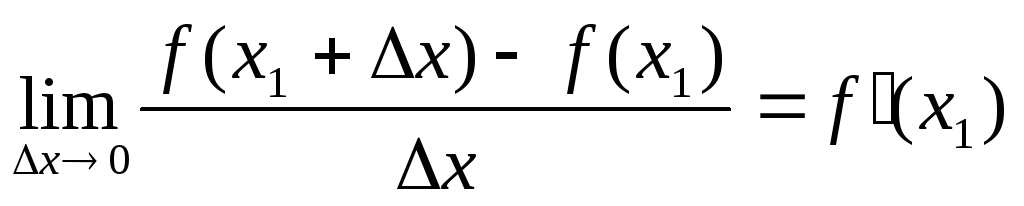
Т.е. если х0, но х<0, то f(x1) 0, а если х0, но х>0, то f(x1) 0.
А возможно это только в том случае, если при х0 f(x1) = 0.
Для случая, если функция f(x) имеет в точке х2 минимум теорема доказывается аналогично.
Теорема доказана.
Следствие. Обратное утверждение неверно. Если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум. Красноречивый пример этого – функция у = х3, производная которой в точке х = 0 равна нулю, однако в этой точке функция имеет только перегиб, а не максимум или минимум.
Определение. Критическими точками функции называются точки, в которых производная функции равна нулю или не существует.
Рассмотренная выше теорема дает нам необходимые условия существования экстремума, но этого недостаточно.
Пример: f(x)
= x Пример: f(x)
= 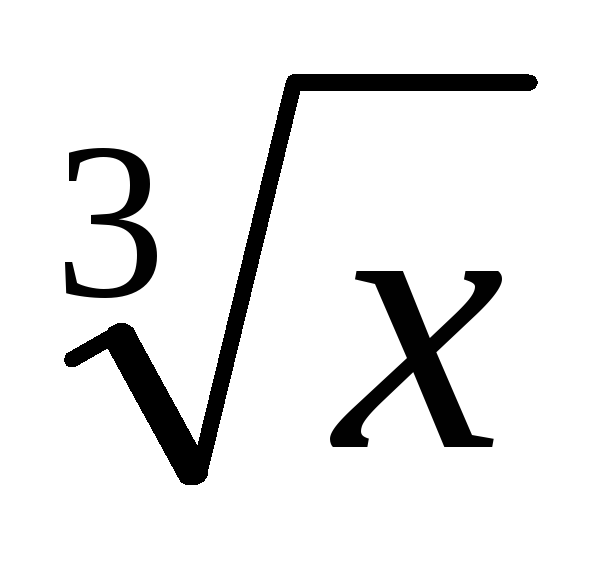
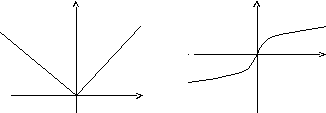 y
y
y
y
x
x
В точке х = 0 функция имеет минимум, но В точке х = 0 функция не имеет не имеет производной. ни максимума, ни минимума, а f(0) = 0
Теорема. (Достаточные условия существования экстремума)
Пусть функция f(x) непрерывна в интервале (a, b), который содержит критическую точку х1, и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки х1).
Если при переходе через точку х1 слева направо производная функции f(x) меняет знак с “+” на “-“, то в точке х = х1 функция f(x) имеет максимум, а если производная меняет знак с “-“ на “+”- то функция имеет минимум.
Доказательство.
Пусть 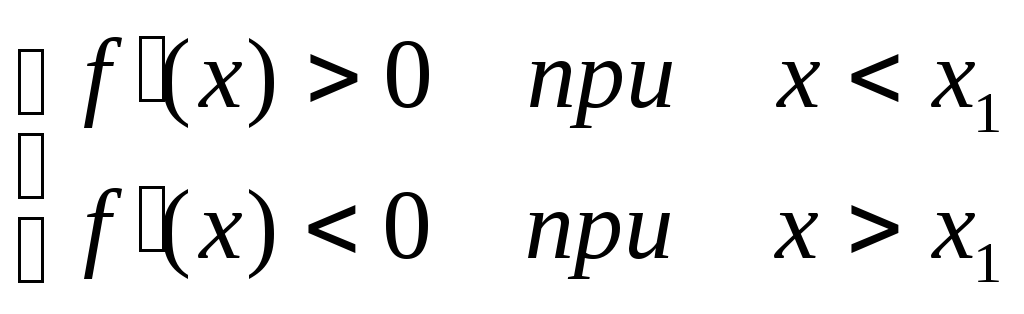
По теореме Лагранжа: f(x) – f(x1) = f()(x – x1), где x < < x1.
Тогда: 1) Если х < x1, то < x1; f()>0; f()(x – x1)<0, следовательно
f(x) – f(x1)<0 или f(x) < f(x1).
2) Если х > x1, то > x1 f()<0; f()(x – x1)<0, следовательно
f(x) – f(x1)<0 или f(x) < f(x1).
Т. к. ответы совпадают, то можно сказать, что f(x) < f(x1) в любых точках вблизи х1, т.е. х1 – точка максимума.
Доказательство теоремы для точки минимума производится аналогично.
Теорема доказана.
На основе вышесказанного можно выработать алгоритм действий при нахождении наибольшего и наименьшего значения функции на отрезке:
Найти критические точки функции.
Найти значения функции в критических точках.
Найти значения функции на концах отрезка.
Выбрать среди полученных значений наибольшее и наименьшее.
Исследование функции с помощью производной (стр. 1 из 3)
МОУ средняя общеобразовательная школа № 18.
«Исследование функции с помощью производной».
Реферат по математике ко Дню науки.
Выполнила:
ученица 11”Б” класса
Бокарева Ирина Николаевна
Руководитель:
учитель математики
Батюкова Галина Викторовна.
Смоленск 2005
План.
Стр.
Введение. 3
Глава I. Развитие понятия функции. 4
Глава II. Основные свойства функции. 7
2.1. Определение функции и графика функции. Область определения и
область значений функции. Нули функции. 7
2.2. Виды функций (четные, нечетные, общего вида, периодические
функции). 8
2.3. Возрастание и убывание функций. Экстремумы. 10
Глава III. Исследование функций. 12
3.1. Общая схема исследования функций. 12
3.2. Признак возрастания и убывания функций. 12
3.3. Критические точки функции, максимумы и минимумы. 13
3.4. Наибольшие и наименьшие значения функции. 14
Глава IV. Примеры применения производной к исследованию функции. 15
Заключение. 22
Список литературы 23
Введение.
Изучение свойств функции и построение ее графика являются одним из самых замечательных приложений производной. Этот способ исследования функции неоднократно подвергался тщательному анализу. Основная причина состоит в том, что в приложениях математики приходилось иметь дело со все более и более сложными функциями, появляющимися при изучении новых явлений. Появились исключения из разработанных математикой правил, появились случаи, когда вообще созданные правила не годились, появились функции, не имеющие ни в одной точке производной.
Целью изучения курса алгебры и начал анализа в 10-11 классах является систематическое изучение функций, раскрытие прикладного значения общих методов математики, связанных с исследованием функций.
Выбрав тему реферата «Исследование функции с помощью производной» я поставила следующие задачи:
— систематизировать свои знания о функции, как важнейшей математической модели;
— усовершенствовать свое умение в применении дифференциального исчисления для исследования элементарных функций.
Развитие функциональных представлений в курсе изучения алгебры и начал анализа на старшей ступени обучения помогает старшеклассникам получить наглядные представления о непрерывности и разрывах функций, узнать о непрерывности любой элементарной функции на области ее применения, научиться строить их графики и обобщить сведения об основных элементарных функциях и осознать их роль в изучении явлений реальной действительности, в человеческой практики.
Работа над содержанием темы «Исследование функций с помощью производной» повысит уровень моей математической подготовки, позволит решать задачи более высокой сложности по сравнению с обязательным курсом.
Глава I. Развитие понятия функции.
Принципиально новая часть курса алгебры посвящена изучению начал анализа. Математический анализ – ветвь математики, оформившаяся в XVIII столетии и включающая в себя две основные части: дифференциальное и интегральное исчисления. Анализ возник благодаря усилиям многих математиков и сыграл громадную роль в развитии естествознания – появился мощный, достаточно универсальный метод исследования функций, возникающих при решении разнообразных прикладных задач. Знакомство с начальными понятиями и методами анализа – одна из важнейших целей курса.
Начиная с XVIII века одним из важнейших понятий является понятие функции. Оно сыграло и поныне играет большую роль в познании реального мира.
Необходимые предпосылки к возникновению понятия функции были созданы, когда возникла аналитическая геометрия, характеризующаяся активным привлечением алгебры к решению геометрических задач.
Идея функциональной зависимости возникла в глубокой древности. Она содержится уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами, в первых формулах для нахождения площади и объема тех или иных фигур и геометрических тел.
Однако явное и вполне сознательное применение понятия функции и систематическое изучение функциональной зависимости берет свое начало в XVII веке в связи с проникновением в математику идеи переменных.
Четкого представления понятия функции в XVII веке еще не было, однако путь к первому такому определению проложил Декарт. Постепенно понятие функции стало отождествляться с понятием аналитического выражения – формулы.
Явное определение функции было впервые дано в 1718 году Иоганном Бернулли : «Функцией переменной величины называют количество, образованное каким угодно способом из этой переменной величины и постоянных».
Леонард Эйлер во «Введении в анализ бесконечных» (1748) примыкает к определению своего учителя И.Бернулли, несколько уточняя его. Правда, он не всегда придерживался вышеуказанного определения. Эйлер придает более широкий смысл функции, понимая ее как кривую, начертанную «свободным влечением руки».
В «Дифференциальном исчислении», вышедшим в свет в 1755 году, Эйлер дает общее определение функции: «Когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называются функциями вторых».
Большой вклад в решение споров внес Жан Батист Жозеф Фурье, который впервые привел примеры функций, которые заданы на различных участках различными аналитическими выражениями.
Во второй половине XIX века понятие функции формулируется следующим образом: если каждому элементу х множества А поставлен в соответствие некоторый определенный элемент у множества В, то говорят, что на множестве А задана функция y=f(x), или что множество А отображено на множество В.
Общее понятие функции применимо, конечно, не только к величинам и числам, но и к другим математическим объектам, например, к геометрическим фигурам.
Это общее определение функции сформировалось уже в XVIII веке и первой половине XIX века. Но уже с самого начала XX века это определение стало вызывать некоторые сомнения среди части математиков.
Дирак ввел так называемую дельта-функцию, которая выходила далеко за рамки классического определения функции.
Сергей Львович Соболев первым рассмотрел частный случай обобщенной функции, включающей и дельта-функцию, и применил созданную теорию к решению ряда задач математической физики.
Важный вклад в развитие теории обобщенных функций внесли ученики и последователи Л.Шварца – И.М.Гельфанд, Г.Е.Шилов и другие.
Краткий обзор развития понятия функции приводит к мысли о том, что эволюция еще далеко не закончена и, вероятно, никогда не закончится, кА никогда не закончится и эволюция математики в целом.
Глава II. Основные свойства функции.
2.1. Определение функции и графика функции. Область определения и область значений функции. Нули функции.
Умение изображать геометрически функциональные зависимости, заданные формулами, особенно важно для успешного усвоения курса высшей математики.
Как известно, функциональной зависимостью называют закон, по которому каждому значению величины х из некоторого множества чисел, называемого областью определения функции, ставится в соответствие одно вполне определенное значение величины у; совокупность значений, которые принимает зависимая переменная у, называется областью изменения функции.
Независимую переменную х называют также аргументом функции. Число у, соответствующее числу х, называют значением функции f в точке х и обозначают f(x).
Функцию можно задать тремя способами: аналитический, табличный, графический.
Аналитический – с помощью формул.
Табличный – с помощью таблиц, где можно указать значения функции, однако лишь для конечного набора значений аргумента.
Графический способ задания функции очень удобен: он дает возможность наглядно представить свойства функции.
Графиком функции f называют множество всех точек (х;у) координатной плоскости, где y=f(x), а х «пробегает» всю область определения функции f.
Пример 1. Найти область определения функции y=lg (2x-3)
y=lg(2x-3)
D(y): 2x-3>0
2x>3
x>1,5
Ответ: D(y)=(1,5; +∞ ).
Одним из понятий для исследования функции является нули функции.
Нули функции – это точки, в которых функция принимает значение нуля.
Пример 2. Найти нули функции y=x2-5x.
y=x2-5x
D(y)=R
По определению :
y=0, тогда
x2-5x=0
x(x-5)=0
x=0 или x=5
Ответ: нулями функции являются точки x=0 и х=5.
Пример 3. Найти нули функции y=4x-8
y=4x-8
D(y)=R
По определению:
у=0, тогда
4х-8=0
4x=8
x=2
Ответ: нулями этой функции является точка х=2.
2.2. Виды функций (четные, нечетные, общего вида, периодические функции).
Рассмотрим функции, области определения которых симметричны относительно начала координат, то есть для любого х из области определения число (-х) также принадлежит области определения. Среди таких функций выделяют четные и нечетные.
Определение: Функция f называется четной, если для любого х из ее области определения f(-x)=f(x).
График четной функции симметричен относительно оси ординат.
Пример 4. Определить вид функции y=2cos2x.
y=2cos2x, D(y)=R
y(-x)=2cos2(-x)=-2cos2x=2cos2x=y(x) – четная.
Пример 5. Определить вид функции y=x4-2x2+2.
y=x4-2x2+2, D(y)=R.
y(-x)=(-x)4-2(-x)2+2=x4-2x2+2=y(x) – четная.
Определение:Функция f называется нечетной, если для любого х из ее области определения f(-x)=-f(x).
График нечетной функции симметричен относительно начала координат.
Пример 6. Определить вид функции y=2sin2x.
y=2sin2x, D(y)=R
y(-x)=2sin2(-x)=-2sin2x=-y(x) – нечетная.
Пример 7. Определить вид функции y=3x+1/3x.
y=3x+1/3x
y(-x)=3(-x)+1/3(-x)=-3x-1/3x=-(3x+1/3x)=-y(x) – нечетная.
Пример 4. Пример 5.
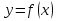
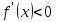 , от промежутка, в котором
, от промежутка, в котором 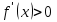 , и точка максимума – в противном случае. Если же в соседних промежутках, разделенных критической точкой
, и точка максимума – в противном случае. Если же в соседних промежутках, разделенных критической точкой  .
.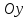 : полагая
: полагая 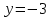 . Точки пересечения графика с осью
. Точки пересечения графика с осью 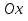 в данном случае найти затруднительно.
в данном случае найти затруднительно.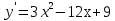 . Далее, имеем
. Далее, имеем  .
.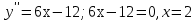 . Точка
. Точка 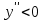 , а во втором
, а во втором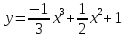 .
.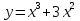 ; б)
; б) 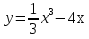 .
.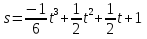
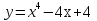 .
.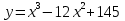 ; б)
; б) 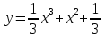 .
.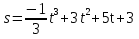 (t — в секундах, s — в метрах). Найдите максимальную скорость движения этой точки.
(t — в секундах, s — в метрах). Найдите максимальную скорость движения этой точки.