Решение тригонометрических уравнений | Математика, которая мне нравится
Простейшие тригонометрические уравнения
Уравнение при решений не имеет,
при имеет решения ,
при имеет решения ,
при имеет решения ,
при всех остальных имеет решения .
Уравнение при решений не имеет,
при имеет решения ,
при имеет решения >,
при имеет решения ,
при всех остальных имеет решения .
Уравнение имеет решения .
Уравнение имеет решения .
Приемы решения тригонометрических уравнений
1. Сведение к одной функции
1. заменяем на , — на .
Пример 1.
Пример 2.
2. заменяем на , — на , — на .
Пример 1.
1) 2) ,
В первом случае решений нет, во втором .
Пример 2.
3. Однородные уравнения относительно .
Если , то деля обе части уравнения на или на , получаем равносильные уравнения. Действительно, пусть — корень уравнения и . Подставляя в уравнение, получаем, что и , а это невозможно.
Пример.
4. Уравнения, приводящиеся к однородным
а) Домножение на
Пример.
б) Переход к половинному аргументу
Пример.
5. Использование формулы
Пример.
6. Замена .
Пример.
Разложение на множители
1. Формулы преобразования суммы в произведение
2. Формулы
Пример 1.
Ответ. .
Пример 2.
, решений нет,
Ответ. , .
Понижение степени
Использование формул
Сравнение левой и правой части
Пример 1.
что невозможно.
Ответ. .
Пример 2.
Ответ. .
Пример 3.
Пусть
Подставляем во второе уравнение:
Ответ. .
Пример 4.
или
Если , то . Если , то .
Ответ. .
hijos.ru
Простейшие тригонометрические уравнения и их решение
К простейшим тригонометрическим уравнениям относятся уравнения вида
Решение простейших тригонометрических уравнений
Рассмотрим подробнее каждое из этих уравнений и их решение.
Уравнение вида . Так как для любого x, то при и уравнение не имеет корней. При , корни этого уравнения находятся по формуле
Особые случаи
Примеры решения задач
Уравнение вида . Так как для любого x, то при и уравнение корней не имеет. При , корни этого уравнения находятся по формуле
Особые случаи:
ПРИМЕР 4| Задание | Решить уравнение — |
| Решение | Косинус – функция ограниченная и лежит в пределах , поэтому данное равенство не имеет смысла. |
| Ответ | Решений нет. |
Простейшие тригонометрические уравнения с тангенсами и котангенсами
Уравнение вида . Для любого действительного a на промежутке существует единственный угол , для которого . Это угол . Учитывая периодичность функции , получим формулы для нахождения корней уравнения :
ПРИМЕР 5
| Задание | Решить уравнение |
| Решение | Выразим из этого равенства тангенс
В последнем равенстве положив , получим простейшее тригонометрическое уравнение , корни которого вычисляются по формуле
Тогда
Сделаем обратную замену
и выразим из полученного уравнения x:
поделим обе части последнего равенства на 2, тогда окончательно получим
|
| Ответ |
Уравнение вида . Для любого действительного a на промежутке существует единственный угол , для которого . Это угол . Учитывая периодичность функции , получим формулы для нахождения корней уравнения :
ПРИМЕР 6
| Задание | Решить уравнение
|
| Решение | Ведем замену , тогда исходное уравнение преобразуется в простейшее тригонометрическое уравнение , корни которого вычисляются по формуле
Тогда
Сделаем обратную замену
и выразим из полученного уравнения x:
поделим обе части последнего равенства на 5, тогда окончательно получим
|
| Ответ |
Приведение тригонометрических уравнений к простейшим
Примеры тригонометрических уравнений, которые приводятся к простейшим тригонометрическим уравнениям с помощью элементарных преобразований или тригонометрических формул.
ПРИМЕР 8| Задание | Решить уравнение |
| Решение | Применим к правой части заданного уравнения формулу суммы синусов:
или
Последнее равенство равносильно совокупности простейших уравнений
|
| Ответ |
| Понравился сайт? Расскажи друзьям! | |||
методика преподавания – статья – Корпорация Российский учебник (издательство Дрофа – Вентана)
1. Синус и косинус любого угла (пропедевтика к изучению тригонометрических уравнений)
Пример задания. Найти приближенно углы, косинусы которых равны 0,8.

Решение. Косинус — это абсцисса соответствующей точки единичной окружности. Все точки с абсциссами, равными 0,8, принадлежат прямой, параллельной оси ординат и проходящей через точку C(0,8; 0). Эта прямая пересекает единичную окружность в двух точках: Pα° и Pβ°, симметричных относительно оси абсцисс.
С помощью транспортира находим, что угол α° приближенно равен 37°. Значит, общий вид углов поворота с конечной точкой Pα°
:α° ≈ 37° + 360°n, где n — любое целое число.
В силу симметрии относительно оси абсцисс точка Pβ° — конечная точка поворота на угол –37°. Значит, для нее общий вид углов поворота:
β° ≈ –37° + 360°n, где n — любое целое число.
Ответ: 37° + 360°n, –37° + 360°n, где n— любое целое число.
Пример задания. Найти углы, синусы которых равны 0,5.
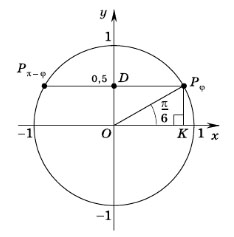
Решение. Синус — это ордината соответствующей точки единичной окружности. Все точки с ординатами, равными 0,5, принадлежат прямой, параллельной оси абсцисс и проходящей через точку D(0; 0,5).
Эта прямая пересекает единичную окружность в двух точках: 
Общий вид углов поворота с конечной точкой Pφ:
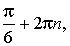
где n — любое целое число. Общий вид углов поворота с конечной точкой Pπ–φ:
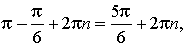
где n — любое целое число.
Ответ: 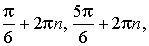 где n — любое целое число.
где n — любое целое число.
2. Тангенс и котангенс любого угла (пропедевтика к изучению тригонометрических уравнений)
Пример 2. Найти общий вид углов, тангенс которых равен –1,2.
Пример задания. Найти общий вид углов, тангенс которых равен –1,2.
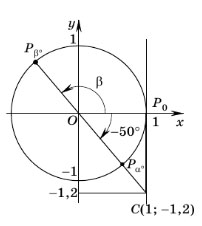
Решение. Отметим на оси тангенсов точку C с ординатой, равной –1,2, и проведем прямую OC. Прямая OC пересекает единичную окружность в точках Pα° и Pβ° — концах одного и того же диаметра. Углы, соответствующие этим точкам, отличаются друг от друга на целое число полуоборотов, т.е. на 180°n (n — целое число). С помощью транспортира находим, что угол
Ответ: –50° + 180°n, n ∈ Z.
По синусу и косинусу углов 30°, 45° и 60° легко найти их тангенсы и котангенсы. Например,
Перечисленные углы довольно часто встречаются в разных задачах, поэтому полезно запомнить значения тангенса и котангенса этих углов.
|
α° |
30° |
45° |
60° |
|
φ рад |
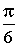
|

|
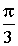
|
|
tg φ |
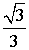
|
1 |
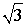
|
|
ctg φ |
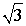
|
1 |
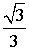
|

Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 11 класс. Базовый уровень
Учебник входит в УМК по математике для 10–11 классов, изучающих предмет на базовом уровне. Теоретический материал разделен на обязательный и дополнительный, система заданий дифференцирована по уровню сложности, каждый пункт главы завершается контрольными вопросами и заданиями, а каждая глава — домашней контрольной работой. В учебник включены темы проектов и сделаны ссылки на интернет-ресурсы.
Купить3. Простейшие тригонометрические уравнения
Вводятся обозначения: arcsin α, arccos α, arctg α, arcctg α. Не рекомендуется торопиться с введением объединенной формулы. Две серии корней значительно удобнее записывать, особенно, когда нужно отбирать корни на интервале.
|
tg φ = α, φ = arctg α + πn, n ∊ Z,
т.е. arctg α — угол из промежутка tg (arctg α) = α. |
|
ctg φ = α, φ = arcctg α + πn, n ∊ Z, 0 < arcctg α < π, т.е. arcctg α — угол из промежутка (0; π), котангенс которого равен α, ctg (arcctg α) = α. |
При изучении темы «простейшие тригонометрические уравнения», уравнения чаще всего сводятся к квадратам.
4. Формулы приведения
Формулы приведения являются тождествами, т. е. они верны для любых допустимых значений φ. Анализируя полученную таблицу, можно заметить, что:
1) знак в правой части формулы совпадает со знаком приводимой функции в соответствующей четверти, если считать φ острым углом;
2) название меняют только функции углов 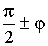 и
и 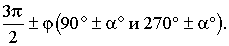
|
α |
φ + 2πn |
– φ |
π – φ |
π + φ |
|
sin α |
sin φ |
– sin φ |
sin φ |
– sin φ |
|
cos α |
cos φ |
cos φ |
– cos φ |
– cos φ |
|
tg α |
tg φ |
– tg φ |
– tg φ |
tg φ |
|
ctg α |
ctg φ |
– ctg φ |
– ctg φ |
ctg φ |
|
α |
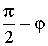
|
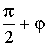
|
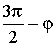
|
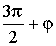
|
|
sin α |
cos φ |
cos φ |
– cos φ |
– cos φ |
|
cos α |
sin φ |
– sin φ |
– sin φ |
sin φ |
|
tg α |
ctg φ |
– ctg φ |
ctg φ |
– ctg φ |
|
ctg α |
tg φ |
— tg φ |
tg φ |
– tg φ |
5. Свойства и график функции y = sin x
Простейшие тригонометрические неравенства решаются либо по графику, либо на окружности. При решении тригонометрического неравенства на окружности важно не перепутать, какую точку указывать первой.
Что ещё почитать?
6. Свойства и график функции y = cos x
Задачу построения графика функции y = cos x можно свести к построению графика функции y = sin x. Действительно, поскольку 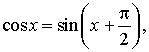 график функции y = cos x можно получить из графика функции y = sin x сдвигом последнего вдоль оси абсцисс влево на
график функции y = cos x можно получить из графика функции y = sin x сдвигом последнего вдоль оси абсцисс влево на 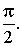
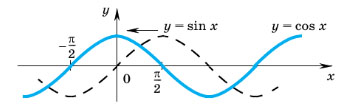
7. Свойства и графики функций y = tg x и y = ctg x
Область определения функции y = tg x включает в себя все числа, кроме чисел вида 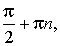 где n ∈ Z. Как и при построении синусоиды, сначала постараемся получить график функции y = tg x на промежутке
где n ∈ Z. Как и при построении синусоиды, сначала постараемся получить график функции y = tg x на промежутке 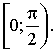
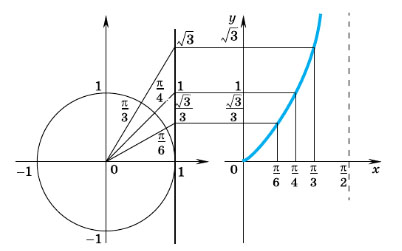
В левом конце этого промежутка тангенс равен нулю, а при приближении к правому концу значения тангенса неограниченно увеличиваются. Графически это выглядит так, как будто график функции y = tg x прижимается к прямой 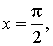 уходя вместе с ней неограниченно вверх.
уходя вместе с ней неограниченно вверх.
8. Зависимости между тригонометрическими функциями одного и того же аргумента
Равенства 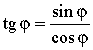 и
и 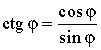 выражают соотношения между тригонометрическими функциями одного и того же аргумента φ. С их помощью, зная синус и косинус некоторого угла, можно найти его тангенс и котангенс. Из этих равенств легко получить, что тангенс и котангенс связаны между собой следующим равенством.
выражают соотношения между тригонометрическими функциями одного и того же аргумента φ. С их помощью, зная синус и косинус некоторого угла, можно найти его тангенс и котангенс. Из этих равенств легко получить, что тангенс и котангенс связаны между собой следующим равенством.
tg φ · ctg φ = 1
Есть и другие зависимости между тригонометрическими функциями.
Уравнение единичной окружности с центром в начале координат x2 + y2= 1 связывает абсциссу и ординату любой точки этой окружности.
Основное тригонометрическое тождество
cos2 φ + sin2 φ = 1
9. Синус и косинус суммы и разности двух углов
Формула косинуса суммы
cos (α + β) = cos α cos β – sin α sin β
Формула косинуса разности
cos (α – β) = cos α cos β + sin α sin β
Формула синуса разности
sin (α – β) = sin α cos β – cos α sin β
Формула синуса суммы
sin (α + β) = sin α cos β + cos α sin β
10. Тангенс суммы и тангенс разности двух углов
Формула тангенса суммы

Формула тангенса разности
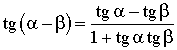

Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 11 класс. Углубленный уровень. Учебник
Учебник входит в УМК по математике для 10–11 классов, изучающих предмет на базовом уровне. Теоретический материал разделен на обязательный и дополнительный, система заданий дифференцирована по уровню сложности, каждый пункт главы завершается контрольными вопросами и заданиями, а каждая глава — домашней контрольной работой. В учебник включены темы проектов и сделаны ссылки на интернет-ресурсы.
Купить11. Тригонометрические функции двойного угла
Формула тангенса двойного угла
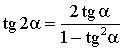
cos2α = 1 – 2sin2α cos2α = 2cos2α – 1
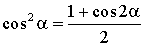
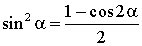
Пример задания. Решить уравнение 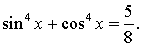
Решение. 
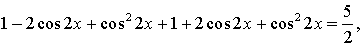
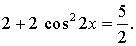
Понизим степень еще раз:
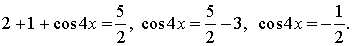
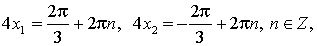
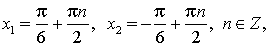
Ответ: 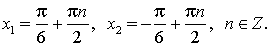
12. Преобразование произведения тригонометрических функций в сумму. Обратное преобразование
Основные формулы
Переход от суммы к произведению
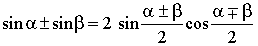

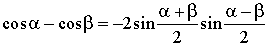
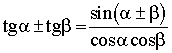
Переход от произведения к сумме
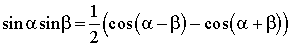
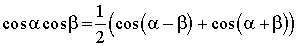
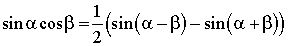
13. Решение тригонометрических уравнений
В большинстве случаев исходное уравнение в процессе решения сводится к простейшим тригонометрическим уравнениям. Однако для тригонометрических уравнений не существует единого метода решения. В каждом конкретном случае успех зависит от знания тригонометрических формул и от умения выбрать из них нужные. При этом обилие различных формул иногда делает этот выбор довольно трудным.
Уравнения, сводящиеся к квадратам
Пример задания. Решить уравнение 2 cos2x + 3 sinx = 0
Решение. С помощью основного тригонометрического тождества это уравнение можно свести к квадратному относительно sinx:
2cos2x + 3sinx = 0, 2(1 – sin2x) + 3sinx = 0,
2 – 2sin2x + 3sinx = 0, 2sin2x – 3sinx – 2 = 0
Введем новую переменную y = sin x, тогда уравнение примет вид: 2y2 – 3y – 2 = 0.
Корни этого уравнения y1 = 2, y2 = –0,5.
Возвращаемся к переменной x и получаем простейшие тригонометрические уравнения:
1) sin x = 2 – это уравнение не имеет корней, так как sin x < 2 при любом значении x;
2) sin x = –0,5, 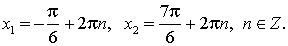
Ответ: 
Однородные тригонометрические уравнения
Пример задания. Решить уравнение 2sin2x – 3sinxcosx – 5cos2x = 0.
Решение. Рассмотрим два случая:
1) cosx = 0 и 2) cosx ≠ 0.
Случай 1. Если cos x = 0, то уравнение принимает вид 2sin2x = 0, откуда sinx = 0. Но это равенство не удовлетворяет условию cosx = 0, так как ни при каком x косинус и синус одновременно в нуль не обращаются.
Случай 2. Если cos x ≠ 0, то можно разделить уравнение на cos2x и получить 2tg2x – 3tgx – 5 = 0. Вводя новую переменную y = tg x, получаем квадратное уравнение 2y2 – 3y — 5 = 0.
Корни этого уравнения y1 = –1, y2 = 2,5.
Возвращаемся к переменной x.
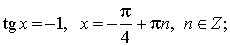
tg x = 2,5,
x = arctg 2,5 + πn, n ∈ Z.
Ответ: 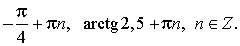
Уравнение, левая часть которого — многочлен, каждый член которого имеет вторую степень, а правая — нуль, называют однородным уравнением второй степени относительно переменных u и v.
Обозначив в исходном уравнении sin x буквой u, а cos x буквой v, получим уравнение вида au2 + buv + cv2 = 0.
Делением на v2 такое уравнение сводится к квадратному относительно 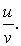
Напоминаем, что апробировать учебник «Алгебра и начало математического анализа. 10 класс», как и многие другие издания, можно на платформе LECTA. Для этого воспользуйтесь предложением «5 учеников бесплатно».
#ADVERTISING_INSERT#
rosuchebnik.ru
Простейшие тригонометрические уравнения и неравенства
\(\blacktriangleright\) Стандартные (простейшие) тригонометричекие уравнения — это уравнения вида
\(\sin x=a,\quad \cos x=a,\quad
\mathrm{tg}\,x=b,\quad
\mathrm{ctg}\,x=b\), которые имеют смысл при \(-1\leq a\leq 1,\quad b\in \mathbb{R}\).
Для решения данных уравнения удобно пользоваться единичной окружностью (радиус равен \(1\)).
\[{\color{red}{\text{Решение простейших тригонометрических уравнений}}}\]
Рассмотрим несколько примеров:
Пример 1. Решить уравнение \(\sin x=\dfrac12\).
Найдем на оси синусов точку \(\dfrac12\) и проведем прямую параллельно оси \(Ox\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, синус которых равен \(\dfrac12\). Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{\pi}6\) и \(\dfrac{5\pi}6\). Все остальные углы можно получить путем прибавления к данным углам \(2\pi\cdot n\), где \(n\) — целое число (т.е. поворотом от данных на целое число полных кругов).
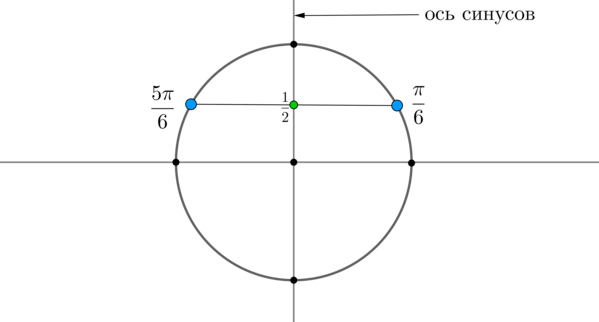
Таким образом, решением являются \(x_1=\dfrac{\pi}6+2\pi n,\
x_2=\dfrac{5\pi}6+2\pi n, \ n\in \mathbb{Z}\).
Пример 2. Решить уравнение \(\cos x=-\dfrac{\sqrt2}{2}\).
Найдем на оси косинусов точку \(-\dfrac{\sqrt2}{2}\) и проведем прямую параллельно оси \(Oy\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, косинус которых равен \(-\dfrac{\sqrt2}{2}\). Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{3\pi}4\) и \(-\dfrac{3\pi}4\). Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\), где \(n\) — целое число.

Таким образом, решением являются \(x_1=\dfrac{3\pi}4+2\pi n,\
x_2=-\dfrac{3\pi}4+2\pi n, \ n\in \mathbb{Z}\).
Пример 3. Решить уравнение \(\mathrm{tg}\,x=\dfrac{\sqrt3}3\).
Найдем на оси тангенсов точку \(\dfrac{\sqrt3}3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, тангенс которых равен \(\dfrac{\sqrt3}3\).Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{\pi}6\) и \(-\dfrac{5\pi}6\). Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\), где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi n\).

Таким образом, решением являются \(x=\dfrac{\pi}6+\pi n, \ n\in \mathbb{Z}\).
Пример 4. Решить уравнение \(\mathrm{ctg}\,x=\sqrt3\).
Найдем на оси котангенсов точку \(\sqrt3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, котангенс которых равен \(\sqrt3\). Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{\pi}6\) и \(-\dfrac{5\pi}6\). Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\), где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi n\).

Таким образом, решением являются \(x=\dfrac{\pi}6+\pi n, \ n\in \mathbb{Z}\).
\(\blacktriangleright\) Решения для любого стандартного тригонометрического уравнения выглядят следующим образом: \[\begin{array}{l|c|c}
\hline \text{Уравнение} & \text{Ограничения} & \text{Решение}\\
\hline &&\\
\sin x=a & -1\leq a\leq 1 & \left[
\begin{gathered}
\begin{aligned}
&x=\arcsin a+2\pi n\\
&x=\pi -\arcsin a+2\pi n
\end{aligned}
\end{gathered}
\right. \ \ , \ n\in \mathbb{Z}\\&&\\
\hline &&\\
\cos x=a & -1\leq a\leq 1 & x=\pm \arccos a+2\pi n, \ n\in
\mathbb{Z}\\&&\\
\hline &&\\
\mathrm{tg}\, x=b & b\in \mathbb{R} & x=\mathrm{arctg}\, b+\pi n, \
n\in
\mathbb{Z}\\&&\\
\hline &&\\
\mathrm{ctg}\,x=b & b\in \mathbb{R} & x=\mathrm{arcctg}\, b+\pi n, \
n\in
\mathbb{Z}\\&&\\
\hline
\end{array}\] Иногда для более короткой записи решение для \(\sin x=a\) записывают как \(x=(-1)^k\cdot \arcsin a+\pi k, \ k\in \mathbb{Z}\).
\(\blacktriangleright\) Любые уравнения вида \(\mathrm{G}\,\big(f(x)\big)=a\), (где \(\mathrm{G}\) — одна из функций \(\sin, \ \cos, \ \mathrm{tg},\ \mathrm{ctg}\), а аргумент \(f(x)\) — некоторая функция) сводятся к стандартным уравнениям путем замены \(t=f(x)\).
Пример 5. Решить уравнение \(\sin{(\pi x+\dfrac{\pi}3)}=1\).
Сделав замену \(t=\pi x+\dfrac{\pi}3\), мы сведем уравнение к виду \(\sin t=1\). Решением данного уравнения являются \(t=\dfrac{\pi}2+2\pi n, n\in\mathbb{Z}\).
Теперь сделаем обратную замену и получим: \(\pi
x+\dfrac{\pi}3=\dfrac{\pi}2+2\pi n\), откуда \(x=\dfrac16+2n,\
n\in\mathbb{Z}\).
\[{\color{red}{\text{Объединение корней}}}\]
Если \(n\) точек, являющихся решением уравнения или системы, разбивают окружность на \(n\) равных частей, то их можно объединить в одну формулу: \(x=\alpha+\dfrac{2\pi}n,\ n\in\mathbb{Z}\), где \(\alpha\) — один из этих углов.
Рассмотрим данную ситуацию на примере:
Пример 6. Допустим, решением системы являются \(x_1=\pm \dfrac{\pi}4+2\pi n, \ x_2=\pm \dfrac{3\pi}4+2\pi n, \ n\in\mathbb{Z}\). Отметим эти точки на окружности:
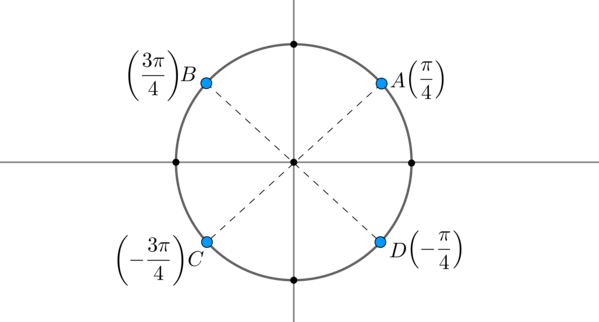
Заметим, что длины дуг \(\buildrel\smile\over{AB},
\buildrel\smile\over{BC}, \buildrel\smile\over{CD},
\buildrel\smile\over{DA}\) равны \(\dfrac{\pi}2\), то есть эти точки разбили окружность на \(4\) равных части. Таким образом, ответ можно записать в виде одной формулы: \(x=\dfrac{\pi}4+\dfrac{\pi}2n, \
n\in\mathbb{Z}\).
\[{\color{red}{\text{Геометрическая интерпретация решений неравенств вида }\mathrm{G}\,(x) \lor a,}}\]
где \(\lor\) — один из знаков \(\leq,\ <,\ >,\ \geq\).
Пример 7. Изобразить на окружности множество решений неравенства \(\sin x >\dfrac12\).
Для начала отметим на окружности корни уравнения \(\sin x =\dfrac12\). Это точки \(A\) и \(B\). Все точки, синус которых больше \(\dfrac12\), находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\), а конец — \(B\).
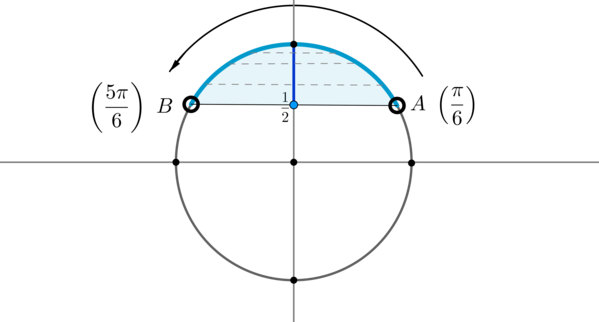
Выберем в точке \(A\) любой угол, например, \(\dfrac{\pi}6\). Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac{\pi}6\), но ближайший к нему, и чтобы синус этого угла также был равен \(\dfrac12\). Это угол \(\dfrac{5\pi}6\). Тогда все числа из промежутка \(\left(\dfrac{\pi}6;\dfrac{5\pi}6\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(\dfrac{\pi}6+2\pi n;\dfrac{5\pi}6+2\pi
n\right), n\in\mathbb{Z}\), т.к. у синуса период \(2\pi\).
Пример 8. Изобразить на окружности множество решений неравенства \(\cos x <\dfrac12\).
Для начала отметим на окружности корни уравнения \(\cos x =\dfrac12\). Это точки \(A\) и \(B\). Все точки, косинус которых меньше \(\dfrac12\), находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\), а конец — \(B\).
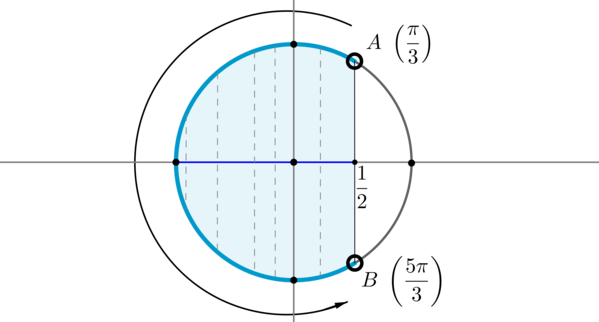
Выберем в точке \(A\) любой угол, например, \(\dfrac{\pi}3\). Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac{\pi}3\), но ближайший к нему, и чтобы косинус этого угла также был равен \(\dfrac12\). Это угол \(\dfrac{5\pi}3\). Тогда все числа из промежутка \(\left(\dfrac{\pi}3;\dfrac{5\pi}3\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(-\dfrac{5\pi}3+2\pi n;-\dfrac{\pi}3+2\pi
n\right), n\in\mathbb{Z}\), т.к. у косинуса период \(2\pi\).
Пример 9. Изобразить на окружности множество решений неравенства \(\mathrm{tg}\, x \geq \dfrac{\sqrt{3}}3\).
Для начала отметим на окружности корни уравнения \(\mathrm{tg}\, x = \dfrac{\sqrt{3}}3\). Это точки \(A\) и \(B\). Все точки, тангенс которых больше или равен \(\dfrac{\sqrt{3}}3\), находятся на выделенных дугах, причем точки \(C\) и \(D\) выколоты, т.к. в них тангенс не определен.
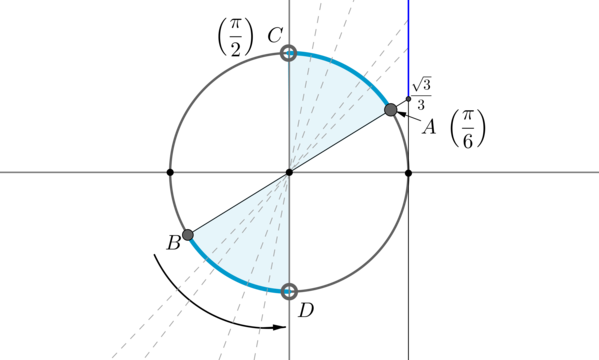
Рассмотрим одну из дуг, например, \(\buildrel\smile\over{AC}\). Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол \(\dfrac{\pi}2\), тогда начало дуги — это угол \(\dfrac{\pi}6\) (угол должен быть меньше \(\dfrac{\pi}2\), но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал \(\Big[\dfrac{\pi}6;\dfrac{\pi}2\Big)\). А все решения данного неравенства будут иметь вид \(\Big[\dfrac{\pi}6+\pi
n;\dfrac{\pi}2+\pi n\Big),
n\in\mathbb{Z}\), т.к. у тангенса период \(\pi\).
Пример 10. Изобразить на окружности множество решений неравенства \(\mathrm{ctg}\, x \leq \sqrt{3}\).
Для начала отметим на окружности корни уравнения \(\mathrm{ctg}\, x = \sqrt{3}\). Это точки \(A\) и \(B\). Все точки, котангенс которых меньше или равен \(\sqrt{3}\), находятся на выделенных дугах, причем точки \(C\) и \(D\) выколоты, т.к. в них котангенс не определен.
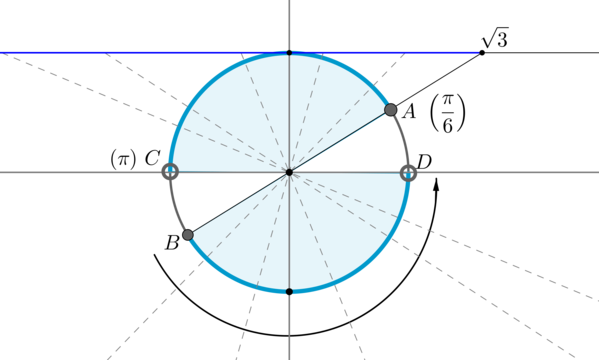
Рассмотрим одну из дуг, например, \(\buildrel\smile\over{AC}\). Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол \(\pi\), тогда начало дуги — это угол \(\dfrac{\pi}6\) (угол должен быть меньше \(\pi\), но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал \(\Big[\dfrac{\pi}6;\pi\Big)\). А все решения данного неравенства будут иметь вид \(\Big[\dfrac{\pi}6+\pi
n;\pi+\pi n\Big), n\in\mathbb{Z}\), т.к. период котангенса \(\pi\).
\[{\color{red}{\text{Отбор корней}}}\]
Геометрический способ (по окружности).
Этот способ заключается в том, что мы отмечаем решения всех уравнений (неравенств) на единичной окружности и пересекаем (объединяем) их.
Пример 11. Найти корни уравнения \(\sin x=-\dfrac12\), если \(\cos x\ne \dfrac{\sqrt3}2\).
В данном случае необходимо пересечь решения первого уравнения с решением второго уравнения.
Решением первого уравнения являются \(x_1=-\dfrac{\pi}6+2\pi n,\
x_2=-\dfrac{5\pi}6+2\pi n,\ n\in \mathbb{Z}\), решением второго являются \(x\ne \pm \dfrac{\pi}6+2\pi n,\ n\in\mathbb{Z}\). Отметим эти точки на окружности:
Видим, что из двух точек, удовлетворяющих первому уравнению, одна точка \(x= -\dfrac{\pi}6+2\pi n\) не подходит. Следовательно, ответом будут только \(x=-\dfrac{5\pi}6+2\pi n, n\in \mathbb{Z}\).
Вычислительный способ.
Этот способ заключается в подстановке решений уравнения (системы) в имеющиеся ограничения. Для данного способа будут полезны некоторые частные случаи формул приведения: \[\begin{aligned}
&\sin{(\alpha+\pi n)}=\begin{cases} \sin \alpha, \text{при } n —
\text{ четном}\\ -\sin \alpha, \text{при } n — \text{ нечетном}
\end{cases}\\
&\cos{(\alpha+\pi n)}=\begin{cases} \cos \alpha, \text{при } n —
\text{ четном}\\ -\cos \alpha, \text{при } n — \text {нечетном}
\end{cases}\\
&\mathrm{tg}\,(\alpha+\pi n)=\mathrm{tg}\,\alpha\\
&\mathrm{ctg}\,(\alpha+\pi n)=\mathrm{ctg}\,\alpha\\
&\sin{\left(\alpha+\dfrac{\pi}2\right)}=\cos\alpha\\
&\cos{\left(\alpha+\dfrac{\pi}2\right)}=-\sin \alpha\\
&\,\mathrm{tg}\,\left(\alpha+\dfrac{\pi}2\right)=-\,\mathrm{ctg}\,\alpha\\
&\,\mathrm{ctg}\,\left(\alpha+\dfrac{\pi}2\right)=-\,\mathrm{tg}\,\alpha
\end{aligned}\]
Пример 12. Решить систему \(\begin{cases} \cos x=\dfrac12\\
\sin x+\cos x>0\end{cases}\)
Решением уравнения являются \(x_1=\dfrac{\pi}3+2\pi n,\ x_2=-\dfrac{\pi}3+2\pi n,\ n\in\mathbb{Z}\). Подставим в неравенство \(\sin x+\cos x>0\) по очереди оба корня:
\(\sin x_1+\cos x_1=\dfrac{\sqrt3}2+\dfrac12>0\), следовательно, корень \(x_1\) нам подходит;
\(\sin x x_2+\cos x_2=-\dfrac{\sqrt3}2+\dfrac12<0\), следовательно, корень \(x_2\) нам не подходит.
Таким образом, решением системы являются только \(x=\dfrac{\pi}3+2\pi
n,\ n\in\mathbb{Z}\).
Алгебраический способ.
Пример 13. Найти корни уравнения \(\sin x=\dfrac{\sqrt2}2\), принадлежащие отрезку \([0;\pi]\).
Решением уравнения являются \(x_1=\dfrac{\pi}4+2\pi n, \
x_2=\dfrac{3\pi}4 +2\pi n, \ n\in\mathbb{Z}\). Для того, чтобы отобрать корни, решим два неравенства: \(0\leq x_1\leq\pi\) и \(0\leq
x_2\leq\pi\):
\(0\leq \dfrac{\pi}4+2\pi n\leq\pi \Leftrightarrow -\dfrac18\leq n\leq\dfrac38\). Таким образом, единственное целое значение \(n\), удовлетворяющее этому неравенству, это \(n=0\). При \(n=0\) \(x_1=\dfrac{\pi}4\) — входит в отрезок \([0;\pi]\).
Аналогично решаем неравенство \(0\leq x_2\leq\pi\) и получаем \(n=0\) и \(x_2=\dfrac{3\pi}4\).
Для следующего примера рассмотрим алгоритм решения линейных уравнений в целых числах:
\[ax+by=c, \quad a,b,c — \text{целые числа}\]
Уравнение будет иметь решение в целых числах относительно \(x\) и \(y\) тогда и только тогда, когда \(c\) делится на \(НОД(a,b)\).
Пример: Уравнение \(2x+4y=3\) не имеет решений в целых числах, потому что \(3\) не делится на \(НОД(2,4)=2\). Действительно, слева стоит сумма двух четных чисел, то есть четное число, а справа — \(3\), то есть нечетное число.
Пример: Решить уравнение \(3x+5y=2\). Т.к. \(НОД(3,5)=1\), то уравнение имеет решение в целых числах. Выразим \(x\) через \(y\):
\[x=\dfrac{2-5y}3=\dfrac{2-2y}3-y\]
Число \(\dfrac{2-2y}3\) должно быть целым. Рассмотрим остатки при делении на \(3\) числа \(y\): \(0\), \(1\) или \(2\).
Если \(y\) при делении на \(3\) имеет остаток \(0\), то оно записывается как \(y=3p+0\). Тогда \[\dfrac{2-2y}3=\dfrac{2-2\cdot
3p}3=\dfrac23-2p\ne \text{целому числу}\]
Если \(y\) при делении на \(3\) имеет остаток \(1\), то оно записывается как \(y=3p+1\). Тогда \[\dfrac{2-2y}3=\dfrac{2-2(3p+1)}3=-2p=\text{целому числу}\]
Значит, этот случай нам подходит. Тогда \(y=3p+1\), а \(x=\dfrac{2-2y}3-y=-5p-1\).
Ответ: \((-5p-1; 3p+1), p\in\mathbb{Z}\).
Перейдем к примеру:
Пример 14. Решить систему \[\begin{cases} \sin \dfrac x3=\dfrac{\sqrt3}2\\[3pt] \cos \dfrac x2=1 \end{cases}\]
Решим первое уравнение системы:
\[\left[ \begin{gathered} \begin{aligned} &\dfrac x3=\dfrac{\pi}3+2\pi n\\[3pt] &\dfrac x3=\dfrac{2\pi}3 +2\pi m \end{aligned} \end{gathered} \right.\quad n,m\in\mathbb{Z} \quad \Leftrightarrow \quad \left[ \begin{gathered} \begin{aligned} &x=\pi+6\pi n\\ &x=2\pi +6\pi m \end{aligned} \end{gathered} \right.\quad n,m\in\mathbb{Z}\]
Решим второе уравнение системы:
\[\dfrac x2=2\pi k, k\in\mathbb{Z} \quad \Leftrightarrow \quad x=4\pi k, k\in\mathbb{Z}\]
Необходимо найти корни, которые удовлетворяют и первому, и второму уравнению системы, то есть пересечь решения первого и второго уравнений.
Найдем целые \(n\) и \(k\), при которых совпадают решения в сериях \(\pi+6\pi n\) и \(4\pi k\):
\[\pi + 6\pi n=4\pi k \quad \Rightarrow \quad 4k-6n=1\]
Т.к. \(НОД(4,6)=2\) и \(1\) не делится на \(2\), то данное уравнение не имеет решений в целых числах.
Найдем целые \(m\) и \(k\), при которых совпадают решения в сериях \(2\pi +6\pi m\) и \(4\pi k\):
\[2\pi +6\pi m=4\pi k \quad \Rightarrow \quad 2k-3m=1\]
Данное уравнение имеет решение в целых числах. Выразим \(k=\frac{3m+1}2=m+\frac{m+1}2\).
Возможные остатки при делении \(m\) на \(2\) — это \(0\) или \(1\).
Если \(m=2p+0\), то \(\frac{m+1}2=\frac{2p+1}2=p+\frac12\ne \) целому числу.
Если \(m=2p+1\), то \(\frac{m+1}2=\frac{2p+1+1}2=p+1= \) целому числу.
Значит, \(m=2p+1\), тогда \(k=3p+2\), \(p\in\mathbb{Z}\).
Подставим либо \(m\), либо \(k\) в соответствующую ему серию и получим окончательный ответ: \(x=4\pi k=4\pi (3p+2)=8\pi+12\pi p, p\in\mathbb{Z}\).
shkolkovo.net
Урок алгебры в 10-м классе. Тема: «Примеры решения тригонометрических уравнений»
Цель урока:
- Закрепить навыки решения простейших тригонометрических уравнений.
- Сформировать понятие решения тригонометрических уравнений сводящихся к квадратным.
- Развивать умения сравнивать, выявлять закономерности, обобщать.
- Воспитывать ответственное отношение к труду.
Оборудование:
- Карточки для повторения формул решения простейших тригонометрических уравнений.
- Плакат с алгоритмом решения тригонометрических уравнений (большой на доску и каждому на стол).
Литература: Учебник Колмагорова “Алгебра и начала анализа, 10-11 класс”.
Ход урока.
I. Повторение
1. sin x = a, cos x = a, tg x = a
При каких значениях а эти уравнения имеют решения?
[sin x и cos x при /а/ 1 tg x при любом a]
2. Повторить формулы решения простейших тригонометрических уравнений (на карточках):
sin x = а х = (-1)к arc sin a+
к, к z
sin x = 0
sin x = 1
sin x = -1
cos x = a x=± arc cos a + 2 , n z
cos x = 0
cos x = 1
cos x = -1
tg x = a x = arc tg a + n, n z
arc sin (-а) = — arc sin а
arc cos (-а) = — arc cos а
arc tg а (-а) = — arc tg а
II. Проверка домашнего задания.
Игра “Поле чудес”. Правила игры несколько изменены, а название оставлено.
Правила игры.
- Учитель берет понравившееся ему высказывание или слова из песни, стихотворения, пословицу. По количеству букв в этом высказывании подбирается столько же примеров или задач так, чтобы одинаковым буквам соответствовали одинаковые ответы.
- Каждому ученику учитель дает карточку с заданиями и ученик сразу начинает решать.
- На доске записаны буквы, которые встречаются в высказывании, и под ними ответы, которые соответствуют этим буквам.
- Ниже записаны числа по порядку (по количеству букв в высказывании).
- Ученик, выполнявший задание, называет номер своей карточки и букву, под которой записан ответ.
- Учитель под числом (…) ставит букву (…). И так далее. Ученики стараются быстрее решить, чтобы получить следующую карточку.
- За правильно решенные 2-3 задания он может получить оценку. Поэтому желательно карточек иметь более чем число.
Ум хорошо, а два лучше
12 3 45 67 8 9 10 11 12 13 14 15 1 6 17
| а | в | д |
| n z | , к z | , n z |
| е | л | м |
| , n z | , n z | , n z |
| о | р | у |
| , n z | , n z | , n z |
| x | ч | ш |
| , n z | , n z | , n z |
Уравнение:
| , n z | у | |
| cos x = -1 | х = +2 n, n z | м |
| , n z | x | |
| , n z | o | |
| , n z | p | |
| , n z | o | |
| , n z | ш | |
| , n z | o | |
| , n z | a | |
| , n z | д | |
| , k z | в | |
| , n x | a | |
| , n z | л | |
| , n z | у | |
| , n z | ч | |
| , n z | ш | |
| , n z | е |
Дополнительные уравнения
| , n z | |
| , k z | |
| , n z | |
| , k z | |
| , n z | |
| , n z | |
| , n z | |
| , n z | |
| , n z | |
| , n z | |
| , k z | |
| , n z | |
| , k z | |
| , k z | |
| , n z | |
| , n z |
III. Объяснение нового.
1.
- В предыдущих параграфах были выведены формулы корней простейших тригонометрических уравнений: sin x=a, cos x=a, tg x=a
- К этим уравнениям сводятся другие тригонометрические уравнения. Для решения большинства из них требуется применение формул преобразований тригонометрических выражений.
- Сегодня на уроке мы рассмотрим уравнение, сводящиеся к квадратным.
2.
- На доске записаны уравнения:
а) 3х-8=х+6 (линейное уравнение)
б) х2+2х-15=0 (квадратное уравнение)
в) х4-5х2+4=0 (квадратное уравнение
относительно х2).
г) 2 cos2x-cosx-1=0 (квадратное уравнение
относительно cosx)
- Какие из них являются квадратными?
- Общий вид квадратного уравнения:
ax2+bx+c=0
,
Корни квадратного уравнения, приведенного, т.е. х2+рх+q=0 можно находить по теореме Виета:
Х1+х2=-р; х1х2=q
- х4-5х2+4=0 – квадратное уравнение относительно х2. Это уравнение назвали биквадратным. Общий вид ах4+вх2+с=0, где а± 0.
- Его легко решить методом введения новой переменной, т.е. х2=а и уравнение принимает вид: а2-5а+4=0
3. Последнее уравнение тоже квадратное, относительно cosx. Для его решения введем новую переменную. Пусть y=cosx, тогда уравнение можно записать виде: 2у2-у-1=0. Получили квадратное уравнение.
Д=1+8=9;
Следовательно:
а) cosx=1 б) cosx=
х=2p n, n z , n z
, n n
Ответ: 2 n, n z; , n z
4. Решим уравнение:
Надо привести уравнение к одной функции. Для этого заменим cos2 x на 1-sin2x. Получим относительно xinx квадратное уравнение:
Пусть xinx=у, тогда 2у2+5у-3=0
Получили квадратное уравнение
Д=25+24=49
;
Следовательно:
а) б) xinx=-3 – решение не имеет
, к z
, к z
Ответ: , к z
5.
tgx-2ctgx=-1. Функции разные. Используя тождество tgx? ctgx=1, выразим , заменим ctgx через tgx.
пусть tgx=у, то у2+у-2=0 (дальше, как в предыдущем случае).
6. Для закрепления
4 xin2x- cosx-1=0
Заменим xin2x на 1- cos2x. Получим
4(1- cos2x)- cosx-1=0
4-4 cos2x- cosx-1=0
-4 cos2x- cosx+3=0
4 cos2x+ cosx-3=0
пусть cosx=у, то
4у2+у-3=0
Д=1-48=49 ;
Следовательно,
а) cosx=-1 б)
х= +2 n, n z , n z
Ответ: +2 n; , n z
7. №164 (в) — cамостоятельно
2 xin2x- xinx-1=0
пусть xinx=у, то
2у2-у-1=0
Д=1+8=9;
Следовательно,
а) xinx=1 б)
, n z , n z
,к z.
Ответ: , n z
, к z
№ 165(б)
2 xin2x+3 cosx=0
Заменим xin2x на 1- cos2x получим
2(1- cos2x)+3 cosx=0
2-2 cos2x+3 cosx=0
-2 cos2x+3 cosx+2=0, т.е.
2 cos2x-3 cosx-2=0
пусть cosx=у, то
2у2-3у=0
Д=9+16=25
;
Следовательно,
а) cosx=2 б)
решение не имеет , n z
, n z
, n z
Ответ: , n z
8.
Итог урока
Алгоритм решения тригонометрических уравнений.
- Привести уравнение к квадратному, относительно тригонометрических функций, применяя тригонометрические тождества.
- Ввести новую переменную.
- Записать данное уравнение, используя эту переменную.
- Найти корни полученного квадратного уравнения.
- Перейти от новой переменной к первоначальной.
- Решить простейшие тригонометрические уравнения.
- Записать ответ.
urok.1sept.ru
Решение простейших тригонометрических уравнений
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Тип урока: урок изучения новой темы.
Класс: 10 класс.
Продолжительность урока: 2 часа (130 минут).
Цели урока:
- дидактические: усвоить навык решения простейших тригонометрических уравнений и их частные случаи;
- развивающие: развитие познавательного интереса, логического мышления, интеллектуальных способностей; формирование математической речи;
- воспитательные: формировать эстетические навыки при оформлении записей в тетради и самостоятельность мышления у учащихся.
Организационный этап.
Девиз:
“Не делай никогда того, чего не знаешь, но научись всему, что следует знать”. (Пифагор)
Сегодня на уроке мы научимся решать с вами простейшие тригонометрические уравнения.
1. Актуализация опорных знаний (устная работа).
В результате выполнения задания мы повторим определения арккосинуса, арксинуса, арктангенса и арккотангенса.
1. Сформулировать определение арксинуса числа.
2. Сформулировать определение арккосинуса числа.
3. Сформулировать определение арктангенса числа.
4. Сформулировать определение арккотангенса числа.
5. С помощью тригонометрической окружности найти все значения из промежутка [-2 которые соответствуют числам , , , , arcsin 0, arcsin (Приложение 1)
6. Проверить, верно ли равенство:
7. Имеет ли смысл выражение:
2. Объяснение новой темы. Простейшие тригонометрические уравнения.
Определение. Уравнения вида f(x) = а, где а – данное число, а f(x) – одна из тригонометрических функций, называются простейшими тригонометрическими уравнениями.
1. Пусть дано простейшее уравнение cos t = a.
Данное уравнение:
a) при -1< t < 1 имеет две серии корней
t1 = arсcos a + 2k, k Z
t 2 = — arсcos a + 2m, m Z.
Эти серии можно записать так
t = ± arсcos a + 2n, n Z ;
б) при а = 1 имеет одну серию решений
t = 2n, n Z ;
в) при а = -1 имеет одну серию решений
t = + 2n, n Z ;
г) при а = 0 имеет две серии корней
t1 = + 2k, k Z
t 2 = — + 2m, m Z. Обе серии можно записать в одну серию
t= + n, n Z.
д) при а > 1 и a < -1 уравнение не имеет корней.
Задание 1. Решить уравнения:
1) cos х = ;
2) cos х = — ;
3) cos 4x = 1
4x = 2n, n Z
.
4)
,
.
5)
,
,
.
6) Решите уравнение ; укажите корни, принадлежащие промежутку [-; -2].
а)
б) сделаем выборку корней, принадлежащих промежутку [-2; -].
1) с помощью окружности
2) с помощью графика функции
Ответ: а) ; б) .
Задание 2. Найти корни уравнения:
1) a) cos x =1 б) cos x = — 1 в) cos x = 0 г) cos x =1,2 д) cos x = 0,2
2) а) б) в) г)
2. Пусть дано простейшее уравнение sin t = a.
Данное уравнение :
a) при -1< t < 1 имеет две серии корней
t1 = arсsin a + 2n, n Z
t 2 = — arсcsin a + 2n, n Z.
Эти серии можно записать так
t = ( -1)karсsin a + k, k Z ;
б) при а = 1 имеет одну серию решений
t= + 2n, n Z
в) при а = -1 имеет одну серию решений
t = — + 2n, n Z;
г) при а = 0 имеет две серии корней
t1 = 2k, k Z,
t2 = + 2m, m Z.
Обе серии можно записать в одну серию
t = n, n Z ;
д) при а > 1 и a < -1 уравнение не имеет корней.
Задание 3. Решить уравнения:
1) sin х = ;
, ; , ; , .Запишем ответ в виде одной серии x= ( -1)k+ k, k Z .
2) sin х = -;
, ; , ; , .Запишем ответ в виде одной серии x= ( -1)k ( — + k, k Z или x= ( -1)k+1+ k, k Z .
Задание 3. Найти корни уравнения :
1) a) sin x =1 б) sin x = — 1 в) sin x = 0 г) sin x =1,2 д) sin x = 0,7
2) а) б) в) г)
3. Пусть дано простейшее уравнение tg t = a.
Данное уравнение при любом а R имеет одну серию решений
х = аrctg a + n, n Z.
1) tg х =
х = аrctg + n, n Z.
x = + n, n Z.
2) tg х = ,
х = аrctg + n, n Z,
x = + n, n Z.
4. Пусть дано простейшее уравнение ctg t = a.
Данное уравнение при любом а R имеет одну серию решений
х = аrcctg a + n, n Z.
1) ctg x = 1
х = аrcctg 1 + n, n Z,
х = + n, n Z.
2) ctg x = — 1
х = аrcctg ( -1) + n, n Z,
х = — аrcctg 1 + n, n Z
х = + n, n Z.
5. Итог урока
Продолжите фразу :
- Сегодня на уроке я повторил …
- Сегодня на уроке я узнал …
- Сегодня на уроке я научился …
Вы молодцы! Каждый из вас “научись тому, что следует знать”. Формулы для решения тригонометрических уравнений записаны на карточке — информаторе. (Приложение 2)
6. Домашнее задание: п.9, пример 1-9, № 137, 139, 141, 142.
Спасибо за урок!
Литература.
- А.Н.Колмогоров Алгебра и начала анализа. 10–11 классы
- С.М. Никольский, М.К. Потапов и др “Алгебра и начала анализа 10”
urok.1sept.ru
Проект «Методы решения тригонометрических уравнений!
Областное государственное автономное
образовательное учреждение
дополнительного профессионального образования
«Белгородский институт развития образования»
Методы решения тригонометрических уравнений
(проектное задание)
Выполнила:
Остапенко Татьяна Ивановна,
учитель математики и физики
МБОУ «Бехтеевская СОШ
Корочанского района
Белгородскойобласти
Руководитель курса:
Вертелецкая О.В.,
старший преподаватель
кафедры естественно-
математического образования
Белгород
СОДЕРЖАНИЕ
стр.
Введение…………………………………………………………………….3
Теоретическая часть……………………………………………………….4-6
Практическая часть………………………………………………………7-18
Заключение………………………………………………………………19-20
Библиография……………………………………………………………….21
Приложение
Введение
Тригонометрические уравнения возникают при решении задач по планиметрии, стереометрии, астрономии, физики и в других областях. Еще древнегреческие математики, используя элементы тригонометрии для решения прямоугольных треугольников, фактически составляли и решали простейшие тригонометрические уравнения. Исторически учение о решении тригонометрических уравнений формировалось с развитием теории тригонометрических функций, а также черпало из алгебры общие методы их решения.
Цель работы: изучить методы решения тригонометрических уравнений, исследовать применение их к решению уравнений повышенной сложности и задач различного содержания.
Теоретическая часть
Уравнение, содержащее неизвестную величину под знаком тригонометрической функции, называется тригонометрическим.
Часть тригонометрических уравнений непосредственно решается сведением их к простейшему виду, иногда – с предварительным разложением левой части уравнения на множители, когда правая часть равна нулю. В некоторых случаях удается произвести замену неизвестных таким образом, что тригонометрическое уравнение преобразуется в «удобное» для решения алгебраическое уравнение.
Простейшие тригонометрические уравнения — это уравнения вида
sin x = a, cos x= a, tq x = a, ctq x = a
Каждое из таких уравнений решается по формулам, которые следует знать.
sinx = a, x = (-1)karcsin a + πk, kЄZ,
arcsin a — угол, содержащийся в промежутке от — π/2 до π/2, синус которого равен a.
cosx= a, x=arccos a +2πk, kЄZ,
arccos a — угол, содержащийся в промежутке от 0 до π, косинус которого равен a.
tq x = a, x = arctq a + πk, kЄZ,
arctg a — угол, содержащийся в промежутке от — π/2 до π/2, тангенс которого равен a.
ctq x = a, x = arcctq a + πk, kЄZ,
arcctg a — угол, содержащийся в промежутке от 0 до π, котангенс которого равен a.
Поскольку каждому значению тригонометрической функции соответствует неограниченное множество углов, то тригонометрическое уравнение, если не сделано каких-либо оговорок, имеет бесчисленное множество решений.
Особо используются частные случаи элементарных тригонометрических уравнений, когда тригонометрические функции равны -1, 0, 1, в которых решение записывается без применения общих формул.
Частные случаи
При решении тригонометрических уравнений важную роль играет период тригонометрических функций.
Рекомендации по решению тригонометрических уравнений
1. Если аргументы функций одинаковые, попробовать получить одинаковые функции, использовав формулы без изменения аргументов.
2. Если аргументы функций отличаются в два раза, попробовать получить одинаковые аргументы, использовав формулы двойного аргумента.
3. Если аргументы функций отличаются в четыре раза, попробовать их привести к промежуточному двойному аргументу.
4. Если есть функции одного аргумента, степени свыше первой, попробовать понизить степень, используя формулы понижения степени или формулы сокращенного умножения.
5. Если есть сумма одноименных функций первой степени с разными аргументами (вне случаев 2,3), попробовать преобразовать сумму в произведение для появления общего множителя.
6. Если есть сумма разноимённых функций первой степени с разными аргументами (вне случаев 2, 3), попробовать использовать формулы приведения, получить затем случай 5.
7. Если в уравнении есть произведение косинусов (синусов) различных аргументов, попробовать свести его к формуле синус двойного аргумента, умножив и разделив это выражение на синус (косинус) подходящего аргумента:
8. Если в уравнении есть числовое слагаемое (множитель), то его можно представить в виде значений функции угла. Например:
Практическая часть
Методы решения тригонометрических уравнений.
При решении тригонометрических уравнений все задачи сводятся к тому, чтобы привести к такому виду, чтобы слева стояла элементарная тригонометрическая функция, а справа – число. После того, как это будет достигнуто, следует найти значение аргумента функции, используя одну из основных формул выражения аргумента через обратные тригонометрические функции.
1. Алгебраические уравнения относительно одной из тригонометрических функций.
Необходимо произвести замену неизвестных таким образом, чтобы тригонометрическое уравнение преобразовалось в «удобное» для решения алгебраическое уравнение.
Примеры
1)Решить уравнение 2sin2 + 3sin —2 = 0.
Это уравнение является квадратным относительно sin.
Его корни: sin = , sin =—2. Второе из полученных простейших уравнений не имеет решений, так как Isinl1, решения первого можно записать так:
+2k,π+ 2k
Если в уравнении встречаются разные тригонометрические функции, то надо заменить их все на какую-нибудь одну, используя тригонометрические тождества.
2) Решить уравнение 2sin + cos = 2.
Если в этом уравнении заменим косинус на синус (по аналогии с предыдущими примерами) или наоборот, то получим уравнение с радикалами. Чтобы избежать этого, используем формулы, выражающие синус и косинус через тангенс половинного угла:
и .
Делая замену, получаем уравнение относительно: .
Квадратное уравнение имеет корни откуда
Это же уравнение можно решить другим способом, вводя вспомогательный угол:
Пусть. Тогда можно продолжить преобразование: . Получаем простейшее уравнение т. е. , откуда , или
Ответ получился в другом виде, однако можно проверить, что решения на самом деле совпадают.
2. Понижение порядка уравнения.
Формулы удвоения позволяют квадраты синуса, косинуса и их произведения заменять линейными функциями от синуса и косинуса двойного угла. Такие замены делать выгодно, так как они понижают порядок уравнения.
Примеры
1)Решить уравнение.
Можно заменить cos2 на 2cos2—1 и получить квадратное уравнение относительно cos, но проще заменитьна и получить линейное уравнение относительно.
2) Решить уравнение
Подставляя вместо, их выражения через, получаем:
,
2
3. Использование тригонометрических формул сложения и следствий из них.
Иногда в уравнениях встречаются тригонометрические функции кратных углов. В таких случаях нужно использовать формулы сложения.
Примеры
1) Решить уравнение.
Сложим два крайних слагаемых:, откуда,. Тогда, .
2) Решить уравнение.
Преобразуем произведение синусов в сумму:,
откуда. Полученное уравнение можно решить разными способами: 1) воспользоваться формулами сложения; 2) преобразовать в произведение. Удобнее воспользоваться условием равенства косинусов двух углов и:.
Получаем два уравнения: .
Здесь решения второй серии содержат в себе все решения первой серии. Учитывая это, ответ можно записать короче:.
4. Однородные уравнения.
Уравнение, в котором каждое слагаемое имеет одну и ту же степень, называется однородным. Его можно решить, выполнив деление на старшую степень синуса (или косинуса).
Так как, то постоянные слагаемые можно считать членами второй степени.
Пример: .
Заменяя 4 на ,получаем:
5. Переход к половинному углу
Рассмотрим этот метод на примере:
Пример 6. Решить уравнение: 3 sin x – 5 cos x = 7.
Решение.
6 sin( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =
= 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,
2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,
tg² ( x / 2 ) – 3 tg ( x / 2 ) + 6 = 0 ,
6. Введение вспомогательного угла
Рассмотрим уравнение вида:
asinx + bcosx = c,
где a, b, c – коэффициенты; x – неизвестное.
Теперь коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль (абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1. Тогда можно обозначить их соответственно как cos и sin ( здесь — так называемый вспомогательный угол ), и наше уравнение принимает вид:
Пример. Решить уравнение:
Приемы решения тригонометрических уравнений, требующих искусственных преобразований.
1. Умножение обеих частей уравнения на одну и ту же тригонометрическую функцию.
Пример. Решите уравнение
Решение. Раскроем скобки и преобразуем произведение
в сумму:
Умножим обе части уравнения на. Заметим, что , не является решением данного уравнения. . Преобразуем левую часть уравнения:
; или тогда
или, т.е.
Исключим из найденных серий корни вида , :
а). Ясно, что — четное число, т.е. , а потому .
б).Tax как , то ,но тогда ,.
Ответ:
2. Прибавление к обеим частям уравнения одного и того же числа, одной и той же тригонометрической функции.
Пример. Решите уравнение.
Решение. Область определения уравнения задается неравенствами:
При6авим к обеим частям уравнения по единице. ;
Разделим обе части уравнения на и после преобразований получим.
Тогда или .
Из первой серии корней области определения принадлежит только , но это серия корней содержится в серии. Нетрудно убедиться, что входит в область определения. Например:что верно, поскольку левая часть — число четное, а правая — нечетное.
Ответ:.
3. Тождественные преобразования одной из частей уравнения.
Пример. Решите уравнение .
Решение. Преобразуем левую часть уравнения:
Откуда , тогда или
Легко видеть, что
Ответ:
4. Использование свойств пропорции.
Необходимо помнить, что применение равенств
и т. д. приводит к изменению области определения уравнения. Так, у пропорции существует ограничение: , а у пропорции место другое ограничение:.
Пример. Решите уравнение
Решение. Применяя формулу тангенса разности, получим уравнение: . Используем свойство пропорции: ;
Область определения исходного уравнения:
В ходе решения произошло сужение области определения, добавились новые, ограничения: откуда
Проверим, удовлетворяют ли исходному уравнению значения
а) -верное равенство,
— решение исходного уравнения.
б) верное равенство.
в)-1 -1 — верное равенство, Ответ:
5. Решение тригонометрических уравнений методом экстремальных значений.
При решении некоторых тригонометрических уравнений бывает удобно использовать ограниченность функций, и. Покажем это на конкретных примерах.
Пример 1. Решите уравнение .
Решение. Так как , то ,, откуда и возможные корни данного уравнения Подставив эти значения в левую часть уравнения, получим а последнее равенство возможно только при .
Следовательно, — решение данного уравнения.
Ответ:
Пример 2. Решите уравнение .
Решение. Легко видеть, что и . Следовательно, , но тогда , , откуда , — возможные корни данного
уравнения. Подстановка в данное уравнение показывает, что эти числа действительно являются его корнями.
Ответ:.
6. Уравнения, содержащие модуль функции и корень четной степени
Пример 1.
При отборе корней нет надобности решать неравенство, достаточно вынести корни на тригонометрический круг и выбрать нужные.
Ответ:
Пример 2.
Решение: Учитывая ОДЗ функций, получим:
Ответ:
Уравнения повышенной сложности
1. (Сканави М.И.8.022)
2sin3 x +2sin2x cos x – sin x cos2x – cos3x = 0 | : cos3x ≠ 0;
т.к. уравнение однородное тригонометрическое 3-ей степени
2tg3x + 2tg2x – tgx – 1 = 0;
Разложим левую часть на множители, сгруппировав члены, получим
(tg x + 1)(2tg2x – 1) = 0;
tgx = -1 х= — + n , n ͼ Z
tgx= ; х= arctg + k, k ͼ Z.
Ответ: — + n , n ͼ Z ;arctg + k, k ͼ Z.
2. ( СканавиМ.И.8.081)
6sin2x + sin x cos x – cos2x = 2;
4sin2x + sin x cos x – 3 cos2x = 0; | : cos2x ≠ 0;
т. к. уравнение однородное тригонометрическое 2-ой степени
4tg2x + tg x – 3 = 0;
tgx = -1, х= — + n , n ͼ Z
tgx= ; х= arctg + k, k ͼ Z.
Ответ: — + n , n ͼ Z;
arctg + k, k ͼ Z.
3. ( Сканави М.И. 8.076)
sinx – sin 2x + sin 5x + sin 8x = 0;
сгруппировав первое с третьим, второе с четвертым слагаемые левой части и применив формулы суммы и разности синусов, получим
2sin 3x cos 2x + 2sin 3x cos 5x = 0;
вынесем в левой части общий множитель за скобки и применим формулу суммы косинусов
2sin 3x ∙ 2 cos cos = 0;
sin 3x = 0, x = , n ͼ Z
cos = 0, x = + , k ͼ Z
cos = 0; x = + , m ͼ Z.
Произведем отбор корней, воспользовавшись тригонометрической окружностью
Ответ: , nͼZ;
+ , kͼZ \ { 7m+3| mͼZ }.
4. ( Сканави М.И. 8.076)
= 2;
воспользуемся формулой косинуса двойного угла
= 2;
sin = 1,
sin ≠ 0;
sin = 1;
х= + 4, kͼZ.
Ответ: + 4, kͼZ.
5. (Сканави М.И. 8.120)
+ — — =0
;понизим степень, воспользовавшись формулами косинуса двойного угла
1 +cos x +1 + cos 3x -1 +cos 4x -1 +cos 8x =0;
сгруппируем слагаемые и воспользуемся формулой суммы косинусов
2cos 2x cos x + 2cos 2x cos 6x =0;
2cos 2x 2cos 3,5x cos 2,5x=0;
произведение всюду определенных множителей равно нулю тогда и только тогда, когда хотя бы один из этих множителей равен нулю
cos 2x=0 2x= + , n ͼ Z
cos 3,5x=0 3,5x= + , m ͼ Z
cos 2,5x=0; 2,5x= + , k ͼ Z;
x= +, n ͼ Z
x= +, m ͼ Z
x= +, k ͼ Z .
Ответ: +, nͼZ;
+, mͼZ;
+, kͼZ .
Заключение.
Изучение тригонометрических уравнений позволяет учащимся овладеть конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, развития умственных способностей, умение извлекать учебную информацию на основе сопоставительного анализа графиков, самостоятельно выполнять различные творческие работы.
В данной работе рассмотрены основные методы решения тригонометрических уравнений, причем, как специфические, характерные только для тригонометрических уравнений, так и общие функциональные методы решения уравнений, применительно к тригонометрическим уравнениям.
Для успешного решения уравнений необходимо знать формулы корней простейших тригонометрических уравнений, значение тригонометрических функций для основных углов и значение обратных тригонометрических функций, универсальные правила решения уравнений. Рассмотрено решение элементарных тригонометрических уравнений, метод разложения на множители, методы сведения тригонометрических уравнений к алгебраическим. Указано, что при решении тригонометрических уравнений широко используются тождества, выражающие соотношение между тригонометрическими функциями одного и разных аргументов.
Приведенные методы не исчерпывают все многообразие способов решений тригонометрических уравнений. Однако рассмотренные типы уравнений встречаются наиболее часто и важно уметь распознавать в данном уравнении тот или иной тип.
Результаты данной работы могут быть использованы в качестве учебного материала при подготовке творческих работ, при составлении факультативных курсов для школьников, так же работа может применяться при подготовке учащихся к Единому государственному экзамену, вступительным экзаменам.
Библиография
1. Алексеев А. Тригонометрические подстановки. // Квант. – 1995. — №2. –с. 40 – 42.
2. Выгодский М. Я. «Справочник по элементарной математике». М., «Наука», 1982 г.
3. Г. И. Глейзер История математики в школе. – М.: «Просвещение» 1983г.
4. Карасев В.А., Лёвшина Г.Д. «12 уроков по тригонометрии» — М.: Илекса, 2013.- 200 с.:ил.
5. Крамор В.С. Тригонометрические функции. – М.: Просвещение, 1979.
6. Сост. Гряда Н. Н. и др. Обобщающее повторение в системе подготовки к ЕГЭ по теме «Тригонометрические уравнения», Армавир, 2005г.
7. Цукарь А.Я. Упражнения практического характера по тригонометрии //Математика в школе. 1993-№3- с 12-15.
8. Шаталов В.Ф. Методические рекомендации для работы с опорными сигналами по тригонометрии. — М.: Новая школа, 1993.
infourok.ru
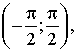 тангенс которого равен α,
тангенс которого равен α,