Неправильные дроби

Мы можем использовать неправильные дроби и смешанные числа для представления одних и тех же значений. Рассмотрим на примере равенство неправильной дроби и смешанного числа :

Перевод неправильной дроби в смешанное число

Для перевода неправильной дроби в смешанное число выполните следующие шаги:

• 1 Разделим числитель на знаменатель 14 ÷ 3, в результате получим 4 целых и 2 в остатке.
• 2 Число 4 будет целой частью смешанного числа.
• 3 Остаток от деления 2 будет числителем дроби, а знаменатель останется прежним, равным 3. В результате получаем

Рассмотрим на примерах как переводить неправильные дроби в смешанные числа.

Пример Перевести неправильные дроби в смешанные числа.

Перевод смешанного числа в неправильную дробь

Для перевода смешанного числа в неправильную дробь выполните следующие шаги:

• 1 Умножим целую часть на знаменатель 2×6 и прибавим числитель 5
  . Полученное число 17=2×6+5запищем в числитель неправильной дроби.
• 2 Запищем в знаменатель неправильной дроби число 6, знаменатель при преобразование в неправильную дробь остается неизменным.
• 3 В результате шагов 1-2 получаем неправильную дробь

Пример Перевести смешанные числа в неправильные дроби.

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Арифметика

Сложение и вычитание дробей

      При сложении (вычитании) дробей с одинаковыми знаменателями получается дробь с тем же знаменателем, а её числитель равен сумме (разности) числителей рассматриваемых дробей.

      Например,

      При сложении (вычитании) дробей с разными знаменателями предварительно нужно привести их к общему знаменателю. Для упрощения вычислений желательно приводить дроби к наименьшему общему знаменателю, хотя это не является обязательным.

      Например,

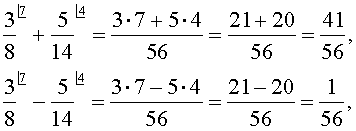
(в уголках сверху здесь обозначены дополнительные множители).

Умножение и деление дробей

      При умножении дробей получается дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.

      Например,

      Деление дробей осуществляется в соответствии со следующим правилом:

      Иногда это правило формулируют так: для того, чтобы разделить первую дробь на вторую, нужно первую дробь умножить на перевернутую вторую.

      В частности,

Действия со смешанными числами

      Для того, чтобы избежать ошибок при выполнении арифметических действий со смешанными числами, рекомендуется сначала обратить смешанные числа в неправильные дроби, затем выполнить нужные арифметические действия, а потом, если это требуется, обратить результат в смешанное число.

      Пример. Найти сумму, разность, произведение и частное смешанных чисел

  и  

      Решение. Преобразуем эти числа в неправильные дроби:

      Далее получаем:

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Смешанные дроби – примеры (5 класс, математика)

Смешанные числа трудны в работе для учеников 5 класса из-за непривычной формы записи. Требуется уметь работать одновременно с дробной и целой частью – это не всегда просто. Поэтому поговорим об основных моментах работы со смешанными числами.

Дробь

Есть два определения дробей:

• Дробью зовется незавершенная операция деления.
• Дробь это разделенное на несколько частей целое. Знаменатель дроби показывает, на сколько частей мы разделили целое. Числитель – сколько частей этого целого было использовано для вычисления

Оба определения обозначают одно и то же. Первая формулировка просто считается более научной.

Любую дробь можно заменить операцией деления и наоборот. В дроби черта обозначает знак деления. То есть дробное число можно заменить делением, подставив числитель на место делимого, а знаменатель на место делителя.

Виды дробей

Можно выделить две больших группы дробей: десятичные и не десятичные. К десятичным относят дроби, записанные в строку. Знаменателем такого числа служит число 10, возведенное в степень, равную количеству знаков после запятой.

Среди не десятичных дробей гораздо больше различных подгрупп:

• Правильные дроби. Это дроби, у которых числитель меньше знаменателя.
• Неправильные дроби. Это дробные числа, у которых числитель больше знаменателя.
• Смешанные числа. Это неправильные дроби, у которых выделили целую часть.

Преобразование смешанных чисел

Неправильную дробь можно преобразовать в смешанное число. Для этого необходимо выполнить следующие действия:

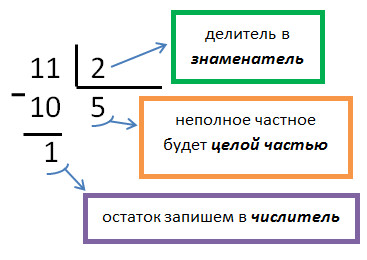
• Числитель разделить на знаменатель с остатком
• Получившееся частное записать в виде целой части дроби
• Остаток – это числитель дробной части смешанного числа.

Можно так же провести обратную процедуру, то есть превратить смешанное число в неправильную дробь. Для этого:

• Целая часть умножается на знаменатель
• Получившееся число прибавляется к числителю
• В результате сложения мы получили числитель неправильной дроби
• Знаменатель неправильной дроби и смешанного числа будет одинаков.

Действия со смешанными числами

Со смешанными числами можно выполнять некоторые действия. Но для правильности решения большинства примеров смешанных дробей придется перевести смешанную дробь в неправильную. По этой же причине целую часть дроби выделяют только в конце всех расчетов, чтобы не выполнять постоянные преобразования.

Смешанные числа без превращения в неправильную дробь можно только складывать и вычитать. Складывают смешанные числа по следующему алгоритму:

• Отдельно складываются целые части
• Отдельно складываются дробные части
• Результат сложения целых частей – целая часть результата, результат сложения дробей – дробная.

Для вычитания порядок действий тот же, но даже для такой простой операции, лучше перевести число в неправильную дробь.

Что мы узнали?

Мы вспомнили, что такое дробь. Поговорили о видах дробей. Отдельно выделили тему «смешанные дроби» и рассказали о правилах выполнения действий с такими числами.

Предыдущая

МатематикаСложение смешанных чисел – правило (5 класс, математика)

Следующая

МатематикаСмешанные числа – правило (5 класс, математика)

правило, алгоритм, примеры с подробным решением

Одни и те же значения в математике можно записать различными выражениями. Использование той или иной записи зависит от конкретного примера. Довольно часто приходится иметь дело со смешанными числами. Их сложение и вычитание опирается на правила простейших арифметических действий с обыкновенными дробями, имеющими одинаковые знаменатели. Другими словами, целую часть в выражении представляют в виде дроби и выполняют необходимое действие.

Понятие смешанных чисел

Число, представленное как сумма натурального числа и правильное отношение, называют смешанным. При этом рациональная дробь будет правильной в том случае, если её делимое будет меньше делителя. Если же числитель выражения равен или превышает её знаменатель, то дробь называют неправильной. Правильная запись дроби будет всегда менее единицы, а неправильная превышать её или быть ей равной.

Любое смешанная дробь состоит из двух частей:

• целой — записывают с левой стороны выражения;
• дробной — указывают после целой части.

Какие-то либо математические знаки между целой и дробной частью не ставят. Например, выражение вида 3 ½ как раз и называют смешанным. При этом число три это целая часть, а ½ — дробная. Следует понимать, что верхнее значение в дробной части указывает на количество имеющихся частей, а нижнее — на сколько их разделяют.

Понимать обозначение записи смешанного выражения очень важно. Например, пусть нужно выполнить сложение числа пять и дроби ¼. Зная, как выполняются действия над дробями, можно записать следующую цепочку решения: 5 + 1/5 = 5/1 + 1 /5 = (5*5) / (1*5) + (1*1) / (5*1) = 25/5 + 1/5 = (25 + 1) / 5 = 26 /5 = 5 1/5.

Обратив внимание на начало записи и конец, можно увидеть, что различие только в опущенном знаке плюс во втором случае: 5 + 1/5 = 5 1/5. То есть фактически имеется свёрнутая и развёрнутая форма записи. Отсюда следует, что если необходимо сложить целую часть и правильного вида выражение, то можно убрать знак сложения, а целое и дробное число записать вместе.

По аналогии со сложением рассматривают и вычитание. Например, от единицы нужно вычесть одну третью. Целую часть можно всегда записать в виде дроби, так как в ней черта, разделяющая числитель и знаменатель, обозначает деление: 1 − 1/3 = 3/3 − 1/3 = (3 − 1) / 3 = 2/3. То есть целое число представляют со знаменателем равным дробной части: 1 − 2/19 = 19/19 − 2/19; 1 − 2 /999 = 999/999 − 2/999.

Когда же целая часть не является единицей, её раскладывают таким образом, чтобы она содержала единичный член, а после используют обозначение смешанного числа при сложении. Например, 3 − 1/3 = 2 + 1 − 1/3 = 2 + 3/3 − 1/3 = 2 + 2/3 = 2 2/3 .

Рассмотренные операции нужно понять так, чтобы их можно было выполнять в уме. В этом случае проблем с нахождением разности смешанных чисел или их суммы возникнуть не должно. При знании материала ответ для примеров вида (4 − 1 ½) быстро вычисляется в уме: (4 − 1 ½) = 4 − (1+ ½) = 4 − 1 − ½ = 3 − ½ = 2 + 1 − ½ = 2 + 2/2 − ½ = 2 + ½ = 2 ½.

Действия над дробями

В пятом классе общеобразовательной школы перед изучением действий над смешанными числами проходят сложение и вычитание дробей с равными знаменателями. Это фундаментальные операции, на них базируются вычисления как в математике, так и в алгебре. Алгоритм вычисления таких примеров довольно прост и состоит всего из трёх действий:

• запись в ответе знаменателя, которым является общее число для всех складываемых членов;
• вычисление числителя путём выполнения арифметических операций над делимыми членами с сохранением их знаков;
• упрощение полученного выражения и при необходимости приведения ответа к смешанной дроби.

Например, ¾ + 7/4 = (3+7) / 4 = 10/4. Объяснить это можно следующим образом. Пусть имеется торт, который разделён на четыре равных куска (части). Три части его забрали. Соответственно в математическом виде это выглядит как ¾. Для второй рассматриваемой дроби получится, что таких тортов два, каждый из которых разделён на четыре одинаковых куска. В первом все части будут забраны, а во втором только три. Всего же получится три торта разрезанных на четыре части каждый с забранными десятью кусками, то есть 10 / 4.

Из полученного выражения можно выделить целую часть — привести к смешанной дроби. Для этого делимое делят на знаменатель «уголком» и остаток переносят в числитель. Для рассматриваемого примера правильным ответом будет 2 ½. Так же выполняют и вычитание. Знаменатель переписывают без изменения, а в числитель представляют как результат вычитания делимых членов: 7/5 − 2/5 = 5/5 = 1. Эти правила справедливы и для вычислений выражений содержащих более двух членов. Например, 17 / 19 + 1 / 19 − 8 / 19 = (17 + 1 − 8) / 19 = 10 / 3 = 3 1/3.

При выполнении действий с отличными знаменателями принцип вычисления заключается в приведении примера к виду, когда все члены получаются с одинаковым делителем. В некоторых случаях проще всего помножить числитель и делитель каждой дроби на число, стоящее в знаменателе другого выражения. Например, 8/9 + 17 /18 = (8*18 / 9*18) + (17 *9) / (18*9). Но такая запись чаще всего громоздкая и неудобная. Поэтому следует научиться находить наименьший общий знаменатель. Вычисляют его путём разложения заданных делителей на множители.

Для рассматриваемого примера справедливым будет следующая цепочка решения: 8/9 + 17 /18 = (8 / (3*3)) + (17 / (3*3*2))= ((8 * 2) + (17 * 2)) / 9. То есть одинаковые члены перемножают и результат записывают в делимое, а оставшиеся используют как множители числителей.

Простые примеры

Важно не только понимать принцип смешанного сложения и вычитания на 5 баллов или 12, то есть на «отлично» (зависит от системы оценок в учебном учреждении), но и уметь применять полученные навыки на практике. Существует ряд примеров, позволяющих практически освоить теоретические навыки. При умении их решать, задачи разной сложности не вызовут затруднений в нахождении правильного ответа.

Вот некоторые из них, в которых необходимо выполнить требуемое действие:

1. Сложить: 12 8/11 + 9 3/11. При решении этого примера следует вспомнить, что 12 8/11 есть не что иное, как сложение и вычитание смешанных чисел 3 + 8/11, а 9 3/11 — иная запись выражения 9 + 3/11. Отсюда следует, что заданное выражение можно переписать как (12 + 8/11) + (9+3/11). Затем применить правило, которое гласит, что для того, чтобы суммировать смешанные части, необходимо выполнить действия отдельно над целыми частями и дробными. То есть верным будет следующее: (12 + 8/11) + (9+3/11) = (12+9) + (8/11+ 3/11) = 21 + ((8+3)/11) = 21 + 11/11 = 21 + 1 = 22.
2. Определить разность двух чисел: 7 3/15 − 2 2/15. Решение выполняют по аналогии с предыдущей задачей: 7 3/15 — 3=2 2/15 = (7 + 3/15) − (2 +2/15) = (7 − 2) + (3/15 − 2/15) = 4 + ((3−2) /15) = 4+ 1/15 = 4 1/15.
3. Немного сложнее пример, в котором получается неправильная дробь: 6 10/13 + 2 9 /13. После суммирования целой и дробной части получится следующий ответ: 8 + 19/11. Делитель с остатком, поэтому ответ приводят к нормальному виду: 8 + 19/13 = 8 + 1 6/13 = 9 3/13.
4. В этом задании нужно от целой части отнять дробную: 2 − 6/7. Целую часть представить в виде двух чисел, одним из которых обязательно должна быть единица: 2 − 6/7 = (2+7/7) — 6/7 = 2 1/7.
5. Последний тип задания подразумевает нахождение результата вычисления сложения или вычитания целого числа и смешанного. Например, 10 − 5 4/23. Девятку нужно представить как 9 +1. Это необходимо для дальнейшего приведения простого числа к дроби. То есть: 10 − 5 4/23 = 9+1 − 5 4/23 = 9 + 23/23 − 5 4/23 = 4 19/7 = 6 6/7.

В простых примерах делать подробные вычисления не нужно. Их следует стараться делать устно, как бы свернуть. При тренировке удобно промежуточные операции проговаривать про себя, пока действия не дойдут до автоматизма.

Задания сложного уровня

При решении задач, касающихся действий над смешанными дробями, нужно всегда использовать правило поочерёдного сложения или вычитания целых и дробных частей выражения. Различные задания могут содержать энное число членов, но при этом правило остаётся неизменным.

Пусть дано выражение вида: 5 15 / 21 + 9 20 / 21 − 6 7/1 3 + 9 5/12 − 6 11/12. Такие примеры проще решать по действиям. Для рассматриваемого примера их будет четыре:

• 5 15 / 21 + 9 20 / 21 = 15 2/3;
• 15 2/3 − 6 7/1 3 = 9 5/39;
• 9 5/39 + 9 5/12 = − 15/52;
• − 15/52 − 6 11/12 = − ((15*52 + 15)/52) − ((6*12 + 11)/12) = − 22 8/39.

Следующая задача требует не только знания правил, но и практического навыка сложения и вычитания чисел. 5 2/3 тонн яблок привезли на овощную базу, а груш доставили на 7/8 тонн меньше, при этом в хранилище уже было персиков на 1/8 тонны больше, чем груш. Спрашивается, сколько всего тонн грузов находится на овощной базе.

Решать её необходимо следующим образом. Из условия известно, что груш меньше, чем яблок на 7/8 тонны. Поэтому верным будет записать, что находится 2 3/8 − 7/8 = 1 + 8/8 + 3/8 − 7/8 = 1 (8 + 3 − 7)/8 = 1 4/8 тонн груш. Используя второе условие, можно найти ранее завезённое количество персиков: 1 4/8 + 1/8 = 1 5/8. Последним действием можно подсчитать общий вес овощей на базе: 2 3/8 + 1 4/8 + 1 5/8 = 4 + 12/8 = 4 + 1 4/8 = 5 4/8 тонны. Таким образом, верно утверждать, что на базе находится пять целых четыре восьмых тонны овощей.

Необходимо отметить, что только самостоятельное решение нескольких заданий позволит закрепить полученные навыки. Для проверки правильности решений можно использовать математические онлайн-калькуляторы.

Это специализированные сайты, выполняющие любые действия над дробями в автоматическом режиме. При этом часто они не только выдают ответ, но и умеют показывать подробное решение, что позволяет проверить правильность алгоритма своих вычислений.

5 класс Смешанные дроби (памятка ученику)

Смешанные дроби

Смешанная Неправильная

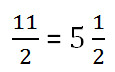
5 =

Сложение и вычитание смешанных дробей

Чтобы сложить смешанные числа, нужно:

1) привести к наименьшему общему знаменателю дробные части;

2) сложить отдельно целые и дробные части;

3) если необходимо, сократить дробную часть;

4) если дробная часть суммы окажется неправильной дробью, выделить из нее целую часть и полученное число прибавить к целой части суммы.

Например:

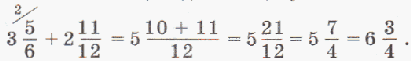
Чтобы вычесть смешанные числа, нужно:

1) привести к наименьшему общему знаменателю дробные части;

2) если дробные части «не вычитаются» (дробная часть уменьшаемого меньше дробной части вычитаемого),то нужно «занять» единицу из целой части;

3) вычесть отдельно целые и дробные части;

4) если необходимо, сократить дробную часть.

Например:

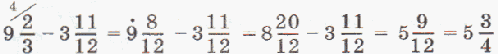
Например:

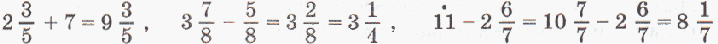
Смешанные дроби

Сложение:

1 шаг: к общ. знам. (НОЗ)

2 шаг: + цел1+цел2,

др1+др2 (числ1+числ2)

3 шаг: неправ. смеш.

4 шаг: сократить

Вычитание:

1 шаг: к общ. знам. (НОЗ)

2 шаг: занять ед. (если нужно)

3 шаг: — цел1 — цел2

др1 — др2 (числ1 — числ2)

4 шаг: сократить

Умножение:

1 шаг: смеш. неправ.

2 шаг: числ1 числ2

зн1 зн2 сократить!

3 шаг: вычислить

4 шаг: неправ. смеш.

Деление:

1 шаг: смеш. неправ.

2 шаг: числ1 зн2

зн1 числ2 сократить!

3 шаг: вычислить

4 шаг: неправ. смеш.