Признаки равенства прямоугольных треугольников. Видеоурок. Геометрия 7 Класс

На этом видеоуроке к изучению предлагается тема «Признаки равенства прямоугольных треугольников». В ходе урока вы сможете продолжить разговор о свойствах прямоугольного треугольника. Учитель напомнит признаки равенства обычных треугольников, а затем перейдет к признакам равенства прямоугольных треугольников, которые тесно связаны между собой.

Вспомним из материала предыдущего урока, прямоугольный треугольником называется треугольник, если у него хотя бы один из углов прямой (т. е. равен 90^о).

Рассмотрим первый признак равенства треугольников: если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.

Проиллюстрируем данный случай:

Рис. 1. Равные прямоугольные треугольники

Доказательство:

Вспомним о первом равенстве произвольных треугольников.

 

 

 

 

 

 

 

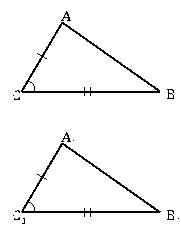
Рис. 2

Если две стороны и угол между ними одного треугольника и соответствующие им две стороны и угол между ними второго треугольника равны, то данные треугольники равны. Об этом гласит первый признак равенства треугольников, то есть:

АВС = .

Аналогичное доказательство следует и для прямоугольных треугольников:

.

Треугольники равны по первому признаку.

Рассмотрим второй признак равенства прямоугольных треугольников. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.

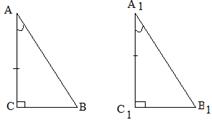
Рис. 3

Доказательство:

Рис. 4

Воспользуемся вторым признаком равенства треугольников:

 

Аналогичное доказательство и для прямоугольных треугольников:

 

Треугольники равны по второму признаку.

Рассмотрим третий признак равенства прямоугольных треугольников: если гипотенуза и прилежащий к ней угол одного прямоугольного треугольника соответственно равны гипотенузе и прилежащему углу другого треугольника, то такие треугольники равны.

Доказательство:

Рис. 5

Вспомним второй признак равенства треугольников:

 Рис. 6

Данные треугольники равны, если:

 

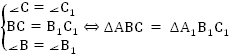
Поскольку известно, что одна пара острых углов у прямоугольных треугольников равна (∠А = ∠А₁), то равенство другой пары углов (∠B = ∠B₁) доказывается следующим образом:

.

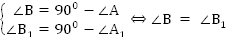Поскольку АВ = А₁

В₁ ( по условию), ∠В = ∠В₁, ∠А = ∠А₁. Поэтому треугольники АВС и А₁В₁С₁ равны по второму признаку.

Рассмотрим следующий признак равенства треугольников:

Если катет и гипотенуза одного треугольника соответственно равны катету и гипотенузе другого треугольника, такие прямоугольные треугольники равны.

 

 

 

 

 

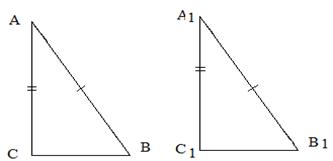
Рис. 7

Доказательство:

Совместим наложением треугольники АВС и А₁В₁С₁. Предположим, что вершины А и А₁, а также С и С₁ совместились наложением, а вершина В и точка В₁ не совпадают. Именно этот случай указан на следующем рисунке:

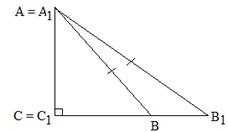
Рис. 8

В данном случае мы можем заметить равнобедренный треугольник АВВ₁ (по определению – по условию АВ = АВ₁). Поэтому по свойству, ∠АВ₁В = ∠АВВ₁. Рассмотрим определение внешнего угла. Внешним углом треугольника называется угол, смежный любому углу треугольника. Его градусная мера равна сумме двух углов треугольника, несмежных с ним. На рисунке указано данное соотношение:

Рис. 9

Угол 5 является внешним углом треугольника и равен ∠5 = ∠1 + ∠2. Отсюда следует, что внешний угол больше каждого из углов, несмежных с ним.

Таким образом, ∠АВВ₁ является внешним углом для треугольника АВС и равен сумме ∠АВВ₁  = ∠САВ + ∠АСВ = ∠АВС  = ∠САВ + 90^о. Таким образом, ∠АВ₁В (что является острым углом в прямоугольном треугольнике АВВ

1) не может быть равен углу ∠АВВ₁, ведь данный угол – тупой по доказанному.

Значит наше предположение касательно расположения точек В и В₁ оказалось неверным, следовательно данные точки совпадают. А значит треугольники АВС и А₁В₁С₁ совместились наложением. Поэтому они равны (по определению).

Таким образом, данные признаки вводятся не зря, ведь их можно использовать при решении некоторых задач.

 

Рекомендованные ссылки на ресурсы интернет

1. Омский государственный университет (Источник).
2. Справочный портал calc.ru (Источник).
3. Учительский портал (Источник).

 

Рекомендованное домашнее задание

1. № 38. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В., под редакцией Садовничего В. А. Геометрия 7. М.: Просвещение. 2010 г.

2. Исходя из данных, указанных на рисунке, укажите равные треугольники, если они есть.

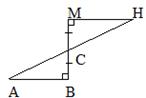
3. Исходя из данных, указанных на рисунке, укажите равные треугольники, если они есть. Учитывайте, что АС = АF.

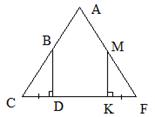
4. В прямоугольном треугольнике к гипотенузе проведены медиана и высота. Угол между ними равен 20^о. Определите величину каждого из острых углов данного прямоугольного треугольника.

Прямоугольный треугольник, свойства, признаки и формулы

Прямоугольный треугольник, свойства, признаки и формулы.

 

 

Прямоугольный треугольник – это треугольник, в котором один угол прямой (то есть составляет 90°).

 

Прямоугольный треугольник (понятие, определение)

Признаки равенства прямоугольных треугольников

Свойства прямоугольного треугольника

Формулы прямоугольного треугольника

Равнобедренный треугольник, равносторонний треугольник

 

Прямоугольный треугольник (понятие, определение):

Прямоугольный треугольник – это треугольник, в котором один угол прямой (то есть составляет 90°).

Сторона, противоположная прямому углу, называется гипотенузой. Гипотенуза (с греч. ὑποτείνουσα – «натянутая») – это самая длинная сторона прямоугольного треугольника, противоположная прямому углу.

Стороны, прилегающие к прямому углу, называются катетами. Катет (с греч. κάθετος – «перпендикуляр, опущенный, отвесный») – одна из двух сторон прямоугольного треугольника, образующих прямой угол.

Для непрямоугольного треугольника гипотенуза и катеты не существуют.

Рис. 1. Прямоугольный треугольник

АВ, АС – катеты прямоугольного треугольника, ВС – гипотенуза прямоугольного треугольника, ∠ ВАС = 90°

Равнобедренный треугольник может быть прямоугольным (равнобедренным прямоугольным треугольником).

Равнобедренный прямоугольный треугольник — это треугольник, являющийся одновременно равнобедренным и прямоугольным. В этом треугольнике каждый острый угол равен 45°.

 

Признаки равенства прямоугольных треугольников:

Признаки равенства прямоугольных треугольников основаны и вытекают из общих признаков равенства треугольников.

1. Равенство по двум катетам.

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.

Рис. 2. Равенство прямоугольных треугольников по двум катетам

АВ = А₁В₁, АС = А₁С₁

2. Равенство по катету и прилежащему острому углу.

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.

Рис. 3. Равенство прямоугольных треугольников по катету и прилежащему углу

АВ = А₁В₁, ∠АВС = ∠А₁В₁С₁

3. Равенство по гипотенузе и острому углу.

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Рис. 4. Равенство прямоугольных треугольников по гипотенузе и острому углу

ВС = В₁С₁, ∠АВС = ∠А₁В₁С₁

4. Равенство по гипотенузе и катету.

Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Рис. 5. Равенство прямоугольных треугольников по гипотенузе и катету

ВС = В₁С₁, АС = А₁С₁ 

5. Равенство по катету и противолежащему острому углу.

Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Рис. 6. Равенство прямоугольных треугольников по катету и противолежащему острому углу

АС = А₁С₁, ∠АВС = ∠А₁В₁С₁

 

Свойства прямоугольного треугольника:

1. В прямоугольном треугольнике сумма двух острых углов равна 90°.

2. В прямоугольном треугольнике катет, лежащий против угла в 30° , равен половине гипотенузы.

И наоборот, если в прямоугольном треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

Рис. 7. Прямоугольный треугольник с острым углом 30˚

b = c / 2

3. Теорема Пифагора:

Сумма квадратов катетов равна квадрату гипотенузы.

c​²​​ = a​²​​ + b​²​​ ,

где a, b – катеты, c – гипотенуза.

Рис. 8. Прямоугольный треугольник

4. В прямоугольном треугольнике центр описанной окружности – есть середина гипотенузы.

И соответственно радиус описанной окружности (R) равен половине гипотенузы.

 ,

где c – гипотенуза.

                         Рис. 9. Прямоугольный треугольник и описанная окружность         

5. В прямоугольном треугольнике медиана, падающая на гипотенузу, равна половине гипотенузы.

 Рис. 10. Прямоугольный треугольник и медиана, падающая на гипотенузу

АМ – медиана прямоугольного треугольника, падающая на гипотенузу, АМ = ВМ = МС, АМ = ВС/2

6. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника подобные исходному.

 Рис. 11. Прямоугольный треугольник и высота, проведенная из вершины прямого угла

АВ/ВС = АН/АС = ВН/АВ

 

Формулы прямоугольного треугольника:

Пусть a и b – длины катетов прямоугольного треугольника, с – длина гипотенузы прямоугольного треугольника, h – высота прямоугольного треугольника, проведенная к гипотенузе (АН), R – радиус описанной окружности, r – радиус вписанной окружности (см. Рис. 9, 11, 12).

Формулы сторон прямоугольного треугольника (a, b, c) по теореме Пифагора:

c​²​​ = a​²​​ + b​²​​ ,

a​²​​ = c​²​​ – b​²​​ ,

b​²​​ = c​² – a​² ​​.

Формула радиуса вписанной окружности (r):

 .

Рис. 12. Прямоугольный треугольник и вписанная окружность

Формула радиуса описанной окружности (R): 

.

Формулы площади (S) прямоугольного треугольника: 

 .

Формулы высоты (h)прямоугольного треугольника:

.

 

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

 

Примечание: © Фото https://www.pexels.com, https://pixabay.com

 

карта сайта

 

Коэффициент востребованности 166

Признаки прямоугольного треугольника, с примерами

ОПРЕДЕЛЕНИЕ

Треугольник, у которого один из углов прямой, называется прямоугольным.

Стороны, которые образуют прямой угол, называются катетами, а сторона, лежащая против прямого угла, – гипотенузой.

Основные признаки прямоугольного треугольника

1. Сумма острых углов треугольника равна :

      

2. Гипотенуза прямоугольного треугольника больше каждого из катетов:

      

3. Катет, лежащий против угла , равен половине гипотенузы.
4. Две высоты прямоугольного треугольника совпадают с его катетами.
5. Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы.
6. Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности:

      

7. Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:

      

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Признаки прямоугольного треугольника | Треугольники

Самые известные признаки прямоугольного треугольника являются обратными теоремами к двум его свойствам.

Признаки прямоугольного треугольника.

1. (Теорема, обратная теореме Пифагора)

Если квадрат стороны треугольника равен сумме квадратов двух других сторон, то этот треугольник — прямоугольный.

2. Если медиана треугольника равна половине стороны, к которой она проведена, то этот треугольник — прямоугольный.

3. Если центр описанной окружности лежит на стороне треугольника, то этот треугольник — прямоугольный.

Сторона, на которой лежит центр описанной около данного треугольника окружности, является гипотенузой.

4. Если радиус окружности, описанной около треугольника, равен половине его стороны, то этот треугольник прямоугольный.

(Если радиус равен половине стороны, то диаметр равен стороне.  Значит, угол, лежащий напротив этой стороны — прямой (как вписанный угол, опирающийся на диаметр)).

Если на основании некоторых данных о треугольнике можно сделать вывод о том, что этот треугольник — прямоугольный, то соответствующее утверждение также может быть названо признаком прямоугольного треугольника.

Пример.

Если площадь треугольника равна половине произведения двух его сторон, то этот треугольник — прямоугольный (а соответствующие стороны — его катеты).

Площадь треугольника можно найти по формуле

   

где a — стороны треугольника, h — высота, проведённая к стороне a. Если

   

то

   

то есть сторона b является высотой, проведённой к стороне a, а значит, стороны a и b перпендикулярны. Следовательно, такой треугольник — прямоугольный.