Исследовательская работа по математике «Числа Фибоначчи»

Введение

Леонардо Пизанский — первый крупный математик средневековой Европы. Наиболее известен под прозвищем Фибоначчи. Отец Фибоначчи по торговым делам часто бывал в Алжире, и Леонардо изучал там математику у арабских учителей. Позже посетил Египет, Сирию, Византию, Сицилию. Леонардо изучал труды математиков стран ислама, по арабским переводам он ознакомился также с достижениями античных и индийских математиков. На основе усвоенных им знаний Фибоначчи написал ряд математических трактатов, представляющих собой выдающееся явление средневековой западноевропейской науки.

Значительную часть усвоенных им знаний он изложил в своей выдающейся «Книге абака» (Liber abaci, 1202 год). Эта книга содержит почти все арифметические и алгебраические сведения того времени, изложенные с исключительной полнотой и глубиной. Первые пять глав книги посвящены арифметике целых чисел на основе десятичной нумерации. В VI и VII главе Леонардо излагает действия над обыкновенными дробями. В VIII-X главах изложены приёмы решения задач коммерческой арифметики, основанные на пропорциях. В XI главе рассмотрены задачи на смешение. В XII главе приводятся задачи на суммирование рядов — арифметической и геометрической прогрессий, ряда квадратов и, впервые в истории математики, возвратного ряда, приводящего к последовательности так называемых чисел Фибоначчи. В XIII главе излагается правило двух ложных положений и ряд других задач, приводимых к линейным уравнениям. В XIV главе Леонардо на числовых примерах разъясняет способы приближённого извлечения квадратного и кубического корней. Наконец, в XV главе собран ряд задач на применение теоремы Пифагора и большое число примеров на квадратные уравнения. Леонардо впервые в Европе использовал отрицательные числа, которые рассматривал как долг.[1]

«Книга абака» резко возвышается над европейской арифметико-алгебраической литературой XII-XIV вв. разнообразием и силой методов, богатством задач, доказательностью изложения. Последующие математики широко черпали из неё как задачи, так и приёмы их решения. По первой книге многие поколения европейских математиков изучали индийскую позиционную систему счисления.

Другая книга Фибоначчи, «Практика геометрии» (Practica geometriae, 1220 год), содержит разнообразные теоремы, относящиеся к измерительным методам. Наряду с классическими результатами Фибоначчи приводит свои собственные — например, первое доказательство того, что три медианы треугольника пересекаются в одной точке (Архимеду этот факт был известен, но если его доказательство и существовало, до нас оно не дошло).

В честь учёного назван числовой ряд, в котором каждое последующее число равно сумме двух предыдущих. Эта числовая последовательность носит название чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368,.. 75025,.. 3478759200, 5628750625,.. 260993908980000,.. 422297015649625,.. 19581068021641812000,..

При этом отношение соседних чисел стремится к золотому сечению:

233 / 144 = 1,618

377 / 233 = 1,618

610 / 377 = 1,618

Учёные, анализируя дальнейшее применение этого числового ряда к природным феноменам и процессам, обнаружили, что эти числа содержатся буквально во всех объектах живой природы, в растениях, в животных и в человеке.

Актуальность выбранной темы заключается в том, что за многовековую историю познания чисел Фибоначчи и их различные инварианты отражаются во всех творениях мироздания, все они продуманы и подчинены единым законам природы и имеют большой практический и теоретический интерес во многих науках.

Целью данной работы является исследование закономерностей числового ряда Фибоначчи.

Задачи исследования:

1. Изучить ряды Фибоначчи;

2. Рассмотреть примеры золотого сечения;

3. Ознакомиться с историей России с помощью ряда Фибоначчи.

Новизна исследования — открытие чисел Фибоначчи в окружающей нас действительности.

Практическая значимость — использование приобретенных знаний и навыков исследовательской работы при изучении других школьных предметов.

Методы исследования:

1. Теоретический (логическая ступень познания).

2. Эмпирический (наблюдение, эксперимент, измерение).

1.Исследование чисел Фибоначчи

1.1 Ряд Фибоначчи и золотое сечение

Ряд Фибоначчи – это не только математическая загадка, мы встречаемся с ним каждый день в повседневной жизни.

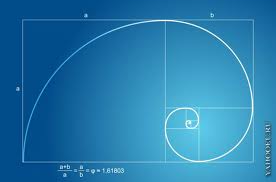
Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей, или, другими словами, меньший отрезок так относится к большему, как больший ко всему (рис. 1).

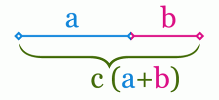
Рис 1. – Соотношение сторон золотого прямоугольника.

Прямоугольник с именно таким отношением сторон стали называть золотым прямоугольником. Его длинные стороны соотносятся с короткими сторонами в соотношении 1,618. [9]

Золотой прямоугольник обладает многими необычными свойствами. Отрезав от золотого прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника, мы снова получим золотой прямоугольник меньших размеров (рис.2).

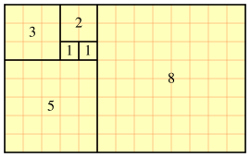
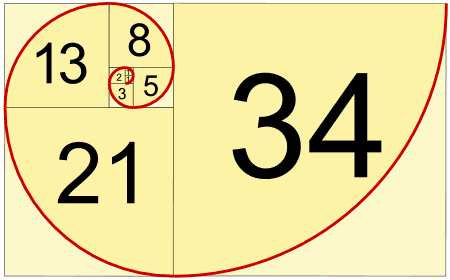
Рис 2. – Золотой прямоугольник.

Этот процесс можно продолжать до бесконечности. Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие золотые прямоугольники. Причем располагаться они будут по логарифмической спирали, имеющей важное значение в математических моделях природных объектов.

Раковина в форме спирали — форма раковины заинтересовала Архимеда, и он выяснил, что увеличение длины завитков раковины – это постоянная величина и равна она 1,618.

Семена в подсолнухе, в шишке располагаются так же в виде спирали. Корзинка подсолнуха имеет число семян = 1000, φ = 137°30’28

На рисунке 3 мы видим, как скачкообразно происходит изменение направления и числа дуг, отвечающих смежным числам Фибоначчи (34, 21), (55, 34), (89, 55).

Рис.3 – Строение семени подсолнечника.

Малейшее отклонение угла φ от значения 137°30’28 приводит к радикальной смене упаковки семян. В этой упаковки семечки находятся не в одинаковом положении относительно своих соседей, т.е. одни семечки имеют большее «жизненное пространство», другие меньшее. Три упаковки семян при трех различных углах φ. Две крайние упаковки не выгодны для выживания семян.[10]

Зато в природе можно найти две равномерных упаковки, показанные на следующем рисунке, которые реализуются при углах 99,5° и 77,9°. Они отвечают рядам Фибоначчи, соответственно, 1, 3, 4, 7, … и 1, 4, 5, 9, 14, … и записываются цепными дробями вида 1 / (3 + φ) и 1 / (4 + φ).[3]

Так как две последние фрактальные упаковки семян встречается реже, то первая упаковка для угла φ является, видимо, оптимальной с точки зрения выживания. Сосновые шишки имеют около 100 чешуек (зерен), которые распределены по 8 «правым» ветвям и 13 «левым». Причем каждая чешуйка, имея четыре стороны, соседствует с четырьмя другими чешуйками. У ананаса имеется не две, а три спиральных дуги с числами Фибоначчи 5, 8 и 13, так что каждая его гексагональная чешуйка соседствует уже с шестью другими чешуйками. Упаковка семян в ананасе и шишке равномерно плотная. Эта оптимальная конфигурация обеспечивается свойствами чисел Фибоначчи. Для ананаса этот факт очевиден: ему нужно, чтобы выполнялось условие 13 = 8 + 5, если вместо 8 рядов будет 9, то возникнет противоречие.

Пауки плетут свою сеть и стадо, на которое нападает хищник, тоже разбегаются по спирали.

Интересно, что спиралью закручивается ураган, облака циклона (рис.4) и это хорошо видно из космоса:

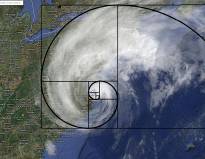
Рис. 4 – Вид урагана с космоса.

Рост растений тоже происходит в соответствии с числовым рядом Фибоначчи – от ствола отходит ветка, на которой появляется лист, затем происходит длинный выброс и снова появляется листок, но он уже короче предыдущего. Затем опять выброс, но и он короче предыдущего. В этой картине, первый выброс равен 100%, второй 62%, а третий 38%(уровни Фибоначчи, используемые в торговле) и т.д. С длиной лепестков все выглядит точно так же.

Ящерица – если поделить ящерицу на хвост и тело, то соотношение их будет 0,62 к 0,38.

Как видно, числовой ряд Фибоначчи широко представлен в нашей жизни: в строении живых существ, сооружений, с его помощью даже описывается устройство Галактик. Все это свидетельствует об универсальности математической загадки числового ряда Фибоначчи. Из Энциклопедии чудес, загадок и тайн.

Многие пытались разгадать секреты пирамиды в Гизе. В отличие от других египетских пирамид это не гробница, а скорее неразрешимая головоломка из числовых комбинаций. Замечательные изобретательность, мастерство, время и труд архитекторов пирамиды, использованные ими при возведении вечного символа, указывают на чрезвычайную важность послания, которое они хотели передать будущим поколениям. Их эпоха была дописьменной, доиероглифической и символы были единственным средством записи открытий.[2]

Ключ к геометро-математическому секрету пирамиды в Гизе, так долго бывшему для человечества загадкой, в действительности был передан Геродоту храмовыми жрецами, сообщившими ему, что пирамида построена так, чтобы площадь каждой из ее граней была равна квадрату ее высоты.

Площадь треугольника

356 x 440 / 2 = 78320

Площадь квадрата

280 x 280 = 78400

Длина грани пирамиды в Гизе равна 783.3 фута (238.7 м), высота пирамиды — 484.4 фута (147.6 м). Длина грани, деленная на высоту, приводит к соотношению Ф=1.618. Высота 484.4 фута соответствует 5813 дюймам (5-8-13) — это числа из последовательности Фибоначчи.

Эти интересные наблюдения подсказывают, что конструкция пирамиды основана на пропорции Ф=1,618. Современные ученые склоняются к интерпретации, что древние египтяне построили ее с единственной целью — передать знания, которые они хотели сохранить для грядущих поколений.

Интенсивные исследования пирамиды в Гизе показали, сколь обширными были в те времена познания в математике и астрологии. Во всех внутренних и внешних пропорциях пирамиды число 1.618 играет центральную роль.

Из истории астрономии известно, что И. Тициус, немецкий астроном XVIII в., с помощью этого ряда нашел закономерность и порядок в расстояниях между планетами солнечной системы.

Однако один случай, который, казалось бы, противоречил закону: между Марсом и Юпитером не было планеты. Сосредоточенное наблюдение за этим участком неба привело к открытию пояса астероидов. Произошло это после смерти Тициуса в начале XIX в. Ряд Фибоначчи используют широко: с его помощью представляют архитектонику и живых существ, и рукотворных сооружений, и строение Галактик. Эти факты — свидетельства независимости числового ряда от условий его проявления, что является одним из признаков его универсальности.

Другой примечательный пример (рис.5) — тело человека. В теле человека отношение длины предплечья к длине руки равно 1.618, т.е. «Золотому сечению».

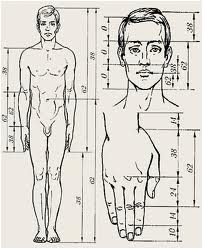
Рис. 5 – Соотношение тела человека.

Другими широко известными примерами в теле человека являются:

1. Отношение между длиной и шириной лица;

2. Отношение расстояния между губами и местом где сходятся брови к длине носа;

3. Отношение размера рта к ширине носа;

4. Отношение расстояния между линией плеч и верхом головы к длине головы;

5. Отношение расстояния между пупком и коленями к расстоянию между коленями и ступням;

6. Отношение расстояния между кончиками пальцев и локтем к расстоянию между запястьем и локтем;

Та же последовательность существует у листьев тополя, вишни, яблони, сливы, дуба и липы. Молекула ДНК закручена двойной спиралью. Гете называл спираль «кривой жизни».

Недавними исследованиями ученых было показано, что волновая структура ДНК в аспектах как свето-цветовых, так и звуко-музыкальных характеристик также базируется на «золотых» закономерностях. Последние характеризуют и процессы белкового синтеза, и цветовую структуру аминокислот. Движение по спирали лежит в основе волновой структуры ДНК и соответствует известной модели ее вещественной структуры (двойная спираль Уотсона-Крика), а при построении спирали учитываются закономерности ряда Фибоначчи.[4]

Наблюдая за ростом и развитием стеблей и цветов, каждая его новая ветвь, прорастая, дает начало другим ветвям. Рассматривая старые и новые ветви совместно, мы обнаружим число Фибоначчи в каждой из горизонтальных плоскостей.

В строении соцветий сложноцветных растений вновь проявляется закономерность Золотого сечения:

Ирис имеет 3 лепестка;

Примула имеет 5 лепестков;

Амброзия полыннолистная имеет 13 лепестков;

Нивяник обыкновенный имеет 34 лепестка;

Астра имеет 55 и 89 лепестков.

Таким образом, суммарной последовательностью Фибоначчи легко можно трактовать закономерность проявлений Золотых чисел, встречаемых в природе. Эти законы действуют в независимости от нашего знания, от чьего-то желания принимать или не принимать их.

В качестве примера (рис. 6) рассмотрим раковину наутилуса. Можно увидеть совершенство рукавов спирали, но если посмотреть на начало, то он не выглядит таким совершенным. Два самых внутренних ее изгиба фактически равны. Второй и третий изгибы чуть ближе приближаются к фи. Потом, наконец, получается эта изящная плавная спираль. Вспомните отношения второго члена к первому, третьего ко второму, четвертого к третьему, и так далее. Будет понятно, что моллюск аккурат следует математике ряда Фибоначчи.

Рис. 6 – Раковина наутилуса.

А теперь рассмотрим свойства цветов радуги.

В данной матрице каждая последующая строка получена из предыдущей с помощью циклического сдвига влево, с перестановкой последнего символа радуги на место первого («И последний становится первым»!)

В этой матрице размерностью 9 х 9 на главной диагонали стоит Великий предел Радуги («Тьма», как единство Белого и фиолетового цветов радуги).

А теперь посмотрим на соотношение одноименных цветов, разделенных в матрице ее главной диагональю, и сравните с данными, приведенными выше

1. Белый цвет: 1+8=9

2. Красный цвет: 2+7=9

3. Оранжевый цвет: 3+6=9

4. Желтый цвет: 4+5=9

4. Зеленый цвет:5+4=9

6. Голубой цвет:6+3=9

7.Синий цвет:7+2=9

8. Фиолетовый цвет:8+1=9

9. Черный цвет: 0+9=9

Данная информация свидетельствует о том, что все «дороги ведут в Рим», т.е. множество периодически повторяющихся случайностей, совпадений, мистификаций и т.д., сливаясь в единый поток, с неизбежностью приводят к выводу о существовании периодической закономерности, отражаемой в ряде Фибоначчи и носящей фундаментальный характер. [5]

Все окружающие нас предметы мы различаем, в том числе и по форме. Какие-то нам нравятся больше, какие-то меньше, некоторые вовсе отталкивают взгляд. Иногда интерес может быть продиктован жизненной ситуацией, а порой красотой наблюдаемого объекта. Симметричная и пропорциональная форма, способствует наилучшему зрительному восприятию и вызывает ощущение красоты и гармонии. Целостный образ всегда состоит из частей разного размера, находящихся в определённом соотношении друг с другом и целым. Золотое сечение — высшее проявление совершенства целого и его частей в науке, искусстве и природе.

Есть предположение, что последовательность Фибоначчи — это попытка природы адаптироваться к более фундаментальной и совершенной золотосечённой логарифмической последовательности, которая практически такая же, только начинается из ниоткуда и уходит в никуда. Природе же обязательно нужно какое-то целое начало, от которого можно оттолкнуться, она не может создать что-то из ничего. Отношения первых членов последовательности Фибоначчи далеки от Золотого Сечения. Но чем дальше мы продвигаемся по ней, тем больше эти отклонения сглаживаются. Для определения любой последовательности достаточно знать три её члена, идущие друг за другом. Но только не для золотой последовательности, ей достаточно двух, она является геометрической и арифметической прогрессией одновременно. Можно подумать, будто она основа для всех остальных последовательностей.

В 1993 году Роберт Фишер издал в «Уайли энд Санз» книгу под рабочим названием «Приложения и стратегии Фибоначчи для биржевых спекулянтов», в которой описывались базовые открытия и изобретения Фибоначчи в приложении к сложным стратегиям успешной коммерции. Книга приобрела и до сих пор сохраняет всеобщий успех. Прошло почти восемь лет. Чем популярнее становилась книга, тем очевиднее становилось, что в первом варианте отсутствует важная составная часть, необходимая, чтобы сделать по-настоящему результативными замечательные принципы Фибоначчи. За прошедшую половину десятилетия, возросшие вычислительные, графические и чертежные возможности современных компьютерных технологий открыли новые неисследованные горизонты. Этот потенциал не должен быть упущен. Заметно прогрессировали компьютерные технологии, а вместе с ними и возможности успешно торговать на рынках, используя инструменты Фибоначчи.

1.2 Исследование истории России с помощью ряда Фибоначчи на основе длительности эпох 

При несложных расчетах проведенных выше была выявлена связь между длительностью двух исторических периодов с 1917 г. по 1973 г. (56 лет), с 1973 г. по 2008 г. (35 года) и числами ряда Фибоначчи. Применив округление поищем и другие исторические периоды кратные числам этого ряда на более широких периодах истории и будущего:

   — в настоящем: нулевая, текущая эпоха 2006 -2027 (21 год)

   — в прошлом (по мере удаления в историю):

• минус первая (от нынешней — нулевой) эпоха 1972 г. — 2006 г. (34 года),

• минус вторая эпоха 1917 г.- 1972 г. (55 лет),

• минус третья эпоха 1828 г. — 1917 г. (89 лет),

• минус четвертая эпоха 1684 г. — 1828 г. (144 лет),

• минус пятая эпоха 1451 г. — 1684 г. (233 года),

• минус шестая эпоха 1074 г. — 1451 г. (377 лет),

• минус восьмая эпоха 464 г. — 1074 г. (610 лет),

• минус девятая эпоха 523 г. до н.э. — 464 г. (987 лет),

• минус десятая эпоха 2120 г. до н.э. — 523 г. до н.э. (1597 лет),

• минус одиннадцатая эпоха 4704 г. до н.э. — 2120 г. до н.э. (2584 лет)

• минус двенадцатая эпоха 8885 г. до н.э. — 4704 г. до н.э. (4181 год)

   — в будущем (по мере удаления в будущее):

• первая (от нынешней нулевой) эпоха 2027 г. — 2040 г. (13 лет),

• вторая эпоха 2040 г. — 2048 г. (8 лет),

• третья эпоха 2048 г. — 2053 г. (5 лет),

• четвертая эпоха 2053 г. — 2056 г. (3 года),

• пятая эпоха 2056 г. — 2058 г. (2 года),

• шестая эпоха 2058 г. — 2059 г. (1 год),

• седьмая эпоха 2059 г. — 2060 г. (1 год),

• восьмая эпоха, эпоха «Х» — 2061 год.

Чтобы убедиться в правильности и достоверности предлагаемого метода применим его на относительно коротком участке истории России, начиная с 1684 года, с минус 4 эпохи, согласно представленным выше периодам Фибоначчи, начавшейся накануне всем известных петровских реформ. Такой выбор обусловлен значимостью ролью Петра 1 для судеб России и поэтому их превосходной освещенностью всех этих и последующих событий в отечественной историографии и, как следствие, минимумом темных пятен. [6]

Итак, на рис. 7 представлена спираль Фибоначчи, показывающая последовательность всех правителей России (за исключением немногих), начиная с 1684 года и до наших дней. Согласно правилам построения спиралей Фибоначчи полученные расчетные даты являются точками перехода от одного историческому периода к другому (в дальнейшем по тексту — точки перехода). Их можно описать следующим образом:

   1684 год — начало 144 — летнего периода (до 1828 года), время предшествующее реформам Петра 1;

   1828 год — начало 89-летнего периода (до 1917 года), почти соответствует началу правления 30-летней эпохи императора Николая 1;

   1917 год — начало 55-летнего периода (до 1972 года), совпадает с февральской и октябрьского революциями и переходу к новой общественно-экономической формации общества в России;

   1972 год — начало 34-летнего периода (до 2006 года), совпадает с серединой т.н. периода брежневского застоя в советское время;

   2006 год — начало нового 21-летнего периода (до 2027 года).

Для более наглядного поиска общего в исторических эпохах удобно спираль Фибоначчи разделить на три подобных волны, гребня так, чтобы каждая из них соединяла собой 3 точки перехода. Первый гребень начинается в 1684 году, второй своей точкой перегиба проходит через 1828 год и заканчивается в 1917 году. Второй гребень аналогично соединяет подобные точки, соответственно, 1917-1972-2006 годы, а третий — 2006- 2027-2040 годы. При этом последние стоит расположить подобно, одна под другой, начиная с более длительной в одном направлении по мере приближения к текущей эпохе (рис.7).

   Таким образом, получается диаграмма, состоящая из подобных трех волн, гребней. Общая длительность волн как сумма двух полуволн составляет:

   — первая волна (сумма двух полуволн): 144+89 = 233 года,

   — вторая волна: 55+34 = 89 лет,

— третья волна: 21+13=34 года.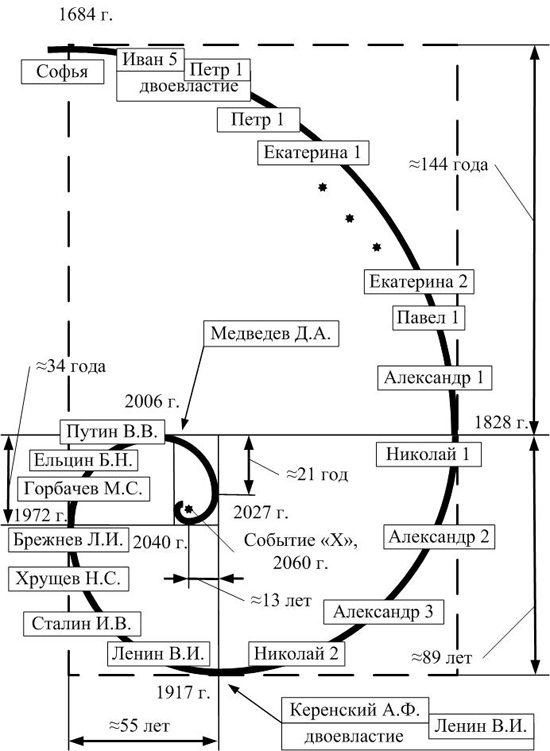

Рис.7 Периоды России согласно циклам Фибоначчи, начиная с 1684 г.

Отношение длительности первой волны ко второй равно квадрату золотой пропорции 233/89 = 1,618² = 2,618 и это означает, что те события, которые ранее развивались в течение длительного времени на следующем гребне ускоряются более чем в 2,5 раза. Ускорение же всех исторических процессов при переходе через один исторический гребень составит 233/34 = 2,618² = 6,85, т.е. почти в 7 раз.

Итак, для данного исследования важно не столько отдельно взятые исторические события, сколько выявление общей схемы, общего рисунка, т.е. повторяемость общих черт от одной эпохи к другой. Выявление этого поможет понять общие «внутренние пружины» исторических процессов в России и способствовать в постижении хотя бы общих контуров будущего. Также полезно поверить «алгеброй… историю», т.е. проверить правильность исторических трактовок «..дел давно минувших дней…».

  

Заключение

Числовой ряд Фибоначчи широко представлен в нашей жизни: в строении живых существ, сооружений, с его помощью даже описывается устройство Галактик, закономерности исторических событий. Все это свидетельствует об универсальности математической загадки числового ряда Фибоначчи.

Мы обнаружили удивительную математическую связь между числом спиралей у растений, числом веток в любой горизонтальной плоскости и числами в последовательности Фибоначчи. Мы увидели, как морфология различных организмов тоже подчиняется этому таинственному закону. Также мы увидели строгую математику в строении человека. Молекула ДНК человека, в которой зашифрована вся программа развития человеческого существа — всё подчиняется определённым числовым соотношениям.

Мы узнали, что сосновые шишки, раковины улиток, волны океана, облака циклона и галактики – все они образуют логарифмические спирали. Даже человеческий палец, который составлен из трех фаланг, находящихся по отношению друг к другу в Золотой пропорции, принимает спиральную форму, когда сжимается.

Вечность времени, и световые годы космоса разделяют сосновую шишку и спиральную галактику, но строение остаётся тем, же самым: коэффициент 1,618! Возможно, это первостепенный закон, управляющий природными явлениями.

Оказывается, закономерность явлений природы, строение и многообразие живых организмов на нашей планете, всё, что нас окружает, поражая воображение своей гармонией и упорядоченностью, законы мироздания, движение человеческой мысли и достижения науки – всё это объясняет суммационная последовательность Фибоначчи.

Наблюдая за явлениями, происходящими в природе, учёные сделали поразительные выводы о том, что вся последовательность событий, происходящих в жизни, революции, крушения, банкротства, периоды процветания, законы и волны развития на фондовом и валютных рынках, циклы семейной жизни, и так далее, организуются на временной шкале в виде циклов, волн. Эти циклы и волны тоже распределяются в соответствии с числовым рядом Фибоначчи!

Опираясь на эти знания, человек научится в будущем прогнозировать различные события и управлять ими.

Список использованных источников и литературы

1. Арутюнов П.А. Теория и применение алгоритмических измерений. Москва: Энергоатомиздат, 1990. -256 с. -6500 экз.

2. Бернулли. Цит. По: Фадеева Т.М. Золотое сечение – формула жизни? //В кн. Фадеева Т.М. Крым в сакральном пространстве. Симферополь: «Бизнес-Информ», 2003. С. 130 -134.

3. Воробьев Н.Н. Числа Фибоначчи – М., Наука, 1984.

4. Гика М. Эстетика пропорций в природе и искусстве. — М., 1936.

5. Дмитриев А. Хаос, фракталы и информация. // Наука и жизнь, № 5, 2001.

6. Львов Е.В. Циклы Фибоначчи в истории России. Материалы международной заочной научно-практической конференции «Актуальные проблемы общественных наук: социология, политология, философия и история» (16 мая 2012 г.), Новосибирск: Изд. «Сибирская ассоциация консультантов», 2012, с.99-121.

7. Кулакова М.А. Волновые принципы организации природных систем. 2008.-200 С. Монография по материалам диссертации доктора технических наук, защищенной в Международном университете фундаментального образования, Санкт-Петербург, 2007г.

8. Стахов А.П. Золотое сечение, священная геометрия и математика гармонии. Сборник «Метафизика. Век XXI». Москва: БИНОМ, 2006, с. 174-21590.

9. Стахов А.П. Под знаком «Золотого Сечения». Исповедь сына студбатовца. Винница: Изд-во «ITI», 2003. – 384 c. — ISBN 966-84320503.

10. Шевелев И.Ш., Марутаев М.А., Шмелев И.П. Золотое сечение/Три взгляда на природу гармонии.-М., 1990.

.

Числа Фибоначчи — презентация, доклад, проект

Описание слайда:

«Пиковая дама» Обратимся вновь к произведениям А.С.Пушкина. Рассмотрим композицию «Пиковой дамы». В этой повести кульминационным моментом является сцена в спальне графини, куда проник Германн в надежде узнать тайну трех карт, сцена, которая оканчивается смертью графини в повести 853 строки. Кульминационный момент повести — это смерть графини. Ему отвечает 535 -я строка. Эта строка расположена в повести почти точно в месте золотого сечения, т.к. 853:535=1,6 . Повесть «Пиковая дама» состоит из шести глав. Посмотрим, не проявляется ли в композиции глав золотая пропорция? В первой главе золотому сечению отвечает 68 строчка (всего в главе 110 строк). Но ведь это же узловая точка повествования, в ней переломный момент всей главы: откроет ли Сен — Жермен свою тайну графине! Вторая глава повести содержит 219 строк. Золотое сечение здесь приходится на 135 строку. Но ведь это кульминационный момент главы, Лиза увидела в окне стоящего на улице Германна! Отсюда начался для нее новый отсчет времени, начались события, определившие всю ее дальнейшую судьбу. А.С.Пушкин совершенно точно определил это место во второй главе: ведь 219:135 = 1,62. Третья глава повести описывает усилия Германна попасть в дом старой графини, выведать у нее тайну трех карт. Это место начинает новый отсчет времени для Германна. Эта ситуация приходится на 131 строку третьей главы, а всего в ней 212 строк. Разделив 212 на 131, мы получим точно золотую пропорцию 1,618! В четвертой главе размером 113 строк золотая пропорция приходится на 70 строку. Это также переломный, трагический момент в жизни Лизы. В пятой главе описано посещение Германна похорон графини. 46 строка пятой главы разделила повествование на две части: первая — похороны графини и вторая — сон Германна. Эта 46 строка также отвечает золотой пропорции, ведь всего в этой главе 75 строк (75:46=1,63). В последней главе повести золотая пропорция приходится на 77 строчку, которая завершает описание первого дня игры Германна в карты и первого его выигрыша. Как видим, и в композиции последней главы повести присутствует золотая пропорция. Золотая пропорция присутствует и в композиции других произведений Пушкина. В рассказе «Станционный смотритель» 377 строк. Кульминационный момент рассказа — это известие о том, что дочь смотрителя уехала с гусаром. Этот момент отражен во фразе, которая является 214 строкой. Здесь почти точное соответствие золотой пропорции. В маленьком рассказе «Гробовщик» всего 229 строк. Со 139 строки начинается описание страшного сна гробовщика. И здесь переломный момент рассказа приходится почти точно на золотую пропорцию (229:1,618=141 строка). Совпадение кульминационных моментов в произведениях А.С.Пушкина с золотой пропорцией удивительно близкое, в пределах 1-3 строк.

Числа фибоначчи | Социальная сеть работников образования

li{counter-increment:lst-ctn-kix_list_3-8}#doc7444413 .lst-kix_list_1-1>li:before{content:»\002022 «}#doc7444413 .lst-kix_list_3-2>li:before{content:»» counter(lst-ctn-kix_list_3-2,lower-roman) «. «}#doc7444413 ol.lst-kix_list_6-3.start{counter-reset:lst-ctn-kix_list_6-3 0}#doc7444413 .lst-kix_list_1-2>li:before{content:»\002022 «}#doc7444413 ol.lst-kix_list_6-2.start{counter-reset:lst-ctn-kix_list_6-2 0}#doc7444413 ol.lst-kix_list_5-8.start{counter-reset:lst-ctn-kix_list_5-8 0}#doc7444413 .lst-kix_list_1-5>li:before{content:»\002022 «}#doc7444413 ol.lst-kix_list_5-3.start{counter-reset:lst-ctn-kix_list_5-3 0}#doc7444413 .lst-kix_list_6-6>li{counter-increment:lst-ctn-kix_list_6-6}#doc7444413 .lst-kix_list_6-3>li:before{content:»» counter(lst-ctn-kix_list_6-3,decimal) «. «}#doc7444413 .lst-kix_list_5-3>li{counter-increment:lst-ctn-kix_list_5-3}#doc7444413 ol.lst-kix_list_6-0.start{counter-reset:lst-ctn-kix_list_6-0 0}#doc7444413 .lst-kix_list_6-7>li:before{content:»» counter(lst-ctn-kix_list_6-7,lower-latin) «. «}#doc7444413 .lst-kix_list_2-3>li:before{content:»\002022 «}#doc7444413 .lst-kix_list_1-4>li:before{content:»\002022 «}#doc7444413 .lst-kix_list_6-2>li:before{content:»» counter(lst-ctn-kix_list_6-2,lower-roman) «. «}#doc7444413 .lst-kix_list_5-1>li{counter-increment:lst-ctn-kix_list_5-1}#doc7444413 .lst-kix_list_3-3>li{counter-increment:lst-ctn-kix_list_3-3}#doc7444413 .lst-kix_list_6-3>li{counter-increment:lst-ctn-kix_list_6-3}#doc7444413 .lst-kix_list_5-7>li:before{content:»» counter(lst-ctn-kix_list_5-7,lower-latin) «. «}#doc7444413 ol.lst-kix_list_3-7.start{counter-reset:lst-ctn-kix_list_3-7 0}#doc7444413 ol.lst-kix_list_6-7.start{counter-reset:lst-ctn-kix_list_6-7 0}#doc7444413 ol.lst-kix_list_6-4.start{counter-reset:lst-ctn-kix_list_6-4 0}#doc7444413 .lst-kix_list_4-3>li:before{content:»\0027a2 «}#doc7444413 .lst-kix_list_2-7>li:before{content:»\002022 «}#doc7444413 .lst-kix_list_3-7>li{counter-increment:lst-ctn-kix_list_3-7}#doc7444413 .lst-kix_list_1-8>li:before{content:»\002022 «}#doc7444413 ol.lst-kix_list_3-6.start{counter-reset:lst-ctn-kix_list_3-6 0}#doc7444413 ol.lst-kix_list_3-0.start{counter-reset:lst-ctn-kix_list_3-0 0}#doc7444413 ol.lst-kix_list_5-0.start{counter-reset:lst-ctn-kix_list_5-0 0}#doc7444413 .lst-kix_list_3-3>li:before{content:»» counter(lst-ctn-kix_list_3-3,decimal) «. «}#doc7444413 .lst-kix_list_3-6>li:before{content:»» counter(lst-ctn-kix_list_3-6,decimal) «. «}#doc7444413 ol.lst-kix_list_6-1.start{counter-reset:lst-ctn-kix_list_6-1 0}#doc7444413 ol.lst-kix_list_3-2.start{counter-reset:lst-ctn-kix_list_3-2 0}#doc7444413 .lst-kix_list_5-2>li:before{content:»» counter(lst-ctn-kix_list_5-2,lower-roman) «. «}#doc7444413 .lst-kix_list_6-4>li:before{content:»» counter(lst-ctn-kix_list_6-4,lower-latin) «. «}#doc7444413 .lst-kix_list_6-1>li:before{content:»» counter(lst-ctn-kix_list_6-1,lower-latin) «. «}#doc7444413 .lst-kix_list_6-8>li:before{content:»» counter(lst-ctn-kix_list_6-8,lower-roman) «. «}#doc7444413 .lst-kix_list_3-2>li{counter-increment:lst-ctn-kix_list_3-2}#doc7444413 .lst-kix_list_6-1>li{counter-increment:lst-ctn-kix_list_6-1}#doc7444413 ol.lst-kix_list_6-8.start{counter-reset:lst-ctn-kix_list_6-8 0}#doc7444413 .lst-kix_list_6-4>li{counter-increment:lst-ctn-kix_list_6-4}#doc7444413 ol.lst-kix_list_5-7.start{counter-reset:lst-ctn-kix_list_5-7 0}#doc7444413 .lst-kix_list_4-7>li:before{content:»\0027a2 «}#doc7444413 .lst-kix_list_5-0>li{counter-increment:lst-ctn-kix_list_5-0}#doc7444413 .lst-kix_list_1-6>li:before{content:»\002022 «}#doc7444413 .lst-kix_list_5-4>li{counter-increment:lst-ctn-kix_list_5-4}#doc7444413 .lst-kix_list_2-6>li:before{content:»\002022 «}#doc7444413 .lst-kix_list_6-5>li:before{content:»» counter(lst-ctn-kix_list_6-5,lower-roman) «. «}#doc7444413 .lst-kix_list_3-6>li{counter-increment:lst-ctn-kix_list_3-6}#doc7444413 ul.lst-kix_list_1-0{list-style-type:none}#doc7444413 ul.lst-kix_list_1-2{list-style-type:none}#doc7444413 ul.lst-kix_list_1-1{list-style-type:none}#doc7444413 .lst-kix_list_2-2>li:before{content:»\002022 «}#doc7444413 ol.lst-kix_list_3-3.start{counter-reset:lst-ctn-kix_list_3-3 0}#doc7444413 ul.lst-kix_list_1-4{list-style-type:none}#doc7444413 .lst-kix_list_6-8>li{counter-increment:lst-ctn-kix_list_6-8}#doc7444413 ul.lst-kix_list_1-3{list-style-type:none}#doc7444413 ul.lst-kix_list_1-6{list-style-type:none}#doc7444413 ul.lst-kix_list_1-5{list-style-type:none}#doc7444413 ul.lst-kix_list_1-8{list-style-type:none}#doc7444413 ul.lst-kix_list_1-7{list-style-type:none}#doc7444413 .lst-kix_list_2-1>li:before{content:»\002022 «}#doc7444413 .lst-kix_list_4-8>li:before{content:»\0027a2 «}#doc7444413 .lst-kix_list_5-5>li:before{content:»» counter(lst-ctn-kix_list_5-5,lower-roman) «. «}#doc7444413 .lst-kix_list_3-0>li{counter-increment:lst-ctn-kix_list_3-0}#doc7444413 .lst-kix_list_2-8>li:before{content:»\002022 «}#doc7444413 .lst-kix_list_6-0>li{counter-increment:lst-ctn-kix_list_6-0}#doc7444413 .lst-kix_list_3-7>li:before{content:»» counter(lst-ctn-kix_list_3-7,lower-latin) «. «}#doc7444413 .lst-kix_list_3-4>li{counter-increment:lst-ctn-kix_list_3-4}#doc7444413 .lst-kix_list_2-0>li:before{content:»\002022 «}#doc7444413 ol.lst-kix_list_3-1{list-style-type:none}#doc7444413 ol.lst-kix_list_3-2{list-style-type:none}#doc7444413 .lst-kix_list_6-6>li:before{content:»» counter(lst-ctn-kix_list_6-6,decimal) «. «}#doc7444413 ol.lst-kix_list_3-3{list-style-type:none}#doc7444413 ol.lst-kix_list_3-4{list-style-type:none}#doc7444413 ol.lst-kix_list_3-0{list-style-type:none}#doc7444413 ol.lst-kix_list_3-6{list-style-type:none}#doc7444413 ol.lst-kix_list_3-5{list-style-type:none}#doc7444413 ol.lst-kix_list_3-8{list-style-type:none}#doc7444413 ol.lst-kix_list_3-7{list-style-type:none}#doc7444413 .lst-kix_list_5-7>li{counter-increment:lst-ctn-kix_list_5-7}#doc7444413 .lst-kix_list_2-4>li:before{content:»\002022 «}#doc7444413 .lst-kix_list_3-5>li:before{content:»» counter(lst-ctn-kix_list_3-5,lower-roman) «. «}#doc7444413 .lst-kix_list_3-5>li{counter-increment:lst-ctn-kix_list_3-5}#doc7444413 ol.lst-kix_list_5-5.start{counter-reset:lst-ctn-kix_list_5-5 0}#doc7444413 .lst-kix_list_4-2>li:before{content:»\0027a2 «}#doc7444413 .lst-kix_list_4-6>li:before{content:»\0027a2 «}#doc7444413 ol.lst-kix_list_6-4{list-style-type:none}#doc7444413 ol.lst-kix_list_5-8{list-style-type:none}#doc7444413 ol.lst-kix_list_6-5{list-style-type:none}#doc7444413 ol.lst-kix_list_5-7{list-style-type:none}#doc7444413 ol.lst-kix_list_6-2{list-style-type:none}#doc7444413 .lst-kix_list_5-3>li:before{content:»» counter(lst-ctn-kix_list_5-3,decimal) «. «}#doc7444413 ol.lst-kix_list_6-3{list-style-type:none}#doc7444413 .lst-kix_list_4-1>li:before{content:»\0027a2 «}#doc7444413 .lst-kix_list_4-5>li:before{content:»\0027a2 «}#doc7444413 ol.lst-kix_list_6-8{list-style-type:none}#doc7444413 ol.lst-kix_list_5-4{list-style-type:none}#doc7444413 ol.lst-kix_list_5-3{list-style-type:none}#doc7444413 ol.lst-kix_list_6-6{list-style-type:none}#doc7444413 ol.lst-kix_list_5-6{list-style-type:none}#doc7444413 .lst-kix_list_5-2>li{counter-increment:lst-ctn-kix_list_5-2}#doc7444413 ol.lst-kix_list_6-7{list-style-type:none}#doc7444413 ol.lst-kix_list_5-5{list-style-type:none}#doc7444413 ol.lst-kix_list_5-0{list-style-type:none}#doc7444413 .lst-kix_list_3-0>li:before{content:»» counter(lst-ctn-kix_list_3-0,decimal) «. «}#doc7444413 ol.lst-kix_list_5-1{list-style-type:none}#doc7444413 .lst-kix_list_1-0>li:before{content:»\002022 «}#doc7444413 .lst-kix_list_2-5>li:before{content:»\002022 «}#doc7444413 ol.lst-kix_list_5-2{list-style-type:none}#doc7444413 ol.lst-kix_list_6-1{list-style-type:none}#doc7444413 .lst-kix_list_5-8>li:before{content:»» counter(lst-ctn-kix_list_5-8,lower-roman) «. «}#doc7444413 ol.lst-kix_list_6-0{list-style-type:none}#doc7444413 .lst-kix_list_5-4>li:before{content:»» counter(lst-ctn-kix_list_5-4,lower-latin) «. «}#doc7444413 .lst-kix_list_4-4>li:before{content:»\0027a2 «}#doc7444413 .lst-kix_list_3-4>li:before{content:»» counter(lst-ctn-kix_list_3-4,lower-latin) «. «}#doc7444413 .lst-kix_list_1-3>li:before{content:»\002022 «}#doc7444413 ol.lst-kix_list_6-6.start{counter-reset:lst-ctn-kix_list_6-6 0}#doc7444413 .lst-kix_list_5-8>li{counter-increment:lst-ctn-kix_list_5-8}#doc7444413 ol.lst-kix_list_6-5.start{counter-reset:lst-ctn-kix_list_6-5 0}#doc7444413 .lst-kix_list_5-0>li:before{content:»» counter(lst-ctn-kix_list_5-0,decimal) «. «}#doc7444413 ul.lst-kix_list_4-8{list-style-type:none}#doc7444413 ul.lst-kix_list_4-7{list-style-type:none}#doc7444413 .lst-kix_list_6-0>li:before{content:»» counter(lst-ctn-kix_list_6-0,decimal) «. «}#doc7444413 .lst-kix_list_6-5>li{counter-increment:lst-ctn-kix_list_6-5}#doc7444413 ul.lst-kix_list_4-6{list-style-type:none}#doc7444413 ul.lst-kix_list_4-1{list-style-type:none}#doc7444413 ul.lst-kix_list_4-0{list-style-type:none}#doc7444413 ol.lst-kix_list_3-5.start{counter-reset:lst-ctn-kix_list_3-5 0}#doc7444413 ol.lst-kix_list_5-6.start{counter-reset:lst-ctn-kix_list_5-6 0}#doc7444413 ul.lst-kix_list_4-5{list-style-type:none}#doc7444413 ul.lst-kix_list_4-4{list-style-type:none}#doc7444413 .lst-kix_list_3-8>li:before{content:»» counter(lst-ctn-kix_list_3-8,lower-roman) «. «}#doc7444413 .lst-kix_list_4-0>li:before{content:»\0027a2 «}#doc7444413 ul.lst-kix_list_4-3{list-style-type:none}#doc7444413 ul.lst-kix_list_4-2{list-style-type:none}#doc7444413 ol.lst-kix_list_3-4.start{counter-reset:lst-ctn-kix_list_3-4 0}#doc7444413 .lst-kix_list_6-2>li{counter-increment:lst-ctn-kix_list_6-2}#doc7444413 ol.lst-kix_list_5-4.start{counter-reset:lst-ctn-kix_list_5-4 0}#doc7444413 .lst-kix_list_5-6>li{counter-increment:lst-ctn-kix_list_5-6}#doc7444413 .lst-kix_list_5-6>li:before{content:»» counter(lst-ctn-kix_list_5-6,decimal) «. «}#doc7444413 .lst-kix_list_3-1>li:before{content:»» counter(lst-ctn-kix_list_3-1,lower-latin) «. «}#doc7444413 ul.lst-kix_list_2-4{list-style-type:none}#doc7444413 ol.lst-kix_list_3-8.start{counter-reset:lst-ctn-kix_list_3-8 0}#doc7444413 ol.lst-kix_list_5-1.start{counter-reset:lst-ctn-kix_list_5-1 0}#doc7444413 ul.lst-kix_list_2-5{list-style-type:none}#doc7444413 ul.lst-kix_list_2-6{list-style-type:none}#doc7444413 .lst-kix_list_1-7>li:before{content:»\002022 «}#doc7444413 ul.lst-kix_list_2-7{list-style-type:none}#doc7444413 .lst-kix_list_5-5>li{counter-increment:lst-ctn-kix_list_5-5}#doc7444413 ul.lst-kix_list_2-0{list-style-type:none}#doc7444413 ul.lst-kix_list_2-1{list-style-type:none}#doc7444413 ol.lst-kix_list_3-1.start{counter-reset:lst-ctn-kix_list_3-1 0}#doc7444413 ol.lst-kix_list_5-2.start{counter-reset:lst-ctn-kix_list_5-2 0}#doc7444413 ul.lst-kix_list_2-2{list-style-type:none}#doc7444413 .lst-kix_list_3-1>li{counter-increment:lst-ctn-kix_list_3-1}#doc7444413 ul.lst-kix_list_2-3{list-style-type:none}#doc7444413 .lst-kix_list_6-7>li{counter-increment:lst-ctn-kix_list_6-7}#doc7444413 .lst-kix_list_5-1>li:before{content:»» counter(lst-ctn-kix_list_5-1,lower-latin) «. «}#doc7444413 ul.lst-kix_list_2-8{list-style-type:none}#doc7444413 ol{margin:0;padding:0}#doc7444413 .c9{line-height:1.1500000000000001;padding-top:0pt;height:11pt;margin-left:36pt;padding-bottom:0pt}#doc7444413 .c1{padding-left:0pt;line-height:1.1500000000000001;padding-top:0pt;margin-left:36pt;padding-bottom:0pt}#doc7444413 .c21{max-width:467.7pt;background-color:#ffffff;padding:35.4pt 42.5pt 42.6pt 85pt}#doc7444413 .c4{color:#7030a0;font-size:12pt;font-family:»Times New Roman»}#doc7444413 .c3{font-size:12pt;font-family:»Times New Roman»;font-weight:normal}#doc7444413 .c18{line-height:1.1500000000000001;padding-top:0pt;padding-bottom:10pt}#doc7444413 .c19{line-height:1.1500000000000001;padding-top:0pt;padding-bottom:0pt}#doc7444413 .c2{color:#7030a0;font-family:»Times New Roman»;font-weight:bold}#doc7444413 .c0{widows:2;orphans:2;direction:ltr}#doc7444413 .c8{font-size:12pt;font-family:»Times New Roman»}#doc7444413 .c11{font-size:14pt;font-family:»Times New Roman»}#doc7444413 .c5{padding-left:0pt;margin-left:36pt}#doc7444413 .c10{margin:0;padding:0}#doc7444413 .c15{color:#000000}#doc7444413 .c20{font-size:11pt}#doc7444413 .c13{height:11pt}#doc7444413 .c6{font-weight:bold}#doc7444413 .c17{font-style:italic}#doc7444413 .c14{font-family:»Times New Roman»}#doc7444413 .c7{font-size:20pt}#doc7444413 .c12{font-weight:normal}#doc7444413 .c16{margin-left:36pt}#doc7444413 .title{widows:2;padding-top:0pt;line-height:1.0;orphans:2;text-align:left;color:#000000;font-size:26pt;font-family:»Brush Script MT»;padding-bottom:15pt;page-break-after:avoid}#doc7444413 .subtitle{widows:2;padding-top:0pt;line-height:1.1500000000000001;orphans:2;text-align:left;color:#4f81bd;font-style:italic;font-size:12pt;font-family:»Brush Script MT»;padding-bottom:10pt;page-break-after:avoid}#doc7444413 li{color:#000000;font-size:11pt;font-family:»Brush Script MT»}#doc7444413 p{color:#000000;font-size:11pt;margin:0;font-family:»Brush Script MT»}#doc7444413 h2{widows:2;padding-top:24pt;line-height:1.1500000000000001;orphans:2;text-align:left;color:#000000;font-size:24pt;font-family:»Brush Script MT»;font-weight:bold;padding-bottom:6pt;page-break-after:avoid}#doc7444413 h3{widows:2;padding-top:10pt;line-height:1.1500000000000001;orphans:2;text-align:left;color:#4f81bd;font-size:13pt;font-family:»Brush Script MT»;font-weight:bold;padding-bottom:0pt;page-break-after:avoid}#doc7444413 h4{widows:2;padding-top:14pt;line-height:1.1500000000000001;orphans:2;text-align:left;color:#000000;font-size:14pt;font-family:»Brush Script MT»;font-weight:bold;padding-bottom:4pt;page-break-after:avoid}#doc7444413 h5{widows:2;padding-top:12pt;line-height:1.1500000000000001;orphans:2;text-align:left;color:#000000;font-size:12pt;font-family:»Brush Script MT»;font-weight:bold;padding-bottom:2pt;page-break-after:avoid}#doc7444413 h5{widows:2;padding-top:11pt;line-height:1.1500000000000001;orphans:2;text-align:left;color:#000000;font-size:11pt;font-family:»Brush Script MT»;font-weight:bold;padding-bottom:2pt;page-break-after:avoid}#doc7444413 h6{widows:2;padding-top:10pt;line-height:1.1500000000000001;orphans:2;text-align:left;color:#000000;font-size:10pt;font-family:»Brush Script MT»;font-weight:bold;padding-bottom:2pt;page-break-after:avoid}#doc7444413 ]]>

Слайд 1.

Тема нашего проекта – «Числа Фибоначчи».

Что привело нас к этой теме?

Еще в 5 классе мы знали только натуральные и дробные числа. В 6 классе наши знания о числах стали шире – мы познакомились с отрицательными числами. И у нас возник вопрос какие еще числа бывают? Изучая литературу по этому вопросу, нас заинтересовали числа Фибоначчи, и мы решили представить вам проект на эту тему.

И наметили план работы над проектом:

Слайд 2.

• Выяснить, какие числа изучают в школе;
• Дать определение чисел Фибоначчи;
• Место чисел Фибоначчи среди других чисел;
• Выяснить, какими свойствами обладают числа Фибоначчи

Слайд 3.

Цели проекта:

• Изучить историю возникновения чисел Фибоначчи;
• Исследовать свойства чисел Фибоначчи.

Слайд 4.

В школе мы познакомились с рациональными числами – к рациональным числам относятся натуральные числа, нуль, числа, противоположные натуральным, дробные (как положительные, так и отрицательные). Так же мы выяснили, что еще бывают иррациональные числа. Но это далеко не все виды чисел. В древности было открыто множество других. Один из древних видов чисел – это числа Фибоначчи.

Слайд 5.

Числа Фибоначчи – это последовательность чисел, в которой каждое число является суммой двух предыдущих. Последовательность Фибоначчи начинается так:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…

Слайд 6.

Около 1170 г. родился Леонардо Пизанский. Он более известен, как сын Благонамеренного (по-итальянски figlio di Bonacci). По жизни он занимался торговлей и только там использовал математику. Во время поездки в Северную Африку он познакомился с работами мусульманских учёных, а именно с индо-арабской системой исчисления. Фибоначчи стал её сторонником и начал распространять её по всей Европе.

Слайд 7.

В 1202 г. Фибоначчи написал книгу, посвящённую вычислениям «Книгу абака» (абак – древний прибор для вычислений). Она продемонстрировала преимущества арабских чисел для вычислений, которые доминировали в то время в Италии. Книга положила конец использованию римских чисел в практике, но это произошло не сразу. В конце концов сторонники арабских цифр, победили.

Слайд 8.

Конечно, она содержала главы о ведении счетов, о распределении прибыли и убытков, а так же об обмене денег.

Но самым известным разделом книги является задача о размножении кроликов, решение которой известно сейчас как последовательность Фибоначчи.

Слайд 9.

«Сколько пар кроликов будет у нас через год, если в январе у нас была одна пара, которая каждый месяц производит на свет другую пару. Начиная с марта новая пара, в свою очередь, производит собственное потомство каждый месяц, начиная со второго месяца».

 Слайд 10.

1. Пусть имеется одна пара кроликов, по условию задачи у нее появляется потомство только со второго месяца.
2. Поэтому в следующем месяце у нас все еще одна пара кроликов.
3. В третьем месяце
4.  у первой пары появляется потомство.
5. Так как в задаче сказано, что потомство у кроликов появляется каждый месяц
6. В четвертом месяце первая пара опять дает потомство
7. Итого у нас уже три пары кроликов
8. В пятом месяце у первой пары
9. появляется потомство
10. И вторая пара тоже радует нас
11. новой парой кроликов
12. Итого в пятом месяце у нас уже пять пар кроликов
13. В шестом месяце снова первая пара
14. дает потомство
15. и вторая пара снова
16. дает потомство
17. третья пара
18. дает потомство
19. Итого в шестом месяце
20. У нас 8 пар кроликов

Слайд 11

Переходим к свойствам чисел Фибоначчи

Слайд 12.

Первое свойство

Если выбрать 10 соседних чисел из последовательности Фибоначчи и сложить их, всегда получится число, кратное 11.

Например,   Примеры зачитать

Слайд 13

Второе свойство

Каждая сумма любых десяти соседних чисел последовательности равна числу 11, умноженному на 7-ое число.

Например,

Сумма десяти последовательных чисел равна 605

В свою очередь, 605 это произведение 11 и седьмого числа из последовательности, а это число 55

Слайд 14

Третье свойство

1. Если пронумеровать все числа последовательности Фибоначчи, то легко заметить, что:

Сумма десяти первых чисел равна разности двенадцатого числа и первого

2. Первое число равно 1, двенадцатое – 144
3. Разность двенадцатого и первого чисел равна 143
4. Сумма первых десяти чисел так же равна 143
5. Это свойство можно использовать для нахождения суммы любого количества последовательных чисел
6. Например: сумма тридцати первых чисел равна тридцать второе число минус первое число

Слайд 15.

Четвертое свойство

Если выбрать три последовательных числа, то произведение крайних чисел будет на единицу больше или меньше, чем квадрат среднего числа.

 Например,    

Рассмотрим три числа – 3, 5, 8

Произведение 3 и 8 равно 24, а пять в квадрате – двадцать пять, а это на 1 больше, чем 24

Рассмотрим три других последовательных числа 5, 8, 13

Найдем произведение 5 и 13 – 65, а это на 1 больше, чем 8 в квадрате.

Слайд 16.

Пятое свойство

Если число последовательности является простым, то оно может занимать место, номер которого так же является простым.

Рассмотрим несколько первых чисел последовательности Фибоначчи

Число 2 занимает третье место (2 и 3 – простые числа), число пять занимает 5 место (5 – простое число), число 13 занимает 7 место (13 и 7 простые числа), число 89 занимает 11 место (89 и 11 – простые числа), 233 занимает 13 место (233 и 13 – простые числа)

Слайд 17

Отношение каждого числа к следующему приближается к 0,618.

Примеры зачитать

Слайд 18

Вывод: при подготовке проекта нами были поставлены цели:

• Изучить историю возникновения чисел Фибоначчи;

Ряд чисел Фибоначчи появился при решении задачи о размножении кроликов.

Вторая цель

• Исследовать свойства чисел Фибоначчи.

Числа Фибоначчи исследованы и найдены несколько свойств этих чисел,

каждое свойство подкреплено примером.  

Цель проекта достигнута.

Спасибо за внимание!!!

 

Числа Фибоначчи применяются при прогнозировании цены, на товарных, фондовых и валютных биржах,     этот вопрос нами не изучался глубоко, поскольку не являлся целью проекта.

Свойства чисел мы нашли в книге, а примеры для них приводили свои

Презентация к уроку по алгебре (9, 10, 11 класс) по теме: Числа Фибоначчи

Слайд 1

Работу выполнила ученица 11 «а» класса Баграева Диана Исследовательский проект по математике на тему «Числа Фибоначчи»

Слайд 2

*Узнать понятие чисел Фибоначчи *Происхождение чисел Фибоначчи * Ч исла Фибоначчи в природе *Числа Фибоначчи в культуре * Ч исла Фибоначчи в стихах *Числа Фибоначчи в музыке *Сделать опрос окружающих, знают ли они числа Фибоначчи * Сделать выводы по исследованию данного проекта Цели исследования:

Слайд 3

Понятие чисел Фибоначчи

Слайд 4

Числа Фибоначчи – это элементы последовательности, 1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765… в которой первые два числа равны либо 1 и 1 ,либо 0 и 1 , а каждое последующее число равно сумме двух предыдущих чисел. Названы они в честь средневекового математика Леонардо Пизанского (известного как Фибоначчи).

Слайд 6

С числами Фибоначчи косвенно связана история «золотого» сечения.

Слайд 7

Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему a : b = b : c или с : b = b : а.

Слайд 8

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор , древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.

Слайд 9

Происхождение чисел Фибоначчи

Слайд 10

Страница Книги абака(лат. Liber abaci ) Фибоначчи из национальной центральной библиотеки Флоренции. В правом блоке демонстрируется последовательность Фибоначчи . Позиции от 0 до 12 обозначены темным цветом римскими цифрами, а значения – красным цветом индо-арабскими цифрами. Последовательность Фибоначчи была хорошо известна в древней Индии,где она применялась в метрических науках( просодии,другими словами-стихосложении ) намного раньше,чем стала известна в Европе.

Слайд 11

Числа Фибоначчи в природе

Слайд 12

Филлотаксис(листорасположение) у растений описывается последовательностью Фибоначчи.

Слайд 13

Семена подсолнуха, сосновые шишки, лепестки цветов, ячейки ананаса также располагаются согласно последовательности Фибоначчи.

Слайд 14

Длины фаланг пальцев человека относятся примерно как числа Фибоначчи.

Слайд 15

Использование чисел Фибоначчи в культуре

Слайд 16

В сериале «Грань» ( Fringe) доктор Уолтер Бишоп перед сном повторял числа 233, 377, 610, 987, 1597, эти числа являются частью последовательности Фибоначчи.

Слайд 17

Американский писатель-фантаст Дэн Браун в книге «Код да Винчи» описал анаграмму на основе последовательности Фибоначчи.

Слайд 18

В фильме 2009 года «Господин Никто» в реальности, где Немо не родился, адрес заброшенного дома 12358, что является частью последовательности Фибоначчи. Номер телефона 123-581-1321 . по которому он должен позвонить Анне, также близок к этой последовательности(лишняя 1 в 581).

Слайд 19

В фильме «Двадцать одно» последовательность Фибоначчи представлена в виде надписи на торте.

Слайд 20

В финале сериала « Звёздный крейсер „Галактика“ » (2004) Кара Трейс набирает числа-координаты для сверхсветового прыжка. Последовательность, что она набирает (1123, 6536, 5321), являются числами Фибоначчи, а именно: 1123 и 5321.

Слайд 21

Числа Фибоначчи в стихах

Слайд 22

0112358… В начале-пустота . Возникла единица- Пусть это буду я, А рядом станешь ты. Мы сложимся- Нас станет двое. Возникнет третий, А за ним еще, Нас станет пять, Как пальцев на руке. Сложенье двух ближайших- Принцип ряда Фибоначчи Единственный. Так продолжая ряд, Дойдем и до великих чисел, Соотношение которых- «сеченье золотое»- Принцип совершенства! Алексей Головко

Слайд 23

Числа Фибоначчи в музыке

Слайд 24

«Фибоначчи» — название песни российской рок-группы «Сплин» из альбома «Обман зрения»(2012).

Слайд 25

У электронного музыканта Брайан Уэйн Трансо (ВТ) есть композиция « Fibonacci Sequence». В тексте называются числа из начала последовательности (1, 1, 2, 3, 5, 8, 13, 21 ).

Слайд 26

Опрос учащихся: -Знаете ли вы числа Фибоначчи ? ДА-10 человек НЕТ-35 человек -Как вы думаете, имеют ли что-то общее числа Фибоначчи в культуре и математике ? ДА-7 человек НЕТ-38 человек Всего опрошено : 45 человек

Слайд 27

Мы узнали, что такое числа Фибоначчи. Как их вычислять. Где они применяются : в кинофильмах, в природе, в музыке, в стихах. Мы опросили учащихся, знакомы ли они с числами Фибоначчи, и как показал наш маленький опрос, мало кто слышал о них. Благодаря этому маленькому исследованию, я узнала много нового для себя. Мне было интересно узнать где применяются числа Фибоначчи. Одно только название вызвало у меня интерес к этой работе. Выводы: