Вариант | Условие |
1 | Докажите, что
для любых множеств A, B, C справедливо равенство: |
2 | Докажите,
что для любых множеств A, B, C справедливо равенство: |
3 | Докажите, что для любых множеств A  ,
и с помощью кругов Эйлера проиллюстрируйте
его. ,
и с помощью кругов Эйлера проиллюстрируйте
его. |
4 | Докажите,
что для любых множеств A, B, C справедливо равенство: |
5 | Докажите,
что для любых множеств A, B, C справедливо равенство: |
6 | Докажите,
что для любых множеств A, B справедливо равенство:  ,
и проиллюстрируйте его с помощью
кругов Эйлера. ,
и проиллюстрируйте его с помощью
кругов Эйлера. |
7 | Докажите,
что для любых множеств A, B справедливо равенство: |
8 | Докажите,
что для любых множеств A, B справедливо равенство: |
9 | Докажите,
что для любых множеств A, B справедливо равенство: |
10 | Докажите,
что для любых множеств A, B справедливо равенство: |
11 | Докажите,
что для любых множеств A, B, C справедливо равенство: |
12 | Докажите,
что для любых множеств A, B, C справедливо равенство: |
13 | Докажите,
что для любых множеств A, B, C справедливо равенство: |
14 | Докажите,
что для любых множеств A, B справедливо равенство: |
15 | Докажите,
что для любых множеств A, B справедливо равенство: |
16 | Докажите,
что для любых множеств A, B справедливо равенство: |
17 | Докажите,
что для любых множеств A, B справедливо равенство: |
18 | Докажите,
что для любых множеств A, B справедливо равенство: |
19 | Докажите, что
для любых множеств A, B, C справедливо равенство: |
20 | Докажите,
что для любых множеств A, B, C справедливо равенство: |
21 | Докажите,
что для любых множеств A, B, C справедливо равенство: |
22 | Докажите,
что для любых множеств A, B, C справедливо равенство: |
23 | Докажите,
что для любых множеств A, B, C справедливо равенство: |
24 | Докажите,
что для любых множеств A, B справедливо равенство: |
25 | Докажите,
что для любых множеств A, B справедливо равенство: |
26 | Докажите, что для любых множеств A 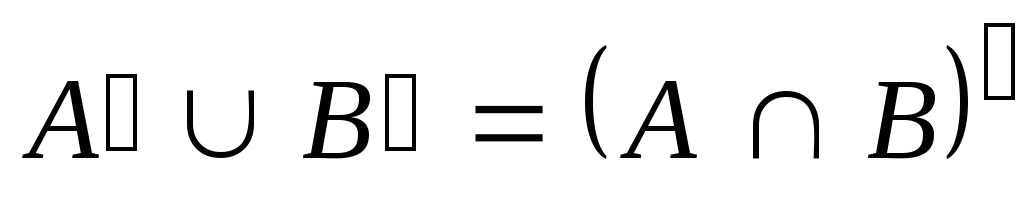 ,
и с помощью кругов Эйлера проиллюстрируйте
его. ,
и с помощью кругов Эйлера проиллюстрируйте
его. |
27 | Докажите,
что для любых множеств A, B, C справедливо равенство: |
28 | Докажите,
что для любых множеств A, B, C справедливо равенство: |
29 | Докажите,
что для любых множеств A, B, C справедливо равенство:  ,
и с помощью кругов Эйлера проиллюстрируйте
его. ,
и с помощью кругов Эйлера проиллюстрируйте
его. |
30 | Докажите,
что для любых множеств A, B справедливо равенство: |
studfile.net
Множества и операции над ними. Решение задач с помощью кругов Эйлера
Современный математический язык более краток и заменяет разговорный язык специальными буквенными и символьными выражениями. Понятия и обозначения языка теории множеств составляет фундамент современного математического языка. Всякий объект, входящий во множество, называют его
Блок 1. Множества и операции над ними.
Презентация. (Слайд 2) Вопросы к слайду 2:
- Перечислите элементы множеств:
а) арабских цифр; (0; 1; 2; 3; 4; 5; 6; 7; 8; 9)
б) натуральных чисел; (1; 2; 3; 4;…)
в) целых чисел (…-2; -1; 0; 1; 2;…). - Как называется множество цветов, стоящих в вазе? (букет).
- Перечислите элементы множества планет солнечной системы. (Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун).
- Как называется множество фруктовых деревьев и кустарников растущих у дома? (сад).
- Приведите примеры множеств, элементами которого являются геометрические фигуры.
- Какие названия применяют для обозначения множеств животных? (млекопитающие, земноводные, хладнокровные и т.п.).
- Перечислите элементы множества видов спорта (футбол, теннис, волейбол и т. п.).
- Какие названия применяют для обозначения множеств кораблей? (флотилия, эскадра).
Задайте сами множество описанием.
(Слайд 3) Множества обычно обозначают большими буквами латинского алфавита: А, В, С, Д, и т. д. Некоторые числовые множества столь часто встречающиеся в различных разделах математики, что для них ввели специальные обозначения:
N – множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
I – множество иррациональных чисел;
R – множество действительных чисел.
(Слайд 4) Чтобы не забыть, что перечисляемые элементы объединены вместе в некоторое множество, такое перечисление производят внутри фигурных скобок {,}.
Например, цифры десятичной системы счисления задаются множеством
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
Если множество состоит из чисел, то при их перечислении иногда удобнее использовать не запятую, а знак препинания “ ; ” – точку с запятой. Так как “перечислительную” запятую можно спутать с “десятичной” запятой.
Элементы множества можно перечислять в произвольном порядке. От изменения порядка перечисления элементов само множество не меняется. Например, множество гласных букв русского алфавита задается {А, Е, Ё, И, О, У, Ы, Э, Ю, Я} или {Э, Е, А, Ё, Я, О, Ы, И, У, Ю}.
Эти множества состоят из одних и тех же элементов, их называют равными, а для записи равенства двух множеств употребляют знак “ = ”.
{А, Е, Ё, И, О, У, Ы, Э, Ю, Я} = {Э, Е, А, Ё, Я, О, Ы, И, У, Ю}.
Чтобы задать конечное множество, можно просто перечислить все его элементы.
Например, запись А = {2; 3; 5; 7; 11; 13} означает, что множество А состоит из первых шести простых чисел.
Однако задавать множество путем перечисления его элементов удобно только в том случае, когда их число невелико. Если число элементов множества достаточно велико или множество бесконечно, то явное перечисление элементов такого множества невозможно.
Способы задания, описания множеств весьма разнообразны. Например, множество всех квадратов натуральных чисел можно записать {1; 4; 9; 16; 25; …}, а множество всех чисел, которые больше 5 и меньше 12 записать {х | 5< х <12} или (5; 12). В примерах использован оборот “ … и так далее” и символ “ | ” внутри фигурных скобок заменяющий комбинацию слов “ … таких, что …”. (Множество всех х таких, что 5< х <12).
Описав словами некоторое множество, нельзя гарантировать, что найдется хотя бы один объект, отвечающий этому описанию. Предположим, о множестве С сказано, что оно состоит из чисел, делящихся на 6, но не делящихся на 3. Таких чисел просто нет. В подобных случаях множество называют пустым и обозначают символом O, в фигурные скобки его не ставят, так как никакого перечисления элементов пустого множества не происходит.
(Слайд 5) Задание 1. [3]
1) Задайте множество цифр, с помощью которых записывается число:
а) 3254; б) 8797; в) 11000; г) 555555.
2) Задайте множество А описанием:
а) А = {1, 3, 5, 7, 9}; б) А = {– 2, – 1, 0, 1, 2}; в) А = {11, 22, 33, 44, 55, 66, 77, 88, 99}; г) А = {0,1; 0,01; 0,001; 0,0001; …}; д) А = {1/2, 2/3, 3/4, 4/5, … }.
3) Задание с выбором ответа. Даны множества: М = {5,4,6}, Р = {4,5,6}, Т = {5,6,7},
S = {4, 6}. Какое из утверждений неверно?
а) М = Р. б) Р S. в) М Т. г) Р = Т.
(Слайд 6) Словесные обороты, как “элемент х принадлежит множеству А” или “х – элемент множества А”, достаточно длинны и не всегда удобны в записи решений конкретных задач.
В математике эти выражения кратко записывают так: х А, где – знак принадлежности.
Например, 5N, лучше читать не буквально, а в “литературном переводе”, “5 – число натуральное”. Наряду со знаком принадлежит используют и его “отрицание” – знак (знак не принадлежит). Запись 0 N означает, что нуль не натуральное число.
(Слайд 7) Задание 2. [3; 1]
1. Запишите на символическом языке следующее утверждение:
а) число 10 – натуральное; б) число – 7 не является натуральным; в) число – 100 является целым; г) число 2,5 – не целое.
2. Верно ли, что:
а) – 5 N; б) -5 Z; в) 2,(45) Q?
3. Верно ли, что:
а) 0,7 {х | х2 – 1 < 0}; б) – 7 {х | х2 + 16х ? – 64}?
(Слайд 8) Возьмем множество А = {2; 4; 6} и В = {1; 2; 3; 4; 5; 6; 7}. Каждый элемент множества А принадлежит также и множеству В. В таких случаях говорят, что множество А является подмножеством множества В, и пишут: А В.
Знак “” называют знаком включения.
Соотношения между множествами А и В можно проиллюстрировать на рисунке с помощью так называемых кругов Эйлера (Леонард Эйлер российский ученый — математик, механик, физик и астроном.). Множество изображается в виде некоторого круга, а его элементы изображаются точками этого круга (рис 1).
Рис. 1
Пустое множество считают подмножеством любого множества. А В. Будем считать, что все элементы рассматриваемых множеств взяты из некоторого одного и того же “универсального” множества К. Это множество будем изображать квадратом, а рассматриваемые множества А, В, С, … – подмножества множества К – кругами (или другими полученными из них фигурами, которые выделим штриховкой).
(Слайд 9) Задание 3. [3; 1]
1. Даны множества: А = {10}, В = {10, 15}, С = {5, 10, 15}, D = {5, 10, 15, 20}.
Поставьте вместо … знак включения ( или ) так, чтобы получилось верное утверждение: а) А… D; б) А…В; в) С…А; г) С…В.
2. Даны три множества А = {1, 2, 3,…, 37}, В = {2, 4, 6, 8, …}, С = {4, 8, 12, 16,…,36}.
Верно ли, что: а) А В; б) В С; в) С А; г) С В?
(Слайд 10) Из данных множеств с помощью специальных операций можно образовывать новые множества:
1) Пересечением множества А и В называют множество, состоящие из всех общих 11элементов множеств А и В, т. е. из всех элементов, которые принадлежат и множеству А, и множеству В (рис. 2). Пересечение множеств А и В обозначают так: АВ. Это определение можно записать и так: АВ = {х | х А и х В}. Иными словами, пересечение двух множеств – это их общая часть. Например, если А = {3; 9; 12} и В = {1; 3; 5; 7; 9; 11}, то АВ = {3; 9}. Если А = {10; 20; …90; 100} и В = {6; 12; 18;…}, то АВ = {30; 60; 90}. Можно рассматривать пересечение не только двух, но трех, четырех и т. д. множеств. Пересечение множеств В, С и D обозначают так: ВСD.
Рис. 2
(Слайд 11) Задание 4. [3; 1]
1. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11}, С = {5; 11}.
Найдите: а) АВ; б) АС; в) СВ.
2. Даны множества: А – множества всех натуральных чисел, кратных 10, В = {1; 2; 3;…, 41}.
Найдите АВ.
3. Даны множества: А = {a, b, c, d}, B = {c, d, e, f}, C = {c, e, g, k}.
Найдите (АВ) С.
(Слайд 12)
2) Объединением множеств А и В называют множество, состоящее из всех элементов, которые принадлежат хотя бы одному из этих множеств – или множеству А, или множеству В (рис. 3). Объединение множеств А и В обозначают так: АUВ.
Рис. 3
Это определение можно записать и так: АUВ = {х | х А или х В}. Например, если А = {3; 9; 12} и В = {1; 3; 5; 7; 9; 11}, то АUВ = {1; 3; 5; 7; 9; 11; 12}. Можно рассматривать объединение не только двух, но трех, четырех и т.д. множеств. Объединение множеств В, С и D обозначают так: ВUСUD.
(Слайд 13) Задание 5. [3; 1]
1. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11}, С = {5; 11}.
Найдите: а) АUВ; б) АUС; в) СUВ.
2. Даны множества: А = {a, b, c, d}, B = {c, d, e, f}, C = {c, e, g, k}.
Найдите (АUВ)UС.
3. Даны три числовых промежутка: А = (7,7; 11), В = [; ], С = (; 13].
Найдите (АUВ)UС.
Продолжение статьи
Приложение
Презентация
urok.1sept.ru
Круги Эйлера онлайн — 4 Июля 2016 — Примеры решений задач
Круги Эйлера, диаграммы Венна
Геометрическое моделирование множеств. Калькулятор.
Для наглядного представления множеств и отношений между ними используется диаграммы Венна (иногда их называют кругами Эйлера или диаграммами Эйлера – Венна).
Универсальное множество изображают в виде прямоугольника, а множества, входящие в универсальное множество, – в виде кругов внутри прямоугольника; элементу множества соответствует точка внутри круга.
С помощью диаграмм Венна удобно иллюстрировать операции над множествами.
Калькулятор для построения кругов Эйлера.
Правила вввода основных обозначений операций над множествами:
| Операция | Обозначение | |
| математическое | в калькуляторе | |
| Дополнение | $\bar{A}$ | A’ |
| Пересечение | (A∩B) | (A intersection B) |
| Объединение | (А⋃B) | (A union B) |
| Симметрическая разность | (A∆B) | (symmetric difference of A and B) |
| Относительное дополнение | (A\B) | (A\B) |
| Правильно | Не правильно |
|---|---|
| (A union B) intersection (A union C) | (AunionB)intersection(AunionC) |
Пример. Изобразить множество D с помощью кругов Эйлера (нарисовать диаграмму Эйлера-Венна):
№ | Множество D | Вводим в калькулятор |
1 | $(A\cap B) \cup C$ | (A intersection B) union C |
2 | $(A\cap B) \cup \bar{C}$ | (A intersection B) union C’ |
3 | $(A\cap \bar{B}) \cup C$ | (A union B’) intersection C |
4 | $(А\cap B) \cup (А\cap C)$ | (A intersection B) union (A intersection C) |
В таблице показано: как правильно вводить в калькулятор выражения для операций над множествами.
www.reshim.su
Круги Эйлера: примеры и возможности
Математика по своей сути наука абстрактная, если отойти от элементарных понятий. Так, на паре-тройке яблок можно наглядно изобразить основные операции, что лежат в основе математики, но, как только плоскость деятельности расширяется, этих объектов становится недостаточно. Кто-нибудь пробовал изобразить на яблоках операции над бесконечными множествами? В том-то и дело, что нет. Чем сложнее становились понятия, которыми оперирует математика в своих суждениях, тем проблематичнее казалось их наглядное выражение, которое было бы призвано облегчить понимание. Однако, на счастье как современных студентов, так и науки в целом, были выведены круги Эйлера, примеры и возможности которых мы рассмотрим ниже.
Немного истории
17 апреля 1707 года мир подарил науке Леонарда Эйлера — замечательного ученого, чей вклад в математику, физику, кораблестроение и даже теорию музыки не переоценить.
 Труды его признаны и востребованы по сей день во всем мире, несмотря на то что наука не стоит на месте. Особо занимательным является тот факт, что господин Эйлер принял непосредственное участие в становлении российской школы высшей математики, тем более что волею судеб он дважды возвращался в наше государство. Ученый обладал уникальной способностью выстраивать прозрачные в своей логике алгоритмы, отсекая все лишнее и в кратчайшие сроки переходя от общего к частному. Не станем перечислять все его заслуги, так как это займет немалое количество времени, и обратимся непосредственно к теме статьи. Именно он предложил использовать графическое изображение операций над множествами. Круги Эйлера решение любой, даже самой сложно составленной задачи, способны изобразить наглядно.
Труды его признаны и востребованы по сей день во всем мире, несмотря на то что наука не стоит на месте. Особо занимательным является тот факт, что господин Эйлер принял непосредственное участие в становлении российской школы высшей математики, тем более что волею судеб он дважды возвращался в наше государство. Ученый обладал уникальной способностью выстраивать прозрачные в своей логике алгоритмы, отсекая все лишнее и в кратчайшие сроки переходя от общего к частному. Не станем перечислять все его заслуги, так как это займет немалое количество времени, и обратимся непосредственно к теме статьи. Именно он предложил использовать графическое изображение операций над множествами. Круги Эйлера решение любой, даже самой сложно составленной задачи, способны изобразить наглядно.В чем же суть?
На практике круги Эйлера, схема которых изображена ниже, могут применяться не только в математике, так как понятия «множества» присущи не только данной дисциплине. Так, они с успехом применяются и в менеджменте.
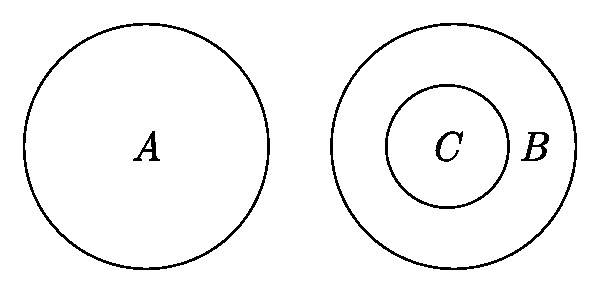
Схема выше показывает отношения множеств А (иррациональные числа), В (рациональные числа) и С (натуральные числа). Круги показывают, что множество С включено в множество В, тогда как множество А с ними никак не пересекается. Пример простейший, но наглядно объясняет специфику «взаимоотношений множеств», которые слишком абстрактны для реального сравнения хотя бы в силу их бесконечности.
Алгебра логики
Данная область математической логики оперирует высказываниями, которые могут носить как истинный, так и ложный характер. Например, из элементарного: число 625 делится нацело на 25, число 625 делится нацело на 5, число 625 является простым. Первое и второе утверждения – истина, тогда как последнее – ложь. Конечно, на практике все сложнее, но суть показана ясно. И, конечно же, в решении опять участвуют круги Эйлера, примеры с их использованием слишком удобны и наглядны, чтобы их игнорировать.
Немного теории:
- Пусть множества А и В существуют и не являются пустыми, тогда для них определены следующие операции пересечения, объединения и отрицания.
- Пересечение множеств А и В состоит из элементов, что принадлежат одновременно как множеству А, так и множеству В.
- Объединение множеств А и В состоит из элементов, что принадлежат множеству А или множеству В.
- Отрицание множества А — это множество, что состоит из элементов, которые не принадлежат множеству А.

Все это изображают опять же круги Эйлера в логике, так как с их помощью каждая задача, вне зависимости от степени сложности, становится очевидной и наглядной.
Аксиомы алгебры логики
Положим, что 1 и 0 существуют и определены во множестве А, тогда:
- отрицание отрицания множества А есть множество А;
- объединение множества А с не_А есть 1;
- объединение множества А с 1 есть 1;
- объединение множества А с самим собой есть множество А;
- объединение множества А с 0 есть множество А;
- пересечение множества А с не_А есть 0;
- пересечение множества А с самим собой есть множество А;
- пересечение множества А с 0 есть 0;
- пересечение множества А с 1 есть множество А.
Основные свойства алгебры логики
Пусть множества А и В существуют и не являются пустыми, тогда:
- для пересечения и объединения множеств А и В действует переместительный закон;
- для пересечения и объединения множеств А и В действует сочетательный закон;
- для пересечения и объединения множеств А и В действует распределительный закон;
- отрицание пересечения множеств А и В есть пересечение отрицаний множеств А и В;
- отрицание объединения множеств А и В есть объединение отрицаний множеств А и В.
Ниже показаны круги Эйлера, примеры пересечения и объединения множеств А, В и С.
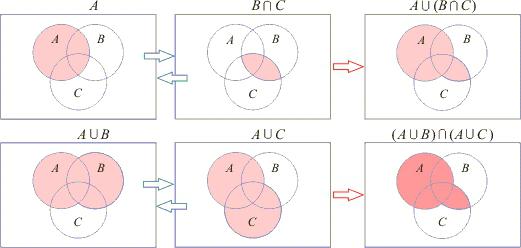
Перспективы
Работы Леонарда Эйлера обоснованно считаются базой современной математики, однако сейчас их с успехом применяют в областях человеческой деятельности, что появились относительно недавно, взять хотя бы корпоративное управление: круги Эйлера, примеры и графики описывают механизмы моделей развития, будь то российская или англо-американская версия.
fb.ru
Исследовательская работа «Применение кругов Эйлера при решении задач»
Муниципальное общеобразовательное учреждение
Доможаковская средняя общеобразовательная школа
МАТЕМАТИКА
Применение кругов Эйлера
к решению задач
Выполнила: Кадушкина
Софья Николаевна, 8 класс
Руководитель: Абрашкин
Евгений Анатольевич,
учитель математики
а.Доможаков, 2010 год
Содержание
Введение………………………………………………………………….3 стр
Жизнеописание Леонарда Эйлера ……………………………………4 стр
Понятие множества ……………………………..……………………..5 стр
Соотношения между множествами…………………………………….6 стр
Решение задач с помощью кругов Эйлера……………………………7 стр
Заключение……………………………………..………………………12 стр
Литература………………………………………………….………….14 стр
Введение
Логические задачи составляют обширный класс нестандартных задач. Сюда относятся, прежде, всего, текстовые задачи, в которых требуется распознать объекты или расположить их в определенном порядке по имеющимся свойствам. При этом часть утверждений условия задачи может выступать с различной оценкой.
Существует множество приемов, которые используются при решении текстовых логических задач. Очень часто решение задачи помогает найти рисунок. Использование рисунка делает решение задачи простым и наглядным. Решение каждой из этих задач можно красиво оформить.
Задачи, решаемые с помощью кругов Эйлера, предлагаются на математических олимпиадах, но в школьной программе не отводятся часы на изучение данной темы.
Логические задачи данного вида загадочны с первого взгляда, поэтому многие считаются неразгаданными. Ценность задач, решаемых с помощью кругов Эйлера, состоит в том, что решения задач с громоздкими условиями и со многими данными, просты и не вызывают особых умозаключений. Актуальность состоит в том, что задачи имеют практический характер, что немаловажно в современной жизни. Задачи заставляют задумываться, подходить к решению какой-либо проблемы с другой стороны, уметь выбирать из множества способов решения, наиболее простой, легкий путь.
Цель: показать применение кругов Эйлера при решении задач.
Задачи: 1. Изучить литературу о жизнеописании Леонарда Эйлера.
2. Раскрыть понятие множества и исследовать отношения между ними.
3. Показать решение задач с помощью кругов Эйлера.
4. Сделать вывод о связи между множествами, о применении кругов Эйлера к решению задач.
Гипотеза: Действительно ли алгебра множеств и круги Леонарда Эйлера упрощают решение задач?
Жизнеописание Леонарда Эйлера
Эйлер принадлежит к числу гениев, чьё творчество стало достоянием всего человечества. До сих пор школьники всех стран изучают тригонометрию и логарифмы в том виде, какой придал им Эйлер. Имя Эйлера дорого всему прогрессивному человечеству, которое чтит в нём одного из величайших геометров мира.
Леонард Эйлер (1707-1783) родился в Базеле (Швейцария) в семье пастыря, получил первоначальное образование у своего отца. Отец предназначал сына к богословскому званию и определил его по окончании средней школы на теологический факультет. Однако Эйлер интересовался не теологией, а математикой, и стал слушать лекции известного профессора математики Иоганна Бернулли.
В 19 – летнем возрасте Эйлер опубликовал первую свою научную работу и принял участие в объявленном Парижской академией наук конкурсе на тему о наилучшем расположении мачт на корабле. В 1727 году Эйлер приехал в Петербург.
В Петербурге Эйлер нашел все необходимые условия для большой научной деятельности и широкие возможности для публикации своих трудов. Здесь он женился, провел большую часть творческого периода своей жизни, став главой первой русской математической школы, написал более 850 научных работ. В одной из них и появились круги.
Решая математические головоломки и развлекательные задачи, Эйлер заложил основы теории графов, ныне широко используемой во многих приложениях математики. Напряженная работа повлияла на зрение ученого. В 1735 году он ослеп на один глаз, а в 1766 на оба. Операция привела к незначительному улучшению: ученый мог лишь разбирать записи, сделанные мелом на черной доске. Но и после этого Эйлер продолжал работу, диктуя ученикам свои статьи.
Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами. Используется в математике, логике, менеджменте и других прикладных направлениях. А впервые он их использовал в письмах к немецкой принцессе. Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления». Позднее аналогичный прием использовал ученый Венн и его назвали «диаграммы Венна». При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов, и они получили название «круги Эйлера».
Понятие множества
В математике, когда какие-нибудь объекты собираются вместе говорят одно и то же слово – множество. Сказать «стадо чашек» нельзя, а множество чашек – можно. Сказать «бригада коров» нельзя, а множество коров – можно.

Предметы или живые существа, входящие во множество, называются элементами этого множества. Между множествами могут быть различные виды отношений. Для наглядной геометрической иллюстрации соотношений между множествами используются диаграммы Эйлера-Венна. Это замкнутая линия, внутри которой расположены элементы данного множества.
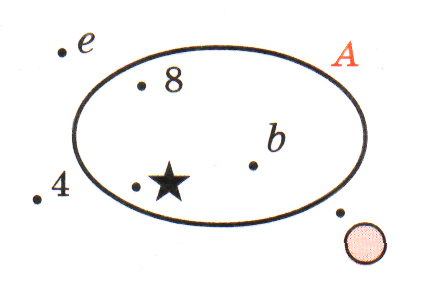
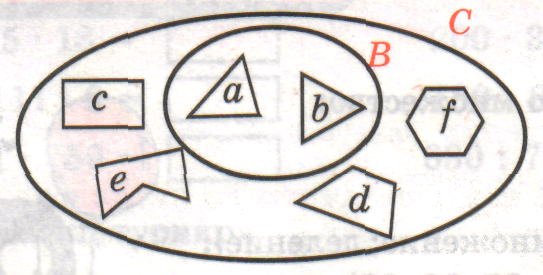
Соотношения между множествами
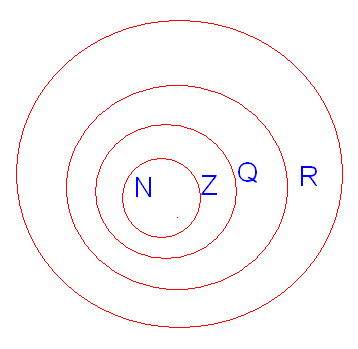
Множество всех действительных чисел Эйлер изобразил с помощью этих кругов: N -множество натуральных чисел, Z — множество целых чисел, Q — множество рациональных чисел, R — множество всех действительных чисел.
Общую часть множеств называют пересечением. Изображают так: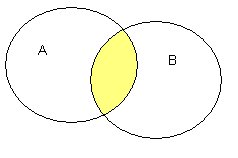
Объединение множеств называют множество всех элементов, принадлежащих данным множествам.
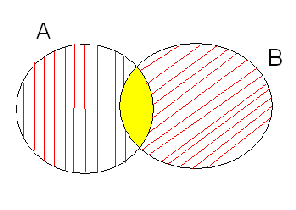
Решение задач с помощью кругов Эйлера
Задача 1
В спортивных соревнованиях участвует школьная команда из 20 человек, каждый из которых имеет спортивный разряд по одному или нескольким из трех видов спорта: легкой атлетике, плаванию и гимнастике. Известно, что 12 из них имеют разряды по легкой атлетике,10 – по гимнастике и 5–по плаванию. Сколько школьников из этой команды имеют разряды по всем видам спорта, если по легкой атлетике и плаванию разряды имеют 2 человека, по легкой атлетике и гимнастике – 4 человека, по плаванию и гимнастике – 2 человека?
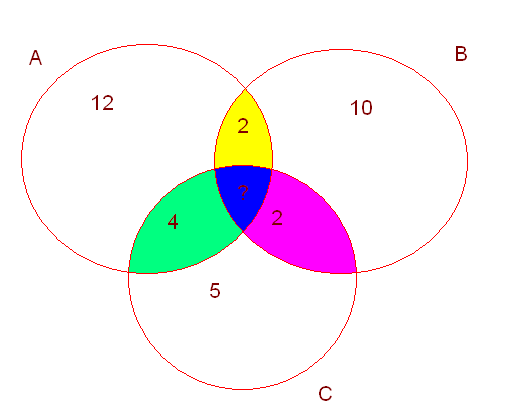
А-множество учащихся имеющих
разряды по легкой атлетике.
В-множество учащихся имеющих разряды по плаванию.
С-множество учащихся имеющих разряды по гимнастики.
Нам надо найти, сколько элементов, то есть учащихся входят в пересечение множеств.
12 -2 = 10 — учащихся только по легкой атлетике.
10 -2 = 8 — учащихся только по плаванию.
5 -4 = 1 — учащихся только по гимнастике.
20-[(12-2)+(10-2)+(5-4)]=20-10-8-1=20-19=1 (уч.) имеют разряд по всем видам спорта.
Задача 2
В классе можно изучать английский или французский язык. Известно, что английский язык изучают 20 школьников, а французский – 17. Всего в классе 32 ученика. Сколько учащихся изучают оба языка: и английский и французский
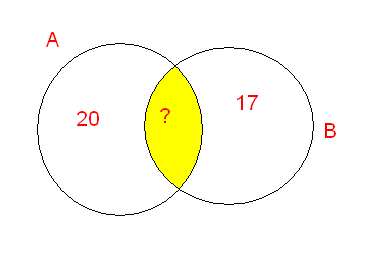
Решение.
А – изучают английский язык
В — изучают французский язык
Надо найти пересечение множеств.
32-(20+17)=5 учащихся
Задача 3
Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят лилии, а пятеро – фиалки. И только у двоих есть и лилии и фиалки. Угадайте сколько у меня подруг?
Решение
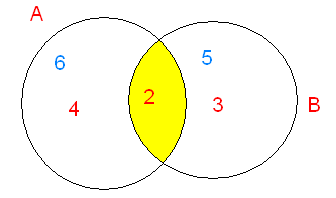
А — лилии
В — фиалки
Пересечение множеств равно 2 ( и лилии, и фиалки)
6 – 2 = 4 – разводят только лилии
5 – 3 = 2 – разводят только фиалки
4 + 3 + 2 = 9 (подруг)
Задача 4
В классе 40 человек. Из них по математике имеют тройки-17 человек, по русскому языку- 19 человек, по физике 22 человека. 4 человека имеют тройки только по русскому языку , 4 только по математике и 11 человек только по физике. Пять человек имеют тройки по русскому языку, математике и физике. Сколько человек учатся без троек?
А – множество учащихся, имеющих тройки по русскому языку.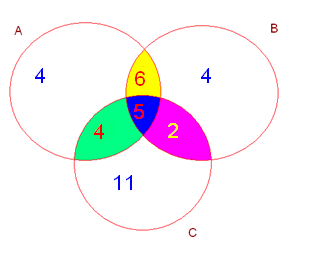
В – множество учащихся,
имеющих тройки по математике.
С – множество учащихся, имеющих тройки по физике.
Всего в множество В входит 17 человек, значит 17-(4+2+5)=6 (чел.) – только по русскому и математике.
Всего в множество А входит 19 человек, значит 19-(4+5+6)=4 (чел.) – только по русскому и физике
Складываем все числа, которые получились на схеме: 4+4+11+6+4+2+5=36.
Всего учащихся 40. Значит без троек учатся 40-36= 4 человека
Задача 5.
В деревне 44 дома, и в каждом доме проживает одна семья. Известно, что 25 семей держат коров , 28 семей – овец и 26 семей – свиней. Причем 15 семей держат коров и овец, 13 семей – овец и свиней, 5 семей – коров, овец и свиней. Сколько семей держат коров и свиней?
А – множество семей, имеющих коров. 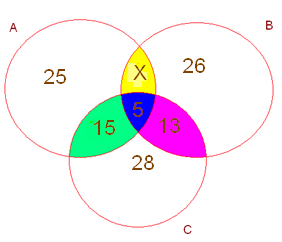
В – множество семей, имеющих свиней.
С – множество семей, имеющих овец.
44-[(25-15)+(28-13)+(26-х)]=5
44-25-26+Х
Х=5-44+51
Х=12
25 – 15 = 10 – семей, имеющих только коров.
28 – 13 = 15 – семей, имеющих только овец.
26 –Х – семей, имеющих только свиней.
Задача 6.
Ученики нашего класса принимали участие в олимпиаде по биологии и русскому языку, часть – только по биологии, а часть в двух олимпиадах. По биологии принимало участие 85%, по русскому языку 75%. Сколько процентов учащихся участвовало в двух олимпиадах?
Решение.
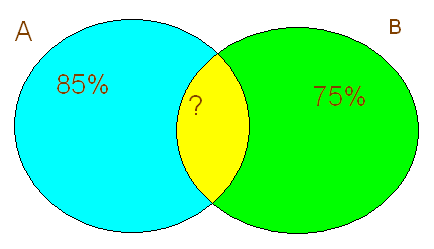
А – множество учеников, принимающих участие в олимпиаде по биологии.
В – множество учеников, принимающих участие в олимпиаде по русскому языку.
100% — все учащиеся.
100% — 85% = 15% Учащиеся, участвующие в олимпиаде только по русскому языку.
75% — 15% = 60% Учащиеся, участвующие в двух олимпиадах.
Задача 7.
В футбольной команде «Спартак» 30 игроков, среди них 18 нападающих, 11 полузащитников, 17 защитников и вратари. Известно, что трое могут быть нападающими и защитниками, 10 защитниками и полузащитниками, 6 нападающими и полузащитниками, а 1 и нападающим, и защитником, и полузащитником. Вратари не заменимы. Сколько в команде «Спартак» вратарей?
Решение.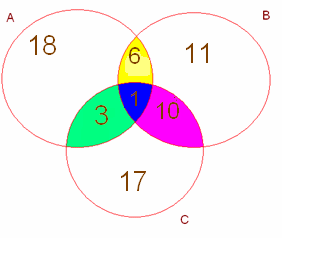
А – множество нападающих.
В– множество полузащитников.
С – защитники.
30 – [(18 – 3) + (17 – 6) + (11 – 10) + 1] = 30 – 15 – 11 – 1 – 1 = 30 – 28 = 2 (вратаря)
Задача 8.
В классе 30 человек. 20 из них каждый день пользуются метро, 15 – автобусом, 23 – троллейбусом, 10 – и метро, и троллейбусом, 12 – и метро, и автобусом, 9 – и троллейбусом, и автобусом. Сколько человек ежедневно пользуется всеми тремя видами транспорта?
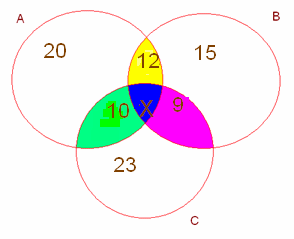
Решение
А – множество человек, которые пользуются метро.
В – множество человек, которые пользуются автобусом.
С – множество человек, которые пользуются троллейбусом.
Пусть Х – пользуются всеми видами транспорта, тогда 20-10=10 – только метро, 23-9=14 – только троллейбусом, 15-12=3 – только автобусом.
Х=30-10-14-3
Х=3
3 человека пользуются всеми видами транспорта.
Заключение
Ты человек, а значит, ты
Обязан рассуждать –
А без логичной простоты
Ты будешь пропадать.
Пусть за собой она зовёт –
Уйми в коленях дрожь!
Коль с Логикой пойдёшь вперёд –
Нигде не пропадёшь!
(С. Алдошин)
Логика, наука о законах и формах правильного мышления, зародилась в Древней Греции. Основоположником логики по праву считают великого учёного Аристотеля (384 – 322 гг. до н.э.). Она лежит в основе различных наук (естественных, общественных и технических), а также в основе любого учебного предмета, изучаемого в общеобразовательной школе. Логику должен знать каждый человек, чтобы мыслить правильно, т.е. определённо, непротиворечиво, доказательно, чётко, и уметь излагать свои мысли понятным языком. Одна из характерных черт любой логики состоит в том, что она позволяет, получив некоторую информацию, извлечь (выявить) содержащиеся в ней новые знания.
Школьникам логика помогает в процессе овладения ими многообразной информацией, с которой они встречаются при изучении различных наук и в практической деятельности. Потом, в ходе дальнейшего самообразования, логика поможет им отделить главное от второстепенного, критически воспринять данные в различных книгах определения и классификации разнообразных понятий, подобрать формы доказательства своих истинных суждений и формы опровержения ложных. И это только некоторые из многих преимуществ, которые даёт человеку изучение интереснейшей и древнейшей из наук – логики, т.е. науки о законах и формах правильного мышления.
Как видно из моей исследовательской работы, задачи состоят из множества данных. Выстроив данные в единую цепочку, можно увидеть, что решение задач подчиняется одному и тому же способу. Для решения задач, решаемых с помощью кругов Эйлера, был составлен алгоритм, состоящий из следующих этапов:
Записываем краткое условие задачи.
Выполняем рисунок.
Записываем данные в круги (или в диаграмму Эйлера).
Выбираем условие, которое содержит больше свойств.
Анализируем, рассуждаем, не забывая записывать результаты в части круга (диаграммы).
Записываем ответ.
Логические задачи заставляют думать, рассуждать, составлять цепочку действий, последовательность, учат алгоритмизации, что немаловажно в современной жизни. А исследовательские работы учат искать информацию из различных источников (включая и интернет) и обрабатывать её, учат находить из большого материала лишь тот, который необходим.
Литература:
Энциклопедический словарь юного математика для среднего и старшего школьного возраста. М.: Педагогика,1989.
Мадер В.В. Математический детектив. Книга дляучащихся. – М.: Просвещение,1992.
Баженов И.И., Порошкин А.Г. и др. Задачи для школьных математических кружков. Сыктывкар, 1994.
Гусев В.А., Орлов А.И., Розенталь А.Л. «Внеклассная работа по математике». М.: Просвещение, 1984.
Гетманова А. Д. Логические основы математики 10 – 11 класс: учебное пособие. – М.: Дрофа, 2005.
Детская энциклопедия «Я познаю мир»
Ю.Н. Макарычев «Алгебра – 8. Дополнительные главы к школьному учебнику»
Г.И. Глейзер «История математики в школе 7 – 9 классы»
infourok.ru
 ,
и с помощью кругов Эйлера проиллюстрируйте
его.
,
и с помощью кругов Эйлера проиллюстрируйте
его. ,
и с помощью кругов Эйлера дайте
графическую иллюстрацию.
,
и с помощью кругов Эйлера дайте
графическую иллюстрацию. ,
и проиллюстрируйте его с помощью
кругов Эйлера.
,
и проиллюстрируйте его с помощью
кругов Эйлера. ,
и с помощью кругов Эйлера проиллюстрируйте
его.
,
и с помощью кругов Эйлера проиллюстрируйте
его. ,
и с помощью кругов Эйлера проиллюстрируйте
его.
,
и с помощью кругов Эйлера проиллюстрируйте
его. ,
и с помощью кругов Эйлера проиллюстрируйте
его.
,
и с помощью кругов Эйлера проиллюстрируйте
его. ,
и с помощью кругов Эйлера проиллюстрируйте
его.
,
и с помощью кругов Эйлера проиллюстрируйте
его. ,
и с помощью кругов Эйлера проиллюстрируйте
его.
,
и с помощью кругов Эйлера проиллюстрируйте
его. ,
и проиллюстрируйте его с помощью
кругов Эйлера.
,
и проиллюстрируйте его с помощью
кругов Эйлера. ,
и с помощью кругов Эйлера проиллюстрируйте
его.
,
и с помощью кругов Эйлера проиллюстрируйте
его. ,
и с помощью кругов Эйлера проиллюстрируйте
его.
,
и с помощью кругов Эйлера проиллюстрируйте
его.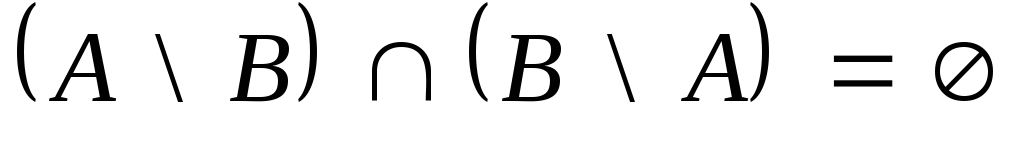 ,
и проиллюстрируйте его с помощью
кругов Эйлера.
,
и проиллюстрируйте его с помощью
кругов Эйлера.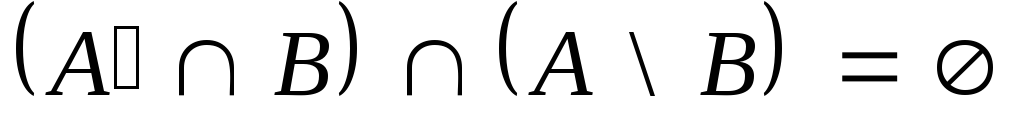 ,
и с помощью кругов Эйлера проиллюстрируйте
его.
,
и с помощью кругов Эйлера проиллюстрируйте
его. ,
и с помощью кругов Эйлера проиллюстрируйте
его.
,
и с помощью кругов Эйлера проиллюстрируйте
его.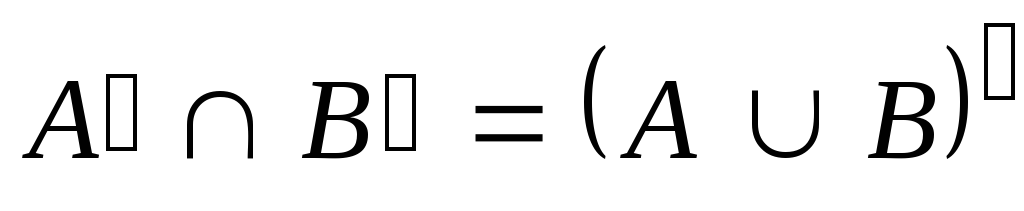 ,
и с помощью кругов Эйлера проиллюстрируйте
его.
,
и с помощью кругов Эйлера проиллюстрируйте
его. ,
и с помощью кругов Эйлера проиллюстрируйте
его.
,
и с помощью кругов Эйлера проиллюстрируйте
его.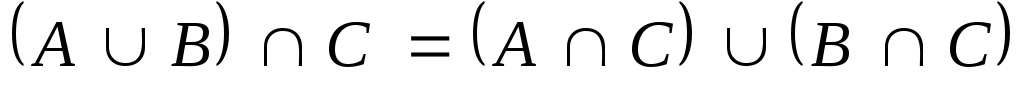 ,
и с помощью кругов Эйлера проиллюстрируйте
его.
,
и с помощью кругов Эйлера проиллюстрируйте
его.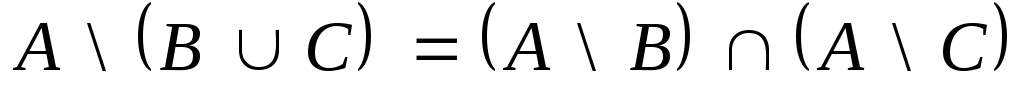
 ,
и с помощью кругов Эйлера проиллюстрируйте
его.
,
и с помощью кругов Эйлера проиллюстрируйте
его. ,
и проиллюстрируйте его с помощью
кругов Эйлера.
,
и проиллюстрируйте его с помощью
кругов Эйлера.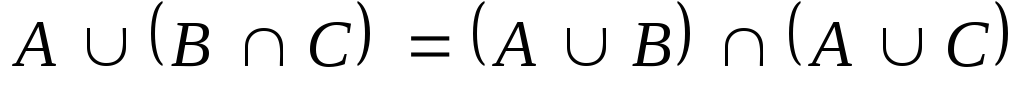
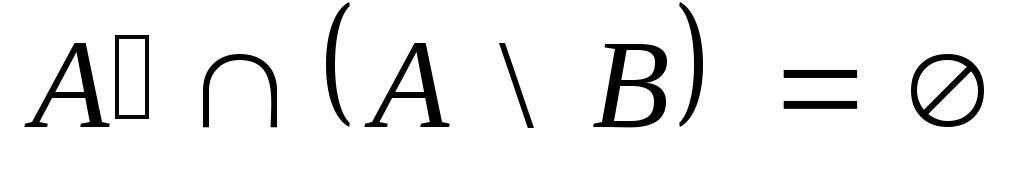 ,
и с помощью кругов Эйлера проиллюстрируйте
его.
,
и с помощью кругов Эйлера проиллюстрируйте
его.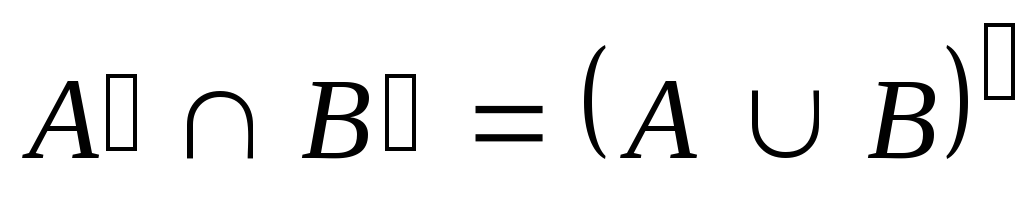 ,
и с помощью кругов Эйлера проиллюстрируйте
его.
,
и с помощью кругов Эйлера проиллюстрируйте
его. ,
и проиллюстрируйте его с помощью
кругов Эйлера.
,
и проиллюстрируйте его с помощью
кругов Эйлера. ,
и с помощью кругов Эйлера проиллюстрируйте
его.
,
и с помощью кругов Эйлера проиллюстрируйте
его. ,
и проиллюстрируйте его с помощью
кругов Эйлера.
,
и проиллюстрируйте его с помощью
кругов Эйлера.