Таблица умножения — Википедия

Табли́ца умноже́ния, она же табли́ца Пифаго́ра — таблица, где строки и столбцы озаглавлены множителями, а в ячейках таблицы находится их произведение. Используется для обучения школьников умножению.

Старейшая известная таблица умножения обнаружена в Древнем Вавилоне и имеет возраст примерно 4000 лет. Она основана на шестидесятеричной системе счисления^[1]. Старейшая десятеричная таблица умножения найдена в Древнем Китае и датируется 305 годом до н. э.^[1]

Иногда изобретение таблицы умножения приписывают Пифагору, в честь которого она названа в различных языках, включая французский, итальянский и русский^[2].

В 493 году Викторий Аквитанский создал таблицу из 98 столбцов, которая представляла в римских числах результат перемножения чисел от 2 до 50^[3].

В России первая таблица умножения была издана в 1682 году в первой печатной математической книге на русском языке, называвшейся «Считание удобное, которым всякий человек, купующий или продающий, зело удобно изыскати может число всякие вещи…» и содержавшей таблицу умножения пар чисел от 1×1 до 100×100, записанных славянскими цифрами

[4]. По экземпляру этой книги хранится, например, в РГБ^[5] и в Научной библиотеке МГУ^[6].

Джон Лесли в книге The Philosophy of Arithmetic (1820)^[7] опубликовал таблицу умножения чисел до 99, позволявшую перемножать цифры парами. Он же рекомендовал ученикам заучивать таблицу умножения до 25.

В своё время введение заучиваемой наизусть таблицы умножения революционизировало устный и письменный счёт. До этого использовались разные хитрые способы вычисления произведений однозначных чисел, которые сильно замедляли весь процесс и служили источником дополнительных ошибок.

В российских школах значения традиционно доходят до 10×10. В Великобритании до 12×12, что связано в том числе с единицами английской системой мер длины (1 фут = 12 дюймов) и денежного обращения (существовавшей до 1971 г.: 1 фунт стерлингов = 20 шиллингам, 1 шиллинг = 12 пенсам).

В Советском Союзе таблицу умножения обычно «задавали на лето» после 1-го класса, а закрепляли на занятиях во 2-м классе (в возрасте 8 лет). В российских школах чаще всего проходят во 2-м классе. По стандартам английского школьного образования таблица умножения должна быть выучена к возрасту 11 лет (планируется ужесточение требования до 9 лет).^[8]

Таблица умножения в десятичной системе

×	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
2	2	4	6	8	10	12	14	16	18	20	22	24	26	28	30	32	34	36	38	40
3	3	6	9	12	15	18	21	24	27	30	33	36	39	42	45	48	51	54	57	60
4	4	8	12	16	20	24	28	32	36	40	44	48	52	56	60	64	68	72	76	80
5	5	10	15	20	25	30	35	40	45	50	55	60	65	70	75	80	85	90	95	100
6	6	12	18	24	30	36	42	48	54	60	66	72	78	84	90	96	102	108	114	120
7	7	14	21	28	35	42	49	56	63	70	77	84	91	98	105	112	119	126	133	140
8	8	16	24	32	40	48	56	64	72	80	88	96	104	112	120	128	136	144	152	160
9	9	18	27	36	45	54	63	72	81	90	99	108	117	126	135	144	153	162	171	180
10	10	20	30	40	50	60	70	80	90	100	110	120	130	140	150	160	170	180	190	200
11	11	22	33	44	55	66	77	88	99	110	121	132	143	154	165	176	187	198	209	220
12	12	24	36	48	60	72	84	96	108	120	132	144	156	168	180	192	204	216	228	240
13	13	26	39	52	65	78	91	104	117	130	143	156	169	182	195	208	221	234	247	260
14	14	28	42	56	70	84	98	112	126	140	154	168	182	196	210	224	238	252	266	280
15	15	30	45	60	75	90	105	120	135	150	165	180	195	210	225	240	255	270	285	300
16	16	32	48	64	80	96	112	128	144	160	176	192	208	224	240	256	272	288	304	320
17	17	34	51	68	85	102	119	136	153	170	187	204	221	238	255	272	289	306	323	340
18	18	36	54	72	90	108	126	144	162	180	198	216	234	252	270	288	306	324	342	360
19	19	38	57	76	95	114	133	152	171	190	209	228	247	266	285	304	323	342	361	380
20	20	40	60	80	100	120	140	160	180	200	220	240	260	280	300	320	340	360	380	400

Как найти результат по таблице умножения[править | править код]

Чтобы узнать результат произведения 4×8 по таблице умножения, нужно найти четвёрку в левом столбце и восьмёрку в верхней строке, провести от 4 горизонтальную линию и от 8 вертикальную. Клетка, на которой линии встречаются, является произведением (в данном случае 32).

×	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	12	14	16	18	20
3	3	6	9	12	15	18	21	24	27	30
4	4	8	12	16	20	24	28	32	36	40
5	5	10	15	20	25	30	35	40	45	50

Помимо широко известного применения классической таблицы умножения для выработки практических навыков умножения натуральных чисел, её можно использовать в некоторых математических доказательствах, например, при выводе формулы суммы кубов натуральных чисел или получении подобного выражения для суммы квадратов^[9].

Наряду с таблицей умножения, в некоторых случаях бывают удобны таблицы сложения.

Таблица Кэли — в общей алгебре, таблица, которая описывает структуру конечных алгебраических систем с одной бинарной операцией. Названа в честь английского математика Артура Кэли. Имеет важное значение в дискретной математике, в частности, в теории групп, в которой в качестве операций рассматриваются умножение и сложение. Таблица позволяет определить, является ли группа абелевой, найти центр группы и обратные элементы по отношению к другим элементам в этой группе.

В высшей алгебре таблицы Кэли могут также использоваться для определения бинарных операций в полях, кольцах и других алгебраических структурах. Также они удобны при проведении действий в данных структурах.

Модулярная арифметика[править | править код]

Все остатки от деления на натуральное число образуют кольцо, а от деления на простое число — поле. Это иллюстрируется таблицами умножения:

Таблица умножения в кольце вычетов по модулю 8

×	0	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6	7
2	0	2	4	6	0	2	4	6
3	0	3	6	1	4	7	2	5
4	0	4	0	4	0	4	0	4
5	0	5	2	7	4	1	6	3
6	0	6	4	2	0	6	4	2
7	0	7	6	5	4	3	2	1

Таблица умножения в поле вычетов по модулю 5

×	0	1	2	3	4
0	0	0	0	0	0
1	0	1	2	3	4
2	0	2	4	1	3
3	0	3	1	4	2
4	0	4	3	2	1

1. ↑ ^{1 2} Jane Qiu. Ancient times table hidden in Chinese bamboo strips (англ.) // Nature : journal. — 2014. — 7 January. — DOI:10.1038/nature.2014.14482.
2. ↑ Например, в Farrar, John. An Elementary Treatise on Arithmetic (англ.).
3. ↑ Maher, David W.; Makowski, John F. Literary evidence for Roman arithmetic with fractions (англ.) // Classical Philology. — 2001. — No. 4 (96). — P. 383.
4. ↑ Депман И. А. История арифметики. Пособие для учителей. — М.: Государственное учебно-педагогическое издательство Министерства Просвещения РСФСР, 1959. — С. 196—198. — 28 000 экз.
5. ↑ Считание удобное : Таблица умножения — карточка электронного каталога РГБ
6. ↑ Считание удобное : Таблица умножения — карточка каталога Научной библиотеки МГУ
7. ↑ Leslie, John. The Philosophy of Arithmetic; Exhibiting a Progressive View of the Theory and Practice of Calculation, with Tables for the Multiplication of Numbers as Far as One Thousand (англ.). — Edinburgh: Abernethy & Walker, 1820.
8. ↑ Children must learn times tables by age nine… // Daily Mail, 17.12.2011
9. ↑ Роу С. Геометрические упражнения с куском бумаги. — 2-е изд. — Одесса: Матезис, 1923. — С. 68—72.

Арифметика — Википедия

Арифме́тика (др.-греч. ἀριθμητική, arithmētikḗ — от ἀριθμός, arithmṓs «число») — раздел математики, изучающий числа, их отношения и свойства. Предметом арифметики является понятие числа (натуральные, целые, рациональные, вещественные, комплексные числа) и его свойства. В арифметике рассматриваются измерения, вычислительные операции (сложение, вычитание, умножение, деление) и приёмы вычислений. Изучением свойств отдельных целых чисел занимается высшая арифметика, или теория чисел. Теоретическая арифметика уделяет внимание определению и анализу понятия числа, в то время как формальная арифметика оперирует логическими построениями предикатов и аксиом. Арифметика является древнейшей и одной из основных математических наук; она тесно связана с алгеброй, геометрией и теорией чисел^[1][2].

Причиной возникновения арифметики стала практическая потребность в счёте и вычислениях, связанных с задачами учёта при централизации сельского хозяйства. Наука развивалась вместе с усложнением задач, требующих решения. Большой вклад в развитие арифметики внесли греческие математики — в частности, философы-пифагорейцы, пытавшиеся с помощью чисел постичь и описать все закономерности мира.

В Средние века арифметику относили, вслед за неоплатониками, к числу так называемых семи свободных искусств. Основными областями практического применения арифметики тогда были торговля, навигация, строительство. В связи с этим особое значение получили приближённые вычисления иррациональных чисел, необходимые, в первую очередь, для геометрических построений. Особенно бурно арифметика развивалась в Индии и странах ислама, откуда новейшие достижения математической мысли проникли в Западную Европу; Россия знакомилась с математическими знаниями «и от греков, и от латин».

С наступлением Нового времени мореходная астрономия, механика, усложнившиеся коммерческие расчёты выдвинули новые требования к технике вычислений и дали толчок к дальнейшему развитию арифметики. В начале XVII века Непер изобрёл логарифмы, а затем Ферма выделил теорию чисел в самостоятельный раздел арифметики. К концу века сформировалось представление об иррациональном числе как о последовательности рациональных приближений, а в течение следующего столетия благодаря трудам Ламберта, Эйлера, Гаусса арифметика включила в себя операции с комплексными величинами, приобретя современный вид.

Последующая история арифметики ознаменована критическим пересмотром её основ, попытками дедуктивного её обоснования. Теоретические обоснования представления о числе связаны, в первую очередь, со строгим определением натурального числа и аксиомами Пеано, сформулированными в 1889 году. Непротиворечивость формального построения арифметики была показана Генценом в 1936 году.

Основам арифметики издавна и неизменно уделяется большое внимание в начальном школьном образовании.

Предметом арифметики являются числовые множества, свойства чисел и действия над числами^[3]. К ней также относят вопросы, связанные с техникой счёта, измерениями^[4], происхождением и развитием понятия числа^[1]. Арифметика изучает, в первую очередь, натуральные числа и дроби^[5]. На основе аксиоматической структуры множества натуральных чисел осуществляется построение других числовых множеств, включая целые, действительные и комплексные числа, проводится их анализ^[1]. Иногда в рамках арифметики рассматривают также кватернионы и другие гиперкомплексные числа. Вместе с тем, из теоремы Фробениуса следует, что расширение понятия числа за пределы комплексной плоскости без потери каких-либо его арифметических свойств невозможно^[6][7].

К основным действиям над числами относят сложение, вычитание, умножение и деление^[3], реже — возведение в степень, извлечение корня^[4] и решение численных уравнений^[3]. Исторически список арифметических действий также включал собственно счёт, удвоение (помимо умножения), деление на два и деление с остатком (помимо деления), поиск суммы арифметической и геометрической прогрессий^[8]. Джон Непер в своей книге «Логистическое искусство» разделил арифметические действия по ступеням: на низшей ступени находятся сложение и вычитание, на следующей — умножение и деление, далее — возведение в степень и извлечение корней^[9]. Известный методист И. В. Арнольд к операциям третьей ступени относил также логарифмирование^[10]. Традиционно арифметикой называют выполнение операций над различными объектами, как то: «арифметика квадратичных форм», «арифметика матриц»^[1].

Собственно математические расчёты и измерения, необходимые для практических нужд (пропорции, проценты, тройное правило), относят к низшей, или практической арифметике^[3], в то время как логический анализ понятия числа относят к теоретической арифметике^[1]. Свойства целых чисел, деление их на части, построение непрерывных дробей являются составной частью теории чисел^[1], которую долгое время считали высшей арифметикой^[3]. Арифметика также тесно связана с алгеброй, которая изучает собственно операции без учёта особенностей и свойств чисел^[1][11]. Такие арифметические действия, как возведение в степень и извлечение корней, являются технической частью алгебры. В этой связи, вслед за Ньютоном и Гауссом, алгебру принято считать обобщением арифметики^[3][4]. Вообще говоря, чётких границ между арифметикой, элементарной алгеброй и теорией чисел не существует. В БСЭ сказано: «Алгебра изучает, пользуясь буквенными обозначениями, общие свойства числовых систем и общие методы решения задач при помощи уравнений; арифметика занимается приёмами вычислений с конкретно заданными числами, а в своих более высоких областях (см. Чисел теория) — более тонкими индивидуальными свойствами чисел»^[12].

Как и прочие академические дисциплины, арифметика сталкивается с принципиальными методологическими проблемами; для неё необходимо исследование вопросов непротиворечивости и полноты аксиом^[3]. Логическими построениями формальной системы предикатов и аксиом арифметики занимается формальная арифметика^[2].

Порядковый счёт, натуральные числа[править | править код]

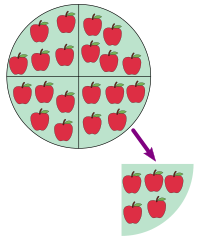
Одно яблоко, два яблока, три яблока. Натуральные числа

Простейшим арифметическим понятием является порядковый счёт. Объектом счёта служат различные элементы или их множества, например, яблоки и корзины яблок. С помощью порядкового счёта можно пронумеровать элементы и обозначить их общее количество.

Порядковый счёт связан со счётом группами, содержащими определённое равное количество элементов — например, счёт десятками яблок. Обычно это пальцы на двух руках (основание равно 10{\displaystyle 10}), но в исторических источниках встречаются группировки по 5,11,12,20,40,60,80{\displaystyle 5,11,12,20,40,60,80}. Количество элементов в группе служит основанием для системы счисления^[11].

Числовой ряд, получаемый при счёте, называют натуральным, а его элементы — натуральными числами. Понятие натурального ряда впервые появилось в работах греческого математика Никомаха в I веке н. э., а натурального числа — у римского автора Боэция в конце V — начале VI века. Всеобщее употребление термина начинается с работ Д’Аламбера в XVIII веке. Архимед в своей работе «Псаммит» указал, что числовой ряд можно продолжать неограниченно, но вместе с тем заметил, что для реальных задач достаточно небольшого отрезка^[13]. Деление натуральных чисел на чётные и нечётные приписывают пифагорейцам, оно также присутствует в египетском папирусе Ринда. Пифагорейцы также определили простые и составные числа^[14].

Сложение, умножение, возведение в степень[править | править код]

3+2=5{\displaystyle 3+2=5}

Для натуральных чисел естественным образом определены операции сложения и умножения. При объединении двух наборов, содержащих некоторое количество предметов, новый набор будет иметь столько предметов, сколько было в первых двух наборах вместе. Если первый набор содержал 3{\displaystyle 3} предмета, а второй — 2{\displaystyle 2} предмета, то их сумма будет содержать 2+3=5{\displaystyle 2+3=5} предметов. Указанное действие носит название сложения и является простейшей бинарной операцией^[4]. Для проверки корректности суммы таблицу сложения знать не обязательно, достаточно пересчитать предметы^[15].

Многократное сложение элементов нескольких одинаковых множеств не зависит от порядка этих множеств, что позволило определить другую бинарную операцию — умножение^[4]. Помимо умножения, в древности существовало отдельное арифметическое действие — удвоение, или умножение на два^[16].

По аналогии с определением умножения через сложение, многократное умножение позволяет определить операцию возведения в степень.

Основные законы арифметики[править | править код]

Переместительный закон умножения

Про свойства этих операций сформулированы пять законов, которые считаются основными законами арифметики^[17]:

• Коммутативность: переместительный закон сложения гласит, что от перемены мест слагаемых сумма не меняется. Аналогичный закон известен и для умножения, но он, конечно, говорит о множителях и произведении. Эти законы можно выразить в алгебраической форме с помощью буквенных обозначений:

a+b=b+a{\displaystyle a+b=b+a}

a⋅b=b⋅a{\displaystyle a\cdot b=b\cdot a}

• Ассоциативность: сочетательный закон сложения гласит, что складывая несколько слагаемых, можно группировать их в любом порядке. Аналогичный закон для умножения говорит о перемножении множителей. Эти законы также можно выразить в алгебраической форме:

(a+b)+c=a+(b+c){\displaystyle (a+b)+c=a+(b+c)}

(a⋅b)⋅c=a⋅(b⋅c){\displaystyle (a\cdot b)\cdot c=a\cdot (b\cdot c)}

(a+b)⋅c=a⋅c+b⋅c{\displaystyle (a+b)\cdot c=a\cdot c+b\cdot c}

Помимо основных законов арифметики, для натуральных чисел выполняются также законы монотонности сложения и умножения^[18][19], в алгебраической форме записываемые так:

a+b>a+c{\displaystyle a+b>a+c} при b>c{\displaystyle b>c};

a⋅b>a⋅c{\displaystyle a\cdot b>a\cdot c} при b>c{\displaystyle b>c} и a>0{\displaystyle a>0}.

Термин «коммутативный» для переместительного закона ввёл в 1814 году французский математик Сервуа. Термин «ассоциативный» для сочетательного закона ввёл в 1853 году Гамильтон^[17].

Пуанкаре рассматривал все арифметические операции и законы с точки зрения интуиции. Утверждая, что законы очевидным образом выполняются для малых чисел, и используя правило индукции, можно прийти к выводу, что они выполняются для всех чисел. При другом подходе интуитивно выполнимыми считаются не все, а только простейшие законы, в то время как дальнейшее доказательство связано с логическими построениями^[20]. Очевидными принимались переместительный и сочетательный законы^[17]. Распределительный, или дистрибутивный закон в своих «Началах» доказывал ещё Евклид, используя геометрический метод^[21].

Операция возведения в степень уже не коммутативна и не ассоциативна, у неё свои правила. Основные правила выполнения этой операции при положительных степенях очевидным образом следуют из её определения^[4]. В алгебраической форме они могут быть записаны следующим образом:

• Дистрибутивность — распределительный закон для операции возведения в степень:

an+m=anam{\displaystyle a^{n+m}=a^{n}a^{m}}

• он же, в случае вычитания, приобретает форму дроби:

an−m=anam,n>m{\displaystyle a^{n-m}={a^{n} \over {a^{m}}},\quad n>m}

• Повторное возведение в степень раскрывается как перемножение степеней:

(an)m=anm{\displaystyle \left(a^{n}\right)^{m}=a^{nm}}.

Обратные операции[править | править код]

У всех операций арифметики есть обратные: у сложения — вычитание, у умножения — деление, у возведения в степень — арифметический корень и логарифм. То, что у сложения и умножения по одной обратной операции, несмотря на их бинарность, объясняется их коммутативностью.

Вычитание: отрицательные числа[править | править код]

5−2=3{\displaystyle 5-2=3}

Вычитание — это операция, обратная сложению: разностью двух чисел 5{\displaystyle 5} и 2{\displaystyle 2} является x{\displaystyle x} из уравнения 2+x=5{\displaystyle 2+x=5}^[4]. Обозначается операция вычитания знаком «−» и записывается в виде 5−2=3{\displaystyle 5-2=3}. Для выполнения операции применяли два приёма: отсчитывание от уменьшаемого числа единиц вычитаемого или подбор такого числа, прибавление которого к вычитаемому давало бы уменьшаемое^[16].

Операция вычитания, если её применять ко всем парам натуральных чисел, а не только к таким, которые могли бы быть суммой и слагаемым в рамках операции сложения, позволяет выйти за пределы натурального ряда, то есть разность двух натуральных чисел не обязательно является натуральным числом — в результате вычитания может получиться ноль или вовсе отрицательное число. Отрицательные числа уже невозможно рассматривать как количество предметов, на числовой оси они расположены левее ноля. Множество чисел, получившееся добавлением к натуральным числам отрицательных чисел и числа ноль, носит название множества целых чисел. Ноль и множество натуральных чисел называются неотрицательные целые числа^[4]. При умножении, чтобы определить, положительным или отрицательным будет произведение чисел, используют «правило знаков»^[22].

Отрицательные числа считали ненастоящими и бессмысленными очень многие математики вплоть до XIX века, что, однако, не мешало их повсеместному формальному использованию. Впервые понятие отрицательных чисел появилось в Индии, где их толковали как «долг» (положительные числа — «имущество»). Распространение же отрицательные числа получили только в XVII веке^[23]. Термин «вычитание» появился ещё у Боэция, термины «вычитаемое» и «уменьшаемое» ввёл в обиход Вольф в 1716 году, «разность» — Видман в 1489 году^[16]. Современное обозначение знаками «+» и «−» было также введено Видманом в конце XV века.

Деление: рациональные числа[править | править код]

Обратной к операции умножения является операция деления. Первое определение деления — это поиск числа, которое содержится в делимом столько раз, сколько единиц содержится в делителе. Такое определение дано в учебниках арифметики XIV века — например, 20:4=5{\displaystyle 20:4=5}. Деление считалось очень сложной и громоздкой операцией. Современный способ деления, использующий частичные произведения делителя на отдельные разряды частного (деление столбиком), представлен в итальянском манускрипте 1460 года^[16].

Для натуральных чисел, не являющихся множителем и произведением, известна операция деление с остатком (а определение собственно остатка от деления также называется деление по модулю). Также существует множество способов, упрощающих деление в различных частных случаях или позволяющих проверить делимость на то или иное число. Например:

• число без остатка делится на два, если его последняя цифра при десятичной записи делится на два;
• число без остатка делится на три, если сумма всех его цифр при десятичной записи делится на три;
• число без остатка делится на десять, если его последняя цифра при десятичной записи — ноль.

Операция деления, если делить не только те числа, которые можно получить умножением натуральных чисел, и при этом не выделять остаток, так же как и вычитание, позволяет выйти за пределы множества натуральных чисел. При делении могут получиться дроби, которые невозможно без остатка сократить до целого. Числа, соответствующие таким дробям, называются рациональными. За счёт осознания основанных на делении рациональных чисел происходит ещё одно расширение перечня известных видов чисел. Исторически сначала появилось понятие дроби, а затем отрицательного числа^[24]. Такой же порядок принят в школьном курсе^[25].

Используется две формы записи дробей — в виде числителя и знаменателя, разделённых горизонтальной или наклонной чертой и часто сокращаемых до минимальных чисел, и в виде цифр дробной части, размещаемых после знака-разделителя целой и дробной части в позиционной записи числа. Например, результат деления 10 на 20 может быть записан как 1020=10/20=5/10=1/2=0,5{\displaystyle {\frac {10}{20}}=10/20=5/10=1/2=0{,}5}.

Извлечение корня: иррациональные и комплексные числа[править | править код]

Одна из двух обратных для возведения в степень операций — извлечение корня, или поиск числа, которое при возведении в соответствующую степень будет давать известный результат. То есть, говоря алгебраически, это поиск корня для уравнения вида xa=b{\displaystyle x^{a}=b}. Вторая обратная операция — поиск логарифма (корня для уравнения вида ax=b{\displaystyle a^{x}=b}). К арифметике, как правило, относят лишь вычисление корня второй степени — квадратного корня.

Операция вычисления корня, если выполнять её не только для тех чисел, которые можно получить возведением в степень натуральных чисел, так же как и остальные обратные операции, позволяет выйти за пределы множества натуральных чисел. Числа, которые получаются при этом, часто не могут быть представлены в виде конечных рациональных дробей и поэтому названы иррациональными. Множество чисел, полученное добавлением к рациональным числам иррациональных, назвали вещественными или действительными.

Ещё в Древней Греции было известно о существовании несоизмеримых отрезков, как минимум, на примере сторон и диагонали квадрата со стороной, принятой за единицу, и проводились попытки получить для них точные числовые значения, что нашло отражение в «Началах» Евклида. Вещественные числа стали объектом исследований только в XVII—XVIII веках. Во второй половине XIX века Дедекинд, Кантор и Вейерштрасс сформулировали свои конструктивные способы определения вещественного числа^[26].

Для операции извлечение корня известно следующее правило^[4]:

• anm=anm{\displaystyle a^{n \over m}={\sqrt[{m}]{a^{n}}}}.

Дальнейшее расширение множества чисел было связано с невозможностью извлечения квадратного корня из отрицательного числа. С подобной задачей сталкивались в древности при решении квадратных уравнений, и такие уравнения просто считали неразрешимыми. В первой половине XVI века стали выражать решения таких уравнений через корни из отрицательных чисел и называть такие корни «мнимыми», «невозможными», «воображаемыми» и т. д.^[27]

Практическая сторона арифметики включает в себя методы, схемы и алгоритмы для осуществления точных арифметических действий, в том числе использование счётных машин и других устройств, а также различные приёмы приближённых вычислений, которые появились в связи с невозможностью получить точный результат при некоторых измерениях и позволяют определить его порядок, то есть первые значащие цифры^[28].

Точные методы[править | править код]

Начиная с XV века предлагались разные алгоритмы для осуществления арифметических операций над многозначными числами, которые отличаются характером записи промежуточных вычислений^[1]. Арифметические алгоритмы построены на действующей позиционной системе счисления, когда любое положительное действительное число x{\displaystyle x} единственным образом представимо в виде

x=(an−1an−2…a1a0,a−1a−2…)b=∑k=−∞n−1akbk{\displaystyle x=(a_{n-1}a_{n-2}\dots a_{1}a_{0},a_{-1}a_{-2}\dots )_{b}=\sum _{k=-\infty }^{n-1}a_{k}b^{k}}, где a{\displaystyle a} — очередная цифра записи числа x{\displaystyle x}, b{\displaystyle b} — основание системы счисления, n{\displaystyle n} — число разрядов целой части числа x{\displaystyle x}.

Все действия над числами используют таблицы сложения и умножения до десяти и основные арифметические законы. В качестве иллюстрации известный популяризатор науки Клейн приводит следующий пример:

7⋅12=7⋅(10+2)=70+14=70+(10+4)=(70+10)+4=80+4=84,{\displaystyle 7\cdot 12=7\cdot (10+2)=70+14=70+(10+4)=(70+10)+4=80+4=84,}

в котором используются распределительный и сочетательный законы^[29].

Потребность в быстрых и точных вычислениях привела к созданию простейших счётных устройств: абака, суаньпаня, юпаны или счёт. Следующим шагом было создание Отредом в 1622 году логарифмической линейки, которая позволяет производить умножение и деление^[30].

Компьютерная арифметика[править | править код]

Копия вычислительной машины Шиккарда

Кнут считал арифметические действия «уделом компьютеров»^[31]. Первые вычислительные машины, которые позволяли механизировать четыре арифметических действия, были сконструированы в XVII веке. «Арифметическая машина» Шиккарда, как он сам её называл, была построена в 1623 году. Операции сложения и вычитания производились посредством вращения цилиндров, специальные цилиндры были также для умножения и деления. Кроме того, машина могла переносить десятки. Машина Паскаля была разработана им в 1642 году для помощи отцу в выполнении финансовых расчётов. Она имела тот же принцип действия, что и машина Шиккарда. Основную часть машины составлял механизм переноса десятков. Вместе с тем, ремесленное изготовление таких машин всё ещё оставалось невыгодным^[32]. Попытки усовершенствовать арифмометр продолжались весь XVIII век, но только в XIX веке применение арифмометров получило широкое распространение^[33].

В XX веке на смену арифмометрам пришли электронные вычислительные машины. В их основе лежат алгоритмы, которые используют наименьшее число элементарных операций для выполнения арифметических действий^[1]. Компьютерная арифметика включает алгоритмы выполнения операций над числами с плавающей запятой, дробями и очень большими числами^[31].

Измерение[править | править код]

Помимо предметов, которые подлежат пересчёту, существуют предметы, которые можно измерить — в первую очередь, это длина и масса^[34].

Как и при счёте, первыми мерами длины у человека были пальцы рук. Затем расстояние стали мерить шагами, двойными шагами, милями (тысяча двойных шагов), стадиями. Кроме того, для измерения длины использовали локти, ладони, сажени, дюймы. В различных регионах устанавливались свои системы мер, которые редко были кратны десяти^[35]. Многообразие мер, в частности, позволяло обойтись без использования дробей^[36][37]. Торговая арифметика включала в себя умение оперировать величинами (денежными единицами, единицами мер и весов) в недесятичной системе счисления^[38].

В конце XVIII века французским революционным правительством на основании временного, а затем и архивного (законом 10 декабря 1799 года) метра была принята метрическая система мер (окончательно Франция перешла на неё с 1 января 1840 года). Вместе с метром был определён и килограмм. В основе метрической системы лежит десятичная система. Именно это обстоятельство позволило ей распространиться почти на весь мир (исключение составляют Великобритания и США). По указу специального Международного бюро мер и весов, расположенного в Париже, в 1888 году из сплава платины и иридия были изготовлены международный метр и международный килограмм — эталоны мер и весов. Помимо мер времени и угла, все остальные единицы мер также связаны с десятичной системой^[39].

Приближённые методы[править | править код]

Исторически приближённые вычисления возникли при поиске длины диагонали единичного квадрата, но получили широкое распространение при переходе к десятичной системе и использовании конечных десятичных дробей вместо иррациональных чисел и чисел, выраженных бесконечной периодической дробью^[40].

Для оценочных вычислений используют, в первую очередь, законы монотонности. Например, чтобы определить порядок произведения 567⋅134{\displaystyle 567\cdot 134}, можно воспользоваться следующей оценкой: 560⋅130<567⋅134<570⋅140{\displaystyle 560\cdot 130<567\cdot 134<570\cdot 140}^[29].

Теория чисел, или высшая арифметика, — это наука о целых числах, которая возникла из арифметических задач, связанных с делимостью чисел^[41]. Элементарная теория чисел имеет дело с проблемами, которые решают элементарными методами, обычно без использования мнимых чисел. К ней относят теорию делимости, теорию сравнений, неопределённые уравнения, разбиение на слагаемые, приближения рациональными числами, цепные дроби^[42]. Основная теорема арифметики — о разбиении числа на простые сомножители единственным образом — также является частью элементарной теории чисел^[43].

Отдельные подклассы целых чисел, такие как простые, составные, квадратные, совершенные числа, были выделены ещё древними греками. Они вывели формулы для определения пифагоровых троек, наибольшего общего делителя, показали бесконечность числа простых чисел. Диофант провёл систематизацию задач, связанных с целыми числами. Работы Диофанта были продолжены Ферма в XVII и Эйлером в XVIII веке. Ферма занимался решением уравнений в целых числах и сформулировал без доказательства малую и великую теоремы Ферма. Эйлер, продолжая исследования Ферма, доказал малую теорему и частный случай великой теоремы Ферма. Он впервые применил математический анализ для решения задач теории чисел и создал аналитическую теорию чисел. Эйлер определил производящие функции, на основе которых были построены круговой метод и метод тригонометрических сумм^[41].

В настоящее время, помимо элементарной и аналитической теории чисел, существуют такие разделы, как аддитивная, алгебраическая, вероятностная, метрическая теория чисел^[41].

В современной математике построение теории представляет собой выбор базовых свойств, или аксиом, из которых требуется вывести все положения теории, или теоремы, с помощью общепринятой логики^[44]. Теоретическое построение арифметики оперирует алгебраическими понятиями. Сложность выделения основных определений арифметики связана с простотой её начальных положений. Пеано, опасаясь ложного ассоциативного ряда при использовании слов, проводил доказательства исключительно на языке символов, опираясь только на принятые им предварительные положения. Кантор и Дедекинд связали числа с множествами и абстрактными отношениями над ними^[20]. Теория множеств рассматривает арифметические действия как особые отн

Умножение или произведение натуральных чисел их свойства

Умножение натурального числа.

Разберем понятие умножение на примере:

Туристы находились в пути три дня. Каждый день они проходили одинаковый путь по 4200 м. Какое расстояние они прошли за три дня? Решите задачу двумя способами.

Решение:
Рассмотрим задачу подробно.

В первый день туристы прошли 4200м. Во-второй день тот же самый путь прошли туристы 4200м и в третий день – 4200м. Запишем математическим языком:
4200+4200+4200=12600м.
Мы видим закономерность число 4200 повторяется три раза, следовательно, можно сумму заменить умножением:
4200⋅3=12600м.
Ответ: туристы за три дня прошли 12600 метров.

Рассмотрим пример:

Чтобы нам не писать длинную запись можно записать ее в виде умножения. Число 2 повторяется 11 раз поэтому пример с умножением будет выглядеть так:
2⋅11=22

Подведем итог. Что такое умножение?

Умножение – это действие заменяющее повторение n раз слагаемого m.

Запись m⋅n и результат этого выражения называют произведением чисел, а числа m и n называют множителями.

Рассмотрим сказанное на примере:
7⋅12=84
Выражение 7⋅12 и результат 84 называются произведением чисел.
Числа 7 и 12 называются множителями.

В математике есть несколько законов умножения. Рассмотрим их:

Переместительный закон умножения.

Рассмотрим задачу:

Мы отдали по два яблока 5 своим друзьям. Математически запись будет выглядеть так: 2⋅5.
Или мы отдали по 5 яблок двум своим друзьям. Математически запись будет выглядеть так: 5⋅2.
В первом и втором случаем мы раздадим одинаковое количество яблок равное 10 штукам.

Если мы умножим  2⋅5=10 и 5⋅2=10, то результат не поменяется.

2⋅5=5⋅2

Свойство переместительного закона умножения:
От перемены мест множителей произведение не меняется.
m⋅n=n⋅m

Сочетательный закон умножения.

Рассмотрим на примере:

(2⋅3)⋅4=6⋅4=24 или 2⋅(3⋅4)=2⋅12=24 получим,
(2⋅3)⋅4=2⋅(3⋅4)
(a⋅b) ⋅c=a⋅(b⋅c)

Свойство сочетательного закона умножения:
Чтобы число умно­жить на про­из­ве­де­ние двух чисел, можно его сна­ча­ла умно­жить на пер­вый мно­жи­тель, а затем по­лу­чен­ное про­из­ве­де­ние умно­жить на вто­рой.

Меняя несколько множителей местами и заключая их в скобки, результат или произведение не изменится.

Эти законы верны для любых натуральных чисел.

Умножение любого натурального числа на единицу.

Рассмотрим пример:
7⋅1=7 или 1⋅7=7
a⋅1=a или 1⋅a=a
При умножении любого натурального числа на единицу произведением будет всегда тоже число.

Умножение любого натурального числа на нуль.

6⋅0=0 или  0⋅6=0
a⋅0=0 или 0⋅a=0
При умножении любого натурального числа на нуль произведение будет равно нулю.

Вопросы к теме “Умножение”:

Что такое произведение чисел?
Ответ: произведением чисел или умножение чисел называется выражение m⋅n, где m – слагаемое, а n – число повторений этого слагаемого.

Для чего нужно умножение?
Ответ: чтобы не писать длинное сложение чисел, а писать сокращенно. Например, 3+3+3+3+3+3=3⋅6=18

Что является результатом умножения?
Ответ: значение произведения.

Что означает запись умножения  3⋅5?
Ответ: 3⋅5=5+5+5=3+3+3+3+3=15

Если умножить миллион на нуль, чему будет равно произведение?
Ответ: 0

Пример №1:
Замените сумму произведением: а) 12+12+12+12+12  б)3+3+3+3+3+3+3+3+3
Ответ: а)12⋅5=60 б) 3⋅9=27

Пример №2:
Запишите в виде произведения: а) а+а+а+а б) с+с+с+с+с+с+с
Решение:
а)а+а+а+а=4⋅а
б) с+с+с+с+с+с+с=7⋅с

Задача №1:
Мама купила 3 коробки конфет. В каждой коробке по 8 конфет. Сколько конфет купила мама?
Решение:
В одной коробке 8 конфет, а у нас таких коробок 3 штуки.
8+8+8=8⋅3=24 конфеты
Ответ: 24 конфеты.

Задача №2:
Учительница рисования сказала приготовить своим восемью ученикам по семь карандашей на урок. Сколько всего карандашей вместе было у детей?
Решение:
Можно посчитать суммой задачу. У первого ученика было 7 карандашей, у второго ученика было 7 карандашей и т.д.
7+7+7+7+7+7+7+7=56
Запись получилась неудобная и длинная, заменим сумму на произведение.
7⋅8=56
Ответ 56 карандашей.

Умножение — это… Что такое Умножение?

Умножение — одно из четырёх основных арифметических действий, бинарная математическая операция, в которой первый аргумент складывается столько раз, сколько показывает второй. В арифметике под умножением понимают краткую запись суммы одинаковых слагаемых. Например, запись 5*3 обозначает «сложить три раза пятёрку (три пятёрки)», то есть является просто краткой записью для 5+5+5. Результат умножения называется произведением, а умножаемые числа — множителями или сомножителями. Существуют также таблицы умножения.

Запись

Умножение обозначается крестиком , звёздочкой или точкой . Записи

обозначают одно и то же. Знак умножения часто пропускают, если это не приводит к путанице. Например, вместо обычно пишут .

Если сомножителей много, то часть их можно заменить многоточием. Например, произведение целых чисел от 1 до 100 может быть записано как .

В буквенной записи применяется также символ произведения: . Например, произведение можно записать кратко так: .

См. также

Умножение — это… Что такое Умножение?

Умножение — одно из четырёх основных арифметических действий, бинарная математическая операция, в которой первый аргумент складывается столько раз, сколько показывает второй. В арифметике под умножением понимают краткую запись суммы одинаковых слагаемых. Например, запись 5*3 обозначает «сложить три раза пятёрку (три пятёрки)», то есть является просто краткой записью для 5+5+5. Результат умножения называется произведением, а умножаемые числа — множителями или сомножителями. Существуют также таблицы умножения.

Запись

Умножение обозначается крестиком , звёздочкой или точкой . Записи

обозначают одно и то же. Знак умножения часто пропускают, если это не приводит к путанице. Например, вместо обычно пишут .

Если сомножителей много, то часть их можно заменить многоточием. Например, произведение целых чисел от 1 до 100 может быть записано как .

В буквенной записи применяется также символ произведения: . Например, произведение можно записать кратко так: .

См. также

умножение — это… Что такое умножение?

УМНОЖЕНИЕ — арифметическое действие. Обозначается точкой . или знаком ? (в буквенном исчислении знаки умножения опускаются). Умножение целых положительных чисел (натуральных чисел) есть действие, позволяющее по двум числам а (множимому) и b (множителю) найти …   Большой Энциклопедический словарь

умножение — Приумножение, размножение, увеличение, накопление, скопление, рост, нарастание, приращение, усиление, собирание, возвышение, удвоение. См …   Словарь синонимов

УМНОЖЕНИЕ — УМНОЖЕНИЕ, умножения, мн. нет, ср. 1. Действие по гл. умножить умножать и состояние по гл. умножиться умножаться. Умножение трех на два. Умножение доходов. 2. Арифметическое действие, повторение данного числа в качестве слагаемого столько раз,… …   Толковый словарь Ушакова

Умножение — Умножение  одно из четырёх основных арифметических действий, бинарная математическая операция, в которой первый аргумент складывается столько раз, сколько показывает второй. В арифметике под умножением понимают краткую запись суммы… …   Википедия

УМНОЖЕНИЕ — УМНОЖЕНИЕ, арифметическая операция, обозначаемая символом (по сути представляет собой многократное СЛОЖЕНИЕ). Например, a3в можно записать иначе как а+а+…+а , где в показывает, сколько раз повторяется операция сложения. В выражении а3в («а»… …   Научно-технический энциклопедический словарь

УМНОЖЕНИЕ — УМНОЖЕНИЕ, я, ср. 1. см. множить, ся. 2. Математическое действие, посредством к рого из двух чисел (или величин) получается новое число (или величина), к рое (для целых чисел) содержит слагаемым первое число столько раз, сколько единиц во втором …   Толковый словарь Ожегова

умножение — — [[http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23]] Тематики защита информации EN multiplication …   Справочник технического переводчика

УМНОЖЕНИЕ — основное арифметическое действие, с помощью которого по двум заданным числам (см.) и (см.) находят третье число (произведение), которое обозначают а∙b или. axb. Между буквами знак умножения обычно не ставят: вместо а∙b пишут ab. Если множимое и… …   Большая политехническая энциклопедия

умножение — ▲ алгебраическая функция ↑ прямое соответствие, от (чего), аргумент (функции) &LT; &GT; математическое деление умножение функция, находящаяся в прямом соответствии от аргументов. умножать. множить. перемножить. помножить …   Идеографический словарь русского языка

умножение — daugyba statusas T sritis automatika atitikmenys: angl. multiplication vok. Multiplikation, f rus. умножение, n pranc. multiplication, f …   Automatikos terminų žodynas