Умножение целых чисел: правила, примеры
В этом материале мы покажем, как правильно выполнять умножение целых чисел. Начнем, как всегда, с основных понятий и обозначений и выясним, какой смысл вкладывается в умножение двух целых чисел. Затем сформулируем правила, по которым перемножают целые положительные и целые отрицательные числа, а также числа, имеющие разные знаки. Как всегда, нашу мысль будем пояснять наглядными примерами решений задач. Далее рассмотрим те случаи, когда один из множителей нулевой или равен единице, посмотрим, как можно проверить верность результата, полученного после умножения, а в конце объясним, как правильно перемножать 3, 4 и большее количество целых чисел.
Основные определения при умножении целых чисел
При умножении целых чисел используются те же термины и знаки, о которых мы говорили ранее в статье об умножении натуральных чисел. У нас есть два множителя, которые являются целыми числами, результат, называемый произведением, и знак умножения в виде точки, звездочки или знака «x» (в целях единообразия в дальнейшем будем использовать точку).
Если обозначить множители и произведение буквами a, b и c, то действие умножения можем записать в виде равенства a·b=c. Само числовое выражение a·b тоже называется произведением. Произведение двух целых чисел также является целым числом.
В чем состоит смысл умножения целых чисел?
До этого мы уже объясняли смысл умножения на примере натуральных чисел. Произведение натуральных чисел a и b представляет собой сумму b слагаемых, каждое из которых равно a.
Целые положительные числа – это натуральные числа, поэтому смысл действия умножения для них точно такой же. В буквенном виде его также можно представить как

(значения a и b – целые положительные числа).
В принципе, этот смысл распространяется на все произведения, где одно слагаемое целое и положительное. Второе при этом также должно быть целым, однако оно может быть отрицательным или даже равным нулю. Так, схема умножения числа -3 на 5 буд
Как объяснить ребенку деление и умножение чисел

Лиана Хазиахметова
Далеко не все дети понимают деление и умножение с первого раза, поэтому родителям приходится дома подробнее разбирать эти процессы. Сегодня расскажем, как это сделать проще для ребенка. В книге «Как объяснить ребенку математику» объяснения строятся на визуальных принципах. Так школьнику будет понятнее, а родителю легче построить общение.
Умножение чисел
При умножении второе число показывает, сколько раз нужно сложить первое число с самим собой. На рисунке ниже в каждой шеренге стоят 13 человек, а всего шеренг 9. Чтобы подсчитать общее количество людей, нужно число 13 сложить само с собой 9 раз. Это и будет произведением чисел 13 на 9.
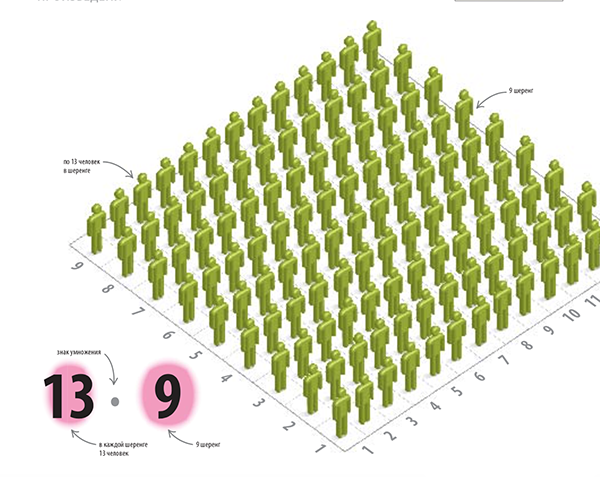
Иллюстрация из книги «Как объяснить ребенку математику»
Количество людей в шеренге (13) умножается на количество шеренг (9). Общее количество людей равно 117.
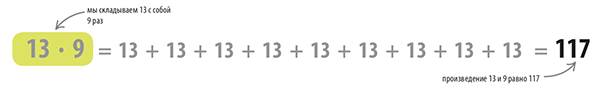
Не имеет значения, в каком порядке перемножаются числа: ответ будет одинаковым. Ниже показаны два способа, как можно вычислить произведение.
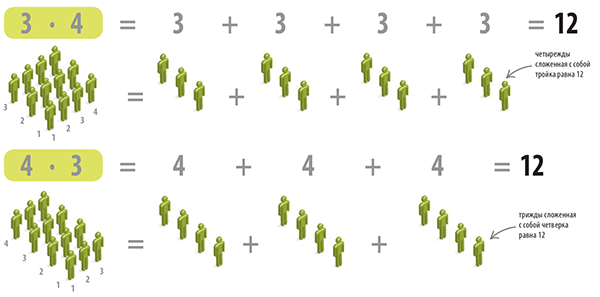
Некоторые числа легко умножать, зная особые приемы. Вот они.
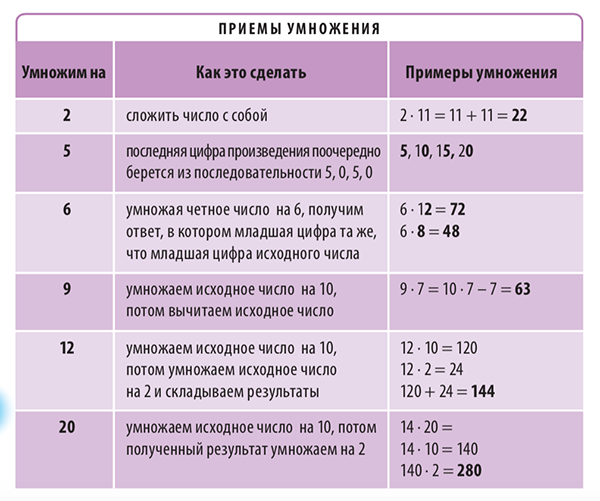
Таблица из книги «Как объяснить ребенку математику»
В таблице показаны приемы быстрого умножения на 2, 5, 6, 9, 12 и 20.
Деление чисел
Деление позволяет найти, сколько раз одно число содержится в другом. Процесс деления можно представить, например, так: если 10 монет раздать 2 людям, то каждый получит по 5 монет. Или так: 10 монет, разложенные в стопки по 2 монеты, дадут 5 стопок.
Деление одного числа (делимого) на другое (делитель) показывает, сколько делителей содержится в делимом. Например, при делении 10 на 2 мы находим, сколько чисел 2 содержится в числе 10. Результат деления называется частным.
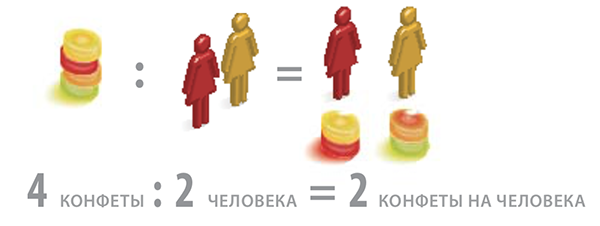
Деление как распределение. Из книги «Как объяснить ребенку математику»
Распределение чего-либо — это, по сути, операция деления. Так, если поровну распределить четыре конфеты между двумя людьми, у каждого из них будет по две конфеты.
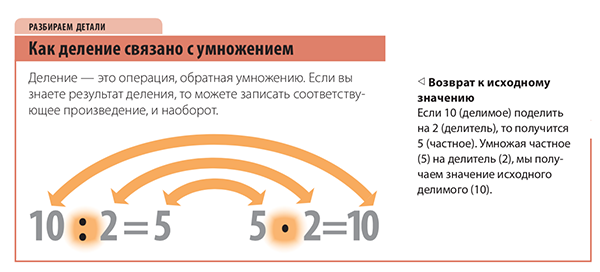
Деление и умножение лучше рассматривать параллельно, чтобы ребенок увидел взаимосвязь. В книге «Как объяснить ребенку математику» есть объяснения более сложных операций, например, деления с остатком, умножения в столбик и так далее. Если визуально показать, как это делается, ребенку легче будет усвоить материал.
Рабочие тетради на деление и умножение
Если ваш ребенок освоил азы деления и умножения, то сейчас ему нужна практика. Японская система Kumon предлагает рабочие тетради «Математика. Деление. Уровень 4»
и «Математика. Умножение. Уровень 4». Постепенно, решая все более сложные задачи, ребенок научится работать с большими цифрами. Ниже — пример одного из последних заданий тетради с делениями.
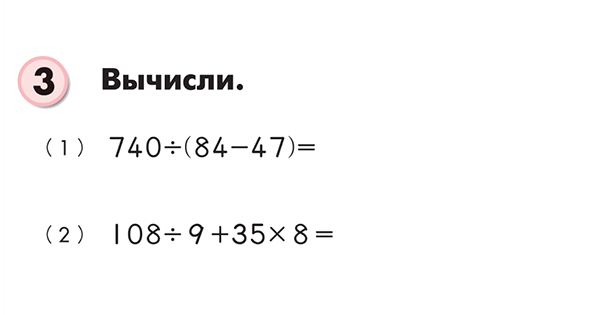
Пример из тетради «Математика. Деление. Уровень 4»
Такие примеры ребенок научится решать легко и быстро, если тренироваться регулярно и по принципу от простого к сложному. Задания нужно усложнять постепенно, тогда школьник будет учиться с чувством «я могу!».
По материалам книги «Как объяснить ребенку математику», рабочих тетрадей «Математика. Деление. Уровень 4» и «Математика. Умножение. Уровень 4».
Обложка поста: pixabay.com
Умножение и деление
Особенно сложны и трудны были в старину действия умножения и деления – особенно последнее.
«Умножение – мое мучение, а с делением – беда», — говорили в старину.
В глубокой древности и почти до восемнадцатого века русские люди в своих вычислениях обходились без умножения и деления: они применяли лишь два арифметических действия — сложение и вычитание, да ещё так называемые «удвоения» и «раздвоение». Сущность русского старинного способа умножения состоит в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам (последовательное раздвоение) при одновременном удвоении другого числа. Если в произведении, например 24∙5, множимое уменьшить в 2 раза («раздвоить»), а множитель увеличить в 2 раза («удвоить»), то произведение не изменится: 24∙5=12∙10=120
Пример:
32∙17
16∙34
8∙68
4∙136
2∙272
1∙544
Деление множимого продолжают до тех пор, пока в частном не получится 1, одновременно удваивая множитель. Последнее удвоенное число и дает искомый результат. Значит 32∙17=1∙544=544. В предлагаемом примере, все числа делятся на 2 без остатка.
А как быть, если деление на 2 происходит с остатком?
Пример:
21∙17
10∙34
5∙68
2∙136
1∙272
357
Если множимое не делится на 2, то от него сначала отнимается единица, а затем уже производится деление на 2. Строчки с четными множимыми вычеркиваются, а правые части строчек с нечетными множимыми складываются.
То есть 21∙17=(20+1)∙17=20∙17+1∙17.
Число 17 запомним (первая строка не вычеркивается), а произведение 20∙17 заменим равным ему произведением 10∙34. но произведение 10∙34, в свою очередь, можно заменить равным ему произведением 5∙68, поэтому вторая строка вычеркивается: 5∙68=(4+1) ∙68= 4∙68+68 Число 68 запомним (третья строка не вычеркивается), а произведение 4∙68 заменим ему равным произведением 2 ∙136. Но произведение 2∙136 можно заменить ему равным произведением 1∙272, поэтому четвертая строка вычеркивается. Значит, чтобы вычислить произведение 21∙17, нужно сложить 17.68.272 – правые части именно с нечетными множимыми.
Произведения же с четными множимыми всегда можно заменить с помощью раздвоения множимого и удвоения множителя равными им произведениями. Поэтому такие строчки исключаются из вычисления окончательного произведения.
Шло время. В ходу была одновременно чуть ли не дюжина различных способов умножения и деления – приемы один другого запутаннее, твердо запомнить которые не в силах был человек средних способностей.
В книге В.Беллюстина «Как постепенно дошли люди до настоящей арифметики» (1941г.) изложено 27 способов умножения, причем автор отмечает; «весьма возможно, что есть и еще (способы), скрытые в тайниках, книгохранилищах, разбросанные в многочисленных, главным образом, рукописных сборниках».
И все эти приемы умножения – «шахматный», «загибанием», «задом наперед», «алмазом» и прочие, а также все способы деления, носившие не менее затейливые наименования, соперничали друг с другом в громоздкости и сложности.
Во времена М.Ломоносова действие умножения уже записывали почти так, как и в наше время. Только множимое называли «еличество», а произведение — «продукт» и, кроме того, не писали знак умножения.
Пример:
48 — Еличество. 8 — Множитель. 384 — Продукт, или произведение.
Известно, что М. В. Ломоносов знал наизусть всю «Арифметику» Магницкого. В соответствии с этим учебником маленький Миша Ломоносов умножение 48 на 8 объяснил бы так: «8-жды 8 есть 64, я 4 пишу под чертою, против 8, а 6 десятиц во уме имею. И дальше 8-жды 4 есть 32, и я З во уме держу, а к 2 приложу 6 десятиц, и будет 8. И сие 8 напишу подле 4, в ряд к левой руке, а 3 пока во уме суть, напишу в ряд подле 8, к левой же руке. И будет из умножения 48 с 8 произведение 384».
Сейчас мы почти так же объясняем, только говорим по-современному, а не по-старинному и, кроме того, называем разряды. Например, 3 надо писать на третьем месте потому, что это будут сотни, а не просто «в ряд подле 8, к левой же руке».
Что касается деления… В учебнике Л.Ф.Магницкого дается несколько способов деления. Некоторые из этих способов настолько трудные, что в них очень легко запутаться.
Разберем сейчас один из этих способов. Магницкий считает его изящным и простым.
Пусть требуется разделить 598432 на 678. Сначала пишем первые цифры делимого 5984, под ним делитель 678. Делим 59 на 7 (678 близко к 700), получаем первую цифру частного 8 и пишем ее справа против делимого, умножаем 8 на 678: восемью восемь 64, отнимаем в уме 4 из 4 и пишем над 4 остаток 0; восемью семь 56, да 6 в уме—62, отнимаем 2 от 8, получаем в остатке 6 и пишем его над 8; 8X6=48, 48 +6=54, 59—54=5, значит, над 59 пишем остаток 5. Теперь к остатку 560 сносим следующую цифру делимого 3 и продолжаем действие в таком же порядке.
Закончив с трудом деление, наши предки считали обязательным проверить его один-два раза. Магницкий в данном случае ограничивается одной проверкой. Он рекомендует умножать с высших разрядов: 678 х 8=5424, еще раз. 678 х 8 = 5424 и 678 х 2= 1356; под этими числами подписывает остаток и складывает. Получает делимое. «Верно разделено» — писали в заключение в старину.
Вот как выглядела запись деления:
436
1792
5603
5984/
882
678
5424
5424
1356
436
598432 верно разделено
Как видим, этот способ очень напоминает тот, которым пользуемся мы. Вероятно, наш современный способ развился из этого. Других способов разбирать не будем, приведем только форму записи делений «ромбом», который встречается у Магницкого.
Разделить 9649378 на 5634:
3
14
259
10
59417
4015530
9649378
5634444
56333
566
5
11 простых математических приемов


Ребята, мы вкладываем душу в AdMe.ru. Cпасибо за то,
что открываете эту
красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте
Если у вас все плохо с математикой — это не ваша вина. Нас просто не научили в школе математическим трюкам, с которыми любые расчеты становятся элементарными.
AdMe.ru публикует приемы, благодаря которым вы легко сможете считать в уме.
Процент от числа

Быстрое возведение в квадрат
Этот прием поможет быстро возвести в квадрат двузначное число, которое заканчивается на 5. Умножьте первую цифру саму на себя + 1, а в конце допишите 25. Вот и все!

Умножение на 9

Умножение на 5
Разделите число на 2. Если в результате получилось целое число, припишите 0 в конце. Если нет, не обращайте внимание на запятую и в конце добавьте 5.

Умножение на 11

Умножение на 4
Хитрость в том, что нужно просто умножить на 2, а затем опять умножить на 2.

Подсчет чаевых
Если вам нужно оставить 15% чаевых, есть простой способ определить, сколько это. Высчитайте 10% (разделите число на 10), а потом добавьте получившееся число к его половине и получите ответ.

Сложное умножение
Если вам нужно умножить большие числа, причем одно из них — четное, вы можете просто перегруппировать их, чтобы получить ответ.

Деление на 5
На самом деле делить большие числа на 5 очень просто. Все, что нужно, — это просто умножить на 2 и перенести запятую.

Вычитание из 1000
Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом: отнимите от 9 все цифры, кроме последней, а последнюю цифру отнимите от 10.

Перевод градусов по Цельсию в градусы по Фаренгейту и наоборот

что делается первым умножение или деление в математике
Эти действия равноправны, поэтому первым выполняется то, с чего начинается серия (отсчёт — слева направо) : А: В*С=(А: В) *С, А*С: В=(А*С): В. Правда, в данном случае результат одинаковый (если вычисления идеально точные) .
что стоит первым то и первое
по моему умножение.. но я не помню уже.. давно в школе учился
Помойму умножение.
без разницы. ответ один и тот же.
ггггг)))) ) Это же одно и то же))))
С лева направо! Если умножение первее стоит то умножение, если деление то деление !
если нет скобок, то без разницы. я обычно делаю в том порядке, в котором проще, в котором меньшие числа надо перемножать или делить.
Совершенно не важно, если нет скобок.
такие примеры решаются по порядку, что первым идет такое действие и выполняете
6 : 2 * 3 = 9 это по порядку 6 : 2 * 3 = 1 это с начало умножение потом деление ответы разные, поэтому очередь имеет значение. Считают слева на право
Действие выполняется в зависимости от порядка. Например: 200*45/1000=9( в данном случае * стоит первым, а деление последним. И поэтому сначала мы будем умножать 200*45, а потом делить 9000/1000=9) Другой пример: 36/9*4=16( в этом случае / стоит первым, а * вторым. И поэтому первым мы будем делит 36/9, а потом умножать 4*4=16) Удачного дня!!!
Эти действия равноправны, поэтому первым выполняется то, с чего начинается серия (отсчёт — слева направо) : А: В*С=(А: В) *С, А*С: В=(А*С): В. Правда, в данном случае результат одинаковый (если вычисления идеально точные) .
конечно! что перьвей стойт и только это клянусь всем что уменя есть!
нумнодайка эээээээ я дебилллл
Умножение или произведение целых чисел
Произведение вы уже проходили в теме умножения натуральных чисел. Отличия произведения натуральных от целых чисел в том, что появляются целые отрицательные числа. Сейчас этой теме мы рассмотрим тему умножение целых чисел подробнее.
Основные понятия, обозначение и смысл произведения целых чисел.
Вспомним, что такое умножение или произведение.
Числа, которые мы умножаем называются множителями, а результат умножения называется произведением.
Обозначается умножение символом таким:
a∙b=c или a*b=c или a×b=c
Произведение в буквенном написании обозначается как a∙b или c.
Так же вспомним смысл произведения.
Произведение 2∙11=22 можно записать в виде суммы мы сложим 11 раз число 2, это будет выглядеть так:

Правило произведения целых чисел.
Определение:
Произведением двух целых чисел не равных нулю называют произведение их модулей и результат будет со знаком плюс, если эти числа одинаковых знаков, и со знаком минус, если они разных знаков.
Самое главное в произведении целых чисел это правильно посчитать знак ответа. Например, оба множителя могут быть положительными или оба отрицательными числами, или один множитель положительный, а другой отрицательный.
Нужно запомнить:
Плюс на плюс дает плюс.
“+ ∙ + = +”
Минус на минус дает плюс.
“– ∙ – =+”
Минус на плюс дает минус.
“– ∙ + = –”
Плюс на минус дает минус.
“+ ∙ – = –”
Каждый случай ниже разберем подробно.
Умножение или произведение положительных целых чисел.
В данном случае мы умножаем два числа положительных знаков, поэтому тут все просто “ плюс на плюс дает плюс”. Произведение положительных целых чисел дает в результате положительное целое число. Рассмотрим пример:
Для наглядности разберем умножение со знаками.
(+5)∙(+8)=(+40)
В умножении не принято писать знак “+”, поэтому его можно опустить. Если перед число не стоит ни какого знака, то считается то перед этим числом стоит знак “+”.
5∙8=40
Умножение отрицательных целых чисел.
Правило умножения двух целых отрицательных чисел:
При умножении двух отрицательных целых чисел, будет равно произведению модулей этих чисел.
|-a|=a и |-b|=b
-a∙(-b)=a∙b
Или другими словами “минус на минус дает плюс”. При произведении двух отрицательных чисел, ответ будет равен положительному целому числу.
Пример:
Вычислите произведение целых чисел -12∙(-3).
Решение:
Два минуса при умножении дают в результате плюс. В ответе число будет с плюсом.
-12∙(-3)=36
Ответ: 36
Произведение целых чисел с разными знаками.
Не важен порядок множителей положительное число умножаем на отрицательное или отрицательное число умножаем на положительное, в результате всегда будет отрицательное целое число.
Правило умножения двух целых чисел с разными знаками:
При умножении двух целых чисел с разными знаками, их произведение будет равно целому отрицательному числу.
Если упростить определение то, обычно говорят:
“Минус на плюс дает минус”.
“Плюс на минус дает минус”.
Разберем пример:
Вычислить произведение целых чисел.
-4∙6=-24
А теперь докажем правильность этого решения.
-4+(-4)+(-4)+(-4)+(-4)+(-4)=-4∙6=-24
Шесть раз сложили число (-4).
Такой же ответ будет, если поменять местами числа.
6∙(-4)=-24
Пример:
-34∙2=-68
Умножение целого числа на нуль.
Правило умножения целых чисел на нуль.
Если любое целое число умножить на нуль, ответ будет равен нулю.
a∙0=0 или 0∙a=0
Пример:
Найдите произведение целого положительного числа 209 на нуль.
Решение:
209∙0=0
Пример:
Найдите произведение целого отрицательного числа (-39) на нуль.
Решение:
0∙(-39)=0
Умножение целого числа на 1.
Правило умножения целого числа на единицу:
Произведение целого числа a и 1 равно a.
a∙1=a или 1∙a=a
Пример:
Вычислить произведение положительного целого числа 49 и единицы.
Решение:
49∙1=49
Пример:
Вычислить произведение отрицательного целого числа (-35 860) и единицы.
Решение:
1∙(-35 860)=-35 860
Пример:
Найдите произведение нуля и единицы.
Решение:
0∙1=0
Проверка результата умножения целых чисел.
Не всегда мы выполняем умножение простых чисел, бывают число объемные и сложные, поэтому нужно уметь проверять правильность выполненного умножения.
Как проверить результат умножения?
Умножение проверяется делением. Мы делим произведение на один из множителей.
Например:
Выполните умножение и сделайте проверку.
5∙12=60
5 – множитель;
12 – множитель;
60 – произведение.
Проверка:
60:12=5 или 60:5=12
Умножение или произведение нескольких целых чисел.
Чтобы посчитать произведение нескольких целых чисел, нужно умножать числа по парно или последовательно, например:
(-3) ∙5∙(-11) ∙(-9) ∙1=((-3) ∙5)∙((-11) ∙(-9)) ∙1=((-15) ∙99) ∙1=(-1485) ∙1=-1485
Сначала сгруппировали по два числа ((-3) ∙5) и ((-11) ∙(-9)), потом ((-15) ∙99) и нашли ответ.
При перемножении целых чисел, результат всегда будет целым числом.
Вопросы по теме:
Как влияет при умножении на целое число (-1)?
Ответ: так как (-1) отрицательное число, при умножении на целое число происходит смена знака числа.
Пример: (-1) ∙3=-3 . Число 3 было со знаком “+”, а стало со знаком “–”.
Еще пример: (-1) ∙(-5)=5 . Число (-5) было со знаком “–”, а стало со знаком “+”.
Пример №1:
Найти произведение двух целых чисел: а) (-2) ∙235 б) (-34) ∙(-17) в) 1∙(-12) г) 0∙4983
Решение:
а) (-2) ∙235=-470
б) (-34) ∙(-17)=578
в) 1∙(-12)=-12
г) 0∙4983=0
Пример №2:
Чему равно произведение последовательных целых чисел, начинающихся числом -100 и оканчивающихся числом 100?
Решение:
Между числами -100 и 100 находится нуль, а любое число, умноженное на 0 равно 0. Поэтому произведение последовательных целых чисел от -100 до 100 равно 0.
Ответ: 0.
Пример №3:
Чему равно произведение всех целых чисел?
Решение:
Целые числа состоят из целых положительных и отрицательных чисел, а также нуля. При умножении любого числа на нуль будет 0. Поэтому произведение всех целых чисел равно 0.
Ответ: 0.