неизвестно начальное значение (метод пропорции)

11 ноября 2013

Этим видео я начинаю целую серию видеоуроков по решению задач B2 на проценты. Мы разберем все — от самых простых задач (таких, как сегодня) до настоящей жести, которая, тем не менее, встречается на настоящем ЕГЭ по математике.

Сегодняшний урок посвящен самым простым задачам B2 и, соответственно, самому простому методу вычисления процентов. А именно, речь пойдет о методе пропорций.

Давайте приступим. Первая задача:

Задача. В школе 204 ученика изучают французский язык, что составляет 24% от числа всех учеников. Сколько учеников учится в школе?

Итак, решаем эту задачу. Переводим ее условие на язык пропорций.

Что нам известно? Нам даны 204 ученика, которые составляют 24% от всех учеников школы. Так и запишем:

204 — 25%

При этом в задаче спрашивается: сколько всего учеников учится в этой школе? Т.е. от нас требуется найти некоторое число x учеников, которое было бы равно общему количеству учеников школы, т.е. 100%. Запишем это:

x — 100%

В результате этих размышлений мы получили по сути таблицу размером 2 × 2, вмещающую в себя все условие задачи:

204 — 25%
x — 100%

Давайте составим из нее пропорцию:

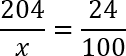
По сути, мы просто добавили дробную черту к приведенной выше конструкции и получили уравнение. Что ж, давайте его решать. Очевидно, что дробь, стоящая справа может быть сокращена: 24 : 4 = 6; 100 : 4 = 25. Перепишем еще раз полученную конструкцию:

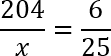
Теперь воспользуемся основным свойством пропорции (произведение крайних членов равно произведению средних членов) и перемножим наши числа крест-накрест. Получим:

204 · 25 = 6 · x

Обратите внимание: между полученными произведениями стоит знак равенства! Не сложение и не вычитание, как думаю многие ученики, а именно равенство. Решаем полученное уравнение:

x = 204 · 25 : 6 = 34 · 25 = 34 · (10 + 10 + 5) = 340 + 340 + 170 = 850

Как вы заметили, мы не стали перемножать числа 34 и 25 столбиком, а просто заметили, что 25 = 10 + 10 + 5, а затем раскрыли скобки.

Итак, мы получили, что x = 850. Это число и является ответом на вопрос, поставленный в задаче: сколько всего учеников учатся в школе. Таких учеников учится 850. Все, задача решена.

Задача на проценты №2

Переходим к следующей задаче:

Задача. 108 выпускников школы собираются учиться в технических вузах. Они составляют 40% от числа выпускников. Сколько в школе выпускников?

Как видим, это снова задача на проценты, и мы снова решаем ее методом пропорций.

Первый шаг. По условию, у нас есть 108 выпускников, которые составляют 40% от общего количества выпускников в школе. А нам надо найти x выпускников, которые составят 100%, т.е. все население школы, которое является выпускниками. Запишем это в виде соотношений:

108 — 40%
x — 100%

Что ж, снова составляем пропорцию. Делим первые два числа друг на друга и вторые два числа друг на друга. Полученные дроби приравниваем:

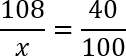
Дробь справа хорошо сокращается (как минимум, на 10). Можно было бы сократить еще и на 2, но дальше нам надо будет перемножать числа согласно основному свойству пропорции. Думаю, что умножить 108 на 10 будет гораздо проще, чем 108 на 5. Умножаем и получаем:

4x = 108 · 10;
4x = 1080.

Осталось решить полученное уравнение, т.е. разделить обе его стороны на 4. Получим:

x = 1080 : 4 = (1000 + 80) : 4 = 250 + 20 = 270

С помощью небольшой хитрости можно делить довольно большие числа без всяких уголков. Вот мы и получили ответ. Всего в школе 270 выпускников.

Как видите, с помощью метода пропорций задачи на проценты решаются очень и очень просто. Единственное, на что хотелось бы обратить внимание — это оформление самих решений. Взгляните: мы везде пишем, что некоторое число — это столько-то процентов. И нигде ни в коем случае не применяем знак равенства.

Это делается неслучайно. Потому что в противном случае мы бы получили выражения вида (на примере последней задачи):

108 = 40

Очевидно, что данное равенство неверно. Как следствие, такая интерпретация условия является некорректной.

В общем, при решении задач на проценты никогда так не пишите. Лучше потратить несколько дополнительных секунд и записать условие правильно, корректно, из которого легко следует пропорция, которая затем не менее легко решается:

108 — 40%

Надеюсь, этот урок поможет тем, кто готовится к ЕГЭ по математике или просто разбирается с задачами на проценты. А у меня на это все. До новых встреч!

Смотрите также:

1. Задачи на проценты: считаем проценты с помощью пропорции
2. Формула простого процента: как найти исходное значение
3. Приведение дробей к общему знаменателю
4. Пробный ЕГЭ 2012. Вариант 10 (без логарифмов)
5. Тест по методу интервалов для строгих неравенств
6. Задача B2: Сложный процент и стандартная формула

Тест. Проценты и пропорции

© 2019, ООО КОМПЭДУ, http://compedu.ru При поддержке проекта http://videouroki.net

Будьте внимательны! У Вас есть 15 минут на прохождение теста. Система оценивания — 5 балльная. Разбалловка теста — 3,4,5 баллов, в зависимости от сложности вопроса. Порядок заданий и вариантов ответов в тесте случайный. С допущенными ошибками и верными ответами можно будет ознакомиться после прохождения теста. Удачи!

Список вопросов теста

Вопрос 1

Выразите число 34 в процентах.

Варианты ответов

Вопрос 2

Выразите число 3,2 в процентах.

Варианты ответов

• 320 %
• 0,032 %
• 32 %
• 0,32 %

Вопрос 3

Найдите 180 % от числа 31,2.

Варианты ответов

Вопрос 4

Разделите число 434 обратно пропорционально числам 2; 3; 5.

Варианты ответов

Вопрос 5

Известно, что 5 % первого числа и 4 % второго составляют в сумме 44, а 4 % первого числа и 5 % второго составляют в сумме 46. Найдите эти числа.

Варианты ответов

Вопрос 6

Разделите число 286 прямо пропорционально числам 2; 3; 8.

Варианты ответов

Вопрос 7

Найдите число, 140 % его равны 182.

Вопрос 8

Яблоки при сушке теряют 85 % массы. Сколько килограммов свежих яблок надо взять, чтобы приготовить 10,5 кг сушеных?

Вопрос 9

На сколько процентов уменьшится дробь, если её числитель уменьшить на 20 %, а знаменатель увеличить на 60 %?

Вопрос 10

Сколько литров пресной воды нужно добавить к 80 л морской, чтобы содержание соли в ней было не 5 %, а 2 %?

Задачи на проценты и пропорции

Задачи на проценты и пропорции при подготовке к ЕГЭ.

Процентом ( от латинского pro cento- с сотни) называется сотая часть. Необходимо помнить, что проценты всегда берутся от каких либо числовых величин и чаще всего от разных. Поэтому складывать, вычитать, умножать и делить проценты не рекомендуется.

Для того, чтобы решить задачу с процентами, необходимо заменить проценты соответствующими десятичными дробями и решать задачу по правилам действия с дробями.

Я подобрала задачи, в которых учащиеся часто встречают затруднения при их решении.

Решение: А =0,4В.Отсюда В=А/0,4=2,5А.Значит, число В составляет от числа А 250%.

Задача1.2. Число А составляет 80% от числа В. Сколько процентов число В составляет от числа А? ( Ответ : 125 %.)

Задача1.3. Число А составляет 25% от числа В. Сколько процентов число В составляет от числа А? ( Ответ : 400 %.)

• Задача 2.Первоначальную цену товара повысили на 25%, а затем понизили на 36% от новой цены. На сколько процентов нужно повысить окончательную цену, чтобы вернуться к первоначальной цене?

Решение: х- первоначальная цена.

х+0,25х=1,25х –цена после повышения;

1,25х-0,36∙ 1,25х=0,8х- цена после понижения;

0,8х+0,01у∙0,8х = х;

0,008у=0,2; у=25 ( Ответ : 25 %.)

Задача2.2.Первоначальную цену товара повысили на 150 %, а затем понизили на 50 % от новой цены. Как нужно изменить окончательную цену, чтобы вернуться к первоначальной цене? ( Ответ : понизить на 20 %.)

Задача2.3. Первоначальную цену товара увеличили на 60 %, а затем ещё на 25 % от новой цены. На сколько процентов нужно уменьшить окончательную цену, чтобы вернуться к первоначальной цене?

( Ответ : 50 %.)

Решение: Так как А=1,12В, а В=(1-0,25)С = 0,75С,то А=1,12 ∙0,75С=0,84С. Это значит, что число А меньше числа С на 16%.( Ответ : 16 %.)

Задача3.2. Число А больше числа В на 35 %. Число В меньше числа С на60 %. На сколько % число А меньше числа С ? ( Ответ : 46 %.)

Задача3.3. Число А больше числа В на 35 %. Число В меньше числа С на 60 %. На сколько % число А меньше числа С ? ( Ответ : 46 %.)

• Задача 4. Доска длины 525см распилили на 2 части так, что одна часть короче другой на 25%. Чему равна длина короткой части?

Решение: Длина большей части доски – 4 условные единицы, тогда длина меньшей части равна 3 у.е. Длина всей доски 7у.е.

525:7=75см- длина 1 у.е.

75∙3=225см-длина короткой части ( Ответ : 225см.)

Задача4.2. Доска длины 436 см распилили на 2 части так, что одна часть длиннее другой на 18 %. Чему равна длина короткой части?

( Ответ : 200см.)

Решение: Пусть вес раствора-5 у.е., тогда соль-1 у.е., вода-4 у.е.

Испарилось 4∙0,25=1у.е. воды. В полученном растворе будет 1 у.е. соли и 3 у. е. воды. Концентрация его равна 1: (1+3)∙100% =25%

( Ответ : 25 %.)

Задача 5.2. Из 25 % раствора соли испарилось 50 % имеющейся в нем воды. Найти концентрацию получившегося раствора.

( Ответ : 40 %.)

Решение:100-45 =55%-сухое вещество в траве.

119∙0,55=65,45кг-вес сухого вещества;

В сене сухого вещества 85%.

Найдем вес сена65,45/0,85=77кг. ( Ответ : 77кг.)

Задача 6.2. Влажность свежескошенной травы составляет 48%. Влажность сена 17%. Сколько сена получится из 166 кг травы?

( Ответ : 104кг.)

Задача 6.3. Влажность свежескошенной травы составляет 60 %. Влажность сена 15 %. Сколько травы нужно скосить, чтобы получить 80кг сена?

( Ответ : 170 кг.)

Решение: Весь путь составляет 100 у.е. Турист прошел 15 у.е, а потом ещё 0,2∙(100-15)=17 у.е.пути. Ему осталось пройти 100-15-17=68у.е., что составляет 17км. Значит, 4 у.е. равны 1км. Весь путь равен100:4=25км

( Ответ : 25км)

Задача 7.2. Турист прошёл 48% всего пути и 40 % оставшегося пути. После этого ему осталось пройти 39 км. Чему равен весь путь ?

( Ответ : 125км)

Задача 7.3. Турист прошёл 4км и 40 % оставшегося пути. После этого ему осталось пройти 30% всего пути. Чему равен весь путь ?

( Ответ : 8км)

• Задача 8.Зарплату рабочего увеличили на 40%, а цены на товары снизили на 20%. На сколько % товаров больше может теперь купить рабочий?

Решение: Пусть з\плата рабочего 100 у.е., а цена единицы товара 5у.е. Тогда, рабочий может купить 100: 5=20 у.е. товара. Новая з/плата равна 140у.е., новая цена товара 4у.е.. Теперь рабочий может купить

140:4 =35у.е.товара. Это на 15у.е.больше, что составляет 15/20=0,75

( Ответ : 75 %)

Задача 8.2. Пенсию повысили на 11%,а цены на продукты повысили на 48%. На сколько % меньше продуктов может теперь купить пенсионер?

( Ответ : 25 %)

• Задача 9.Велосипедист ехал от одного города до другого со скоростью 10км/ч, а обратно со скоростью 15км/ч. Чему равна средняя скорость движения велосипедиста?

Решение: Велосипедист тратит на каждый км пути туда 6 мин,

а обратно 4 минуты. В среднем, на каждый км всего пути он тратит (6+4):2=5 минут. Средняя скорость равна 60:5=12км/ч

Задача 9.2. Мотоциклист ехал от одного города до другого со скоростью 40км/ч, а обратно со скоростью 60км/ч. Чему равна средняя скорость движения мотоциклиста?

( Ответ: 48км/ч)

Задача 9.3. Турист прошел 2/9 намеченного пути со скоростью 4км
/ч. Остаток пути он проехал на велосипеде со скоростью 7км/ч. Чему равна средняя скорость движения туриста?

( Ответ: 6 км/ч)

• Задача 10. Пассажирский поезд идет со скоростью 50 км/ч. Пассажир, смотревший в окно, заметил, что встречный поезд проехал мимо него за 4 секунды. Какова скорость движения встречного поезда, если его длина равна 100метров?

Решение: Встречный поезд двигался относительно пассажира со скоростью 100:4=25м/с или 25м/с=25∙3600:1000=90 км/ч.

Собственная скорость встречного поезда равна 90-50=40км/ч
( Ответ: 40 км/ч)

Задача 10.2. Пассажирский поезд идет со скоростью 60 км/ч. Пассажир, смотревший в окно, заметил, что встречный поезд проехал мимо него за 3 секунды. Какова скорость движения встречного поезда, если его длина равна 120метров?

( Ответ: 48 км/ч)

Контрольная работа «Пропорции и проценты»

Контрольная работа

Пропорции и проценты

Вариант 1

1.Для обозначения процента используют а) ÷ б)%

2.Представьте в виде десятичной дроби: а)27 %   б)0,14% в)3%

3.Перевести в проценты: а)34 б)5,67 в)8

4.Найти неизвестный член пропорции а:5,6=10:21

5.Маршрут составил 200 км, из которых 23 % горная местность. Сколько км занимает горная часть?

6.Лена прочла 120 страниц, что составило 75 % всей книги. Сколько страниц в книге?

7. Из 7,5 кг свежих грибов получается 1500 г сушеных грибов. Найдите, сколько сушеных грибов получится из 17,5 кг свежих.

8. В спортивном отряде было 16 футболистов и 8 волейболистов. Составить круговую диаграмму распределения спортсменов в отряде.

9.Три курицы за 4 дня снесли 8 яиц. Сколько яиц снесли две курицы за три дня.

10.Стороны прямоугольника относятся как 4:5. Найти отношение периметра прямоугольника к меньшей стороне.

Контрольная работа

Пропорции и проценты

Вариант 2

1.Процент это…а)1/10 б)1/100

2. Представьте в виде десятичной дроби: а)32 %   б)0,18% в)6%

3.Перевести в проценты: а)44 б)5,87 в) 9

4.Найти неизвестный член пропорции 1,2:а=0,6:21

5.Маршрут составил 200 км, из которых равнина занимает 56 %, какова длина равнинного участка?

6. Вспахали 16 га поля, что составляет 40 % всей пашни. Какова площадь пашни?

7.Из 1,4 т золотистого песка намывают 0,7 г золота. Найдите, сколько золота можно намыть из 2170 т золотистого песка.

8. В месяце было 12 солнечных и 18 пасмурных дней. Составить круговую диаграмму распределения солнечных и пасмурных дней.

9.Четыре солдата за 3 ч начистили 2 ведра картошки. Сколько ведер картошки начистили бы три солдата за 2 ч, если бы работали с той же производительностью.

10. Стороны прямоугольника относятся как 3:4. Найти отношение периметра прямоугольника к большей стороне.