Обсуждение:Прямая — Википедия
нельзя определять слого через него же.
Почему убрали категорию Конические сечения? Анатолий 09:46, 27 апреля 2006 (UTC)
- А зачем? если кто ищет что-то про коническое сечение то прямую он уже нашёл. —Тоша 10:16, 30 апреля 2006 (UTC)
- Чтобы категория включала в себя все объекты, подпадающие по смыслу. Анатолий 21:04, 30 апреля 2006 (UTC)
Не следует быть формалистом, хотя прямая это вырожденный случай конического сечения она сюда не подходит. Кроме того она находится в над-категории и в этом случае вставлять её в подкатегорию не следует без особых на то причин. —Тоша 23:17, 30 апреля 2006 (UTC)
Цитата: «Утверждение о том, что параллельные прямые не пересекаются принимается аксиоматически, существуют геометрии, в которых это утверждение не верно, например, геометрия Лобачевского». Разве это правда? Ведь параллельные прямые не пересекаются по определению!—Qwertic 18:37, 18 мая 2006 (UTC)
- Дык у нас вроде была статья про распространённые математические заблуждения, и там был этот самый пример! —AndyVolykhov 18:39, 18 мая 2006 (UTC)
Я, короче, сидел и меня вдохновило! Я придумал определение прямой, зацените! (ну, если что не так — исправьте, плиз. Я не учёный, мне всего 16, так что не будьте ко мне строги!)
- Очень класное определение, но я его убрал за ненаучность. —Тоша 16:06, 5 августа 2006 (UTC)
- Отличное определение! Кстати, я тоже недавно придумал определение линии: линия — это то, вдоль чего можно мерить Александр Дмитриев 03:54, 15 февраля 2009 (UTC)
94.199.64.35 04:29, 9 марта 2010 (UTC)
Люди! Это же определение только для евклидова пространства![править код]
А как же более другиме пространства? И вообще, нужно давать определение независимо от метрики! И про параллельность упоминать не надо ВААЩЕ, поскольку это слишком индивидуально для каждой метрики. — Вот что вы скажете о параллельности прямых и об их пересечении в геометрии на сфере или в геометрии Лобачевского ?
Переделайте определение! наподобие определения геодезической линии, которое, кстати, отсутствует в википедии
Вот, посмотрите сюда: топик на эту тему на membrana.ru (кстати, хороший форум!) -Eugene- 05:03, 8 сентября 2006 (UTC)
- Поддерживаю. Надо рассказать о прямых в других геометриях. Например, в модели Пуанкаре прямые — полуокружности, а в сферической геометрии — дуги больших кругов. infovarius 20:30, 21 октября 2010 (UTC)
Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.
1) Тогда как определяется линия? 2) Если у нас есть понятие расстояния то у нас введены координаты (неважно какие). Поэтому нет смысла вводить через линию если можно сразу сказать, что это множество точек удовлетворяющее уравнению 1 порядка. Про уравнение 1-го порядка — это определение с привлечением дифференциальной геометрии. А нужно дать чисто геометрическое определение
«Точка и прямая» — действительно фундаментальные понятия. Рассказать о них людям, ещё детям, в школе — очень важно. И нужны РАЗНЫЕ выражения и определения, заумные и вплоть до ПРОСТЕЙШИХ! Вот мой вариант для людей «среднего ума»: Точка — мысленная , без размеров и массы, метка на прямой, плоскости или в пространстве. У неё есть координаты. Прямая — совокупность точек, лежащих в выбранном направлении. Линия — прямая, которую изогнули в нужном направлении или которая образовалась из прямой при изгибе прямой, лежащей на плоскости или на поверхности. Беру прямую проволоку, укладываю её на плоскость и изгибаю её вместе с плоскостью. Или: черчу прямую линию на листе бумаги и изгибаю лист — дети ВИДЯТ как прямая превращается в кривую линию. Меня понимали сразу и без лишних вопросов даже самые слабые ученики. Педагог Бирюков ВИ Валентин Иванович 18:28, 14 августа 2009 (UTC)
== Альтернативное определение для прямой? ==
Как это не странно но за 2000 лет так и не дали простого определения для прямой. Почему то для окружности оно существует. (Множество точек которые расположены на одинаковом расстоянии не равном нулю вокруг одной точки являющейся её центром). Возможно что прямую правильней определить через окружности? К примеру так: Прямая это множество точек касания окружностей «расходящихся» из двух точек являющихся их центрами. Под «расходящимися» окружностями я подразумеваю множество окружностей с одним центром радиус которых плавно увеличивается.
Shefon 11:54, 15 декабря 2009 (UTC)
- Дело в том, что определение для окружности зависит от многих других определений, например расстояния (знаете, что квадрат — это тоже окружность?). А определение расстояния зависит от определения прямой, так что это получится замкнутый круг. infovarius 21:32, 25 декабря 2009 (UTC)
- Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.
Shefon 14:19, 28 декабря 2009
- А я еще в школе придумал, что в двумерной системе координат прямая — множество всех точек, каждая из которых равноудалена от двух заданных точек. Таким образом я использовал только термины «точка» и «расстояние». Таким же образом можно определить плоскость в трехмерной системе координат. И даже, наверно, пространство в четырехмерной, хотя в этом я не уверен, ибо представить — мозг перегревается. 94.199.64.35 04:30, 9 марта 2010 (UTC) Павел
Предлагаю: «Прямая — это пересечение двух плоскостей», т.к. она в геометрии константа как и точка. Несогласным, могу пояснить. «Линия — путь от одной точки до другой», т.к. нет точного определения линии, пришлось определить самому. Соответственно «Прямая линия — это векторный путь от одной точки до другой».
Syrik 85.26.235.124 22:59, 19 марта 2010 (UTC)
- «Прямая — это пересечение двух плоскостей» — не совсем корректно. Как минимум «совокупность всех точек, одновременно принадлежащих двум плоскостям». Однако, даже это не вполне удовлетворительно, так как в таком определении мы оперируем терминами, более комплексными, чем прямая: «плоскость», «пересечение». К тому же, прямая может фигурировать и в двумерном пространстве, тогда как плоскость как минимум в трехмерном. Посему остаюсь при своем мнении (см. выше). Кстати, о линии. «Линия — путь от одной точки до другой» тогда следует вводить понятие «путь» 94.199.64.35 05:58, 29 марта 2010 (UTC) Павел
Shefon
- Прямая — множество всех точек, каждая из которых равноудалена от двух заданных точек. Наверное стоит добавить что эти две заданные точки не принадлежат прямой. По моему замечательное определение. Но как обычно кто то может придраться к расстоянию. Хотя возможно «равноудаленние» к расстоянию не относится.
Shefon 10:46, 14 апреля 2010 (UTC)
Надо написать, что прямая — это одномерное пространство. 79.172.102.0 13:28, 20 января 2011 (UTC)
Хочу предложить своё определение прямой:
- Прямая — это такая линия, что, если взять на ней три точки, то расстояние между двумя крайними точками равно сумме расстояний между крайними и средней точкой.
Ну как? Еще у меня было определение линии, но я забыл. ChASnock 04:42, 17 апреля 2011 (UTC)
- орисс — X7q 04:56, 17 апреля 2011 (UTC)
путь вдоль которой равен расстоянию между двумя точками.[править код]
это отрезок, а не прямая! у прямой нету точек79.139.187.32 22:52, 24 января 2011 (UTC)Анька
- Вы, наверно, хотите сказать что у прямой в отличие от отрезка нет не точек, а концов. Потому что прямая свободно может проходить через две точек, а точнее и, вообще, через любое количество точек. И если взять две произвольные точки, то через них проходит какая-та прямая, и часть прямой между этими точками является отрезком. Подробнее об этом вы можете узнать в учебниках по геометрии средней школы. AntiKrisT 08:04, 25 января 2011 (UTC)
О нормальном уравнении прямой.[править код]
Нормальное уравнение прямой записывается xcosα+ysinα−p=0{\displaystyle x\cos \alpha +y\sin \alpha -p=0}. Утверждается, что значение p{\displaystyle p} в этом уравнении равно длине перпендикуляра, проведённого из начала координат к прямой xcosα+ysinα−p=0{\displaystyle x\cos \alpha +y\sin \alpha -p=0}. Это правильно только при xcosα≥0{\displaystyle x\cos \alpha \geq 0} и ysinα≥0{\displaystyle y\sin \alpha \geq 0}. Иначе значение p{\displaystyle p} не равно длине перпендикуляра, проведённого из начала координат к прямой xcosα+ysinα−p=0{\displaystyle x\cos \alpha +y\sin \alpha -p=0}. Это следует из хода доказательства получения нормального уравнения прямой.
Вадим Шловиков 10:00, 23 октября 2011 (UTC)
- А никто и не спорит. xcosα≥0{\displaystyle x\cos \alpha \geq 0} и ysinα≥0{\displaystyle y\sin \alpha \geq 0} выполняется всегда. DziedMaroztalk 19:38, 23 октября 2011 (UTC)
- Да, мы не правы. Значение p{\displaystyle p} в нормальном уравнении прямой xcosα+ysinα−p=0{\displaystyle x\cos \alpha +y\sin \alpha -p=0} равно перпендикуляру, проведённому из начала координат к прямой. Вадим Шловиков 12:15, 24 октября 2011 (UTC)
Самая короткая прямая — это точка… (андроид) 91.205.25.30 02:54, 10 июля 2013 (UTC)
А можно ли задать через гомотетию? То есть прямая — это одна из геометрических фигур, гомотетия которой в любой точке и с любым коэффициентом даст конгруэнтную фигуру. Аналогично к точке и плоскости можно применить. И ещё, можно в это определение включить пространство, но я не знаю как. Alldark 09:11, 9 марта 2015 (UTC)
- Определить можно многими способами, но в Википедию лучше добавлять только те определения, которые используются в авторитетных источниках. То, что Вы предлагаете, по-моему, не слишком сильно отличается от задания параметрического уравнения (прямая переходит в себя при гомотетии относительно лежащей на ней точки). Danneks 20:48, 9 марта 2015 (UTC)
В статье написано «Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются параллельными». Если две прямые могут совпадать, то придётся признать это как четвёртый случай взаимного расположения двух прямых в трёхмерном пространстве (прямые совпадают). Либо утверждение неверно, так как не бывает двух совпадающих прямых — это одна прямая. Dorogusha-w (обс.) 17:53, 10 апреля 2019 (UTC)
- Вы правы. Добавил слово «несовпадающих» для прямых в пространстве. — Алексей Копылов 20:31, 11 апреля 2019 (UTC)
- Тогда следует добавить, что: Через любые две несовпадающие точки можно провести любое количество совпадающих прямых (в частности одну единственную). Dorogusha-w (обс.) 19:59, 15 апреля 2019 (UTC)
- Нет. Когда в математике говорят «даны две точки a и b», то обычно не подразумевается две различные точки, вполне возможно, что a=b. Поэтому лучше уточнить, что мы имеем в виду несовпадающие точки. Фраза «можно провести единственную прямую» явно говорит, что прямая единственна, тут никаких уточнений не нужно. Можно даже сказать «единственность» объекта с некоторым свойством означает, что любые два объекта с этим свойством совпадают. Я знаю, математики странные люди. — Алексей Копылов 03:04, 16 апреля 2019 (UTC)
Отрезок — это… Что такое Отрезок?
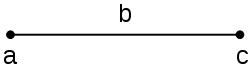
Отрезком может называться одно из двух близких понятий в геометрии и математическом анализе. Отрезок — множество точек, которое обычно изображается ограниченной частью прямой.
Отрезок в геометрии
Отрезок прямой — это множество (часть прямой), состоящее из двух различных точек и всех точек, лежащих между ними. При этом сама точка в геометрии является абстрактным объектом, не имеющим никакой длины и вообще каких-либо измеряемых характеристик. Отрезок прямой, соединяющий две точки и (которые называются концами отрезка), обозначается следующим образом — . Если в обозначении отрезка опускаются квадратные скобки, то пишут «отрезок ». Любая точка, лежащая между концами отрезка, называется его внутренней точкой. Расстояние между концами отрезка называют его длиной и обозначают как .
Отрезок числовой прямой
Отрезок числовой (координатной) прямой (числовой отрезок, сегмент) — множество вещественных чисел , удовлетворяющих неравенству , где заранее заданные вещественные числа и называются концами (граничными точками) отрезка. В противоположность им, остальные числа , удовлетворяющие неравенству , называются внутренними точками отрезка.[1]
Отрезок обычно обозначается :
- .
Любой отрезок заведомо включён в множество вещественных чисел. Отрезок является замкнутым промежутком.
Число называется длиной числового отрезка .
Стягивающаяся система сегментов
Система сегментов — это бесконечная последовательность элементов множества отрезков на числовой прямой .
Система сегментов обозначается . Подразумевается, что каждому натуральному числу поставлен в соответствие отрезок .
Система сегментов называется стягивающейся, если[2]
- каждый следующий отрезок содержится в предыдущем;
- соответствующая последовательность длин отрезков бесконечно мала.
У любой стягивающейся системы сегментов существует единственная точка, принадлежащая всем сегментам этой системы.
Этот факт следует из свойств монотонной последовательности.
Направленный отрезок
Обычно у отрезка прямой неважно, в каком порядке рассматриваются его концы: то есть отрезки и представляют собой один и тот же отрезок. Если у отрезка определить направление, то есть порядок перечисления его концов, то такой отрезок называется направленным. Например, выше указанные направленные отрезки не совпадают. Особого обозначения у направленных отрезков нет — то, что у отрезка важно его направление обычно указывается особо.
Дальнейшее обобщение приводит к понятию вектора — класса всех равных по длине и сонаправленных направленных отрезков.
Примечания
См. также
отрезок прямой — это… Что такое отрезок прямой?
- отрезок программы
- отрезок рассеяния
Смотреть что такое «отрезок прямой» в других словарях:
отрезок прямой — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN intercept … Справочник технического переводчика
откладывать отрезок (прямой) — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN mark off … Справочник технического переводчика
Отрезок — Отрезком может называться одно из двух близких понятий в геометрии и математическом анализе. Отрезок множество точек, к … Википедия
Прямой круговой конус — Конус тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. Иногда конусом называют часть такого тела, полученную объединением всех отрезков, соединяющих вершину и точки… … Википедия
ОТРЕЗОК — ОТРЕЗОК, зка, муж. 1. Небольшой отрезанный кусок чего н. 2. Часть чего н., измеряемого в пространстве или во времени. О. пути. О. прямой (в математике: часть прямой, лежащая между двумя её точками). О. времени (промежуток времени). Толковый… … Толковый словарь Ожегова
ОТРЕЗОК — (сегмент) в математике множество чисел или точек на прямой между двумя числами или точками a и b, включая сами точки a и b; обозначается ОТРЕПЬЕВ Григорий Богданович по утверждению правительства Бориса Годунова, беглый дьякон московского Чудова… … Большой Энциклопедический словарь
ОТРЕЗОК — часть прямой, заключённая между двумя её точками и включающая обе эти точки … Большая политехническая энциклопедия
отрезок — зка; м. 1. Часть чего л. измеряемого в пространстве или во времени. О. линии. О. времени. О. пути. О. прямой (часть прямой, лежащая между двумя её точками). 2. только мн.: отрезки, ов. Ист. = Отрезные земли. ◁ Отрезочек, чка; м. Разг. Уменьш. * * … Энциклопедический словарь
Отрезок — сегмент (в математике), множество точек на прямой, расположенных между двумя точками А и В, включая сами точки А и В. Иначе говоря, О. есть множество точек на прямой, координаты которых удовлетворяют условиям а ≤ х ≤ b (а и b координаты… … Большая советская энциклопедия
отрезок — зка; м. см. тж. отрезочек 1) Часть чего л. измеряемого в пространстве или во времени. Отре/зок линии. Отре/зок времени. Отре/зок пути. Отре/зок прямой (часть прямой, лежащая между двумя её точками) … Словарь многих выражений
ОТРЕЗОК — сегмент, множество точек на прямой, расположенных между двумя данными точками а, b и удовлетворяющих условию вида обозначают [a, b]. См. также Интервал и сегмент … Математическая энциклопедия
Направленный отрезок — это… Что такое Направленный отрезок?
Под направленным отрезком 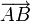 в геометрии понимают упорядоченную пару точек, первая из которых — точка A — называется его началом, а вторая — B — его концом.
в геометрии понимают упорядоченную пару точек, первая из которых — точка A — называется его началом, а вторая — B — его концом.
Определение
Вектором в простейшем случае называется направленный отрезок, а в других случаях различные векторы — это разные классы эквивалентности направленных отрезков, определяемые неким конкретным отношением эквивалентности. Причем отношение эквивалентности может быть разным, определяя тип вектора («свободный», «фиксированный» итд). Проще говоря, внутри класса эквивалентности все входящие в него направленные отрезки рассматриваются как совершенно равные, и каждый может равно представлять весь класс.
Учитывая изоморфизм между множеством свободных векторов и множеством их параллельных переносов пространства, если операцию сложения отождествить с композицией переносов, можно использовать множество параллельных переносов пространства даже для определения вектора.
Большую роль играют векторы в изучении бесконечно малых трансформаций пространства.
- Вектор, начало которого совпадает с его концом, называют нулевым:

- Вектор
 называют противоположным вектору
называют противоположным вектору  .
.
- Длиной вектора, или модулем вектора, называют длину соответствующего направленного отрезка:
 .
.
Свободные, скользящие и фиксированные векторы
Иногда, вместо того, чтобы рассматривать в качестве векторов множество всех равных направленных отрезков, берут только некоторую модификацию этого множества (фактормножество). Так, говорят о «свободных» (когда отождествляются все равные по длине и направлению направленные отрезки, считаясь полностью равными или одним и тем же вектором), «скользящих» (отождествляются между собой все направленные отрезки, равные в смысле свободных векторов, начала и концы которых расположены на одной прямой) и «фиксированных» векторах (по сути дела, просто о направленных отрезках, когда разное начало означает уже неравенство векторов).
Определение. Говорят, что свободные векторы 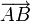 и
и 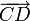 равны, если найдутся точки E и F такие, что четырёхугольники ABFE и CDFE — параллелограммы.
равны, если найдутся точки E и F такие, что четырёхугольники ABFE и CDFE — параллелограммы.
- Замечание. «Ухищрение» (введение дополнительных точек) в определении равенства касается, прежде всего, случая, когда точки A,B,C,D располагаются на одной прямой. В противном случае определение выглядит проще:
Определение. Говорят, что свободные векторы 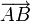 и
и 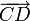 , не лежащие на одной прямой, равны, если четырёхугольник ABDC — параллелограмм.
, не лежащие на одной прямой, равны, если четырёхугольник ABDC — параллелограмм.
Определение. Говорят, что скользящие векторы 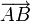 и
и 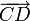 равны, если
равны, если
- точки A,B,C,D располагаются на одной прямой,
- векторы
 и
и  равны между собой как свободные векторы.
равны между собой как свободные векторы.
Неформально говоря, скользящему вектору разрешено двигаться вдоль его прямой без изменения величины и направления.
- Замечание. Скользящие векторы особо употребимы в механике. Простейший пример скользящего вектора в механике — сила. Перенос такого начала вектора вдоль прямой, на котой он лежит, не меняет момента силы ни относительно какой точки; перенос же его на другую прямую, даже если не менять величины и направления вектора, может вызвать изменение его момента (скорее даже почти всегда вызовет): поэтому нельзя рассматривать силу как свободный вектор.
Определение. Говорят, что фиксированные векторы 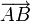 и
и 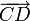 равны, если попарно совпадают точки A и C, B и D.
равны, если попарно совпадают точки A и C, B и D.
Операции над векторами
Сложение векторов
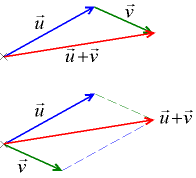
Два вектора u, v и вектор их суммы
Сложение двух свободных векторов можно осуществлять как по правилу параллелограмма, так и по правилу треугольника.
Правило треугольника. Для сложения двух векторов 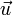 и
и 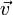 по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора.
по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора.
Правило параллелограмма. Для сложения двух векторов 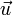 и
и 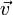 по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.
по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.
Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Тогда каждый из векторов переносится вдоль своей прямой в точку пересечения этих прямых, после чего сложение осуществляется по правилу параллелограмма.
Сложение двух фиксированных векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма.
Сложение коллинеарных скользящих векторов
Если скользящие векторы параллельны, то при их сложении главная трудность состоит в определении прямой, на которой будет расположена их сумма. (Величину и направление вектора суммы было бы естественно определить точно так же, как и в случае сложения свободных векторов.) В механике при изучении статики для решения вопроса о сложении параллельных сил, которые, как известно, задаются скользящими векторами, вводится дополнительная гипотеза: к системе векторов можно добавить два вектора, равных по величине, противоположных по направлению и расположенных на одной прямой, пересекающей прямые, на которых расположены данные вектора. Пусть, например, надо сложить скользящие векторы 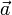 и
и 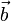 , расположенные на параллельных прямых. Добавим к ним векторы
, расположенные на параллельных прямых. Добавим к ним векторы 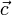 и
и 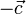 , расположенные на одной прямой. Прямые, на которых расположены векторы
, расположенные на одной прямой. Прямые, на которых расположены векторы 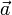 и
и 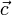 ,
, 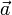 и
и 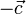 пересекаются. Поэтому определены векторы
пересекаются. Поэтому определены векторы
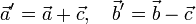
Прямые, на которых расположены векторы 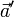 и
и 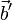 , пересекаются всегда, за исключением случая, когда векторы
, пересекаются всегда, за исключением случая, когда векторы 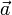 и
и 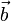 равны по величине и противоположны по направлению, в котором говорят, что векторы
равны по величине и противоположны по направлению, в котором говорят, что векторы 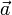 и
и 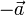 образуют пару (векторов).
образуют пару (векторов).
Таким образом, под суммой векторов 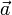 и
и 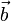 можно понимать сумму векторов
можно понимать сумму векторов 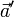 и
и 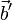 , и эта сумма векторов определена корректно во всех случаях, когда векторы
, и эта сумма векторов определена корректно во всех случаях, когда векторы 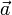 и
и 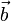 не образуют пару.
не образуют пару.
Произведение вектора на число
Произведением вектора 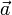 и числа λ называется вектор, обозначаемый
и числа λ называется вектор, обозначаемый 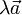 (или
(или 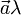 ), модуль которого равен
), модуль которого равен  , а направление совпадает с направлением вектора
, а направление совпадает с направлением вектора 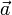 , если
, если 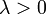 , и противоположно ему, если
, и противоположно ему, если 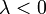 . Если же
. Если же 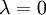 , или вектор
, или вектор 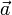 нулевой, тогда и только тогда произведение
нулевой, тогда и только тогда произведение 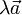 — нулевой вектор.
— нулевой вектор.
- Обычно принято в записи произведения числа и вектора число записывать слева, но в принципе допустим и обратный порядок, хотя все же обычное соглашение состоит в том, чтобы его избегать, если нет прямой необходимости. Так или иначе,
 .
.
Из определения произведения вектора на число легко вывести следующие свойства:
- если
 , то
, то  . Наоборот, если
. Наоборот, если  , то при некотором λ верно равенство
, то при некотором λ верно равенство  ;
; - всегда
 °, то есть каждый вектор равен произведению его модуля на орт.
°, то есть каждый вектор равен произведению его модуля на орт.
Скалярное произведение
Скалярным произведением векторов 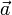 и
и 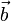 называют число, равное
называют число, равное 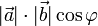 , где
, где 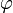 — угол между векторами
— угол между векторами 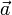 и
и 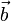 . Обозначения:
. Обозначения: 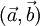 или
или 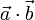 .
.
Если один из векторов является нулевым, то несмотря на то, что угол 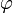 не определён, произведение равно нулю.
не определён, произведение равно нулю.
Свойства скалярного произведения векторов:
 — коммутативность.
— коммутативность. — дистрибутивность.
— дистрибутивность. — линейность по отношению к умножению на число.
— линейность по отношению к умножению на число. — норма вектора.
— норма вектора.
Геометрически скалярное произведение есть произведение длины одного из сомножителей на ортогональную проекцию другого на направление первого (или наоборот). Скалярное произведение какого-то вектора 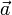 с единичным вектором есть ортогональная проекция вектора
с единичным вектором есть ортогональная проекция вектора 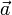 на направление единичного вектора.
на направление единичного вектора.
Векторное произведение
Векторным произведением вектора a на вектор b называется вектор c, удовлетворяющий следующим требованиям:
- длина вектора c равна произведению длин векторов a и b на синус угла φ; между ними
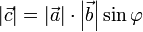
- вектор c ортогонален каждому из векторов a и b
- вектор c направлен так, что тройка векторов abc является правой.
Обозначение: ![\vec c = \left[ \vec a \vec b \right] = \left[ \vec a, \vec b \right] = \vec a \times \vec b](/800/600/https/dic.academic.ru/pictures/wiki/files/56/8a8df77cfa301a9a6e5c4e01235165ad.png)
Геометрически векторное произведение 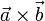 есть ориентированная площадь параллелограмма, построенного на векторах
есть ориентированная площадь параллелограмма, построенного на векторах 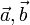 , представленная псевдовектором, ортогональным этому параллелограмму.
, представленная псевдовектором, ортогональным этому параллелограмму.
Свойства векторного произведения:
- При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е
- Векторное произведение обладает сочетательным свойством относительно скалярного множителя, то есть
- Векторное произведение обладает распределительным свойством:
Смешанное произведение
Сме́шанное произведе́ние 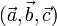 векторов
векторов 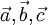 — скалярное произведение вектора
— скалярное произведение вектора 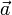 на векторное произведение векторов
на векторное произведение векторов 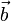 и
и 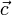 :
:
(равенство записано для разных обозначений скалярного и векторного произведения).
Иногда смешанное произведение называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).
Геометрически смешанное произведение 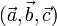 есть (ориентированный) объем параллелепипеда, построенного на векторах
есть (ориентированный) объем параллелепипеда, построенного на векторах 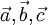 .
.
Условие перпендикулярности векторов
Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.
Пример
Даны два вектора 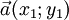 и
и 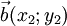 . Эти векторы будут перпендикулярны, если выражение x1x2 + y1y2 = 0.
. Эти векторы будут перпендикулярны, если выражение x1x2 + y1y2 = 0.
Условие коллинеарности векторов
Векторы являются коллинеарными тогда и только тогда, когда их векторное произведение равно нулю.
Пример
Даны два вектора 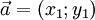 и
и 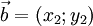 . Эти векторы коллинеарны, если x1 = λx2 и y1 = λy2, где
. Эти векторы коллинеарны, если x1 = λx2 и y1 = λy2, где 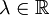
См. также
Ссылки
Wikimedia Foundation. 2010.
ОТРЕЗОК — это… Что такое ОТРЕЗОК?
отрезок — См. часть… Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. отрезок кусок, часть; сегмент, хорда, медиана, отрезочек, составная часть, этап Словарь русских синонимов … Словарь синонимов
ОТРЕЗОК — (сегмент) в математике множество чисел или точек на прямой между двумя числами или точками a и b, включая сами точки a и b; обозначается ОТРЕПЬЕВ Григорий Богданович по утверждению правительства Бориса Годунова, беглый дьякон московского Чудова… … Большой Энциклопедический словарь
ОТРЕЗОК — ОТРЕЗОК, зка, муж. 1. Небольшой отрезанный кусок чего н. 2. Часть чего н., измеряемого в пространстве или во времени. О. пути. О. прямой (в математике: часть прямой, лежащая между двумя её точками). О. времени (промежуток времени). Толковый… … Толковый словарь Ожегова
отрезок — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN spline … Справочник технического переводчика
ОТРЕЗОК — часть прямой, заключённая между двумя её точками и включающая обе эти точки … Большая политехническая энциклопедия
Отрезок — Отрезком может называться одно из двух близких понятий в геометрии и математическом анализе. Отрезок множество точек, к … Википедия
отрезок — ОТРЕЗОК1, зка, м Небольшая часть предмета, отделенная от целого с помощью режущего инструмента, орудия (ножа, ножниц и т.п.). Короткий отрезок веревки изогнулся под стулом, как змея. ОТРЕЗОК2, зка, м Часть чего л. измеряемого в пространстве или… … Толковый словарь русских существительных
отрезок — зка; м. 1. Часть чего л. измеряемого в пространстве или во времени. О. линии. О. времени. О. пути. О. прямой (часть прямой, лежащая между двумя её точками). 2. только мн.: отрезки, ов. Ист. = Отрезные земли. ◁ Отрезочек, чка; м. Разг. Уменьш. * * … Энциклопедический словарь
отрезок — ▲ фрагмент ↑ линия отрезок кусок линии; часть последовательности между двумя точками, включая и эти точки; конечная последовательность; внутренняя часть плюс оконечности. на отрезке. тире (сине зеленый. юго восток. 10 22 штук). двоеточие (1:7).… … Идеографический словарь русского языка
отрезок — tarpsnis statusas T sritis Kūno kultūra ir sportas apibrėžtis Periodas, nuotolio dalis, tarpas. atitikmenys: angl. period; phase vok. Abschnitt, m; Periode, f rus. отрезок; период … Sporto terminų žodynas
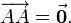
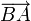 называют противоположным вектору
называют противоположным вектору 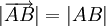 .
.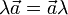 .
.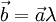 , то
, то 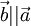 . Наоборот, если
. Наоборот, если 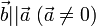 , то при некотором λ верно равенство
, то при некотором λ верно равенство 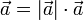 °, то есть каждый вектор равен произведению его модуля на орт.
°, то есть каждый вектор равен произведению его модуля на орт.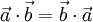 — коммутативность.
— коммутативность.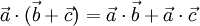 — дистрибутивность.
— дистрибутивность.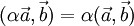 — линейность по отношению к умножению на число.
— линейность по отношению к умножению на число.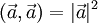 — норма вектора.
— норма вектора.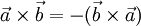
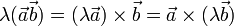
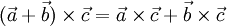
![(\vec{a}, \vec{b}, \vec{c}) = \left(\vec{a}, [\vec{b}, \vec{c}]\right) = \vec{a}\cdot\left(\vec{b}\times\vec{c}\right)](/800/600/https/dic.academic.ru/pictures/wiki/files/50/2def1ecac1759e7c06c5e879e157d6eb.png)