1 класс. Математика. Точка. Прямая, кривая и ломаная линии. — Прямая линия. Кривая линия. Ломаная линия.
Комментарии преподавателя
На данном уроке Вы изучите простейшие геометрические понятия, о которых вам расскажет мама дракончиков. Вместе с дракончиками Вы изучите такие основные понятия, как прямая линия, луч, отрезок, угол, ломаная и кривая линия. У Вас будет возможность изучить предложенный материал на наглядных примерах.
Тема: Наглядная геометрия
Урок: Начальные геометрические понятия
На этом уроке будут изучены простейшие геометрические понятия. Для лучшего понимания рассмотрим сказку про дракончиков.
Далеко-далеко в горах живет большая-большая семья драконов: папа-дракон, мама-дракониха и много маленьких дракончиков. Когда дракончики были маленькие, они учились ползать, бегать, летать, прыгать, узнавали, что такое снег, дождь, звёзды, учились в горах ориентироваться, учились даже огнём дышать.
Рис. 1
Мама-дракониха сказала, что эта линия называется прямая. Это такое геометрическое понятие.
Прямая линия – это линия, которая совершенно бесконечна.
Прямая линия идет бесконечно в одну сторону и в другую сторону. Есть такое даже выражение «Летит в небе по прямой».
Потом мама нарисовала точку и от неё провела линию. (рис. 2)
Рис. 2
Она объяснила, что точка – это начало, от нее идет линия в бесконечность. Это называется луч.
Это называется луч.
Луч — это полупрямая, которая имеет точку начала и не имеет конца.
Он так называется потому, что она как луч света. У луча света всегда есть начало. Он всегда начинается либо на солнце, либо на свечки, либо в фонарике, либо на звезде далекой. Дракончики поняли, что такое луч.
Потом мама-дракониха попросила представить дракончиков, что они от прямой отрежут кусочек. Такая фигура называется отрезок. (рис. 3)
Рис. 3
Отрезок — это часть прямой, которая ограничена с двух сторон.
Отрезок может быть длинным или коротким. Дракончики сразу не поняли. Тогда мама нарисовала еще несколько отрезков: длинные и короткие. (рис. 4)
Рис. 4
Это всё отрезки. Теперь дракончики все поняли.
Потом мама-дракониха из одной точки отложила два луча, получилась фигура, которая называется угол. (рис. 5)
(рис. 5)
Рис. 5
Причем углом называется как вся фигура, так и что находится внутри неё.
Угол – это геометрическая фигура, образованная двумя лучами, выходящими из одной точки.
Потом мама-дракониха решила нарисовать еще одну форму линии. (рис. 6)
Рис. 6
Такая линия называется ломаная линия. Потому что взяли фактически прямую линию и поломали ее. И каждый кусочек на этой линии называется звено. Ломаные линии могут быть самые разные, по разному поломанные.
Следом мама нарисовала загогулину. (рис. 7)
Рис. 7
Это кривая линия. Таких кривых линий можно нарисовать много-много самых разных.
Потом мама-дракониха спросила у маленьких дракончиков, по какой линии они летаете в небе. Дракончики задумались. И один сказал, что он летает по кривой линии, он делает всякие пируэты, закладывает спирали, петли делает. А другой дракончик сказал, что когда они в снежки играли, он повисал в воздухе, махал крылышками, а в него кидали снежками. Он улетал от них и дёргался туда-сюда, туда-сюда. Получалась ломаная линия. Мама-дракониха сказала, что дракончики все поняли правильно. Драконы летают и по кривой линии, и по ломаной, иногда просто по прямой.
А другой дракончик сказал, что когда они в снежки играли, он повисал в воздухе, махал крылышками, а в него кидали снежками. Он улетал от них и дёргался туда-сюда, туда-сюда. Получалась ломаная линия. Мама-дракониха сказала, что дракончики все поняли правильно. Драконы летают и по кривой линии, и по ломаной, иногда просто по прямой.
И тут мама заметила, что дракончики уже стали скучать и как-то вертеться, уже плохо её слушают. Она поняла, что пора их отпустить, она сказала, что урок закончен. Дракончики замахали крылышками, взлетели в небо, разлетелись над горами, весело кричали, смеялись. Мама смотрела на них и улыбалась, махала им лапой.
Итак, на уроке мы выучили такие простейшие геометрические понятия, как прямая линия, отрезок, луч, угол. Также мы рассмотрели ломаную и кривую линию. После изученного урока Вы будете знать простейшие геометрические понятия не хуже маленьких дракончиков.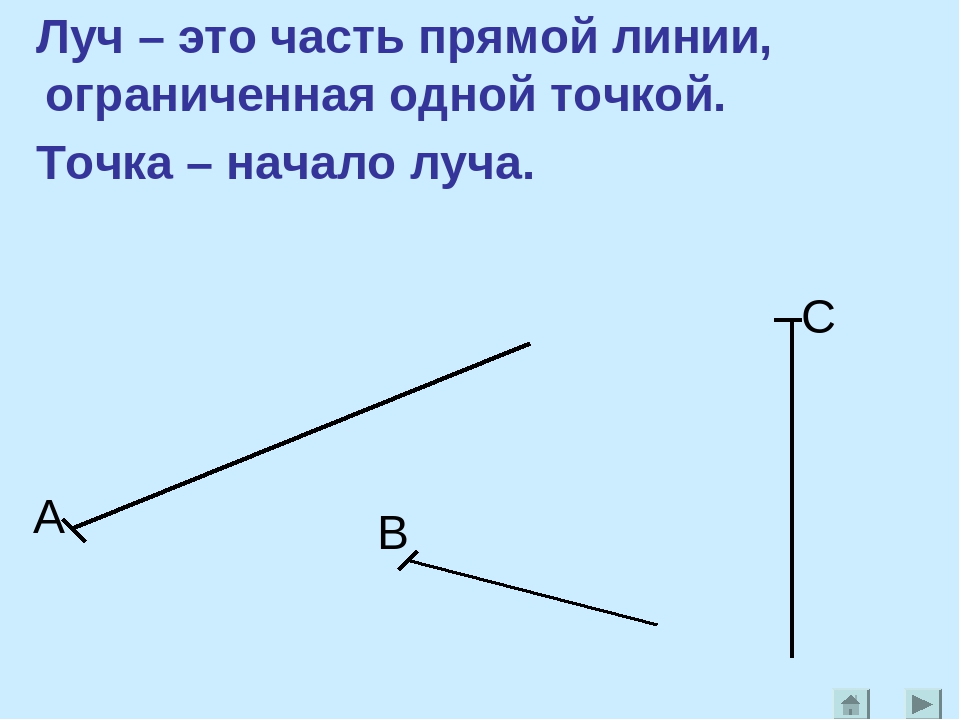
Источник конспекта: http://interneturok.ru/ru/school/matematika/1-klass/beksperimentb/nachalnye-geometricheskie-ponyatiya?seconds=0
Источник видео: https://www.youtube.com/watch?v=o8Pu_Q8YFjk
Что Такое Прямая Линия?
Определение линии происходит «прямо» от Евклида Александрийского, первого математика, который собрал определения и аксиомы геометрии, которые древние греки разработали к 300 году до нашей эры. Что шокирует, так это то, что более 2000 лет спустя ни один математический «физик» на Земле не может сказать вам, что такое линия или даже является ли она геометрической фигурой. Если вы хотите получить высшее образование и иметь будущее в качестве математического «физика», вы должны наизусть прочитать 1-мерный четок: «линия остается неопределенной». Тот факт, что стратегические термины геометрии, такие как точка и линия, по-прежнему омрачены тайной, может показаться тривиальным, пока вы не поймете, что математические «физики» говорят всем, что математика — это язык того, что они называют «физикой». Заблудшие люди, возглавляющие мир науки, убедили мир в том, что «математика — это определение», что эти определения и аксиомы безупречны и объективны, а геометрия стоит на твердой почве. Думаю об этом. Все теории общей теории относительности, квантовой механики и теории струн в значительной степени опираются на эти две концепции. Все квантовые частицы обозначены как «точки». Общая теория относительности не может обойтись без расстояний и геодезических (то есть «прямых» линий). И теория струн полностью исчезнет, если пресловутая 1D линия (то есть «строка») перестанет вибрировать. Конечно, если эти «респектабельные» ветви математической «физики» опираются на основы, которые, как показано, прогнили до глубины души, все здание рухнет.
Заблудшие люди, возглавляющие мир науки, убедили мир в том, что «математика — это определение», что эти определения и аксиомы безупречны и объективны, а геометрия стоит на твердой почве. Думаю об этом. Все теории общей теории относительности, квантовой механики и теории струн в значительной степени опираются на эти две концепции. Все квантовые частицы обозначены как «точки». Общая теория относительности не может обойтись без расстояний и геодезических (то есть «прямых» линий). И теория струн полностью исчезнет, если пресловутая 1D линия (то есть «строка») перестанет вибрировать. Конечно, если эти «респектабельные» ветви математической «физики» опираются на основы, которые, как показано, прогнили до глубины души, все здание рухнет.Таинственные неверные строки Евклида
В своем оригинальном сборнике «Элементы» Евклид различал термины «линия» и «прямая линия».
«Линия безгранична». (Определение 2, Книга I Элементов)
«Прямая линия — это линия, которая лежит равномерно с точками на себе».
Первый невообразим, потому что Евклид говорит нам, что он простирается навсегда в обоих направлениях. И это заставляет задуматься, намекает ли он даже на геометрическую фигуру. «Бескрайняя длина» Евклида несовместима с его определением фигуры, приведенным ниже в его книге:
«Фигура — это то, что содержится в любой границе или границах». (Определение 14, Книга I)
Линия Евклида не ограничена границами на обоих концах.
Более того, сегодня преемники Евклида до сих пор строят свою «бесконечную» линию, и это, безусловно, гарантирует им сохранение рабочих мест до конца вечности. Евклид относится не к существительному, а к глаголу. Евклид приравнивает «линию» к «длине», что в настоящем контексте может быть истолковано только как пройденное расстояние. Евклид говорит о маршруте, а не о палке.
Этот аргумент подкрепляется тем фактом, что длина Евклида «не имеет ширины», что означает, что Евклид сжимает свою линию в одно измерение: длину. Евклид явно имеет в виду не двумерную палку, которую он нарисовал на доске, а скорее воображаемую линию, состоящую из локаций (т.
Определение Евклидом прямой линии подтверждает, что он говорит о маршруте, если, как он описывает, он «равномерно связан с точками на себе». Он ясно дал понять, что его точка «не является частью» — это местоположение, а не точка. Слово «точка» — это не пятно. Слово «точка» относится к абстрактному понятию: упорядоченная пара (x, y). Следовательно, его прямая линия «сделана» из местоположений, что означает, что он снова ссылается на прямолинейный маршрут, а не на 2-мерную или 3-мерную автономную палку.
Всемогущая линия математической «физики»
Открывает глаза на то, что ученики Евклида не делали ничего лучше на протяжении веков. Не требуется лишь поверхностного анализа современной Геометрии, чтобы понять, что Математическое Учреждение в конечном итоге привело к еще большему беспорядку в линии Евклида, чем он.
Германом Вейлем был один из выдающихся математических «физиков», который сделал исчерпывающий обзор основ геометрии как вступления к своему великому опусу об общей теории относительности. В «Пространстве-времени» Вейль начинает с понятия истеблишмента, а затем продолжает анализировать загадочную словесную линию. Но когда вы читаете и следите за ходом мыслей Вейля, становится очевидно, что бедняга был бредовым. Его сюрреалистическая линия превращается из одного абзаца в следующий:
В «Пространстве-времени» Вейль начинает с понятия истеблишмента, а затем продолжает анализировать загадочную словесную линию. Но когда вы читаете и следите за ходом мыслей Вейля, становится очевидно, что бедняга был бредовым. Его сюрреалистическая линия превращается из одного абзаца в следующий:
1. «Двухточечная» линия Вейля…
«Прямая линия … определяется двумя ее точками» (стр. 12)
2. Линия «расстояния» Вейля…
«Прямая линия лежит равномерно между ее точками» (стр. 12)
3. Петля Вейля
«Не только прямая линия, но и плоскость основана на свойстве вращения. »(Стр. 13)
4. Линия «ряд яблок»
«Конгруэнтное преобразование, которое преобразует А в себя, и все точки справа от А в точки справа от А, а все точки слева от А в точки слева от А, оставляют все точки прямой без изменений , »(Стр. 12)
«Мы получим массив точек на строящейся прямой» (стр. 16)
5. Линия «катящегося яблока»
«Пусть a будет переводом, который переводит точку Ao в A. » (стр. 15)
» (стр. 15)
«Прямая линия выводится из точки бесконечным повторением
того же бесконечно малого перевода и его обратного. »(Стр. 16)
6. Палка Вейля
«Все точки, которые мы получаем, в конечном итоге сливаются в линейный континуум, в
которые они встраиваются, отказываясь от своего индивидуального существования (это
описание основано на нашей интуиции непрерывности). »(стр. 16)
7. Линия вспашки
«Существует один и только один перевод, который переносит произвольную точку A на g в произвольную точку A * на той же прямой линии». (Стр. 14)
8. Строка «номер»
«Если мы возьмем все возможные целые числа в качестве значений n, этот массив станет более плотным по мере увеличения n» (стр. 16)
Что мы можем сказать? Линия Вейля слишком сложна для разумного человека. Возможно, его коллеги смогут поработать над этим чуть больше в течение следующих 2000 лет.
Реальная линия, пожалуйста, встаньте?
Переменная линия Вейля показывает, что математики установили всю свою структуру геометрии на хрупких зыбучих песках. Основы дисциплины действительно прогнили до глубины души. Геометрические плоскости и твердые тела построены с гибкими и постоянно изменяющимися точками и линиями. В тот момент, когда вы думали, что стороны этого идеального, цельного куба, который смотрит на вас в лицо, состоят из непрерывных линий, математик говорит вам проснуться, потереть глаза и снова посмотреть. Вы смотрите на маршруты. Или, может быть, вы все еще галлюцинируете и видите миражи. Линия была фактически рядом дискретных точек. И только когда вы подумали, что угол, который вы рассматриваете, состоит из двух палочек, геометр смотрит на вас так, как будто вы пришли с Марса. «Что с тобой не так? Разве ты не видишь, что это явно два перпендикулярных ряда чисел?
Основы дисциплины действительно прогнили до глубины души. Геометрические плоскости и твердые тела построены с гибкими и постоянно изменяющимися точками и линиями. В тот момент, когда вы думали, что стороны этого идеального, цельного куба, который смотрит на вас в лицо, состоят из непрерывных линий, математик говорит вам проснуться, потереть глаза и снова посмотреть. Вы смотрите на маршруты. Или, может быть, вы все еще галлюцинируете и видите миражи. Линия была фактически рядом дискретных точек. И только когда вы подумали, что угол, который вы рассматриваете, состоит из двух палочек, геометр смотрит на вас так, как будто вы пришли с Марса. «Что с тобой не так? Разве ты не видишь, что это явно два перпендикулярных ряда чисел?
В этот момент здравомыслящий человек начинает задумываться: «О чем в мире говорят геометры? Они в своем уме? Является ли линия (а) рядом яблок, (б) траекторией одного яблока или (в) цельной палкой? Является ли это (a) безразмерным маршрутом, (b) автономным, 1-мерным «длиной» или (c) явно очевидным 2-мерным вытянутым прямоугольником, который нарисовал мел на доске? Как, в любом случае, 0-мерная «точка» или серия из них образуют 1-мерную линию? Если линия представляет собой серию следов, почему торговец змеиным маслом называет это линией? Это ввести в заблуждение и запутать толпу? Почему бы не назвать это маршрут или траектория или перемещение? Ну, возможно, это потому, что маршрут — это не геометрическая фигура! Может быть, поэтому! Но тогда, какое отношение имеет «маршрутная линия» к геометрии? И если линия — это палка, сделанная из одного куска, как геометры могут согласовать это с рядом дискретных точек? Как палка напоминает ряд чисел? Ответ на все эти вопросы: «бесконечное дыхание»!
Если по прошествии более 2500 лет математические «физики» не смогли определить суть геометрии — точку и линию — это потому, что они не смогли различить объекты и понятия. Объект — это то, что имеет форму. Концепция — это то, чего нет. Если геометр вводит линию как фигуру в Суде Физики, он по праву принадлежит Геометрии. Но затем геометру отказывают в праве отрывать кожу от несчастной фигуры, сбрасывать ее форму и поверхность в мусорную корзину и выполнять его приказы с указанием местоположений и чисел. То, что явно смотрит нам в лицо, это вытянутый прямоугольник. Вот что перед нами. Если математик не может использовать эту двумерную фигуру, он не должен указывать на нее, называть ее линией, а затем вызывать несвязанные абстрактные понятия для объяснения своей теории.
Объект — это то, что имеет форму. Концепция — это то, чего нет. Если геометр вводит линию как фигуру в Суде Физики, он по праву принадлежит Геометрии. Но затем геометру отказывают в праве отрывать кожу от несчастной фигуры, сбрасывать ее форму и поверхность в мусорную корзину и выполнять его приказы с указанием местоположений и чисел. То, что явно смотрит нам в лицо, это вытянутый прямоугольник. Вот что перед нами. Если математик не может использовать эту двумерную фигуру, он не должен указывать на нее, называть ее линией, а затем вызывать несвязанные абстрактные понятия для объяснения своей теории.
Математический «физик» имеет единственный выход, и он должен использовать его термины последовательно, если он хочет быть частью науки. Если он намеревается говорить о маршрутах, он должен использовать слово «маршрут». Если он собирается говорить о местах, он должен использовать слово местоположение. И если он собирается говорить о цифрах, он должен называть их номерами. Ни один из них не является ни точками, ни линиями. Точки и палочки принадлежат миру фигур: геометрия. Местоположения, маршруты и числа принадлежат исключительно абстрактному миру понятий: философия.
Точки и палочки принадлежат миру фигур: геометрия. Местоположения, маршруты и числа принадлежат исключительно абстрактному миру понятий: философия.
Математический «физик» может утверждать, что те, кто хорошо разбирается в геометрии, не смущаются языком. Члены гильдии привыкли к жаргону за эти годы. Он может добавить, что геометры знают, как сохранить свои точки и местоположения, палки и маршруты разграниченными.
Да! Конечно! И тогда тот же самый народ сделает следующий шаг и с полной искренностью скажет вам, что частица на самом деле является возбужденным «полем» и что абстрактное понятие «масса» обладает способностью перемещать звезды вокруг.
.
.
.
Точка, линия, прямая, луч, отрезок, ломанная. Точка, линия, прямая, луч, отрезок, ломанная На рисунке 3 объекта отрезок прямой
ПОВТОРЯЕМ ТЕОРИЮ
16. Заполните пропуски.
1) Точка и отрезок являются примерами геометрических
фигур.
2) Измерить отрезок означает подсчитать, сколько единых отрезков
в нем помещается.
3) Если на отрезке АВ ометить точку С, то длинна отрезка АВ равна сумме длин
отрезков АС +СВ
4) Два отрезка называют равными, если они совпадают при наложении
.
5) Равные отрезки имеют равные
длины.
6) Расстоянием между точками А и В называют длину отрезка
АВ.
РЕШАЕМ ЗАДАЧИ
17. Обозначьте отрезки, изображенные на рисунке, и измерьте их длины.
18. Проведите все возможные отрезки с концами в точках A, B, C и D. Запишите обозначения всех проведенных отрезков.
AB, ВC, СD, АD, АС, ВD
19. Запишите все отрезки, изображенные на рисунке.
20. Начертите отрезки СК и АD так, чтобы СК=4 см 6 мм, АD=2 см 5 мм.
21. Начертите отрезок ВЕ, длина которого равна 5 см 3 мм. Отметьте на нем точку А так, чтобы ВА = 3 см 8 мм. Какова длина отрезка АЕ?
АЕ=ВЕ-ВА= 5 см 3 мм — 3см 8мм = 1 см 5мм
22. Выразите данную величину в указанных единицах измерения.
Выразите данную величину в указанных единицах измерения.
23. Запишите звенья ломаной и измерьте их длины (в миллиметрах). Вычислите длину ломаной.
24. Отметьте точку В, расположенную на 6 клеток левее и на 1 клетку ниже точки А; точку С, расположенную на 3 клетки правее и на 3 клетки ниже точки В; точку D, расположенную на 7 клеток правее и на 2 клетки выше точки С. Соедините последовательно отрезками точки А, В, С и D.
Образовалась ломаная АВСD, состоящая из 3 звеньев.
25. Вычислите длину ломаной, изображенной на рисунке.
а) 5*36 = 180 мм
б) 3*28 = 84 мм
в) 10*10+15*4 = 160 мм
26. Постройте ломаную DСЕК так, чтобы DС=18 мм, СЕ=37 мм, ЕК=26 мм. Вычислите длину ломаной.
27. Известно, что АС=17 см, ВD=9см, ВС=3 см. Вычислите длину отрезка АD.
28. Известно, что МК=KN=NP=PR=RT=3 см. Какие еще равные отрезки есть на этом рисунке? Найдите их длины.
29. На прямой отметили точки так, что расстояние между двумя любыми соседними точками равно 4 см, а между крайними точками — 36 см. Сколько точек отмечено?
30. Начертите, не отрывая карандаша от бумаги, фигуры, изображенные на рисунке. По каждой линии можно проводить карандашом только один раз.
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение
Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
A B Cточка 1, точка 2, точка 3
1 2 3Можно нарисовать на листке бумаги три точки «А» и предложить ребёнку провести линию через две точки «А». Но как понять через какие? A A A
Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
линия a, линия b, линия c
a b cЛиния может быть
- замкнутой, если её начало и конец находятся в одной точке,
- разомкнутой, если её начало и конец не соединены
замкнутые линии
разомкнутые линии
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру. Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.- самопересекающейся
- без самопересечений
самопересекающиеся линии
линии без самопересечений
- прямой
- ломанной
- кривой
прямые линии
ломанные линии
кривые линии
Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны
Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны
Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия a
aпрямая линия AB
B AПрямые могут быть
- пересекающимися, если имеют общую точку.
 Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке.- перпендикулярными, если пересекаются под прямым углом (90°).
- параллельными, если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону
У луча света на картинке начальной точкой является солнце
солнышко
Точка разделяет прямую на две части — два луча A A
Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
луч a
aлуч AB
B AЛучи совпадают, если
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
C B AОтрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. Длина отрезка — это расстояние между его начальной и конечной точками
Длина отрезка — это расстояние между его начальной и конечной точками
Через одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
B Aпрямая линия AB
B AОт прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками. ✂ B A ✂
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок
отрезок AB
B AЗадача: где прямая , луч , отрезок , кривая ?
Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
A B C D E 64 62 127 52Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Задача: какая ломанная длиннее
, а у какой больше вершин
? У первой линии все звенья одинаковой длины, а именно по 13см. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
Многоугольник — это замкнутая ломанная линия
Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и вершина B являются соседними
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
сторона CD и сторона DE являются смежными
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются смежными
A B C D E F 120 60 58 122 98 141Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т. д.
д.
Прямой называется линия (множество точек имеющих лишь длину) которая не искривляется и не имеет ни начала ни конца.
Отрезок это прямая ограниченная с двух концов.
Луч это прямая ограниченная с одного конца.
Точка не имеет никаких измерительных характеристик, в задачах важно только ее местоположение.
Отметим три точки на прямой
Прямая не является трехмерной фигурой, более того она не искривляется, а бесконечно продолжается не имея ни ширины ни высоты в 1 плоскости. Поэтому и точки можно ставить на протяжении всей бесконечной длины где угодно, это повлияет только на длину отрезков, отсекаемых этими точками.
Количество отрезков
Так как точек три, расположим их произвольно на прямой и назовем а, b, c. Таким образом три точки ограничивают прямую, превращая в отрезки три раза, то есть мы имеем три отрезка
Количество лучей
Теперь разберемся с лучами. Прямая не ограниченна ни с начала ни с конца, а луч должен быть ограничен с одной стороны.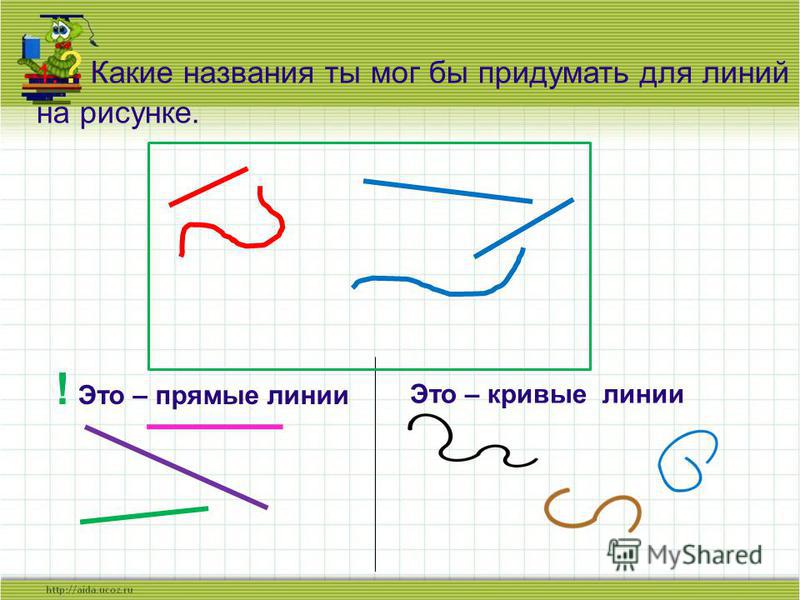
- если мы поставим на прямой 1 точку соответственно ограничив ее в этой точке то получим 2 луча,
- если поставим 2 точки мы ограничим прямую в двух местах, логично было бы предположить что и лучей у нас будет больше 2х, но ограничив в двух местах мы получили отрезок, т. к. он ограничен с двух сторон, и 2 луча, т. к. имеем еще начало и конец прямой, которые не ограничены,
- если поставим три точки? правильно, ситуация повторится, только увеличится количество отрезков
Ответ
Прямая на которой отмечены три точки делится этими точками на три отрезка и два луча.
Нарисуем прямую и отметим на ней три точки А, В, С. (см. рисунок)
Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными ее точками.
Или проще говоря, отрезок это часть прямой, ограниченная двумя точками.
На рисунке получилось три отрезка:
АВ (рис. 1)
АС (рис. 3)
Луч – часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной точки. Любая точка на прямой разделяет прямую на два луча.
Любая точка на прямой разделяет прямую на два луча.
Точка А делит прямую на лучи: а и АС. (рис. 4)
Точка В делит прямую на лучи: ВА и ВС. (рис. 5)
Точка С делит прямую на лучи: СА и с. (рис. 6)
Получилось три отрезка и шесть лучей.
Отрезок. Длина отрезка. Треугольник.
1. В этом параграфе вы познакомитесь с некоторыми понятиями геометрии. Геометрия — наука об «измерении земли». Это слово происходит от латинских слов: geo — земля и metr — мера, мерить. В геометрии изучаются различные геометрические объекты , их свойства, их связи с окружающим миром. Простейшие геометрические объекты — это точка, линия, поверхность. Более сложные геометрические объекты, например, геометрические фигуры и тела, образованы из простейших.
Если приложить к двум точкам А и В линейку и вдоль нее провести линию, соединяющую эти точки, то мы получим отрезок, который называют АВ или ВА (читаем: «а — бэ», «бэ- а»). Точки А и В называются концами отрезка (рисунок 1). Расстояние между концами отрезка, измеренное в единицах длины, называется длиной отрез ка .
Расстояние между концами отрезка, измеренное в единицах длины, называется длиной отрез ка .
Единицы длины: м — метр, см — сантиметр, дм — дециметр, мм — миллиметр, км — километр и др. (1 км = 1000 м; 1м =10 дм; 1 дм = 10 см; 1 см = 10 мм). Для измерения длины отрезков используют линейку, рулетку. Измерить длину отрезка, значит, выяснить, сколько раз в нем укладывается та или иная мера длины.
Равными называются два отрезка, которые можно совместить, наложив один на другой (рисунок 2). Например, можно вырезать реально или мысленно один из отрезков и приложить к другому так, чтобы совпали их концы. Если отрезки АВ и СК равны, то пишут АВ = СК. Равные отрезки имеют равные длины. Верно обратное: два отрезка, имеющие равные длины, равны. Если два отрезка имеют различные длины, то они не равны. Из двух неравных отрезков меньше тот, который составляет часть другого отрезка. Сравнивать отрезки наложением можно, используя циркуль.
Если мысленно продлить отрезок АВ в обе стороны до бесконечности, то мы получим представление о прямой АВ (рисунок 3).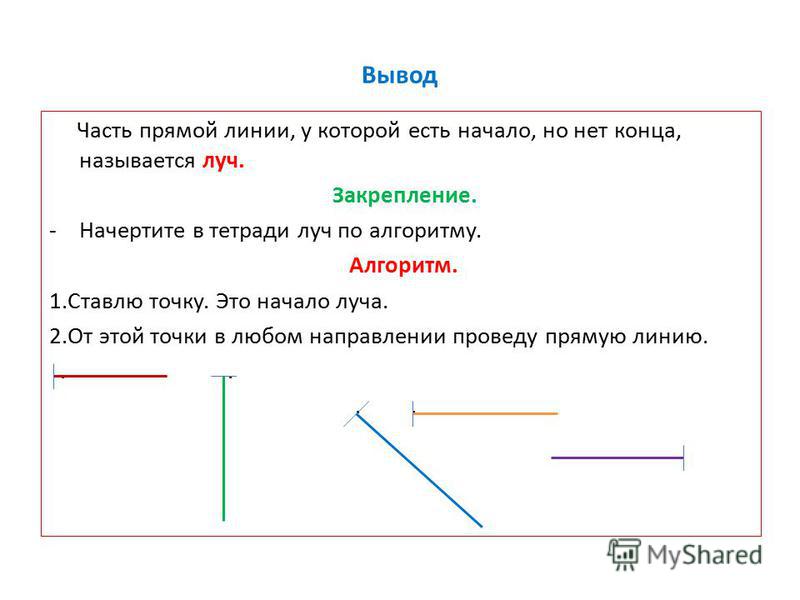 Любая точка, лежащая на прямой, разбивает ее на два луча (рисунок 4). Точка С разбивает прямую АВ на два луча СА и СВ. Тоска С называется началом луча .
Любая точка, лежащая на прямой, разбивает ее на два луча (рисунок 4). Точка С разбивает прямую АВ на два луча СА и СВ. Тоска С называется началом луча .
2. Если три точки, не лежащие на одной прямой, соединить отрезками, то получим фигуру, называемую треугольником. Данные точки называются вершинами треугольника, а отрезки, их соединяющие, сторонами треугольника (рисунок 5). FNM — треугольник, отрезки FN, NM, FM — стороны треугольника, точки F, N, M — вершины треугольника. Стороны всех треугольников обладают следующим свойством: длина любой из сторон треугольника всегда меньше суммы длин двух других его сторон.
Если мысленно продлить во все стороны, например, поверхность крышки стола, то получим представление о плоскости . Точки, отрезки, прямые, лучи располагаются на плоскости (рисунок 6).
Блок 1. Дополнительный
Мир, в котором мы живем, все, что нас окружает, древние называли природой или космосом. Пространство, в котором мы живем, считается трехмерным, т.е. имеет три измерения. Их часто называют: длина, ширина и высота (например, длина комнаты 4 м, ширина комнаты 2 м и высота 3 м).
Пространство, в котором мы живем, считается трехмерным, т.е. имеет три измерения. Их часто называют: длина, ширина и высота (например, длина комнаты 4 м, ширина комнаты 2 м и высота 3 м).
Представление о геометрической (математической) точке дает нам звезда на ночном небе, точка в конце этого предложения, след от иглы и т.д. Однако все перечисленные объекты имеют размеры, в отличие от них размеры геометрической точки считаются равными нулю (её измерения равны нулю). Поэтому реальную математическую точку можно лишь мысленно представить. Можно также сказать, в каком месте она находится. Поставив авторучкой в тетради точку, мы не изобразим геометрическую точку, но будем считать, что построенный объект есть геометрическая точка (рисунок 6). Точки обозначают заглавными буквами латинского алфавита: A , B , C , D , (читают «точка а, точка бэ, точка цэ, точка дэ» ) (рисунок 7).
Провода, висящие на столбах, видимая линия горизонта (граница между небом и землей или водой), русло реки, изображенное на карте, гимнастический обруч, струя воды, бьющая из фонтана дают нам представление о линиях.
Различают замкнутые и незамкнутые линии, гладкие и негладкие линии, линии с самопересечением и без самопересечения (рисунки 8 и 9).
Лист бумаги, лазерный диск, оболочка футбольного мяча, картон упаковочной коробки, новогодняя пластиковая маска и т.д. дают нам представление о поверхностях (рисунок 10). Когда красят пол комнаты или автомобиль, то покрывают краской именно поверхность пола или автомобиля.
Тело человека, камень, кирпич, головка сыра, мяч, ледяная сосулька и т.д. дают нам представление о геометрических телах (рисунок 11).
Наиболее простая из всех линий — это прямая . Приложим к листу бумаги линейку и проведем карандашом вдоль неё прямую линию. Мысленно продолжив эту линию до бесконечности в обе стороны, мы получим представление о прямой. Считают, что прямая имеет одно измерение — длину, а два других ее измерения равны нулю (рисунок 12).
При решении задач прямую изображают в виде линии, которую проводят вдоль линейки карандашом или мелом. Прямые обозначаются строчными латинскими буквами: a, b, n, m (рисунок 13). Можно обозначать прямую также двумя буквами, соответствующими точкам, лежащим на ней. Например, прямую n на рисунке 13 можно обозначить: АВ или ВА, А D или D А, D В или В D .
Прямые обозначаются строчными латинскими буквами: a, b, n, m (рисунок 13). Можно обозначать прямую также двумя буквами, соответствующими точкам, лежащим на ней. Например, прямую n на рисунке 13 можно обозначить: АВ или ВА, А D или D А, D В или В D .
Точки могут лежать на прямой (принадлежать прямой) и не лежать на прямой (не принадлежать прямой). На рисунке 13 изображены точки A, D, B, лежащие на прямой AB (принадлежащие прямой AB). При этом пишут. Читают: точка A принадлежит прямой AB, точка В принадлежит AB, точка D принадлежит АВ. Точка D принадлежит также и прямой m, ее называют общей точкой. В точке D прямые AB и m пересекаются. Точки P и R не принадлежат прямым AB и m:
Через любые две точки всегда можно провести прямую и причем только одну .
Из всех видов линий, соединяющих любые две точки, наименьшую длину имеет отрезок, концами которого служат данные точки (рисунок 14).
Фигура, которая состоит из точек и соединяющих их отрезков называется ломаной (рисунок 15). Отрезки, образующие ломаную, называются звеньями ломаной, а их концы — вершинами ломаной. Называют (обозначают) ломаную, перечисляя по порядку все ее вершины, например, ломаная ABCDEFG. Длиной ломаной называется сумма длин ее звеньев. Значит, длина ломаной ABCDEFG равна сумме: AB + BC + CD + DE + EF + FG.
Замкнутая ломаная называется многоугольником , ее вершины называются вершинами многоугольника , а ее звенья сторонами многоугольника (рисунок 16). Называют (обозначают) многоугольник, перечисляя по порядку все его вершины, начиная с любой, например, многоугольник (семиугольник) ABCDEFG , многоугольник (пятиугольник) RTPKL:
Сумма длин всех сторон многоугольника называется периметром многоугольника и обозначается латинской буквой p (читаем: пэ ). Периметры многоугольников на рисунке 13:
P ABCDEFG = AB + BC + CD + DE + EF + FG + GA.
P RTPKL = RT + TP + PK + KL + LR.
Мысленно продлив поверхность крышки стола или оконного стекла до бесконечности во все стороны, получим представление о поверхности, которая называется плоскостью (рисунок 17). Обозначают плоскости малыми буквами греческого алфавита: α, β, γ, δ, … (читаем: плоскость альфа, бетта, гамма, дельта, и т.д. ).
Блок 2. Словарь.
Составьте словарь новых терминов и определений из §2. Для этого в пустые строки таблицы впишите слова из списка терминов, приведенного ниже. В таблице 2 укажите номера терминов в соответствии с номерами строк. Рекомендуется перед заполнением словаря еще раз внимательно просмотреть §2 и блок 2.1.
Блок 3. Установите соответствие (УС).
Геометрические фигуры.
Блок 4. Самопроверка.
Измерение отрезка с помощью линейки.
Напомним, что измерить отрезок АВ в сантиметрах, значит, сравнить его с отрезком длиной 1см и узнать, сколько таких отрезков по 1см помещается в отрезке АВ. Чтобы измерить отрезок в других единицах длины, поступают подобным же образом.
Чтобы измерить отрезок в других единицах длины, поступают подобным же образом.
Для выполнения заданий работайте по плану, приведенному в левой колонке таблицы. При этом правую колонку рекомендуем закрыть листом бумаги. Затем вы сможете сопоставить свои выводы с решениями, приведенными в таблице справа.
Блок 5. Установление последовательности действий (УП).
Построение отрезка заданной длины.
Вариант 1 . В таблице записан перепутанный алгоритм (перепутанный порядок действий) построения отрезка заданной длины (например, построим отрезок ВС = 7см). В левом столбце указание к действию в правом результат выполнения этого действия. Переставьте строки таблицы так, чтобы получился верный алгоритм построения отрезка заданной длины. Запишите верную последовательность действий.
Вариант 2. В следующей таблице приведен алгоритм построения отрезка КМ = n см, где вместо n можно подставить любое число. В этом варианте нет соответствия между действием и результатом.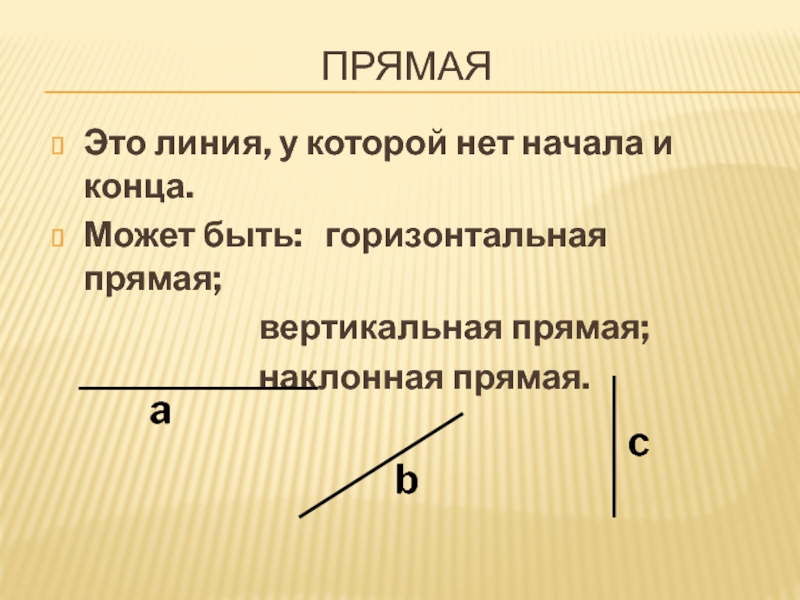 Поэтому необходимо установить последовательность действий, затем для каждого действия выбрать его результат. Ответ запишите в виде: 2а, 1в, 4б и т.д.
Поэтому необходимо установить последовательность действий, затем для каждого действия выбрать его результат. Ответ запишите в виде: 2а, 1в, 4б и т.д.
Вариант 3. Используя алгоритм варианта 2, постройте в тетради отрезки при n = 3 см, n = 10 см, n = 12 см.
Блок 6. Фасетный тест.
Отрезок, луч, прямая, плоскость.
В задачах фасетного теста используются рисунки и записи под номерами 1 — 12, приведённые в таблице 1. Из них формируются данные задач. Затем к ним добавляются требования задач, которые в тесте помещены после соединительного слова «ТО». Ответы к задачам помещены после слова «РАВНО». Набор задач приведён в таблице 2. Например, задача 6.15.19 составляется следующим образом: «ЕСЛИ в задаче используется рисунок 6, з атем к нему добавляется условие под номером 15, требование задачи стоит под номером 19.»
13) построить четыре точки так, чтобы каждые три из них не лежали на одной прямой;
14) провести через каждые две точки прямую;
15) каждую из поверхностей коробки продлить мысленно во все стороны до бесконечности;
16) количество различных отрезков на рисунке;
17) количество различных лучей на рисунке;
18) количество различных прямых на рисунке;
19) количество получившихся различных плоскостей;
20) длина отрезка АС в сантиметрах;
21) длина отрезка АВ в километрах;
22) длина отрезка DC в метрах;
23) периметр треугольника PRQ;
24) длина ломаной QPRMN;
25) частное периметров треугольников RMN и PRQ;
26) длина отрезка ED;
27) длина отрезка BE;
28) количество получившихся точек пересечения прямых;
29) количество получившихся треугольников;
30) количество частей, на которые оказалась разделена плоскость;
31) периметр многоугольника, выраженный в метрах;
32) периметр многоугольника, выраженный в дециметрах;
33) периметр многоугольника, выраженный в сантиметрах;
34) периметр многоугольника, выраженный в миллиметрах;
35) периметр многоугольника, выраженный в километрах;
РАВНО (равна, имеет вид):
а) 70; б) 4; в) 217; г) 8; д) 20; е) 10; ж) 8∙b; з) 800∙b; и) 8000∙b; к) 80∙b; л) 63000; м) 63; н) 63000000; о) 3; п) 6; р) 630000; с) 6300000; т) 7; у) 5; ф) 22; х) 28
Блок 7. Давай поиграем.
Давай поиграем.
7.1. Математический лабиринт.
Лабиринт состоит из десяти комнат с тремя дверьми каждая. В каждой из комнат находится по одному геометрическому объекту (он нарисован на стене комнаты). Сведения об этом объекте находятся в «путеводителе» по лабиринту. Читая его, надо переходить в ту комнату, о которой написано в путеводителе. Проходя по комнатам лабиринта, рисуйте свой маршрут. В двух последних комнатах имеются выходы.
Путеводитель по лабиринту
- Войти в лабиринт надо через комнату, где находится геометрический объект, у которого нет начала, но есть два конца.
- Геометрический объект этой комнаты не имеет размеров, он подобен далёкой звезде на ночном небе.
- Геометрический объект этой комнаты составлен из четырёх отрезков, имеющих три общие точки.
- Этот геометрический объект состоит из четырёх отрезков с четырьмя общими точками.
- В этой комнате находятся геометрические объекты, каждый из которых имеет начало, но не имеет конца.

- Здесь два геометрических объекта, не имеющих ни начала, ни конца, но с одной общей точкой.
- Представление об этом геометрическом объекте даёт полет артиллерийских снарядов
(траектория движения).
- В этой комнате находится геометрический объект с тремя вершинами, но это не горные
- Об этом геометрическом объекте даёт представление полёт бумеранга (охотничье
оружие коренных жителей Австралии). В физике эту линию называют траекторией
движения тела.
- Представление об этом геометрическом объекте даёт поверхность озера в
безветренную погоду.
Теперь можете выходить из лабиринта.
В лабиринте находятся геометрические объекты: плоскость, незамкнутая линия, прямая, треугольник, точка, замкнутая линия, ломаная, отрезок, луч, четырёхугольник.
7.2. Периметр геометрических фигур.
В рисунках выделите геометрические фигуры: треугольники, четырёхугольники, пяти — и шестиугольники. С помощью линейки (в миллиметрах) определите периметры некоторых из них.
С помощью линейки (в миллиметрах) определите периметры некоторых из них.
7.3. Эстафета геометрических объектов.
В заданиях эстафеты есть пустые рамки. В них запишите пропущенное слово. Затем перенесите это слово в другую рамку, куда показывает стрелка. При этом можно изменять падеж этого слова. Проходя по этапам эстафеты, выполняйте требуемые построения. Если эстафету пройдёте правильно, то в конце получите слово: периметр .
7.4. Крепость геометрических объектов.
Прочитайте § 2, выпишите из его текста названия геометрических объектов. Затем впишите эти слова в пустые клетки «крепости».
Точка, отрезок, луч, прямая — числовая прямая
Мы рассмотрим каждую из тем, а в конце будут даны тесты по темам.
Точка в математике
Что такое точка в математике? Математическая точка не имеет размеров и обозначается заглавными латинскими буквами: A, B, C, D, F и т.д.
На рисунке можно видеть изображение точек A, B, C, D, F, E, M, T, S.
Отрезок в математике
Что такое отрезок в математике? На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка. Концы отрезка — две граничные точки.
На рисунке мы видим следующее: отрезки [A;C],[C;D],[D;M],[M;F],[F;E] и [E;T], а также две точки B и S.
Прямая в математике
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности. Прямая в математике обозначается двумя любыми точками прямой. Для объяснения понятия прямой ученику можно сказать, что прямая — это отрезок, который не имеет двух концов.
На рисунке изображены две прямые: CD и EF.
Луч в математике
Что же такое луч? Определение луча в математике: луч — часть прямой, которая имеет начало и не имеет конца. В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
На рисунке изображены лучи: DC, KC, EF, MT, MS. Лучи KC и KD — один луч, т.к. у них общее начало.
Числовая прямая в математике
Определение числовой прямой в математике: прямая, точки которой отмечают числа, называют числовой прямой.
На рисунке изображена числовая прямая, а также луч OD и ED
Нужна помощь в учебе?
Предыдущая тема: Сложение и вычитание дробей с одинаковыми знаменателями: ПРИМЕРЫ
Следующая тема:   Чтение и запись больших натуральных чисел: разряды, классы + ПРИМЕР
прямая линия — Перевод на английский — примеры русский
На основании Вашего запроса эти примеры могут содержать грубую лексику.
На основании Вашего запроса эти примеры могут содержать разговорную лексику.
В Евклидовой геометрии прямая линия представляет собой кратчайшее расстояние между двумя точками.
Мне не нравится эта большая прямая линия.
В сакральной геометрии прямая линия считается мужской, а кривая — женской.
In sacral geometry the direct line is considered men, and a curve — female.Они звонят мне, словно у меня прямая линия с Овальным кабинетом.
They call me, like I’ve got some direct line to the Oval…Щёлкнул выключателем — вот тебе и прямая линия.
Не прямая линия, не дуга, ничего.
Таким образом, действительно, решение — это прямая линия, заданная в полярных координатах.
Thus, indeed, the solution is a straight line given in polar coordinates.Ранее была прямая линия из Рендсбурга в Хузум через Эрфде, в отличие от нынешнего маршрута через Юбек.
There used to be a direct line from Rendsburg to Husum via Erfde, as distinct from the current route via Jübek.Вот моя прямая линия и номер мобильного.
Думаю, это его прямая линия, управляющий Хан.
Потому что прослеживается очень прямая линия от Диллона и Спрингера к тебе.
Это была его прямая линия, Фил
И эта… твоя прямая линия.
Если ветер все еще дует с юго-запада, получается прямая линия от Кру.
If the wind’s still blowing from the southwest it’s in direct line from Crewe.Они чрезвычайно сложны, и редко существует прямая линия от А до Я.
They are extremely complex, and there is rarely a straight line from A to Z. Так что улететь от всего этого стоять на планете, не окутаной дымом, где единственная прямая линия — солнечный луч. ..
..
Идея Кальвино о быстром пути между двумя пунктами — это косвенный путь, не прямая линия.
It’s Calvino’s idea of the quickest way between two points is the circuitous line, not the straight line.Смотрите, если соединить раны так, получится сплошная прямая линия, Точно поперек тела и вокруг плеча.
See, if you line the wounds up, they form a single straight line, right across the body, and around the shoulder. Пожалуйста, обратите внимание, что данное расстояние рассчитывается как прямой маршрут (прямая линия) и не учитывает расстояние, которое необходимо преодолеть автомобилю.
Понимаете, говорится следующее, вот темпы роста Китая, вот темпы роста США, и вот получается прямая линия.
You know, everything says, here’s the growth rate of China, here’s the growth rate of the U.S., here it goes — straight line.Кремль отложил «Прямую линию с Путиным» на неопределенный срок. Объясняем возможные причины
- Владимир Дергачев, Петр Козлов, Сергей Горяшко, Наталия Зотова
- Би-би-си
Автор фото, EPA
Подпись к фото,В 2019 году «Прямая линия с Путиным» стала 17-й по счету и длилась более четырех часов
«Прямая линия с Владимиром Путиным» не планируется в июле, рассказал Би-би-си пресс-секретарь президента России Дмитрий Песков.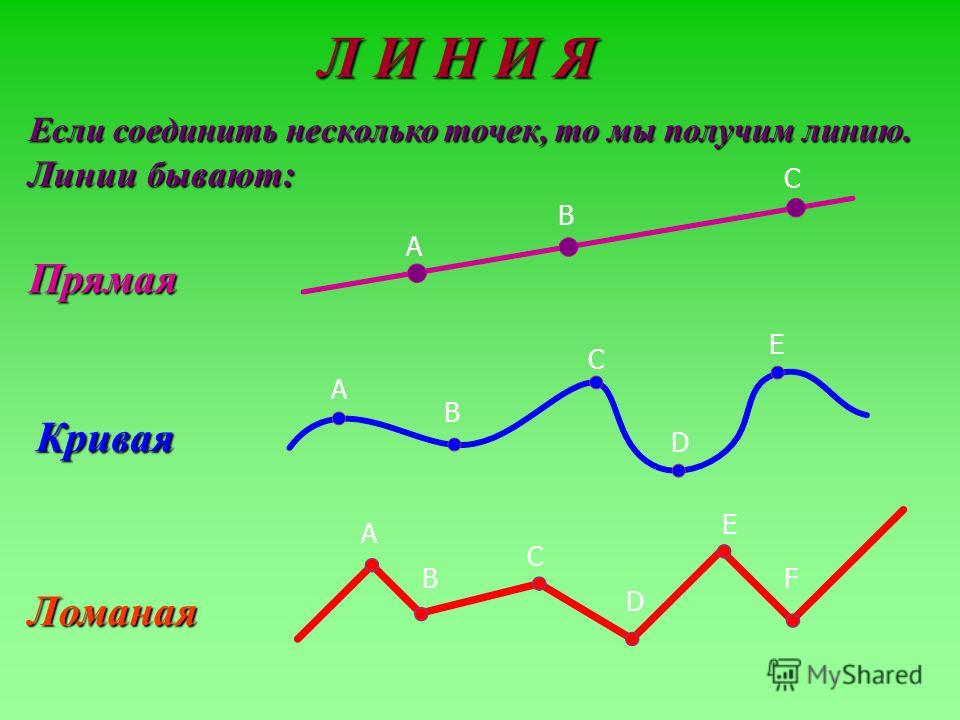 До этого он говорил журналистам, что «линия» пройдет после голосования по поправкам к Конституции РФ 1 июля.
До этого он говорил журналистам, что «линия» пройдет после голосования по поправкам к Конституции РФ 1 июля.
В последние годы «линия» проходила в июне — планы Кремля провести ее в привычные сроки нарушила пандемия.
Этот формат существует с 2001 года, но от такого «общения с народом» мог устать сам президент, считает политолог Татьяна Становая.
Тем не менее во вторник Дмитрий Песков рассказал журналистам, что ежегодная «Прямая линия с президентом России Владимиром Путиным» состоится — после голосования по поправкам к Конституции 1 июля. «Это будет полноформатная прямая линия общения Путина с людьми», — подчеркнул он.
В четверг пресс-секретарь президента заявил Би-би-си, что «линия» пройдет не в июле, а позднее. Назвать более точные сроки он отказался.
Технически мероприятие готовится не так долго — оборудовать площадку и развернуть колл-центр можно за 10-14 дней. Об этом сказал Би-би-си источник, знакомый с подготовкой «линии», но не имеющий полномочий давать официальные комментарии.
Песков призвал не сравнивать формат прямой линии с совещанием 15 июня по мерам поддержки экономики и социальной сферы. Участие в нем, кроме чиновников и бизнеса, приняли обычные россияне. «Все-таки это совсем разные форматы», — пояснил пресс-секретарь президента.
Последняя «линия» в июне 2019 года стала 17-й по счету и длилась более четырех часов.
Важная роль в подготовке «линии» принадлежит внутриполитическому блоку администрации президента (АП), который курирует Сергей Кириенко. Однако в июне АП оказалась занята подготовкой голосования по Конституции, а провести «Прямую линию» в условиях пандемии оказалось сложно, признает политолог Григорий Казанков: «Никто же не отменял противовирусных ограничений, а «Прямая линия» — красивая история, там много людей в зале, большие группы на прямой связи, картинка красивая. А тут чего, все из дома будут выходить в эфир?»
В итоге провести «линию» в июне не представилось возможным, хотя в изначальном политическом календаре она логично выглядела сразу после планировавшегося на 22 апреля «референдума» по Конституции.
«Политический календарь Путина сломался, и это заставляет поддерживать линейку мобилизационных мероприятий — среди них парад и голосование по Конституции, — сказал Би-би-си руководитель программы «Российская внутренняя политика» московского центра Карнеги Андрей Колесников. — Но мобилизационный эффект сильно преувеличен Кремлем, и не очевидно, что высокие результаты голосования и «Прямая линия» вслед за ним пойдут в плюс Путину».
По словам эксперта, впереди длинный период восстановления доходов и рынка труда — если оно вообще начнется, — и нарочито мобилизационные действия власти могут начать раздражать значительную часть общества. В политтехнологическом плане плюсы от проведения «Прямой линии» в ближайшее время неочевидны, считает Колесников.
Казанков тоже считает, что мобилизационная роль «линии» неочевидна: «К тому же в июле странно ее проводить — время мертвое».
Популярность «линии» в последние годы падала, и в Кремле пытались привлечь к ней интерес
«Прямая линия с Владимиром Путиным» — ежегодная телепередача с участием главы государства, в ходе которой он отвечает на вопросы граждан. Часть вопросов присылают в редакцию, часть — задают зрители в студии и участники телемостов из регионов. В 2016 году Би-би-си выяснила, что вопросы участников репетировали в подмосковном пансионате.
Часть вопросов присылают в редакцию, часть — задают зрители в студии и участники телемостов из регионов. В 2016 году Би-би-си выяснила, что вопросы участников репетировали в подмосковном пансионате.
Первые десять прямых линий с 2001 года проходили в декабре или осенью. В 2012 году она не проводилась, официально — из-за переноса на теплое время года. В СМИ это связывали с ростом протестных настроений в обществе,
После 2012-го мероприятие стало проходить в апреле, а в 2017 году впервые было организовано летом — в июне. С тех пор оно проходило в первом месяце лета.
Постепенно интерес россиян к формату угасал. В 2018 году его аудитория оказалась самой малочисленной за последние шесть лет, свидетельствовали данные компании Mediascope. И это несмотря на то, что Кремль пробовал новые форматы мероприятия.
В 2018-м президент впервые за историю формата отчитывал губернаторов и министров в режиме конференц-связи, а в предыдущие годы к «линии» подключили соцсети «ВКонтакте» и «Одноклассники». К линии старались привлечь внимание и через трансляцию «неудобных вопросов» президенту бегущей строкой.
К линии старались привлечь внимание и через трансляцию «неудобных вопросов» президенту бегущей строкой.
Эксперты перечисляют причины переноса, среди которых — и усталость президента от такого формата
Политконсультант Дмитрий Фетисов видит в переносе «линии» идеологические и технологические предпосылки.
Голосование по поправкам в Конституцию — одно из важнейших событий за последние 20 лет, и логично использовать «линию» для подведения итогов, указал эксперт. Накануне голосования Путин выступит со специальным обращением к гражданам с просьбой поддержать поправки, прогнозирует Фетисов.
Технологический аспект переноса «линии», по его мнению, заключается в нецелесообразности отвлекать кремлевскую администрацию от подготовки к голосованию.
Формат «линии» варьируется в зависимости от задач политического планирования, полагает политолог Евгений Минченко. Проведение мероприятия уже после голосования по Конституции он объяснил тем, что рассказы граждан о своих проблемах на «линии» преждевременны.
Для просмотра этого контента вам надо включить JavaScript или использовать другой браузер
Подпись к видео,«Вы меня видите, слышите?»: Владимир Путин и видеосвязь
«Люди бы говорили ему [президенту] — у меня кран течет, у меня соседи шумят, у меня финансовые проблемы. Они не спрашивали бы про обнуление [президентских сроков в поправках к Конституции]. А зачем ему сейчас это, когда ключевая повестка — голосование по поправкам к Конституции? — рассуждает Минченко. — Логично сначала провести голосование, которое касается принципиальных вопросов организации государственной власти, а потом перейти к жанру «президент решает конкретные проблемы людей».
В ситуации с коронавирусом на первый план для президента выходят мероприятия, которые отменять нельзя — референдум и, что намного важнее для Путина, парад Победы 24 июня, считает руководитель аналитической фирмы Rpolitik Татьяна Становая.
Для Путина эта прямая линия давно перестала играть «сакрально-социальную роль» и «превращается в ежегодную пытку», полагает Становая. Она считает, что мероприятие и вовсе могут перенести на сентябрь-октябрь.
Она считает, что мероприятие и вовсе могут перенести на сентябрь-октябрь.
«Для него [президента] прямая линия — традиция, ритуал, который он должен выполнять ежегодно, чтобы поддерживать прямую связь с электоратом, доносить свои идеи, получать обратную связь, — объясняет она. — Он это видит как возможность воздействия на элиту, возможность исправлять ошибки. Для него это обременение, которое нельзя сбрасывать».
По ее мнению, глава государства находится вне логики лидеров западных демократических систем, где избранный глава государства имеет свой электорат, рейтинг и соперников.
«Путин живет в мире, где у него нет альтернативы, у него автоматическая поддержка. Ему не нужно специальных кампаний, мероприятий, чтобы подстраховать результат на референдуме или выборах, потому что то, что он делает, обслуживает интересы нации — он верит в это. Он давно превратился в миссионера», — говорит эксперт.
Точка линия прямая луч отрезок. «Прямая» в геометрии
У луча света на картинке начальной точкой является солнце
Точка разделяет прямую на две части — два луча A A
Луч обозначается строчной (маленькой) латинской буквой.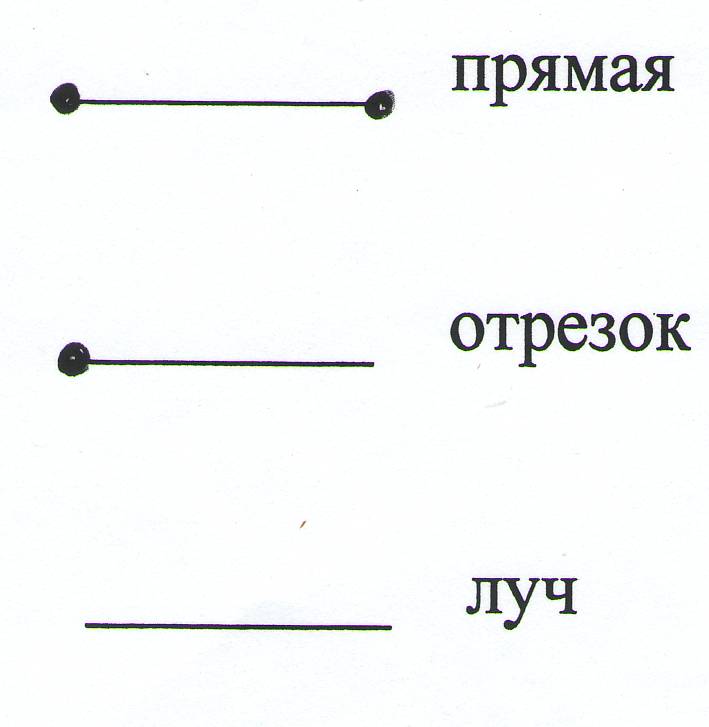 Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
лучи AB и AC совпадают
лучи CB и CA совпадают
Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. Длина отрезка — это расстояние между его начальной и конечной точками
Через одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
прямая линия AB
От прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками.
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок
отрезок AB
Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Многоугольник — это замкнутая ломанная линия
Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.
Смежные стороны многоугольника — это смежные звенья ломанной.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и вершина B являются соседними
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
сторона CD и сторона DE являются смежными
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются смежными
A B C D E F 120 60 58 122 98 141
Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т. д.
д.
shpargalkablog.ru
Основы геометрии
Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства.
Познакомимся с основными геометрическими понятиями, изучаемыми в начальной школе .
Точка — это основная и самая простая геометрическая фигура.
В геометрии точка обозначается заглавной латинской буквой или цифрой. Многие латинские буквы по написанию похожи на английские буквы.
В тексте точку обозначают следующим символом: « (·) A » — точка « А ».
Прямая — это самая простая геометрическая фигура, которая не имеет ни начала, ни конца.
Слова «не имеет ни начала, ни конца» говорят о том, что прямая бесконечна.
Способы обозначения прямых
Двумя заглавными латинскими буквами в том случае, если этими буквами обозначены точки, расположенные на прямой.
Луч — это часть прямой линии, которая расположена по одну сторону от какой-либо точки. У луча есть начало, но нет конца.
Способы обозначения лучей
Двумя заглавными латинскими буквами в том случае, когда первая точка — начало луча, а вторая точка лежит на луче.
Отрезок — это часть прямой линии, которая ограничена двумя точками (концами отрезка). У отрезка есть и начало, и конец.
Основное свойство отрезка — это его длина.
Длина отрезка — это расстояние между его концами.
В математике отрезок обозначается заглавными латинскими буквами.
Ломаная — это геометрическая фигура, состоящая из точек, которые соединены отрезками.
Вершины ломаной — это точки, в которых соединяются отрезки, образующие ломаную.
Звенья ломаной — это отрезки ломаной.
В математике ломаная обозначается заглавными латинскими буквами.
Ломаная « ABCD ».
Вершины ломаной — A, B, C, D .
Звенья ломаной — AB, BC, CD.
Чтобы найти длину ломаной, необходимо сложить длины всех её звеньев (отрезков), из которых она состоит.
KLCM = KL + LC + CM = 3 см + 2 см + 2 см = 7 см
Вот мы и познакомились с основами геометрии . Теперь мы готовы рассмотреть не менее важную геометрическую фигуру — угол. Для этого перейдите на следующую страницу, нажав на кнопку «Посмотреть содержание темы» вверху страницы.
Точка. Отрезок. Луч. Прямая. Числовая прямая
Мы рассмотрим каждую из тем, а в конце будут даны тесты по темам.
Точка в математике
Что такое точка в математике? Математическая точка не имеет размеров и обозначается заглавными латинскими буквами: A, B, C, D, F и т.д.
На рисунке можно видеть изображение точек A, B, C, D, F, E, M, T, S.
Отрезок в математике
Что такое отрезок в математике? На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка. Концы отрезка — две граничные точки.
Концы отрезка — две граничные точки.
На рисунке мы видим следующее: отрезки ,,,, и , а также две точки B и S.
Прямая в математике
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности. Прямая в математике обозначается двумя любыми точками прямой. Для объяснения понятия прямой ученику можно сказать, что прямая — это отрезок, который не имеет двух концов.
На рисунке изображены две прямые: CD и EF.
Луч в математике
Что же такое луч? Определение луча в математике: луч — часть прямой, которая имеет начало и не имеет конца. В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
На рисунке изображены лучи: DC, KC, EF, MT, MS. Лучи KC и KD — один луч, т.к. у них общее начало.
Числовая прямая в математике
Определение числовой прямой в математике: прямая, точки которой отмечают числа, называют числовой прямой.
На рисунке изображена числовая прямая, а также луч OD и ED
Основные геометрические фигуры
К основным геометрическим фигурам на плоскости относятся точка и прямая линия . Отрезок , луч , ломаная линия — простейшие геометрические фигуры на плоскости.
Точка — это самая малая геометрическая фигура , которая является основой всех прочих построений (фигур) в любом изображении или чертеже.
Всякая более сложная геометрическая фигура — это множество точек , которые обладают определенным свойством, характерным только для этой фигуры.
Прямую линию, или прямую, можно представить себе как бесчисленное множество точек , которые расположены на одной линии, не имеющей ни начала, ни конца. На листе бумаги мы видим только часть прямой линии, так как она бесконечна. Прямая изображается так:
Часть прямой линии , ограниченная с двух сторон точками , называется отрезком прямой, или отрезком. Отрезок изображается так:
Отрезок изображается так:
Луч — это направленная полупрямая, которая имеет точку начала и не имеет конца. Луч изображается так:
Если на прямой вы поставили точку , то этой точкой прямая разбивается па два луча , противоположно направленных. Такие лучи называются дополнительными.
Ломаная линия — это несколько отрезков , соединенных между собой так, что конец первого отрезка является началом второго отрезка, а конец второго отрезка — началом третьего отрезка и т. д., при этом соседние (имеющие одну общую точку ) отрезки расположены не на одной прямой. Если конец последнего отрезка не совпадает с началом первого, то такая ломаная линия называется незамкнутой.
Выше изображена трехзвенная ломаная линия .
Если конец последнего отрезка ломаной совпадает с началом первого отрезка, то такая ломаная линия называется замкнутой. Примером замкнутой ломаной служит любой многоугольник:
Четырехзвенная замкнутая ломаная линия — четырехугольник
Трехзвенная замкнутая ломаная линия — треугольник
Плоскость, как и прямая, — это первичное понятие, не имеющее определения. У плоскости, как и у прямой, нельзя видеть ни начала, ни конца. Мы рассматриваем только часть плоскости, которая ограничена замкнутой ломаной линией.
У плоскости, как и у прямой, нельзя видеть ни начала, ни конца. Мы рассматриваем только часть плоскости, которая ограничена замкнутой ломаной линией.
Примером плоскости является поверхность вашего рабочего стола, тетрадный лист, любая гладкая поверхность. Плоскость можно изобразить как заштрихованную
геометрическую фигуру:
1 класс. Математика. Точка. Прямая, кривая и ломаная линии. — Прямая линия. Кривая линия. Ломаная линия.
Комментарии преподавателя
.На данном уроке Вы изучите простейшие геометрические понятия, о которых вам расскажет мама дракончиков. Вместе с дракончиками Вы изучите такие основные понятия, как прямая линия, луч, отрезок, угол, ломаная и кривая линия. У Вас будет возможность изучить предложенный материал на наглядных примерах.
Тема: Наглядная геометрия
Урок: Начальные геометрические понятия
На этом уроке будут изучены простейшие геометрические понятия. Для лучшего понимания рассмотрим сказку про дракончиков.
Для лучшего понимания рассмотрим сказку про дракончиков.
Далеко-далеко в горах живет большая-большая семья драконов: папа-дракон, мама-дракониха и много маленьких дракончиков. Когда дракончики были маленькие, они учились ползать, бегать, летать, прыгать, узнавали, что такое снег, дождь, звёзды, учились в горах, учились даже огнём дышать. Когда дракончики немножко подросли, мама решила их научить математики, в том числе геометрии.Дракончики очень удивились, они не поняли о чём идет речь. Мама предложила им сесть на площадке перед большой скалой и смотреть, что она будет рисовать. Она начала рисовать мелом на этом плоском куске скалы различные геометрические вещи, начиная с самых простых. Вначале мама-дракониха нарисовала линию, которая изображена на рисунке. (рис. 1)
Рис. 1
Мама-дракониха сказала, что эта линия называется прямая.Это такое геометрическое понятие.
Прямая линия — это линия, которая совершенно бесконечна.
Прямая линия идет бесконечно в одну сторону и в другую сторону. Есть такое даже выражение «Летит в небе по прямой».
Потом мама нарисовала точку и от нее провела линию. (рис. 2)
Рис. 2
Она объяснила, что точка — это начало, от нее идет линия в бесконечность. Это называется луч.
Луч — это полупрямая, которая имеет точку начала и не имеет конца.
Он так называется, что она как луч света. У луча света всегда есть начало. Он всегда начинается либо на солнце, либо на свечки, либо в фонарике, либо на звезде далекой. Дракончики поняли, что такое луч.
Потом мама-дракониха попросила представить дракончиков, что они от прямого отрежут кусочек. Такая фигура называется отрезок.(рис. 3)
Рис. 3
Отрезок — это часть, которая прямой ограничена с двух сторон.
Отрезок может быть длинным или коротким. Дракончики сразу не поняли. Тогда мама нарисовала еще несколько отрезков: длинные и короткие. (рис. 4)
(рис. 4)
Рис. 4
Это всё отрезки. Теперь дракончики все поняли.
Потом мама-дракониха из одной точки отложила два луча, получилась фигура, которая называется угол.(рис. 5)
Рис. 5
Причем угла называется вся фигура.
Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки.
Потом мама-дракониха решила нарисовать еще одну форму линии. (рис. 6)
Рис. 6
Такая линия называется ломаная линия . Потому что взяли фактически прямую линию и поломали ее.И каждый кусочек на этой линии называется звено . Ломаные линии могут быть самые разные, по разному поломанные.
Следом мама нарисовала загогулину. (рис. 7)
Рис. 7
Это кривая линия . Таких кривых линий можно нарисовать много-много самых разных.
Потом мама-дракониха спросила у маленьких дракончиков, по какой линии они летаете в небе. Дракончики задумались.И, что он летает по кривой линии, он делает всякие пируэты, закладывает спирали, петли делает. А другой дракончик сказал, когда они в снежки играли, он повисал в воздухе, махал крылышками, а в нем кидали снежками. Он улетал от них и дёргался туда-сюда, туда-сюда. Получалась ломаная линия. Мама-дракониха сказала, что дракончики все поняли правильно. Драконы летают и по кривой линии, и по ломаной, иногда просто по прямой.
Дракончики задумались.И, что он летает по кривой линии, он делает всякие пируэты, закладывает спирали, петли делает. А другой дракончик сказал, когда они в снежки играли, он повисал в воздухе, махал крылышками, а в нем кидали снежками. Он улетал от них и дёргался туда-сюда, туда-сюда. Получалась ломаная линия. Мама-дракониха сказала, что дракончики все поняли правильно. Драконы летают и по кривой линии, и по ломаной, иногда просто по прямой.
И тут мама заметила, что дракончики уже стали скучать и как-то вертеться, уже плохо её слушают. Она поняла, что пора их отпустить, она сказала, что урок закончен. Дракончики замахали крылышками, взлетели в небо, разлетелись над горами, кричали, смеялись. Мама смотрела на них и улыбалась, махала им лапой.
Итак, на уроке мы выучили такие простейшие геометрические понятия, как прямая линия, отрезок, луч, угол.Также мы рассмотрели ломаную и кривую линию. После изученного урока Вы будете знать простейшие геометрические понятия не хуже маленьких дракончиков.
Источник конспекта: http://interneturok.ru/ru/school/matematika/1-klass/beksperimentb/nachalnye-geometricheskie-ponyatiya?seconds=0
Источник видео: https://www.youtube.com/watch?v=o8Pu_Q8YFjk
Отрезок
Отрезок. Длина отрезка. Треугольник.
1.В этом параграфе вы познакомитесь с некоторыми понятиями геометрии. Геометрия — наука об «измерении земли». Это слово происходит от латинских слов: geo — земля и metr — мера, мерить. В геометрии изучаются различные геометрические объекты , их свойства, их связи с окружающим миром. Простейшие геометрические объекты — это точка, линия, поверхность. Более сложные геометрические объекты, например, геометрические фигуры и тела, образованы из простейших.
Если приложить к точкам А и В линейку и вдоль нее провести линию, соединяющую эти точки, то мы получим отрезок, который называют АВ или ВА (читаем: «а — бэ», «бэ– а»).Точки А и В называются концами отрезка (рисунок 1). Расстояние между концами отрезка, измеренное в единицах длины, называется длиной отрезком ка .
Расстояние между концами отрезка, измеренное в единицах длины, называется длиной отрезком ка .
Единицы длины: м — метр, см — сантиметр, дм — дециметр, мм — миллиметр, км — километр и др. (1 км = 1000 м; 1м = 10 дм; 1 дм = 10 см; 1 см = 10 мм). Для измерения длины отрезков использовать линейку, рулетку. Измерить длину отрезка, значит выяснить, сколько раз в нем укладывается та или иная мера длины.
Равными называются два отрезка, которые можно совместить, наложив один на другой (рисунок 2). Например, можно вырезать реально или мысленно один из их отрезков и приложить к другому так, чтобы совпали концы. Если отрезки АВ и СК равны, то пишут АВ = СК. Равные отрезки имеют равную длину. Верно обратное: два отрезка, имеющие равные длины, равны. Если два отрезка имеют длину, то они не равны. Из двух неравных отрезков меньше тот, который составляет часть другого отрезка.Сравнивать отрезки наложением можно, используя циркуль.
Если мысленно продлить отрезок АВ в обе стороны до бесконечности, то прямой получим представление о АВ (рисунок 3). Любая точка, лежащая на прямой, разбивает ее на два луча (рисунок 4). Точка С разбивает прямую АВ на два луча СА и СВ. Тоска С называется Начало луча .
2. Если три точки, не лежащий на одной прямой, соединить отрезками, то получим фигуру, называемую треугольником. Данные точки называются вершинами ика, а отрезки, их соединяющие, стороны треугольника (рисунок 5). FNM — треугольник, отрезки FN, NM, FM — стороны треугольника, точки F, N, M — вершины треугольника. Стороны всех треугольников своим следующим своим: д лина любой из сторон треугольника всегда меньше суммы двух других его сторон.
Если мысленно продлить во все стороны, например, поверхность крышки стола, то получим представление о плоскости .Точки, отрезки, прямые, лучи располагаются на плоскости (рисунок 6).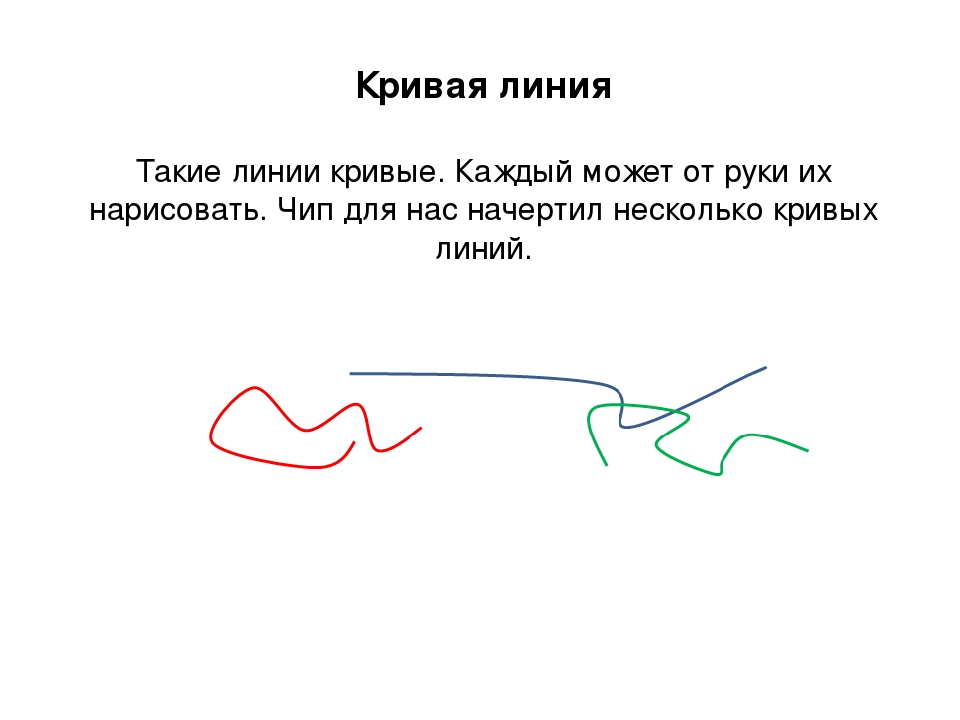
Блок 1. Дополнительный
Мир, в котором мы живем, все, что нас окружает, древние называли природой или космосом. Пространство, в котором мы живем, считается трехмерным, т.е. имеет три измерения. Их часто называют: длина, ширина и высота (например, длина комнаты 4 м, ширина комнаты 2 м и высота 3 м).
Представление о геометрической (математической) точке дает нам звезда на ночном небе, точка в конце этого предложения, след от иглы и т.д. Однако все перечисленные объекты имеют размеры, в отличие от размеров геометрической точки равными нулю (измерения равны нулю). Поэтому реальную математическую точку можно лишь мысленно представить. Можно также сказать, в каком месте она находится. Поставив авторучкой в геометрическую точку, мы не изобразим геометрическую точку, но будем считать, что построенный объект есть геометрическая точка (рисунок 6). Точки обозначают заглавными буквами латинского алфавита: A , B , C , D , (читают « точка а, точка бэ, точка цэ, точка дэ» ) рисунок 7).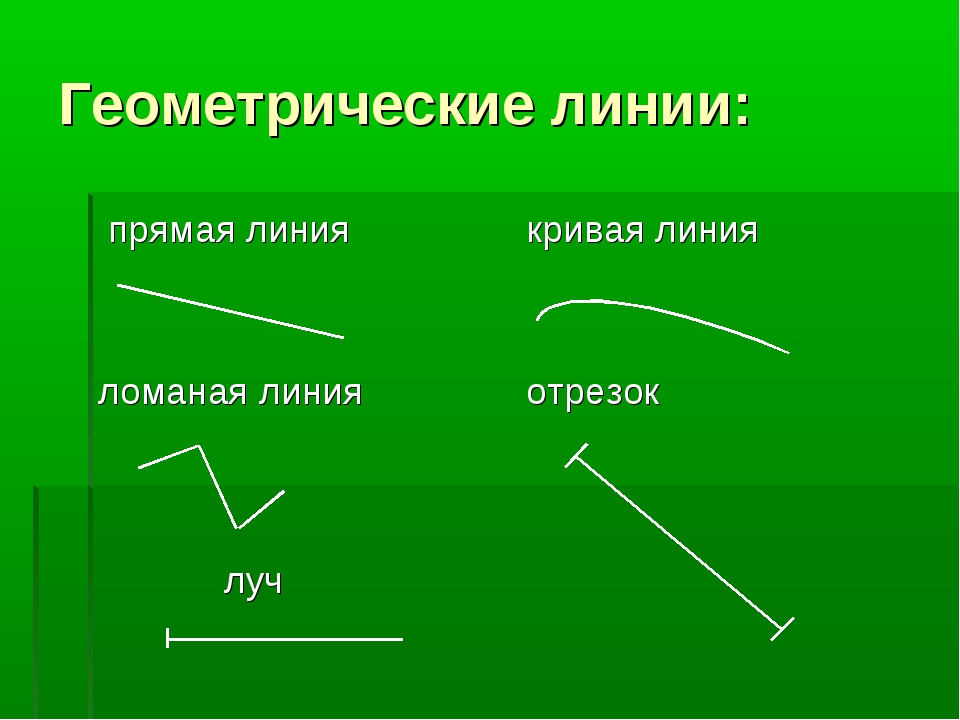
Провода, висящие на столбах, видимая линия горизонта (граница между небом и землей или водой), русло реки, изображенное на карте, гимнастический обруч, струя воды, бьющая из фонтана дают представление о линиях.
Различают замкнутые и незамкнутые линии, гладкие и негладкие линии, линии с самопересечением и без самопересечения (рисунки 8 и 9).
Лист бумаги, лазерный диск, оболочка футбольного мяча, картон упаковочной коробки, новогодняя пластиковая маска и т.д. дают нам представление о поверхностях (рисунок 10). Когда красят пол комнаты или автомобиль, то покрывают краской именно поверхность пола или автомобиля.
Тело человека, камень, кирпич, головка сыра, мяч, ледяная сосулька и т.д. дают нам представление о геометрических телах (рисунок 11).
Наиболее простая из всех линий — это прямая . Приложим к листу линейку и проведем карандашом вдоль нее прямую линию. Мысленно продолжив эту линию до бесконечности в обе стороны, мы получим представление о прямой. Считают, что прямая имеет одно измерение — длину, а два других ее измерения равны нулю (рисунок 12).
Мысленно продолжив эту линию до бесконечности в обе стороны, мы получим представление о прямой. Считают, что прямая имеет одно измерение — длину, а два других ее измерения равны нулю (рисунок 12).
При решении задач прямую изображают в виде линии, которую проводят вдоль линейки карандашом или мелом. Прямые обозначаются строчными латинскими буквами: a, b, n, m (рисунок 13). Можно обозначать также двумя буквами, точкам, лежащим на ней. Например ,ую n на рисунке 13 можно прямить: АВ или ВА, А D D А, D В или В D .
Точки могут лежать на прямой (принадлежать прямой) и не лежать на прямой (не принадлежать). На рисунке 13 изображены точки A, D, B, лежащие на прямой AB (принадлежащие прямой AB). При этом пишут. Читают: точка A принадлежит прямой AB, точка В принадлежит AB, точка D принадлежит АВ. Точка D принадлежит также и прямой м, ее называют общей точкой. В точке D прямых AB и m пересекаются. Точки P и R не принадлежат прямым AB и m:
В точке D прямых AB и m пересекаются. Точки P и R не принадлежат прямым AB и m:
Через любые две точки всегда можно провести прямую и причем только одну .
Из всех видов линий, соединяющих любые две точки, наименьшую длину имеет отрезок, концами которого данные точки (рисунок 14).
Фигура, которая из точек и соединяющих их отрезков состоит из ломаной (рисунок 15). Отрезки, образующие ломаную, называются звеньями ломаной, а их концы — вершинами ломаной. Называют (обозначают) ломаную, перечисляя по порядку все ее вершины, например, ломаная ABCDEFG.Длиной ломаной сумма называется длин ее звеньев. Значит, длина ломаной ABCDEFG равна сумме: AB + BC + CD + DE + EF + FG.
Замкнутая ломаная называется многоугольником , ее вершины называются вершинами многоугольника , а ее звенья связаны многоугольника (рисунок 16). Называют (обозначают) многоугольник, перечисляя по порядку все его вершины, начиная с любого, например, многоугольник (семиугольник) ABCDEFG, многоугольник (пятиугольник) RTPKL:
Называют (обозначают) многоугольник, перечисляя по порядку все его вершины, начиная с любого, например, многоугольник (семиугольник) ABCDEFG, многоугольник (пятиугольник) RTPKL:
Сумма длин всех сторон многоугольника называется периметром многоугольника и обозначается латинской буквой p (читаем: пэ ).Периметры многоугольников на рисунке 13:
P ABCDEFG = AB + BC + CD + DE + EF + FG + GA.
П РТПКЛ = RT + TP + PK + KL + LR.
Мысленно продлив поверхность крышки стола или оконного стекла до бесконечности во все стороны, получим представление о поверхности, которая называется плоскостью (рисунок 17). Обозначают плоскости малыми буквами греческого алфавита: α, β, γ, δ, … (читаем: плоскость альфа, бетта, гамма, дельта, и т.д. ).
Блок 2. Словарь.
Составьте словарь новых терминов и определений из §2. Для этого в пустые строки таблицы впишите слова из терминов, приведенного ниже. В таблице 2 укажите номера терминов в соответствии с номерами строк. Рекомендуется перед заполнением словаря еще раз внимательно просмотреть §2 и блок 2.1.
Для этого в пустые строки таблицы впишите слова из терминов, приведенного ниже. В таблице 2 укажите номера терминов в соответствии с номерами строк. Рекомендуется перед заполнением словаря еще раз внимательно просмотреть §2 и блок 2.1.
Блок 3. Установите соответствие (УС).
Геометрические фигуры.
Блок 4. Самопроверка.
Измерение отрезка с помощью линейки.
Напомним, что измерить отрезок АВ в сантиметрах, значит сравнить его с отрезком длиной 1см и узнать, сколько отрезков по 1см помещается в отрезке АВ. Чтобы измерить отрезок в других единицах, поступают подобным же образом.
Для выполнения заданий работайте по плану, приведенному в левой колонке таблицы.При этом правую колонку рекомендуем закрыть листом бумаги. Затем вы сможете сопоставить свои выводы и решения, приведенными в таблице справа.
Блок 5. Установление действий (УП).
Построение отрезка заданной длины.
Вариант 1 . В таблице перепутанный алгоритм (перепутанный порядок действий) построим отрезка заданной длины (например, построим отрезок ВС = 7см).В левом столбце указание к действию в правом результате выполнения этого действия. Переставьте строки таблицы так, чтобы получился верный алгоритм построения отрезка заданной длины. Запишите верную последовательность действий.
Вариант 2. В следующей таблице алгоритм построения отрезка КМ = n см, где вместо n можно подставить любое число. В этом варианте нет соответствующего между этим и результатом. Поэтому необходимо установить последовательность действий, затем для каждого действия выбрать его результат.Ответ запишите в виде: 2а, 1в, 4б и т.д.
Вариант 3. Используя алгоритм варианта 2, постройте в тетради отрезки при n = 3 см, n = 10 см, n = 12 см.
Блок 6. Фасетный тест.
Отрезок, луч, прямая, плоскость.
В задачах фасетного теста используются рисунки и записи под номерами 1–12, приведены в таблице 1. Из них формируются данные задач. Затем к ним добавляются требования задач, которые в тесте помещены после соединительного слова «ТО».Ответы к задачам помещены после слова «РАВНО». Набор задач приведён в таблице 2. Задача 6.15.19 составляется следующим образом: «ЕСЛИ в задаче используется 6 , с добавляется условие под номером 15, требование стоит под номером 19.»
Содержание теста.
13) построить четыре точки так, чтобы каждые три из них не лежали на одной прямой;
14) провести через каждые две точки прямую;
15) каждую из поверхностей коробки продлить мысленно во все стороны до бесконечности;
ТО:
16) количество различных отрезков на рисунке;
17) количество различных лучей на рисунке;
18) количество различных прямых на рисунке;
19) количество получившихся различных плоскостей;
20) длина отрезка АС в сантиметрах;
21) длина отрезка АВ в километрах;
22) длина отрезка DC в метрах;
23) периметр треугольника PRQ;
24) длина ломаной QPRMN;
25) частное периметров треугольников RMN и PRQ;
26) длина отрезка ED;
27) длина отрезка BE;
28) количество получившихся точек пересечения прямых;
29) количество получившихся треугольников;
30) количество частей, которые оказались разделена плоскость;
31) периметр многоугольника, выраженный в метрах;
32) периметр многоугольника, выраженный в дециметрах;
33) периметр многоугольника, выраженный в сантиметрах;
34) периметр многоугольника, выраженный в миллиметрах;
35) периметр многоугольника, выраженный в километрах;
РАВНО (равна, имеет вид):
а) 70; б) 4; в) 217; г) 8; д) 20; е) 10; ж) 8 ∙ б; з) 800 ∙ б; и) 8000 ∙ б; к) 80 ∙ б; л) 63000; м) 63; н) 63000000; о) 3; п) 6; р) 630000; с) 6300000; т) 7; у) 5; ф) 22; х) 28
Блок 7. Давай поиграем.
Давай поиграем.
7.1. Математический лабиринт.
Лабиринт состоит из десяти комнат с тремя дверьми каждую. В комнате по одному геометрическому объекту (он находится на каждой стене комнаты). Сведения об этом объекте находятся в «путеводителе» по лабиринту. Читая его, надо переходить в ту комнату, о которой написано в путеводителе. Проходя по комнатам лабиринта, рисуйте свой маршрут. В двух последних комнатах имеются выходы.
Путеводитель по лабиринту
- Войти в лабиринт надо через комнату, где находится геометрический объект, у которого нет начала, но есть два конца.
- Геометрический объект этой комнаты не имеет размеров, он подобен далёкой звезде на ночном небе.
- Геометрический объект этой составной комнаты из четырёх отрезков, имеющего три общие точки.
- Этот геометрический объект состоит из четырёх отрезков с четырьмя общими точками.
- В этой комнате находятся геометрические объекты, каждый из которых имеет начало, но не имеет конца.

- Здесь два геометрических объекта, не имеющих ни начала, ни конца, но с одной общей точкой.
- Представление об этом геометрическом объекте даёт полет артиллерийских снарядов
(траектория движения).
- В этой комнате геометрический объект с тремя вершинами, но это не горные
вершины.
- Об этом геометрическом объекте даёт представление полёт бумеранга (охотничье )
оружие популяризатора Австралии). В физике эту линию называют траекторией
движения тела.
- Представление об этом геометрическом объекте даёт поверхность озера в
безветренную погоду.
Теперь можете выходить из лабиринта.
В лабиринте геометрические объекты: плоскость, незамкнутая линия, прямая, треугольник, точка, замкнутая линия, ломаная, отрезок, луч, четырёхугольник.
7.2. Периметр геометрических фигур.
В рисунках выделите геометрические фигуры: треугольники, четырёхугольники, пяти — и шестиугольники.С помощью линейки (в миллиметрах) определите периметры некоторых из них.
7.3. Эстафета геометрических объектов.
В заданиях эстафеты есть пустые рамки. В них запишите пропущенное слово. Затем перенесите это слово в другую рамку, куда показывает стрелка. При этом можно виноват падеж этого слова. Проходя по этапам эстафеты, выполняйте требуемые построения. Если эстафету пройдёте правильно, то в конце получите слово: периметр .
7.4. Крепость геометрических объектов.
Прочитайте § 2, выпишите из его текста названия геометрических объектов. Затем впишите эти слова в пустые клетки «крепости».
Что Такое Прямая Линия?
Определение линии происходит «прямо» от Евклида Александрийского, первого математика, который собрал определения и аксиомы геометрии, которые древние греки разработали к 300 году до нашей эры. Что шокирует, так это то, что более 2000 лет спустя ни один математический «физик» на Земле может сказать вам, что такое линия или является ли она геометрической фигурой. Если вы хотите получить высшее образование и получить будущее в качестве математического «физика», вы должны наизусть прочитать 1-мерный четок: «линия остается неопределенной». Тот факт, что стратегические термины геометрии, такие как точка и линия, по-прежнему омрачены тайной, может показаться тривиальным, пока вы не поймете, что математические «физики» говорят всем, что математика — это язык того, что они называют «физикой» .Заблудшие люди, лидеры мира науки, убедили мир в том, что эти определения и аксиомы безупречны и объективны, а геометрия стоит на твердой почве. Думаю об этом. Все теории общей теории относительности, квантовой механики и теории теории в основе опираются на эти две концепции. Все квантовые частицы обозначены как «точки». Общая теория не может обойтись без относительных расстояний и геодезических (то есть есть «прямых» линий).
Что шокирует, так это то, что более 2000 лет спустя ни один математический «физик» на Земле может сказать вам, что такое линия или является ли она геометрической фигурой. Если вы хотите получить высшее образование и получить будущее в качестве математического «физика», вы должны наизусть прочитать 1-мерный четок: «линия остается неопределенной». Тот факт, что стратегические термины геометрии, такие как точка и линия, по-прежнему омрачены тайной, может показаться тривиальным, пока вы не поймете, что математические «физики» говорят всем, что математика — это язык того, что они называют «физикой» .Заблудшие люди, лидеры мира науки, убедили мир в том, что эти определения и аксиомы безупречны и объективны, а геометрия стоит на твердой почве. Думаю об этом. Все теории общей теории относительности, квантовой механики и теории теории в основе опираются на эти две концепции. Все квантовые частицы обозначены как «точки». Общая теория не может обойтись без относительных расстояний и геодезических (то есть есть «прямых» линий). И теория струн полностью исчезнет, если пресловутая 1D линия (то есть «строка») перестанет вибрировать.Конечно, если эти «респектабельные» ветви математической «физики» опираются на основы, которые, как показано, прогнили до глубины души, все здание рухнет.
И теория струн полностью исчезнет, если пресловутая 1D линия (то есть «строка») перестанет вибрировать.Конечно, если эти «респектабельные» ветви математической «физики» опираются на основы, которые, как показано, прогнили до глубины души, все здание рухнет.
Таинственные неверные строки Евклида
В своем оригинальном сборнике «Элементы» Евклид различал термины «линия» и «прямая линия».
«Линия безгранична». (Определение 2, Книга I Элементов)
«Прямая линия — это линия, которая равномерно с точками на себе». (Определение 4, Книга I)
Первый невообразим, потому что Евклид говорит нам, что он простирается навсегда в обоих направлениях.И это заставляет задуматься, намекает ли он даже на геометрическую фигуру. «Бескрайняя длина» Евклида несовместима с его определением фигуры, приведенным ниже в его книге:
«Рисунок — это то, что содержится в любой границе или границах». (Определение 14, Книга I)
Линия Евклида не ограничена границами на обоих концах.
Более того, сегодня преемники Евклида до сих порят свою «бесконечную» линию, безусловно, гарантирует им сохранение рабочих мест до конца вечности.Евклид относится не к существительному, а к глаголу. Евклид приравнивает «линию» к «длине», что в настоящем контексте может быть истолковано только как пройденное расстояние. Евклид говорит о маршруте, а не о палке.
Этот аргумент подкрепляется тем фактом, что длина Евклида «не имеет ширины», что означает, что Евклид сжимает свою линию в одно измерение: длина. Евклид явно имеет в виду не двумерную палку, которую он нарисовал на доске, а скорее воображаемую линию, состоящую из локаций (т.Е. Точек «без деталей», которые он определил в определении 1). Евклид говорит о смещении, а не об отдельной геометрической фигуре.
Определение Евклидом прямой линии подтверждает, что он говорит о маршруте, если, как он, он «равномерно связан с точками на себе». Он ясно дал понять, что его точка «не является частью» — это местоположение, а не точка. Слово «точка» — это не пятно. Слово «точка» относится к абстрактному понятию: упорядоченная пара (x, y). Следовательно, его прямая линия «сделана» из местоположений, что означает, что он снова указан на прямолинейный маршрут, а не на 2-мерную или 3-мерную автономную палку.
Слово «точка» — это не пятно. Слово «точка» относится к абстрактному понятию: упорядоченная пара (x, y). Следовательно, его прямая линия «сделана» из местоположений, что означает, что он снова указан на прямолинейный маршрут, а не на 2-мерную или 3-мерную автономную палку.
Всемогущая линия математической «физики»
Открывает глаза на то, что ученики Евклида не делали ничего лучше на протяжении веков. Не требуется поверхностного анализа современной Геометрии, чтобы понять, что такое Математическое Учреждение наступило до достижения большего беспорядку в линии Евклида, чем он.
Германом Вейлем был один из выдающихся математических «физиков», который сделал исчерпывающий обзор геометрии вступления к своему великому опусу об общей теории относительности.В «Пространстве-времени» Вейль начинает с понятия истеблишмента, а затем продолжает анализировать загадочную словесную линию. Но когда вы читаете и следите за ходом мыслей Вейля, становится очевидно, что бедняга был бредовым. Его сюрреалистическая линия превращается из одного абзаца в следующий:
Его сюрреалистическая линия превращается из одного абзаца в следующий:
1. «Двухточечная» линия Вейля…
«Прямая линия … определяет ее точками» (стр. 12)
2. Линия «двумя расстояниями» Вейля…
«Прямая линия равномерно между ее точками» (стр.12)
3. Петля Вейля
«Не только прямая линия, но и плоскость на своем вращении. »(Стр. 13)
4. Линия« ряд яблок »
« Конгруэнтное преобразование, которое преобразует А в себя, и все точки справа от А в точке справа от А, все точки слева от А в точки слева от А , оставляют все точки прямой без изменений, »(Стр. 12)
« Мы получим массив точек на строящейся прямой »(стр. 16)
5. Линия« катящегося яблока »
« Пусть a будет переводом, который переводит точку Ao в A.»(Стр. 15)
« Прямая линия вывода из точки бесконечным повторением
того же бесконечно малого перевода и его обратного. »(Стр. 16)
6. Палка Вейля
« Все точки, которые в конечном итоге получают, в конечном итоге создаются в линейном континууме, в
, которые они встраиваются, отказываясь от своего индивидуального описания (это
описание на нашей интуиции непрерывности) ). »(Стр. 16)
»(Стр. 16)
7. Линия вспашки
« Существует один и только один перевод, переносящий произвольную точку A на g в произвольную точку A * на той же прямой линии ».(Стр. 14)
8. Строка «номер»
«Если мы возьмем все возможные целые числа в качестве значений n, этот массив станет более плотным по мере увеличения n» (стр. 16)
Что мы можем сказать? Линия Вейля слишком сложна для разумного человека. Возможно, его коллеги смог поработать над этим чуть больше в течение следующих 2000 лет.
Реальная линия, пожалуйста, встаньте?
Переменная линия Вейля показывает, что математики установили всю свою структуру геометрии на хрупких зыбучих песках.Основы дисциплины действительно прогнили до глубины души. Геометрические плоскости и твердые тела построены с гибкими и изменяемыми точками и линиями. В тот момент, когда вы думали, что стороны этого идеального, цельного куба, который смотрит на вас в лицо, состоят из непрерывных линий, математик говорит вам проснуться, потереть глаза и снова посмотреть.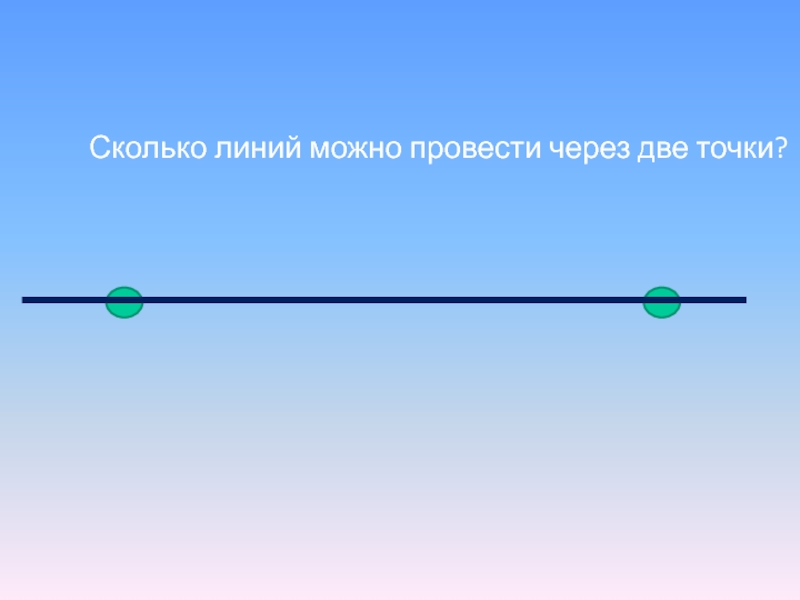 Вы смотрите на маршруты. Вы все еще галлюцинируете и видите миражи. Линия была фактически рядом дискретных точек. И только когда вы подумали, что угол, который вы рассматриваете, состоит из двух палочек, геометр смотрит на вас так, как будто вы пришли с Марса.
Вы смотрите на маршруты. Вы все еще галлюцинируете и видите миражи. Линия была фактически рядом дискретных точек. И только когда вы подумали, что угол, который вы рассматриваете, состоит из двух палочек, геометр смотрит на вас так, как будто вы пришли с Марса.
Этот момент здравомыслящий человек начинает задумываться: «Что с тобой не видишь, что это явно два перпендикулярных ряда чисел?»
В этот момент здравомыслящий человек начинает задумываться: «О чем в мире говорят геометры? яблоко, (б) траекторией одного яблока или (в) цельной палкой? Является ли это (a) безразмерным маршрутом, (b) автономным, 1-мерным «длиной» или (c) явно очевидным 2-мерным вытянутым прямоугольником, который нарисовал мел на доске? Как, в любом случае, 0-мерная «точка» или серия из них образуют 1-мерную линию? Почему бы линия представляет собой серию следов, почему торговец змеиным маслом называет это линией? не назвать это маршрут или траектория или перемещение? Ну, возможно, это потому, что маршрут — это не геометрическая фигура! Может быть, поэтому! Какое отношение имеет «маршрутная линия» к геометрии? из одного куска, как геометры могут согласовать это с рядо м дискретных точек? Как палка напоминает ряд чисел? Ответ на все эти вопросы: «бесконечное дыхание»!
Если по прошествии более 2500 лет математические «физики» не смогли определить суть геометрии — точку и линию — это потому, что они не смогли выявить объекты и понятия.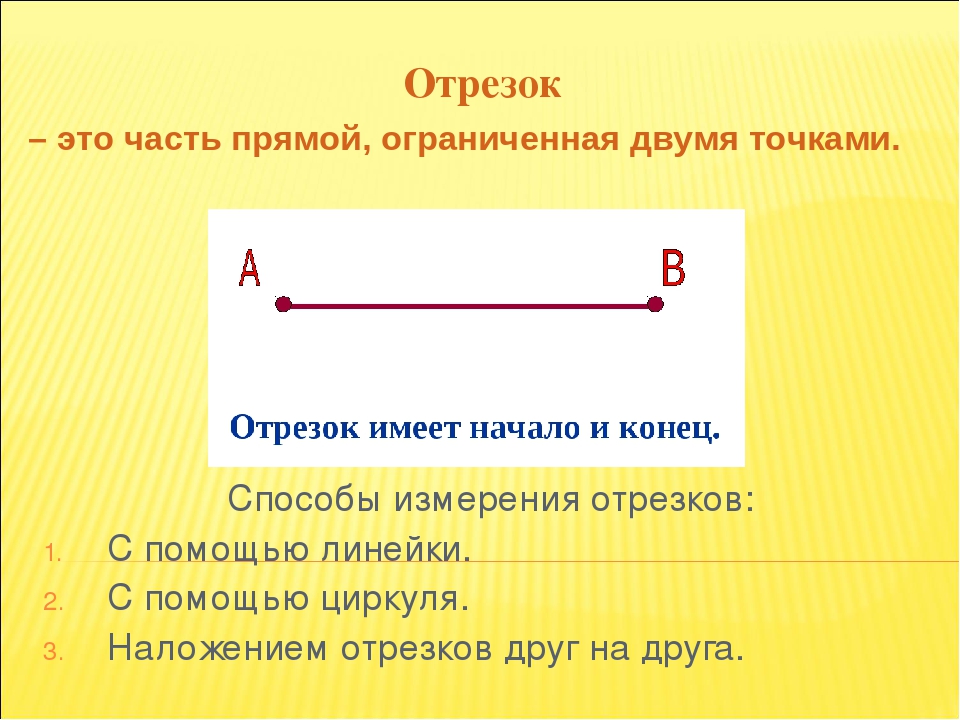 Объект — это то, что имеет форму. Концепция — это то, чего нет. Если геометр вводит линию как фигуру в Суде Физики, он по праву принадлежит Геометрии. Но затем геометру отказывают в праве отрывать кожу от несчастной фигуры, сбрасывать ее форму и поверхность в мусорную корзину и выполнять его приказы с помощью местоположений и чисел. То, что явно смотрит нам в лицо, это вытянутый прямоугольник. Вот что перед нами. Если математик не может использовать эту двумерную фигуру, он не должен указывать на нее, называть ее линией, а затем вызывать несвязанные абстрактные понятия для объяснения своей теории.
Объект — это то, что имеет форму. Концепция — это то, чего нет. Если геометр вводит линию как фигуру в Суде Физики, он по праву принадлежит Геометрии. Но затем геометру отказывают в праве отрывать кожу от несчастной фигуры, сбрасывать ее форму и поверхность в мусорную корзину и выполнять его приказы с помощью местоположений и чисел. То, что явно смотрит нам в лицо, это вытянутый прямоугольник. Вот что перед нами. Если математик не может использовать эту двумерную фигуру, он не должен указывать на нее, называть ее линией, а затем вызывать несвязанные абстрактные понятия для объяснения своей теории.
Математический «физик» имеет единственный выход, и он должен использовать его термины последовательно, если он хочет быть частью науки. Если он намеревается говорить о маршрутах, он должен использовать слово «маршрут». Он должен использовать слово местоположение. И если он собирается говорить о цифрах, он должен называть их номерами. Ни один из них не является ни точками, ни линиями. Точки и палочки принадлежат миру фигуррия. Местоположения, маршруты и числа исключительно абстрактному миру понятий: философия.
Местоположения, маршруты и числа исключительно абстрактному миру понятий: философия.
Математический «физик» может утверждать, что те, кто хорошо разбирается в геометрии, не смущаются языком. Члены гильдии привыкли к жаргону за эти годы. Он может добавить, что геометры знают, как сохранить свои точки и местоположения, палки и маршруты разграниченными.
Да! Конечно! И тогда тот же самый народ сделает следующий шаг и с полной искренностью скажет вам, что частица на деле возбужденным «полем» и что абстрактное понятие «масса» обладает способностью перемещать звезды вокруг.
.
.
.
«Это будет очень непростая прямая линия» — Коммерсантъ FM —
Прямая линия президента пройдет после 1 июля. Как пояснил его пресс-секретарь Дмитрий Песков, это будет полноформатный диалог главы государства с народом. Точную дату и время мероприятия Кремль озвучит позже. Ранее были сообщения о том, что Владимир Путин ответит на вопросы россиян прямо в канун проголосовал по поправкам в Конституцию. Однако Песков фактически опроверг эти утверждения. Политический обозреватель «Ъ FM» Дмитрий Дризе считает, что на этот разение с электоратом не обещает быть легким.
Однако Песков фактически опроверг эти утверждения. Политический обозреватель «Ъ FM» Дмитрий Дризе считает, что на этот разение с электоратом не обещает быть легким.
Прямая линия — это обязательной инструмент кремлевской политики, поэтому ее просто не может не быть. Сложилась традиция: летом — прямая линия, зимой под Новый год — пресс-конференция. Но вот вмешался коронавирус и порушил все устойчивые конструкции. Сначала пришлось сдвигать по срокам голосование по поправкам, а затем и общение с народом.И даже сейчас, как мы видим, точная дата не определена. Однако сильно затягивать нельзя — коронавирус грозит вернуться. К тому же диалог с гражданами и прессой необходимо развести по срокам. И как можно дальше.
Что здесь важно отметить? Какая-либо внутренняя линия перестала существовать последние лет пять-шесть, как-то больше, несмотря на титанические старания организаторов, как-то оживить аудиторию и вдохнуть в мероприятие новую жизнь. Привлекались и блогеры, и перспективная молодежь, и министры с вице-премьерами держали в прямом эфире ответ перед населением. Доставалось на орехи губернаторам, местным чиновникам, а также жадным и вороватым работодателям. Однако на выходе все равно получалось одно и тоже — всероссийская книга жалоб. И это признается официально. Даже можно сказать, что возник некий кризис прямых линий. Президент даже засомневался: не может же быть так плохо, что пожарный получает зарплату ниже каких бы то ни было нормативов. И так от линии к линии.
Доставалось на орехи губернаторам, местным чиновникам, а также жадным и вороватым работодателям. Однако на выходе все равно получалось одно и тоже — всероссийская книга жалоб. И это признается официально. Даже можно сказать, что возник некий кризис прямых линий. Президент даже засомневался: не может же быть так плохо, что пожарный получает зарплату ниже каких бы то ни было нормативов. И так от линии к линии.
И, тем не менее, сейчас к предстоящему событию возникает некоторый интерес.
Есть тезис, что поправки к Конституции означают перезагрузку российской политической системы. Иными словами — на прямой линии может появиться некий новый образ высшей государственной власти.
Что это может быть — выбор по большому счету невелик. Первое, что приходит в голову, — это провести такую мысль: в период испытаний власть и народ проявили единение, и поэтому страна вышла из всего этого с минимальными потерями. Об этом уже было сказано в недавнем президентском интервью.То есть система доказала свою эффективность, в отличие от Запада, который охвачен пожарами протестов.
Дальше народу нужно разъяснить, что поправки — это во благо, что дальше будет лучше, иначе, зачем все это затевалось. Конечно, есть недостатки, но мы их опять же вместе сумеем преодолеть. Ну а электорат по прямому итогу линии, наверное, должен как бы со всем с этим согласиться и с уверенностью в завтрашний день. Но есть одна сложность. Во-первых, результат пока что неизвестен.И здесь хоть с малой долей вероятности, но сюрпризы возможны. Во-вторых, и это главное, коронавирус выявил так много проблем, что они рискуют затмить собой радость победы. Хотя бы потому, что пандемия продолжается и не внемлет приказам убираться вон. Люди все равно болеют, здравоохранение в плачевном состоянии, и компенсацию многие не получили, и работы нет. И кризис следом идет и многое, и многое другое. И тогда разговор может выйти не из приятных. Можно, конечно, причесать вопросы, результат в кадр радостную молодежь и благодарный рабочий класс.Но здесь большой риск — ведь не поверят, и результат выйдет прямо противоположенный.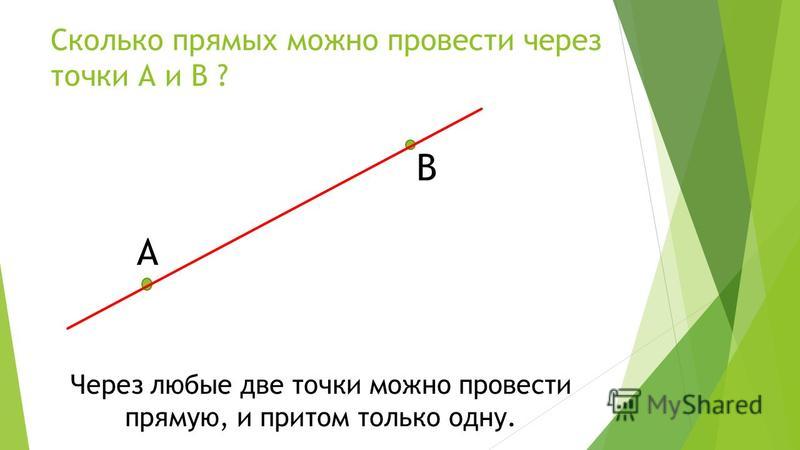 Это будет очень непростая прямая линия. В первую очередь потому, что вопросов намного больше, чем ответов.
Это будет очень непростая прямая линия. В первую очередь потому, что вопросов намного больше, чем ответов.
Точка, линия, прямая, луч, отрезок, ломанная. Точка, линия, прямая, луч, отрезок, ломанная На рисунке 3 объекта отрезок прямой
ПОВТОРЯЕМ ТЕОРИЮ
16. Заполните пропуски.
1) Точка и отрезок являются примерами геометрических
фигур.
2) Измерить отрезок означает подсчитать, сколько единиц отрезков
в нем помещается.
3) Если на отрезке АВ ометить точку С, тона отрезка АВ равна сумме длин длин
отрезков АС + СВ
4) Два отрезка называют равными, если они совпадают при наложении
.
5) Равные отрезки равные
длина.
6) Расстоянием между точками А и В называют длинным отрезка
АВ.
РЕШАЕМ ЗАДАЧИ
17. Обозначьте отрезки, изображенные на рисунке, и измерьте их длину.
18. Проведите все возможные отрезки с концами в точках A, B, C и D. Запишите обозначения всех проведенных отрезков.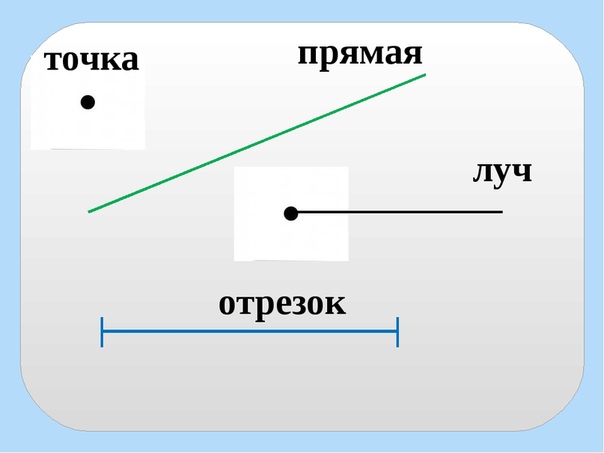
AB, ВС, СD, АD, АС, ВD
19. Запишите все отрезки, изображенные на рисунке.
20. Начертите отрезки СК и АD так, чтобы СК = 4 см 6 мм, АD = 2 см 5 мм.
21. Начертите отрезок ВЕ, длина которого равна 5 см 3 мм. Отметьте на нем точку А так, чтобы ВА = 3 см 8 мм.Какова длина отрезка АЕ?
АЕ = ВЕ-ВА = 5 см 3 мм — 3см 8мм = 1 см 5мм
22. Выразите параметры в указанных размерах.
23. Запишите звенья ломаной и измерьте их длину (в миллиметрах). Вычислите длину ломаной.
24. Установите точку В, расположенную на 6 клетках левее и на 1 клетку ниже точки А; точку С, расположенную на 3 клетки правее и на 3 клетки ниже точки В; точку D, расположенную на 7 клетках правее и на 2 клетки выше точки С.Соедините последовательно отрезками точки А, В, С и D.
Образовалась ломаная АВСD, состоящая из 3 звеньев.
25. Вычислите длину ломаной, изображенной на рисунке.
Вычислите длину ломаной, изображенной на рисунке.
а) 5 * 36 = 180 мм
б) 3 * 28 = 84 мм
в) 10 * 10 + 15 * 4 = 160 мм
26. Постройте ломаную DСЕК так, чтобы DС = 18 мм , СЕ = 37 мм, ЕК = 26 мм. Вычислите длину ломаной.
27. Известно, что АС = 17 см, ВD = 9см, ВС = 3 см.Вычислите длину отрезка АD.
28. Известно, что МК = KN = NP = PR = RT = 3 см. Какие еще равные отрезки есть на этом рисунке? Найдите их длину.
29. На прямой отметили точки так, что расстояние между двумя любыми соседними точками равно 4 см, а между крайними точками — 36 см. Сколько точек принято?
30. Начертите, не отрывая карандаша от бумаги, фигуры, изображенные на рисунке. По каждой линии можно проводить карандашом только один раз.
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи только важно его местоположение
Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
А B Cточка 1, точка 2, точка 3
1 2 3Можно нарисовать на листке бумаги три точки «А» и предложить ребёнку провести линию через две точки «А».Но как понять через какие? А А А
Линия — это множество точек. У нее измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
линия а, линия б, линия с
а б cЛиния может быть
- замкнутой, если ее начало и конец находятся в одной точке,
- разомкнутой, если ее начало и конец не соединены
замкнутые линии
разомкнутые линии
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру.Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.- самопересекающейся
- без самопересечений
самопересекающиеся линии
линии без самопересечений
- прямой
- ломанной
- кривой
прямые линии
ломанные линии
кривые линии
Прямая линия — это линия, которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обеих сторонах
Даже когда виден небольшой прямой юридический вопрос, что она бесконечно продолжается в обеих сторонах
Обозначается строчной (маленькой) латинской буквой.Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия а
апрямая линия AB
B AПрямые могут быть
- пересекающиеся, если имеют общую точку.
 Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке.- перпендикулярными, если пересекаются под прямым углом (90 °).
- параллельные, если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
Луч — это часть прямой, которая имеет начало, но не имеет конца, ее можно бесконечно продолжать только в одну сторону
У луча света на картинке начальной точкой является солнце
солнышко
Точка разделяет прямую на две части — два луча А A
Луч обозначается строчной (маленькой) латинской буквой.Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
луч а
алуч AB
B AЛучи совпадают, если
- расположены прямо на одной и той же,
- возникают в одной точке,
- движутся в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
C B А Отрезок — это часть прямого, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить ее длину. Длина отрезка — это расстояние между его начальной и конечной точками
Длина отрезка — это расстояние между его начальной и конечной точками
Через одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
B Апрямая линия AB
B AОт прямого «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками. ✂ B А ✂
Отрезок обозначается двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, имеющая отрезок
отрезок AB
B AЗадача: где прямая , луч , отрезок , кривая ?
Ломанная линия — это линия, состоящая из последовательно соединенных отрезков не под углом 180 °
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из состоящих из ломаной.Смежные звенья — это звенья, у которых один конец звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, которые соединяются отрезками, образующие ломаную, точка, заканчивающаяся ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются дополнительными
звено BC и звено CD являются дополнительными
звено CD и звено DE являются смежными
А B C D E 64 62 127 52Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Задача: какая ломанная длиннее
, а у какой больше вершин
? У первой линии все звенья одинаковой длины, а именно по 13см.У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
У третьей линии все звенья одинаковой длины, а именно по 41см.
Многоугольник — это замкнутая ломанная линия
Сторона многоугольника (поможет запомнить выражение: «пойти на все четыре стороны дома», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это дополнительные звенья ломанной.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точка конца одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
CD и сторона DE соответствуют
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются собственными
А B C D E F 120 60 58 122 98 141Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т.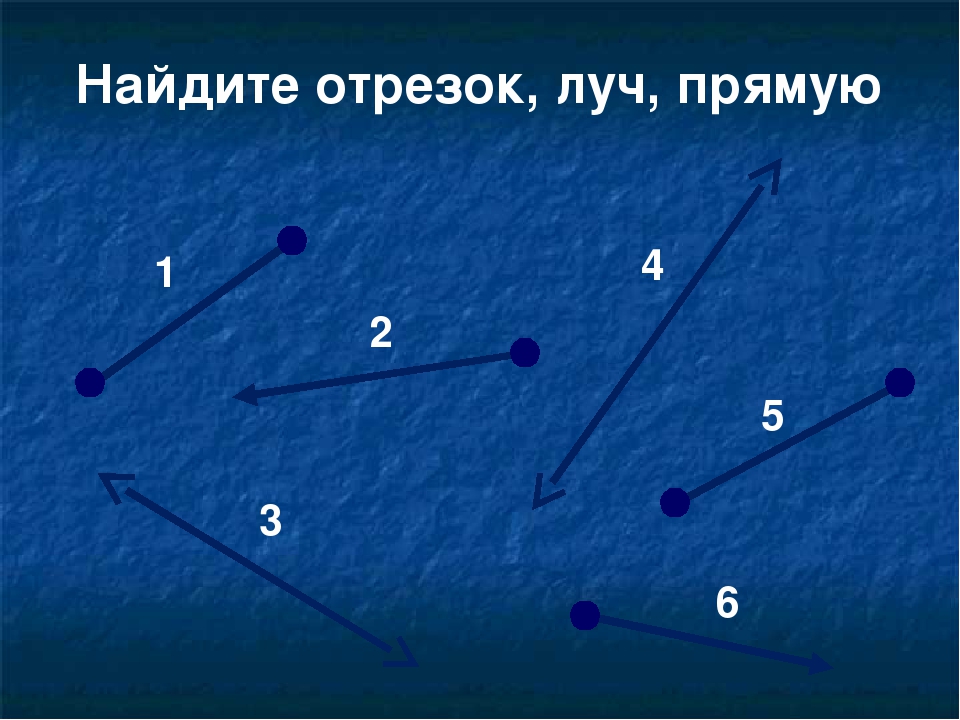 д.
д.
Прямой линия называется множеством точек лишь длины), которая не имеет ни начала ни конца.
Отрезок это прямая ограниченная с двух концов.
Луч это прямая ограниченная с одного конца.
Точка не имеет никаких измерительных характеристик, в задаче важно только ее местоположение.
Отметим три точки на прямой
Прямая не является трехмерной фигурой, более того она не искривляется, а бесконечно продолжается не имея ширины ни высоты в 1 плоскости.Поэтому и точки можно ставить на всей бесконечной длины где угодно, это повлияет только на длину отрезков, отсекаемых точками.
Количество отрезков
Так как точек три, расположим их произвольно на прямой и назовем а, b, c. Таким образом три точки ограничивают прямую, превращая в отрезки три раза, то есть мы имеем три отрезка
Количество лучей
Теперь разберемся с лучами. Прямая не ограниченна ни с начала ни с конца, а луч должен быть ограничен с одной стороны.
- , если мы поставим на прямую 1 точку соответственно ограничив ее в этой точке то получим 2 луча,
- , если поставим 2 точки, мы ограничим прямую в двух местах, логично было предположить, что и лучей у нас будет больше 2х, но ограничим в двух местах, мы получили отрезок, т. к. он ограничен с двух сторон, и 2 луча, т. к. имеем еще начало и конец прямой, которые не ограничены,
- если поставим три точки? правильно, ситуация повторится, только увеличится количество отрезков
Ответ
Прямая на которой отмечены три точки делится этим точками на три отрезка и два луча.
Нарисуем прямую и отметим на ней три точки А, В, С. (см. рисунок)
Отрезком называется часть прямой, которая состоит из всех точек этой, лежащих между двумя данными ее точками.
Или проще говоря, отрезок это прямой, ограниченная двумя точками.
На рисунке получилось три отрезка:
АВ (рис. 1)
АС (рис. 3)
Луч — часть прямой, которая состоит из всех точек этой прямой, лежащих по одной стороне от данной точки. Любая точка на прямой разделяет прямую на два луча.
Любая точка на прямой разделяет прямую на два луча.
Точка А делит прямую на лучи: а и АС. (рис. 4)
Точка В делит прямую на лучи: ВА и ВС. (рис. 5)
Точка С делит прямую на лучи: СА и с. (рис. 6)
Получилось три отрезка и шесть лучей.
Отрезок. Длина отрезка. Треугольник.
1. В этом параграфе вы познакомитесь с некоторыми понятиями геометрии. Геометрия — наука об «измерении земли». Это слово происходит от латинских слов: geo — земля и metr — мера, мерить.В геометрии изучаются различные геометрические объекты , их свойства, их связи с окружающим миром. Простейшие геометрические объекты — это точка, линия, поверхность. Более сложные геометрические объекты, например, геометрические фигуры и тела, образованы из простейших.
Если приложить к точкам А и В линейку и вдоль нее провести линию, соединяющую эти точки, то мы получим отрезок, который называют АВ или ВА (читаем: «а — бэ», «бэ- а»). Точки А и В называются концами отрезка (рисунок 1).Расстояние между концами отрезка, измеренное в единицах длины, называется длиной. отрезка ка .
Точки А и В называются концами отрезка (рисунок 1).Расстояние между концами отрезка, измеренное в единицах длины, называется длиной. отрезка ка .
Единицы длины: м — метр, см — сантиметр, дм — дециметр, мм — миллиметр, км — километр и др. (1 км = 1000 м; 1м = 10 дм; 1 дм = 10 см; 1 см = 10 мм). Для измерения длины отрезков использовать линейку, рулетку. Измерить длину отрезка, значит выяснить, сколько раз в нем укладывается та или иная мера длины.
Равными называются два отрезка, которые можно совместить, наложив один на другой (рисунок 2).Например, можно вырезать реально или мысленно один из их отрезков и приложить к другому так, чтобы совпали концы. Если отрезки АВ и СК равны, то пишут АВ = СК. Равные отрезки имеют равную длину. Верно обратное: два отрезка, имеющие равные длины, равны. Если два отрезка имеют длину, то они не равны. Из двух неравных отрезков меньше тот, который составляет часть другого отрезка. Сравнивать отрезки наложением можно, используя циркуль.
Сравнивать отрезки наложением можно, используя циркуль.
Если мысленно продлить отрезок АВ в обе стороны до бесконечности, то прямой получим представление о АВ (рисунок 3).Любая точка, лежащая на прямой, разбивает ее на два луча (рисунок 4). Точка С разбивает прямую АВ на два луча СА и СВ. Тоска С называется Начало луча. .
2. Если три точки, не лежащий на одной прямой, соединить отрезками, то получим фигуру, называемую треугольником. Данные точки называются вершинами треугольника, а отрезки, их соединяющие, соединяют треугольника (рисунок 5). FNM — треугольник, отрезки FN, NM, FM — стороны треугольника, точки F, N, M — вершины треугольника.Стороны всех треугольников своим следующим своим: д лина любой из сторон треугольника всегда меньше суммы двух других его сторон.
Если мысленно продлить во все стороны, например, поверхность крышки стола, то получим представление о плоскости . Точки, отрезки, прямые, лучи располагаются на плоскости (рисунок 6).
Точки, отрезки, прямые, лучи располагаются на плоскости (рисунок 6).
Блок 1. Дополнительный
Мир, в котором мы живем, все, что нас окружает, древние называли природой или космосом.Пространство, в котором мы живем, считается трехмерным, т.е. имеет три измерения. Их часто называют: длина, ширина и высота (например, длина комнаты 4 м, ширина комнаты 2 м и высота 3 м).
Представление о геометрической (математической) точке дает нам звезда на ночном небе, точка в конце этого предложения, след от иглы и т.д. Однако все перечисленные объекты имеют размеры, в отличие от размеров геометрической точки равными нулю (измерения равны нулю). Поэтому реальную математическую точку можно лишь мысленно представить.Можно также сказать, в каком месте она находится. Поставив авторучкой в геометрическую точку, мы не изобразим геометрическую точку, но будем считать, что построенный объект есть геометрическая точка (рисунок 6). Точки обозначают заглавными буквами латинского алфавита: A , г.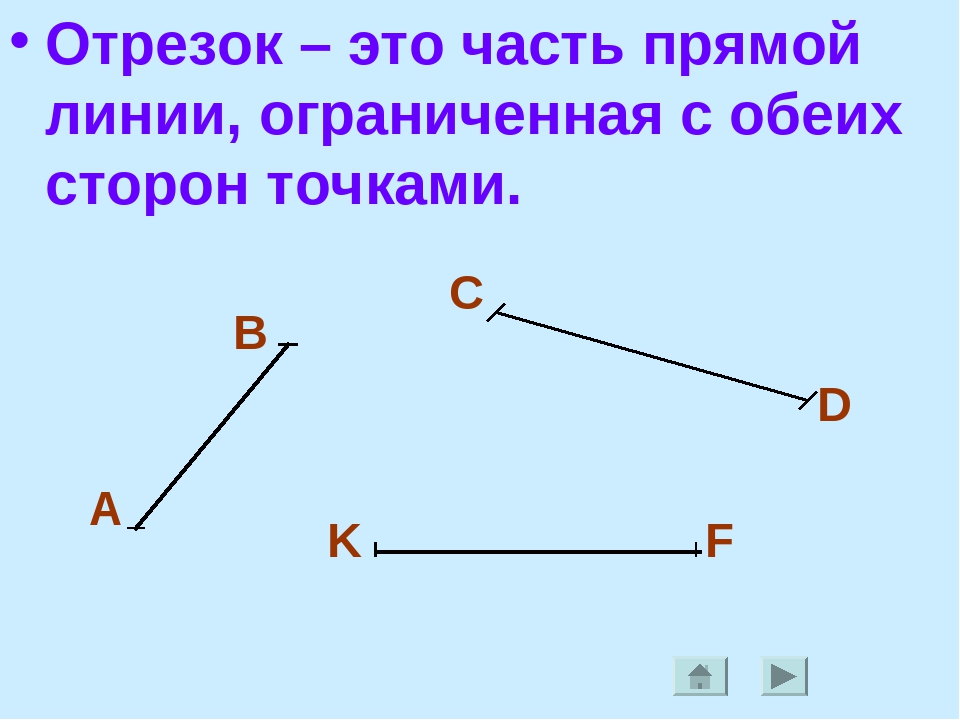 B , г. С , г. D , г. (читают « точка а, точка бэ, точка цэ, точка дэ» ) (рисунок 7).
B , г. С , г. D , г. (читают « точка а, точка бэ, точка цэ, точка дэ» ) (рисунок 7).
Провода, висящие на столбах, видимая линия горизонта (граница между небом и землей или водой), русло реки, изображенное на карте, гимнастический обруч, струя воды, бьющая из фонтана дают представление о линиях.
Различают замкнутые и незамкнутые линии, гладкие и негладкие линии, линии с самопересечением и без самопересечения (рисунки 8 и 9).
Лист бумаги, лазерный диск, оболочка футбольного мяча, картон упаковочной коробки, новогодняя пластиковая маска и т.д. дают нам представление о поверхностях (рисунок 10). Когда красят пол комнаты или автомобиль, то покрывают краской именно поверхность пола или автомобиля.
Тело человека, камень, кирпич, головка сыра, мяч, ледяная сосулька и т.д. дают нам представление о геометрических телах (рисунок 11).
Наиболее простая из всех линий — это прямая. . Приложим к листу линейку и проведем карандашом вдоль нее прямую линию. Мысленно продолжив эту линию до бесконечности в обе стороны, мы получим представление о прямой. Считают, что прямая имеет одно измерение — длину, а два других ее измерения равны нулю (рисунок 12).
При решении задач прямую изображают в виде линии, которую проводят вдоль линейки карандашом или мелом.Прямые обозначаются строчными латинскими буквами: a, b, n, m (рисунок 13). Можно обозначать также двумя буквами, точкам, лежащим на ней. Например, прямую n на рисунке 13 можно обозначить: АВ или ВА, А D или D А, D В или В D .
Точки могут лежать на прямой (принадлежать прямой) и не лежать на прямой (не принадлежать).На рисунке 13 изображены точки A, D, B, лежащие на прямой AB (принадлежащие прямой AB). При этом пишут. Читают: точка A принадлежит прямой AB, точка В принадлежит AB, точка D принадлежит АВ. Точка D принадлежит также и прямой м, ее называют общей точка. В точке D прямых AB и m пересекаются. Точки P и R не принадлежат прямым AB и m:
Читают: точка A принадлежит прямой AB, точка В принадлежит AB, точка D принадлежит АВ. Точка D принадлежит также и прямой м, ее называют общей точка. В точке D прямых AB и m пересекаются. Точки P и R не принадлежат прямым AB и m:
Через любые две точки всегда можно провести прямую и причем только одну .
Из всех видов линий, соединяющих любые две точки, наименьшую длину имеет отрезок, концами которого данные точки (рисунок 14).
Фигура, которая из точек и соединяющих их отрезков состоит из ломаной (рисунок 15). Отрезки, образующие ломаную, называются звеньями ломаной, а их концы — вершинами ломаной. Называют (обозначают) ломаную, перечисляя по порядку все ее вершины, например, ломаная ABCDEFG.Длиной ломаной сумма называется длин ее звеньев. Значит, длина ломаной ABCDEFG равна сумме: AB + BC + CD + DE + EF + FG.
Замкнутая ломаная называется многоугольником , ее вершины называются вершинами многоугольника , а ее звенья касается многоугольника (рисунок 16). Называют (обозначают) многоугольник, перечисляя по порядку все его вершины, начиная с любого, например, многоугольник (семиугольник) ABCDEFG, многоугольник (пятиугольник) RTPKL:
Называют (обозначают) многоугольник, перечисляя по порядку все его вершины, начиная с любого, например, многоугольник (семиугольник) ABCDEFG, многоугольник (пятиугольник) RTPKL:
Сумма длин всех сторон многоугольника называется периметром многоугольника и обозначается латинской буквой п (читаем: пэ ).Периметры многоугольников на рисунке 13:
P ABCDEFG = AB + BC + CD + DE + EF + FG + GA.
П РТПКЛ = RT + TP + PK + KL + LR.
Мысленно продлив поверхность крышки стола или оконного стекла до бесконечности во все стороны, получим представление о поверхности, которая называется плоскостью (рисунок 17). Обозначают плоскости малыми буквами греческого алфавита: α, β, γ, δ, … (читаем: плоскость альфа, бетта, гамма, дельта, и т.д. ).
Блок 2. Словарь.
Составьте словарь новых терминов и определений из §2. Для этого в пустые строки таблицы впишите слова из терминов, приведенного ниже. В таблице 2 укажите номера терминов в соответствии с номерами строк. Рекомендуется перед заполнением словаря еще раз внимательно просмотреть §2 и блок 2.1.
В таблице 2 укажите номера терминов в соответствии с номерами строк. Рекомендуется перед заполнением словаря еще раз внимательно просмотреть §2 и блок 2.1.
Блок 3. Установите соответствие (УС).
Геометрические фигуры.
Блок 4. Самопроверка.
Измерение отрезка с помощью линейки.
Напомним, что измерить отрезок АВ в сантиметрах, значит сравнить его с отрезком длиной 1см и узнать, сколько отрезков по 1см помещается в отрезке АВ. Чтобы измерить отрезок в других единицах, поступают подобным же образом.
Для выполнения заданий работайте по плану, приведенному в левой колонке таблицы.При этом правую колонку рекомендуем закрыть листом бумаги. Затем вы сможете сопоставить свои выводы и решения, приведенными в таблице справа.
Блок 5. Установление действий (УП).
Построение отрезка заданной длины.
Вариант 1 . В таблице перепутанный алгоритм (перепутанный порядок действий) построим отрезка заданной длины (например, построим отрезок ВС = 7см).В левом столбце указание к действию в правом результате выполнения этого действия. Переставьте строки таблицы так, чтобы получился верный алгоритм построения отрезка заданной длины. Запишите верную последовательность действий.
Вариант 2. В следующей таблице приведен алгоритм построения отрезка КМ = n см, где вместо n можно подставить любое число. В этом варианте нет соответствующего между этим и результатом. Поэтому необходимо установить последовательность действий, затем для каждого действия выбрать его результат.Ответ запишите в виде: 2а, 1в, 4б и т.д.
Вариант 3. Используя алгоритм 2, постройте в тетради отрезки при n = 3 см, n = 10 см, n = 12 см.
Блок 6. Фасетный тест.
Отрезок, луч, прямая, плоскость.
В задачах фасетного теста используются рисунки и записи под номерами 1–12, приведены в таблице 1. Из них формируются данные задач. Затем к ним добавляются требования задач, которые в тесте помещены после соединительного слова «ТО».Ответы к задачам помещены после слова «РАВНО». Набор задач приведён в таблице 2. Задача 6.15.19 составляется следующим образом: «ЕСЛИ в задаче используется рисунок 6 , з атем к нему добавляется условие под номером 15, требование стоит под номером 19. »
Из них формируются данные задач. Затем к ним добавляются требования задач, которые в тесте помещены после соединительного слова «ТО».Ответы к задачам помещены после слова «РАВНО». Набор задач приведён в таблице 2. Задача 6.15.19 составляется следующим образом: «ЕСЛИ в задаче используется рисунок 6 , з атем к нему добавляется условие под номером 15, требование стоит под номером 19. »
13) построить четыре точки так, чтобы каждые три из них не лежали на одной прямой;
14) провести через каждые две точки прямую;
15) каждую из поверхностей коробки продлить мысленно во все стороны до бесконечности;
16) количество различных отрезков на рисунке;
17) количество различных лучей на рисунке;
18) количество различных прямых на рисунке;
19) количество получившихся различных плоскостей;
20) длина отрезка АС в сантиметрах;
21) длина отрезка АВ в километрах;
22) длина отрезка DC в метрах;
23) периметр треугольника PRQ;
24) длина ломаной QPRMN;
25) частное периметров треугольников RMN и PRQ;
26) длина отрезка ED;
27) длина отрезка BE;
28) количество получившихся точек пересечения прямых;
29) количество получившихся треугольников;
30) количество частей, которые оказались разделена плоскость;
31) периметр многоугольника, выраженный в метрах;
32) периметр многоугольника, выраженный в дециметрах;
33) периметр многоугольника, выраженный в сантиметрах;
34) периметр многоугольника, выраженный в миллиметрах;
35) периметр многоугольника, выраженный в километрах;
РАВНО (равна, имеет вид):
а) 70; б) 4; в) 217; г) 8; д) 20; е) 10; ж) 8 ∙ б; з) 800 ∙ б; и) 8000 ∙ б; к) 80 ∙ б; л) 63000; м) 63; н) 63000000; о) 3; п) 6; р) 630000; с) 6300000; т) 7; у) 5; ф) 22; х) 28
Блок 7. Давай поиграем.
Давай поиграем.
7.1. Математический лабиринт.
Лабиринт состоит из десяти комнат с тремя дверьми каждую. В комнате по одному геометрическому объекту (он находится на каждой стене комнаты). Сведения об этом объекте находятся в «путеводителе» по лабиринту. Читая его, надо переходить в ту комнату, о которой написано в путеводителе. Проходя по комнатам лабиринта, рисуйте свой маршрут. В двух последних комнатах имеются выходы.
Путеводитель по лабиринту
- Войти в лабиринт надо через комнату, где находится геометрический объект, у которого нет начала, но есть два конца.
- Геометрический объект этой комнаты не имеет размеров, он подобен далёкой звезде на ночном небе.
- Геометрический объект этой составной комнаты из четырёх отрезков, имеющего три общие точки.
- Этот геометрический объект состоит из четырёх отрезков с четырьмя общими точками.
- В этой комнате находятся геометрические объекты, каждый из которых имеет начало, но не имеет конца.

- Здесь два геометрических объекта, не имеющих ни начала, ни конца, но с одной общей точкой.
- Представление об этом геометрическом объекте даёт полет артиллерийских снарядов
(траектория движения).
- В этой комнате находится геометрический объект с тремя вершинами, но это не горные
- Об этом геометрическом объекте даёт представление полёт бумеранга (охотничье )
оружие популяризатора Австралии). В физике эту линию называют траекторией
движения тела.
- Представление об этом геометрическом объекте даёт поверхность озера в
безветренную погоду.
Теперь можете выходить из лабиринта.
В лабиринте геометрические объекты: плоскость, незамкнутая линия, прямая, треугольник, точка, замкнутая линия, ломаная, отрезок, луч, четырёхугольник.
7.2. Периметр геометрических фигур.
В рисунках выделите геометрические фигуры: треугольники, четырёхугольники, пяти — и шестиугольники. С помощью линейки (в миллиметрах) определите периметры некоторых из них.
С помощью линейки (в миллиметрах) определите периметры некоторых из них.
7.3. Эстафета геометрических объектов.
В заданиях эстафеты есть пустые рамки. В них запишите пропущенное слово. Затем перенесите это слово в другую рамку, куда показывает стрелка. При этом можно виноват падеж этого слова. Проходя по этапам эстафеты, выполняйте требуемые построения. Если эстафету пройдёте правильно, то в конце получите слово: периметр .
7.4. Крепость геометрических объектов.
Прочитайте § 2, выпишите из его текста названия геометрических объектов. Затем впишите эти слова в пустые клетки «крепости».
«Прямая линия, пунктирная линия, истории в Инстаграме» — Интернет на TJ
{«id»: 83276, «url»: «https: \ / \ / tjournal.ru \ / internet \ / 83276-mem-pryamaya-liniya-punktirnaya-liniya-istorii-v-instagrame», «title»: » \ u041c \ u0435 \ u043c: \ u00ab \ u041f \ u0440 \ u044f \ u043c \ u0430 \ u044f \ u043b \ u0438 \ u043d \ u0438 \ u044f, \ u043f \ u0443 \ u043d \ u043d \ u044043 \ u043d \ u043d \ u043d \ u043d \ u043d \ u043d \ u043d \ u04404 \ u044f \ u043b \ u0438 \ u043d \ u0438 \ u044f, \ u0438 \ u0441 \ u0442 \ u043e \ u0440 \ u0438 \ u0438 \ u0432 \ u0418 \ u043d \ u0441 \ u0432 \ u0418 \ u043d \ u0441 \ u0442 \ u0442 \ u0435 \ u0435 \ u0435 \ u0442 \ u0442 \ u0435 \ u0435 u00bb «,» услуги «: {» vkontakte «: {» url «:» https: \ / \ / vk. com \ /share.php? url = https: \ / \ / tjournal.ru \ / internet \ / 83276-mem-прямая-линия-пунктирная-линия-история-v-instagrame & title = \ u041c \ u0435 \ u043c: \ u00ab « u0438 \ u044f, \ u0438 \ u0441 \ u0442 \ u043e \ u0440 \ u0438 \ u0438 \ u0432 \ u0418 \ u043d \ u0441 \ u0442 \ u0430 \ u0433 \ u0440 \ u0430 \ u043c «,» title «:» \ u0412 \ u041a \ u043e \ u043d \ u0442 \ u0430 \ u043a \ u0442 \ u0435 «,» width «: 600,» height «: 450},» facebook «: {» url «:» https: \ / \ / www.facebook.com \ / sharer \ /sharer.php? u = https: \ / \ / tjournal.ru \ / internet \ / 83276-mem-прямая-линия-пунктирная-линия-истории-v-instagrame «,» краткое_имя » : «FB», «title»: «Facebook», «width»: 600, «height»: 450}, «twitter»: {«url»: «https: \ / \ / twitter.com \ / intent \ / tweet? url = https: \ / \ / tjournal.ru \ / internet \ / 83276-мем-прямая-линия-пунктирная-линия-истории-v-instagrame & text = \ u041c \ u0435 \ u043c: \ u00ab \ u041f \ u0440 \ u044f \ u043c \ u0430 \ u044f \ u043b \ u0438 \ u043d \ u0438 \ u044f, \ u043f \ u0443 \ u043d \ u043a \ u0442 \ u0438 \ u0440 \ u043d \ u0430 \ u438 \ u0440 \ u043d \ u0430 \ u0440 \ u0440 \ u0430 \ u0440 \ u0438 \ u0440 \ u0438 \ u0440 \ u044f u0438 \ u0441 \ u0442 \ u043e \ u0440 \ u0438 \ u0438 \ u0432 \ u0418 \ u043d \ u0441 \ u0442 \ u0430 \ u0433 \ u0440 \ u0430 \ u043c \ u0435 \ u00bb «,» название «,» : «Twitter», «width»: 600, «height»: 450}, «telegram»: {«url»: «tg: \ / \ / msg_url? Url = https: \ / \ / tjournal.
com \ /share.php? url = https: \ / \ / tjournal.ru \ / internet \ / 83276-mem-прямая-линия-пунктирная-линия-история-v-instagrame & title = \ u041c \ u0435 \ u043c: \ u00ab « u0438 \ u044f, \ u0438 \ u0441 \ u0442 \ u043e \ u0440 \ u0438 \ u0438 \ u0432 \ u0418 \ u043d \ u0441 \ u0442 \ u0430 \ u0433 \ u0440 \ u0430 \ u043c «,» title «:» \ u0412 \ u041a \ u043e \ u043d \ u0442 \ u0430 \ u043a \ u0442 \ u0435 «,» width «: 600,» height «: 450},» facebook «: {» url «:» https: \ / \ / www.facebook.com \ / sharer \ /sharer.php? u = https: \ / \ / tjournal.ru \ / internet \ / 83276-mem-прямая-линия-пунктирная-линия-истории-v-instagrame «,» краткое_имя » : «FB», «title»: «Facebook», «width»: 600, «height»: 450}, «twitter»: {«url»: «https: \ / \ / twitter.com \ / intent \ / tweet? url = https: \ / \ / tjournal.ru \ / internet \ / 83276-мем-прямая-линия-пунктирная-линия-истории-v-instagrame & text = \ u041c \ u0435 \ u043c: \ u00ab \ u041f \ u0440 \ u044f \ u043c \ u0430 \ u044f \ u043b \ u0438 \ u043d \ u0438 \ u044f, \ u043f \ u0443 \ u043d \ u043a \ u0442 \ u0438 \ u0440 \ u043d \ u0430 \ u438 \ u0440 \ u043d \ u0430 \ u0440 \ u0440 \ u0430 \ u0440 \ u0438 \ u0440 \ u0438 \ u0440 \ u044f u0438 \ u0441 \ u0442 \ u043e \ u0440 \ u0438 \ u0438 \ u0432 \ u0418 \ u043d \ u0441 \ u0442 \ u0430 \ u0433 \ u0440 \ u0430 \ u043c \ u0435 \ u00bb «,» название «,» : «Twitter», «width»: 600, «height»: 450}, «telegram»: {«url»: «tg: \ / \ / msg_url? Url = https: \ / \ / tjournal. ru \ / internet \ / 83276-мем-прямая-линия-пунктирная-линия-история-v-instagrame & text = \ u041c \ u0435 \ u043c: \ u00ab \ u041f \ u0440 \ u044f \ u043c \ u0430 \ u044f \ u043c \ u0430 \ u044f \ u043d \ u0438 \ u044f, \ u043f \ u0443 \ u043d \ u043a \ u0442 \ u0438 \ u0440 \ u043d \ u0430 \ u044f \ u043b \ u0438 \ u043d \ u0438 \ u044f \ u0440 \ u0438 \ u0438 \ u0438 \ u0438 \ u0438 u0438 \ u0432 \ u0418 \ u043d \ u0441 \ u0442 \ u0430 \ u0433 \ u0440 \ u0430 \ u043c \ u0435 \ u00bb «,» short_name «:» TG «,» title «:» Telegram «,» width «: 600,» height «: 450},» одноклассники «: {» url «:» http: \ / \ / connect.ok.ru \ / dk? st.cmd = WidgetSharePreview & service = odnoklassniki & st.shareUrl = https: \ / \ / tjournal.ru \ / internet \ / 83276-mem-прямая-линия-пунктирная-линия-истории-v-instagrame «,» краткое_имя «:» OK «,» title «:» \ u041e \ u0434 \ u043d \ u043e \ u043a \ u043b \ u0430 \ u0441 \ u0441 \ u043d \ u0438 \ u043a \ u0438 «,» width «: 600,» height «: 450 }, «email»: {«url»: «mailto:? subject = \ u041c \ u0435 \ u043c: \ u00ab \ u041f \ u0440 \ u044f \ u043c \ u0430 \ u044f \ u043b \ u0438 \ u043d \ u0438 \ u044f, \ u043f \ u0443 \ u043d \ u043a \ u0442 \ u0438 \ u0440 \ u043d \ u0430 \ u044f \ u043b \ u0438 \ u043d \ u0438 \ u044f, \ u0438 \ u0441 \ u0442 \ u4180 \ u0438 \ u0441 \ u0442 \ u0430 \ u043e \ u0441 \ u0442 \ u0430 \ u0433 \ u0440 \ u0430 \ u043c \ u0435 \ u00bb & body = https: \ / \ / tjournal.
ru \ / internet \ / 83276-мем-прямая-линия-пунктирная-линия-история-v-instagrame & text = \ u041c \ u0435 \ u043c: \ u00ab \ u041f \ u0440 \ u044f \ u043c \ u0430 \ u044f \ u043c \ u0430 \ u044f \ u043d \ u0438 \ u044f, \ u043f \ u0443 \ u043d \ u043a \ u0442 \ u0438 \ u0440 \ u043d \ u0430 \ u044f \ u043b \ u0438 \ u043d \ u0438 \ u044f \ u0440 \ u0438 \ u0438 \ u0438 \ u0438 \ u0438 u0438 \ u0432 \ u0418 \ u043d \ u0441 \ u0442 \ u0430 \ u0433 \ u0440 \ u0430 \ u043c \ u0435 \ u00bb «,» short_name «:» TG «,» title «:» Telegram «,» width «: 600,» height «: 450},» одноклассники «: {» url «:» http: \ / \ / connect.ok.ru \ / dk? st.cmd = WidgetSharePreview & service = odnoklassniki & st.shareUrl = https: \ / \ / tjournal.ru \ / internet \ / 83276-mem-прямая-линия-пунктирная-линия-истории-v-instagrame «,» краткое_имя «:» OK «,» title «:» \ u041e \ u0434 \ u043d \ u043e \ u043a \ u043b \ u0430 \ u0441 \ u0441 \ u043d \ u0438 \ u043a \ u0438 «,» width «: 600,» height «: 450 }, «email»: {«url»: «mailto:? subject = \ u041c \ u0435 \ u043c: \ u00ab \ u041f \ u0440 \ u044f \ u043c \ u0430 \ u044f \ u043b \ u0438 \ u043d \ u0438 \ u044f, \ u043f \ u0443 \ u043d \ u043a \ u0442 \ u0438 \ u0440 \ u043d \ u0430 \ u044f \ u043b \ u0438 \ u043d \ u0438 \ u044f, \ u0438 \ u0441 \ u0442 \ u4180 \ u0438 \ u0441 \ u0442 \ u0430 \ u043e \ u0441 \ u0442 \ u0430 \ u0433 \ u0440 \ u0430 \ u043c \ u0435 \ u00bb & body = https: \ / \ / tjournal. ru \ / internet \ / 83276-мем-прямая-линия-пунктирная-линия-истории-v-instagrame «,» short_name «:» Email «,» title «:» \ u041e \ u0442 \ u043f \ u0440 \ u0430 \ u0432 \ u0438 \ u0442 \ u044c \ u043d \ u0430 \ u043f \ u043e \ u0447 \ u0442 \ u0443 «,» width «: 600,» height «: 450}},» isFavorited «: false}
ru \ / internet \ / 83276-мем-прямая-линия-пунктирная-линия-истории-v-instagrame «,» short_name «:» Email «,» title «:» \ u041e \ u0442 \ u043f \ u0440 \ u0430 \ u0432 \ u0438 \ u0442 \ u044c \ u043d \ u0430 \ u043f \ u043e \ u0447 \ u0442 \ u0443 «,» width «: 600,» height «: 450}},» isFavorited «: false}
24 799 просмотров
1) отрезок, луч, прямая (обозначение, определение) 2) середина отрезка
1) Отрезок — часть прямая, ограниченная двумя точками.Обозначают двумя латинскими буквами: АВ, CD, EF.
Луч — это часть, прямая ограниченная одна точка. Луч имеет начало, но не имеет конца. Обозначение — как и у отрезка, но можно и малыми латинскими буквами: а, с, b, m. Обычно название луча читают с начала.
Прямая — прямая линия, определения не существует, т.к. это одно из основных неопределяемых понятий, таких, как точка, прямая и плоскость. Прямую можно представить как туго натянутую нить, бесконечную в обе стороны.Обозначают, как и луч — 9 двумя 1489 большими латинскими буквами или одной маленькой: АВ или а.
Прямую можно представить как туго натянутую нить, бесконечную в обе стороны.Обозначают, как и луч — 9 двумя 1489 большими латинскими буквами или одной маленькой: АВ или а.
2) Середина отрезка — точка на заданном отрезке, которая делит отрезок на две равные части.
3) Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки и плоскости плоскости, которые они ограничивают.
Виды: следующие, вертикальные, острые (<90 °), прямые (= 90 °), тупые (> 90 °, но <180 °), развернутые (= 180 °), полные (= 360 °).
4) Биссектриса угла — луч, выходящий из вершины угла и делящий этот угол на два равных угла.
5) Смежные углы — это углы, одна общая сторона, две другие дополнительные лучами (т.е. дополняют друг друга до прямого). Свойство : сумма соответствующих углов равна 180 °.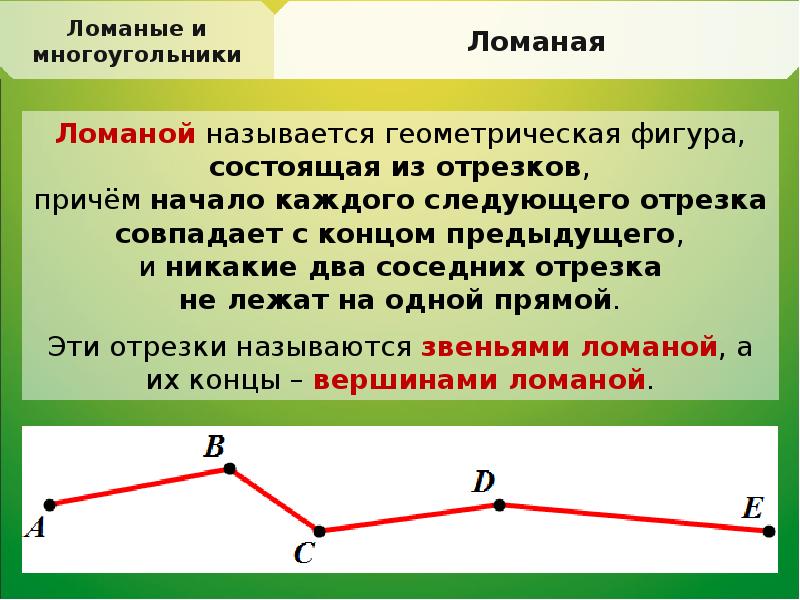
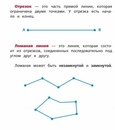 Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке. Длина отрезка — это расстояние между его начальной и конечной точками
Длина отрезка — это расстояние между его начальной и конечной точками
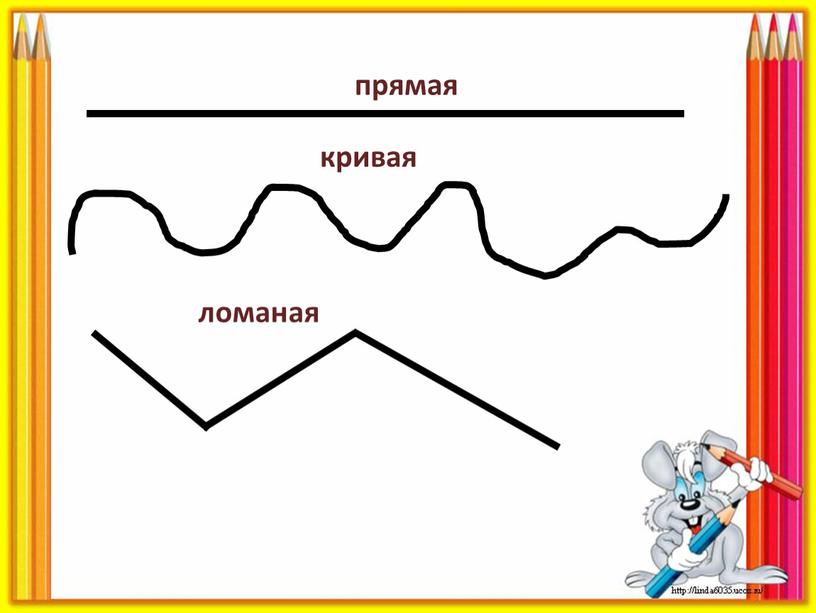
 Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке.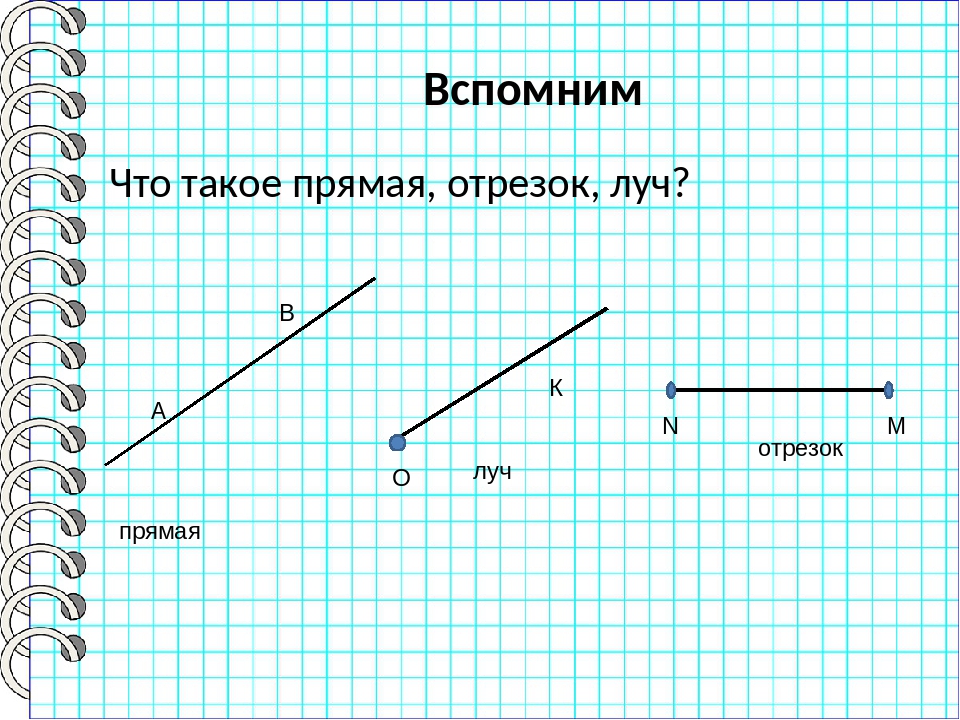 Длина отрезка — это расстояние между его начальной и конечной точками
Длина отрезка — это расстояние между его начальной и конечной точками 