3. Прямая и точка в плоскости. Прямые уровня плоскости.
Позиционными задачами называются задачи, в результате решения которых можно ответить на вопрос о взаимном расположении заданных геометрических фигур. Они бывают двух видов:
Задачи на пересечение (a) построениe линий пересечения двух поверхностей, б) определение точек пересечения линии с поверхностью
Задачи на взаимную принадлежность геометрических элементов (например, на принадлежность точки поверхности).
Прямая и точка в плоскости.
Точка принадлежит плоскости, если она принадлежит какой-нибудь прямой, лежащей в этой плоскости.
Из элементарной геометрии известно, что прямая принадлежит плоскости, если:
oна проходит через две точки, принадлежащие плоскости;
oна проходит через 1 точку, принадлежащую плоскости, и параллельна прямой, лежащей в плоскости.
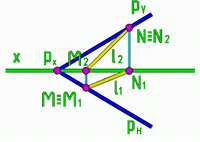
Из первого положения следует, что если прямая принадлежит плоскости, то ее одноименные следы лежат на одноименных следах плоскости.
Рис.1 |
Рис.2 | Пусть следами задана плоскость общего положения Р, построим в этой плоскости прямую l. |
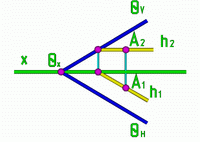
Главные линии плоскости.
Прямые, принадлежащие заданной плоскости и плоскости уровня, называются линиями уровня.
Прямые, принадлежащие плоскости и перпендикулярные к линиям уровня, называются линиями наибольшего наклона плоскости к плоскости проекций. Иногда линию наибольшего наклона плоскости к плоскости Н называют линией наибольшего ската.
Рис.3 |
Линии уровня.
Бывают трех видов:
Горизонталь плоскости

Фронталь плоскости

Профильная прямая плоскости

Пример: Построить линию наибольшего
ската плоскости и определить угол
наклона плоскости  к
плоскости проекций Н.
к
плоскости проекций Н.
У линии наибольшего ската на эпюре горизонтальная проекция всегда перпендикулярна горизонтальной проекции горизонтали или горизонтальному следу.
Рис.7 |
Пример: Найти недостающую проекцию
точки А, лежащей в плоскости 
Так как A
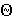
 A
A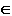 l
l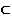
В качестве прямой l следует брать линию уровня плоскости, так как построение ее ортогональных проекций проще, чем построение проекций любой другой прямой, принадлежащей плоскости.
Рис.8 |
Взаимное положение плоскостей.
Две плоскости в пространстве могут пересекаться по собственной и несобственной прямой, следовательно они могут пересекаться или быть параллельными.
4. Параллельность плоскостей.
Из элементарной геометрии известна теорема (признак параллельности плоскостей):
Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
Следствие: если плоскости заданы следами и одноименные следы плоскостей параллельны, то и плоскости параллельны.
(QH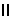 PH)
PH) (QV
(QV
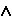 (QW
(QW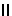 PW)
PW)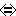 Q
Q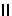 P
PИз этого соотношения следует, что если хотя бы одна пара одноименных следов пересекается, то и плоскости пересекаются.
Из этих определений легко вывести способ построения параллельных плоскостей на чертеже.
Пример: Через точку А провести плоскость, параллельно заданной.
h1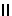 QH,
так как QH
QH,
так как QH
 Q
по условию).
Q
по условию). Для плоскостей общего положения (QH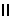 PH)
PH)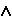 (QV
(QV PV)
PV)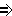 (QW
(QW PW)
PW)
Условие параллельности QWи PWпроверяется построением.
Прямая Эйлера — Википедия
Материал из Википедии — свободной энциклопедии
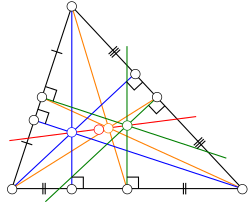
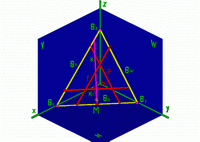
Пряма́я Э́йлера может быть определена как прямая, проходящая через центр описанной окружности и ортоцентр треугольника.
- Прямая Эйлера проходит через:
 Точка Шиффлера Sp{\displaystyle S_{p}} — точка пересечения прямых Эйлера трёх треугольников: △BCI,△CAI{\displaystyle \triangle BCI,\;\triangle CAI}и △ABI{\displaystyle \triangle ABI}.
Точка Шиффлера Sp{\displaystyle S_{p}} — точка пересечения прямых Эйлера трёх треугольников: △BCI,△CAI{\displaystyle \triangle BCI,\;\triangle CAI}и △ABI{\displaystyle \triangle ABI}.- Теорема Шиффлера утверждает следующее: Если в треугольнике ABC с центром вписанной окружности I рассмотреть три треугольника BCI, CAI и ABI, то их три (первые) прямые Эйлера, а также (первая) прямая Эйлера треугольника ABC (все четыре прямые) пересекутся в одной точке — точке Шиффлера Sp (см. рис. справа).
Вторая прямая Эйлера (прямая Эйлера — Нагеля)[править | править код]
Указанную выше прямую Эйлера иногда называют (первой) обобщённой прямой Эйлера[1]. На этой прямой лежат 4 точки:
Вторую прямую Эйлера или прямую Эйлера-Нагеля определяет следующая Теорема Хузеля.
- {IS=SM;IG=2GS;MG=2IG.{\displaystyle \left\{{\begin{matrix}IS=SM;\\IG=2GS;\\MG=2IG.\end{matrix}}\right.}
Указанную прямую иногда называют второй прямой Эйлера или прямой Эйлера-Нагеля. На этой прямой лежат 4 точки:
Если брать у треугольника ABC любую пару сторон, а третьей стороной брать первую прямую Эйлера треугольника ABC, то перебором трёх вариантов можно построить три треугольника. Их первые прямые Эйлера образуют треугольник AgBgCg, конгруэнтный треугольнику ABC (равный ему, но повернутый на некоторый угол). Три пары отрезков, соединяюшие сходственные вершины этих двух конгруэнтных треугольников пересекутся в точке Pg, называемой
Перспектор Госсарда (Gossard Perspector) http://faculty.evansville.edu/ck6/tcenters/recent/gosspersp.html
Теорема Эйлера была доказана в 1765 году Л. Эйлером. Тогда же он обнаружил и тот факт, что середины сторон треугольника и основания его высот лежат на одной окружности — окружности Эйлера.
- Leonhard Euler. Solutio facilis problematum quorundam geometricorum difficillimorum // Novi Commentarii academiae scientiarum imperialis Petropolitanae. 1767, т. 11. — С. 103—123. Перепечатано в Opera Omnia, ser. I, vol. XXVI, pp. 139—157, Societas Scientiarum Naturalium Helveticae, Lausanne, 1953, MR0061061.
- Дм. Ефремов. Новая геометрия треугольника. — 1902.
- Коксетер Г. С. М., Грейтцер С. П. Новые встречи с геометрией. — М.: Наука, 1978. — Т. 14. — (Библиотека математического кружка).
- Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 96—97. — 383 с. — ISBN 5-09-001287-3..
- Зетель С.И. Новая геометрия треугольника. Пособие для учителей. 2-е издание.. — М.: Учпедгиз, 1962. — 153 с.
Точка пересечения прямой и плоскости онлайн
С помощю этого онлайн калькулятора можно найти точку пересечения прямой и плоскости. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямой и плоскости задайте вид уравнения прямой («канонический» или «параметрический» ), введите данные в уравнения прямой и плоскости и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Точка пересечения прямой и плоскости − теория, примеры и решения
1. Точка пересечения плоскости и прямой, заданной в каноническом виде
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямая L1:
 , , | (1) |
и плоскость α:
где M1(x1, y1, z1) − точка, лежащая на прямой L1, q1={m1, p1, l1} − направляющий вектор прямой L1, а n={A,B,C} − нормальный вектор плоскости α.
Найти точку пересечения прямой L1 и плоскости α (Рис.1).
Запишем уравнение (1) в виде системы двух линейных уравнений:
Сделаем перекрестное умножение в уравнениях (3) и (4):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Решим систему линейных уравнений (2), (5), (6) с тремя неизвестными x, y, z. Для этого в уравнении (2) переведем свободный член в правую часть уравнения и запишем эту систему в матричном виде:
Как решить систему линейных уравнений (11)(или (2), (5), (6)) посмотрите на странице Метод Гаусса онлайн или на примерах ниже. Если система линейных уравнениий (7) несовместна, то прямая L1 и плоскость α не пересекаются. Если система (7) имеет множество решений, то прямая L1 лежит на плоскости α. Единственное решение системы линейных уравнений (7) указывает на то, что это решение определяет координаты точки пересечения прямой L1 и плоскости α.
Замечание. Если прямая задана параметрическим уравнением, то уранение прямой нужно приводить к каноническому виду и применить метод, описанный выше, или же
2. Точка пересечения плоскости и прямой, заданной в параметрическом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L1 в параметрическом виде:
и плоскость α:
где M1(x1, y1, z1) − точка, лежащая на прямой L1, q1={m1, p1, l1} − направляющий вектор прямой L1, а n={A,B,C} − нормальный вектор плоскости α.
Задачу нахождения нахождения точки пересечения прямых L1 и плоскости α можно решить разными методами.
Метод 1. Приведем уравнения прямой L1 к каноническому виду.
Для приведения уравнения (8) к каноническому виду, выразим параметр t через остальные переменные:
Так как левые части уравнений (10) равны, то можем записать:
Далее, для нахождения точки пересечения прямой и плоскости нужно воспользоваться параграфом 1.
Метод 2. Для нахождения точки пересечения прямой L1 и плоскости α решим совместно уравнения (8) и (9). Из уравнений (8) подставим x, y, z в (9):
Откроем скобки и найдем t:
Если числитель и знаменатель в уравнении (14) одновременно равны нулю, то это значит, что прямая L1 лежит на полскости α. Если в уравнении (14) числитель отличен от нуля, а знаменатель равен нулю, то прямая и плоскость параллельны.
Если же числитель и знаменатель в уравнении (14) отличны от нуля, то прямая и плоскость пересекаются в одной точке. Для нахождения координат точки пересечения прямой L1 и плоскости α подставим полученное значение t из (14) в (8).
3. Примеры нахождения точки пересечения прямой и плоскости.
Пример 1. Найти точку пересечения прямой L1:
и плоскости α:
Представим уравнение (15) в виде двух уравнений:
Сделаем перекрестное умножение в уравнениях (17) и (18):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Упростим:
Для нахождения точки пересечения прямой L1 и плосклсти α нужно решить совместно уравнения (2), (19) и (20). Для этого переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (19) и (20):
Решим систему линейных уравнений (21) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −7/3:
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 3 со строкой 2, умноженной на 4/3:
Второй этап. Обратный ход Гаусса.
Исключим элементы 3-го столбца матрицы выше элемента a33. Для этого сложим строку 2 со строкой 3, умноженной на −3/2:
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на 1/2:
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
Запишем решение:
Ответ. Точка пересечения прямой L1 и плоскости α имеет следующие координаты:
Пример 2. Найти точку пересечения прямой L1:
и плоскости α:
Представим уравнение (22) в виде двух уравнений:
Сделаем перекрестное умножение в уравнениях (24) и (25):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Упростим:
Для нахождения точки пересечения прямой L1 и плосклсти α нужно решить совместно уравнения (2), (26) и (27). Переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (26) и (27):
Решим систему линейных уравнений (21) отностительно x, y, z. Для этого построим расширенную матрицу:
Обозначим через aij элементы i-ой строки и j-ого столбца.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строку 3 со строкой 1, умноженной на 6/5:
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 3 со строкой 2, умноженной на −1/5:
Из расширенной матрицы восстановим систему линейных уравнений:
Легко можно заметить, что последнее уравнение в (29) несовместна, так как несуществуют такие x, y, z чтобы выполнялось это равенство. Следовательно система линейных уравнений (2), (26) и (27) несовместна. Тогда прямая L1 и плоскость α не пересекаются, т.е. они параллельны.
Ответ. Прямая L1 и плоскость α параллельны, т.е. не имеют общую точку.
Пример 3. Найти точку пересечения прямой в параметрическом виде L1:
и плоскости α:
Решение. Для нахождения точки пересечения прямой L1 и плоскости α нужно найти такое значение t, при котором точка M(x, y, z) удовлетворяет уравнению (31). Поэтому подставим значения x, y, z из (30) в (31):
Откроем скобки:
Упростив уравнение, получим:
Как видим, любое значение t удовлетворяет уравнению (33), т.е. любая точка на прямой L1 удовлетворяет уравнению плоскости α. Следовательно прямая L1 лежит на плоскости α.
Ответ. Прямая L1 лежит на плоскости α.
Пересечение прямых. Точка пересечения двух прямых
Точка пересечения двух прямых на плоскости
Методы решения. Существует два метода решения плоских задач на определение координат точки пересечения прямых:- графический
- аналитический
Графический метод решения. Используя уравнения, начертить графики прямых и с помощью линейки найти координаты точки пересечения.
Аналитический метод решения. Необходимо объединить уравнения прямых в систему, решение которой, позволит определить точные координаты точки пересечения прямых.Если система уравнений:
- имеет единственное решение, то прямые пересекаются;
- имеет бесконечное множество решений, то прямые совпадают;
- не имеет решений, то прямые не пересекаются (прямые параллельны между собой)
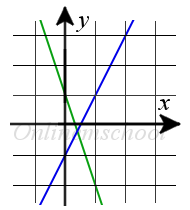 Пример 1. Найти точку пересечения прямых y = 2x — 1 и y = -3x + 1.
Пример 1. Найти точку пересечения прямых y = 2x — 1 и y = -3x + 1.Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
y = 2x — 1y = -3x + 1Вычтем из первого уравнения второе
y — y = 2x — 1 — (-3x + 1)y = -3x + 1 => 0 = 5x — 2y = -3x + 1
Из первого уравнения найдем значение x
5x = 2y = -3x + 1 => x = 25 = 0.4y = -3x + 1
Подставим значение x во второе уравнение и найдем значение y
x = 0.4y = -3·(0.4) + 1 = -1.2 + 1 = -0.2
Ответ. Точка пересечения двух прямых имеет координаты (0.4, -0.2)
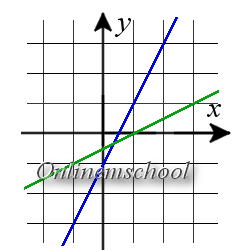 Пример 2. Найти точку пересечения прямых y = 2x — 1 и x = 2t + 1y = t.
Пример 2. Найти точку пересечения прямых y = 2x — 1 и x = 2t + 1y = t.Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
y = 2x — 1x = 2t + 1y = tВ первое уравнение подставим значения x и y из второго и третьего уравнений.
t = 2·(2t + 1) — 1x = 2t + 1y = t => t = 4t + 1x = 2t + 1y = t =>
-3t = 1x = 2t + 1y = t => t = -13x = 2t + 1y = t
Подставим значение t во второе и третье уравнение
t = -13x = 2·(-13) + 1 = -23 + 1 = 13y = -13
Ответ. Точка пересечения двух прямых имеет координаты (13, -13)
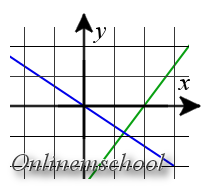 Пример 3 Найти точку пересечения прямых 2x + 3y = 0 и x — 23 = y4.
Пример 3 Найти точку пересечения прямых 2x + 3y = 0 и x — 23 = y4.Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
2x + 3y = 0x — 23 = y4
Из второго уравнения выразим y через x
2x + 3y = 0y = 4·x — 23
Подставим y в первое уравнение
2x + 3·4·x — 23 = 0y = 4·x — 23 => 2x + 4·(x — 2) = 0y = 4·x — 23 =>
2x + 4x — 8 = 0y = 4·x — 23 => 6x = 8y = 4·x — 23 =>
x = 86 = 43y = 4·x — 23 => x = 86 = 43y = 4·4/3 — 23 = 4·-2/3 3 = -89
Ответ. Точка пересечения двух прямых имеет координаты (43, -89)
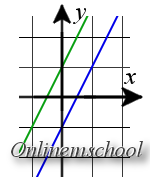 Пример 4. Найти точку пересечения прямых y = 2x — 1 и y = 2x + 1.
Пример 4. Найти точку пересечения прямых y = 2x — 1 и y = 2x + 1.Решение: Обе прямые заданы уравнениями с угловым коэффициентом. Так как k1 = k2 = 2, то прямые параллельны. Так как эти прямые не совпадают то точек пересечения нет.
Решим также эту задачу используя систему уравнений:
y = 2x — 1y = 2x + 1Вычтем из первого уравнения второе
y — y = 2x — 1 — (2x + 1)y = -3x + 1 => 0 = -2y = -3x + 1
В первом уравнении получили противоречие (0 ≠ -2), значит система не имеет решений — отсутствуют точки пересечения прямых (прямые параллельны).
Ответ. Прямые не пересекаются (прямые параллельны).
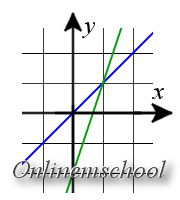 Пример 5. Проверить является ли точка N(1, 1) точкой пересечения прямых y = x и y = 3x — 2.
Пример 5. Проверить является ли точка N(1, 1) точкой пересечения прямых y = x и y = 3x — 2.Решение: Подставим координаты точки N в уравнения прямых.
1 = 1
1 = 3·1 — 2 = 1
Ответ. Так как оба уравнения превратились в тождества, то точка N — точка пересечения этих прямых.
Точка пересечения двух прямых в пространстве
Метод решения. Для определение координат точки пересечения прямых в пространстве, необходимо объединить уравнения прямых в систему, решение которой, позволит определить точные координаты точки пересечения прямых.Если система уравнений:
- имеет единственное решение, то прямые пересекаются;
- имеет бесконечное множество решений, то прямые совпадают;
- не имеет решений, то прямые не пересекаются (прямые параллельны или скрещиваются между собой)
Решение: Составим систему уравнений
x — 1 = ay — 1 = az — 1 = ax — 3-2 = b2 — y = bz = b => x = a + 1y = a + 1z = a + 1x — 3-2 = b2 — y = bz = b =>
Подставим значения x, y, z из 1, 2, 3 уравнений в 4, 5, 6 уравнения
x = a + 1y = a + 1z = a + 1a + 1 — 3-2 = b2 — (a + 1) = ba + 1 = b => x = a + 1y = a + 1z = a + 1a — 2-2 = b1 — a = ba + 1 = b
К шестому уравнению добавим пятое уравнение
x = a + 1y = a + 1z = a + 1a — 2-2 = b1 — a = ba + 1 + (1 — a) = b + b => x = a + 1y = a + 1z = a + 1a — 2-2 = b1 — a = bb = 1
Подставим значение b в четвертое и пятое уравнения
x = a + 1y = a + 1z = a + 1a — 2-2 = 11 — a = 1b = 1 => x = a + 1y = a + 1z = a + 1a — 2 = -2a = 0b = 1 =>
x = a + 1y = a + 1z = a + 1a = 0a = 0b = 1 => x = 0 + 1 = 1y = 0 + 1 = 1z = 0 + 1 = 1a = 0a = 0b = 1
Ответ. Прямые пересекаются в точке с координатами (1, 1, 1).
Замечание. Если уравнения прямых заданы параметрически, и в обоих уравнениях параметр задан одной и той же буквой, то при составлении системы в одном из уравнений необходимо заменить букву отвечающую за параметр.
Пример 7. Найти точку пересечения прямых x = 2t — 3y = tz = -t + 2 и x = t + 1y = 3t — 2z = 3.Решение: Составим систему уравнений заменив во втором уравнении параметр t на a
x = 2t — 3y = tz = -t + 2x = a + 1y = 3a — 2z = 3
Подставим значения x, y, z из 1, 2, 3 уравнений в 4, 5, 6 уравнения
x = 2t — 3y = tz = -t + 22t — 3 = a + 1t = 3a — 2-t + 2 = 3 => x = 2t — 3y = tz = -t + 22t = a + 4t = 3a — 2t = -1 =>Подставим значение t из шестого уравнения в остальные уравнения
x = 2·(-1) — 3y = (-1)z = -(-1) + 22·(-1) = a + 4-1 = 3a — 2t = -1 => x = -5y = -1z = 3a = -6a = 13t = -1
Ответ. Так как -6 ≠ 13, то прямые не пересекаются.
Идеальная точка — Википедия

Несобственная точка, идеальная точка, омега-точка или бесконечно удалённая точка[1] — это вполне определенная[en] точка вне гиперболической плоскости или пространства. Если дана прямая l и точка P вне l, справа и слева параллельные в пределе к прямой l и проходящие через P прямые сходятся к l в идеальных точках.
В отличие от проективного случая, идеальные точки образуют границу, а не подмногообразие. Таким образом, эти прямые не пересекаются в идеальной точке и такие точки, хотя они вполне определены[en], не принадлежат самому гиперболическому пространству.
Идеальные точки вместе образуют абсолют Кэли[en] или границу гиперболической геометрии. Например, единичная окружность образует абсолют Кэли дисковой модели Пуанкаре и дисковой модели Клейна. В это же время вещественная прямая образует абсолют Кэли модели полуплоскости[2].
Аксиома Паша и теорема о внешнем угле треугольника выполняются для омега-треугольника, который определяется двумя точками гиперболического пространства и омега-точкой[3].
- Гиперболическое расстояние между идеальными точками и любой другой точкой или другой точкой равно бесконечности.
- Центры орициклов и орисфер являются идеальными точками. Два орицикла концентричны, когда они имеют один и тот же центр.
Многоугольники с идеальными вершинами[править | править код]
Идеальные треугольники[править | править код]
Если все вершины треугольника являются идеальными точками, треугольник является идеальным треугольником.
Идеальные треугольники имеют несколько интересных свойств:
- Все идеальные треугольники конгруэнтны.
- Внутренние углы идеального треугольника все равны нулю.
- Любой идеальный треугольник имеет бесконечный периметр.
- Любой идеальный треугольник имеет площадь π/−K{\displaystyle \pi /-K}, где K равно (отрицательной) кривизне плоскости[4].
Идеальные четырёхугольники[править | править код]
Если все вершины четырёхугольника являются идеальными точками, четырёхугольник является идеальным четырёхугольником.
В то время как все идеальные треугольники конгруэнтны, не все четырёхугольники конгруэнтны, диагонали могут пересекаться под разными углами, что приводит к неконгруэнтности четырёхугольников, при этом:
- Внутренние углы идеального четырёхугольника все равны нулю.
- Любой идеальный четырёхугольник имеет бесконечный периметр.
- Любой идеальный (выпуклый без пересечений) четырёхугольник имеет площадь 2π/−K{\displaystyle 2\pi /-K}, где K равно (отрицательной) кривизне плоскости.
Идеальный квадрат[править | править код]
Идеальный четырёхугольник, у которого две диагонали перпендикулярны образует идеальный квадрат.
Идеальный квадрат использовал Фердинанд Карл Швейкарт в его меморандуме, в которой он упоминает «астральную геометрию». Это была одна из первых публикаций, допускающих возможность гиперболической геометрии[5].
Идеальные n-угольники[править | править код]
Как n-угольники могут быть разделены на (n − 2) идеальных треугольников, и площадь многоугольника будет равна площади идеального треугольника, умноженной на (n − 2).
Представления в моделях гиперболической геометрии[править | править код]
В дисковой модели Кляйна и дисковой модели Пуанкаре гиперболической плоскости идеальными точками являются единичные окружности (для гиперболической плоскости) или единичная сфера (для пространств большей размерности), которые являются недостижимой границей гиперболического пространства.
Одна и та же гиперболическая прямая в дисковой модели Кляйна и дисковой модели Пуанкаре будет проходить через те же две идеальные точки.
Дисковая модель Клейна[править | править код]
Если даны две различные точки p и q в открытом единичном диске, единственная прямая, соединяющая их, пересекает единичную окружность в двух идеальных точках, a и b (предполагается, что точки идут в порядке a, p, q, b), так что |aq| > |ap| и |pb| > |qb|. Тогда гиперболическое расстояние между p и q выражается формулой
- d(p,q)=12log|qa||bp||pa||bq|,{\displaystyle d(p,q)={\frac {1}{2}}\log {\frac {\left|qa\right|\left|bp\right|}{\left|pa\right|\left|bq\right|}},}
Дисковая модель Пуанкаре[править | править код]
Если заданы две различные точки p и q в открытом единичном диске, то единственная дуга окружности ортогональная границе и соединяющая точки пересекает единичную окружность в двух идеальных точках, a и b (предполагается, что точки идут в порядке a, p, q, b), так что |aq| > |ap| и |pb| > |qb|. Тогда гиперболическое расстояние между p и q выражается формулой
- d(p,q)=log|qa||bp||pa||bq|,{\displaystyle d(p,q)=\log {\frac {\left|qa\right|\left|bp\right|}{\left|pa\right|\left|bq\right|}},}
Здесь расстояние измеряется вдоль (прямых) отрезков aq, ap, pb и qb.
Модель полуплоскости Пуанкаре[править | править код]
В модели полуплоскости идеальные точки — это точки на граничной оси. Существует также другая идеальная точка, которая не принадлежит модели полуплоскости (но лучи, параллельные положительной полуоси y, приближаются к ней).
Гиперболическая модель[править | править код]
В гиперболоидной модели нет никаких несобственных точек.
- ↑ Комацу, 1981, с. 103-104.
- ↑ Struve, Struve, 2010, с. 151–170.
- ↑ Hvidsten, 2005, с. 276–283.
- ↑ Thurston, 2012.
- ↑ Bonola, 1955, с. 75–77.
- Мацуо Комацу. Многообразие геометрии. — М.: Знание, 1981.
- Thomas Q. Sibley. The geometric viewpoint : a survey of geometries. — Reading, Mass.: Addison-Wesley, 1998. — С. 109. — ISBN 0-201-87450-4.
- Horst Struve, Rolf Struve. Non-euclidean geometries: the Cayley-Klein approach // Journal of Geometry. — 2010. — Т. 89, вып. 1. — ISSN 0047-2468. — DOI:10.1007/s00022-010-0053-z.
- Michael Hvidsten. Geometry with Geometry Explorer. — New York, NY, 2005. — ISBN 0-07-312990-9.
- Roberto Bonola. Non-Euclidean geometry : a critical and historical study of its developments. — New York, NY: Dover, 1955. — С. 75–77. — ISBN 0486600270.
- Dylan. 274 Curves on Surfaces, Lecture 5. — 2012.
Проекция точки на прямую онлайн
С помощю этого онлайн калькулятора можно найти проекцию точки на прямую. Дается подробное решение с пояснениями. Для вычисления проекции точки на прямую, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точки и элементы уравнения в ячейки и нажимайте на кнопку «Решить».
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Проекция точки на прямую − теория, примеры и решения
Рассмотрим эту задачу в двухмерном и трехмерном пространствах.
1. Пусть в двухмерном пространстве задана точка M0(x0, y0) и прямая L:
где q=(m,p) направляющий вектор прямой L.
Найдем проекцию точки M0 на прямую (1)(Рис.1).
Алгоритм нахождения проекции точки на прямую L содержит следующие шаги:
- построить прямую L1, проходящую через точку M0 и перпендикулярную прямой L,
- найти пересечение прямых L и L1(точка M1)
Уравнение прямой, проходящей через точку M0(x0, y0) имеет следующий вид:
где n=(A,B) нормальный вектор прямой L1.
Как видно из рисунка Рис.1, для того, чтобы прямая L1 была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n прямой L1, поэтому в качестве нормального вектора прямой L1 достаточно взять направляющий вектор прямой L. Тогда уравнение прямой L1, представленной уравнением (2) можно записать так:
Откроем скобки
Для нахождения точки пересечения прямых L и L1, которая и будет проекцией точки M0 на прямую L, можно решить систему из двух уравнений (1) и (3) с двумя неизвестными x и y. Выражая неизвестную x из одного уравнения и подставляя в другое уравнение получим координаты точки M1(x1, y1).
Найдем точку пересечения прямых L и L1 другим методом.
Выведем параметрическое уравнение прямой (1):
Подставим значения x и y в (4):
Мы нашли такое значение t=t’, при котором координаты x и y точки на прямой L удовлетворяют уравнению прямой L1(4). Следовательно, подставляя значение t’ в (5) получим координаты проекции точки M0 на прямую L:
где x1=mt’+x’, y1=pt’+y’.
Пример 1. Найти проекцию точки M0(1, 3) на прямую
Решение.
Направляющий вектор прямой (6) имеет вид:
Т.е. m=4, p=5. Из уравнения прямой (6) видно, что она проходит через точку M’ (x’, y’)=(2, −3)(в этом легко убедится − подставляя эти значения в (6) получим тождество 0=0), т.е. x’=2, y’=-3. Подставим значения m, p, x0, y0, x’, y’ в (5′):
Подставляя значение t в (5), получим:
Ответ:
Проекцией точки M0(1, 3) на прямую (6) является точка:
2. Пусть в трехмерном пространстве задана точка M0(x0, y0, z0) и прямая L:
где q=(m, p, l) направляющий вектор прямой L.
Найдем проекцию точки M0 на прямую (7)(Рис.2).
Нахождение проекцию точки на прямую L содержит следующие шаги:
- построить плоскость α, проходящую через точку M0 и перпендикулярную прямой L,
- найти пересечение плоскости α и прямой L(точка M1)
Уравнение плоскости, проходящей через точку M0(x0, y0, z0) имеет следующий вид:
где n=(A,B,C) нормальный вектор плоскости α.
Как видно из рисунка Рис.2, для того, чтобы плоскость α была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n плоскости α, поэтому в качестве нормального вектора плоскости α достаточно взять направляющий вектор прямой L. Тогда уравнение плоскости α, представленной уравнением (8) можно записать так:
Откроем скобки
Для нахождения точки пересечения плоскости α и прямой L, которая и будет проекцией точки M0 на прямую L, выведем параметрическое уравнение прямой (7):
Подставим значения x и y в (9):
Мы нашли такое значение t=t’, при котором координаты x,y и z точки на прямой L удовлетворяют уравнению плоскости (9). Следовательно, подставляя значение t’ в (10) получим координаты проекции точки M0 на прямую L:
где x1=mt’+x’, y1=pt’+y’, z1=lt’+z’.
Пример 2. Найти проекцию точки M0(3, −1, −2) на прямую
Решение.
Направляющий вектор прямой (11) имеет вид:
Т.е. m=2, p=3, l=−4. Из уравнения прямой (11) видно, что она проходит через точку M’ (x’, y’, z’)=(2, 1, 1)(в этом легко убедится − подставляя эти значения в (11) получим тождество 0=0=0), т.е. x’=2, y’=1, z’=1. Подставим значения m, p, l x0, y0, z0 x’, y’, z’ в (10′):
Подставляя значение t=t’ в (10), получим:
Ответ:
Проекцией точки M0(3, −1, −2) на прямую (11) является точка: