Т. Понятия кинематики — PhysBook

Основные понятия кинематики

Кинематика — раздел механики, изучающий движение тел без учета причин, вызвавших это движение.

Основной задачей кинематики является нахождение положения тела в любой момент времени, если известны его положение, скорость и ускорение в начальный момент времени.

Механическое движение — это изменение положения тел (или частей тела) относительно друг друга в пространстве с течением времени.

Для описания механического движения надо выбрать систему отсчета.

Тело отсчета — тело (или группа тел), принимаемое в данном случае за неподвижное, относительно которого рассматривается движение других тел.

Система отсчета — это система координат, связанная с телом отсчета, и выбранный способ измерения времени (рис. 1).

Рис. 1

Положение тела можно определить с помощью радиуса-вектора \(~\vec r\) или с помощью координат.

Радиус-вектор \(~\vec r\) точки Μ — направленный отрезок прямой, соединяющий начало отсчета

О с точкой Μ (рис. 2).

Рис. 2

Координата x точки Μ — это проекция конца радиуса-вектора точки Μ на ось Ох. Обычно пользуются прямоугольной системой ко ординат. В этом случае положение точки Μ на линии, плоскости и в пространстве определяют соответственно одним (x), двумя (х, у) и тремя (х, у, z) числами — координатами (рис. 3).

Рис. 3

В элементарном курсе физики изучают кинематику движения материальной точки.

Материальная точка — тело, размерами которого в данных условиях можно пренебречь.

Этой моделью пользуются в тех случаях, когда линейные размеры рассматриваемых тел много меньше всех прочих расстояний в данной задаче или когда тело движется поступательно.

Поступательным называется движение тела, при котором прямая, проходящая через любые две точки тела, перемещается, оставаясь параллельной самой себе. При поступательном движении все точки тела описывают одинаковые траектории и в любой момент времени имеют одинаковые скорости и ускорения. Поэтому для описания такого движения тела достаточно описать движение его одной произвольной точки.

В дальнейшем под словом «тело» будем понимать «материальная точка».

Линия, которую описывает движущееся тело в определенной системе отсчета, называется траекторией. На практике форму траектории задают с помощью математических формул (y = f(x) — уравнение траектории) или изображают на рисунке. Вид траектории зависит от выбора системы отсчета. Например, траекторией тела, свободно падающего в вагоне, который движется равномерно и прямолинейно, является прямая вертикальная линия в системе отсчета, связанной с вагоном, и парабола в системе отсчета, связанной с Землей.

В зависимости от вида траектории различают прямолинейное и криволинейное движение.

Путь s — скалярная физическая величина, определяемая длиной траектории, описанной телом за некоторый промежуток времени. Путь всегда положителен:

s > 0.

Перемещение \(~\Delta \vec r\) тела за определенный промежуток времени — направленный отрезок прямой, соединяющий начальное (точка M₀) и конечное (точка М) положение тела (см. рис. 2):

\(~\Delta \vec r = \vec r — \vec r_0,\)

где \(~\vec r\) и \(~\vec r_0\) — радиусы-векторы тела в эти моменты времени.

Проекция перемещения на ось Ox\[~\Delta r_x = \Delta x = x — x_0\], где x₀ и x — координаты тела в начальный и конечный моменты времени.

Модуль перемещения не может быть больше пути\[~|\Delta \vec r| \le s\].

Знак равенства относится к случаю прямолинейного движения, если направление движения не изменяется.

Зная перемещение и начальное положение тела, можно найти его положение в момент времени t:

\(~\vec r = \vec r_0 + \Delta \vec r;\) \(~\left\{ \begin{matrix} x = x_0 + \Delta r_x ; \\ y = y_0 + \Delta r_y . \end{matrix} \right.\)

Скорость — мера механического состояния тела. Она характеризует быстроту изменения положения тела относительно данной системы отсчета и является векторной физической величиной.

Средняя скорость \(~\mathcal h \vec \upsilon \mathcal i\) — векторная физическая величина, численно равная отношению перемещения к промежутку времени, за который оно произошло, и направленная вдоль перемещения (рис. 4):

\(~\mathcal h \vec \upsilon \mathcal i = \frac{\Delta \vec r}{\Delta t}; \qquad \mathcal h \vec \upsilon \mathcal i \upuparrows \Delta \vec r .\)

Рис. 4

В СИ единицей скорости является метр в секунду (м/с).

Средняя скорость, найденная по этой формуле, характеризует движение только на том участке траектории, для которого она определена. На другом участке траектории она может быть другой.

Иногда пользуются средней скоростью пути\[~\mathcal h \upsilon \mathcal i = \frac{s}{\Delta t}\], где s — путь, пройденный за промежуток времени Δ

t. Средняя скорость пути — это скалярная величина.

Мгновенная скорость \(~\vec \upsilon\) тела — скорость тела в данный момент времени (или в данной точке траектории). Она равна пределу, к которому стремится средняя скорость за бесконечно малый промежуток времени \(~\vec \upsilon = \lim_{\Delta t \to 0} \frac{\Delta \vec r}{\Delta t} = \vec r \ ‘\). Здесь \(~\vec r \ ‘\) — производная от радиуса-вектора по времени.

В проекции на ось Ох:

\(~\upsilon_x = \lim_{\Delta t \to 0} \frac{\Delta x}{\Delta t} = x’.\)

Мгновенная скорость тела направлена по касательной к траектории в каждой ее точке в сторону движения (см. рис. 4).

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. Оно показывает, на какую величину изменяется скорость тела за единицу времени.

Среднее ускорение — физическая величина, численно равная отношению изменения скорости ко времени, за которое оно произошло:

\(~\mathcal h \vec a \mathcal i = \frac{\Delta \vec \upsilon}{\Delta t} = \frac{\vec \upsilon — \vec \upsilon_0}{\Delta t} .\)

Вектор \(~\mathcal h \vec a \mathcal i\) направлен параллельно вектору изменения скорости \(~\Delta \vec \upsilon\) (\(~\mathcal h \vec a \mathcal i \upuparrows \Delta \vec \upsilon\)) в сторону вогнутости траектории (рис. 5).

Рис. 5

Мгновенное ускорение:

\(~\vec a = \lim_{\Delta t \to 0} \frac{\Delta \vec \upsilon}{\Delta t} = \vec \upsilon \ ‘ .\)

В СИ единицей ускорения является метр на секунду в квадрате (м/с²).

В общем случае мгновенное ускорение направлено под углом к скорости. Зная траекторию, можно определить направление скорости, но не ускорения. Направление ускорения определяется направлением равнодействующей сил, действующих на тело.

При прямолинейном движении с возрастающей по модулю скоростью (рис. 6, а) векторы \(~\vec a\) и \(~\vec \upsilon_0\) сонаправлены (\(~\vec a \upuparrows \vec \upsilon_0\)) и проекция ускорения на направление движения положительна.

При прямолинейном движении с убывающей по модулю скоростью (рис. 6, б) направления векторов \(~\vec a\) и \(~\vec \upsilon_0\) противоположны (\(~\vec a \uparrow \downarrow \vec \upsilon_0\)) и проекция ускорения на направление движения отрицательна.

Рис. 6

Вектор \(~\vec a\) при криволинейном движении можно разложить на две составляющие, направленные вдоль скорости \(~\vec a_{\tau}\) и перпендикулярно скорости \(~\vec a_n\) (рис. 1.7), \(~\vec a_{\tau}\) — тангенциальное ускорение, характеризующее быстроту изменения модуля скорости при криволинейном движении, \(~\vec a_n\) — нормальное ускорение, характеризующее быстроту изменения направления вектора скорости при криволинейном движении Модуль ускорения \(~a = \sqrt{a^2_{\tau} + a^2_n}\).

Рис. 7

Литература

1. Аксенович Л.А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л.А. Аксенович, Н.Н.Ракина, К.С. Фарино; Под ред. К.С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C.5-8.

Перемещение. Видеоурок. Физика 9 Класс

Первой характеристикой движения, введенной нами ранее, был пройденный путь. Напомним, что обозначается он буквой S (иногда встречается обозначение L) и измеряется в СИ в метрах.

Пройденный путь – это скалярная величина, т. е. величина, которая характеризуется только числовым значением. А значит, предсказать, где тело окажется в нужный нам момент времени, мы не сможем. Можно говорить только о пройденном телом общем расстоянии (рис. 1).

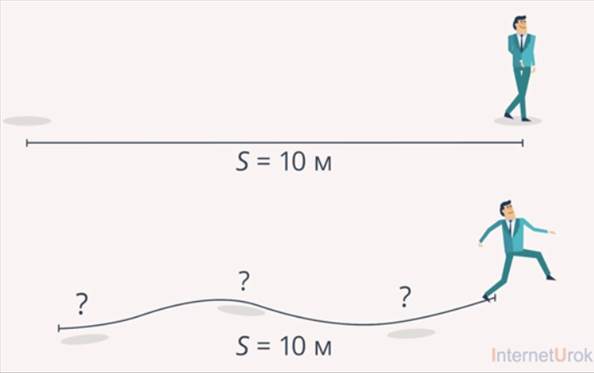
Рис. 1. Зная только пройденный путь, нельзя определить положение тела в произвольный момент времени

Чтобы охарактеризовать местоположение тела в произвольный момент, вводится величина, которая называется перемещение. Перемещение – векторная величина, т. е. это величина, которая характеризуется не только числовым значением, но и направлением.

Перемещение обозначается так же, как пройденный путь, буквой S, но, в отличие от пройденного пути, над буквой ставится стрелочка, подчеркивая тем самым, что это величина векторная: .

То, что перемещение и пройденный путь обозначаются одной буквой, вводит в некоторое заблуждение, но мы должны четко понимать разницу между пройденным путем и перемещением. Еще раз отметим, что иногда путь обозначается L. Это позволяет избежать путаницы.

Определение

Перемещение – это вектор (направленный отрезок прямой), который соединяет начальную точку движения тела с его конечной точкой (рис. 2).

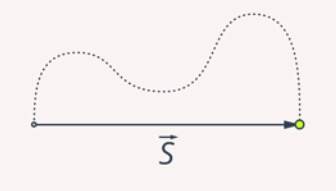
Рис. 2. Перемещение – векторная величина

Напомним, что пройденный путь – это длина траектории. А значит, путь и перемещение – это совершенно разные физические величины, хотя иногда случаются ситуации, когда они численно совпадают.

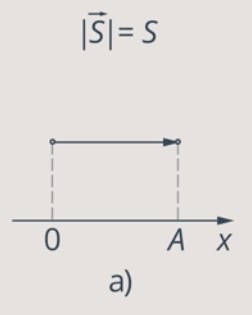
Рис. 3. Путь и модуль перемещения совпадают

На рис. 3 рассмотрен самый простой случай, когда тело движется вдоль прямой (оси Ох). Тело начинает свое движение из точки 0 и попадает в точку А. В этом случае мы можем говорить о том, что модуль перемещения 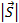 равен пройденному пути: .

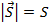Примером такого движения может служить перелет самолета (например, из Санкт-Петербурга в Москву). Если движение было строго прямолинейным, то тогда модуль перемещения будет равен пройденному пути.

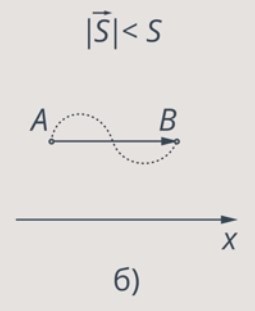
Рис. 4. Величина пути больше модуля перемещения

На рис. 4 тело движется вдоль кривой линии, т. е. движение криволинейное (из точки А в точку В). Из рисунка видно, что модуль перемещения (прямая линия) будет меньше пройденного пути, т. е. длина пройденного пути и длина вектора перемещения не равны.

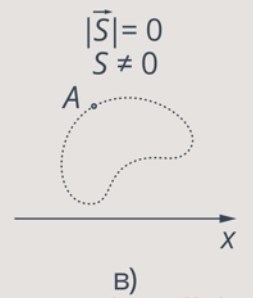
Рис. 5. Замкнутая траектория

На рис. 5 тело движется по замкнутой кривой. Выходит из точки А и в эту же точку возвращается. Модуль перемещения равен 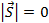, а пройденный путь – это длина всей кривой, .

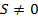Данный случай можно характеризовать следующим примером. Ученик вышел из дома утром, пошел в школу, целый день отзанимался, кроме этого, побывал еще в нескольких местах (магазин, спортзал, библиотека) и вернулся домой. Обратите внимание: в итоге ученик оказался дома, а значит, его перемещение равно 0 (рис. 6).

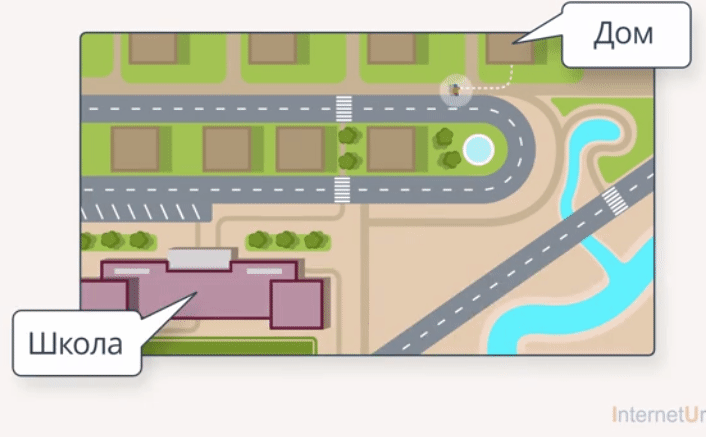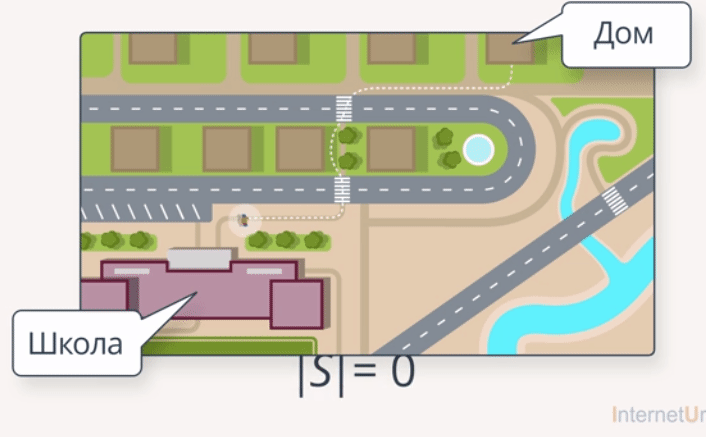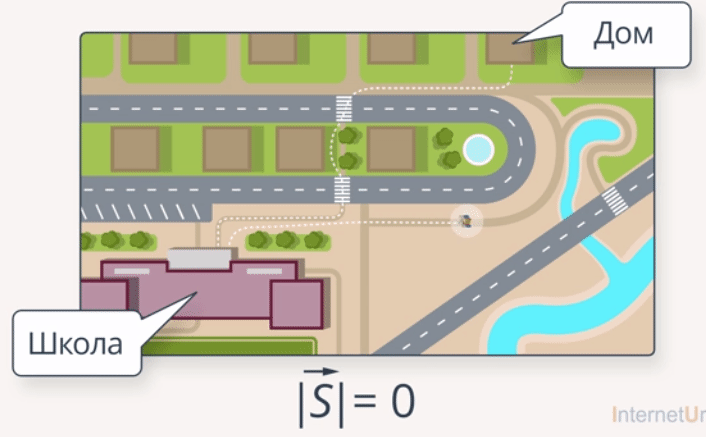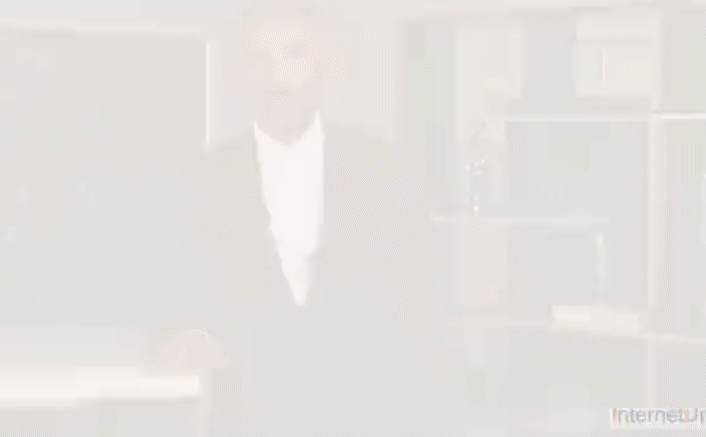
Рис. 6. Перемещение ученика равно нулю

Когда речь идет о перемещении, важно помнить, что перемещение зависит от системы отсчета, в которой рассматривается движение.

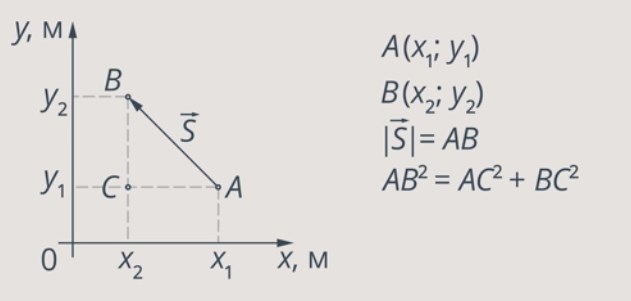
Рис. 7. Определение модуля перемещения тела

Тело движется в плоскости XOY. Точка А – начальное положение тела. Ее координаты 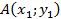. Тело перемещается в точку 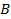. Вектор  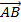– это перемещение тела: .

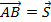Рассчитать модуль перемещения можно как гипотенузу прямоугольного треугольника 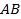, используя теорему Пифагора: 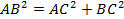. Для нахождения же вектора перемещения  необходимо найти угол между осью Ох и вектором перемещения.

Мы можем выбрать систему произвольно, то есть направить координатные оси так, как нам удобно, главное – проекции всех векторов в дальнейшем рассматривать в одной и той же выбранной системе координат.

Заключение

В заключение можно отметить, что мы познакомились с важной величиной – перемещением. Еще раз обратите внимание на то, что перемещение и путь могут совпадать только в случае прямолинейного движения, без смены направления такого движения.

Список литературы

1. Кикоин И.К., Кикоин А.К. Физика: учебник для 9 класса средней школы. – М.: Просвещение.
2. Перышкин А.В., Гутник Е.М., Физика. 9 кл.: учебник для общеобразоват. учреждений/А. В. Перышкин, Е. М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300.
3. Соколович Ю.А., Богданова Г.С. Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «vip8082p.vip8081p.beget.tech» (Источник)
2. Интернет-портал «foxford.ru» (Источник)

 

Домашнее задание

1. Что такое путь и перемещение? Чем они отличаются?
2. Мотоциклист выехал из гаража и направился на север. Проехал 5 км, затем повернул на запад и проехал также 5 км. На каком расстоянии от гаража он будет находиться?
3. Минутная стрелка прошла полный круг. Определите перемещение и пройденный путь для точки, которая находится на конце стрелки (радиус часов – 10 см).

Основные понятия кинематики

Кинематика — это один из разделов механики, который изучает движение тел без выяснения причин этого движения.

Механическое движение — это движение, при котором происходит изменение его положения в пространстве относительно других тел с течением времени, например, движение небесных тел, движение живых существ.

Система отсчета — это система координат, которая определяет механическое движение тела в любой момент времени.

Тело отсчета — это тело, по отношению, к которому рассматривается движение.

Всякому телу присущи такие свойства, как форма, размер, могут быть способность к деформированию и другое. Тела, которые не обладают такими свойствами, считаются абстрактными, например материальная точка.

Материальная точка — это абстрактное тело, которое имеет очень маленькую массу и размер по сравнению с расстоянием до других тел.

Любое тело можно принять за материальную точку, пренебрегая его размерами.

Траектория движения — линия, по которой происходит движение точки тела.

Перемещение — это отрезок прямой, имеющий направление, соединяет начальное положение тела с его последующим положением и определяется формулой:

Пройденный путь — это длина траектории, которую тело пройдет за время t, от начальной точки до конечной.

В кинематике рассматривается равномерное или поступательное движение, вращательное движение, равноускоренное движение.

Равномерное движение — это такое движение твердого тела, при котором все части тела движутся одинаково, имеют равные скорости и ускорения.

Вращательное движение — это такое движение твердого тела, при котором все точки тела движутся по окружностям вокруг прямой, центры которых лежат на этой прямой, т. е. оси вращения.

Равноускоренное движение — это такое движение, при котором вектор ускорения не изменяется ни по модулю, ни направлению.

Например, движение камня, брошенного под некоторым углом к горизонту.
Перемещение является векторной величиной, а путь — скалярной величиной.

Скорость — это физическая величина, которая определяется отношением пройденного пути к отрезку времени, за который был пройден этот путь.

Ускорение — это физическая величина, которая определяется пределом отношения небольшого изменения скорости к небольшому промежутку времени, в течение которого происходило изменение скорости. Обычно в физике и математике ускорение делится на касательное (тангенсальное) и нормальное.

Касательное ускорение ориентирует, насколько быстро будет изменяется скорость тела по модулю.

Нормальное ускорение ориентирует, насколько быстро скорость тела будет изменяется по направлению.

 

Вопросы, на которые нельзя не ответить!

1. Путь, перемещение и радиус кривизны.

Путь– скалярная физическая величина, определяемая длиной траектории, описанной телом за некоторый промежуток времени.

Перемещение(s{век}) — вектор, соединяющий начальную и конечную точки траектории; измеряется в метрах (м).

Радиус кривизны— величина, обратная кривизне кривой. Радиус кривизны характеризует величину соответствия кривой от прямой. 

2. Связь радиус-вектора, скорости и ускорения. Смысл скорости и ускорения.

v=dr/dt

a=dv/dt

Скоростьхарактеризует быстроту изменения положения тела относительно данной системы отсчета и является векторной физической величиной.

Ускорение– векторная физическая величина, характеризующая быстроту изменения скорости.

3. Нормальное и тангенциальное ускорение.

Тангенциальное ускорение– ускорение, характеризующее быстроту изменения модуля скорости при криволинейном движении.

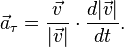
Нормальное ускорение– ускорение, характеризующее быстроту изменения направления вектора скорости при криволинейном движении.

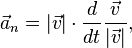
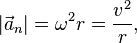где ω — угловая скоростьотносительно центра вращения, а r — радиус окружности.

4. Связь угла поворота, угловой скорости и углового ускорения.

Угловая скорость —векторнаяфизическая величина, характеризующая скоростьвращенияматериальной точкивокруг центра вращения. Вектор угловой скорости по величине равенуглуповорота точки вокруг центра вращения в единицу времени:

,

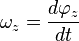а направлен пооси вращениясогласноправилу буравчика, то есть, в ту сторону, в которую ввинчивался быбуравчикс правой резьбой, если бы вращался в ту же сторону.

Угловое ускорение —псевдовекторнаяфизическая величина, характеризующая быстроту измененияугловой скоростиматериальной точки. При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости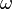по времени, то есть

,

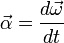и направлен по касательной кгодографувектора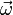в соответствующей его точке.

5. Связь угловых и линейных величин.

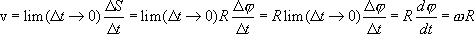
6. Законы Ньютона.

1) Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения.

2) В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.

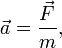
3) Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

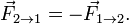
7. Силы в механике (вид, к чему приложена, куда направлена, чему равна). Сюда относятся силы упругости, сила трения, сила тяжести, вес.

Сила– физическая величина, являющаяся количественной мерой воздействия одного тела на другое, в результате которого тело приобретает ускорение или деформируется.

Сила упругости— сила, возникающая при деформации тела и противодействующая этой деформации. Действует в любом сечении деформированного тела, а также в месте его контакта с телом, вызывающим деформации. Вектор силы противоположен направлению деформации тела (смещению его молекул). Природа упругих сил электромагнитная.

Закон Гука:

Силой трения — сила, которая возникает при движении одного тела по поверхности другого. Сила трения всегда направлена вдоль поверхности соприкосновения в сторону, противоположную движению. Сила трения прямо пропорциональна весу тела (P) и силе нормальной реакции (N) и зависит от того, насколько сильно тела прижаты друг к другу.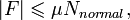

Сила тяжести– сила, действующая на тело со стороны Земли и сообщающая телу ускорение свободного падения (Fт=mg). Направление силы тяжести — вертикаль в данной точке земной поверхности. По закону всемирного тяготения на поверхности Земли (или вблизи этой поверхности) на тело массой m действует сила тяжести Fт=GMm/R² .СИЛА ТЯЖЕСТИ, сила P, действующая на любое тело, находящееся вблизи земной поверхности, и определяемая как геометрическая сумма силы притяжения Земли F и центробежной силы инерции Q, учитывающей эффект суточного вращения Земли.

Вес тела– сила, в которой вследствие притяжения к Земле тело действует на свою опору или подвес. В отличие от силы тяжести, являющейся гравитационной силой, приложенной к телу, вес — это упругая сила, приложенная к опоре или подвесу (т. е. к связи). Вес тела направлен в одну сторону с силой тяжести и равен P=m(g±a).

физики помогите! дайте определения словам и формулы к ним!

Плотность — это скалярная физическая величина, которая показывает сколька массы содержится в единице объёма. Равнодействующая всех сил — это векторная физическая величина, равная сумме всех сил, приложеных к телу. F = F1+F2+F3+…+Fn (все «эфки» с чёрточками или стрелочками — это векторная величина, и сумма тоже векторная) Объём — это ёмкость физического тела, т. е. та часть пространства, которая ограничена одной или несколькими поверхностями. В ощем случае объем тела даётся интегральной формулой (я думаю, вам это ещё рановато 🙂 ), но в наиболее распространённых случаях это произведение площади основания фигуры на высоту. Сила давления — это векторная физическая величина, равная давлению, которое оказывает тело на единицу площади. Пройденый путь — это скалярная физическая величина, равная длинне траектории тела, или более просто: это длина пути, пройденого телом. Работа — это скалярная физическая величина, характеризующая действие некоторой силы на определённом пути. Численно равна потере энергии на преодоление некоторого пути или деформации тела. Выражается как произведение силы на пройденый путь: A = F*s В общем случае — это контурный интеграл по пути от силы этому самому контуру. Измеряется в Джоулях.

То есть одного моего ответа вам мало? Ну хорошо, мне не жалко повторить. Плотность это единица массы, приходящаяся на единицу объема. Равнодействующая сила — это сила, действие которой на тело эквивалентно сумме нескольих сил. (Fр= Summ(F), векторно) . По второму закону Ньютона: summ(F) = m*a Объем — это вместимость пространства занимаемого телом. Формула через плотность: V = m/p. Другие формулы для разных тел смотрите в учебнике по геометрии. Давление — сила действующая на единицу площади. P = F/S Пройденый путь — длина участка траектории материальной точки, пройденного ею за определённое время. (для прямого участка S = v*t — равномерное движение, S = v0*t+a*t^2/2 — равноускоренное) Работа (в механике, действительно обозначается буквой А) — количественная характеристика действия силы, на процесс. A=F*v*dt = (F;S) = F*S*cos(a). Что такое косинус тоже расписывать?

Плотность — это скалярная физическая величина, которая показывает сколька массы содержится в единице объёма. Равнодействующая всех сил — это векторная физическая величина, равная сумме всех сил, приложеных к телу. F = F1+F2+F3+…+Fn (все «эфки» с чёрточками или стрелочками — это векторная величина, и сумма тоже векторная) Объём — это ёмкость физического тела, т. е. та часть пространства, которая ограничена одной или несколькими поверхностями. В ощем случае объем тела даётся интегральной формулой (я думаю, вам это ещё рановато 🙂 ), но в наиболее распространённых случаях это произведение площади основания фигуры на высоту. Сила давления — это векторная физическая величина, равная давлению, которое оказывает тело на единицу площади. Пройденый путь — это скалярная физическая величина, равная длинне траектории тела, или более просто: это длина пути, пройденого телом. Работа — это скалярная физическая величина, характеризующая действие некоторой силы на определённом пути. Численно равна потере энергии на преодоление некоторого пути или деформации тела. Выражается как произведение силы на пройденый путь: A = F*s В общем случае — это контурный интеграл по пути от силы этому самому контуру. Измеряется в Джоулях.

Плотность — это скалярная физическая величина, которая показывает сколька массы содержится в единице объёма. Равнодействующая всех сил — это векторная физическая величина, равная сумме всех сил, приложеных к телу. F = F1+F2+F3+…+Fn (все «эфки» с чёрточками или стрелочками — это векторная величина, и сумма тоже векторная) Объём — это ёмкость физического тела, т. е. та часть пространства, которая ограничена одной или несколькими поверхностями. В ощем случае объем тела даётся интегральной формулой (я думаю, вам это ещё рановато 🙂 ), но в наиболее распространённых случаях это произведение площади основания фигуры на высоту. Сила давления — это векторная физическая величина, равная давлению, которое оказывает тело на единицу площади. Пройденый путь — это скалярная физическая величина, равная длинне траектории тела, или более просто: это длина пути, пройденого телом. Работа — это скалярная физическая величина, характеризующая действие некоторой силы на определённом пути. Численно равна потере энергии на преодоление некоторого пути или деформации тела. Выражается как произведение силы на пройденый путь: A = F*s В общем случае — это контурный интеграл по пути от силы этому самому контуру. Измеряется в Джоулях.

Траектория путь перемещение скорость ускорение определение

⇐ ПредыдущаяСтр 2 из 6Следующая ⇒

Линию, вдоль которой движется материальная точка, называют траекторией. Длину траектории называют путем. Единица пути — метр.
Путь = скорость* время. S=v*t.
Направленный отрезок прямой, проведенный из начального положения движущейся точки в ее конечное положение, называется перемещением (s). Перемещение — величина векторная. Единица перемещения — метр.
Скорость — векторная физическая величина, характеризующая быстроту перемещения тела, численно равная отношению перемещения за малый промежуток времени к величине этого промежутка времени.
Формула скорости имеет вид v = s/t. Единица скорости — м/с
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло. Формула для вычисления ускорения: a=(v-v0)/t; Единица ускорения – метр/(секунда в квадрате).

Составляющие ускорения тангенциальное и нормальное ускорения

Тангенциальное ускорение направлено по касательной к траектории

Нормальное ускорение направлено по нормали к траектории

 

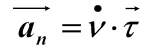
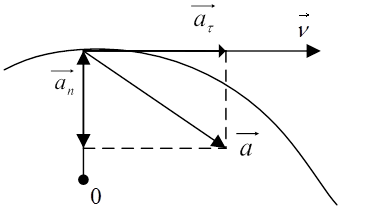
Тангенциальное ускорение характеризует изменение скорости по величине. Если скорость по величине не изменяется, то тангенциальная составляющая равна нулю, а нормальная составляющая ускорения равна полному ускорению.

Нормальное ускорение характеризует изменение скорости по направлению. Если направление скорости не изменяется, движение происходит по прямолинейной траектории.

 

В общем случае полное ускорение:

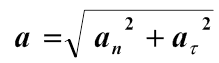
Итак, нормальная составляющая вектора ускорения

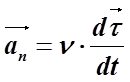
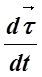быстрота изменения со временем направления касательной к траектории. Она тем больше ( 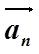), чем больше искривлена траектория и чем быстрее перемещается частица по траектории.

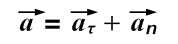
4)Угловой путь

Угловой путь – это элементарный угол поворота:

, .

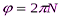Радиан – это угол, который вырезает на окружности дугу, равную радиусу.

Направление углового пути определяется правилом правого винта: если головку винта вращать в направлении движения точки по окружности, то поступательное движение острия винта укажет направление .

Угловая скорость (средняя и мгновенная)

Средняя угловая скорость – это физическая величина, численно равная отношению углового пути к промежутку времени:

, .

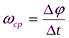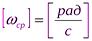Мгновенная угловая скорость – это физическая величина, численно равная изменения пределу отношения углового пути к промежутку времени при стремлении данного промежутка к нулю, или является первой производной углового пути по времени:

, .

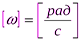Угловое ускорение (среднее и мгновенное)

Среднее угловое ускорение – это физическая величина, численно равная отношению изменения угловой скорости к промежутку времени, за который это изменение произошло:

, .

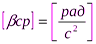Мгновенное угловое ускорение – это физическая величина, численно равная пределу отношения изменения угловой скорости к промежутку времени при стремлении данного промежутка к нулю, или является первой производной угловой скорости по времени, или второй производной углового пути по времени:

, .

 

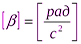При ускоренном движении угловое ускорение совпадает по направлению с угловой скоростью. При замедленном вращении угловое ускорение направлено в противоположную относительно угловой скорости сторону.

Законы Ньютона

Первый закон Ньютона

• Инерциальной называется та система отсчёта, относительно которой любая, изолированная от внешних воздействий, материальная точка либо покоится, либо сохраняет состояние равномерного прямолинейного движения.
• Первый закон Ньютона гласит:

Инерциальные системы отсчёта существуют.

По сути, этот закон постулирует инерцию тел, что сегодня кажется очевидным. Но это было далеко не так на заре исследования природы. Аристотель вот утверждал, что причиной всякого движения является сила, т. е. движения по инерции для него не существовало. ^{[источник?]}

 

Второй закон Ньютона

Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и её ускорением.

Второй закон Ньютона утверждает, что

в инерциальной системе отсчета (ИСО) ускорение, которое получает материальная точка, прямо пропорционально приложенной силе и обратно пропорционально массе.

При подходящем выборе единиц измерения этот закон можно записать в виде формулы:

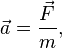
где — ускорение тела;

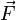— сила, приложенная к телу;

m — масса тела.

Или в более известном виде:

Если на тело действуют несколько сил, то второй закон Ньютона записывается:

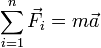
В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется в общем виде: скорость изменения импульса точки равна действующей на неё силе.

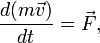
где 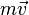— импульс (количество движения) точки;

t — время;

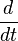— производная по времени.

Второй закон Ньютона действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта.

Третий закон Ньютона

Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой , а второе — на первое с силой 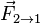. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.

Сам закон:

Тела действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль одной и той же прямой, равными по модулю и противоположными по направлению:

Выводы

Из законов Ньютона сразу же следуют некоторые интересные выводы. Так, третий закон Ньютона говорит, что, как бы тела ни взаимодействовали, они не могут изменить свой суммарный импульс: возникает закон сохранения импульса. Далее, надо потребовать, чтобы потенциал взаимодействия двух тел зависел только от модуля разности координат этих тел U( | r₁ − r₂ | ). Тогда возникает закон сохранения суммарной механической энергии взаимодействующих тел:

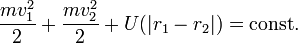
Законы Ньютона являются основными законами механики. Из них могут быть выведены все остальные законы механики.



ЛК_№1-Кинематика

3

ЛИТЕРАТУРА.

1. И.В.Савельев, Курс общей физики. М: Изд. «Наука».1970г.

2. Т.И.Трофимова, Курс физики. М: Изд.«Высшая школа».2001г.

3. А.И.Черноуцан, Краткий курс физики. М: Изд.«Высшая школа».2004г.

4. Б.М.Яворский, А.А.Детлаф, Справочник по физике для инженеров и студентов ВУЗов. М: Изд.»Наука».1978. – 939с.

Раздел. МЕХАНИКА

Тема 1. Кинематика.

Лекция_№1.

1. Физические величины, основные свойства.

2. Кинематика материальной точки,общие определения.

1. Физические величины, основные свойства.

Что такое физическая величина? В чём её основные отличительные свойства?

Критерием достоверности знаний о материальном мире является опыт.

Проведение опыта – это определение физической величины, то есть её наблюдение и измерение. Таким образом физическая величина должна обладать свойством быть наблюдаемой и измеряемой.

Требование достоверности означает, что физический опыт должен быть повторяемым. Это значит, что при повторении опыт, проведенный в равных условиях, должен приводить всякий раз к одинаковому результату. Таким образом, физическая величина должна обладать свойством повторяемости.

Наконец, физические величины должны обладать свойством размерности.

Под размерностью физической величины понимают совокупность параметров, необходимых для ее определения. Например, простые физические величины — это длина, время и масса. Они имеют собственные размерности, обозначаемые соответственно буквами [L], [T] и [M], потому что для их определения никаких других измерений производить не нужно. Но для определения скорости тела необходимо произвести два независимых измерения — длины L и времени T. Поэтому размерность скорости есть отношение [L/T] .

Подчеркнем, что размерность физической величины и единицы ее измерения — это разные понятия. Например, скорость может измеряться в см/с, или в м/с, или в км/ч, а размерность ее при этом не меняется — она всегда есть [L/T], потому что независимо от того, в каких единицах мы измеряем скорость, мы всегда производим измерения одних и тех же двух параметров — длины L, и времени T.

Размерность физической величины представляет ее важнейшее свойство. Часто приходится сравнивать между собой различные величины. Физические величины можно сравнивать, только если они обладают одинаковой размерностью. Например, нельзя сравнивать между собой длину пути и отрезки времени: это бессмысленно — они обладают разной размерностью.

Итак, важнейшими свойствами физических величин являются:

2.Кинематика материальной точки, общие определения.

Материальная точка – это идеализация реальных физических объектов.

Определение 1.

Материальная точка – это физическое тело, обладающее массой, размерами которого можно пренебречь при рассмотрении его движения.

При движении пространственное положение материальной точки фиксируется

тройкой чисел в какой-либо системе координат. Кроме системы координат, необходимо устройство для измерения времени. Образно говоря, такое устройство назовем часами.

Итак, выбранная система координат и связанные с ней часы образуют систему отсчета.

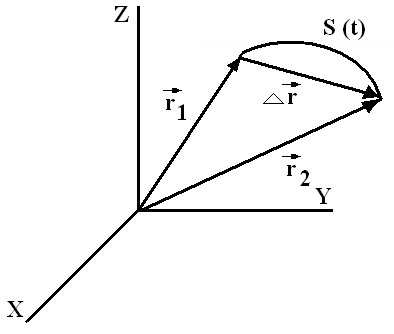
Например, в декартовой прямоугольной системе координат {X,Y,Z} радиус-вектор 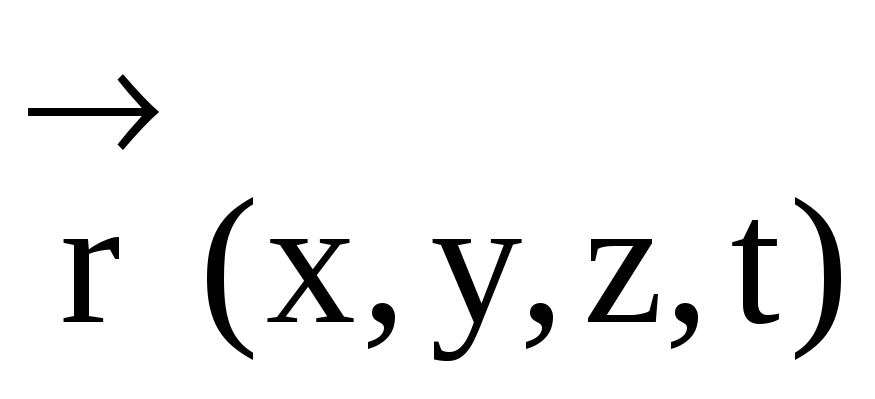описывает траекторию материальной точки. Длина траектории точки представляет собой величину пройденного пути S(t).

Путь S(t)— скалярная величина.

Наряду с величиной пройденного пути, перемещение точки характеризуется направлением, в котором она движется. В отличие от пути перемещение есть векторная величина.

Определение 2.

Разность двух радиус-векторов, взятых в различные моменты времени, образует вектор

перемещения точки (см. рис.), .

Изменение положения точки в пространстве характеризуется её скоростью.

Определение 3.

Под средней скоростью движения по траектории за конечное время t понимают отношение пройденного за это время конечного пути S ко времени:

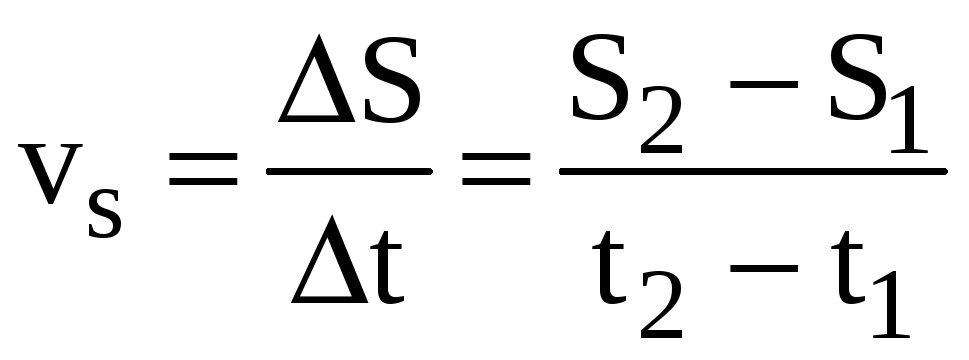. (1)

Определение 4.

В терминах дифференциального исчисления мгновенная скорость точки определяется соотношением:

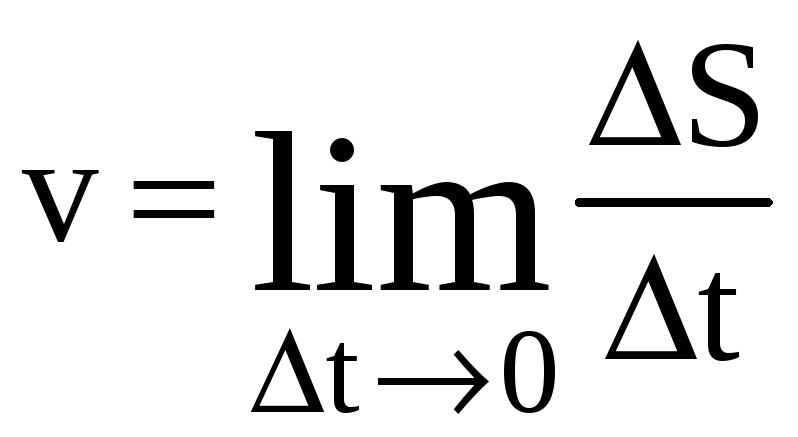. (2)

Скорость движения точки по траектории — скалярная величина. Наряду с ней в механике вводится средняя скорость перемещения точки.

Определение 5.

Средняя скорость перемещения — это величина, направленная вдоль вектора перемещения,

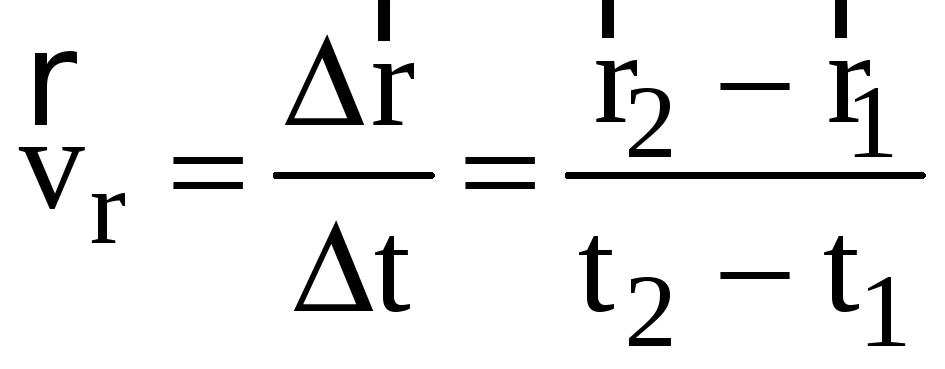. (3)

Определение 6.

Производная радиус-вектора 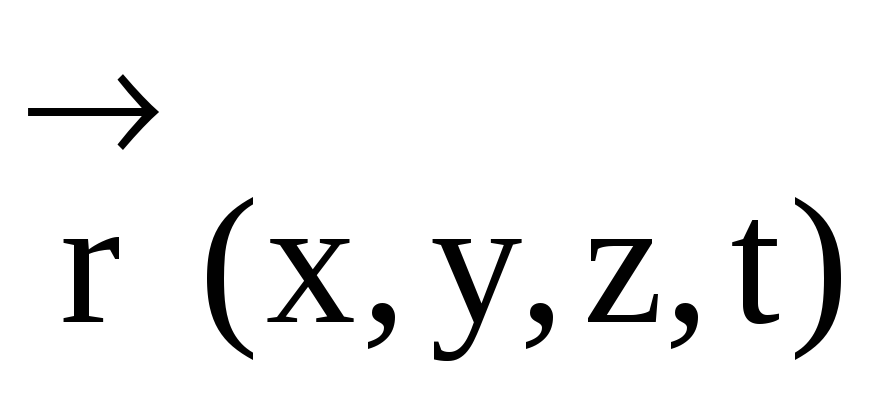по времени определяет мгновенную скорость перемещения точки.

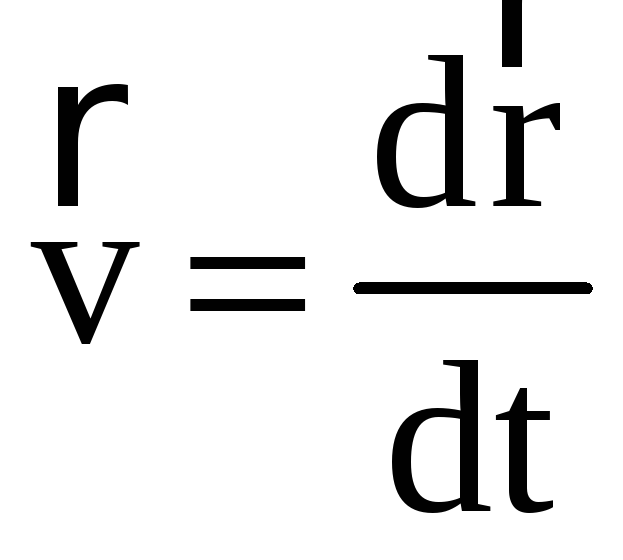. (4)

Поскольку перемещение совпадает с бесконечно малым элементом траектории , то вектор скорости направлен по касательной к траектории, а его величина (модуль вектора!):

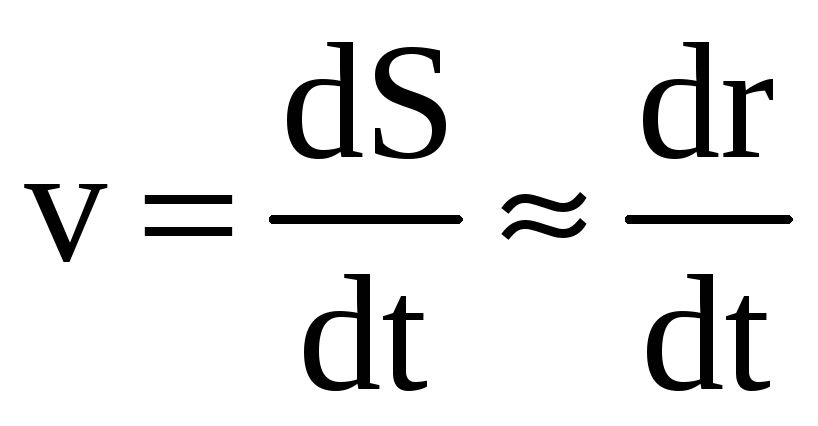. (5)

Интегрируя выражение (5) в интервале времени от t₀ до t, можно вычислить путь, пройденный телом за время t—t₀ , если известна зависимость от времени его скорости v(t) (точнее приращение пути!)

. (6)

В случае равномерного движения, когда скорость сохраняет свое постоянное значение во все время движе­ния, v=const; следует выражение

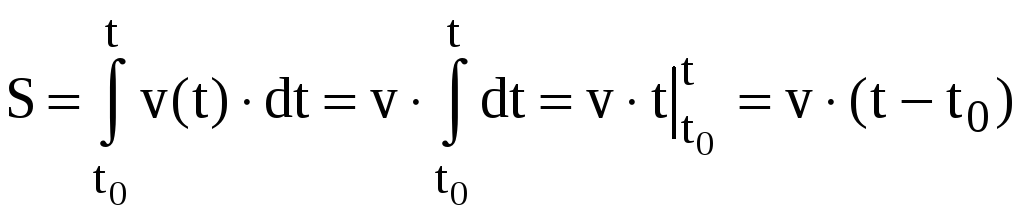. (6а)

Если к начальному моменту времени – 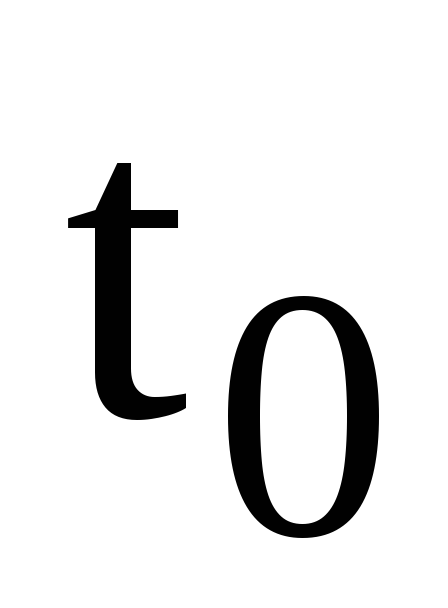был пройден путь – 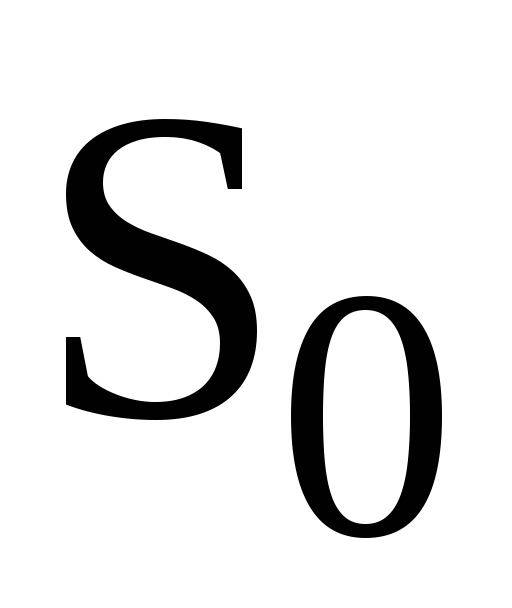, то

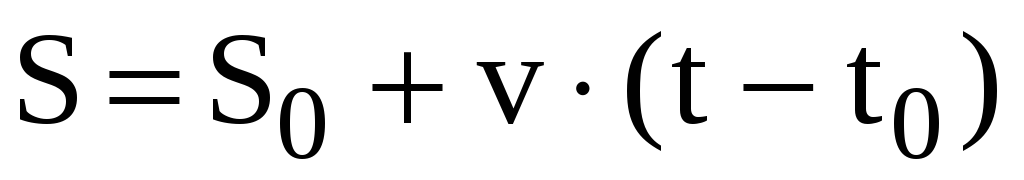, (7)

Определение 7.

Производную скорости по времени, которая является второй производной по времени от радиус-вектора, называют ускорением точки:

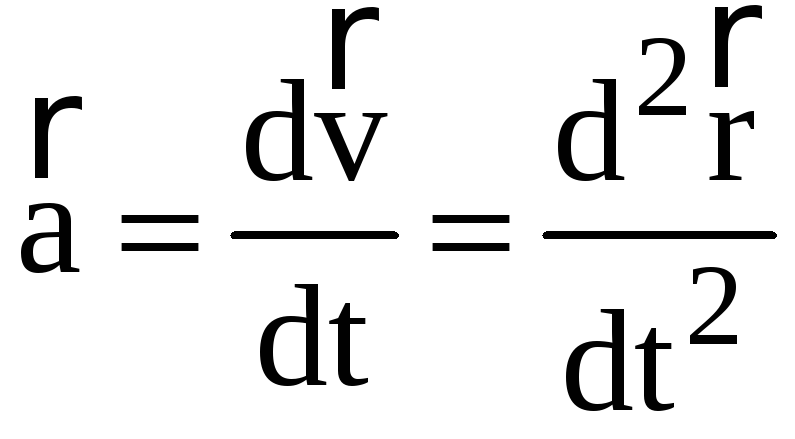. (8)

Вектор ускорения а направлен вдоль вектора приращения скорости dv.

Пусть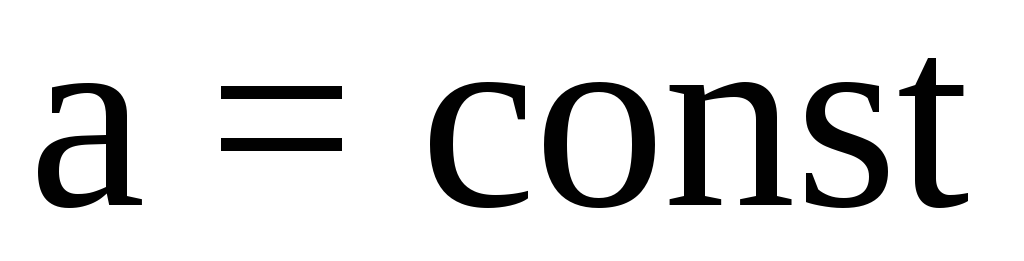. Этот важный и часто встречаемый случай носит название равноускоренного или равнозамедленного движения (в зависимости от знака ускорения – !) .

Проинтегрируем выражение (8) в пределах от t = 0 до t, получим, что

(9)

. (10)