Разработка темы «Рациональные неравенства. Системы рациональных неравенств. Рациональные неравенства с параметрами» в профильном классе
Рациональные неравенства. Системы рациональных неравенств. Рациональные неравенства с параметрами.
Нестандартные методы решения неравенств и их систем (МЗМ). Решение неравенств с двумя переменными.
|
1 |
Повторить теорию: Никольский п. 2.9, 2.10, 2.11 |
На оценку проверяется: |
|
2 |
Решить задачи: Никольский — № 2.70, — 2.72, 2.78, 2.79, 2.88-2.92, 2.98-2.100, № 84, 85, 89, 94, 101, 102, 105 (стр. 373 — 376). |
|
|
3* |
Изучить теорию и разобрать примеры: Коропец п. 1, 2, 3 |
|
|
4* |
Решить задачи: Коропец: №1-31 стр. 19-20, № 1-49 стр. 37-39. |
|
|
|
|
|
|
Решение иррациональных неравенств. 10-й класс
Цели урока.
Обучающий аспект.
1. Закрепить знания и умения решения неравенств.
2. Научиться решать иррациональные неравенства по составленному на уроке алгоритму.
Развивающий аспект.
1. Развивать грамотную математическую речь при ответе с места и у доски.
2. Развивать мышление посредством:
— анализа и синтеза при работе над выводом алгоритма
— постановки и решения проблемы (логические умозаключения при возникновении проблемной ситуации и ее разрешении)
3. Развивать умение проводить аналогии при решении иррациональных неравенств.
Воспитывающий аспект.
1. Воспитывать соблюдение норм поведения в коллективе, уважение к мнению окружающих при совместной деятельности в группах.
Тип урока. Урок изучения новых знаний.
Этапы урока.
- Подготовка к активной учебно-познавательной деятельности.
- Усвоение нового материала.
- Первичная проверка понимания.
- Домашнее задание.
- Подведение итогов урока.
Учащиеся знают и умеют: умеют решать иррациональные уравнения, рациональные неравенства.
Учащиеся не знают: способ решения иррациональных неравенств.
| Этапы урока, образовательные задачи | Содержание учебного материала |
| Подготовка к активной
учебно-познавательной деятельности. Обеспечение мотивации познавательной деятельности учащихся. Актуализация опорных знаний и умений. Создание условий для самостоятельной формулировки учащимися темы и целей урока. |
Выполните устно: 1. Найди ошибку: у(х)= 2. – Ответ: (- 3. Решите неравенство у(х) , используя рисунок.
4. Решите уравнение: А) 1 Повторение. Решите уравнение:(один учащийся у доски дает ответ с полным комментарием решения, все остальные решают в тетради) Решите устно неравенство 5. ; Чем будем заниматься на уроке , дети должны сформулировать сами. Решение иррациональных неравенств. 6. Неравенство под №5 решить устно сложно. Сегодня на уроке мы научимся решать иррациональные неравенства вида , создав при этом алгоритм их решения. Тема урока записывается в тетрадь “Решение иррациональных неравенств”. |
| Усвоение нового
материала. Организация деятельности учащихся по выводу алгоритма решения уравнений, приводимых к квадратным, путем введения вспомогательной переменной. Восприятие, осмысление, первичное запоминание изучаемого материала. |
Учащиеся делятся на две группы. Одна выводит алгоритм решения неравенства вида , а другая вида Представитель каждой группы обоснует свой вывод, остальные слушают, делают комментарии Используя выведенный алгоритм решения, учащимся предлагается решить следующие неравенства самостоятельно, разделившись на пары, с последующей проверкой. Решить неравенства: ; 2) 5) |
| Первичная проверка
понимания. Установление правильности и осознанности усвоения алгоритма |
Далее у доски с полным
комментарием решают уравнения:
|
| Первичный контроль | Самостоятельная работа 1) |
| Домашнее задание Обеспечение понимания цели, содержания и способов выполнения домашнего задания. |
Домашняя работа на оценку “5” — 9-10 заданий; “4” — 7-8 заданий; “3” — 5-6 заданий; в остальных случаях “2”. 1)
8) 9) |
| Подведение итогов урока |
Приложение
Иррациональные неравенства. Видеоурок. Алгебра 11 Класс
Тема: Уравнения и неравенства. Системы уравнений и неравенств
Урок: Иррациональные неравенства
При решении иррациональных неравенств довольно часто необходимо возводить обе части неравенства в некоторую степень, это довольно ответственная операция. Напомним особенности.
Обе части неравенства можно возвести в квадрат, если обе они неотрицательны, только тогда мы получаем из верного неравенства верное неравенство.
Обе части неравенства можно возвести куб в любом случае, если исходное неравенство было верным, то при возведении в куб мы получим верное неравенство.
Рассмотрим неравенство вида:

Подкоренное выражение должно быть неотрицательным. Функция  может принимать любые значения, необходимо рассмотреть два случая.
может принимать любые значения, необходимо рассмотреть два случая.
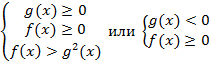
В первом случае обе части неравенства неотрицательны, имеем право возвести в квадрат. Во втором случае правая часть отрицательна, и мы не имеем права возводить в квадрат. В таком случае необходимо смотреть на смысл неравенства: здесь положительное выражение (квадратный корень) больше отрицательного выражения, значит, неравенство выполняется всегда.
Итак, имеем следующую схему решения:
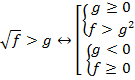
В первой системе мы не защищаем отдельно подкоренное выражение, т. к. при выполнении второго неравенства системы подкоренное выражение автоматически должно быть положительно.
Пример 1 – решить неравенство:
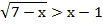
Согласно схеме, переходим к эквивалентной совокупности двух систем неравенств:
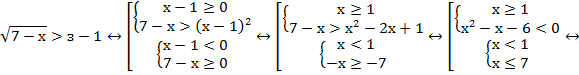
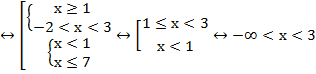
Проиллюстрируем:

Рис. 1 – иллюстрация решения примера 1
Ответ:
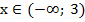
Как мы видим, при избавлении от иррациональности, например, при возведении в квадрат, получаем совокупность систем. Иногда эту сложную конструкцию можно упростить. В полученной совокупности мы имеем право упростить первую систему и получить эквивалентную совокупность:
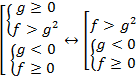
В качестве самостоятельного упражнения необходимо доказать эквивалентность данных совокупностей.
Рассмотрим неравенство вида:
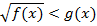
Аналогично предыдущему неравенству, рассматриваем два случая:

В первом случае обе части неравенства неотрицательны, имеем право возвести в квадрат. Во втором случае правая часть отрицательна, и мы не имеем права возводить в квадрат. В таком случае необходимо смотреть на смысл неравенства: здесь положительное выражение (квадратный корень) меньше отрицательного выражения, значит, неравенство противоречиво. Вторую систему рассматривать не нужно.
Имеем эквивалентную систему:
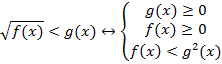
Иногда иррациональное неравенство можно решить графическим методом. Данный способ применим, когда соответствующие графики можно достаточно легко построить и найти их точки пересечения.
Пример 2 – решить неравенства графически:
а) 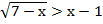
б) 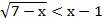
Первое неравенство мы уже решали и знаем ответ.
Чтобы решить неравенства графически, нужно построить график функции, стоящей в левой части, и график функции, стоящей в правой части.
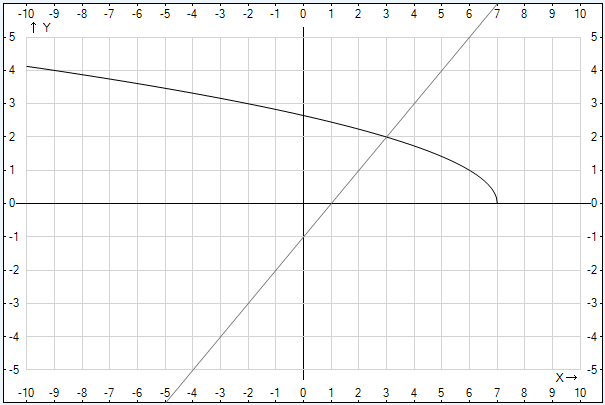
Рис. 2. Графики функций  и
и 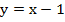
Для построения графика функции  необходимо преобразовать параболу
необходимо преобразовать параболу 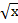 в параболу
в параболу 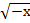 (зеркально отобразить относительно оси у), полученную кривую сместить на 7 единиц вправо. График подтверждает, что данная функция монотонно убывает на своей области определения.
(зеркально отобразить относительно оси у), полученную кривую сместить на 7 единиц вправо. График подтверждает, что данная функция монотонно убывает на своей области определения.
График функции 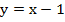 – это прямая, ее легко построить. Точка пересечения с осью у – (0;-1).
– это прямая, ее легко построить. Точка пересечения с осью у – (0;-1).
Первая функция монотонно убывает, вторая монотонно возрастает. Если уравнение имеет корень, то он единственный, по графику легко его угадать: 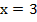 .
.
Когда значение аргумента меньше корня, парабола находится выше прямой. Когда значение аргумента находится в пределах от трех до семи, прямая проходит выше параболы.
Имеем ответ:
а) 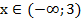 ; б)
; б) 
Эффективным методом решения иррациональных неравенств является метод интервалов.
Пример 3 – решить неравенства методом интервалов:
а) 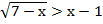
б) 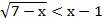
согласно методу интервалов, необходимо временно отойти от неравенства. Для этого перенести в заданном неравенстве все в левую часть (получить справа ноль) и ввести функцию, равную левой части:

теперь необходимо изучить полученную функцию.
ОДЗ: 
Корни: 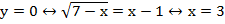
Данное уравнение мы уже решали графически, поэтому не останавливаемся на определении корня.
Теперь необходимо выделить интервалы знакопостоянства и определить знак функции на каждом интервале:
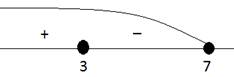
Рис. 3. Интервалы знакопостоянства к примеру 3
Напомним, что для определения знаков на интервале необходимо взять пробную точку и подставить ее в функцию, полученный знак функция будет сохранять на всем интервале.
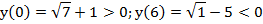
Проверим значение в граничной точке:
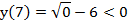
Очевиден ответ:
а) 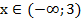 ; б)
; б) 
Рассмотрим следующий тип неравенств:
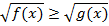
Сначала запишем ОДЗ:
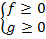
Корни существуют, они неотрицательны, обе части можем возвести в квадрат. Получаем:
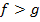
Получили эквивалентную систему:
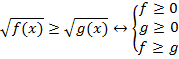
Полученную систему можно упростить. При выполнении второго и третьего неравенств первое истинно автоматически. Имеем:: 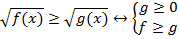
Пример 4 – решить неравенство:
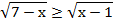
Действуем по схеме – получаем эквивалентную систему:
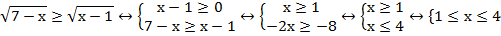
Ответ: 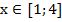
Рассмотрим неравенства вида:
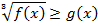
В данном случае имеем дело с корнем нечетной степени, в левой и правой части неравенства могут стоять любые (как положительные, так и отрицательные) числа. Имеем эквивалентное неравенство:
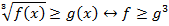
Пример 5 – решить неравенство:
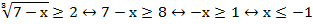
Ответ: 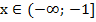
Итак, мы рассмотрели решение различных типовых иррациональных неравенств, привели несколько методов решения и решили примеры. Далее будем рассматривать неравенства с модулем.
Список литературы
1. Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
2. Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
3. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. ЕГЭ по математике (Источник).
2. Math.md (Источник).
3. Diffur.kemsu.ru (Источник).
Домашнее задание
1. Решить неравенство:
а) 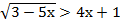 ;
;
б) 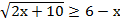 ;
;
в) 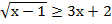 ;
;
г) 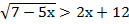 ;
;
2. Решить неравенство:
а) 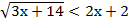 ;
;
б)  ;
;
в) 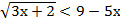 ;
;
г) 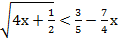 ;
;
3. Решить неравенство:
а) 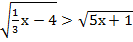 ;
;
б) 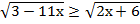 ;
;
в) 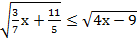 ;
;
г) 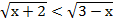 ;
;
План-конспект урока по алгебре (10 класс) на тему: Системы рациональных неравенств.
Тема урока «Решение систем рациональных неравенств»
Класс 10
Тип урока: поисковый
Цель: поиск способов решения неравенств с модулем, применение метода интервалов в новой ситуации.
Задачи урока:
— проверить умения и навыки в решении рациональных неравенств и их систем; — показать учащимся возможности применения метода интервалов при решении неравенств с модулем;
— научить логически мыслить;
— выработать навык самооценки своей работы;
— научить выражать свои мысли,
— научить аргументированно отстаивать свою точку зрения;
— сформировать у учащихся положительный мотив учения;
— развить самостоятельность учащихся.
Ход урока
I. Организационный момент (1мин)
Здравствуйте, сегодня мы с вами продолжим изучение темы «Система рациональных неравенств», будем применять свои знания и умения в новой ситуации.
Запишите число и тему урока «Решение систем рациональных неравенств». Сегодня я вас приглашаю в путешествие по дорогам математики, где вас ожидают испытания, проверка на прочность. У вас на партах лежат дорожные карты с заданиями, путевой лист самооценки, который в конце путешествия сдадите мне (диспетчеру).
Девизом путешествия будет служить афоризм «Дорогу осилит идущий, а математику мыслящий». Возьмите с собой ваш багаж знаний. Включите мыслительный процесс и в путь. В дороге нас будет сопровождать дорожное радио. Звучит фрагмент музыки (1 мин). Потом резкий звук сигнала.
II. Этап проверки знаний. Работа в группах. «Досмотр багажа»,
Вот и первое испытание «Досмотр багажа», проверка ваших знаний по теме
Сейчас вы разделитесь на группы по 3 или 4 человека. У каждого на парте есть листок с заданием. Распределите эти задания между собой, решите их, на общем листе запишите готовые ответы. Группа, состоящая из 3 человек, выбирает 3 любые задания. Кто выполнит все задания, сообщит об этом учителю. Я или мои помощники сверим ответы, и если хоть один ответ будет неверным, группе возвращается листок на перепроверку. (ответы дети не видят, им только сообщается, в каком задании неверный ответ). Победит та группа, которая первой без ошибок справиться со всеми заданиями. Вперёд за победой.
Звучит очень тихая музыка.
Если закончат работу две или три группы одновременно, то учителю поможет проверить кто-то из ребят другой группы. Ответы на листе у учителя (4 экземпляра).
Работа останавливается, когда появится группа-победитель.
Не забудьте заполнить путевой лист самооценки. И едем дальше.
Лист с заданием для «Досмотра багажа»
1) 3)
2) 4)
III. Этап актуализации знаний и открытие новых знаний. «Эврика»
Досмотр показал, что багаж знаний у вас есть.
Но в дороге всякие ситуации бывают, иногда требуется смекалка, а не забыли ли вы прихватить её с собой, проверим.
Вы научились решать системы рациональных неравенств методом интервалов. Сегодня мы посмотрим, при решении каких задач целесообразно применение этого метода. Но сначала вспомним, что такое модуль .
1. Продолжите предложения «Модуль числа равен самому числу, если…» (устно)
«Модуль числа равен противоположному числу, если…»
2. Пусть А(Х) -многочлен от x
Продолжите запись:
Ответ:
На доске пишет ученик, ребята, записывают в тетради.
Запишите выражение, противоположное выражению А(х)
А(х) = 5 — 4х; А(х) = 6х2 — 4х + 2
-А(х)= -А(х)=
На доске пишет ученик, ребята, записывают в тетради.
3. Сейчас попробуем найти способ решения квадратичного неравенства с модулем
Ваши предложения по решению этого неравенства.
Выслушать предложения ребят.
Если предложений не будет, то задать вопрос: «Можно ли решить это неравенство с помощью систем неравенств?»
Выходит ученик, решает.
IV. Этап первичного закрепления новых знаний, составление алгоритма решения. Пополнение багажа.
(Работа в группах по 4 человека).
Сейчас я вам предлагаю пополнить ваш багаж. Будете работать в группах. Каждой группе выдаются по 2 карточки с заданиями.
На первой карточке нужно записать системы для решения неравенств, представленных на доске и разработать алгоритм решения подобных неравенств, решать не нужно.
Первая карточка у групп разная, вторая одинаковая
1.Запишите две системы неравенств для решения квадратичного неравенства с модулем
|
1.Запишите две системы неравенств для решения квадратичного неравенства с модулем
|
1.Запишите две системы неравенств для решения квадратичного неравенства с модулем
|
1.Запишите две системы неравенств для решения квадратичного неравенства с модулем
|
2. Разработать алгоритм решения подобных неравенств по шагам. |
Что получилось?
Под каждым уравнением на доске нужно написать совокупность систем.
Выходят 4 ученика, и пишут системы. В это время с классом обсуждаем алгоритм.
V. Этап закрепления знаний. «Дорога домой».
Багаж пополнен, теперь пора в обратный путь. Сейчас решите самостоятельно любое из предложенных неравенств с модулем в соответствии с составленным алгоритмом.
С вами в пути опять будет дорожное радио.
Включить тихую фоновую музыку. Учитель проверяет оформление и при необходимости консультирует.
Задания на доске.
Работу закончили. Сверьте ответы (они на обратной стороне доски), заполните путевой лист самооценки.
Постановка домашнего задания.
Запишите домашнее задание (перепишите в тетрадь неравенства, которые не сделали или сделали с ошибками, дополнительно № 84 (а) на стр. 373 учебника по желанию)
VI. Этап релаксации.
Чем полезно было для вас это путешествие?
Чему вы научились?
Подведите итоги. Подсчитайте, сколько баллов каждый из вас заработал. (ребята называют итоговый балл). Листы с самооценкой сдайте диспетчеру, то есть мне.
Закончить урок я хочу притчей.
«Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому по вопросу. У первого спросил: «Что ты делал целый день?», и тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал целый день?», и тот ответил: «А я добросовестно выполнял свою работу», а третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве Храма!»»
— Ребята! Оцените каждый свою работу за урок, задумайтесь, что для каждого из вас учёба в школе: тяжёлые камни, или выполненная работа, или закладывание фундамента вашей будущей успешной жизни?
Урок окончен.
Лист самооценки
Фамилия, имя, класс | Количество баллов | |
Работа в группе по решению неравенств или систем неравенств. | 2 балла, если выполнил верно без посторонней помощи; 1 балл, если выполнил верно с посторонней помощью; 0 баллов, если не выполнил задание 1 балл дополнительный за победу группы | |
Работа в группе по составлению алгоритма | 1 балл за активную работу | |
Самостоятельная работа | 2 балла за каждое задание, если выполнил верно без посторонней помощи; 1 балл, если выполнил верно с посторонней помощью; 0 баллов, если не выполнил задание. | |
Всего |
Методическая разработка по алгебре (10 класс): «Методы решения иррациональных неравенств».
«Методы решения иррациональных неравенств».
Ахметова Гюзяль Абузяровна-
учитель математики МБОО-Старокулаткинская СШ №1.
2016 г.
Методы решения иррациональных неравенств.
Если в неравенство входят функции под знаком корня, то такие неравенства называют иррациональными.
Стандартный метод решения этих неравенств заключается в возведении обеих частей неравенства в нужную степень: если в неравенство входит квадратный корень, то в квадрат; входит корень третьей степени − в куб и т. д. Однако, Правило : Если f (x) ≥ 0, g (x) ≥ 0 на множестве X, то неравенства
равносильны на этом множестве , преобразования неравенств, возводить в квадрат, не нарушая равносильности, можно только неравенство, у которого обе части неотрицательны. При возведении же в квадрат неравенств, части которых имеют разные знаки, могут получиться неравенства, как равносильные исходному, так и неравносильные ему. Простой пример: –1 − тоже верное неравенство. Несмотря на то, что –4 уже верным не является.
Как получить равносильные системы для некоторых часто встречающихся типов неравенств.
Неравенства вида:
Если x лежит в ОДЗ: f (x) ≥ 0, то левая часть неравенства существует и неотрицательна. Поскольку для всех x, являющихся решением данного неравенства, правая часть больше левой, то g (x) > 0. Следовательно, обе части неравенства неотрицательны (для тех x, которые являются решениями неравенства, другие x нас не интересуют). Значит, возведение в квадрат не нарушает равносильности и можно записать равносильную нашему неравенству систему неравенств:
Пример 1
Решение:
Неравенство равносильно системе: Ответ. |
Пример 2
Решение:
Неравенства вида
ОДЗ данного неравенства f (x) ≥ 0. Пусть для каких-то x из ОДЗ g (x) x − решения, так как при этих x левая часть определена (x ОДЗ) и неотрицательна, в то время как правая часть g (x)
Для других x из ОДЗ g (x) ≥ 0. Для них обе части неравенства неотрицательны, и его можно возвести в квадрат: Значит, данное неравенство равносильно совокупности неравенств:
Заметим, что в последнюю систему не входит требование f (x) ≥ 0. Оно и не нужно, так как выполняется автоматически ибо полный квадрат всегда неотрицателен.
Пример 3
Решите неравенство
Решение:
ОДЗ неравенства: x ≥ –3. 1. Если то все эти x ОДЗ, для которых верно x − первая часть ответа. 2. Если то обе части неравенства неотрицательны, и его можно возвести в квадрат. Имеем: Получаем, что решениями являются все Объединяя результаты пунктов 1 и 2, получаем: Ответ. |
Пример 4
Решение:
Неравенства вида
ОДЗ данного неравенства: Обе части неравенства неотрицательны в ОДЗ, и потому можно возводить в квадрат. Получим равносильную систему
Заметим, что из неравенства следует, что то есть дополнительно это требовать и включать это неравенство в систему не нужно.
Отметим полезное следствие. Предположим, что ОДЗ неравенства уже найдено, и мы будем отбирать решения только из ОДЗ (это разумно, поскольку вне ОДЗ решений нет). Тогда исходное неравенство равносильно следующему: а та система, которой это неравенство равносильно, может быть представлена (для x из ОДЗ) в виде Следовательно, в ОДЗ
Эти же рассуждения применимы и для знака неравенства ≥. Отсюда можно сделать вывод:
Знак разности совпадает со знаком выражения
Отсюда же получается ещё одно следствие:
в ОДЗ:
Пример 5
Решить неравенство:
Перейдём к равносильной системе:
Решая эту систему методом интервалов, получаем:
Ответ.
Пример 6
Решить неравенство.
Решение:
ОДЗ неравенства:
Заметим, что в ОДЗ x ≥ 0, поэтому существует и значит,
Мы воспользовались здесь тем, что в ОДЗ x ≥ 0, (x – 5)(x – 6) ≥ 0 и потому существуют выписанные в последней строчке корни. Кроме того, мы вынесли за скобку который по вышесказанному существует. Этот корень неотрицателен и потому не влияет на знак неравенства, следовательно, на него можно сократить, не забывая, что он может ещё обратиться в нуль и те x, для которых корень обращается в нуль, являются решениями неравенства. Таким образом, в ответ необходимо включить число x = 5. При x = 6 корень обращается в нуль, но x = 6 не входит в ОДЗ неравенства. Воспользуемся теперь тем, что знак разности корней совпадает со знаком разности подкоренных выражений. Имеем:
Учтём теперь ОДЗ и получим:
Ответ.
Неравенства вида
ОДЗ данного неравенства: Предположим, что функции f (x) и g (x) не имеют общих корней. Рассмотрим вспомогательное неравенство
(*) |
1. Если g (x) x из ОДЗ выполнено
2. Если g (x) ≥ 0, то выражение может иметь любой знак, но выражение всегда строго положительно. Умножая обе части неравенства (*) на строго положительное число не меняя знака неравенства, перейдём к равносильному неравенству
Таким образом, в ОДЗ
Значит, при g (x) ≥ 0, знак разности совпадает со знаком разности в ОДЗ.
Получаем следующие условия равносильности.
Запоминать приведённые системы неравенств не нужно, важно понимать, как они получаются.
Пример 7
Решить неравенство:
Решение:
Выполним равносильные в ОДЗ преобразования :.
Не случайно сделано последнее преобразование. Важно знать, чему конкретно равняется функция g (x) = 2x – 8. Часто ошибкой является считать, что g (x) = 2x + 8.
ОДЗ данного неравенства: то есть Перейдём к равносильной системе.
С учётом ОДЗ сразу получаем:
Ответ.
Вывод.
Иррациональными называются неравенства, в которых переменная содержится под знаком корня.
Иррациональное неравенство сводится к равносильной системе (или совокупности систем) неравенств:
Литература:
1.Математика: алгебра и начала математического анализа. 10-11 классы: учеб. для общеобразоват. организаций : базовый и углубленный уровни /( Ш.А. Алимов, Ю.М.Колягин и др.)-М. : Просвещение, 2016.
2.Дорофеев Г., Потапов М., Розов Н. Математика для поступающих в вузы. М.: Дрофа, 2002.
Презентация +конспект урока алгебры в 10 классе на тему: «Иррациональные неравенства»
Урок «Решение иррациональных неравенств»,
10 класс,
Цель: познакомить учащихся с иррациональными неравенствами и методами их решения.
Тип урока: изучение нового материала.
Оборудование: учебное пособие «Алгебра и начала анализа. 10- 11 класс», Ш.А. Алимов, справочный материал по алгебре, презентация по данной теме.
План урока:
№
Этап урока
Цель этапа
Время
1
Организационный момент
Сообщение темы урока; постановка цели урока; сообщение этапов урока.
2 мин
2
Устная работа
Пропедевтика определения иррационального уравнения.
4 мин
3
Изучение нового материала
Познакомить с иррациональными неравенствами и со способами их решения
20 мин
4
Решение задач
Формировать умение решать иррациональные неравенства
14 мин
5
Итог урока
Повторить определение иррационального неравенства и способы его решения.
3 мин
7
Домашнее задание
Инструктаж по домашнему заданию.
2 мин
Ход урока
Организационный момент.
Устная работа (Слайд 4,5)
— Какие уравнения называются иррациональными?
— Какие из следующих уравнений являются иррациональными?
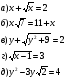
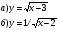 — Найти область определения
— Найти область определения
— Объясните, почему эти уравнения не имеют решения на множестве действительных чисел
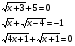
— Древнегреческий учёный – исследователь, который впервые доказал существование иррациональных чисел (Слайд 6)
— Кто впервые ввёл современное изображение корня (Слайд 7)
Изучение нового материала.
В тетради со справочным материалом запишите определение иррациональных неравенств: (Слайд 8) Неравенства, содержащие неизвестное под знаком корня, называются иррациональными.
Иррациональные неравенства – это довольно сложный раздел школьного курса математики. Решение иррациональных неравенств осложняется тем обстоятельством, что здесь, как правило, исключена возможность проверки, поэтому надо стараться делать все преобразования равносильными.
Чтобы избежать ошибки при решении иррациональных неравенств, следует рассматривать только те значения переменной, при которых все входящие в неравенства функции определены, т.е. найти ООН, а затем обоснованно осуществлять равносильный переход на всей ООН или её частях.
Основным методом решения иррациональных неравенств является сведение неравенства к равносильной системе или совокупности систем рациональных неравенств. В тетради со справочным материалом запишем основные методы решения иррациональных неравенств по аналогии с методами решения иррациональных уравнений. (Слайд 9)
При решении иррациональных неравенств следует запомнить правило: (Слайд 10)1. при возведении обеих частей неравенства в нечётную степень всегда получается неравенство, равносильное данному неравенству; 2. если обе части неравенства возводят в чётную степень, то получится неравенство, равносильное исходному только в том случае, если обе части исходного неравенства неотрицательны.
Рассмотрим решение иррациональных неравенств, в которых правая часть является числом. (Слайд 11)
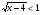 1.
1.
Возведём в квадрат обе части неравенства, но в квадрат мы можем возводить только неотрицательные числа. Значит, найдём ООН, т.е. множество таких значений х, при которых имеют смысл обе части неравенства. Правая часть неравенства определена при всех допустимых значениях х, а левая при
х-4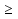 0. Данное неравенство равносильно системе неравенств:
0. Данное неравенство равносильно системе неравенств:
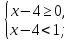
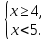
Ответ. [4;5)
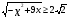 2.
2.
Это неравенство равносильно системе неравенств:
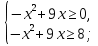
Т.к. каждое решение 2 неравенства является решением 1 неравенства системы, то система равносильна 2 неравенству
—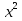 +9х
+9х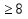 .
.
Ответ.[1;8]
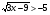 3.
3.
Правая часть отрицательна, а левая часть неотрицательна при всех значениях х, при которых она определена. Это означает, что левая часть больше правой при всех значениях х , удовлетворяющих условию х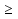 3.
3.
Ответ.[3; +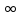 )
)
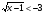 4.
4.
При всех допустимых значениях х, т.е. х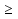 1, левая часть неотрицательна.
1, левая часть неотрицательна.
Ответ. Решений нет.
На следующем уроке рассмотрим решение неравенств вида (Слайд 12,13)
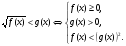
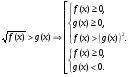
Решение задач.
№ 167(1,3), 168(3)
Итог урока.
Какие неравенства мы решали на уроке?
Дайте определение иррационального неравенства.
Каким методом можно решить иррациональное неравенство?
Рефлексия.
Домашнее задание. П. 10(1-5). 167 (2,4), 169 (4)
Тестирование по теме «Решение неравенств»(10 класс)
Тест по теме: «Решение неравенств».
1. Решить неравенство 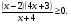
а)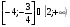
б)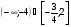
в)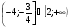
г)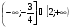
2. Решить неравенство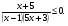
а)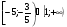
б)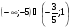
в)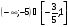
г)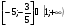
3. Решите неравенство 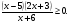
а)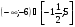
б)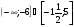
в)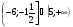
г)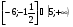
4. Решите неравенство 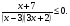
а)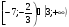
б)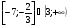
в)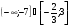
г)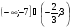
5. Решите неравенство 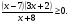
а)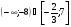
б)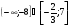
в)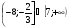
г)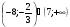
6. Решите неравенство 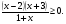
а)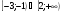
б)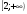
в)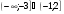
г)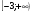
7. Решите неравенство 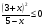 и укажите наименьшее целое решение этого неравенства.
и укажите наименьшее целое решение этого неравенства.
а)-3
б)-2
в)-1
г)4
8. Решите неравенство 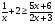
а)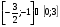
б)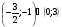
в)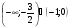
г)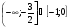
9. Решите неравенство 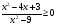
а)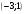
б)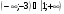
в)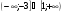
г)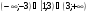
10. Решите неравенство 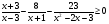
а)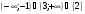
б)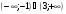
в)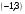
г)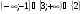
11. Решением неравенства x2 + 2x – 48 < 0 является промежуток
а)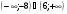
б)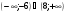
в)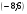
г)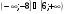
12. Решите неравенство (х – 2)(х – 5)(х – 4) > 0
а) (4; 5)
б)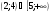
в)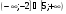
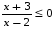 г)
г)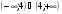 .
.
13.Решите неравенство
а)(.;.— 3)(2; ),
б)(— 3; 2]
в)(— ; — 3)[2; ),
г)(— 3; 2).
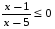
14.Решите неравенство
а) (— ; 1](5; ),
б) (1; 5)
в) (— ; 1)(5; ),
г) [1; 5).
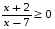
15.Решите неравенство
а) (— ; — 2](7; ),
б) [— 2; 7),
в) (— ; — 2)(7; ),
г) (— 2; 7).



