Степень с рациональным показателем — Алгебра и геометрия
Свойства степеней с рациональными показателями
Степень с дробным показателем мы определяли, распространяя на нее свойства степени с целым показателем. Иными словами, степени с дробными показателями обладают теми же свойствами, что и степени с целыми показателями. А именно:
- свойство произведения степеней с одинаковыми основаниями при a>0, а если и , то при a≥0;
- свойство частного степеней с одинаковыми основаниями при a>0;
- свойство произведения в дробной степени при a>0 и b>0, а если и , то при a≥0 и (или) b≥0;
- свойство частного в дробной степени при a>0 и b>0, а если , то при a≥0 и b>0;
- свойство степени в степени при a>0, а если и , то при a≥0;
- свойство сравнения степеней с равными рациональными показателями: для любых положительных чисел a и b, a<b и рациональном p при p>0 справедливо неравенство ap<bp, а при p<0 – неравенство ap>bp;
- свойство сравнения степеней с рациональными показателями и равными основаниями: для рациональных чисел p и q, p>q при 0<a<1 выполняется неравенство ap<aq, а при a>0 – неравенство ap>aq.

Доказательство свойств степеней с дробными показателями базируется на определении степени с дробным показателем, на свойствах арифметического корня n-ой степени и на свойствах степени с целым показателем. Приведем доказательства.
По определению степени с дробным показателем и , тогда . Свойства арифметического корня позволяют нам записать следующие равенства . Дальше, используя свойство степени с целым показателем, получаем , откуда по определению степени с дробным показателем имеем , а показатель полученной степени можно преобразовать так: . На этом доказательство завершено.
Абсолютно аналогично доказывается второе свойство степеней с дробными показателями:
По схожим принципам доказываются и остальные равенства:
Переходим к доказательству следующего свойства. Докажем, что для любых положительных a и b, a<b и рациональном p при p>0 справедливо неравенство ap<bp, а при p<0 – неравенство ap>bp. Запишем рациональное число p как m/n, где m – целое число, а n – натуральное. Условиям p<0 и p>0 в этом случае будут эквивалентны условия m<0 и m>0 соответственно. При m>0 и a<b по свойству степени с целым положительным показателем должно выполняться неравенство am<bm. Из этого неравенства по свойству корней имеем , а так как a и b – положительные числа, то на основе определения степени с дробным показателем полученное неравенство можно переписать как , то есть, ap<bp.
Запишем рациональное число p как m/n, где m – целое число, а n – натуральное. Условиям p<0 и p>0 в этом случае будут эквивалентны условия m<0 и m>0 соответственно. При m>0 и a<b по свойству степени с целым положительным показателем должно выполняться неравенство am<bm. Из этого неравенства по свойству корней имеем , а так как a и b – положительные числа, то на основе определения степени с дробным показателем полученное неравенство можно переписать как , то есть, ap<bp.
Аналогично, при m<0 имеем am>bm, откуда , то есть, и ap>bp.
Осталось доказать последнее из перечисленных свойств. Докажем, что для рациональных чисел p и q, p>q при 0<a<1 выполняется неравенство ap<aq, а при a>0 – неравенство ap>aq. Мы всегда можем привести к общему знаменателю рациональные числа p и q, пусть при этом мы получим обыкновенные дроби и , где m1 и m2 – целые числа, а n — натуральное. При этом условию p>q будет соответствовать условие m1>m2, что следует из правила сравнения обыкновенных дробей с одинаковыми знаменателями. Тогда по свойству сравнения степеней с одинаковыми основаниями и натуральными показателями при 0<a<1 должно быть справедливо неравенство am1<am2, а при a>1 – неравенство am1>am2. Эти неравенства по свойствам корней можно переписать соответственно как и . А определение степени с рациональным показателем позволяет перейти к неравенствам и соответственно. Отсюда делаем окончательный вывод: при p>q и 0<a<1 выполняется неравенство ap<aq, а при a>0 – неравенство ap>aq.
При этом условию p>q будет соответствовать условие m1>m2, что следует из правила сравнения обыкновенных дробей с одинаковыми знаменателями. Тогда по свойству сравнения степеней с одинаковыми основаниями и натуральными показателями при 0<a<1 должно быть справедливо неравенство am1<am2, а при a>1 – неравенство am1>am2. Эти неравенства по свойствам корней можно переписать соответственно как и . А определение степени с рациональным показателем позволяет перейти к неравенствам и соответственно. Отсюда делаем окончательный вывод: при p>q и 0<a<1 выполняется неравенство ap<aq, а при a>0 – неравенство ap>aq.
1.
|
Выражения, которые имеют смысл
Сложность: лёгкое |
4 |
| 2. |
Степень с дробным показателем (обыкновенная дробь)
|
1 |
3.
|
Степень с дробным показателем (смешанное число)
Сложность: лёгкое |
2 |
| 4. |
Степень с дробным показателем (десятичная дробь)
Сложность: лёгкое |
2 |
5.
|
Корень степени n из обыкновенной дроби
Сложность: лёгкое |
1 |
| 6. | Корень степени n из степени Сложность: лёгкое | 1 |
7.
|
Степень с рациональным показателем
Сложность: лёгкое | 2 |
| 8. |
Произведение степеней с рациональными показателями
Сложность: лёгкое |
2 |
9.
|
Частное степеней с рациональными показателями
Сложность: лёгкое |
1 |
| 10. |
Возведение степени в степень (рациональные показатели)
|
1 |
11.
|
Значение степени с рациональным показателем
Сложность: среднее |
4 |
| 12. |
Упрощение выражения, содержащего радикалы, замена переменных
Сложность: сложное |
5 |
13.
|
Степень с целым показателем
Сложность: среднее |
6 |
| 14. | Произведение степени и корня Сложность: среднее | 2,5 |
15.
|
Свойства степеней с рациональными показателями (десятичные и обыкновенные дроби)
Сложность: среднее |
3 |
| 16. |
Свойства степеней с рациональными показателями (десятичные дроби)
Сложность: среднее |
6 |
17.
|
Произведение в рациональной степени (степень и дробь)
Сложность: среднее |
6 |
| 18. |
Сумма корней и степеней
Сложность: среднее |
4 |
19.
|
Свойства степеней с рациональными показателями (дробь)
Сложность: среднее |
4 |
| 20. |
Произведение бинома на одночлен
Сложность: среднее |
5 |
21.
|
Квадрат бинома
Сложность: среднее |
4 |
| 22. |
Произведение суммы и разности (степень и число)
Сложность: среднее |
3 |
23.
|
Сокращение дроби
Сложность: среднее |
4 |
| 24. |
Упрощение выражения, содержащего радикалы, формула разложения на множители кв. трехчлена
Сложность: среднее |
4 |
25.
|
Произведение суммы и разности двух степеней
Сложность: сложное |
4 |
29 Степень с рациональным показателем
29 Степень с рациональным показателем
Задача № 1
Показать ответОтвет:
Показать решениеРешение:
Ответ:
Задача № 2
Показать ответОтвет:
Показать решениеРешение:
Ответ:
Задача № 3
Показать ответОтвет:
Показать решениеРешение:
Ответ:
Задача № 4
Показать ответОтвет:
Показать решениеРешение:
Ответ:
Задача № 5
Показать ответОтвет:
Показать решениеРешение:
Ответ:
Задача № 6
Показать ответОтвет:
Показать решениеРешение:
Ответ:
Задача № 7
Показать ответОтвет:
Показать решениеРешение:
Ответ:
Задача № 8
Показать ответОтвет:
Показать решениеРешение:
Ответ:
Задача № 9
Показать ответОтвет:
Показать решениеРешение:
Ответ:
Задача № 10
Показать ответОтвет:
Показать решениеРешение:
Ответ:
Задача № 11
Показать ответОтвет:
Показать решениеРешение:
Ответ:
Задача № 12
Показать ответОтвет:
Показать решениеРешение:
Ответ:
Задача № 13
Показать ответОтвет:
Показать решениеРешение:
Ответ:
Задача № 14
Показать ответОтвет:
Показать решениеРешение:
Ответ:
Задача № 15
Показать ответОтвет:
Показать решениеРешение:
Ответ:
Задача № 16
Показать ответОтвет:
Показать решениеРешение:
Ответ:
© 2017-2019 Математушка
11 класс.
 Алгебра. Степени и корни. Степенные функции. Преобразование выражений, содержащих радикалы. Свойства и графики степенных функций. — Обобщение понятия о показателе степени — начальные сведения.Комментарии преподавателя
Алгебра. Степени и корни. Степенные функции. Преобразование выражений, содержащих радикалы. Свойства и графики степенных функций. — Обобщение понятия о показателе степени — начальные сведения.Комментарии преподавателяЧтобы обобщить понятие о показателе степени, вспомним, что такое степень.
– степень с натуральным показателем, здесь а – основание степени, n – показатель степени;
n штук
Кроме того, напомним, что:
и ;
Выражение не существует.
Основные свойства степеней:
1. ;
Для того чтобы умножить степени с одинаковым основанием, нужно сложить их показатели, основание оставить тем же самым.
2. ;
Можно разделить степени с одинаковым основанием, для этого их показатели нужно вычесть, а основание оставить тем же самым;
3. ;
Для того чтобы степень возвести в степень, нужно перемножить показатели степени, основание оставить без изменений.
4. ;
При умножении степеней с одинаковым показателем, нужно перемножить основания и возвести результат в исходную степень;
5. ;
Чтобы разделить степени с одинаковыми показателями, нужно разделить основания и возвести результат в исходную степень;
Напомним основные числовые множества:
– натуральные числа;
– целые числа;
– рациональные числа;
Числа, которые не могут быть представлены в виде дроби , назвали иррациональными, например . Если к множеству рациональных чисел прибавить множество иррациональных чисел, получим множество действительных чисел
– действительные числа;
Напомним связь между множеством действительных чисел и числовой осью. Между множеством действительных чисел и множеством точек числовой оси существует взаимооднозначное соответствие. То есть, если мы говорим, что есть число , то ему на оси соответствует единственная точка. Точно так же каждой точке соответствует единственное действительное число.
Точно так же каждой точке соответствует единственное действительное число.
Рис. 1. Числовая ось
Определение:
Степенью неотрицательного числа а с рациональным положительным показателем называется число
Например:
Пример 1 – вычислить:
Пример 2 – вычислить:
Пример 3 – вычислить:
Пример 4 – представить в виде степени:
Пример 5 – представить в виде степени:
Пример 6 – представить в виде степени:
Пример 7 – представить в виде степени:
Определение:
Степенью положительного числа а с рациональным отрицательным показателем называется число .
Например:
Пример 8 – вычислить:
Пример 9 – вычислить:
Пример 10 – вычислить:
Обратим внимание на типовую ошибку. Вычислить:
Вычислить:
Ответ: не существует
Пояснение:
– выражение 1;
Данное равенство неверно, так как наше определение не должно противоречить определениям, данным ранее, например основному свойству дроби:
– выражение 2;
Из выражений 1 и 2 получили , неверное числовое равенство.
Запомним:
определено только при .
Пример 11 – построить графики функций:
График первой функции нам известен, он проходит через три фиксированные точки: (0;0), (1;1) и (-1;-1), область определения .
График второй функции по определению соответствует графику функции при .
Отличие заданных функций наглядно продемонстрировано на графиках 2 и 3.
Рис. 2. График функции
Рис. 3. График функции
Пример 12 – найти область определения выражения:
По определению положительного рационального показателя степени:
По определению отрицательного рационального показателя степени:
По определению положительного рационального показателя степени:
По определению отрицательного рационального показателя степени:
Итак, мы рассмотрели понятие степени с рациональным показателем, дали важные определения.
Напомним, что такое множество рациональных чисел.
– рациональные числа.
Каждая дробь может быть представлена в десятичном виде, например :
Итак, рациональное число может быть представлено как бесконечная десятичная дробь с периодом.
Напомним определение: для выполняется равенство:
Например: ; ; (нужно перевести бесконечную периодическую дробь в обыкновенную).
Рассмотрим свойства степени с рациональным показателем, они аналогичны свойствам степени с натуральным показателем, здесь s и r – рациональные числа:
1. .
Для того чтобы умножить степени с одинаковым основанием, нужно сложить их показатели, основание оставить без изменений.
2. .
Можно разделить степени с одинаковым основанием, для этого их показатели нужно вычесть, а основание оставить без изменений.
3. .
Для того чтобы степень возвести в степень, нужно перемножить показатели степени, основание оставить без изменений.
4. .
При умножении степеней с одинаковым показателем, нужно перемножить основания и возвести результат в исходную степень.
5. .
Чтобы разделить степени с одинаковыми показателями, нужно разделить основания и возвести результат в исходную степень.
Вышеперечисленные свойства справедливы для любых рациональных показателей. Докажем первое свойство:
Доказательство:
s и r – рациональные числа, , ,
.
Приведем корни к одинаковому показателю:
.
Преобразуем полученное выражение согласно свойствам корня:
.
По определению степени с рациональным показателем:
.
Согласно свойствам степени:
.
Итак, получили:
.
Докажем третье свойство:
Доказательство:
s и r – рациональные числа, , , .
Схема доказательства стандартная: от степеней перейти к корням, выполнить преобразования с корнями и вернуться к степеням.
Остальные свойства доказываются аналогично.
Перейдем к решению типовых задач.
Пример 1 – имеет ли смысл выражение:
а)
Ответ: нет.
б)
Ответ: да ().
в)
Ответ: да, т. к. -4 – целое число ().
г)
Ответ: нет.
Пример 2 – вычислить:
Рассмотрим слагаемые отдельно:
.
Получаем:
.
Пример 3 – упростить выражение:
Упростим знаменатель:
.
Получаем:
.
Отметим, что обязательно в данном случае .
Пример 4 – упростить выражение:
Возводим в квадрат двучлен:
.
Получили выражение:
.
В данной задаче могут быть поставлены дополнительные вопросы, например, допустимы ли отрицательные значения с. Ответ: нет, т. к. с имеет рациональный показатель степени и по определению является неотрицательным.
Пример 5 – упростить выражение:
Комментарий: ограничение на х наложено в связи с тем, что он имеет отрицательный рациональный показатель степени.
Итак, мы рассмотрели свойства степеней с рациональным показателем.
ИСТОЧНИК
http://interneturok.ru/ru/school/algebra/11-klass/stepeni-i-korni-stepennye-funktsii/obobschenie-ponyatiya-o-pokazatele-stepeni-nachalnye-svedeniya
http://interneturok.ru/ru/school/algebra/11-klass/stepeni-i-korni-stepennye-funktsii/stepen-s-ratsionalnym-pokazatelem-prosteyshie-zadachi
http://www. youtube.com/watch?v=lxaxSszE22I
youtube.com/watch?v=lxaxSszE22I
http://www.youtube.com/watch?v=Q-XBCtZuQ3g
http://metodtest.ru/index.php/kontrolnye-raboty/50-samostoyatelnye-raboty-po-algebre-7-11-klass/617-samostoyatelnaya-rabota-s-7-obobshchenie-ponyatiya-o-pokazatele-stepeni-11-klass.html
http://www.mathematics-repetition.com/tag/primer-na-svoystva-stepeni-s-naturalynm-pokazatelem
http://www.nado5.ru/e-book/stepen-s-racionalnym-pokazatelem
Свойства степени с рациональным показателем
1. Свойства степени с рациональным показателем.
Бродецкая Т. А.,учитель математики
МОУ «Гимназия № 4»,
г.о. Электросталь
2. Вспомним теорию
1Вспомним теорию
Арифметическим корнем n – ой степени (n N, n 2) из
неотрицательного числа a называется такое
неотрицательное число, n – я степень которого равна а:
2 n 1
2n
nk
a
a
a
2 n 1
2n
mn
a,
n N
;
a ,
n N
;
k
a
m
,
при
a 0.

2
1)
m
n
Степень с рациональным
показателем.
a a ,
m
0,
n
Если
m Z , n N , a 0;
где
m
n
то
m
n
a n am
при
a 0.
2) При a > 0, b > 0, p и q — рациональные числа:
a a a
p
q
(a ) a
p q
p
a p a
( ) p
b
b
p q
pq
p
a
p q
a
q
a
(ab) a b
p
p
p
4. Тренировочные упражнения
51) Вычислить:
2
3 3 27 9 5
64
3
3
2) Найдите значение выражения
3) Упростить выражение
c c
5
c
1
5
5
=-26,5
6 2 17 5 6 2 17 = -2
=1
4
4) Найдите значение выражения
(
2с
2с
d
d
5) Упростить выражение
2c
2c
d
) (
d
1
2
d
2c
1
3
1
2
2c
)
d
125 8 5 5 49
1
2
6) Упростить выражение
a 2 2 a 1 a 2 2 a 1
2
2
2
2
= 2
=
4
= 7 5 35
Задания для самостоятельной работы
Вычислить: 1)
2)
3)
4)
5)
2
3) :
3
5( 27
(( 4 2 4 8 ) 2 6)(( 4 2 4 8 ) 2 6)
8 28 8 28
64
5
6
(0,125)
1
3
4
32 2 16
1
1
2
(3 ) 4
0 4
(3 100 23 5 23 2 )( 3 10 3 4 )
Упростить:
6)
3
b b
3
7)
(
0,5а
1
4
(2 а)
3
4
b
2
4
1
4
(2 а) а
2
3
4
) : ( 2а а 2 )
3
4
Проверка
1)
2)
2
5
(
3
3
3
)
3
5( 27 3 ) :
15
3
2
(( 2 8 ) 6)(( 2 8 ) 6)
4
2
4
4
4
2
( 2 8 2 2 8 6)( 2 8 2 2 8 6)
4
4
( 2 8 2)( 2 8 2) ( 2 8 ) 4
2
2 8 2 16 4 14
Проверка
3)
8 28 8 28
1 2 7 7 1 2 7 7 (1 7 ) 2 (1 7 ) 2
1 7 1 7 7 1 1 7 2
4)
5
6
1
3
64 (0,125) 32 2 4 16
5
6
6
(2 )
1
3 3
(0,5 )
4
1
1
2
(30 ) 4 4
3
4
2
2 2 (2 )
5
1 4
1 1
6
5
5
2 ( ) 2 2 4 2 2 2 4 2
2
5
5)
Проверка
3
3
3
3
3
( 100 2 5 2 2 )( 10 4 )
(а аb b )(a b) a b следует
3
3
3
3
( 10 ) ( 4 ) 10 4 6
По формуле
b3 b 2
6)
3
b
4
2
2
2 4
1
3 3
b
3
1
3
b
3
3
b
Проверка
7)
(
0,5а
1
4
(2 а)
1
4
(2 а) а
2
3
4
1
4
1)
3
4
3
4
2 0,5a (2 a) (2 a ) a
2 (2 a)
3
4
2)
1
4
1 a (2 a)
3
4
a (2 a)
3
4
3
4
1
3
4
) : ( 2а а 2 )
3
4
1
3
4
a (2 a)
3
4
3
4
;
1
10.
 Задание на дом. • Тренировочный тест по теме «Свойства степени с
Задание на дом. • Тренировочный тест по теме «Свойства степени срациональным показателем» (проверка на
следующем уроке).
11. Тренировочный тест.
11. Найдите значение выражения: 6 8 3 .
1) 12; 2) 6; 3) 3; 4) –3.
2. Выберите верное неравенство:
1
1
1
3
1) 2 2 3 2 ; 2) 0 ,3 0 ,5 ; 3) 1,5 1; 4) 3-8
3. Среди данных чисел выберите наибольшее:
1) 5 ;
2) 5 ;
3) 5 ;
4) 5 .
4. Представьте данное выражение в виде степени:
1,7
2,8
1,5
у у у .
1) у -3; 2) у -7,14; 3) у 3;
4) у 6.
5. Упростите выражение: b 0,2 : b 0,7 .
2
1
0,9
1) b ;
2) b ;
3) b
; 4) b 7 .
1
2
1
2
1
3
1
2
1
4
12. Тренировочный тест (продолжение).
23
-1,5) .
6. Упростите выражение:
(а
5
1
5
6
6
1) а;
2) а ; 3) а ;
4) a . 36 3
.
2
7.
 Найдите значение выражения: 125
Найдите значение выражения: 125 5
6
36
1) 6 ; 2) 1,2 ;
3) 125 ;
4) 25 .
8. Найдите значение выражения: 2 3 3 2
1) -4;
2) 9;
3) -5;33
4) 5.
x 1
.
9. Сократите дробь:
33
22
11
x x x
11
1
x11
x 11 1
x
1
1) x11 1 ;
2) 11 ; 3) 11 ;
4)
.
11
x
x
x
10. Найдите значение выражения:
х х
при х = 0,0625
1
6
5
3
1
2
1) 0,5;
1
3
1
3
3
4
х 3 х 1
2) 2;
3) 4;
4) 0,25.
5
3
1
3
3 6 .
Тренировочный тест (продолжение).
11. Вычислите: -24·1251-39. 1) -1139; 2) -159; 3) -81; 4)81.
33
12. Вычислите: 4,7 — 8 ·2
. 1) -11,3; 2) 5,3; 3) -7,3; 4) 11,3.
1
1
3 2
13. Вычислите:
.
1)
1;
2)
2;
3)
;
4)
.
36
3
2
0
,
216
14.
 Вычислите:
Вычислите:.
1
2
1
2
4
4
9
3
1) 0,04;
3
2
1
0 ,09 4 0 ,027 6
2) 0,4;
15. Вычислите: 18 27 0 ,4.
16. Упростите выражение
23
3) 4;
4) 0,16.
1) 1,6; 2) 161,6; 3) 2,6; 4) 5,6.
3
1 у2
2 у.
1
1 у2 у
1) 1 + у ; 2) 1 + 2 у ; 3) 2 у -1; 4) (1 — у )2.
а 16
а .
17. Упростите выражение:
а 4
1) -4; 2) 4; 3) –2а ;
4) 0.
18. Вычислите: 81 1 .
4
1 16
1
1) 2; 2) 2 2 ;
3) 3;
4) 1 2 .
2
3
1
3
1
3
1
4
1
3
1
2
Тренировочный тест (продолжение).
9
4
0 ,216 .
8
27
19. Найдите значение выражения
1) 0,36;
2) 3,6;
3) 0,6;
4) 0,18.
0 ,16 . 1) 0,04; 2) 0,4; 3) 0,2; 4) 0,8.
20. Вычислите: 0 ,064
23
32
0 3
0 ,5
3
21. Вычислите: 9 ( 5 ) 3 ( 0,01 ) 9 3 27 .
1) 13;
2) 7;
3) 3;
4) .

22. Вычислите: 5·250,5 –1 2. 1) 8; 2) 23; 3) 123; 4) 125- 2.
23. Вычислите: 24·16 -21 6. 1) 0; 2) 6; 3) 42; 4)90.
35 2
4 .
24. Вычислите:
1
28
25 2
1) 5 ;
2) 1;
3) 3,5;
4) 14.
25. Вычислите: 23·2-2 + 2-3·22 +1,25.
1
6
1) 1
9
;
32
2) 2,5;
1
1
4
1
3) 3,75;
26. Вычислите:
.
5 4 2 2 10 2
1) -63;
2) 63;
3)
25
1296
4) 1,25.
;
4) 0.
Тренировочный
тест
(продолжение).
1
2
Вычислите: 64 31 0 ,8
27.
.
1) 1,3;
2) 5,2;
3) 8,8;
4) 16,8.
1
28. Упростите выражение: а 4 : а 0,75
.
1
1
1
1) а 2 ;
2) а ;
3) а 2 ;
4) а .
6
1
1
29. Упростите выражение: а 2 : а 7
. 7
9
9
9
1) а14 ; 2) а 14 ;
3) а 7 ;
4) а 4 .
1
9
3
при
р
30. Найдите значение выражения
.

2
1) 0 ;
2) 1;
3) 9;
4) 3.
31. Найдите значение выражения 3 1 при р 2 .
3
1
1) 9 ;
2) 4 ;
3) 320 ;
4) 81.
3
32. Найдите наименьшее число:
1
1
1
1) 12 ;
2) 2 2 ;
3) 1 2 ;
4) 4 2 .
3р
6 р
4 р
1
2
1
р
Тренировочный тест (ответы).
№ 1
воп
рос
а
Отв 3
ет
2
3
4
5
6
7
8
9
10
11
12 13 14 15 16
1
4
3
1
4
2
3
4
1
2
1
3
3
1
1
№ 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
воп
рос
а
Отв 2 1 1 2 2 2
4
3 3 4 3
4 2
4 4 4
ет
Используемая литература
• Алгебра и начала анализа. Учебник для 10-11 классов
общеобразовательных учреждений. А. Н. Колмогоров, А. М.
Абрамов, Ю. П. Дудницын и др. Москва.
«Просвещение»
2010г.
• Журнал «Математика.
 Первое сентября» № 19, 2008г.,
Первое сентября» № 19, 2008г.,«Подготовка к ЕГЭ».
• Сборники для подготовки к ЕГЭ по математике.
• Интернет – ресурс. Сайт http://www.mathege.ru. Открытый
банк задач по математике.
• Тест по теме «Свойства степени с рациональным
показателем»:
http://ov1098.jimdo.com/%D1%83%D1%87%D0%B0%D1%89%
D0%B8%D0%BC%D1%81%D1%8F/11%D0%BA%D0%BB%D0%B0%D1%81%D1%81%D1%82%D0%B5%D1%81%D1%82%D1%8B/
Корень n-я степени, степень с рациональным показателем и их свойства [wiki.eduVdom.com]
Число, n-я степень которого равна a, называется корнем n-й степени из числа $a (n\in\mathbb{N}) и обозначается $\sqrt[n]{a}$.
Неотрицательное число, n-я степень которого равна неотрицательному числу а, называется арифметическим корнем n-и степени из числа а.
Свойства арифметического корня n-й степени:
Если $a\geq 0 ; b \geq 0 \text{ , то } \sqrt[n]{ab} = \sqrt[n]{a}\cdot\sqrt[n]{b}$
Если $a \geq 0; b \geq 0 \text{ , то } \sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}$
Если $n,\,k\in,\,a\geq 0\text{ , то } \sqrt[n]{\sqrt[k]{a}} = \sqrt[nk]{a}$
Если $n,\,k\in,\,a\geq 0\text{ , то } \sqrt[nk]{a^{mk}} = \sqrt[n]{a^m}$
Если $a>0\text{ , те }\mathbb{Z},\,n\in\mathbb{N}\text{ , то }a^{\frac{m}{n}} = \sqrt[n]{m} $. {\frac{2}{3}}$
{\frac{2}{3}}$
Существование корня. Степень с рациональным показателем
Содержание:
Существование корня. Степень с рациональным показателем
Существование корня. Степень с рациональным показателем. Определение умножения (и деления) действительного числа, как обычно, непосредственно приводит к определению его степени по показателю положительного целого числа (и отрицательного целого числа).Если вы посмотрите в определенной степени на рациональные показатели в целом, вы в первую очередь сосредоточитесь на вопросе о наличии корня. 1 проверьте, насколько хорошо расширение заполнило старый зазор (он не создает новый зазор). пусть a-произвольное вещественное число, а l-натуральное число. Как известно, корни порядка l из a являются вещественными числами€.
Как мы помним, отсутствие простейших корней в поле рациональных чисел является одной из причин расширения этого поля. Людмила Фирмаль
- Ограничиваясь случаем, когда a положительно, ищем положительное b, удовлетворяющее этому соотношению, так называемому арифметическому значению корня.
 Докажите, что такое число 6 всегда присутствует и только 1 больше. Однако последнее объяснение единственности числа€сразу же вытекает из того факта, что разным положительным числам соответствуют разные их степени. Для 05$’, это bn b’N. если существует положительное рациональное число r, n-я степень которого равна a, то это искомое число 6.Поэтому в дальнейшем достаточно ограничиться предположением, что такого рационального числа не существует. Теперь мы построим сечение X \ X в области всех рациональных чисел следующим образом.
Докажите, что такое число 6 всегда присутствует и только 1 больше. Однако последнее объяснение единственности числа€сразу же вытекает из того факта, что разным положительным числам соответствуют разные их степени. Для 05$’, это bn b’N. если существует положительное рациональное число r, n-я степень которого равна a, то это искомое число 6.Поэтому в дальнейшем достаточно ограничиться предположением, что такого рационального числа не существует. Теперь мы построим сечение X \ X в области всех рациональных чисел следующим образом.
- Классифицировать X как все отрицательные рациональные числа и нули, а XA a для рациональных чисел q. классифицировать класс X как положительное рациональное число x(X’N> c). Легко видеть, что эти классы не пусты и X содержит положительные числа. Например, используя натуральное число m, h > 1 Это-и Т, и тем более-гг а Тл, число которых содержится в-а, т т м т И число m находится в X’. Другие требования поперечного сечения быстро проверяются.
 хм. Очевидно, что x принадлежит классу X, а x ’принадлежит классу X, и по определению этих классов х, Нуа, стр. Однако разница x’ x может быть меньше любого числа;> 0(n * 4, примечания), и ничто не мешает вам видеть x меньше, чем предварительно фиксированное число x’0.In в этом случае разница н-х-хп =(**)(х-Эн〜1 + х * х н〜х + … + ху-1)е * в NX? То есть он может быть сколь угодно малым*).по Лемме 2 это означает, что число и a равны. и проверяется, что обычные правила, оцененные в ходе элементарной алгебры, справедливы для таких степеней. АР * О!»АР + Р>, АГ: аг= на *、 (аг = ’ РЛ (арг =’ р-р ’、 П Он также подчеркивает, что в случае a> 1 порядок ar увеличивается по мере увеличения рационального показателя r.
хм. Очевидно, что x принадлежит классу X, а x ’принадлежит классу X, и по определению этих классов х, Нуа, стр. Однако разница x’ x может быть меньше любого числа;> 0(n * 4, примечания), и ничто не мешает вам видеть x меньше, чем предварительно фиксированное число x’0.In в этом случае разница н-х-хп =(**)(х-Эн〜1 + х * х н〜х + … + ху-1)е * в NX? То есть он может быть сколь угодно малым*).по Лемме 2 это означает, что число и a равны. и проверяется, что обычные правила, оцененные в ходе элементарной алгебры, справедливы для таких степеней. АР * О!»АР + Р>, АГ: аг= на *、 (аг = ’ РЛ (арг =’ р-р ’、 П Он также подчеркивает, что в случае a> 1 порядок ar увеличивается по мере увеличения рационального показателя r.
Смотрите также:
Решение задач по математическому анализу
рациональных выражений
Выражение, представляющее собой отношение двух многочленов:
Это похоже на дробь, но с многочленами.
Другие примеры:
| x 3 + 2x — 1 6x 2 | 2x + 9 x 4 — x 2 |
Также
| 1 2 — x 2 | Верхний полином равен «1», и это нормально. |
| 2x 2 + 3 | Да, это так! Так же можно было бы написать: 2x 2 + 3 1 |
Но не
| 2 — √ (x) 4 — x | вершина не является многочленом (квадратный корень из переменной не допускается) | |
| 1 / x не допускается в полиноме |
В целом
Рациональная функция — это отношение двух многочленов P (x) и Q (x), как это
f (x) = P (x) Q (x)
За исключением того, что Q (x) не может быть нулем (и везде, где Q (x) = 0 не определено)
Поиск корней рациональных выражений
«Корень» (или «ноль») — это выражение , равное нулю : |
Чтобы найти корни рационального выражения , нам нужно только найти корни верхнего многочлена , если рациональное выражение находится в «наименьших членах».
Итак, что означает «Самые низкие термины»?
Наименьшие условия
Ну, дробь находится в наименьшем числе, когда верх и низ не имеют общих множителей.
Пример: дроби
2 6 , а не в самых низких показателях
, поскольку 2 и 6 имеют общий множитель «2»
Но:
1 3 — это в низком выражении,
, поскольку 1 и 3 не имеют общих множителей
Точно так же рациональное выражение находится в наименьших членах, когда верх и низ не имеют общих множителей.
Пример: рациональные выражения
x 3 + 3x 2 2x — это , а не в самом низком выражении,
как x 3 + 3x 2 и 2x
имеют общий множитель «х»
Но
x 2 + 3x 2 — это в низком выражении,
as x 2 + 3x и 2 не имеют общих множителей
Итак, чтобы найти корни рационального выражения :
- Сократите рациональное выражение до наименьших членов,
- Затем найдите корни верхнего полинома
Как нам найти корни? Прочтите «Решение многочленов», чтобы узнать, как это сделать.
Правильное против неправильного
| Дроби могут быть правильными или неправильными: |
| (В «Неправильном» нет ничего плохого, просто другой тип) |
И аналогично:
Рациональное выражение также может быть правильным или неправильным !
Но что делает многочлен больше или меньше?
Степень!
Для полинома с одной переменной Степень является наибольшим показателем этой переменной.
Примеры степеней:
| 4x | Степень: 1 (переменная без экспоненты фактически имеет показатель степени 1) | |
| 4x 3 — x + 3 | Степень 3 (наибольший показатель x) |
Итак, вот как узнать, является ли рациональное выражение правильным или неправильным :
Правильный: степень верха меньше степени низа.
| Правильный: | 1 х + 1 | град (вверху) <градус (внизу) |
Другой пример: x x 3 — 1
Неправильно: степень верха больше или равна степени низа.
| Неправильно: | x 2 — 1 x + 1 | град (верх) ≥ град (низ) |
Другой пример: 4x 3 -3 5x 3 + 1
Если полином неправильный, мы можем упростить его с помощью полиномиального деления в длину
Асимптоты
Рациональные выражения могут иметь асимптоты (линия , к которой кривая приближается по мере приближения к бесконечности):
Рациональное выражение может иметь:
- любое количество вертикальных асимптот,
- только нулевая или одна горизонтальная асимптота,
- только нулевая или одна наклонная (наклонная) асимптота
Поиск горизонтальных или наклонных асимптот
Найти их довольно просто. ..
..
… но это зависит от степени полинома сверху и снизу .
Быстрее всего будет расти тот, у кого большая степень.
То же, что «Правильный» и «Неправильный», но на самом деле существует четырех возможных случаев, показано ниже.
(я показываю тестовое значение x = 1000 для каждого случая, просто чтобы показать, что происходит)
Давайте рассмотрим каждый из этих примеров по очереди:
Степень верха
Меньше нижеНижний многочлен будет доминировать, а горизонтальная асимптота равна нулю.
Пример: f (x) = (3x + 1) / (4x
2 +1)Когда x равен 1000:
f (1000) = 3001/4000001 = 0,00075 …
И чем больше x, тем больше f (x) приближается к 0
градус верха
равен низу Ни один из них не доминирует … асимптота задается старшими членами каждого полинома.
Пример: f (x) = (3x + 1) / (4x + 1)
Когда x равен 1000:
f (1000) = 3001/4001 = 0.750 …
И чем больше x, тем больше f (x) приближается к 3/4
Почему 3/4? Поскольку «3» и «4» являются «старшими коэффициентами» каждого полинома
Члены отсортированы в порядке убывания степени
(Технически 7 — это постоянная величина, но здесь их все легче представить как коэффициенты.)
Метод простой:
Разделите старший коэффициент верхнего многочлена на старший коэффициент нижнего многочлена.
Вот еще один пример:
Пример: f (x) = (8x
3 + 2x 2 — 5x + 1) / (2x 3 + 15x + 2)Степени равны (обе имеют степень 3)
Достаточно взглянуть на старшие коэффициенты каждого полинома:
- Верх 8 (от 8x 3 )
- Снизу 2 (из 2x 3 )
Итак, существует горизонтальная асимптота на 8/2 = 4
Степень верха
1 больше низа Это особый случай: существует наклонная асимптота , и нам нужно найти уравнение прямой.
Чтобы решить эту проблему, используйте полиномиальное деление в столбик: разделите верхнюю часть на нижнюю, чтобы найти частное (остаток игнорируйте).
Пример: f (x) = (3x
2 +1) / (4x + 1)Степень вершины равна 2, а степень основания равна 1, поэтому будет наклонная асимптота
Нам нужно разделить 3x 2 +1 на 4x + 1 , используя полиномиальное деление в столбик:
Ответ: (3/4) x- (3/16) (без остатка):
Асимптота «уравнение линии»: (3/4) x- (3/16)
Степень верха:
больше, чем на 1, больше , чем нижний уголКогда верхний многочлен на более чем на 1 градус, на выше нижнего многочлена, не существует горизонтальной или наклонной асимптоты .
Пример: f (x) = (3x
3 +1) / (4x + 1)Степень верха равна 3, а степень низа 1.
Верх более чем на 1 градус выше низа, поэтому нет горизонтальной или наклонной асимптоты .
Поиск вертикальных асимптот
Существует еще один тип асимптоты, который вызван нижним многочленом только .
Но сначала: убедитесь, что рациональное выражение выражено в минимальных терминах!
Когда нижний многочлен равен нулю (любой из его корней), мы получаем вертикальную асимптоту.
Прочтите раздел Решение многочленов, чтобы узнать, как найти корни
Из нашего примера выше:
Пример: (x
2 -3x) / (2x-2)Нижний полином равен 2x-2 , который разлагается на: 2 (х-1) А множитель (x-1) означает, что существует вертикальная асимптота при x = 1 (потому что 1-1 = 0) |
Полный пример
Пример: эскиз (x − 1) / (x
2 −9)Прежде всего, мы можем разложить на множители нижний многочлен (это разница двух квадратов):
x − 1 (x + 3) (x − 3)
Теперь мы видим:
Корни верхнего многочлена: +1 (здесь пересекает ось x )
Корни нижнего многочлена: −3 и +3 (это вертикальные асимптоты )
Это пересекает ось y , когда x = 0, поэтому давайте установим x равным 0:
Пересекает ось Y в: 0−1 (0 + 3) (0−3) = −1 −9 = 1 9
Мы также знаем, что степень вершины меньше степени основания, поэтому существует горизонтальная асимптота в точке 0
.
Итак, мы можем набросать всю эту информацию:
И теперь мы можем набросать кривую:
(Сравните это с графиком (x-1) / (x 2 -9))
рациональных функций | Безграничная алгебра
Введение в рациональные функции
Рациональная функция — это такая функция, что [latex] f (x) = \ frac {P (x)} {Q (x)} [/ latex], где [latex] Q (x) \ neq 0 [/ latex] ; область определения рациональной функции может быть вычислена.
Цели обучения
Описать рациональные функции, включая их области
Основные выводы
Ключевые моменты
- Рациональная функция — это любая функция, которую можно записать как отношение двух полиномиальных функций, где многочлен в знаменателе не равен нулю.
- Область [latex] f (x) = \ frac {P (x)} {Q (x)} [/ latex] — это набор всех точек [latex] x [/ latex], знаменатель которых [latex] ] Q (x) [/ latex] не равно нулю.

- Ограничения области рациональной функции можно определить, установив знаменатель равным нулю и решив. Значения [latex] x [/ latex], при которых знаменатель равен нулю, называются сингулярностями и не находятся в области определения функции.
Ключевые термины
- домен : Набор всех входных значений ([latex] x [/ latex]), по которым определяется функция.
- рациональная функция : Любая функция, значение которой может быть выражено как частное двух многочленов (где многочлен в знаменателе не равен нулю).
- особенности : Значения [latex] x [/ latex], при которых рациональная функция не определена, для которых знаменатель [latex] Q (x) [/ latex] равен нулю.
- вертикальная асимптота : вертикальная прямая линия, к которой кривая приближается произвольно близко, уходя в бесконечность.
- знаменатель : Число или выражение, записанное под чертой в виде дроби (например, [latex] 2 [/ latex] в [latex] \ frac {1} {2} [/ latex]).

Рациональные функции
Рациональная функция — это любая функция, которую можно записать как отношение двух полиномиальных функций.Ни коэффициенты многочленов, ни значения, принимаемые функцией, не обязательно являются рациональными числами.
Любая функция одной переменной, [latex] x [/ latex], называется рациональной функцией, если и только если она может быть записана в форме:
[латекс] f (x) = \ dfrac {P (x)} {Q (x)} [/ латекс]
, где [латекс] P [/ латекс] и [латекс] Q [/ латекс] являются полиномиальными функциями от [латекса] x [/ латекса] и [латекса] Q (x) \ neq 0 [/ latex].
Обратите внимание, что каждая полиномиальная функция является рациональной функцией с [latex] Q (x) = 1 [/ latex].Функция, которую нельзя записать в виде многочлена, например [latex] f (x) = \ sin (x) [/ latex], не является рациональной функцией. Однако прилагательное «иррациональное» обычно не используется для обозначения функций.
Постоянная функция, такая как [latex] f (x) = \ pi [/ latex], является рациональной функцией, поскольку константы являются полиномами. Обратите внимание, что сама функция рациональна, хотя значение [latex] f (x) [/ latex] иррационально для всех [latex] x [/ latex].
Обратите внимание, что сама функция рациональна, хотя значение [latex] f (x) [/ latex] иррационально для всех [latex] x [/ latex].
Область рациональной функции
Область определения рациональной функции [latex] f (x) = \ frac {P (x)} {Q (x)} [/ latex] — это набор всех значений [latex] x [/ latex], для которых знаменатель [латекс] Q (x) [/ латекс] не равен нулю.
В качестве простого примера рассмотрим рациональную функцию [latex] y = \ frac {1} {x} [/ latex]. Домен состоит из всех значений [latex] x \ neq 0 [/ latex].
Ограничения домена могут быть рассчитаны путем нахождения сингулярностей, которые представляют собой значения [latex] x [/ latex], для которых знаменатель [latex] Q (x) [/ latex] равен нулю. Рациональная функция не определена для таких значений [latex] x [/ latex], и эти значения исключаются из набора предметных областей функции.
Факторизация числителя и знаменателя рациональной функции помогает выявить особенности алгебраических рациональных функций. 2 [/ latex] должно быть равно [latex] -2 [/ latex]. Поскольку это условие не может быть удовлетворено действительным числом, область определения функции — все действительные числа.
2 [/ latex] должно быть равно [latex] -2 [/ latex]. Поскольку это условие не может быть удовлетворено действительным числом, область определения функции — все действительные числа.
Асимптоты
Рациональная функция может иметь не более одной горизонтальной или наклонной асимптоты и много возможных вертикальных асимптот; их можно рассчитать.
Цели обучения
Определите, когда асимптота рациональной функции будет горизонтальной, наклонной или вертикальной
Основные выводы
Ключевые моменты
- Асимптота кривой — это линия, расстояние между которой и кривой приближается к нулю, поскольку они стремятся к бесконечности.
- Асимптоты бывают трех видов: горизонтальные, вертикальные и наклонные.
- Рациональная функция имеет не более одной горизонтальной асимптоты или наклонной (наклонной) асимптоты и, возможно, несколько вертикальных асимптот.
- Вертикальные асимптоты встречаются в особенностях рациональной функции или точках, в которых функция не определена.
 Они возникают только в сингулярностях, где соответствующий линейный множитель в знаменателе остается после отмены.
Они возникают только в сингулярностях, где соответствующий линейный множитель в знаменателе остается после отмены. - Существование горизонтальной или наклонной асимптоты зависит от степеней полиномов в числителе и знаменателе
.
Ключевые термины
- асимптота : прямая линия, к которой кривая приближается произвольно близко, уходя в бесконечность.
- наклонный : Непрямой или перпендикулярный; ни параллельно, ни под прямым углом к основанию; косой; склонен.
- рациональная функция : Любая функция, значение которой может быть выражено как частное двух многочленов (где многочлен в знаменателе не равен нулю).
Типы асимптот
В аналитической геометрии асимптота кривой — это такая линия, что расстояние между кривой и линией приближается к нулю, поскольку они стремятся к бесконечности.
Существует три вида асимпт: горизонтальная , вертикальная и наклонная . Горизонтальные асимптоты кривых — это горизонтальные линии, к которым график функции приближается, поскольку [latex] x [/ latex] стремится к [latex] + \ infty [/ latex] или [latex] — \ infty [/ latex]. Горизонтальные асимптоты параллельны оси [latex] x [/ latex].
Горизонтальные асимптоты кривых — это горизонтальные линии, к которым график функции приближается, поскольку [latex] x [/ latex] стремится к [latex] + \ infty [/ latex] или [latex] — \ infty [/ latex]. Горизонтальные асимптоты параллельны оси [latex] x [/ latex].
Вертикальные асимптоты — это вертикальные линии, вблизи которых функция неограниченно растет. Они параллельны оси [латекс] y [/ латекс].
Асимптота, которая не является ни горизонтальной, ни вертикальной, называется наклонной (или наклонной) асимптотой. Это диагональные линии, так что разница между кривой и линией приближается к [латексу] 0 [/ латексу], поскольку [латекс] x [/ латекс] стремится к [латексу] + \ infty [/ latex] или [латексу] — \ инфты [/ латекс].
Каждый тип асимптоты показан на графике ниже.
График с асимптотами: График функции с горизонтальной ([latex] y = 0 [/ latex]), вертикальной ([latex] x = 0 [/ latex]) и наклонной асимптотой (синяя линия).
Пример 1
Рассмотрим график уравнения [latex] f (x) = \ frac {1} {x} [/ latex], показанный ниже. Координаты точек на кривой имеют вид [latex] (x, \ frac {1} {x}) [/ latex], где [latex] x [/ latex] — это число, отличное от 0.
Координаты точек на кривой имеют вид [latex] (x, \ frac {1} {x}) [/ latex], где [latex] x [/ latex] — это число, отличное от 0.
График [latex] f (x) = 1 / x [/ latex]: Обе оси [latex] x [/ latex] и [latex] y [/ latex] являются асимптотами.
Обратите внимание, что по мере того, как положительные значения [latex] x [/ latex] становятся все больше и больше, соответствующие значения [latex] y [/ latex] становятся бесконечно малыми.Однако независимо от того, насколько большим становится [латекс] x [/ latex], [latex] \ frac {1} {x} [/ latex] никогда не бывает [latex] 0 [/ latex], поэтому кривая никогда не касается [ латекс] х [/ латекс] -ось. Ось [latex] x [/ latex] — это горизонтальная асимптота кривой.
Аналогичным образом, когда положительные значения [латекс] x [/ латекс] становятся все меньше и меньше, соответствующие значения [латекс] y [/ латекс] становятся все больше и больше. Таким образом, кривая тянется все дальше и дальше вверх по мере приближения к оси [латекс] y [/ латекс]. [Latex] y [/ latex] -ось — это вертикальная асимптота кривой.
[Latex] y [/ latex] -ось — это вертикальная асимптота кривой.
Асимптоты рациональных функций
Рациональная функция имеет не более одной горизонтальной или наклонной асимптоты и, возможно, несколько вертикальных асимптот.
Вертикальные асимптоты возникают только тогда, когда знаменатель равен нулю. Другими словами, вертикальные асимптоты возникают в особенностях или точках, в которых рациональная функция не определена. Вертикальные асимптоты возникают только в сингулярностях, когда соответствующий линейный множитель в знаменателе остается после сокращения.
Например, рассмотрим функцию:
[латекс] f (x) = \ dfrac {(x-1) (x + 2)} {(x-1) (x + 1)} [/ latex]
Из линейных множителей в знаменателе можно определить, что существуют две особенности: [latex] x = 1 [/ latex] и [latex] x = -1 [/ latex]. Однако линейный коэффициент [латекс] (x-1) [/ latex] отменяется коэффициентом в числителе. Таким образом, единственная вертикальная асимптота для этой функции — [latex] x = -1 [/ latex].
Степень числителя и степень знаменателя определяют, существуют ли горизонтальные или наклонные асимптоты.
Существование горизонтальной асимптоты зависит от степени полинома в числителе ([латекс] n [/ латекс]) и степени полинома в знаменателе ([латекс] m [/ латекс]). Возможны три случая:
- Если [latex] n> m [/ latex], то горизонтальной асимптоты нет (Однако, если [latex] n = m + 1 [/ latex], то наклонная асимптота существует).
- Если [latex] n
- Если [латекс] n = m [/ latex], то существует горизонтальная асимптота и уравнение:
[latex] \ quad \ quad y = \ frac {\ text {Коэффициент члена наивысшей степени в числителе}} {\ text {Коэффициент члена наивысшей степени в знаменателе}} [/ latex]
Когда числитель рациональной функции имеет степень ровно на единицу больше знаменателя, функция имеет наклонную (наклонную) асимптоту.2 (x + 1)} [/ латекс].
Обратите внимание, что, исходя из линейных множителей в знаменателе, сингулярности существуют при [latex] x = 1 [/ latex] и [latex] x = -1 [/ latex]. Также обратите внимание, что один линейный коэффициент [латекс] (x-1) [/ latex] отменяется с числителем. Однако один линейный коэффициент [латекс] (x-1) [/ латекс] остается в знаменателе, потому что он возведен в квадрат. Следовательно, существует вертикальная асимптота при [latex] x = 1 [/ latex]. Линейный коэффициент [латекс] (x + 1) [/ латекс] также не отменяет; таким образом, вертикальная асимптота также существует при [latex] x = -1 [/ latex].2 + 16} [/ латекс].
Поскольку многочлены в числителе и знаменателе имеют одинаковую степень ([latex] 2 [/ latex]), мы можем определить, что существует одна горизонтальная асимптота и нет наклонной асимптоты.
Коэффициент при наивысшей степени мощности равен [латекс] 2 [/ латекс] в числителе и [латекс] 1 [/ латекс] в знаменателе. Следовательно, горизонтальная асимптота имеет вид:
[латекс] y = \ frac {2} {1} = 2 [/ латекс]
Решение задач с помощью рациональных функций
[latex] x [/ latex] -перехваты рациональных функций находятся путем установки полинома в числителе равным [latex] 0 [/ latex] и решения для [latex] x [/ latex].
Цели обучения
Используйте числитель рациональной функции, чтобы найти ее нули
Основные выводы
Ключевые моменты
- Перехваты [latex] x [/ latex] (также известные как нули или корни) функции — это точки, в которых график пересекает ось [latex] x [/ latex]. Рациональные функции могут иметь ноль, один или несколько [latex] x [/ latex] -перехватов.
- Для любой функции перехватчики [latex] x [/ latex] являются значениями [latex] x [/ latex], для которых функция имеет нулевое значение: [latex] f (x) = 0 [/ latex] .
- Для рациональных функций существуют перехватчики [latex] x [/ latex], когда числитель равен [latex] 0 [/ latex]. Для [латекс] f (x) = \ frac {P (x)} {Q (x)} [/ latex], если [latex] P (x) = 0 [/ latex], то [latex] f (x ) = 0 [/ латекс].
Ключевые термины
- знаменатель : Число или выражение, записанное под чертой в виде дроби (например, [латекс] 2 [/ латекс] в [латекс] \ frac {1} {2} [/ латекс]).
 2 — x — 1} [/ латекс]
2 — x — 1} [/ латекс]Рациональные функции можно изобразить на координатной плоскости.Мы можем использовать алгебраические методы для вычисления их [latex] x [/ latex] -перехватов (также известных как нули или корни), то есть точек, где график пересекает ось [latex] x [/ latex]. Рациональные функции могут иметь ноль, один или несколько [latex] x [/ latex] -перехватов.
Для любой функции перехватчики [latex] x [/ latex] являются значениями [latex] x [/ latex], для которых функция имеет нулевое значение: [latex] f (x) = 0 [/ latex] .
В случае рациональных функций, перехватчики [latex] x [/ latex] существуют, когда числитель равен [latex] 0 [/ latex].2 — 3x + 2 \\ & = (x — 1) (x — 2) \ end {align} [/ latex]
Решения для этого многочлена: [latex] x = 1 [/ latex] или [latex] x = 2 [/ latex]. Это означает, что эта функция имеет [latex] x [/ latex] -перехваты в [latex] 1 [/ latex] и [latex] 2 [/ latex].
Пример 2
Найдите [latex] x [/ latex] -перехваты функции:
[латекс] f (x) = \ dfrac {1} {x} [/ латекс]
Здесь числитель является константой и, следовательно, не может быть установлен равным [латекс] 0 [/ латекс].
 2 — 10} [/ latex]: [latex] x [/ latex] -перехватов существуют в [latex] x = — \ sqrt {2}, 0, \ sqrt {2} [/ latex].
2 — 10} [/ latex]: [latex] x [/ latex] -перехватов существуют в [latex] x = — \ sqrt {2}, 0, \ sqrt {2} [/ latex].Упрощение, умножение и деление рациональных выражений
Рациональное выражение можно рассматривать как дробь, и им можно управлять с помощью умножения и деления.
Цели обучения
Практика упрощения, умножения и деления рациональных выражений
Основные выводы
Ключевые моменты
- Рациональное выражение — это частное двух многочленов, где многочлен в знаменателе не равен нулю.
- Рациональные выражения часто можно упростить, удалив термины, которые можно вычесть из числителя и знаменателя. Это могут быть числа или функции [latex] x [/ latex].
- Рациональные выражения можно перемножать. Числители каждого умножаются вместе, а также их знаменатели. Иногда можно упростить получившуюся дробь.
- Рациональные выражения можно разделить друг на друга. Это соответствует правилам деления дробей, где дивиденд умножается на обратную величину делителя.
 0 [/ latex].Важно отметить, что поскольку все показатели положительные, невозможно разделить на [латекс] х [/ латекс].
0 [/ latex].Важно отметить, что поскольку все показатели положительные, невозможно разделить на [латекс] х [/ латекс].
Рациональное выражение — это дробь, содержащая многочлены, где многочлен в знаменателе не равен нулю. Как и дробь, состоящая из чисел, рациональное выражение можно упрощать, умножать и делить. Правила выполнения этих операций часто отражают правила упрощения, умножения и деления дробей. Выполнение этих операций с рациональными выражениями часто включает в себя выведение полиномиальных выражений из числителя и знаменателя.2 + 5x + 2} [/ латекс]
Это выражение необходимо сначала разложить на множители, чтобы получить выражение
[латекс] \ displaystyle \ frac {(x + 2) (x + 3)} {(2x + 1) (x + 2)} [/ латекс]
, который после исключения общего множителя [латекс] (x + 2) [/ latex] из числителя и знаменателя дает упрощенное выражение
[латекс] \ displaystyle \ frac {x + 3} {2x + 1} [/ латекс]
Умножение рациональных выражений
Рациональные выражения можно умножать и делить аналогично дробям.
 2 + x — 2} [/ латекс]
2 + x — 2} [/ латекс]Выражение не подлежит дальнейшему упрощению.
Неполные дроби
Частичное разложение на дробь — это процедура, используемая для уменьшения степени числителя или знаменателя рациональной функции.
Цели обучения
Практика разбиения рациональной функции на частичные дроби
Основные выводы
Ключевые моменты
- Частичное дробное разложение — это процедура, используемая для уменьшения степени числителя или знаменателя рациональной функции, и включает в себя разделение одного отношения на несколько более простых соотношений.С математической точки зрения, разложение на частичные дроби превращает функцию вида [латекс] \ frac {f (x)} {g (x)} [/ latex], где [latex] f [/ latex] и [latex] g [ / latex] оба многочлены, в функцию вида [latex] \ sum_ {j} \ frac {f_ {j} (x)} {g_ {j} (x)} [/ latex], где [latex] g_ {j} (x) [/ latex] — многочлены, которые являются множителями [latex] g (x) [/ latex].
- Основная мотивация разложения рациональной функции на сумму более простых дробей состоит в том, чтобы упростить выполнение линейных операций над суммой.
 3 -7x -6} = \ frac {1} {x + 2} + \ frac {3} {x-3} + \ гидроразрыв {4} {x + 1} [/ латекс]
3 -7x -6} = \ frac {1} {x + 2} + \ frac {3} {x-3} + \ гидроразрыв {4} {x + 1} [/ латекс]С математической точки зрения, расширение частичной дроби используется для изменения рациональной функции в форме [latex] \ frac {f (x)} {g (x)} [/ latex], где [latex] f [/ latex] и [latex] g [/ latex] — многочлены в функцию вида [latex] \ sum_ {j} \ frac {f_ {j} (x)} {g_ {j} (x)} [/ latex].Знаменатели членов этого суммирования, [латекс] g_ {j} (x) [/ latex], являются многочленами, которые являются множителями [latex] g (x) [/ latex], и, как правило, имеют более низкую степень.
Основная мотивация разложения рациональной функции на сумму более простых дробей состоит в том, чтобы упростить выполнение линейных операций над суммой. Сокращение сложных математических задач с помощью частичной декомпозиции дроби позволяет нам сосредоточиться на вычислении каждого отдельного элемента разложения, а не на более сложной рациональной функции.
Шаги к разложению рациональной функции
Допустим, у нас есть рациональная функция [latex] R (x) = \ frac {f (x)} {g (x)} [/ latex], где степень числителя меньше степени знаменателя.
 Предположим, [latex] R (x) [/ latex] имеет знаменатель, который учитывается в других выражениях, например, [latex] g (x) = P (x) \ cdot Q (x) [/ latex], и что нет повторяющиеся корни.
Предположим, [latex] R (x) [/ latex] имеет знаменатель, который учитывается в других выражениях, например, [latex] g (x) = P (x) \ cdot Q (x) [/ latex], и что нет повторяющиеся корни.Первый шаг к разложению функции [латекс] R (x) [/ latex] — разложить ее знаменатель на множители:
[латекс] \ Displaystyle R (x) = \ frac {f (x)} {(x — a_1) (x — a_2) \ cdots (x — a_p)} [/ латекс]
где [латекс] a_1,…, a_p [/ latex] — корни [латекса] g (x) [/ latex].
Тогда мы можем записать [латекс] R (x) [/ latex] как сумму частичных дробей:
[латекс] R (x) = \ frac {c_1} {(x — a_1)} + \ frac {c_2} {(x — a_2)} + \ cdots + \ frac {c_p} {(x — a_p)} [/ латекс]
где [латекс] c_1,…, c_p [/ latex] — константы.
Чтобы завершить процесс, мы должны определить значения этих коэффициентов [latex] c_i [/ latex]. Чтобы найти коэффициент, умножьте связанный с ним знаменатель на рациональную функцию [латекс] R (x) [/ latex]:
[латекс] c_i = (x — a_i) R (x) [/ латекс]
Это даст выражение со значением [latex] x [/ latex].
 2 (x + 3)} [/ latex], для которого [latex] x = 1 [/ latex] является повторяющимся корнем), необходимо предпринять дополнительные шаги для декомпозиции функции.
2 (x + 3)} [/ latex], для которого [latex] x = 1 [/ latex] является повторяющимся корнем), необходимо предпринять дополнительные шаги для декомпозиции функции. - Для рациональной функции [latex] R (x) = \ frac {f (x)} {g (x)} [/ latex], если степень [latex] f (x) [/ latex] больше, чем или равна степени [latex] g (x) [/ latex], функция не может быть разложена прямым способом. Необходимо выполнить евклидово деление [латекса] f [/ latex] на [latex] g [/ latex] с использованием полиномиального деления в столбик, в результате чего [latex] f (x) = E (X) g (x) + h (x) [/ латекс].Разделив на [латекс] g (x) [/ latex], получим [латекс] \ frac {f (x)} {g (x)} = E (x) + \ frac {h (x)} {g (x )} [/ latex], который затем можно выполнить разложение на [latex] \ frac {h (x)} {g (x)} [/ latex].
Рациональная степень — обзор
2 ПРИРОДА ЛОГИКИ
Декарт не написал отдельного трактата по логике, но разработал свой метод в неопубликованных Правилах управления сознанием и его более позднем Рассуждениях о методе.
 Рукопись Правил была предоставлена Арно и Николь, и они даже включили часть этой работы в свою собственную. 4 Декарт сосредоточился на прояснении простых идей и разработке метода, который приведет к новым истинам. Его точка зрения заключалась в том, что у ума не было проблем с выводами, 5 , но что у него действительно были проблемы с четким и отчетливым различением того, что было до него. Его метод был разработан, чтобы помочь уму решать проблемы и более ясно различать истины. Декарт распознал две операции интеллекта, которые помогают ему достичь этой цели, — интуицию и дедукцию. Интуиция, по его словам, была не «колеблющимся свидетельством чувства или обманчивым суждением воображения … но концепцией ясного и внимательного ума, которая настолько легка и отчетлива, что не может быть места для сомнений в том, кто мы такие. понимание »[Адам и Таннери, 1964-76, X, 368; Cottingham et al., 1985-1991, I, 14].Он был менее ясен в том, что он имел в виду под дедукцией, но предположил, что дедукция необходима, поскольку «очень многие факты, которые не являются самоочевидными, известны с уверенностью, при условии, что они выводятся из истинных и известных принципов посредством непрерывного и непрерывного движения мысль, в которой каждое отдельное предложение ясно интуитивно интуитивно »[Адам и Таннери, 1964-76, X, 369; Cottingham et al.
Рукопись Правил была предоставлена Арно и Николь, и они даже включили часть этой работы в свою собственную. 4 Декарт сосредоточился на прояснении простых идей и разработке метода, который приведет к новым истинам. Его точка зрения заключалась в том, что у ума не было проблем с выводами, 5 , но что у него действительно были проблемы с четким и отчетливым различением того, что было до него. Его метод был разработан, чтобы помочь уму решать проблемы и более ясно различать истины. Декарт распознал две операции интеллекта, которые помогают ему достичь этой цели, — интуицию и дедукцию. Интуиция, по его словам, была не «колеблющимся свидетельством чувства или обманчивым суждением воображения … но концепцией ясного и внимательного ума, которая настолько легка и отчетлива, что не может быть места для сомнений в том, кто мы такие. понимание »[Адам и Таннери, 1964-76, X, 368; Cottingham et al., 1985-1991, I, 14].Он был менее ясен в том, что он имел в виду под дедукцией, но предположил, что дедукция необходима, поскольку «очень многие факты, которые не являются самоочевидными, известны с уверенностью, при условии, что они выводятся из истинных и известных принципов посредством непрерывного и непрерывного движения мысль, в которой каждое отдельное предложение ясно интуитивно интуитивно »[Адам и Таннери, 1964-76, X, 369; Cottingham et al. , 1985-1991, I, 15]. Дедукция для Декарта, по-видимому, включает интуицию необходимой связи между двумя отчетливо интуитивными идеями.Интуитивно понятные предметы называются «объектами» [ objectum ] [Adam and Tannery, 1964-76, X, 365; Cottingham et al., 1985-1991, I, 12], но также и «предложения» [ propositionis ] [Adam and Tannery, 1964-76, X, 379; Cottingham et al., 1985-1991, I, 20]. В «Дискурсе », также метод был сосредоточен на достижении знания, разбивая проблемы на их простейшие объекты, а затем, переходя от «простейших и наиболее легко узнаваемых объектов» к «постепенному восхождению, шаг за шагом, к знанию о них». самый сложный… »[Адам и Таннери, 1964-76, VII, 18; Cottingham et al., 1985-1991, I, 120].Примеры, которые он имеет в виду, кажутся простыми пропорциями, которые сохраняются между длинами строк. 6
, 1985-1991, I, 15]. Дедукция для Декарта, по-видимому, включает интуицию необходимой связи между двумя отчетливо интуитивными идеями.Интуитивно понятные предметы называются «объектами» [ objectum ] [Adam and Tannery, 1964-76, X, 365; Cottingham et al., 1985-1991, I, 12], но также и «предложения» [ propositionis ] [Adam and Tannery, 1964-76, X, 379; Cottingham et al., 1985-1991, I, 20]. В «Дискурсе », также метод был сосредоточен на достижении знания, разбивая проблемы на их простейшие объекты, а затем, переходя от «простейших и наиболее легко узнаваемых объектов» к «постепенному восхождению, шаг за шагом, к знанию о них». самый сложный… »[Адам и Таннери, 1964-76, VII, 18; Cottingham et al., 1985-1991, I, 120].Примеры, которые он имеет в виду, кажутся простыми пропорциями, которые сохраняются между длинами строк. 6 В то время как Декарт был озабочен пониманием простых предложений и отношениями между ними, он также был озабочен прояснением простых идей и видением отношений между простыми идеями.
 Понимание отношений разной длины берется в качестве модели для ясного и отчетливого восприятия, которое затем используется для объяснения непосредственных выводов от одного предложения к другому.
Понимание отношений разной длины берется в качестве модели для ясного и отчетливого восприятия, которое затем используется для объяснения непосредственных выводов от одного предложения к другому.Взгляд Декарта на логику как инструмент для открытия истин и его критика старой логики также присутствует в Port-Royal Logic . В «Логике » присутствует критика формальной логики как бесполезной для открытия истин. Однако Арно и Николь обсуждали такие формальные темы, как преобразование суждений и обоснованность силлогизмов. Но даже при обсуждении этих тем они сразу заметили, что не считают эти вопросы важными.Ярким свидетельством их антиформализма является полное отсутствие переменных в экспозиции. Авторы приводят конкретные примеры различных силлогизмов, и ясно, что речь идет о вопросах формы, но они никогда не представляют силлогизмы или категориальные предложения с переменными.
Арно и Николь видели в логике «искусство мышления», которое они понимали вместе с Декартом как искусство отличать истину от лжи (15).
 Другие в то время классифицировали логику как искусство хорошо рассуждать 7 , но во втором дискурсе Арно и Николь специально отвергли эту характеристику как слишком узкую: «… цель логики — дать правила для всех действий разума, и для простых идей, а также для суждений и умозаключений… »(27).Рассматриваемые правила — это правила, помогающие отличить истинное от ложного (15). Правила для веских аргументов будут составлять часть этой дисциплины, но только небольшую часть. Арно и Николь также включили правила для определения истинности простых суждений или идей и, фактически, вслед за Декартом, считали этот вопрос более актуальным. Однако, в отличие от Декарта, Арно и Николь действительно считали, что правила для фигур силлогизмов имеют некоторую пользу (22), но что более формальные темы, такие как демонстрация действительности этих правил и правила преобразования, были менее полезны и были включены только как упражнения для ума.В первое издание было включено сокращение силлогизмов до силлогизмов первой фигуры, но они опустили это в более поздних изданиях, посчитав это бесполезным.
Другие в то время классифицировали логику как искусство хорошо рассуждать 7 , но во втором дискурсе Арно и Николь специально отвергли эту характеристику как слишком узкую: «… цель логики — дать правила для всех действий разума, и для простых идей, а также для суждений и умозаключений… »(27).Рассматриваемые правила — это правила, помогающие отличить истинное от ложного (15). Правила для веских аргументов будут составлять часть этой дисциплины, но только небольшую часть. Арно и Николь также включили правила для определения истинности простых суждений или идей и, фактически, вслед за Декартом, считали этот вопрос более актуальным. Однако, в отличие от Декарта, Арно и Николь действительно считали, что правила для фигур силлогизмов имеют некоторую пользу (22), но что более формальные темы, такие как демонстрация действительности этих правил и правила преобразования, были менее полезны и были включены только как упражнения для ума.В первое издание было включено сокращение силлогизмов до силлогизмов первой фигуры, но они опустили это в более поздних изданиях, посчитав это бесполезным.
Стандартные логические работы были организованы с разделами, посвященными терминам, предложениям и аргументам, и часто заключительным разделом по методам. Эту организацию можно прочесть в «Органоне» Аристотеля , с категориями , относящимися к терминам, De Interpretation , относящимся к предложениям, Prior Analytics , имеющим дело с аргументами, и Posterior Analytics и Topics с методом .Такой способ разделения темы был довольно распространен в средневековье. Авторы Port Royal следовали этому образцу, но их выбор названий предполагает, что их заботили именно операции разума, а не язык. Они организуют Logic следующим образом:
Часть I Содержит размышления об идеях или первое действие ума, которое называется зачатием.
Часть II Содержит размышления людей о своих суждениях.
Часть III О рассуждениях
Часть IV О методе.
Из этого содержания обвинение в психологизме кажется оправданным, так как оно, кажется, предполагает исследование работы ума, а не логики как таковой.
 Однако, хотя некоторые не относящиеся к делу психологические соображения проникли в обсуждение логики, в целом они сведены к минимуму. Верно, что вслед за Декартом, Арно и Николь считали, что наш разум устроен так, чтобы давать правильные концепции и суждения, когда мы правильно используем наши рассуждения, и поэтому они рассматривали логику или искусство мышления как искусство, помогающее совершенствоваться. наши естественные познавательные способности.Таким образом, заголовки разделов предполагают, что предметом исследования являются когнитивные способности, а не объекты этих способностей. Однако анализ, который дают Арно и Николь, касается оцениваемых концепций и суждений, а не действий разума, которые к ним ведут. По большей части соображения эмпирической психологии не мешают обсуждению логики. Однако, как это часто бывает с работами по неформальной логике даже сегодня, их обсуждение ошибок в формировании понятий и выводов действительно ссылается на психологические тенденции и даже на теологические проблемы.
Однако, хотя некоторые не относящиеся к делу психологические соображения проникли в обсуждение логики, в целом они сведены к минимуму. Верно, что вслед за Декартом, Арно и Николь считали, что наш разум устроен так, чтобы давать правильные концепции и суждения, когда мы правильно используем наши рассуждения, и поэтому они рассматривали логику или искусство мышления как искусство, помогающее совершенствоваться. наши естественные познавательные способности.Таким образом, заголовки разделов предполагают, что предметом исследования являются когнитивные способности, а не объекты этих способностей. Однако анализ, который дают Арно и Николь, касается оцениваемых концепций и суждений, а не действий разума, которые к ним ведут. По большей части соображения эмпирической психологии не мешают обсуждению логики. Однако, как это часто бывает с работами по неформальной логике даже сегодня, их обсуждение ошибок в формировании понятий и выводов действительно ссылается на психологические тенденции и даже на теологические проблемы. 8
8 Хотя вклад во все, что мы теперь признаем формальной логикой, невелик, Logic действительно содержит более сложную семантику, чем может показаться на первый взгляд, и использует эту семантику, особенно различие между пониманием и расширением, сделанное в первая книга, чтобы позже использовать их при анализе предложений и аргументов.
3.5 — Рациональные функции и асимптоты
3.5 — Рациональные функции и асимптотыРациональная функция — это функция, которая можно записать как отношение двух многочлены, где знаменатель не ноль.
f (x) = p (x) / q (x)
Домен
Область определения рациональной функции — это все действительные значения, кроме знаменателя q (x) = 0.
Корни
Корни, нули, решения, пересечения по оси x (как хотите их называть) рациональной функции. будут места, где p (x) = 0. То есть полностью игнорировать знаменатель. Что бы ни делало нулевой числитель будет корнями рациональной функции, точно так же, как они были корнями полиномиальная функция ранее.

Если вы можете записать его в факторизованной форме, то вы можете сказать, будет ли он пересекать или касаться оси x в каждое пересечение по x зависит от того, является ли кратность множителя нечетной или четной.
Вертикальные асимптоты
Асимптота — это линия, к которой кривая приближается, но не пересекает. Уравнения вертикали асимптоты можно найти, найдя корни q (x). Полностью игнорируйте числитель, когда при поиске вертикальных асимптот имеет значение только знаменатель.
Если вы можете записать его в факторизованной форме, то вы можете сказать, будет ли граф асимптотическим в в том же направлении или в разных направлениях в зависимости от того, четная или нечетная множественность.
Асимптотика в одном направлении означает, что кривая будет идти вверх или вниз как слева, так и правые части вертикальной асимптоты. Асимптотика в разные стороны означает, что одна сторона кривой будет идти вниз, а другая сторона кривой будет идти вверх на вертикальной асимптоте.

Горизонтальные асимптоты
Горизонтальная линия — это асимптота только в крайнем левом и крайнем правом углу график. «Дальний» левый или «крайнее правое» определяется как что-либо за вертикальными асимптотами или пересечениями по оси x.Горизонтальные асимптоты не асимптотичны в середине. Это нормально пересечь горизонтальная асимптота в середина.
Положение горизонтальной асимптоты определяется по степеням числитель (n) и знаменатель (m).
- Если n
- Если n = m, то y = a n / b m — горизонтальная асимптота. То есть соотношение ведущих коэффициенты.
- Если n> m, горизонтальная асимптота отсутствует.Однако, если n = m + 1, имеется наклонный или наклонный асимптота.
Отверстия
Иногда множитель появляется в числителе и знаменателе. Предположим, что коэффициент (x-k) находится в числителе и знаменателе. Поскольку множитель стоит в знаменателе, x = k не будет в домене функции.
 Это означает, что может произойти одно из двух. Там
будет либо вертикальная асимптота при x = k, либо будет дыра при x = k.
Это означает, что может произойти одно из двух. Там
будет либо вертикальная асимптота при x = k, либо будет дыра при x = k.Давайте посмотрим, что будет в каждом из этих случаев.
- В знаменателе больше (x-k) множителей. После разделения всех повторяющихся факторов (x-k) по-прежнему в знаменателе. Множители в знаменателе дают вертикальные асимптоты. Следовательно, будет вертикальная асимптота при x = k.
- В числителе больше (x-k) множителей. После разделения всех повторяющихся факторов (x-k) все еще стоит в числителе. Множители в числителе дают пересечение по оси x. Но потому что вы не можете использовать x = k, на графике по оси x будет дыра.
- В числителе и знаменателе одинаковое количество (x-k) множителей. После разделения
из всех факторов (потому что есть равные количества), не остается (x-k) вообще. Потому что там
нет (x-k) в знаменателе, нет вертикальной асимптоты при x = k. Потому что нет (х-к)
в числителе нет точки пересечения с x при x = k.
 На графике просто дыра, где-то
кроме оси абсцисс. Чтобы найти точное местоположение, подставьте x = k в сокращенную функцию
(вы не можете подключить его к оригиналу, он там undefined) и посмотрите, какое значение y вы получите.
На графике просто дыра, где-то
кроме оси абсцисс. Чтобы найти точное местоположение, подставьте x = k в сокращенную функцию
(вы не можете подключить его к оригиналу, он там undefined) и посмотрите, какое значение y вы получите.
Косые асимптоты
Когда степень числителя ровно на единицу больше степени знаменателя, график рациональной функции будет иметь наклонную асимптоту. Другое название косой асимптота — наклонная асимптота.
Чтобы найти уравнение наклонной асимптоты, выполните деление в столбик (синтетическое, если оно работает) на деление знаменателя на числитель. Поскольку x становится очень большим (это крайний левый или крайний правый о чем я говорил) остальная часть становится совсем маленькой, почти нулевой.Итак, чтобы найти уравнение наклонной асимптоты, выполнить деление в длину и отбросить остаток.
Графические рациональные функции, n = m — Концепция
При создании графиков рациональных функций необходимо учитывать различные характеристики.
 С графиками рациональных функций, где степень функции числителя равна степени функции знаменателя, мы можем найти горизонтальную асимптоту. Когда степень числителя меньше или больше степени знаменателя, существуют другие методы построения графиков рациональных функций .
С графиками рациональных функций, где степень функции числителя равна степени функции знаменателя, мы можем найти горизонтальную асимптоту. Когда степень числителя меньше или больше степени знаменателя, существуют другие методы построения графиков рациональных функций .Я хочу поговорить о графическом изображении рациональных функций, когда степень числителя такая же, как степень знаменателя. Давайте немного поговорим о том, какой будет горизонтальная асимптота в этом случае.
Если f для x равно n плюс da da da над bx к m плюс da da da, тогда и это наши главные члены для числителя и знаменателя, тогда числитель имеет степень n, а знаменатель — степень m, и поэтому, если эти степени одинаковы, тогда ваша рациональная функция f от x будет приближаться к a над b, к дроби a над b, которая является долей ведущих коэффициентов, когда x стремится к бесконечности и когда x стремится к отрицательной бесконечности, и это означает, что y равно a над b будет вашей горизонтальной асимптотой, тогда очень легко найти горизонтальную асимптоту. Теперь вы должны знать одну вещь, если степень числителя больше степени знаменателя, то не существует горизонтальной асимптоты. Давайте посмотрим на пример.
Теперь вы должны знать одну вещь, если степень числителя больше степени знаменателя, то не существует горизонтальной асимптоты. Давайте посмотрим на пример.
Он говорит: найдите горизонтальную асимптоту. Итак, все, что вам нужно сделать, это сначала спросить себя, одинаковы ли степени, и если они, то горизонтальная асимптота будет ведущим коэффициентом над ведущим коэффициентом, поэтому горизонтальная асимптота будет y = -4 над 1, -4, y = — 4 это наш ответ.
Теперь в этом случае степень числителя больше, чем степень знаменателя, поэтому нет горизонтальной асимптоты, я сокращу ее ha, и в этом случае степени равны 1, они одинаковы, поэтому мы смотрим на ведущие коэффициенты снова 3 и 1, поэтому y равно 3 по сравнению с 1 y = 3, это наша горизонтальная асимптота.
Итак, действительно легко найти горизонтальные асимптоты, когда степень числителя такая же, как степень знаменателя. Горизонтальные асимптоты всегда легко найти. Если степень числителя меньше степени знаменателя, всегда y = 0. К случаю, когда степень числителя больше, мы подойдем позже.
К случаю, когда степень числителя больше, мы подойдем позже. Графические рациональные функции, n менее m — Концепция
При построении графиков рациональных функций следует учитывать различные характеристики.Когда строит график рациональных функций , где степень функции числителя меньше степени функции знаменателя, мы знаем, что y = 0 является горизонтальной асимптотой. Когда степень числителя равна или больше степени знаменателя, существуют другие методы построения графиков рациональных функций.
Мне нужны графические рациональные функции, и мы собираемся начать с рациональных функций, в которых степень числителя меньше степени знаменателя, поэтому давайте немного поговорим о горизонтальных асимптотах.
Если рациональная функция f от x равна p от x над q от x, p и q будут полиномиальными функциями. Предположим, что числитель имеет степень n, а знаменатель имеет степень f, теперь, если степень числителя меньше степени знаменателя, тогда функция f от x стремится к 0, когда x стремится к бесконечности, и она также переходит к 0, когда x стремится к отрицательной бесконечности, и это означает, что y = 0 — горизонтальная асимптота. Теперь очень важно знать, что если степень числителя не меньше степени знаменателя, если она больше или равна степени знаменателя, то y = 0 не является горизонтальной асимптотой, поэтому давайте возьмем посмотрите на некоторые рациональные функции.
Предположим, что числитель имеет степень n, а знаменатель имеет степень f, теперь, если степень числителя меньше степени знаменателя, тогда функция f от x стремится к 0, когда x стремится к бесконечности, и она также переходит к 0, когда x стремится к отрицательной бесконечности, и это означает, что y = 0 — горизонтальная асимптота. Теперь очень важно знать, что если степень числителя не меньше степени знаменателя, если она больше или равна степени знаменателя, то y = 0 не является горизонтальной асимптотой, поэтому давайте возьмем посмотрите на некоторые рациональные функции.
Теперь это f из x 1 + 3x над 1-x, степени числителя и знаменателя равны, степени одинаковы, и поэтому y = 0 здесь не горизонтальная асимптота.
А как насчет g от x, градус вверху равен 2, градус внизу будет равен 3, верно? Степень знаменателя больше, чем числитель, поэтому здесь y = 0, так что да, но нет.
И, наконец, здесь степень числителя больше, чем степень знаменателя, поэтому нет, y = o не является горизонтальной асимптотой, поэтому снова y = 0 является горизонтальной асимптотой, когда степень числителя меньше, чем эта степень знаменателя, и это единственный пример рациональной функции, которая обладает этим свойством.
Математических изображений | Рациональные функции (2): знаменатель степени 2
Рациональные функции (2): Знаменатель степени 2
Ваш браузер не поддерживает видео тег.После изучения линейных рациональных функций мы собираемся рассмотреть рациональные функции, которые имеют знаменатель, который является многочленом степени 2 (парабола).
В простейшем случае числитель является константой, а знаменатель — многочленом степени 2.
Такой вид рациональных функций может иметь две вертикальные асимптоты:
Только одна вертикальная асимптота:
Или вообще никакой вертикальной асимптоты. Это зависит от корней знаменателя (и в некоторой степени зависит от корней числителя).
Корни знаменателя — это значения, для которых функция не определена. На ноль делить нельзя. Эти значения называются особенностями функции. Интересно изучить поведение функции вблизи особенности.
 В некоторых случаях, в зависимости от поведения вблизи особенности,
рациональная функция имеет вертикальную асимптоту, как мы уже видели в некоторых примерах.
В некоторых случаях, в зависимости от поведения вблизи особенности,
рациональная функция имеет вертикальную асимптоту, как мы уже видели в некоторых примерах.В общем, если x 0 и x 1 являются двумя корнями знаменателя
Тогда область определения рациональной функции:
Если мы рассмотрим крайний случай, когда числитель равен 0, рациональной функцией будет горизонтальная линия y = 0, но с двумя отверстиями, одним отверстием или без отверстий.
У таких функций всегда есть одна горизонтальная асимптота (y = 0)
Теперь рассмотрим рациональные функции, в числителе которых есть многочлен степени 1 (негоризонтальная прямая):
В следующей математике вы можете поиграть с двумя элементами такого рода рациональной функции: прямой линией (числитель выделен синим цветом) и параболой. (знаменатель оранжевым)
Ваш браузер не поддерживает видео тег.Как и раньше, эта рациональная функция может иметь 2, 1 или 0 особенностей.
 Интересно изучить поведение вблизи особенностей в зависимости от положения точки, в которой прямая линия пересекает ось x:
Интересно изучить поведение вблизи особенностей в зависимости от положения точки, в которой прямая линия пересекает ось x:Когда функция имеет две особенности и числитель отсекает ось абсцисс в одной из этих точек, то в этой особенности мы не имеем асимптота, но «дыра». Мы называем эту особенность сингулярностью, которой можно избежать.
Например, на предыдущем графике формула выглядит так:
Обратите внимание, что числитель и знаменатель имеют (x-1) как общий множитель.
Другой другой случай — это когда функция имеет особенность, но степени 2 (парабола касается только оси x, многочлен степени 2 от де знаменатель имеет двойной корень) и числитель имеет тот же корень, то у нас есть асимптота.
Например, на предыдущем графике формула выглядит так:
Вы можете видеть, что в некоторых случаях график функции срезает горизонтальную асимптоту y = 0:
Вы можете добавить постоянную функцию p к правильной рациональной функции со знаменателем степени 2:
В следующем видео мы можем увидеть три элемента такого рода рациональной функции: число p (зеленая горизонтальная линия), числитель (прямая линия, синий цвет) и знаменатель (парабола, оранжевый цвет)
Ваш браузер не поддерживает видео тег.
Этот вид рациональных функций имеет горизонтальную асимптоту:
Когда мы говорим, что рациональная функция с многочленом степени 2 в знаменателе может иметь две, одну или ни одной особенности, мы имеем в виду реальные особенности. Когда мы рассматриваем эти функции как сложные, тогда эти функции всегда имеют две (действительные или) комплексные особенности. (Это следствие фундаментальной теоремы алгебры, доказанной Гауссом).
РЕКОМЕНДАЦИИ
ГРАММ.Шилов, Исчисление рациональных функций, Издательство Мир, Москва.
Гельфанд И. Глаголева, Е.Е.Шнол, Функции и графики, Dover Publications, Inc., Минеола, Нью-Йорк.
СЛЕДУЮЩИЙ
Для больших абсолютных значений x некоторые рациональные функции ведут себя как наклонная прямая линия, мы называем эту линию наклонной или наклонной асимптотой.
ПРЕДЫДУЩИЙ
Рациональные функции можно записать как отношение двух многочленов.Линейные рациональные функции — самые простые из таких функций.

БОЛЬШЕ ССЫЛКИ
Вы можете добавить многочлен к правильной рациональной функции. Конечное поведение этой рациональной функции очень похоже на многочлен.
Две точки определяют прямую линию. Как функцию мы называем это линейной функцией. Мы можем видеть наклон линии и то, как мы можем получить уравнение прямой через две точки. Мы также изучаем точки пересечения по оси x и оси y линейного уравнения.
Многочлены степени 2 — это квадратичные функции. Их графики — параболы. Чтобы найти точки пересечения по оси x, мы должны решить квадратное уравнение. Вершина параболы — это максимум минимума функции.
Степень с натуральными показателями — простые и важные функции. Их обратные функции — это степени с рациональными показателями (радикал или корень n-й степени)
Многочлены степени 3 — это кубические функции. Реальная кубическая функция всегда пересекает ось x хотя бы один раз.
Мы можем рассматривать полиномиальную функцию, проходящую через серию точек плоскости.
 Это проблема интерполяции, которая здесь решается с помощью интерполяционного полинома Лагранжа.
Это проблема интерполяции, которая здесь решается с помощью интерполяционного полинома Лагранжа.Функция имеет особенность в -1. Многочлены Тейлора относительно начала координат приближают функцию от -1 до 1.
Функция имеет особенность в -1. Многочлены Тейлора относительно начала координат приближают функцию от -1 до 1.
Эта функция имеет две действительные особенности в точках -1 и 1.Многочлены Тейлора аппроксимируют функцию в интервале с центром в центре ряда. Его радиус — это расстояние до ближайшей особенности.
Это непрерывная функция, не имеющая реальных особенностей. Однако ряд Тейлора приближает функцию только в интервале. Чтобы понять это поведение, мы должны рассмотреть сложную функцию.
Мы увидим, как многочлены Тейлора аппроксимируют функцию внутри круга сходимости.
Комплексные степенные функции с натуральным показателем имеют в начале координат нуль (или корень) кратности n.
Многочлен степени 2 имеет два нуля или корня.
 На этом изображении вы видите овалы Кассини и лемнискату.
На этом изображении вы видите овалы Кассини и лемнискату.Комплексный полином степени 3 имеет три корня или ноль.
Каждый комплексный многочлен степени n имеет n нулей или корней.
Производная линейной функции — постоянная функция.
Производная квадратичной функции — это линейная функция, то есть прямая линия.
Производная кубической функции — это квадратичная функция, парабола.
Интегральное понятие ассоциируется с понятием площади. Мы начали рассматривать область, ограниченную графиком функции и осью абсцисс между двумя вертикальными линиями.
.

 Докажите, что такое число 6 всегда присутствует и только 1 больше. Однако последнее объяснение единственности числа€сразу же вытекает из того факта, что разным положительным числам соответствуют разные их степени. Для 05$’, это bn b’N. если существует положительное рациональное число r, n-я степень которого равна a, то это искомое число 6.Поэтому в дальнейшем достаточно ограничиться предположением, что такого рационального числа не существует. Теперь мы построим сечение X \ X в области всех рациональных чисел следующим образом.
Докажите, что такое число 6 всегда присутствует и только 1 больше. Однако последнее объяснение единственности числа€сразу же вытекает из того факта, что разным положительным числам соответствуют разные их степени. Для 05$’, это bn b’N. если существует положительное рациональное число r, n-я степень которого равна a, то это искомое число 6.Поэтому в дальнейшем достаточно ограничиться предположением, что такого рационального числа не существует. Теперь мы построим сечение X \ X в области всех рациональных чисел следующим образом. хм. Очевидно, что x принадлежит классу X, а x ’принадлежит классу X, и по определению этих классов х, Нуа, стр. Однако разница x’ x может быть меньше любого числа;> 0(n * 4, примечания), и ничто не мешает вам видеть x меньше, чем предварительно фиксированное число x’0.In в этом случае разница н-х-хп =(**)(х-Эн〜1 + х * х н〜х + … + ху-1)е * в NX? То есть он может быть сколь угодно малым*).по Лемме 2 это означает, что число и a равны. и проверяется, что обычные правила, оцененные в ходе элементарной алгебры, справедливы для таких степеней. АР * О!»АР + Р>, АГ: аг= на *、 (аг = ’ РЛ (арг =’ р-р ’、 П Он также подчеркивает, что в случае a> 1 порядок ar увеличивается по мере увеличения рационального показателя r.
хм. Очевидно, что x принадлежит классу X, а x ’принадлежит классу X, и по определению этих классов х, Нуа, стр. Однако разница x’ x может быть меньше любого числа;> 0(n * 4, примечания), и ничто не мешает вам видеть x меньше, чем предварительно фиксированное число x’0.In в этом случае разница н-х-хп =(**)(х-Эн〜1 + х * х н〜х + … + ху-1)е * в NX? То есть он может быть сколь угодно малым*).по Лемме 2 это означает, что число и a равны. и проверяется, что обычные правила, оцененные в ходе элементарной алгебры, справедливы для таких степеней. АР * О!»АР + Р>, АГ: аг= на *、 (аг = ’ РЛ (арг =’ р-р ’、 П Он также подчеркивает, что в случае a> 1 порядок ar увеличивается по мере увеличения рационального показателя r.

 Они возникают только в сингулярностях, где соответствующий линейный множитель в знаменателе остается после отмены.
Они возникают только в сингулярностях, где соответствующий линейный множитель в знаменателе остается после отмены. 2 — x — 1} [/ латекс]
2 — x — 1} [/ латекс] 2 — 10} [/ latex]: [latex] x [/ latex] -перехватов существуют в [latex] x = — \ sqrt {2}, 0, \ sqrt {2} [/ latex].
2 — 10} [/ latex]: [latex] x [/ latex] -перехватов существуют в [latex] x = — \ sqrt {2}, 0, \ sqrt {2} [/ latex]. 0 [/ latex].Важно отметить, что поскольку все показатели положительные, невозможно разделить на [латекс] х [/ латекс].
0 [/ latex].Важно отметить, что поскольку все показатели положительные, невозможно разделить на [латекс] х [/ латекс]. 2 + x — 2} [/ латекс]
2 + x — 2} [/ латекс] 3 -7x -6} = \ frac {1} {x + 2} + \ frac {3} {x-3} + \ гидроразрыв {4} {x + 1} [/ латекс]
3 -7x -6} = \ frac {1} {x + 2} + \ frac {3} {x-3} + \ гидроразрыв {4} {x + 1} [/ латекс] Предположим, [latex] R (x) [/ latex] имеет знаменатель, который учитывается в других выражениях, например, [latex] g (x) = P (x) \ cdot Q (x) [/ latex], и что нет повторяющиеся корни.
Предположим, [latex] R (x) [/ latex] имеет знаменатель, который учитывается в других выражениях, например, [latex] g (x) = P (x) \ cdot Q (x) [/ latex], и что нет повторяющиеся корни. 2 (x + 3)} [/ latex], для которого [latex] x = 1 [/ latex] является повторяющимся корнем), необходимо предпринять дополнительные шаги для декомпозиции функции.
2 (x + 3)} [/ latex], для которого [latex] x = 1 [/ latex] является повторяющимся корнем), необходимо предпринять дополнительные шаги для декомпозиции функции. Рукопись Правил была предоставлена Арно и Николь, и они даже включили часть этой работы в свою собственную. 4 Декарт сосредоточился на прояснении простых идей и разработке метода, который приведет к новым истинам. Его точка зрения заключалась в том, что у ума не было проблем с выводами, 5 , но что у него действительно были проблемы с четким и отчетливым различением того, что было до него. Его метод был разработан, чтобы помочь уму решать проблемы и более ясно различать истины. Декарт распознал две операции интеллекта, которые помогают ему достичь этой цели, — интуицию и дедукцию. Интуиция, по его словам, была не «колеблющимся свидетельством чувства или обманчивым суждением воображения … но концепцией ясного и внимательного ума, которая настолько легка и отчетлива, что не может быть места для сомнений в том, кто мы такие. понимание »[Адам и Таннери, 1964-76, X, 368; Cottingham et al., 1985-1991, I, 14].Он был менее ясен в том, что он имел в виду под дедукцией, но предположил, что дедукция необходима, поскольку «очень многие факты, которые не являются самоочевидными, известны с уверенностью, при условии, что они выводятся из истинных и известных принципов посредством непрерывного и непрерывного движения мысль, в которой каждое отдельное предложение ясно интуитивно интуитивно »[Адам и Таннери, 1964-76, X, 369; Cottingham et al.
Рукопись Правил была предоставлена Арно и Николь, и они даже включили часть этой работы в свою собственную. 4 Декарт сосредоточился на прояснении простых идей и разработке метода, который приведет к новым истинам. Его точка зрения заключалась в том, что у ума не было проблем с выводами, 5 , но что у него действительно были проблемы с четким и отчетливым различением того, что было до него. Его метод был разработан, чтобы помочь уму решать проблемы и более ясно различать истины. Декарт распознал две операции интеллекта, которые помогают ему достичь этой цели, — интуицию и дедукцию. Интуиция, по его словам, была не «колеблющимся свидетельством чувства или обманчивым суждением воображения … но концепцией ясного и внимательного ума, которая настолько легка и отчетлива, что не может быть места для сомнений в том, кто мы такие. понимание »[Адам и Таннери, 1964-76, X, 368; Cottingham et al., 1985-1991, I, 14].Он был менее ясен в том, что он имел в виду под дедукцией, но предположил, что дедукция необходима, поскольку «очень многие факты, которые не являются самоочевидными, известны с уверенностью, при условии, что они выводятся из истинных и известных принципов посредством непрерывного и непрерывного движения мысль, в которой каждое отдельное предложение ясно интуитивно интуитивно »[Адам и Таннери, 1964-76, X, 369; Cottingham et al. , 1985-1991, I, 15]. Дедукция для Декарта, по-видимому, включает интуицию необходимой связи между двумя отчетливо интуитивными идеями.Интуитивно понятные предметы называются «объектами» [ objectum ] [Adam and Tannery, 1964-76, X, 365; Cottingham et al., 1985-1991, I, 12], но также и «предложения» [ propositionis ] [Adam and Tannery, 1964-76, X, 379; Cottingham et al., 1985-1991, I, 20]. В «Дискурсе », также метод был сосредоточен на достижении знания, разбивая проблемы на их простейшие объекты, а затем, переходя от «простейших и наиболее легко узнаваемых объектов» к «постепенному восхождению, шаг за шагом, к знанию о них». самый сложный… »[Адам и Таннери, 1964-76, VII, 18; Cottingham et al., 1985-1991, I, 120].Примеры, которые он имеет в виду, кажутся простыми пропорциями, которые сохраняются между длинами строк. 6
, 1985-1991, I, 15]. Дедукция для Декарта, по-видимому, включает интуицию необходимой связи между двумя отчетливо интуитивными идеями.Интуитивно понятные предметы называются «объектами» [ objectum ] [Adam and Tannery, 1964-76, X, 365; Cottingham et al., 1985-1991, I, 12], но также и «предложения» [ propositionis ] [Adam and Tannery, 1964-76, X, 379; Cottingham et al., 1985-1991, I, 20]. В «Дискурсе », также метод был сосредоточен на достижении знания, разбивая проблемы на их простейшие объекты, а затем, переходя от «простейших и наиболее легко узнаваемых объектов» к «постепенному восхождению, шаг за шагом, к знанию о них». самый сложный… »[Адам и Таннери, 1964-76, VII, 18; Cottingham et al., 1985-1991, I, 120].Примеры, которые он имеет в виду, кажутся простыми пропорциями, которые сохраняются между длинами строк. 6 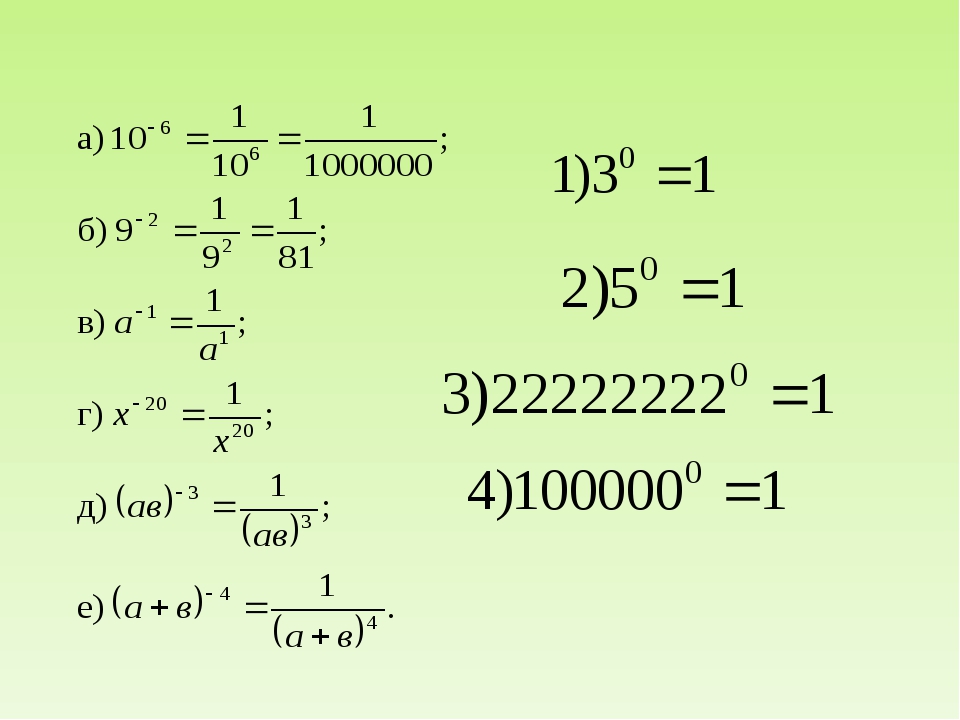 Понимание отношений разной длины берется в качестве модели для ясного и отчетливого восприятия, которое затем используется для объяснения непосредственных выводов от одного предложения к другому.
Понимание отношений разной длины берется в качестве модели для ясного и отчетливого восприятия, которое затем используется для объяснения непосредственных выводов от одного предложения к другому. Другие в то время классифицировали логику как искусство хорошо рассуждать 7 , но во втором дискурсе Арно и Николь специально отвергли эту характеристику как слишком узкую: «… цель логики — дать правила для всех действий разума, и для простых идей, а также для суждений и умозаключений… »(27).Рассматриваемые правила — это правила, помогающие отличить истинное от ложного (15). Правила для веских аргументов будут составлять часть этой дисциплины, но только небольшую часть. Арно и Николь также включили правила для определения истинности простых суждений или идей и, фактически, вслед за Декартом, считали этот вопрос более актуальным. Однако, в отличие от Декарта, Арно и Николь действительно считали, что правила для фигур силлогизмов имеют некоторую пользу (22), но что более формальные темы, такие как демонстрация действительности этих правил и правила преобразования, были менее полезны и были включены только как упражнения для ума.В первое издание было включено сокращение силлогизмов до силлогизмов первой фигуры, но они опустили это в более поздних изданиях, посчитав это бесполезным.
Другие в то время классифицировали логику как искусство хорошо рассуждать 7 , но во втором дискурсе Арно и Николь специально отвергли эту характеристику как слишком узкую: «… цель логики — дать правила для всех действий разума, и для простых идей, а также для суждений и умозаключений… »(27).Рассматриваемые правила — это правила, помогающие отличить истинное от ложного (15). Правила для веских аргументов будут составлять часть этой дисциплины, но только небольшую часть. Арно и Николь также включили правила для определения истинности простых суждений или идей и, фактически, вслед за Декартом, считали этот вопрос более актуальным. Однако, в отличие от Декарта, Арно и Николь действительно считали, что правила для фигур силлогизмов имеют некоторую пользу (22), но что более формальные темы, такие как демонстрация действительности этих правил и правила преобразования, были менее полезны и были включены только как упражнения для ума.В первое издание было включено сокращение силлогизмов до силлогизмов первой фигуры, но они опустили это в более поздних изданиях, посчитав это бесполезным.
 Однако, хотя некоторые не относящиеся к делу психологические соображения проникли в обсуждение логики, в целом они сведены к минимуму. Верно, что вслед за Декартом, Арно и Николь считали, что наш разум устроен так, чтобы давать правильные концепции и суждения, когда мы правильно используем наши рассуждения, и поэтому они рассматривали логику или искусство мышления как искусство, помогающее совершенствоваться. наши естественные познавательные способности.Таким образом, заголовки разделов предполагают, что предметом исследования являются когнитивные способности, а не объекты этих способностей. Однако анализ, который дают Арно и Николь, касается оцениваемых концепций и суждений, а не действий разума, которые к ним ведут. По большей части соображения эмпирической психологии не мешают обсуждению логики. Однако, как это часто бывает с работами по неформальной логике даже сегодня, их обсуждение ошибок в формировании понятий и выводов действительно ссылается на психологические тенденции и даже на теологические проблемы.
Однако, хотя некоторые не относящиеся к делу психологические соображения проникли в обсуждение логики, в целом они сведены к минимуму. Верно, что вслед за Декартом, Арно и Николь считали, что наш разум устроен так, чтобы давать правильные концепции и суждения, когда мы правильно используем наши рассуждения, и поэтому они рассматривали логику или искусство мышления как искусство, помогающее совершенствоваться. наши естественные познавательные способности.Таким образом, заголовки разделов предполагают, что предметом исследования являются когнитивные способности, а не объекты этих способностей. Однако анализ, который дают Арно и Николь, касается оцениваемых концепций и суждений, а не действий разума, которые к ним ведут. По большей части соображения эмпирической психологии не мешают обсуждению логики. Однако, как это часто бывает с работами по неформальной логике даже сегодня, их обсуждение ошибок в формировании понятий и выводов действительно ссылается на психологические тенденции и даже на теологические проблемы. 8
8 

 Это означает, что может произойти одно из двух. Там
будет либо вертикальная асимптота при x = k, либо будет дыра при x = k.
Это означает, что может произойти одно из двух. Там
будет либо вертикальная асимптота при x = k, либо будет дыра при x = k. На графике просто дыра, где-то
кроме оси абсцисс. Чтобы найти точное местоположение, подставьте x = k в сокращенную функцию
(вы не можете подключить его к оригиналу, он там undefined) и посмотрите, какое значение y вы получите.
На графике просто дыра, где-то
кроме оси абсцисс. Чтобы найти точное местоположение, подставьте x = k в сокращенную функцию
(вы не можете подключить его к оригиналу, он там undefined) и посмотрите, какое значение y вы получите. С графиками рациональных функций, где степень функции числителя равна степени функции знаменателя, мы можем найти горизонтальную асимптоту. Когда степень числителя меньше или больше степени знаменателя, существуют другие методы построения графиков рациональных функций .
С графиками рациональных функций, где степень функции числителя равна степени функции знаменателя, мы можем найти горизонтальную асимптоту. Когда степень числителя меньше или больше степени знаменателя, существуют другие методы построения графиков рациональных функций .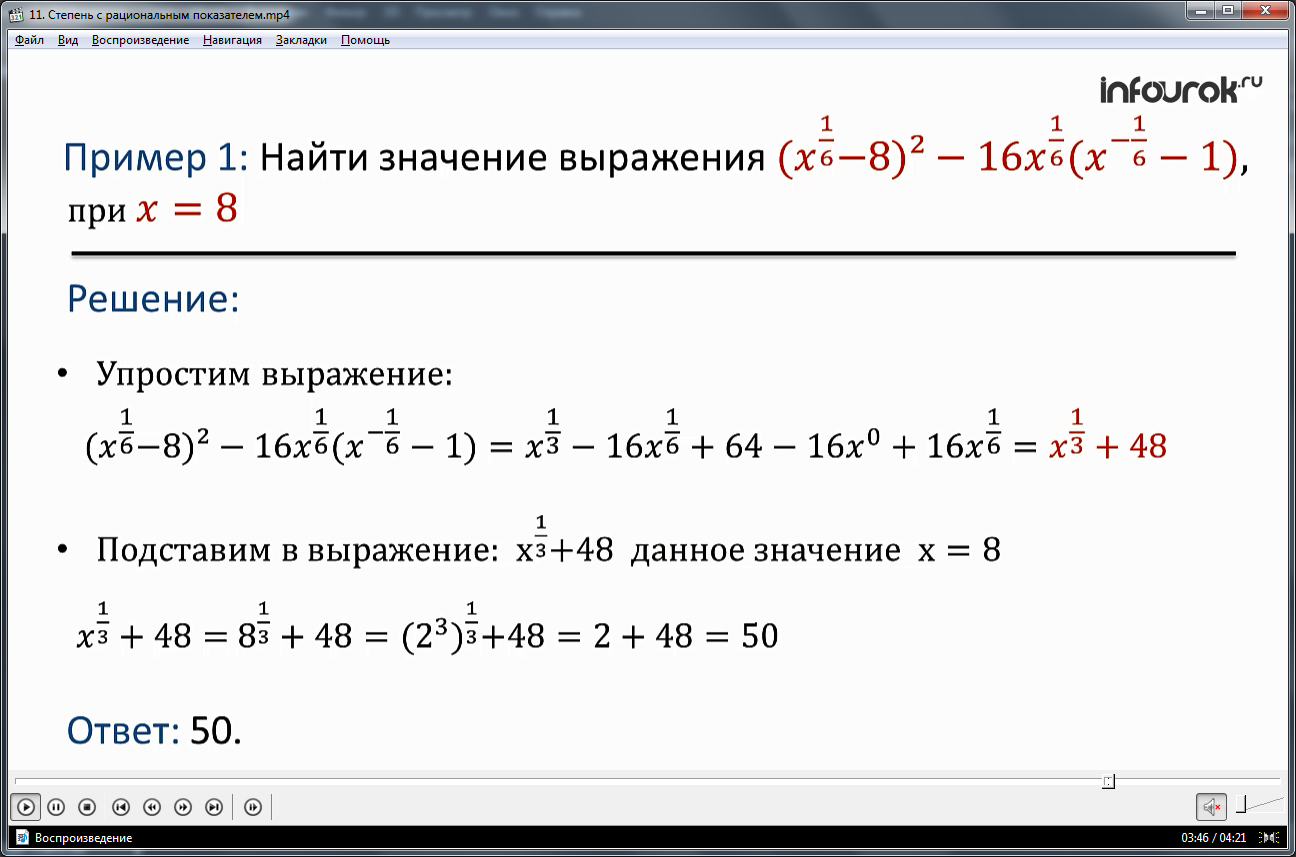 Теперь вы должны знать одну вещь, если степень числителя больше степени знаменателя, то не существует горизонтальной асимптоты. Давайте посмотрим на пример.
Теперь вы должны знать одну вещь, если степень числителя больше степени знаменателя, то не существует горизонтальной асимптоты. Давайте посмотрим на пример.  К случаю, когда степень числителя больше, мы подойдем позже.
К случаю, когда степень числителя больше, мы подойдем позже.  Предположим, что числитель имеет степень n, а знаменатель имеет степень f, теперь, если степень числителя меньше степени знаменателя, тогда функция f от x стремится к 0, когда x стремится к бесконечности, и она также переходит к 0, когда x стремится к отрицательной бесконечности, и это означает, что y = 0 — горизонтальная асимптота. Теперь очень важно знать, что если степень числителя не меньше степени знаменателя, если она больше или равна степени знаменателя, то y = 0 не является горизонтальной асимптотой, поэтому давайте возьмем посмотрите на некоторые рациональные функции.
Предположим, что числитель имеет степень n, а знаменатель имеет степень f, теперь, если степень числителя меньше степени знаменателя, тогда функция f от x стремится к 0, когда x стремится к бесконечности, и она также переходит к 0, когда x стремится к отрицательной бесконечности, и это означает, что y = 0 — горизонтальная асимптота. Теперь очень важно знать, что если степень числителя не меньше степени знаменателя, если она больше или равна степени знаменателя, то y = 0 не является горизонтальной асимптотой, поэтому давайте возьмем посмотрите на некоторые рациональные функции.
 В некоторых случаях, в зависимости от поведения вблизи особенности,
рациональная функция имеет вертикальную асимптоту, как мы уже видели в некоторых примерах.
В некоторых случаях, в зависимости от поведения вблизи особенности,
рациональная функция имеет вертикальную асимптоту, как мы уже видели в некоторых примерах. Интересно изучить поведение вблизи особенностей в зависимости от положения точки, в которой прямая линия пересекает ось x:
Интересно изучить поведение вблизи особенностей в зависимости от положения точки, в которой прямая линия пересекает ось x:

 Это проблема интерполяции, которая здесь решается с помощью интерполяционного полинома Лагранжа.
Это проблема интерполяции, которая здесь решается с помощью интерполяционного полинома Лагранжа. На этом изображении вы видите овалы Кассини и лемнискату.
На этом изображении вы видите овалы Кассини и лемнискату.