Вложенные радикалы — Википедия

Материал из Википедии — свободной энциклопедии

В алгебре вложенным радикалом называется радикал, содержащийся в другом радикале. Например

5−25 ,{\displaystyle {\sqrt {5-2{\sqrt {5}}\ }},}

или более сложный пример

2+3+43 3.{\displaystyle {\sqrt[{3}]{2+{\sqrt {3}}+{\sqrt[{3}]{4}}\ }}.}

Некоторые вложенные радикалы могут быть упрощены. Например:

3+22=1+2,{\displaystyle {\sqrt {3+2{\sqrt {2}}}}=1+{\sqrt {2}}\,,}

23−13=1−23+4393.{\displaystyle {\sqrt[{3}]{{\sqrt[{3}]{2}}-1}}={\frac {1-{\sqrt[{3}]{2}}+{\sqrt[{3}]{4}}}{\sqrt[{3}]{9}}}\,.}

В общем случае упрощение является сложной проблемой, если оно вообще возможно. Следующая формула позволяет произвести упрощение в случае, когда R=a2−b2c{\displaystyle R={\sqrt {a^{2}-b^{2}c}}} рационально:

a±bc=a+R2±a−R2.{\displaystyle {\sqrt {a\pm b{\sqrt {c}}}}={\sqrt {\frac {a+R}{2}}}\pm {\sqrt {\frac {a-R}{2}}}.}

Например,

a±a2−b2=a+b2±a−b2(a≥b).{\displaystyle {\sqrt {a\pm {\sqrt {a^{2}-b^{2}}}}}={\sqrt {\frac {a+b}{2}}}\pm {\sqrt {\frac {a-b}{2}}}\quad (a\geq b).}

В частности, для комплексных чисел (c=−1{\displaystyle c=-1}):

a+bi=±(|z|+a2+isgn⁡(b)|z|−a2),{\displaystyle {\sqrt {a+bi}}=\pm \left({\sqrt {\frac {\left|z\right|+a}{2}}}+i\operatorname {sgn}(b){\sqrt {\frac {\left|z\right|-a}{2}}}\right),} где |z|=a2+b2.{\displaystyle \left|z\right|={\sqrt {a^{2}+b^{2}}}.}

Общие положения[править | править код]

В некоторых случаях бесконечно вложенные радикалы могут быть тождественны некоторому рациональному числу, например выражение

x=2+2+2+2+⋯{\displaystyle x={\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2+\cdots }}}}}}}}}

равно 2. Для того чтобы это увидеть, возведем обе части выражения в квадрат и отнимем 2:

x2−2=2+2+2+⋯=x{\displaystyle x^{2}-2={\sqrt {2+{\sqrt {2+{\sqrt {2+\cdots }}}}}}=x};

x2−x−2=0{\displaystyle x^{2}-x-2=0};

x1=2,x2=−1{\displaystyle x_{1}=2,x_{2}=-1}.

Очевидно, что −1{\displaystyle -1} не может являться значением исходного радикала. В общем случае:

a+a+a+a+⋯=1+1+4a2{\displaystyle {\sqrt {a+{\sqrt {a+{\sqrt {a+{\sqrt {a+\cdots }}}}}}}}={\frac {1+{\sqrt {1+4a}}}{2}}}

Тривиальные случаи[править | править код]

Нетривиальные случаи[править | править код]

• Формула Рамануджана:

  x+n+a=ax+(n+a)2+xa(x+n)+(n+a)2+(x+n)a(x+2n)+(n+a)2+(x+2n)⋯{\displaystyle x+n+a={\sqrt {ax+(n+a)^{2}+x{\sqrt {a(x+n)+(n+a)^{2}+(x+n){\sqrt {a(x+2n)+(n+a)^{2}+(x+2n){\sqrt {\cdots }}}}}}}}}

Частные случаи[править | править код]

• Золотое сечение:

  ϕ=1+1+1+⋯{\displaystyle \phi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {\cdots }}}}}}}}}

• Пластическое число:

  ρ=1+1+1+⋯3333{\displaystyle \rho ={\sqrt[{3}]{1+{\sqrt[{3}]{1+{\sqrt[{3}]{1+{\sqrt[{3}]{\cdots }}}}}}}}}

• Число Пи:

  2π=1212+121212+1212+1212⋯{\displaystyle {\frac {2}{\pi }}={\sqrt {\frac {1}{2}}}{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}}}\cdots }

Преобразование выражений, содержащих радикалы. Алгебра, 11 класс: уроки, тесты, задания.

1.	Произведение разности и суммы (одночлен и корень) Сложность: лёгкое	2
2.	Вынесение множителя из-под знака корня (буквы) Сложность: лёгкое	2
3.	Сравнение корней Сложность: лёгкое	4
4.	Внести множитель под корень (числа) Сложность: лёгкое	2
5.	Внести множитель под корень (обыкновенная дробь) Сложность: лёгкое	4
6.	Внести множитель под корень (произведение) Сложность: лёгкое	4
7.	Вынесение множителя из-под знака корня (числа) Сложность: среднее	2
8.	Вынесение множителя из-под знака корня (произведение) Сложность: среднее	3
9.	Разность корней Сложность: среднее	4
10.	Вычисление значения выражения с корнем и модулем Сложность: среднее	1
11.	Квадрат бинома Сложность: среднее	4
12.	Формула сокращённого умножения Сложность: среднее	3
13.	Сокращение дроби (буквы) Сложность: среднее	5
14.	Сокращение дроби (разность квадратов) Сложность: среднее	5
15.	Вынесение множителя из-под знака корня (дробь) Сложность: среднее	5
16.	Корень из корня Сложность: среднее	3
17.	Корень из произведения Сложность: среднее	4
18.	Алгебраическая сумма корней (метод группировки) Сложность: среднее	3
19.	Значение выражения, содержащего радикалы (корни пятой степени) Сложность: среднее	3
20.	Упрощение выражения, содержащего радикалы, сумма алгебраических дробей Сложность: среднее	4
21.	Значение выражения, содержащего радикалы Сложность: среднее	1
22.	Сокращение дроби, содержащей радикалы Сложность: сложное	5
23.	Сокращение дроби, содержащей радикалы (корни различной степени) Сложность: сложное	5

Уединение радикала (корня), определение, примеры

Иррациональные уравнения, решение иррациональных уравнений

Эта статья про уединение радикала или, как его еще называют, уединение корня. Здесь мы разъясним, что понимают под уединением радикала, что понимают под уединением произведения и дроби с радикалом, приведем примеры и укажем основную сферу применения.

Определение

Словосочетания «уединение радикала» и «уединение корня» фигурируют в школьных учебниках по алгебре, например, [1, c. 194-195; 2, с. 240]. Но там сильно не разъясняется, что понимается под уединением радикала. Однако, приведенной в учебниках информации достаточно для формирования представления о предмете нашего разговора. Для себя можно принять следующее:

Определение

Уединение радикала — это такое преобразование уравнения, при котором в одной части уравнения оставляют один единственный корень с переменной под ним (уединяют его) и ничего кроме него, а все остальное собирают в другой части уравнения.

Обычно уединения радикала добиваются последовательным выполнением некоторых основных преобразований уравнения, например, переносом слагаемых из одной части уравнения в другую.

К началу страницы

Примеры

Приведем пару примеров уединения радикала (корня).

Если из левой части уравнения перенести все слагаемые, кроме корня, в правую часть, естественно, изменив их знаки на противоположные, то мы получим уравнение с уединенным радикалом: .

Рассмотрим еще одно уравнение . В его записи три корня, каждый из которых можно уединить. Уединим первый радикал. Для этого оставляем его в левой части, а два других корня переносим в правую часть с противоположными знаками: . Аналогично можно было уединить второй радикал, вместо первого: для этого нужно было оставить в левой части только нужный нам радикал вместе с его знаком , а дальше избавиться от минуса перед ним, выполнив умножение обеих частей уравнения на минус единицу, что дало бы уравнение . А можно было провести уединение третьего радикала. Для этого нужно было оставить слева третий корень и отправить два оставшихся корня в правую часть: .

К началу страницы

Уединение произведения или дроби с радикалом

На практике бывает полезно уединять не корень, а произведение, одним или несколькими множителями которого являются корни, или дробь, в числителе и/или знаменателе которой присутствуют корни. То есть, можно говорить не только об уединении радикала, но и об уединении произведения радикалов, в том числе и с числовым коэффициентом, про уединение дроби с корнем в числителе и/или знаменателе и т.п.

Обычно уединение перечисленных математических объектов достигается переносом слагаемых в другую часть уравнения. Приведем несколько примеров.

Вот пример уединения произведения корней с числовым коэффициентом: от уравнения переходим к уравнению . А в уравнении можно уединить дробь с корнем и перейти к уравнению .

К началу страницы

Где применяется уединение радикала

Осталось разобраться с главным: понять, для чего нужно уединение радикала, уединение произведений и дробей с радикалами. В основном уединение радикала используется при решении иррациональных уравнений. Оно позволяет подготовить уравнение к дальнейшему возведению его обеих частей в одну и ту же натуральную степень, что в дальнейшем позволяет избавиться от знаков корней и тем самым перейти к решению сравнительно простого уравнения. В этом и состоит суть уединения радикала.

Для иллюстрации возьмем иррациональное уравнение . Если не уединять радикал, а сразу возвести обе его части в квадрат, то это не приведет к избавлению от корня: , . А если сначала провести уединение радикала, осуществив перенос минус единицы в правую часть с противоположным знаком, а уже потом возводить обе части в квадрат, то это позволит избавиться от корня: , , x=1.

Некогда разбираться?

Закажите решение

Литература

1. Алгебра и начала математического анализа. 10 класс : учеб. для общеобразоват. учреждений : базовый и профил. уровни / [Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин]; под ред. А. Б. Жижченко. — 3-е изд. — М.: Просвещение, 2010.- 368 с.: ил.-ISBN 978-5-09-022771-1.
2. Мордкович А. Г. Алгебра и начала математического анализа. 11 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А. Г. Мордкович, П. В. Семенов. — 2-е изд., стер. — М.: Мнемозина, 2008. — 287 с.: ил. ISBN 978-5-346-01027-2.

К началу страницы

Уравнение, не решаемое в радикалах

Среди великих ученых прошлого выделяется человек, не доживший и до двадцати одного года, но успевший за столь короткую жизнь сделать великое открытие в области алгебры. Все его научные труды занимают всего 60 страниц, содержание которых не давало покоя математикам всего мира в течение целого столетия. Это выдающийся французский математик Эварист Галуа.

В предрассветные часы 30 мая 1832 года, перед дуэлью, на которой оборвется его жизнь, Галуа написал своему другу Огюсту Шевалье: «Я открыл в анализе кое-что новое. Некоторые из этих открытий касаются теории уравнений, другие — функций, определяемых интегралами.

В теории уравнений я исследовал, в каких случаях уравнения разрешаются в радикалах, что дало мне повод углубить эту теорию и описать все возможные преобразования уравнения, допустимые даже тогда, когда оно не решается в радикалах.

Из этого можно сделать три мемуара…

Обратись публично к Якоби и Гауссу и попроси их высказать свое мнение, но не о верности теорем, а об их значении.

Я надеюсь, что после этого найдутся люди, которые сочтут для себя полезным навести порядок во всей этой неразберихе».

 

Открытие математики

Эварист Галуа родился 25 октября 1811 года в городе Бур-ла-Рен близ Парижа. Его отец Никола Габриэль Галуа был сторонником Наполеона; он был избран мэром Бур-ла-Рена в 1815 году, во время наполеоновских «Ста дней».

Официально обучение Галуа началось в 1823 году, когда он поступил в Королевский лицей Людовика Великого — парижскую приготовительную школу, в которой в свое время учились Робеспьер и Виктор Гюго (эта школа существует и по сей день). В лицее сформировались политические взгляды Галуа. Антироялистские симпатии, переданные ему родителями, совпадали с политическими взглядами большинства лицеистов.

В первый год пребывания Галуа в лицее отношения между лицеистами и новым директором школы были весьма натянутыми. Лицеисты подозревали его в намерении отдать школу иезуитам, которые символизировали реакцию, пришедшую на смену наполеоновской эпохе. Ученики доступными им средствами выражали свой протест: отказывались петь в церкви, отвечать в классе, провозглашать тост за здоровье Людовика XVIII на школьных банкетах. Директор исключил сразу сорок учеников как зачинщиков. Галуа не исключили (и неизвестно, принимал ли он участие во всем этом), но произвол директора, несомненно, усилил недоверие Галуа к властям.

Французский математик и астроном Жозеф Луи Лагранж

Wikipedia

В первые годы обучения Галуа завоевал несколько наград по греческому и латыни и получил полдюжины хвалебных отзывов. Правда, на третьем курсе лицея он недостаточно хорошо занимался по классу риторики и был оставлен на второй год. Галуа было тогда пятнадцать лет. Занятия в его классе вел Ипполит Жан Вернье, который пробудил в Галуа интерес к математике. Без труда освоив учебную программу, он сразу взялся за работы выдающихся ученых того времени, увлеченнно изучил книгу геометра Лежандра и труды Лагранжа «Решение алгебраических уравнений», «Теория аналитических функций» и «Лекции по дифференциальному исчислению». По-видимому, Вернье по достоинству оценил талант своего ученика: в отзыве на отчет Галуа за триместр он пишет о «старании и успехе», «старании и очень заметном прогрессе».

Открыв для себя мир математики, Галуа сильно переменился. Он стал небрежно относиться к занятиям по другим предметам, чем вызвал недовольство учителей по гуманитарным наукам. Преподаватели риторики называют его рассеянным, в отчете за триместр и в отзывах появляются слова «замкнутый», «странный», «своеобразный». Даже Вернье, который не стремился охладить страсть Галуа к математике, советовал ему заниматься более систематически. Галуа не последовал совету: он решил держать вступительный экзамен в Политехнический институт на год раньше и без обычного подготовительного курса по математике. И провалился, так как недостаточно глубоко знал ее основы.

 

У истоков теории групп

Галуа считал, что с ним обошлись несправедливо, провал еще более настроил его против властей. Тем не менее он продолжал делать успехи в математике и записался в лицее в математический класс более высокого уровня, который вел очень опытный преподаватель Луи Поль Эмиль Ришар. Ришар сразу понял, сколь одарен Галуа, и обратился с просьбой принять в Политехнический институт без экзаменов. Просьба эта последствий не возымела, но одобрение Ришара оказало на юношу чудесное влияние. В марте 1829 года, когда Галуа был еще студентом, вышла его первая статья. Она называлась «Доказательство одной теоремы о периодических непрерывных дробях» и появилась в журнале Annales de mathématiques pures et appliquées, который издавал Жозеф Диаз Жергон.

Однако тема статьи была в стороне от главных научных интересов Галуа. В то время он уже обратился к теории алгебраических уравнений, которую начал изучать по трудам Лагранжа. В возрасте семнадцати лет Галуа взялся за одну из самых трудных в математике проблем, которая сто с лишним лет заводила ученых в тупик.

В 1829 году центральной проблемой теории уравнений был вопрос, каким должен быть метод решения уравнения с одним неизвестным x, все коэффициенты которого являются рациональными числами, причем член наивысшей степени равен xⁿ. Метод должен быть общим, применяться ко всем подобным уравнениям и включать в себя лишь четыре элементарные операции (сложение, вычитание, умножение и деление) и операцию извлечения корня. Если решения (корни) уравнения можно получить из коэффициентов уравнения только при помощи этих операций, то говорят, что уравнение разрешимо в радикалах.

Накопленный опыт как будто подсказывал, что решение уравнения n-й степени не потребует более сложных операций, чем извлечение корня n-й степени. Решение квадратного уравнения общего вида или уравнения второй степени ax² + bx + c = 0, известное еще вавилонянам, требует извлечения квадратного корня из некоторой комбинации коэффициентов, а именно из выражения b² − 4ac. Таким образом, общее квадратное уравнение разрешимо в радикалах. Точно так же общее решение кубического уравнения, которое нашли в начале XVI века итальянские математики Сципион дель Ферро и Никколо Фонтана (Тарталья), сводится к извлечению кубического корня из некоторой комбинации коэффициентов. Решение уравнения четвертой степени общего вида, впервые полученное итальянским математиком Лудовико Феррари примерно в то же время, требует извлечения корней четвертой степени.

До Галуа почти триста лет никому не удавалось решить в радикалах общее уравнение пятой степени или выше. Многие математики склонялись к мысли, что общее решение такого вида невозможно, хотя в частных случаях, например в случае уравнения x⁷ − 2 = 0, решение можно найти в радикалах. (В этом примере одно из решений — ⁷√2.) Галуа нашел окончательные критерии, которые позволили определить, существует ли решение данного уравнения в радикалах. Его исследования привели к теории, ныне называемой теорией групп, приложения которой выходят далеко за рамки теории уравнений.

Свою первую статью в той области, которая в дальнейшем превратится в теорию групп, Галуа представил во Французскую академию наук 25 мая 1829 года, незадолго до окончания лицея. Менее чем через два месяца ему снова предстояло держать вступительный экзамен в Политехнический институт, однако события приняли несчастливый оборот. Второго июля, за несколько недель до экзамена, отец Эвариста покончил жизнь самоубийством, не вынеся скандала вокруг своего имени. (Приходский священник-иезуит Бур-ла-Рена оклеветал старшего Галуа, распространив среди родственников и знакомых Галуа злые эпиграммы на него.) Обстановка для экзамена сложилась крайне неблагоприятная. Кроме того, на экзамене Эварист, по-видимому, отказался следовать предложенной экзаменатором схеме ответа; в результате Галуа провалился опять, на этот раз окончательно.

 

Отвергнутый академией

Вынужденный теперь подумать о менее престижной Эколь Нормаль, Галуа в ноябре 1829 года выдержал необходимый для поступления экзамен. На этот раз его приняли благодаря очень высокому баллу по математике, и примерно в то же время, когда его статья по теории групп была представлена в Академию наук, он стал студентом. Однако статья Галуа не была зачитана на заседании академии.

Дело в том, что рецензентом назначили Огюстена Луи Коши — самого известного в ту пору французского математика, который был верным сторонником консервативной реставрации. Коши уже занимался комбинаторикой, предшественницей теории групп; позднее он написал много работ, посвященных этой теории. Распространена версия, что Коши потерял, забыл или выбросил рукопись Галуа; но больше похоже на правду, что Коши, понимая ее значение, обращался с ней бережно. Действительно, из письма, обнаруженного Татоном в 1971 году в архивах академии, явствует, что 18 января 1830 года Коши намеревался выступить на заседании академии с изложением результатов Галуа.

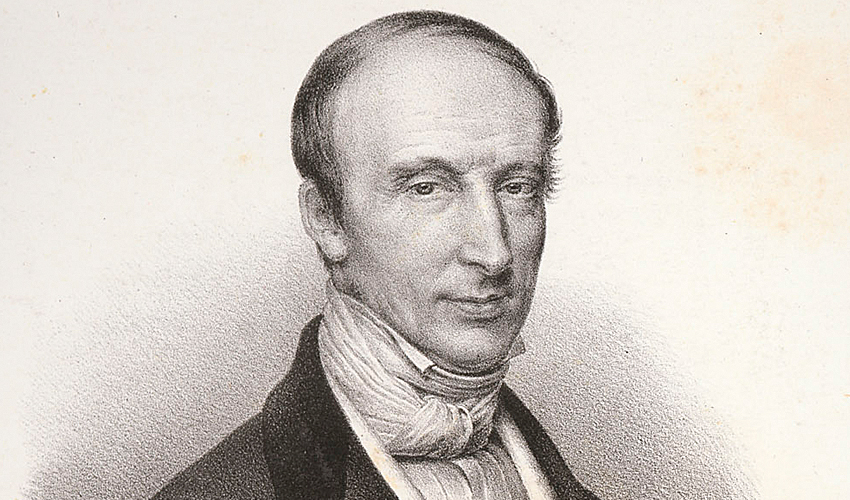
Французский математик Огюстен Луи Коши

dic.academic.ru

Однако на следующей неделе, когда Коши выступал перед академией со своим собственным докладом, он не представил работу Галуа. Почему так получилось — остается предметом догадок. По мнению историка Татона, Коши настаивал на том, чтобы Галуа расширил свою статью и представил ее на соискание высшей награды академии по математике. Хотя предположение Татона не подтверждается документами, Галуа действительно представил свою работу на конкурс в феврале, за месяц до истечения срока конкурса. Статья была послана постоянному секретарю академии Жану-Батисту Фурье, математику, разработавшему метод анализа, который ныне называют анализом Фурье. Однако в мае Фурье умер, и рукопись Галуа среди его бумаг не нашли. Впоследствии Галуа приписывал свое невезение козням со стороны Академии, обвиняя конкурсную комиссию в произволе: его работу отклонили только потому, что его фамилия Галуа и он всего лишь студент.

Несмотря на неудачи, Галуа продолжал плодотворно работать и начал публиковать свои труды в Bulletin des sciences mathématiques, astronomiques, physiques et chimiques, издававшемся бароном Феруссаком, — менее видном издании, чем публикации Академии наук. Из его статей ясно, что в 1830 году он ушел далеко вперед в исследовании условий, определяющих разрешимость уравнений, хотя еще и не получил полного решения этой проблемы. В январе 1831 года он завершил работу и, следуя настоятельным советам математика Симеона Дени Пуассона, представил ее в Академию наук. Эта статья — самая значительная работа Галуа, и тот факт, что она вышла в свет более чем за год до дуэли, лишает смысла историю о том, что все свои работы по теории групп Галуа написал за одну ночь.

Чтобы понять работу Галуа, бесполезно изучать его оригинальные статьи. Пуассон, несомненно, старался разобраться в рукописи 1831 года, но в конце концов рекомендовал Академии наук отклонить ее, посоветовав Галуа расширить статью и сделать изложение более ясным. Пуассон также отверг одно из доказательств Галуа, посчитав его неверным. Действительно, как считают историки науки, аргументация Галуа была очень кратка и сжата, что чрезвычайно затрудняет ее понимание; кроме того, встречаются и неточности. Это было не случайно. Галуа сознательно пренебрегал разъяснениями. Он писал: «Вместо алгебраических формул они [его критики] используют длинные рассуждения — и к громоздкости математических преобразований добавляют громоздкость словесного описания этих преобразований, пользуясь языком, не приспособленным для выполнения таких задач. Эти математики отстали на сто лет».

Теория групп, у истоков которой стоял Галуа, ныне является одной из самых плодотворных областей математики. Ученый и изобретатель Александр Белл писал, что она на сотни лет дала математикам пищу для исследований. А известный математик Иэн Стюарт отметил, что «никто не мог бы предположить, что вопросы о разрешимости уравнений приведут к одной из ключевых концепций в математике — концепции группы или что группы окажутся языком, на котором описывается симметрия. Еще менее того можно было полагать, что симметрии откроют нам дверь к тайнам физического мира».

 

Математика и революция

Когда Галуа заканчивал работу над теорией групп, в его жизнь ворвались политические события. В июле 1830 года республиканцы — противники восстановленной монархии вышли на улицы. Карл X был вынужден эмигрировать. В то время как революционно настроенные студенты Политехнического института активно участвовали в этих событиях, Галуа и его товарищей по Эколь Нормаль заперли внутри школы по приказу директора. Возмущенный Галуа пытался сбежать, но ему это не удалось, так что он остался в стороне от событий июльской революции.

Отречение Карла X казалось большой победой республиканцев, однако на троне оказался Луи-Филипп, к великому разочарованию Галуа и других республиканцев. В последовавшие за революцией месяцы Галуа посещал собрания республиканцев, встречался с их лидерами (особенно с Франсуа Венсаном Распаем) и, по-видимому, принимал участие в волнениях и демонстрациях, лихорадивших Париж. Он вступил в артиллерию Национальной гвардии — подразделение милиции, состоявшее почти исключительно из республиканцев. В декабре Галуа написал в одну из парижских газет письмо, в котором называл директора Эколь Нормаль предателем, имея в виду его поведение во время июльской революции; неудивительно, что после этого Галуа исключили.

Жан-Виктор Шнец «Сражение за ратушу. Париж. 28 июля 1830 года»

Wikipedia

В противоположность традиционной легенде, Галуа вовсе не производит впечатления жертвы обстоятельств. Напротив, он, похоже, был сорвиголовой и постоянно попадал в переделки. Из письма математика Софи Жермен следует, что Галуа регулярно присутствовал на заседаниях Академии наук и обычно всячески нападал на выступающих. Когда Галуа исключили из Эколь Нормаль, он переехал в парижский дом своей матери, но ей оказалось трудно с ним ужиться, и она уехала.

Для Галуа кульминация бурной весны 1831 года наступила 9 мая во время банкета республиканцев, которые праздновали оправдание девятнадцати артиллерийских офицеров, обвиненных в заговоре против правительства. В своих мемуарах Александр Дюма-отец, который присутствовал на этом банкете, пишет, что Галуа встал и предложил тост за Луи-Филиппа, при этом одновременно с бокалом он поднял кинжал. На следующий день Галуа арестовали, и он провел больше месяца в тюрьме св. Пелагеи.

На суде защитник Галуа утверждал, что тост на самом деле звучал так: «За Луи-Филиппа, если он предаст», однако конец фразы потонул в шуме. Либо судьи поверили защите, либо их тронула молодость Галуа, но они его оправдали. Тем не менее в день взятия Бастилии, 14 июля 1831 года — не прошло и месяца после суда, — Галуа снова арестовали, на этот раз за незаконное ношение формы артиллерийской гвардии. Гвардия была распущена как угроза короне, поэтому поступок Галуа был вызывающим. На этот раз он провел в тюрьме св. Пелагеи восемь месяцев.

Сохранившиеся рукописи Галуа свидетельствуют, что и попав в тюрьму, он продолжал вести математические изыскания и не оставлял их вплоть до самой смерти. То, что он мог продуктивно работать в таких условиях, говорит о необыкновенной силе его воображения и интеллекта

 

«Подлая кокетка»

Но тюремное заключение не прошло даром: он впадал то в ярость, то в уныние. Его приятель Распай, который находился в тюрьме в это же время, позже вспоминал, что однажды Галуа в состоянии опьянения пытался покончить с собой. Согласно Распаю, Галуа говорил, что его преследует видение собственной кончины: «Я умру на дуэли по вине какой-нибудь кокетки низкого пошиба. Почему? Потому что она заставит меня защищать ее честь, которую оскорбит другой». Когда погиб один из заключенных, Галуа, по-видимому, обвинил тюремного надзирателя в том, что тот подстроил убийство. За это Галуа посадили в карцер.

Самой большой неприятностью было то, что статьи, написанные Галуа в течение 1831 года, не напечатали. В исполненном горечи предисловии к тюремным запискам он утверждал: «Мне некого благодарить ни за совет, ни за поддержку. Благодарность была бы ложью».

В середине марта 1832 года из-за свирепствовавшей тогда в Париже эпидемии холеры Галуа перевели из тюрьмы св. Пелагеи в частную лечебницу Фолтрие. По-видимому, именно здесь он и встретил ту самую «подлую кокетку». Роман был коротким, однако нелепо утверждать, что героиня его была продажной женщиной или платным агентом и намеренно подстроила убийство. Согласно свидетельству Распая, фразу о кокетке низкого пошиба Галуа произнес за год до дуэли; вполне возможно, что это слова самого Распая. Кроме того, 25 мая, за шесть дней до смерти, в письме к Огюсту Шевалье Галуа намекает, что его роман оборвался: «Но как изгладить следы той бури страстей, через которую я прошел? Как утешиться, когда за один месяц исчерпан до дна источник самого сладостного блаженства, отпущенного человеку, когда он выпит без радости и без надежды, когда знаешь, что он иссяк навсегда?» Кто же была эта женщина? Имя женщины, которую Галуа обвиняет в своих бедах в письме, написанном в ночь накануне дуэли, часто появляется на полях статей Галуа. На факсимиле под именем Эварист можно прочесть имя Стефания; Галуа также объединил буквы «С» и «Э» в монограмме. Из писем и других рукописей ясно, что злой эпитет «подлая кокетка» вышел из-под пера Галуа в связи с разочарованием в любви к женщине, которую он встретил всего за несколько месяцев до дуэли. Ее личность установлена: это Стефания Фелисия Потерэн дю Мотель, дочь парижского врача.

Брат Галуа Альфред утверждал, что Эвариста убили преднамеренно, но маловероятно, чтобы убийцу подкупили антиреспубликанцы. Согласно Дюма, противником Галуа был Пеше д’Эрбенвиль, пылкий республиканец. В самом деле, д’Эрбенвиль — один из тех девятнадцати офицеров, чье оправдание послужило поводом для вызывающего тоста Галуа. Кроме того, когда во время революции 1848 года разоблачали агентов короля, имя д’Эрбенвиля не упоминалось. Историки считают, что дуэль происходила между друзьями и представляла собой что-то вроде «русской рулетки», когда заряжают только один пистолет.

Дуэль Эвариста Галуа и Пеше д’Эрбенвиля

bbvaopenmind.com

В предрассветные часы 30 мая 1832 года Эварист Галуа писал своим друзьям Лебону и Делонэ: «Меня вызвали на дуэль два патриота… Я не мог отказаться. Простите, что я не дал знать никому из вас. Противники взяли с меня честное слово, что я не предупрежу никого из патриотов. Ваша задача очень проста: вам надо подтвердить, что я дрался против воли, то есть после того, как были исчерпаны все средства мирно уладить дело, и что я не способен лгать даже в таком пустяке, как тот, о котором шла речь. Не забывайте меня! Ведь судьба не дала мне прожить столько, чтобы мое имя узнала родина.

Умираю вашим другом. Э. Галуа».

В десять часов утра 31 мая 1832 года Галуа скончался от смертельного ранения.

Математические работы Галуа, по крайней мере те, что сохранились,

составляют всего шестьдесят страниц. Как заметил кто-то из математиков, никогда еще труды столь малого объема не приносили автору такой широкой известности.

Исполняя желание Эвариста Галуа, его младший брат Альфред и Огюст Шевалье разослали копии рукописи Карлу Гауссу, Карлу Якоби и другим известным математикам. Но прошло почти десять лет, прежде чем его работа была оценена по достоинству. Это произошло в 1846 году, когда одна из копий была вручена выдающемуся французскому математику Жозефу Лиувиллю. Ученый уделил много времени работе Галуа, отредактировал его мемуары и опубликовал в своем престижном издании — «Журнале чистой и прикладной математики» (Journal de Mathèmatiques pures et appliquées).

откуда берутся, вред, как нейтрализовать

Каждую секунду в нашем теле происходят тысячи химических реакций: передаются нервные импульсы, рождаются новые клетки, отмирают старые. Поэтому организм, как огромная электростанция, потребляет гигантское количество энергии. При её высвобождении образуются такие «страшные и ужасные» свободные радикалы.

Что такое свободные радикалы

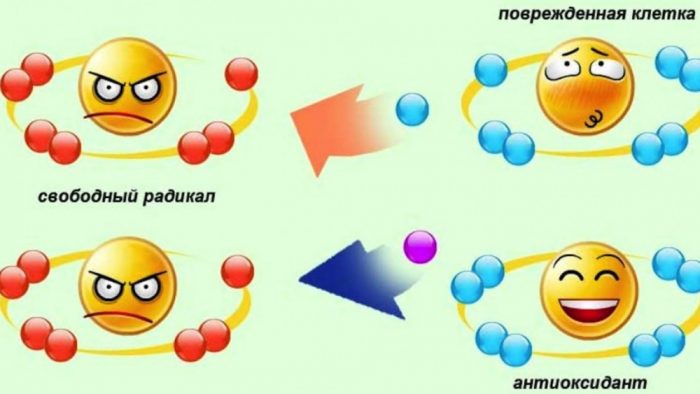
Что же происходит внутри нас? Наши клетки состоят из множества молекул. Когда эти клетки стабильны, они воспроизводятся, сохраняя организм молодым и свободным от болезней. Стабильность молекулы определяется наличием спаренных электронов.

Однако, существуют клетки с одиночными, неспаренными электронами. Это и есть свободные радикалы.

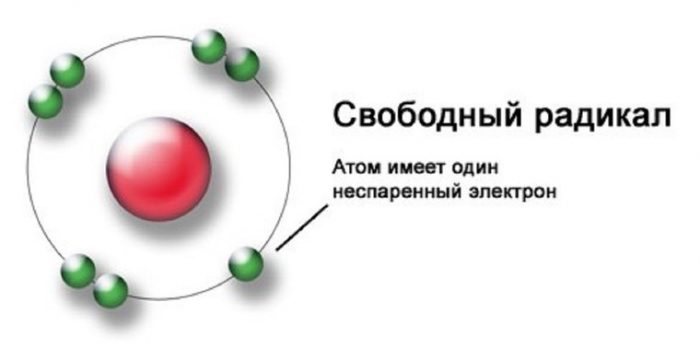
Они крайне нестабильны и очень активны. Поскольку им не хватает электрона, они нападают на другие молекулы, вырывая из их атомов электрон для себя. Уже вторая клетка становится свободным радикалом. Повреждённая клетка ищет на освободившееся место новый электрон, отбирая его из соседнего атома. Так запускается цепная реакция.

Свободные радикалы — это простыми словами рейдеры, которые захватывают в личное владение чужую собственность. Причём здесь жертва становится нападающим, и так выстраиваются огромные «рейдерские сети».

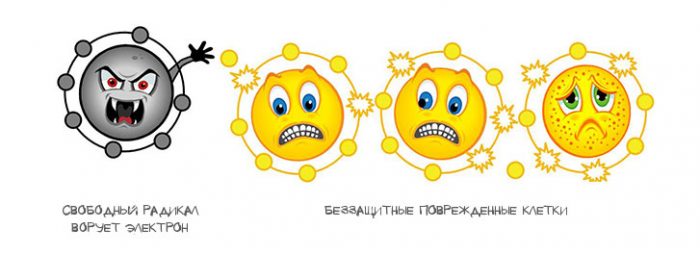
Чем это плохо? Тем, что свободный радикал способен повредить любой элемент нашей клеточной структуры. В первую очередь страдает оболочка клетки, с повреждённой оболочкой клетка становится нежизнеспособной. Это как пробить броню на танке – следующий удар станет смертельным.

Свободный радикал может повредить святая святых наших клеток: ДНК. А в ДНК, как на жёстком диске компьютера, записана вся информация о всех органах и клетках в нашем теле, о том, как функционирует наш организм и как он должен строится.

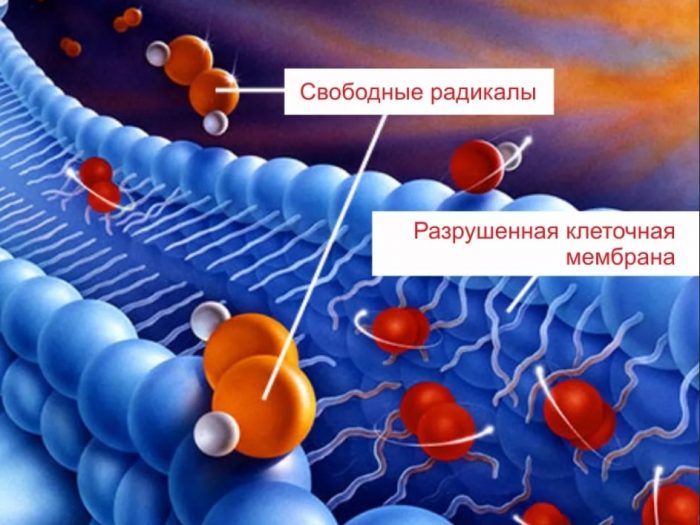
После такой атаки информация с ДНК считывается либо плохо, либо с ошибкой. Со временем, каждый раз, когда такая клетка делится, ошибки наслаиваются друг на друга.

Факт: клетка не прекращает делиться на протяжении всей жизни человека, и происходит это миллиарды раз. Существует теория, что в течение семи лет все наши клетки полностью обновляются. То есть каждые семь лет наше тело как бы заново рождается.

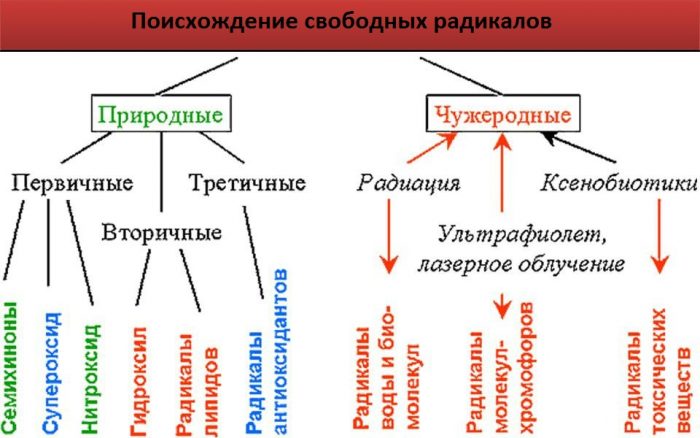
Свободные радикалы: откуда же они берутся

Зарождается свободный радикал во время естественных процессов, происходящих в организме. Клетка дышит, питается, делится, используя незаменимый химический элемент – кислород. Именно он даёт нам могучую энергию, окисляя разнообразнейшие органические соединения, которые мы получаем с пищей. Но, параллельно, он окисляет молекулы до суперактивной формы, делая их нестабильными.

То есть, наш организм в процессе своей жизнедеятельности постоянно производит свободные радикалы.

Но мы каждый день читаем в соцсетях, слышим от знакомых и узнаём из телепередач о детях и достаточно молодых людях с серьёзными заболеваниями. Их первопричина – это огромное количество свободнорадикальных агрессоров, с которыми растущий организм не в силах справиться. Когда же они успели «нажить» их в свои то годы?

Ответ очевиден: свободные радикалы поступают в организм извне.

Учёные, исследующие пути попадания оксидантов в тело человека, выделяют несколько основных:

• радиационное излучение. В эту группу входит не только обычное рентгеновское облучение во время обследований.  Доказано опасное радиационное воздействие строительных материалов, особенно асбеста и шлакоблоков. Также источниками излучения являются микроволновки, смартфоны, телевизоры, телефонные вышки;
• ультрафиолетовые лучи, если они в избытке;
• курение, как активное, так и пассивное;
• выхлопные газы и дым от химических и строительных заводов;
• неправильное питание, — когда мы едим слишком много жареного, жирного, копчёностей, сладостей;
• пищевая химия – это различные пищевые красители, усилители вкуса и запаха, консерванты: знаменитые Ешки на упаковках;
• бытовая химия: стиральные порошки и гели, некачественные средства гигиены;
• неконтролируемый приём антибиотиков, снотворных, антидепрессантов, гормональных и других лекарственных препаратов.

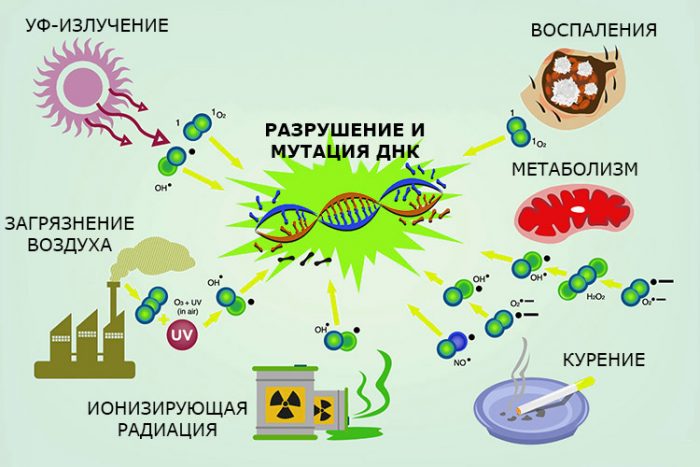
Что касается образования свободных радикалов самим нашим организмом, то к резкому скачку их роста приводят различные бактериальные и вирусные инфекции, а также стрессы.

Воздействие свободных радикалов на организм человека

Свободные радикалы – естественные обитатели нашего тела. Они живут внутри нас, осуществляя свои функции и выполняя конкретные задачи. Они не плохие и не хорошие. Не стоит демонизировать их, потому что всё есть лекарство и всё есть яд – вопрос в дозировке.

Вред от свободных радикалов

Старение клетки, накопление в ней ошибок как раз и запускает глобальный процесс старения организма. Кожа становится менее упругой, кости более хрупкими, уставшие органы не хотят работать в прежнем темпе, качество крови ухудшается, сосуды теряют эластичность, снижается память и, как следствие, появляются болезни.

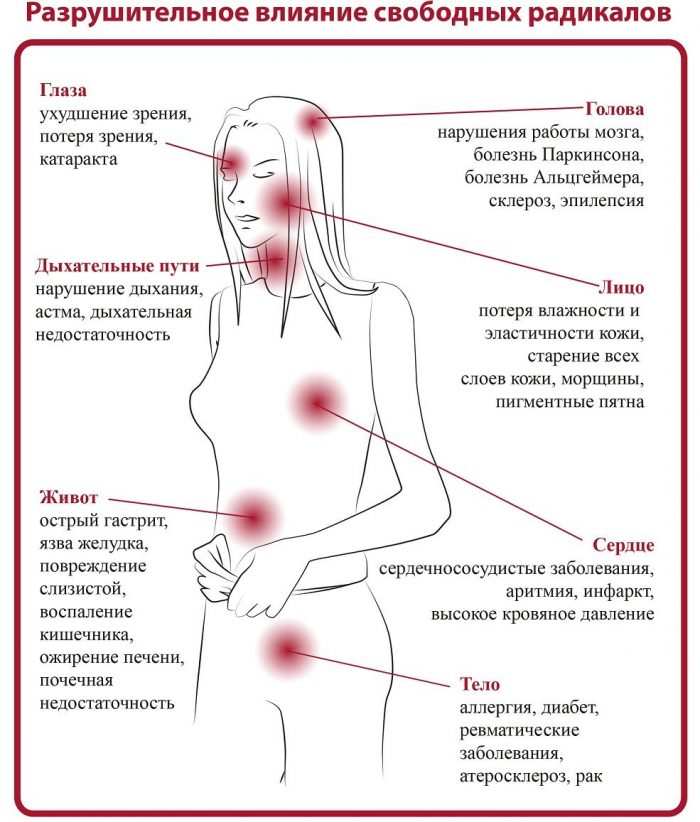
Разрушение и смерть повреждённых клеток происходит не одномоментно – на это требуется время. Этот процесс принято называть окислительным или оксидативным стрессом организма.

Результаты таких длительных активных действий свободных радикалов на здоровые клетки плачевны. Они напрямую влияют на возникновение и развитие массы заболеваний:

• патологии ЦНС: деменция, болезни Альцгеймера и Паркинсона, различные нейродегенеративные нарушения;
• инсульты, инфаркты, атеросклероз, тромбофлебит и другие сердечно-сосудистые аномалии;
• эндокринные: проблемы щитовидной железы, сахарный диабет, панкреатит, разнообразные гормональные нарушения;
• аутоиммунные болезни: ревматоидный артрит, эндометриоз, рассеянный склероз;
• генетические: синдром Дауна, аутизм;
• возрастные изменения: седеют и выпадают волосы, ухудшается зрение и обоняние, кожа становится сухой и появляются морщины…

На самом деле, этот список будет размером с томик «Мёртвых душ».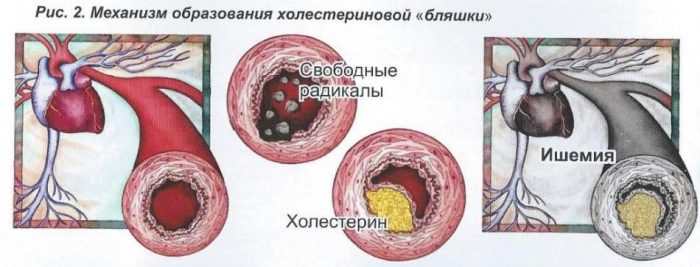

Когда оксидант приносит пользу

Но, не всё так однозначно. Свободные радикалы на самом деле могут быть нам полезными. Они играют положительную роль в работе иммунной системы. Как это возможно? Судите сами.

В организм попала инфекция, вирус или вы травмировались. Что происходит: иммунная система моментально начинает действовать и первым даёт неспецифический ответ. А именно, заставляет свои клетки-защитники макрофаги и нейтрофилы преобразоваться в безумное количество тех самых свободных радикалов, которые устремляются к очагу поражения. Они уничтожают большую часть враждебных клеток, а оставшиеся локализуют на небольшом участке.

Факт: Неспецифический (врождённый) иммунитет первый этап борьбы с инфекцией: разрушает её и локализует очаг воспаления.

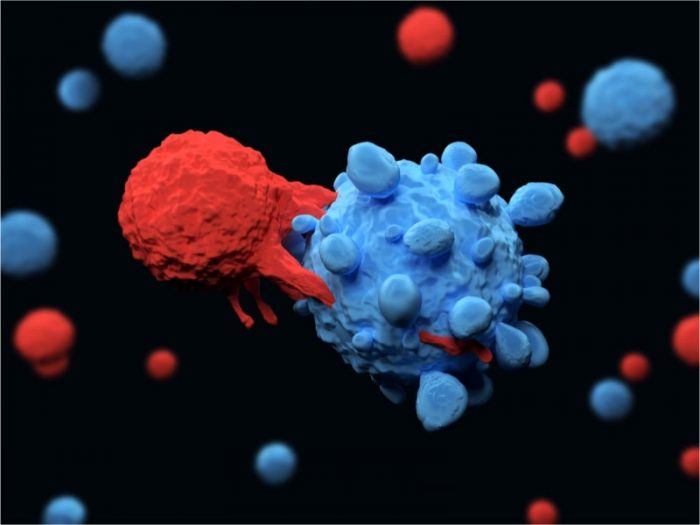
Затем иммунитет даёт специфический ответ: распознаёт чужеродные антигены, активизирует и направляет в очаг воспаления лимфоциты и Т-клетки, и устраняет врага.

Факт: Специфический (приобретённый) иммунитет второй этап защиты организма: распознаёт врага, вырабатывает стратегию и средства защиты.

Но, чтобы сформировался специфический ответ, необходимо время. Неспецифический же ответ формируется в доли секунды: «команда зачистки», выдирая электроны из чужих клеток, делает их нежизнеспособными.

Плюсы свободных радикалов:

• они не дают инфекции распространится по организму, локализуя её;
• резкое увеличение их количества даёт сигнал, который активизирует наш иммунитет.

Как защититься от воздействия свободных радикалов

Первый и самый лучший способ – правильное питание. Придерживаясь основных правил ПП, ваш организм будет функционировать и развиваться так, как заложено в нём природой. Это позволит вам дольше не стареть.

Здесь стоит подчеркнуть значимость про- и пребиотиков, которые содержаться в кисломолочных продуктах, зелени, овощах и фруктах. Здоровая кишечная флора легко справляется с молекулами, которые могут преобразовываться в оксиданты, полностью разрушая их.

Физическая активность – действенный способ защиты. Упражнения в зале, йога, езда на велосипеде, пешие прогулки, плавание, закаливание – помогут держать тело в тонусе, устранить отёки и сутулость от сидячей работы, улучшат кровообращение и питание клеток, и как следствие, укрепят иммунитет.

Важно не переусердствовать с загаром – большое количество ультрафиолета стимулирует высокую активность свободных радикалов, да и солнечные ожоги кожу не украсят. Но полностью отказываться от солнца нельзя, ведь мы знаем, что витамин D₃ вырабатывается в организме только под воздействием солнечного света.

Незаменимое средство защиты от воздействия свободных радикалов – антиоксиданты. Это маленькие, но сильные патрульные: они нейтрализуют клетки-окислители и блокируют развитие цепных окислительных реакций.

Как бороться со свободными радикалами в организме

Химическая структура у свободного радикала такая, что, распадаясь он создаёт три новых. Помните сказку, когда богатырь рубил Змею Горынычу голову, а на её месте вырастало три? Так и свободные радикалы растут в геометрической прогрессии: был 1 — затем 3 – потом стало 9 – 27 – 81 — 243 и т.д.

Эта агрессивная стая мигрирует по организму, вырывая электроны у всех встретившихся в дороге клеток. После единичного нападения молекула ещё способна восстановиться, но после нескольких атак шансов уже нет.

Как мы помним, повреждённая клетка становится свободным радикалом, — и создаётся целая армия клеток-крушителей.

Так что же делать: как бороться со свободными радикалами в организме, когда их слишком много?

Наш организм очень умный и стремится держать баланс во всём. Создавая свободные радикалы, он создаёт и средство борьбы с ними – антиоксиданты.

Антиоксидантные системы могут работать как ловушки – нейтрализовать уже существующие свободные радикалы, и как щит – не допускать создание новых.

Что такое антиоксиданты, откуда их взять и как они работают, — рассмотрим подробнее.

Свободные радикалы и антиоксиданты

Антиоксиданты – это молекулы, которые по доброй воле делятся своим электроном со свободным радикалом, чтобы нейтрализовать его. При этом они преобразуются в свободный радикал: теряя электрон, антиоксидант теряет стабильность.

 

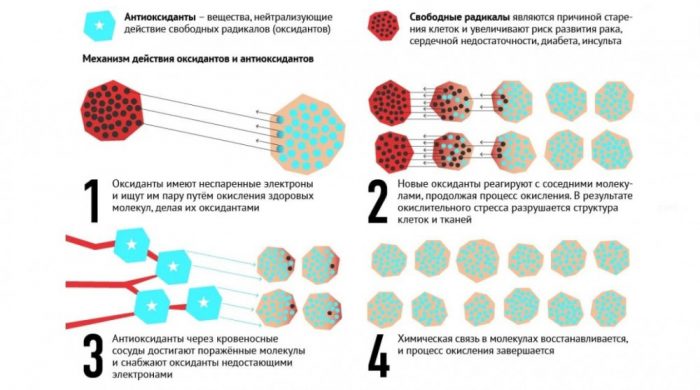
Но, родившийся таким способом новый оксидант живёт гораздо меньше, чем его предшественник, и становится малоактивным либо вообще неактивным. Соответственно и ущерб от него практически сводится к нулю.

Факт: такой антиоксидант, перешедший на сторону врага, не способен вызывать повреждения в молекулах ДНК.

Однако, антиоксидант можно вернуть в работу, восстановив утраченную часть. Они очень эффективно работают группами. Когда один из них теряет свой электрон, другой делится с напарником. Доказано, например, что молекула витамина С восстанавливает повреждённую клетку витамина Е. В таком случае, молекула антиоксиданта не теряет своей стабильности.

Так наш организм борется с постоянно создающимися в процессе клеточного дыхания свободными радикалами.

Виды антиоксидантов

По происхождению антиоксиданты бывают ферментными и неферментными.

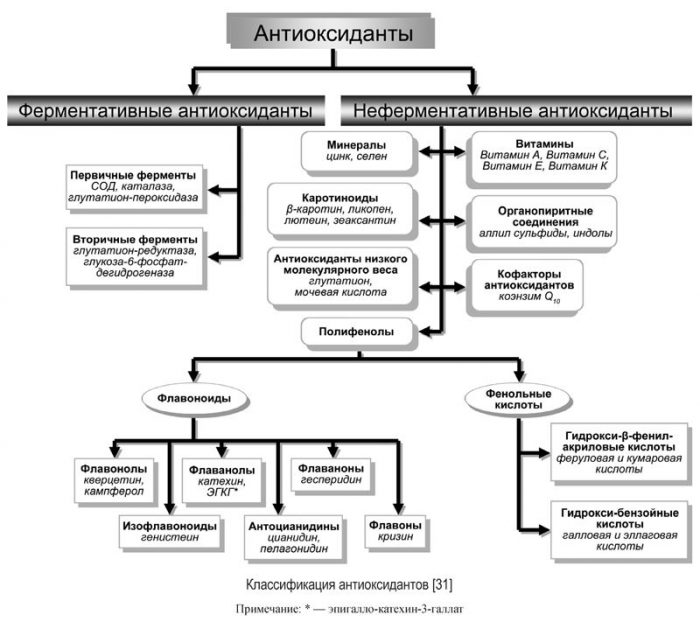
Ферментные антиокислители создаются внутри нашего организма и представляют собой важнейший элемент «встроенной» антиоксидантной защиты. Наиболее изученные это супероксиддисмутаза, каталаза и пероксидазы.

Ферментные антиоксиданты создают хитрые химические реакции, в ходе которых нестабильные агрессивные клетки преобразуются в безобидные, а сами антиоксиданты остаются неизменно устойчивыми.

Неферментные антиоксиданты мы получаем из продуктов, трав и специй. Самые известные из них:

• витамины: С, Е, А, коэнзим Q10, ликопин, группа витаминов В, РР, витамин К;
• флавоноиды: кверцетин, рутин, апигенин, ресвератрол, танины, катехины;
• аминокислоты: L-Аргинин, цистин, пролин, метионин, глутамин, таурин;
• микроэлементы: селен, цинк, железо, медь, сера.

По способу растворения антиоксиданты делятся на две подгруппы: гидрофильные – растворимые в воде и липофильные – растворимые в липидах.

Водорастворимые защищают плазму крови и клетку от окисления изнутри. Жирорастворимые оберегают от повреждения внешнюю оболочку клетки – мембрану.

Если своих антиоксидантов у нас недостаточно, то получается лавинное повреждение органов и систем организма. Чтобы этого не допустить, мы должны повысить количество своих «защитников», получая их из внешних источников.

 

Природные продукты, богатые антиоксидантами: таблица ТОП 100

Природа позаботилась о том, чтобы выживать в различных неблагоприятных и экстремальных условиях, внедрив средства защиты и борьбы с агрессорами в каждое своё творенье. Так, для борьбы с заболеваниями, вирусами и всевозможными поражениями каждое растение на планете в разных количествах содержит антиоксиданты. И щедро ними делится с нами.

Природные продукты антиоксиданты, попадая в наш организм, помогают ему справляться с окислительным стрессом, выступая на страже здоровых клеток и обезвреживая свободные радикалы.

Орехи

Грецкие орехи, арахис, кешью, фундук, миндаль, кедровые орешки, фисташки – просто кладезь антиоксидантов. Из них, мы получаем витамины Е, А, D, В, С, йод, магний, железо, фосфор, цинк, фитостерин, ресвератрол.

Бобовые и семена

Порция бобовых даст нашим клеткам ресвератрол, кемпферол, витамины Е, С, А, РР, биофлавоноиды, фитостерины.

Семечки подсолнечника и тыквенные, семена льна, кунжута, люцерны, чиа, киноа, зёрна граната содержат полифенолы, танины, элаговую кислоту, лигнаны, витамины группы В, витамины Е и А.

Сухофрукты

Сушёные изюм, курага, клюква, яблоки, груши, чернослив, финики, инжир богаты на олеанолевую кислоту, железо, калий, магний, фосфор, токоферол, ретинол, витамин С.

Свежие ягоды и фрукты

Первое место в этом списке занимают черника, голубика, клубника, смородина, черешня, облепиха, ягоды годжи и асаи. Они богаты антоцианами, глицином, флавоноидами, марганцем, цинком, селеном, витаминами С, К, Е, каротиноидами.

В цитрусовых и киви очень высокое содержание витамина С и альфа-токоферолов. Яблоки богаты железом, цинком и пектином.

Овощи и корнеплоды

Капуста, свекла, спаржа, морковь, картофель, помидоры, огурцы – хранят в себе ликопины, альфа- и бета-каротин, лютеин, полифенолы, аллилгликозиды, витамины Е, А, С, В, микроэлементы.

В чесноке и луке огромные запасы флавоноидов, аллилсульфидов, соединений селена и цинка.

Самые мощные природные антиоксиданты среди трав и специй

В шпинате, базилике, петрушке, чабреце, листьях салата и прочей зелени содержатся: аскорбиновая и никотиновая кислоты, витамины А, Е, йод, селен, цинк, магний, железо, коэнзим Q 10, каротиноиды, полифенолы.

Специи и пряности лидируют по концентрации антиоксидантных веществ. Больше всего в них содержание полифенолов, которые придают специям неповторимый вкус и аромат: капсаицин, коричная кислота, куркумин, ресвератрол, розмариновая кислота.

Другие продукты, содержащие антиоксиданты

Лидирующие позиции среди продуктов антиоксидантов занимают морские водоросли, где высокая концентрация астаксантина, альфа-токоферола, каротиноидов и почти все микроэлементы из таблицы Менделеева: йод, селен, железо, цинк и другие.

Чёрный шоколад и какао содержат теобромин, анандамид, фенилэтиламин, флавоноиды.

В белом, чёрном и зелёном чае есть танины, катехины, теафлавины и немного витамина С.

Натуральный кофе содержит гидрокоричную, хлорогеновую и феруловую кислоты, полифенолы.

Антиоксиданты в продуктах питания учёные исследуют очень давно. И в конце ХХ века они были сведены в единую таблицу под названием ORAC:

№	Продукт	индекс ORAC			№	Продукт	индекс ORAC
1	Гвоздика	314,446			51	Черная фасоль	8,040
2	Семейство сумаховых (фисташки, манго, кешью)	312,400			52	Фисташки	7,983
3	Корица	267,536			53	Смородина	7,960
4	Сорго	240,000			54	Пинто-бобы	7,779
5	Орегано сушеный	200,129			55	Сливы	7,581
6	Куркума	159,277			56	Молочный шоколад	7,528
7	Ягода асаи	102,700			57	Чечевица	7,282
8	Сорго, отруби, черные	100,800			58	Агава	7,274
9	Сумак, зерно, сыр	90,100			59	Яблоки сушеные	6,681
10	Какао-порошок	80,933			60	Чесночный порошок	6,665
11	Семена тмина	76,800			61	Голубика	6,552
12	Ягоды маки (порошок)	75,000			62	Чернослив	6,552
13	Петрушка (высушенная)	74,349			63	Сорго (отруби белые)	6,400
14	Сорго (отруби красные)	71,000			64	Лимонник (листья)	5,997
15	Базилик (сушенный)	67,553			65	Соевые бобы	5,764
16	Шоколад (без сахара)	49,926			66	Луковый порошок	5,735
17	Порошок карри	48,504			67	Ежевика	5,347
18	Сорго (зерно)	45,400			68	Чеснок сырой	5,346
19	Шоколад (порошок)	40,200			69	Листья кинзы	5,141
20	Сок ягод маки	40,000			70	Вино (Каберне Совиньон)	5,034
21	Шалфей	32,004			71	Малина	4,882
22	Горчичные зерна	29,257			72	Базилик (свежий)	4,805
23	Имбирь	28,811			73	Миндаль	4,454
24	Перец черный	27,618			74	Укроп	4,392
25	Тимьян свежий	27,426			75	Вигна китайская	4,343
26	Марджорам (свежие)	27,297			76	Яблоки красные	4,275
27	Ягоды Годжи	25,300			77	Персики сушеные	4,222
28	Рис	24,287			78	Изюм белый	4,188
29	Порошок чили	23,636			79	Яблоки	3,898
30	Сорго черный (зерно)	21,900			80	Финики	3,895
31	Шоколад (темный)	20,823			81	Вино красное	3,873
32	Семена льна	19,600			82	Земляника	3,577
33	Шоколад (полусладкий)	18,053			83	Арахисное масло	3,432
34	Пекан	17,940			84	Красная смородина	3,387
35	Паприка	17,919			85	Рис	3,383
36	Плоды аронии	16,062			86	Черешня	3,365
37	Эстрагон (свежий)	15,542			87	Крыжовник	3,277
38	Корень имбиря	14,840			88	Абрикос сушеный	3,234
39	Плоды бузины	14,697			89	Арахис, все виды	3,166
40	Сорго красный (зерно)	14,000			90	Капуста краснокачанная	3,145
41	Мята перечная	13,978			91	Брокколи	3,083
42	Орегано (свежий)	13,978			92	Яблоки	3,082
43	Грецкие орехи	13,541			93	Изюм	3,037
44	Фундук	9,645			94	Груши	2,941
45	Клюква	9,584			95	Плоды агавы	2,938
46	Груши (сушеные)	9,496			96	Сок черники	2,906
47	Савойская капуста	9,465			97	Кардамон	2,764
48	Артишоки	9,416			98	Гуава	2,550
49	Фасоль (красные бобы)	8,459			99	Красный салат листовой	2,380
50	Фасоль (розовые бобы )	8,320			100	Виноградный сок	2,377

Факт: индекс ORAC в продуктах измеряется их способностью поглощать свободные радикалы. Учёные Национального института здравоохранения США, разработавшие эту систему, рекомендуют каждый день употреблять антиоксидантных продуктов в размере 3000-5000 единиц ORAC.

Вконтакте

Facebook

Twitter

Google+

Одноклассники

Мой мир