Модули — Математика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Базовые сведения о модуле
К оглавлению…
Определение модуля может быть дано следующим образом: Абсолютной величиной числа a (модулем) называется расстояние от точки, изображающей данное число a на координатной прямой, до начала координат. Из определения следует, что:
Таким образом, для того чтобы раскрыть модуль необходимо определить знак подмодульного выражения. Если оно положительно, то можно просто убирать знак модуля. Если же подмодульное выражение отрицательно, то его нужно умножить на «минус», и знак модуля, опять-таки, больше не писать.
Основные свойства модуля:
Некоторые методы решения уравнений с модулями
К оглавлению…
Существует несколько типов уравнений с модулем, для которых имеется предпочтительный способ решения. При этом данный способ не является единственным. Например, для уравнения вида:
При этом данный способ не является единственным. Например, для уравнения вида:
Предпочтительным способом решения будет переход к совокупности:
А для уравнений вида:
Также можно переходить к почти аналогичной совокупности, но так как модуль принимает только положительные значения, то и правая часть уравнения должна быть положительной. Это условие нужно дописать в качестве общего ограничения для всего примера. Тогда получим систему:
Оба этих типа уравнений можно решать и другим способом: раскрывая соответствующим образом модуль на промежутках где подмодульное выражение имеет определённый знак. В этом случае будем получать совокупность двух систем. Приведем общий вид решений получающихся для обоих типов уравнений приведённых выше:
Для решения уравнений в которых содержится более чем один модуль применяется метод интервалов, который состоит в следующем:
- Сначала находим точки на числовой оси, в которых обращается в ноль каждое из выражений, стоящих под модулем.

- Далее делим всю числовую ось на интервалы между полученными точками и исследуем знак каждого из подмодульных выражений на каждом интервале. Заметьте, что для определения знака выражения надо подставить в него любое значение x из интервала, кроме граничных точек. Выбирайте те значения x, которые легко подставлять.
- Далее на каждом полученном интервале раскрываем все модули в исходном уравнении в соответствии с их знаками на данном интервале и решаем полученное обычное уравнение. В итоговый ответ выписываем только те корни этого уравнения, которые попадают в исследуемый промежуток. Еще раз: такую процедуру проводим для каждого из полученных интервалов.
Раскрытие модулей но определению в математике с примерами решения
Раскрытие модулей но определениюЕсли в задаче содержится модуль (как правило, один), то рассматривают два случая: когда выражение под знаком модуля больше либо равно нулю и когда оно меньше нуля.
Аналогично можно решать неравенства вида где знак заменяет любой из знаков неравенства.
Замечание. Раскрывать модули по определению можно и в случаях, когда их количество в задаче больше одного, но тогда, например, при решении уравнения придётся рассмотреть четыре случая:
(и в каждом случае раскрывать модули и решать уравнение), в то время как при использовании метода интервалов — всего три:
что эффективнее. Рас-смотрим соответствующие примеры.
Пример №257.Решить уравнение
Решение:
Рассмотрим два случая:
Пример №258.
Решить неравенство
Решение:
Раскладывая левую часть неравенства на множители, имеем
Пример №259.Решить уравнение
Решение:
ОДЗ: Рассмотрим два случая:
Ответ:
Пример №260.Решить уравнение
Ответ:
Пример №261.Найти все пары (х;у), удовлетворяющие условию
Решение:
1) При x = 0 неравенство верно при любом действительном у. Отсюда получаем пары чисел где
2) При x >0 имеем: откуда получаем пары чисел вида где
3) При имеем: т. е. получили пары
е. получили пары
Ответ:
Пример №262.Решить неравенство
Решение:
Здесь целесообразно вначале «отделить» параметр от переменной , и уже затем раскрывать модуль, но только над x .
1) При имеем:
Если , то решением будет Пересекая с промежутком получаем Если то решением будет Пересекая с промежутком получаем Если то неравенство примет вид что не выполняется ни при каких x .
2) При имеем:
Пересекая с промежутком получаем, что при всех а реше-нием будет любое Осталось объединить полученные решения.
Ответ: при при
Пример №263.Найти сумму целых решений неравенства
Решение:
В этой задаче имеются вложенные модули. Раскроем их, начиная с внутреннего модуля. Для этого рассмотрим два случая.
Раскроем их, начиная с внутреннего модуля. Для этого рассмотрим два случая.
1) Посколь-ку на рассматриваемом промежутке то оставшийся модуль раскрывается со знаком «минус», и получаем Пересекая с данным промежутком, имеем результат:
2) раскрывая внутренний модуль, получаем . Если при этом то имеемпересекая с данным промежутком, получаем решения если же то имеем или, с учётом промежутка, Объединяя результаты, находим множество всех решений неравенства:
Ответ:
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Предмет математика
Эти страницы возможно вам будут полезны:
Уравнение с модулем
Что такое уравнение с модулем и как его решить?
В уравнениях с модулем неизвестное значение содержится под знáком модуля. Например:
Например:
|x − 2| = 5
Уравнения с модулем бывают разными и решаются они различными методами. Нельзя сказать что какой-то метод наиболее рационален. Всё зависит от исходного уравнения.
Например, в каких-то уравнениях можно просто угадать корень, в то время как в других нужно логически мыслить, раскрывать модули, выполнять тождественные преобразования. Человек волен выбирать каким методом решения пользоваться.
К примеру, решим вышеприведённое уравнение |x − 2| = 5. Допустим, что мы не знаем ни одного метода решения. Как бы мы его решили?
Прежде всего заметим, что правая часть данного уравнения равна числу 5. Слева же располагается модуль из выражения | x − 2|. Это означает что подмодульное выражение x − 2 должно равняться числу 5 или −5
Значит нужно выяснить при каких значениях переменной x подмодульное выражение x − 2 будет обращаться в число 5 или −5.
Искомые значения x найдутся если приравнять подмодульное выражение к числу 5 и −5, а затем поочерёдно решить каждое из уравнений:
Значит корнями уравнения |x − 2| = 5 являются числа 7 и −3.
Большинство элементарных уравнений с модулем можно решить используя правило раскрытия модуля. Для этого раскрывают модуль содержащийся в уравнении, затем получившееся выражение подставляют в исходное уравнение вместо выражения с модулем.
Раскрывать модуль нужно для каждого из случаев: когда подмодульное выражение больше или равно нулю, и когда подмодульное выражение меньше нуля.
Решим наше уравнение |x − 2| = 5 с помощью правила раскрытия модуля. Выпишем отдельно его модуль и раскроем его:
В этой конструкции говорится, что если подмодульное выражение x − 2 больше или равно нулю, то модуль раскроется как x − 2, и тогда исходное уравнение примет вид x − 2 = 5, откуда x = 7
А если же подмодульное выражение x − 2 меньше нуля, то модуль раскроется как −(x − 2). Тогда исходное уравнение примет вид −(x − 2) = 5, откуда x = −3
Итак, уравнение |x − 2|= 5 имеет корни 7 и −3. Для проверки подстáвим числа 7 и −3 в исходное уравнение вместо x. Тогда получим верное равенство:
Для проверки подстáвим числа 7 и −3 в исходное уравнение вместо x. Тогда получим верное равенство:
Подмодульное выражение как правило содержит такое x, которое может обращать всё подмодульное выражение как в положительное число, так и в отрицательное, либо вообще в ноль.
Поэтому модуль и раскрывается для каждого из случаев: когда подмодульное выражение больше или равно нулю, и когда подмодульное выражение меньше нуля. Каждый из случаев будет давать независимое уравнение со своим корнем.
Вернёмся теперь к моменту, где мы раскрывали модуль:
Условия x − 2 ≥ 0 и x − 2 < 0 являются неравенствами, которые можно решить, тем самым приведя их к простому виду:
Символ ⇔ означает равносильность. В данном случае указывается, что условие x − 2 ≥ 0 равносильно условию x ≥ 2, а условие x − 2 < 0 равносильно условию x < 2.
Такой вид записи условий позволяет однозначно сказать при каких x модуль будет раскрываться с плюсом, а при каких с минусом.
В первом случае получилось условие x ≥ 2. Это значит что при всех x бóльших либо равных 2, модуль |x − 2| будет раскрываться с плюсом. Так, при x = 7, подмодульное выражение станет равно 5
|7 − 2| = |5|
А значит дальнейшее раскрытие будет с плюсом
|7 − 2| = |5| = 5
Таким же образом модуль |x − 2| будет вести себя и с другими значениями x на промежутке x ≥ 2. То есть, будет раскрываться с плюсом. Примеры:
При x = 3, |3 − 2|=|1| = 1
При x = 4, |4 − 2|=|2| = 2
При x = 2, |2 − 2|=|0| = 0
При x = 13, |13 − 2|=|11| = 11
А во втором случае получилось условие x < 2. Это значит что при всех x мéньших 2, модуль будет раскрываться с минусом. Так, при x = −3, подмодульное выражение опять же станет равно 5. Но в промежуточных вычислениях можно увидеть, что модуль раскрывается с минусом:
Но в промежуточных вычислениях можно увидеть, что модуль раскрывается с минусом:
|−3 − 2| = |−5| = −(−5) = 5
Модуль |x − 2| будет вести себя так же и с другими значениями x на промежутке x < 2. Примеры:
При x = 1, |1 − 2|=|−1| = −(−1) = 1
При x = 0, |0 − 2|=|−2| = −(−2) = 2
При x = −1, |−1 − 2|=|−3| = −(−3) = 3
При x = −9,|−9 − 2|=|−11| = −(−11) = 11
Число 2 является своего рода точкой перехода, в которой модуль |x − 2| меняет свой порядок раскрытия.
Можно представить как модуль |x − 2| двигался по маршруту от минус бесконечности до числа 2, раскрываясь в каждой точке с минусом. Попав в точку 2, модуль поменял свой порядок раскрытия — а именно раскрывшись в точке 2 с плюсом, он далее стал раскрываться с плюсом, двигаясь в правую часть к плюс бесконечности.
С помощью координатной прямой это можно представить так:
Красные знаки минуса и плюса указывают, как будет раскрываться модуль |x − 2| на промежутках x < 2 и x ≥ 2.
Точку перехода можно найти для любого модуля. Для этого нужно узнать при каких x подмодульное выражение равно нулю. Ноль это то значение, до и после которого модуль всегда сохраняет свой знак. Это следует из правила раскрытия модуля:
В этом примере в момент когда x станет равным нулю, модуль |x| раскроется с плюсом и далее при всех x, бóльших нуля, будет раскрываться с плюсом. Напротив, при всех x, мéньших нуля модуль будет раскрываться с минусом:
А например для модуля |2x + 6| точкой перехода будет число −3, потому что при его подстановке в подмодульное выражение 2x + 6 вместо x, данное подмодульное выражение станет равно нулю. Изобразим это на рисунке:
При всех x, бóльших либо равных −3, модуль будет раскрываться с плюсом. Примеры:
При x = −3, |2 × (−3) + 6| = |0| = 0
При x = 4, |2 × 4 + 6| = |14| = 14
При x = 5, |2 × 5 + 6| = |16| = 16
А при всех x, мéньших 3, модуль будет раскрываться с минусом. Примеры:
Примеры:
При x = −4, |2 × (−4) + 6| = |−2| = −(−2) = 2
При x = −5, |2 × (−5) + 6| = |−4| = −(−4) = 4
При x = −6, |2 × (−6) + 6| = |−6| = −(−6) = 6
Пример 2. Решить уравнение |x| + 3x = −2
Решение
Раскроем модуль, который содержится в левой части уравнения:
Если x ≥ 0, то модуль раскроется со знаком плюс и тогда исходное уравнение примет вид x + 3x = −2. Сразу решим это уравнение:
Теперь рассмотрим второй случай — когда x < 0. В этом случае модуль в исходном уравнении раскроется со знаком минус, и тогда получится уравнение −x + 3x = −2. Решим и это уравнение:
Получили корни и −1.
Выполним проверку, подставив найденные корни в исходное уравнение. Проверим корень
Видим, что при подстановке корня исходное уравнение не обращается в верное равенство. Значит не является корнем исходного уравнения.
Значит не является корнем исходного уравнения.
Проверим теперь корень −1
Получили верное равенство. Значит из двух найденных решений только −1 является корнем уравнения.
Ответ: −1.
Здесь можно сделать важный вывод. В уравнениях с модулем найденные корни не всегда удовлетворяют исходному уравнению. Чтобы убедиться в правильности своего решения, нужно выполнять проверку, подставляя найденные корни в исходное уравнение.
Кроме того, проверить является ли найденное значение корнем уравнения можно с помощью условия, согласно которому был раскрыт модуль.
Так, в данном примере мы раскрывали модуль |x| для случаев когда подмодульное выражение больше или равно нулю, и когда подмодульное выражение меньше нуля:
Условия x≥0 и x<0 являются неравенствами. В эти неравенства можно подставлять найденные корни. Если неравенства окажутся верными, значит корни удовлетворяют исходному уравнению.
Так, при раскрытии модуля со знаком плюс, получилось уравнение x + 3x = −2. Корнем этого уравнения стало число . Это число не удовлетворяет условию x ≥ 0, согласно которому был раскрыт модуль |x| и согласно которому было получено уравнение x + 3x = −2. Действительно, при подстановке числа в неравенство x ≥ 0 получается неверное неравенство.
А при раскрытии модуля со знаком минус, получилось уравнение −x + 3x = −2. Корнем этого уравнения стало число −1. Это число удовлетворяет условию x<0, согласно которому был раскрыт модуль |x| и согласно которому было получено уравнение −x + 3x = −2. Действительно, при подстановке числа −1 в неравенство x < 0 получается верное неравенство.
Пример 3. Решить уравнение |1 − 2x| − 4x = −6
Решение
Раскроем модуль:
При раскрытии модуля |1 − 2x| со знаком плюс, получим уравнение 1 − 2x − 4x = −6. Решим его:
Решим его:
При раскрытии модуля |1 − 2x| со знаком минус, получим уравнение −1 + 2x − 4x = −6. Решим его:
Получили корни и .
Корень не удовлетворяет условию , значит не является корнем исходного уравнения.
Корень удовлетворяет условию , значит является корнем исходного уравнения. Проверка также покажет это:
Ответ: .
Пример 4. Решить уравнение |x2 − 3x| = 0
Решение
Если модуль числа равен нулю, то подмодульное выражение тоже равно нулю:
То есть можно не раскрывать модуль. Достаточно узнать при каких значениях x подмодульное выражение равно нулю. В данном случае для этого нужно решить неполное квадратное уравнение:
Получили корни 0 и 3. Оба корня удовлетворяют исходному уравнению. Проверка показывает это:
Пример 5. Решить уравнение x2 − 5|x| + 6 = 0
Выпишем отдельно модуль |x| и раскроем его:
При раскрытии модуля |x| со знаком плюс, исходное уравнение примет вид x2 − 5x + 6 = 0. Это квадратное уравнение. Решим его с помощью дискриминанта:
Это квадратное уравнение. Решим его с помощью дискриминанта:
Оба корня удовлетворяют условию x ≥ 0, значит являются корнями исходного уравнения.
При раскрытии модуля |x| со знаком минус, исходное уравнение примет вид x2 + 5x + 6 = 0. Это тоже квадратное уравнение. Решим его как и предыдущее:
При условии x ≥ 0, модуль из уравнения раскрылся с плюсом, получились корни 3 и 2. Оба корня удовлетворяют условию x ≥ 0, значит удовлетворяют и исходному уравнению.
При условии x < 0, модуль из уравнения раскрылся с минусом, получились корни −2 и −3. Оба корня удовлетворяют условию x < 0, значит удовлетворяют и исходному уравнению.
Ответ: 3, 2, −2 и −3.
Сведéние уравнения с модулем в совокупность
Большинство элементарных уравнений с модулем можно решить сведéнием их к так называемой совокупности уравнений.
Элементарными мы будем называть те уравнения с модулем, в которых левая часть является модулем из какого-то выражения, а правая часть — числом. Например, |x| = 3 или |2x − 1| = 3.
Решим наше самое первое уравнение |x − 2| = 5 сведéнием его к совокупности уравнений. Корнями этого уравнения были числа 7 и −3. Это уравнение тоже считается элементарным.
Если раскрыть модуль |x − 2| со знаком плюс, то уравнение |x − 2| = 5 примет вид x − 2 = 5.
Если раскрыть модуль |x − 2| со знаком минус, то уравнение |x − 2| = 5 примет вид −(x − 2) = 5, то есть −x + 2 = 5.
Видим, что из уравнения |x − 2| = 5 получилось два уравнения: x − 2 = 5 и −x + 2 = 5. Причём каждое из уравнений имеет свой собственный корень. Уравнение x − 2 = 5 имеет корень 7, а уравнение −x + 2 = 5 — корень −3
Выпишем уравнения x − 2 = 5 и −x + 2 = 5 и объединим их квадратной скобкой:
Такой вид записи называют совокупностью уравнений.
Совокупность уравнений — это несколько уравнений, объединённых квадратной скобкой, и имеющих множество решений, которые удовлетворяют хотя бы одному из уравнений, входящих в данную совокупность.
Так, число 7 является решением совокупности потому что это число удовлетворяет первому уравнению х − 2 = 5.
Число −3 тоже является решением данной совокупности, поскольку удовлетворяет второму уравнению −х + 2 = 5.
Вместе же числа 7 и −3 образуют множество решений данной совокупности.
В отличие от системы уравнений, совокупность состоит из уравнений, которые не зависят друг от друга. Для каждого уравнения, входящего в совокупность, значение переменной x будет разным. А в системе уравнений значение переменной x удовлетворяет как первому уравнению, так и второму.
Решить совокупность уравнений означает найти множество решений, которые удовлетворяют хотя бы одному из уравнений, входящих в данную совокупность.
Решим каждое уравнение совокупности по-отдельности. Это обычные линейные уравнения, которые легко решаются:
Символ ⇔ как было ранее сказано означает равносильность. В данном случае он указывает на то, что все получающиеся совокупности равносильны друг другу.
Итак, мы получили корни 7 и −3. Поскольку эти два числа являются решениями совокупности , то значит являются и решениями уравнения |x − 2| = 5.
В исходную совокупность можно включать условия, согласно которым был раскрыт модуль. В этом случае каждое уравнение вместе со своим условием обрамляется знаком системы.
Дополним предыдущую совокупность условиями, согласно которым был раскрыт модуль. К первому уравнению x − 2 = 5 добавим условие x − 2 ≥ 0, а ко второму уравнению −x + 2 = 5 добавим условие x − 2 < 0
Решение каждого уравнения должно удовлетворять своему условию. Поэтому условия и уравнения обрамлены знáком системы.
Решим получившуюся совокупность с условиями. Условия являются неравенствами, которые тоже можно решать:
В первом случае получили корень 7, который удовлетворяет своему условию x ≥ 2. Во втором случае получили корень −3, который удовлетворяет своему условию x < 2.
Не следует бояться таких записей. Это лишь подробное решение, показывающее что откуда взялось. Чаще всего решение можно записать покороче.
Существует схема для сведéния в совокупность уравнения вида |x| = a. Выглядит эта схема так:
Данная схема легко позволяет свести уравнение с модулем в совокупность. Эту схему можно прочитать так: «Если выражение |x| равно a, то подмодульное выражение равно a или −a»
Квадратная скобка в совокупностях заменяет собой слово «или».
Например, уравнение |x| = 5 можно свести в совокупность, рассуждая так: если выражение |x| равно 5, то подмодульное выражение равно 5 или −5.
А применительно к нашему предыдущему примеру можно рассуждать так: если |x − 2| равно 5, то подмодульное выражение равно 5 или −5
Это та же самая совокупность, что и в прошлый раз. Убедитесь в этом, умножив обе части второго уравнения на −1.
В уравнениях где слева модуль, а справа число, мы будем чаще использовать именно такой способ записи совокупности. Он позволяет не прибегать к правилу раскрытия модуля, а сразу получить совокупность.
Но надо помнить, что эта схема будет работать только для уравнений вида |x| = a. То есть для уравнений, у которого слева модуль, а справа число.
Пример 2. Решить уравнение |2x − 1| = 3
Решение
У этого уравнения слева модуль, а справа число. Значит его можно свести в совокупность, воспользовавшись схемой
Если выражение |2x − 1| равно 3, то подмодульное выражение 2x − 1 равно 3 или −3
Теперь решим каждое уравнение совокупности по отдельности:
Ответ: 2 и −1.
Пример 3. Решить уравнение |x + 2| − 3 = 8
Решение
В некоторых случаях прежде чем свести исходное уравнение в совокупность, его следует упростить.
Так, в данном случае −3 следует перенести в правую часть, изменив знак:
Получили уравнение |x + 2| = 11. Если выражение |x + 2| равно 11, то подмодульное выражение x + 2 равно 11 или −11
Решим данную совокупность:
Ответ: 9 и −13.
Пример 4. Решить уравнение 4|x| + 4 = 2|x| + 10
Решение
Перенесём 2|x| из правой части в левую часть, а 4 перенесём из левой части в правую часть:
4|x| − 2|x| = 10 − 4
2|x| = 6
Разделим обе части получившегося уравнения на 2. Тогда получится простое уравнение с модулем:
Ответ: 3 и −3.
Пример 5. Решить уравнение
Решить уравнение
Решение
Если выражение |2 − 5x2| равно 3, то подмодульное выражение 2 − 5x2 равно 3 или −3
В обоих уравнениях перенесём 2 в правую часть, изменив знак:
В первом уравнении разделим обе части на −5. Во втором уравнении так же разделим обе части на −5. Тогда получим два квадратных уравнения
Первое уравнение не имеет корней, потому что квадрат любого числа положителен, а в данном случае он равен отрицательному числу. Корнями второго уравнения являются числа 1 и −1, поскольку вторая степень этих чисел равна единице.
Ответ: 1 и −1.
Пример 6. Решить уравнение |x + 6| + 4x = 5
Решение
Данное уравнение не является уравнением вида |x| = a, значит не получится воспользоваться схемой .
Чтобы свести данное уравнение в совокупность, нужно сначала раскрыть его модуль, затем записать совокупность из получившихся уравнения.
Раскроем модуль |x + 6|
Если x + 6 ≥ 0 , то модуль раскроется со знаком плюс и тогда исходное уравнение примет вид x + 6 + 4x = 5
Если x + 6 < 0, то модуль раскроется со знаком минус и тогда исходное уравнение примет вид −x − 6 + 4x = 5. Получим следующую совокупность:
Дальнейшее решение элементарно:
Из найденных корней только является корнем исходного уравнения, поскольку удовлетворяет условию x ≥ −6. А корень не является корнем уравнения, поскольку не удовлетворяет условию x < −6.
Ответ:
Наиболее простой вид
Наиболее простой вид уравнения с модулем выглядит так:
| x | = a
где x — корень уравнения, a — произвольное число, бóльшее или рáвное нулю. То есть a ≥ 0
Если условие a ≥ 0 не выполнено, то уравнение |x|= a корней не имеет. Это следует из определения модуля. Действительно, модуль всегда неотрицателен.
Это следует из определения модуля. Действительно, модуль всегда неотрицателен.
Приведем несколько примеров уравнений вида |x| = a
Пример 1. Решить уравнение |x| = 2
Решение
В данном случае сразу видно, что корнями являются числа 2 и −2. Ведь если вместо x подставить эти числа, то получим верное равенство: |−2| = 2 и |2| = 2. Решение для этого уравнения можно записать, сведя его в совокупность:
«Если выражение |x| равно 2, то подмодульное выражение x равно 2 или −2«
Ответ: 2 и −2
Пример 2. Решить уравнение |−x| = 4
Решение
Если выражение |−x| равно 4, то подмодульное выражение равно 4 или −4
Умножим оба уравнения на −1
Ответ: −4 и 4.
Пример 3. Решить уравнение |x| = −7
В данном случае корней нет, поскольку модуль всегда неотрицателен. А в данном случае модуль равен отрицательному числу.
А в данном случае модуль равен отрицательному числу.
Если уравнение с модулем не имеет корней, обычно пишут что x принадлежит пустому множеству:
x ∈ ø
Напомним, что пустым называют множество, не имеющее элементов.
Модуль внутри модуля
Рассмотрим уравнение:
В этом уравнении слева располагается модуль, который в свою очередь содержит внутри себя другой модуль, а справа уравнения располагается число. Такой вид уравнения с модулем можно решить, сведя его в совокупность с помощью схемы, которую мы рассмотрели ранее:
В нашем случае если выражение равно 9, то подмодульное выражение |2 + x| + 3 равно 9 или −9
В получившейся совокупности имеется два уравнения с модулем. Эти уравнения тоже в свою очередь следует свести в совокупность. Но сначала немного упростим эти уравнения. В первом и во втором уравнении перенесем 3 в правую часть, изменив знак. Тогда получим:
Теперь сведём эти уравнения в совокупности. Первое уравнение распадётся на следующую совокупность:
Первое уравнение распадётся на следующую совокупность:
Сразу решим совокупность . Первый корень равен 4, второй −8.
Теперь решим второе уравнение |2 + x| = −12. Но замечаем, что его правая часть равна отрицательному числу. Это уравнение не имеет корней, потому что модуль не может равняться отрицательному числу.
Значит уравнение имеет корни 4 и −8. Проверим эти корни, подставив их в исходное уравнение
В данном случае оба корня удовлетворяют исходному уравнению.
Ответ: 4 и −8.
Вообще, уравнение с модулем внутри которого содержится другой модуль, тоже решается различными способами. Какой способ использовать зависит от самогó уравнения. Решим например следующее уравнение:
Здесь уже нельзя использовать схему потому что слева располагается не только модуль, но и переменная x. Конечно, переменную x можно перенести в правую часть, и тогда можно будет свести данное уравнение в совокупность:
Но тогда справа появляется переменная x, на которую нужно будет вводить дополнительное ограничение, чтобы правая часть уравнения не стала отрицательной. Такой способ решения мы рассмотрим позже. А пока решим исходное уравнение с помощью правила раскрытия модуля.
Такой способ решения мы рассмотрим позже. А пока решим исходное уравнение с помощью правила раскрытия модуля.
Чтобы раскрыть модули данного уравнения нужно сначала определиться где внешний и где внутренний модуль.
В уравнении внешним модулем является полностью левая часть , а внутренним модулем — выражение
Значение внешнего модуля зависит от внутреннего модуля, и раскрываться внешний модуль будет исходя от результата который получился в результате вычисления его подмодульного содержимого.
Например, если x = 3, то внутренний модуль |3 − x| примет значение 0, и в результате всё подмодульное выражение внешнего модуля станет равно −2. А это значит что внешний модуль будет раскрываться с минусом.
||3 − x| − x + 1| = ||3 − 3| − 3 + 1| = ||0| − 3 + 1| = |−2| = −(−2) = 2
А если например x = −2, то внутренний модуль |3 − x| примет значение 5, и в результате всё подмодульное выражение внешнего модуля станет равно 8. А это значит что внешний модуль будет раскрываться с плюсом:
А это значит что внешний модуль будет раскрываться с плюсом:
||3 − x| − x + 1| = ||3 − (−2)| − (−2) + 1| = ||5| − (−2) + 1| = | 8 |=8
Поэтому решение будем начинать с раскрытия внутреннего модуля.
Если внутренний модуль раскроется с плюсом, то есть если 3 − x ≥ 0 (что равносильно неравенству x ≤ 3), то исходное уравнение примет вид:
Теперь уравнение имеет только внешний модуль. Решим его раскрыв модуль:
Если −2x + 4 ≥ 0, то:
Сейчас нас интересуют только те значения x при которых внутренний модуль раскрывается с плюсом, а это произойдет при условии x ≤ 3. Поэтому для наглядности рядом с найденным корнем указано, что он удовлетворяет условию x ≤ 3
Решаем далее. Если −2x + 4 < 0, то:
Несмотря на то, что оба найденных корня удовлетворяют уравнению |−2x+4|=6−x, мы исключаем корень из решений, потому что нас сейчас интересуют только те значения x, при которых внутренний модуль изначального уравнения раскрывается с плюсом. Поэтому рядом с корнем указано, что он не удовлетворяет условию x ≤ 3.
Поэтому рядом с корнем указано, что он не удовлетворяет условию x ≤ 3.
Итак, если внутренний модуль раскрывается с плюсом, исходное уравнение принимает вид |−2x + 4| = 6 − x и корнем этого уравнения является число −2.
Теперь решим исходное уравнение для случая, когда внутренний модуль раскрывается с минусом, то есть когда 3 − x < 0 (что равносильно неравенству x > 3). Внутренний модуль будет раскрываться с минусом при всех значениях x больших 3.
Если внутренний модуль раскроется с минусом, то исходное уравнение примет вид:
Модуль −2 равен 2. Тогда получаем простейшее линейное уравнение, корень которого равен 4
Получили корень 4, который удовлетворяет условию x > 3.
В итоге корнями уравнения являются числа −2 и 4.
Ответ: 2 и 4.
Пример 3. Решить уравнение ||x − 1| − 7| = 10
Решить уравнение ||x − 1| − 7| = 10
Решение
Слева располагается модуль, а справа число, значит можно применить схему:
В данном случае если выражение ||x − 1| − 7| равно 10, то подмодульное выражение |x − 1| − 7 равно 10 или −10. Получится совокупность из двух уравнений:
Упростим получившиеся уравнения. Перенесём число −7 в обоих уравнениях в правую часть, изменив знак:
Второе уравнение корней не имеет. Первое уравнение распадется на совокупность , корни которой 18 и −16.
Ответ: 18 и −16.
Решим это же уравнение с помощью раскрытия модулей. Начнем с внутреннего модуля.
Если x − 1 ≥ 0 (что равносильно x ≥ 1), то исходное уравнение примет вид:
Решим получившееся уравнение раскрыв модуль:
Далее решаем уравнение для случаев когда x − 8 ≥ 0 и x − 8 < 0
Сейчас нас интересуют те значения, при которых внутренний модуль исходного уравнения раскрывается с плюсом. А это будет при условии, что x ≥ 1. Этому условию удовлетворяет только значение 18, поэтому мы пометили его зеленой галочкой для наглядности.
А это будет при условии, что x ≥ 1. Этому условию удовлетворяет только значение 18, поэтому мы пометили его зеленой галочкой для наглядности.
Теперь решим исходное уравнение для случая, когда внутренний модуль раскрывается с минусом, то есть когда x − 1 < 0 (или что равносильно неравенству x < 1).
Если x − 1 < 0, то исходное уравнение примет вид:
Решим получившееся уравнение раскрыв модуль:
Далее решаем уравнение для случаев когда −x − 6 ≥ 0 и −x − 6 < 0
Из найденных корней только −16 удовлетворяет условию x < 1.
В итоге корнями уравнения ||x − 1| − 7| = 10 являются числа 18 и −16.
Видно, что с помощью схемы данное уравнение решилось легче и быстрее, чем способом раскрытия модулей.
Слева модуль, а справа выражение с переменной
Решим следующее уравнение с модулем:
|4x − 3| = 3x
Здесь так же применима схема:
То есть, если выражение |4x − 3| равно 3x, то подмодульное выражение 4x − 3 должно равняться 3x или −3x.
Но в исходном уравнении переменная x содержится не только под знáком модуля, но и в правой части. Нам пока неизвестно какое значение примет переменная x. Если x примет отрицательное значение, то правая часть станет полностью отрицательной. В этом случае корней не будет, потому что модуль не может равняться отрицательному числу.
Поэтому, если мы хотим решить данное уравнение, то при сведéнии его в совокупность, дополнительно следует ввести ограничение в виде условия 3x ≥ 0. Это будет означать, что правая часть уравнения |4x − 3| = 3x должна быть больше либо равна нулю:
Совокупность и условие обрамлены знаком системы, потому что решения совокупности должны удовлетворять условию 3x ≥ 0.
Итак, решим совокупность. Условие 3x ≥ 0 является неравенством, которое тоже можно решить:
Получившиеся корни можно подставить в условие x ≥ 0 и посмотреть выполняется ли оно. Если выполняется, то найденные корни удовлетворяют уравнению. В данном случае при подстановке обеих корней в неравенство, оно выполняется. Проверка также показывает, что корни удовлетворяют уравнению:
Пример 2. Решить уравнение |2x − 1| = 5x − 10
Решение
Решим это уравнение таким же образом, как и предыдущее. Введём условие, требующее чтобы правая часть была больше либо равна нулю:
В данном случае только значение 3 удовлетворяет условию x ≥ 2. Оно же является единственным корнем исходного уравнения. Проверка показывает это:
А число не удовлетворяет условию x ≥ 2 и не является корнем исходного уравнения. Проверка также показывает это:
Видим, что модуль стал равен отрицательному числу, а это противоречит определению модуля и нашему условию x ≥ 2.
Пример 3. Решить уравнение
Решение
Это уравнение мы решили, когда учились решать уравнения с модулем внутри которых другой модуль. Теперь данное уравнение можно решить, сведя его в совокупность.
Для начала перенесём x в правую часть, изменив знак:
Теперь сведём данное уравнение в совокупность. Дополнительно введём условие в виде неравенства 6 − x ≥ 0
В левой части первого уравнения оставим модуль, остальные члены перенесём в правую часть. Тоже самое сделаем и со вторым уравнением. Также будем решать неравенство 6 − x ≥ 0, оно позволит в конце проверять найденные корни на соответствие:
Решим первое уравнение. Оно распадётся на следующую совокупность:
Получились корни −2 и 8. Из них только −2 удовлетворяет условию x ≤ 6.
Теперь решим второе уравнение. Оно является уравнением, содержащим переменную в правой части. При сведении его в совокупность дополним его условием −7 + 2x ≥ 0
Дальнейшее элементарно:
При решении второго уравнения получились корни и 4.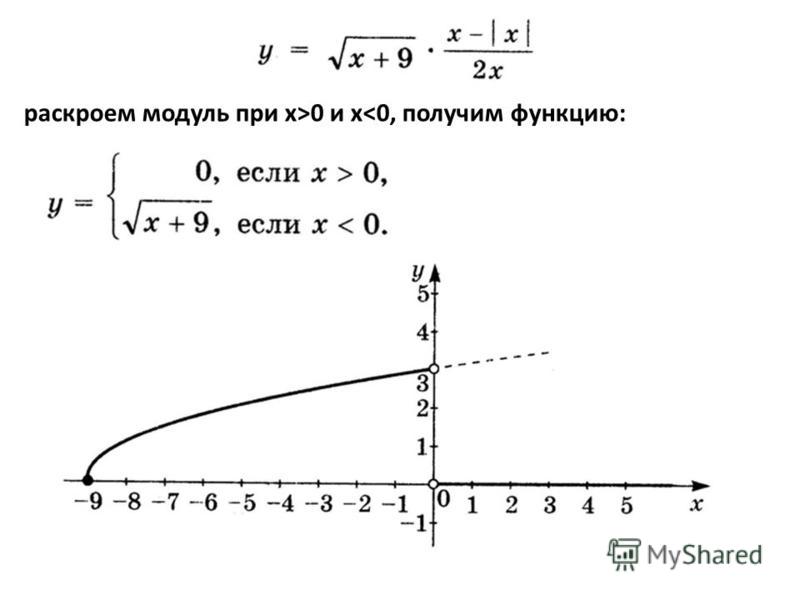 Прежде чем сверять их с условием x ≤ 6 следует сверить их с условием под которое решалось уравнение |3 − x| = −7 + 2x. Условию удовлетворяет только корень 4.
Прежде чем сверять их с условием x ≤ 6 следует сверить их с условием под которое решалось уравнение |3 − x| = −7 + 2x. Условию удовлетворяет только корень 4.
В итоге корнями исходного уравнения являются числа −2 и 4.
Пример 4. Решить уравнение |4x + 20| = −6x
Решение
На первый взгляд покажется, что данное уравнение не имеет решений, потому что правая часть отрицательна. Но это не совсем так. Правая часть содержит переменную x, которая может принять отрицательное значение или ноль, и это приведёт к тому что правая часть станет положительной либо равной нулю. А такое уравнение имеет право на существование.
В данном случае мы решим это уравнение, сведя его в совокупность. Но при этом укажем, что правая часть должна быть больше или равна нулю:
Из найденных корней только корень −2 удовлетворяет исходному уравнению. Также он удовлетворяет нашему условию x ≤ 0.
Ответ: −2.
Когда обе части — модули
Решим следующее уравнение:
|x + 7| = |1 + 3x|
Обе части этого уравнения являются модулями. Раскроем эти модули. Будем учитывать все возможные случаи при их раскрытии.
Случай 1. Если x + 7 ≥ 0 и 1 + 3x ≥ 0, то модули в обеих частях раскроются со знаком плюс и тогда исходное уравнение примет вид:
x + 7 = 1 + 3x
Это простейшее линейное уравнение. Решим его:
Случай 2. Если x + 7 < 0 и 1 + 3x < 0, то модули в обеих частях раскроются со знаком минус и тогда исходное уравнение примет вид:
−(x + 7) = −(1 + 3x)
Раскроем скобки, получим:
−x − 7 = −1 − 3x
Замечаем, что если умножить обе части этого уравнения на −1, то получается уравнение x + 7 = 1 + 3x. А это уравнение мы получали в результате раскрытия модулей со знаком плюс.
То есть уравнения x + 7 = 1 + 3x и −x − 7 = −1 − 3x являются равносильными, а значит имеют одни и те же корни. Убедимся в этом, решив уравнение −x − 7 = −1 − 3x
Поэтому, раскрыв модули со знаком плюс, нет необходимости раскрывать их со знаком минус, потому что в обоих случаях получаются уравнения, имеющие одни и те же корни.
Следующий случай это когда x + 7 ≥ 0 и 1 + 3x < 0. Тогда исходное уравнение примет вид x + 7 = −1 − 3x. Найдём корень этого уравнения:
И последний случай это когда x + 7 < 0 и 1 + 3x ≥ 0. Тогда уравнение примет вид −x − 7 = 1 + 3x. Если умножить это уравнение на −1, то получим уравнение x + 7 = −1 − 3x. А это уравнение мы получали, когда рассматривали предыдущий случай (случай x + 7 ≥ 0 и 1 + 3x < 0).
Следовательно, уравнение −x − 7 = 1 + 3x равносильно предыдущему уравнению x + 7 = −1 − 3x. Убедимся в этом решив уравнение −x − 7 = 1 + 3x
Убедимся в этом решив уравнение −x − 7 = 1 + 3x
Значит раскрыв левую часть со знаком плюс, а правую часть со знаком минус, нет необходимости раскрывать левую часть со знаком минус, а правую часть со знаком плюс, потому что в обоих случаях получаются уравнения, имеющие одни и те же корни.
Вообще, если в уравнении обе части являются модулями как в данном примере, то это уравнение можно свести в следующую совокупность:
В этой конструкции уравнение вида |a| = |b| сведено в совокупность из двух уравнений a = b и a = −b. Видно что первое уравнение получается путем раскрытия обоих модулей со знаком плюс, а второе уравнение — путем раскрытия модуля |a| со знаком плюс, а модуля|b|— со знаком минус.
Важно. Данная схема работает только тогда, когда обе части являются модулями без посторонних членов. Проще говоря, если будет дано уравнение, например |a| = |b| + c, то приведенную схему использовать нельзя.
Пример 2. Решить уравнение |2 − 3x| = |x + 5|
Решение
Обе части данного уравнения являются модулями. Воспользуемся схемой:
У нас получится совокупность из двух уравнений. В первом уравнении оба модуля будут раскрыты со знаком плюс, во втором уравнении — модуль |2 − 3x| будет раскрыт со знаком плюс, а модуль |x + 5| со знаком минус:
Выполним проверку:
Ответ: и
Пример 3. Решить уравнение |x2 − 13x + 35|=|35 − x2|
Решение
Обе части данного уравнения являются модулями. Воспользуемся схемой:
У нас получится совокупность из двух уравнений. В первом уравнении оба модуля будут раскрыты со знаком плюс. Во втором уравнении — модуль |x2 − 13x + 35| будет раскрыт со знаком плюс, а модуль |35 − x2| со знаком минус:
Приведём подобные члены в обоих уравнениях:
Первое уравнение является неполным квадратным. Решим его, вынеся x за скобки. Второе уравнение решается элементарно:
Решим его, вынеся x за скобки. Второе уравнение решается элементарно:
Ответ: , , 0.
Когда решение — числовой промежуток
Нередко приходиться решать уравнения с модулем, где корнями являются не один или два числа, а числовой промежуток. Таковым, например, является уравнение:
|5x + 3| = −5x − 3
Раскроем модуль этого уравнения:
Если раскрыть модуль со знаком плюс, то получается уравнение 5x + 3 = −5x − 3. Решим его:
А если раскрыть модуль со знаком минус, то получится уравнение −5x − 3 = −5x − 3. В этом уравнении обе части являются одинаковыми, а значит данное равенство является тождеством. Оно будет верно при любом значении x. Значит корнями уравнения −5x − 3 = −5x − 3 являются все числа от минус бесконечности до плюс бесконечности:
x ∈ (−∞; +∞)
Но надо помнить про условия, согласно которым были раскрыты модули. В первом случае мы получили корень . Он будет верен только при условии что . Это условие соблюдено. Проверка также показывает что корень подходит:
В первом случае мы получили корень . Он будет верен только при условии что . Это условие соблюдено. Проверка также показывает что корень подходит:
Значит один из корней уравнений равен
Во втором случае мы получили множество корней от минус бесконечности до плюс бесконечности. Но это будет верно только при условии что
Например, если взять любое число из промежутка (−∞; +∞), но которое не будет удовлетворять условию , то это число не будет обращать наше уравнение в верное равенство.
Например, число 2 принадлежит промежутку (−∞; +∞), но не удовлетворяет условию , а значит число 2 не является корнем исходного уравнения. Проверка также покажет это:
А если взять к примеру число −5, то оно будет принадлежать промежутку (−∞; +∞) и удовлетворять условию , а значит будет обращать исходное уравнение в верное равенство:
Поэтому ответ надо записать так, чтобы были выполнены оба условия и . Для наглядности нарисуем координатную прямую и обозначим её как x
Отметим на ней наш первый корень
Раскрыв модуль со знаком минус и решив получившееся уравнение, мы получили в ответе множество всех чисел от минус бесконечности до плюс бесконечности, но при этом было дано условие . Значит более точным ответ в этом случае будет таким:
Значит более точным ответ в этом случае будет таким:
Корнями уравнения −5x − 3 = −5x − 3 при условии являются все числа от минус бесконечности до
Значит на координатной прямой нужно заштриховать область слева от числа . Они будут иллюстрировать числа, меньшие
Число тоже является верным корнем исходного уравнения. Он был получен при раскрытии модуля со знаком плюс. Поэтому на координатной прямой пустой кружок нужно закрасить. Так мы включим число во множество решений:
Тогда окончательный ответ будет выглядеть так:
Ответ:
Также, можно решить это уравнение сведя его в совокупность, дополнительно указав, что правая часть должна быть больше либо равна нулю:
Пример 2. Решить уравнение |2x − 3| = 3 − 2x
Решение
Решим исходное уравнение для случаев когда 2x − 3 ≥ 0 и 2x − 3 < 0
Ответ:
Использование координатной прямой
Рассмотрим ещё один способ решения элементарных уравнений с модулем — с помощью координатной прямой. Этот способ используется редко, но знать о нём не помешает.
Этот способ используется редко, но знать о нём не помешает.
Решим наше самое первое уравнение |x − 2| = 5 с помощью координатной прямой. Напомним, что корнями этого уравнения были числа 7 и −3.
Модуль есть расстояние от начала координат до точки A. Либо расстояние между двумя числами на координатной прямой.
Расстояние между двумя числами выражается в виде разности |x1 − x2|, где x1 — первое число, x2 — второе число.
Если внимательно посмотреть на уравнение |x − 2|= 5, то можно увидеть что его левая часть это расстояние от x до 2 (или от 2 до x) и это расстояние равно 5. Отмéтим на координатной прямой число x и число 2
Правая часть уравнения |x − 2|= 5 говорит о том, что расстояние от x до 2 составляет пять единиц:
Если расстояние от x до 2 равно 5, то и расстояние от 2 до x тоже равно 5. Это позволяет отсчитать пять целых шагов от числа 2 к числу x и таким образом узнать значение x
Это позволяет отсчитать пять целых шагов от числа 2 к числу x и таким образом узнать значение x
Видно, что отсчитав пять шагов влево мы попали в точку с координатой −3. А это один из корней, который мы находили для уравнения |x − 2|= 5.
Но пять целых шагов от числа 2 можно отсчитать не только влево, но и вправо:
Если отсчитать пять целых шагов вправо, то попадём в точку с координатой 7. Это тоже был корень уравнения |x − 2|= 5
Несколько модулей в одной части
Решим следующее уравнение:
|x − 5| − |x| = 1
Это уравнение содержит два модуля в левой части. Чтобы решить данное уравнение нужно раскрыть его модули. Рассмотреть нужно каждый из случаев:
- когда оба модуля больше либо равны нулю;
- когда оба модуля меньше нуля;
- когда первый модуль больше либо равен нулю, а второй модуль меньше нуля;
- когда первый модуль меньше нуля, а второй модуль больше либо равен нулю.

Не будем комментировать каждый случай, а сразу приведём решение:
Первые два случая корней не дали. В третьем случае нашелся корень 3, но он не удовлетворяет условиям x − 5 ≥ 0 и x < 0, поэтому не является корнем исходного уравнения.
В четвёртом случае нашёлся корень 2, который удовлетворяет условиям x − 5 < 0 и x ≥ 0. Также он удовлетворяет исходному уравнению.
Заметно, что такой способ решения уравнения неудобен. Если модулей в уравнении будет три, четыре или более, то придётся рассматривать намного больше случаев. Человек запутавшись, может забыть рассмотреть какой-то из случаев, и получится что уравнение решено не полностью.
Поэтому такой вид уравнения как в данном примере удобнее решать методом интервалов. Об этом мы поговорим в следующем уроке.
Задания для самостоятельного решения
Задание 1. Решить уравнение:
Решение:
Задание 2. Решить уравнение:
Решить уравнение:
Решение:
Задание 3. Решить уравнение:
Решение:
Задание 4. Решить уравнение:
Решение:
Ответ: .Задание 5. Решить уравнение:
Решение:
Ответ: .Задание 6. Решить уравнение:
Решение:
Ответ: .Задание 7. Решить уравнение:
Решение:
Ответ: .Задание 8. Решить уравнение:
Решение:
Ответ: .Задание 9. Решить уравнение:
Решение:
Ответ: .Задание 10. Решить уравнение:
Решение:
Ответ: .Задание 11. Решить уравнение:
Решение:
Ответ: .Задание 12. Решить уравнение:
Решение:
Ответ: 0, 5.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Что такое модуль примеры.
 Калькулятор онлайн.Решение уравнений и неравенств с модулями
Калькулятор онлайн.Решение уравнений и неравенств с модулямиРешение уравнений и неравенств с модулем часто вызывает затруднения. Однако, если хорошо понимать, что такое модуль числа , и как правильно раскрывать выражения, содержащие знак модуля , то наличие в уравнении выражения, стоящего под знаком модуля , перестает быть препятствием для его решения.
Немного теории. Каждое число имеет две характеристики: абсолютное значение числа, и его знак.
Например, число +5, или просто 5 имеет знак «+» и абсолютное значение 5.
Число -5 имеет знак «-» и абсолютное значение 5.
Абсолютные значения чисел 5 и -5 равны 5.
Абсолютное значение числа х называется модулем числа и обозначается |x|.
Как мы видим, модуль числа равен самому числу, если это число больше или равно нуля, и этому числу с противоположным знаком, если это число отрицательно.
Это же касается любых выражений, которые стоят под знаком модуля.
Правило раскрытия модуля выглядит так:
|f(x)|= f(x), если f(x) ≥ 0, и
|f(x)|= — f(x), если f(x)
Например |x-3|=x-3, если x-3≥0 и |x-3|=-(x-3)=3-x, если x-3
Чтобы решить уравнение, содержащее выражение, стоящее под знаком модуля, нужно сначала раскрыть модуль по правилу раскрытия модуля .
Тогда наше уравнение или неравенство преобразуется в два различных уравнения, существующих на двух различных числовых промежутках.
Одно уравнение существует на числовом промежутке, на котором выражение, стоящее под знаком модуля неотрицательно.
А второе уравнение существует на промежутке, на котором выражение, стоящее под знаком модуля отрицательно.
Рассмотрим простой пример.
Решим уравнение:
|x-3|=-x 2 +4x-3
1. Раскроем модуль.
|x-3|=x-3, если x-3≥0, т.е. если х≥3
|x-3|=-(x-3)=3-x, если x-3
2. Мы получили два числовых промежутка: х≥3 и х
Рассмотрим, в какие уравнения преобразуется исходное уравнение на каждом промежутке:
А) При х≥3 |x-3|=x-3, и наше уранение имеет вид:
Внимание! Это уравнение существует только на промежутке х≥3!
Раскроем скобки, приведем подобные члены:
и решим это уравнение.
Это уравнение имеет корни:
х 1 =0, х 2 =3
Внимание! поскольку уравнение x-3=-x 2 +4x-3 существует только на промежутке х≥3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х 2 =3.
Б) При x
Внимание! Это уравнение существует только на промежутке х
Раскроем скобки, приведем подобные члены. Получим уравнение:
х 1 =2, х 2 =3
Внимание! поскольку уравнение 3-х=-x 2 +4x-3 существует только на промежутке x
Итак: из первого промежутка мы берем только корень х=3, из второго — корень х=2.
МБОУ СОШ №17 г. Иванова
«Уравнения с модулем»
Методическая разработка
Составлена
учителем математики
Лебедевой Н.В.20010 г.
Пояснительная записка
Глава 1. Введение
Раздел 2. Основные свойства Раздел 3. Геометрическая интерпретация понятия модуля числа Раздел 4. График функции у = |х| Раздел 5. Условные обозначения
График функции у = |х| Раздел 5. Условные обозначения Глава 2. Решение уравнений, содержащих модуль
Раздел 1.Уравнения вида |F(х)| = m (простейшие) Раздел 2. Уравнения вида F(|х|) = m Раздел 3. Уравнения вида |F(х)| = G(х) Раздел 4. Уравнения вида |F(х)| = ± F(х) (красивейшие) Раздел 5. Уравнения вида |F(х)| = |G(х)| Раздел 6. Примеры решения нестандартных уравнений Раздел 7. Уравнения вида |F(х)| + |G(х)| = 0 Раздел 8. Уравнения вида |а 1 х ± в 1 | ± |а 2 х ± в 2 | ± …|а n х ± в n | = m Раздел 9. Уравнения, содержащие несколько модулейГлава 3. Примеры решения различных уравнений с модулем.
Раздел 1. Тригонометрические уравнения Раздел 2. Показательные уравнения Раздел 3. Логарифмические уравнения Раздел 4. Иррациональные уравнения Раздел 5. Задания повышенной сложности Ответы к упражнениям Список литературы Понятие абсолютной величины (модуля) действительного числа является одной из существенных его характеристик. Это понятие имеет широкое распространение в различных разделах физико-математических и технических наук. В практике преподавания курса математики в средней школе в соответствии с Программой МО РФ понятие «абсолютная величина числа» встречается неоднократно: в 6 – м классе вводиться определение модуля, его геометрический смысл; в 8 – м классе формируется понятие абсолютной погрешности, рассматривается решение простейших уравнений и неравенств, содержащих модуль, изучаются свойства арифметического квадратного корня; в 11 – м классе понятие встречается в разделе «Корень n -ой степени». Опыт преподавания показывает, что учащиеся часто сталкиваются с трудностями при решении заданий, требующих знания данного материала, а нередко пропускают, не приступая к выполнению. В текстах экзаменационных заданий за курс 9 – ого и 11 – ого классов также включены подобные задания. Кроме того, требования, которые предъявляют к выпускникам школ Вузы отличаются, а именно, более высокого уровня, чем требования школьной программы.
Это понятие имеет широкое распространение в различных разделах физико-математических и технических наук. В практике преподавания курса математики в средней школе в соответствии с Программой МО РФ понятие «абсолютная величина числа» встречается неоднократно: в 6 – м классе вводиться определение модуля, его геометрический смысл; в 8 – м классе формируется понятие абсолютной погрешности, рассматривается решение простейших уравнений и неравенств, содержащих модуль, изучаются свойства арифметического квадратного корня; в 11 – м классе понятие встречается в разделе «Корень n -ой степени». Опыт преподавания показывает, что учащиеся часто сталкиваются с трудностями при решении заданий, требующих знания данного материала, а нередко пропускают, не приступая к выполнению. В текстах экзаменационных заданий за курс 9 – ого и 11 – ого классов также включены подобные задания. Кроме того, требования, которые предъявляют к выпускникам школ Вузы отличаются, а именно, более высокого уровня, чем требования школьной программы. Для жизни в современном обществе очень важным является формирование математического стиля мышления, проявляющегося в определённых умственных навыках. В процессе решения задач с модулями требуется умение применять такие приёмы, как обобщение и конкретизация, анализ, классификация и систематизация, аналогия. Решение подобных заданий позволяет проверить знание основных разделов школьного курса, уровень логического мышления, первоначальные навыки исследовательской деятельности.
Данная работа посвящена одному из разделов – решению уравнений, содержащих модуль. Она состоит из трёх глав. В первой главе вводятся основные понятия и наиболее важные теоретические выкладки. Во второй главе предлагаются девять основных типов уравнений, содержащих модуль, рассматриваются методы их решения, разбираются примеры разного уровня сложности. В третьей главе предлагаются более сложные и нестандартные уравнения (тригонометрические, показательные, логарифмические и иррациональные). К каждому типу уравнений есть упражнения для самостоятельного решения (ответы и указания прилагаются).
Для жизни в современном обществе очень важным является формирование математического стиля мышления, проявляющегося в определённых умственных навыках. В процессе решения задач с модулями требуется умение применять такие приёмы, как обобщение и конкретизация, анализ, классификация и систематизация, аналогия. Решение подобных заданий позволяет проверить знание основных разделов школьного курса, уровень логического мышления, первоначальные навыки исследовательской деятельности.
Данная работа посвящена одному из разделов – решению уравнений, содержащих модуль. Она состоит из трёх глав. В первой главе вводятся основные понятия и наиболее важные теоретические выкладки. Во второй главе предлагаются девять основных типов уравнений, содержащих модуль, рассматриваются методы их решения, разбираются примеры разного уровня сложности. В третьей главе предлагаются более сложные и нестандартные уравнения (тригонометрические, показательные, логарифмические и иррациональные). К каждому типу уравнений есть упражнения для самостоятельного решения (ответы и указания прилагаются). Основное назначение данной работы – это оказание методической помощи преподавателям при подготовке к урокам и при организации факультативных курсов. Материал также может быть использован в качестве учебного пособия для старшеклассников. Задания, предлагаемые в работе, интересны и не всегда просты в решении, что позволяет сделать учебную мотивацию учащихся более осознанной, проверить свои способности, повысить уровень подготовки выпускников школ к поступлению в Вузы. Дифференцированный подбор предлагаемых упражнений предполагает переход от репродуктивного уровня усвоения материала к творческому, а также возможность научить применять свои знания при решении нестандартных задач. Определение : Абсолютной величиной (модулем) действительного числа а называется неотрицательное число: а или –а. Обозначение: │ а │ Запись читается следующим образом: «модуль числа а» или «абсолютная величина числа а»
Основное назначение данной работы – это оказание методической помощи преподавателям при подготовке к урокам и при организации факультативных курсов. Материал также может быть использован в качестве учебного пособия для старшеклассников. Задания, предлагаемые в работе, интересны и не всегда просты в решении, что позволяет сделать учебную мотивацию учащихся более осознанной, проверить свои способности, повысить уровень подготовки выпускников школ к поступлению в Вузы. Дифференцированный подбор предлагаемых упражнений предполагает переход от репродуктивного уровня усвоения материала к творческому, а также возможность научить применять свои знания при решении нестандартных задач. Определение : Абсолютной величиной (модулем) действительного числа а называется неотрицательное число: а или –а. Обозначение: │ а │ Запись читается следующим образом: «модуль числа а» или «абсолютная величина числа а»│ а, если а > 0
│а│ = │ 0, если а = 0 (1)
│ — а, если аПримеры: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 — √2│ = √2 – 1
- Раскрыть модуль выражения:
Раздел 2.
 Основные свойства. Рассмотрим основные свойства абсолютной величины. Свойство №1: Противоположные числа имеют равные модули, т.е. │а│=│- а│ Покажем верность равенства. Запишем определение числа – а : │— а│ = (2) Сравним совокупности (1) и (2). Очевидно, что определения абсолютных величин чисел а и – а совпадают. Следовательно, │а│=│- а│
Основные свойства. Рассмотрим основные свойства абсолютной величины. Свойство №1: Противоположные числа имеют равные модули, т.е. │а│=│- а│ Покажем верность равенства. Запишем определение числа – а : │— а│ = (2) Сравним совокупности (1) и (2). Очевидно, что определения абсолютных величин чисел а и – а совпадают. Следовательно, │а│=│- а│ При рассмотрении следующих свойств ограничимся их формулировкой, так как их доказательство приводится в Свойство №2: Абсолютная величина суммы конечного числа действительных чисел не превосходит суммы абсолютных величин слагаемых: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │+ … + │а n │ Свойство №3: Абсолютная величина разности двух действительных чисел не превосходит суммы их абсолютных величин: │а — в│ ≤│а│+│в│ Свойство №4: Абсолютная величина произведения конечного числа действительных чисел равна произведению абсолютных величин множителей: │а · в│=│а│·│в│ Свойство №5: Абсолютная величина частного действительных чисел равна частному их абсолютных величин:
Раздел 3.
 Геометрическая интерпретация понятия модуля числа. Каждому действительному числу можно поставить в соответствие точку на числовой прямой, которая будет геометрическим изображением данного действительного числа. Каждой точке на числовой прямой соответствует её расстояние от начала отсчёта, т.е. длина отрезка от начала отсчёта до данной точки. Это расстояние рассматривается всегда как величина неотрицательная. Поэтому длина соответствующего отрезка и будет геометрической интерпретацией абсолютной величины данного действительного числа
Геометрическая интерпретация понятия модуля числа. Каждому действительному числу можно поставить в соответствие точку на числовой прямой, которая будет геометрическим изображением данного действительного числа. Каждой точке на числовой прямой соответствует её расстояние от начала отсчёта, т.е. длина отрезка от начала отсчёта до данной точки. Это расстояние рассматривается всегда как величина неотрицательная. Поэтому длина соответствующего отрезка и будет геометрической интерпретацией абсолютной величины данного действительного числа Представленная геометрическая иллюстрация наглядно подтверждает свойство №1, т.е. модули противоположных чисел равны. Отсюда легко понимается справедливость равенства: │х – а│= │а — х│. Также более очевидным становиться решение уравнения │х│= m, где m ≥ 0, а именно х 1,2 = ± m. Примеры: 1) │х│= 4 х 1,2 = ± 4 2) │х — 3│= 1
х 1,2 = 2; 4
Раздел 4. График функции у = │х│
Область определения данной функции все действительные числа.
Раздел 5. Условные обозначения.
В дальнейшем при рассмотрении примеров решения уравнений будут использованы следующие условные обозначения: { — знак системы [ — знак совокупности При решение системы уравнений (неравенств) находится пересечение решений входящих в систему уравнений (неравенств). При решении совокупности уравнений (неравенств) находится объединение решений входящих в совокупность уравнений (неравенств). В этой главе мы рассмотрим алгебраические способы решения уравнений, содержащих один или более модуль.Раздел 1. Уравнения вида │F (х)│= m
Уравнение данного вида называется простейшим. Оно имеет решение тогда и только тогда, когда m ≥ 0. По определению модуля, исходное уравнение равносильно совокупности двух уравнений: │F (х)│= mПримеры:
№1. Решите уравнение: │7х — 2│= 9
Ответ: х 1 = — 1; х 2 = 1 4 / 7 №2
│х 2 + 3х + 1│= 1
х 2 + 3х + 2 = 0 х 2 +3х = 0 х 1 = -1; х 2 = -2 х · (х + 3) = 0 х 1 = 0; х 2 = -3 Ответ: сумма корней равна — 2 .
 №3
№3 │х 4 -5х 2 + 2│= 2 х 4 – 5х 2 = 0 х 4 – 5х 2 + 4 = 0 х 2 · (х 2 – 5) = 0 обозначим х 2 = m, m ≥ 0 х = 0; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 – оба значения удовлетворяют условию m ≥ 0 х 2 = 1 х 2 = 4 х = ± 1 х = ± 2 Ответ: количество корней уравнения 7. Упражнения:
№1. Решите уравнение и укажите сумму корней: │х — 5│= 3№2 . Решите уравнение и укажите меньший корень: │х 2 + х│= 0№3 . Решите уравнение и укажите больший корень: │х 2 – 5х + 4│= 4№4 .Решите уравнение и укажите целый корень: │2х 2 – 7х + 6│= 1№5 .Решите уравнение и укажите количество корней: │х 4 – 13х 2 + 50│= 14
Раздел 2. Уравнения вида F(│х│) = m
Аргумент функции в левой части находится под знаком модуля, а правая часть не зависит от переменной. Рассмотрим два способа решения уравнений данного вида.1 способ: По определению абсолютной величины исходное уравнение равносильно совокупности двух систем. В каждой из которых накладывается условие на подмодульное выражение. F (│х│) = m
В каждой из которых накладывается условие на подмодульное выражение. F (│х│) = m Так как функция F(│х│) – чётная на всей области определения, то корни уравнений F(х) = m и F(- х) = m – это пары противоположных чисел. Поэтому достаточно решить одну из систем (при рассмотрении примеров указанным способом будет приводиться решение одной системы).2 способ: Применение метода введения новой переменной. При этом вводиться обозначение │х│= а, где а ≥ 0. Данный способ менее объёмный по оформлению.
Примеры: №1 . Решите уравнение: 3х 2 – 4│х│= — 1 Воспользуемся введением новой переменной. Обозначим │х│= а, где а ≥ 0. Получим уравнение 3а 2 — 4а + 1 = 0 Д = 16 – 12 = 4 а 1 = 1 а 2 = 1 / 3 Возвращаемся к исходной переменной: │х│=1 и │х│= 1 / 3 . Каждое уравнение имеет два корня. Ответ: х 1 = 1; х 2 = — 1; х 3 = 1 / 3 ; х 4 = — 1 / 3 .
 №2. Решите уравнение: 5х 2 + 3│х│- 1 = 1 / 2 │х│ + 3х 2
№2. Решите уравнение: 5х 2 + 3│х│- 1 = 1 / 2 │х│ + 3х 2 Найдём решение первой системы совокупности: 4х 2 + 5х – 2 =0 Д = 57 х 1 = -5+√57 / 8 х 2 = -5-√57 / 8 Заметим, что х 2 не удовлетворяет условию х ≥ 0. Решением второй системы будет число, противоположное значению х 1 . Ответ: х 1 = -5+√57 / 8 ; х 2 = 5-√57 / 8 .№3 . Решите уравнение: х 4 – │х│= 0 Обозначим │х│= а, где а ≥ 0. Получим уравнение а 4 – а = 0 а · (а 3 – 1) = 0 а 1 = 0 а 2 = 1 Возвращаемся к исходной переменной: │х│=0 и │х│= 1 х = 0; ± 1 Ответ: х 1 = 0; х 2 = 1; х 3 = — 1.
Упражнения: №6. Решите уравнение: 2│х│ — 4,5 = 5 – 3 / 8 │х│ №7 . Решите уравнение, в ответе укажите количество корней: 3х 2 — 7│х│ + 2 = 0 №8 . Решите уравнение, в ответе укажите целые решения: х 4 + │х│ — 2 = 0
Раздел 3.
 Уравнения вида │F(х)│ = G(х) Правая часть уравнения данного вида зависит от переменной и, следовательно, имеет решение тогда и только тогда, когда правая часть функция G(х) ≥ 0. Исходное уравнение можно решить двумя способами:1 способ: Стандартный, основан на раскрытии модуля исходя из его определения и заключается в равносильном переходе к совокупности двух систем. │F (х)│ = G (х)
Уравнения вида │F(х)│ = G(х) Правая часть уравнения данного вида зависит от переменной и, следовательно, имеет решение тогда и только тогда, когда правая часть функция G(х) ≥ 0. Исходное уравнение можно решить двумя способами:1 способ: Стандартный, основан на раскрытии модуля исходя из его определения и заключается в равносильном переходе к совокупности двух систем. │F (х)│ = G (х) Данный способ рационально использовать в случае сложного выражения для функции G(x) и мене сложного – для функции F(х), так как предполагается решение неравенств с функцией F(х).2 способ: Состоит в переходе к равносильной системе, в которой накладывается условие на правую часть. │F (x )│= G (x )
Данный способ удобнее применять, если выражение для функции G(х) мене сложное, чем для функции F(х), так как предполагается решение неравенства G(х) ≥ 0. Кроме того, в случае нескольких модулей этот способ рекомендуется применять второй вариант.
 Примеры: №1. Решите уравнение: │х + 2│= 6 -2х
Примеры: №1. Решите уравнение: │х + 2│= 6 -2х (1 способ) Ответ: х = 1 1 / 3 №2.
│х 2 – 2х — 1│= 2·(х + 1)
(2 способ) Ответ: Произведение корней – 3.
№3. Решите уравнение,в ответе укажите сумму корней:
│х — 6│= х 2 — 5х + 9
Ответ: сумма корней равна 4.
Упражнения: №9. │х + 4│= — 3х№10. Решите уравнение, в ответе укажите число решений:│х 2 + х — 1│= 2х – 1№11 . Решите уравнение, в ответе укажите произведение корней:│х + 3│= х 2 + х – 6
Раздел 4. Уравнения вида │F(x)│= F(x) и │F(x)│= — F(x)
Уравнения данного вида иногда называют «красивейшими». Так как правая часть уравнений зависит от переменной, решения существуют тогда и только тогда, когда правая часть неотрицательна. Поэтому исходные уравнения равносильны неравенствам:│F(x)│= F(x) F(x) ≥ 0 и │F(x)│= — F(x) F(x) Примеры: №1 .
 Решите уравнение, в ответе укажите меньший целый корень: │5х — 3│= 5х – 3 5х – 3 ≥ 0 5х ≥ 3 х ≥ 0,6 Ответ: х = 1 №2. Решите уравнение, в ответе укажите длину промежутка: │х 2 — 9│= 9 – х 2 х 2 – 9 ≤ 0 (х – 3) (х + 3) ≤ 0 [- 3; 3] Ответ: длина промежутка равна 6. №3 . Решите уравнение, в ответе укажите число целых решений: │2 + х – х 2 │= 2 + х – х 2 2 + х – х 2 ≥ 0 х 2 – х – 2 ≤ 0 [- 1; 2] Ответ: 4 целых решения. №4 . Решите уравнение, в ответе укажите наибольший корень:
Решите уравнение, в ответе укажите меньший целый корень: │5х — 3│= 5х – 3 5х – 3 ≥ 0 5х ≥ 3 х ≥ 0,6 Ответ: х = 1 №2. Решите уравнение, в ответе укажите длину промежутка: │х 2 — 9│= 9 – х 2 х 2 – 9 ≤ 0 (х – 3) (х + 3) ≤ 0 [- 3; 3] Ответ: длина промежутка равна 6. №3 . Решите уравнение, в ответе укажите число целых решений: │2 + х – х 2 │= 2 + х – х 2 2 + х – х 2 ≥ 0 х 2 – х – 2 ≤ 0 [- 1; 2] Ответ: 4 целых решения. №4 . Решите уравнение, в ответе укажите наибольший корень:│4 – х —
│= 4 – х –
х 2 – 5х + 5 = 0 Д = 5 х 1,2 =
≈ 1,4
Ответ: х = 3.
Упражнения: №12. Решите уравнение, в ответе укажите целый корень: │х 2 + 6х + 8│= х 2 + 6х + 8№13. Решите уравнение, в ответе укажите число целых решений: │13х – х 2 — 36│+ х 2 – 13х + 36 = 0№14. Решите уравнение, в ответе укажите целое число, не являющееся корнем уравнения:
Раздел 5.
 Уравнения вида │F(x)│= │G(x)│ Так как обе части уравнения неотрицательные, то решение предполагает рассмотрение двух случаев: подмодульные выражения равны или противоположны по знаку. Следовательно, исходное уравнение равносильно совокупности двух уравнений: │F (x )│= │ G (x )│
Уравнения вида │F(x)│= │G(x)│ Так как обе части уравнения неотрицательные, то решение предполагает рассмотрение двух случаев: подмодульные выражения равны или противоположны по знаку. Следовательно, исходное уравнение равносильно совокупности двух уравнений: │F (x )│= │ G (x )│ Примеры: №1. Решите уравнение, в ответе укажите целый корень: │х + 3│=│2х — 1│
Ответ: целый корень х = 4. №2. Решите уравнение: │ х – х 2 — 1│=│2х – 3 – х 2 │
Ответ: х = 2. №3 . Решите уравнение, в ответе укажите произведение корней:
Корниуравнения 4х 2 + 2х – 1 = 0 х 1,2 = — 1±√5 / 4 Ответ: произведение корней равно – 0,25. Упражнения: №15 . Решите уравнение, в ответе укажите целое решение:│х 2 – 3х + 2│= │х 2 + 6х — 1│ №16. Решите уравнение, в ответе укажите меньший корень:│5х — 3│=│7 — х│ №17 . Решите уравнение, в ответе укажите сумму корней:
Решите уравнение, в ответе укажите сумму корней:
Раздел 6. Примеры решения нестандартных уравнений
В данном разделе мы рассмотрим примеры нестандартных уравнений, при решении которых абсолютная величина выражения раскрывается по определению. Примеры:№1. Решите уравнение, в ответе укажите сумму корней: х · │х│- 5х – 6 = 0
Ответ: сумма корней равна 1 №2. . Решите уравнение, в ответе укажите меньший корень: х 2 — 4х ·
— 5 = 0
Ответ: меньший корень х = — 5. №3. Решите уравнение:
Ответ: х = -1. Упражнения: №18. Решите уравнение и укажите сумму корней: х · │3х + 5│= 3х 2 + 4х + 3
№19. Решите уравнение: х 2 – 3х =
№20. Решите уравнение:
Раздел 7. Уравнения вида │F(x)│+│G(x)│=0
Нетрудно заметить, что в левой части уравнения данного вида сумма неотрицательных величин. Следовательно, исходное уравнение имеет решение тогда и только тогда, когда оба слагаемых одновременно равны нулю. Уравнение равносильно системе уравнений: │F (x )│+│ G (x )│=0
Следовательно, исходное уравнение имеет решение тогда и только тогда, когда оба слагаемых одновременно равны нулю. Уравнение равносильно системе уравнений: │F (x )│+│ G (x )│=0 Примеры: №1 . Решите уравнение:
Ответ: х = 2. №2. Решите уравнение: Ответ: х = 1. Упражнения: №21. Решите уравнение: №22 . Решите уравнение, в ответе укажите сумму корней: №23 . Решите уравнение, в ответе укажите количество решений:
Раздел 8. Уравнения вида │а 1 х + в 1 │±│а 2 х + в 2 │± … │а n х +в n │= m
Для решения уравнений данного вида применяется метод интервалов. Если его решать последовательным раскрытием модулей, то получим n совокупностей систем, что очень громоздко и неудобно. Рассмотрим алгоритм метода интервалов: 1). Найти значения переменной х , при которых каждый модуль равен нулю (нули подмодульных выражений):2).
 Найденные значения отметить на числовой прямой, которая разбивается на интервалы (количество интервалов соответственно равно n +1 ) 3). Определить, с каким знаком раскрывается каждый модуль на каждом из полученных интервалов (при оформлении решения можно использовать числовую прямую, отметив на ней знаки) 4). Исходное уравнение равносильно совокупности n +1 систем, в каждой из которых указывается принадлежность переменной х одному из интервалов. Примеры: №1 . Решите уравнение, в ответе укажите наибольший корень:
Найденные значения отметить на числовой прямой, которая разбивается на интервалы (количество интервалов соответственно равно n +1 ) 3). Определить, с каким знаком раскрывается каждый модуль на каждом из полученных интервалов (при оформлении решения можно использовать числовую прямую, отметив на ней знаки) 4). Исходное уравнение равносильно совокупности n +1 систем, в каждой из которых указывается принадлежность переменной х одному из интервалов. Примеры: №1 . Решите уравнение, в ответе укажите наибольший корень: 1). Найдём нули подмодульных выражений: х = 2; х = -3 2). Отметим найденные значения на числовой прямой и определим, с каким знаком раскрывается каждый модуль на полученных интервалах:
х – 2 х – 2 х – 2 — — + — 3 2 х 2х + 6 2х + 6 2х + 6 — + + 3)
— нет решений Уравнение имеет два корня. Ответ: наибольший корень х = 2. №2. Решите уравнение, в ответе укажите целый корень:
1).
 Найдём нули подмодульных выражений: х = 1,5; х = — 1 2). Отметим найденные значения на числовой прямой и определим, с каким знаком раскрывается каждый модуль на полученных интервалах: х + 1 х + 1 х + 1 — + +
Найдём нули подмодульных выражений: х = 1,5; х = — 1 2). Отметим найденные значения на числовой прямой и определим, с каким знаком раскрывается каждый модуль на полученных интервалах: х + 1 х + 1 х + 1 — + +-1 1,5 х 2х – 3 2х – 3 2х – 3 — — +
3).
Последняя система не имеет решений, следовательно, уравнение имеет два корня. В ходе решения уравнения следует обратить внимание на знак « — » перед вторым модулем. Ответ: целый корень х = 7. №3. Решите уравнение, в ответе укажите сумму корней: 1). Найдём нули подмодульных выражений: х = 5; х = 1; х = — 2 2). Отметим найденные значения на числовой прямой и определим, с каким знаком раскрывается каждый модуль на полученных интервалах: х – 5 х – 5 х – 5 х – 5 — — — +
-2 1 5 х х – 1 х – 1 х – 1 х – 1 — — + + х + 2 х + 2 х + 2 х + 2 — + + +
3).
Уравнение имеет два корня х = 0 и 2. Ответ: сумма корней равна 2. №4 . Решите уравнение: 1). Найдём нули подмодульных выражений: х = 1; х = 2; х = 3.
 2). Определим, с каким знаком раскрывается каждый модуль на полученных интервалах. 3).
2). Определим, с каким знаком раскрывается каждый модуль на полученных интервалах. 3). Объединим решения первых трёх систем. Ответ: ; х = 5.
Упражнения: №24. Решите уравнение:
№25. Решите уравнение, в ответе укажите сумму корней: №26. Решите уравнение, в ответе укажите меньший корень:№27. Решите уравнение, в ответе укажите больший корень:
Раздел 9. Уравнения, содержащие несколько модулей
Уравнения, содержащие несколько модулей, предполагают наличие абсолютных величин в подмодульных выражениях. Основной принцип решения уравнений данного вида – это последовательное раскрытие модулей, начиная с «внешнего». В ходе решения используются приёмы, рассмотренные в разделах №1, №3.Примеры: №1. Решите уравнение:
Ответ: х = 1; — 11. №2. Решите уравнение:
Ответ: х = 0; 4; — 4. №3. Решите уравнение, в ответе укажите произведение корней:
Ответ: произведение корней равно – 8. №4. Решите уравнение:
№4. Решите уравнение:
Обозначим уравнения совокупности (1) и (2) и рассмотрим решение каждого из них отдельно для удобства оформления. Так как оба уравнения содержат более одного модуля, то удобнее осуществить равносильный переход к совокупностям систем.(1)
(2)
Ответ:
Упражнения: №36. Решите уравнение, в ответе укажите сумму корней: 5 │3х-5│ = 25 х №37. Решите уравнение, если корней более одного, в ответе укажите сумму корней: │х + 2│ х – 3х – 10 = 1 №38. Решите уравнение: 3 │2х -4│ = 9 │х│ №39. Решите уравнение, в ответе укажите количество корней на : 2 │ sin х│ = √2 №40 . Решите уравнение, в ответе укажите количество корней:
Раздел 3. Логарифмические уравнения.
Перед решением следующих уравнений необходимо повторить свойства логарифмов и логарифмической функции. Примеры: №1. Решите уравнение, в ответе укажите произведение корней: log 2 (х+1) 2 + log 2 │x+1│ = 6 О.Д.З. х+1≠0 х≠ — 1
Решите уравнение, в ответе укажите произведение корней: log 2 (х+1) 2 + log 2 │x+1│ = 6 О.Д.З. х+1≠0 х≠ — 11 случай: если х ≥ — 1, то log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – удовлетворяет условию х ≥ — 1 2 случай: если х log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = — 5 – удовлетворяет условию х — 1
Ответ: произведение корней равно – 15.
№2. Решите уравнение, в ответе укажите сумму корней: lg
О.Д.З.
Ответ: сумма корней равна 0,5.
№3. Решите уравнение: log 5
О.Д.З.
Ответ: х = 9. №4. Решите уравнение: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ О.Д.З. х > 0 Воспользуемся формулой перехода к другому основанию. │2 — log 5 x│+ 3 = │1 + log 5 x│
│2 — log 5 x│- │1 + log 5 x│= — 3 Найдём нули подмодульных выражений: х = 25; х = Эти числа делят область допустимых значений на три интервала, поэтому уравнение равносильно совокупности трёх систем.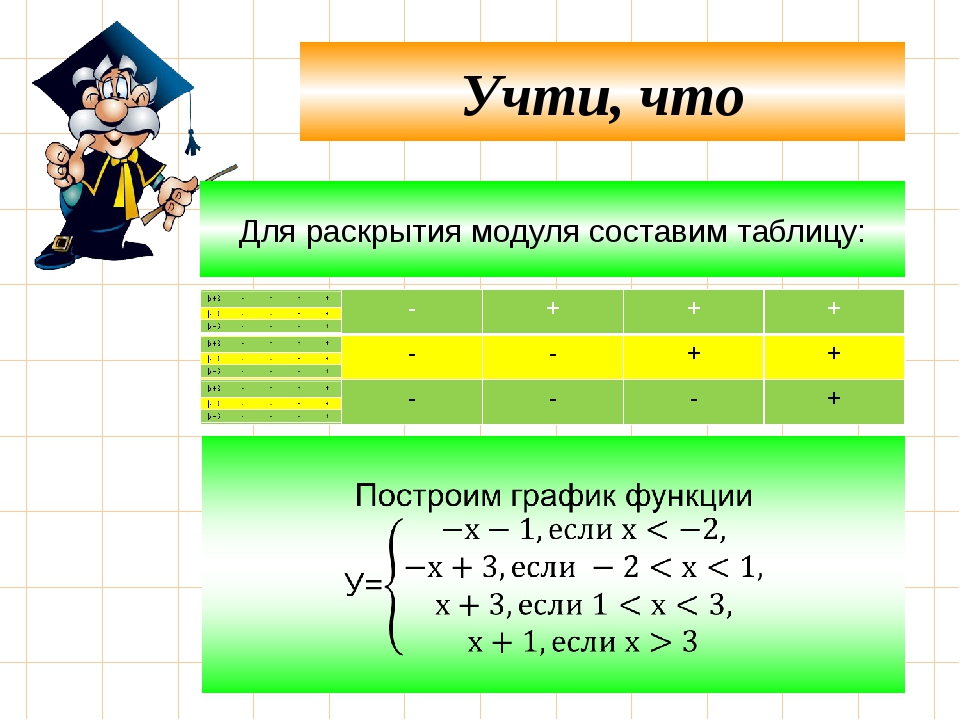
Ответ: }
Методические разработки по теме «решение уравнений с модулем в курсе алгебры 8 класса»
МЕТОДИЧЕСКИЕ РАЗРАБОТКИ ПО ТЕМЕ: «Решение уравнений с модулем в курсе алгебры 8 класса»
Давыдова Наталья Александровна, учитель математики МОУ «Лицей №4» Волжского района города Саратова
2008 год
Практически каждый учитель знает, какие проблемы вызывают у учащихся задания, содержащие модуль. Это один из самых трудных материалов, с которыми школьники сталкиваются на экзаменах.
Выбор темы обусловлен тем, что,
во-первых, задачи, связанные с абсолютными
величинами, часто встречаются на
математических олимпиадах и на
вступительных экзаменах в ВУЗы, во-вторых,
это понятие широко применяется не только
в различных разделах школьного курса
математики, но и в курсе высшей математики.
Так в математическом анализе понятие
абсолютной величины числа используется
при определении основных понятий:
предела, ограниченности функции и
других. В теории приближенных вычислений
употребляется понятие абсолютной
погрешности. В механике, в геометрии
изучается понятие вектора, одной из
характеристик которого служит его длина
(модуль вектора).
В теории приближенных вычислений
употребляется понятие абсолютной
погрешности. В механике, в геометрии
изучается понятие вектора, одной из
характеристик которого служит его длина
(модуль вектора).
Несмотря на то, что тема «Модуль числа» проходит «красной нитью» через весь курс школьной и высшей математики, для ее изучения по программе отводится очень мало времени (в 6 классе -2 часа, в 8 классе — 4 часа).
Исходя из всего вышесказанного,
учителю необходимо находить разнообразные
методические приемы, использовать
различные подходы и методы в обучении
решению задач с модулем. Разнообразие
методов будет способствовать сознательному
усвоению математических знаний,
вовлечению учащихся в творческую
деятельность, а также решению ряда
методических задач, встающих перед
учителем в процессе обучения, в частности,
реализации внутрипредметных связей
(алгебра-геометрия), расширению области
использования графиков, повышению
графической культуры учеников.
Указанные обстоятельства обусловили выбор темы творческой работы. Цель работы: показать необходимость более глубокого рассмотрения темы «Решение уравнений с модулем» в школьной программе; разработать методические рекомендации по использованию различных методов при решении задач с модулем.
Основные способы, используемые при решении уравнений, содержащих модуль.
Напомним основные понятия, используемые в данной теме. Уравнением с одной переменной называют равенство, содержащее переменную. Корнями уравнения называются значения переменной, при которых уравнение обращается в верное равенство. Решить уравнение – значит, найти все его корни или доказать, что корней нет. Уравнением с модулем называют равенство, содержащее переменную под знаком модуля.
При решении уравнений, содержащих
знак абсолютной величины, мы будем
основываться на определении модуля
числа и свойствах абсолютной величины
числа.
Существует несколько способов решения уравнений с модулем. Рассмотрим подробнее каждый из них.
1 способ. Метод последовательного раскрытия модуля.
Опорная информация:
Пример 1. Решим уравнение |х-5|=4.
Исходя из определения модуля, произведем следующие рассуждения. Если выражение, стоящее под знаком модуля неотрицательно, то есть х-5≥0, то уравнение примет вид х-5=4. Если значение выражения под знаком модуля отрицательно, то по определению оно будет равно – (х-5)=4 или х-5= -4. Решая полученные уравнения, находим: х1=9, х2=1.
Ответ: 9; 1.
Решим этим же способом уравнение, содержащее «модуль в модуле».
Пример 2. Решим уравнение ||2х-1|-4|=6.
Рассуждая аналогично, рассмотрим два случая.
1). |2х-1|-4=6, |2х-1|=10. Используя еще
раз определение модуля, получим: 2х-1=10
либо 2х-1= -10. Откуда х1=5,5,
х2= -4,5.
|2х-1|-4=6, |2х-1|=10. Используя еще
раз определение модуля, получим: 2х-1=10
либо 2х-1= -10. Откуда х1=5,5,
х2= -4,5.
2). |2х-1|-4= -6, |2х-1|= -2. Понятно, что в этом случае уравнение не имеет решений, так как по определению модуль всегда неотрицателен.
Ответ: 5,5; -4,5.
2 способ. Метод интервалов.
Опорная информация:
Метод интервалов – это метод разбиения числовой прямой на промежутки, в которых по определению модуля знак абсолютной величины можно будет снять. Для каждого из промежутков необходимо решить уравнение и сделать вывод относительно получившихся корней. Корни, удовлетворяющие промежуткам, и дадут окончательный ответ.
Пример 3. Решим уравнение |х+3|+|х-1|=6.
Найдем корни (нули) каждого
выражения, содержащегося под знаком
модуля: х+3=0, х= -3; х-1=0, х=1. Эти значения х
разбивают числовую прямую на три
промежутка:
Эти значения х
разбивают числовую прямую на три
промежутка:
Решим уравнение отдельно в каждом из получившихся промежутков. В первом промежутке (х < -3) оба выражения, стоящие под знаком модуля отрицательны, поэтому при записи уравнения без абсолютной величины знаки этих выражений меняем на противоположные. Получим уравнение:
-х-3-х+1=6. Откуда х= -4. Число -4 является решением данного уравнения, так как оно принадлежит рассматриваемому промежутку. Во втором промежутке (-3 ≤ х < 1) первое выражение положительно, а второе отрицательно. Рассуждая аналогично, получим уравнение: х+1-х+1=6, откуда получаем неверное числовое равенство, то есть в рассматриваемом промежутке уравнение корней не имеет. В последнем промежутке (х ≥ 1) оба выражения положительны, поэтому уравнение записывается так: х+3+х-1=6. Откуда х=2. Это значение удовлетворяет неравенству х ≥ 1. Ответ: -4; 2.
Пример 4. |2-х|=2х+1.
Прежде всего, следует установить область допустимых значений. Возникает естественный вопрос, почему в предыдущих примерах не было необходимости этого делать. В этом уравнении в правой части стоит выражение с переменной, которое может быть отрицательным. Таким образом, область допустимых значений – это промежуток [-½; +∞). Найдем нуль выражения, стоящего под знаком модуля: 2-х=0, х=2.
В первом промежутке: 2-х=2х+1, х=⅓. Это значение принадлежит ОДЗ, значит, является корнем уравнения.
Во втором промежутке: -2+х=2х+1, х= -3. -3 не принадлежит ОДЗ, а следовательно не является корнем уравнения. Ответ: ⅓.
3 способ. Графический метод.
Суть данного метода заключается
в использовании графиков функций для
нахождения корней уравнения. Этот метод
реже других применяют для решения
уравнений, содержащих модуль, так как,
во-первых, он занимает достаточно много
времени и не всегда рационален, а,
во-вторых, результаты, полученные при
построении графиков, не всегда являются
точными.
Пример 5. |х+1|=2. Построим графики функций у=|х+1| и у=2.
Для построения графика у=|х+1|, построим график функции у=х+1, а затем отразим часть прямой, лежащую ниже оси ОХ. Абсциссы точек пересечения графиков и есть корни уравнения: х1=1, х2= -3. Ответ: 1; -3.
Пример 6. |х2-1|=|4-х2|.
Построим графики функций у=|х2-1| и у=|4-х2|. Для этого построим графики функций у= х2-1 и у=4-х2, а затем отобразим часть графиков, лежащую ниже оси ОХ.
х1≈1,6; х2≈-1,6.
4 способ. Метод решения при помощи зависимостей между числами а и в, их модулями и квадратами этих чисел.
Опорная информация:
|а|=|в| а=в или а=-в;
а2=в2 а=в или а=-в; (1)
|а|=|в| а2=в2 (2)
Пример 7. Решим
уравнение |х2-8х+5|=|х2-5|.
Решим
уравнение |х2-8х+5|=|х2-5|.
Учитывая соотношение (1), получим:
х2-8х+5= х2-5 или х2-8х+5= -х2+5
х=1,25 х=0 или х=4.
Таким образом, корни исходного уравнения: х1=1,25; х2=0; х3=4.
Ответ: 1,25; 0; 4.
Пример 8. |х+3|=|х-5|.
В силу соотношения (2) получаем: (х+3)2=(х-5)2;
х2+6х+9= х2-10х+25;
х=1.
Ответ:1.
Пример 9. (1-3х)2=(х-2)2.
Учитывая соотношение (2), получаем: |1-3х|=|х-2|, откуда из соотношения (1), имеем:
1-3х=х-2 или 1-3х= -х+2
х=0,75 х= -0,5.
Ответ: 0,75; -0,5.
5 способ. Использование геометрической интерпретации модуля.
Опорная информация: геометрический смысл модуля разности величин – это расстояние между ними. Например, геометрический смысл выражения |х-а| — длина отрезка координатной оси, соединяющей точки с абсциссами а и х. Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких решений.
Пример 10. |х-2|+|х-3|=1.
Исходя из геометрической интерпретации модуля, левая часть уравнения представляет собой сумму расстояний от некоторой точки с абсциссой х до двух фиксированных точек с абсциссами 2 и 3. Тогда очевидно, что все точки с абсциссами, принадлежащими отрезку [2;3] обладают требуемым свойством, а точки, расположенные вне этого отрезка – нет. Отсюда, множеством решений уравнения является отрезок [2;3].
Ответ: [2;3].
Пример 11. |х-2|-|х-3|=1.
|х-2|-|х-3|=1.
Рассуждая аналогично, получим, что разность расстояний до точек с абсциссами 2 и 3 равна 1 только для точек, расположенных на координатной оси правее числа 3. Следовательно, решением данного уравнения будет являться луч, выходящий из точки 3, и направленный в положительном направлении оси ОХ.
Ответ: [3;+∞).
О
|х-а|+|х-в|=в-а, где в ≥ а а ≤ х ≤ в
|х-а|-|х-в|=в-а, где в ≥ а х ≥ в
бобщением вышеприведенных уравнений 10 и 11 являются следующие равносильные переходы:Проанализировав представленные способы решения уравнений, содержащих модуль, можно сделать вывод, что ни один из них не является универсальным и для получения наилучших результатов необходимо добиваться того, чтобы ученик овладел возможно большим количеством методов решения, оставляя право выбора решения за собой.
Методические
рекомендации по использованию методов
решения уравнений, содержащих модуль.
Практика обучения учащихся 7-8 классов способам решения уравнений, содержащих модули, позволила выявить достоинства и недостатки каждого способа, которые для удобства сведены в таблицу.
Способы | Достоинства | Недостатки |
Метод последовательного раскрытия модулей | 1). Объявляя условие раскрытия одного модуля, можно пользоваться им для раскрытия других модуле тем самым, выигрывая время в решении задачи. 2). Последовательность действий, направленных на поиск ответа, позволяет контролировать и проверять промежуточные результаты. | Необходимость раскрытия модуля, что для некоторых заданий приводит к потере темпа в получении ответа. |
Метод интервалов | Самый
эффективный способ, так как сопровождается
относительно небольшим объемом работы. | В силу необходимости нахождения концов интервалов может возникнуть ситуация, когда соответствующее уравнение либо вызывает серьезные затруднения при определении корней, либо недоступно ученику на данном этапе обучения. |
Графический метод | Данный способ имеет очень широкое применение в других темах школьного курса математики. | Ответ определяется приблизительно. |
Метод решения при помощи зависимостей между числами, их модулями и квадратами этих чисел | В некоторых случаях применение данного способа позволяет решать уравнения определенного вида на более раннем этапе. | В некоторых
случаях выбор данного способа приводит
к громоздкому решению, а иногда решение
сводится к уравнению, недоступному
для ученика на данном этапе обучения. |
Геометрическая интерпретация модуля | Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких решений. | Применение данного способа ограничивается уравнениями определенного вида. |
Проанализировав достоинства и недостатки каждого из указанных способов, можно с уверенностью сказать, что на мотивационном этапе формирования умения решать уравнения с модулем ученикам следует показывать все, доступные на данном этапе обучения способы решения, и, главное, на конкретных примерах доказывать, что первый этап решения – выбор самого эффективного способа.
Рассмотрим пример |х2+4х+3|=|х2-3|.
Решим это уравнение методом
интервалов. Для этого
найдем концы интервалов, решив уравнения
х2+4х+3=0 и
х2-3=0. В
результате х1=
-1, х2= -3, х3=,
х4=
-.
Видим, что первое уравнение –
квадратное, поэтому его решение недоступно
ученику седьмого класса, впрочем, также
как и второе уравнение, для решения
которого необходимо знание арифметического
квадратного корня. Кроме того, отметив
полученные числа на координатном луче,
получим пять промежутков, в каждом из
которых, предварительно сняв знак модуля
необходимо опять решить квадратное
уравнение.
В
результате х1=
-1, х2= -3, х3=,
х4=
-.
Видим, что первое уравнение –
квадратное, поэтому его решение недоступно
ученику седьмого класса, впрочем, также
как и второе уравнение, для решения
которого необходимо знание арифметического
квадратного корня. Кроме того, отметив
полученные числа на координатном луче,
получим пять промежутков, в каждом из
которых, предварительно сняв знак модуля
необходимо опять решить квадратное
уравнение.
Если же использовать четвертый способ (метод решения при помощи зависимостей между числами, их модулями и квадратами этих чисел), то это уравнение можно решить на более раннем этапе. Итак,
|х2+4х+3|=|х2-3| х2+4х+3=х2-3 или х2+4х+3= -х2+3.
х1= -1,5; х2=0; х3= -2.
Ответ: -1,5; -2; 0.
Ясно, что способ решения при помощи зависимостей между величинами, их модулями и квадратами величин, является самым эффективным для решения этого уравнения.
Рассмотрим пример |х-7|-|х-8|=1.
Решим это уравнение двумя способами.
а) метод интервалов: Найдем концы интервалов: х=7 и х=8. Отметим эти числа на координатной прямой, а затем решим уравнение в каждом из получившихся промежутков:
-х+7+х-8=1, х-7+х-8=1, х-7-х+8=1,
-1≠1, 2х=16, 1=1,
х=8 х – любое число
Ответ: [8;+∞).
б) использование
геометрической интерпретации. Использование равносильных переходов,
вытекающих из геометрической интерпретации,
позволяют сразу найти ответ: [8;+∞).
Использование равносильных переходов,
вытекающих из геометрической интерпретации,
позволяют сразу найти ответ: [8;+∞).
3. Рассмотрим пример |(х-1)(х-3)|=х-3. Это уравнение можно решить тремя способами.
а) последовательное раскрытие модуля:
Если (х-1)(х-3) ≥ 0, то Если (х-1)(х-3) < 0, то
х2-4х+3=х-3, х2-4х+3= -х+3,
х2-5х+6=0, х2-3х=0,
х1=3, х2=2. х1=0, х2=3.
2 – не удовлетворяет условию. 0, 3 — не удовлетворяет условию.
Ответ: 3.
б) метод интервалов: найдем концы интервалов, решив уравнение
(х-1)(х-3)=0, откуда х1=1,
х2=3.
(х-1)(х-3)=х-3, -(х-1)(х-3)=х-3, (х-1)(х-3)=х-3,
х1=2, х2=3. х1=0, х2=3. х1=2, х2=3.
2 (-∞; 1), 0 [1; 3). 2 [3; +∞).
3 (-∞; 1).
Ответ: 3.
в) графический метод: для решения уравнения построим в одной системе координат графики функций у=|х2-4х+3| и у=-3.
Построим у=|х2-4х+3|.
Для этого сначала рассмотрим функцию
у=х2-4х+3,
графиком которой является парабола,
ветви направлены вверх. Вершина параболы
в точке (2; -1). Строим график и отображаем
часть параболы, которая лежит ниже оси
ОХ в верхнюю полуплоскость. Далее в этой
же системе координат строим график
у=х-3. Графики функций пересеклись в
точке с абсциссой 3.
Графики функций пересеклись в
точке с абсциссой 3.
Ответ: 3.
Завершая рассмотрение различных способов решения уравнений, содержащих знак модуля, еще раз отметим тот важный факт, что ни один из них не является универсальным и для получения наилучших результатов необходимо добиваться того, чтобы ученик овладел возможно большим количеством методов решения, оставляя право выбора решения за собой.
Над проблемой применения различных способов для решения уравнений с модулем я работаю пятый год. За это время мною разработана и внедрена в практику методика обучения учащихся решению уравнений с модулем. Цель внедрения данной методики заключается в стремлении повысить качество умения решать уравнения, содержащие абсолютную величину.
Я работаю как в лицейских, так и
в общеобразовательных классах, где
интерес учащихся к математике невелик.
Исследование уровня обученности
показало, что решение уравнений,
содержащих знак абсолютной величины,
составляет большую трудность для
учащихся. В начале обучения использованию
различных методов для решения уравнений
ученики относились к ним настороженно,
стараясь, как можно чаще использовать
один метод для решения всех уравнений,
что иногда приводило к затруднениям.
Однако, со временем, поняв, что к каждому
уравнению можно подобрать наиболее
эффективный метод решения, дети стали
использовать для решения все способы
в зависимости от уравнения. Это привело
к повышению качества обученности решению
уравнений с модулем.
В начале обучения использованию
различных методов для решения уравнений
ученики относились к ним настороженно,
стараясь, как можно чаще использовать
один метод для решения всех уравнений,
что иногда приводило к затруднениям.
Однако, со временем, поняв, что к каждому
уравнению можно подобрать наиболее
эффективный метод решения, дети стали
использовать для решения все способы
в зависимости от уравнения. Это привело
к повышению качества обученности решению
уравнений с модулем.
Таким образом, можно сделать следующий вывод: систематическое использование различных способов для решения уравнений, содержащих абсолютную величину, приводит не только к повышению интереса к математике, повышению творческой активности школьников, но и повышает уверенность детей в собственных силах, так как у них имеется возможность выбора того способа решения, который наиболее эффективен в каждом конкретном случае.
Решение уравнений содержащих неизвестную под знаком модуля
1. 1.Определение модуля. Решение по определению.
1.Определение модуля. Решение по определению.По определению, модуль, или абсолютная величина,
неотрицательного числа a совпадает с самим числом, а модуль
отрицательного числа равен противоположному числу, то есть – a:
а, если а 0,
a
а, если а 0
Запишем решение простейших уравнений в общем виде:
x b, b 0
x b x 0, b 0
,
b 0
Пример. Решить уравнение |x –3| = 3 – 2x.
Рассматриваем два случая.
При x – 3> 0 уравнение принимает вид x – 3 = 3 – 2x, откуда x = 2. Но это
значение не удовлетворяет неравенству x – 3 > 0, потому не входит в ответ
исходного уравнения.
При x – 3
соответствующему условию x – 3
Итак, ответ к исходному уравнению: x = 0.
Ответ: х = 0.
1.2. Решение уравнений по правилам
1-е правило:
f ( x) g ( x),
f ( x) 0;
|f(x)| = g(x)
f ( x) g ( x),
f ( x) 0;
g ( x) 0;
2-е правило: |f(x)| = g(x) f ( x) g ( x),
f ( x) g ( x).
ЗАМЕЧАНИЕ.
 Фигурные скобки обозначают системы, а
Фигурные скобки обозначают системы, аквадратные – совокупности.
Решения системы уравнений – это значения переменной,
одновременно удовлетворяющие всем уравнениям системы.
Решениями совокупности уравнений являются все
значения переменной, каждое из которых есть корень хотя бы
одного из уравнений совокупности.
f ( x) g ( x),
|f(x)| = |g(x)|
f ( x) g ( x)
Пример . Решить уравнение |x2 – x – 6| = |2×2 + x – 1|.
Решение. Мы уже знаем, что рассматривать (целых 4) варианта
распределения знаков выражений под модулями здесь не нужно: это
уравнение равносильно совокупности двух квадратных уравнений без
каких-либо дополнительных неравенств:
x 2 x 6 2 x 2 x 1,
2
2
x
x
6
2
x
x 1.
Которая равносильна:
x 2 2 x 5 0,
2
3 x 7.
Первое уравнение совокупности решений не имеет (его дискриминант
отрицателен), второе уравнение имеет два корня .
Ответ:
7 7
;
3 3
Третий способ освобождения от модуля –
замена переменной
Пример .
 Решить уравнение:
Решить уравнение:x 7
2
x 7 30.
2
Решение. Заметим, что ( x 7) x 7 , тогда уравнение примет вид:
2
x 7 x 7 30 0.
2
Пусть
2
x 7 t , t 0 , тогда решим квадратное уравнение: t t 30 0
Его корни
t1 6, t2 5 , условию t 0
удовлетворяет первый корень.
Возвращаясь к переменной х, получаем уравнение
решая которое находим:
Ответ: .
x 13, x 1
x 13, x 1
x 7 6
Задачи с несколькими модулями.
Два основных подхода к решению.
«последовательное»
раскрытие модулей
Сначала один из модулей
изолируется в одной части
уравнения (или неравенства) и
раскрывается
одним
из
описанных
ранее
методов.
Затем
то
же
самое
повторяется с каждым из
получившихся в результате
уравнений с модулями и так
продолжается, пока мы не
избавимся ото всех модулей.
«параллельное»
раскрытие модулей
Можно снять сразу все модули
в уравнении или неравенстве и
выписать все возможные
сочетания знаков
подмодульных выражений.

При снятии модуля может
получить один из двух знаков –
плюс или минус. Эти области
определяются знаками
выражений под модулями.
Пример. Решить уравнение: 1 3х 4 3 х 12
Решение.
Уединим второй модуль и раскроем его, пользуясь первым
способом, то есть просто определением абсолютной величины:
К полученным двум уравнениям применяем второй способ освобождения от
модуля:
Наконец, решаем получившиеся
четыре
линейных
уравнения
и
отбираем те их корни, которые
удовлетворяют
соответствующим
неравенствам :
23
Ответ: -1;
7
Пример. Решить уравнение: 1 3х 4 3 х 12
Решение.
Рассмотрим 4 возможных набора знаков выражений под модулями.
Лишь первый и третий из этих корней удовлетворяют
соответствующим неравенствам, а значит, и исходному
уравнению.
Ответ: -1;
23
7
Метод интервалов в задачах с модулями.
Пусть имеется уравнение, в которое входят три модуля от
линейных выражений; например: |x – a| + |x – b| + |x – c| = m.

Первый модуль равен x – a при x ³ a и a – x при x
Второй равен x – b или b – x при x ³ b и x
Аналогично раскрывается и третий модуль. Нарисуем эти
области и возьмем их пересечения.
В
частности,
если все выражения под модулями
рациональны, то достаточно отметить на оси их корни, а
также точки, где они не определены, то есть корни их
знаменателей. Отмеченные точки и задают искомые
промежутки знакопостоянства.
Пример. Решить уравнение: x 2 x 3 x
.
Решение.
Найдем нули функции x+2=0 или x+3=0 , откуда x=-2 , x=-3.
Рассмотрим 3 возможных набора знаков выражений под модулями.
Решаем задачу на каждом интервале:
1) x 3 : x 2 x 3 x, 3 x 5 x
5
; 3
3
2) 3 x 2 : x 2 x 3 x, x 5 x 5 -3;-2
3) x 2 : x 2 x 3 x, x 5 x 5 -2;+
Итак, данное уравнение не имеет решений.
Ответ:
Вложенные модули
Последовательное
раскрытие
модулей
наиболее
эффективно в «задачах-матрешках», где внутри одного
модуля находится другой, а то и несколько.

Пример. Решить уравнение: x 1 2 3
Решение.
Освободимся от внешнего модуля, получим:
x 1 2 3,
x 1 1,
x 1 2 3;
x 1 5.
Второе уравнение совокупности решений не имеет, так как
модуль всегда положителен, а первое уравнение
x 1 1,
x 2,
равносильно совокупности:
x 1 1 x 0.
Ответ: 0; 2.
Модули и квадраты
Существует простой и быстрый способ освобождения от знака
f ( x) g ( x) f 2 x g 2 x
модуля в уравнениях вида |f(x)| = |g(x)|:
Он основан на двух очевидных соображениях. Вопервых, из двух неотрицательных чисел то больше, квадрат
которого больше, а если квадраты равны, то и числа равны:
a > b a2 > b2; a = b a2 = b2.
Во-вторых, квадрат модуля числа равен квадрату
самого числа: |a|2 = a2. Поэтому допускается такое
равносильное преобразование:
f ( x) g ( x)
2
2
f ( x) g ( x) f x g x f ( x) g ( x) f ( x) g ( x)
f ( x) g ( x)
Эту же идею можно применить к уравнениям или
неравенствам, одна часть которых равна нулю, а другая
содержит разность модулей как сомножитель.
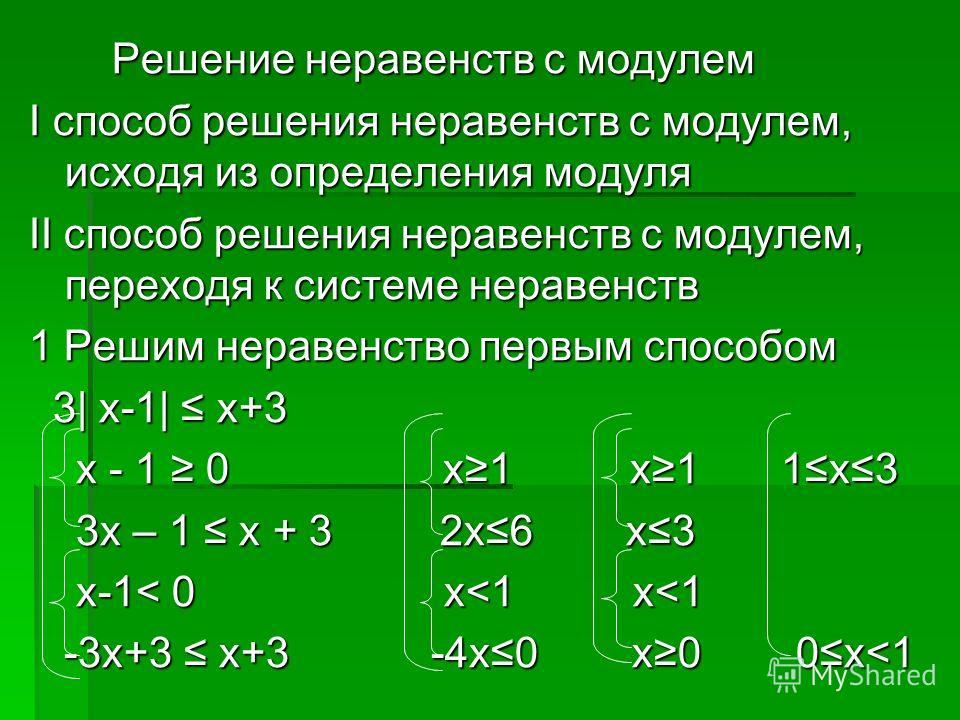 В такой задаче
В такой задачеразность модулей можно заменить разностью квадратов тех
2
2
же выражений: f ( x) g ( x) h( x) 0 f ( x) g ( x) h( x) 0
Модули неотрицательных выражений.
Пример 1. Решить уравнение: … x 1 … 10 55
Решение.
Нетрудно догадаться, что все выражения, стоящие под знаком
второго, третьего и т.д. модулей положительны. И поскольку модуль
положительного выражения равен самому этому выражению, получим
… x 1 … 10 55
x 1 2 … 10 55 x 0 x 0
Ответ: 0
Пример 2. Решить уравнение:
x2 2 x 1 x2 4 x 4 3
Решение.
f 2 ( x) f ( x)
Воспользуемся тождеством
, и получим
уравнение
x 1 x 2 3 , решая которое методом интервалов
получим ответ
Ответ:
x 2;
Графическое решение уравнений,
содержащих знак абсолютной величины.
Решить уравнение :
3| x + 2 | + x 2 + 6x + 2 = 0.
Для решения уравнения графическим способом,
надо построить графики функций
y 3 x 2
y x2 6x 2
Парабола пересеклась с «уголком» в
точках с координатами (-4; 6) и (-1; 3),
следовательно, решениями уравнения
будут абсциссы точек: x 1, x 4
Ответ:
x 1, x 4
Графическое решение уравнений,
содержащих знак абсолютной величины.

Решить равнение: | 4 – x | + | (x – 1)(x – 3) | = 3.
Для решения уравнения графическим
способом, надо построить графики функций
y 3 4 x
y x 1 x 3
Парабола пересеклась с «уголком» в
точках с координатами (1; 0), (2; 1) и
(4; 3), следовательно, решениями
уравнения будут абсциссы точек:
x 1, x 2, x 4
Ответ:
x 1, x 2, x 4
Графическое решение уравнений,
содержащих знак абсолютной величины.
1 x 2 y
Решить графически уравнение
x y 5
Для решения уравнения
графическим способом, надо
построить графики:
y 5 x
y 1 x2
-2
Эти графики пересекаются в
двух точках (-2; -3) и (2; 3),
следовательно, исходное
уравнение имеет два решения
x 2, x 2
Ответ:
x 2, x 2
2
Найти все значения а, при которых уравнение
(а 4 х х 1)(а 1 х 2 ) 0
2
имеет ровно три корня?
a x 4 x 1 0
Данное уравнение равносильно совокупности
Выражая параметр а, получаем:
a x 2 1 0
2
a x2 4 x 1
a x 2 1
График этой совокупности –
объединение
уголка
и
параболы.

Прямая а 1
-2
пересекает полученное
объединение в трех точках.
Ответ:
а 1
а
1
х
1
-1
-1
2
3
4
5
а = -1
Уравнение с модулем и параметром примеры. §6. Решение уравнений с модулями и параметрами. Сбор и использование персональной информации
10x − 5y − 3z = − 9,
6 x + 4 y − 5 z = − 1,3 x − 4 y − 6 z = − 23.
Уравняем коэффициенты при x в первом и втором уравнениях, для этого умножим обе части первого уравнения на 6, а второго уравнения – на 10, получаем:
60x − 30 y − 18z = − 54,60x + 40 y − 50z = − 10.
Вычитаем из второго уравнения полученной системы первое урав-
нение, получаем: 70 y − 32 z = 44, 35 y − 16 z = 22.
Из второго уравнения исходной системы вычитаем третье уравнение, умноженное на 2, получаем: 4 y + 8 y − 5 z + 12 z = − 1 + 46,
12 y + 7z = 45.
Теперь решаем новую систему уравнений:
35y
−
16z
=
22,12 y
+
7z
=
45.
К первому уравнению новой системы, умноженному на 7, прибавляем второе уравнение, умноженное на 16, получаем:
35 7 y + 12 16y = 22 7 + 45 16,
Теперь подставляем y = 2, z = 3 в первое уравнение исходной сис-
темы, получаем: 10x − 5 2 − 3 3 = − 9, 10x − 10 − 9 = − 9, 10x = 10, x = 1.
Ответ: (1; 2;3) . ▲
ax + 4 y = 2 a,
Рассмотрим систему уравнений
x + ay = a.
2010-2011 уч. год., № 3, 8 кл. Математика. Системы уравнений.
В этой системе, на самом деле, три переменные, а именно: a , x , y . Неизвестными считают x и y , a называют параметром. Требуется найти решения (x , y ) данной системы при каждом значении параметра a .
Покажем, как решают такие системы. Выразим переменную x из второго уравнения системы: x = a − ay . Подставляем это значение для x в первое уравнение системы, получаем:
a (a − ay) + 4 y = 2 a,
(2 − a )(2 + a ) y = a (2 − a ) .
Если a
=
2,
то получаем уравнение 0
y
=
0. Этому уравнению удовлетворяет любое число y
,
и тогда x
=
2
−
2
y
,
т. е. при a
=
2
пара чисел (2
−
2
y
;
y
)
является решением системы. Так как y
может быть
Этому уравнению удовлетворяет любое число y
,
и тогда x
=
2
−
2
y
,
т. е. при a
=
2
пара чисел (2
−
2
y
;
y
)
является решением системы. Так как y
может быть
любым числом, то система при a = 2 имеет бесконечно много решений.
Если a = − 2, то получаем уравнение 0 y = 8. Это уравнение не имеет ни одного решения.
Если теперь a ≠ ± 2, | то y = | a (2 − a) | |||||||
(2 − a )(2 + a ) | 2 + a | ||||||||
x = a − ay = a − | |||||||||
2 + a | |||||||||
Ответ: При a = 2 система имеет бесконечно много решений вида (2 − 2 y ; y ) , где y − любое число;
при a = − 2 система не имеет решений; | ||||||
при a ≠ ± 2, система имеет единственное решение | . | |||||
2 + a | 2 + a |
Мы решили эту систему и установили, при каких значениях параметра a система имеет одно решение, когда имеет бесконечно много решений и при каких значениях параметра a она не имеет решений.
Пример 1. Решите систему уравнений
© 2010, ФЗФТШ при МФТИ. Составитель: Яковлева Тамара Харитоновна
2010-2011 уч. год., № 3, 8 кл. Математика. Системы уравнений.
−3 | y − 1 | |||||||||||
3x
−
2 y
=
5. | ||||||||||||
Из второго уравнения системы выражаем x через y , получаем | ||||||||||||
2 y + 5 | подставляем это значение для x в первое уравнение сис- | |||||||||||
темы, получаем: | 2y + 5 | −3 | y − 1 | −3 | −1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5 = 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Выражение | y = − | y > − | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
; если | −5 | = −y | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Выражение y − 1 = 0, | если y
=
1. | y > 1, то | y − 1 | Y − 1, а ес- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ли y | y − 1 | 1 − y . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если y ≥ 1, то | y − 1 | Y −1 и | получаем уравнение: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
−3 (y | − 1) = 3, | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
−3 y | 3, − | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(2 2 + | 5
)
=
3. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
шением системы. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пусть теперь | 5 ≤ y | y − 1 | − y ; | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
нахождения | получаем | уравнение | 3 y −3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4 y + 10 | 3 y = 6, | 13 y = 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
© 2010, ФЗФТШ при МФТИ. Составитель: Яковлева Тамара Харитоновна
Составитель: Яковлева Тамара Харитоновна
2010-2011 уч. год., № 3, 8 кл. Математика. Системы уравнений.
(2 y + 5) = | ||||||||||||||||||||||||||||||
Но меньше, чем | поэтому пара чисел | |||||||||||||||||||||||||||||
является решением системы. | ||||||||||||||||||||||||||||||
y | то получаем уравнение: | 3 y −3 | ||||||||||||||||||||||||||||
4 y − | 3y = 6, | 5 y = | 28
,
y
=
28
. | значение | ||||||||||||||||||||||||||
поэтому решений нет. | ||||||||||||||||||||||||||||||
Таким образом, система имеет два решения (3;2) и 13
27
;
13
8
. ▲
▲
§ 4. Решение задач с помощью систем уравнений
Пример 1. Путь от города до посёлка автомобиль проезжает за 2,5 часа. Если он увеличит скорость на 20 км/ч, то за 2 часа он пройдёт путь на 15 км больший, чем расстояние от города до посёлка. Найдите это расстояние.
Обозначим через S расстояние между городом и посёлком и через V скорость автомобиля. Тогда для нахождения S получаем систему из двух уравнений
2,5V = S ,
(V + 20) 2 = S + 15.
© 2010, ФЗФТШ при МФТИ. Составитель: Яковлева Тамара Харитоновна
2010-2011 уч. год., № 3, 8 кл. Математика. Системы уравнений.
во второе уравнение: | S + 20 2 | S +15, | S = 25, | S = 125. | ||
Ответ:
125 км. ▲
▲
Пример 2. Сумма цифр двузначного числа равна 15. Если эти цифры поменять местами, то получится число, которое на 27 больше исходного. Найдите эти числа.
Пусть данное число ab , т.е. число десятков равно a , а число единиц равно b . Из первого условия задачи имеем: a + b = 15. Если из числа ba вычесть число ab , то получится 27, отсюда получаем второе уравнение: 10 b + a − (10 a + b ) = 27. x
2010-2011 уч. год., № 3, 8 кл. Математика. Системы уравнений.
Умножим обе части уравнения на 20, получим: x + 8 y = 840. Для нахождения x и y получили систему уравнений
Ответ: 40 т, 100 т. ▲
Пример 4. Оператор ЭВМ, работая с учеником, обрабатывает задачу за 2 ч 24 мин. Если оператор будет работать 2 ч, а ученик 1 ч, то бу-
дет выполнено 2 3 всей работы. Сколько времени потребуется операто-
ру и ученику в отдельности на обработку задачи?
Обозначим всю работу за 1, производительность оператора за x и производительность ученика за y . Учитываем, что
2 ч
24 мин
=
2 5
2
ч
=
12
5
ч
.
Из первого условия задачи следует, что (x+y ) 12 5 = 1. Из второго условия задачи следует, что 2 x + y = 2 3 . Получили систему уравнений
(x+y) | |||||||||||||||||||||||||||
2 x + y = | |||||||||||||||||||||||||||
Решаем эту систему методом подстановки: | |||||||||||||||||||||||||||
− 2 x ; | |||||||||||||||||||||||||||
−2 x | −x | − 1; | |||||||||||||||||||||||||
; x = | ; y = | ||||||||||||||||||||||||||
© 2010, ФЗФТШ при МФТИ. Составитель: Яковлева Тамара Харитоновна
Составитель: Яковлева Тамара Харитоновна
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цель урока. Решение уравнений с параметрами и модулями, применяя свойства функций в неожиданных ситуациях и освоение геометрических приемов решения задач. Нестандарные уравнения.
Задачи:
- Образовательные : научить решать некоторые виды уравнений уравнений модулями и параметрами;
- Развивающие : развивать культуру мысли, культуру речи и умение работать с тетрадью и доской.
- Воспитательные : воспитывать самостоятельность и умение преодолевать трудности.
Оборудование: наглядный материал для
устного счёта и объяснения новой темы. Интерактивная доска, мультимедийное
оборудование урока.
Интерактивная доска, мультимедийное
оборудование урока.
Структура урока:
- Повторение изученного материала (устный счёт).
- Изучение нового материала.
- Закрепление изученного материала.
- Итог урока.
- Домашнее задание.
ХОД УРОКА
1. Повторение важнейшего теоретического материала по темам: «Уравнения, содержащие модуль», «Решение уравнений с параметрами»
1) «Уравнения, содержащие модуль»
Абсолютной величиной или модулем числа a называется число a , если a > 0, число – a , если a a = 0. Или
Из определения следует, что | a | > 0
и | a | > a для всех a € R .
Неравенство | x | a
, (если a > 0) равносильно двойному неравенству – a х
a
.
Неравенство | x | a
, (если a 0.
Неравенство | x | > a , (если a > 0)
равносильно двум неравенствам
Неравенство | x | > a , (если a х
€ R.
2) «Решение уравнений с параметрами»
Решить уравнение с параметрами – значит указать, при каких значениях параметров существуют решения и каковы они.
а) определить множество допустимых значений неизвестного и параметров;
б) для каждой допустимой системы значений параметров найти соответствующие множества решений уравнения.
2. Устные упражнения
1. Решить уравнение | x – 2 | = 5; Ответ : 7; – 3
| x – 2 | = – 5; Ответ : решения нет
| x – 2 | = х + 5; Ответ : решения нет; 1,5
| x – 2 | = | x + 5 |; Ответ : решения нет; – 1,5; решения нет; – 1,5;
2. Решить уравнение: | x + 3 | + | y – 2 | = 4;
Расcмотрим четыре случая
| { | x + 3 > 0 | { | x > – 3 |
| y – 2 > 0 | y > 2 | ||
| x + 3 + y – 2 = 4 | y = – x + 3 |
| { | x + 3 > 0 | { | x > – 3 |
| y – 2 | y | ||
| x + 3 – y + 2 = 4 | y = x + 1 |
| { | x + 3 | { | x |
| y + 2 > 0 | y > – 2 | ||
| – x – 3 – y – 2 = 4 | y = x + 9 |
| { | x + 3 | { | x |
| y + 2 | y | ||
| – x – 3 – y – 2 = 4 | y = – x – 9 |
В результате мы получаем квадрат, центр
которого (–3; 2), а длина диагонали равна 8, причем
диагонали параллельны осям координат.
Из наглядных соображений можно сделать вывод: что уравнение вида | х + a | + | у + b | = с ; задает на плоскости квадрат с центром в точке (– а ; – b ), диагоналями параллельными осям OX и ОУ, и длина каждой диагонали равна 2с . Ответ : (– 3; 2).
2. Решить уравнение aх = 1
Ответ : если a = 0, то нет решения; если a = 0, то х = 1/ a
3. Решить уравнение (а 2 – 1) х = а + 1.
Решение .
Нетрудно сообразить, что при решении этого уравнения достаточно рассмотреть такие случаи:
1) а = 1; тогда уравнение принимает вид ОX = 2 и не имеет решения
2) а = – 1; получаем ОX = О, и очевидно х – любое.
1
3) если а = + 1, то х = –––
а – 1
Ответ:
если а = – 1, то х – любое;
если а = 1, то нет решения;
1
если а = + 1 , то х = –––
а – 1
3. Решения примеров (из вариантов С)
Решения примеров (из вариантов С)
1. При каком значении параметра р уравнение | х 2 – 5х + 6 | + | х 2 – 5х + 4 | = р имеет четыре корня.
Рассмотрим функцию у = | х 2 – 5х + 6 | + | х 2 – 5х + 4 |
Так как х 2 – 5х + 6 = (х – 2)(х – 3) и х 2 – 5х + 4 = (х – 1)(х – 4), то y = | (х – 2)(х – 3) | + | (х – 1)(х – 4) |, корни квадратных трехчленов отметим на числовой прямой
1 2 3 4 х
Числовая прямая при этом разбивает на 5 промежутков
| { | x | { | x |
| y = x 2 – 5x + 6 + x 2 – 5x + 4 | y = 2x 2 – 10x + 10 |
| { | 1 x | { | 1 x |
| y = x 2 – 5x + 6 – x 2 + 5x – 4 | y = 2 |
| { | 2 x | { | 2 x |
| y = – 2x 2 + 10x – 10 | y = – x 2 + 5x – 6 – x 2 + 5x – 4 |
| { | 3 x | { | 3 x |
| y = 2 | y = x 2 – 5x + 6 – x 2 + 5x – 4 |
| { | x > 4 | { | x > 4 |
| y = 2x 2 – 10x + 10 | y = x 2 – 5x + 6 + x 2 –5x + 4 |
Для случая 3) х 0 = – b | 2a = 2, y 0 = 25: 2 + 25 – 10 = 2,5
Итак, (2,5; 2,5) – координаты вершины параболы y = – 2x 2 + 10x – 10.
Построим график функции, заданной равенством
Как видно из рисунка, исходное уравнение имеет четыре корня, если 2 а
Ответ : при 2 а
4. Самостоятельная работа по уровням
1 уровень
1. Решить уравнение х 2 – | x | = 6
2. При каких целых значениях а имеет единственное
решение уравнение ах 2 – (а + 1) + а 2
+ а = 0?
2 уровень
1. Решить уравнение: | x – 5 | – | 2x + 3 | = 10
а –12) х 2 + 2 =
2(12 – а ) имеет два различных корня?
3 уровень
1. Решить уравнение | x – 5 | – | 2x + 3| = 10
2. Найти все значениях параметра а, при
которых уравнение (а – 12) х 2 + 2 = 2(12
– а ) имеет два различных корня?
5. Итог урока
1. Определение модуля.
2. Что значит решить уравнение с параметром?
6. Задание на дом. C5 варианта №11 Ф.Ф.
Лысенко. Математика, 2012
Задание на дом. C5 варианта №11 Ф.Ф.
Лысенко. Математика, 2012
1. Системы линейных уравнений с параметром
Системы линейных уравнений с параметром решаются теми же основными методами, что и обычные системы уравнений: метод подстановки, метод сложения уравнений и графический метод. Знание графической интерпретации линейных систем позволяет легко ответить на вопрос о количестве корней и их существовании.
Пример 1.
Найти все значения для параметра а, при которых система уравнений не имеет решений.
{х + (а 2 – 3)у = а,
{х + у = 2.
Решение.
Рассмотрим несколько способов решения данного задания.
1 способ . Используем свойство: система не имеет решений, если отношение коэффициентов перед х равно отношению коэффициентов перед у, но не равно отношению свободных членов (а/а 1 = b/b 1 ≠ c/c 1). Тогда имеем:
1/1 = (а 2 – 3)/1 ≠ а/2 или систему
{а 2 – 3 = 1,
{а ≠ 2.
Из первого уравнения а 2 = 4, поэтому с учетом условия, что а ≠ 2, получаем ответ.
Ответ: а = -2.
2 способ . Решаем методом подстановки.
{2 – у + (а 2 – 3)у = а,
{х = 2 – у,
{(а 2 – 3)у – у = а – 2,
{х = 2 – у.
После вынесения в первом уравнении общего множителя у за скобки, получим:
{(а 2 – 4)у = а – 2,
{х = 2 – у.
Система не имеет решений, если первое уравнение не будет иметь решений, то есть
{а 2 – 4 = 0,
{а – 2 ≠ 0.
Очевидно, что а = ±2, но с учетом второго условия в ответ идет только ответ с минусом.
Ответ: а = -2.
Пример 2.
Найти все значения для параметра а, при которых система уравнений имеет бесконечное множество решений.
{8х + ау = 2,
{ах + 2у = 1.
Решение.
По свойству, если отношение коэффициентов при х и у одинаковое, и равно отношению свободных членов системы, то она имеет бесконечное множество решений (т. е. а/а 1 = b/b 1 = c/c 1). Следовательно 8/а = а/2 = 2/1. Решая каждое из полученных уравнений находим, что а = 4 – ответ в данном примере.
е. а/а 1 = b/b 1 = c/c 1). Следовательно 8/а = а/2 = 2/1. Решая каждое из полученных уравнений находим, что а = 4 – ответ в данном примере.
Ответ: а = 4.
2. Системы рациональных уравнений с параметром
Пример 3.
{3|х| + у = 2,
{|х| + 2у = a.
Решение.
Умножим первое уравнение системы на 2:
{6|х| + 2у = 4,
{|х| + 2у = a.
Вычтем из первого второе уравнение, получим 5|х| = 4 – а. Это уравнение будет иметь единственное решение при а = 4. В других случаях это уравнение будет иметь два решения (при а 4).
Ответ: а = 4.
Пример 4.
Найти все значения параметра а, при которых система уравнений имеет единственное решение.
{х + у = а,
{у – х 2 = 1.
Решение.
Данную систему решим с использованием графического метода. Так, графиком второго уравнения системы является парабола, поднятая по оси Оу вверх на один единичный отрезок. Первое уравнение задает множество прямых, параллельных прямой y = -x (рисунок 1) . Из рисунка хорошо видно, что система имеет решение, если прямая у = -х + а является касательной к параболе в точке с координатами (-0,5; 1,25). Подставив в уравнение прямой вместо х и у эти координаты, находим значение параметра а:
Первое уравнение задает множество прямых, параллельных прямой y = -x (рисунок 1) . Из рисунка хорошо видно, что система имеет решение, если прямая у = -х + а является касательной к параболе в точке с координатами (-0,5; 1,25). Подставив в уравнение прямой вместо х и у эти координаты, находим значение параметра а:
1,25 = 0,5 + а;
Ответ: а = 0,75.
Пример 5.
Используя метод подстановки, выясните, при каком значении параметра а, система имеет единственное решение.
{ах – у = а + 1,
{ах + (а + 2)у = 2.
Решение.
Из первого уравнения выразим у и подставим во второе:
{у = ах – а – 1,
{ах + (а + 2)(ах – а – 1) = 2.
Приведем второе уравнение к виду kx = b, которое будет иметь единственное решение при k ≠ 0. Имеем:
ах + а 2 х – а 2 – а + 2ах – 2а – 2 = 2;
а 2 х + 3ах = 2 + а 2 + 3а + 2.
Квадратный трехчлен а 2 + 3а + 2 представим в виде произведения скобок
(а + 2)(а + 1), а слева вынесем х за скобки:
(а 2 + 3а)х = 2 + (а + 2)(а + 1).
Очевидно, что а 2 + 3а не должно быть равным нулю, поэтому,
а 2 + 3а ≠ 0, а(а + 3) ≠ 0, а значит а ≠ 0 и ≠ -3.
Ответ: а ≠ 0; ≠ -3.
Пример 6.
Используя графический метод решения, определите, при каком значении параметра а, система имеет единственное решение.
{х 2 + у 2 = 9,
{у – |х| = а.
Решение.
Исходя из условия, строим окружность с центром в начале координат и радиусом 3 единичных отрезка, именно ее задает первое уравнение системы
х 2 + у 2 = 9. Второе уравнение системы (у = |х| + а) – ломаная. С помощью рисунка 2 рассматриваем все возможные случаи ее расположения относительно окружности. Легко видеть, что а = 3.
Ответ: а = 3.
Остались вопросы? Не знаете, как решать системы уравнений?
Чтобы получить помощь репетитора – .
Первый урок – бесплатно!
blog.сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
«Линейное уравнение с двумя переменными» — Равенство, содержащее две переменные, называется уравнением с двумя переменными. -Что называется уравнением с двумя переменными? Приведите примеры. -Какое уравнение с двумя переменными называется линейным? Линейное уравнение с двумя переменными. Определение: Алгоритм доказательства, что данная пара чисел является решением уравнения:
«Решение показательных уравнений» — Сведение к одному основанию. Вынесение за скобки. Т. Виета. Графический способ. Показательным уравнением называют уравнение, содержащее переменную в показателе степени. Решение показательных уравнений. Устная работа. ab+ac=a(b+c). Степени. 2.Решить уравнение: Свойство. Виды и способы решения показательных уравнений.
«Графический способ решения уравнений» — Ответ: один корень, х=-1. Два корня. Решить графически уравнение (х+1)/(х-2)=2. Построить график функции y=x?+6x+8. Практикум по решению уравнений графическим способом Подготовка к зачету. Построить графики функций. Построить график функции y=(x+1)/(x-2). 1. Перенесем 8 в правую часть уравнения. Корней нет.
Построить график функции y=(x+1)/(x-2). 1. Перенесем 8 в правую часть уравнения. Корней нет.
«Решение целых уравнений» — «Уравнения, в которых скопом Корни, степень, неравенств бездна. Три великих математика. Удачи в дальнейшем изучении методов решения уравнений. Осевая симметрия присуща большинству видов растений и животных. Центральная. В животном мире 2 вида симметрии. Диктант. Осевая. Определите методы решения уравнений.
«Уравнения с логарифмами» — Логарифмические уравнения. Реши устно уравнения. Формулы преобразования логарифмов. Уравнение. Определение. Таблицы логарифмов. Определение логарифма. Определение и свойства логарифма. Логарифмическая линейка. Функция. Наушники или колонки. Область определения. Подходы к решению. Решить уравнение. Гимназия.
«Иррациональные уравнения» — На контроль д/з выполнили: №419 (в,г) Сафиуллина, №418(в,г) Кульмухаметов, №420(в,г)Шагеев. 2 урок Решение систем уравнений. Урок 1 Тема: Решение иррациональных уравнений. 1.Какие из следующих уравнений являются иррациональными: Цели: Познакомить учащихся с решениями некоторых видов иррациональных уравнений.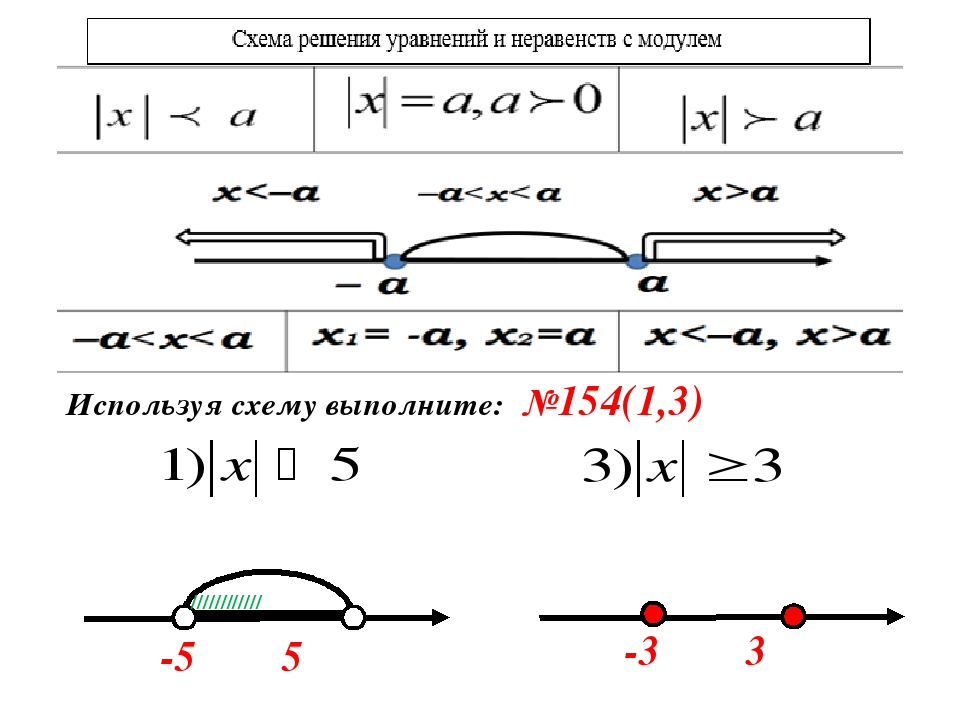
Всего в теме 49 презентаций
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
6.3: Объединение законов газа: уравнение идеального газа и общее уравнение газа
Цели обучения
- Чтобы использовать закон идеального газа для описания поведения газа.

В этом модуле описываются отношения между давлением, температурой, объемом и количеством газа, а также то, как эти отношения могут быть объединены для получения общего выражения, описывающего поведение газа.
Вывод закона об идеальном газе
Любой набор взаимосвязей между одной величиной (например, V) и несколькими другими переменными (\ (P \), \ (T \) и \ (n \)) может быть объединен в одно выражение, описывающее все взаимосвязи. одновременно.Три отдельных выражения выглядят следующим образом:
\ [V \ propto \ dfrac {1} {P} \; \; \ text {@ constant n и T} \]
\ [V \ propto T \; \; \ text {@ constant n и P} \]
\ [V \ propto n \; \; \ text {@ постоянные T и P} \]
Объединение этих трех выражений дает
\ [V \ propto \ dfrac {nT} {P} \ tag {6.3.1} \]
, который показывает, что объем газа пропорционален количеству молей и температуре и обратно пропорционален давлению.Это выражение также можно записать как
\ [V = {\ rm Cons. } \ Left (\ dfrac {nT} {P} \ right) \ tag {6.3.2} \]
} \ Left (\ dfrac {nT} {P} \ right) \ tag {6.3.2} \]
По соглашению, константа пропорциональности в уравнении 6.3.1 называется газовой постоянной, которая обозначается буквой \ (R \). Вставка R в уравнение 6.3.2 дает
\ [V = \ dfrac {Rnt} {P} = \ dfrac {nRT} {P} \ tag {6.3.3} \]
Удаление дробей путем умножения обеих частей уравнения 6.3.4 на \ (P \) дает
\ [PV = nRT \ tag {6.3.4} \]
Это уравнение известно как закон для идеального газа .
Идеальный газ определяется как гипотетическое газообразное вещество, поведение которого не зависит от сил притяжения и отталкивания и может быть полностью описано законом идеального газа. На самом деле идеального газа не существует, но идеальный газ — это полезная концептуальная модель, которая позволяет нам понять, как газы реагируют на изменяющиеся условия. Как мы увидим, при многих условиях большинство реальных газов демонстрируют поведение, очень близкое к поведению идеального газа. Таким образом, закон идеального газа можно использовать для предсказания поведения реальных газов в большинстве условий.Закон идеального газа плохо работает при очень низких температурах или очень высоких давлениях, где чаще всего наблюдаются отклонения от идеального поведения.
Таким образом, закон идеального газа можно использовать для предсказания поведения реальных газов в большинстве условий.Закон идеального газа плохо работает при очень низких температурах или очень высоких давлениях, где чаще всего наблюдаются отклонения от идеального поведения.
Примечание
Значительные отклонения от поведения идеального газа обычно возникают при низких температурах и очень высоких давлениях.
Однако, прежде чем мы сможем использовать закон идеального газа, нам необходимо знать значение газовой постоянной R. Ее форма зависит от единиц, используемых для других величин в выражении. Если V выражается в литрах (л), P в атмосферах (атм), T в кельвинах (K) и n в молях (моль), то
\ [R = 0.5 \; Па \]
Обратите внимание, что STP в части определен иначе. Старое определение было основано на стандартном давлении 1 атм.
Мы можем рассчитать объем 1.000 моль идеального газа при стандартных условиях, используя вариант закона идеального газа, приведенный в уравнении 6. 3.4:
3.4:
\ [V = \ dfrac {nRT} {P} \ tag {6.3.7} \]
Таким образом, объем 1 моля идеального газа равен 22,71 л при STP и 22,41 л при 0 ° C и 1 атм , что примерно эквивалентно объему трех баскетбольных мячей.Молярные объемы нескольких реальных газов при 0 ° C и 1 атм приведены в таблице 10.3, которая показывает, что отклонения от поведения идеального газа довольно малы. Таким образом, закон идеального газа хорошо аппроксимирует поведение реальных газов при 0 ° C и 1 атм. Отношения, описанные в разделе 10.3 как законы Бойля, Чарльза и Авогадро, являются просто частными случаями закона идеального газа, в котором два из четырех параметров (P, V, T и n) остаются фиксированными.
| Газ | Молярный объем (л) |
|---|---|
| He | 22. 434 434 |
| Ар | 22,397 |
| H 2 | 22,433 |
| № 2 | 22,402 |
| О 2 | 22,397 |
| CO 2 | 22,260 |
| NH 3 | 22.079 |
Применение закона об идеальном газе
Закон идеального газа позволяет нам вычислить значение четвертой переменной для газовой пробы, если мы знаем значения любых трех из четырех переменных ( P , V , T и n ).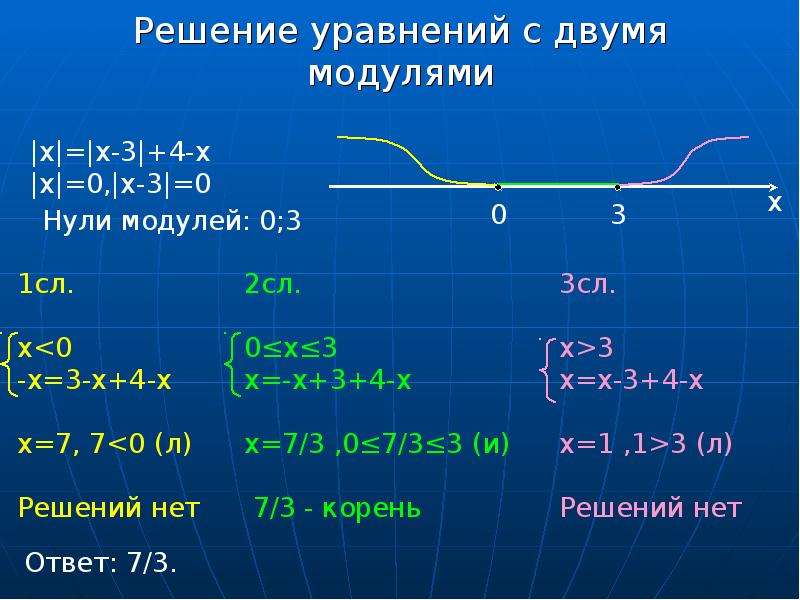 Это также позволяет нам предсказать конечное состояние образца газа (то есть его конечную температуру, давление, объем и количество) после любых изменений условий, если параметры ( P , V , T и n ) указаны для начального состояния . Некоторые приложения показаны в следующих примерах. Подход, используемый повсюду, всегда заключается в том, чтобы начинать с одного и того же уравнения — закона идеального газа — а затем определять, какие количества даны, а какие необходимо рассчитать. Давайте начнем с простых случаев, когда нам даны три из четырех параметров, необходимых для полного физического описания газового образца.
Это также позволяет нам предсказать конечное состояние образца газа (то есть его конечную температуру, давление, объем и количество) после любых изменений условий, если параметры ( P , V , T и n ) указаны для начального состояния . Некоторые приложения показаны в следующих примерах. Подход, используемый повсюду, всегда заключается в том, чтобы начинать с одного и того же уравнения — закона идеального газа — а затем определять, какие количества даны, а какие необходимо рассчитать. Давайте начнем с простых случаев, когда нам даны три из четырех параметров, необходимых для полного физического описания газового образца.
Пример \ (\ PageIndex {1} \)
Воздушный шар, который Чарльз использовал во время своего первого полета в 1783 году, был разрушен, но мы можем оценить, что его объем составлял 31 150 л (1100 футов 3 ), учитывая размеры, зарегистрированные в то время.Если температура на уровне земли составляла 86 ° F (30 ° C), а атмосферное давление составляло 745 мм рт. Ст., Сколько молей газообразного водорода требовалось для заполнения воздушного шара?
Ст., Сколько молей газообразного водорода требовалось для заполнения воздушного шара?
Дано: объем, температура и давление
Запрошено: количество газа
Стратегия:
- Решите закон идеального газа для неизвестной величины, в данном случае n .
- Убедитесь, что все величины указаны в единицах, совместимых с единицами газовой постоянной.При необходимости преобразуйте их в соответствующие единицы, вставьте их в полученное уравнение, а затем вычислите необходимое количество молей газообразного водорода.
Решение:
A Нам даны значения для P , T и V и попросили вычислить n . Если мы решим закон идеального газа (уравнение 6.3.4) для n , мы получим
\ [\ rm745 \; мм рт. Ст. \ Раз \ dfrac {1 \; атм} {760 \; мм рт. Ст.} = 0,980 \; атм \]
B P и T даны в единицах, которые несовместимы с единицами измерения газовой постоянной [ R = 0. 3 \; моль \]
3 \; моль \]
Упражнение \ (\ PageIndex {1} \)
Предположим, что «пустой» баллончик с аэрозольной краской имеет объем 0,406 л и содержит 0,025 моль газа-вытеснителя, такого как CO 2 . Какое давление газа при 25 ° C?
Ответ: 1,5 атм
В примере \ (\ PageIndex {1} \) нам были даны три из четырех параметров, необходимых для описания газа при определенном наборе условий, и нам было предложено вычислить четвертый. Мы также можем использовать закон идеального газа для расчета влияния изменений в любом из указанных условий на любой из других параметров, как показано в примере \ (\ PageIndex {5} \).
Общее уравнение газа
Когда газ описывается в двух разных условиях, уравнение идеального газа должно применяться дважды — к начальному и конечному условию. Это:
\ [\ begin {array} {cc} \ text {Initial condition} (i) & \ text {Final condition} (f) \\ P_iV_i = n_iRT_i & P_fV_f = n_fRT_f \ end {array} \]
Оба уравнения можно переставить так, чтобы получилось:
\ [R = \ dfrac {P_iV_i} {n_iT_i} \ hspace {1cm} R = \ dfrac {P_fV_f} {n_fT_f} \]
Два уравнения равны друг другу, поскольку каждое из них равно одной и той же константе \ (R \). Следовательно, имеем:
Следовательно, имеем:
\ [\ dfrac {P_iV_i} {n_iT_i} = \ dfrac {P_fV_f} {n_fT_f} \ tag {6.3.8} \]
Уравнение называется общим уравнением газа . Уравнение особенно полезно, когда одно или два свойства газа поддерживаются постоянными между двумя условиями. В таких случаях уравнение можно упростить, исключив эти постоянные свойства газа.
Пример \ (\ PageIndex {2} \)
Предположим, что Чарльз изменил свои планы и выполнил свой первый полет не в августе, а в холодный январский день, когда температура на уровне земли была -10 ° C (14 ° F).Какого размера ему понадобился бы воздушный шар, чтобы в нем содержалось такое же количество газообразного водорода при том же давлении, что и в примере \ (\ PageIndex {1} \)?
Дано: температура, давление, количество и объем в августе; температура января
Запрошено: объема в январе
Стратегия:
- Используйте результаты из примера \ (\ PageIndex {1} \) для августа в качестве начальных условий, а затем вычислите изменение объема из-за изменения температуры с 30 ° C до -10 ° C.
 Начните с построения таблицы, показывающей начальные и конечные условия.
Начните с построения таблицы, показывающей начальные и конечные условия. - Упростите общее уравнение газа, исключив величины, которые остаются постоянными между начальными и конечными условиями, в данном случае \ (P \) и \ (n \).
- Найдите неизвестный параметр.
Решение:
A Чтобы точно увидеть, какие параметры изменились, а какие являются постоянными, подготовьте таблицу начальных и конечных условий:
| Начальное (август) | Финал (январь) |
| \ (T_i = 30 \) ° С = 303 К | \ (T_f = \) -10 ° С = 263 К |
| \ (P_i = \) 0.980 атм | \ (P_f = \) 0,980 атм |
| \ (n_i = \) 1,23 × 103 моль | \ (n_f = \) 1,23 × 103 моль |
| \ (V_i = 31150 \) L | \ (V_f =? \) |
B И \ (n \), и \ (P \) одинаковы в обоих случаях (\ (n_i = n_f, P_i = P_f \)). Следовательно, уравнение можно упростить до:
Следовательно, уравнение можно упростить до:
\ [\ dfrac {V_i} {T_i} = \ dfrac {V_f} {T_f} \]
Эту связь впервые заметил Чарльз.4 \; L \]
Важно проверить свой ответ, чтобы убедиться, что он имеет смысл, на тот случай, если вы случайно перевернули количество или умножили, а не разделили. В этом случае температура газа понижается. Поскольку мы знаем, что объем газа уменьшается с понижением температуры, конечный объем должен быть меньше начального, поэтому ответ имеет смысл. Мы могли бы рассчитать новый объем, подставив все заданные числа в закон идеального газа, но, как правило, гораздо проще и быстрее сосредоточиться только на тех количествах, которые меняются.
Упражнение \ (\ PageIndex {2} \)
На вечеринке в лаборатории наполненный гелием баллон объемом 2,00 л при 22 ° C опускают в большой контейнер с жидким азотом (T = -196 ° C). Каков конечный объем газа в баллоне?
Ответ : 0,52 л
Пример \ (\ PageIndex {1} \) иллюстрирует взаимосвязь, первоначально наблюдаемую Чарльзом. Мы могли бы проработать аналогичные примеры, иллюстрирующие обратную зависимость между давлением и объемом, отмеченную Бойлем ( PV = константа), и взаимосвязь между объемом и количеством, наблюдаемую Авогадро ( V, / n = постоянная).Однако мы не будем этого делать, потому что более важно отметить, что исторически важные законы газа — это только частные случаи закона идеального газа, в котором две величины меняются, а две другие остаются фиксированными. Метод, использованный в Примере \ (\ PageIndex {1} \), может быть применен в в любом таком случае , как мы демонстрируем в Примере \ (\ PageIndex {2} \) (который также показывает, почему нагревание закрытого баллона с газом (например, баллончик с бутановой зажигалкой или аэрозольный баллончик, могут вызвать взрыв).
Мы могли бы проработать аналогичные примеры, иллюстрирующие обратную зависимость между давлением и объемом, отмеченную Бойлем ( PV = константа), и взаимосвязь между объемом и количеством, наблюдаемую Авогадро ( V, / n = постоянная).Однако мы не будем этого делать, потому что более важно отметить, что исторически важные законы газа — это только частные случаи закона идеального газа, в котором две величины меняются, а две другие остаются фиксированными. Метод, использованный в Примере \ (\ PageIndex {1} \), может быть применен в в любом таком случае , как мы демонстрируем в Примере \ (\ PageIndex {2} \) (который также показывает, почему нагревание закрытого баллона с газом (например, баллончик с бутановой зажигалкой или аэрозольный баллончик, могут вызвать взрыв).
Пример \ (\ PageIndex {3} \)
Аэрозольные баллончики имеют заметную этикетку с предупреждением, например: «Не сжигайте пустой контейнер.Предположим, что вы не заметили этого предупреждения и бросили «пустой» аэрозольный баллон в упражнении 5 (0,025 моль в 0,406 л, первоначально при 25 ° C и внутреннем давлении 1,5 атм) в огонь при температуре 750 ° C. \ circ C = 1023 \; K \)
\ circ C = 1023 \; K \)
И \ (V \), и \ (n \) одинаковы в обоих случаях (\ (V_i = V_f, n_i = n_f \)). Следовательно, уравнение можно упростить до:
\ [P_iT_i = P_fT_f \]
Решая уравнение для \ (P_f \), получаем:
\ [P_f = P_i \ times \ dfrac {T_i} {T_f} = \ rm1.5 \; atm \ times \ dfrac {1023 \; K} {298 \; K} = 5.1 \; atm \]
Этого давления более чем достаточно, чтобы разорвать контейнер из тонкого листового металла и вызвать взрыв!
Упражнение \ (\ PageIndex {3} \)
Предположим, что огнетушитель залит СО 2 до давления 20.0 атм при 21 ° C на заводе, случайно оставлен на солнце в закрытом автомобиле в Тусоне, штат Аризона, в июле. Температура в салоне автомобиля повышается до 160 ° F (71,1 ° C). Какое внутреннее давление в огнетушителе?
Ответ : 23,4 атм
В примерах \ (\ PageIndex {1} \) и \ (\ PageIndex {2} \) два из четырех параметров ( P , V , T и n ) были исправлены, а одному было разрешено варьироваться, и нас интересовало влияние на ценность четвертого. Фактически, мы часто сталкиваемся со случаями, когда две из переменных P , V и T могут изменяться для данного образца газа (следовательно, n является постоянным), и мы заинтересованы в изменении в стоимости третьего в новых условиях.
Фактически, мы часто сталкиваемся со случаями, когда две из переменных P , V и T могут изменяться для данного образца газа (следовательно, n является постоянным), и мы заинтересованы в изменении в стоимости третьего в новых условиях.
Пример \ (\ PageIndex {4} \)
В примере \ (\ PageIndex {1} \) мы видели, что Чарльз использовал воздушный шар объемом 31 150 л для своего начального подъема и что воздушный шар содержал 1,23 × 10 3 моль газа H 2 первоначально при 30 ° C. ° C и 745 мм рт.Предположим, что Гей-Люссак также использовал этот аэростат для своего рекордного подъема на высоту 23 000 футов и что давление и температура на этой высоте составляли 312 мм рт. Ст. И –30 ° C соответственно. До какого объема пришлось бы расшириться воздушному шару, чтобы удерживать такое же количество газообразного водорода на большей высоте?
Дано: начальное давление, температура, количество и объем; конечное давление и температура
Запрошено: окончательный том
Стратегия:
Следуйте стратегии, описанной в примере \ (\ PageIndex {5} \). 4 \; L \]
4 \; L \]
Имеет ли смысл этот ответ? В этой проблеме работают два противоположных фактора: уменьшение давления ведет к увеличению объема газа, а снижение температуры ведет к уменьшению объема газа. Что мы ожидаем преобладать? Давление падает более чем в два раза, а абсолютная температура падает только примерно на 20%. Поскольку объем пробы газа прямо пропорционален как T , так и 1/ P , наиболее изменяющаяся переменная будет иметь наибольшее влияние на V .В этом случае преобладает эффект снижения давления, и мы ожидаем увеличения объема газа, как мы обнаружили в нашем расчете.
Мы также могли бы решить эту проблему, решив закон идеального газа для V и затем подставив соответствующие параметры для высоты 23000 футов:
За исключением разницы, вызванной округлением до последней значащей цифры, это тот же результат, который мы получили ранее. Часто существует несколько «правильных» способов решения химических проблем.
Упражнение \ (\ PageIndex {4} \)
Стальной баллон со сжатым аргоном объемом 0,400 л был заполнен до давления 145 атм при 10 ° C. При давлении 1,00 атм и температуре 25 ° C сколько ламп накаливания объемом 15,0 мл можно залить из этого цилиндра? (Подсказка: найдите количество молей аргона в каждом контейнере.)
Ответ: 4,07 × 10 3
Использование закона идеального газа для расчета плотности и молярной массы газа
Закон идеального газа также можно использовать для расчета молярных масс газов на основе экспериментально измеренных плотностей газа.Чтобы увидеть, как это возможно, сначала изменим закон идеального газа, чтобы получить
\ [\ dfrac {n} {V} = \ dfrac {P} {RT} \ tag {6.3.9} \]
В левой части представлены единицы измерения в молях на единицу объема (моль / л). Количество молей вещества равно его массе (\ (m \), в граммах), деленной на его молярную массу (\ (M \), в граммах на моль):
\ [n = \ dfrac {m} {M} \ tag {6. 3.10} \]
3.10} \]
Подстановка этого выражения для \ (n \) в уравнение 6.3.9 дает
\ [\ dfrac {m} {MV} = \ dfrac {P} {RT} \ tag {6.3.11} \]
Поскольку \ (m / V \) — это плотность \ (d \) вещества, мы можем заменить \ (m / V \) на \ (d \) и переставить, чтобы получить
\ [\ rho = \ dfrac {m} {V} = \ dfrac {MP} {RT} \ tag {6.3.12} \]
Расстояние между частицами в газах велико по сравнению с размером частиц, поэтому их плотность намного ниже плотности жидкостей и твердых тел. Следовательно, плотность газа обычно измеряется в граммах на литр (г / л), а не в граммах на миллилитр (г / мл).
Пример \ (\ PageIndex {5} \)
Рассчитайте плотность бутана при 25 ° C и давлении 750 мм рт.
Дано: соединение, температура и давление
Запрошено: плотность
Стратегия:
- Рассчитайте молярную массу бутана и преобразуйте все количества в соответствующие единицы для значения газовой постоянной.

- Подставьте эти значения в уравнение 6.3.12, чтобы получить плотность.
Решение:
A Молярная масса бутана (C 4 H 10 ) составляет
\ [M = (4) (12.011) + (10) (1,0079) = 58,123 мкм г / моль]
Использование 0,08206 (л • атм) / (K • моль) для R означает, что нам нужно преобразовать температуру из градусов Цельсия в кельвины ( T = 25 + 273 = 298 K) и давление из миллиметров ртутного столба. до атмосфер:
\ [P = \ rm750 \; мм рт. Ст. \ Раз \ dfrac {1 \; атм} {760 \; мм рт. Ст.} = 0,987 \; атм \]
B Подстановка этих значений в уравнение 6.3.12 дает
\ [\ rho = \ rm \ dfrac {58.123 \; г / моль \ times0.987 \; атм} {0.08206 \ dfrac {L \ cdot atm} {K \ cdot mol} \ times298 \; K} = 2.35 \; г / л \]
Упражнение \ (\ PageIndex {5} \)
Радон (Rn) — радиоактивный газ, образующийся при распаде природного урана в таких породах, как гранит. Он имеет тенденцию скапливаться в подвалах домов и представляет значительный риск для здоровья, если присутствует в воздухе внутри помещений. Многие штаты теперь требуют, чтобы дома проверялись на радон перед продажей. Вычислите плотность радона при давлении 1,00 атм и температуре 20 ° C и сравните ее с плотностью газообразного азота, который составляет 80% атмосферы, в тех же условиях, чтобы понять, почему радон находится в подвалах, а не на чердаках.
Он имеет тенденцию скапливаться в подвалах домов и представляет значительный риск для здоровья, если присутствует в воздухе внутри помещений. Многие штаты теперь требуют, чтобы дома проверялись на радон перед продажей. Вычислите плотность радона при давлении 1,00 атм и температуре 20 ° C и сравните ее с плотностью газообразного азота, который составляет 80% атмосферы, в тех же условиях, чтобы понять, почему радон находится в подвалах, а не на чердаках.
Ответ: радон, 9,23 г / л; N 2 , 1,17 г / л
Уравнение 6.3.12 обычно используется для определения молярной массы неизвестного газа путем измерения его плотности при известной температуре и давлении. Этот метод особенно полезен для идентификации газа, образовавшегося в результате реакции, и его нетрудно осуществить. Колбу или стеклянную колбу известного объема осторожно сушат, вакуумируют, герметично закрывают и взвешивают. Затем он заполняется пробой газа при известной температуре и давлении и повторно взвешивается. Разница в массе между двумя показаниями и есть масса газа. Объем колбы обычно определяется путем взвешивания пустой колбы, наполненной жидкостью известной плотности, например водой. Использование измерений плотности для расчета молярных масс показано в примере \ (\ PageIndex {6} \).
Разница в массе между двумя показаниями и есть масса газа. Объем колбы обычно определяется путем взвешивания пустой колбы, наполненной жидкостью известной плотности, например водой. Использование измерений плотности для расчета молярных масс показано в примере \ (\ PageIndex {6} \).
Пример \ (\ PageIndex {6} \)
Реакция медного пенни с азотной кислотой приводит к образованию красно-коричневого газообразного соединения, содержащего азот и кислород.Проба газа при давлении 727 мм рт. Ст. И температуре 18 ° C весила 0,289 г в колбе объемом 157,0 мл. Вычислите молярную массу газа и предложите разумную химическую формулу соединения.
Дано: давление, температура, масса и объем
Запрошено: Молярная масса и химическая формула
Стратегия:
- Решите уравнение 6.3.12 для молярной массы газа, а затем вычислите плотность газа на основе предоставленной информации.
- Преобразуйте все известные величины в соответствующие единицы используемой газовой постоянной.
 Подставьте известные значения в уравнение и найдите молярную массу.
Подставьте известные значения в уравнение и найдите молярную массу. - Предложите разумную эмпирическую формулу, используя атомные массы азота и кислорода и рассчитанную молярную массу газа.
Решение:
A Решение уравнения 6.3.12 для молярной массы дает
\ [M = \ dfrac {mRT} {PV} = \ dfrac {dRT} {P} \]
Плотность — это масса газа, деленная на его объем:
\ [\ rho = \ dfrac {m} {V} = \ dfrac {0.289 \ rm g} {0,17 \ rm L} = 1,84 \ rm г / л \]
B Мы должны преобразовать другие величины в соответствующие единицы, прежде чем вставлять их в уравнение:
\ [T = 18 + 273 = 291 К \]
\ [P = 727 \ rm мм рт. Ст. \ Раз \ dfrac {1 \ rm атм} {760 \ rm мм рт. Ст.} = 0,957 \ rm атм \]
Таким образом, молярная масса неизвестного газа равна
.\ [\ rho = \ rm \ dfrac {1,84 \; г / л \ times0.08206 \ dfrac {L \ cdot atm} {K \ cdot mol} \ times291 \; K} {0,957 \; атм} = 45,9 г / моль \]
C Атомные массы N и O составляют примерно 14 и 16 соответственно, поэтому мы можем составить список, показывающий массы возможных комбинаций:
\ [M ({\ rm NO}) = 14 + 16 = 30 \ rm \; г / моль \]
\ [M ({\ rm N_2O}) = (2) (14) + 16 = 44 \ rm \; г / моль \]
\ [M ({\ rm NO_2}) = 14+ (2) (16) = 46 \ rm \; г / моль \]
Наиболее вероятный выбор — NO 2 , что согласуется с данными. Красно-коричневый цвет смога также является следствием присутствия газа NO 2 .
Красно-коричневый цвет смога также является следствием присутствия газа NO 2 .
Упражнение \ (\ PageIndex {6} \)
Вы отвечаете за интерпретацию данных беспилотного космического зонда, который только что приземлился на Венеру и отправил отчет о ее атмосфере. Данные следующие: давление 90 атм; температура, 557 ° С; плотность 58 г / л. Основным компонентом атмосферы (> 95%) является углерод. Рассчитайте молярную массу основного газа и определите его.
Ответ : 44 г / моль; \ (CO_2 \)
Сводка
Закон идеального газа выводится из эмпирических соотношений между давлением, объемом, температурой и числом молей газа; его можно использовать для расчета любого из четырех свойств, если известны три других.
Уравнение идеального газа : \ (PV = nRT \),
, где \ (R = 0,08206 \ dfrac {\ rm L \ cdot atm} {\ rm K \ cdot mol} = 8,3145 \ dfrac {\ rm J} {\ rm K \ cdot mol} \)
Общее уравнение газа : \ (\ dfrac {P_iV_i} {n_iT_i} = \ dfrac {P_fV_f} {n_fT_f} \)
Плотность газа: \ (\ rho = \ dfrac {MP} {RT} \)
Эмпирические зависимости между объемом, температурой, давлением и количеством газа могут быть объединены в закон идеального газа , PV = nRT . Константа пропорциональности, R , называется газовой постоянной и имеет значение 0,08206 (л • атм) / (К • моль), 8,3145 Дж / (К • моль) или 1,9872 кал / (К • моль). , в зависимости от используемых единиц. Закон идеального газа описывает поведение идеального газа , гипотетического вещества, поведение которого можно количественно объяснить с помощью закона идеального газа и кинетической молекулярной теории газов. Стандартные температура и давление (STP) 0 ° C и 1 атм. Объем 1 моля идеального газа на СТП равен 22.41 л, стандартный молярный объем . Все эмпирические газовые зависимости являются частными случаями закона идеального газа, в котором два из четырех параметров остаются постоянными. Закон идеального газа позволяет нам вычислить значение четвертой величины ( P , V , T или n ), необходимой для описания газовой пробы, когда другие известны, а также спрогнозировать значение этих величин.
Константа пропорциональности, R , называется газовой постоянной и имеет значение 0,08206 (л • атм) / (К • моль), 8,3145 Дж / (К • моль) или 1,9872 кал / (К • моль). , в зависимости от используемых единиц. Закон идеального газа описывает поведение идеального газа , гипотетического вещества, поведение которого можно количественно объяснить с помощью закона идеального газа и кинетической молекулярной теории газов. Стандартные температура и давление (STP) 0 ° C и 1 атм. Объем 1 моля идеального газа на СТП равен 22.41 л, стандартный молярный объем . Все эмпирические газовые зависимости являются частными случаями закона идеального газа, в котором два из четырех параметров остаются постоянными. Закон идеального газа позволяет нам вычислить значение четвертой величины ( P , V , T или n ), необходимой для описания газовой пробы, когда другие известны, а также спрогнозировать значение этих величин. количества после изменения условий, если исходные условия (значения P , V , T и n ) известны.Закон идеального газа также можно использовать для расчета плотности газа, если его молярная масса известна, или, наоборот, молярной массы неизвестного образца газа, если его плотность измерена.
количества после изменения условий, если исходные условия (значения P , V , T и n ) известны.Закон идеального газа также можно использовать для расчета плотности газа, если его молярная масса известна, или, наоборот, молярной массы неизвестного образца газа, если его плотность измерена.
Расширение газа — Chemistry LibreTexts
- Последнее обновление
- Сохранить как PDF
- Изотермическое расширение
- Изотермический необратимый / обратимый процесс
- Адиабатическое расширение
- Обратимое адиабатическое расширение
- Ссылки

Показывает расширение газа при постоянной температуре в зависимости от веса объекта (м) на поршне.Температура поддерживается постоянной, поэтому изменение энергии равно нулю (U = 0). Таким образом, количество тепла, поглощаемого газом, равно работе, совершаемой идеальным газом над окружающей средой. Изменение энтальпии также равно нулю, потому что изменение энергии равно нулю, а давление и объем постоянны.
Изотермический необратимый / обратимый процесс
Графики ясно показывают, что проделанная работа (площадь под кривой) больше при обратимом процессе.
Адиабатическое расширение
Адиабатическое расширение означает, что во время расширения между системой и окружающей средой не происходит теплообмена и температура больше не поддерживается постоянной.
Обратимое адиабатическое расширение
Это уравнение показывает взаимосвязь между PV и полезно только тогда, когда оно применяется к идеальному газу и обратимому адиабатическому изменению. Уравнение очень похоже на закон Бойля, за исключением того, что у него есть показатель степени (гамма) из-за изменения температуры. Работа, выполняемая адиабатическим обратимым процессом, определяется следующим уравнением:
Уравнение очень похоже на закон Бойля, за исключением того, что у него есть показатель степени (гамма) из-за изменения температуры. Работа, выполняемая адиабатическим обратимым процессом, определяется следующим уравнением:
, где T 2 меньше, чем T 1 . Внутренняя энергия системы уменьшается по мере расширения газа.Работу можно рассчитать двумя способами, потому что внутренняя энергия (U) не зависит от пути. График показывает, что в адиабатическом обратимом процессе выполняется меньше работы, чем в изотермическом обратимом процессе.
Ссылки
- Chang, Raymond. Физическая химия для биологических наук. Саусалито, Калифорния: Университетская наука, 2005.
1.3 Тепловое расширение — Университетская физика Том 2
Задачи обучения
К концу этого раздела вы сможете:
- Ответить на качественные вопросы о эффектах теплового расширения
- Решение проблем, связанных с тепловым расширением, в том числе с тепловым напряжением
Расширение спирта в градуснике — один из многих часто встречающихся примеров теплового расширения, которое представляет собой изменение размера или объема данной системы при изменении ее температуры. Самый наглядный пример — расширение горячего воздуха. Когда воздух нагревается, он расширяется и становится менее плотным, чем окружающий воздух, который затем оказывает (направленное вверх) силу на горячий воздух и заставляет пар и дым подниматься, воздушные шары плавают и т. Д. То же самое происходит со всеми жидкостями и газами, вызывая естественный теплоперенос вверх в домах, океанах и погодных системах, как мы обсудим в следующем разделе. Твердые тела также подвергаются тепловому расширению. Например, железнодорожные пути и мосты имеют компенсаторы, позволяющие им свободно расширяться и сжиматься при изменении температуры, как показано на Рисунке 1.5.
Самый наглядный пример — расширение горячего воздуха. Когда воздух нагревается, он расширяется и становится менее плотным, чем окружающий воздух, который затем оказывает (направленное вверх) силу на горячий воздух и заставляет пар и дым подниматься, воздушные шары плавают и т. Д. То же самое происходит со всеми жидкостями и газами, вызывая естественный теплоперенос вверх в домах, океанах и погодных системах, как мы обсудим в следующем разделе. Твердые тела также подвергаются тепловому расширению. Например, железнодорожные пути и мосты имеют компенсаторы, позволяющие им свободно расширяться и сжиматься при изменении температуры, как показано на Рисунке 1.5.
Фигура 1.5 (а) Такие термические компенсаторы на мосту через гавань Окленда в Новой Зеландии (б) позволяют мостам изменять длину без потери устойчивости. (кредит: модификация работ «ŠJů» / Wikimedia Commons)
Какова основная причина теплового расширения? Как упоминалось ранее, повышение температуры означает увеличение кинетической энергии отдельных атомов. В твердом теле, в отличие от газа, молекулы удерживаются на месте силами соседних молекул; как мы видели в «Колебаниях», силы можно моделировать как гармонические пружины, описываемые потенциалом Леннарда-Джонса.Энергия в простом гармоническом движении показывает, что такие потенциалы асимметричны в том смысле, что потенциальная энергия возрастает более круто, когда молекулы приближаются друг к другу, чем когда они удаляются дальше. Таким образом, при данной кинетической энергии пройденное расстояние больше, когда соседи удаляются друг от друга, чем когда они движутся навстречу друг другу. В результате повышенная кинетическая энергия (повышенная температура) увеличивает среднее расстояние между молекулами — вещество расширяется.
В твердом теле, в отличие от газа, молекулы удерживаются на месте силами соседних молекул; как мы видели в «Колебаниях», силы можно моделировать как гармонические пружины, описываемые потенциалом Леннарда-Джонса.Энергия в простом гармоническом движении показывает, что такие потенциалы асимметричны в том смысле, что потенциальная энергия возрастает более круто, когда молекулы приближаются друг к другу, чем когда они удаляются дальше. Таким образом, при данной кинетической энергии пройденное расстояние больше, когда соседи удаляются друг от друга, чем когда они движутся навстречу друг другу. В результате повышенная кинетическая энергия (повышенная температура) увеличивает среднее расстояние между молекулами — вещество расширяется.
Для большинства веществ в обычных условиях это отличное приближение, что нет предпочтительного направления (т. Е. Твердое тело является «изотропным»), а увеличение температуры увеличивает размер твердого тела на определенную долю в каждом измерении.Следовательно, если твердое тело может расширяться или сжиматься, его пропорции остаются прежними; изменяется только его общий размер.
Линейное тепловое расширение
Согласно экспериментам, зависимость теплового расширения от температуры, вещества и исходной начальной длины резюмируется в уравнении
, где dLdTdLdT — мгновенное изменение длины при изменении температуры, L — длина, а αα — коэффициент линейного расширения, свойство материала, которое незначительно изменяется в зависимости от температуры.Поскольку αα почти постоянна, а также очень мала, для практических целей мы используем линейное приближение:
, где ΔLΔL — это изменение длины, а ΔTΔT — изменение температуры.
В таблице 1.2 приведены типичные значения коэффициента линейного расширения. Как отмечалось ранее, ΔTΔT одинаково независимо от того, выражено ли оно в градусах Цельсия или в кельвинах; таким образом, αα может иметь единицы 1 / ° C1 / ° C или 1 / K с одинаковым значением в любом случае. Аппроксимация αα как константы достаточно точна для небольших изменений температуры и достаточна для большинства практических целей, даже для больших изменений температуры. Мы рассмотрим это приближение более подробно в следующем примере.
Мы рассмотрим это приближение более подробно в следующем примере.
| Материал | Коэффициент линейного расширения α (1 / ° C) α (1 / ° C) | Коэффициент объемного расширения β (1 / ° C) β (1 / ° C) |
|---|---|---|
| Твердые вещества | ||
| Алюминий | 25 × 10-625 × 10-6 | 75 × 10–675 × 10–6 |
| Латунь | 19 × 10-619 × 10-6 | 56 × 10–656 × 10–6 |
| Медь | 17 × 10-617 × 10-6 | 51 × 10–651 × 10–6 |
| Золото | 14 × 10-614 × 10-6 | 42 × 10–642 × 10–6 |
| Чугун или сталь | 12 × 10-612 × 10-6 | 35 × 10-635 × 10-6 |
| Инвар (железо-никелевый сплав) | 0. 9 × 10–60,9 × 10–6 9 × 10–60,9 × 10–6 | 2,7 × 10–62,7 × 10–6 |
| Свинец | 29 × 10-629 × 10-6 | 87 × 10–687 × 10–6 |
| Серебро | 18 × 10-618 × 10-6 | 54 × 10–654 × 10–6 |
| Стекло (обычное) | 9 × 10–69 × 10–6 | 27 × 10-627 × 10-6 |
| Стекло (Pyrex®) | 3 × 10–63 × 10–6 | 9 × 10–69 × 10–6 |
| Кварц | 0,4 × 10-60,4 × 10-6 | 1 × 10–61 × 10–6 |
| Бетон, кирпич | ~ 12 × 10-6 ~ 12 × 10-6 | ~ 36 × 10-6 ~ 36 × 10-6 |
| Мрамор (средний) | 2. 5 × 10–62,5 × 10–6 5 × 10–62,5 × 10–6 | 7,5 × 10–67,5 × 10–6 |
| Жидкости | ||
| Эфир | 1650 × 10-6 1650 × 10-6 | |
| Этиловый спирт | 1100 × 10-6 1100 × 10-6 | |
| Бензин | 950 × 10–6950 × 10–6 | |
| Глицерин | 500 × 10–6500 × 10–6 | |
| Меркурий | 180 × 10–6180 × 10–6 | |
| Вода | 210 × 10–62 10 × 10–6 | |
| Газы | ||
| Воздух и большинство других газов при атмосферном давлении | 3400 × 10-6 3400 × 10-6 | |
Таблица
1. 2
Коэффициенты теплового расширения
2
Коэффициенты теплового расширения
В биметаллической полосе используется тепловое расширение (рис. 1.6). Это устройство можно использовать как термометр, если изогнутая полоска прикреплена к стрелке на шкале. Его также можно использовать для автоматического включения или выключения переключателя при определенной температуре, как в старых или аналоговых термостатах.
Пример 1.2
Расчет линейного теплового расширения
Главный пролет моста Золотые Ворота в Сан-Франциско в самые холодные дни составляет 1275 м в длину.Мост подвергается воздействию температур от –15 ° C – 15 ° C до 40 ° C40 ° C. Каково его изменение длины между этими температурами? Предположим, что мост полностью стальной.Стратегия
Используйте уравнение линейного теплового расширения ΔL = αLΔTΔL = αLΔT, чтобы рассчитать изменение длины, ΔLΔL. Используйте коэффициент линейного расширения αα для стали из Таблицы 1.2 и обратите внимание, что изменение температуры ΔTΔT составляет 55 ° C и 55 ° C.
Решение
Подставьте все известные значения в уравнение, чтобы найти ΔLΔL: ΔL = αLΔT = (12 × 10−6 ° C) (1275 м) (55 ° C) = 0.84 м. ΔL = αL ΔT = (12 × 10−6 ° C) (1275 м) (55 ° C) = 0,84 м.Значение
Это изменение длины заметно, хотя и невелико по сравнению с длиной моста. Обычно он распространяется на многие компенсаторы, поэтому расширение в каждом стыке невелико.Тепловое расширение в двух и трех измерениях
Неограниченные объекты расширяются во всех измерениях, как показано на Рисунке 1.7. То есть их площадь и объем, а также длина увеличиваются с температурой. Поскольку пропорции остаются неизменными, отверстия и объемы контейнеров также увеличиваются с температурой.Если вы прорежете отверстие в металлической пластине, оставшийся материал расширится точно так же, как если бы кусок, который вы удалили, все еще был на месте. Кусок станет больше, поэтому и отверстие должно стать больше.
Тепловое расширение в двух измерениях
Для небольших изменений температуры изменение площади ΔAΔA равно
ΔA = 2αAΔTΔA = 2αAΔT 1. 3
3
, где ΔAΔA — это изменение площади A, ΔTA, ΔT — изменение температуры, а αα — коэффициент линейного расширения, который незначительно изменяется в зависимости от температуры.(Вывод этого уравнения аналогичен выводу более важного уравнения для трех измерений, приведенного ниже.)
Фигура 1,7 Как правило, объекты расширяются во всех направлениях при повышении температуры. На этих чертежах исходные границы объектов показаны сплошными линиями, а расширенные границы — пунктирными линиями. (а) Площадь увеличивается из-за увеличения как длины, так и ширины. Увеличивается и площадь круглой пробки. (b) Если заглушку удалить, оставшееся отверстие становится больше с повышением температуры, как если бы расширяющаяся заглушка все еще оставалась на месте.(c) Объем также увеличивается, потому что все три измерения увеличиваются.
Тепловое расширение в трех измерениях
Связь между объемом и температурой dVdTdVdT определяется выражением dVdT = βVdVdT = βV, где ββ — коэффициент объемного расширения. Как вы можете показать в упражнении 1.60, β = 3αβ = 3α. Это уравнение обычно записывается как
Как вы можете показать в упражнении 1.60, β = 3αβ = 3α. Это уравнение обычно записывается как
1.4
Обратите внимание, что значения ββ в Таблице 1.2 равны 3α3α, за исключением округления.
Объемное расширение определяется для жидкостей, но линейное расширение и расширение по площади — нет, поскольку изменение линейных размеров и площади жидкости зависит от формы ее контейнера.Таким образом, в таблице 1.2 показаны значения ββ для жидкостей, но не αα.
Как правило, объекты расширяются с повышением температуры. Вода — самое важное исключение из этого правила. Вода действительно расширяется с повышением температуры (ее плотность уменьшается на ) при температурах выше 4 ° C (40 ° F) и 4 ° C (40 ° F). Однако он наиболее плотный при + 4 ° C + 4 ° C и расширяется с при понижении температуры между + 4 ° C + 4 ° C и 0 ° C0 ° C (от 40 ° F до 32 ° F, 40 ° F до 32 ° F), как показано. на рисунке 1.8. Ярким следствием этого явления является замерзание воды в пруду.Когда вода у поверхности охлаждается до 4 ° C, 4 ° C, она становится плотнее, чем оставшаяся вода, и опускается на дно. Этот «оборот» оставляет у поверхности слой более теплой воды, которая затем охлаждается. Однако, если температура в поверхностном слое опускается ниже 4 ° C4 ° C, эта вода менее плотная, чем вода внизу, и, таким образом, остается около вершины. В результате поверхность пруда может замерзнуть. Слой льда изолирует жидкую воду под ним от низких температур воздуха. Рыба и другие водные животные могут выжить в воде с температурой 4–4 ° C подо льдом благодаря этой необычной характеристике воды.
на рисунке 1.8. Ярким следствием этого явления является замерзание воды в пруду.Когда вода у поверхности охлаждается до 4 ° C, 4 ° C, она становится плотнее, чем оставшаяся вода, и опускается на дно. Этот «оборот» оставляет у поверхности слой более теплой воды, которая затем охлаждается. Однако, если температура в поверхностном слое опускается ниже 4 ° C4 ° C, эта вода менее плотная, чем вода внизу, и, таким образом, остается около вершины. В результате поверхность пруда может замерзнуть. Слой льда изолирует жидкую воду под ним от низких температур воздуха. Рыба и другие водные животные могут выжить в воде с температурой 4–4 ° C подо льдом благодаря этой необычной характеристике воды.
 Уменьшение плотности ниже 4 ° C4 ° C происходит из-за того, что жидкая вода приближается к твердой кристаллической форме льда, которая содержит больше пустого пространства, чем жидкость.
Уменьшение плотности ниже 4 ° C4 ° C происходит из-за того, что жидкая вода приближается к твердой кристаллической форме льда, которая содержит больше пустого пространства, чем жидкость.Пример 1.3
Расчет теплового расширения
Допустим, вам 60.Стальной бензобак объемом 0 л (15,9 галлона (15,9 галлона)) заполнен газом, который является прохладным, потому что его только что выкачали из подземного резервуара. Теперь и резервуар, и бензин имеют температуру 15,0 ° C. .15,0 ° C. Сколько бензина вылилось к тому времени, когда он нагрелся до 35,0 ° C35,0 ° C?Стратегия
Бак и бензин увеличиваются в объеме, но бензин увеличивается больше, поэтому количество разлитого является разницей в изменении их объема. Мы можем использовать уравнение объемного расширения, чтобы рассчитать изменение объема бензина и бака.(Бензобак можно рассматривать как твердый стальной.)Решение
- Используйте уравнение для объемного расширения, чтобы рассчитать увеличение объема стального резервуара:
ΔVs = βsVsΔT.
 ΔVs = βsVsΔT.
ΔVs = βsVsΔT. - Увеличение объема бензина определяется следующим уравнением: ΔVgas = βgasVgasΔT.ΔVgas = βgasVgasΔT.
- Найдите разницу в объеме, чтобы определить количество разлитого в виде Vspill = ΔVgas — ΔVs.Vspill = ΔVgas — ΔVs.
В качестве альтернативы мы можем объединить эти три уравнения в одно уравнение.(Обратите внимание, что исходные объемы равны.)
Vspill = (βgas − βs) VΔT = [(950−35) × 10−6 / ° C] (60.0L) (20.0 ° C) = 1.10L. Vspill = (βgas − βs) VΔT = [(950−35 ) × 10-6 / ° C] (60,0 л) (20,0 ° C) = 1,10 л.Значение
Это значительное количество, особенно для бака объемом 60,0 л. Эффект такой поразительный, потому что бензин и сталь быстро расширяются. Скорость изменения тепловых свойств обсуждается далее в этой главе. Если вы попытаетесь плотно закрыть резервуар, чтобы предотвратить переполнение, вы обнаружите, что он все равно протекает либо вокруг крышки, либо в результате разрыва резервуара.Сильное сжатие расширяющегося газа эквивалентно его сжатию, и как жидкости, так и твердые тела сопротивляются сжатию с чрезвычайно большими силами. Чтобы избежать разрыва жестких контейнеров, в этих контейнерах есть воздушные зазоры, которые позволяют им расширяться и сжиматься, не нагружая их.
Чтобы избежать разрыва жестких контейнеров, в этих контейнерах есть воздушные зазоры, которые позволяют им расширяться и сжиматься, не нагружая их.
Проверьте свое понимание 1.1
Проверьте свое понимание Указывает ли данное показание шкалы бензина на большее количество бензина в холодную или жаркую погоду, или температура не имеет значения?
Термическое напряжение
Если вы измените температуру объекта, не допуская его расширения или сжатия, объект подвергнется напряжению, которое будет сжимающим, если объект будет расширяться в отсутствие ограничений, и растяжением, если он будет сжиматься.Это напряжение, возникающее в результате изменений температуры, известно как термическое напряжение. Он может быть довольно большим и может вызвать повреждение.
Чтобы избежать этого стресса, инженеры могут проектировать компоненты так, чтобы они могли свободно расширяться и сжиматься. Например, на автомагистралях между блоками намеренно оставляют промежутки, чтобы предотвратить развитие теплового напряжения. Когда нельзя оставлять зазоров, инженеры должны учитывать термическое напряжение в своих конструкциях. Таким образом, арматурные стержни в бетоне изготавливаются из стали, поскольку коэффициент линейного расширения стали почти равен коэффициенту линейного расширения бетона.
Например, на автомагистралях между блоками намеренно оставляют промежутки, чтобы предотвратить развитие теплового напряжения. Когда нельзя оставлять зазоров, инженеры должны учитывать термическое напряжение в своих конструкциях. Таким образом, арматурные стержни в бетоне изготавливаются из стали, поскольку коэффициент линейного расширения стали почти равен коэффициенту линейного расширения бетона.
Чтобы рассчитать тепловое напряжение в стержне, оба конца которого жестко закреплены, мы можем представить себе напряжение как развивающееся в два этапа. Во-первых, позвольте концам свободно расширяться (или сжиматься) и обнаруживать расширение (или сжатие). Во-вторых, найдите напряжение, необходимое для сжатия (или удлинения) стержня до его первоначальной длины, с помощью методов, которые вы изучали в статье Статическое равновесие и упругость по статическому равновесию и упругости. Другими словами, ΔLΔL теплового расширения равняется ΔLΔL упругой деформации (за исключением того, что знаки противоположные).
Пример 1.4
Расчет термического напряжения
Бетонные блоки выкладываются на шоссе рядом друг с другом без промежутков между ними, поэтому они не могут расширяться. Строительная бригада выполняла работы в зимний день, когда температура составляла 5 ° C5 ° C. Найдите напряжение в блоках в жаркий летний день, когда температура составляет 38 ° C38 ° C. Модуль Юнга бетона при сжатии составляет Y = 20 × 109 Н / м2Y = 20 × 109 Н / м2.Стратегия
Согласно главе, посвященной статическому равновесию и упругости, напряжение F / A определяется как, где Y — модуль Юнга материала, в данном случае бетона.При тепловом расширении ΔL = αL0ΔT.ΔL = αL0ΔT. Мы объединяем эти два уравнения, отмечая, что два ΔL’sΔL’s равны, как указано выше. Поскольку нам не даны L0L0 или A , мы можем получить числовой ответ, только если они оба сокращаются.
Решение
Подставляя уравнение теплового расширения в уравнение упругости, получаем FA = YαL0ΔTL0 = YαΔT, FA = YαL0ΔTL0 = YαΔT,и, как мы надеялись, L0L0 был отменен, и A появляется только в F / A , обозначении количества, которое мы вычисляем.
Теперь нам нужно только вставить числа:
FA = (20 × 109 Н / м2) (12 × 10–6 / ° C) (38 ° C – 5 ° C) = 7,9 × 106 Н / м2. FA = (20 × 109 Н / м2) (12 × 10–6 / ° C) (38 ° C — 5 ° C) = 7,9 × 106 Н / м2.Значение
Предел прочности бетона на сжатие составляет 20 × 106 Н / м2, 20 × 106 Н / м2, поэтому блоки вряд ли разобьются. Однако предел прочности бетона на сдвиг составляет всего 2 × 106 Н / м2,2 × 106 Н / м2, поэтому некоторые из них могут отколоться.Проверьте свое понимание 1.2
Проверьте свое понимание Два объекта A и B имеют одинаковые размеры и одинаково связаны. A изготовлен из материала с более высоким коэффициентом теплового расширения, чем B . Если предметы нагреваются одинаково, будет ли A испытывать большее напряжение, чем B ?
уравнений для фотоэлектрических систем | PVEducation
Основные уравнения
Плотность состояний в полосе проводимости и валентности
Функция Ферми:
Концентрация носителей в равновесии
Закон массового действия:
Концентрации носителей:
Материал n-типа:
Материал p-типа:
Концентрация носителей при смещении
Поколение
Количество фотонов:
Скорость генерации:
Поколение, однородный полупроводник: G = const:
Тип P:
Тип N:
Рекомбинация
Общая скорость рекомбинации СРГ:
В условиях низкого впрыска:
Для электронов:
Для отверстий:
Набор базовых уравнений для PN-соединения
1.Уравнение Пуассона:
2. Уравнения переноса:
3. Уравнения неразрывности:
Общее решение для постоянного поколения без электричества
Уравнения для PN-переходов
Встроенное напряжение pn переход:
Общее уравнение идеального диода:
I 0 для диода с широкой базой:
I 0 для диода с узкой базой:
Уравнение тока полного насыщения диода:
Рекомбинация области истощения:
Уравнения солнечных батарей
для постоянного G, широкое основание
Материальные константы и общие единицы
Концентрация собственных носителей:
Эффективная плотность состояний:
Уровень внутренней энергии:
Коэффициент диффузии
Диффузионная длина неосновных носителей:
Удельное сопротивление и проводимость:
Сопротивление, однородное:
Разрешение:
Энергия излучения
Длина волны и энергия фотона:
Если E выражено в эВ, а λ — в мкм:
Спектральная освещенность для черного тела:
Плотность мощности неидеального черного тела:
Поток фотонов и плотность мощности:
| Материал | млн * / м0 | мп * / м0 | EG (эВ) | ni (см-3) | с (эВ) | ES |
| Si | 1.18 | 0,81 | 1,12 | 1,0 × 10 10 | 4,03 | 11,8 |
| Ge | 0,55 | 0,36 | 0,66 | 2,0 × 10 13 | 4,13 | 16,0 |
| GaAs | 0,066 | 0,52 | 1,42 | 1,8 × 10 6 | 4,07 | 13,1 |
| InP | 0,08 | 0.6 | 1,34 | 1,3 × 10 7 | 4,38 | 12,5 |
9.6 Неидеальное поведение газа — химия
Цели обучения
К концу этого раздела вы сможете:
- Опишите физические факторы, которые приводят к отклонениям от характеристик идеального газа
- Объясните, как эти факторы представлены в уравнении Ван-дер-Ваальса
- Определите сжимаемость (Z) и опишите, как ее изменение с давлением отражает неидеальное поведение
- Количественная оценка неидеального поведения путем сравнения расчетов свойств газа с использованием закона идеального газа и уравнения Ван-дер-Ваальса
До сих пор закон идеального газа, PV = nRT , применялся к множеству различных типов задач, начиная от стехиометрии реакции и задач эмпирических и молекулярных формул до определения плотности и молярной массы газа.Однако, как упоминалось в предыдущих модулях этой главы, поведение газа часто неидеально, а это означает, что наблюдаемые отношения между его давлением, объемом и температурой не точно описываются газовыми законами. В этом разделе рассматриваются причины этих отклонений от поведения идеального газа.
Один из способов определения точности PV = nRT — это сравнение фактического объема 1 моля газа (его молярный объем, V м ) с молярным объемом идеального газа при том же температура и давление.Это отношение называется коэффициентом сжимаемости (Z) с:
[латекс] \ text {Z} = \ frac {\ text {молярный объем газа при одном и том же} \; T \; \ text {and} \; P} {\ text {при этом молярный объем идеального газа} \ ; T \; \ text {and} \; P} = (\ frac {PV_m} {RT}) _ {\ text {измерено}} [/ latex]
Таким образом, идеальное поведение газа обозначается, когда это отношение равно 1, а любое отклонение от 1 указывает на неидеальное поведение. На рисунке 1 показаны графики Z в большом диапазоне давлений для нескольких обычных газов.
Рис. 1. График зависимости коэффициента сжимаемости (Z) от давления показывает, что газы могут демонстрировать значительные отклонения от поведения, предсказываемого законом идеального газа.Как видно из рисунка 1, закон идеального газа плохо описывает поведение газа при относительно высоких давлениях. Чтобы определить, почему это так, рассмотрите различия между свойствами реального газа и тем, что ожидается от гипотетического идеального газа.
Частицы гипотетического идеального газа не имеют значительного объема и не притягиваются и не отталкиваются друг от друга.В общем, реальные газы приближаются к такому поведению при относительно низких давлениях и высоких температурах. Однако при высоких давлениях молекулы газа сжимаются ближе друг к другу, и количество пустого пространства между молекулами уменьшается. При этих более высоких давлениях объем самих молекул газа становится заметным по сравнению с общим объемом, занимаемым газом (рис. 2). Следовательно, газ становится менее сжимаемым при таких высоких давлениях, и хотя его объем продолжает уменьшаться с увеличением давления, это уменьшение не является пропорциональным , как предсказывается законом Бойля.
Рис. 2. Повышение давления газа увеличивает долю его объема, занимаемую молекулами газа, и делает газ менее сжимаемым.При относительно низких давлениях молекулы газа практически не притягиваются друг к другу, потому что они (в среднем) так далеко друг от друга и ведут себя почти как частицы идеального газа. Однако при более высоких давлениях сила притяжения также перестает быть незначительной. Эта сила притягивает молекулы немного ближе друг к другу, немного уменьшая давление (если объем постоянный) или уменьшая объем (при постоянном давлении) (рис. 3).Это изменение более выражено при низких температурах, потому что молекулы имеют более низкий KE по сравнению с силами притяжения, и поэтому они менее эффективны в преодолении этого притяжения после столкновения друг с другом.
Рис. 3. (a) Притяжения между молекулами газа служат для уменьшения объема газа при постоянном давлении по сравнению с идеальным газом, молекулы которого не испытывают сил притяжения. (б) Эти силы притяжения уменьшат силу столкновений между молекулами и стенками емкости, тем самым уменьшив оказываемое давление по сравнению с идеальным газом.Существует несколько различных уравнений, которые лучше описывают поведение газа, чем закон идеального газа. Первый и самый простой из них был разработан голландским ученым Йоханнесом ван дер Ваальсом в 1879 году. Уравнение Ван дер Ваальса улучшает закон идеального газа, добавляя два члена: один для учета объема молекул газа и другой для сил притяжения между ними.
Константа a соответствует силе притяжения между молекулами определенного газа, а константа b соответствует размеру молекул определенного газа.2} [/ latex], а «поправка» к объему — nb . Обратите внимание, что когда V относительно велико, а n относительно мало, оба этих поправочных члена становятся незначительными, и уравнение Ван-дер-Ваальса сводится к закону идеального газа, PV = nRT . Такое состояние соответствует газу, в котором относительно небольшое количество молекул занимает относительно большой объем, то есть газу с относительно низким давлением. Экспериментальные значения констант Ван-дер-Ваальса некоторых распространенных газов приведены в таблице 3.
| Газ | a (L 2 атм / моль 2 ) | b (л / моль) |
|---|---|---|
| N 2 | 1,39 | 0,0391 |
| O 2 | 1,36 | 0,0318 |
| CO 2 | 3,59 | 0,0427 |
| H 2 O | 5,46 | 0.0305 |
| He | 0,0342 | 0,0237 |
| CCl 4 | 20,4 | 0,1383 |
| Таблица 3. Значения констант Ван-дер-Ваальса для некоторых распространенных газов | ||
При низких давлениях поправка на межмолекулярное притяжение, a , более важна, чем поправка на молекулярный объем, b . При высоких давлениях и малых объемах поправка на объем молекул становится важной, потому что сами молекулы несжимаемы и составляют значительную часть от общего объема.При некотором промежуточном давлении две поправки оказывают противоположное влияние, и газ, кажется, следует соотношению, заданному формулой PV = nRT в небольшом диапазоне давлений. Такое поведение отражается в «провалах» на некоторых кривых сжимаемости, показанных на рисунке 1. Сила притяжения между молекулами изначально делает газ более сжимаемым, чем идеальный газ, по мере увеличения давления (Z уменьшается с увеличением P ). При очень высоких давлениях газ становится менее сжимаемым (Z увеличивается с P ), поскольку молекулы газа начинают занимать все более значительную долю от общего объема газа.
Строго говоря, уравнение идеального газа хорошо работает, когда межмолекулярное притяжение между молекулами газа пренебрежимо мало, а сами молекулы газа не занимают заметной части всего объема. Этим критериям удовлетворяются условия при низком давлении и при высокой температуре. Говорят, что в таких условиях газ ведет себя идеально, а отклонения от газовых законов достаточно малы, чтобы ими можно было пренебречь — однако очень часто это не так.
Пример 1
Сравнение закона идеального газа и уравнения Ван-дер-Ваальса
Колба объемом 4,25 л содержит 3,46 моль CO 2 при 229 ° C. Рассчитайте давление этого образца CO 2 :
(а) из закона идеального газа
(б) из уравнения Ван-дер-Ваальса
(c) Объясните причину (ы) разницы.
Решение
(a) Из закона идеального газа:
[латекс] P = \ frac {nRT} {V} = \ frac {3.2} [/ латекс]
Это окончательно дает P = 32,4 атм.
(c) Это не сильно отличается от значения из закона идеального газа, потому что давление не очень высокое, а температура не очень низкая. Значение несколько отличается, потому что молекулы CO 2 действительно имеют некоторый объем и притяжение между молекулами, а закон идеального газа предполагает, что они не имеют объема или притяжения.
Проверьте свои знания
Колба на 560 мл содержит 21 штуку.3 г N 2 при 145 ° C. Рассчитайте давление N 2 :
(а) из закона идеального газа
(б) из уравнения Ван-дер-Ваальса
(c) Объясните причину (ы) разницы.
Ответ:
(а) 46,562 атм; б) 46,594 атм; (c) Уравнение Ван-дер-Ваальса учитывает объем самих молекул газа, а также межмолекулярные притяжения.
Молекулы газа обладают конечным объемом и испытывают силы притяжения друг к другу.Следовательно, поведение газа не обязательно хорошо описывается законом идеального газа. В условиях низкого давления и высокой температуры этими факторами можно пренебречь, уравнение идеального газа является точным описанием поведения газа, и говорят, что газ демонстрирует идеальное поведение. Однако при более низких температурах и более высоких давлениях требуются поправки на молекулярный объем и молекулярное притяжение, чтобы учесть конечный размер молекулы и силы притяжения. Уравнение Ван-дер-Ваальса — это модифицированная версия закона идеального газа, которую можно использовать для объяснения неидеального поведения газов в этих условиях.2}) \ times (V — nb) = nRT [/ latex]
Химия: упражнения в конце главы
- Далее следуют графики, показывающие поведение нескольких различных газов. Поведение какого из этих газов существенно отличается от поведения идеальных газов?
- Объясните, почему график PV для CO 2 отличается от графика для идеального газа.
- При каком из следующих наборов условий реальный газ ведет себя больше всего как идеальный газ и при каких условиях ожидается, что реальный газ будет отклоняться от идеального? Объяснять.
(а) высокое давление, малый объем
(б) высокая температура, низкое давление
(в) низкая температура, высокое давление
- Опишите факторы, ответственные за отклонение поведения реальных газов от поведения идеального газа.
- Для какого из следующих газов поправка на молекулярный объем должна быть наибольшей:
CO, CO 2 , H 2 , He, NH 3 , SF 6 ?
- Колба на 0,245 л содержит 0.467 моль CO 2 при 159 ° C. Рассчитайте давление:
(a) с использованием закона идеального газа
(b) с использованием уравнения Ван-дер-Ваальса
(c) Объясните причину разницы.
(d) Определите, какая поправка (для P или V) является доминирующей и почему.
- Ответьте на следующие вопросы:
(a) Если бы XX вел себя как идеальный газ, как бы выглядел его график зависимости Z от P?
(b) На протяжении большей части этой главы мы проводили расчеты, считая газы идеальными.Было ли это оправдано?
(c) Как объем молекул газа влияет на Z? При каких условиях этот эффект невелик? Когда он большой? Объясните, используя соответствующую схему.
(d) Как межмолекулярное притяжение влияет на значение Z? При каких условиях этот эффект невелик? Когда он большой? Объясните, используя соответствующую схему.
(e) В целом, при каких температурных условиях вы ожидаете, что Z будет иметь наибольшие отклонения от Z для идеального газа?
Глоссарий
- Коэффициент сжимаемости (Z)
- отношение экспериментально измеренного молярного объема газа к его молярному объему, вычисленное по уравнению идеального газа
- уравнение Ван-дер-Ваальса
- модифицированная версия уравнения идеального газа, содержащая дополнительные члены для учета неидеального поведения газа
Решения
1.Газы C, E и F
3. Поведение газа наиболее похоже на поведение идеального газа при условиях, указанных в (b). Молекулы имеют высокие скорости и перемещаются на большие расстояния между столкновениями; у них также более короткое время контакта, и взаимодействия менее вероятны. Отклонения возникают при условиях, описанных в (a) и (c). В условиях (а) некоторые газы могут сжижаться. В условиях пункта (c) большинство газов сжижается.
5. SF 6
7. (a) Прямая горизонтальная линия в точке 1.0; (b) Когда реальные газы находятся при низких давлениях и высоких температурах, они ведут себя достаточно близко к идеальным газам, что их можно аппроксимировать как таковые, однако в некоторых случаях мы видим, что при высоком давлении и температуре приближение идеального газа нарушается и значительно отличается от давления, рассчитанного по уравнению идеального газа (c) Чем больше сжимаемость, тем больше значение имеет объем. При низких давлениях поправочный коэффициент для межмолекулярного притяжения более значителен, и влияние объема молекул газа на Z будет небольшим снижением сжимаемости.При более высоких давлениях влияние объема самих молекул газа на Z увеличит сжимаемость (см. Рисунок 1). (D) И снова при низких давлениях влияние межмолекулярного притяжения на Z будет более важным, чем поправочный коэффициент для объем самих молекул газа, хотя, возможно, все еще небольшой. При более высоких давлениях и низких температурах эффект межмолекулярного притяжения будет сильнее. См. Рисунок 1. (e) низкие температуры
Биномиальная теорема: формулы (стр. 1 из 2) Разделы: формулы, Работает примеры Биномиальная теорема быстрый способ (хорошо, это менее медленный способ) расширения (или умножения out) биномиальное выражение, которое было возведено в некоторые (обычно неудобно большая) мощность.Например, выражение (3 x 2) 10 будет будет очень больно размножать вручную. К счастью, кто-то подумал формулу для этого расширения, и мы можем подставить бином 3 x 2 и степень 10 в эту формулу, чтобы получить эту расширенную (умноженную) форму. Формальное выражение биномиальная теорема имеет следующий вид: Да, я знаю; эта формула мне тоже никогда особо не помогало.И не помогает то, что разные тексты используйте разные обозначения для обозначения одного и того же. Бит в скобках выше есть эти эквиваленты: Напомним, что факториал запись « n !» означает «произведение всех целых чисел от 1 и n «, так, например, 6! = 123456. Тогда обозначение « 10 C 7 » (часто произносится как «десять, выберите семь») означает:
Как вы понимаете, рисунок Треугольник Паскаля каждый раз, когда вам нужно расширять бином, будет довольно долгий процесс, особенно если у бинома большой показатель степени на Это. Люди сделали много исследований по Треугольник Паскаля, но с практической точки зрения, вероятно, лучше всего используйте свой калькулятор, чтобы найти n C r , вместо использования треугольника.Полагаю, Треугольник симпатичный, но он не очень полезно в этом контексте, отнимает больше времени, чем что-либо еще. Например, на тесте вы хотите оценить « 10 C 7 » вычислив одиннадцать рядов Треугольника или нажав четыре кнопки на вашем калькуляторе? Я никогда не мог вспомнить формулу биномиальной теоремы, поэтому вместо этого я только что выучил как это работало.Я заметил, что полномочия каждого члена в расширении всегда добавляется к n было, и что термы отсчитывались от нуля до n . Возвращаясь к нашему исходному примеру (3 x 2) 10 , г. силы на каждом сроке расширения будут в сумме до 10, и полномочия по условиям будут увеличиваться путем отсчета от нуля до 10: (3 х 2) 10 = 10 C 0 (3 x ) 10 0 (2) 0 + 10 К 1 (3 x ) 10 1 (2) 1 + 10 К 2 (3 x ) 10 2 (2) 2 + 10 К 3 (3 x ) 10 3 (2) 3 + 10 К 4 (3 x ) 10 4 (2) 4 + 10 К 5 (3 x ) 10 5 (2) 5 + 10 К 6 (3 x ) 10 6 (2) 6 + 10 К 7 (3 x ) 10 7 (2) 7 + 10 К 8 (3 x ) 10 8 (2) 8 + 10 К 9 (3 x ) 10 9 (2) 9 + 10 К 10 (3 x ) 10 10 (2) 10 Обратите внимание, как выделено номер счетчика отсчитывается от нуля до 10, с множителями на концах каждого члена, имеющими номер счетчика, и коэффициент в середине, где номер счетчика вычитается из 10.Этот шаблон — все, что вам действительно нужно знать о биномиальной теореме; вот как это работает. Ваш первый шаг, учитывая бином для расширения, следует включить его в теорему, точно так же, как Я сделал выше. Не пытайтесь делать слишком много шагов одновременно. Только после того, как ты настройте свой бином по образцу теоремы, если вы начнете упрощать условия. Биномиальная теорема лучше всего работает как «заткнись». процесс, но вы должны сначала подключить; выпить позже.Я сделал «затыкание» выше; теперь «пыхтение» дает мне: (1) (59049) x 10 (1) + (10) (19683) x 9 (2) + (45) (6561) x 8 (4) + (120) (2187) x 7 (8) + (210) (729) x 6 (16) + (252) (243) x 5 (32) + (210) (81) x 4 (64) + (120) (27) x 3 (128) + (45) (9) x 2 (256) + (10) (3) x (512) + (1) (1) (1) (1024) = 59049 x 10 393660 x 9 + 1180980 x 8 2099520 x 7 + 2449440 x 6 1959552 x 5 Так же мучительно, как теорема бинома процесс, это все же проще, чем пытаться умножить это на рука.Так что не позволяйте Формуле вас отпугнуть. Это просто другое дело запомни, так что запомни, по крайней мере, для следующего теста. Самый большой источник ошибок в биномиальной теореме (кроме забвения теоремы) это процесс упрощения. Не пытайтесь делать это в своей голове или пытайтесь делать слишком много шагов одновременно. Пишите красиво и ясно, как я сделал выше, поэтому у вас будет больше шансов получить правильный ответ. (И было бы хорошо выполнить кучу практических задач, так что процесс практически автоматически к моменту прохождения следующего теста.) Верх | 1 | 2 | Возвращение к указателю Вперед >>
|
Тепловое расширение: определение, уравнения и примеры — видео и стенограмма урока
Уравнение
Это уравнение описывает линейное тепловое расширение, которое мы рассмотрим в контексте расширения металлического стержня и увеличения его длины:
В этом уравнении дельта L — это изменение длины стержня, дельта T — это изменение температуры стержня, L — исходная длина до изменения температуры, а альфа — линейный коэффициент теплового расширения.Коэффициент — это просто число, которое показывает, насколько материал расширяется. Например, металлы склонны к расширению больше, чем пластмассы.
Пример
Мы уже говорили об открытии непроходимой банки, но еще одним примером теплового расширения являются стыки моста. Мосты строятся из бетона и других относительно твердых материалов, но эти материалы расширяются, как и все остальное. Когда это произойдет, мост может сломаться и рухнуть. Чтобы этого не произошло, на больших мостах ставят компенсаторы.Таким образом, поскольку температура меняется в течение года, мост может становиться длиннее или короче, не вызывая трещин или поломок.
Итак, допустим, длина моста составляет 50 метров в день, когда температура составляет 15 градусов Цельсия, а коэффициент расширения моста составляет 0,0005. Как долго будет стоять мост в день, когда температура составляет 35 градусов по Цельсию?
Ну, это изменение температуры на 20 градусов (35-15 = 20), поэтому дельта Т равна 20.И мы знаем как исходную длину, так и коэффициент расширения. Итак, все, что нам нужно сделать, это вставить три числа и решить. Изменение длины будет равно:
0,0005 * 50 * 20 = 0,5 метра
Поскольку мост расширяется, это означает, что общая длина моста составит:
50,5 метра (50 + 0,5)
Если вы применяете это уравнение в трех отдельных измерениях, вы можете вывести уравнение для увеличения площади или даже для полного трехмерного увеличения объема.
Резюме урока
Тепловое расширение — это место, где объект расширяется и становится больше из-за изменения его температуры.Более высокая температура означает, что в среднем молекулы движутся быстрее, в результате чего они занимают больше места. Следовательно, нагретые предметы увеличиваются в размерах.
Изменение длины объекта можно рассчитать с помощью следующего уравнения:
Помните, что линейный коэффициент показывает, насколько расширяется конкретный материал, поскольку некоторые материалы расширяются больше, чем другие.
Обзор теплового расширения
- Тепловое расширение происходит, когда объект расширяется или становится больше из-за повышения его температуры.




 ▲
▲
 Если
Если Число 2
>
1,
так что пара (3;2) является ре-
Число 2
>
1,
так что пара (3;2) является ре-


 д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
 Начните с построения таблицы, показывающей начальные и конечные условия.
Начните с построения таблицы, показывающей начальные и конечные условия.
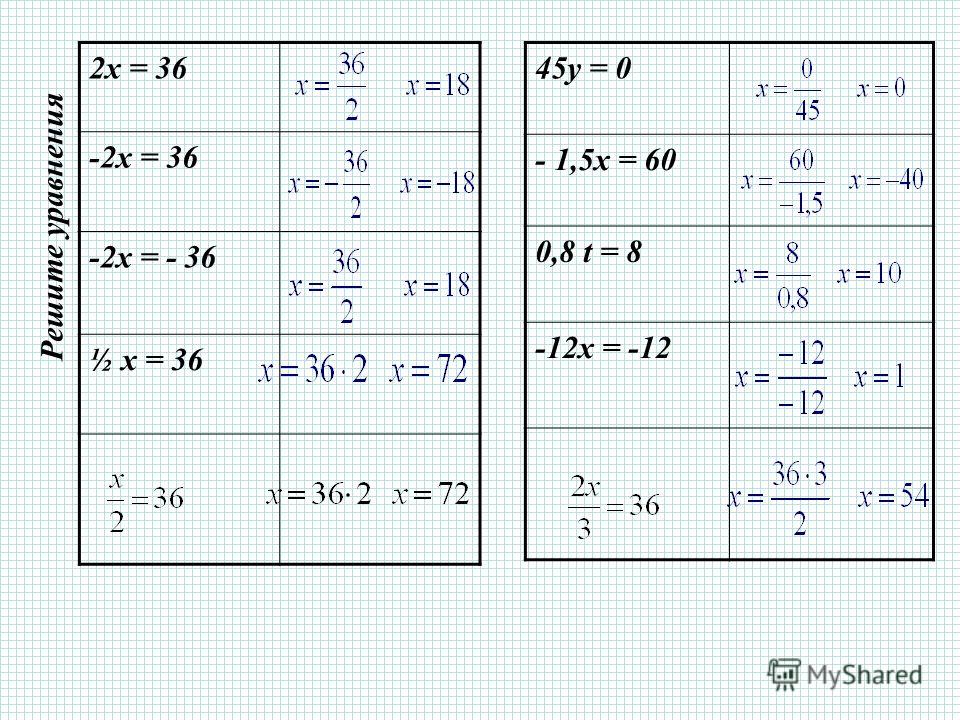 Подставьте известные значения в уравнение и найдите молярную массу.
Подставьте известные значения в уравнение и найдите молярную массу. ΔVs = βsVsΔT.
ΔVs = βsVsΔT.