§ 26. Расстояние от точки до плоскости в координатах

§ 26.Расстояние от точки до плоскости в координатах

Напомним, что расстояние от данной точки M0 до плоскости α равно длине перпендикуляра M0M1_{(M1∈ α), опущенного из точки M0 на плоскость α (рис. 228).}

Проведём через точку M0(x0; y0; z0), не лежащую на плоскости α, прямую h, перпендикулярную α. Так как вектор нормали плоскости α является направляющим вектором прямой h, то для поиска координат x1, y1, z1 точки M1 пересечения прямой h и плоскости α достаточно, как и в предыдущем параграфе, решить систему уравнений относительно параметра t:

Решением этой системы является

t0 =  = ,

что позволяет нам найти искомые координаты точки пересечения прямой h и плоскости α:

Тогда находим длину отрезка M0M1, равную искомому расстоянию d от точки M0 до плоскости α:

d = | M0M1 | =

= =

=  = 

= |t0| =

= •=

= .

Если точка M0 лежит на данной плоскости, то

Ax0 + By0 + Cz0 + D = 0

и искомое расстояние равно нулю, что также следует из полученной формулы

d = .

Расстояние от начала координат O(0; 0; 0) до плоскости α равно

.

Приведём ещё один способ рассуждений.

Расстояние от точки M0 до плоскости α обозначим: d = | M0; α | = | M0M1|, где точка M1 — основание перпендикуляра, опущенного из точки M0 на плоскость α (см. рис. 228).

Пусть в системе координат Oxyz плоскость α задана уравнением

Ax + By + Cz + D = 0,(1)

точки M0 и M1 имеют координаты: M0(x0; y0; z0), M1(x1; y1; z1).

Заметим, что

M1 ∈ α ⇒ Ax1 + By1 + Cz1 + D = 0.(2)

Вектор (x0 – x1; y0 – y1; z0 – z1) и вектор нормали (A; B; C) плоскости α коллинеарны, так как каждый из них перпендикулярен плоскости α, поэтому

• = |  |•|  |•(±1) = ±d•|  |;

(+1, если  ↑↑ ; – 1, если  ↑↓ ).

Тогда

|M0; α | = d = |  | =  = .

Раскроем в числителе скобки и, пользуясь соотношением (2), заменим выражение –Ax1 – By1 – Cz1 числом D. Получаем

d = .(3)

Сравните два приведённых способа рассуждений и выберите для себя наиболее понятный.

ЗадаЧа 7.182. Найти расстояние от точки K(1; –2; 3) до плоскости 3x + 2y – 6z + 5 = 0.

Решение. Находим координаты вектора нормали плоскости: (3; 2; –6). Тогда

d =  =  = 2.

Ответ: 2.

ЗадаЧа 7.183. Найти множество точек, равноудалённых от плоскостей 2x + 2y – z – 3 = 0 и 3x + 4y + 12z – 13 = 0.

Решение. Пусть точка M(x; y; z) равноудалена от данных плоскостей, тогда

 = , т. е.

 = .

Данное уравнение распадается на совокупность двух уравнений

 = ,

или  = – .

После упрощения получим уравнения двух плоскостей

17x + 14y – 49z = 0 и 35x + 38y + 23z – 78 = 0.

Подумайте, почему эти плоскости получились взаимно перпендикулярными и как они связаны с данными в задаче плоскостями.

Задания для работы с интернет-ресурсами

1. Вы можете найти в Интернете дополнительный материал по темам «Декартова прямоугольная система координат в пространстве», «Координаты вектора», «Условие параллельности двух векторов в координатах», «Скалярное произведение векторов в координатах», «Условие перпендикулярности двух векторов в координатах», «Проекция вектора на ось в координатах».

2. Найдите и изучите дополнительные материалы и презентации по темам: «Простейшие задачи стереометрии в координатах», «Уравнения и неравенства, задающие множества точек в пространстве», «Уравнение сферы и неравенство шара».

3. Найдите и выпишите знакомые и незнакомые формулы по теме «Плоскость в пространстве в координатах».

4. Найдите и выпишите знакомые и незнакомые формулы по темам «Прямая в координатах», «Взаимное расположение прямой и плоскости в координатах».

5. Набрав в поисковой системе слова «Прямая и плоскость в пространстве», «Параллельность прямой и плоскости», вы увидите, как можно использовать векторы и координаты при изучении вопросов параллельности прямой и плоскости.

6. Посмотрите статьи по теме «Аналитическая геометрия». Этот раздел математики вы будете изучать в высших учебных заведениях, но многими формулами и приёмами координатного метода изучения свойств геометрических фигур вы владеете уже сейчас. Попытайтесь узнать об этом ещё больше.

Вопросы для самооценки

1. Оцените результаты изучения этой главы. Довольны ли вы ими?

2. Что нового вы узнали в этой главе?

3. Как могут пригодиться вам эти знания в повседневной жизни?

4. Какие задания в этой главе были для вас самыми трудными? Почему?

5. Использовали ли вы при выполнении заданий дополнительные источники: справочники, пособия, интернет-ресурсы?

6. Обращались ли вы за помощью к одноклассникам, родителям, учителю?

11 класс. Геометрия. Метод координат в пространстве. Уравнение плоскости. Движения пространства. — Уравнение плоскости.

Комментарии преподавателя

Урав­не­ние плос­ко­сти

Урав­не­ние с тремя пе­ре­мен­ны­ми x, у, z на­зы­ва­ет­ся урав­не­ни­ем дан­ной по­верх­но­сти P в си­сте­ме ко­ор­ди­нат Охуz, если этому урав­не­нию удо­вле­тво­ря­ют ко­ор­ди­на­ты любой точки по­верх­но­сти Р и не удо­вле­тво­ря­ют ко­ор­ди­на­ты ни­ка­кой точки, не ле­жа­щей на этой по­верх­но­сти. Из всех воз­мож­ных по­верх­но­стей нас се­год­ня будет ин­те­ре­со­вать урав­не­ние плос­ко­сти.

Урав­не­ние плос­ко­сти через точку и век­тор

Пусть дана неко­то­рая точка M0(x0;y0;z0) и нену­ле­вой век­тор . Через точку M0 можно про­ве­сти толь­ко одну плос­кость α пер­пен­ди­ку­ляр­ную век­то­ру  (см. рис. 1).

Рис. 1. 

Вы­ве­дем урав­не­ние плос­ко­сти α. Пусть М — про­из­воль­ная точка про­стран­ства. Оче­вид­но, что точка М при­над­ле­жит плос­ко­сти α толь­ко тогда, когда век­тор  пер­пен­ди­ку­ля­рен век­то­ру . По­это­му урав­не­ние плос­ко­сти, про­хо­дя­щей через точку M0 пер­пен­ди­ку­ляр­но век­то­ру, можно за­пи­сать в виде: .

 

Урав­не­ние плос­ко­сти, про­хо­дя­щей через точку пер­пен­ди­ку­ляр­но век­то­ру фор­му­ла

Итак, фор­му­ла урав­не­ния плос­ко­сти, про­хо­дя­щей через точку, пер­пен­ди­ку­ляр­но век­то­ру:

Век­тор  в урав­не­нии  на­зы­ва­ет­ся нор­маль­ным век­то­ром плос­ко­сти. В ка­че­стве нор­маль­но­го век­то­ра можно взять любой век­тор, пер­пен­ди­ку­ляр­ный плос­ко­сти.

Пусть ко­ор­ди­на­ты век­то­ра равны . И обо­зна­чим ко­ор­ди­на­ты про­из­воль­ной точки М через x, y и z. Тогда век­тор имеет ко­ор­ди­на­ты .

Урав­не­ние плос­ко­сти через точку

Те­перь можно за­пи­сать урав­не­ние плос­ко­сти через ко­ор­ди­на­ты век­то­ра и век­то­ра :

Это урав­не­ние на­зы­ва­ет­ся урав­не­ни­ем плос­ко­сти, про­хо­дя­щей через точку M0(x0;y0;z0) пер­пен­ди­ку­ляр­но век­то­ру (А; В; С). Рас­кро­ем скоб­ки и пе­ре­груп­пи­ру­ем сла­га­е­мые, обо­зна­чив сла­га­е­мые, не со­дер­жа­щие пе­ре­мен­ные за D:

;

;

.

Рас­сто­я­ние от точки до плос­ко­сти

Зная урав­не­ние плос­ко­сти, можно найти рас­сто­я­ние от точки, не ле­жа­щей на плос­ко­сти до самой плос­ко­сти.

Рас­сто­я­ние от точки до плос­ко­сти за­да­ча

Дано: В неко­то­рой де­кар­то­вой си­сте­ме ко­ор­ди­нат урав­не­ние Ax+By +Cz+D=0, опи­сы­ва­ю­щее плос­кость. M0(x0, y0, z0) — точка про­стран­ства, за­дан­ная сво­и­ми ко­ор­ди­на­та­ми в той же си­сте­ме ко­ор­ди­нат (см. рис. 2).

Рис. 2.

Найти: рас­сто­я­ние от точки М0 до плос­ко­сти.

Ре­ше­ние: Пусть точка М1(x1;y1;z1)-про­ек­ция точки М0 на плос­кость. Зна­чит, нам необ­хо­ди­мо найти длину от­рез­ка M0M1. Чтобы найти рас­сто­я­ние d, вы­ра­зим век­тор  через век­тор нор­ма­ли, ко­ор­ди­на­ты ко­то­ро­го мы знаем по урав­не­нию плос­ко­сти —  (А; В; С): .

Так как век­тор  и век­тор  — кол­ли­не­ар­ны, зна­чит, можно вы­ра­зить ко­ор­ди­на­ты век­то­ра  двумя спо­со­ба­ми: , .

По­лу­ча­ем си­сте­му урав­не­ний:

Вы­ра­жа­ем ко­ор­ди­на­ты точки M1:

Под­ста­вим ко­ор­ди­на­ты точки M1 в урав­не­ние плос­ко­сти, так как эта точка лежит в плос­ко­сти α:

.

От­сю­да вы­ра­жа­ем ко­эф­фи­ци­ент k:

.

Фор­му­ла рас­сто­я­ния от точки до плос­ко­сти

Те­перь вы­ве­дем фор­му­лу для на­хож­де­ния рас­сто­я­ния от точки до плос­ко­сти:

.

Урав­не­ние плос­ко­сти за­да­чи

За­да­ча 1.

Дано: Тре­уголь­ник с вер­ши­на­ми в точ­ках А1{-5;2;7), А2(5;0;6), А3(0;-1;2). А1М0 – ме­ди­а­на (см. рис. 3). Найти: урав­не­ние плос­ко­сти, про­хо­дя­щей через точку М0 пер­пен­ди­ку­ляр­но ме­ди­ане А1М0.

Рис. 3.

Ре­ше­ние:

Чтобы на­пи­сать урав­не­ние плос­ко­сти, мы долж­ны знать ко­ор­ди­на­ты точки М0, при­над­ле­жа­щей плос­ко­сти, и ко­ор­ди­на­ты век­то­ра нор­ма­ли. За нор­маль­ный век­тор плос­ко­сти можно при­нять век­тор . Опре­де­лим его ко­ор­ди­на­ты. Точка М0— се­ре­ди­на от­рез­ка А2А3, по­это­му, ее ко­ор­ди­на­ты равны .

Ко­ор­ди­на­ты нор­маль­но­го век­то­ра  на­хо­дим, вы­чи­тая из ко­ор­ди­нат конца ко­ор­ди­на­ты на­ча­ла век­то­ра: .

Те­перь под­ста­вим все нуж­ные числа в урав­не­ние плос­ко­сти:

;

.

Ответ: .

Рас­сто­я­ние от точки до плос­ко­сти за­да­ча 2

За­да­ча 2.

Дано: пря­мо­уголь­ный па­рал­ле­ле­пи­пед (см. рис. 4), AB=4; AD=3; AA1=2. A1K:KD1=2:1; K∈α; ; . Найти: а) Рас­сто­я­ние от B1 до α, б) Рас­сто­я­ние от M до D1.

Рис. 4.

Ре­ше­ние: Вве­дем пря­мо­уголь­ную си­сте­му ко­ор­ди­нат, как по­ка­за­но на ри­сун­ке.

а) Чтобы найти нуж­ное нам рас­сто­я­ние на­пи­шем урав­не­ние плос­ко­сти α. Для этого узна­ем ко­ор­ди­на­ты точки K и ко­ор­ди­на­ты век­то­ра нор­ма­ли к плос­ко­сти. Век­тор нор­ма­ли в дан­ном слу­чае – это век­тор . Так как это ра­ди­ус-век­тор, его ко­ор­ди­на­ты сов­па­да­ют с ко­ор­ди­на­та­ми точки С1. ; K(0;2;2).

Тогда урав­не­ние плос­ко­сти α имеет вид ,

Или .

Ис­ко­мое рас­сто­я­ние от точки В1 до плос­ко­сти α на­хо­дим по фор­му­ле: .

Ко­ор­ди­на­ты точки В1 равны (4;0;2). Тогда .

б) Чтобы узнать необ­хо­ди­мое рас­сто­я­ние най­дем ко­ор­ди­на­ты точек M и D1, D1(0;3;2).По усло­вию, точка M на­хо­дит­ся на пря­мой BC, зна­чит M(4;y;0). Так как точка М(4;y;0) при­над­ле­жит плос­ко­сти α, то ее ко­ор­ди­на­ты можно под­ста­вить в урав­не­ние плос­ко­сти, ко­то­рое мы уже знаем — 

По­лу­чи­ли: 16+3y-10=0. Тогда y=-2, M(4;-2;0).

Те­перь най­дем мо­дуль век­то­ра , как ко­рень из суммы квад­ра­тов раз­но­сти ко­ор­ди­нат конца и на­ча­ла век­то­ра: .

Ответ: ; .

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/11-klass/bmetod-koordinat-v-prostranstveb/uravnenie-ploskosti

http://www.youtube.com/watch?v=M5RfXWoz5jQ

http://www.youtube.com/watch?v=Zpv7yKF1QXI

http://www.cleverstudents.ru/line_and_plane/normal_equation_of_plane.html

http://www.mathprofi.ru/uravnenie_ploskosti.html

http://dealer-auto.spb.ru/blog.php?snjqf=/rcxdfcn/statistika_naseleniya_zadachi_s_resheniem_2626_3.jpg

http://mypresentation.ru/download/uravnenie_ploskosti_v_prostranstve

Определить расстояние от точки m до плоскости. Расстояние от точки до плоскости онлайн. Вывод формулы для координатного метода поиска расстояния от точки до плоскости в пространстве

Рассмотрим в пространстве некоторую плоскость π и произвольную точку M 0 . Выберем для плоскости единичный нормальный вектор n с началом в некоторой точке М 1 ∈ π, и пусть р(М 0 ,π) — расстояние от точки М 0 до плоскости π. Тогда (рис. 5.5)

р(М 0 ,π) = | пр n M 1 M 0 | = |nM 1 M 0 |, (5.8)

так как |n| = 1.

Если плоскость π задана в прямоугольной системе координат своим общим уравнением Ax + By + Cz + D = 0, то ее нормальным вектором является вектор с координатами {A; B; C} и в качестве единичного нормального вектора можно выбрать

Пусть (x 0 ; y 0 ; z 0) и (x 1 ; y 1 ; z 1) координаты точек M 0 и M 1 . 2) } } = 0,85 $$

Ответ:

Данная статья рассказывает об определении расстояния от точки до плоскости. произведем разбор методом координат, который позволит находить расстояние от заданной точки трехмерного пространства. Для закрепления рассмотрим примеры нескольких задач.

Расстояние от точки до плоскости находится посредством известного расстояния от точки до точки, где одна из них заданная, а другая – проекция на заданную плоскость.

Когда в пространстве задается точка М 1 с плоскостью χ , то через точку можно провести перпендикулярную плоскости прямую. Н 1 является общей точкой их пересечения. Отсюда получаем, что отрезок М 1 Н 1 – это перпендикуляр,который провели из точки М 1 к плоскости χ , где точка Н 1 – основание перпендикуляра.

Определение 1

Называют расстояние от заданной точки к основанию перпендикуляра, который провели из заданной точки к заданной плоскости.

Определение может быть записано разными формулировками.

Определение 2

Расстоянием от точки до плоскости называют длину перпендикуляра, который провели из заданной точки к заданной плоскости.

Расстояние от точки М 1 к плоскости χ определяется так: расстояние от точки М 1 до плоскости χ будет являться наименьшим от заданной точки до любой точки плоскости. Если точка Н 2 располагается в плоскости χ и не равна точке Н 2 , тогда получаем прямоугольный треугольник вида М 2 H 1 H 2 , который является прямоугольным, где имеется катет М 2 H 1 , М 2 H 2 – гипотенуза. Значит, отсюда следует, что M 1 H 1 считается наклонной, которая проводится из точки М 1 до плоскости χ . Мы имеем, что перпендикуляр, проведенный из заданной точки к плоскости, меньше наклонной, которую проводят из точки к заданной плоскости. Рассмотрим этот случай на рисунке, приведенном ниже.

Расстояние от точки до плоскости – теория, примеры, решения

Существует ряд геометрических задач, решения которых должны содержать расстояние от точки до плоскости. Способы выявления этого могут быть разными. Для разрешения применяют теорему Пифагора или подобия треугольников. Когда по условию необходимо рассчитать расстояние от точки до плоскости, заданные в прямоугольной системе координат трехмерного пространства, решают методом координат. Данный пункт рассматривает этот метод.

По условию задачи имеем, что задана точка трехмерного пространства с координатами M 1 (x 1 , y 1 , z 1) с плоскостью χ , необходимо определить расстояние от М 1 к плоскости χ . Для решения применяется несколько способов решения.

Первый способ

Данный способ основывается на нахождении расстояния от точки до плоскости при помощи координат точки Н 1 , которые являются основанием перпендикуляра из точки М 1 к плоскости χ . Далее необходимо вычислить расстояние между М 1 и Н 1 .

Для решения задачи вторым способом применяют нормальное уравнение заданной плоскости.

Второй способ

По условию имеем, что Н 1 является основанием перпендикуляра, который опустили из точки М 1 на плоскость χ . Тогда определяем координаты (x 2 , y 2 , z 2) точки Н 1 . Искомое расстояние от М 1 к плоскости χ находится по формуле M 1 H 1 = (x 2 — x 1) 2 + (y 2 — y 1) 2 + (z 2 — z 1) 2 , где M 1 (x 1 , y 1 , z 1) и H 1 (x 2 , y 2 , z 2) . Для решения необходимо узнать координаты точки Н 1 .

Имеем, что Н 1 является точкой пересечения плоскости χ с прямой a , которая проходит через точку М 1 , расположенную перпендикулярно плоскости χ . Отсюда следует, что необходимо составление уравнения прямой, проходящей через заданную точку перпендикулярно к заданной плоскости. Именно тогда сможем определить координаты точки Н 1 . Необходимо произвести вычисление координат точки пересечения прямой и плоскости.

Алгоритм нахождения расстояния от точки с координатами M 1 (x 1 , y 1 , z 1) к плоскости χ :

Определение 3

• составить уравнение прямой а, проходящей через точку М 1 и одновременно
• перпендикулярной к плоскости χ ;
• найти и вычислить координаты (x 2 , y 2 , z 2) точки Н 1 , являющимися точками
• пересечения прямой a с плоскостью χ ;
• вычислить расстояние от М 1 до χ , используя формулу M 1 H 1 = (x 2 — x 1) 2 + (y 2 — y 1) 2 + z 2 — z 1 2 .

Третий способ

В заданной прямоугольной системе координат О х у z имеется плоскость χ , тогда получаем нормальное уравнение плоскости вида cos α · x + cos β · y + cos γ · z — p = 0 . Отсюда получаем, что расстояние M 1 H 1 с точкой M 1 (x 1 , y 1 , z 1) , проведенной на плоскость χ , вычисляемое по формуле M 1 H 1 = cos α · x + cos β · y + cos γ · z — p . Эта формула справедлива, так как это установлено благодаря теореме.

Теорема

Если задана точка M 1 (x 1 , y 1 , z 1) в трехмерном пространстве, имеющая нормальное уравнение плоскости χ вида cos α · x + cos β · y + cos γ · z — p = 0 , тогда вычисление расстояния от точки до плоскости M 1 H 1 производится из формулы M 1 H 1 = cos α · x + cos β · y + cos γ · z — p , так как x = x 1 , y = y 1 , z = z 1 .

Доказательство

Доказательство теоремы сводится к нахождению расстояния от точки до прямой. Отсюда получаем, что расстояние от M 1 до плоскости χ — это и есть модуль разности числовой проекции радиус-вектора M 1 с расстоянием от начала координат к плоскости χ . Тогда получаем выражение M 1 H 1 = n p n → O M → — p . Нормальный вектор плоскости χ имеет вид n → = cos α , cos β , cos γ , а его длина равняется единице, n p n → O M → — числовая проекция вектора O M → = (x 1 , y 1 , z 1) по направлению, определяемым вектором n → .

Применим формулу вычисления скалярных векторов. Тогда получаем выражение для нахождения вектора вида n → , O M → = n → · n p n → O M → = 1 · n p n → O M → = n p n → O M → , так как n → = cos α , cos β , cos γ · z и O M → = (x 1 , y 1 , z 1) . Координатная форма записи примет вид n → , O M → = cos α · x 1 + cos β · y 1 + cos γ · z 1 , тогда M 1 H 1 = n p n → O M → — p = cos α · x 1 + cos β · y 1 + cos γ · z 1 — p . Теорема доказана.

Отсюда получаем, что расстояние от точки M 1 (x 1 , y 1 , z 1) к плоскости χ вычисляется при помощи подстановки в левую часть нормального уравнения плоскости cos α · x + cos β · y + cos γ · z — p = 0 вместо х, у, z координаты x 1 , y 1 и z 1 ,относящиеся к точке М 1 , взяв абсолютную величину полученного значения.

Рассмотрим примеры нахождения расстояния от точки с координатами до заданной плоскости.

Пример 1

Вычислить расстояние от точки с координатами M 1 (5 , — 3 , 10) к плоскости 2 x — y + 5 z — 3 = 0 .

Решение

Решим задачу двумя способами.

Первый способ начнется с вычисления направляющего вектора прямой a . По условию имеем, что заданное уравнение 2 x — y + 5 z — 3 = 0 является уравнением плоскости общего вида, а n → = (2 , — 1 , 5) является нормальным вектором заданной плоскости. Его применяют в качестве направляющего вектора прямой a , которая перпендикулярна относительно заданной плоскости. Следует записать каноническое уравнение прямой в пространстве, проходящее через M 1 (5 , — 3 , 10) с направляющим вектором с координатами 2 , — 1 , 5 .

Уравнение получит вид x — 5 2 = y — (- 3) — 1 = z — 10 5 ⇔ x — 5 2 = y + 3 — 1 = z — 10 5 .

Следует определить точки пересечения. Для этого нежно объединить уравнения в систему для перехода от канонического к уравнениям двух пересекающихся прямых. Данную точку примем за Н 1 . Получим, что

x — 5 2 = y + 3 — 1 = z — 10 5 ⇔ — 1 · (x — 5) = 2 · (y + 3) 5 · (x — 5) = 2 · (z — 10) 5 · (y + 3) = — 1 · (z — 10) ⇔ ⇔ x + 2 y + 1 = 0 5 x — 2 z — 5 = 0 5 y + z + 5 = 0 ⇔ x + 2 y + 1 = 0 5 x — 2 z — 5 = 0

После чего необходимо разрешить систему

x + 2 y + 1 = 0 5 x — 2 z — 5 = 0 2 x — y + 5 z — 3 = 0 ⇔ x + 2 y = 1 5 x — 2 z = 5 2 x — y + 5 z = 3

Обратимся к правилу решения системы по Гауссу:

1 2 0 — 1 5 0 — 2 5 2 — 1 5 3 ~ 1 2 0 — 1 0 — 10 — 2 10 0 — 5 5 5 ~ 1 2 0 — 1 0 — 10 — 2 10 0 0 6 0 ⇒ ⇒ z = 0 6 = 0 , y = — 1 10 · 10 + 2 · z = — 1 , x = — 1 — 2 · y = 1

Получаем, что H 1 (1 , — 1 , 0) .

Производим вычисления расстояния от заданной точки до плоскости. Берем точки M 1 (5 , — 3 , 10) и H 1 (1 , — 1 , 0) и получаем

M 1 H 1 = (1 — 5) 2 + (- 1 — (- 3)) 2 + (0 — 10) 2 = 2 30

Второй способ решения заключается в том, чтобы для начала привести заданное уравнение 2 x — y + 5 z — 3 = 0 к нормальному виду. Определяем нормирующий множитель и получаем 1 2 2 + (- 1) 2 + 5 2 = 1 30 . Отсюда выводим уравнение плоскости 2 30 · x — 1 30 · y + 5 30 · z — 3 30 = 0 . Вычисление левой части уравнения производится посредствам подстановки x = 5 , y = — 3 , z = 10 , причем нужно взять расстояние от M 1 (5 , — 3 , 10) до 2 x — y + 5 z — 3 = 0 по модулю. Получаем выражение:

M 1 H 1 = 2 30 · 5 — 1 30 · — 3 + 5 30 · 10 — 3 30 = 60 30 = 2 30

Ответ: 2 30 .

Когда плоскость χ задается одним из способов раздела способы задания плоскости, тогда нужно для начала получить уравнение плоскости χ и вычислять искомое расстояние при помощи любого метода.

Пример 2

В трехмерном пространстве задаются точки с координатами M 1 (5 , — 3 , 10) , A (0 , 2 , 1) , B (2 , 6 , 1) , C (4 , 0 , — 1) . Вычислить расстяние от М 1 к плоскости А В С.

Решение

Для начала необходимо записать уравнение плоскости, проходящее через заданные три точки с координатами M 1 (5 , — 3 , 10) , A (0 , 2 , 1) , B (2 , 6 , 1) , C (4 , 0 , — 1) .

x — 0 y — 2 z — 1 2 — 0 6 — 2 1 — 1 4 — 0 0 — 2 — 1 — 1 = 0 ⇔ x y — 2 z — 1 2 4 0 4 — 2 — 2 = 0 ⇔ ⇔ — 8 x + 4 y — 20 z + 12 = 0 ⇔ 2 x — y + 5 z — 3 = 0

Отсюда следует, что задача имеет аналогичное предыдущему решение. Значит, расстояние от точки М 1 к плоскости А В С имеет значение 2 30 .

Ответ: 2 30 .

Нахождение расстояния от заданной точки на плоскости или к плоскости, которым они параллельны, удобнее, применив формулу M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 — p . Отсюда получим, что нормальные уравнения плоскостей получают в несколько действий.

Пример 3

Найти расстояние от заданной точки с координатами M 1 (- 3 , 2 , — 7) к координатной плоскости О х у z и плоскости, заданной уравнением 2 y — 5 = 0 .

Решение

Координатная плоскость О у z соответствует уравнению вида х = 0 . Для плоскости О у z оно является нормальным. Поэтому необходимо подставить в левую часть выражения значения х = — 3 и взять модуль значения расстояния от точки с координатами M 1 (- 3 , 2 , — 7) к плоскости. Получаем значение, равное — 3 = 3 .

После преобразования нормальное уравнение плоскости 2 y — 5 = 0 получит вид y — 5 2 = 0 . Тогда можно найти искомое расстояние от точки с координатами M 1 (- 3 , 2 , — 7) к плоскости 2 y — 5 = 0 . Подставив и вычислив, получаем 2 — 5 2 = 5 2 — 2 .

Ответ: Искомое расстояние от M 1 (- 3 , 2 , — 7) до О у z имеет значение 3 , а до 2 y — 5 = 0 имеет значение 5 2 — 2 .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Пусть существует плоскость . Проведем нормаль
через начало координат О. Пусть заданы
– углы, образованные нормальюс осями координат.
. Пусть– длина отрезка нормали
до пересечения с плоскостью. Считая известными направляющие косинусы нормали, выведем уравнение плоскости.

Пусть
) – произвольная точка плоскости. Вектор единичной нормали имеет координаты. Найдем проекцию вектора
на нормаль.

Поскольку точка М принадлежит плоскости, то

.

Это и есть уравнение заданной плоскости, называющееся нормальным .

Расстояние от точки до плоскости

Пусть дана плоскость ,М *
– точка пространства,d – её расстояние от плоскости.

Определение. Отклонением точки М* от плоскости называется число (+ d ), если M * лежит по ту сторону от плоскости, куда указывает положительное направление нормали , и число (-d ), если точка расположена по другую сторону плоскости:

.

Теорема . Пусть плоскость с единичной нормальюзадана нормальным уравнением:

Пусть М *
– точка пространства Отклонение т.M * от плоскости задаётся выражением

Доказательство. Проекцию т.
* на нормаль обозначимQ . Отклонение точки М* от плоскости равно

.

Правило. Чтобы найти отклонение т. M * от плоскости, нужно в нормальное уравнение плоскости подставить координаты т. M * . Расстояние от точки до плоскости равно .

Приведение общего уравнения плоскости к нормальному виду

Пусть одна и та же плоскость задана двумя уравнениями:

Общее уравнение,

Нормальное уравнение.

Поскольку оба уравнения задают одну плоскость, их коэффициенты пропорциональны:

Первые три равенства возведем в квадрат и сложим:

Отсюда найдем – нормирующий множитель:

. (10)

Умножив общее уравнение плоскости на нормирующий множитель, получим нормальное уравнение плоскости:

Примеры задач на тему «Плоскость».

Пример 1. Составить уравнение плоскости , проходящей через заданную точку
(2,1,-1) и параллельной плоскости.

Решение . Нормаль к плоскости :
. Поскольку плоскости параллельны, то нормальявляется и нормалью к искомой плоскости. Используя уравнение плоскости, проходящей через заданную точку (3), получим для плоскостиуравнение:

Ответ:

Пример 2. Основанием перпендикуляра, опущенного из начала координат на плоскость , является точка
. Найти уравнение плоскости.

Решение . Вектор
является нормалью к плоскости. ТочкаМ 0 принадлежит плоскости. Можно воспользоваться уравнением плоскости, проходящей через заданную точку (3):

Ответ:

Пример 3. Построить плоскость , проходящую через точки

и перпендикулярную плоскости :.

Следовательно, чтобы некоторая точка М (x , y , z ) принадлежала плоскости , необходимо, чтобы три вектора
были компланарны:

=0.

Осталось раскрыть определитель и привести полученное выражение к виду общего уравнения (1).

Пример 4. Плоскость задана общим уравнением:

Найти отклонение точки
от заданной плоскости.

Решение . Приведем уравнение плоскости к нормальному виду.

,

.

Подставим в полученное нормальное уравнение координаты точки М* .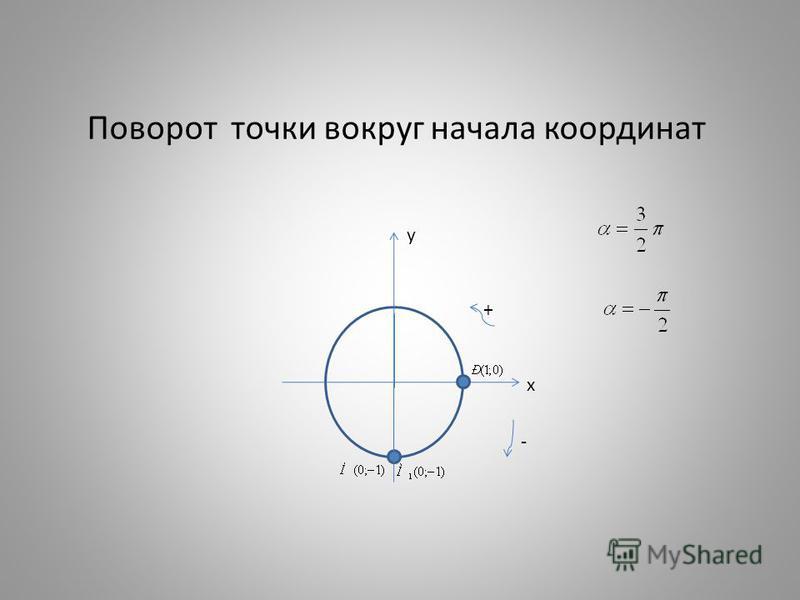

.

Ответ:
.

Пример 5. Пересекает ли плоскость отрезок.

Решение . Чтобы отрезок АВ пересекал плоскость, отклонения иот плоскостидолжны иметь разные знаки:

.

Пример 6. Пересечение трех плоскостей в одной точке.

.

Система имеет единственное решение, следовательно, три плоскости имеют одну общую точку.

Пример 7. Нахождение биссектрис двугранного угла, образованного двумя заданными плоскостями.

Пусть и- отклонение некоторой точки
от первой и второй плоскостей.

На одной из биссектральных плоскостей (отвечающей тому углу, в котором лежит начало координат) эти отклонения равны по модулю и знаку, а на другой – равны по модулю и противоположны по знаку.

Это уравнение первой биссектральной плоскости.

Это уравнение второй биссектральной плоскости.

Пример 8. Определение местоположения двух данных точек иотносительно двугранных углов, образованных данными плоскостями.

Пусть
. Определить: в одном, в смежных или в вертикальных углах находятся точкии.

а). Если илежат по одну сторону оти от, то они лежат в одном двугранном углу.

б). Если илежат по одну сторону оти по разные от, то они лежат в смежных углах.

в). Если илежат по разные стороны оти, то они лежат в вертикальных углах.

Системы координат 3

Линии на плоскости 8

Линии первого порядка. Прямые на плоскости. 10

Угол между прямыми 12

Общее уравнение прямой 13

Неполное уравнение первой степени 14

Уравнение прямой “в отрезках” 14

Совместное исследование уравнений двух прямых 15

Нормаль к прямой 15

Угол между двумя прямыми 16

Каноническое уравнение прямой 16

Параметрические уравнения прямой 17

Нормальное (нормированное) уравнение прямой 18

Расстояние от точки до прямой 19

Уравнение пучка прямых 20

Примеры задач на тему «прямая на плоскости» 22

Векторное произведение векторов 24

Свойства векторного произведения 24

Геометрические свойства 24

Алгебраические свойства 25

Выражение векторного произведения через координаты сомножителей 26

Смешанное произведение трёх векторов 28

Геометрический смысл смешанного произведения 28

Выражение смешанного произведения через координаты векторов 29

Примеры решения задач

, Конкурс «Презентация к уроку»

Класс: 11

Презентация к уроку

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели:

• обобщение и систематизация знаний и умений учащихся;
• развитие умений анализировать, сравнивать, делать выводы.

Оборудование:

• мультимедийный проектор;
• компьютер;
• листы с текстами задач

ХОД ЗАНЯТИЯ

I. Организационный момент

II. Этап актуализации знаний (слайд 2)

Повторяем как определяется расстояние от точки до плоскости

III. Лекция (cлайды 3-15)

На занятии мы рассмотрим различные способы нахождения расстояния от точки до плоскости.

Первый метод: поэтапно-вычислительный

Расстояние от точки М до плоскости α:
– равно расстоянию до плоскости α от произвольной точки Р, лежащей на прямой a, которая проходит через точку М и параллельна плоскости α;
– равно расстоянию до плоскости α от произвольной точки Р, лежащей на плоскости β, которая проходит через точку М и параллельна плоскости α.

Решим следующие задачи:

№1. В кубе А…D 1 найти расстояние от точки С 1 до плоскости АВ 1 С.

Осталось вычислить значение длины отрезка О 1 Н.

№2. В правильной шестиугольной призме А…F 1 , все ребра которой равны 1, найдите расстояние от точки А до плоскости DEA 1 .

Следующий метод: метод объемов .

Если объем пирамиды АВСМ равен V, то расстояние от точки М до плоскости α, содержащей ∆АВС вычисляется по формуле ρ(М; α) = ρ(М; АВС) =
При решении задач мы используем равенство объемов одной фигуры, выраженные двумя различными способами.

Решим следующую задачу:

№3. Ребро AD пирамиды DABC перпендикулярно плоскости основания АВС. Найдите расстояние от А до плоскости, проходящей через середины ребер АВ, АС и АD, если.

При решении задач координатным методом расстояние от точки М до плоскости α можно вычислить по формуле ρ(М; α) = , где М(х 0 ; у 0 ; z 0), а плоскость задана уравнением ax + by + cz + d = 0

Решим следующую задачу:

№4. В единичном кубе A…D 1 найдите расстояние от точки А 1 до плоскости ВDC 1 .

Введем систему координат с началом в точке А, ось у пройдет по ребру АВ, ось х – по ребру АD, ось z – по ребру АА 1 . Тогда координаты точек В (0; 1; 0) D (1; 0; 0;) C 1 (1; 1; 1)
Составим уравнение плоскости, проходящей через точки В, D, C 1 .

Тогда – dx – dy + dz + d = 0 x + y – z – 1= 0. Следовательно, ρ =

Следующий метод, который можно использовать при решении задач данного типа – метод опорных задач.

Применение данного метода состоит в применении известных опорных задач, которые формулируются как теоремы.

Решим следующую задачу:

№5. В единичном кубе А…D 1 найдите расстояние от точки D 1 до плоскости АВ 1 С.

Рассмотрим применение векторного метода.

№6. В единичном кубе А…D 1 найдите расстояние от точки А 1 до плоскости ВDС 1 .

Итак, мы рассмотрели различные способы, которые можно использовать при решении данного типа задач. Выбор того или иного метода зависит от конкретной задачи и ваших предпочтений.

IV. Работа в группах

Попробуйте решить задачу разными способами.

№1. Ребро куба А…D 1 равно . Найдите расстояние от вершины С до плоскости BDC 1 .

№2. В правильном тетраэдре АВСD с ребром найдите расстояние от точки А до плоскости BDC

№3. В правильной треугольной призме АВСА 1 В 1 С 1 все ребра которой равны 1, найдите расстояние от А до плоскости ВСА 1 .

№4. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите расстояние от А до плоскости SCD.

V. Итог урока, домашнее задание, рефлексия

Отклонение точки от прямой

В данной статье мы рассмотрим понятие отклонения точки от прямой на плоскости. Приведем примеры нахождения отклонения точки от прямой.

Отклонение точки от прямой на плоскости − это расстояние от точки до прямой, взятой со знаком «+», если эта точка и начало координат лежат по разные стороны прямой, и со знаком «−», если точка и начало координат лежат по одну сторону от прямой.

Если прямая проходит через начало координат, то отклонение точки от прямой предполагается равным расстоянию от точки до прямой, взятой со знаком «+», если точка лежит по ту сторону от прямой, куда направлен пормальный вектор прямой, и равным расстоянию от точки до прямой, взятой со знаком «−», в противном случае.

Обозначим отклонение точки от прямой символом δ, а расстояние от точки до прямой символом d. На рисунке Рис.1 отклонение точки M₁ от прямой L равно δ=+d₁, так как точка M₁ и начало координат O лежат по разные стороны прямой L, а отклонение точки M₂ от прямой L равно δ=−d₂, так как точка M₂ и начало координат O лежат по одну сторону от прямой L.

На рисунке Рис.2 прямая L проходит через начало координат. Поэтому, отклонение точки M₁ от прямой L равно δ=+d₁, так как точка M₁ лежит по ту сторону прямой L, куда направлен нормальный вектор n прямой L, а отклонение точки M₂ от прямой L равно δ=−d₂, так как точка M₂ лежит по противоположную сторону прямой, куда направлен нормальный вектор n прямой L

 

Рассмотрим нормальное уравнение прямой L (Рис.3):

где r− расстояние начала координат до прямой L, а φ− угол между нормальным вектором прямой L и осью Ox.

Покажем, что левая часть нормального уравнения прямой дает отклонение точки M(x,y) от прямой, заданной уравнением (1). Для этого докажем следующую теорему:

Теорема 1. Пусть прямая L определяется нормальным уравнением прямой (1). Тогда отклонением точки M с координатами x, y от прямой L равно δ=xcosφ+ysinφ−r.

Доказательство. Проведем через нормальный вектор прямой L линию OQ (Рис.3). Проекция точки М на прямую OQ будет точка S. Отклонение δ точки M от прямой L будет равно SR.

Тогда

Но

где n− единичный нормальный вектор прямой L, α−угол между векторами n и .

Из (3) и (4) следует:

С другой стороны

так как нормальный вектор прямой имеет координаты n={cosφ, sinφ}, а точка M − M(x, y).

Сопоставляя (2), (5) и (6), получим:

Теорема доказана.

Таким образом, как следует из теоремы 1, для вычисления отклонения некоторой точки M₀(x₀, y₀) от прямой, нужно в левую часть нормированного уравнения прямой (1) подставить координаты точки M₀:

Заметим, расстояние от точки M₀ до прямой L будет равно модулю отклонения данной точки от прямой.

Пример 1. Задано нормальное уравнение прямой:

Найти отклонение точки M(5,-3) от прямой (7).

Решение. Подставим координаты точки M(5,−3) в левую часть уравнения (7):

Ответ. Отклонение точки M(5,−3) от прямой (7) равно:

Пример 2. Задано общее уравнение прямой:

Найти отклонение точки M(1,1) от прямой (8).

Решение. Один из простых методов решения − это приведение общего уравнения прямой к нормальному виду (подробнее об этом читайте в статье «нормальное уравнение прямой»). Для приведения уравнения (8) к нормальному виду, нужно умножить данное уравнение на нормирующий множитель:

Так как в уравнении (8) третий коэффициент равен +1, то знак нормирующего множителя должен быть противоположным:

Умножив уравнение (8) на нормирующий множитель, получим:

Теперь найдем отклонение точки M(1,1) от прямой (8). Для этого вставим координаты точки M в левую часть уравнения(8):

Ответ. 2}}\right|.$$

 

Прямоугольная система координат

Прежде чем приступить к созданию первой управляющей программы, вы должны вспомнить, что такое прямоугольная система координат. Ведь именно прямоугольная система координат служит математической базой программирования обработки. Более 300 лет назад французский математик Декарт придумал систему, которая позволяет человеку описать положение любой точки в пространстве. В простейшем случае прямоугольная система координат представляет собой две пересекающиеся под прямым углом линии. Эти линии называются осями, а точка их пересечения является началом координат.

Рис. 3.1. Прямоугольная система координат на плоскости

Оси обозначаются буквами X и Y. Координатная система с двумя осями X и Y позволяет описать положение точки на плоскости. Расстояние от начала координат до точки А вдоль оси X является х-координатой этой точки. Расстояние от начала координат до точки А вдоль оси Y является у-координатой этой точки.

Координаты точки принято указывать в скобках. Сначала пишется координата по оси X, а затем по оси Y. Таким образом, на рис. 3.1 находится точка А(1; 5). У каждой оси есть положительное и отрицательное направления. Когда координата имеет отрицательное значение, то это означает, что точка лежит либо левее начала координат, либо ниже. Например, точка В имеет следующие координаты: х = –2, у = –5. Если точка лежит на какой-либо оси, то одна из ее координат обязательно равна нулю.

Пересечение трех взаимно перпендикулярных плоскостей образует трехмерную систему координат, которая используется для описания положения точки в пространстве. К двум имеющимся осям X и Y добавляется третья ось Z. Координаты точки также указываются в скобках и идут в алфавитном порядке (x; y; z).

Рис. 3.2. Прямоугольная пространственная система координат

Как инструменты близости вычисляют расстояние—Справка

Как определяется расстояние

Расстояние между любыми двумя объектами вычисляется как минимальный интервал между ними, т.е., там, где два объекта расположены ближе всего друг к другу. Эта логика действует во всех инструментах геообработки, которые вычисляют расстояние, включая такие инструменты, как Ближайший объект, Построить таблицу ближайших объектов, Расстояние между точками и Пространственное соединение (с опцией ближайших совпадений).

Измерения расстояний имеют наибольшую точность, если входные данные используют систему координат равнопромежуточной проекции. Хотя вычисление расстояния может быть выполнено независимо от системы координат, результат может оказаться не точным или даже бессмысленным, если данные используют географическую систему координат или система координат задана неправильно.

Более подробно о географических системах координат и системах координат проекции

Для дальнейшего обсуждения, расстоянием всегда будет считаться минимальный интервал между двумя объектами.

Особые соображения

• Несколько объектов могут оказаться на одинаковом удалении от другого объекта. В таком случае один из равноудаленных объектов будет выбираться в качестве ближайшего случайным образом.
• Если один из объектов содержит другой или находится внутри другого объекта, расстояние между ними равно 0.
  • Это означает, что если объект находится внутри полигона, расстояние между ним и окружающим его полигоном равно 0.
• Расстояние между двумя объектами равняется нулю всякий раз, когда у них имеется хотя бы одна общая координата x,y.
  • Это означает, что при пересечении, перекрытии или касании двух объектов, расстояние между ними равняется 0.
• Расстояние всегда вычисляется до границы полигонального объекта, не до центра или центроида полигона.
  • Как отмечено выше, если объект полностью находится внутри полигона, расстояние между ним и окружающим его полигоном равно 0.
• Расстояние между двумя объектами (любого типа) не меняется в зависимости от направления измерения.

Основные операции для определения расстояния

Вычисление расстояния зависит от типа геометрии объектов, а также от других факторов, таких как система координат. Однако есть три основных правила, подробнее описанные ниже, которые определяют способ вычисления расстояния.

1. Расстояние между двумя точками является прямой линией, соединяющей их.
2. Расстояние от точки до линии измеряется либо как перпендикуляр, либо как расстояние до ближайшей вершины.
3. Расстояние между полилиниями определяется вершинами сегментов.

Правило 1: расстояние между двумя точками является прямой линией, соединяющей их

На рисунке ниже показано расстояние между двумя точками, вместе с несколькими ключевыми словами и объектами, использующимися инструментами близости.

Ключевые слова в вышеуказанных выносках (IN_FID, NEAR_DIST, NEAR_FID, NEAR_X, NEAR_Y и NEAR_ANGLE) являются полями, добавляемыми к выходным данным инструментами Построить таблицу ближайших объектов и Расстояние между точками, а также к входному классу объектов при использовании инструмента Ближайший объект.

Расстояние между мультиточками

Для особого случая, когда определяется расстояние между мультиточками, вычисляются расстояния от каждой точки входного мультиточечного объекта до каждой точки ближайшего мультиточечного объекта с помощью Правила 1, минимальное из этих трех расстояний станет расстоянием между мультиточечными объектами.

Кроме того, когда одна из точек мультиточечного объекта находится поверх одной из точек другого мультиточечного объекта, расстояние между ними равняется 0. Это справедливо для всех составных объектов.

Правило 2: расстояние от точки до полилинии измеряется либо как перпендикуляр, либо как расстояние до ближайшей вершины

В ArcGIS линейные объекты называются полилиниями. Эти два термина, линия и полилиния, взаимозаменяемы. Полилиния является упорядоченным набором точек, эти точки называются вершинами. An individual vertice is a vertex. Полилиния может иметь любое количество вершин. Линия, заданная двумя вершинами, называется сегментом. Две вершины, которые задают сегмент линии, называются конечными вершинами.

Сходным образом, полигон является замкнутой областью, заданной одной или несколькими полилиниями.

Кратчайшим расстоянием от точки до сегмента линии является перпендикуляр к ней. Если в пределах конечных вершин сегмента перпендикуляр провести не удается, кратчайшим расстоянием будет расстояние до ближайшей конечной вершины.

Расстояние от точки до полилинии

Если полилиния содержит только один сегмент, для вычисления расстояния применяется Правило 2.

Если полилиния состоит из нескольких сегментов (чаще всего), сначала определяется ближайший к точке сегмент линии, затем для вычисления расстояния применяется Правило 2.

Расстояние от точки до полигона

Поскольку полигон является замкнутой областью, образованной набором сегментов линий, вычисление расстояния от точки до полигона включает определение ближайшего к точке сегмента, затем применяется Правило 2.

Расстояние будет определяться, только если точка находится вне полигона; иначе, расстояние равно 0.

На рисунке выше, для точек 2 и 3 расстояние равно 0, для точек 1 и 4 – расстояние положительно.

Правило 3: расстояние между полилиниями определяется вершинами сегментов линии

Для двух объектов, не являющихся точками, таких как два сегмента линий:

1. Расстояние вычисляется от каждой из конечных вершин входного сегмента до ближайшего сегмента с использованием Правила 2.
2. Расстояние вычисляется от каждой из конечных вершин ближайшего сегмента до входного сегмента.

Минимальное из этих двух значений принимается за расстояние между двумя сегментами.

Расстояние от полилинии до полилинии

В простейшем случае, предположим, что оба полилинейных объекта состоят из одного сегмента. На рисунке ниже показан перпендикуляр CX от вершины C до сегмента, заданного вершинами AB. Перпендикуляр от вершины D также вычисляется, но это расстояние больше, чем расстояние CX. Поэтому CX является кратчайшим расстоянием от сегмента CD до сегмента AB.

Обратите внимание, что перпендикуляр от вершины A или B до сегмента CD провести нельзя, поэтому, кратчайшее расстояние вычисляется от вершин A и B до вершины C. В результате, именно AC является кратчайшим расстоянием между сегментами AB и CD.

Из двух вычисленных расстояний (AC и CX), CX является кратчайшим между двумя сегментами, поскольку это минимальное расстояние из всех расстояний между вершинами и сегментом.

Когда обе полилинии состоят из нескольких сегментов, определяются два наиболее близкорасположенных друг к другу сегмента, затем вычисляется расстояние, согласно Правилу 3.

Расстояние от полилинии до полигона

При вычислении расстояния между полилинией и полигоном определяются два наиболее близкорасположенных сегмента: один сегмент полилинии и один сегмент из образующих границу полигона. Расстояние между этими двумя сегментами определяется так же, как описано в Правиле 3.

Краткая информация

На следующем рисунке показано, как измеряется расстояние между объектами различных типов и определяется положение ближайших объектов. Показаны не все возможные комбинации.

Связанные темы

Отзыв по этому разделу?

Видео с вопросом: Определение расстояния между точкой и исходной точкой с использованием формулы расстояния между двумя точками

Стенограмма видеозаписи

Найдите расстояние между отрицательной точкой два, четыре и исходной точкой.

Чтобы помочь нам понять, что означает этот вопрос, я нарисовал небольшой набросок. На самом деле я показал это на паре осей. Итак, на самом деле у нас есть два момента. У нас отрицательные два, четыре.А у нас ноль, ноль. И это ноль, ноль, потому что это источник. И мы пытаемся найти расстояние между этими двумя точками. И я изобразил это розовой линией.

Для этого нам нужно использовать формулу расстояния или формулу расстояния между двумя точками. И формула такова, что расстояние равно квадратному корню два минус 𝑥 один все в квадрате плюс 𝑦 два минус 𝑦 один все в квадрате.

На самом деле это означает квадратный корень из разницы между нашими-координатами в квадрате плюс разность между нашими 𝑦-координатами в квадрате.Но почему это дает нам расстояние? Что ж, причина, по которой мы получили эту формулу, в том, что она исходит из теоремы Пифагора.

Итак, я нарисовал небольшой треугольник, чтобы помочь нам понять, что это будет. Итак, у меня получился прямоугольный треугольник. А наше расстояние на самом деле наша гипотенуза. Наша разница в 𝑦 — одна из наших коротких сторон. А разница в 𝑥-координатах — это на самом деле наша другая более короткая сторона. Таким образом, мы сможем адаптировать нашу теорему Пифагора, чтобы на самом деле дать нам гипотенузу или, в данном случае, расстояние.

Хорошо, отлично! Давайте воспользуемся формулой, чтобы вычислить расстояние между нашей точкой и исходной точкой. Итак, во-первых, я обозначил наши координаты. И я сделал это, чтобы мы знали, что мы собираемся вернуть в нашу формулу, не совершая ошибок. А затем мы фактически подставим эти значения в нашу формулу.

Итак, мы имеем, что расстояние равно квадратному корню из нуля минус два минус два, все в квадрате. И это потому, что это 𝑥 два, то есть ноль, минус один, что отрицательно.И тогда все в квадрате. И это будет плюс ноль минус четыре в квадрате. И это потому, что это наши ценности два и 𝑦 один. Таким образом, это даст нам, что расстояние равно квадратному корню из двух в квадрате плюс отрицательные четыре в квадрате.

И, как вы можете видеть на этом этапе, мы фактически возводим в квадрат разности каждой из наших 𝑥-координат и 𝑦-координат. Так что на самом деле это будет означать, что не имеет значения, в каком направлении у нас есть очки. Так что, если бы наши 𝑥 один и 𝑦 один поменяли местами с нашими 𝑥 два и 𝑦 два, это все равно работало бы, потому что мы фактически возводим разницу в квадрат.Так что ответ всегда будет положительным.

Итак, теперь мы можем продолжить и сказать, что расстояние равно корню 20. Хорошо, это окончательный ответ? О да, здесь у нас есть ответ. Но я всегда говорю: если вы получите резкий ответ, постарайтесь упростить, где это возможно. Итак, мы попытаемся еще больше упростить это.

Чтобы еще больше упростить это, мы будем использовать это правило surd, которое гласит, что корень 𝑎, умноженный на корень 𝑏, равен корню, помня, что мы действительно хотим, чтобы 𝑎 или 𝑏 были наивысшим квадратным множителем, равным 20. , что означает, что мы можем сказать, что корень 20 равен корню четыре, умноженному на корень пять.И мы не можем упростить это дальше.

Итак, мы можем сказать, что расстояние между отрицательной точкой два, четыре и исходной точкой будет равно двум корням пять. И в этом вопросе у нас просто нет единиц. Вместо этого мы часто можем сказать, что это две единицы длины корня пятью.

Расстояние по перпендикуляру от точки до линии

(Кстати — нам действительно не нужно говорить «перпендикулярно», потому что расстояние от точки до линии всегда означает кратчайшее расстояние.2`

После доказательства приведено несколько примеров использования этой формулы.

Доказательство формулы перпендикулярного расстояния

Начнем с строки Ax + By + C = 0 и обозначим DE. Имеет наклон «-A / B».

У нас есть точка P с координатами ( м , n ). Мы хотим найти расстояние по перпендикуляру от точки P до линии DE (то есть расстояние «PQ»).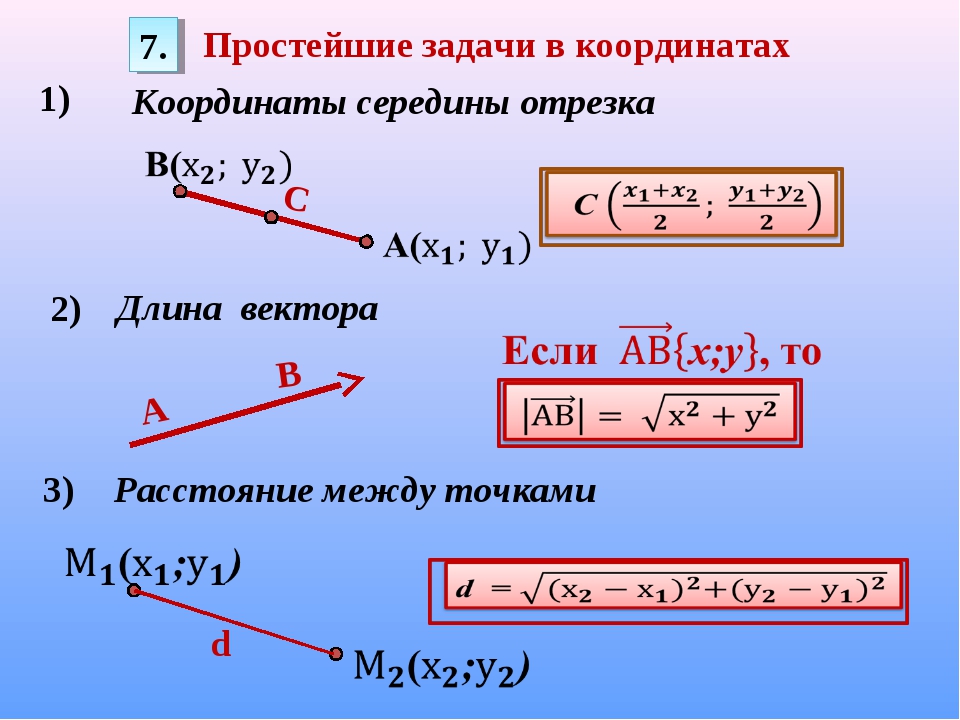 2))`

Знак абсолютного значения необходим, поскольку расстояние должно быть положительным значением, и определенные комбинации A, m, B, n и C могут дать отрицательное число в числителе.2`

`= (| (-2) (5) + (3) (6) +4 |) / (sqrt (4 + 9)`

`= 3,328`

Вот график ситуации. Мы видим, что наш ответ чуть более 3 единиц является разумным.

Таким образом, требуемое расстояние составляет «3,3» единицы с точностью до 1 десятичного знака.

Пример 2

Найдите расстояние от точки `(-3, 7)` до линии

`y = 6 / 5x + 2`

Ответ

Сначала нам нужно выразить данную строку в стандартной форме.2`

`= (| (6) (- 3) + (- 5) (7) +10 |) / sqrt (36 + 25)`

`= | -5,506 |`

`= 5,506`

Таким образом, требуемое расстояние составляет 5,506 единиц с точностью до 3 десятичных знаков.

Найдите точку на прямой, которая является ближайшей к калькулятору исходной точки

Этот калькулятор свободного уклона рассчитывает несколько параметров, включая уклон и уравнение линии. Он принимает входные данные двух известных точек или одной известной точки, а вертикальная линия имеет неопределенный наклон, так как это приведет к дроби с 0 в качестве знаменателя.См. Приведенное ниже уравнение.

Калькулятор среднего, медианы, режима и диапазона. Рассчитайте среднее значение и диапазон. Введите числа справа, ставя между ними запятую. Значение в наборе, наиболее близкое к середине диапазона. Режим. Как найти режим. Единственное число, которое появляется несколько раз, — 3, так что это режим.

3 февраля 2020 г. · Пример 10.3, 5 Найдите точки на оси x, расстояние между которыми от прямой / 3 + 𝑦 / 4 = 1 равно 4 единицам. Нам нужно найти точку на оси x. Пусть любая точка на оси x будет P (x, 0). Учитывая, что расстояние по перпендикуляру от точки P (x, 0) до данной прямой 𝑥 / 3 + 𝑦 / 4 = 1 равно 4. Упрощение уравнения

18 ноября 2007 г. · В моем последнем тесте с вычислением они спросили f (x) = 10x + 5, какая точка в функции ближе всего к началу координат? Я решил это, найдя нормальную линию, которая пересекает начало координат, а затем нашел, где эта линия пересекает f (x).(Мы еще не получили тесты, поэтому я не знаю, как это сработало) В любом случае …

Я хочу найти точку, которая находится ближе всего к моей точке на плоскости. Другими словами, я хочу найти точку на линии $ (1,1,1) + t (2,2,1) $, но на моей плоскости. Обратите внимание, что вектор $ (2,2,1) $ — это мой нормальный вектор, и поэтому я хочу найти точку, параллельную этому вектору, но из моей исходной точки. Мне нужен толчок, чтобы решить эту проблему! Спасибо …

Шаблон статьи библиографического веб-сайта в стиле Чикаго.Служба писателей академических эссе esl для mba. Контрольный лист книги успеваемости по написанию тезисов. Форматы предложений по проектам маркетинговых исследований. Педиатрические системы раннего предупреждения для обнаружения и. Математические мелочи книги в формате pdf отвечают на вопросы.

Независимо от того, как указаны линии, вы должны иметь возможность сгенерировать две разные точки вдоль линии, а затем сгенерировать A, B и C. Теперь предположим, что у вас есть линии, заданные уравнениями: A 1 x + B 1 y = C 1 A 2 x + B 2 y = C 2. Чтобы найти точку, в которой две прямые пересекаются, нам просто нужно решить два уравнения для двух…

Расстояние от точки до линии

У нас есть общая линия ax + by + c = 0ax + by + c = 0ax + by + c = 0 с именем LLL. Эта прямая имеет наклон −ab- \ frac {a} {b} −ba. У нас также есть общая точка P = (x0, y0) P = (x_0, y_0) P = (x0, y0). Расстояние между линией LLL и точкой PPP можно представить другой линией, перпендикулярной L; L; L; назовем это ТТТ. TTT будет иметь уклон ba \ frac {b} {a} ab, поскольку он перпендикулярен LLL. Теперь, чтобы найти расстояние между точкой PPP и линией L, L, L, мы можем использовать небольшой геометрический трюк и получить другую линию, параллельную LLL, которая проходит через PPP; назовем это SSS. Точно так же у нас может быть другая линия, на этот раз параллельная TTT, которая проходит через начало координат (0,0) (0,0) (0,0); назовем это RRR.

Теперь, когда время рисования закончилось, пора работать.

Во-первых, поскольку SSS проходит через PPP и имеет тот же наклон, что и LLL, его уравнение составляет

y − y0 = −ab (x − x0) ⟹ y = −ax + ax0 + by0b.y — y_0 = — \ dfrac {a} {b} (x — x_0) \ подразумевает y = \ dfrac {-ax + ax_0 + by_0} {b} .y − y0 = −ba (x − x0) ⟹y = b − ax + ax0 + by0.

Линия RRR имеет уравнение

y = bax.2}}. \ end {align} d = (- a2 + b2ac −a2 + b2a (ax0 + by0)) 2 + (- a2 + b2bc −a2 + b2b (ax0 + by0)) 2 = (a2 + b2) 2 [−a (ax0 + by0 + c)] 2 + [- b (ax0 + by0 + c) v] 2 = (a2 + b2) 2 (a2 + b2 ) (ax0 + by0 + c) 2 = a2 + b2 (ax0 + by0 + c) 2 = a2 + b2 ∣ax0 + by0 + c∣.

Знак абсолютного значения необходим, так как расстояние должно быть положительным значением. □ _ \ квадрат □

Здесь мы представляем геометрическое доказательство.

Сначала мы рисуем линию, параллельную LLL, которая проходит через PPP, которая имеет уравнение ax + by- (ax0 + by0) = 0ax + by- (ax_0 + by_0) = 0ax + by- (ax0 + by0) = 0.2}}. \ _ \ Square \ end {align} 21 ∣ax0 + by0 + c∣aba2 + b2 × d⇒d = 21 ∣ax0 + by0 + c∣2ab1 = a2 + b2 ∣ax0 + by0 + c∣. □

Ближайшая точка к исходной точке | Сессия 29: Проблемы оптимизации | Часть B: Оптимизация, соответствующие ставки и метод Ньютона | 2. Приложения дифференцирования | Исчисление одной переменной | Математика

КРИСТИН БРЕЙНЕР: С возвращением к чтению.

Сегодня мы займемся проблемой оптимизации. Итак, я хочу, чтобы мы ответили на вопрос: какая точка кривой y, равная квадратному корню из x плюс 4, ближе всего к началу координат? Я нарисовал набросок этой кривой.Масштаб в этом направлении — каждая решетка — это одна единица в направлении x, каждая решетка здесь — одна единица в направлении y. Просто хочу указать на два простых места, где можно определить расстояние до начала координат. Здесь, где кривая начинается с отрицательного значения 4,0, расстояние до начала координат составляет 4 единицы. А здесь в (0, 2) расстояние до начала координат составляет две единицы. Это, наверное, можно смело сказать, подальше отсюда.

Итак, мы ожидаем, что где-то на кривой в этом регионе мы должны найти наше место, которое ближе всего к исходной точке.Единственная причина, по которой я указываю на это, заключается в том, что, когда вы решаете эти проблемы самостоятельно, вы всегда должны стараться и примерно предвидеть, где что-то должно произойти, в каком регионе, чтобы вы не … Начните думать: если вы сделаете что-то не так и получите x равное 100, а затем вернетесь и посмотрите на кривую, вы сразу поймете, что это не имеет никакого смысла. Итак, мы хотим всегда думать, решая проблемы, имеет ли мой ответ смысл?

Так что я дам вам немного времени, чтобы вы поработали над этим самостоятельно, а потом я вернусь и тоже поработаю над этим.

С возвращением. Надеюсь, вам удалось довольно далеко разобраться в этой проблеме. Итак, я сейчас начну над этим работать.

Итак, снова вопрос в том, что мы хотим оптимизировать — в данном случае минимизировать — расстояние до начала координат от этой кривой. Итак, что мы действительно пытаемся сделать, так это то, что у нас есть ограничение, ограничение в том, что мы должны быть на кривой, а затем у нас также есть что-то, что мы пытаемся минимизировать. И то, что мы пытаемся минимизировать, — это расстояние. И поэтому мы должны убедиться, что понимаем два уравнения, которые нам нужны: уравнение оптимизации или уравнение ограничений и уравнение оптимизации.

Итак, чтобы оптимизировать, нам нужно знать, как измерять расстояние в двухмерном пространстве. И я хочу отметить один момент: если вы хотите оптимизировать расстояние, вы можете также оптимизировать квадрат расстояния, потому что это намного проще. Позвольте мне вкратце обосновать это, а затем мы продолжим.

Итак, я хочу оптимизировать квадрат расстояния до начала координат. Это, ну, как вы помните, расстояние между двумя точками (x, y) и (a, b) — это что-то в этой форме. Квадрат расстояния — это разница между квадратом значения x и разницей между квадратом значения y.Это в конечном итоге должно напомнить вам о теореме Пифагора.

Итак, в нашем случае расстояние до начала координат равно x в квадрате плюс y в квадрате. Квадрат расстояния равен x в квадрате плюс y в квадрате. Я только что сказал вам, что вместо того, чтобы пытаться оптимизировать расстояние, мы можем оптимизировать квадрат расстояния. Это почему? Что ж, помните, что при оптимизации вы ищете место, где производная интересующей функции равна 0. Итак, я хочу отметить, что когда вы возьмете производную от расстояния в квадрате и найдете, где это 0, это будет то же самое, что и место, где производная расстояния равна 0.

Итак, давайте это заметим. Так что это небольшое обоснование для боковой панели. Обратите внимание: d простое число в квадрате равно 2d d простому числу. Откуда это пришло? Это неявное дифференцирование по x и цепное правило. Итак, если я хочу, чтобы d простое было равно 0, я также могу найти, где d в квадрате простого числа равно 0. Я предполагаю — обратите внимание, что расстояние никогда не находится в начале координат — поэтому расстояние никогда не равно нулю. беспокоиться об этом. Это небольшая боковая панель, но просто чтобы объяснить, почему мы можем это сделать.

А теперь вернемся к проблеме.

Какова наша задача оптимизации, уравнение, которое мы хотим минимизировать? Мы хотим минимизировать это уравнение относительно определенного ограничения. Что за ограничение? Ограничение — это то, что есть y. y зависит от x. И поэтому, когда я решу эти проблемы, мне придется заменить свое ограничение. Итак, y в квадрате — это квадратный корень из x плюс 4 величины в квадрате, поэтому я просто получаю x плюс 4.

Итак, теперь у меня есть уравнение оптимизации.Как найти минимум или максимум? Я беру производную и устанавливаю ее равной 0. Так что позвольте мне дать себе немного больше места и сделать это здесь. Итак, d возведенное в квадрат простое число, теперь я получаю, что производная от x в квадрате равна 2x. Производная x равна 1, а производная 4 равна 0. Это будет оптимизировано, если оно равно 0. Итак, 0 равно 2x плюс 1. Таким образом, x равен минус 1/2.

Проходит ли это, как мы бы сказали, тест на запах? Для нас это нормально пахнет? Ответ будет положительным. Потому что помните, мы сказали, что где-то в этой области x мы ожидаем, что у нас будет ближайшее расстояние, точка, ближайшая к началу координат.Итак, мы подошли к значению x. Теперь нам нужно найти значение y, чтобы решить проблему. Но это пока не очень удивительно. Кажется, может быть, это правильно.

Теперь у нас есть x. Итак, как нам найти y? Что ж, мы знаем, что это такое. y равен квадратному корню из x плюс 4, поэтому он равен квадратному корню из отрицательной 1/2 плюс 4, что упрощенно составляет 3 и 1/2, что, как мне кажется, составляет 7/2. Таким образом, точка — это отрицательный квадратный корень 1/2 запятой из 7/2.

И затем вы просто хотите дважды проверить и убедиться, я спрашивал расстояние или я спрашивал точку? А сейчас у нас есть точка, поэтому давайте подойдем и убедимся, какая точка на кривой ближе всего к началу координат.Итак, теперь мы знаем, что ответили на правильный вопрос.

Итак, опять же, это была проблема максимизации … извините, это была проблема минимизации. Это была проблема оптимизации, когда мы хотели минимизировать расстояние. У нас было уравнение связи. У нас было то, что мы хотели минимизировать. Затем мы взяли производную минимизатора, установили ее — оптимизирующего уравнения, установили ее равной 0, решили для x, а затем нашли ответ на конкретный вопрос, найдя значение y.

И я думаю, что остановлюсь на этом.

Прямоугольная система координат

Точка, которая делит пополам отрезок прямой, образованный двумя точками (x1, y1) и (x2, y2), называется средней точкой. Имеются две точки (x1, y1) и (x2, y2), середина — это упорядоченная пара, заданная формулой (x1 + x22, y1 + y22). и задается следующей формулой:

Средняя точка — это упорядоченная пара, образованная путем нахождения среднего значения x и среднего значения y данных точек.

Пример 8: Вычислите среднюю точку между (-1, -2) и (7, 4).

Решение: Сначала вычислите среднее значение x — и y — значений данных точек.

Затем сформируйте среднюю точку в виде упорядоченной пары, используя усредненные координаты.

Чтобы убедиться, что это действительно средняя точка, вычислите расстояние между двумя заданными точками и убедитесь, что результат равен сумме двух равных расстояний от конечных точек до этой средней точки. Эта проверка предоставляется читателю в качестве упражнения.

Попробуй! Найдите середину между (−6, 5) и (6, −11).

Тематические упражнения

Часть A: Заказанные пары

Укажите координаты точек A , B , C , D и E .

1.

2.

3.

4.

5.

6.

Изобразите данный набор упорядоченных пар.

7. {(−4, 5), (−1, 1), (−3, −2), (5, −1)}

8.{(−15, −10), (−5, 10), (15, 10), (5, −10)}

9. {(−2, 5), (10, 0), (2, −5), (6, −10)}

10. {(−8, 3), (−4, 6), (0, −6), (6, 9)}

11. {(−10, 5), (20, −10), (30, 15), (50, 0)}

12. {(−53, −12), (- 13, 12), (23, −1), (53, 1)}

13. {(-35, -43), (25, 43), (1, -23), (0, 1)}

14. {(−3,5, 0), (−1,5, 2), (0, 1,5), (2,5, −1,5)}

15. {(-0,8, 0.2), (−0,2, −0,4), (0, −1), (0,6, −0,4)}

16. {(-1,2, -1,2), (-0,3, -0,3), (0, 0), (0,6, 0,6), (1,2, 1,2)}

Укажите квадрант, в котором находится данная точка.

17. (−3, 2)

18. (5, 7)

19. (−12, −15)

20. (7, −8)

21 (-3,8, 4,6)

22. (17,3, 1,9)

23. (−18, −58)

24.(34, −14)

25. x> 0 и y <0

26. x <0 и y <0

27. x <0 и y> 0

28. x> 0 и y> 0

Средняя цена галлона обычного неэтилированного бензина в городах США представлена ​​на следующем линейном графике. Используйте график, чтобы ответить на следующие вопросы.

Источник: Бюро статистики труда.

29. Какова была средняя цена галлона неэтилированного бензина в 2004 году?

30. Какова была средняя цена галлона неэтилированного бензина в 1976 году?

31. В какие годы средняя цена галлона неэтилированного бензина составляла 1,20 доллара США?

32. Насколько выросла цена галлона бензина с 1980 по 2008 год?

33. Каков процент увеличения цены галлона неэтилированного бензина с 1976 по 1980 год?

34.На сколько процентов увеличилась цена галлона неэтилированного бензина с 2000 по 2008 год?

Средняя цена на универсальную белую муку в городах США с 1980 по 2008 год представлена ​​на следующем линейном графике. Используйте график, чтобы ответить на следующие вопросы.

Источник: Бюро статистики труда.

35. Какова была средняя цена за фунт универсальной белой муки в 2000 году?

36.Какова была средняя цена за фунт универсальной белой муки в 2008 году?

37. В каком году мука стоила в среднем 0,25 доллара за фунт?

38. В какие годы цена на муку составляла в среднем 0,20 доллара за фунт?

39. Каков процент увеличения объема муки с 2000 по 2008 год?

40. Каков процент увеличения муки с 1992 по 2000 год?

Используя следующие данные, создайте линейный график.

41. Процент от общего числа выпускников средней школы, поступивших в колледж.

Год	Процент
1969	36%
1979	40%
1989	47%
1999	42%

Источник: Сборник статистики образования.

42. Средняя дневная температура в мае в градусах Фаренгейта.

Экзамен	Температура
8:00	60
12:00	72
16:00	75
20:00	67
12:00	60
4:00	55

Вычислите площадь формы, образованной соединением следующего набора вершин.

43. {(0, 0), (0, 3), (5, 0), (5, 3)}

44. {(−1, −1), (−1, 1), (1, −1), (1, 1)}

45. {(−2, −1), (−2, 3), (5, 3), (5, −1)}

46. {(−5, −4), (−5, 5), (3, 5), (3, −4)}

47. {(0, 0), (4, 0), (2, 2)}

48. {(−2, −2), (2, −2), (0, 2)}

49. {(0, 0), (0, 6), (3, 4)}

50. {(−2, 0), (5, 0), (3, −3)}

Часть B: Формула расстояния

Рассчитайте расстояние между заданными двумя точками.

51. (−5, 3) и (−1, 6)

52. (6, −2) и (−2, 4)

53. (0, 0) и (5, 12)

54. (−6, −8) и (0, 0)

55. (−7, 8) и (5, −1)

56. (-1, -2) и (9, 22)

57. (−1, 2) и (−7/2, −4)

58. (−12, 13) и (52, −113)

59. (−13, 23) и (1, −13)

60. (12, −34) и (32, 14)

61.(1, 2) и (4, 3)

62. (2, −4) и (−3, −2)

63. (-1, 5) и (1, -3)

64. (1, −7) и (5, −1)

65. (−7, −3) и (−1, 6)

66. (0, 1) и (1, 0)

67. (-0,2, -0,2) и (1,8, 1,8)

68. (1,2, −3,3) и (2,2, −1,7)

Для каждой задачи покажите, что три точки образуют прямоугольный треугольник.

69.(−3, −2), (0, −2) и (0, 4)

70. (7, 12), (7, −13) и (−5, −4)

71. (-1,4, 0,2), (1, 2) и (1, -3)

72. (2, -1), (-1, 2) и (6, 3)

73. (−5, 2), (−1, −2) и (−2, 5)

74. (1, −2), (2, 3) и (−3, 4)

Равнобедренные треугольники имеют две стороны равной длины. Для каждой задачи покажите, что следующие точки образуют равнобедренный треугольник.

75.(1, 6), (-1, 1) и (3, 1)

76. (−6, −2), (−3, −5) и (−9, −5)

77. (−3, 0), (0, 3) и (3, 0)

78. (0, -1), (0, 1) и (1, 0)

Вычислите площадь и периметр треугольников, образованных следующим набором вершин.

79. {(−4, −5), (−4, 3), (2, 3)}

80. {(−1, 1), (3, 1), (3, −2)}

81. {(−3, 1), (−3, 5), (1, 5)}

82.{(−3, −1), (−3, 7), (1, −1)}

Часть C: Формула средней точки

Найдите середину между заданными двумя точками.

83. (−1, 6) и (−7, −2)

84. (8, 0) и (4, −3)

85. (-10, 0) и (10, 0)

86. (−3, −6) и (−3, 6)

87. (−10, 5) и (14, −5)

88. (0, 1) и (2, 2)

89. (5, −3) и (4, −5)

90.(0, 0) и (1, 1)

91. (-1, -1) и (4, 4)

92. (3, −5) и (3, 5)

93. (−12, −13) и (32, 73)

94. (34, −23) и (18, −12)

95. (53, 14) и (−16, −32)

96. (−15, −52) и (710, −14)

97. Дан прямоугольный треугольник, образованный вершинами (0, 0), (6, 0) и (6, 8), покажите, что середины сторон образуют прямоугольный треугольник.

98. Для равнобедренного треугольника, образованного вершинами (−10, −12), (0, 12) и (10, −12), покажите, что середины сторон также образуют равнобедренный треугольник.

99. Вычислите площадь треугольника, образованного вершинами (−4, −3), (−1, 1) и (2, −3). (Подсказка: вершины образуют равнобедренный треугольник.)

100. Вычислите площадь треугольника, образованного вершинами (−2, 1), (4, 1) и (1, −5).

Часть D. Темы дискуссионной доски

101. Изучите и обсудите жизнь и вклад в математику Рене Декарта.

102. Изучите и обсудите историю прямоугольного треугольника и теоремы Пифагора.

103. Что такое тройка Пифагора? Приведите несколько примеров.

104. Объясните, почему нельзя использовать линейку для вычисления расстояния на графике.

105. Как разделить отрезок пополам с помощью циркуля и линейки?

Соединить исходные точки с пунктами назначения — Справка ArcGIS Online

Инструмент Соединить исходные точки с пунктами назначения измеряет время в пути или расстояние между парами точек с использованием либо прямых линий, либо сетевых режимов перемещения.

Примечания по использованию

Требуются два слоя входных точек: один с исходными точками, а другой с конечными точками. Соединения, создаваемые между исходными и конечными точками, зависят от количества исходных и конечных точек и представлены в следующей таблице:

94529

Количество исходных	Количество назначений	Подключения
Один	Один	Исходная точка соединяется с местом назначения.
Один	Более одного	Исходная точка соединяется со всеми пунктами назначения.
Более одного	Один	Все исходные пункты связаны с пунктом назначения.
Более одного	Более одного	Соединения «многие ко многим» создаются с использованием совпадающих полей идентификатора.Каждый источник подключается к каждому пункту назначения, имеющему соответствующее значение поля идентификатора.

Пункты отправления и назначения могут быть соединены с использованием расстояния по прямой линии или одного из нескольких режимов перемещения по сети. В некоторых режимах движения есть возможность использовать условия движения. Когда используются условия движения, они могут быть основаны на реальных условиях или типичных условиях для определенного дня недели и времени. Условия реального трафика могут быть компенсированы до 12 часов от текущего времени.Время для типичных условий может быть установлено с 15-минутными интервалами для всего дня и ночи.

Режимы передвижения может настраивать администратор вашей организации. Администратор также может добавить новые режимы передвижения или удалить режимы передвижения, которые не нужны вашей организации. Измерение расстояния по умолчанию будет в милях или километрах, в зависимости от настроек единиц в вашем профиле.

В следующей таблице описаны сетевые режимы перемещения по умолчанию, доступные для инструмента Соединить исходные точки с пунктами назначения:

Время в пути

Режим движения	Описание	Технические характеристики
	Следует по тропинкам и дорогам, допускающим пешеходное движение, и находит решения, оптимизирующие время в пути. Скорость ходьбы установлена ​​на 5 километров в час.	Скорость ходьбы установлена ​​на уровне 5 километров (3,1 мили) в час. Скорость ходьбы может быть настроена администратором вашей организации.
Расстояние проезда в сельской местности	Моделирует движение автомобилей и других подобных небольших автомобилей, таких как пикапы, и находит решения, которые оптимизируют расстояние проезда. Путешествуйте по дорогам с односторонним движением, избегайте незаконных поворотов и соблюдайте другие правила, характерные для автомобилей, но не препятствующие передвижению по грунтовым дорогам.	Нет
Время вождения	Моделирует движение легковых и других подобных небольших автомобилей, таких как пикапы, и находит решения, которые оптимизируют время в пути. Путешествуйте по дорогам с односторонним движением, избегайте незаконных поворотов и соблюдайте другие правила, характерные для автомобилей. Когда вы указываете время начала, используются динамические скорости движения в зависимости от загруженности дорог там, где это возможно.	Использовать трафик по умолчанию отключен.Скорость движения будет основываться на исторических данных и данных о трафике в реальном времени. Трафик может быть основан на реальных условиях или типичных условиях для указанного дня недели и времени. Проверьте, доступны ли данные о трафике в вашем региона, щелкнув ссылку Просмотреть доступность на панели инструментов.
Driving Distance	Моделирует движение легковых и других подобных небольших автомобилей, таких как пикапы, и находит решения, которые оптимизируют расстояние проезда. Путешествуйте по дорогам с односторонним движением, избегайте незаконных поворотов и соблюдайте другие правила, характерные для автомобилей.	Нет
Пешком	Прослеживает пути и дороги, допускающие пешеходное движение, и находит решения, которые оптимизируют расстояние проезда.	Нет
Время вождения в сельской местности	Моделирует движение легковых и других подобных небольших автомобилей, таких как пикапы, и находит решения, оптимизирующие время в пути.Путешествуйте по дорогам с односторонним движением, избегайте незаконных поворотов и соблюдайте другие правила, характерные для автомобилей, но не препятствующие передвижению по грунтовым дорогам. Когда вы указываете время начала, используются динамические скорости движения в зависимости от загруженности дорог там, где это возможно.	Использовать трафик по умолчанию отключен. Скорость движения в сельской местности будет основываться на исторических данных и данных о загруженности дорог. Трафик может быть основан на реальных условиях или типичных условиях для указанного дня недели и времени. Проверьте, доступны ли данные о трафике в вашем региона, щелкнув ссылку Просмотреть доступность на панели инструментов.
Время в пути	Моделирует базовое движение грузовика, выбирая обозначенные маршруты грузовика, и находит решения, которые оптимизируют время в пути. Маршруты должны соответствовать дорогам с односторонним движением, избегать запрещенных поворотов и т. Д. Когда вы указываете время начала, динамические скорости движения на основе трафика используются там, где это возможно, вплоть до допустимого ограничения скорости грузовика. Соблюдает правила, применимые к большегрузным автомобилям.	Скорость грузоперевозок будет основываться либо на исторических средних скоростях для автомобилей, либо на опубликованных ограничениях скорости для грузовиков, в зависимости от того, что меньше. Использовать трафик по умолчанию отключен. Скорость грузоперевозок будет основываться на исторических данных и текущих данных трафика, но не будет превышать заявленную скорость грузоперевозок. Трафик может быть основан на реальных условиях или типичных условиях для указанного дня недели и времени.
Расстояние грузового транспорта	Моделирует базовое движение грузовика, выбирая обозначенные маршруты грузовика, и находит решения, которые оптимизируют расстояние проезда. Маршруты должны соответствовать дорогам с односторонним движением, избегать запрещенных поворотов и т. Д. Соблюдает правила, применимые к большегрузным автомобилям.	Нет

Защитные слои Select параметр может использоваться для указания одного или нескольких функции, которые действуют как временные ограничения при поездках на основные улицы.

Параметр Форма маршрута определяет, как будут отображаться выходные маршруты при соединении исходных точек с местами назначения. Прямая линия (по умолчанию) генерирует прямые линии (также называемые линиями желаний) между исходной точкой и пунктом назначения, тогда как Следовать по улицам возвращает маршруты в форме уличной сети. Один и тот же расчет для сопоставления пунктов отправления и назначения используется независимо от выбранной формы маршрута. Расчет всегда основан на выбранном вами режиме передвижения. Если вместо режима движения используется расстояние по прямой, в качестве параметра Форма маршрута доступна только Прямая линия.

Выходной слой содержит линии маршрута, включая измерения между каждой исходной точкой и пунктом назначения.

Если вы выбираете Включить слои маршрута, каждый маршрут из результата также сохраняется как слой маршрута. Слой маршрута включает всю информацию для конкретного маршрута, такую ​​как остановки, назначенные маршруту, а также направления движения.

Если установлен флажок Использовать текущий экстент карты, при анализе будут учитываться только те объекты, которые видны в текущем экстенте карты.Если этот флажок не установлен, будут учитываться все объекты входного слоя, даже если они находятся за пределами текущего экстента карты.

Совет:

Щелкните Показать кредиты перед запуском анализа, чтобы проверить, сколько кредитов будет использовано.

Как работает Connect Origins to Destinations

Инструмент Соединить истоки с пунктами назначения использует геодезический метод при поиске пространственных объектов с расстоянием по прямой, а не евклидов метод. Геодезические линии определяют фактическую форму Земли (эллипсоид или, точнее, геоид).Расстояния рассчитываются между двумя точками на криволинейной поверхности (геоид), а не между двумя точками на плоской поверхности (декартова плоскость).

Опция Live traffic использует текущее время в качестве отправления. Скорость движения прогнозируется для поездки с использованием текущих скоростей, исторических скоростей и текущих событий, таких как погода.

Когда используются типичные условия для дня недели и времени, скорости движения основываются на исторических скоростях, усредненных по 5-минутным интервалам за всю неделю.Выбранное время соответствует местному времени в часовом поясе, в котором находятся ваши данные. При использовании любого из условий трафика инструмент «Подключить источник к пункту назначения» учитывает изменяющиеся условия движения в зависимости от времени, прошедшего с момента отправления.

Создание слоев маршрута полезно, если вы хотите поделиться отдельными маршрутами с другими членами вашей организации или для дальнейшего изменения маршрутов с помощью кнопки «Маршруты» в Map Viewer Classic. Слои маршрута используют имя, предоставленное для векторного слоя, в качестве префикса, а имя маршрута, созданное как часть анализа, добавляется для создания уникального имени для каждого слоя маршрута.

Источники и места назначения ввода

Инструмент «Подключить источники к получателям» ведет себя немного по-разному в зависимости от количества исходных и конечных точек ввода, используемых в анализе.

Использование одного источника или одного пункта назначения

Если введенные вами данные содержат только один пункт отправления или один пункт назначения, никаких специальных полей идентификатора не требуется. Использование одного источника и одного или нескольких пунктов назначения приводит к соединению между этим источником и всеми пунктами назначения. Использование одного пункта назначения и одного или нескольких пунктов отправления приводит к соединению каждого пункта назначения с одним пунктом назначения.

Использование нескольких источников и пунктов назначения

Если введенные вами данные содержат более одного источника и более одного пункта назначения, каждая таблица пунктов отправления и назначения должна содержать поле идентификатора, которое можно использовать для сопоставления каждого источника с пунктом назначения. Результаты включают соединение между каждым источником и каждым пунктом назначения с совпадающими идентификаторами.

Например, предположим, что учащиеся школьного округа имеют право ездить на школьном автобусе только в том случае, если они живут на расстоянии более одной мили пешком от школы, которую они посещают. Чтобы определить, какие учащиеся имеют право пользоваться автобусом, школьный округ должен рассчитать расстояние пешком между домом каждого учащегося и назначенной школой.

Школьный округ имеет слой домов учащихся, которые используются в качестве исходных данных в анализе. В слое есть поле School, в котором указано название школы, которую посещает ученик.

Школьный округ также имеет слой с местоположениями школ, которые используются в качестве пунктов назначения в анализе.Слой местоположения школы включает в себя поле «Имя», в котором указывается название школы.

Поскольку значения поля School в источниках соответствуют значениям поля Name в пунктах назначения, вы можете использовать эти два поля в качестве специальных полей идентификатора, которые указывают, какой источник должен подключаться к какому пункту назначения. Задайте для поля ID в параметре origin значение School, а для поля Matching ID в параметре destinations — значение Name.

Результирующий анализ содержит линию, соединяющую каждого ученика с назначенной им школой, и аналитик может посмотреть на значения полей в выходных данных, чтобы определить, какие ученики живут дальше, чем пороговое значение в одну милю, чтобы иметь право пользоваться автобусом.

Похожие инструменты

Используйте функцию «Подключить исходные точки к пунктам назначения» для измерения времени или расстояния между парами точек. Другие инструменты могут быть полезны при решении похожих, но немного разных проблем.

Map Viewer Классические инструменты анализа

Чтобы найти объекты, наиболее близкие к входному слою, используйте инструмент «Найти ближайший».

Чтобы спланировать маршрут движения с несколькими остановками, используйте инструмент «Планирование маршрутов».

Инструменты анализа ArcGIS Pro

Инструмент Подключить исходные точки к пунктам назначения выполняет ту же функцию, что и решатель маршрутов в дополнительном модуле ArcGIS Network Analyst.