Расстояние между двумя точками на плоскости

Posted on 30.12.202031.12.2019 by alexxlab

Содержание

Каждая точка А плоскости характеризуется своими координатами (х, у). Они совпадают с координатами вектора 0А, выходящего из точки 0 — начала координат .

Пусть А и В — произвольные точки плоскости с координатами (х₁ y₁) и (х₂, у₂) соответственно.

Тогда вектор AB имеет, очевидно, координаты (х₂ — х₁, y₂ — y₁). Известно, что квадрат длины вектора равен сумме квадратов его координат. Поэтому расстояние d между точками А и В, или, что то же самое, длина вектора АВ, определяется из условия

d² = (х₂ — х₁)² + (y₂ — y₁)².

Отсюда

$$ d = \sqrt{(x_2 — x_1)^2 + (y_2 — y_1)^2} $$

Полученная формула позволяет находить расстояние между любыми двумя точками плоскости, если только известны координаты этих точек

Каждый раз, говоря о координатах той или иной точки плоскости, мы имеем в виду вполне определенную систему координат х0у. А вообще-то систему координат на плоскости можно выбирать по-разному. Так, вместо системы координат х0у можно рассмотреть систему координат хִу , которая получается в результате поворота старых осей координат вокруг начальной точки 0 против часовой стрелки на угол α.

Если некоторая точка плоскости в системе координат х0у имела координаты (х, у), то в новой системе координат хִу она будет иметь уже другие координаты (х, у).

В качестве примера рассмотрим точку М, расположенную на оси 0х и отстоящую от точки 0 на расстоянии, равном 1.

Очевидно, что в системе координат x0у эта точка имеет координаты (cos α, sin α), а в системе координат хִу координаты (1,0).

Координаты любых двух точек плоскости А и В зависят от того, как в этой плоскости задана система координат. А вот расстояние между этими точками не зависит от способа задания системы координат.

razdupli.ru

2.2.2. Расстояние между двумя точками на плоскости

Даны две точки на плоскости с координатами A (x₁, y₁) и B (x₂, y₂).

y₂B

y₁A C

0 x₁ x₂ X

Из треугольника ABC:

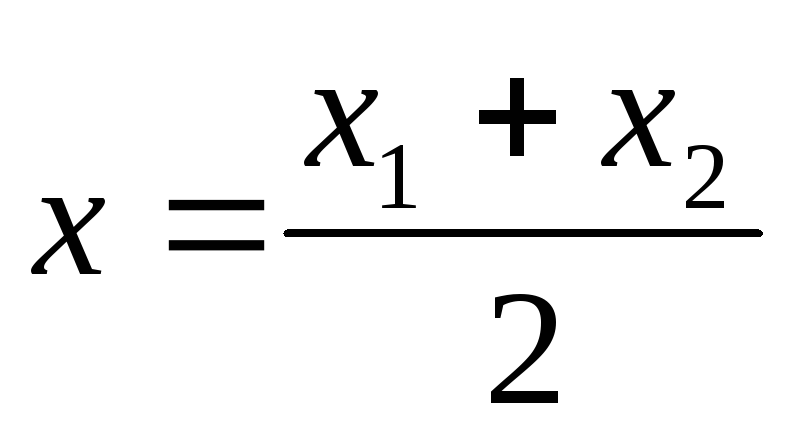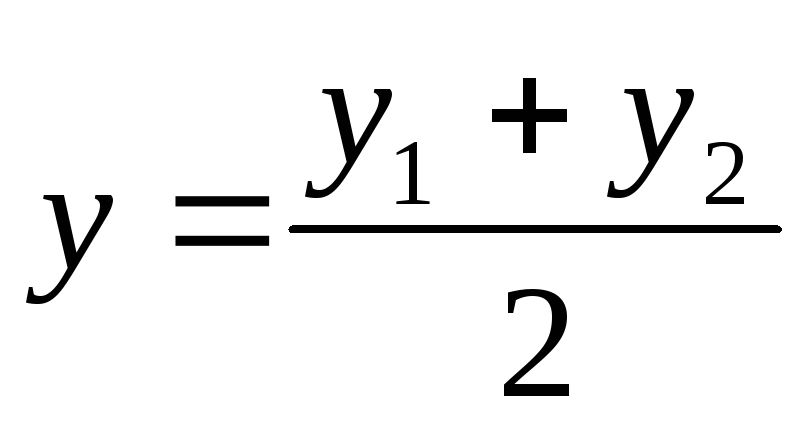, — формулы для нахождения координат середины отрезка.

2.2.3. Общее уравнение прямой

Теорема 1.Всякое невырожденное уравнение первой степени с двумя переменными определяет на плоскости некоторую прямую, и наоборот.

Аx+Вy+С=0 — общее уравнение прямой,

— условие невырожденности.

Рассмотрим различные случаи расположения прямой на плоскости в зависимости от коэффициентов общего уравнения.

1) С = 0, Ax + By = 0 — прямая проходит через начало координат;

А= 0,By+C= 0 — прямая проходит параллельно осиОХ;

В= 0,Ax+C= 0 — прямая проходит параллельно осиОУ;

2) A = C= 0,By= 0 — прямая совпадает с осьюОХ;

B = C =0,Ax= 0 — прямая совпадает с осьюОУ.

Расстояние от точки M₀ (x₀,y₀) до прямой, заданной общим уравнениемAx +

By + C= 0, находится по формуле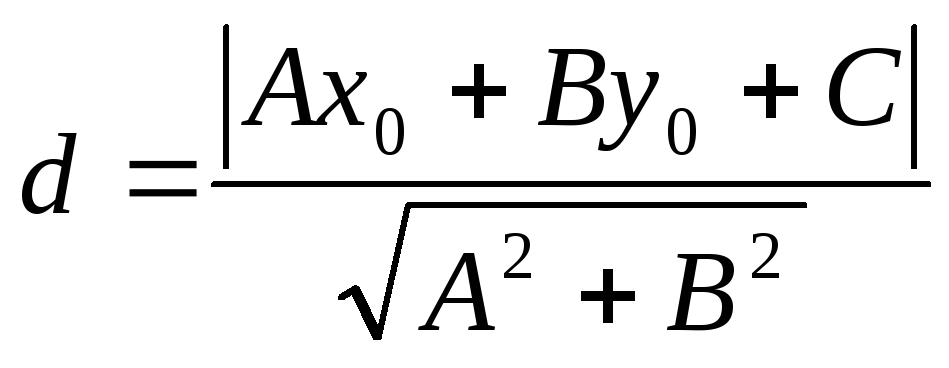

2.2.4. Уравнение прямой с угловым коэффициентом

Предположим, что прямая расположена под углом jк осиОХи отсекает от осиОУотрезок вbединиц. Составим уравнение этой прямой.

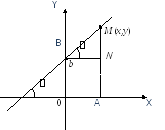
Возьмем произвольную точку M (x, y), лежащую на этой прямой, инайдем уравнение, связывающее переменные x и y. Из рисунка видно:AM = AN + NM, где AM = y, AN = b. Из треугольника BMN: MN = BN · tg j.Обозначим tg j = k и назовем его угловым коэффициентом прямой.MN

= k · x. Подставляя в равенствоAM = AN + NM выражения отрезковAM = y,AN = b,MN = k · x; получимy = k · x + b — уравнение прямой с угловым коэффициентом.

2.2.5. Уравнение прямой, проходящей

через данную точку в данном направлении

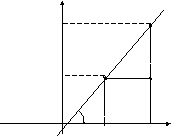
Предположим, что прямая проходит через точку M₁(x₁,y₁) и образует с осьюOX

угол j. Составим уравнение этой прямой.

y M(x,y)

у₁ M₁(x₁,y₁)N

0 х1 х Х

Будем искать уравнение прямой в виде уравнения с угловым коэффициентом:y = k · x + b. Угловой коэффициент прямой можно найти, зная угол наклонаk =tgj. Возьмем произвольную точкуM (x, y), лежащую на этой прямой, и найдем уравнение, связывающее переменныеxиy. Так как точкиМиM₁лежат на прямой, то их координаты удовлетворяют уравнению прямой:y = k · x + b,y₁ = k · x₁ +

b.Вычитая эти равенства, получим:

y — y₁ = k · (x — x₁) — уравнение прямой, проходящей через данную точку в данном направлении.

2.2.6. Уравнение прямой, проходящей через две данные точки

Даны две точки M₁ (x₁, y₁) иM₂ (x₂, y₂). Составим уравнение прямой, проходящей через две эти точки,

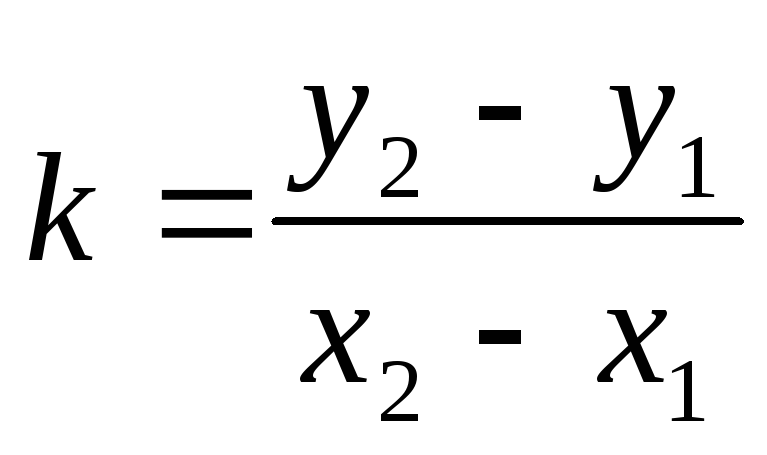
— угловой коэффициент прямой, проходящей через две данные точки.

Воспользуемся уравнением прямой, проходящей через данную точку M₁ и в данномнаправлении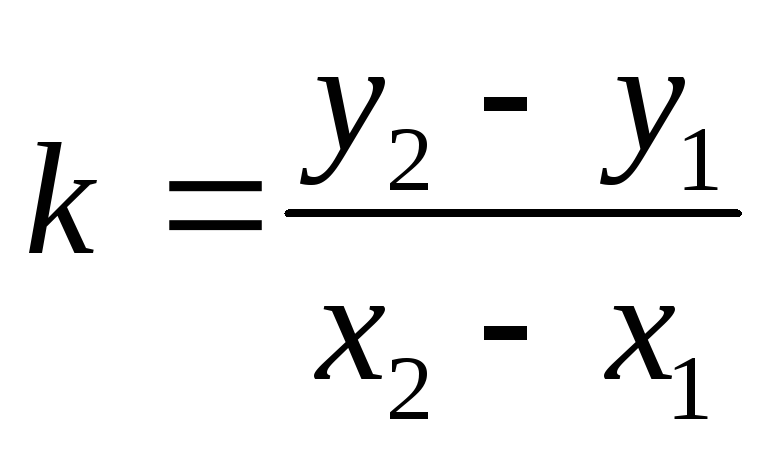

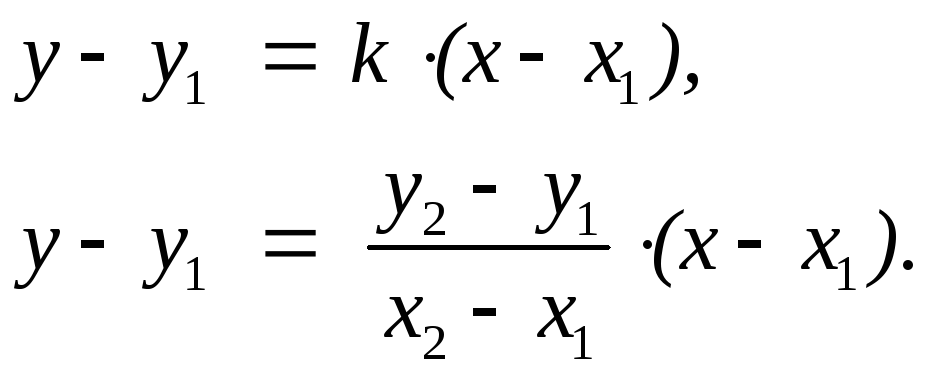
получим

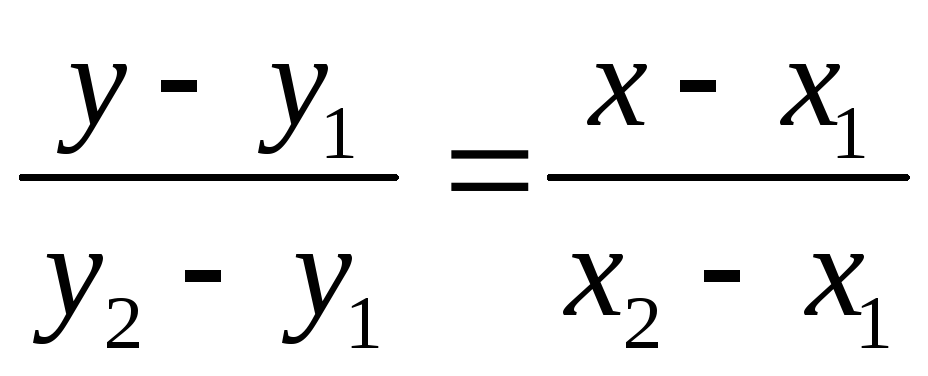— уравнение прямой, проходящей через две данные точки.

2.2.7. Угол между двумя прямыми. Условие параллельности. Условие перпендикулярности прямых

Определение 1.Углом между двумя прямымиIиIIназываетсяугол, отсчитываемый в положительном направлении от прямой I к прямой II.

Пусть даны две прямые, заданные уравнениями с угловыми коэффициентами

y = k₁ · x + b₁, y = k₂ ·

x + b₂.

Найдем угол между первой и второй прямыми. Обозначим углы наклона прямых φ1 и φ2. Тогда

k₁ = tgφ1, k₂ = tgφ2.

Проведем через точку пересечения прямую, параллельную оси OX.

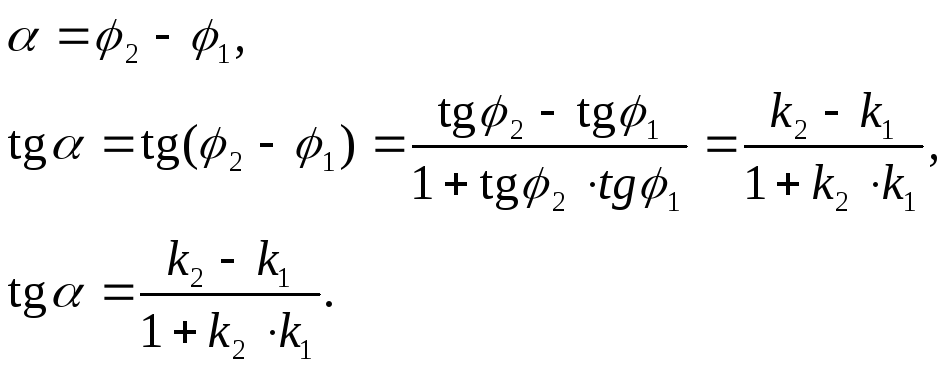
— формула для вычисления угла между двумя прямыми.

1. Предположим, что прямые параллельны:

ÞtgÞ

k₁ = k₂ — условие параллельности прямых.

2. Предположим, что прямые перпендикулярны:

⁰Þtgне существуетÞctg

= 0Þ

Þ k₁· k₂= -1 — условие перпендикулярности прямых

Вопросы для самопроверки.

1. Как выглядит общее уравнение прямой7 Опишите частные случаи этого уравнения.

2. Условие параллельности прямых.

3. Условие перпендикулярности прямых.

4. Напишите уравнение прямой с угловым коэффициентом.

5. Напишите уравнение прямой, проходящей через данные точки.

Резюме.

studfile.net

Формула расстояния между точками | Треугольники

Формула для нахождения расстояния между двумя точками A(x1;x2) B(x2;y2) на плоскости:

Доказательство:

Сначала рассмотрим частные случаи.

1) Если y1=y2,

то

К этой же формуле придём, если подставим координаты точек A и B в общую формулу:

2) Аналогично, если x1=x2:

Эту же формулу получим, подставив координаты A и B в общую формулу:

3) Если x1=x2 и y1=y2, AB=0. Формула для этого случая также верна.

4) Если x1≠x2, y1≠y2.

Проведём через точки A и B прямые, перпендикулярные координатным осям. Обозначим точку пересечения этих прямых через C.

Из прямоугольного треугольника ABC по теореме Пифагора

Поскольку

или

Отсюда

Что и требовалось доказать.

www.treugolniki.ru

Расстояние между двумя точками на поверхности Земли: yu_xuan — LiveJournal

Представим, что для чего-то понадобилось измерить расстояние между двумя точками на поверхности Земли, например, расстояние между Красной площадью и Эрмитажем. Конечно, можно попробовать решить задачу в лоб и посчитать евклидово расстояние по формуле:

но этот подход не заработает по той простой причине, что евклидова метрика предназначена для вычисления расстояния на плоскости, а поверхность Земли — это всё-таки фигура, очень близкая к сфере.

Для решения такой задачи нужно обратиться к редко используемым тригонометрическим функциям.

Одна из таких функций, называется синус-верзус, или, по-другому, версинус. Он представляет собой расстояние от центральной точки дуги, измеряемой удвоенным данным углом, до центральной точки хорды, стягивающей дугу. Вычисляется версинус по формуле:

Гаверсинус — это просто половина версинуса, и именно эта функция поможет нам в решении задачи с поиском расстояния:

Для любых двух точек на сфере гаверсинус центрального угла между ними вычисляется по формуле:

В этой формуле:

d — это центральный угол между двумя точками, лежащими на большом круге

r — радиус сферы

φ₁ и φ₂ — широта первой и второй точек в радианах

λ₁ и λ₂ — долгота первой и второй точек в радианах

Обозначим временно гаверсинус отношения длины к радиусу как переменную h:

Тогда длину d можно вынести за знак равенства:

а для того, чтобы избавиться от дроби, выразим гаверсинус через арксинус:

затем раскроем переменную h:

подставим формулу гаверсинуса и получаем формулу вычисления расстояния:

Теперь вернёмся к исходной задаче поиска расстояния между Красной площадью и Эрмитажем.

Для Красной площади Гугл подсказал координаты (55.7539° N, 37.6208° E), а для Эрмитажа — (59.9398° N, 30.3146° E).

Прежде, чем подставлять координаты в формулу, их нужно перевести в радианы.

Для того, чтобы вычислить длину, в соответствии с формулой, нужно полученное значение арксинуса умножить на два радиуса сферы. Подсчёты усложняет тот факт, что Земля не является идеальной сферой и её радиус немного варьируется. Воспользуемся усреднённым значением радиуса, который, в соответствии со стандартом WGS84 приблизительно равен 6371км:

Произведя умножение, получаем искомое значение, которое приблизительно равно 634.57 км.

Кстати, из-за того, что Земля — не идеальная сфера, погрешность расчётов с использованием этой формулы, составляет около 0,5%.

yu-xuan.livejournal.com

Расстояние между двумя точками на прямой

Расстояние между двумя точками на координатной прямой равно модулю разности их координат.

Формула расстояния между точками на координатной прямой:

AB = |a — b|,

где A и B – это произвольные точки, расстояние между которыми надо найти, то есть, найти длину отрезка AB, a и b – координаты точек.

Выражение |a — b| можно заменить выражением |b — a|, так как a — b и b — a являются противоположными числами и их модули равны.

Следовательно, чтобы найти расстояние между точками координатной прямой надо из координаты одной точки вычесть координату другой точки.

Пример 1. Найти расстояние между точками L(-3) и M(5), отмеченными на координатной прямой.

Решение. Чтобы найти расстояние между точками L и M надо из координаты точки L вычесть координату точки M или наоборот, а в качестве ответа взять модуль полученного результата:

|-3 — 5| = |-8| = 8 или |5 — (-3)| = |5 + 3| = 8

Ответ. Расстояние между точками L и M равно 8.

Пример 2. Найдите координаты середины отрезка AB, если A(-5) и B(5).

Решение. Обозначим середину отрезка точкой C. Так как C – середина отрезка AB, то |AC| = |CB|. Значит, чтобы найти координату точки C, надо сначала вычислить длину отрезка AB и разделить её на 2, то есть, на две равные части AC и CB:

AB = |-5 — 5| = |-10| = 10

10 : 2 = 5, значит |AC| = |CB| = 5

Как видно из чертежа, чтобы найти координату середины отрезка, надо половину длины отрезка либо прибавить к точке с наименьшей координатой, либо отнять от точки с наибольшей координатой:

-5 + 5 = 0 или 5 — 5 = 0

Ответ. Координата середины отрезка C(0).

Пример 3. Найдите координату точки C, которая является серединой отрезка с концами в точках A(7) и B(25).

Решение.

AB = |7 — 25| = |-18| = 18

AC = CB = 18 : 2 = 9

7 + 9 = 16 или 25 — 9 = 16

Ответ. Координата точки C – 16.

naobumium.info

Расстояние между двумя точками.

⇐ ПредыдущаяСтр 2 из 18Следующая ⇒

Пусть задана прямоугольная система координат.

Теорема 1.1.Для любых двух точек М₁(х₁;у₁) и М₂(х₂;у₂) плоскости расстояние d между ними выражается формулой

d = (3)

Доказательство.Опустим из точек М₁ и М₂ перпендикуляры М₁В и М₂А соответственно

на оси Оу и Ох и обозначим через К точку пересечения прямых М₁В и М₂А (рис. 1.4). Возможны следующие случаи:

1)Точки М₁, М₂ и К различны. Очевидно, что точка К имеет координаты (х₂;у₁). Нетрудно заметить что М₁К = ôх₂ – х₁ô, М₂К = ôу₂ – у₁ô. Т.к. ∆М₁КМ₂ прямоугольный, то по теореме Пифагора d = М₁М₂ = = .

2) Точка К совпадает с точкой М₂, но отлична от точки М₁ (рис. 1.5). В этом случае у₂ = у₁

и d = М₁М₂ = М₁К = ôх₂ – х₁ô= =

= .

3) Точка К совпадает с точкой М₁, но отлична от точки М_{2 .} В этом случае х₂ = х₁ и d =

М₁М₂ = КМ₂ = ôу₂— у₁ô= = .

4) Точка М₂ совпадает с точкой М₁. Тогда х₁ = х₂ , у₁ = у₂ и

d = М₁М₂ = О = .

Деление отрезка в данном отношении.

Пусть на плоскости дан произвольный отрезок М₁М₂ и пусть М ─ любая точка этого

отрезка, отличная от точки М₂ (рис. 1.6). Число l, определяемое равенством l = , называется отношением,в котором точка М делит отрезок М₁М₂.

Теорема 1.2.Если точка М(х;у) делит отрезок М₁М₂ в отношении l, то координаты этой определяются формулами

х = , у = ,(4)

где (х₁;у₁) ─ координаты точки М₁, (х₂;у₂) ─ координаты точки М₂.

Доказательство.Докажем первую из формул (4). Вторая формула доказывается аналогично. Возможны два случая.

1) Прямая М₁М₂ перпендикулярна оси Ох. Тогда х₁ = х = х₂ и поэтому

х = х₁ = = = .

2) Прямая М₁М₂ не перпендикулярна оси Ох (рис. 1.6). Опустим перпендикуляры из точек М₁, М, М₂ на ось Ох и обозначим точки их пересечения с осью Ох соответственно Р₁, Р, Р₂. По теореме о пропорциональных отрезках = l.

Т.к. Р₁Р = ôх – х₁ô, РР₂ = ôх₂ – хô и числа (х – х₁) и (х₂ – х) имеют один и тот же знак (при х₁ < х₂они положительны, а при х₁ > х₂отрицательны), то

l = = ,

х – х₁ = l(х₂ – х), х + lх = х₁ + lх₂,

х = .

Следствие 1.2.1.Если М₁(х₁;у₁) и М₂(х₂;у₂) ─ две произвольные точки и точка М(х;у) ─ середина отрезка М₁М₂, то

х = , у = (5)

Доказательство. Так как М₁М = М₂М, то l = 1 и по формулам (4) получаем формулы (5).

Площадь треугольника.

Теорема 1.3.Для любых точек А(х₁;у₁), В(х₂;у₂) и С(х₃;у₃), не лежащих на одной

прямой, площадь S треугольника АВС выражается формулой

S = ô(х₂ – х₁)(у₃ – у₁) – (х₃ – х₁)(у₂ – у₁)ô (6)

Доказательство.Площадь ∆ АВС, изображённого на рис. 1.7, вычисляем следующим

образом:

S_ABC = S_ADEC + S_BCEF – S_ABFD_.

Вычисляем площади трапеций:

S_ADEC = ,

S_BCEF =

S_ABFD =

Теперь имеем

S_ABC = ((х₃ – х₁)(у₃ + у₁) + (х₃ – х₂)(у₃ + у₂) — (х₂ – -х₁)(у₁ + у₂)) = (х₃у₃ – х₁у₃ + х₃у₁ – х₁у₁+ + х₂у₃ – -х₃у₃ + х₂у₂ – х₃у₂ – х₂у₁ + х₁у₁ – х₂у₂ + х₁у₂) = (х₃у₁ – х₃у₂ + х₁у₂ – х₂у₁ + х₂у₃ –

— х₁у₃) = (х₃(у₁ – у₂) + х₁у₂ – х₁у₁ + х₁у₁ – х₂у₁ + у₃(х₂ – х₁)) = (х₁(у₂ – у₁) – х₃(у₂ – у₁) + +у₁(х₁ – х₂) – у₃(х₁ – х₂)) = ((х₁ – х₃)(у₂ – у₁) + (х₁ – х₂)(у₁ – у₃)) = ((х₂ – х₁)(у₃ – у₁) –

— (х₃ – х₁)(у₂ – у₁)).

Для другого расположения ∆ АВС формула (6) доказывается аналогично, но может получиться со знаком «-». Поэтому в формуле (6) ставят знак модуля.

Лекция 2.

Уравнение прямой линии на плоскости: уравнение прямой с главным коэффициентом, общее уравнение прямой, уравнение прямой в отрезках, уравнение прямой, проходящей через две точки. Угол между прямыми, условия параллельности и перпендикулярности прямых на плоскости.

2.1. Пусть на плоскости задана прямоугольная система координат и некоторая линия L.

Определение 2.1.Уравнение вида F(x;y) = 0, связывающее переменные величины x и y, называется уравнение линии L(в заданной системе координат), если этому уравнению удовлетворяют координаты любой точки, лежащей на линии L, и не удовлетворяют координаты никакой точки, не лежащей на этой прямой.

Примеры уравнений линий на плоскости.

1) Рассмотрим прямую, параллельную оси Oy прямоугольной системы координат (рис. 2.1). Обозначим буквой A точку пересечения этой прямой с осью Ox, (a;o) ─ её ор-

динаты. Уравнение x = a является уравнением данной прямой. Действительно, этому уравнению удовлетворяют координаты любой точки M(a;y) этой прямой и не удовлетворяют координаты ни одной точки, не лежащей на прямой. Если a = 0, то прямая совпадает с осью Oy, которая имеет уравнение x = 0.

2) Уравнение x — y = 0 определяет множество точек плоскости, составляющих биссектрисы I и III координатных углов.

3) Уравнение x²— y² = 0 ─ это уравнение двух биссектрис координатных углов.

4) Уравнение x² + y² = 0 определяет на плоскости единственную точку O(0;0).

5) Уравнение x² + y² = 25 ─ уравнение окружности радиуса 5 с центром в начале координат.

Рекомендуемые страницы:

lektsia.com