Признаки равенства прямоугольных треугольников / Соотношения между сторонами и углами треугольника / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Соотношения между сторонами и углами треугольника
- Признаки равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников позволяют сравнивать прямоугольные треугольники лишь по двум элементам, так как любые два прямых угла равны.
1. Признак равенства по двум катетам
| Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны |
Данный признак следует из первого признака равенства треугольников.
Пример:
ABC = A1B1C1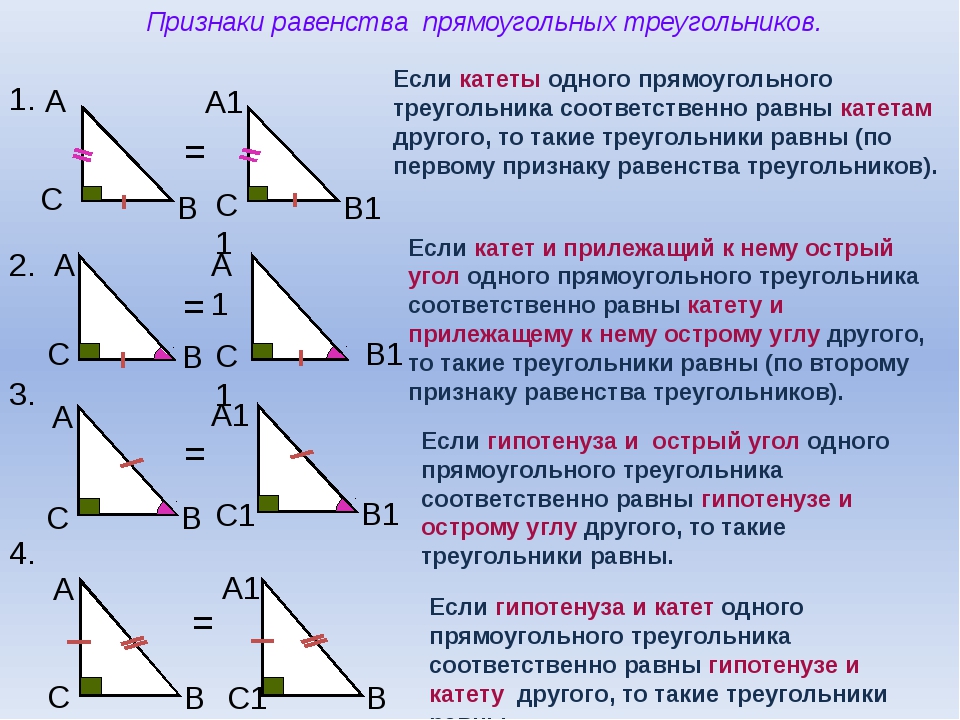 к. AB = A1B1 иAC = A1C1.
к. AB = A1B1 иAC = A1C1.
2. Признак равенства по катету и острому углу
| Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны |
Данный признак следует из второго признака равенства треугольников.
Пример:
ABC = A1B1C1, т.к. AC = A1C1, C = C1
3. Признак равенства по гипотенузе и острому углуТеорема
| Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого,то такие треугольники равны |
Пример:
ABC = A1B1C1, т.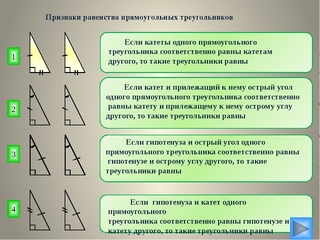 к. BC = B1C1, B = B1
к. BC = B1C1, B = B1
Доказательство
Так как сумма двух острых углов прямоугольного треугольника равна 900, то в таких треугольниках два других острых угла также равны, поэтому данные треугольники равны по второму признаку треугольников, т.е. по
4. Признак равенства по катету и гипотенузе
Теорема
| Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны |
Пример:
ABC = A1B1C1, т.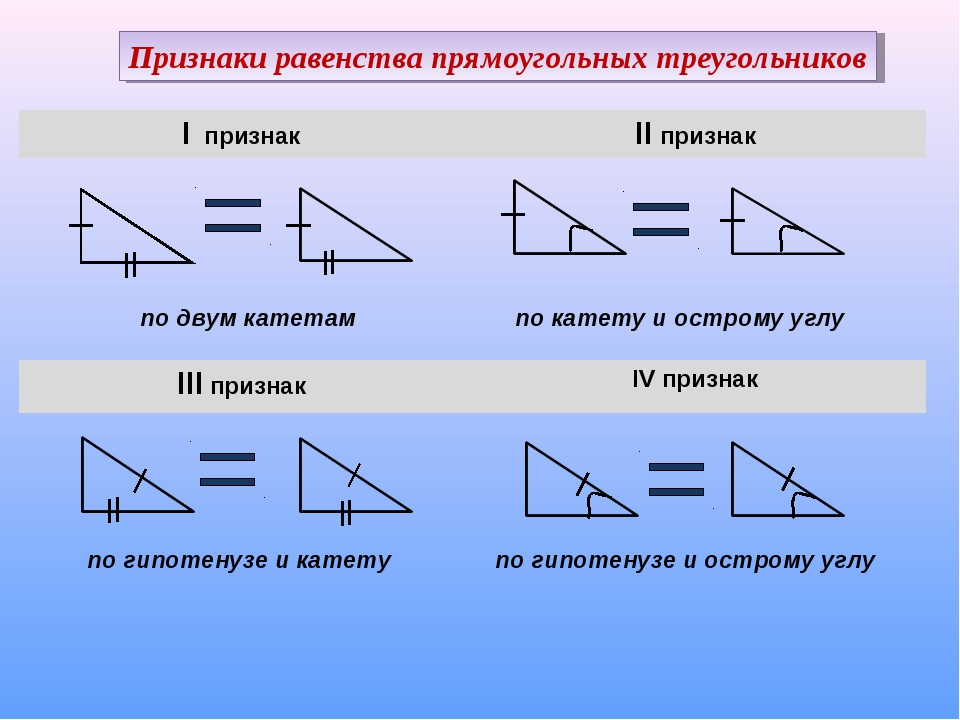 к. BC = B1C1, AB = A1B1
к. BC = B1C1, AB = A1B1
Доказательство
Дано: ABC, A1B1C1, BC = B1C1, AB = A1B1
Доказать: ABC = A1B1C1
Доказательство:
Рассмотрим данные треугольники:
Так как A = A1, то ABC можно наложить на A1B1C1 так, что вершина A совместится с вершиной A1, а стороны AC и AB наложатся соответственно на лучи A1C1 и A1B1.
В C1B1C2 углы при основании не равны (C2 — острый
, а C1 — тупой, так как он смежный с угломB1C1A1, который является острым). А это невозможно, так как у равнобедренного треугольника углы у основания равны, следовательно, вершина C совместится с вершиной C1. А это значит, что полностью совместятся треугольники ABC, A1B1C1, т.е. они равны, что и требовалось доказать.
А это невозможно, так как у равнобедренного треугольника углы у основания равны, следовательно, вершина C совместится с вершиной C1. А это значит, что полностью совместятся треугольники ABC, A1B1C1, т.е. они равны, что и требовалось доказать.Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Теорема о сумме углов треугольника
Остроугольный, прямоугольный и тупоугольный треугольники
Теорема о соотношениях между сторонами и углами треугольника
Неравенство треугольника
Некоторые свойства прямоугольных треугольников
Уголковый отражатель
Расстояние от точки до прямой
Расстояние между параллельными прямыми
Построение треугольника по двум сторонам и углу между ними
Построение треугольника по стороне и двум прилежащим к ней углам
Построение треугольника по трем его сторонам
Соотношения между сторонами и углами треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 266, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 267, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 482, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 644, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 5, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 833, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 839, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 20, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 5, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1175, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5. com, 2022
com, 2022
Пользовательское соглашение
Copyright
Признаки равенства прямоугольных треугольников
Первый признак равенства треугольников:
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Второй признак равенства треугольников:
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Воспользуемся первым и вторым признаками равенства треугольников и докажем следующие признаки равенства прямоугольных треугольников.
Теорема (о равенстве прямоугольных треугольников по двум катетам):
Если
катеты одного прямоугольного треугольника соответственно равны катетам другого
прямоугольного треугольника, то такие треугольники равны.
Доказательство:
Возьмём
два прямоугольных треугольника АВС и А1В1С1.
Пусть катет АС=А1С1, а катет ВС=В1С1.
В прямоугольном треугольнике угол между катетами прямой, а любые два прямых
угла равны. То есть ∠С=С1=90 градусов.
Получаем, что треугольники АВС и А
Теорема (о равенстве прямоугольных треугольников по катету и прилежащему острому углу):
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Доказательство:
Пусть
АВС и А1В1С1 — прямоугольные треугольники, и
катет АС=А1С1, а ∠А=∠А1. А также ∠С=∠С1=90
градусов. Следовательно, получаем, что треугольники АВС и А1В1С1
равны по второму признаку равенства треугольников. Теорема доказана.
А также ∠С=∠С1=90
градусов. Следовательно, получаем, что треугольники АВС и А1В1С1
равны по второму признаку равенства треугольников. Теорема доказана.
Теорема (о равенстве прямоугольных треугольников по гипотенузе и острому углу):
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Доказательство:
Пусть АВС и А1В1С1 — прямоугольные треугольники, у которых ∠С=∠С1=90 градусов. Гипотенузы АВ и А1В1 равны. Углы А и А1 также равны. В прямоугольном треугольнике сумма острых углов равна 90 градусов, то есть:
Получаем:
Таким
образом, получили, что гипотенуза АВ и два прилежащих к ней угла треугольника
АВС соответственно равны гипотенузе А1В1 и двум
прилежащим к ней углам треугольника А1В1С1. Следовательно, треугольники равны по второму признаку равенства треугольников.
Теорема доказана.
Следовательно, треугольники равны по второму признаку равенства треугольников.
Теорема доказана.
Теорема (о равенстве прямоугольных треугольников по гипотенузе и катету):
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольнике равны.
Доказательство:
Пусть АВС и А1В1С1 — прямоугольные треугольники, у которых ∠С=∠С1=90 градусов. Гипотенуза АВ=А1В1 и катет АС=А1С1.
Приложим треугольники друг к другу равными катетами, получаем:
Получили равнобедренный треугольник В1АВ. АС — высота, проведённая из вершины. Тогда АС является и медианой, то есть В1С=СВ.
В
результате получаем, что у прямоугольных треугольников АВС и А1В1С1
равны и вторые катеты. А следовательно, эти
треугольники равны по трём сторонам (или по двум катетам). Теорема доказана.
А следовательно, эти
треугольники равны по трём сторонам (или по двум катетам). Теорема доказана.
Пример.
На рисунке отрезки СА и DB перпендикулярны прямой АВ, отрезок ОА=ОВ. Доказать, что отрезок СА=DB.
Рассмотрим прямоугольные треугольники АСО и BDO. АО=OB по условию задачи. Углы AOC и BOD равны как вертикальные.
Тогда треугольники АСО и ВDО равны по катету и острому углу. Откуда отрезки СА и DB равны как стороны равных треугольников. Что и требовалось доказать.
Пример.
В треугольниках АВС и А1В1С1 углы С и С1 — прямые, а отрезки АD и A1D1 — биссектрисы. Доказать, что треугольники АВС и А1В1С1 равны, если АD=А1D1 и ∠ВАС=∠В1А1С1.
Рассмотрим
прямоугольные треугольники АСD и А1С1D1.
У них гипотенуза АD=А1D1. Углы САD
и С1А1D1
равны
как половины равных углов САВ и С1А1В1.
Получаем, что треугольники АСD и А1С1D1равны
по гипотенузе и острому углу. Следовательно, АС и А1С1
равны как стороны равных треугольников. Тогда и треугольники АВС и А1В1С1
равны, так как катет АС=А1С1 и ∠ВАС=∠В1А1С1.
Что и требовалось доказать.
Углы САD
и С1А1D1
равны
как половины равных углов САВ и С1А1В1.
Получаем, что треугольники АСD и А1С1D1равны
по гипотенузе и острому углу. Следовательно, АС и А1С1
равны как стороны равных треугольников. Тогда и треугольники АВС и А1В1С1
равны, так как катет АС=А1С1 и ∠ВАС=∠В1А1С1.
Что и требовалось доказать.
Прямоугольные треугольники 7 класс онлайн-подготовка на Ростелеком Лицей
110. Прямоугольные треугольники.
Ранее мы уже знакомились с признаками равенства треугольников. Напомним их:
1-й признак (по 2 сторонам и углу между ними): если у треугольников равны две стороны и угол между ними, то такие треугольники равны между собой.
2-й признак (по стороне и двум прилежащим углам): если у треугольников равны сторона и два угла, прилежащие к данной стороне, то такие треугольники равны между собой.
Примечание: пользуясь тем, что сумма углов треугольника постоянна и равна 180°, легко доказать, что условие «прилежания» углов не является необходимым, то есть признак будет верен и в такой формулировке: «… равны сторона и два угла, то …».
3-й признак (по 3 сторонам): если у треугольников равны все три стороны, то такие треугольники равны между собой.
Естественно, все эти признаки остаются верными и для прямоугольных треугольников. Однако у прямоугольных треугольников есть одна существенная особенность – у них всегда есть пара равных прямых углов. Поэтому данные признаки для них упрощаются. Итак, сформулируем признаки равенства прямоугольных треугольников.
1-й признак (по двум катетам): если у прямоугольных треугольников катеты попарно равны, то такие треугольники равны между собой.
Дано:
АС = A1C1
BC = B1C1
Доказать: △ABC =△A1B1C1
Доказательство: вспомним, что в прямоугольных треугольниках: ∠C = ∠C1 =90°. Значит, мы можем воспользоваться первым признаком равенства треугольников (по 2 сторонам и углу между ними) и получить: △ABC =△A1B1C1.
2-й признак (по катету и углу): если катет и острый угол одного прямоугольного треугольника равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны между собой.
Дано:
AC = A1C1
∠A = ∠A1
Доказать: △ABC =△A1B1C1
Доказательство же данного признака сводится к использованию второго признака равенства треугольников (по 2 углам и стороне). Действительно, по условию равны катеты и пара прилежащих к ним углов. Но вторая пара прилежащих к ним углов состоит из углов ∠C = ∠C1 =90°. Значит, мы можем воспользоваться вторым признаком равенства треугольников и получить: △ABC =△A1B1C1.
Но вторая пара прилежащих к ним углов состоит из углов ∠C = ∠C1 =90°. Значит, мы можем воспользоваться вторым признаком равенства треугольников и получить: △ABC =△A1B1C1.
3-й признак (по гипотенузе и углу): если гипотенуза и острый угол одного прямоугольного треугольника равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны между собой.
Дано:
AB = A1B1
∠A = ∠A1
Доказать: △ABC =△A1B1C1
Доказательство: для доказательства этого признака можно сразу воспользоваться вторым признаком равенства треугольников – по стороне и двум углам (точнее, следствием, в котором указано, что углы не обязательно должны быть прилежащими к стороне). Действительно, по условию: AB = A1B1, ∠A = ∠A1, а из свойств прямоугольных треугольников следует, что ∠C = ∠C1 =90°. Значит, мы можем воспользоваться вторым признаком равенства треугольников, и получить: △ABC =△A1B1C1.
Значит, мы можем воспользоваться вторым признаком равенства треугольников, и получить: △ABC =△A1B1C1.
4-й признак (по гипотенузе и катету): если гипотенуза и катет одного прямоугольного треугольника равны соответственно гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны между собой.
Дано:
AB = A1B1
AC = A1C1
Доказать:△ABC =△A1B1C1
Доказательство: так как ∠C = ∠C1 =90°, то треугольник АВС можно наложить на треугольник А1B1C1 так, что вершина С совместится с вершиной С1, а стороны СА и СВ наложатся соответственно на лучи С1А1 и С1В1. Поскольку AC=A1C1, то вершина А совместится с вершиной А1. Но тогда вершины В и В1 также совместятся. В самом деле, если предположить, что точка В совместится с некоторой другой точкой В2 луча С1В1, то получим равнобедренный треугольник А1В1В2, в котором углы при основании В1В2 не равны (∠В2 – острый, а ∠В1 – тупой как смежный с острым углом А1В1С1). Но это невозможно, поэтому вершины В и В1 совместятся. Следовательно, полностью совместятся треугольники △ABC и△A1B1C1, то есть они равны.
В самом деле, если предположить, что точка В совместится с некоторой другой точкой В2 луча С1В1, то получим равнобедренный треугольник А1В1В2, в котором углы при основании В1В2 не равны (∠В2 – острый, а ∠В1 – тупой как смежный с острым углом А1В1С1). Но это невозможно, поэтому вершины В и В1 совместятся. Следовательно, полностью совместятся треугольники △ABC и△A1B1C1, то есть они равны.
Свойства прямоугольного треугольника.
Свойство 1. Сумма двух острых углов прямоугольного треугольника равна 900.
Доказательство. Вспомним, что сумма углов любого треугольника равна 180°. Учитывая тот факт, что ∠C = 90°, получаем, что сумма оставшихся двух углов равна 90°. То есть, ∠А + ∠В= 90°
Свойство 2. Катет, лежащий против угла в 30°, в 2 раза меньше гипотенузы.
Катет, лежащий против угла в 30°, в 2 раза меньше гипотенузы.
Дано:
∠CAB = 30°
Доказать: AB=2ВС
Доказательство: выполним дополнительное построение: продлим прямую ВС за точку С на отрезок, равный ВС. Получим точку D. Так как углы ACB и ACD – смежные, то их сумма равна 180°. Поскольку ∠ACB = 90°, то и ∠ACD = 90°.
Значит, прямоугольные треугольники ACB и ACD равны (по двум катетам: AC – общий, BC = CD – по построению) – первый признак равенства прямоугольных треугольников.
Из равенства треугольников следует равенство всех соответствующих элементов. Значит, ∠BAC = ∠DAC = 30° . Откуда: ∠DAB = 60°. Кроме того, ∠B = ∠D (из равенства всё тех же треугольников). Значит, треугольник ⊿DAB – равнобедренный (так как у него равны углы при основании), но равнобедренный треугольник, один из углов которого равен 60°, – равносторонний. Из этого следует, в частности, что AB = DB = 2BC, что и требовалось доказать.
Стоит отметить, что верно и обратное утверждение: если в прямоугольном треугольнике гипотенуза в два раза больше одного из катетов, то острый угол, лежащий напротив этого катета, равен 30°.
Урок геометрии в 7-м классе по теме: «Признаки равенства прямоугольных треугольников»
Тема: “Признаки равенства прямоугольных треугольников”
Цель: закрепление знаний (свойства прямоугольных треугольников), знакомство с некоторыми признаками равенства прямоугольных треугольников.
Ход урока:
I. Оргмомент.II. Устно.
1. Ответить на вопросы:
- Назвать элементы прямоугольного треугольника.
- Какими свойствами обладают элементы прямоугольного треугольника?
- Докажите, что катет прямоугольного
треугольника, лежащий против угла в 300 ,
равен половине гипотенузы.

- Докажите, что если катет прямоугольного треугольника равен половине гипотенузы, то угол лежащий против этого катета равен 300.
- Найти x. Ответ выбрать из треугольника. Буквы какого-то слова находятся в секторах треугольника. Обсуждение в парах (3 мин).
Рисунок 1.
Составили слово “признак”.
III. Изучение нового материалаИзучая треугольники, мы говорим, что он обладает некоторыми свойствами и признаками. А какие признаки равенства треугольников вам известны? Мы сформулировали и доказали свойства прямоугольных треугольников, а сегодня рассмотрим признаки равенства прямоугольных треугольников, будем решать задачи с их применением.
Доказывая равенство треугольников, сколько пар соответственно равных элементов отыскивали? А возможно ли доказать равенство прямоугольных треугольников по двум катетам?
Перед вами два прямоугольных треугольника АВС
и А1В1С1, у них соответственно
равны катеты. Докажите, если это возможно, их
равенство.
Докажите, если это возможно, их
равенство.
№1. (По двум катетам)
Рисунок 2.
Дано: АВС и А1В1С1 , В=В1=900, АВ = А1В1, ВС = В1С1
Доказать: АВС = А1В1С1
Как прозвучит признак? (Затем задача №1)
№2. (По катету и прилежащему к нему острому углу)
Рисунок 3.
Дано: АВС и А1В1С1 , В=В1=900, ВС = В1С1,С= С1
Доказать: АВС = А1В1С1
Как прозвучит признак? (Затем задача №2)
№3. (По гипотенузе и острому углу)
Рисунок 4.
Дано: АВС и А1В1С1 , В=В1=900, АС = А1С1,А= А1
Доказать: АВС = А1В1С1
Как прозвучит признак? (Затем задача №3)
Задачи. Найти равные треугольники и доказать их
равенство.
Найти равные треугольники и доказать их
равенство.
Рисунок 5.
IV. Закрепление изученного на уроке.Решить следующую задачу.
Рисунок 6.
Дано: АВС, А1В1С1, DAB=CBA=900, АD = BD
Доказать: CAB=DBA.
Обсуждение в четверках (3 мин).
Зачем задача из учебника №261 с записью.
№ 261.
Рисунок 7.
Дано: АВС – равнобедренный, AD и CE – высота АВС
Доказать: AD = CE
Доказательство:
- Треугольники ADC и CEA прямоугольные, так как AD и CE высоты АВС.
- Рассмотрим прямоугольные треугольники ADC и CEA: AC – общая гипотенуза, A=C (как углы при основании равнобедренного треугольника АВС). Значит ADC=CEA (по гипотенузе и острому углу)
- Вывод: так как ADC=CEA, то AD=CE.
 Что и
требовалось доказать.
Что и
требовалось доказать.
V. Задание на дом.
П.35 (три признака), №261 (доказать, что АОС — равнобедренный), №268 (признак равенства прямоугольных треугольников по катету и противолежащему углу).
На следующем уроке геометрии мы продолжим знакомство с признаками равенства прямоугольных треугольников. Отметки выставлю также в следующий раз по результатам за 2 урока.
Дополнительно. Найти равные треугольники.
Рисунок 8.
Признаки равенства прямоугольных треугольников
Треугольник называется прямоугольным, если у него есть прямой угол. Так как сумма углов треугольника равна 180˚, то у прямоугольного треугольника один угол прямой, а два других угла острые, причём их сумма равна 90˚. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны называются катетами.
Из общих признаков равенства треугольников для прямоугольных треугольников можно сформулировать свои признаки равенства.
В прямоугольном треугольнике угол между двумя катетами – прямой, значит в двух любых прямоугольных треугольниках уже равные углы. Исходя из этого, можем сделать следующие выводы:
- если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны;
- если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
Из второго признака равенства треугольников можно убрать прилежащий к катету прямой угол, потому что прямые углы в двух треугольниках равные, и получается:
- если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.

Рассмотрим еще один признак равенства прямоугольных треугольников.
Из теоремы о сумме углов мы знаем, что сумма углов треугольника равна 180˚, один угол в прямоугольном треугольнике прямой. И если один острый угол в прямоугольнике соответственно равен острому углу второго треугольника, то и оставшиеся острые углы треугольников будут равны. Это второй признак равенства треугольников: по стороне и прилежащим к ней углам.
Значит, в прямоугольном треугольнике для определения равенства можно рассматривать только гипотенузу и один острый угол:
- если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Признаки равенства прямоугольных треугольников с примерами решения
Содержание:
Признаки равенства прямоугольных треугольников:
Вы уже знаете три признака равенства треугольников. Поскольку часто приходится иметь дело с прямоугольными треугольниками, то выделяют пять признаков равенства прямоугольных треугольников. Сформулируем и докажем их.
Поскольку часто приходится иметь дело с прямоугольными треугольниками, то выделяют пять признаков равенства прямоугольных треугольников. Сформулируем и докажем их.
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Дано:
Доказать:
Доказательство:
по стороне и двум прилежащим к ней углам.
Третий признак (по катету и противолежащему острому углу)
Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и противолежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Дано: (рис. 264).
Доказать:
Доказательство:
Сумма острых углов прямоугольного треугольника равна 90°. Из того, что следует, что Тогда по стороне и двум прилежащим к ней углам.
Из того, что следует, что Тогда по стороне и двум прилежащим к ней углам.
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Дано: (рис. 265).
Доказать:
Доказательство:
Сумма острых углов прямоугольного треугольника равна 90°. Из того, что следует, что Тогда по стороне и двум прилежащим к ней углам.
Пятый признак (по катету и гипотенузе).Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.
Дано: (рис. 266).
Доказать:
Доказательство:
Приложим треугольников А1В1С1 к треугольнику АВС так, чтобы совместились равные катеты А1С1 и АС, а вершины В1 и В лежали по разные стороны от прямой АС.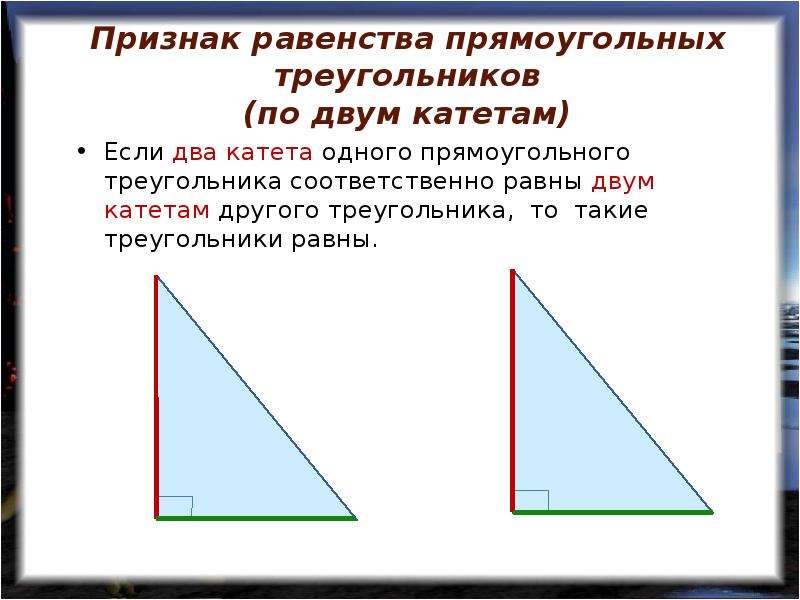 Треугольник А1В1С1 займет положение треугольника АВ2С. Так как B2CB — развернутый и АВ2 = АВ, то треугольник В2АВ — равнобедренный, катет АС — его высота. По свойству равнобедренного треугольника высота, проведенная к основанию, будет и медианой. Тогда В2С=СВ и треугольники ABC и АВ2С равны по двум катетам.
Треугольник А1В1С1 займет положение треугольника АВ2С. Так как B2CB — развернутый и АВ2 = АВ, то треугольник В2АВ — равнобедренный, катет АС — его высота. По свойству равнобедренного треугольника высота, проведенная к основанию, будет и медианой. Тогда В2С=СВ и треугольники ABC и АВ2С равны по двум катетам.
Отсюда
Пример:
На рисунке 267
Доказать равенство треугольников: а) АВС и ADC б) АОВ и COD.
Доказательство:
а) Рассмотрим прямоугольные треугольники ABC и ADC. У них гипотенуза АС — общая, катеты AD и ВС равны по условию. Тогда АВС =ADC по катету и гипотенузе.
б) Из равенства треугольников ABC и ADC следует равенство сторон АВ и CD (доказано в пункте а). Тогда АОВ =COD. по катету (АВ = CD) и противолежащему острому углу (AOB =COD как вертикальные).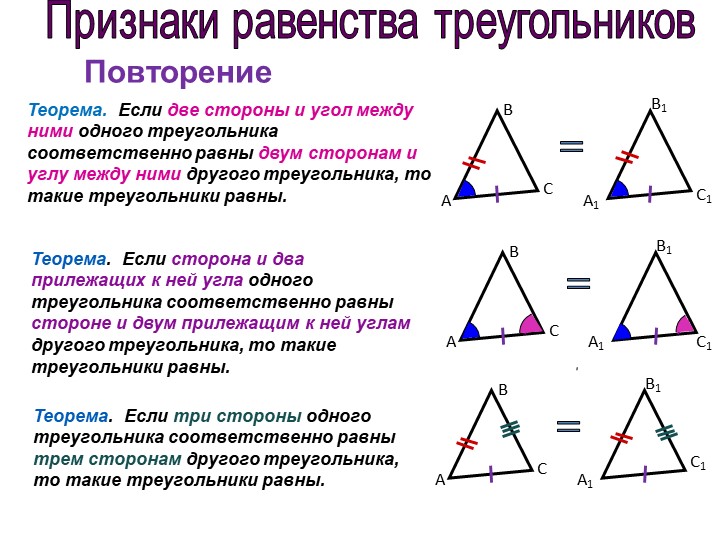
Пример:
Дан треугольник ABC, АК и СМ — его высоты, проведенные к боковым сторонам, О — точка их пересечения (рис. 268). Доказать, что если треугольники АОМ и СОК равны, то треугольник ABC — равнобедренный.
Доказательство:
Так как AOM =COK как вертикальные, то MAO =KCO (сумма острых углов прямоугольного треугольника 90°). Из равенства треугольников АОМ и СОК следует равенство гипотенуз АО и СО. Треугольник АОС — равнобедренный,OAC =OCA как углы при основании равнобедренного треугольника. Тогда BAC =BCA как составленные из равных углов. Треугольник ABC равнобедренный по признаку равнобедренного треугольника. Что и требовалось доказать.
| facebook.com/groups/DPVA.ru»>Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. / / Признаки равенства треугольников. Признаки равенства прямоугольных треугольников. Признаки подобия треугольников. Признаки подобия прямоугольных треугольников. Поделиться:
 Введите свой запрос: Введите свой запрос: | ||||||||||
| Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | |||||||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | ||||||||||
Как определить конгруэнтность прямоугольных треугольников
Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно
или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному агенту, указанному ниже. Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права. Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы подать уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \
достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем
а
ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
Отправьте жалобу нашему назначенному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Конгруэнтность прямоугольного треугольника
Конгруэнтность ног
Если стороны прямоугольного треугольника
конгруэнтный
соответствующим сторонам другого прямоугольного треугольника, то эти треугольники равны.
На рисунке А Б ¯ ≅ Икс Д ¯ и Б С ¯ ≅ Д Z ¯ .
Так, Δ А Б С ≅ Δ Икс Д Z .
Конгруэнтность угла гипотенузы
Если гипотенуза и острый угол прямоугольного треугольника равны гипотенузе и соответствующему острому углу другого прямоугольного треугольника, то треугольники равны.
На рисунке А С ¯ ≅ Икс Z ¯ и ∠ С ≅ ∠ Z .
Так, Δ А Б С ≅ Δ Икс Д Z .
Конгруэнтность угла ноги
Если катет и острый угол прямоугольного треугольника соответственно равны катету и соответствующему ему острому углу другого прямоугольного треугольника, то такие треугольники равны.
На рисунке А Б ¯ ≅ Икс Д ¯ и ∠ С ≅ ∠ Z .
Так, Δ А Б С ≅ Δ Икс Д Z .
Гипотенуза-конгруэнтность катетов
Если гипотенуза и катет прямоугольного треугольника равны гипотенузе и соответствующему катету другого прямоугольного треугольника, то такие треугольники равны.
На рисунке А Б ¯ ≅ Икс Д ¯ и А С ¯ ≅ Икс Z ¯ .
Так, Δ А Б С ≅ Δ Икс Д Z .
Конгруэнтность прямоугольного треугольника — Уроки Византа
Равнобедренные и равнобедренные треугольники — не единственные классификации
треугольников с особыми характеристиками. Прямоугольные треугольники также важны
Прямоугольные треугольники также важны
при изучении геометрии
и, как мы увидим, мы сможем эффективно доказать конгруэнтность прямоугольных треугольников
.
Однако, прежде чем мы начнем изучать это, важно разбить прямоугольные треугольники
на части. Изучение терминов, относящихся к частям прямоугольного треугольника, поможет нам избежать путаницы в этом разделе.
Все прямоугольные треугольники имеют два катета , которые могут быть конгруэнтны, а могут и не конгруэнтны.
катетов прямоугольного треугольника пересекаются под прямым углом . Другая сторона треугольника
(которая не образует ни одной части прямого угла) называется гипотенузой
прямоугольного треугольника. Эта сторона прямоугольного треугольника всегда будет самой длинной
из всех трех сторон. Углы прямоугольного треугольника, не являющиеся прямым углом
, должны быть острыми.
Теперь давайте узнаем, что такое теорема о катете-гипотенузе и как ее применять.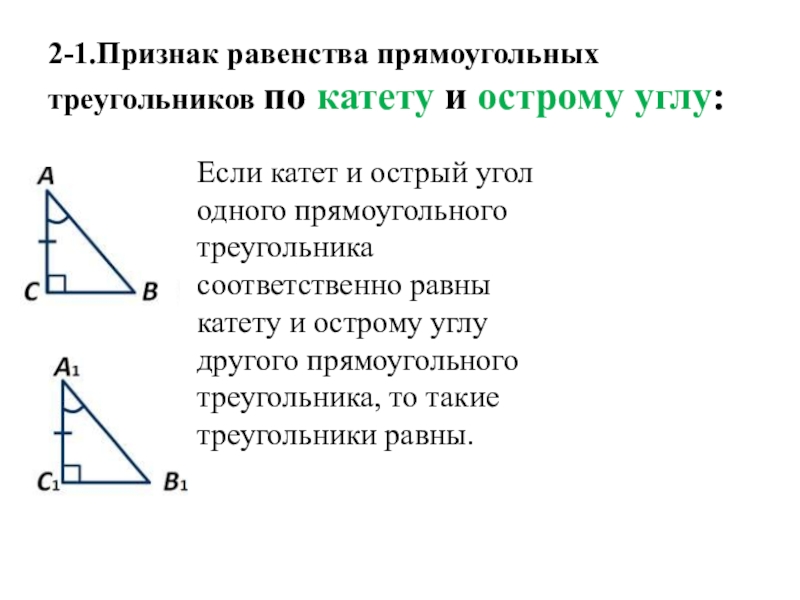
Теорема гипотенузы-нога (HL)
Если гипотенуза и катет прямоугольного треугольника равны гипотенузе и
катету другого прямоугольного треугольника, то два прямоугольных треугольника равны.
Напомним, что критерии наших постулатов о конгруэнтности требовали трех пар
конгруэнтных частей между треугольниками. Теорема HL, по сути, просто требует конгруэнтности между двумя частями: гипотенузой и катетом.Давайте посмотрим на иллюстрацию
, на которой показано правильное использование теоремы о гипотенузе-катете.
На рисунке у нас есть конгруэнтные гипотенузы (AB?DE) и конгруэнтные катеты (CA?FD).
Мы готовы приступить к практике с теоремой HL. Давайте выполним следующие
упражнения, чтобы понять, как использовать эту полезную теорему.
Упражнение 1
Какая дополнительная информация нам нужна, чтобы доказать, что треугольники меньше
конгруэнтны по теореме о гипотенузе-катете?
Ответ:
Обратите внимание, что оба треугольника являются прямоугольными, потому что они оба имеют один прямой угол
. Поэтому, если мы сможем доказать, что гипотенузы треугольников
Поэтому, если мы сможем доказать, что гипотенузы треугольников
и один катет каждого треугольника конгруэнтны, мы сможем применить теорему HL.
Глядя на схему, замечаем, что отрезки SQ и VT
конгруэнтны. Напомним, что сторона прямоугольного треугольника, которая не образует ни одной части
прямого угла, называется гипотенузой. Итак, на диаграмме видно, что у нас
конгруэнтных гипотенузы.
Однако никакой другой информации о треугольниках нам не дано. Если бы нам дали
, что другая пара катетов конгруэнтна, то наши критерии для использования теоремы HL
были бы удовлетворены. Ниже мы показываем две ситуации, в которых мы могли бы использовать
, используя теорему HL, чтобы доказать, что ?QRS??TUV .
На приведенной выше диаграмме нам дана вся та же информация, что и в оригинале,
, а также тот факт, что отрезки QR и TU конгруэнтны. В этой ситуации мы могли бы применить
В этой ситуации мы могли бы применить
теорему HL для доказательства конгруэнтности.
На приведенной выше диаграмме мы отмечаем, что вся исходная информация была предоставлена нам
, а также тот факт, что RS и UV конгруэнтны. Здесь мы могли бы применить
теорему HL, чтобы доказать конгруэнтность треугольников.
Упражнение 2
На каком из следующих рисунков мы можем использовать теорему о катете-гипотенузе, чтобы показать
, что треугольники конгруэнтны?
(а)
(б)
(с)
(г)
Ответ:
Давайте внимательно рассмотрим все диаграммы, чтобы определить, какие из них показывают
пару конгруэнтных треугольников по теореме HL.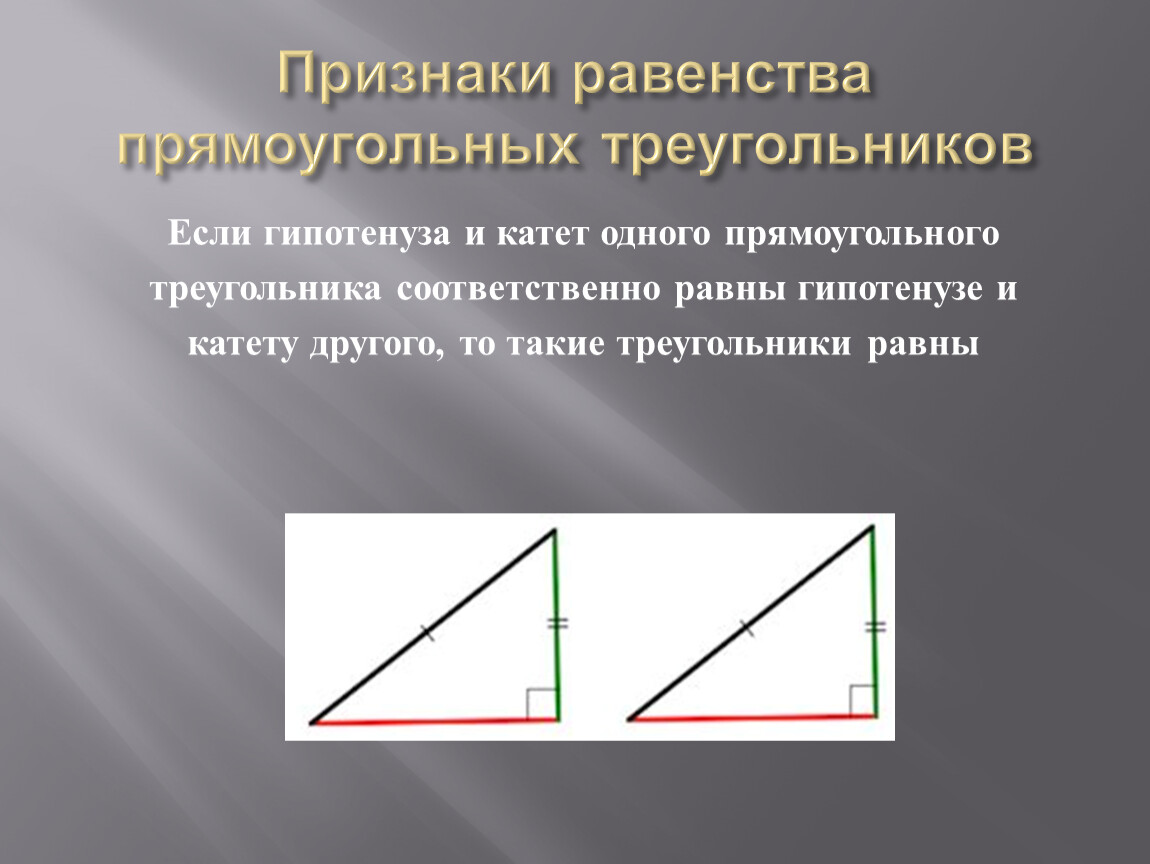
В (a) кажется, что мы могли бы использовать теорему HL. Однако при внимательном рассмотрении
отметим, что углы при вершинах А и
D не прямые. Поскольку квадрат не используется для обозначения того, что
углы прямые, мы не можем использовать теорему HL. Напомним, что единственным типом треугольника, для которого справедлива эта теорема, является прямоугольный треугольник, поэтому мы не можем
применить ее в данной ситуации.
Рисунок (b) показывает два треугольника, которые конгруэнтны, но не по теореме HL
. Нам дано, что отрезок FG конгруэнтен отрезку HG
, а отрезок EG сравним с отрезком IG . У нас также
есть прямые углы, которые образуют G . Поскольку у нас есть две стороны и
включенный угол одного треугольника, конгруэнтные соответствующим частям другого
треугольника, мы знаем, что треугольники конгруэнтны по постулату SAS .
Однако нам не дали никакой информации о гипотенузах ?EGF
и ?IHG , поэтому мы не можем применить теорему HL, чтобы доказать, что треугольники
конгруэнтны.
Теперь давайте посмотрим на (с) . Обратите внимание, что у нас есть два прямых угла на рисунке:
?JLK и ?JLM . Кроме того, нам дали тот факт, что отрезок
JK конгруэнтен отрезку JM .Эти отрезки
на самом деле являются гипотенузами треугольников, потому что они лежат на стороне, противоположной
прямого угла. Более того, два треугольника на рисунке имеют общий сегмент JL .
По транзитивности мы знаем, что отрезок конгруэнтен сам себе. Таким образом, мы можем
применить теорему HL, чтобы доказать, что ?JKL??JML , поскольку мы знаем, что
треугольники прямоугольные, их гипотенузы конгруэнтны, и у них есть
пары конгруэнтных катетов.
Наконец, у нас есть цифра для (d) . Нам известно, что при вершинах O и Q имеется
прямых угла. Мы также можем предположить, что
?NPO и ?RPQ равны, потому что они являются вертикальными
углами. Однако это не поможет нам в попытке доказать конгруэнтность треугольников по теореме HL
. Мы ищем информацию о катетах или гипотенузах
треугольников.Поскольку мы не можем вывести из диаграммы больше фактов, которые нам помогут, мы не можем применить теорему HL в этой ситуации.
Следовательно, мы можем применить теорему HL только к (c) , чтобы показать, что треугольники
конгруэнтны.
Упражнение 3
Ответ:
Мы хотим изучить информацию, которая была дана нам в задаче.Мы
знаем, что отрезок RV перпендикулярен отрезку SK ,
и что отрезки SR и KR
5 конгруэнтны. Давайте попробуем
Давайте попробуем
вывести больше информации из данных утверждений, которые могут помочь нам доказать, что
?RSV??RKV .
Поскольку нам известно, что RV и SK перпендикулярны,
мы знаем, что существуют прямые углы при ?RVS и ?RVK 35.
Этот факт является ключевым компонентом нашего доказательства, поскольку мы знаем, что треугольники ?RSV
и ?RKV являются прямоугольными. Таким образом, мы можем попытаться использовать теорему HL
, чтобы доказать, что они конгруэнтны друг другу.
Нам уже было дано, что гипотенузы конгруэнтны, поэтому все, что осталось показать, это конгруэнтность пары катетов треугольников. Поскольку они оба разделяют
отрезок RV , мы можем использовать переходное свойство , чтобы сказать, что
отрезок конгруэнтен самому себе.
Всего мы нашли прямые углы, конгруэнтные гипотенузы и конгруэнтные катеты между
треугольниками, поэтому мы применяем теорему HL, чтобы сказать, что ?RSV??RKV . Наша новая диаграмма
Наша новая диаграмма
и геометрическое доказательство в два столбца показаны ниже.
Теорема HL будет использоваться в оставшейся части нашего изучения геометрии. Существуют и другие теоремы, относящиеся к прямоугольным треугольникам, которые мы не будем подробно изучать, поскольку они эквивалентны постулатам конгруэнтности, которые мы уже изучили.Эти теоремы и эквивалентные им постулаты поясняются ниже.
Нога-нога (LL) Теорема
Если катеты одного прямоугольного треугольника равны катетам другого прямоугольного треугольника,
то два прямоугольных треугольника конгруэнтны.
Это утверждение совпадает с постулатом SAS , о котором мы узнали, потому что
включает две стороны треугольника, а также угол между ними (который является прямым углом
).
Теорема острого угла ноги (LA)
Если катет и острый угол одного прямоугольного треугольника равны соответствующим
частям другого прямоугольного треугольника, то два прямоугольных треугольника равны.
Это утверждение эквивалентно постулату ASA , о котором мы узнали, потому что
включает в себя прямые углы (которые конгруэнтны), пару сторон одинаковой меры,
и конгруэнтные острые углы.
Теорема гипотенузы-острого угла (HA)
Если гипотенуза и острый угол прямоугольного треугольника равны гипотенузе
и острому углу другого прямоугольного треугольника, то эти два треугольника равны.
Это утверждение совпадает с постулатом AAS , потому что оно включает
прямых угла (которые конгруэнтны), два конгруэнтных острых угла и пару конгруэнтных
гипотенуз.
Конгруэнтность прямоугольных треугольников: определение теорем LA и LL — видео и расшифровка урока
Теорема ЛА
Начнем с теоремы ЛА. Теорема Лос-Анджелеса — это моя теория о дорожном движении в Лос-Анджелесе, подождите, подождите. .. этот Лос-Анджелес не имеет ничего общего с Лос-Анджелесом. Теорема LA in LA относится к острой ноге. Он гласит, что если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
.. этот Лос-Анджелес не имеет ничего общего с Лос-Анджелесом. Теорема LA in LA относится к острой ноге. Он гласит, что если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Вот это да. Объяснение этой теоремы занимает примерно столько же времени, сколько требуется, чтобы добраться куда-нибудь в пробках Лос-Анджелеса. Я почти уверен, что оркестры двигались бы быстрее на 405-м. Что касается теоремы Лос-Анджелеса, если подумать, она очень логична.
Давайте посмотрим на два треугольника, ABC и DEF.
Они определенно выглядят так, будто вместе играют в марширующем оркестре, не так ли? Мы знаем, что они оба прямоугольные.Углы В и Е равны по 90 градусов. И мы знаем, что AB конгруэнтен DE, а угол A конгруэнтен углу D.
Используя теорему LA, мы могли бы сказать: «Хорошо, два прямоугольных треугольника. И у нас есть катет и острый угол, которые совпадают, так что они конгруэнтны. Но почему это правда?
И у нас есть катет и острый угол, которые совпадают, так что они конгруэнтны. Но почему это правда?
Обратите внимание, что, поскольку B и E также конгруэнтны, это на самом деле просто постулат «угол-сторона-угол». Тот факт, что это прямоугольные треугольники, просто дает нам короткий путь. Это как родиться с трубой в руках.Хм, может быть, это не очень хорошая идея.
Но даже если бы мы не включали стороны, как здесь AB и DE, это все равно было бы точно так же, как ASA. Что, если мы знаем, что A и D конгруэнтны, но тогда BC и EF? Что ж, поскольку сумма внутренних углов треугольника равна 180, мы знаем, что C и F также должны быть конгруэнтны друг другу. Таким образом, мы по-прежнему получаем наш угол-бок-угол.
Теорема ЛЛ
Теперь поговорим о теореме ЛЛ. LL Теорема рассказывает о розничной торговле спортивными товарами в штате Мэн…подождите, нет. Это Л.Л. Бин. Другая вещь. Теорема LL — это теорема о ноге. Теорема LA является остротой ноги, поэтому имеет смысл, что LL является ногой. Он гласит, что если катеты одного прямоугольного треугольника равны катетам другого прямоугольного треугольника, то треугольники равны.
Он гласит, что если катеты одного прямоугольного треугольника равны катетам другого прямоугольного треугольника, то треугольники равны.
Это как оркестр с одинаковыми штанами. Ноги у них похожи, да?
Внизу два треугольника: MNO и XYZ.
Возможно, MNO играет на тромбоне, а XYZ играет на ксилофоне.Мы знаем, что это прямоугольные треугольники. Углы N и Y равны по 90 градусов. Если мы знаем, что MN конгруэнтно XY, а NO конгруэнтно YZ, то у нас есть две ноги. Это позволяет нам сказать, что они конгруэнтны на основании теоремы LL.
Теорема LL на самом деле просто постулат SAS, или сторона-угол-сторона. Помните, что стороны прямоугольного треугольника всегда пересекаются под прямым углом, поэтому мы всегда знаем угол между ними.
Использование теорем
Итак, мы узнали об LA, или теореме об острой ноге, и LL, или теореме о ноге. Они дополняются теоремами HA и HL. Теорема HA является теоремой гипотенуза-угол , а теорема HL является теоремой катет гипотенузы . (Посмотрите уроки по этим двум другим теоремам, чтобы узнать больше о каждой из них.) Давайте посмотрим на несколько треугольников и посмотрим, как мы можем определить конгруэнтность.
Они дополняются теоремами HA и HL. Теорема HA является теоремой гипотенуза-угол , а теорема HL является теоремой катет гипотенузы . (Посмотрите уроки по этим двум другим теоремам, чтобы узнать больше о каждой из них.) Давайте посмотрим на несколько треугольников и посмотрим, как мы можем определить конгруэнтность.
Вот два треугольника, LMN и NOL, образованные из прямоугольника:
Вот что происходит, когда два участника группы маршируют друг на друга.Будьте осторожны, чтобы не попасть под валторну. Они конгруэнтны? Итак, мы говорим, что углы OLN и MNL равны. И они имеют общую гипотенузу. Следовательно, мы можем сказать, что они конгруэнтны на основании HA или теоремы гипотенуза-угол.
А эти двое?
Они сразу не выглядят конгруэнтными. Они выглядят как марширующие в разных направлениях. Но обратите внимание, что BC конгруэнтна ST, а углы A и R конгруэнтны.Следовательно, мы можем использовать теорему LA, чтобы определить, что они конгруэнтны. Это тот пример, когда нам точно не дан угол-сторона-угол, но мы знаем, что углы B и S также должны быть равны.
Они выглядят как марширующие в разных направлениях. Но обратите внимание, что BC конгруэнтна ST, а углы A и R конгруэнтны.Следовательно, мы можем использовать теорему LA, чтобы определить, что они конгруэнтны. Это тот пример, когда нам точно не дан угол-сторона-угол, но мы знаем, что углы B и S также должны быть равны.
Вот еще два, которые идут своим путем:
Может быть, деревянные духовые наконец-то устали от духовых. В любом случае, AB и YZ конгруэнтны. Так же как и BC и XZ. Это две пары ног? Нет, AB и YZ расположены напротив прямого угла.Что находится напротив прямого угла? Гипотенуза. Итак, у нас есть гипотенуза и катет. Угадай, что? Это HL, или теорема о катете гипотенузы.
Хорошо, время для еще одного. Вот два треугольника, которые выглядят так, как будто они находятся в какой-то формации:
Может быть, это одна из тех групп, хореография которых создана для создания крутых форм. Хорошо, что мы знаем? FH конгруэнтно LK. И HG конгруэнтно JK.Это все ноги. Подходящих брюк здесь предостаточно. Ноги и ноги? Это теорема нога-нога, или LL.
Хорошо, что мы знаем? FH конгруэнтно LK. И HG конгруэнтно JK.Это все ноги. Подходящих брюк здесь предостаточно. Ноги и ноги? Это теорема нога-нога, или LL.
Итоги урока
Итак, мы узнали о двух полезных теоремах о конгруэнтности прямоугольных треугольников.
Во-первых, теорема Лос-Анджелеса. Это теорема об острой ноге. Он гласит, что если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Далее мы узнали о теореме ЛЛ.Это теорема нога-нога. Этот утверждает, что если катеты одного прямоугольного треугольника конгруэнтны катетам другого прямоугольного треугольника, то треугольники конгруэнтны.
Мы также научились применять эти теоремы для установления конгруэнтности прямоугольных треугольников. Они дополняют две другие теоремы о прямоугольном треугольнике, теорему об угле-гипотенузе, или HA, и теорему о катете-гипотенузе, или HL.
Результаты обучения
Понимание фактов из этого урока может помочь вам сделать следующее:
- Перечислить характеристики прямоугольных треугольников
- Укажите LA, или теорему об острой ноге, и LL, или теорему о ноге
- Подробно изложите, как эти две теоремы соотносятся с теоремами об угле-гипотенузе и катете-гипотенузе
конгруэнтных прямоугольных треугольников в геометрии
Что такое конгруэнтные прямоугольные треугольники? Мы можем использовать свойства специальных треугольников (таких как равнобедренные треугольники или прямоугольные треугольники), чтобы помочь нам идентифицировать соответствующие части, которые равны. Давайте рассмотрим пример:
Давайте рассмотрим пример:
Проблема
Два прямоугольных треугольника ΔABC и ΔDEF имеют равные гипотенузы и равные катеты. Докажите, что треугольники равны.
Стратегия
Глядя на два треугольника, мы видим, что у нас две равные стороны — катеты AB и DE, а гипотенузы AC и DF — это было указано в условии задачи.
У нас также есть одна пара конгруэнтных углов — прямые углы ∠ABC и ∠DEF, так как оба треугольника прямоугольные.
К сожалению, мы не можем использовать постулат Сторона-Угол-Сторона, потому что конгруэнтный угол не находится между двумя сторонами.
Заманчиво попытаться найти другую пару углов, но мы просто ничего не знаем о двух других углах. НО мы знаем кое-что еще о прямоугольных треугольниках, а именно об отношении между их катетами и гипотенузой — теорема Пифагора: a² + b² = c².
Здесь у нас уже есть 2 равные стороны, поэтому мы можем алгебраически показать, что третья сторона также должна быть равна, и доказать, что треугольники конгруэнтны, используя постулат Сторона-Сторона-Сторона.
Доказательство
(1) AB = DE //данные
(2) AC = DF //данные
(3) m∠ABC = m∠DEF=90° // Определение прямоугольного треугольника
(4) AB² + BC² = AC² / /Теорема Пифагора
(5) DE² + EF² = DF² // Теорема Пифагора
(6) AB² + EF² = AC² // подстановка с использованием (1), (2) и (5)
(7) BC = EF // 4) & (6)
(8) ΔABC ≅ΔDEF // Сторона-сторона-сторона постулат
Иногда вы увидите, что это называется еще одним методом демонстрации конгруэнтности треугольников, применимым только к прямоугольным треугольникам, который называется «гипотенуза-контур» (или сокращенно HL) — если два прямоугольных треугольника имеют одинаковую гипотенузу и один катет, они конгруэнтны.
Теорема о катете гипотенузы – объяснение и примеры
В этой статье мы узнаем о теореме катета гипотенузы (HL) . Подобно SAS, SSS, ASA и AAS, это также один из постулатов конгруэнтности треугольника.
Разница в том, что остальные 4 постулата применимы ко всем треугольникам. В то же время теорема о катете гипотенузы верна только для прямоугольных треугольников , поскольку, очевидно, гипотенуза является одним из катетов прямоугольного треугольника.
Что такое теорема о катете гипотенузы?
Теорема о катете гипотенузы — это критерий, используемый для доказательства конгруэнтности заданного набора прямоугольных треугольников.
Теорема о катете гипотенузы (HL) утверждает, что; данный набор треугольников конгруэнтен, если соответствующие длины их гипотенузы и одного катета равны.
В отличие от других постулатов конгруэнтности, таких как; SSS, SAS, ASA и AAS, проверяются три величины, с теоремой о катете гипотенузы (HL), рассматриваются только две стороны прямоугольного треугольника.
.
от Pythagorean Theorem,
AC 2 = AB 2 + BC 2 + BC 2 + BC 2 2 и PQ 2 = RP 2 + RP 2
с AC = PQ, Заменитель получить;
AB 2 + BC 2 = RQ 2 + RP 2 + RP 2
, но ab = rq = RQ,
по замене;
RQ 2 + BC 2 = RQ 2 + RP 2
Собери одинаковые условия, чтобы получить;
BC 9072 2 = RP 2 = RP 2 = RP 2
0 abc ab ab ≅≅ PQRПример 1
9 Если PR ⊥ QS, Докажите, что PQR и PRS конгруэнтны
Решение
Треугольники PQR и PRS являются прямоугольными треугольниками, потому что они оба имеют угол 90-09°09 R.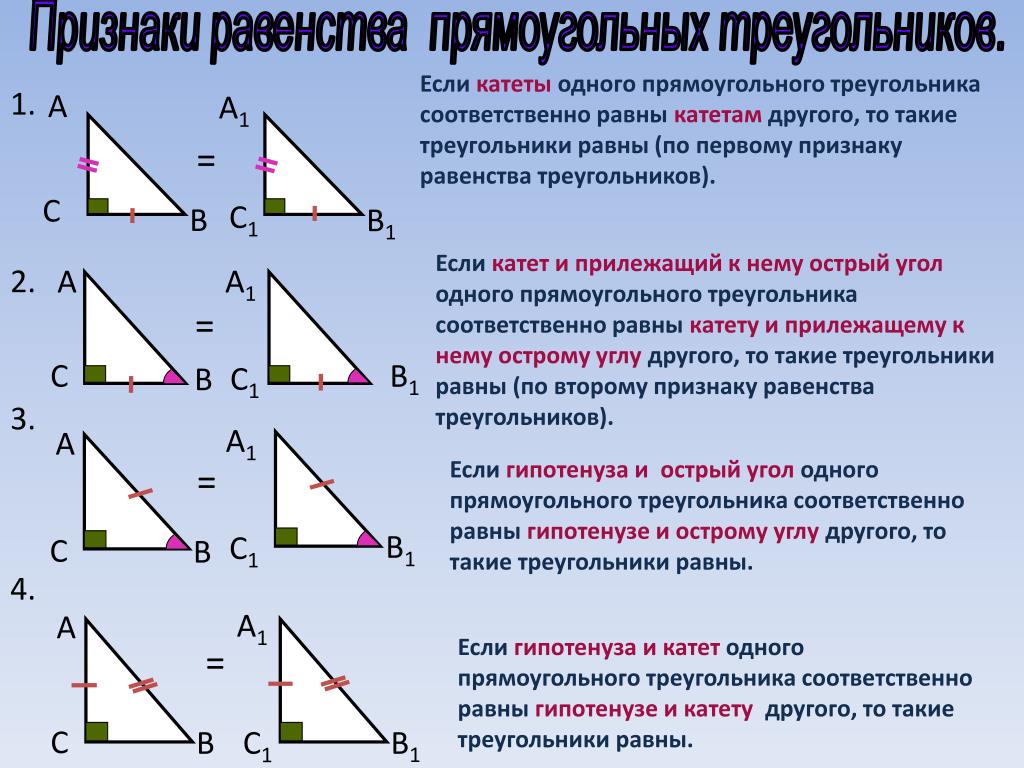 098 в точке.
098 в точке.
Дано;
- PQ = PS (гипотенузы)
- PR = PR (общая сторона)
- Следовательно, путем гипотенузы — теорема ногой (HL), △ PQR ≅ △ PR.
Пример 2
Если FB = DB, BA = BC , FB ⊥ AE и DB ⊥ CE , показывают, что AE = CE.
Отсюда доказано. Пример 3 Учитывая, что ∆ ABC равнобедренный треугольник и ∠ BAM = ∠ MAD . Докажите, что M — это середина BD. Решение Учитывая ∠ BAM = ∠ MAD , тогда линия AM является биссектрисой ∠ BAD . Пример 4 Проверить конгруэнтность ∆ XYZ и ∆ STR . Решение Пример 5 : ∠ ∠ ∠ ∠ C = C = градусов , AD = BC .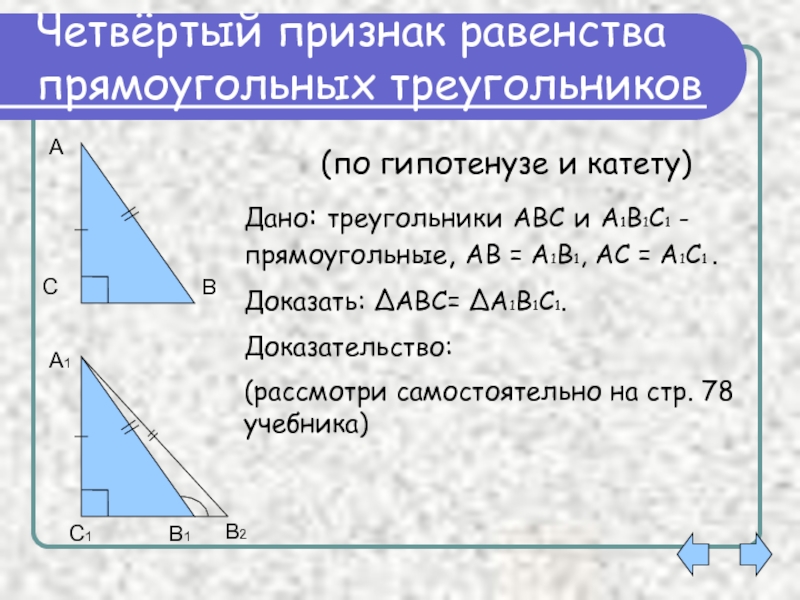
 Покажите, что △ ABD ≅ △ DBC.
Покажите, что △ ABD ≅ △ DBC.
Дано,
- AD = BC (равная нога)
- ∠ a = ∠ C (прямой угол)
- BD = DB (Общая сторона, гипотенузность)
- by, с помощью гипотенузы ноги (HL) теорема, △ ABD ≅ △ DBC
Пример 6
Prepaperse ∠ W = ∠ Z = 90 градусов, а M является средней точкой WZ и XY. Докажите, что два треугольника WMX и YMZ равны.
2
01
- △
- △
- △ WMX и △ YMZ являются правыми треугольниками, потому что они оба имеют угол 90 0 (прямые углы)
- WM = MZ (нога)
- XM = MY (гипотенуза)
- Следовательно, , по теореме гипотенузы-поля (HL), △ WMX ≅ △ YMZ.

Пример 7
Вычислите значение x в следующих конгруэнтных треугольниках.
Решение
Учитывая, что два треугольника конгруэнтны, тогда;
⇒ 2x + 2 = 5x — 19
⇒ 2x — 5x = -19 — 2
⇒ -3x = — 21
x = — 21/-3
x = 7.
3,
3, x = 7
Доказательство:
⇒ 2x + 2 = 2(7) + 2
⇒ 14 + 2 = 16
⇒ 5x -19 = 5(7) – 19
– 6 ⇒ 3 5 5
Да, сработало!
Пример 8
Если ∠ A = ∠ C = 90 градусов и AD = BC Найдите значение x и y, при котором два треугольника ABD и DBC равны.
2
1ABD ≅ △ DBC DBC
Рассчитайте значение x
⇒ 6x — 7 = 4x + 2
⇒ 6x — 4x = 2 + 7
⇒ 2x = 9
⇒ x = 9/2
x = 4,5
Вычислите значение y.

⇒ 4Y + 25 = 7Y — 5
⇒ 4Y — 77 002 ⇒ — 25
⇒ -3Y = -30
y = -30 / -3 = 10
Следовательно, △ abd ≅ △ ДБК , когда х = 4.2\)
Теперь давайте сохраним еще одну сторону равной в обоих треугольниках и посмотрим на результат.
Да, на изображении выше \(\треугольник ABC \cong \треугольник PQR\).
Мы можем разместить оба треугольника друг на друге без каких-либо зазоров и перекрытий.
Следовательно, \(\triangle ABC \cong \triangle PQR\) с использованием правила соответствия RHS.
Укажите и докажите, равны ли данные треугольники или нет.
\(\следовательно \треугольник ZXY \cong \треугольник PQR\), по критерию правосторонней конгруэнтности.
- Критерий соответствия RHS применим только в прямоугольных треугольниках.
- По правилу RHS мы рассматриваем только гипотенузу и одну соответствующую сторону данных двух прямоугольных треугольников, чтобы доказать конгруэнтность треугольников.

- Два равных треугольника всегда равны по площади.
- Когда мы кладем два конгруэнтных прямоугольных треугольника друг на друга, между ними нет зазоров и перекрытий. Они полностью подходят друг другу.
Теперь взгляните на некоторые примеры критериев RHS для более глубокого понимания.
Решенные примерыВ заданном равнобедренном треугольнике \(\треугольник PQR\) докажите, что высота \(PO\) делит пополам основание треугольника \(QR\).
Раствор
В заданном треугольнике \(\треугольник PQR\) образованы два малых прямоугольных треугольника: \(\треугольник POQ\) и \(\треугольник POR\),
Высота \(PO\) делит пополам \(QR\), когда \(OQ=OR\).
Итак, докажем, что \(\треугольник POQ \cong \треугольник POR\).о\)
Итак, по критерию соответствия RHS
\(\треугольник POQ \cong \треугольник POR\)
\(OQ=OR\) (по CPCT)
\(\следовательно\) Высота треугольника \(\треугольник PQR\) делит пополам основание \(QR\) треугольника.

В заданном треугольнике \(\треугольник ABD\), если \(AC\) делит пополам сторону \(BD\) и \(CE=CF\), докажите, что площади треугольников \(\треугольник BCE\) и \(\треугольник DCF\) равны.
Раствор
Мы знаем, что площади двух равных треугольников всегда равны.о\конец{выравнивание}\)
\(\следовательно \треугольник BCE \cong \треугольник DCF\) (по критерию RHS конгруэнтности)
Следовательно, \(\треугольник BCE\) и \(\треугольник DCF\) равны по площади.
Интерактивные вопросы по RHSВот несколько упражнений для практики. Выберите/введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Подведем итогиМини-урок был посвящен увлекательной концепции RHS.Математическое путешествие по RHS началось с того, что ученик уже знал, и продолжилось творческим созданием новой концепции в умах молодых.
О Куэмате Сделано таким образом, что это не только понятно и легко для понимания, но и останется с ними навсегда.
Сделано таким образом, что это не только понятно и легко для понимания, но и останется с ними навсегда.В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу «обучение-преподавание-обучение» учителя изучают тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любая другая форма отношений, это логическое мышление и разумный подход к обучению, в которые мы в Cuemath верим.
Часто задаваемые вопросы по RHS 1. Что такое правила соответствия?Существует 5 основных правил конгруэнтности треугольников, а именно:
- SSS (сторона сторона сторона) правило
- ASA (угол сторона угол) правило
- SAS (боковой угол боковой) правило
- Правило AAS (угол угол стороны)
- Правило RHS (прямоугольная сторона гипотенузы)
 Что такое критерий RHS в треугольниках? Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и соответствующему катету другого прямоугольного треугольника, то такие треугольники равны. 3. Как вы используете правило RHS? По правилу RHS мы показываем, что в двух прямоугольных треугольниках длина гипотенузы равна длине другой соответствующей стороны треугольников. Если мы можем это доказать, это означает, что данные треугольники конгруэнтны, иначе нет. 4. В чем разница между SAS и RHS? В правиле SAS мы считаем угол между двумя сторонами равными, но в RHS расположение угла не имеет значения, поскольку мы берем гипотенузу и любую из двух других соответствующих сторон. 5. Какова полная форма правила соответствия RHS? Полная форма RHS — это прямоугольная сторона гипотенузы. 6. Где мы используем правило соответствия RHS? Правило RHS используется для нахождения длины недостающей стороны в прямоугольных треугольниках, для нахождения площади треугольников, для проектирования зданий и башен и т.
Что такое критерий RHS в треугольниках? Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и соответствующему катету другого прямоугольного треугольника, то такие треугольники равны. 3. Как вы используете правило RHS? По правилу RHS мы показываем, что в двух прямоугольных треугольниках длина гипотенузы равна длине другой соответствующей стороны треугольников. Если мы можем это доказать, это означает, что данные треугольники конгруэнтны, иначе нет. 4. В чем разница между SAS и RHS? В правиле SAS мы считаем угол между двумя сторонами равными, но в RHS расположение угла не имеет значения, поскольку мы берем гипотенузу и любую из двух других соответствующих сторон. 5. Какова полная форма правила соответствия RHS? Полная форма RHS — это прямоугольная сторона гипотенузы. 6. Где мы используем правило соответствия RHS? Правило RHS используется для нахождения длины недостающей стороны в прямоугольных треугольниках, для нахождения площади треугольников, для проектирования зданий и башен и т.
- △
- △

 Что и
требовалось доказать.
Что и
требовалось доказать.
 Признаки подобия треугольников. Признаки подобия прямоугольных треугольников.
Признаки подобия треугольников. Признаки подобия прямоугольных треугольников.




 Сделано таким образом, что это не только понятно и легко для понимания, но и останется с ними навсегда.
Сделано таким образом, что это не только понятно и легко для понимания, но и останется с ними навсегда. Что такое критерий RHS в треугольниках? Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и соответствующему катету другого прямоугольного треугольника, то такие треугольники равны. 3. Как вы используете правило RHS? По правилу RHS мы показываем, что в двух прямоугольных треугольниках длина гипотенузы равна длине другой соответствующей стороны треугольников. Если мы можем это доказать, это означает, что данные треугольники конгруэнтны, иначе нет. 4. В чем разница между SAS и RHS? В правиле SAS мы считаем угол между двумя сторонами равными, но в RHS расположение угла не имеет значения, поскольку мы берем гипотенузу и любую из двух других соответствующих сторон. 5. Какова полная форма правила соответствия RHS? Полная форма RHS — это прямоугольная сторона гипотенузы. 6. Где мы используем правило соответствия RHS? Правило RHS используется для нахождения длины недостающей стороны в прямоугольных треугольниках, для нахождения площади треугольников, для проектирования зданий и башен и т.
Что такое критерий RHS в треугольниках? Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и соответствующему катету другого прямоугольного треугольника, то такие треугольники равны. 3. Как вы используете правило RHS? По правилу RHS мы показываем, что в двух прямоугольных треугольниках длина гипотенузы равна длине другой соответствующей стороны треугольников. Если мы можем это доказать, это означает, что данные треугольники конгруэнтны, иначе нет. 4. В чем разница между SAS и RHS? В правиле SAS мы считаем угол между двумя сторонами равными, но в RHS расположение угла не имеет значения, поскольку мы берем гипотенузу и любую из двух других соответствующих сторон. 5. Какова полная форма правила соответствия RHS? Полная форма RHS — это прямоугольная сторона гипотенузы. 6. Где мы используем правило соответствия RHS? Правило RHS используется для нахождения длины недостающей стороны в прямоугольных треугольниках, для нахождения площади треугольников, для проектирования зданий и башен и т.