Признаки равенства прямоугольных треугольников / Соотношения между сторонами и углами треугольника / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Соотношения между сторонами и углами треугольника
- Признаки равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников позволяют сравнивать прямоугольные треугольники лишь по двум элементам, так как любые два прямых угла равны.
1. Признак равенства по двум катетам
| Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны |
Данный признак следует из первого признака равенства треугольников.
Пример:
A1B1C1, т.к. AB = A1B1 иAC = A1C1.2. Признак равенства по катету и острому углу
| Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны |
Данный признак следует из второго признака равенства треугольников.
Пример:
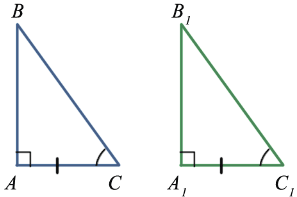
A1B1C1, т.к. AC = A1C1, 
C = C13. Признак равенства по гипотенузе и острому углу
Теорема
| Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого,то такие треугольники равны |
Пример:
A1B1C1, т.к. BC = B1C1, B = B1Доказательство
Так как сумма двух острых углов прямоугольного треугольника равна 900, то в таких треугольниках два других острых угла также равны, поэтому данные треугольники равны по второму признаку треугольников, т.е. по стороне(по гипотенузе) и двум прилежащим к ней углам, что и требовалось доказать.
4. Признак равенства по катету и гипотенузе
Теорема
| Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны |
Пример:
ABC = A1B1C1, т.к. BC = B1C1, AB = A1B1
Доказательство
Дано: ABCA1B1C1, BC = B1C1, AB = A1B1
Доказать: ABC = A1B1C1
Доказательство:
Рассмотрим данные треугольники:
Так как A = A 1, то ABC можно наложить на A1B1C1 так, что вершина A совместится с вершиной A1, а стороны AC и AB наложатся соответственно на лучи A1C1 и A1B1. При этом вершина B совместится с вершиной B1, потому что AB = A1B1. Но тогда вершина C также совместится с вершиной C1. Действительно, если
В C1B1C2 углы при основании не равны (C2 — острый, а C1 — тупой, так как он смежный с угломB1C1A1, который является острым). А это невозможно, так как у равнобедренного треугольника углы у основания равны, следовательно, вершина C совместится с вершиной C1. А это значит, что полностью совместятся треугольники ABC, A1B1C1, т.е. они равны, что и требовалось доказать.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Теорема о сумме углов треугольника
Остроугольный, прямоугольный и тупоугольный треугольники
Теорема о соотношениях между сторонами и углами треугольника
Неравенство треугольника
Некоторые свойства прямоугольных треугольников
Уголковый отражатель
Расстояние от точки до прямой
Расстояние между параллельными прямыми
Построение треугольника по двум сторонам и углу между ними
Построение треугольника по стороне и двум прилежащим к ней углам
Построение треугольника по трем его сторонам
Соотношения между сторонами и углами треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 267, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 357, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 408, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 434, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 437, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 616, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 5, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 839, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1175, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1305, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5.com, 2019
Пользовательское соглашение
budu5.com
Признаки равенства прямоугольных треугольников
Первый признак равенства треугольников:
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Второй признак равенства треугольников:
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Воспользуемся первым и вторым признаками равенства треугольников и докажем следующие признаки равенства прямоугольных треугольников.
Теорема (о равенстве прямоугольных треугольников по двум катетам):
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
Доказательство:
Возьмём два прямоугольных треугольника АВС и А1В1С1. Пусть катет АС=А1С1, а катет ВС=В1С1. В прямоугольном треугольнике угол между катетами прямой, а любые два прямых угла равны. То есть ∠С=С1=90 градусов. Получаем, что треугольники АВС и А1В1С1 равны по первому признаку равенства треугольников. Теорема доказана.
Теорема (о равенстве прямоугольных треугольников по катету и прилежащему острому углу):
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Доказательство:
Пусть АВС и А1В1С1 — прямоугольные треугольники, и катет АС=А1С1, а ∠А=∠А1. А также ∠С=∠С1=90 градусов. Следовательно, получаем, что треугольники АВС и А1В1С1 равны по второму признаку равенства треугольников. Теорема доказана.
Теорема (о равенстве прямоугольных треугольников по гипотенузе и острому углу):
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Доказательство:
Пусть АВС и А1В1С1 — прямоугольные треугольники, у которых ∠С=∠С1=90 градусов. Гипотенузы АВ и А1В1 равны. Углы А и А1 также равны. В прямоугольном треугольнике сумма острых углов равна 90 градусов, то есть:
Получаем:
Таким образом, получили, что гипотенуза АВ и два прилежащих к ней угла треугольника АВС соответственно равны гипотенузе А1В1 и двум прилежащим к ней углам треугольника А1В1С1. Следовательно, треугольники равны по второму признаку равенства треугольников. Теорема доказана.
Теорема (о равенстве прямоугольных треугольников по гипотенузе и катету):
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольнике равны.
Доказательство:
Пусть АВС и А1В1С1 — прямоугольные треугольники, у которых ∠С=∠С1=90 градусов. Гипотенуза АВ=А1В1 и катет АС=А1С1.
Приложим треугольники друг к другу равными катетами, получаем:
Получили равнобедренный треугольник В1АВ. АС — высота, проведённая из вершины. Тогда АС является и медианой, то есть В1С=СВ.
В результате получаем, что у прямоугольных треугольников АВС и А1В1С1 равны и вторые катеты. А следовательно, эти треугольники равны по трём сторонам (или по двум катетам). Теорема доказана.
Пример.
На рисунке отрезки СА и DB перпендикулярны прямой АВ, отрезок ОА=ОВ. Доказать, что отрезок СА=DB.
Рассмотрим прямоугольные треугольники АСО и BDO. АО=OB по условию задачи. Углы AOC и BOD равны как вертикальные.
Тогда треугольники АСО и ВDО равны по катету и острому углу. Откуда отрезки СА и DB равны как стороны равных треугольников. Что и требовалось доказать.
Пример.
В треугольниках АВС и А1В1С1 углы С и С1 — прямые, а отрезки АD и A1D1 — биссектрисы. Доказать, что треугольники АВС и А1В1С1 равны, если АD=А1D1 и ∠ВАС=∠В1А1С1.
Рассмотрим прямоугольные треугольники АСD и А1С1D1. У них гипотенуза АD=А1D1. Углы САD и С1А1D1 равны как половины равных углов САВ и С1А1В1. Получаем, что треугольники АСD и А1С1D1равны по гипотенузе и острому углу. Следовательно, АС и А1С1 равны как стороны равных треугольников. Тогда и треугольники АВС и А1В1С1 равны, так как катет АС=А1С1 и ∠ВАС=∠В1А1С1. Что и требовалось доказать.
videouroki.net
Признаки равенства прямоугольных треугольников
Для прямоугольных треугольников можно сформулировать следующие признаки равенства треугольников:
Первый признак равенства (по двум катетам)
1 признак (по двум катетам). Если два катета одного прямоугольного треугольника равны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники равны (рис. 1)
Второй признак равенства (по катету и гипотенузе)
2 признак (по катету и гипотенузе). Если катет и гипотенуза одного прямоугольного треугольника равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны (рис. 2).
Третий признак равенства (по гипотенузе и острому углу)
3 признак (по гипотенузе и острому углу). Если гипотенуза и острый угол одного прямоугольного треугольника равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны (рис. 3).
Четвертый признак равенства (по катету и острому углу)
4 признак (по катету и острому углу). Если катет и острый угол одного прямоугольного треугольника равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны (рис. 4).
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Равенство по катету и острому углу
Теорема 1
(Признак равенства прямоугольных треугольников по катету и прилежащему острому углу)
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Дано:
ΔABC, ΔA1B1C1,
∠C=90°, ∠C1=90°,
BC=B1C1, ∠B=∠B1
Доказать: ΔABC= ΔA1B1C1
Доказательство:
По условию, в треугольниках ABC и ΔA1B1C1:
1) BC=B1C1;
2)∠C=∠C1;
3) ∠B=∠B1.
Следовательно, ΔABC= ΔA1B1C1(по стороне и двум прилежащим к ней углам).
Что и требовалось доказать.
Теорема 2
(Признак равенства прямоугольных треугольников по катету и противолежащему углу)
Если катет и противолежащий ему угол одного прямоугольного треугольника соответственно равны катету и противолежащему ему углу другого прямоугольного треугольника, то такие треугольники равны.
Дано:
ΔABC, ΔA1B1C1,
∠C=90°, ∠C1=90°, BC=B1C1,
∠A=∠A1
Доказать: ΔABC= ΔA1B1C1
Доказательство:
По условию, в треугольниках ABC и ΔA1B1C1:
1) BC=B1C1;
2)∠C=∠C1;
3)Так как сумма острых углов прямоугольного треугольника равна 90°,
то есть ∠ B=∠ B1.
Следовательно, ΔABC= ΔA1B1C1(по стороне и двум прилежащим к ней углам).
Что и требовалось доказать.
www.treugolniki.ru
Признаки равенства прямоугольных треугольников [wiki.eduVdom.com]
Так как в прямоугольном треугольнике угол между двумя катетами прямой, а любые два прямых угла равны, то из первого признака равенства треугольников вытекает следствие.
Следствие 1. Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
Далее, из второго признака равенства треугольников вытекает следствие.
Следствие 2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
Рассмотрим еще два признака равенства прямоугольных треугольников.
Теорема 1. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
Доказательство. Из следствия 1 следует, что в таких треугольниках два других острых угла также равны, поэтому треугольники равны по второму признаку равенства треугольников. Теорема доказана.
Теорема 2. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны (рис.1).
Рис.1
Пример 1. Доказать, что каждая точка биссектрисы угла равноудалена от его сторон.
Решение. Пусть l — биссектриса ∠ АОВ (рис.2).
Рис.2
Рассмотрим произвольную точку М, лежащую на луче l. Опустим из точки М перпендикуляры МС и MD на стороны угла АОВ. Прямоугольные треугольники ОМС и OMD равны по теореме 1: у них гипотенуза ОМ общая, а углы СОМ и DOM равны по условию. Отсюда следует, что МС = MD.
Пример 2. Доказать, что точка плоскости, равноудаленная от сторон угла, лежит на биссектрисе этого угла.
Решение. Пусть точка М равноудалена от сторон угла АОВ (см. рис.3), т. е. перпендикуляры МС и MD к сторонам угла равны.
Рис.2
Тогда Δ ОМС = Δ OMD по теореме 2. Отсюда ∠ СОМ = ∠ DOM, и, следовательно, луч ОМ является биссектрисой угла АОВ.
Замечание. Предложения, установленные в примерах 1 и 2 выражают свойства биссектрисы угла. Из этих предложений следует, что биссектрисы треугольника пересекаются в одной точке.
Пример 3. Доказать, что в прямоугольном треугольнике с углом 30° катет, противолежащий этому углу, равен половине гипотенузы.
Решение. Пусть ABC — прямоугольный треугольник с прямым углом С и острым углом В, равным 30° (рис.3).
Рис.3
Отложим на продолжении стороны АС отрезок CD, равный АС.
Прямоугольные треугольники АСВ и DCB (углы при вершине С прямые) равны по двум катетам (сторона ВС общая, а АС = CD по построению).
Из равенства треугольников следует, что ∠ D = ∠ А = 60°, ∠ CBD = ∠ CBA = 30°, а значит, ∠ ABD= 60°. Отсюда следует, что треугольник ABD равносторонний. Поэтому АС = 1/2 * AD = 1/2 * АВ, что и требовалось доказать.
wiki.eduvdom.com
Признаки равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников
Прямоугольный треугольник
Прямоугольный треугольник
- Треугольник называется прямоугольным, если у него есть прямой угол.
- ABC – прямоугольный
C = 90°
A + B = 90°
Сумма острых углов прямоугольного треугольника равна 90 °.
- Сторона прямоугольного треугольника, противолежащая прямому углу называется гипотенузой.
- Две другие стороны называются катетами.
- по двум катетам
по двум сторонам и углу между ними
Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.
- по гипотенузе и
острому углу
по стороне и двум
прилежащим к ней углам
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
- по катету и прилежащему острому углу
по стороне и двум прилежащим к ней углам
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
- по катету и противолежащему острому углу
по стороне и двум прилежащим углам
Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и противолежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.
- по гипотенузе и катету
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
по двум катетам
по гипотенузе и катету
по гипотенузе и острому углу
по катету и
противолежащему
острому углу
по катету и
прилежащему
острому углу
Дано: B = D = 90°
BC || AD
Доказать: ABC = CDA .
1) Рассмотрим ABC и CDA
— треугольники прямоугольные по условию;
— AC — общая гипотенуза;
- BCA = CAD — т. к. они внутренние накрест лежащие
при параллельных прямых BC и AD и секущей AC .
по гипотенузе и острому углу
2) ABC = CDA
Из точки D , лежащей на биссектрисе A, опущены перпендикуляры DB и DC на стороны угла. Докажите, что A D B = AD C.
Дано: AD — биссектриса A
DB AB, DC AC.
Доказать: A D B = AD C.
1) Рассмотрим A D B и AD C.
— треугольники прямоугольные т. к. DB AB, DC AC .
— AD — общая гипотенуза.
— BAD = CAD т. к. AD — биссектриса A.
2) A D B = AD C по гипотенузе и острому углу .
Дано: C = D = 90°
AD = BC
Доказать: ABC = BAD .
- Рассмотрим ABC и BAD .
— треугольники прямоугольные т. к. C= D=90°.
— AD = BC
— AB — общая гипотенуза
2) ABC = BAD
по гипотенузе и катету
Дано: AB BC ; CD BC ;
O — середина AD ;
AB = 3 см.
Найти: CD .
1) Рассмотрим ABO и DCO.
• треугольники прямоугольные т. к. AB BC и CD BC .
• AO = OD т. к. O — середина AD.
• AOB = DOC как вертикальные.
2) ABO = DCO по гипотенузе и острому углу .
3) Из равенства треугольников следует AB = CD = 3 см.
CD = 3 см.
Домашнее задание.
Устно : формулировки признаков .
Письменно:
Дано: DA AB
FB AB
BD = AF
Доказать: ABD = BAF
№ 1.
№ 2. Докажите, что два равнобедренных прямоугольных треугольника равны, если равны их гипотенузы.
№ 3 Докажите равенство прямоугольных треугольников по катету и высоте, опущенной на гипотенузу.
Сколько существует внешних углов при одной вершине ?
1
3
2
4
B
30 º
70 º
?
D
A
C
70 º
30 º
100 º
80 º
B
?
100 º
D
A
C
50 º
80 º
40 º
20 º
B
40 º
D
A
C
?
K
70 º
40 º
140 º
130 º
Свойство катета, лежащего против угла в 30 .
BC = AB
Катет, лежащий против угла в 30 , равен половине гипотенузы.
Докажите, что в прямоугольном треугольнике с углом 30 ° катет, противолежащий этому углу, равен половине гипотенузы.
Дано: ABC
C = 90° , B = 30° .
Доказать: АС = АВ.
1) Построим DBC = ABC , как показано на рисунке.
2) ABC — равносторонний, так как все его углы равны
60 ° и AB = BD = AD .
3) AC = AD или AC = AB .
В равнобедренном треугольнике угол, противолежащий основанию, равен 120 °, а медиана, проведенная к основанию, равна 3 см. Найдите углы при основании и боковые стороны треугольника.
Дано: ABC — равнобедренный
с основанием AC ;
B =120° ;
BD — медиана; BD = 3 см.
Найти: A, C, AB и BC.
1) ABC — равнобедренный по условию .
BD — медиана, биссектриса и высота.
- ABC – равнобедренный
по условию .
BD — медиана, биссектриса и высота.
60 º
60 º
30 º
2) AB D = CB D = 120° : 2 = 60 ° т. к. BD — биссектриса .
3 ) AB D — прямоугольный т. к. ADB = 90°.
4 ) A + AB D = 90° как острые углы прямоугольного треугольника .
A = 90° — 60° = 30°.
5 ) BD = AB по свойству катета, лежащего против угла в 30°.
AB = 3 • 2 = 6 см. AB = BC = 6 см.
6) A = C = 30° как углы при основании равнобедренного
треугольника.
A = C = 30° ; AB = BC = 6 см.
по двум катетам
по гипотенузе и катету
по гипотенузе и острому углу
по катету и
противолежащему
острому углу
по катету и
прилежащему
острому углу
Докажите, что у равных треугольников высоты, проведенные из соответствующих вершин, равны.
Дано: ABC = A 1 B 1 C 1
BD AC, B 1 D 1 A 1 C 1
Доказать: BD = B 1 D 1 .
- Рассмотрим ABD и A 1 B 1 D 1 .
- треугольники прямоугольные т. к. BD AC и B 1 D 1 A 1 C 1 .
- AB = A 1 B 1 из равенства
- A = A 1 ABC = A 1 B 1 C 1
2) ABD = A 1 B 1 D 1 по гипотенузе и острому углу.
3) Из равенства треугольников следует BD = B 1 D 1 .
Докажите, что сумма трех внешних углов треугольника, взятых по одному при каждой вершине, равна 360 º .
Домашнее задание.
Устно : формулировки признаков и формулировка
задачи №43.
Письменно:
c
Дано: a | | b ; с – секущая; ∠ 3 больше суммы ∠ 1 + ∠ 2 в 4 раза.
Найти все образовавшиеся углы.
№ 1.
1
a
2
b
3
№ 2. Докажите, что равносторонние треугольники равны, если равны их высоты.
№ 3. Докажите равенство остроугольных треугольников по двум углам и высоте, проведенной из вершины третьего угла.
Свойство катета, лежащего против угла в 30 .
BC = AB
Катет, лежащий против угла в 30 , равен половине гипотенузы.
videouroki.net
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Типы треугольников
Рассмотрим три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки (рис. 1).
Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника, а концы отрезков (три точки, не лежащие на одной прямой) – вершинами треугольника.
Рис.1
В таблице 1 перечислены все возможные типы треугольников в зависимости от величины их углов.
Таблица 1 – Типы треугольников в зависимости от величины углов
| Рисунок | Тип треугольника | Определение |
 | Остроугольный треугольник | Треугольник, у которого все углы острые, называют остроугольным |
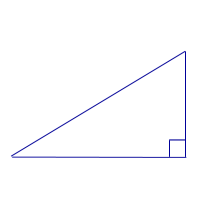 | Прямоугольный треугольник | Треугольник, у которого один из углов прямой, называют прямоугольным |
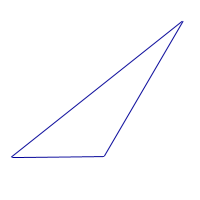 | Тупоугольный треугольник | Треугольник, у которого один из углов тупой, называют тупоугольным |
| Остроугольный треугольник |
Определение: Треугольник, у которого все углы острые, называют остроугольным |
| Прямоугольный треугольник |
Определение: Треугольник, у которого один из углов прямой, называют прямоугольным |
| Тупоугольный треугольник |
Определение: Треугольник, у которого один из углов тупой, называют тупоугольным |
В зависимости от длин сторон выделяют два важных типа треугольников.
Таблица 2 – Равнобедренный и равносторонний треугольники
| Рисунок | Тип треугольника | Определение |
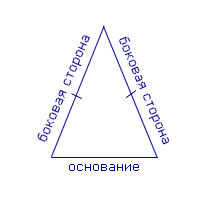 | Равнобедренный треугольник | Треугольник, у которого две стороны равны, называют равнобедренным треугольником. В этом случае две равные стороны называют боковыми сторонами, а третью сторону называют основанием равнобедренного треугольника |
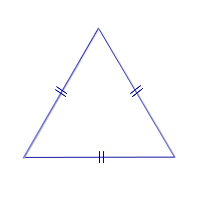 | Равносторонний (правильный) треугольник | Треугольник, у которого все три стороны равны, называют равносторонним или правильным треугольником |
| Равнобедренный треугольник |
Определение: Треугольник, у которого две стороны равны, называют равнобедренным треугольником. В этом случае две равные стороны называют боковыми сторонами, а третью сторону называют основанием равнобедренного треугольника |
| Равносторонний (правильный) треугольник |
Определение: Треугольник, у которого все три стороны равны, называют равносторонним или правильным треугольником |
Признаки равенства треугольников
Треугольники называют равными, если их можно совместить наложением.
В таблице 3 приведены признаки равенства треугольников.
Таблица 3 – Признаки равенства треугольников
| Рисунок | Название признака | Формулировка признака |
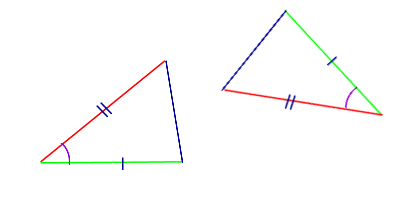 | Признак равенства треугольников по двум сторонам и углу между ними | Если две стороны одного треугольника и угол между ними соответственно равны двум сторонам другого треугольника и углу между ними, то такие треугольники равны |
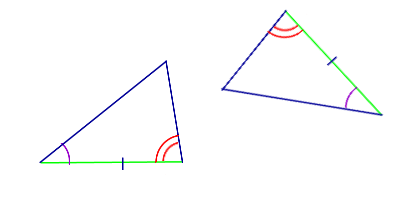 | Признак равенства треугольников по стороне и двум прилежащим к ней углам | Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны |
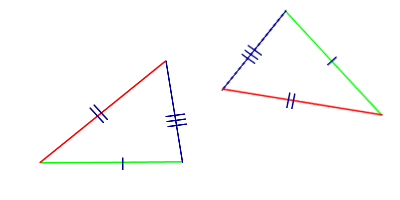 | Признак равенства треугольников по трём сторонам | Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны |
Признаки равенства прямоугольных треугольников
Для сторон прямоугольных треугольников принято использовать следующие названия.
Гипотенузой называют сторону прямоугольного треугольника, лежащую против прямого угла (рис. 2), две другие стороны называют катетами.
Рис.2
Таблица 4 – Признаки равенства прямоугольных треугольников
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
www.resolventa.ru