Сферические шары. Разница между шаром и сферой

Определение.

Сфера (поверхность шара ) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение.

Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).

Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение. Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).

Определение. Диаметр сферы (шара)

(D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.

Формула. Объём шара :

V =	4	π R 3 =	1	π D 3
	3		6

Формула. Площадь поверхности сферы через радиус или диаметр:

S = 4π R 2 = π D 2

Уравнение сферы

1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат :

x 2 + y 2 + z 2 = R 2

2. Уравнение сферы с радиусом R и центром в точке с координатами (x 0 , y 0 , z 0) в декартовой системе координат :

(x — x 0) 2 + (y — y 0) 2 + (z — z 0) 2 = R 2

Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.

Основные свойства сферы и шара

1. Все точки сферы одинаково удалены от центра.

2. Любое сечение сферы плоскостью является окружностью.

3. Любое сечение шара плоскостью есть кругом.

4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.

5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.

6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.

7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.

8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются , а в плоскости пересечения образуется круг.

Секущая, хорда, секущая плоскость сферы и их свойства

Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются

точками протыкания поверхности или точками входа и выхода на поверхности.

Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).

Определение. Секущая плоскость — это плоскость, которая пересекает сферу.

Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или ша

alluz.ru

Разница между Кругом и Сферой | Разница Между

Ключевое отличие: И круги, и сферы являются круглыми объектами. Круг — это двумерная фигура, а сфера — это трехмерная фигура.

Круг — это круглая плоская фигура, граница которой (окружность) состоит из точек, равноудаленных от неподвижной точки (центра). Круг существует в двухмерном и в плоскости. Это простая форма евклидовой геометрии, в которой набор всех точек на плоскости находится на фиксированном заданном расстоянии от заданной фиксированной точки, известной как центр. Круг — это простая замкнутая кривая, которая делит плоскость на две области: внутреннюю и внешнюю. Технически это называется диском. Это кривая, которая сохраняет фиксированное расстояние, когда она отслеживается центральной точкой. Его изучение и разработка применима в области математики, геометрии, астрономии и исчисления. Примеры реального мира — колеса, тарелка, поверхность монеты и т. Д.

Терминология круга включает в себя следующие определения:

• Центр: точка на равном расстоянии от точек на окружности.
• Радиус: отрезок, соединяющий центр круга с любой точкой на самом круге; или длина такого отрезка, равная половине диаметра.
• Диаметр: отрезок, конечные точки которого лежат на окружности и который проходит через центр; или длина такого отрезка, который является наибольшим расстоянием между любыми двумя точками на окружности. Это особый случай аккорда, а именно самого длинного аккорда, и он вдвое больше радиуса.
• Окружность: длина одного круга по кругу.
• Аккорд: отрезок, конечные точки которого лежат на окружности.
• Касательная: копланарная прямая, которая касается круга в одной точке.
• Дуга: любая связанная часть круга.

Сфера — это круглая сплошная фигура по своей поверхности, каждая точка которой находится на равном расстоянии от своего центра. Это трехмерная фигура, которая состоит из объема. Это напоминает форму шара. Это расстояние r является

ru.natapa.org

Сфера и шар

На этом уроке мы рассмотрим понятия сферы и шара. Дадим их определения. Назовем некоторые из элементов сферы и шара. А также узнаем, как находят объем шара и площадь сферы.

Итак, рассмотрим понятия сферы и шара. Нас окружают различные тела. Формы предметов окружающего мира очень разнообразны. Среди них встречаются так называемые «круглые тела». Особое место среди круглых тел занимает шар.

Итак, шар – это геометрическое тело. Форму, близкую к форме шара, имеют арбуз, апельсин, планеты. Некоторые архитектурные сооружения.

Декоративным растениям также придают форму шара.

Поверхность шара называют сферой. Можно сказать, что сфера – это как-бы оболочка или граница шара. Как окружность, есть граница круга, так и сфера – это граница шара. Представление о сфере дают полые круглые предметы, например, футбольный и теннисный мяч, мыльные пузыри или, ставший в наше время популярным видом отдыха, «аквазорбинг». Зорб дает представление о сфере.

Чтобы уяснить разницу между понятиями шар и сфера, давайте внимательно посмотрим на рисунок.

Перед вами изображены воздушный шар и бильярдный шар. Оба этих предмета называют шарами. Однако в первом случае мы имеем дело со сферой, а во втором с полноценным шаром со своим содержимым внутри.

Определение. Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.

Данная точка называется центром сферы, а данное расстояние – радиусом сферы.

Любой отрезок, соединяющий центр сферы с какой-либо ее точкой, также называется радиусом сферы.

Отрезок, соединяющий две точки сферы, называется хордой сферы.

Отрезок, соединяющий две точки сферы и проходящий через ее центр, называется диаметром сферы. Понятно, что .

Тело, ограниченное сферой, называется шаром.

Определение. Шар – это совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного.

Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара. Т.е. отрезок, соединяющий любую точку сферы с центром шара, называется радиусом шара.

Отрезок, соединяющий две точки сферы и проходящий через центр шара, называется диаметром шара. Диаметр шара равен двум радиусам.

Рассмотрим чертеж.

Перед нами математическое изображение шара. Точка О – это центр шара. Все точки поверхности шара одинаково удалены от центра шара. Понятно, что шар радиуса r с центром О содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем r (включая саму точку О), и не содержит других точек.

Хотелось бы обратить внимание на то, что шар может быть получен путем вращения полукруга вокруг его диаметра. При этом сфера образуется в результате вращения полуокружности.

Пользуясь принципом Кавальери, можно доказать, что .

В отличие от боковых поверхностей цилиндра и конуса сферу нельзя развернуть так, чтобы получилась плоская фигура.

Поэтому для сферы не подходит способ вычисления площади с помощью развертки.

Вопрос о том, что понимать под площадью сферы и как ее вычислять, мы будем подробно рассматривать в курсе стереометрии в одиннадцатом классе.

 

Сейчас только отметим, что для площади S сферы радиуса r получается формула: .

Если шар разрезать, то фигура, образованная на срезе, есть круг.

Сам же срез называют сечением. В свою очередь, сечение сферы плоскостью есть окружность.

Задача. Найдите объем шара и площадь сферы с радиусом

 метра. Число .

Решение:

 

 

  (м³)

 (м²)

Ответ: , .

Немного из истории. Оба слова «шар» и «сфера» происходят от греческого слова «сфайра» – мяч, шар.

В древности сфера и шар были в большом почете.

Пифагорейцы учили о существовании десяти сфер Вселенной, по которым якобы двигаются небесные тела. Они утверждали, что расстояние этих тел друг от друга пропорциональны интервалам музыкальной гаммы. В этом усматривали элементы мировой гармонии. Отсюда пошло выражение «музыка сферы».

Аристотель считал, что шарообразная форма, как наиболее совершенная, свойственна Солнцу, Земле, Луне и всем мировым телам. Так же он полагал, что Земля окружена рядом концентрических сфер.

Подведем итоги урока. На этом уроке мы рассмотрели понятия сферы и шара. Узнали, что сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. А шар – это совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного. Назвали некоторые из элементов сферы и шара. А также узнали, как находят объем шара и площадь сферы.

videouroki.net

формула, свойства, площадь поверхности нашей планеты

Сфера — это одно из первых тел, обладающих высокой симметрией, свойства которого изучают в школьном курсе геометрии. В данной статье рассматривается формула сферы, ее отличие от шара, а также приводится расчет площади поверхности нашей планеты.

Сфера: понятие в геометрии

Чтобы лучше понять формулу поверхности, которая будет дана ниже, необходимо познакомиться с понятием сферы. В геометрии она представляет собой трехмерное тело, которое заключает в себе некоторый объем пространства. Математическое определение сферы следующее: это совокупность точек, которые лежат на определенном одинаковом расстоянии от одной фиксированной точки, называемой центром. Отмеченное расстояние — это радиус сферы, который обозначается r или R и измеряется в метрах (километрах, сантиметрах и других единицах длины).

На рисунке ниже приведена описанная фигура. Линии показывают контуры ее поверхности. Черная точка — центр сферы.

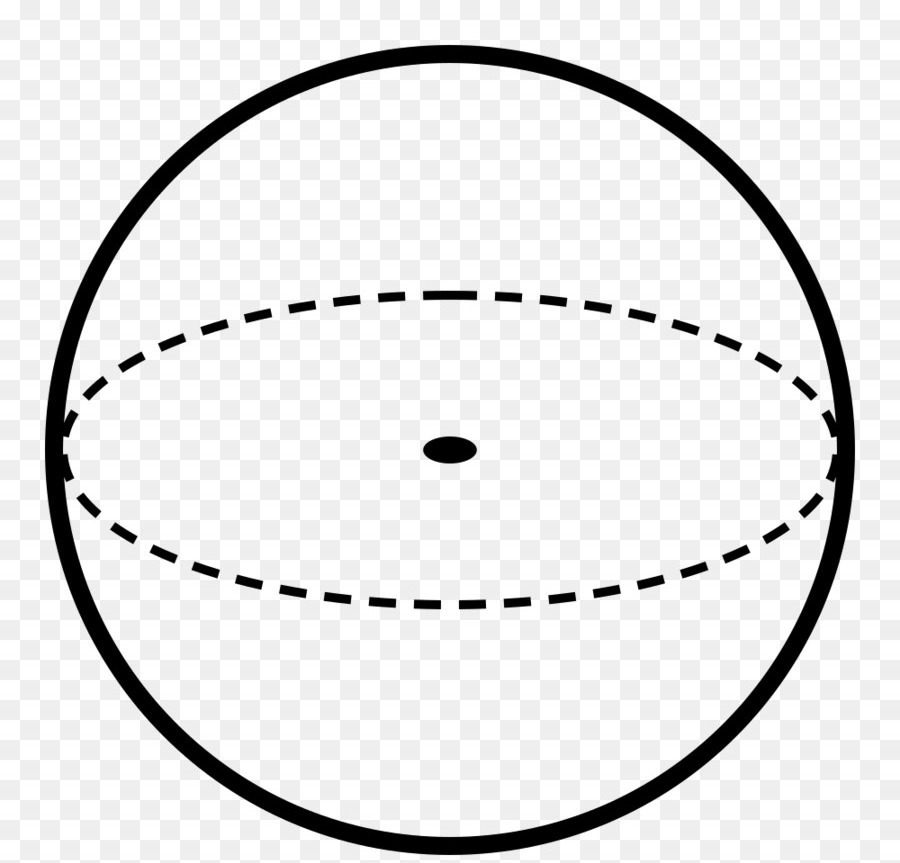
Получить эту фигуру можно, если взять окружность и начать ее вращать вокруг любой из осей, проходящей через диаметр.

Сфера и шар: в чем разница и в чем сходство?

Часто школьники путают эти две фигуры, которые внешне похожи друг на друга, но обладают совершенно разными физическими свойствами. Сфера и шар в первую очередь отличаются своей массой: сфера — это бесконечно тонкий слой, шар же — это объемное тело конечной плотности, которая одинакова во всех его точках, ограниченных сферической поверхностью. То есть шар обладает конечной массой и является вполне реальным объектом. Сфера — это фигура идеальная, не имеющая массы, которая в действительности не существует, но она является удачной идеализацией в геометрии при изучении ее свойств.

Примерами реальных объектов, форма которых практически соответствует сфере, являются новогодняя игрушка в виде шарика для украшения елки или мыльный пузырь.

Что касается сходства между рассматриваемыми фигурами, то можно назвать следующие их признаки:

• обе они обладают одинаковой симметрией;
• для обеих формула площади поверхности является одинаковой, более того, они обладают равной площадью поверхности, если их радиусы равны;
• обе фигуры при равных радиусах занимают одинаковый объем в пространстве, только шар его заполняет полностью, а сфера лишь ограничивает своей поверхностью.

Сфера и шар равного радиуса приведены на рисунке ниже.

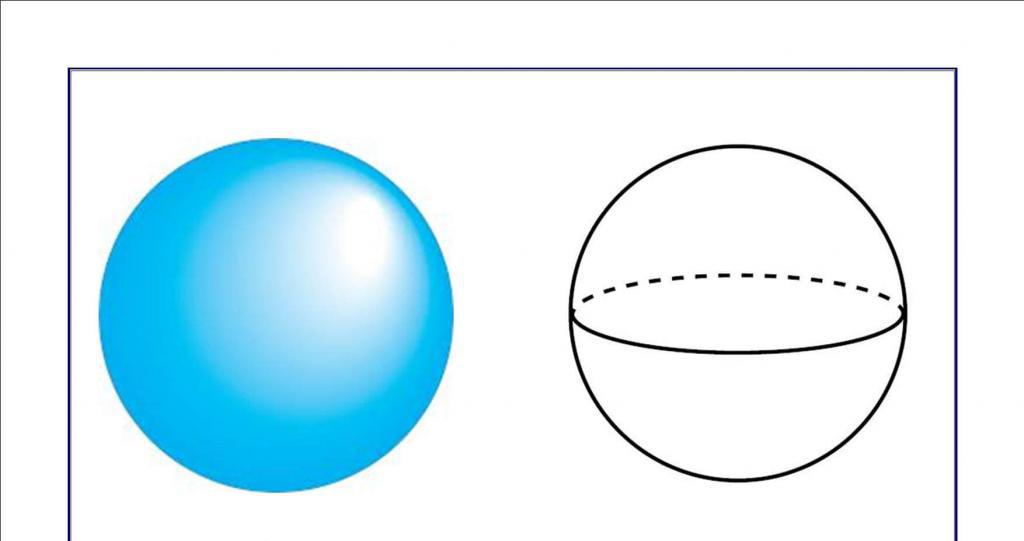
Заметим, что шар, так же как и сфера, является телом вращения, поэтому его можно получить, если вращать вокруг диаметра круг (не окружность!).

Элементы сферы

Так называются геометрические величины, знание которых позволяет описать либо всю фигуру, либо отдельные ее части. Основными ее элементами являются следующие:

• Радиус r, который уже был упомянут ранее. Он является расстоянием от центра фигуры до сферической поверхности. По сути, это единственная величина, которая описывает все свойства сферы.
• Диаметр d, или D. Это отрезок, концы которого лежат на сферической поверхности, а середина проходит через центральную точку фигуры. Диаметр сферы можно провести бесконечным числом способов, но все полученные отрезки будут иметь одинаковую длину, которая равна удвоенному радиусу, то есть D = 2*R.
• Площадь поверхности S — двумерная характеристика, формула для которой будет приведена ниже.
• Связанные со сферой трехмерные углы измеряются в стерадианах. Один стерадиан — это угол, вершина которого лежит в центре сферы, и который опирается на часть сферической поверхности, имеющей площадь R².

Геометрические свойства сферы

Из приведенного описания этой фигуры можно самостоятельно догадаться об этих свойствах. Они следующие:

• Любая прямая, которая пересекает сферу и проходит через ее центр, является осью симметрии фигуры. Поворот сферы вокруг этой оси на любой угол переводит ее в саму себя.
• Плоскость, которая пересекает рассматриваемую фигуру через ее центр, делит сферу на две равные части, то есть является плоскостью отражения.

Площадь поверхности фигуры

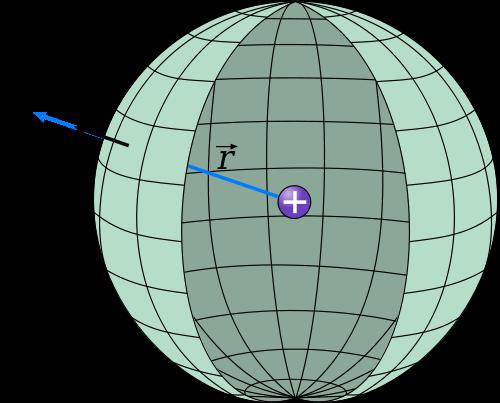
Эта величина обозначается латинской буквой S. Формула вычисления площади сферы имеет следующий вид:

S = 4*pi*R², где pi ≈ 3,1416.

Формула демонстрирует, что площадь S может быть вычислена при условии знания радиуса фигуры. Если же известен ее диаметр D, тогда формулу сферы можно записать так:

S = pi*D².

Иррациональное число pi, для которого приведены четыре знака после запятой, в ряде математических расчетов можно использовать с точностью до сотых, то есть 3,14.

Любопытно также рассмотреть вопрос, скольким стерадианам соответствует вся поверхность рассматриваемой фигуры. Исходя из определения этой величины, получаем:

Ω = S/R² = 4*pi*R²/R² = 4*pi стерадиан.

Для вычисления любого объемного угла следует в выражение выше подставить соответствующее значение площади S.

Поверхность планеты Земля

Формулу сферы можно применить для определения площади поверхности планеты, на которой мы живем. Перед тем как приступать к вычислениям, следует сделать пару оговорок:

• Во-первых, Земля не обладает идеальной сферической поверхностью. Ее экваториальный и полярный радиусы равны 6378 км и 6357 км соответственно. Отличие между этими цифрами не превышает 0,3%, поэтому для расчета можно взять средний радиус 6371 км.
• Во-вторых, рельеф поверхности Земли является трехмерным, то есть на ней имеются впадины и горы. Эти характерные особенности планеты приводят к увеличению ее площади поверхности, тем не менее, в расчете их учитывать не будем, поскольку даже самая большая гора, Эверест, составляет 0,1% от земного радиуса (8,848/6371).

Используя формулу сферы, получаем:

S = 4*pi*R² = 4*3,1416*6371² ≈ 510,066 млн. км².

Россия, по официальным данным, занимает площадь 17,125 млн км², что составляет 3,36% от поверхности планеты. Если же учесть, что к суше относятся лишь 150,387 млн км², тогда площадь нашей страны составит 11,4% от всей территории, не покрытой водой.

fb.ru

Шар и сфера, объем шара, площадь сферы, формулы

Шар и сфера — это прежде всего геометрические фигуры, и если шар — это геометрическое тело, то сфера — это поверхность шара. Этими фигурами интересовались еще многие тысячи лет назад до н.э.

Впоследствии когда было открыто, что Земля — это шар, а небо — небесная сфера, получило развитие новое увлекательное направление в геометрии — геометрия на сфере или сферическая геометрия. Для того, чтобы рассуждать о размере и объеме шара, нужно сначала дать ему определение.

Шар

Шаром радиуса R с центром в точке О в геометрии называют тело, которое создано всеми точками пространство, имеющими общее свойство. Эти точки находятся на расстоянии, не превышающем радиуса шара, то есть заполняют все пространство меньше радиуса шара во все стороны от его центра. Если мы рассмотрим только те точки, которые равноудалены от центра шара — мы будем рассматривать его поверхность или оболочку шара.

Как можно получить шар? Мы можем вырезать из бумаги круг и начать его вращать вокруг его же диаметра. То есть диаметр круга будет осью вращения. Образованная фигура — будет шар. Поэтому шар называют также телом вращения. Потому что он может быть образован путем вращения плоской фигуры — круга.

Возьмем какую-нибудь плоскость и разрежем ею наш шар. Подобно тому как мы режем ножом апельсин. Кусок, который мы отсечем от шара, называется шаровым сегментом.

В Древней Греции умели не только работать с шаром и сферой, как с геометрическими фигурами, например, использовать их при строительстве, а также умели расчитывать площадь поверхности шара и объем шара.

Сфера

Сферой иначе называется поверхность шара. Сфера — это не тело — это поверхность тела вращения. Однако так как и Земля и многие тела имеют сферическую форму, например капля воды, то изучение геометрических соотношений внутри сферы получило большое распространение.

Например, если мы соединим две точки сферы между собой прямой линией, то эта прямая линия назовется хордой, а если эта хорда пройдет через центр сферы, который совпадает с центром шара, то хорда назовется диаметром сферы.

Если мы проведем прямую линию, которая коснется сферы всего в одной точке, то эта линия будет называться касательной. Кроме того, эта касательная к сфере в этой точке будет перпендикулярна к радиусу сферы, проведенному в точку касания.

Если мы продолжим хорду до прямой в одну и другую сторону от сферы, то эта хорда станет называться секущей. Или можно сказать иначе — секущая к сфере содержит в себе ее хорду.

Объем шара

Формула для вычисления объема шара имеет вид:

V=4/3 πR³,

где R — радиус шара.

Если нужно найти объем шарового сегмента — воспользуйтесь формулой:

V _сег=πh²(R-h/3),  h — высота шарового сегмента.

Площадь поверхности шара или сферы

Чтобы вычислить площадь сферы или площадь поверхности шара (это одно и то же):

S=4πR,

где R — радиус сферы.

Архимед очень любил шар и сферу, он даже попросил оставить на его гробницу рисунок, на котором в цилиндр вписан шар. Архимед считал, что объем шара и его поверхность равны двум третьим от объема и поверхности цилиндра, в который вписан шар»

 

 

 

novstudent.ru

Сфера и шар. Уравнение сферы

На этом уроке мы вспомним понятия сферы и шара. Дадим их определения. Рассмотрим их основные элементы. А также выведем уравнение сферы радиуса  с центром в точке .

Итак, рассмотрим понятия сферы и шара. В окружающем мире предметы имеют очень разнообразные формы. Среди них встречаются так называемые «круглые тела». Особое место среди круглых тел занимает шар.

Итак, шар – это геометрическое тело.

Форму, близкую к форме шара, имеют шарики мороженного, снежный ком, бусинки, светильники.

Некоторые архитектурные сооружения.

Декоративным растениям также придают форму шара.

Поверхность шара называют сферой. Можно сказать, что сфера – это как-бы оболочка или граница шара. Как окружность, есть граница круга, так и сфера – это граница шара.

Представление о сфере дают полые круглые предметы, например, мячи (футбольный, баскетбольный, волейбольный и т.д.), шарики для украшения ёлки, мыльные пузыри.

А также ставший популярным видом отдыха в наше время «аквазорбинг». Зорб даёт представление о сфере.

Сфера входит в число наиболее привлекательных пространственных фигур. Использование в строительстве и архитектуре конструкций, имеющих форму сферы, придает сооружениям особое величие и служит подтверждением тому, что сфера – достаточно гармоничная геометрическая фигура.

Чтобы уяснить разницу между понятиями шар и сфера, давайте внимательно посмотрим на экран.

Перед вами изображены воздушный шар и бильярдный шар. Отметим, что оба этих предмета называют шарами. Однако в первом случае мы имеем дело со сферой, а во втором с полноценным шаром со своим содержимым внутри.

Определение:

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.

А теперь назовём основные элементы сферы.

Данная точка называется центром сферы (в нашем случае это точка О), а данное расстояние – радиусом сферы. Радиус сферы часто обозначают латинской буквой .

Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Все радиусы одной сферы равны между собой.

Хордой сферы называется отрезок, соединяющий две точки сферы.

Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы. Любой диаметр сферы равен двум радиусам .

Тело, ограниченное сферой, называется шаром.

Определение:

Шар – это совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного.

Центр, радиус, хорда и диаметр сферы называются также центром, радиусом, хордой и диаметром шара.

Т.е. отрезок, соединяющий любую точку сферы с центром шара, называется радиусом шара.

Отрезок, соединяющий две точки сферы называется хордой шара.

Отрезок, соединяющий две точки сферы и проходящий через центр шара, называется диаметром шара. Диаметр шара равен двум радиусам .

Рассмотрим чертёж.

Перед нами математическое изображение шара. Точка О – это центр шара. Все точки поверхности шара одинаково удалены от центра шара. Понятно, что шар радиуса  с центром О содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем  (включая саму точку О), и не содержит других точек.

Хотелось бы обратить внимание на то, что шар может быть получен путём вращения полукруга вокруг его диаметра.

При этом сфера образуется в результате вращения полуокружности вокруг её диаметра.

Задача: отрезок  – хорда сферы, не проходящая через центр сферы . Вычислите расстояние от центра сферы до середины хорды , если радиус сферы равен  см, а длина хорды  равна  см.

Решение: обозначим середину хорды  точкой .

Рассмотрим . Он равнобедренный, т.е. , так как . А как мы знаем, все радиусы одной сферы равны между собой. Отсюда,  (см).

Теперь рассмотрим . Он прямоугольный, так как отрезок  является серединным перпендикуляром проведённым к хорде . Его катет  (см).

Воспользовавшись теоремой Пифагора найдём катет , который как раз таки и есть расстояние от центра сферы до середины хорды . Получаем, что  (см).

Запишем ответ.

Перейдём к уравнению сферы.

Для начала вспомним, что уравнение с тремя переменными , ,  называется уравнением поверхности , если этому уравнению удовлетворяют координаты любой точки поверхности  и не удовлетворяют координаты никакой точки, не лежащей на этой поверхности.

Напомним, что уравнение плоскости, проходящей через точку  и перпендикулярной к ненулевому вектору  имеет следующий вид:

где

Теперь давайте выведем уравнение сферы радиуса  с центром в точке .

Напомним, что расстояние от произвольной точки  до точки  вычисляется по формуле:

Если точка  лежит на данной сфере, то расстояние , или , т.е. координаты точки  удовлетворяют уравнению:

Если же точка  не лежит на данной сфере, то расстояние , или , т.е. координаты точки  не удовлетворяют уравнению сферы.

Следовательно, в прямоугольной системе координат уравнение сферы радиуса  с центром в точке :

Если уравнение относительно прямоугольных координат  определяет поверхность в пространстве, то ею является сфера.

Задача: напишите уравнение сферы с центром в точке  радиусом равным  см.

Решение: запишем уравнение сферы в общем виде, где ,  и  – координаты центра сферы.

Подставим заданные координаты центра сферы в уравнение. Получим, что уравнение данной нам сферы выглядит так:

Запишем ответ.

Задача: найдите координаты центра и радиус сферы, заданной уравнением: .

Решение: запишем уравнение сферы в общем виде, где ,  и  – координаты центра сферы.

Тогда не трудно заметить, что координаты центра сферы будут равны 2, — 1, 0.

А радиус заданной сферы равен .

Не забудем записать ответ.

Задача: какую поверхность определяет уравнение

 ?

Решение: запишем уравнение сферы в общем виде, где ,  и  – координаты центра сферы.

Преобразуем наше уравнение.

Разделим почленно это уравнение на 4.

Получим, .

Затем выделим полные квадраты. Получим, .  

Преобразуем слагаемые получившегося выражения. Получим, .

Теперь сравним последнее уравнение с уравнением сферы в общем виде. Заметим, что исходное уравнение определяет сферу с центром в точке  и .

Запишем ответ.

Итоги:

На этом уроке мы вспомнили понятия сферы и шара. Узнали, что сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. А шар – это совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного. Назвали основные элементы сферы и шара. А также вывели уравнение сферы радиуса  с центром в точке .

videouroki.net

Методическая разработка (4 класс) на тему: Шар и Сфера

Слайд 1

Шар. Сфера.

Слайд 2

Цель занятия: Формирование ценностного отношения к совместной познавательной деятельности по изучению геометрических фигур: шара, сферы.

Слайд 4

Чем отличается шар от сферы?

Слайд 5

Сфера и шар

Слайд 6

ШАР-символ будущего

Слайд 7

Слово «сфера» , «шар» произошли от греческого слова « сфайра », которое переводится на русский язык как «мяч».

Слайд 8

Сказка о возникновении шара. Однажды , оставшись один дома, красавец Полукруг долго принаряживался и жеманился перед небольшим в оловянных рамках зеркалом и не мог налюбоваться собою. «Что людям вздумалось расславлять , будто я хорош?- говорил он. – Лгут люди , я совсем не хорош. Почему девушки провозгласили , что лучшего парня и не было еще никогда и не будет никогда на селе Хатанга?». Полукруг знал и слышал все, что про него говорили , и был капризным, как красавец . Он мог целый день любоваться собой перед зеркалом , рассматривая себя со всех сторон . И вдруг случилось чудо, когда Полукруг повернулся перед зеркалом вокруг себя, он увидел в зеркале собственное отражение в форме Шара.

Слайд 9

Найти сходство и различие Шаром принято называть тело, ограниченное сферой, т.е. шар и сфера – это разные геометрические тела Шар — это тело, состоящее из всех точек пространства, находящихся от данной точки на одинаковом расстоянии. Шар — это тело правильно геометрической формы, ограниченное поверхностью шара. Шар возможно получить, методом вращения полукруга. Сферой называется поверхность, состоящая из всех точек пространства, расположенных на определенном расстоянии от данной точки. Сфера является поверхностью (границей) шара с центром и радиусом

Слайд 10

Письмо от принцессы “- Ах, ужасно плохо я спала! — пишет принцесса — я всю ночь не сомкнула глаза. Бог знает, что там у меня было в постели! Я лежала на чём-то твердом и теперь у меня всё тело в синяках! Это просто ужас что такое!”. — Принцесса интересуется — на чём она спала?

Слайд 11

Письмо от барона “- Я стоял рядом с огромной пушкой, которая полила по турецкому городу, и когда из пушки вылетело ядро, вскочил на него и понёсся вперёд. Все в один голос воскликнули — Браво, браво барон!”. Барон интересуется, какой формы был этот предмет? — Какую форму имело ядро у барона?

Слайд 12

Письмо третье Просит старик: — испеки мне, старая, колобок. Я колобок, колобок! По амбару метён По сумкам скребён , На сметане сажён На окошке стужён Я от дедушки ушёл Я от бабушки ушёл.

Слайд 13

Сфера полая, в то время как шар является заполненным внутри телом. воздушный шар – это сфера бильярдный шар – это полноценный шар.

Слайд 14

Сказка про Сферу и Шар Поспорили однажды Сфера и Шар, кто из них важнее. — Я, — кричит Сфера, — важнее тебя! У меня даже в названии букв больше! — Нет, — сердится Шар, — я важнее, мое имя люди каждый день произносят! Разругались они и решили больше никогда не дружить друг с другом. Подслушал этот разговор злой волшебник, Антигеометрий , и решил уничтожить их, чтобы на Земле осталось поменьше геометрических фигур. Пока они спали, схватил их и бросил в вязкую тину, где обитали страшные крокозябры , поедатели фигур. Обрадовались крокозябры , плывут к нашим фигурам, чтобы сожрать. Бедная Сфера не может плыть, так как слишком легкая, ветер назад ее уносит. Тогда Шар, который был потяжелее, схватил Сферу и быстро вместе с ней покатил по волнам к берегу. Вытолкнул он ее на берег, а сам вылезти не может. А злые крокозябры уже вот-вот его схватят. Тут Сфера быстро взлетела, так как она была пустая внутри и очень легкая, подлетела к Шару, схватила его и вынесла по воздуху на берег. Так друзья поняли, что каждый из них очень важен в жизни. С тех пор они не спорят, а всегда помогают друг другу.

nsportal.ru