Члены геометрической прогрессии | Онлайн калькулятор

Члены геометрической прогрессии представляют собой числа, выстроенные строго по порядковым номерам, где непосредственно порядковый номер определяет значение члена последовательности. Первый член геометрической прогрессии может быть любым числом, кроме нуля (b≠0). Для того чтобы найти n член геометрической прогрессии необходимо первый член умножить на знаменатель прогрессии нужное количество раз.

Знаменателем прогрессии является заданное число, которое неизменно на протяжении всего числового ряда. Для того чтобы увидеть суть последовательности, рассмотрим числовой ряд, где выписаны b_n— это первые несколько членов прогрессии с порядковым номером n, а q — это знаменатель прогрессии.
b₁
b₂=b₁ q
b₃=b₂ q=b₁ qq=b₁ q^{2
b₄=b₃ q=b₁ q2 q=b₁ q3
…}

Отсюда наглядно видно, что знаменатель геометрической прогрессии собирается в степень, показателем которой является число на одну единицу меньше порядкового номера члена прогрессии, который нужно найти, и все члены зависят от первого. Общая формула членов геометрической прогрессии будет выглядеть так: b_n=b₁ q^(n-1)

Исходя из этого, зная первый член геометрической прогрессии, можно найти первые три, четыре члена прогрессии, умножая на знаменатель в нужной степени. Подобный онлайн калькулятор рассчитывает и в обратную сторону, то есть, зная любой из членов последовательности, можно найти первый. Чтобы проделать подобную операцию, калькулятор переворачивает формулу, в которой первый член геометрической прогрессии будет равен отношению заданного по условиям задачи члена к знаменателю, возведенному в степень n-1, где n — это порядковый номер известного члена.

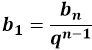
Другой способ найти первый член геометрической прогрессии заложен в определении суммы первых нескольких членов прогрессии. Сама сумма равна произведению первого члена прогрессии на разность знаменателя в степени порядкового номера последнего участвующего члена и единицы, затем полученный результат необходимо разделить на еще одну разность знаменателя, в этот раз без степени, и единицы: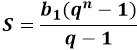

Порядок уменьшаемого и вычитаемого в скобках может меняться, это не будет влиять на результат до тех пор, пока это происходит синхронно:

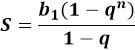
Тогда при перераспределении параметров в формуле выходит, что первый член прогрессии равен произведению суммы с разностью единицы и знаменателя, деленной на разность единицы и знаменателя в степени н: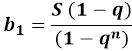

Арифметическая и геометрическая прогрессии. Решения

На Ваше рассмотрение представлены решения примеров повышенной сложности на арифметическую и геометрическую прогрессии. Методика вычислений является полезной для практических занятий как в школе, так и ВУЗах и соответствует школьной программе. Если приведенные примеры для Вас трудны прочтите для начала простые задачи на арифметическую и геометрическую прогрессию.

Пример 1. В геометрической прогрессии b₁₀* b₁₄* b₂₁=-0,125. Вычислить b₁₅.
Решение. Приведем методику которая упростит решение подобных примеров. Для начала найдем сумму индексов членов прогрессии.
10+14+21=45.
Сумма 45 нацело делится на 15 и получаем 3. Заданное произведение членов прогресии можно представить в виде
b₁₀* b₁₄* b₂₁=(b₁₅)^3
Это следует и со свойств геометрической прогреси.
Отсюда вычисляем искомый член прогрессии

Итак, 15 член прогрессии равен -0,5.

 

Пример 2. Сумма трех чисел, представляющих возрастающую арифметическую прогрессию равна 21. Если к ним, соответственно, добавить 2, 3, и 9 то образованные числа составят геометрическую прогрессию. Найти наибольшее из искомых членов проргресии.
Решение. Таким заданием можно проверить знание формул арифметической и геометрической прогрессии.
Обозначим члены возрастающей прогрессии через a-d, a, a+d.
Тогда их сумма равна 3a=21, откуда a=21/3=7.
Такое быстрое решение получили за счет удачного выбора формул членов прогресии. Таким образом средний член арифметической прогрессии известен.
Далее найдем неизвестные члены геометрической прогрессии
Первый – a-d+2=7-d+2=9-d
второй a+3=7+3=10.
третий a+d+9=7+d+9=16+d.
По свойству геометрической прогрессии о среднем геометрическом значении получим что квадрат среднего ее члена равен произведению равноудаленных, т.е.

Подставим члены геометрической прогрессии в формулу
(9-d)(16+d)=10^2=100.
Думаю Ви знаете что делать с подобным уравнением.
Раскроем скобки и сведем к квадратному уравнению относительно разницы арифметической прогрессии.


Находим дискриминант

и шаг арифметической прогрессии

Отсюда находим нужный член арифметической прогрессии
a+d=7+4=11.
Вот такие сложные задачи на прогрессию Вам могут встретиться в обучении.

 

Пример 3. Три числа которые составляют возрастающую арифметическую прогрессию дают в сумме 15. Если к первому и второму из них добавить по единице, а к третьему числу прибавить 4, то новые числа составят геометрическую прогрессию. Найти старшый член заданной прогресии.
Решение. Задача аналогична предыдущей. Вводим те же обозначения что и в предыдущем примере, тогда средний член арифметической прогрессии равен 15/3=5, а соседние – 5-d и 5+d.
По условию запишем члены геометрической прогрессии
(5-d+1)=6-d; 5+1=6; 5+d+4=9+d
и составим из них уравнение
(6-d)(9+d)=6*6=36.
Раскрываем скобки и сводим к квадратному уравнению


Вычисляем дискриминант

и разницу арифметической прогрессии
d=(-3+9)/2=3.
Больший из членов прогресии равен 8
a+d=5+3=8.

 

Пример 4. Три числа b₁, b₂, b₃ образуют возрастающую геометрическую прогрессию. Вычислить b₃ если b₁*b₂*b₃=64, b₁+b₂+b₃=14.
Решение. Опять имеем задание на составление уравнения. Обозначим члены геометрической прогрессии в нужном для нас виде
b/q;b;b*q.
Подставив в условие можно найти средний член геометрической прогрессии
b/q*b*b*q=b^3=64.
Отсюда средний член геометрической прогрессии равен корню кубическому из 64

С учетом найденного значения, запишем второе условие задания

b₁+b₂+b₃=14;

Умножым на знаменатель прогресии

и сведем к квадратному уравнению

Вычислим дискриминант уравнения

и знаменатель геометрической прогрессии

Второе значение отбрасываем, так как при нем геометрическая прогрессия становится убывающей, а по условию мы ищем возрастающую прогрессию.
Теперь без труда находим старший член геометрической прогрессии
b*q=4*2=8.

 

Пример 5. Три числа b₁, b₂, b₃ образуют убивающую геометрическую прогрессию. Вычислить b₃ если b₁*b₂*b₃=27, b₁+b₂+b₃= 13.
Решение. По свойству геометрической прогрессии имеем
b₂/q*b₂*b₂*q=2^3=27.
Отсюда второй член геометрической прогресии равен b[2]=3.
Из второго условия получим уравнение

Решение задач на геометрическую прогрессию

Этот калькулятор может решать два типа задач на геометрическую прогрессию:

1. Найти n-ный член геометрической прогрессии если известен m-ный член и знаменатель прогрессии. Пример задачи: Знаменатель прогрессии равна -1 и 1-ый член прогрессии равен 10. Найти 8-ой член прогрессии.

2. Найти n-ный член геометрической прогрессии если известны i-тый и j-тый члены. Пример задачи: 3-ий член геометрической прогрессии равен 1/2 и 5-ый член равен 8. Найти 8-ой член.

Формулы расчета приведены под калькулятором.

Решение задач на геометрическую прогрессию

Тип задачиНайти член прогрессии по другому члену и знаменателю прогрессииНайти член прогрессии по двум другим членам

Первый член прогрессии

 

Знаменатель прогрессии

 

Формула n-го члена прогрессии

 

Значение неизвестного члена

 

save Сохранить share Поделиться extension Виджет

Геометрическая прогрессия

Напомним, что геометрической прогрессией называется последовательность чисел, каждый член которой, начиная со второго, равен предыдущему члену умноженному на ненулевое, постоянное для этой последовательности число, называемое знаменателем прогрессии.

Таким образом, формула для n-ного члена прогрессии выглядит как

где r — знаменатель прогрессии.

Первый тип задач можно решить, вычислив сначала первый член прогресии

и применив затем общую формулу для n-ного члена

Для второго типа задач сначала надо найти знаменатель прогрессии. Для этого выведем формулу из деления одного известного члена на другой

После чего задача сводится к первому типу.

Для удобства калькулятор в любом случае рассчитывает и выводит первый член прогрессии, знаменатель прогрессии и общую формулу для n-ного члена.

геометрическая прогрессия | C++ для приматов

Задача взята с сайта e-olymp.

Задача

Как-то наконец земляне нашли обитаемую планету, назвали ее ТТВ, и отправили вместе с кораблем туда одного кролика. Кролику понравился климат новой планеты и через месяц он произвел на свет еще одного кролика. Известно, что каждый месяц каждый кролик, присутствующий на планете, производил на свет еще одного кролика. На планете откуда-то взялся монстр, который в начале месяца съедал [latex] k [/latex] кроликов, если только их становилось строго больше [latex] k [/latex]. В задаче необходимо определить количество кроликов, которое будет на планете через [latex] n [/latex]месяцев после прибытия туда космического корабля с первым кроликом.

Входные данные

Первая строка содержит количество месяцев [latex] n [/latex] [latex] (0 ≤ n ≤ 100) [/latex], вторая — число кроликов [latex] k [/latex] [latex]  (0 ≤ k ≤ 10000) [/latex], которое съедал монстр.

Выходные данные

Определить количество кроликов, которое будет находиться на планете ТТВ через [latex] n [/latex] месяцев после поселения туда первого кролика. Известно, что результат для любого теста всегда не больше [latex] 2 \cdot 10^9 [/latex].

Тесты

#	Входные данные	Выходные данные
1	0 10	1
2	1 10	2
3	10 7	128
4	7 128	12
5	30 0	1073741824
6	29 29	2
7	20 20	16
8	90 90	64

Cпособ 1 (с циклом)

Код

#include <iostream> using namespace std; int main() {     long int r = 1, n, k;     cin >> n >> k;     for (int i = n; i > 0; i—){         if (r > k) r -= k;         r *= 2;     }     cout << r;     return 0; }

 

Решение

Известно, что изначально на планете был один кролик. Создадим цикл, который будет высчитывать популяцию кроликов на планете через [latex] n [/latex] месяцев после прибытия. Цикл будет работать до тех пор, пока количество месяцев будет больше нуля. В нем будем высчитывать популяцию кроликов по простой формуле [latex] r = r \cdot 2 [/latex], где [latex] r [/latex] — количество кроликов. Если же количество кроликов, съедаемых монстром в начале месяца строго больше того количества, которое уже есть на планете, то от этой популяции отнимем [latex]  k [/latex]кроликов : [latex] r = r[/latex] $-$ [latex] k [/latex]. Внутри цикла также не забываем от данного количества [latex] n [/latex] месяцев отнимать по одному каждый раз.

Способ 2 (без цикла)

Код

#include <iostream> using namespace std;   int f2(long int r, long int n, long int k){     if (n == 0) return r;     if (r <= k) return f2(r * 2, n — 1, k);     return f2(2 * (r-k), n — 1, k); }     int main() {     long int n, k, r = 1;     cin >> n >> k;     cout << f2(r, n, k);     return 0; }

Решение

Сам алгоритм похож на 1 способ, однако здесь мы будем использовать рекурсивную функцию, а не цикл. Функция  int f2();  будет вызывать сама себя до тех пор, пока количество месяцев [latex] n [/latex] не станет равным нулю.

Ссылки

Засчитанное решение на e-olymp.

1 Код в ideone.

2 Код в ideone.

Прикладная математика. Одесский Национальный Университет имени И.И. Мечникова