Как решить логарифмическое уравнение: подробное объяснение

Как решить логарифмическое уравнение? Этим вопросом задаются многие школьники, особенно в преддверии сдачи ЕГЭ по математике. Ведь в задании С1 профильного ЕГЭ могут встретиться именно логарифмические уравнения.

Уравнение, в котором неизвестное находится внутри логарифмов, называется логарифмическим. Причем неизвестное может находится как в аргументе логарифма, так и в его основании.

Способов решения таких уравнений существует несколько. В этой статье мы разберем способ, который легко понять и запомнить.

1. Как решать уравнения с логарифмами: 2 способа с примерами
2. Пример решения логарифмического уравнения с разными основаниями
3. Пример решения логарифмического уравнения с переменными основаниями
4. Как сделать проверку – это важно

Как решать уравнения с логарифмами: 2 способа с примерами

Решить логарифмическое уравнение можно разными способами. Чаще всего в школе учат решать логарифмическое уравнение с помощью определения логарифма. То есть мы имеем уравнение вида:Вспоминаем определение логарифма и получаем следующее:Таким образом мы получаем простое уравнение, которое сможем легко решить.

При решении логарифмических уравнений важно помнить об области определения логарифма, т.к. аргумент f(x) должен быть больше ноля. Поэтому после решения логарифмического уравнения мы всегда делаем проверку!

Давайте посмотрим, как это работает на примере:

Воспользуемся определением логарифма и получим:

2х + 3 = 3²

Теперь перед нами простейшее уравнение, решить которое не составит труда:

2х + 3 = 9

2х = 6

х = 3

Сделаем проверку. Подставим найденный Х в исходное уравнение:Так как 3² = 9, то последнее выражение верно. Следовательно,  х = 3 является корнем уравнения.

Ответ: х = 3

Основной минус данного метода решения логарифмических уравнений в том, что многие ребята путают, что именно нужно возводить в степень. То есть при преобразовании log_af(x) = b, многие возводят не a в степень b, а наоборот b в степень a. Такая досадная ошибка может лишить вас драгоценных баллов на ЕГЭ.

Поэтому мы покажем еще один способ решения логарифмических уравнений.

Чтобы решить логарифмическое уравнение, нам нужно привести его к такому виду, когда и в правой, и в левой части уравнения будут стоять логарифмы с одинаковыми основаниями. Это выглядит вот так:

Когда уравнение приведено к такому виду, то мы можем «зачеркнуть» логарифмы и решить простое уравнение. Давайте разбираться на примере.

Решим еще раз то же самое уравнение, но теперь этим способом:В левой части у нас логарифм с основанием 2. Следовательно, правую часть логарифма нам нужно преобразовать так, чтобы она тоже содержала логарифм с основанием 2.

Для этого вспоминаем свойства логарифмов. Первое свойство, которое нам здесь понадобится – это логарифмическая единица. Напомним его:То есть в нашем случае:Возьмем правую часть нашего уравнения и начнем ее преобразовывать:Теперь нам нужно 2 тоже внести в логарифмическое выражение. Для этого вспоминаем еще одно свойство логарифма:

Воспользуемся этим свойством в нашем случае, получим:Мы преобразовали правую часть нашего уравнения в тот вид, который нам был нужен и получили:Теперь в левой и в правой частях уравнения у нас стоят логарифмы с одинаковыми основаниями, поэтому мы можем их зачеркнуть. В результате, получим такое уравнение:

2х + 3 = 3²

2х + 3 = 9

2х = 6

х = 3

Ответ: х = 3

Да, действий в этом способе больше, чем при решении с помощью определения логарифма. Но все действия логичны и последовательны, в результате чего шансов ошибиться меньше. К тому же данный способ дает больше возможностей для решения более сложных логарифмических уравнений.

Разберем другой пример:Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом:После преобразования правой части наше уравнение принимает следующий вид:Теперь можно зачеркнуть логарифмы и тогда получим:Вспоминаем свойства степеней:

3х – 5 = 4

3х = 9

х = 3

Теперь делаем проверку:то последнее выражение верно. Следовательно,  х = 3 является корнем уравнения.

Ответ: х = 3

Еще один пример решения логарифмического уравнения:Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим:Теперь преобразуем правую часть уравнения:Выполнив преобразования правой и левой частей уравнения, мы получили:Теперь мы можем зачеркнуть логарифмы:

Решим данное квадратное уравнение, найдем дискриминант:

Сделаем проверку, подставим х₁ = 1 в исходное уравнение:Верно, следовательно, х₁ = 1 является корнем уравнения.

Теперь подставим х₂ = -5 в исходное уравнение:Так как аргумент логарифма должен быть положительным, выражение не является верным. Следовательно, х₂ = -5 – посторонний корень.

Ответ: х = 1

Пример решения логарифмического уравнения с разными основаниями

Выше мы решали логарифмические уравнения, в которых участвовали логарифмы с одинаковыми основаниями. А что же делать, если основания у логарифмов разные? Например,

Правильно, нужно привести логарифмы в правой и левой части к одному основанию!

Итак, разберем наш пример:Преобразуем правую часть нашего уравнения:

Мы знаем, что 1/3 = 3^-1. Еще мы знаем свойство логарифма, а именно вынесение показателя степени из логарифма:Применяем эти знания и получаем:Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма:

Тогда получим:Вот теперь в правой и левой части уравнения у нас стоят логарифмы с одинаковыми основаниями и мы можем их зачеркнуть:Делаем проверку:Если мы преобразуем правую часть, воспользовавшись свойствами логарифма, то получим:Верно, следовательно, х = 4 является корнем уравнения.

Ответ: х = 4.

Пример решения логарифмического уравнения с переменными основаниями

Выше мы разобрали примеры решения логарифмических уравнений, основания которых были постоянными, т.е. определенным значением – 2, 3, ½ … Но в основании логарифма может содержаться Х, тогда такое основание будет называться переменным. Например, log_x+1(х²+5х-5) = 2. Мы видим, что основание логарифма в данном уравнении – х+1. Как же решать уравнение такого вида? Решать мы его будем по тому же принципу, что и предыдущие. Т.е. мы будем преобразовывать наше уравнение таким образом, чтобы слева и справа были логарифмы с одинаковым основанием.Преобразуем правую часть уравнения:Теперь логарифм в правой части уравнения имеет такое же основание, как и логарифм в левой части:Теперь мы можем зачеркнуть логарифмы:Но данное уравнение неравносильно исходному уравнению, так как не учтена область определения. Запишем все требования, относящиеся к логарифму:

1. Аргумент логарифма должен быть больше ноля, следовательно:

2. Основание логарифма должно быть больше 0 и не должно равняться единице, следовательно:

Сведем все требования в систему:

Данную систему требований мы можем упростить. Смотрите х²+5х-5 больше ноля, при этом оно приравнивается к (х + 1)², которую в свою очередь так же больше ноля. Следовательно, требование х²+5х-5 > 0 выполняется автоматически и мы можем его не решать. Тогда наша система будет сведена к следующему:Перепишем нашу систему:Следовательно, наша система примет следующий вид:Теперь решаем наше уравнение:Справа у нас квадрат суммы:Данный корень удовлетворяет наши требования, так как 2 больше -1 и не равно 0. Следовательно, х = 2 – корень нашего уравнения.

Для полной уверенности можем выполнить проверку, подставим х = 2 в исходное уравнение:

Т.к. 3²=9, то  последнее выражение верно.

Ответ: х = 2

Как сделать проверку

Еще раз обращаем ваше внимание, что при решении логарифмических уравнений необходимо учитывать область допустимых значений. Так, основание логарифма должно быть больше ноля и не должно равняться единице. А его аргумент должен быть положительным, т.е. больше ноля.

Если наше уравнение имеет вид log_a (f(x)) = log_a (g(x)), то должны выполняться следующие ограничения:

После решения логарифмического уравнения нужно обязательно сделать проверку. Для этого вам необходимо подставить получившееся значения в исходное уравнение и посчитать его. Времени это займет немного, зато позволит не записать в ответ посторонние корни. Ведь так обидно правильно решить уравнение и при этом неправильно записать ответ!

Итак, теперь вы знаете, как решить логарифмическое уравнение с помощью определения логарифма и с помощью преобразования уравнения, когда в обеих его частях стоят логарифмы с одинаковыми основаниями, которые мы можем «зачеркнуть». Отличное знание свойств логарифма, учет области определения, выполнение проверки – залог успеха при решении логарифмических уравнений.

Логарифмические уравнения. Способы решения и примеры

С уравнениями мы все знакомы с начальных классов. Еще там мы учились решать самые простые примеры, и надо признать, что они находят свое применение даже в высшей математике. С уравнениями все просто, в том числи и с квадратными. Если у вас проблемы с этой темой, настоятельно рекомендуем вам повторить ее.

Логарифмы вы, вероятно, тоже уже прошли. Тем не менее, считаем важным рассказать, что это для тех, кто еще не знает. Логарифм приравнивается к степени, в которую нужно возвести основание, чтобы получилось число, стоящее справа от знака логарифма. Приведем пример, исходя из которого, вам все станет ясно.

Если вы возведете 3 в четвертую степень получится 81. Теперь подставьте по аналогии числа, и поймете окончательно, как решаются логарифмы. Теперь осталось лишь совместить два рассмотренных понятия. Изначально ситуация кажется чрезвычайно сложной, но при ближайшем рассмотрении весе становится на свои места. Мы уверены, что после этой короткой статьи у вас не будет проблем в этой части ЕГЭ.

Как правильно решать?

Сегодня выделяют множество способов решения подобных конструкций. Мы расскажем о самых простых, эффективных и наиболее применимых в случае заданий ЕГЭ. Решение логарифмических уравнений должно начинаться с самого простого примера. Простейшие логарифмические уравнения состоят из функции и одной переменной в ней.

Важно учесть, что x находится внутри аргумента. A и b должны быть числами. В таком случае вы можете попросту выразить функцию через число в степени. Выглядит это следующим образом.

Разумеется, решение логарифмического уравнения таким методом приведет вас к верному ответу. Ног проблема подавляющего большинства учеников в этом случае заключается в том, что они не понимают, что и откуда берется. В результате приходится мириться с ошибками и не получать желаемых баллов. Самой обидной ошибкой будет, если вы перепутаете буквы местами. Чтобы решить уравнение этим способом, нужно зазубрить эту стандартную школьную формулу, потому что понять ее сложно.

Чтобы было проще, можно прибегнуть к другому способу – канонической форме. Идея крайне проста. Снова обратите внимание на задачу. Помните, что буква a – число, а не функция или переменная. A не равно одному и больше нуля. На b никаких ограничений не действует. Теперь из всех формул вспоминаем одну. B можно выразить следующим образом.

Из этого следует, что все исходные уравнения с логарифмами можно представить в виде:

Теперь мы можем отбросить логарифмы. Получится простая конструкция, которую мы уже видели ранее.

Удобство данной формулы заключается в том, что ее можно применять в самых разных случаях, а не только для самых простых конструкций.

Не переживайте насчет ООФ!

Многие опытные математики заметят, что мы не уделили внимание области определения. Сводится правило к тому, что F(x) обязательно больше 0. Нет, мы не упустили этот момент. Сейчас мы говорим об еще одном серьезном преимуществе канонической формы.

Лишних корней здесь не возникнет. Если переменная будет встречаться лишь в одном месте, то область определения не является необходимостью. Она выполняется автоматически. Чтобы убедиться в данном суждении, займитесь решением нескольких простых примеров.

Как решать логарифмические уравнения с разными основаниями

Это уже сложные логарифмические уравнения, и подход к их решению должен быть особым. Здесь редко получается ограничиться пресловутой канонической формой. Начнем наш подробный рассказ. Мы имеем следующую конструкцию.

Обратите внимание на дробь. В ней находится логарифм. Если вы увидите такое в задании, стоит вспомнить один интересный прием.

Что это значит? Каждый логарифм можно представить в виде частного двух логарифмов с удобным основанием. И у данной формулы есть частный случай, который применим с этим примером (имеем ввиду, если c=b).

Именно такую дробь мы и видим в нашем примере. Таким образом.

По сути, перевернули дробь и получили более удобное выражение. Запомните этот алгоритм!

Теперь нужно, что логарифмическое уравнение не содержало разных оснований. Представим основание дробью.

В математике есть правило, исходя из которого, можно вынести степень из основания. Получается следующая конструкция.

Казалось бы, что мешает теперь превратить наше выражение в каноническую форму и элементарно решить ее? Не все так просто. Дробей перед логарифмом быть не должно. Исправляем эту ситуацию! Дробь разрешается выносить в качестве степени.

Соответственно.

Если основания одинаковые, мы можем убрать логарифмы и приравнять сами выражения. Так ситуация станет в разы проще, чем была. Останется элементарное уравнение, которое каждый из нас умел решать еще в 8 или даже в 7 классе. Расчеты вы сможете произвести сами.

Мы получили единственно верный корень этого логарифмического уравнения. Примеры решения логарифмического уравнения достаточно просты, не так ли? Теперь и у вас получится самостоятельно разобраться даже с самыми сложными задачами для подготовки и сдачи ЕГЭ.

Что в итоге?

В случае с любыми логарифмическими уравнениями мы исходим из одного очень важного правила. Необходимо действовать так, чтобы привести выражение к максимально простому виду. В таком случае у вас будет больше шансов не просто решить задание правильно, но еще и сделать это максимально простым и логичным путем. Именно так всегда действуют математики.

Настоятельно не рекомендуем вам искать сложных путей, особенно в этом случае. Запомните несколько простых правил, которые позволят преобразовать любое выражение. К примеру, привести два или три логарифма к одному основанию или вывести степень из основания и выиграть на этом.

Также стоит помнить о том, что в решении логарифмических уравнений необходимо постоянно тренироваться. Постепенно вы будете переходить ко все более сложным конструкциям, а это приведет вас к уверенному решению всех вариантов задач на ЕГЭ. Готовьтесь к экзаменам заблаговременно, и удачи вам!

Похожие статьи

Рекомендуем почитать:

Методическая разработка «Методы решение логарифмических уравнений»

Процесс решения любого логарифмического уравнения заключается в переходе от уравнения с логарифмами к уравнению без них

И это решение состоит из двух равноценных частей:

1) нахождение области допустимых значений (ОДЗ),

2) решение самого уравнения.

Эти части решаются независимо друг от друга. Главное — в самом конце не забыть результаты сопоставить, лишнее выбросить.

ОДЗ — это те значения х, которые  разрешены для исходного примера. А как искать ОДЗ? Внимательно осматриваем пример и ищем опасные места. Места, в которых возможны запретные действия. Таких запретных действий в математике очень мало. ( Нельзя делить на ноль, в корнях чётной степени подкоренное выражение должно быть неотрицательным, выражение стоящее под логарифмом должно быть неотрицательным и основание логарифма а >0 и а ≠1.)

Простейшие логарифмические уравнения

Умение решать простейшие логарифмические уравнения — это очень важно. Дело в том, что даже самые злые и замороченные уравнения обязательно сводятся к простейшим! Собственно, простейшие уравнения — это финишная часть решения любых уравнений.

Уравнения вида log_а f(х) = log_а g(х)

Простейшее уравнение log_а f(х) = log_а g(х) решается методом потенцирования. Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их:
log_а f(х) = log_а g(х) f(х) = g(х), при f(х)>0, g(х)>0 , а > 0, а≠ 1. т.е. если равны логарифмы по одному и тому же основанию, то и равны логарифмируемые выражения. В виде равносильного перехода:

Ликвидировать логарифмы безо всяких опасений можно, если у них:

а) одинаковые числовые основания

в) логарифмы слева-справа чистые (безо всяких коэффициентов) и находятся в гордом одиночестве

-В уравнении log₃х = 2log₃(3х-1) убирать логарифмы нельзя. Двойка справа не позволяет

. Коэффициент.

— В примере log₃х+log₃(х+1) = log₃(3+х) тоже нельзя потенцировать уравнение. В левой части нет одинокого логарифма. Их там два.

Короче, убирать логарифмы можно, если уравнение выглядит так и только так: log_а(…..) = log_а(…..)

В скобках, где многоточие, могут быть какие угодно выражения. Простые, суперсложные, всякие. Какие угодно. Важно то, что после ликвидации логарифмов у нас остаётся более простое уравнение

Пример 1. Решите уравнение:   

Решение: способ 1. В область допустимых значений (ОДЗ) входят только те x, при которых выражение, находящееся под знаком логарифма, больше нуля. Эти значения определяются следующей системой неравенств:

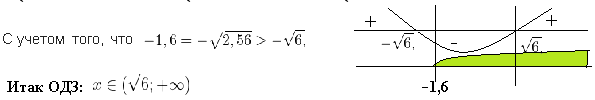
Видим логарифмы по одному и тому же основанию равны, значит, равны и логарифмируемые выражения. 

     

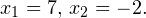
В область допустимых значений входит только первый корень. Ответ:  7. ОДЗ можно было не решать, а просто записать. В конце каждый корень подставить в ОДЗ. Если с каждым неравенством ОДЗ получится верное числовое неравенство, то он идет в Решение: способ 2. Если это уравнение решим путем равносильных переходов, то ОДЗ нашли бы без всяких квадратных неравенств и пересечений. Итак

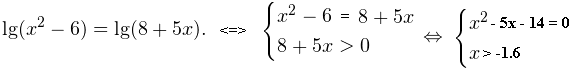Уравнение х² — 5х – 14 = 0 имеет корни х₁ = 7, х₂ = -2. В область допустимых значений входит только первый корень. Ответ: x = 7.

Пример 2. Решите уравнение

Решение. Решим методом равносильных переходов. Тогда уравнение равносильно системе

Корни уравнения -2 и 5. Только -2 ϵ ОДЗ. Ответ: -2

Итак уравнения такого вида решили 2-мя способами: 1)отдельно найдя ОДЗ и отдельно решив само уравнение; 2)используя равносильные переходы. Какой способ вам по душе?

Уравнения вида log_a f (x) = b

Уравнение log_a f (x) = b — простейшее логарифмическое уравнение, где а и b — числа; а >0, a≠1. Переменная х присутствует только внутри аргумента.

Способы решения :

1) Применение определения логарифма

2)Представление числа в виде логарифма: b = log_a a^b

1. Решение уравнений применением определения логарифма

Решение уравнения
основано на применении определения логарифма и в решении равносильного уравнения

Для уравнений log_a f (x) = b записывать область определения не нужно (f (x) >0), потому что она будет выполняться автоматически. Так как в какую бы степень мы бы не возводили положительное число а, на выходе мы все равно получим положительное число, т.е. если а > 0, то a^b > 0 всегда => f (x) = a^b > 0.

Пример 1. Решите уравнение log₅(x – 2) = 1

Решение: Переменная х встречается лишь в одном log и стоит в его аргументе, значит находить ОДЗ не надо. log₅(x – 2) = 1  x – 2 = 5¹  x – 2 = 5  x = 7. Ответ: 7.

Пример 2. Решите уравнение

Решение: Три раза выполним переход: log_a f(x) = b f(x) = a^b

   x = 8.

Ответ: 8

2). Решение простейшего логарифмического уравнения log_a f (x) = b представлением числа в виде логарифма b = log_aa^b (методом потенцирования).

(log_a f (x) = b  log_a f (x) = log_aa^b  f (x) = a^b)

Пример 3. Решите уравнение:

Решение: Это простейшее логарифмическое уравнение, поэтому нет необходимости найти ОДЗ, потому что 3х – 1>0 будет выполняться автоматически. Слева у нас стоит выражение с логарифмом, а справа – число. Что делать? Нужно сделать так, чтобы справа тоже было выражение с логарифмом по основанию 0,5 а затем просто сбросить логарифмы. Так как −3 = −3*1 = -3*log_0,5 0,5=log_0,5 0,5⁻³ тогда уравнение примет вид: log_0,5 (3x − 1) = log_0,5 0,5⁻³

3x − 1 = 0,5⁻³

Все десятичные дроби переводите в обычные, когда вы решаете логарифмическое уравнение.

Заметим что 0,5^-3 = (1/2) ⁻³ = (2^-1)^-3 = 2³ = 8 и получим

3x − 1 = 8
3x = 9
x = 3 Ответ: 3.

Пример 4. Решите уравнение

Решение: Это простое логарифмическое уравнение, поэтому можно не найти ОДЗ. Первый шаг- дробь справа представим в виде логарифма. Получим:

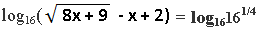Учитывая, что 16^1/4 = (2⁴)^1/4 = 2

избавляемся от знака логарифма и получаем обычное иррациональное уравнение: где надо будет учесть ОДЗ.

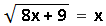, решим равносильным переходом к системе:

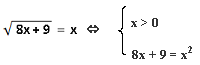
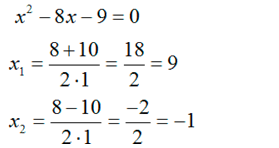
Из полученных корней нас устраивает только первый, так как второй корень меньше нуля. Единственным ответом будет число 9. Ответ: 9.

Уравнения, решаемые применением свойств логарифмов

Схема решения не простых логарифмических уравнений

1. Привести уравнение с помощью свойств логарифмов к виду:

log _а f(x) = b или log_а f(x) = log_а g(x).

2. Решить равносильное уравнение

f(x) = a ^b или f(x) = g(x) по их алгоритму.

Пример 1. Решите уравнение

Если lg(x – 1) переведем в правую часть уравнения, то получим уравнение вида log_а f(х) = log_а g(х).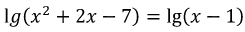

Если неравенства неудобные, ОДЗ можно не решать. Достаточно подставить результаты уравнения в записанные условия ОДЗ и проверить, какие решения проходят. Их и взять за ответы

Пример 2. Решите уравнение

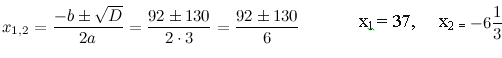
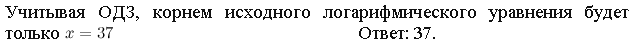
Если в уравнении содержатся логарифмы с разными основаниями, то, прежде всего, следует свести все логарифмы к одному основанию, используя формулы перехода 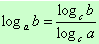, и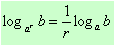

Пример 3. Решите уравнение

Решение. ОДЗ: х > 0. Сразу видно, что у логарифмов основания разные. Используя формулу придем к одинаковому основанию

x = 8

Уравнения, решаемые введением новой переменной

Если, в уравнение неоднократно, встречается некоторое определенное выражение, то оно решается введением новой переменной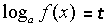

Пример 1. Решите уравнение

ОДЗ: x > 0. Введем новую переменную тогда получим квадратное уравнение:

y² – y = 2,

y² – y – 2 = 0,

y₁ = 2 или y₂ = -1

или

x = 25 или x = 5^-1

x =

Ответ: 25;

Пример 2. Решите уравнение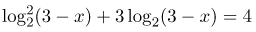

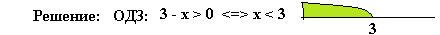
Оба корня удовлетворяют ОДЗ нашего уравнения.

Пример 3. Решите уравнение 4 log₂₅5x + log²₅x – 5 = 0; ОДЗ: x > 0.

Тут 2 основания, выполним переход к основанию 5, используя формулу

2 log₅5x + log²₅x – 5 = 0; Применим формулу log_axy = log_ax + log_ay

2(log₅5 + log₅x) + log²₅x – 5 = 0.

2(1 + log₅x) + log²₅x – 5 = 0.

Пусть log₅x = t, тогда 2(1 + t) + t² – 5 = 0;

t² + 2t – 3 = 0;

(t + 3)(t – 1) = 0;

t = – 3 или t = 1; Обратно переходим на обозначение log₅x = t:

log₅x = – 3, log₅x = 1;

x = 5^-3, x = 5;

x = 1/125. Оба корня удовлетворяют ОДЗ. Ответ:

Пример 4. Решите уравнение Решение: Область допустимых значений:

Решать систему необходимости нет. Пусть log₂(5x – 1) = t, тогда

Уравнения, содержащие неизвестное и в основании и в аргументе.

Уравнения вида log _f(x)g(x) = b

Уравнение log _f(x)g(x) = b похоже простейшему уравнению log_a f (x) = b Сходство: в обеих уравнениях в левой части log, в правой число b. Отличие в том, что в первой переменная х присутствует не только внутри аргумента, но и в основании логарифма.

Но мы должны учесть определенные требования. 1) аргумент каждого из логарифмов должен быть больше 0: 2) основание должно быть не только больше 0, но и отлично от 1

Способы решения :

1) Применение определения логарифма

2)Представление числа в виде логарифма

Пример 1. Решить уравнение: log _{x – 1}(x² – 5x + 10) = 2. 

Решение: ОДЗ: x² – 5x + 10 > 0, x – 1 > 0, x – 1 ≠ 1.

По определению логарифма х² – 5х + 10 = (х — 1)² х² – 5х + 10 =:х² – 2х + 1, -3х = -9 х = 3

Проверим  принадлежность х = 3 ОДЗ: 3² – 5*3 + 10 > 0 верно, 3 – 1 > 0 верно 3 – 1 ≠ 1 верно

Ответ: 3.

Пример 2. Решите уравнение log _х+1(2x²+1)=2 Решение: Решим методом равносильных переходов. Заменяем 2 на так как 2=2*1=2* log _{х + 1}(х+1)= log _{х + 1}(х+1)² тогда получим: log _х+1(2x²+1)= log _х+1(x+1)²

Наше уравнение содержит неизвестное и в основании и в аргументе. Поэтому 1) аргумент каждого из логарифмов должен быть больше 0. 2) основание должно быть не только больше 0, но и ≠ 1. В итоге получим систему:

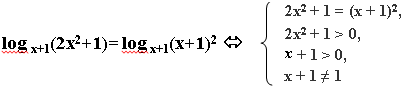
Решим уравнение 2х²+1=(х+1)², 2х² + 1 = х² + 2х + 1 х² — 2x = 0  x(x — 2) = 0  x=2 или x=0. х=0 не соответствует системе. Ответ: 2.

Способ 2. ОДЗ: по определению логарифма получим: 2х²+1 = (х+1)², 2х²+1 = х² + 2х + 1, х² – 2х = 0  x(x – 2) = 0  x = 0, x = 2. Корень х = 0 не удовлетворяет третьему неравенству ОДЗ.

Ответ: 2

Уравнения вида log _h(x)f(x) = log _h(x)g(x)

Пример 1. Решите уравнение log _3x(x² – 5x) = log _3x(4x – 8)

Показательно – логарифмические уравнения

 
При решении уравнений, содержащих переменную и в основании, и в показателе степени, используется метод логарифмирования. Если при этом в показателе степени содержится логарифм, то обе части уравнения надо прологарифмировать по основанию этого логарифма.

Пример 1. Решить уравнение: х^{1 – lgx} = 0.01. Решение: ОДЗ: x > 0, x ≠ 1. Прологарифмировав обе части уравнения по основанию 10, получим уравнение:

(1 – lg x)*lg x = -2

Положив t = lg x, придем к уравнению t² – t – 2 = 0, откуда t₁ = -1, t₂ = 2. Таким образом, задача свелась к решению следующей совокупности уравнений:

Оба найденных значения входят в ОДЗ. Ответ: 0,1; 100

Пример 2. Решить уравнение 3^2log4 ^x+2=16x².

Решение. Область определения x >0. Прологарифмируем обе части по основанию 4.

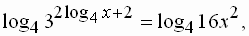
Используя свойства логарифмов, получим

Ответ: x = 1/4

Функционально – графический метод.

Пример 1. Решите уравнение log₂x = 3 – x

В одной и той же системе координат строим графики функции у= log₂x и у = 3 – x

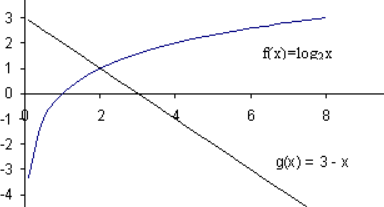Ответ: 2.

Обычно графически метод применяется, если трудно найти других методов. Графически метод менее точный. Целесообразно его использовать, если стоит вопрос «Сколько корней имеет уравнение».

Метод использования монотонности функции

Есть способ, позволяющий не строить графики. Он заключается в следующем: если одна из функции y = f(x) возрастает, а другая y = g(x) убывает на промежутке Х, то уравнение f(x) = g(x) имеет не более одного корня на промежутке Х.

Если корень имеется, то его можно угадать.

Пример 1. Решить уравнение: log₃ x = 4- x Решение: ОДЗ х > 0. Так как функция у= log₃ х возрастающая, а функция у = 4-х убывающая на (0; + ∞ ), то заданное уравнение на этом интервале имеет один корень. Подбором определяем х = 3. Ответ: 3.

Пример 2. Решите уравнение : log₃(x + 1) + log₄(5x + 6) = 3. ОДЗ: х > -1

Решение: у = log₃(x + 1) – возрастающая функция, y = log₃(x + 1) – тоже возрастающая. Сумма двух возрастающих функции дает возрастающую функцию. В правой части постоянная функция у = 3. Значит уравнение имеет не более одного корня. Подбором определяем х = 2. Ответ: 2.

Урок математики на тему «Методы решения логарифмических уравнений»

Цель урока: выработка умений самостоятельного применения знаний в стандартных и нестандартных ситуациях.

Задачи урока распределяются по 3 уровням:

• 1 уровень – уметь решать простейшие логарифмические уравнения, применяя определение логарифма, свойства логарифмов;
• 2 уровень – уметь решать логарифмические уравнения, выбирая самостоятельно способ решения;
• 3 уровень – уметь применять знания и умения в нестандартных ситуациях.

Тип урока: комплексное применение знаний.

Ход урока

Организационный момент

Сообщение учителем темы, целей и задач урока, его основных моментов.

Актуализация комплекса знаний

Фронтальный опрос класса:

• Что понимают под логарифмическим уравнением?
• Что называют корнем уравнения?
• Что значит “решить уравнение”?
• Какие уравнения называются равносильными?
• На доске записаны формулы. Какие из них неверные?

Диктант (с последующей взаимопроверкой)

Возможные ответы: “да” — , “нет” —

Результаты диктанта анализируются, оцениваются и выставляются в оценочный лист.

Определяется готовность учащихся к комплексному применению знаний.

Рассматриваются методы решения логарифмических уравнений

Преобразование логарифмических уравнений.

При решении уравнений, содержащих логарифмические функции, иногда применяют различные преобразования, сводящие заданное уравнение к простейшему виду. При этом важно, чтобы ОДЗ не менялась.

Пример 1. Решите уравнение 2 + 6 log₈ x = log₂ (6x + 18).

Решение. Данное уравнение равносильно:

1. log₂ 4 + 2 log₂. x = log₂ (6 + 18) o
2. log₂4x²= Iog₂(6x + 18), o 14x² — 6x + 18, x>0 .
3. x>0.

Преобразование 2 log₂ x = log₂ x² расширяет область определения уравнения, поэтому к полученному уравнению необходимо добавить неравенство х > 0. Далее решим квадратное уравнение и “отбросим” отрицательный корень.

Ответ: 3.

Пример 2. Решите уравнение lg (х + 4) + lg {2х + 3) = lg (1 — 2х).

Решение. Данное уравнение равносильно:

1. lg (x + 4)(2x + 3) = lg (1- 2x) 2x² + 13x + 11 = 0,
2. 2х + 3 > О, o — 1,5 < x < 0,5.
3. 1 — 2х > О

Ответ: -1.

Для решения уравнений, содержащих логарифмы с разными основаниями, используется формула перехода от одного основания к другому:

— log_a b = .

Пример 3. Решите уравнение log₂ x + log₄x + log₁₆x = 7.

Решение. Перепишем уравнение в виде:

4 log₂ х + 2 log₂x + log₂ x = 28 o log₂ x = 4.

Ответ: 16.

Пример 4. Решите уравнение log₄х² + log₂ (х + 2) = 0.

Решение. Поскольку

log₄х² = = log_2,

то уравнение примет вид:

log₂ | x ! + log₂ (x + 2) = 0 <=> log₂ | x(x + 2) = log₂ 1 и х ? 0 .

осталось рассмотреть два случая:

x² + 2x – 1 = 0, где х > 0

x = - 1

2) x² + 2x + 1 = 0, где х < 0

X = — 1.

Ответ: — 1; — 1.

Замена переменных в уравнениях.

Некоторые логарифмические уравнения сводятся к алгебраическим уравнениям с помощью замены переменных.

Пример 5. Решите уравнение 4 – lg x = 3 .

Решение. Воспользуемся методом замены. Пусть = t, тогда данное уравнение примет вид t² + 3t – 4 = 0, откуда t₁ = 1, t₂ = — 4 (посторонний корень).

Следовательно, = 1, lg x = 1, х = 10.

Ответ: 10.

Логарифмирование уравнений.

Иногда встречаются уравнения, в которых фигурирует функция вида у = f(x)^g(х), при этом подразумевают, что f(x) > 0. Так будем поступать и мы. Такие уравнения удобно решать почленным логарифмированием.

Пример 5. Решите уравнение х^х+2 = х⁵.

Решение. х^х+2 = х⁵ o lg x^x+2 = lg x⁵ o (x + 2) lg x = 5 lg x o ( x – 3 ) lg x = 0.

Ответ: 1; 3.

4.Самостоятельное комплексное применение знаний.

1 уровень:

1 вариант

• log ₃ x= 4
• log ₂ x= -6
• log_x 64 = 6
• — log _x64 = 3
• 2 log _x8 + 3 = 0

2 вариант

• log ₂ x= 5
• log ₅ x= -3
• log _x81 = 4
• — log _x625= 4
• 3 log_x 64 + 2 = 0

Работа проверяется, оценивается. Верное решение всех заданий дает право учащемуся приступить к выполнению второго уровня. В противном случае ученик корректирует свою работу и выполняет задания другого варианта этого же уровня. При успешном выполнении данной работы, приступает к следующему уровню.

2 уровень.

1 вариант

• log ₃ (2х — 1) = log ₃ 27
• log ₃ (4х+5)+log ₃ (х +2) = log ₃ (2х +3)
• log ₂ х = — log ₂ (6х — 1)
• 4 + log ₃(3-х) = log ₃ (135-27х)
• log(х — 2) + log ₃ (х — 2) = 10

2 вариант

• log ₂ (х + 3) = log ₂ 16
• 2 log ₅ (3-4х)-log ₅ (2х +1)² = 0
• 2 log ₃ (7х — 10) = log ₃ х
• lg_{(х -1)+lg х = lg(5х-8)}
• -lg(х — 1)-lg= -6

Самоконтроль работы (правильные ответы у учителя), занесение результатов в оценочный лист.

Успешное выполнение 2 уровня дает право на решение 3 уровня.

3 уровень.

1 вариант

• 2log ²₃ х — 7 log ₃ х + 3 = 0
• lg ² х — 3 lg х — 4 = 0
• log ² ₃ х — log ₃ х — 3 = 2 ^lоg ₂ ³

2 вариант

• log² ₃ х — 3 log ₃ х + 2 = 0
• lg ² х — 2 lg х — 3 = 0
• 3log ² ₈ х +2 log ₈ х +2 = 0,5 ^lоg _0,53

3 вариант

• log ₇ (х ² — 2х + 1) = 1
• log ² ₃ х — log ₃ х = 2
• 2 log ₅ (х + 3)+log _0,2 (х +4) = log ₂ 5

4 вариант

• log ₆ (х ² — 5х + 40) = 2
• log ²₃ х + 2 log ₂ х = 3
• log ₅ 7 = 2 log ₇ х — log ₇ (х+4)

Работы оцениваются. Подводят итоги всей работы. Коррекция проводится на каждом этапе работы. Ошибки анализируются вместе с учителем и при необходимости для закрепления положительного результата ученик выполняет задания этого же уровня другого варианта.

5. Итог урока.

Мы с вами в ходе комплексного применения знаний выработали навык самостоятельного применения полученных знаний в стандартных и нестандартных ситуациях. В результате выполнения работ каждый смог оценить себя и определить свой уровень, сделать выводы.

6. Задания для самостоятельного домашнего решения:

(Для ребят увлеченных математикой)

а) log ₉ (2 • 3^2х — 27) = х

б) -4 = log _0,5 (1 + 3х) + log _0,5 (х — 4)

в) log ₅ (5 + 3х) = log ₅ 3 • log ₃ (2х + 10)

г) 4 log ₅ + log ²₅х = 5

д) log ₂ х + log ₅ х = 1

е) 2 (log ₃ х ² — 3) • log ₅ = 2 log ₅ + log ₃ .

Оценочный лист

Номер варианта——————————————

Фамилия, имя———————————————

Класс——————————————————

Вид работы	диктант	1 уровень	2 уровень	3 уровень	итог
Результат работы (оценка)

Решение логарифмических уравнений — 3

В этой статье мы рассмотрим решение логарифмических уравнений с логарифмом в показателе степени. Общий подход к решению уравнений этого типа я покажу на примере решения вот этого логарифмического уравнения:

Как всегда, сначала выпишем ОДЗ уравнения:

Обе части уравнения строго больше нуля, и мы можем взять логарифм от правой и левой части. Собственно, уравнения с логарифмом в показателе степени в большинстве случаев решаются логарифмирование правой и левой части уравнения по тому же основанию, что и у логарифма в показателе степени. В нашем уравнении в показателе степени стоит десятичный логарифм, поэтому будем логарифмировать по основанию 10:

Вынесем показатели степени за знак логарифма:

Получили уравнение:

Для того, чтобы облегчить себе жизнь, введем замену :

Получим уравнение относительно t:

Решим биквадратное уравнение:

,

, ,  ,  

Вернемся к исходной переменной:

, ,  ,  

Отсюда:

, ,  ,  

Ответ:  {10; 0,1; 100; 0,01}

 

А теперь давайте решим, с виду, очень простое уравнение:

Так как уравнение содержит логарифм в показателе степени, возьмем от правой и левой части уравнения логарифм по основанию х (как у логарифма в показателе степени):

Вынесем показатель степени за знак логарифма:

«Растащим» выражения, стоящие под знаком логарифма — наша задача разложить их на простые «кирпичики»:

Мы видим, что неизвестное присутствует в уравнении в составе двух выражений:

и

Чтобы структура уравнения стала более «прозрачной», введем замену:

 и  

Получим уравнение:

Приведем его к виду

И решим как квадратное относительно 

Теперь можем вернуться к исходным переменным:

, ,

, ,

Вот такое длинное решение получилось у такого коротенького уравнения.

Ответ: ,

Решение  логарифмических уравнений остальных типов мы рассмотрим здесь и здесь

И.В. Фельдман, репетитор по математике.

 

 

Некоторые методы решения логарифмических уравнений

Рассмотрим некоторые типы логарифмических уравнений, которые не так часто рассматриваются на уроках математики в школе, но широко используются при составлении конкурсных заданий, в том числе и для ЕГЭ.

1. Уравнения, решаемые методом логарифмирования

При решении уравнений, содержащих переменную и в основании и в показателе степени, используют метод логарифмирования. Если, при этом, в показателе степени содержится логарифм, то обе части уравнения надо логарифмировать по основанию этого логарифма.

Пример 1.

Решить уравнение: х^log2^х+2 = 8.

Решение.

Прологарифмируем левую и правую части уравнения по основанию 2. Получим

log₂ (х^log2^х+2) =  log₂ 8,                  

(log₂ х + 2) · log₂ х = 3. 

Пусть log₂ х = t.

Тогда (t + 2)t = 3. 

t² + 2t – 3 = 0.

D = 16. t₁ = 1; t₂ = -3.

Значит log₂ х = 1 и х₁ = 2 или log₂ х = -3 и х₂ =1/8

Ответ: 1/8; 2.

2.  Однородные логарифмические уравнения.

Пример 2.

Решить уравнение log²₃ (х² – 3х + 4) – 3log₃ (х + 5) log₃ (х² – 3х + 4) – 2log²₃ (х + 5) = 0

Решение.

Область определения уравнения

{х² – 3х + 4 > 0,
{х + 5 > 0. → х > -5.

log₃ (х + 5) = 0 при х = -4. Проверкой определяем, что данное значение х не является корнем первоначального уравнения. Следовательно можно разделить обе части уравнения на log² ₃ (х + 5).

Получим log²₃ (х² – 3х + 4) / log²₃ (х + 5) – 3 log₃ (х² – 3х + 4) / log₃ (х + 5) + 2 = 0.

Пусть log₃ (х² – 3х + 4) / log₃ (х + 5) = t. Тогда t ²– 3 t + 2 = 0. Корни данного уравнения 1; 2. Возвратившись к первоначальной переменной , получим совокупность двух уравнений

[log₃ (х² – 3х + 4) / log₃ (х + 5) = 1

[log₃ (х² – 3х + 4) / log₃ (х + 5) = 2. Отсюда

[log₃ (х² – 3х + 4) = log₃ (х + 5),

[log₃ (х² – 3х + 4) = 2log₃ (х + 5).

Выполнив потенцирование, получим

 [х² – 3х + 4 = х + 5,

 [х² – 3х + 4 = (х + 5)² ;

 [х² – 4х – 1 = 0,

 [-13х = 21.

 [х = 2 – √5,

 [х = 2 + √5, [х = -21/13. Все корни входят в область определения.

Ответ: ,-21/13; 2 – √5; 2 + √5.

3. Уравнения, содержащие переменную и в основании логарифма и в выражении, стоящем под знаком логарифма

Пример 3.

Найдите среднее арифметическое корней уравнения log_3х+7 (9 + 12х + 4х²) + log_2х+3 (6х² + 23х + 21) = 4.

Решение.

9 + 12х + 4х² = (2х + 3)²;  6х² + 23х + 21 = (2х + 3)(3х + 7).

Область определения уравнения

{2х + 3 > 0,
{2х + 3 ≠ 1,

{3х + 7 > 0,
{3х + 7 ≠ 1.

Следовательно х > -1,5 и х ≠ -1

Тогда log_3х+7 (2х + 3)² + log_2х+3 (2х + 3)(3х + 7) = 4;

2log_3х+7 (2х + 3) + log_2х+3 (2х + 3)+ log_2х+3 (3х + 7) = 4;

2log_3х+7 (2х + 3) + 1 + log_2х+3 (3х + 7) = 4;

2log_3х+7 (2х + 3) + 1/log_3х+7 (2х + 3) = 3;

Введём новую переменную log_3х+7 (2х + 3) = t. Получим 2t + 1/t = 3. 2t² – 3t + 1 = 0. Корни уравнения 1/2; 1.

Возвращаемся к исходной переменной.

Получаем log_3х+7 (2х + 3) = 1/2  или log _3х+7 (2х + 3) = 1

2х + 3 = (3х + 7)^1/2;                    

(2х + 3)² = 3х + 7;

4х² + 9х + 2 = 0.

Корни уравнения -2; -0,25.

log_3х+7 (2х+3) = 1.

2х + 3 = 3х + 7.

Х = -4.

В область определения уравнения входит только число -0,25.

Среднее арифметическое -0,25,

Ответ: -0,25.

4. Уравнения, требующие использования свойств логарифмических функций (т.е. решаемые функциональным методом).

Пример 4. Какой наибольший корень в уравнении log₃ (8 + 2х – х²) = 2^х-1 + 2^1-х

Решение.

Рассмотрим функцию у = 8 + 2х – х². Её график – парабола, ветви которой направлены вниз. Координаты вершины (1; 9). Область значений функции (-∞; 9]. Но с учётом существования логарифма нужно рассматривать лишь значения (0; 9]. Значит выражение в левой части принимает наибольшее значение 2 при х = 1. Рассмотрим теперь функцию у = 2^х-1 + 2^1-х . Если принять t = 2^x-1,, то она примет вид у = t + 1/t, где t > 0. При таких условиях она имеет единственную критическую точку t = 1. Это точка минимума. У_vin = 2. И достигается он при х = 1.

Теперь очевидно, что графики рассматриваемых функций могут пересекаться лишь один раз в точке (1; 2). Получается, что х = 1 единственный корень решаемого уравнения.

Ответ: х = 1.

Пример 5. Решить уравнение log²₂ х + (х – 1) log₂ х = 6 – 2х

Решение.

Решим данное уравнение относительно log₂ х. Пусть log₂ х = t. Тогда t² + (х – 1) t – 6 + 2х = 0.

D = (х – 1)² – 4(2х – 6) = (х – 5)². t₁ = -2; t₂ = 3 – х.

Получим уравнение log₂ х = -2 или log₂ х = 3 – х.

Корень первого уравнения х₁ = 1/4.

Корень уравнения log₂ х = 3 – х найдём подбором. Это число 2. Этот корень единственный, так как функция у = log₂ х возрастающая на всей области определения, а функция у = 3 – х – убывающая.

Проверкой легко убедится в том, что оба числа являются корнями уравнения

Ответ:1/4; 2.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Методы решения логарифмических уравнений

Цель: дать представление о логарифмических уравнениях.

Задачи:

• образовательная: формирование знаний о разных способах решения логарифмических уравнений, умений применять их в каждой конкретной ситуации и выбирать для решения любой способ;

• развивающая: развитие умений наблюдать, сравнивать, применять знания в новой ситуации, выявлять закономерности, обобщать; формирование навыков взаимоконтроля и самоконтроля;

• воспитательная: воспитание ответственного отношения к учебному труду, внимательного восприятия материала на уроке, аккуратности ведения записей.

Тип урока: урок ознакомления с новым материалом.

Оборудование: мультимедиа проектор, презентация к уроку.

Технологии, используемые на уроке: педагогика сотрудничества, групповая технология, информационно-коммуникативная технология.

Ход урока

1. Организационный момент.

2. Постановка цели урока.

Изученные определение логарифма, свойства логарифмов и логарифмической функции позволят нам решать логарифмические уравнения. Все логарифмические уравнения, какой бы сложности они не были, решаются по единым алгоритмам. Эти алгоритмы рассмотрим сегодня на уроке. Их немного. Если их освоить, то любое уравнение с логарифмами будет посильно каждому из вас.

— Запишите в тетради тему урока: «Методы решения логарифмических уравнений».

3. Актуализация опорных знаний.

Подготовимся к изучению темы урока. Каждое задание вы решаете и записываете ответ, условие можно не писать. Работайте в парах. (Демонстрируется слайды с заданиями для устной работы).

4. Изучение нового материала.

1) При каких значениях х имеет смысл функция:

а)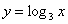

б) 

в)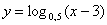

г)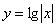

(По каждому слайду сверяются ответы и разбираются ошибки).

2) Совпадают ли графики функций?

а) y = x и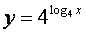  

б) 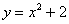 и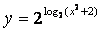

3) Перепишите равенства в виде логарифмических равенств:

 

4) Запишите числа в виде логарифмов с основанием 2:

4 =

— 2 =

0,5 =

1 =

5) Вычислите: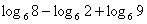

4. Ознакомление с новым материалом.

Попробуйте сформулировать определение логарифмического уравнения. (Уравнение, содержащее неизвестное под знаком логарифма).

Рассмотрим простейшее логарифмическое уравнение: log _аx = b (где а>0, a ≠ 1). Так как логарифмическая функция возрастает (или убывает) на множестве положительных чисел и принимает все действительные значения, то по теореме о корне следует, что для любого b данное уравнение имеет, и притом только одно, решение, причем положительное.

Вспомните определение логарифма. (Логарифм числа х по основанию а – это показатель степени, в которую надо возвести основание а, чтобы получить число х). Из определения логарифма сразу следует, что а^b является таким решением.

Запишите подзаголовок «Методы решения логарифмов».

1 метод. По определению логарифма.

Так решаются простейшие уравнения вида .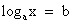

 

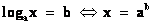
Решить уравнение :

Как вы предлагаете его решать? (По определению логарифма).

Решение. 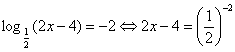, Отсюда 2х – 4 = 4; х = 4.

Ответ: 4.

В этом задании 2х – 4 > 0, так как > 0, поэтому посторонних корней появиться не может, и проверку нет необходимости делать. Условие 2х – 4 > 0 в этом задании выписывать не надо.

2 метод. Потенцирование (переход от логарифма данного выражения к самому этому выражению).

Рассмотрим пример :

Какую особенность вы заметили? (Основания одинаковы и логарифмы двух выражений равны). Что можно сделать? (Потенцировать).

При этом надо учитывать, что любое решение содержится среди всех х, для которых логарифмируемые выражение положительны.

Решение 1. ОДЗ: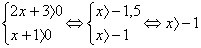

Потенцируем исходное уравнение 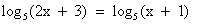, получим уравнение 2x + 3 = х + 1.

Решаем его: х = -2. Это решение не подходит ОДЗ, значит, данное уравнение корней не имеет.

Можно решить это уравнение иначе – переходом к равносильной системе:

Уравнение

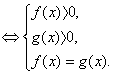
(Система содержит избыточное условие – одно из неравенств можно не рассматривать).

Решение 2. Уравнение 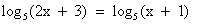 равносильно системе:

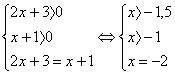
Эта система решений не имеет.

Есть еще один вариант решения – переход к следствию из данного уравнения. При неравносильных преобразованиях найденное решение необходимо проверить подстановкой в исходное уравнение.

Решение 3. .

Сделаем проверку: неверно, так как не имеет смысла.

Ответ: корней нет.

Вопрос классу: Какое из этих трех решений вам больше всего понравилось? (Обсуждение способов).

Вы имеете право решать любым способом.

3. Введение новой переменной.

Рассмотрим пример. .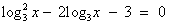

Что вы заметили? (Это квадратное уравнение относительно log3x).

Ваши предложения? (Ввести новую переменную)

Решение. ОДЗ: х > 0.

Пусть 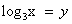, тогда уравнение примет вид: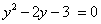. Дискриминант D > 0. Корни по теореме Виета:.

Вернемся к замене: или .

Решив простейшие логарифмические уравнения, получим:

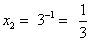; . Ответ: 27;

4. Логарифмирование обеих частей уравнения.

Решить уравнение:.

Решение: ОДЗ: х>0, прологарифмируем обе части уравнения по основанию 10:

Применим свойство логарифма степени:

(lgx + 3) lgx =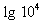

(lgx + 3) lgx = 4

Пусть lgx = y, тогда (у + 3)у = 4

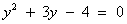, (D > 0) корни по теореме Виета: у1 = -4 и у2 = 1.

Вернемся к замене, получим: lgx = -4,; lgx = 1, .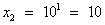

Ответ: 0,0001; 10.

5. Приведение к одному основанию.

Решите уравнение:

Решение: ОДЗ: х>0. Перейдем к основанию 3.

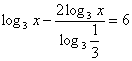  или ; .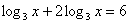

Ответ: 9.

6. Функционально-графический метод.

Решить графически уравнение: 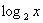= 3 – x.

Как вы предлагаете решать? (Строить по точкам графики двух функций у = log2x и y = 3 – x и искать абсциссу точек пересечения графиков).

Посмотрите ваше решение на слайде.

Есть способ, позволяющий не строить графики. Он заключается в следующем: если одна из функций у = f(x) возрастает, а другая y = g(x) убывает на промежутке Х, то уравнение f(x)= g(x) имеет не более одного корня на промежутке Х.

Если корень имеется, то его можно угадать.

В нашем случае функция 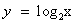возрастает при х>0, а функция y = 3 – x убывает при всех значениях х, в том числе и при х>0, значит, уравнение имеет не более одного корня. Заметим, что при х = 2 уравнение обращается в верное равенство, так как .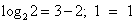

Ответ: 2.

5. Закрепление изученного материала.

Предложите метод решения уравнений:

1)

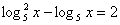
2)

3)

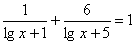
4)

5)

6)

6. Подведение итогов урока.

— Какие методы решения логарифмических уравнений мы рассмотрели на уроке?

7. Домашнее задание: карточки (решить задания двумя способами).

На следующих уроках рассмотрим более сложные уравнения. Для их решения пригодятся изученные методы.