Неравенства с переменными, их частные и общее решение

Неравенства, содержащие переменную, занимают основную долю в общем объеме изучения темы «Неравенства» школьной программы математики и алгебры. Данная статья содержит базовый материал: определение понятия неравенства с переменными и их решений, способ записи решений неравенств. Также для наглядности приведем решение практических задач.

Определение неравенств с переменными

Числовые неравенства мы разобрали в соответствующей статье, выяснив что числовыми неравенствами являются два числовых выражения, между которыми располагается какой-либо из знаков неравенства. Заменив хотя бы одно из числовых выражений выражением с переменной, мы получим неравенство с переменными. Такое определение дано по виду записи подобных неравенств. Выделяют неравенства с одной, двумя, тремя и большим количеством переменных по числу переменных, использующихся в записи неравенства.

Неравенства с одной переменной

Определение 1

Неравенство с одной переменной – это неравенство, в записи которого используется одна переменная.

К примеру, k < 7 – неравенство с одной переменной k; 8 ≥ d2 – 3 – неравенство с одной переменной d.  При этом возможно, что переменная будет участвовать в записи несколько раз, например:

((2·x — 5·t2) · (t-1) < 1t  или t-1+ 4 ≥ 1t- t3t+3

Неравенства с двумя переменными

Определение 2

Неравенство с двумя переменными – это неравенство, в записи которого используются две неодинаковые переменные.

Например, m3+15· n2>13 – неравенство с двумя переменными m и n;

                    (f+2·g)37+3< 7 — ff2+1 – неравенство с двумя переменными f и g.

По записи неравенства с двумя переменными схожи с неравенствами с параметром и одной переменной. Но тогда, как правило, в условиях всегда указывается, какие буквы служат обозначением параметров, поэтому вопрос о том, сколько переменных в заданном неравенстве, обычно не возникает.

Неравенства с тремя или больше переменными

Определение 3

Неравенства с тремя, четырьмя и т.д. переменными – это неравенства, в записи которых используются три, четыре и т.д. переменных.

В школьной программе подобные неравенства встречаются редко, но тем не менее существуют. Например, шар, радиус которого равен 2 и центр которого со

zaochnik.com

Подборка материала по математике «Решение неравенств с двумя переменными»

Решение неравенств с двумя переменными

Графическое решение неравенств

Неравенство с двумя переменными х и у f(x;y) > 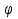(х;у) можно записать в виде F(x;y)>0 (1), где f(x;y),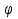(x;y),

 F(x;y) — мног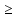очлены с указанными переменными. Неравенства, содержащие неизвестные, могут быть и другого вида:

F(x;y) < 0,F(x;y)  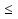0,F(x;.y)  0.

Решением неравенства (1) называется упорядоченная пара действительных чисел (х₀; у₀), обращающая это неравенство в верное числовое неравенство. Графически это соответствует заданию точки (х₀; у₀) координатной плоскости. Решить неравенство — значит, найти множество всех его решений. Совокупность всех точек, координаты которых удовлетворяют неравенству (1), называется областью его решений.

Неравенства называются равносильными, если они имеют одну и ту же область решений.

Полезно будет напомнить здесь одно простое
утверждение: график уравнения F(x;y) = y — f(x) = 0, где f(x) — многочлен, делит координатную плоскость на две области так, что при переходе из одной области в другую значение выражения F(x;y) меняет знак на противоположный.

Рис. 1cnh 62

Действительно, если взять любую точку (рис. 1), лежащую выше графика, то ее ордината будет больше, чем ордината точки, имеющей такую же абсциссу, но лежащей на графике. То есть множество точек плоскости, расположенных выше графика, будет геометрическим изображением решения неравенства у > f(x), т.е. F(x;y) > 0 . Для точек, лежащих ниже графика, имеет место неравенство F(x;y) < 0.

Аналогично можно сформулировать утверждение для графика уравнения F(y,x) = х – 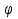(у) = 0, где  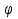(у) —многочлен.

Многочлен можно заменить на элементарную функцию. Например, для выражений F(x;y) = y — log₂x иF(x;y) = y — 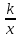 (k>0) на рисунках 2 и 3 соответственно представлены решения неравенства F(x;y)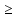 

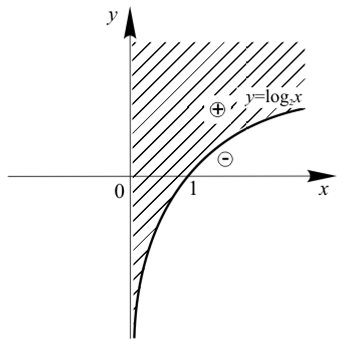
0.

Рис. 2

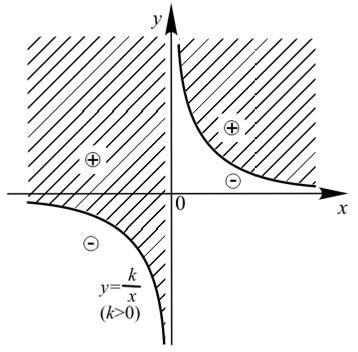
Рис. 3

Указанные утверждения удобно использовать, если в неравенстве удается выразить переменную у(или х) в явном виде, то есть уединить эту переменную в одной из частей неравенства. 

Области знакопостоянства линейного многочлена F(x;y) =px + qy + r

Уравнение px + qy + r = 0, где p²+q²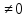, задает прямую линию. Геометрической интерпретацией решения линейного неравенства с двумя переменными является следующая теорема.

Теорема 1. Прямая px + qy + r = 0, где p²+q²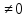, разбивает координатную плоскость на две открытые полуплоскости так, что координаты точек одной полуплоскости удовлетворяют неравенству рх + qy + r > 0, а другой — неравенствуpx + qy + r <0.

Исходя из теоремы 1, можно сформулировать свойство чередования знака для линейного многочлена Ф(х;у) = px

 + qy + r (p²+q²,):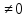 

при переходе через точку прямой px + qy + r = 0 из одной полуплоскости в другую знак значения многочлена Ф(х;у) меняется на противоположный.

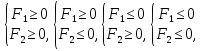 задает на координатной плоскости множество внутренних точек угла, включая границы. Например, совокупность  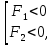соответствующая системе неравенств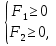 

задает оставшуюся часть, исключая границы (координатную плоскость с «вырезанным» углом). Аналогичные утверждения верны и для других пар систем и совокупностей неравенств. Другими словами, в алгебре указанные совокупность и система неравенств являются логическими отрицаниями друг друга, а на координатной плоскости им соответствующие множества точек являются дополнениями друг друга до всей плоскости.

• Неравенство (a₁x + b₁y +c₁)(a₂x + b₂y + c₂) 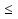0 (или (a₁

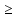x + b₁y +c₁)(a₂x + b₂y + c₂) 0), где a_i² +b_i² 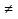0 (i = 1; 2), 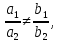задает на координатной плоскости множество внутренних точек вертикальных углов, включая границы.

Метод областей и его обобщения

• Рассмотрим выражение F(x;y)=F₁(x;y) F₂(x;y) × … × F_n(x;y), (2)

где F_i (х; у) = p_ix + q_iy + r_i, причем прямые p_ix + q_iy + r_i =0 и p_jx + q_jy + r_j =0 попарно различны (i = 1,2,…,n; у = 1,2,…,n; i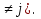  

Выражению (2) соответствует разбиение плоскости на области прямыми линиями p_ix + q_iy + r_i =0 (i = 1,2,…,n). Точки пересечения прямых будем называть особыми точками границы области, другие точки —обыкновенными. Метод областей опирается на следующее свойство чередования знака выражения (2): при переходе через обыкновенную точку прямой p_ix + q_iy + r_i =0 (границы области) из одной области в смежную знак значения выражения (2) меняется на противоположный.

Действительно, при переходе через прямую линию p_ix + q_iy + r_i =0 в выражении (2) меняет знак только один множитель p_ix + q_iy + r_i.

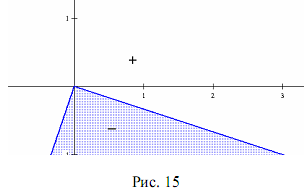
Пример . Решите графически неравенство (у + х)(х – у — 1)(х + 2)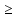0.

Решение. На координатной плоскости хОу строим сплошными линиями график уравнения (у + х)(х – у — 1)(х + 2) = 0, состоящий из трех прямых у = -х, у = х — 1 и х = -2 (рис.4). Многочлену F(x; у) = (у + х)(х — у — 1)(х + 2) соответствует разбиение плоскости (х;у) на семь областей. Возьмем пробную точку (3;0) и определим знак значения выражения F(x;y) в этой точке: F(3;0) = 30; 30 > 0. Ставим знак плюс в области, содержащей точку (3;0). Далее, используя свойство чередования знака выражения F(x;y) вида (2), расставляем знаки в остальных областях. Нумерация областей на рисунке показывает последовательность их обхода (последовательность обхода может быть и другой). Выбираем области, содержащие знак плюс и решения уравнения F(x;y) = 0.

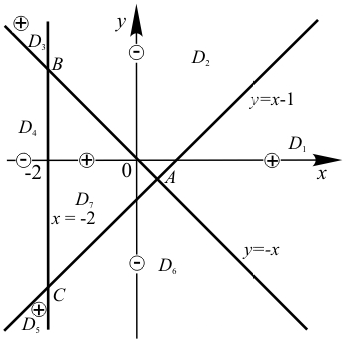
Рис. 4

• Пусть дано выражение вида F(x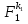;y) =(x;y) 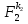(x;y) 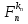 …  (x;y) (3), где F_j{x;y) = p_ix + q_iy + r_i , причем прямые p_ix + q_iy + r_i =0 и p_jx + q_jy + r_j =0 попарно различны (i = 1,2,…,n; у = 1,2,…,n; i 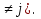k₁,k₂,…,k_n — фиксированные натуральные числа и выражению F(x;y) соответствует разбиение плоскости на области.

Для решения неравенства (1), где выражение F(x; у)имеет вид (3), используется обобщенный метод областей, который опирается на следующее правило чередования знака выражения: при переходе через обыкновенную точку прямой p_ix + q_iy + r_i =0(границы области) из одной области в смежную знак значения выражения (3) меняется на противоположный, если к_i — нечетное число, и не меняется, если k_i — четное число.

Области знакопостоянства многочленов F(x; у) второй степени

Рассмотрим кривые второго порядка: эллипс (в частности, окружность), гиперболу, параболу.

Теорема 2. Окружность (х — т)² +(у — n)² = R² (с центром в точке А(т;n) и радиуса R > 0) делит координатную плоскость на две части так, что координаты точек, лежащих вне окружности, удовлетворяют неравенству (х — т)² +(у — n)² > R²,а расположенных внутри окружности неравенству (х — т)² +(у — n)^2 2.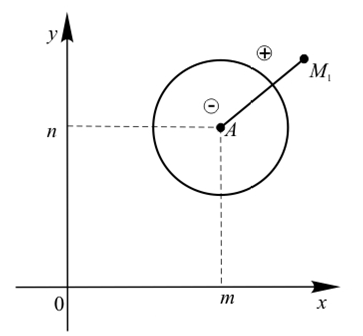

Рис. 5 

Теорема 3. Эллипс, заданный каноническим уравнением 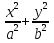= 1, делит координатную плоскость на две части так, что координаты точек, лежащих вне эллипса, удовлетворяют неравенству  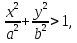а расположенных внутри эллипса — неравенству  1. 

Для эллипса 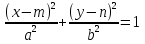аналогично формулируется утверждение о знакочередовании значения выражения F(x; y) = .

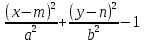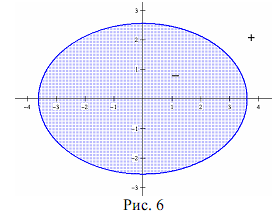
Отсюда как следствие вытекает теорема 2. 

Теорема 4. Гипербола ху — k = 0 (k 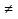 0) делит координатную плоскость на три области так, что при переходе из одной области в смежную выражение F(x;y) = ху — k меняет знак на противоположный.

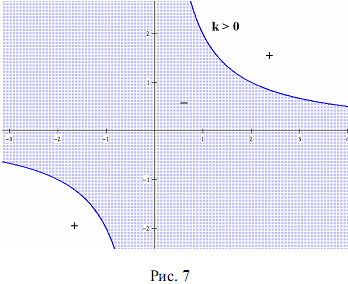
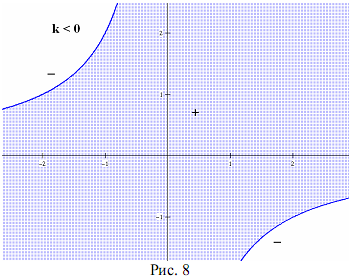
Аналогичное свойство знакочередования формулируется для гиперболы (х — т)(у — n) — k = 0 (k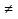 0)

Теорема 5. Гипербола, заданная каноническим уравнением 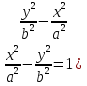 = 1), делит координатную плоскость на три области так, что при переходе из одной области в смежную значение выражения F(x; y) =  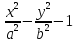(F(x; y) =  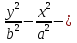1) меняет знак на противоположный.

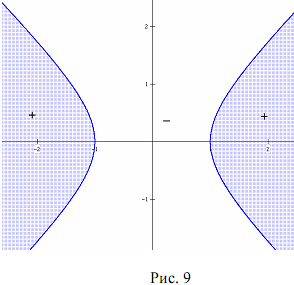
Аналогичное свойство формулируется для гипербол 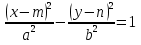 и 

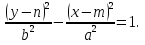
Теорема 6. Парабола, заданная каноническим уравнением у²= 2рх (р > 0 или р < 0), делит координатную плоскость на две области так, что при переходе из одной области в другую значение выражения F(x;y) = у² -2рх меняет знак на противоположный.

Аналогичное свойство формулируется для параболы (у — n)²= 2р(х — т).

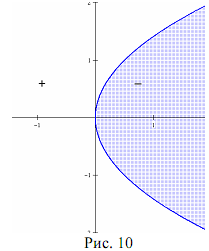
Области знакопостоянства выражений, содержащих знак модуля

Для решения неравенств с двумя переменными, содержащих знак модуля, обычно разбивают координатную плоскость на отдельные области так, чтобы на каждой из них можно было записать неравенство, не используя знака абсолютной величины.

В некоторых случаях удобно использовать известные области знакопостоянства выражений с модулями.

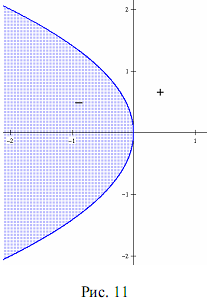
Теорема 7. Ромб, заданный уравнением 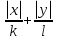= 1, где k > 0, l > 0, делит координатную плоскость на две части так, что координаты точек, лежащих вне ромба, удовлетворяют неравенству  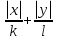> 1, а расположенных внутри ромба — неравенству .

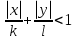По аналогии с существующей терминологией «уравнение прямой в отрезках», уравнение 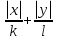= 1, где k > 0, l > 0, можно назвать «уравнением ромба в отрезках».

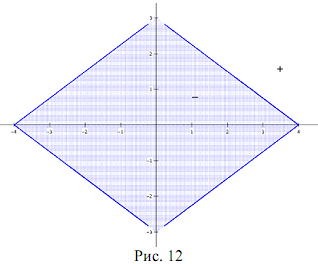
Теорема 8. Фигура, заданная уравнением 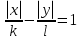, где k> 0, l > 0, делит координатную плоскость на три области так, что при переходе из одной области в смежную значение выражения F(x; y) =  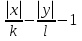меняет знак на противоположный.

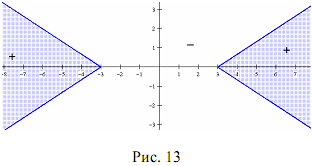
Теорема 9.Фигура, заданная уравнением или k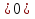, делит координатную плоскость на две области так, что при переходе из одной области в другую значение выражения F(x; y) =  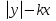меняет знак на противоположный.

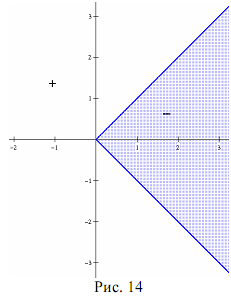
Теорема 10. Неравенство a₁x + b₁y +c₁÷ 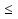 a₂x + b₂y + c₂,где a_i² + b_i² 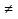0 (i = 1; 2), 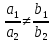, задает на координатной плоскости множество внутренних точек угла, включая границы.

Теорема 11.Неравенство a₁x + b₁y+c₁÷ 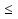a₂x + b₂y +c₂ , где a_i² +b_i² 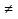0 (i = 1; 2),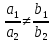, задает на координатной плоскости множество внутренних точек вертикальных углов, включая границы.

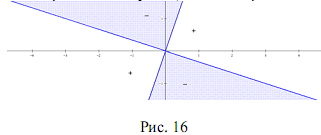
Теорема 12. Пара параллельных прямых, заданных уравнением 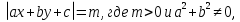разбивает координатную плоскость на три области так, что при переходе из одной плоскости в другую значение выражения F(x; y) = ax + by + c — m меняет знак на противоположный.

Конкретизируем данную теорему: неравенство 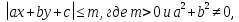 задает на координатной плоскости множество внутренних точек «полосы», включая границы. В частности, «полоса» 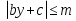параллельна оси Ох, а «полоса»  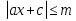параллельна оси Оу.

Теорема 13. Неравенство a₁x + b₁y +c₁÷ 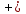 a₂x 

infourok.ru

Решение неравенств с двумя переменными

Решение неравенств

с двумя переменными

9 класс

Автор:

Сидорова А.В.

МБОУ СОШ № 31

Г. Мурманска

Устная работа

• 1. Какие из следующих чисел: –2; –1; 0; 2; 3 – являются решением неравенства х 3 – 2 х ≥ 1?
• 2. Подберите два каких-нибудь числа разных знаков, чтобы их сумма была больше 5.
• 3. Является ли пара чисел х = 2, у = 5 решением неравенства: 2 х 2 – у

Определение

• Решением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное неравенство в верное числовое неравенство.

Определение

• Линейным неравенством с двумя переменными называется неравенство вида ах + by с, где х и у — переменные, а, b и с — некоторые числа.

Пример 1.

• Изобразим на координатной плоскости множество решений неравенства 2у+3х≤6.
• Решение.
• Строим прямую 2у+3х=6

у=3-1,5х

х

у

0

2

3

0

х

у

0

2

3

0

У

2у+3х≤6

B

1

A

Х

0

1

Возьмем из каждой области по контрольной

точке: А(1;1) :

В(1;3):

верно

2·1+3·1≤6, 5≤6

неверно

2·3+3·1≤6

ПЛАН ВЫПОЛНЕНИЯ ЗАДАНИЯ

• Заменить знак неравенства на равно.
• Выразить переменную у через переменную х.
• Построить график полученного

уравнения.

• Выбираем любую из полученных областей и рассматриваем в ней произвольную точку.
• Подставляем координаты точки в

неравенство.

• Если в результате проверки получается верное числовое неравенство, то заключаем, что исходное неравенство выполняется во всей области, которой принадлежит выбранная точка.
• Если в результате проверки получается неверное числовое неравенство, то множеством решений неравенства будет вторая область, которой выбранная точка не принадлежит.

Пример 2.

• Изобразим на координатной плоскости множество решений неравенства 2у+3х
• Решение.
• Строим прямую 2у+3х=6

у=3-1,5х

х

у

0

2

3

0

У

2у+3х

1

A

Х

1

0

Возьмем контрольную

точку: А(1;1) :

верно

2·1+3·1

Пример 3

Изобразить на координатной плоскости множество точек, координаты которых удовлетворяют неравенству

Выполняем задание по плану.

1 2 + 2 неверно Y 5 4 3 y = x 2 + 2 2 A 1 X O -2 2 1 «

А (1;1)

1 1 2 + 2

неверно

Y

5

4

3

y = x 2 + 2

2

A

1

X

O

-2

2

1

Задание 3.

Изобразить на координатной плоскости множество точек, координаты которых удовлетворяют неравенству

х 2 + y 2

План выполнения задания

1. Заменить знак неравенства на равно:

х 2 + y 2 = 16

2. Определить, какая фигура задаётся таким уравнением:

х 2 + y 2 = 16 – уравнение окружности, с центром в начале координат, R = 4.

х 2 + y 2

1 2 + 1 2

А (1;1)

У

верно

A

1

Х

0

1

СПАСИБО за

внимание !

videouroki.net

Графическое решение систем неравенств с двумя переменными

Просмотр содержимого документа
«Графическое решение систем неравенств с двумя переменными»

Системы неравенств

с двумя переменными

К учебнику Ю.Н.Макарычева

Алгебра, 9 класс, Глава III §

Автор: Софронова Наталия Андреевна,

учитель математики высшей категории

МОУ «Упшинская основная общеобразовательная школа»

Оршанского района Республики Марий Эл

Решение системы неравенств

с двумя переменными

Решением системы неравенств с двумя переменными называется пара значений этих переменных, являющаяся как решением первого неравенства, так и второго неравенства системы.

(1; 2) – решение ?

( 2; 1) – решение ?

(1; 2) – решение

( 2; 1) –не решение

Изображение множества решений неравенства с двумя переменными на координатной плоскости

Парабола разбивает координатную плоскость на две области. Решением неравенства является область с точкой А.

у

у

А

О

О

О

х

В

Изображение множества решений системы неравенств с двумя переменными на координатной плоскости

Множеством решений системы неравенств с двумя переменными является пересечение множеств решений неравенств, входящих в систему. На координатной плоскости множество решений системы неравенств изображается множеством точек, являющихся общей частью множеств, представляющих собой решения каждого неравенства системы.

х = 2

у

• Построим прямую х = 2.
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

О

х

• Построим прямую у = -3.
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

у = -3

Решениями данной системы являются координаты точек пересечения множеств решений неравенств системы (прямой угол)

у

х

у

0

3

2

0

• Построим прямую 2у + 3х = 6
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

О

х

х

у

0

2

-3

1

• Построим прямую у — 2х = -3
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются координаты точек пересечения множеств решений неравенств системы (угол)

у

х

у

0

1

1

3

• Построим прямую у = 2 х + 1
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

О

х

х

у

0

1

-1

1

• Построим прямую у = 2 х — 1
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются координаты точек пересечения множеств решений неравенств системы (полоса)

у

• Построим окружность х 2 + у 2 = 1
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

х

О

х

у

0

1

0

-2

• Построим прямую 2х + у = 0
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются точки полукруга

у

• Построим параболу у = (х — 1) 2 -2
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

х

О

• Построим окружность (х-1) 2 +(у+2) 2 =1
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются точки пересечения множеств решений неравенств системы

Изобразить множество точек, которые являются решениями системы и вычислить площадь получившейся фигуры

у

х

О

у

О

х

multiurok.ru

Презентация к уроку по алгебре (9 класс) на тему: Графическое решение неравенств с двумя переменными

Урок алгебры в 9 классе

Графическое решение неравенств, систем неравенств с двумя переменными.

Учитель математики  Прокофьева И.Л.

МБОУ лицей №8 г. Ставрополь

 Цели и задачи урока:

1. Ввести понятие системы неравенств с двумя переменными.

 Составить алгоритм решения систем неравенств

 Формировать навыки решения систем неравенств

2. Развивать « критическое» мышление и интерес к предмету у учащихся в процессе решения проблемных ситуаций и заданий творческого характера.

Оборудование: Ноутбук ,  мультимедийный проектор, 

Этапы урока

•  Организация начала занятия.
• Проверка выполнения домашнего задания.
• Подготовка к усвоению новых знаний.
• Изучение нового материала.
• Первичная проверка знаний.
• Закрепление знаний.
• Подведение итогов занятий.
• Домашнее задание.

Ход урока. 1. Организационный момент.     

    На предыдущих уроках мы решали системы уравнений графическим способом. Сегодня мы переходим к изучению новой темы «Графическое решение неравенств, систем неравенств с двумя переменными». Повторим материал прошлого урока.

2. Устная работа учащихся с использованием проектора.

Из данных 6 функций выберите те, которые будут изображаться на экране.

               

 Даны функции  (записаны на доске)

   3.Изучение новой темы .

 Неравенство с двумя неизвестными можно представить так: f(x;y)>, где   f(x;y), – многочлен двух переменных х и у. Его можно записать в виде.

Неравенства содержащие неизвестные могут быть вида

F(x,y)0, F(x,y) 0, F(x,y) 0.

• Решением неравенства называется упорядоченная пара действительных чисел  , обращающая это неравенство в верное числовое неравенство.
• Графически это соответствует заданию точки     координатной плоскости.
• Решить неравенство — значит найти множество его решений

Если одно из неравенств системы представлено в виде  нестрогого неравенства, то график изображается сплошной линией, если строгое, то пунктирной.

Если одно из неравенств системы представлено в виде у ≥f(x).  То это неравенство задает на плоскости область, которая лежит не ниже графика.

Если одно из неравенств системы представлено в виде у ≤f(x).  То это неравенство задает на плоскости область, которая лежит не ниже графика.

 Если линия f(x.у)- замкнутая, например окружность, или замкнутая ломанная, то неравенство f(x.у≥0, задает область лежащую внутри замкнутой линии., а неравенство f(x.у)≤0- область лежащую вне.

 И наиболее универсальное, полезное для проверки правило- Правило пробной точки

• Построить   F(x;y)=0
• Взяв из какой — либо области пробную точку установить, являются ли ее координаты решением неравенства
• Сделать вывод о решении неравенства

Рассмотрим многочлен F(x;y)=y+x-1, тогда

   

В следующем примере дано уравнение окружности.

 Необходимо расставить знаки неравенств >,,используя правило пробной точки О(0,0).

   

• Решаем вместе .

 Рассмотрим примеры.

1. Решить неравенство:│х-0,5│-1,5≤0
2. Решить неравенство:
3. Решить неравенство:

Тестирование.

Системой неравенств  с двумя переменными  является система вида.

Алгоритм решения систем неравенств.

• Построить F(x;y)=0 и  G(x;y)=0
• Взяв из каждой области пробную точку установить, являются ли ее координаты решением системы

Объединение полученных областей- решение системы неравенств

• Решаем вместе .

1. Решить систему неравенств:

2. Решить систему неравенств:

3 Решить графически неравенство:  

Подведение итогов урока. Домашнее задание.

Литература:

1. Ю.Н.МакарычевН.Г.Миндюк, К.Н.Нешков Алгебра. 9кл. учебник для класса с углубленным изучением математики Изд. Мнемозина, 2004-2006
2. Мордкович А.Г.. Алгебра, 9 кл. Учебник для классов с углубленным изучением математики. Изд. Мнемозина, 2004-2006
3. Мордкович А.Г.. Алгебра, 9 кл. Задачник для классов с углубленным изучением математики. Изд. Мнемозина, 2004-2006
4. А.Корянов Неравенства с двумя переменными: графическое и аналитическое решения Библиотека «Первого сентября, серия «Математика», выпуск 22,Москва, Чистые пруды,2008

nsportal.ru

План-конспект урока по алгебре (9 класс) на тему: урок «Неравенства с двумя переменными»

Урок алгебры в 9 классе

Графическое решение неравенств с двумя переменными.

Цели и задачи урока:

1. Ввести понятие системы неравенств с двумя переменными.

 Составить алгоритм решения систем неравенств

 Формировать навыки решения систем неравенств

2. Развивать « критическое» мышление и интерес к предмету у учащихся в процессе решения проблемных ситуаций и заданий творческого характера.

Оборудование: Ноутбук ,  мультимедийный проектор, 

Этапы урока

•  Организация начала занятия.
• Проверка выполнения домашнего задания.
• Подготовка к усвоению новых знаний.
• Изучение нового материала.
• Первичная проверка знаний.
• Закрепление знаний.
• Подведение итогов занятий.
• Домашнее задание.

Ход урока. 1. Организационный момент.     

    На предыдущих уроках мы решали системы уравнений графическим способом. Сегодня мы переходим к изучению новой темы «Графическое решение неравенств с двумя переменными». Повторим материал прошлого урока.

2. Устная работа учащихся с использованием проектора.

Из данных 6 функций выберите те, которые будут изображаться на экране.

               

 Даны функции  (записаны на доске)

   3.Изучение новой темы .

 Неравенство с двумя неизвестными можно представить так: f(x;y)>, где   f(x;y), – многочлен двух переменных х и у. Его можно записать в виде.

Неравенства содержащие неизвестные могут быть вида

F(x,y)0, F(x,y) 0, F(x,y) 0.

• Решением неравенства называется упорядоченная пара действительных чисел  , обращающая это неравенство в верное числовое неравенство.
• Графически это соответствует заданию точки     координатной плоскости.
• Решить неравенство — значит найти множество его решений

Если одно из неравенств системы представлено в виде  нестрогого неравенства, то график изображается сплошной линией, если строгое, то пунктирной.

Если одно из неравенств системы представлено в виде у ≥f(x).  То это неравенство задает на плоскости область, которая лежит не ниже графика.

Если одно из неравенств системы представлено в виде у ≤f(x).  То это неравенство задает на плоскости область, которая лежит не ниже графика.

 Если линия f(x.у)- замкнутая, например окружность, или замкнутая ломанная, то неравенство f(x.у≥0, задает область лежащую внутри замкнутой линии., а неравенство f(x.у)≤0- область лежащую вне.

 И наиболее универсальное, полезное для проверки правило- Правило пробной точки

• Построить   F(x;y)=0
• Взяв из какой — либо области пробную точку установить, являются ли ее координаты решением неравенства
• Сделать вывод о решении неравенства

Рассмотрим многочлен F(x;y)=y+x-1, тогда

   

В следующем примере дано уравнение окружности.

 Необходимо расставить знаки неравенств >,,используя правило пробной точки О(0,0).

   

• Решаем вместе .

 Рассмотрим примеры.

1. Решить неравенство:│х-0,5│-1,5≤0
2. Решить неравенство:
3. Решить неравенство:

Тестирование.

Системой неравенств  с двумя переменными  является система вида.

Алгоритм решения систем неравенств.

• Построить F(x;y)=0 и  G(x;y)=0
• Взяв из каждой области пробную точку установить, являются ли ее координаты решением системы

Объединение полученных областей- решение системы неравенств

• Решаем вместе .

1. Решить систему неравенств:

2. Решить систему неравенств:

3 Решить графически неравенство:  

Подведение итогов урока. Домашнее задание.

nsportal.ru

19.2. Решение систем mлинейных неравенств с двумя переменными

Дана система т линейных неравенств с двумя переменными

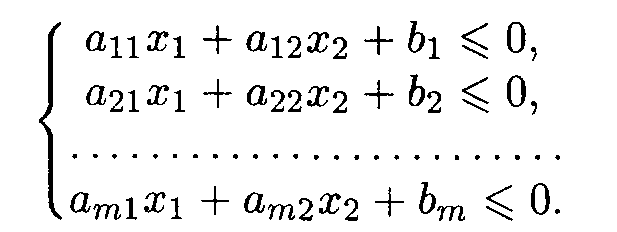
Знаки некоторых или всех неравенств могут быть ≥.

Рассмотрим первое неравенство в системе координат Х₁ОХ₂. Построим прямую

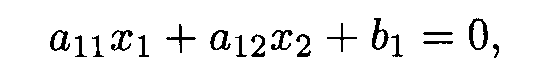
которая является граничной прямой.

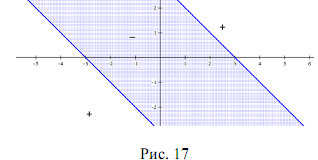
Эта прямая делит плоскость на две полуплоскости 1 и 2 (рис. 19.4).

Полуплоскость 1 содержит начало координат, полуплос­кость 2 не содержит начала координат.

Для определения, по какую сторону от граничной прямой расположена заданная полуплоскость, надо взять произволь­ную точку на плоскости (лучше начало координат) и подста­вить координаты этой точки в неравенство. Если неравенство справедливо, то полуплоскость обращена в сторону этой точки, если не справедливо, то в противоположную от точки сторону.

Направление полуплоскости на рисунках показываем стрел­кой.

Определение 15. Решением каждого неравенства систе­мы является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от нее.

Определение 16. Пересечение полуплоскостей, каждая из ко­торых определяется соответствующим неравенством системы, называется областью решения системы (ОР).

Определение 17. Область решения системы, удовлетворяю­щая условиям неотрицательности (x_j ≥ 0, j = ), называ­ется областью неотрицательных, или допустимых, решений (ОДР).

Если система неравенств совместна, то ОР и ОДР могут быть многогранником, неограниченной многогранной облас­тью или одной точкой.

Если система неравенств несовместна, то ОР и ОДР — пус­тое множество.

Пример 1. Найти ОР и ОДР системы неравенств и опреде­лить координаты угловых точек ОДР

Решение. Найдем ОР первого неравенства: х₁ + 3x₂ ≥ 3. Построим граничную прямую х₁ +3x₂ – 3 = 0 (рис. 19.5). Под­ставим координаты точки (0,0) в неравенство: 1∙0 + 3∙0 > 3; так как координаты точки (0,0) не удовлетворяют ему, то решени­ем неравенства (19.1) является полуплоскость, не содержащая точку (0,0).

Аналогично найдем решения остальных неравенств систе­мы. Получим, что ОР и ОДР системы неравенств является выпуклый многогранник ABCD.

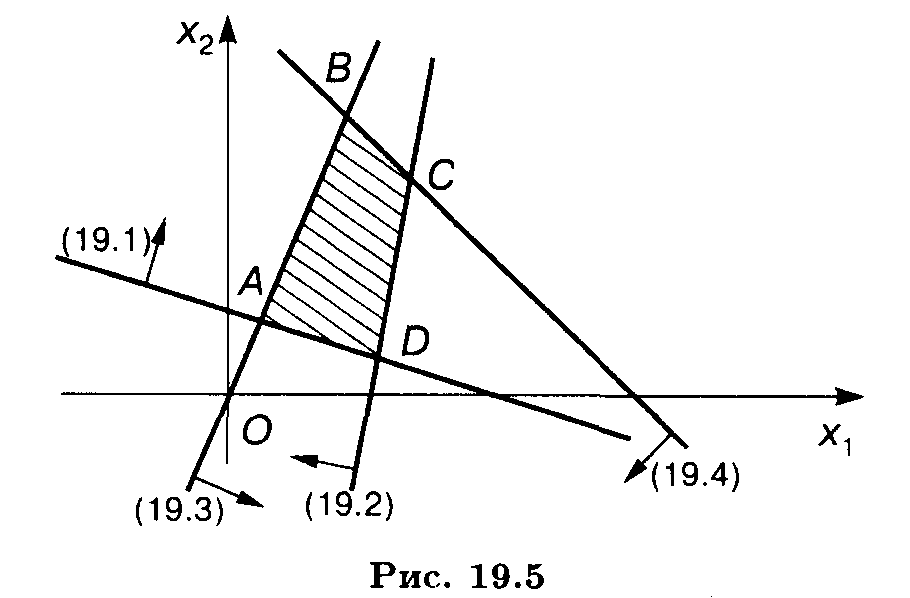
Найдем угловые точки многогранника. Точку А определим как точку пересечения прямых

Решая систему, получим А(3/7, 6/7).

Точку В найдем как точку пересечения прямых

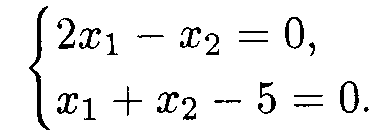
Из системы получим B(5/3, 10/3). Аналогично найдем коорди­наты точек С и D: С(11/4; 9/14), D(3/10; 21/10).

Пример 2. Найти ОР и ОДР системы неравенств

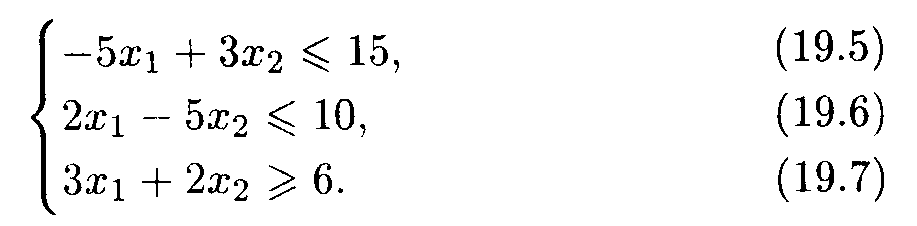
Решение. Построим прямые и определим решения не­равенств (19.5)-(19.7). ОР и ОДР являются неограниченные многогранные области ACFM и ABDEKM соответственно (рис. 19.6).

Пример 3. Найти ОР и ОДР системы неравенств

Решение. Найдем решения неравенств (19.8)-(19.10) (рис. 19.7). ОР представляет неограниченную многогранную область ABC; ОДР — точка В.

Пример 4. Найти OP и ОДР системы неравенств

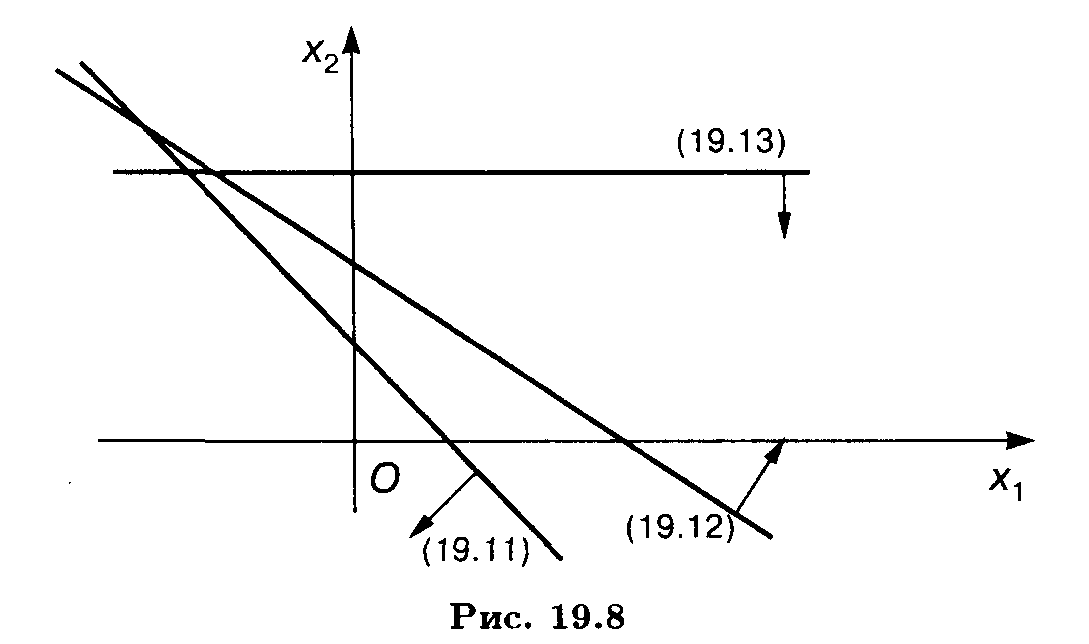
Решение. Построив прямые, найдем решения неравенств системы. ОР и ОДР несовместны (рис. 19.8).

Упражнения

Найти ОР и ОДР систем неравенств

Глава 20. Графический метод

20.1. Постановка задачи

Наиболее простым и наглядным методом линейного про­граммирования является графический метод. Он применяется для решения задач ЛП с двумя переменными, заданными в не­канонической форме, и многими переменными в канонической форме при условии, что они содержат не более двух свободных переменных.

С геометрической точки зрения в задаче линейного про­граммирования ищется такая угловая точка или набор точек из допустимого множества решений, на котором достигается самая верхняя (нижняя) линия уровня, расположенная дальше (ближе) остальных в направлении наискорейшего роста.

Для нахождения экстремального значения целевой функ­ции при графическом решении задач ЛП используют вектор L() на плоскости Х₁ОХ₂, который обозначим . Этот вектор показывает направление наискорейшего изменения це­левой функции, он равен

где е₁ и е₂ — единичные векторы по осям OX₁ и ОX₂ соответ­ственно; таким образом, = (∂L/∂х₁, ∂L/∂х₂). Координатами вектора являются коэффициенты целевой функции L().

studfile.net