Тест 1. Показательные неравенства. | Тест 1. Показательные неравенства. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вариант 13. | Вариант 14. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1. Найти наибольшее целое решение неравенства
| 1. Найти наименьшее целое решение неравенства
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2. Найти наименьшее целое решение неравенства
| 2. Найти наибольшее целое решение неравенства
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3. Найти число целых решений неравенства
| 3. Найти число целых решений неравенства принадлежащих промежутку (-2;5).
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4. Найти среднее арифметическое целых решений неравенства принадлежащих промежутку
| 4.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5. Решить неравенство
| 5. Решить неравенство
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Тест 1. Показательные неравенства. | Тест 1. Показательные неравенства. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вариант 15. | Вариант 16. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1. Найти наибольшее целое решение неравенства
| 1. Найти наименьшее целое решение неравенства
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2. Найти наименьшее целое решение неравенства
| 2. Найти наибольшее целое решение неравенства
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3. Найти число целых решений неравенства
| 3. Найти число целых решений неравенства принадлежащих промежутку
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4. Найти среднее арифметическое целых решений неравенства принадлежащих промежутку
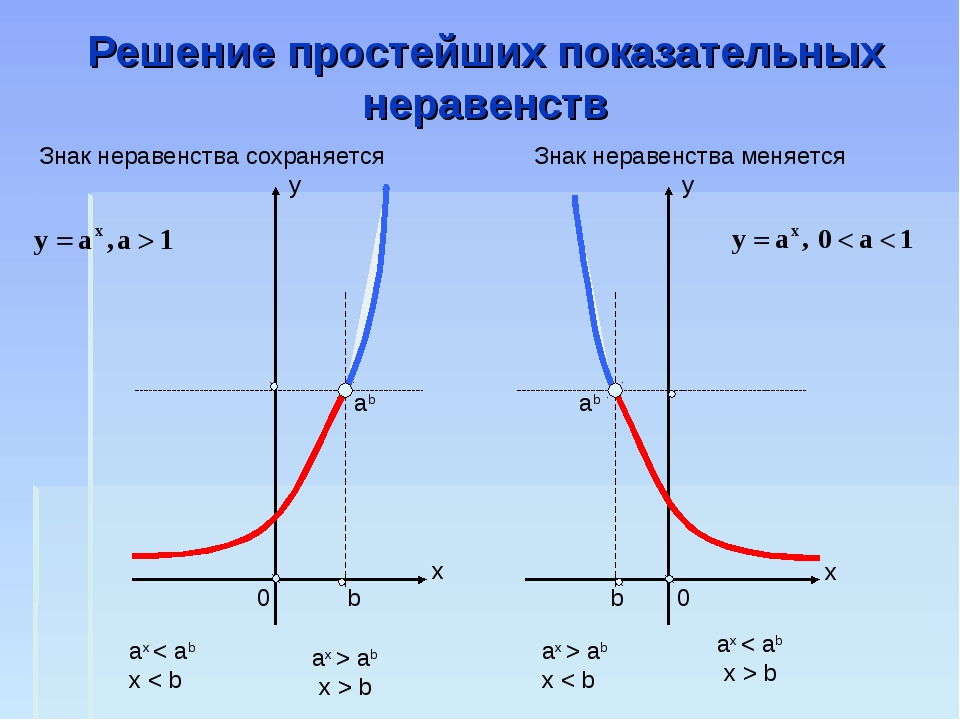
| 4. Ответ: \(x\in[-1;0)\cup(0;2]\). 3.2.6. Показательные и логарифмические неравенстваГлава 3. Решение уравнений и неравенств3.2.3.2.6.Рассмотрим неравенство и неравенство, ему равносильное: Для его решения исследуем знак разности Итак, выясним, что следует из того, что 1) Если a > 1, то f (x) > g (x), а это значит, что (a – 1)(f (x) – g (x)) > 0. 2) Если 0 < a < 1, то f (x) < g (x), и опять (a – 1)(f (x) – g (x)) > 0. Верно и обратное. Если то при имеем то есть а при получаем то есть Таким образом, мы доказали, что:
А это как раз обозначает, что получено условие равносильности:
Решить неравенство Пример 2 Решите неравенство Рассмотрим теперь неравенство
и найдём соответствующие ему условия равносильности. Если a > 1, то тогда и только тогда, когда f (x) > 1 в ОДЗ (f (x) < 1), то есть Если 0 < a < 1, то тогда и только тогда, когда f (x) < 1 в ОДЗ (f (x) > 1), то есть опять Верно и обратное, если то при a > 1 имеем f (x) > 1 в ОДЗ (f (x) < 1), а при 0 < a < 1 имеем f (x) < 1 в ОДЗ (f (x) > 1). Таким образом, получаем следующие условия равносильности. Отсюда следует, что:
Рассмотрим теперь неравенство вида где ОДЗ этого неравенства: Перепишем данное неравенство в виде:
Решите неравенство Пример 4 Решите неравенство
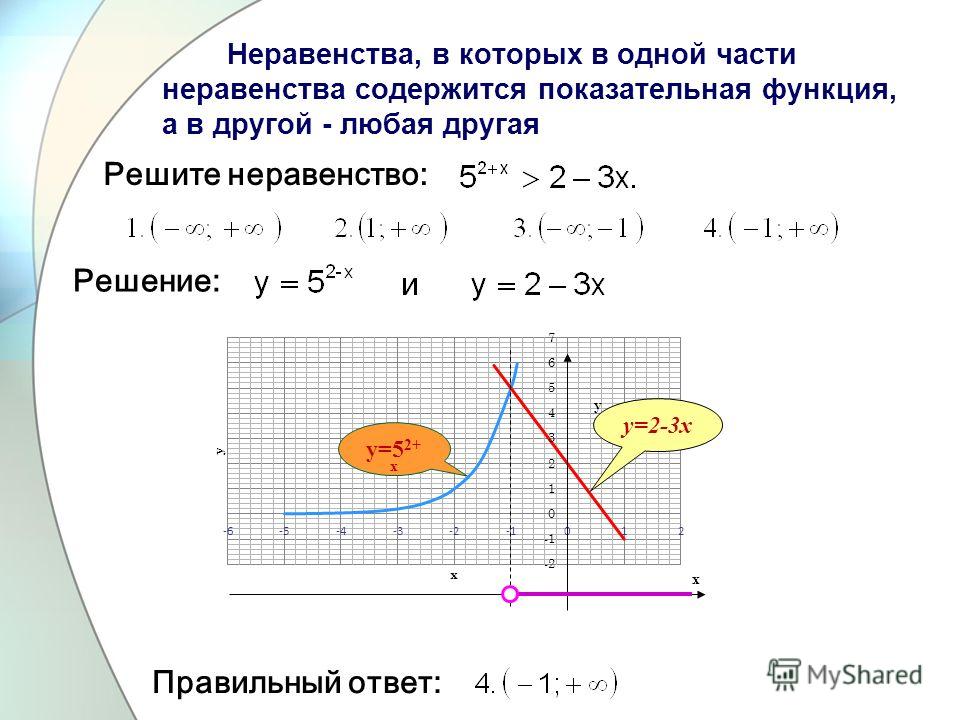
Как решать показательные неравенства графически. Показательные уравнения и неравенства. Выделение устойчивого выражения и замена переменнойУрок и презентация на тему: «Показательные уравнения и показательные неравенства»Дополнительные материалы $(x-3)(x+5)≥0$. Воспользуемся интервальным методом решения: Ответ: $(-∞;-5]U» title=»Rendered by QuickLaTeX.com»> Группируем степени с одинаковыми основаниями. Удобнее для этого развести их по разные стороны неравенства: Title=»Rendered by QuickLaTeX.com»> Из каждой пары степеней выносим за скобки общий множитель — степень с меньшим показателем. Вынести за скобки общий множитель- значит, каждое слагаемое разделить на этот множитель. При делении степеней с одинаковыми основаниями основание оставляем прежним, а показатели вычитаем: Title=»Rendered by QuickLaTeX.com»> Title=»Rendered by QuickLaTeX.com»> Делить можно сразу на 20 (20=4∙5), но практика показывает, что деление в два этапа позволяет избежать возможных ошибок: Title=»Rendered by QuickLaTeX.com»> Title=»Rendered by QuickLaTeX.com»> Title=»Rendered by QuickLaTeX.com»> Title=»Rendered by QuickLaTeX.com»> Title=»Rendered by QuickLaTeX. Title=»Rendered by QuickLaTeX.com»> Так как основание 2/5 убывает, поэтому знак неравенства между показателями степеней изменяется на противоположный: Квадратичное неравенство решим методом интервалов . Нули функции, стоящей в левой части неравенства — x1=-1; x2=2. Отмечаем их на числовой прямой. Для проверки знака возьмем нуль: 0²-0-2=-2, в промежуток, которому принадлежит нуль, ставим «-«. Остальные знаки расставляем в шахматном порядке. Так как решаем неравенство, в котором левая часть меньше нуля, выбираем промежуток со знаком «-«. Ответ: x ∈ (-1; 2). Вариант неравенств такого вида — все степени имеют одинаковые основания, но отличаются коэффициентами при x в показателях. В левой части выносим за скобки степень с наименьшим показателем Title=»Rendered by QuickLaTeX.com»> Пришли к показательному неравенству . Так как основание 7>1, функция возрастает, знак неравенства между показателями не изменяется: Чтобы решить это неравенство методом интервалов перенесем все слагаемые в левую часть и приведём дроби к Показательными уравнениями и неравенствами считают такие уравнения и неравенства, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения а х = а b , где а > 0, а ≠ 1, х – неизвестное. Это уравнение имеет единственный корень х = b, так как справедлива следующая теорема: Теорема. Если а > 0, а ≠ 1 и а х 1 = а х 2 , то х 1 = х 2 . Обоснуем рассмотренное утверждение. Предположим, что равенство х 1 = х 2 не выполняется, т.е. х 1 1, то показательная функция у = а х возрастает и поэтому должно выполняться неравенство а х 1 а х 2 . В обоих случаях мы получили противоречие условию а х 1 = а х 2 . Рассмотрим несколько задач. Решить уравнение 4 ∙ 2 х = 1. Решение. Запишем уравнение в виде 2 2 ∙ 2 х = 2 0 – 2 х+2 = 2 0 , откуда получаем х + 2 = 0, т.е. х = -2. Ответ. х = -2. Решить уравнение 2 3х ∙ 3 х = 576. Решение. Так как 2 3х = (2 3) х = 8 х, 576 = 24 2 , то уравнение можно записать в виде 8 х ∙ 3 х = 24 2 или в виде 24 х = 24 2 . Отсюда получаем х = 2. Ответ. х = 2. Решить уравнение 3 х+1 – 2∙3 х — 2 = 25. Решение. Вынося в левой части за скобки общий множитель 3 х — 2 , получаем 3 х — 2 ∙ (3 3 – 2) = 25 – 3 х — 2 ∙ 25 = 25, откуда 3 х — 2 = 1, т.е. х – 2 = 0, х = 2. Решить уравнение 3 х = 7 х. Решение. Так как 7 х ≠ 0, то уравнение можно записать в виде 3 х /7 х = 1, откуда (3/7) х = 1, х = 0. Ответ. х = 0. Решить уравнение 9 х – 4 ∙ 3 х – 45 = 0. Решение. Заменой 3 х = а данное уравнение сводится к квадратному уравнению а 2 – 4а – 45 = 0. Решая это уравнение, находим его корни: а 1 = 9, а 2 = -5, откуда 3 х = 9, 3 х = -5. Уравнение 3 х = 9 имеет корень 2, а уравнение 3 х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения. Ответ. х = 2. Решение показательных неравенств часто сводится к решению неравенств а х > а b или а х Рассмотрим некоторые задачи. Решить неравенство 3 х Решение. Запишем неравенство в виде 3 х 1, то функция у = 3 х является возрастающей. Следовательно, при х Таким образом, при х 3 х Ответ. х Решить неравенство 16 х +4 х – 2 > 0. Решение. Обозначим 4 х = t, тогда получим квадратное неравенство t2 + t – 2 > 0. Это неравенство выполняется при t 1. Так как t = 4 х, то получим два неравенства 4 х 1. Первое неравенство не имеет решений, так как 4 х > 0 при всех х € R. Второе неравенство запишем в виде 4 х > 4 0 , откуда х > 0. Ответ. х > 0. Графически решить уравнение (1/3) х = х – 2/3. Решение. 1) Построим графики функций у = (1/3) х и у = х – 2/3. 2) Опираясь на наш рисунок, можно сделать вывод, что графики рассмотренных функций пересекаются в точке с абсциссой х ≈ 1. Проверка доказывает, что х = 1 – корень данного уравнения: (1/3) 1 = 1/3 и 1 – 2/3 = 1/3. Иными словами, мы нашли один из корней уравнения. 3) Найдем другие корни или докажем, что таковых нет. Функция (1/3) х убывающая, а функция у = х – 2/3 возрастающая. Следовательно, при х > 1 значения первой функции меньше 1/3, а второй – больше 1/3; при х 1 и х Ответ. х = 1. Заметим, что из решения этой задачи, в частности, следует, что неравенство (1/3) х > х – 2/3 выполняется при х 1. сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна. Решение большинства математических задач так или иначе связано с преобразованием числовых, алгебраических или функциональных выражений. Сказанное в особенности относится к решению . В вариантах ЕГЭ по математике к такому типу задач относится, в частности, задача C3. Научиться решать задания C3 важно не только с целью успешной сдачи ЕГЭ, но и по той причине, что это умение пригодится при изучении курса математики в высшей школе. Выполняя задания C3, приходится решать различные виды уравнений и неравенств. Прежде чем приступить к разбору конкретных показательных уравнений и неравенств , как репетитор по математике, предлагаю вам освежить в памяти некоторый теоретический материал, который нам понадобится. Показательная функцияЧто такое показательная функция?Функцию вида y = a x , где a > 0 и a ≠ 1, называют показательной функцией . Основные свойства показательной функции y = a x : График показательной функцииГрафиком показательной функции является экспонента : Графики показательных функций (экспоненты) Решение показательных уравненийПоказательными называются уравнения, в которых неизвестная переменная находится только
в показателях каких-либо степеней. Для решения показательных уравнений требуется знать и уметь использовать следующую несложную теорему: Теорема 1. Показательное уравнение a f (x ) = a g (x ) (где a > 0, a ≠ 1) равносильно уравнению f (x ) = g (x ). Помимо этого, полезно помнить об основных формулах и действиях со степенями: Title=»Rendered by QuickLaTeX.com»> Пример 1. Решите уравнение: Решение: используем приведенные выше формулы и подстановку: Уравнение тогда принимает вид: Дискриминант полученного квадратного уравнения положителен: Title=»Rendered by QuickLaTeX.com»> Это означает, что данное уравнение имеет два корня. Находим их: Переходя к обратной подстановке, получаем: Второе уравнение корней не имеет, поскольку показательная функция строго положительна на всей области определения. Решаем второе: С учетом сказанного в теореме 1 переходим к эквивалентному уравнению: x = 3. Ответ: x = 3. Пример 2. Решите уравнение: Решение: ограничений на область допустимых значений у уравнения нет, так как подкоренное выражение имеет смысл при любом значении x (показательная функция y = 9 4 -x положительна и не равна нулю). Решаем уравнение путем равносильных преобразований с использованием правил умножения и деления степеней: Последний переход был осуществлен в соответствии с теоремой 1. Ответ: x = 6. Пример 3. Решите уравнение: Решение: обе части исходного уравнения можно поделить на 0,2 x . Данный переход будет являться равносильным, поскольку это выражение больше нуля при любом значении x (показательная функция строго положительна на своей области определения). Тогда уравнение принимает вид: Ответ: x = 0. Пример 4. Решение: упрощаем уравнение до элементарного путем равносильных преобразований с использованием приведенных в начале статьи правил деления и умножения степеней: Деление обеих частей уравнения на 4 x , как и в предыдущем примере, является равносильным преобразованием, поскольку данное выражение не равно нулю ни при каких значениях x . Ответ: x = 0. Пример 5. Решите уравнение: Решение: функция y = 3 x , стоящая в левой части уравнения, является возрастающей. Функция y = —x -2/3, стоящая в правой части уравнения, является убывающей. Это означает, что если графики этих функций пересекаются, то не более чем в одной точке. В данном случае нетрудно догадаться, что графики пересекаются в точке x = -1. Других корней не будет. Ответ: x = -1. Пример 6. Решите уравнение: Решение: упрощаем уравнение путем равносильных преобразований, имея в виду везде, что показательная функция строго больше нуля при любом значении x и используя правила вычисления произведения и частного степеней, приведенные в начале статьи: Ответ: x = 2. Решение показательных неравенствПоказательными называются неравенства, в которых неизвестная переменная содержится только в показателях каких-либо степеней. Для решения показательных неравенств требуется знание следующей теоремы: Теорема 2. Если a > 1, то неравенство a f (x ) > a g (x ) равносильно неравенству того же смысла: f (x ) > g (x ). Если 0 a a f (x ) > a g (x ) равносильно неравенству противоположного смысла: f (x ) g (x ). Пример 7. Решите неравенство: Решение: представим исходное неравенство в виде: Разделим обе части этого неравенства на 3 2x , при этом (в силу положительности функции y = 3 2x ) знак неравенства не изменится: Воспользуемся подстановкой: Тогда неравенство примет вид: Итак, решением неравенства является промежуток: переходя к обратной подстановке, получаем: Левое неравенства в силу положительности показательной функции выполняется автоматически. Поскольку в основании степени стоит число, большее единицы, эквивалентным (по теореме 2) будет переход к следующему неравенству: Итак, окончательно получаем ответ: Пример 8. Решите неравенство: Решение: используя свойства умножения и деления степеней, перепишем неравенство в виде: Введем новую переменную: С учетом этой подстановки неравенство принимает вид: Умножим числитель и знаменатель дроби на 7, получаем следующее равносильное неравенство: Итак, неравенству удовлетворяют следующие значения переменной t : Тогда, переходя к обратной подстановке, получаем: Поскольку основание степени здесь больше единицы, равносильным (по теореме 2) будет переход к неравенству: Окончательно получаем ответ: Пример 9. Решение: Делим обе части неравенства на выражение: Оно всегда больше нуля (из-за положительности показательной функции), поэтому знак неравенства изменять не нужно. Получаем: t , находящиеся в промежутке: Переходя к обратной подстановке получаем, что исходное неравенство распадается на два случая: Первое неравенство решений не имеет в силу положительности показательной функции. Решаем второе: Пример 10. Решите неравенство: Решение: Ветви параболы y = 2x +2-x 2 направлены вниз, следовательно она ограничена сверху значением, которое она достигает в своей вершине: Ветви параболы y = x 2 -2x +2, стоящей в показателе, направлены вверх, значит она ограничена снизу значением, которое она достигает в своей вершине: Вместе с этим ограниченной снизу оказывается и функция y = 3 x 2 -2x +2 , стоящая в правой части уравнения. Ответ: x = 1. Для того, чтобы научиться решать показательные уравнения и неравенства, необходимо постоянно тренироваться в их решении. В этом нелегком деле вам могут помочь различные методические пособия, задачники по элементарной математике, сборники конкурсных задач, занятия по математике в школе, а также индивидуальные занятия с профессиональным репетитором. Искренне желаю вам успехов в подготовке и блестящих результатов на экзамене. P. S. Уважаемые гости! Пожалуйста, не пишите в комментариях заявки на решение ваших уравнений. Здравствуйте! Дорогие мои ученики, в этой статье мы научимся с вами решать показательные неравенства. Каким бы сложным не показалось вам показательное неравенство, после некоторых преобразований (о них мы поговорим чуть позже) все неравенства сводятся к решению простейших показательных неравенств : а х > b , a x и a x ≥ b , a x ≤ b . Давайте попробуем разобраться как же решаются такие неравенства. Мы рассмотрим решение строгих неравенств . Отличие при решении нестрогих неравенств заключается только в том, что полученные соответствующие корни включаются в ответ. Пусть надо решить неравенство вида а f (x) > b , где a>1 и b>0 . Посмотрите на схему решения таких неравенств (рисунок 1): Сейчас рассмотрим конкретный пример. Так как 5 > 1 и 125 > 0, то Ответ: (4; +∞) . А каким же будет решение этого же неравенства а f (x) >b , если 0 и b>0 ? Итак, схема на рисунке 2 Пример: Решить неравенство (1/2) 2x — 2 ≥ 4 Применяя правило (рисунок 2), получаем Ответ: (–∞; 0] . Снова рассмотрим это же неравенство а f (x) > b , если a>0 и b. Итак, схема на рисунке 3: Пример решения неравенства (1/3) х + 2 > –9 . Как мы замечаем, какое бы число мы не подставили вместо х, (1/3) х + 2 всегда больше нуля. Ответ: (–∞; +∞) . А как же решаются неравенства вида а f (x) , где a>1 и b>0 ? Схема на рисунке 4: И следующий пример: 3 3 – х ≥ 8 . Ответ: (0; 3–log 3 8) . Как же измениться решение неравенства а f (x) , при 0 и b>0 ? Схема на рисунке 5: И следующий пример: Решить неравенство 0,6 2х – 3 . Cледуя схеме на рисунке 5, получаем Ответ: (2,5; +∞) . Рассмотрим последнюю схему решения неравенства вида а f (x) , при a>0 и b, представленную на рисунке 6: Например, решим неравенство: Замечаем, что какое бы число мы не подставили вместо х, левая часть неравенства всегда больше нуля, а у нас это выражение меньше -8, т.е. и нуля, значит решений нет. Ответ: решений нет . Зная как решаются простейшие показательные неравенства, можно приступить и к решению показательных неравенств . Пример 1. Найти наибольшее целое значение х, удовлетворяющее неравеству Так как 6 х больше нуля (ни при каком х знаменатель в ноль не обращается), умножим обе части неравенства на 6 х, получим: 440 – 2· 6 2х > 8, тогда x Ответ: 1 . Пример 2 . Решить неравенство 2 2 x – 3·2 x + 2 ≤ 0 Обозначим 2 х через у, получим неравенство у 2 – 3у + 2 ≤ 0, решим это квадратное неравенство. у 2 – 3у +2 = 0, Ветви параболы направлены вверх, изобразим график: Тогда решением неравенства будет неравенство 1 Ответ: (0; 1) . Пример 3 . Решите неравенство 5 x +1 – 3 x +2 5 x +1 – 2·5 x Вынесем в левой части неравенства за скобки 5 x , а в правой части неравенства 3 х и получим неравенство 5 х (5 – 2) 3·5 х Разделим обе части неравенства на выражение 3·3 х, знак неравенства не изменится, так как 3·3 х положительное число, получим неравенство: х 1). Ответ: (–∞; 2) . Если у вас возникнут вопросы по решению показательных неравенств или вы захотите попрактиковаться в решении подобных примеров, записывайтесь ко мне на уроки. Репетитор Валентина Галиневская . сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна. Экзамены, тесты по математике. Показательные уравнения и неравенстваУважаемые школьники, выпускники, абитуриенты, этот раздел поможет подготовиться к экзаменам, тестам, внешнему независимому тестированию по математике в 2015 году. Ответы к тестам помогут Вам понять материал и методику вычислений, систематизировать и повысить накопленный уровень знаний по математике. Решение примеров будут интересны для школьников 9, 10, 11 классов, а так же их родителей. Раздел II. Уравнения и неравенстваЗадача 2.24 (Т-07, 45) Решите показательное уравнение .
Задача 2.25 Если показательное уравнение имеет вид то решение х=
Задача 2.26 Решите неравенство:
Задача 2.27 Решите показательное неравенство
Задача 2.28 Решите неравенство .
Алгоритм решения показательных уравнений и неравенств. Показательные неравенства Показательные неравенстваНа данном уроке мы рассмотрим различные показательные неравенства и научимся их решать, основываясь на методике решения простейших показательных неравенств 1. Определение и свойства показательной функцииНапомним определение и основные свойства показательной функции. Именно на свойствах базируется решение всех показательных уравнений и неравенств. Показательная функция — это функция вида , где основание степени и Здесь х — независимая переменная, аргумент; у — зависимая переменная, функция. Рис. 1. График показательной функции На графике показаны возрастающая и убывающая экспоненты, иллюстрирующие показательную функцию при основании большем единицы и меньшем единицы, но большим нуля соответственно. Обе кривые проходят через точку (0;1) Свойства показательной функции : Область определения: ; Область значений: ; Функция монотонна, при возрастает, при убывает. Монотонная функция принимает каждое свое значение при единственном значении аргумента. При , когда аргумент возрастает от минус до плюс бесконечности, функция возрастает от нуля не включительно до плюс бесконечности, т. е. при данных значениях аргумента мы имеем монотонно возрастающую функцию (). При наоборот, когда аргумент возрастает от минус до плюс бесконечности, функция убывает от бесконечности до нуля не включительно, т. е. при данных значениях аргумента мы имеем монотонно убывающую функцию (). 2. Простейшие показательные неравенства, методика решения, примерНа основании вышесказанного приведем методику решения простейших показательных неравенств: Методика решения неравенств: Уравнять основания степеней; Сравнить показатели, сохранив или изменив на противоположный знак неравенства. Решение сложных показательных неравенств заключается, как правило, в их сведении к простейшим показательным неравенствам. Основание степени больше единицы, значит, знак неравенства сохраняется: Преобразуем правую часть согласно свойствам степени: Основание степени меньше единицы, знак неравенства необходимо поменять на противоположный: Для решения квадратного неравенства решим соответствующее квадратное уравнение: По теореме Виета находим корни: Ветви параболы направлены вверх. Таким образом, имеем решение неравенства: Несложно догадаться, что правую часть можно представить как степень с нулевым показателем: Основание степени больше единицы, знак неравенства не меняется, получаем: Напомним методику решения таких неравенств. Рассматриваем дробно-рациональную функцию: Находим область определения: Находим корни функции: Функция имеет единственный корень, Выделяем интервалы знакопостоянства и определяем знаки функции на каждом интервале: Рис. 2. Интервалы знакопостоянства Таким образом, получили ответ. Ответ: 3. Решение типовых показательных неравенствРассмотрим неравенства с одинаковыми показателями, но различными основаниями. Одно из свойств показательной функции — она при любых значениях аргумента принимает строго положительные значения, значит, на показательную функцию можно разделить. Выполним деление заданного неравенства на правую его часть: Основание степени больше единицы, знак неравенства сохраняется. Проиллюстрируем решение: На рисунке 6.3 изображены графики функций и . Очевидно, что когда аргумент больше нуля, график функции расположен выше, эта функция больше. Когда же значения аргумента отрицательны, функция проходит ниже, она меньше. При значении аргумента функции равны, значит, данная точка также является решением заданного неравенства. Рис. 3. Иллюстрация к примеру 4 Преобразуем заданное неравенство согласно свойствам степени: Приведем подобные члены: Разделим обе части на : Теперь продолжаем решать аналогично примеру 4, разделим обе части на : Основание степени больше единицы, знак неравенства сохраняется: 4. Графическое решение показательных неравенствПример 6 — решить неравенство графически: Рассмотрим функции, стоящие в левой и правой части и построим график каждой из них. Функция — экспонента, возрастает на всей своей области определения, т. е. при всех действительных значениях аргумента. Функция — линейная, убывает на всей своей области определения, т. е. при всех действительных значениях аргумента. Если данные функции пересекаются, то есть система имеет решение, то такое решение единственное и его легко можно угадать. Для этого перебираем целые числа () Несложно заметить, что корнем данной системы является : Таким образом, графики функций пересекаются в точке с аргументом, равным единице. Теперь нужно получить ответ. Смысл заданного неравенства в том, что экспонента должна быть больше или равна линейной функции, то есть быть выше или совпадать с ней. Очевиден ответ: (рисунок 6.4) Рис. 4. Иллюстрация к примеру 6 Итак, мы рассмотрели решение различных типовых показательных неравенств. Далее перейдем к рассмотрению более сложных показательных неравенств. Список литературы Мордкович А. Г. Алгебра и начала математического анализа. — М.: Мнемозина. Муравин Г. К., Муравина О. В. Алгебра и начала математического анализа. Math. md . Mathematics-repetition. com . Diffur. kemsu. ru . Домашнее задание 1. Алгебра и начала анализа, 10-11 класс (А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын) 1990, № 472, 473; 2. Решить неравенство: 3. Решить неравенство. Показательными уравнениями и неравенствами считают такие уравнения и неравенства, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения а х = а b , где а > 0, а ≠ 1, х – неизвестное. Это уравнение имеет единственный корень х = b, так как справедлива следующая теорема: Теорема. Если а > 0, а ≠ 1 и а х 1 = а х 2 , то х 1 = х 2 . Обоснуем рассмотренное утверждение. Предположим, что равенство х 1 = х 2 не выполняется, т.е. х 1 1, то показательная функция у = а х возрастает и поэтому должно выполняться неравенство а х 1 а х 2 . Рассмотрим несколько задач. Решить уравнение 4 ∙ 2 х = 1. Решение. Запишем уравнение в виде 2 2 ∙ 2 х = 2 0 – 2 х+2 = 2 0 , откуда получаем х + 2 = 0, т.е. х = -2. Ответ. х = -2. Решить уравнение 2 3х ∙ 3 х = 576. Решение. Так как 2 3х = (2 3) х = 8 х, 576 = 24 2 , то уравнение можно записать в виде 8 х ∙ 3 х = 24 2 или в виде 24 х = 24 2 . Отсюда получаем х = 2. Ответ. х = 2. Решить уравнение 3 х+1 – 2∙3 х — 2 = 25. Решение. Вынося в левой части за скобки общий множитель 3 х — 2 , получаем 3 х — 2 ∙ (3 3 – 2) = 25 – 3 х — 2 ∙ 25 = 25, откуда 3 х — 2 = 1, т.е. х – 2 = 0, х = 2. Ответ. х = 2. Решить уравнение 3 х = 7 х. Решение. Так как 7 х ≠ 0, то уравнение можно записать в виде 3 х /7 х = 1, откуда (3/7) х = 1, х = 0. Ответ. х = 0. Решить уравнение 9 х – 4 ∙ 3 х – 45 = 0. Решение. Заменой 3 х = а данное уравнение сводится к квадратному уравнению а 2 – 4а – 45 = 0. Решая это уравнение, находим его корни: а 1 = 9, а 2 = -5, откуда 3 х = 9, 3 х = -5. Уравнение 3 х = 9 имеет корень 2, а уравнение 3 х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения. Ответ. х = 2. Решение показательных неравенств часто сводится к решению неравенств а х > а b или а х Рассмотрим некоторые задачи. Решить неравенство 3 х Решение. Запишем неравенство в виде 3 х 1, то функция у = 3 х является возрастающей. Следовательно, при х Таким образом, при х 3 х Ответ. х Решить неравенство 16 х +4 х – 2 > 0. Решение. Обозначим 4 х = t, тогда получим квадратное неравенство t2 + t – 2 > 0. Это неравенство выполняется при t 1. Так как t = 4 х, то получим два неравенства 4 х 1. Первое неравенство не имеет решений, так как 4 х > 0 при всех х € R. Второе неравенство запишем в виде 4 х > 4 0 , откуда х > 0. Ответ. х > 0. Графически решить уравнение (1/3) х = х – 2/3. Решение. 1) Построим графики функций у = (1/3) х и у = х – 2/3. 2) Опираясь на наш рисунок, можно сделать вывод, что графики рассмотренных функций пересекаются в точке с абсциссой х ≈ 1. Проверка доказывает, что х = 1 – корень данного уравнения: (1/3) 1 = 1/3 и 1 – 2/3 = 1/3. Иными словами, мы нашли один из корней уравнения. 3) Найдем другие корни или докажем, что таковых нет. Функция (1/3) х убывающая, а функция у = х – 2/3 возрастающая. Следовательно, при х > 1 значения первой функции меньше 1/3, а второй – больше 1/3; при х 1 и х Ответ. х = 1. Заметим, что из решения этой задачи, в частности, следует, что неравенство (1/3) х > х – 2/3 выполняется при х 1. сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна. Но вернёмся к нашей задаче. Попробуем в этот раз обойтись без рационализации. Вспоминаем: основание степени больше единицы, поэтому тройки можно просто зачеркнуть — знак неравенства при этом не поменяется. Получим: \[\begin{align} & -\frac{8x}{3} \lt 4-4x; \\ & 4x-\frac{8x}{3} \lt 4; \\ & \frac{4x}{3} \lt 4; \\ & 4x \lt 12; \\ & x \lt 3. \\\end{align}\] Вот и всё. Окончательный ответ: $x\in \left(-\infty ;3 \right)$. Выделение устойчивого выражения и замена переменнойВ заключение предлагаю решить ещё четыре показательных неравенства, которые уже являются довольно сложными для неподготовленных учеников. Конечно, все эти числа при желании можно восстановить в уме, просто последовательно умножая их друг на друга. Однако, когда вам предстоит решить несколько показательных неравенств, причём каждое следующее сложнее предыдущего, то последнее, о чём хочется думать — это степени каких-то там чисел. И в этом смысле данные задачи являются более сложными, нежели «классические» неравенства, которые решаются методом интервалов. белгородский государственный университет КАФЕДРА алгебры, теории чисел и геометрии Тема работы: Показательно-степенные уравнения и неравенства. Дипломная работа студента физико-математического факультета Научный руководитель: ______________________________ Рецензент: _______________________________ ________________________ Белгород. 2006 г.
Введение. «…радость видеть и понимать…» А.Эйнштейн. В этой работе я попыталась передать свой опыт работы учителем математики, передать хоть в какой-то степени свое отношение к ее преподаванию — человеческому делу, в котором удивительным образом переплетаются и математическая наука, и педагогика, и дидактика, и психология, и даже философия. Мне довелось работать с малышами и выпускниками, с детьми, стоящими на полюсах интеллектуального развития: теми, кто состоял на учете у психиатра и кто действительно интересовался математикой Мне довелось решать множество методических задач. Я попытаюсь рассказать о тех из них, которые мне удалось решить. Но еще важнее самого опыта — учительские размышления и сомнения: а почему он именно такой, этот опыт? И лето нынче на дворе иное, и разворот образования стал поинтереснее. «Под юпитерами» нынче не поиски мифической оптимальной системы обучения «всех и всему», а сам ребенок. Но тогда — с необходимостью — и учитель. В школьном курсе алгебры и начал анализа, 10 – 11 класс, при сдаче ЕГЭ за курс средней школы и на вступительных экзаменах в ВУЗы встречаются уравнения и неравенства, содержащее неизвестное в основании и показатели степени – это показательно-степенные уравнения и неравенства. В школе им мало уделяется внимания, в учебниках практически нет заданий на эту тему. Однако, овладение методикой их решения, мне кажется, очень полезным: оно повышает умственные и творческие способности учащихся, перед нами открываются совершенно новые горизонты. При решении задач ученики приобретают первые навыки исследовательской работы, обогащается их математическая культура, развиваются способности к логическому мышлению. Работать над данной темой дипломного исследования я начала еще с написания курсовой. В ходе, которой я глубже изучила и проанализировала математическую литературу по этой теме, выявила наиболее подходящий метод решения показательно-степенных уравнений и неравенств. Он заключается в том, что помимо общепринятого подхода при решении показательно-степенных уравнений (основание берется больше 0) и при решении тех же неравенств (основание берется больше 1 или больше 0, но меньше 1), рассматриваются еще и случаи, когда основания отрицательны, равны 0 и 1. Анализ письменных экзаменационных работ учащихся показывает, что неосвещенность вопроса об отрицательном значении аргумента показательно-степенной функции в школьных учебниках, вызывает у них ряд трудностей и ведет к появлению ошибок. Чтобы учащиеся смогли успешно сдать выпускные и вступительные экзамены, я считаю, необходимо уделять больше внимания решению показательно-степенных уравнений и неравенств на учебных занятиях, либо дополнительно на факультативах и кружках. Таким образом тема , моей дипломной работы определена следующим образом: «Показательно-степенные уравнения и неравенства». Целями настоящей работы являются: 1. Проанализировать литературу по данной теме. 2. Дать полный анализ решения показательно-степенных уравнений и неравенств. 3. Привести достаточное число примеров по данной теме разнообразных типов. 4. Проверить на урочных, факультативных и кружковых занятиях как будет восприниматься предлагаемые приемы решения показательно-степенных уравнений и неравенств. Дать соответствующие рекомендации к изучению этой темы. Предметом нашего исследования является разработка методики решения показательно-степенных уравнений и неравенств. Цель и предмет исследования потребовали решения следующих задач: 1. Изучить литературу по теме: «Показательно-степенные уравнения и неравенства». 2. Овладеть методиками решения показательно-степенных уравнений и неравенств. 3. Подобрать обучающий материал и разработать систему упражнений разных уровней по теме: «Решение показательно-степенных уравнений и неравенств». В ходе дипломного исследования было проанализировано более 20 работ, посвященных применению различных методов решения показательно-степенных уравнений и неравенств. Отсюда получаем. План дипломной работы: Введение. Глава I. Анализ литературы по теме исследования. Глава II. Функции и их свойства, используемые при решении показательно-степенных уравнений и неравенств. II.1. Степенная функция и ее свойства. II.2. Показательная функция и ее свойства. Глава III. Решение показательно-степенных уравнений, алгоритм и примеры. Глава IV. Решение показательно-степенных неравенств, план решения и примеры. Глава V. Опыт проведения занятий со школьниками по данной теме. 1.Обучающий материал. 2.Задачи для самостоятельного решения. Заключение. Выводы и предложения. Список использованной литературы. В I главе проанализирована литература а x = b — простейшее показательное уравнение. В нем a больше нуля и а не равняется единице. Решение показательных уравненийИз свойств показательной функции знаем, что ее область значений ограничена положительными вещественными числами. Тогда если b = 0, уравнение не имеет решений. Теперь положим, что b>0. Если в показательной функции основание a больше единицы, то функция будет возрастающей на всей области определения. Если в показательной функции для основания а выполнено следующее условие 0 Исходя из этого и применяя теорему о корне, получим, что уравнение a x = b иметь один единственный корень, при b>0 и положительном a не равном единице. Чтобы его найти, необходимо представить b в виде b = a c . Рассмотрим следующий пример: решить уравнение 5 (x 2 — 2*x — 1) = 25. Представим 25 как 5 2 , получим: 5 (x 2 — 2*x — 1) = 5 2 . Или что равносильно: x 2 — 2*x — 1 = 2. Решаем полученное квадратное уравнение любым из известных способов. Получаем два корня x = 3 и x = -1. Ответ: 3;-1. Решим уравнение 4 x — 5*2 x + 4 = 0. Сделаем замену: t=2 x и получим следующее квадратное уравнение: t 2 — 5*t + 4 = 0. Теперь решаем уравнения 2 x = 1 и 2 x = 4. Ответ: 0;2. Решение показательных неравенствРешение простейших показательных неравенств основывается тоже на свойствах возрастания и убывания функции. Если в показательной функции основание a больше единицы, то функция будет возрастающей на всей области определения. Если в показательной функции для основания а выполнено следующее условие 0, то данная функция будет убывающей на всем множестве вещественных чисел. Рассмотрим пример: решить неравенство (0.5) (7 — 3*x) Заметим, что 4 = (0.5) 2 . Тогда неравенство примет вид (0.5)(7 — 3*x) Получим: 7 — 3*x>-2. Отсюда: х Ответ: х Если бы в неравенстве основание было больше единицы, то при избавлении от основания, знак неравенства менять было бы не нужно. Задача 15 (С3). Показательные неравенства. — МатематикаФайл к уроку – Показательные неравенства. Показательным называется неравенство, которое содержит неизвестную величину в показателе степени при постоянном основании A (A 0). Методы решения показательных неравенств те же, что и для уравнений:
Принципиально новым методом является метод рационализации, или еще его называют метод оптимизации –процедура, позволяющая упростить неравенство и свести его к рациональному неравенству, которое решается методом интервалов. Рассмотрим неравенство
Теорема: Сравнение , где знак заменяет один из знаков . Получается, что знак неравенства совпадает со знаком неравенства при любом положительном а, и при решении неравенств рациональнее заменить сравнение или его часть на равносильную по знаку часть . Пример: Решить неравенство Решение:
Решая методом интервалов и учитывая ОДЗ, получаем ответ Задачи к уроку:
Ответ: .
Ответ: .
Ответ: .
Ответ: .
Ответ:
Ответ: .
Ответ: .
Ответ: .
Ответ:
Ответ:
Ответ:
Ответ:
Ответ:
 □ _ \ квадрат □ □ _ \ квадрат □Напомним, что отрицательные основания хорошо работают только с целыми показателями; в противном случае результат обычно бывает сложным. Следовательно, любое значение, которое делает основание отрицательным, должно также делать показатель степени целым, чтобы выражение оставалось четко определенным. Решите неравенство (х2 + х-2) х2-х-2> 0.2-x-4 = 0 \ подразумевает x = \ frac {1 \ pm \ sqrt {17}} {2} x2 − x − 4 = 0⟹x = 21 ± 17. Только 1−172∈ [−2,1] \ frac {1- \ sqrt {17}} {2} \ in [-2,1] 21−17 ∈ [−2,1], так что это единственное решение в этом подслучае. Суммируя случаи, набор решений составляет х <-2, х = 1-172, х = -1, х = 0, х> 1. □ x <-2, \ x = \ frac {1- \ sqrt {17}} {2}, \ x = -1, \ x = 0, \ x> 1. \ _ \ squarex <−2, x = 21−17, х = -1, х = 0, х> 1. □ Показатели и неравенства — GMAT Math Study GuideОпределения
Работая с неравенством: экспонентыПри работе с неравенствами, включающими показатели степени, эти неравенства ведут себя во многом как традиционные уравнения.Неравенства с четным показателем обычно имеют два решения, а неравенства с нечетным показателем имеют одно решение. Нечетные экспоненты Неравенство с нечетным показателем ведет себя точно так же, как неравенство без показателя степени или традиционное уравнение с нечетным показателем. Единственное предостережение — которое также относится к неравенствам без показателей — это то, что вы должны знать знак переменной, прежде чем вы сможете делить или умножать ее (см. Умножение и деление с неравенствами). x 3 <27 2x 3 + 14> 30 Четные экспоненты Как указано выше, неравенство с четным показателем обычно имеет два решения. x 2 > 16 Случай 1: x положителен Случай 2: x отрицателен Решение можно представить графически. 3x 2 <27 Множественные неравенства Множественные неравенства с показателями решаются так же, как решаются множественные неравенства без показателей. 1.) Решите каждое неравенство отдельно. x 2 <9 2.) Объедините каждое неравенство и найдите перекрытие (т. Е. Области, в которых выполняется каждое неравенство — эта область является решением). Область перекрытия, то есть решение набора неравенств, — это где x <2 и x> -2 Для многих студентов вышеуказанный набор неравенств лучше всего можно понять графически. Решением множества неравенств является перекрывающаяся графическая область. 6.3: Экспоненциальные уравнения и неравенства В разделе \ ref {ExpEquations} мы решили уравнения и неравенства, включающие экспоненциальные функции, используя одну из двух основных стратегий. Теперь мы обратим наше внимание на уравнения и неравенства, включающие логарифмические функции, и неудивительно, что есть две основные стратегии на выбор. Этапы решения уравнения с логарифмическими функциями
Пример \ (\ PageIndex {1} \): Решите следующие уравнения.2-3 \ right)} {\ ln (117)} \) и мы видим, что они пересекаются только в точке \ (x = -4 \). Чтобы увидеть, что случилось с решением \ (x = 1 \), мы подставляем его в наше исходное уравнение, чтобы получить \ (\ log_ {117} (- 2) = \ log_ {117} (- 2) \). Хотя эти выражения выглядят одинаково, ни одно из них не является действительным числом, \ footnote {Однако они представляют одно и то же \ textbf {семейство} комплексных чисел.
\ [\ begin {array} {rclr} 1 & = & 2 \ log_ {2} (x) — 2 \ left (\ frac {1} {2} \ log_ {2} (x + 1) \ right ) & \\ 1 & = & 2 \ log_ {2} (x) — \ log_ {2} (x + 1) & \\ 1 & = & \ log_ {2} \ left (x ^ 2 \ right) — \ log_ {2} (x + 1) & \ text {Правило мощности} \\ 1 & = & \ log_ {2} \ left (\ dfrac {x ^ {2}} {x + 1} \ right) & \ текст {Правило частного} \\ \ end {array} \] Переписывая это в экспоненциальной форме, мы получаем \ (\ frac {x ^ {2}} {x + 1} = 2 \) или \ (x ^ 2 -2x-2 = 0 \). По крайней мере, Пример \ ref {LogEqnsEx1} демонстрирует важность проверки на наличие посторонних решений \ footnote {Напомним, что постороннее решение — это полученный аналитически ответ, который не удовлетворяет исходному уравнению.} при решении уравнений, содержащих логарифмы. Несмотря на то, что мы проверили наши ответы графически, посторонние решения легко обнаружить — любое предполагаемое решение, которое вызывает отрицательное число внутри логарифма, должно быть отброшено. Как и в случае с уравнениями в примере \ ref {expeqnsex1}, многое можно узнать, проверив все ответы в примере \ ref {LogEqnsEx1} аналитически. Решение \ item Мы начинаем решать \ (\ frac {1} {\ ln (x) +1} \ leq 1 \), получая \ (0 \) на одной стороне неравенства: \ (\ frac {1} {\ ln (x) +1} — 1 \ leq 0 \). Получение общего знаменателя дает \ (\ frac {1} {\ ln (x) +1} — \ frac {\ ln (x) +1} {\ ln (x) +1} \ leq 0 \), который сводится к \ (\ frac {- \ ln (x)} {\ ln (x) +1} \ leq 0 \) или \ (\ frac {\ ln (x)} {\ ln (x) +1} \ geq 0 \). Мы определяем \ (r (x) = \ frac {\ ln (x)} {\ ln (x) +1} \) и приступаем к поиску области и нулей \ (r \).2 \) находится ниже графика \ (y = g (x) = \ frac {2 \ ln (x)} {\ ln (2)} + 3 \) на интервале решения.  Мы определяем \ (r (x) = x \ log (x + 1) — x \ (и из-за наличия логарифма мы требуем \ (x + 1> 0 \) или \ (x> -1 \). ). Чтобы найти нули \ (r \), положим \ (r (x) = x \ log (x + 1) — x = 0 \). Факторируя, получаем \ (x \ left (\ log ( x + 1) — 1 \ right) = 0 \), что дает \ (x = 0 \) или \ (\ log (x + 1) — 1 = 0 \).{1} \), допускающий \ (x = 9 \). Мы выбираем тестовые значения \ (x \) так, чтобы \ (x + 1 \) было степенью \ (10 \), и получаем \ (- 1 <-0.9 <0 <\ sqrt {10} -1 <9 <99 \). Наша знаковая диаграмма дает решение \ ((- 1,0] \ cup [9, \ infty) \). Калькулятор показывает, что график \ (y = f (x) = x \ log (x + 1) \) находится выше \ (y = g (x) = x \) на интервалах решения, и графики пересекаются в \ (х = 0 \) и \ (х = 9 \). Мы определяем \ (r (x) = x \ log (x + 1) — x \ (и из-за наличия логарифма мы требуем \ (x + 1> 0 \) или \ (x> -1 \). ). Чтобы найти нули \ (r \), положим \ (r (x) = x \ log (x + 1) — x = 0 \). Факторируя, получаем \ (x \ left (\ log ( x + 1) — 1 \ right) = 0 \), что дает \ (x = 0 \) или \ (\ log (x + 1) — 1 = 0 \).{1} \), допускающий \ (x = 9 \). Мы выбираем тестовые значения \ (x \) так, чтобы \ (x + 1 \) было степенью \ (10 \), и получаем \ (- 1 <-0.9 <0 <\ sqrt {10} -1 <9 <99 \). Наша знаковая диаграмма дает решение \ ((- 1,0] \ cup [9, \ infty) \). Калькулятор показывает, что график \ (y = f (x) = x \ log (x + 1) \) находится выше \ (y = g (x) = x \) на интервалах решения, и графики пересекаются в \ (х = 0 \) и \ (х = 9 \).В следующем примере мы вновь возвращаемся к понятию pH, впервые представленному в упражнениях в Разделе \ ref {IntroExpLogs}.{-1} (x) \) и проверьте свой ответ графически с помощью калькулятора. Решение Сначала мы пишем \ (y = f (x) \), затем меняем местами \ (x \) и \ (y \) и решаем относительно \ (y \). Окончательное решение — это объединение решений первого и второго случая, т.е. решение: $$ x \ in \ left <- \ infty, 0 \ right> \ cup \ left [1, \ infty \ right>. $$ % PDF-1.6
%
95 0 объект
>
эндобдж
xref
95 80
0000000016 00000 н.
0000002574 00000 н.
0000002637 00000 н.
0000002888 00000 н.
0000003022 00000 н.
0000003156 00000 п.
0000003288 00000 н.
0000003429 00000 н.
0000003570 00000 н.
0000003711 00000 н.
0000003846 00000 н.
0000004076 00000 н.
0000004852 00000 н.
0000005521 00000 н.
0000006303 00000 н.
0000007037 00000 п.
0000007911 00000 п.
0000008546 00000 н.
0000009262 00000 п.
0000009905 00000 н.
0000010036 00000 п.
0000010170 00000 п.
0000010300 00000 п.
0000010431 00000 п.
0000010563 00000 п. Решение абсолютных уравнений и неравенств (Алгебра 1, Линейные неравенства) — MathplanetАбсолютное число числа a записывается как $$ \ осталось | a \ right | $$ And представляет собой расстояние между a и 0 на числовой прямой. Уравнение абсолютного значения — это уравнение, которое содержит выражение абсолютного значения. Уравнение $$ \ осталось | x \ right | = a $$ Имеет два решения x = a и x = -a, потому что оба числа находятся на расстоянии a от 0. Чтобы решить уравнение абсолютного значения как $$ \ осталось | x + 7 \ вправо | = 14 $$ Вы начинаете с того, что превращаете его в два отдельных уравнения, а затем решаете их по отдельности. $$ x + 7 = 14 $$ $$ x + 7 \, {\ color {green} {- \, 7}} \, = 14 \, {\ color {green} {- \, 7}} $$ $$ x = 7 $$ или $$ x + 7 = -14 $$ $$ x + 7 \, {\ color {green} {- \, 7}} \, = -14 \, {\ color {green} {- \, 7}} $$ $$ x = -21 $$ Уравнение абсолютного значения не имеет решения, если выражение абсолютного значения равно отрицательному числу, поскольку абсолютное значение никогда не может быть отрицательным. Неравенство $$ \ осталось | х \ право | <2 $$ Представляет расстояние между x и 0, которое меньше 2 Тогда как неравенство $$ \ осталось | x \ right |> 2 $$ Представляет расстояние между x и 0, которое больше 2 Вы можете записать неравенство по абсолютным значениям как составное неравенство. $$ \ осталось | x \ right | <2 \: или $$ — 2 Это верно для всех неравенств по абсолютным значениям. $$ \ осталось | ax + b \ right | $$ = — c $$ \ осталось | ax + b \ right |> c, \: где \: c> 0 $$ $$ = ax + b <-c \: или \: ax + b> c $$ Вы можете заменить> выше на ≥ и <на ≤. При решении неравенства абсолютного значения необходимо сначала выделить выражение абсолютного значения на одной стороне неравенства, прежде чем решать неравенство. Пример Решите неравенство абсолютных значений $$ 2 \ влево | 3x + 9 \ вправо | <36 $$ $$ \ frac {2 \ left | 3x + 9 \ right |} {2} <\ frac {36} {2} $$ $$ \ осталось | 3x + 9 \ вправо | <18 $$ $$ — 18 <3x + 9 <18 $$ $$ — 18 \, {\ color {green} {- \, 9}} <3x + 9 \, {\ color {green} {- \, 9}} <18 \, {\ color {green} { - \, 9}} $$ $$ — 27 <3x <9 $$ $$ \ frac {-27} {{\ color {green} 3}} <\ frac {3x} {{\ color {green} 3}} <\ frac {9} {{\ color {green} 3} } $$ $$ — 9 Решите уравнение абсолютного значения $$ 4 \ влево | 2x -1 \ вправо | -2 = 10 $$ youtube.com/embed/eVsG7_GfgmY?fs=1&hl=sv_SE&rel=0″ allowfullscreen=»»/> Рисунок 1 Попасть в список почета в большинстве ведущих университетов непросто. Предположим, студенты должны были пройти курс не менее 12 кредитных часов и поддерживать средний балл 3,5 или выше. Как можно математически выразить эти требования к списку почета? В этом разделе мы рассмотрим различные способы выражения различных наборов чисел, неравенств и неравенств по абсолютным значениям. Указать решение неравенства, такого как x≥4x≥4, можно несколькими способами. Мы можем использовать числовую линию, как показано на рисунке 2 . Синий луч начинается с x = 4x = 4 и, как указано стрелкой, продолжается до бесконечности, что показывает, что набор решений включает все действительные числа, большие или равные 4. Рисунок 2 Мы можем использовать нотацию конструктора множеств: {x | x≥4}, {x | x≥4}, что переводится как «все действительные числа x , такие, что x больше или равно 4.Обратите внимание, что фигурные скобки используются для обозначения набора. Третий метод — это интервальная запись, в которой наборы решений указываются круглыми или квадратными скобками. Решения x≥4x≥4 представлены как [4, ∞). [4, ∞). Это, пожалуй, самый полезный метод, поскольку он применим к концепциям, изучаемым позже в этом курсе, и к другим курсам математики более высокого уровня. Основная концепция, которую следует запомнить, заключается в том, что круглые скобки представляют решения, которые больше или меньше числа, а скобки представляют решения, которые больше или равны или меньше или равны числу.Используйте круглые скобки для обозначения бесконечности или отрицательной бесконечности, поскольку положительная и отрицательная бесконечность не являются числами в обычном смысле слова и, следовательно, не могут быть «равны». Таблица 1 Используйте обозначение интервала для обозначения всех действительных чисел, больших или равных -2. Используйте квадратную скобку слева от −2−2 и круглые скобки после бесконечности: [−2, ∞). [- 2, ∞). Скобка указывает, что −2−2 включен в набор со всеми действительными числами от −2−2 до бесконечности. Попробуй # 1 Используйте обозначение интервала, чтобы указать все действительные числа от −3−3 до 5,5 включительно. Запишите интервал, выражающий все действительные числа, меньшие или равные -1-1 или больше или равные 1.1. Для этого примера мы должны написать два интервала. Первый интервал должен указывать все действительные числа, меньшие или равные 1. Во втором интервале должны отображаться все действительные числа, большие или равные 1,1, что записывается как [1, ∞). [1, ∞). Однако мы хотим объединить эти два набора. Мы достигаем этого, вставляя символ объединения, ∪, ∪, между двумя интервалами. Попробуй # 2 Выразите все действительные числа меньше -2-2 или больше или равные 3 в виде интервалов. Когда мы работаем с неравенствами, мы обычно можем относиться к ним аналогично, но не точно так, как мы относимся к равенствам. Мы можем использовать свойство сложения и свойство умножения, чтобы помочь нам решить их. Единственное исключение — это когда мы умножаем или делим на отрицательное число; при этом символ неравенства меняется на противоположное. Эти свойства также применимы к a≤b, a≤b, a> b, a> b и a≥b.a≥b. Проиллюстрируйте свойство сложения неравенств, решив каждое из следующих решений: Свойство сложения для неравенств гласит, что если неравенство существует, добавление или вычитание одного и того же числа с обеих сторон не меняет неравенства. Попробуй # 3 Решить: 3x − 2 <1,3x − 2 <1. Проиллюстрируйте свойство умножения неравенств, решив каждое из следующих решений: Попробуй # 4 Решите: 4x + 7≥2x − 3.4x + 7≥2x − 3. Как показали примеры, мы можем выполнять те же операции с обеими сторонами неравенства, как и с уравнениями; совмещаем похожие сроки и выполняем операции.Чтобы решить, мы изолируем переменную. Решите неравенство: 13−7x≥10x − 4.13−7x≥10x − 4. Решение этого неравенства аналогично решению уравнения до последнего шага. Множество решений задается интервалом (−∞, 1], (- ∞, 1] или всеми действительными числами, меньшими 1 включительно. Попробуй # 5 Решите неравенство и запишите ответ в интервале: −x + 4 <12x + 1. − x + 4 <12x + 1. Решите следующее неравенство и запишите ответ в интервальной записи: −34x≥ − 58 + 23x.−34x≥ − 58 + 23x. Мы начинаем решать так же, как и при решении уравнения. Множеством решений является интервал (−∞, 1534]. (- ∞, 1534]. Попробуй # 6 Решите неравенство и запишите ответ в интервале: −56x≤34 + 83x. − 56x≤34 + 83x. Сложное неравенство включает в себя два неравенства в одном утверждении. Утверждение, такое как 4 Решите составное неравенство: 3≤2x + 2 <6.3≤2x + 2 <6. Первый способ — написать два отдельных неравенства: 3≤2x + 23≤2x + 2 и 2x + 2 <6. Затем мы можем переписать решение как составное неравенство, таким же образом проблема началась. В интервальной записи решение записывается как [12,2). [12,2). Второй метод — оставить составное неравенство неповрежденным и выполнить процедуры решения для трех частей одновременно. Получим такое же решение: [12,2).[12,2). Попробуй # 7 Решите составное неравенство: 4 <2x − 8≤10,4 <2x − 8≤10. Решите составное неравенство с переменными во всех трех частях: 3 + x> 7x − 2> 5x − 10,3 + x> 7x − 2> 5x − 10. Попробуем первый способ. Запишем два неравенства : Рисунок 3 Попробуй # 8 Решите составное неравенство: 3y <4−5y <5 + 3y.3y <4−5y <5 + 3y. Как мы знаем, абсолютное значение величины — это положительное число или ноль.От начала координат точка, расположенная в (−x, 0) (- x, 0), имеет абсолютное значение x, x, так как она находится на расстоянии x единиц. Неравенство по абсолютной величине — это уравнение вида Где A , а иногда B , представляет алгебраическое выражение, зависящее от переменной x. Решение неравенства означает нахождение набора всех xx — значений, которые удовлетворяют задаче. Обычно этот набор представляет собой интервал или объединение двух интервалов и включает диапазон значений. Существует два основных подхода к решению абсолютных неравенств: графический и алгебраический. Преимущество графического подхода в том, что мы можем прочитать решение, интерпретируя графики двух уравнений. Предположим, мы хотим знать все возможные доходы от инвестиций, если бы мы могли заработать некоторую сумму денег в пределах от 200 до 600 долларов. Мы можем решить алгебраически для набора из x- значений, так что расстояние между xx и 600 меньше или равно 200. Мы представляем расстояние между xx и 600 как | x − 600 |, | x − 600 |, и, следовательно, | x − 600 | ≤200 | x − 600 | ≤200 или Это означает, что наша прибыль составит от 400 до 800 долларов США. Для решения неравенств по абсолютным значениям, как и для уравнений с абсолютными значениями, мы записываем два неравенства и затем решаем их независимо. Для алгебраического выражения X, и k> 0, k> 0 неравенство по модулю является неравенством вида Эти утверждения также применимы к | X | ≤k | X | ≤k и | X | ≥k. Опишите все значения xx на расстоянии 4 от числа 5. Мы хотим, чтобы расстояние между xx и 5 было меньше или равно 4. Мы можем нарисовать числовую линию, например, на рис. 4 , , чтобы представить условие, которое должно быть выполнено. Рисунок 4 Расстояние от xx до 5 может быть представлено с помощью символа абсолютного значения | x − 5 |.| х − 5 |. Запишите значения xx, которые удовлетворяют условию, как неравенство по абсолютной величине. Нам нужно написать два неравенства, так как всегда есть два решения уравнения абсолютного значения. Если набор решений x≤9x≤9 и x≥1, x≥1, то решение set — интервал, включающий все действительные числа от 1 до 9 включительно. Итак, | x − 5 | ≤4 | x − 5 | ≤4 эквивалентно [1,9] [1,9] в обозначении интервалов. Попробуй # 9 Опишите все значения x- на расстоянии 3 от числа 2. Решить | x − 1 | ≤3 | x − 1 | ≤3. Учитывая уравнение y = −12 | 4x − 5 | + 3, y = −12 | 4x − 5 | +3, определите значения x , для которых значения y отрицательны. Мы пытаемся определить, где y <0, y <0, то есть когда −12 | 4x − 5 | +3 <0.−12 | 4х − 5 | +3 <0. Начнем с выделения абсолютного значения. Затем мы решаем равенство | 4x − 5 | = 6. | 4x − 5 | = 6. Теперь мы можем изучить график, чтобы увидеть где значения y- отрицательны. Мы наблюдаем, где ветви находятся ниже оси x- .Обратите внимание, что не важно, как именно выглядит график, если мы знаем, что он пересекает горизонтальную ось в точках x = −14x = −14 и x = 114, x = 114, и что график открывается вниз. См. Рисунок 5 . Рисунок 5 Попробуй # 10 Решить −2 | k − 4 | ≤ − 6. − 2 | k − 4 | ≤ − 6. При решении неравенства объясните, что произошло с шага 1 по шаг 2: Шаг 1-2x> 6 Шаг 2x <−3 Шаг 1-2x> 6 Шаг 2x <−3 Решая неравенство, получаем: х + 2 <х + 32 <3х + 2 <х + 32 <3 Объясните, что представляет собой наш набор решений. При записи нашего решения в интервальной записи, как мы представляем все действительные числа? Решая неравенство, получаем: х + 2> х + 32> 3х + 2> х + 32> 3 Объясните, что представляет собой наш набор решений. Опишите, как построить график y = | x − 3 | y = | x − 3 | Для следующих упражнений решите неравенство.Напишите окончательный ответ в виде интервалов. 3x + 2≥7x − 13x + 2≥7x − 1 −2x + 3> x − 5−2x + 3> x − 5 4 (x + 3) ≥2x − 14 (x + 3) ≥2x − 1 −12x≤ − 54 + 25x − 12x≤ − 54 + 25x −5 (x − 1) +3> 3x − 4−4x − 5 (x − 1) +3> 3x − 4−4x −3 (2x + 1)> — 2 (x + 4) −3 (2x + 1)> — 2 (x + 4) x + 38 − x + 55≥310x + 38 − x + 55≥310 x − 13 + x + 25≤35x − 13 + x + 25≤35 Для следующих упражнений решите неравенство с абсолютным значением.Напишите окончательный ответ в виде интервалов. | х − 2 | + 4≥10 | х − 2 | + 4≥10 | −2x + 7 | ≤13 | −2x + 7 | ≤13 | х-20 |> -1 | х-20 |> -1 Для следующих упражнений опишите все значения x в пределах или включая расстояние от заданных значений. Дистанция 5 единиц от номера 7 Расстояние 3 единицы от номера 9 Дистанция 10 единиц от номера 4 Расстояние 11 единиц от номера 1 Для следующих упражнений решите сложное неравенство. Выразите свой ответ, используя знаки неравенства, а затем запишите свой ответ, используя интервальную нотацию. −4 <3x + 2≤18−4 <3x + 2≤18 3x + 1> 2x − 5> x − 73x + 1> 2x − 5> x − 7 3y <5−2y <7 + y3y <5−2y <7 + y 2x − 5 <−11or 5x + 1≥62x − 5 <−11or 5x + 1≥6 Постройте график функции для следующих упражнений.Наблюдая за точками пересечения, заштрихуйте ось x , представляющую решение, заданное неравенством. Покажите свой график и напишите окончательный ответ в виде интервалов. Для следующих упражнений нарисуйте обе прямые линии (левая сторона — y1, а правая сторона — y2) на одних и тех же осях. Найдите точку пересечения и решите неравенство, наблюдая, где оно истинно, сравнивая значения y линий. 12x + 1> 12x − 512x + 1> 12x − 5 Для следующих упражнений запишите набор в интервальной записи. {x | xis все действительные числа} {x | xis все действительные числа} Для следующих упражнений запишите интервал в нотации конструктора множеств. [−4,1] ∪ [9, ∞) [- 4,1] ∪ [9, ∞) Для следующих упражнений запишите набор чисел, представленных в числовой строке, в интервальной записи. Для следующих упражнений введите левую часть неравенства в виде графика Y1 в графической утилите.Введите y2 = правую часть. Ввод абсолютного значения выражения находится в меню MATH, Num, 1: abs (. Найдите точки пересечения, вспомните (2 nd CALC 5: пересечение, 1 st curve, enter, 2 nd кривой, введите, угадайте, введите). Скопируйте эскиз графика и заштрихуйте ось x для вашего решения, установленного на неравенство. Запишите окончательные ответы в виде интервалов. Решите | 3x + 1 | = | 2x + 3 || 3x + 1 | = | 2x + 3 | x − 5x + 7≤0, x − 5x + 7≤0, x ≠ −7x ≠ −7 p = −x2 + 130x − 3000p = −x2 + 130x − 3000 — формула прибыли для малого бизнеса. В химии объем для определенного газа определяется как V = 20T, V = 20T, где V измеряется в кубических сантиметрах, а T — температура в ºC. Если температура колеблется от 80ºC до 120ºC, найдите набор значений объема. Базовый пакет сотовой связи стоит 20 долларов в месяц. в течение 60 минут звонка с дополнительной оплатой в размере 0,30 доллара за минуту по истечении этого времени .. Формула расчета стоимости будет следующей: C = 20 + 0,30 (x − 60) .C = 20 + 0,30 (x − 60). Если вам необходимо выставить счет на сумму не более 50 долларов, какое максимальное количество минут вы можете использовать? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Найти среднее арифметическое целых решений неравенства
Найти среднее арифметическое целых решений неравенства 2- x-2\le 0\\ \end{cases} \Rightarrow \begin{cases}x\ne 0 \\ -1 \le x \le2\\ \end{cases} \Rightarrow x\in[-1;0)\cup(0;2].\)
2- x-2\le 0\\ \end{cases} \Rightarrow \begin{cases}x\ne 0 \\ -1 \le x \le2\\ \end{cases} \Rightarrow x\in[-1;0)\cup(0;2].\)
 ОДЗ этого неравенства: f (x) > 0.
ОДЗ этого неравенства: f (x) > 0.

 com»>
com»>



 Среди них — рациональные, иррациональные, показательные, логарифмические, тригонометрические, содержащие модули (абсолютные величины), а также комбинированные. В этой статье рассмотрены основные типы показательных уравнений и неравенств, а также различные методы их решений. О решении остальных видов уравнений и неравенств читайте в рубрике « » в статьях, посвященных методам решения задач C3 из вариантов ЕГЭ по математике.
Среди них — рациональные, иррациональные, показательные, логарифмические, тригонометрические, содержащие модули (абсолютные величины), а также комбинированные. В этой статье рассмотрены основные типы показательных уравнений и неравенств, а также различные методы их решений. О решении остальных видов уравнений и неравенств читайте в рубрике « » в статьях, посвященных методам решения задач C3 из вариантов ЕГЭ по математике.
 Это и будет являться ответом к заданию.
Это и будет являться ответом к заданию. Решите уравнение:
Решите уравнение:
 Воспользовавшись известным свойством логарифма, переходим к эквивалентному неравенству:
Воспользовавшись известным свойством логарифма, переходим к эквивалентному неравенству: Решите неравенство:
Решите неравенство: Она достигает своего наименьшего значения в той же точке, что и парабола, стоящая в показателе, и это значение равно 3 1 = 3. Итак, исходное неравенство может оказаться верным только в том случае, если функция слева и функция справа принимают в одной точке значение, равное 3 (пересечением областей значений этих функций является только это число). Это условие выполняется в единственной точке x = 1.
Она достигает своего наименьшего значения в той же точке, что и парабола, стоящая в показателе, и это значение равно 3 1 = 3. Итак, исходное неравенство может оказаться верным только в том случае, если функция слева и функция справа принимают в одной точке значение, равное 3 (пересечением областей значений этих функций является только это число). Это условие выполняется в единственной точке x = 1. К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно.
К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно. Решить неравенство: 5 х – 1 > 125 .
Решить неравенство: 5 х – 1 > 125 .


 Сведем справа и слева формулы к одному основанию (2)
Сведем справа и слева формулы к одному основанию (2) Запишем неравенство в виде
Запишем неравенство в виде



 — М.: Дрофа. Колмогоров А. Н., Абрамов А. М., Дудницын Ю. П. и др. Алгебра и начала математического анализа. — М.: Просвещение.
— М.: Дрофа. Колмогоров А. Н., Абрамов А. М., Дудницын Ю. П. и др. Алгебра и начала математического анализа. — М.: Просвещение. В обоих случаях мы получили противоречие условию а х 1 = а х 2 .
В обоих случаях мы получили противоречие условию а х 1 = а х 2 .

 {n}}$. До тех пор, пока у вас слева или справа есть какие-то левые множители, дополнительные константы и т.д., никакую рационализацию и «зачёркивание» оснований выполнять нельзя ! Бесчисленное множество задач было выполнено неправильно из-за непонимания этого простого факта. Я сам постоянно наблюдаю эту проблему у моих учеников, когда мы только-только приступаем к разбору показательных и логарифмических неравенств.
{n}}$. До тех пор, пока у вас слева или справа есть какие-то левые множители, дополнительные константы и т.д., никакую рационализацию и «зачёркивание» оснований выполнять нельзя ! Бесчисленное множество задач было выполнено неправильно из-за непонимания этого простого факта. Я сам постоянно наблюдаю эту проблему у моих учеников, когда мы только-только приступаем к разбору показательных и логарифмических неравенств.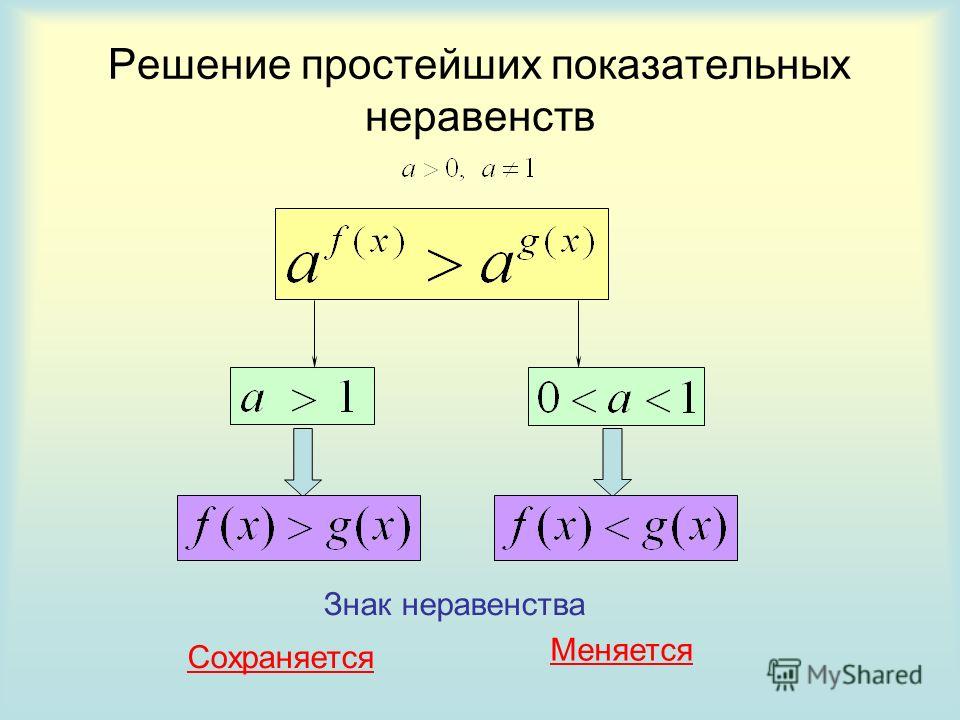 {5}}=3125. \\\end{align}\]
{5}}=3125. \\\end{align}\]
 2.
2.  Но еще больше — не удалось, да и в тех, что вроде бы решены, появляются новые вопросы.
Но еще больше — не удалось, да и в тех, что вроде бы решены, появляются новые вопросы. У школьников формируются такие качества личности как целеустремленность, целеполагание, самостоятельность, которые будут полезны им в дальнейшей жизни. А также происходит повторение, расширение и глубокое усвоение учебного материала.
У школьников формируются такие качества личности как целеустремленность, целеполагание, самостоятельность, которые будут полезны им в дальнейшей жизни. А также происходит повторение, расширение и глубокое усвоение учебного материала. А также у них возникают проблемы на этапе систематизации полученных результатов, где могут в силу перехода к уравнению – следствию или неравенству – следствию, появиться посторонние корни. С целью устранения ошибок мы используем проверку по исходному уравнению или неравенству и алгоритм решения показательно-степенных уравнений, либо план решения показательно-степенных неравенств.
А также у них возникают проблемы на этапе систематизации полученных результатов, где могут в силу перехода к уравнению – следствию или неравенству – следствию, появиться посторонние корни. С целью устранения ошибок мы используем проверку по исходному уравнению или неравенству и алгоритм решения показательно-степенных уравнений, либо план решения показательно-степенных неравенств.
 Такая же ситуация имеет место быть, в уравнении где b
Такая же ситуация имеет место быть, в уравнении где b




 Причина в том, что x может быть как положительным, так и отрицательным. Следовательно, при вычислении четной экспоненты в неравенстве мы имеем дело с двумя случаями: x положительный, x отрицательный.
Причина в том, что x может быть как положительным, так и отрицательным. Следовательно, при вычислении четной экспоненты в неравенстве мы имеем дело с двумя случаями: x положительный, x отрицательный.
 Например, предположим, что мы хотим решить \ (\ log_ {2} (x) = \ log_ {2} (5) \). Теорема \ ref {explogsonetoone} говорит нам, что \ textit {only} решением этого уравнения является \ (x = 5 \).{3} = x \) или \ (x = 8 \). Мы резюмируем два распространенных способа решения логарифмических уравнений ниже.
Например, предположим, что мы хотим решить \ (\ log_ {2} (x) = \ log_ {2} (5) \). Теорема \ ref {explogsonetoone} говорит нам, что \ textit {only} решением этого уравнения является \ (x = 5 \).{3} = x \) или \ (x = 8 \). Мы резюмируем два распространенных способа решения логарифмических уравнений ниже. {3} = \ frac { x + 3} {6-x} \] Это сводится к линейному уравнению \ (8 (6-x) = x + 3 \), которое дает нам \ (x = 5 \).Когда мы строим график \ (f (x) = \ frac {\ ln (x + 3)} {\ ln (2)} \) и \ (g (x) = \ frac {\ ln (6-x)} { \ ln (2)} + 3 \), мы обнаруживаем, что они пересекаются в точке \ (x = 5 \).
{3} = \ frac { x + 3} {6-x} \] Это сводится к линейному уравнению \ (8 (6-x) = x + 3 \), которое дает нам \ (x = 5 \).Когда мы строим график \ (f (x) = \ frac {\ ln (x + 3)} {\ ln (2)} \) и \ (g (x) = \ frac {\ ln (6-x)} { \ ln (2)} + 3 \), мы обнаруживаем, что они пересекаются в точке \ (x = 5 \). Используя формулу корней квадратного уравнения, получаем \ (x = 1 \ pm \ sqrt {3} \). Построение графика \ (f (x) = 1 + \ frac {2 \ ln (x + 1)} {\ ln (4)} \) и \ (g (x) = \ frac {2 \ ln (x)} { \ ln (2)} \), мы видим, что графики пересекаются только в точке \ (x = 1 + \ sqrt {3} \ приблизительно 2.732 \). Решение \ (x = 1 — \ sqrt {3} <0 \), что означает, что если подставить в исходное уравнение, член \ (2 \ log_ {2} \ left (1 - \ sqrt {3} \ right) \) не определено.
Используя формулу корней квадратного уравнения, получаем \ (x = 1 \ pm \ sqrt {3} \). Построение графика \ (f (x) = 1 + \ frac {2 \ ln (x + 1)} {\ ln (4)} \) и \ (g (x) = \ frac {2 \ ln (x)} { \ ln (2)} \), мы видим, что графики пересекаются только в точке \ (x = 1 + \ sqrt {3} \ приблизительно 2.732 \). Решение \ (x = 1 — \ sqrt {3} <0 \), что означает, что если подставить в исходное уравнение, член \ (2 \ log_ {2} \ left (1 - \ sqrt {3} \ right) \) не определено. Мы оставляем это читателю и обратим внимание на неравенства, содержащие логарифмические функции. Поскольку логарифмические функции непрерывны в своей области определения, мы можем использовать знаковые диаграммы.2 <2 \ log_ {2} (x) + 3 \)
Мы оставляем это читателю и обратим внимание на неравенства, содержащие логарифмические функции. Поскольку логарифмические функции непрерывны в своей области определения, мы можем использовать знаковые диаграммы.2 <2 \ log_ {2} (x) + 3 \) 2-t-3 = 0 $.x <0 $ - это $ x \ in \ left <0, \ infty \ right> $. Следовательно, решением второго случая является пересечение решений обоих неравенств: $ x \ in \ left [1, \ infty \ right> $.
2-t-3 = 0 $.x <0 $ - это $ x \ in \ left <0, \ infty \ right> $. Следовательно, решением второго случая является пересечение решений обоих неравенств: $ x \ in \ left [1, \ infty \ right> $. 0000010695 00000 п.
0000010827 00000 п.
0000010958 00000 п.
0000011089 00000 п.
0000011222 00000 п.
0000011355 00000 п.
0000011488 00000 п.
0000011619 00000 п.
0000011751 00000 п.
0000011882 00000 п.
0000044499 00000 н.
0000045105 00000 п.
0000045795 00000 п.
0000065093 00000 п.
0000065476 00000 п.
0000065994 00000 п.
0000085689 00000 п.
0000086122 00000 п.
0000086873 00000 п.
0000103376 00000 н.
0000103761 00000 п.
0000104441 00000 н.
0000123630 00000 н.
0000124019 00000 н.
0000124732 00000 н.
0000137242 00000 н.
0000137522 00000 н.
0000138189 00000 п.
0000150609 00000 н.
0000151196 00000 н.
0000151846 00000 н.
0000161922 00000 н.
0000162320 00000 н.
0000163023 00000 н.
0000170764 00000 н.
0000171022 00000 н.
0000171670 00000 н.
0000194299 00000 н.
0000194755 00000 н.
0000195398 00000 н.
0000228344 00000 н.
0000228765 00000 н.
0000229424 00000 н.
0000253662 00000 н.
0000254232 00000 н.
0000254897 00000 н.
0000272979 00000 н.
0000273340 00000 н.
0000010695 00000 п.
0000010827 00000 п.
0000010958 00000 п.
0000011089 00000 п.
0000011222 00000 п.
0000011355 00000 п.
0000011488 00000 п.
0000011619 00000 п.
0000011751 00000 п.
0000011882 00000 п.
0000044499 00000 н.
0000045105 00000 п.
0000045795 00000 п.
0000065093 00000 п.
0000065476 00000 п.
0000065994 00000 п.
0000085689 00000 п.
0000086122 00000 п.
0000086873 00000 п.
0000103376 00000 н.
0000103761 00000 п.
0000104441 00000 н.
0000123630 00000 н.
0000124019 00000 н.
0000124732 00000 н.
0000137242 00000 н.
0000137522 00000 н.
0000138189 00000 п.
0000150609 00000 н.
0000151196 00000 н.
0000151846 00000 н.
0000161922 00000 н.
0000162320 00000 н.
0000163023 00000 н.
0000170764 00000 н.
0000171022 00000 н.
0000171670 00000 н.
0000194299 00000 н.
0000194755 00000 н.
0000195398 00000 н.
0000228344 00000 н.
0000228765 00000 н.
0000229424 00000 н.
0000253662 00000 н.
0000254232 00000 н.
0000254897 00000 н.
0000272979 00000 н.
0000273340 00000 н. 0000274055 00000 н.
0000283959 00000 н.
0000284346 00000 п.
0000285041 00000 н.
0000302356 00000 п.
0000302673 00000 н.
0000001896 00000 н.
трейлер
] >>
startxref
0
%% EOF
174 0 объект
> поток
xb«a«_ Ab @ YI2ooLeO} 9C & ˁ? wj ɠKI 㒪 LPmYV099mӋ ٚ \ & d ԗW \ 86ww # D \ xy \ Ythf% * szy \ T {WyS
N] & j ~ fM: c7oΞg # pH’S & \ f] lV ޚ s ~ _ʻ / 7rly 㱱} YeZE2 & u4 ՚:% bkai) g = H5 + 0X8ww @ A * ‘Rebp 5o: 9iɑ ݒ Hq8u30ԀS / + r03u2133fL @ A | AV3Ljwd143q? Cdbi0fTcg $ G͐Ya *: `y @ ۧ 001 D0i3020_fPĤjeaL
0000274055 00000 н.
0000283959 00000 н.
0000284346 00000 п.
0000285041 00000 н.
0000302356 00000 п.
0000302673 00000 н.
0000001896 00000 н.
трейлер
] >>
startxref
0
%% EOF
174 0 объект
> поток
xb«a«_ Ab @ YI2ooLeO} 9C & ˁ? wj ɠKI 㒪 LPmYV099mӋ ٚ \ & d ԗW \ 86ww # D \ xy \ Ythf% * szy \ T {WyS
N] & j ~ fM: c7oΞg # pH’S & \ f] lV ޚ s ~ _ʻ / 7rly 㱱} YeZE2 & u4 ՚:% bkai) g = H5 + 0X8ww @ A * ‘Rebp 5o: 9iɑ ݒ Hq8u30ԀS / + r03u2133fL @ A | AV3Ljwd143q? Cdbi0fTcg $ G͐Ya *: `y @ ۧ 001 D0i3020_fPĤjeaL

 Несколько примеров интервала или набора чисел, в которые попадает решение: [−2,6), [- 2,6) или все числа от −2−2 до 6,6, включая −2, −2, но не включая 6; 6; (−1,0), (- 1,0), все действительные числа между, но не включая −1−1 и 0; 0; и (−∞, 1], (- ∞, 1], все действительные числа, меньшие, чем 1.1, включая 1.1. В таблице 1 показаны возможные варианты.
Несколько примеров интервала или набора чисел, в которые попадает решение: [−2,6), [- 2,6) или все числа от −2−2 до 6,6, включая −2, −2, но не включая 6; 6; (−1,0), (- 1,0), все действительные числа между, но не включая −1−1 и 0; 0; и (−∞, 1], (- ∞, 1], все действительные числа, меньшие, чем 1.1, включая 1.1. В таблице 1 показаны возможные варианты. −2.
−2. Итак, этот интервал начинается с −∞ − ∞ и заканчивается на −1, −1, что записывается как (−∞, −1]. (- ∞, −1].
Итак, этот интервал начинается с −∞ − ∞ и заканчивается на −1, −1, что записывается как (−∞, −1]. (- ∞, −1].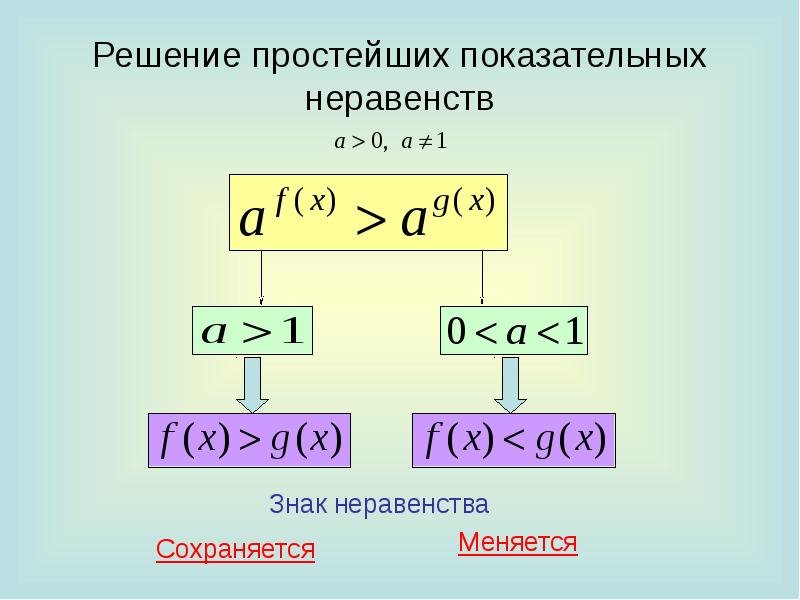 7≥x6≥x − 16 + 1≥x − 1 + 1 Прибавить 1 к обеим сторонам. 7≥x
7≥x6≥x − 16 + 1≥x − 1 + 1 Прибавить 1 к обеим сторонам. 7≥x 5 − x> 10 − x> 5 ( −1) (- x)> (5) (- 1) Умножить на −1.x <−5 Отменить неравенство.
5 − x> 10 − x> 5 ( −1) (- x)> (5) (- 1) Умножить на −1.x <−5 Отменить неравенство. −17x≥ − 17 Выделите член переменной. X≤1 Разделение обеих частей на −17 отменяет неравенство.
−17x≥ − 17 Выделите член переменной. X≤1 Разделение обеих частей на −17 отменяет неравенство. −1712x≥ − 58x≤ − 58 (−1217) Умножение на отрицательное число отменяет неравенство.x≤1534
−1712x≥ − 58x≤ − 58 (−1217) Умножение на отрицательное число отменяет неравенство.x≤1534 2x + 2 <6. Решаем их самостоятельно.
2x + 2 <6. Решаем их самостоятельно.
 Считайте абсолютное значение расстоянием от одной точки до другой точки. Независимо от направления, положительного или отрицательного, расстояние между двумя точками представляется как положительное число или ноль.
Считайте абсолютное значение расстоянием от одной точки до другой точки. Независимо от направления, положительного или отрицательного, расстояние между двумя точками представляется как положительное число или ноль. Преимущество алгебраического подхода состоит в том, что решения являются точными, поскольку точные решения иногда трудно прочитать с графика.
Преимущество алгебраического подхода состоит в том, что решения являются точными, поскольку точные решения иногда трудно прочитать с графика. | X | ≥k.
| X | ≥k.
 | 4x − 5 |> 6−12 | 4x − 5 | <−3 Умножьте обе части на –2 и отмените неравенство. | 4x − 5 |> 6
| 4x − 5 |> 6−12 | 4x − 5 | <−3 Умножьте обе части на –2 и отмените неравенство. | 4x − 5 |> 6



 Найдите набор значений x , которые сохранят эту прибыль положительной.
Найдите набор значений x , которые сохранят эту прибыль положительной.