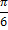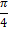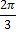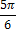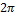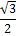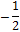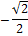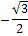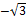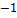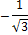Задачи с решением — Тригонометрические уравнения

1.       Решить уравнение cos2x = 1/2.

Используем метод решения простейших тригонометрических уравнений и получаем:

2x = ±arccos(1/2) + 2πn = ±π/3 + 2πn (здесь и далее, n ∈ Z).

Откуда x = ±π/6 + πn.

Ответ: x = ±π/6 + πn.

2.       Решить уравнение sin(3 — 2x) = -1/2.

Используем формулу из методов решений, имеем:

3 — 2x = (-1)n(arcsin(-1/2)) + πn = (-1)n(-π/6) + πn (здесь и далее n ∈ Z).

Делаем преобразование и получаем x = 3/2 + π/12(-1)n — πn/2.

Ответ: x = 3/2 + π/12(-1)n — πn/2.

3.       Решить уравнение cos2x — 3sinx = 2.

 

Воспользуемся формулой удвоенного угла косинуса (cos2a = 1 — 2sin2a) и получим:

1 — 2sin2x — 3sinx = 2.

Воспользуемся методом замены, обозначим sinx = y. Уравнение примет вид:

2y2 + 3y + 1 = 0.

Находим его корни: y1 = -1, y2 = -1/2.

Возвращаемся к исходной переменной и получаем совокупность sinx = -1 и sinx = -1/2.

Из первого получаем решение — x = -π/2 + 2πn, из второго — x = (-1)m(-π/6) + πm (m, n ∈ Z).

Ответ: x = -π/2 + 2πn или x = (-1)m(-π/6) + πm.

4.       Решить уравнение 2tgx — 3ctgx = 1.

Так как ctgx = 1/tgx при x ≠ πn/2 (n ∈ Z) получаем уравнение

2tgx — 3/tgx = 1 или 2tg2x — tgx — 3 = 0.

Вводим новую переменную tgx = y и решаем квадратное уравнение 2y2 — y — 3 = 0 относительно y.

Оно имеет два решения y1 = 3/2, y2 = -1.

Возвращаемся к исходной переменной и решаем два уравнения:

tgx = 3/2, откуда x = arctg(3/2) + πn, n ∈ Z.

tgx = -1, откуда x = arctg(-1) + πm = -π/4 + πm, m ∈ Z.

Ответ: x = arctg(3/2) + πn или x = -π/4 + πm.

5.       Решить уравнение 3cosx — sin2x = 1 — sin3x.

Сделаем следующее преобразование 3(cosx + sinx) = 1 + sin2x.

Замена cosx + sinx = t приведет к уравнению 3t = t2. Оно имеет корни t1 = 0, t2 = 3.

Берем первый корень, возвращаем замену и получаем cosx + sinx = 0, делим на cosx ≠ 0, откуда tgx = -1, x = -π/4 + πn (n ∈ Z).

Второй корень t2 дает уравнение cosx + sinx = 3. Это уравнение не имеет решений, т.к. и cosx, и cosx меньше равны 1, в сумме меньше равны 2.

Ответ: x = -π/4 + πn.

6.       Решить уравнение cos2x + cos4x + cos6x = 0.

Проделаем следующие преобразования

(cos2x + cos6x) + cos4x = 0;

2cos4xcos2x + cos4x = 0;

cos4x(2cos2x + 1) = 0.

Имеем два случая:

cos4x = 0, откуда 4x = π/2 + πn, x = π/8 + πn/4 (n ∈ Z).

2cos2x + 1 = 0 или cos2x = -1/2, откуда 2x = ±2π/3 + 2πm, x = ±π/3 + πm (m ∈ Z).

Ответ: x = π/8 + πn/4 или x = ±π/3 + πm.

7.       Решить уравнение cos5x = cos2x.

Переносим в одну сторону и применяем формулу разницы косинусов:

-2sin(7x/2)sin(3x/2)

www.sites.google.com

Практические задачи с использованием тригонометрии.

Практические задачи с использованием тригонометрии.

Существует ряд практических ситуаций, в которых необходимо использовать тригонометрию для определения неизвестных сторон и углов треугольников.

Пример 1

Здание шириной 10 м имеет двускатную крышу с наклоном 35^o с одной стороны и 41^o — с другой. Найти длину скатов крыши с точностью до сантиметра.

Пример 2

На рис. показаны два вектора напряжения, V₁=50В и V₂=90В . Определить величину результирующего вектора. (т.е. длину СА) и угол между результирующим вектором и V₁

Пример 3

На рис. ниже показан кривошипно-шатунный механизм бензинового двигателя. Плечо ОА имеет длину 11 см и вращается по часовой стрелке вокруг О. Шатун АВ имеет длину 32 см, и конец В движется горизонтально. Определить угол между шатуном АВ и горизонталью и длину ОВ в положении, показанном на рис.

Пример 4

Поле имеет форму четырехугольника ABCD, показанного на рис. ниже. Определить площадь поля.

 

Пример 1

Здание шириной 10 м имеет двускатную крышу с наклоном 35^o с одной стороны и 41^o — с другой. Найти длину скатов крыши с точностью до сантиметра.

 

Решение:

Угол конька крыши В=180^o — 35^o— 41^o=104^o

По теореме синусов

,

Откуда

.

Также по теореме синусов:

Откуда

.

(используется таблица синусов)

Следовательно, длины скатов крыши равны 6 м и 7 м с точностью до см.

Примечание: сторона а — сторона против угла А, сторона с — сторона против угла С.

Пример 2

На рис. показаны два вектора напряжения, V₁=50В и V₂

=90В . Определить величину результирующего вектора. (т.е. длину СА) и угол между результирующим вектором и V₁.

 

Решение:

<CAB=180^o — 45^o=135^o.

Согласно теореме косинусов:

СА² = V₁²+V₂² — 2V₁V₂ cosCBA=

=50² + 90² — 2*50*90cos135^o=16963.(по таблице косинусов)

Результирующий вектор CA=(16963)^1/2 =130,2B.

Cогласно теореме синусов,

,

Откуда

,

Следовательно угол АСВ приблизительно равен 29^о. (по таблице синусов)

Итак, результирующий вектор напряжения равен 130,2В и составляет угол в 29^о с V₁

Пример 3

На рис. ниже показан кривошипно-шатунный механизм бензинового двигателя. Плечо ОА имеет длину 11 см и вращается по часовой стрелке вокруг О. Шатун АВ имеет длину 32 см, и конец В движется горизонтально. Определить угол между шатуном АВ и горизонталью и длину ОВ в положении, показанном на рис.

Решение:

По теореме синусов,

, откуда

Значит, В=arcsin0,2431≈ 14 ^o (по таблице синусов )

Следовательно, шатун AB составляет угол 14 ^o с горизонталью.

<ОАВ=180^o-45^o-14^o=121^o

По теореме синусов:

, откуда

Пример 4

Поле имеет форму четырехугольника ABCD, показанного на рис. Определить площадь поля.

Проведенная из В в D диагональ делит четырехугольник на два треугольника.

 

 Решение:

 Площадь четырехугольника ABCD= площадь треугольника ABD+площадь треугольника BCD, т.е.

 S_ABCD =1/2*(40)*(21)*sin115^o + 1/2*(45)*(23)*sin55

o=804,582 м²

 

tehtab.ru

Урок 10. Тригонометрические функции. Тригонометрические уравнения и их системы. Теория

Подготовка к ЕГЭ по математике

Эксперимент

Урок 10. Тригонометрические функции. Тригонометрические уравнения и их системы.

 

Теория

 

Конспект урока

Мы с вами уже многократно применяли термин «тригонометрическая функция». Еще на первом уроке этой темы мы определили их с помощью прямоугольного треугольника и единичной тригонометрической окружности. Используя такие способы задания тригонометрических функций, мы уже можем сделать вывод, что для них одному значению аргумента (или угла) соответствует строго одно значение функции, т.е. мы вправе называть синус, косинус, тангенс и котангенс именно функциями.

На этом уроке самое время попробовать абстрагироваться от рассмотренных ранее способов вычисления значений тригонометрических функций. Сегодня мы перейдем к привычному алгебраическому подходу работы с функциями, мы рассмотрим их свойства и изобразим графики.

Что касается свойств тригонометрических функций, то особое внимание следует обратить на:

— область определения и область значений, т.к. для синуса и косинуса есть ограничения по области значений, а для тангенса и котангенса ограничения по области определения;

— периодичность всех тригонометрических функций, т.к. мы уже отмечали наличие наименьшего ненулевого аргумента, добавление которого не меняет значение функции. Такой аргумент называют периодом функции и обозначают буквой . Для синуса/косинуса и тангенса/котангенса эти периоды различны.

Рассмотрим функцию:

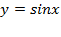
Основные свойства этой функции:

1) Область определения ;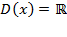

2) Область значений ;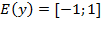

3) Функция нечетная ;

4) Функция не является монотонной на всей своей области определения;

5) Функция периодична с периодом .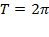

 

Построим график функции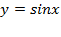

. При этом удобно начинать построение с изображения области, которая ограничивает график сверху числом 1 и снизу числом , что связано с областью значений функции. Кроме того, для построения полезно помнить значения синусов нескольких основных табличных углов, например, что  Это позволит построить первую полную «волну» графика и потом перерисовывать ее вправо и влево, пользуясь тем, что картинка будет повторяться со смещением на период, т.е. на .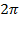

Теперь рассмотрим функцию:

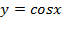
Основные свойства этой функции:

1) Область определения ;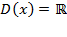

2) Область значений ;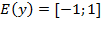

3) Функция четная  Из этого следует симметричность графика функции относительно оси ординат;

4) Функция не является монотонной на всей своей области определения;

5) Функция периодична с периодом .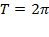

Построим график функции 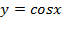. Как и при построении синуса удобно начинать с изображения области, которая ограничивает график сверху числом 1 и снизу числом , что связано с областью значений функции. Также нанесем на график координаты нескольких точек, для чего необходимо помнить значения косинусов нескольких основных табличных углов, например, что 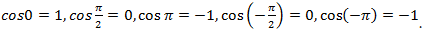 С помощью этих точек мы можем построить первую полную «волну» графика и потом перерисовывать ее вправо и влево, пользуясь тем, что картинка будет повторяться со смещением на период, т.е. на .

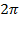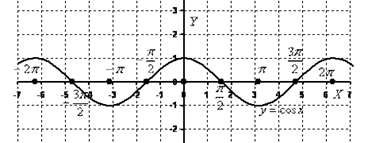
Перейдем к функции:

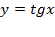
Основные свойства этой функции:

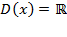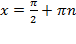1) Область определения  кроме , где 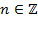. Мы уже указывали в предыдущих уроках, что  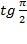не существует. Это утверждение можно обобщить, учитывая период тангенса;

2) Область значений 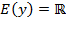, т.е. значения тангенса не ограничены;

3) Функция нечетная ;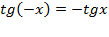

4) Функция монотонно возрастает в пределах своих так называемых веток тангенса, которые мы сейчас увидим на рисунке;

5) Функция периодична с периодом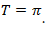 

 

Построим график функции 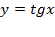. При этом удобно начинать построение с изображения вертикальных асимптот графика в точках, которые не входят в область определения, т.е.  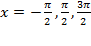и т.д. Далее изображаем ветки тангенса внутри каждой из образованных асимптотами полосок, прижимая их к левой асимптоте и к правой. При этом не забываем, что каждая ветка монотонно возрастает. Все ветки изображаем одинаково, т.к. функция имеет период, равный 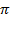. Это видно по тому, что каждая ветка получается смещением соседней на  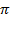вдоль оси абсцисс.

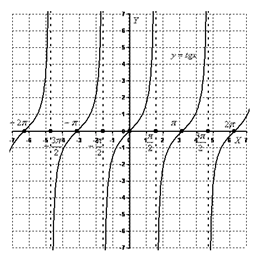
И завершаем рассмотрением функции:

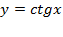
Основные свойства этой функции:

 

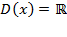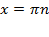1) Область определения  кроме , где 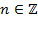. По таблице значений тригонометрических функций мы уже знаем, что  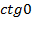не существует. Это утверждение можно обобщить, учитывая период котангенса;

2) Область значений 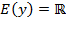, т.е. значения котангенса не ограничены;

3) Функция нечетная ;

4) Функция монотонно убывает в пределах своих веток, которые похожи на ветки тангенса;

5) Функция периодична с периодом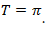 

 

Построим график функции 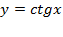. При этом, как и для тангенса, удобно начинать построение с изображения вертикальных асимптот графика в точках, которые не входят в область определения, т.е.  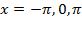и т.д. Далее изображаем ветки котангенса внутри каждой из образованных асимптотами полосок, прижимая их к левой асимптоте и к правой. В этом случае учитываем, что каждая ветка монотонно убывает. Все ветки аналогично тангенсу изображаем одинаково, т.к. функция имеет период, равный .

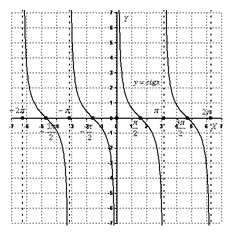
Отдельно следует отметить тот факт, что у тригонометрических функций со сложным аргументом может быть нестандартный период. Речь идет о функциях вида:

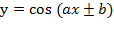
У них период равен 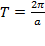. И о функциях:

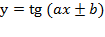
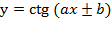
У них период равен .

Как видим, для вычисления нового периода стандартный период просто делится на множитель при аргументе. От остальных видоизменений функции он не зависит.

Подробнее разобраться и понять, откуда берутся эти формулы, вы сможете в уроке про построение и преобразование графиков функций.

Мы подошли к одной из самых главных частей темы «Тригонометрия», которую мы посвятим решению тригонометрических уравнений. Умение решать такие уравнения важно, например, при описании колебательных процессов в физике. Представим, что вы на спортивной машине проехали несколько кругов на картинге, определить сколько времени вы уже участвуете в гонке в зависимости от положения машины на трассе поможет решение тригонометрического уравнения. 

Запишем простейшее тригонометрическое уравнение:

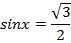
Решением такого уравнения являются аргументы, синус которых равен 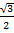. Но мы уже знаем, что из-за периодичности синуса таких аргументов существует бесконечное множество. Таким образом, решением этого уравнения будут  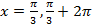и т.п. То же самое относится и к решению любого другого простейшего тригонометрического уравнения, их будет бесконечное количество.

Тригонометрические уравнения делятся на несколько основных типов. Отдельно следует остановиться на простейших, т.к. все остальные к ним сводятся. Таких уравнений четыре (по количеству основных тригонометрических функций). Для них известны общие решения, их необходимо запомнить.

Простейшие тригонометрические уравнения и их общие решения выглядят следующим образом:

1)

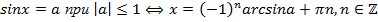
2)

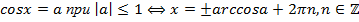
3)

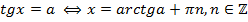
4)

Обратите внимание, что на значения синуса и косинуса необходимо учитывать известные нам ограничения. Если, например, 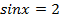, то уравнение не имеет решений и применять указанную формулу не следует. 

Кроме того, указанные формулы корней содержат параметр в виде произвольного целого числа . В школьной программе это единственный случай, когда решение уравнения без параметра содержит в себе параметр. Это произвольное целое число показывает, что можно выписать бесконечное количество корней любого из указанных уравнений просто подставляя вместо  по очереди все целые числа.

Ознакомиться с подробным получением указанных формул вы можете, повторив главу «Тригонометрические уравнения» в программе алгебры 10 класса.

Отдельно необходимо обратить внимание на решение частных случаев простейших уравнений с синусом и косинусом. Эти уравнения имеют вид:

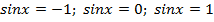 и

.

К ним не следует применять формулы нахождения общих решений. Такие уравнения удобнее всего решаются с использованием тригонометрической окружности, что дает более простой результат, чем формулы общих решений.

Например, решением уравнения 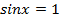 является 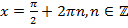. Попробуйте сами получить этот ответ и решить остальные указанные уравнения.

 

Кроме указанного наиболее часто встречающегося типа тригонометрических уравнений существуют еще несколько стандартных. Перечислим их с учетом тех, которые мы уже указали:

1) Простейшие, например, ;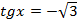

2) Частные случаи простейших уравнений, например, ;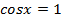

3) Уравнения со сложным аргументом, например, ;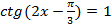

4) Уравнения, сводящиеся к простейшим путем вынесения общего множителя, например, ;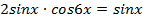

5) Уравнения, сводящиеся к простейшим путем преобразования тригонометрических функций, например, ;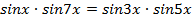

6) Уравнения, сводящиеся к простейшим с помощью замены, например, ;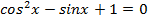

7) Однородные уравнения, например, ;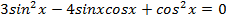

8) Уравнения, которые решаются с использованием свойств функций, например, 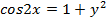. Пусть вас не пугает, что в этом уравнении две переменные, оно при этом решается;

А также уравнения, которые решаются с использованием различных методов.

Кроме решения тригонометрических уравнений необходимо уметь решать и их системы.

Наиболее часто встречаются системы следующих типов:

1) В которых одно из уравнений степенное, например, ;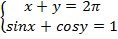

2) Системы из простейших тригонометрических уравнений, например, .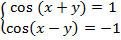

 

На сегодняшнем уроке мы рассмотрели основные тригонометрические функции, их свойства и графики. А также познакомились с общими формулами решения простейших тригонометрических уравнений, указали основные типы таких уравнений и их систем.

В практической части урока мы разберем методы решения тригонометрических уравнений и их систем.

 

Вставка 1. Решение частных случаев простейших тригонометрических уравнений.

Как мы уже говорили в основной части урока частные случаи тригонометрических уравнений с синусом и косинусом вида:

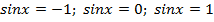 и

 

имеют более простые решения, чем дают формулы общих решений.

Для этого используется тригонометрическая окружность. Разберем метод их решения на примере уравнения .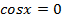

Изобразим на тригонометрической окружности точку, в которой значение косинуса равно нулю, оно же является координатой по оси абсцисс. Как видим, таких точек две. Наша задача указать чему равен угол, который соответствует этим точкам на окружности.

 

 

 

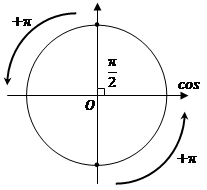Начинаем отсчет от положительного направления оси абсцисс (оси косинусов) и при откладывании угла 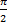 попадаем в первую изображенную точку, т.е. одним из решений будет это значение угла. Но нас же еще устраивает угол, который соответствует второй точке. Как попасть в нее?

Для этого необходимо к уже отложенному углу добавить развернутый угол 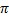. Второй угол, который является решением уравнения, равен 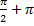. Но нельзя забывать, что это еще не все, т.к. мы можем построить угол больший полного круга, и он еще раз попадет в первую точку и также будет решением нашего уравнения. Для этого необходимо прибавить ко второму вычисленному углу еще раз 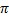, и получим значение

interneturok.ru

Тригонометрические уравнения. Задания ЕГЭ по математике (профильный уровень)

а) 1. Согласно формуле приведения, ctg\left( \frac{3\pi }2-x\right) =tgx. Областью определения уравнения будут такие значения x, что \cos x \neq 0 и tg x \neq -1. Преобразуем уравнение, пользуясь формулой косинуса двойного угла 2 \cos ^2 \frac x2=1+\cos x. Получим уравнение: 5(1+\cos x) =\frac{11+5tgx}{1+tgx}.

Заметим, что \frac{11+5tgx}{1+tgx}= \frac{5(1+tgx)+6}{1+tgx}= 5+\frac{6}{1+tgx}, поэтому уравнение принимает вид: 5+5 \cos x=5 +\frac{6}{1+tgx}. Отсюда \cos x =\frac{\dfrac65}{1+tgx}, \cos x+\sin x =\frac65.

2. Преобразуем \sin x+\cos x по формуле приведения и формуле суммы косинусов: \sin x=\cos \left(\frac\pi 2-x\right), \cos x+\sin x= \cos x+\cos \left(\frac\pi 2-x\right)= 2\cos \frac\pi 4\cos \left(x-\frac\pi 4\right)= \sqrt 2\cos \left( x-\frac\pi 4\right) = \frac65.

Отсюда \cos \left(x-\frac\pi 4\right) =\frac{3\sqrt 2}5. Значит, x-\frac\pi 4= arc\cos \frac{3\sqrt 2}5+2\pi k, k \in \mathbb Z,

или x-\frac\pi 4= -arc\cos \frac{3\sqrt 2}5+2\pi t, t \in \mathbb Z.

Поэтому x=\frac\pi 4+arc\cos \frac{3\sqrt 2}5+2\pi k,k \in \mathbb Z,

или x =\frac\pi 4-arc\cos \frac{3\sqrt 2}5+2\pi t,t \in \mathbb Z.

Найденные значения x принадлежат области определения.

б) Выясним сначала куда попадают корни уравнения при k=0 и t=0. Это будут соответственно числа a=\frac\pi 4+arccos \frac{3\sqrt 2}5 и b=\frac\pi 4-arccos \frac{3\sqrt 2}5.

1. Докажем вспомогательное неравенство:

\frac{\sqrt 2}{2}<\frac{3\sqrt 2}2<1.

Действительно, \frac{\sqrt 2}{2}=\frac{5\sqrt 2}{10}<\frac{6\sqrt2}{10}=\frac{3\sqrt2}{5}.

Заметим также, что \left( \frac{3\sqrt 2}5\right) ^2=\frac{18}{25}<1^2=1, значит \frac{3\sqrt 2}5<1.

2. Из неравенств (1) по свойству арккосинуса получаем:

arccos 1<arc\cos \frac{3\sqrt 2}5<arc\cos \frac{\sqrt 2}2,

0<arccos\frac{3\sqrt2}{5}<\frac{\pi}{4}.

Отсюда \frac\pi 4+0<\frac\pi 4+arc\cos \frac{3\sqrt 2}5<\frac\pi 4+\frac\pi 4,

0<\frac\pi 4+arccos \frac{3\sqrt 2}5<\frac\pi 2,

0<a<\frac\pi 2.

Аналогично, -\frac\pi 4<arccos\frac{3\sqrt2}{5}<0,

0=\frac\pi 4-\frac\pi 4<\frac\pi 4-arccos \frac{3\sqrt 2}5< \frac\pi 4<\frac\pi 2,

0<b<\frac\pi 2.

При k=-1 и t=-1 получаем корни уравнения a-2\pi и b-2\pi.

\Bigg( a-2\pi =-\frac74\pi +arccos \frac{3\sqrt 2}5,\, b-2\pi =-\frac74\pi -arccos \frac{3\sqrt 2}5\Bigg). При этом -2\pi <a-2\pi <-\frac{3\pi }2,

-2\pi <b-2\pi <-\frac{3\pi }2. Значит, эти корни принадлежат заданному промежутку \left( -2\pi , -\frac{3\pi }2\right).

При остальных значениях k и t корни уравнения не принадлежат заданному промежутку.

Действительно, если k\geqslant 1 и t\geqslant 1, то корни больше 2\pi. Если k\leqslant -2 и t\leqslant -2, то корни меньше -\frac{7\pi }2.

academyege.ru

Формулы приведения и решение типовых задач. Видеоурок. Алгебра 10 Класс

Тема: Тригонометрические функции

Урок: Формулы приведения и решение типовых задач

Формулы приведения подчиняются двум правилам, которые мы рассмотрели на прошлом уроке. Они позволяют привести значения тригонометрических функций к более удобным углам. Особенно важны углы, кратные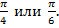

Рассмотрим таблицу значений тригонометрических функций для таких углов. 

α	0								π
sinα	0				1				0				-1				0
cosα	1				0				-1				0				1
tgα	0		1						0		1		—				0
ctgα	—		1		0				—		1		0				—

  

По вертикали отложены функции, по горизонтали – углы, кратные 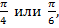  на отрезке

Держать такую таблицу в голове довольно сложно. Надо иметь способ быстрого получения значений тригонометрических функций для этих углов. Применение формул приведения и есть такой способ. Для этого достаточно запомнить значения тригонометрических функций для углов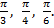   

Рассмотрим расположение углов на числовой оси и числовой окружности.

Углы из отрезка 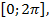 кратные  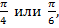на координатной оси (рис. 1).

Углы из отрезка 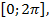 кратные  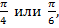на единичной окружности (рис. 2).

 

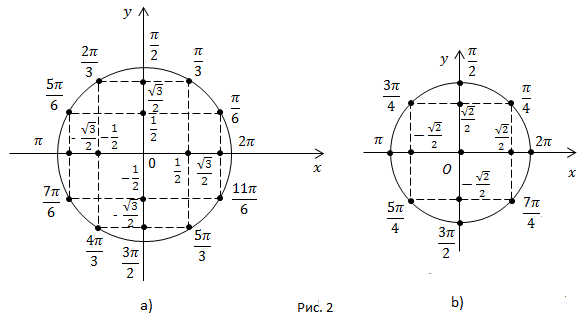
a) Значения  кратные

interneturok.ru

Тригонометрические уравнения | Материалы для подготовки к ЕГЭ по математике ЕГЭ-Студия

Ну что, перечисляем обе серии (1) и (2) в ответе через запятую? Нет! Серия (2) является в данном случае частью серии (1). Действительно, если в формуле (1) число n кратно 5, то мы получаем все решения серии (2).
Поэтому ответ:

3. Бывает, что перед разложением суммы или разности тригонометрических функций в произведение надо проделать обратную процедуру: превратить произведение в сумму (разность).

Решим уравнение:

Домножаем обе части на 2, преобразуем левую часть в разность косинусов, а правую часть — в сумму косинусов:

Ответ:

4. Ещё пример, где финальное разложение на множители поначалу замаскировано:
Здесь используем формулу понижения степени:
(которая является ни чем иным, как переписанной в другом виде формулой косинуса двойного
угла). Получаем:
и дальше ясно.

5. Многие оказываются в ступоре при виде следующего уравнения:
Переносим косинус влево и применяем формулу приведения
Дальше — дело техники.

6. А в этом примере нужны совсем другие манипуляции:
Раскладываем синус двойного угла, всё собираем в левой части и группируем:
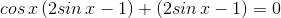
Цель достигнута.

Рассмотрим уравнение:
Степень каждого слагаемого в левой части равна двум. Точно так же, как в обычном многочлене
степень каждого слагаемого равна двум (степень одночлена — это сумма степеней входящих в него сомножителей).
Поскольку степени всех слагаемых одинаковы, такое уравнение называют однородным. Для однородных уравнений существует стандартный приём решения — деление обеих его частей на . Возможность этого деления, однако, должна быть обоснована: а что, если косинус равен нулю?

Следующий абзац предлагаем выучить наизусть и всегда прописывать его при решении однородных уравнений.

Предположим, что . Тогда в силу уравнения и 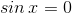, что противоречит основному тригонометрическому тождеству. Следовательно, любое решение данного уравнения удовлетворяет условию , и мы можем поделить обе его части на .

В результате деления приходим к равносильному квадратному уравнению относительно тангенса:

и дальнейший ход решения трудностей не представляет

1. Рассмотрим уравнение
Если бы в правой части стоял нуль, уравнение было бы однородным. Мы поправим ситуацию изящным приёмом: заменим число 3 на выражение :
и дело сделано.

2. Неожиданным образом сводится к однородному следующее уравнение:
Казалось бы, где тут однородность? Переходим к половинному углу!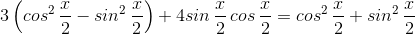
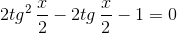
откуда

(3)

Мы не случайно довели это уравнение до ответа. В следующем разделе оно будет решено другим методом, и ответ окажется внешне непохожим на этот.

Введение дополнительного угла

Этот метод применяется для уравнений вида . Он присутствует в школьных учебниках. Правда, в них рассматриваются только частные случаи — когда числа a и b являются значениями синуса и косинуса углов в 30°, 45° или 60°.

1. Рассмотрим уравнение
Делим обе части на 2:
Замечаем, что  :

В левой части получили синус суммы:
,
откуда и

2. Другой пример:
Делим обе части на
Сделаем теперь для разнообразия в левой части косинус разности:
3. Рассмотрим теперь общий случай — уравнение
Делим обе части на :

(4)

Для чего мы выполнили это деление? Всё дело в получившихся коэффициентах при косинусе и синусе. Легко видеть, что сумма их квадратов равна единице:

Это означает, что данные коэффициенты сами являются косинусом и синусом некоторого угла :

Соотношение (4) тогда приобретает вид:
,
или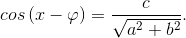

Исходное уравнение сведено к простейшему. Теперь понятно, почему рассматриваемый метод называется введением дополнительного угла. Этим дополнительным углом как раз и является угол .

4. Снова решим уравнение
Делим обе части на :
Существует угол такой, что 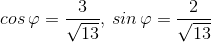. Например, . Получаем:
,
,
,
,

В предыдущем разделе мы решили это уравнение, сведя его к однородному, и получили в качестве ответа выражение (3). Сравните с полученным только что выражением. А ведь это одно и то же множество решений!

Универсальная подстановка

Запомним две важные формулы: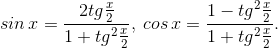

Их ценность в том, что они позволяют выразить синус и косинус через одну и ту же функцию — тангенс половинного угла. Именно поэтому они получили название универсальной подстановки. Единственная неприятность, о которой не надо забывать: правые части этих формул не определены при . Поэтому если применение универсальной подстановки приводит к сужению ОДЗ, то данную серию нужно проверить непосредственно.

1. Решим уравнение
Выражаем , используя универсальную подстановку:
Делаем замену :
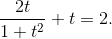Получаем кубическое уравнение:
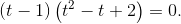Оно имеет единственный корень . Стало быть, , откуда .
Сужения ОДЗ в данном случае не было, так как уравнение с самого начала содержало .

2. Рассмотрим уравнение
А вот здесь использование универсальной подстановки сужает ОДЗ. Поэтому сначала непосредственно подставляем в уравнение и убеждаемся, что это — решение.
Теперь обозначаем  и применяем универсальную подстановку:
После простых алгебраических преобразований приходим к уравнению:
Следовательно, и .
Ответ: .

Метод оценок

В некоторых уравнениях на помощь приходят оценки .

3. Рассмотрим уравнение
Так как оба синуса не превосходят единицы, данное равенство может быть выполнено лишь в
том случае, когда они равны единице одновременно:
Таким образом, должны одновременно выполняться следующие равенства:
Обратите внимание, что сейчас речь идёт о пересечении множества решений (а не об их объединении, как это было в случае разложения на множители). Нам ещё предстоит понять, какие значения x удовлетворяют обоим равенствам. Имеем: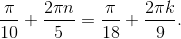
Умножаем обе части на 90 и сокращаем на π: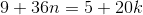
Правая часть, как видим, должна делиться на 5. Число n при делении на 5 может давать остатки от 0 до 4; иначе говоря, число n может иметь один из следующих пяти видов: 5n, 5m + 1, 5m + 2, 5m + 3 и 5m + 4, где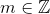. Для того, чтобы 9n+ 1 делилось на 5, годится лишь n = 5m + 1.

Искать k, в принципе, уже не нужно. Сразу находим x:

Ответ: .

4. Рассмотрим уравнение
Ясно, что данное равенство может выполняться лишь в двух случаях: когда оба синуса одновременно равны 1 или −1. Действуя так, мы должны были бы поочерёдно рассмотреть две системы уравнений.

Лучше поступить по-другому: умножим обе части на 2 и преобразуем левую часть в разность косинусов:
Тем самым мы сокращаем работу вдвое, получая лишь одну систему:
Имеем:
Ищем пересечение:
Умножаем на 21 и сокращаем на π:
Данное равенство невозможно, так как в левой части стоит чётное число, а в правой — нечётное.
Ответ: решений нет.

5. Страшное с виду уравнение
также решается методом оценок. В самом деле, из неравенств следует, что . Следовательно, , причём равенство возможно в том и только в том случае, когда
Остаётся решить полученную систему. Это не сложно.

Учёт тригонометрических неравенств

Рассмотрим уравнение:

Перепишем его в виде, пригодном для возведения в квадрат:

Тогда наше уравнение равносильно системе:

Решаем уравнение системы:

,
,

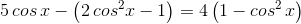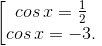
Второе уравнение данной совокупности не имеет решений, а первое даёт две серии:

Теперь нужно произвести отбор решений в соответствии с неравенством . Серия  не удовлетворяет этому неравенству, а серия удовлетворяет ему. Следовательно, решением исходного уравнения служит только серия .
Ответ: .

Специальные приёмы

В этом разделе рассматриваются некоторые типы уравнений, приёмы решения которых нужно знать обязательно.

1. Рассмотрим уравнение

Это сравнительно редкий случай, когда используется исходная формула косинуса двойного угла:
,
,
,

Каждое из уравнений полученной совокупности мы решать умеем.

2. Теперь рассмотрим такое уравнение:

Метод решения будет совсем другим. Сделаем замену . Как выразить 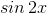 через t? Имеем:
,
откуда . Получаем:
,
,
,

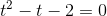Как действовать дальше, мы знаем.

3. Надо обязательно помнить формулы косинуса и синуса тройного угла (чтобы не изобретать их на экзамене):
,

Вот, например, уравнение: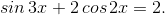

Оно сводится к уравнению относительно :
,
,

Дальше всё понятно.

4. Как бороться с суммой четвёртых степеней синуса и косинуса? Рассмотрим уравнение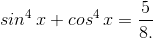

Выделяем полный квадрат!
,
,
,
,
,
,

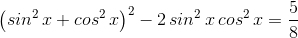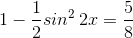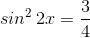5. А как быть с суммой шестых степеней? Рассмотрим такое уравнение:

Раскладываем левую часть на множители как сумму кубов: .
Получим:
,

С суммой четвёртых степеней вы уже умеете обращаться.

Мы рассмотрели основные методы решения тригонометрических уравнений. Знать их нужно обязательно, это — необходимая база.

В более сложных и нестандартных задачах нужно ещё догадаться, как использовать те или иные методы. Это приходит только с опытом. Именно этому мы и учим на наших занятиях.

 

ege-study.ru

Задание 6 — геометрия с элементами тригонометрии

14 апреля 2011

Сегодня рассмотрим задачи B8 c тригонометрией в ее классическом понимании, где изучаются обычные прямоугольные треугольники. Поэтому никаких тригонометрических окружностей и отрицательных углов сегодня не будет — только обычные синусы и косинусы.

Такие задачи составляют примерно 30% от общего числа. Помните: если в задаче B8 хоть раз упоминается угол π, она решается совсем другими способами. Мы обязательно рассмотрим их в ближайшее время. А сейчас — главное определение урока:

Треугольник — фигура на плоскости, состоящая из трех точек и отрезков, которые их соединяют. Фактически, это замкнутая ломаная из трех звеньев. Точки называются вершинами треугольника, а отрезки — сторонами. Важно заметить, что вершины не должны лежать на одной прямой, иначе треугольник вырождается в отрезок.

Довольно часто треугольником называют не только саму ломаную, но и часть плоскости, которая этой ломаной ограничена. Таким образом, можно определить площадь треугольника.

Два треугольника называются равными, если один можно получить из другого путем одного или нескольких движений плоскости: сдвига, поворота или симметрии. Кроме того, существует понятие подобных треугольников: их углы равны, а соответствующие стороны пропорциональны…

Все, что написано выше, можно было не читать. Потому что это не нужно. Вы что, не знаете, что такое треугольник? Вы действительно не знаете, как он выглядит? Хорошо, я сейчас покажу.

Это треугольник ABC. Более того, это прямоугольный треугольник: в нем ∠C = 90°. Именно такие чаще всего и встречаются в задаче B8.

Все, что надо знать для решения задачи B8 — это несколько простых фактов из геометрии и тригонометрии, а также общая схема решения, в которой эти факты используются. Затем останется просто «набить руку».

Начнем с фактов. Они разбиты на три группы:

1. Определения и следствия из них;
2. Основные тождества;
3. Симметрии в треугольнике.

Нельзя сказать, что какая-то из этих групп важнее, сложнее или проще. Но информация, которая в них содержится, позволяет решить любую задачу B8. Поэтому знать надо все. Итак, поехали!

Группа 1: определения и следствия из них

Рассмотрим треугольник ABC, где ∠C — прямой. Для начала — определения:

Синус угла — это отношение противолежащего катета к гипотенузе.

Косинус угла — это отношение прилежащего катета к гипотенузе.

Тангенс угла — это отношение противолежащего катета к прилежащему.

Один угол или отрезок может входить в разные прямоугольные треугольники. Более того, очень часто один и тот же отрезок является катетом в одном треугольнике и гипотенузой — в другом. Но об этом — дальше, а пока будем работать с обычным углом А. Тогда:

1. sin A = BC : AB;
2. cos A = AC : AB;
3. tg A = BC : AC.

Основные следствия из определения:

1. sin A = cos B; cos A = sin B — самые часто используемые следствия
2. tg A = sin A : cos A — связывает тангенс, синус и косинус одного угла
3. Если ∠A + ∠B = 180°, т.е. углы смежные, то: sin A = sin B; cos A = −cos B.

Хотите — верьте, хотите — нет, но этих фактов достаточно, чтобы решить примерно треть всех тригонометрических задач B8.

Группа 2: основные тождества

Первое и самое главное тождество — теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Применительно к треугольнику ABC, рассмотренному выше, эту теорему можно записать так:

AC ² + BC ² = AB ²

И сразу — небольшое замечание, которое убережет читателя от множества ошибок. Когда решаете задачу, всегда (слышите, всегда!) записывайте теорему Пифагора именно в таком виде. Не пытайтесь сразу выражать катет, как это обычно требуется. Возможно, вы сэкономите пару строчек вычислений, но именно на этой «экономии» было потеряно больше баллов, чем где-либо еще в геометрии.

Второе тождество — из тригонометрии. Выглядит следующим образом:

sin ²A + cos ²A = 1

Оно так и называется: основное тригонометрическое тождество. С его помощью можно через синус выразить косинус и наоборот.

Группа 3: Симметрии в треугольнике

То, что написано ниже, относится только к равнобедренным треугольникам. Если в задаче таковой не фигурирует, то для решения достаточно фактов из первых двух групп.

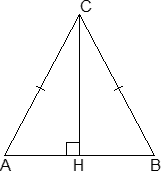
Итак, рассмотрим равнобедренный треугольник ABC, где AC = BC. Проведем к основанию высоту CH. Получим следующие факты:

1. ∠A = ∠B. Как следствие, sin A = sin B; cos A = cos B; tg A = tg B.
2. CH — не только высота, но и биссектриса, т.е. ∠ACH = ∠BCH. Аналогично, равны и тригонометрические функции этих углов.
3. Также CH — это медиана, поэтому AH = BH = 0,5 · AB.

Теперь, когда все факты рассмотрены, перейдем непосредственно к методам решения.

Общая схема решения задачи B8

Геометрия отличается от алгебры тем, что в ней нет простых и универсальных алгоритмов. Каждую задачу приходится решать с нуля — и в этом ее сложность. Тем не менее, общие рекомендации дать все-таки можно.

Для начала, следует обозначить неизвестную сторону (если таковая имеется) за X. Затем применяем схему решения, которая состоит из трех пунктов:

1. Если в задаче есть равнобедренный треугольник, применить к нему все возможные факты из третьей группы. Найдите равные углы и выразите их тригонометрические функции. Кроме того, равнобедренный треугольник редко бывает прямоугольным. Поэтому ищите в задаче прямоугольные треугольники — они там обязательно есть.
2. Применить к прямоугольному треугольнику факты из первой группы. Конечная цель — получить уравнение относительно переменной X. Найдем X — решим задачу.
3. Если фактов из первой группы оказалось недостаточно, применяем факты из второй группы. И снова ищем X.

Примеры решения задач

А теперь попробуем с помощью полученных знаний решить наиболее распространенные задачи B8. Не удивляйтесь, что с таким арсеналом текст решения окажется не намного длиннее, чем исходное условие. И это радует 🙂

Задача. В треугольнике ABC угол C равен 90°, AB = 5, BC = 3. Найдите cos A.

По определению (группа 1), cos A = AC : AB. Гипотенуза AB нам известна, а вот катет AC придется искать. Обозначим его AC = x.

Переходим к группе 2. Треугольник ABC — прямоугольный. По теореме Пифагора:

AC ² + BC ² = AB ²;
x² + 3² = 5²;
x² = 25 − 9 = 16;
x = 4.

Теперь можно найти косинус:

cos A = AC : AB = 4 : 5 = 0,8.

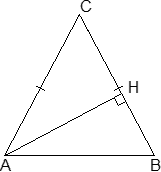
Задача. В треугольнике ABC угол B равен 90°, cos A = 4/5, BC = 3. BH — высота. Найдите AH.

Обозначим искомую сторону AH = x и рассмотрим треугольник ABH. Он прямоугольный, причем ∠AHB = 90° по условию. Поэтому cos A = AH : AB = x : AB = 4/5. Это пропорция, ее можно переписать так: 5 · x = 4 · AB. Очевидно, мы найдем x, если будем знать AB.

Рассмотрим треугольник ABC. Он также прямоугольный, причем cos A = AB : AC. Ни AB, ни AC нам не известны, поэтому переходим ко второй группе фактов. Запишем основное тригонометрическое тождество:

sin ²A + cos ²A = 1;
sin ²A = 1 − cos ²A = 1 − (4/5)² = 1 − 16/25 = 9/25.

Поскольку тригонометрические функции острого угла положительны, получаем sin A = 3/5. С другой стороны, sin A = BC : AC = 3 : AC. Получаем пропорцию:

3 : AC = 3 : 5;
3 · AC = 3 · 5;
AC = 5.

Итак, AC = 5. Тогда AB = AC · cos A = 5 · 4/5 = 4. Наконец, находим AH = x:

5 · x = 4 · 4;
x = 16/5 = 3,2.

Задача. В треугольнике ABC AB = BC, AC = 5, cos C = 0,8. Найдите высоту CH.

Обозначим искомую высоту CH = x. Перед нами равнобедренный треугольник ABC, в котором AB = BC. Следовательно, из третьей группы фактов имеем:

∠A = ∠C ⇒ cos A = cos C = 0,8

Рассмотрим треугольник ACH. Он прямоугольный (∠H = 90°), причем AC = 5 и cos A = 0,8. По определению, cos A = AH : AC = AH : 5. Получаем пропорцию:

AH : 5 = 8 : 10;
10 · AH = 5 · 8;
AH = 40 : 10 = 4.

Осталось воспользоваться второй группой фактов, а именно теоремой Пифагора для треугольника ACH:

AH ² + CH ² = AC ²;
4² + x² = 5²;
x² = 25 − 16 = 9;
x = 3.

Задача. В прямоугольном треугольнике ABC ∠B = 90°, AB = 32, AC = 40. Найдите синус угла CAD.

Поскольку нам известна гипотенуза AC = 40 и катет AB = 32, можно найти косинус угла A: cos A = AB : AC = 32 : 40 = 0,8. Это был факт из первой группы.

Зная косинус, можно найти синус через основное тригонометрическое тождество (факт из второй группы):

sin ²A + cos ²A = 1;
sin ²A = 1 − cos ²A = 1 − 0,8² = 0,36;
sin A = 0,6.

При нахождении синуса вновь был использован тот факт, что тригонометрические функции острого угла положительны. Осталось заметить, что углы BAC и CAD смежные. Из первой группы фактов имеем:

∠BAC + ∠CAD = 180°;
sin CAD = sin BAC = sin A = 0,6.

Задача. В треугольнике ABC AC = BC = 5, AB = 8, CH — высота. Найдите tg A.

Треугольник ABC — равнобедренный, CH — высота, поэтому заметим, что AH = BH = 0,5 · AB = 0,5 · 8 = 4. Это факт из третьей группы.

Теперь рассмотрим треугольник ACH: в нем ∠AHC = 90°. Можно выразить тангенс: tg A = CH : AH. Но AH = 4, поэтому остается найти сторону CH, которую обозначим CH = x. По теореме Пифагора (факт из группы 2) имеем:

AH ² + CH ² = AC ²;
4² + x² = 5²;
x² = 25 − 16 = 9;
x = 3.

Теперь все готово, чтобы найти тангенс: tg A = CH : AH = 3 : 4 = 0,75.

Задача. В треугольнике ABC AC = BC, AB = 6, cos A = 3/5. Найдите высоту AH.

Обозначим искомую высоту AH = x. Снова треугольник ABC — равнобедренный, поэтому заметим, что ∠A = ∠B, следовательно, cos B = cos A = 3/5. Это факт из третьей группы.

Рассмотрим треугольник ABH. По условию, он прямоугольный (∠AHB = 90°), причем известна гипотенуза AB = 6 и cos B = 3/5. Но cos B = BH : AB = BH : 6 = 3/5. Получили пропорцию:

BH : 6 = 3 : 5;
5 · BH = 6 · 3;
BH = 18/5 = 3,6.

Теперь найдем AH = x по теореме Пифагора для треугольника ABH:

AH ² + BH ² = AB ²;
x² + 3,6² = 6²;
x² = 36 − 12,96 = 23,04;
x = 4,8.

Дополнительные соображения

Бывают нестандартные задачи, где рассмотренные выше факты и схемы бесполезны. Увы, в таком случае нужен действительно индивидуальный подход. Подобные задачи любят давать на всевозможных «пробных» и «демонстрационных» экзаменах.

Ниже приведены две реальные задачи, которые предлагались на пробном ЕГЭ в Москве. Справились с ними единицы, что свидетельствует о высокой сложности этих задач.

Задача. В прямоугольном треугольнике ABC из угла C = 90° провели медиану и высоту. Известно, что ∠A = 23°. Найдите ∠MCH.

Заметим, что медиана CM проведена к гипотенузе AB, поэтому M — центр описанной окружности, т.е. AM = BM = CM = R, где R — радиус описанной окружности. Следовательно, треугольник ACM — равнобедренный, и ∠ACM = ∠CAM = 23°.

Теперь рассмотрим треугольники ABC и CBH. По условию, оба треугольника прямоугольные. Кроме того, ∠B — общий. Следовательно, треугольники ABC и CBH подобны по двум углам.

В подобных треугольника соответствующие элементы пропорциональны. В частности:

BCH = BAC = 23°

Наконец, рассмотрим ∠C. Он прямой, и, кроме того, ∠C = ∠ACM + ∠MCH + ∠BCH. В этом равенстве ∠MCH — искомый, а ∠ACM и ∠BCH известны и равны 23°. Имеем:

90° = 23° + MCH + 23°;
MCH = 90° − 23° − 23° = 44°.

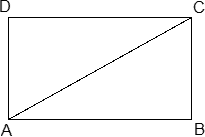
Задача. Периметр прямоугольника равен 34, а площадь равна 60. Найдите диагональ этого прямоугольника.

Обозначим стороны прямоугольника: AB = x, BC = y. Выразим периметр:

P_ABCD = 2 · (AB + BC) = 2 · (x + y) = 34;
x + y = 17.

Аналогично выразим площадь: S_ABCD = AB · BC = x · y = 60.

Теперь рассмотрим треугольник ABC. Он прямоугольный, поэтому запишем теорему Пифагора:

AB ² + BC ² = AC²;
AC ² = x² + y².

Заметим, что из формулы квадрата разности следует равенство:

x² + y² = (x + y)² − 2 · x · y = 17² − 2 · 60 = 289 − 120 = 169

Итак, AC ² = 169, откуда AC = 13.

Смотрите также:

1. Задача B8: отрезки и углы в треугольниках
2. Центральные и вписанные углы в задании 6
3. Дополнительные соображения
4. Тест к уроку «Площади многоугольников на координатной сетке» (средний)
5. Сложные логарифмические неравенства
6. Задача B5: площадь фигуры без клеток

www.berdov.com