Решение систем показательных уравнений
Цели урока:
Образовательная: научить решать системы показательны уравнений; закрепить навыки решения уравнений входящих в эти системы
Воспитательная: воспитать аккуратность.
Развивающая: развить культуру письменной и устной речи.
Оборудование: компьютер; мультимедийный проектор.
Ход урока
Организационный момент
Учитель. Сегодня мы продолжим изучение главы “Показательная функция”. Тему урока сформулируем чуть позже. В течение урока вы будите заполнять бланки ответов, которые лежат у вас на столах (см. приложение №1). Ответы будут суммироваться.
Актуализация знаний.
Учащиеся отвечают на вопросы:
- Какой вид имеет показательная функция?
Устная работа. Работа по слайдам с 1 по 5.
- Какое уравнение называется показательным?
- Какие методы решения вам известны?
Устная работа по слайдам с 6 по 10.
- Какое свойство показательной функции используют при решении показательного неравенства?
Устная работа по слайдам с 11 по 15.
Задание. Записать ответы на эти вопросы в бланке ответов №1. (см. приложение №1). (слайды с 16 по 31)
Проверка домашнего задания
.Домашнюю работу проверяем следующим образом.
Замените корни уравнений на соответствующую букву и отгадайте слово.
Учащиеся смотрят в бланк ответов №2 (приложение 1). Учитель демонстрирует слайд №33
(Учащиеся называют слово (слайд №34)).
Учитель:
- Какие явления протекают по законам этой функции?
Учащимся предлагается решить задания из ЕГЭ В12 (слайд 35) и записать решение в бланк ответа №3 (приложение 1).
Учитель.
В ходе проверки домашней работы и решая задание В12, мы повторим методы решения показательных уравниваний.
Какие еще способы вы знаете?
Далее учащимся предлагается уравнение (слайд № 36) и класс подбирает способ его решения.
Учащиеся приходят к выводу, что для решения уравнения с двумя переменными требуется еще одно уравнение.
Затем формулируется тема урока (слайд № 37).
В тетрадях записывается система (слайд № 38).
Что бы решить эту систему, повторяем метод подстановки (слайд № 39).
Метод сложения повторяется в ходе решения системы (слайд с 38 по 39).
Первичное закрепление изученного материала
:Учащиеся самостоятельно решают системы уравнений в бланках ответа № 4 (приложение 1), получая индивидуальные консультации учителя.
Подведение итогов. Рефлексия.
Продолжите фразы.
- Сегодня на уроке я повторил…
- Сегодня на уроке я закрепил…
- Сегодня на уроке я научился…
- Сегодня на уроке я узнал…
В конце урока учащиеся записывают домашнее задание, сдают бланки ответов
Задание на дом:
№ 59 (четные) и № 62 (четные).Литература
- Все задания группы ЕГЭ 3000 задач – Издательство “Экзамен” Москва, 2011. Под редакцией А.Л. Семенова, И.В. Ященко.
- С.А. Шестаков, П.И. Захаров ЕГЭ 2010 математика задача С1 под редакцией А.Л. Семенова, И.В. Ященко Москва издательство “МЦНМО”.
- Учебное пособие Алгебра и начала математического анализа,10 класс Ю.М.Колягин Москва “Просвещение”, 2008.
Презентация
Конспект урока 11 класс «Решение показательных уравнений и систем уравнений».


 Тема: «Решение показательных уравнений и систем уравнений».
Тема: «Решение показательных уравнений и систем уравнений».Цель: 1. Систематизировать виды показательных выражений,
рассмотреть способы решений уравнений и систем уравнений.
Задачи:
Научить систематизировать показательные уравнения и их системы.
Развить умение применять алгоритмы решений показательных уравнений к различным видам уравнений и их систем.
Воспитывать ответственное отношение к изучаемой теме.
Ход урока:
Организационный момент. Сообщение темы и цели урока.
Повторение и закрепление пройденного материала.
ответы на вопросы по домашнему заданию (разбор нерешённых заданий).
Устный фронтальный опрос по теме «Показательная функция».
В.1. Какая функция называется показательной?
(ответ: Функция вида у = ах, где а 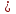 о, а ≠ 1, х — переменная, называется показательной функцией).
о, а ≠ 1, х — переменная, называется показательной функцией).
В.2. Почему основание а не должно быть равным 1 (а ≠ 1)?
(ответ: т.к при а=1 степень ах при любом значении х равнялась бы 1 и тогда она не зависела бы от х).
В.3. Почему основание а должно быть обязательно положительным (а 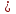
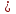 о степень ах для многих значений х не была бы действительным числом. Например а = — 5,
о степень ах для многих значений х не была бы действительным числом. Например а = — 5, 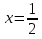 , то ах будет
, то ах будет 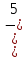 , что не является действительным числом).
, что не является действительным числом).В.4. Какое число берётся из всех значений, если х равен дроби, ах означает корень некоторой степени?
(ответ: берётся только одно арифметическое значение, т.е. неотрицательное число).
В.5. Повторить свойства:
ах
* ау= а х+уах : ау = а х-у
(ах)у = а х*у
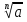 m =
m = 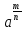
Изучение нового материала
Определение: Показательным уравнением называется уравнение котором неизвестное Х входит только в показатель степени при некоторых постоянных основаниях.
а) 2х =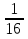 ; б)
; б) 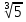
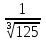 ; в) 3х+1 + 3х = 108
; в) 3х+1 + 3х = 108Способы решения показательных уравнений
Способ приведения к общему основанию
Алгоритм:
1) обе части уравнения приводим к одинаковому основанию;
2) приравниваем показатели степеней левой и правой частей уравнения, в результате чего получаем уравнение, способ решения которого известен;
3) Решаем полученное уравнение;
4) с помощью проверки определяем, какие из полученных значений переменной являются корнями данного показательного уравнения.
ПРИМЕР: 27 х = 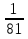
1. Обе части уравнения приводим к основанию 3 (33)х =3— 4
2. Приравниваем показатели 3х = — 4
3. Решив полученное уравнение имеем Х= —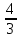
4. Проверим: 
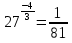
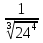 =
= 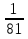
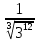 =
= 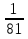
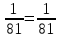 Ответ: —
Ответ: — 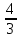
Способ введения новой переменной
Алгоритм:
Делаем замену переменной, приводящую к алгебраическому уравнению;
Решаем полученное алгебраическое уравнение;
Найденные значения корней алгебраического уравнения подставив в равенство, определяющее замену;
Найдём корни полученного уравнения;
С помощью проверки определяем, какие из этих корней являются корнями данного показательного уравнения.
ПРИМЕР: 3 2х+5 = 3 х+2 + 2
3 2х * 35 = 3х * 32 +2
(3х)2 * 243 = 3х *9+2
3х = у, тогда
243у2 – 9*у-2 = 0 решив это уравнение, имеем
у1=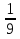 ; у2 = —
; у2 = — 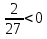
не может быть 3х 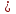 0.
0.
берём только у = 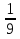 3х =
3х =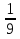 3х = 3-2 х = -2
3х = 3-2 х = -2
ответ: _______
Графический способ.
Используется в тех случаях, когда в показательном уравнении ах = в, число В нельзя представить в виде степени числа а. Для решения уравнения на одной координатной плоскости строят графики функций у=ах и у=в. Абсциссы точек пересечения графиков указанных функций будут решениями данного показательного уравнения.
Решение системы показательных уравнений.
ПРИМЕР 1:
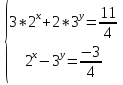 умножим обе части второго уравнения на 2
умножим обе части второго уравнения на 2
+ 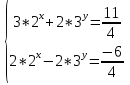 почленно сложим уравнения
почленно сложим уравнения
5 * 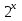 =
= 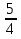
2х = 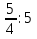
2х = 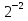 х=2 –подставим во второе уравнение системы
х=2 –подставим во второе уравнение системы
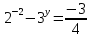 ;
;
—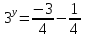 ;
;
—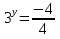 ;
;
3у = 1;
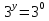 ;
;
у = 0. Ответ: (-2; 0).
ПРИМЕР 2.
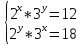
1-ый способ:
Первое уравнение почленно умножим на второе
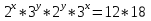
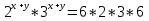
(2 * 3)х+у = 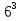
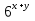 =
= 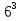
х + у = 3
у = 3 – х подставим в первое уравнение:
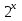 *
* 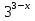 = 12
= 12
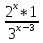 = 12
= 12
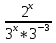 = 12
= 12
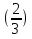 х = 12
х = 12
(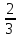 )х =
)х = 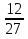
(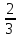 )х = (
)х = (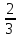 )2
)2
х = 2, у = 3 – 2 = 1. Ответ: (2;1)
Решение показательных уравнений, требующие применения различных алгебраических приёмов преобразования уравнений.
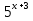 — 3 *
— 3 * 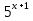 — 10 *
— 10 * 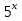 = 4
= 4
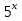 — можно вынести за скобки
— можно вынести за скобки
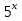 *
* 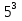 —
— 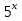 *
* 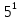 * 3 – 10 *
* 3 – 10 * 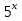 = 4
= 4
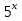 (
(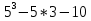 ) = 4
) = 4
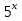 * 100 = 4
* 100 = 4
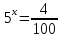
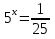
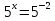
х = — 2
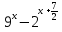 =
= 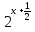 —
— 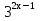
Сгруппируем члены уравнение, содержащие степени числа 3, в левой части, а члены, содержащие степени числа 2, — в правой.
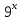 +
+ 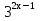 =
= 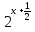 +
+ 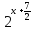
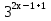 +
+ 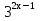 =
= 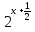 +
+ 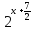
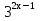 * (3+1) =
* (3+1) = 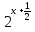 * (1+
* (1+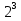 )
)
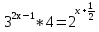 * 9
* 9
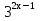 *
* 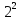 =
= 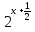 *
* 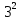 разделим обе части этого уравнения на правую часть
разделим обе части этого уравнения на правую часть
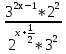 = 1 по свойствам степени
= 1 по свойствам степени
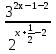 = 1
= 1
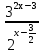 = 1
= 1
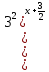 = 1
= 1
(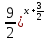 = (
= (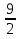 )0
)0
х — 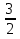 = 0
= 0
х = 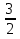
Уравнение, решаемые разложением на множители
 *
* 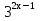 *
* 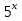 = 5400
= 5400
 *
* 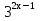 *
* 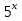 =
= 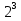 *
* 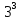 *
* 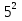
Разделим обе части уравнения на его правую часть, получим
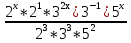 = 1 по свойствам степеней
= 1 по свойствам степеней
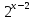 *
* 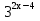 *
* 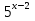 = 1
= 1
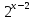 *
* 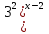 *
* 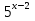 = 1
= 1
(2 * 9 * 5)х-2 = 1
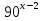 = 900
= 900
х-2 = 0
х = 2
Уравнения, содержащие помимо показательных другие функции.
2 * 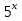
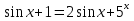
Перенесём все члены уравнения в левую часть, сгруппируем их и вынесем общие множители за скобки и имеем:
2 * 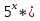
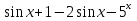 = 0
= 0
(2 * 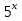
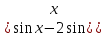 + (1-
+ (1- 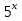 ) = 0
) = 0
2 * 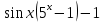 (
(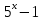 ) = 0
) = 0
(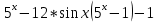 ) * (2
) * (2 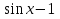 ) = 0
) = 0
т.к. произведение равно 0, если хотя бы один из множителей равен 0.
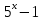 = 0 или 2
= 0 или 2 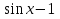 = 0
= 0
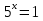 2
2 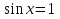
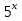 =
=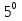
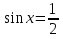
х = 0 х = (-1)n arcsin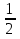 + π n,
+ π n,
х = (-1)n 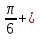 π n, n € z
π n, n € z
Есть показательные уравнения, в которых для решения приходится вводить две новые переменные.
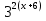 +
+ 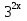 ² — 2 *
² — 2 * 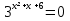
(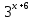 )2 + (
)2 + (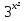 )2 – 2 *
)2 – 2 * 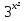 *
* 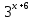 = 0
= 0
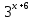 = а
= а
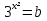 получаем
получаем
а2 + b2 – 2 аb = 0
по формуле сокращенного умножения
(а — b)2 = 0 следовательно а = b
т.е. 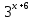 =
= 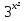
х + 6 = х2
х2 – х – 6 = 0
D=25, х1 = — 2, х2 = 3
Уравнения, решаемые с помощью их специфики.
7х + 24х = 25х
Можно угадать, что корень уравнения равен 2.
х = 2, действительно 72 + 242 = 252
Разделим все члены уравнения на его правую часть, получим
(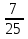 )х + (
)х + (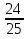 )х = 2
)х = 2
Функции (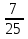 )х и (
)х и (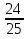 )х убывающие, т.к. основания меньше 1.
)х убывающие, т.к. основания меньше 1.
Сумма этих функций является функцией убывающей. Поэтому по теореме о корне данное уравнение имеет единственное решение. у
Уравнения, решаемые графически.
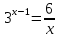 3 у2
3 у2
построим график функции у1 = 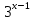 и у2 =
и у2 = 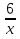 у1 х
у1 х
Видно, что графики этих функций пересекаются 2
в единственной точке А, абсцисса х = 2 которой
является решением данного уравнения.
Закрепление новой темы. Решить в классе упр.596,598,600,602(нечетные)
Д/З упр.596,598,600(четные)
Урок по алгебре в 11 классе «Решение показательных уравнений и их систем»
2. Актуализация знаний:
Учитель: На прошлом уроке вы познакомились с показательным уравнением и способом их решения.
Тема сегодняшнего урока Показательные уравнения и их системы, сформулируйте цель урока самостоятельно.
Подготовительная работа:
1 устный опрос
2 работа по карточке (решение показательных уравнений)
3. Работа у доски:
1)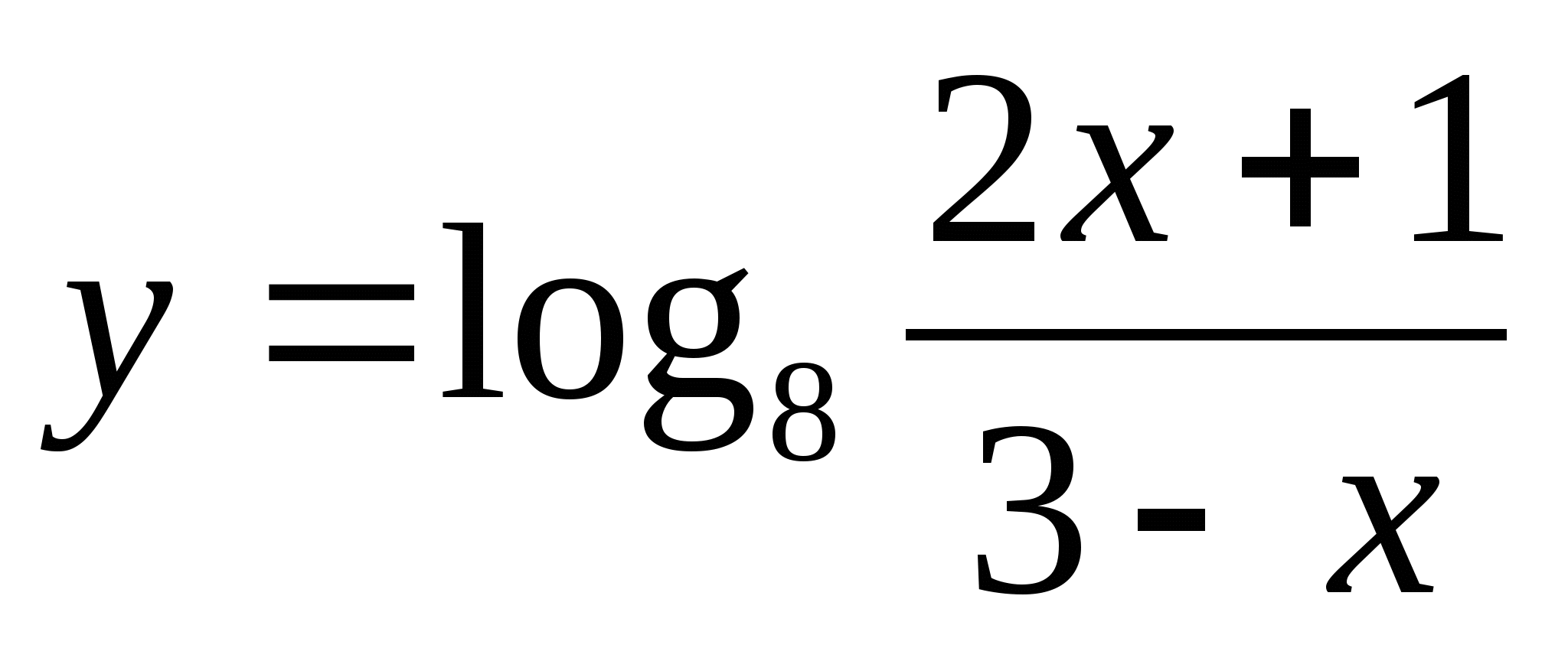
2)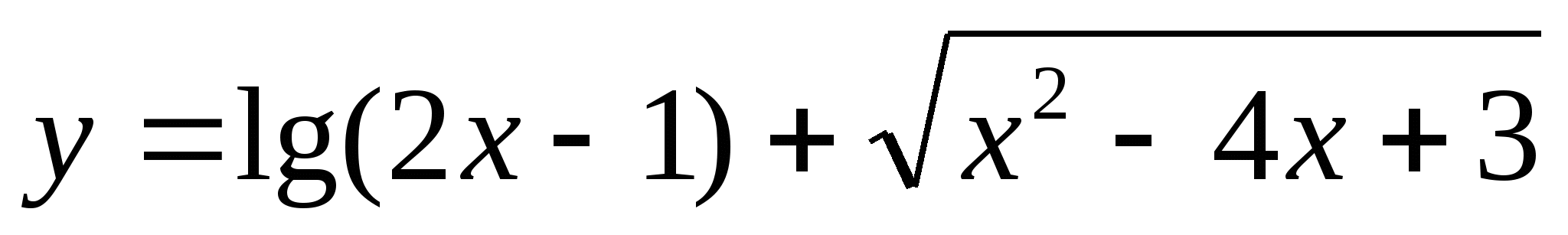
3)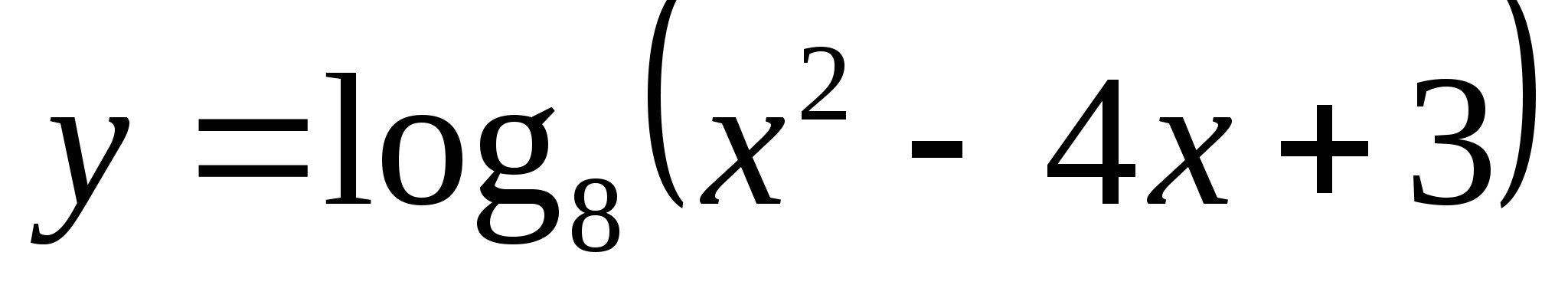
4)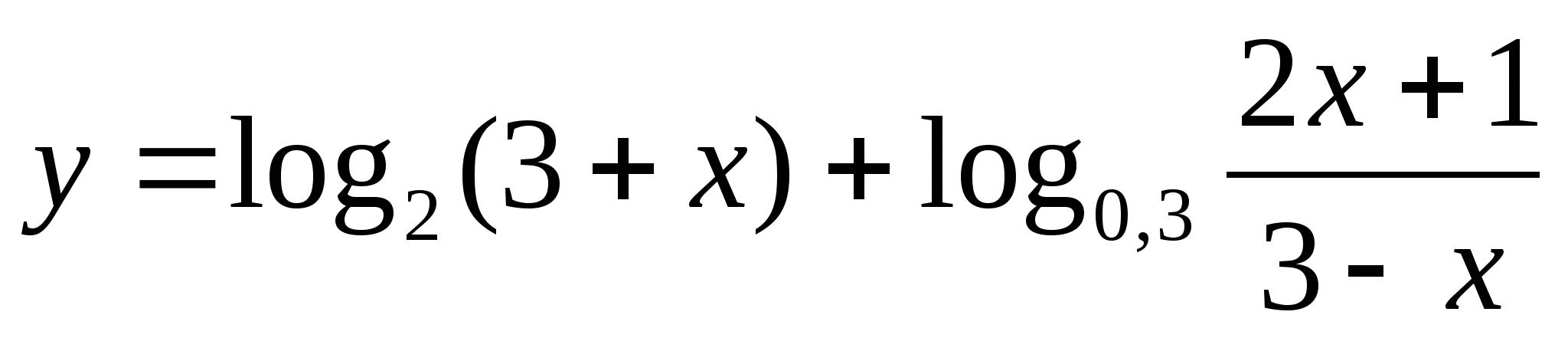
5) 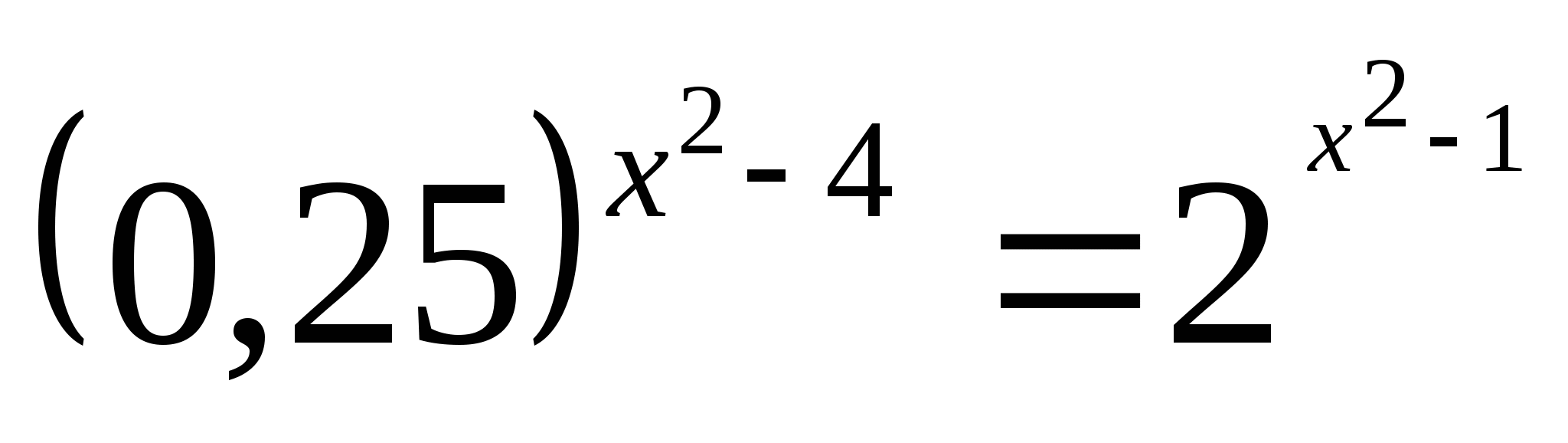
6) 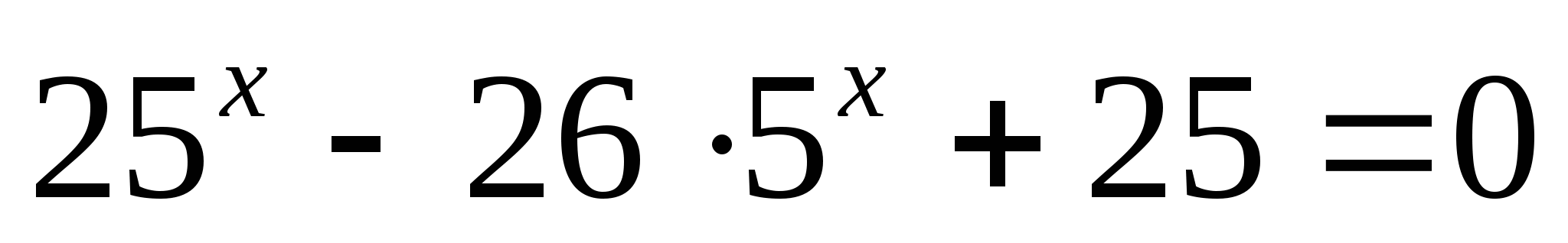
7) 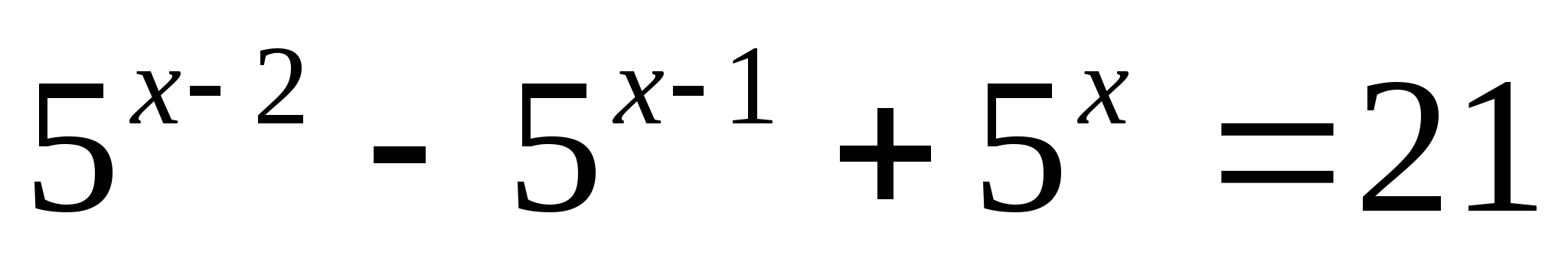
8) 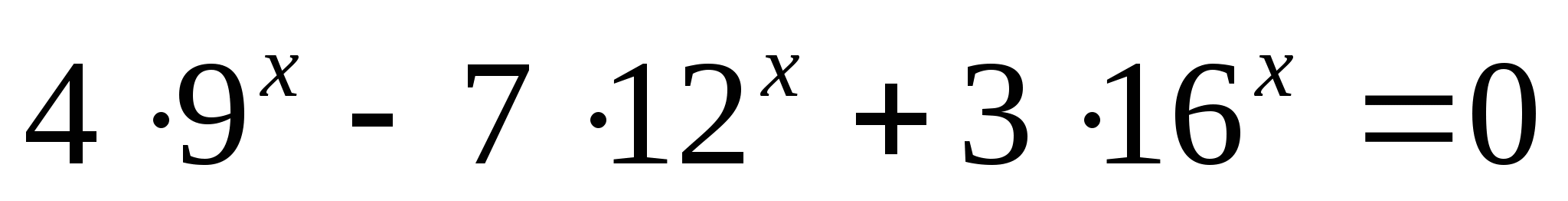
3. Изучение нового материала. Стадия содержания.
Предлагается учащимся поработать в группах с таблицей для исследования (технология «Зигзаг»).
Составить алгоритм решения способов показательных уравнений:
1)простейшие
2)разложение на множители
3)приводимые к квадратным
3)однородные
Учитель координирует деятельность учащихся
Переходят за стол под своим номером и обсуждают с коллегами заполнение таблицы, при необходимости вносят корректировку и дополнения
4. Заполнение таблицы после изучения материала
По ходу выступления учащиеся заполняют таблицу.
ИТОГ: каждый ученик получает сводную таблицу алгоритмов решения показательных уравнений.
5. Работа в группе.
Деление учащихся на группы (с целью дифференциации и выполнения разно уровневых заданий)
Используя таблицу, решить системы уравнений
1 группа (простейшие)
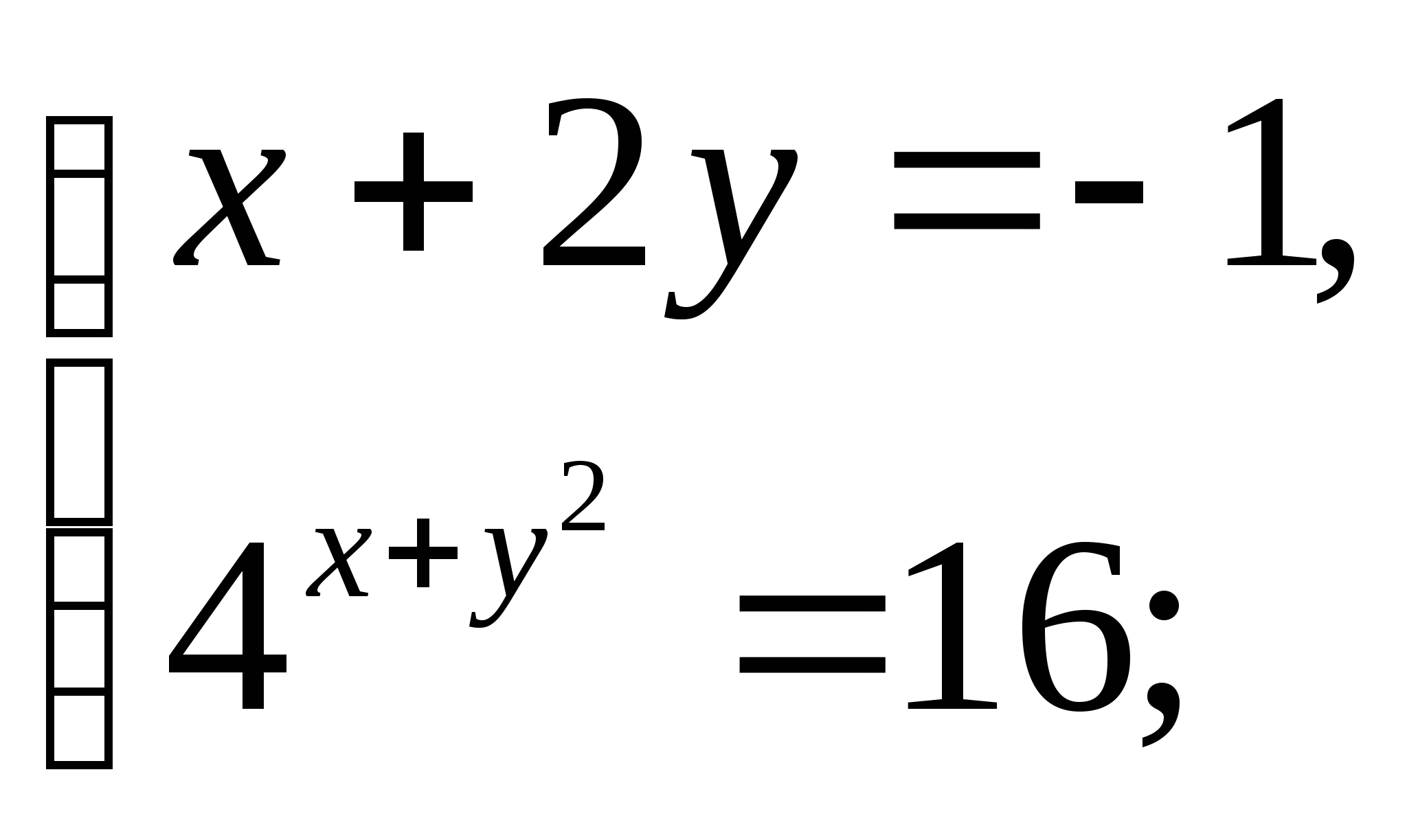 (способ подстановки)
(способ подстановки)
2 группа
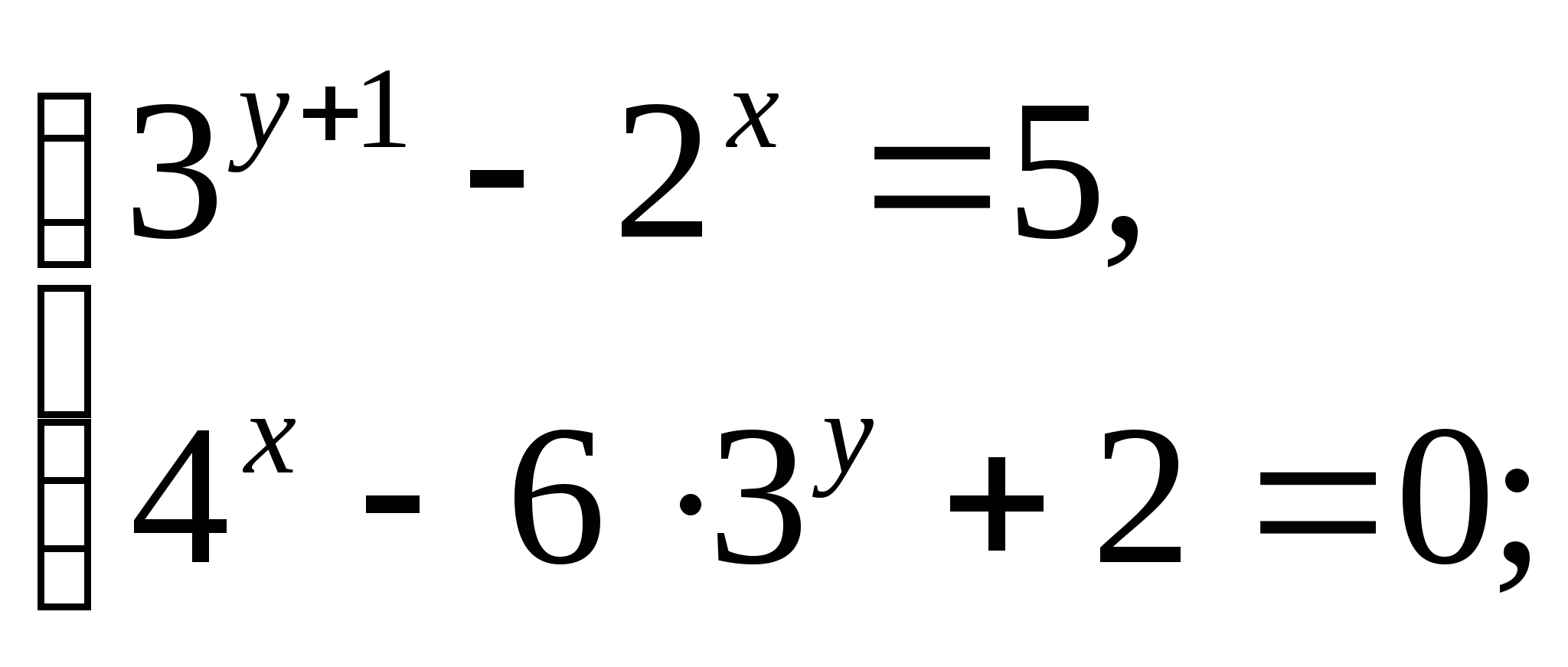 (способ замены)
(способ замены)
3 группа
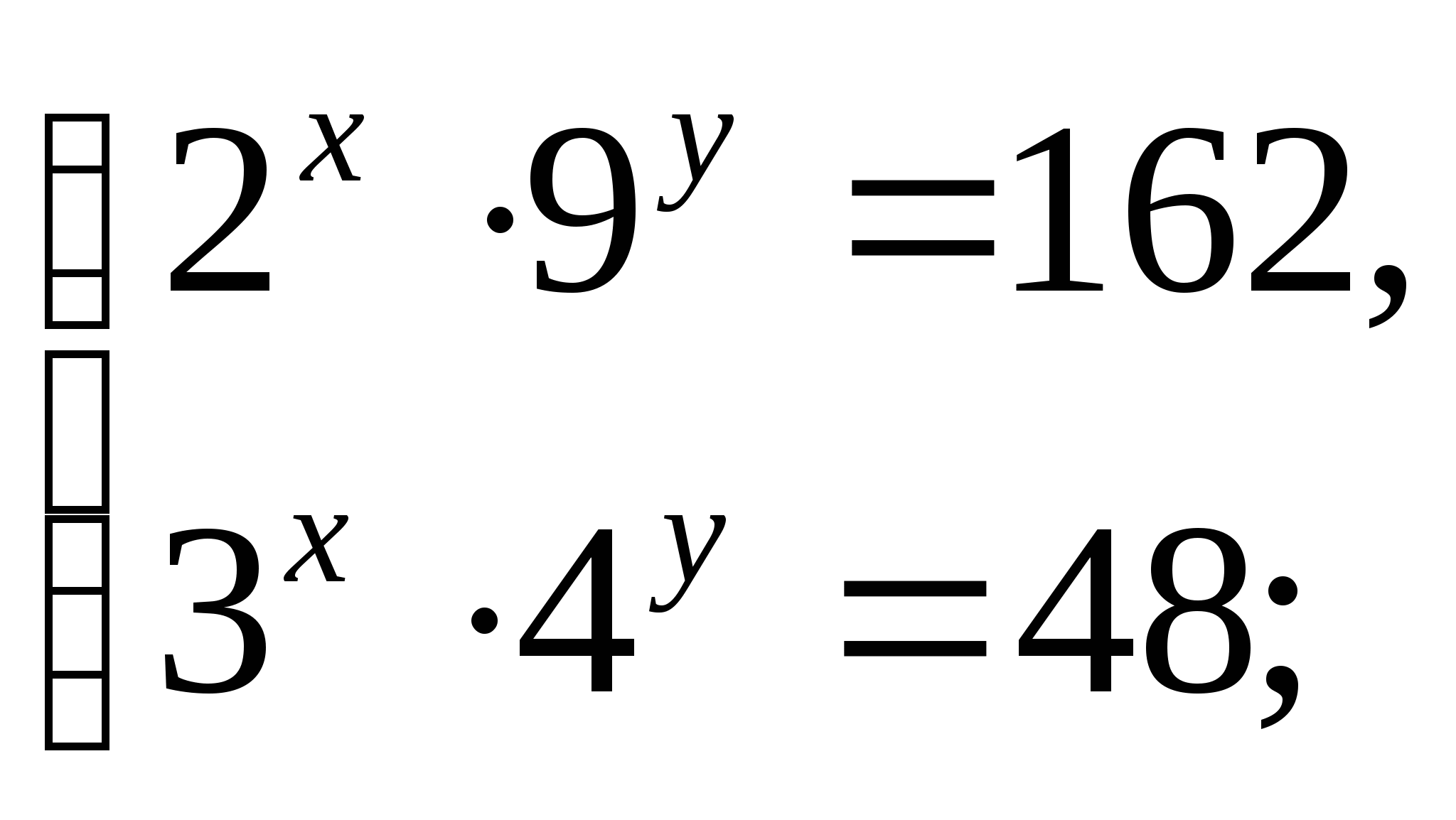 (способ перемножения)
(способ перемножения)
4 группа
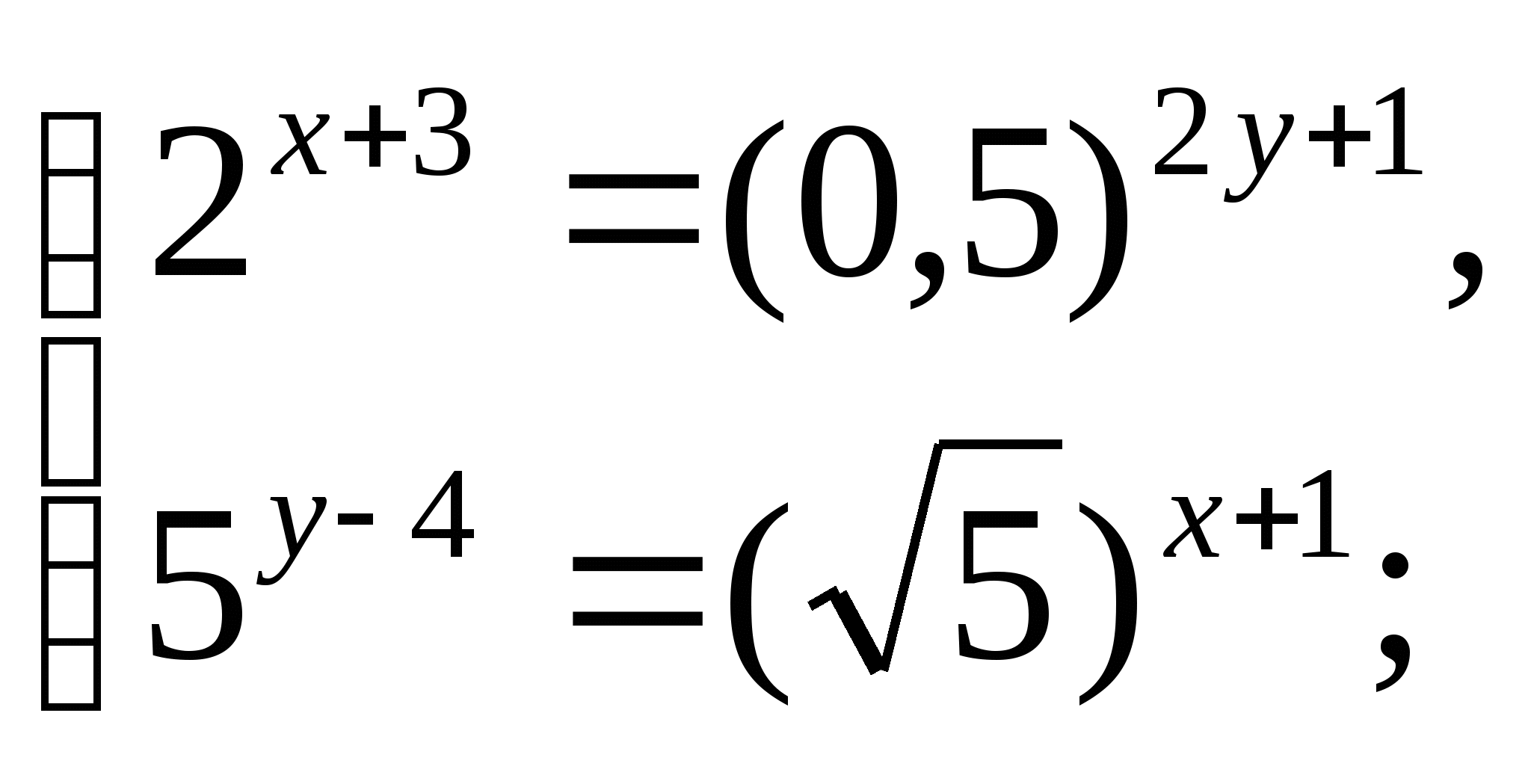 (простейшие уравнения)
(простейшие уравнения)
7.Обратная связь.
Самостоятельная работа по карточкам по системам:
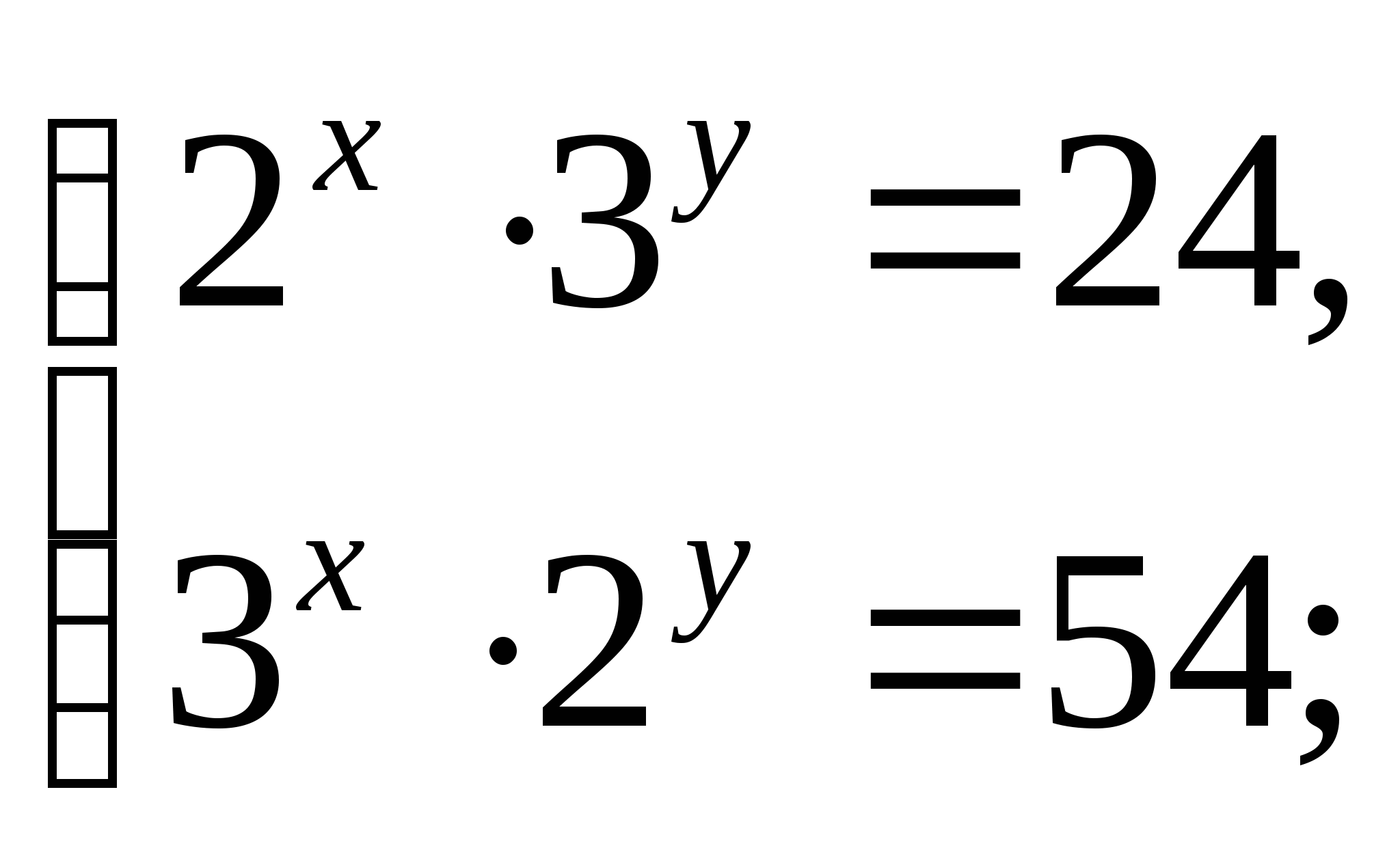
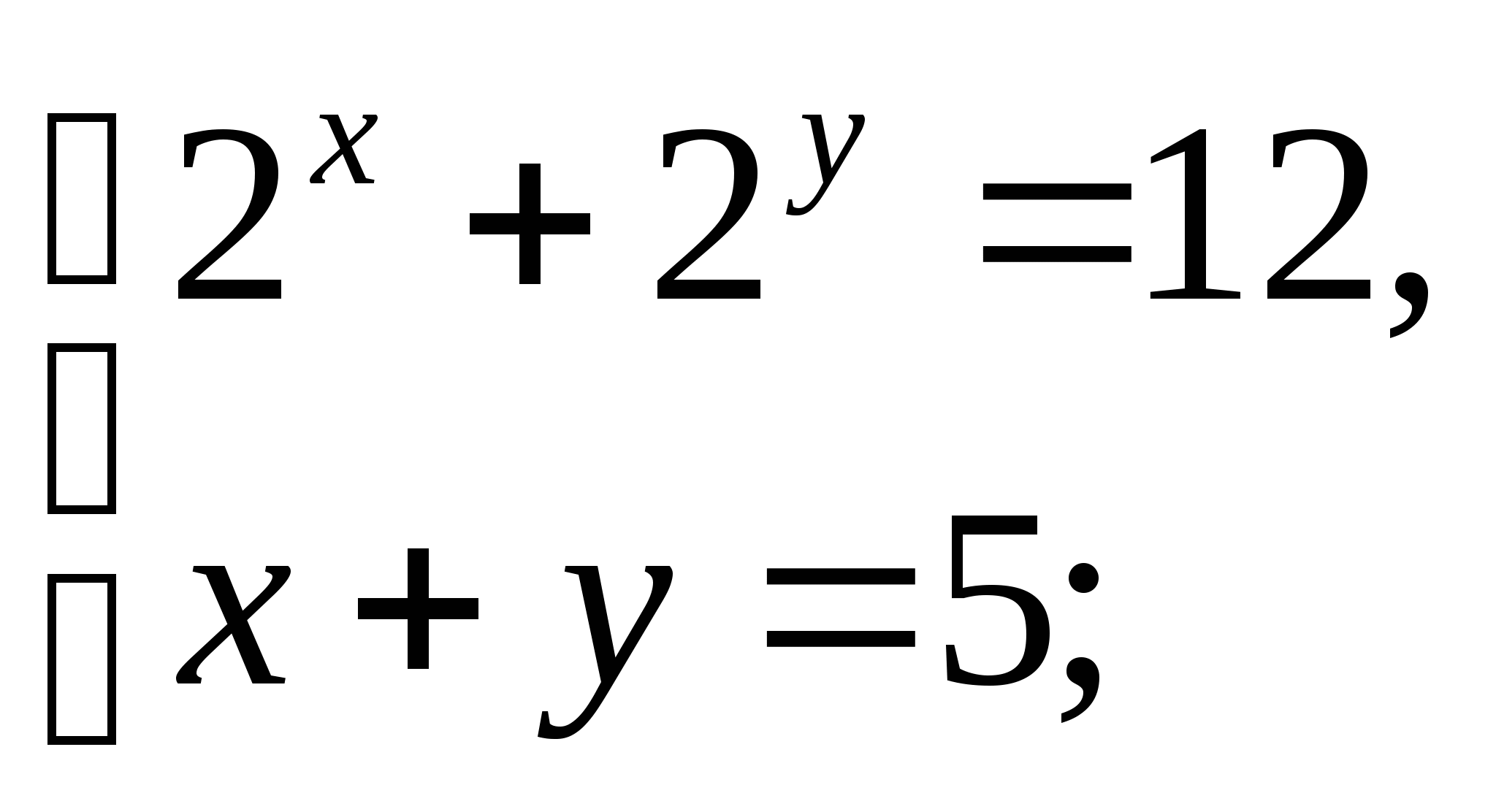
7. Домашнее задание:
264, 265.
Урок математики в 11-м классе по теме «Системы показательных уравнений»
Цель урока:
- Обобщение и систематизация способов решения показательных уравнений;
- Формирование навыков решения систем показательных уравнений;
- Выявление знаний и степени усвоения материала по теме.
Ход урока
1. Организационный момент.
Сегодня мы с вами повторим способы решения показательных уравнений и рассмотрим решение систем показательных уравнений.
Эпиграфом к уроку являются слова Конфуция “Три пути ведут к знанию: путь размышления — это путь самый благородный, путь подражания- это путь самый легкий и путь опыта- это путь самый горький” (Приложение 1)
2. Устная работа. (Приложение 2)
1) Найдите область определения функции.
у =
у =
2) Укажите множество значений функции.
у =
у =
3) Решите уравнения.
В это время 4 человека работают за компьютерами и выполняют тест (в формате STRATUM) (Приложение 3)
3. Актуализация знаний.
Просматриваются презентации, подготовленные тремя учащимися дома по методам решения показательных уравнений (Приложения 4, 5, 6)
4. Изучение темы.
Рассмотрим следующие системы (Приложение 7, 8)
Вывод: значит, все методы решения показательных уравнений применимы и при решении систем показательных уравнений.
5. Закрепление.
1.
Ответ: (0;1)
Обсуждается план решения и учащиеся решают сами, ответ записан на доске и закрыт. После решения ответ открывается.
№1840(б) – учебник А.Г.Мордкович, Л.О.Денищева “Алгебра и начала анализа”. 10-11 кл.
Ответ: (-1,6; -2)
6. Подведение итогов урока.
7. Домашнее задание: 1840(а), 1841, 1842(б),1843