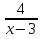Урок «Решение рациональных уравнений» 9 класс




































 Урок обобщения и систематизации знаний.
Урок обобщения и систематизации знаний.Тема: Решение рациональных уравнений (80 мин.)
Цель урока: Обобщение и углубление знаний учащихся по изученной теме.
Задачи: — систематизировать и расширить знания, умения и навыки
учащихся по решению рациональных уравнений;
— формировать умения работать с дополнительными источниками
информации, применять приемы сравнения, обобщения,
выделения главного; умения классифицировать материал,
устанавливать причинно-следственные связи; пользоваться
исследовательскими умениями при переносе знаний в новую
нестандартную ситуацию;
— развивать логическое мышление и творческие способности
путем решения заданий, содержащих модули, параметры,
уравнения 3-ей, 4-ой, 5-ой степени;
— воспитывать организованность, стремление преодолевать
трудности, самоконтроль и взаимоконтроль.
Оборудование: мультимедийный проектор
интерактивная доска
Структура урока: 1. Организационный этап
2. Постановка цели и мотивация учебной деятельности
учащихся
3. Воспроизведение и коррекция опорных знаний
4. повторение, обобщение и анализ основных фактов
5. Систематизация знаний, применение их в
стандартной ситуации. Первичный контроль
6. Перенос знаний в новую ситуацию
7. защита проекта по теме
8. Подведение итогов. Рефлексия.
9. Постановка домашнего задания.
Тезис урока:
«Три пути ведут к знанию: путь
размышлений – это путь самый
благородный, путь подражания –
это путь самый легкий и путь
опыта – это путь самый горький»
Конфуций
Ход урока
Организационный этап (2 мин)
Цель: Приветствие учащихся, организация внимания, фиксация отсутствующих.
Постановка цели и мотивация знаний учащихся (3 мин)
Цель: Донести до учащихся практическую значимость материала, раскрыть
Общую идею и цель урока
Вводная беседа: один девятиклассник, решая уравнение, рассуждал так:
На экран выводится слайд:
Пример 1. х (х +8) = 3х Разделим обе части уравнения на х
х + 8 = 3
х = — 5 ответ: — 5
Пример 2: х
2 = х – 1 _ 4х – 3 Т. к. знаменатели дробей равны,х – 1 х – 1 то равны и их числители:
х2 + х – 1 = 4х – 3
х2 – 3х + 2 = 0
х1 = 1; х2 = — 2 ответ: — 2 ; 1.
Какие ошибки допустил ученик? Почему при решении уравнений нельзя
Избавиться от всего «лишнего»?
Вывод: В результате преобразования в примере 1 мы потеряли корень х = 0,
а в примере 2 не определили ОДЗ уравнения и появился посторонний корень
х = 1. Как не допускать подобных ошибок? Прежде всего нужно четко понимать,
какие действия надо выполнить в ходе решения уравнения.
Сегодня на уроке мы повторим, обобщим и систематизируем изученные виды, методы и приемы решения рациональных уравнений.
Воспроизведение и коррекция опорных знаний (10 мин)
Цель: Воспроизведение ранее изученного материала для установления преемственности прежних и новых знаний, применения их в нестандартной ситуации.
Проверка домашнего задания (приложение 1)
На доску проецируется текст домашнего задания. Ученики отвечают по готовым записям. Работа ведется фронтально, но пары обмениваются тетрадями и проводят взаимопроверку.
Критерии оценки: «5» — нет ошибок
«4» — 2-3 ошибки
«3» — более 3-х ошибок
«2» — 5 и более ошибок
Из задания №2 разбирается наиболее интересный пример.
В результате проверки домашнего задания и обсуждения выясняется важность умения решать уравнения:
Вывод: 1. Уравнения являются математическими моделями очень многих
физических и других явлений. Поэтому решение различных
практических задач сводится к решению уравнений.
2. Уравнением с одним неизвестным называется запись вида:
А(х) = В(х), где А(х) и В(х) – выражения от неизвестной х.
3.Областью определения уравнения называется множество всех
значений х, при которых определены обе части уравнения.
Корнем или решением уравнения называется значение
неизвестного, которое обращает уравнение в верное числовое
равенство. Решить уравнение – значит найти все его корни или
доказать, что их нет.
На доску проецируется схема (приложение 2) – классификация уравнений по видам. Ученики обсуждают, делают выводы по классификации.
Работа в группах.
Цель: проверка навыков решения простейших уравнений, обеспечение первичного усвоения материла.
На доску проецируется 3 варианта заданий (приложение 3). Учащиеся совещаются в группах, обсуждая вид и способы решения уравнений. Затем по команде учителя обсуждения прекращаются и каждый учащийся записывает на отдельный лист № варианта и номера уравнений, напротив каждого номера записываются только ответы (после решения). Напротив задания, вызвавшего затруднения, ставится прочерк. По команде учителя листы подписываются и сдаются, после чего на доске открываются номера уравнений и список правильных ответов. Работы проверяются, учащиеся выставляют оценки в оценочную таблицу.
Критерии оценки: «5» — за 12 верно выполненных
«4» — за 10 верно выполненных
«3»- за 6-9 верно выполненных
«2» — менее 6 правильных ответов
4.Обобщение и анализ основных фактов (12 мин)
Цель: Установить связи между корнями квадратного уравнения и его коэффициентами, повторить и систематизировать методы решения рациональных уравнений.
На доске демонстрируется слайд (приложение №4). Учащиеся обсуждают и делают выводы.
Фронтальная работа с классом. Задание: решить уравнение х2 – 4х +3 = 0
пятью различными способами (пять учащихся решают на доске).
Способы решения: а) с помощью дискриминанта;
б) по теореме Виета;
в) графически;
г) разложением на множители левой части;
д) выделением квадрата двучлена.
Сформулируйте идею графического метода. В каких случаях его удобно использовать? ( Когда необходимо определить число корней уравнения, указать знаки корней, найти их приближенные значения). Этот метод красив, прост, но не дает 100% гарантии точного решения.
Сформулируйте известные вам аналитические способы решения
а) способ группировки;
б) вынесение общего множителя за скобки;
в) использование формул сокращенного умножения;
г) выделение полного квадрата;
д) разложение на множители.
Все эти приемы объединяет метод разложения на множители
Первичный контроль знаний, умений, навыков.
Работа в парах. На доске задания для 1-го и 2-го варианта – решить уравнение
несколькими способами.
Вариант 1. Вариант 2.
х2 – 6х + 8 = 0 х2 + 2х – 8 =0
Ученики обмениваются тетрадями, комментируют, выставляют оценки.
Критерии оценивания: »5» — за 5 верно выполненных способов
«4» — за 4 верно выполненных способов
«3» — за 1-3 верно выполненных
Практическое применение знаний в новой ситуации (13 мин).
Цель: Разобрать на примерах использование методов разложения на множители
к уравнениям 3-ей и более степеней, уравнениям с модулями и параметрами.
Решение уравнений, содержащих параметр.
На доске демонстрируется слайд (приложение 5). Решить уравнение с параметром – значит для каждого значения параметра найти значение
переменной, обращающее это уравнение в верное равенство.
а) Решим уравнение: ах2 – 2х + 4 = 0
1) при а= 0 уравнение превращается в линейное: — 2х + 4=0
х = 2
При а ≠ 0 оно квадратное, D = 4 – 16 а
а) если D > 0, то 4 – 16 а >0, а < 0,25 2 решения
х1,2 = 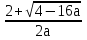 =
= 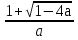
б) если D= 0, то а = 0,25 и х = 4
в) если D< 0, то а >0,25 и решений нет.
Ответ: при а = 0 х = 2
при а > 0,25 решений нет
при а = 0,25 х = 4
при а < 0,25, а ≠ 0 два решения : х1,2 = 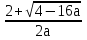 =
= 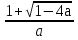
Двое учащихся решают у доски (1) и (3), комментируя решения.
2)Решить уравнение: (х2 + х + 4)2 +8х( х2 + х + 4) + 15х2 = 0
(решает на доске учитель)
1-ый способ: выполним разложение на множители способом группировки
(представим 8х( х2 + х + 4) как 5х( х2 + х + 4) + 3х( х2 + х + 4)
(х2 + х + 4)2 + 5х( х2 + х + 4) + 3х( х2 + х + 4) + 15х2 = 0
(х2 + х + 4)(х2 + х +4 + 3х) + 5х(х2 + х +4 + 3х) = 0
(х2 + х + 4)( х2 + 4х +4) + 5х(х2 + 4х +4 ) = 0
(х2 + х + 4)( х2 + 6х +4) = 0
х1 = — 2 , х2,3 = — 3 ± 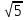
2 способ: обозначим (х2 + х + 4) = у, тогда у2 + 8ху + 15х2 = 0
Решим как квадратное относительно у по теореме Виета:
У1 + у2 = -8х
У1 ∙ у2 = 15х2, откуда у1 = -3х, у2 = — 5х
Уравнение примет вид: (у + 3х)(у + 5х) = 0
При у = -3х: х2 + х +4 = -3х При у = -5х: х2 + х +4 = -5х
х1 = -2 х2,3 = -3 ±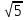
На доску проецируются следующие уравнения:
х4 — 2х2 – 3 = 0 (1) ! Каждое из этих уравнений можно
х2 – 2 |х| = 0 (2) несколькими способами, но к каждому
(х + 2)2 – 2 |х + 2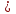 — 3 = 0 (3) удобно применить свой способ
— 3 = 0 (3) удобно применить свой способ
х(х – 1)(х – 2)(х – 3) = 24 (4) решения.
Биквадратное, решается введением новой переменной
Раскрытие модуля по определению
, (4) замена переменных
Решим (2) : х2 – 2 |х| = 0
При х< 0: х2 + 2х = 0; х = 0; — 2 0 не подходит
При х ≥0: х2 – 2х = 0 х = 0; 2
Ответ: 0; — 2 ; 2
Решим (4): х(х – 1)(х – 2)(х – 3) = 24
Сгруппируем 1-ый и 4-ый множитель, 2-й и 3-й:
(х2 – 3х)( х2 – 3х + 2) = 24 х2 – 3х = у
у(у +2) = 24
у1 = 4; у2 = — 6
х2 – 3х = 4 х2 – 3х = — 6
х = — 1 ; 4 Ø
Ответ: — 1 ; 4
Дифференцированная самостоятельная работа по теме.
Группа А
Группа В
Группа С
1
х3 – 5х2 — 6х = 0
х6 – 5х5 + 6х4 – х2 +5х -6 =0
(х2 -5х – 6)(1 — |2х -1|)=0
2
х4 – 6х2 +5 =0
(х2 +1)2 – 6(х2 +1) + 5 = 0
х2 – 6 |х| + 5 =0
Работа выполняется под копирку. После сдачи работы записи сравнивают с правильными ответами. Учитель выполняет проверку по шаблону и объявляет результаты. Ученики выставляют оценку в оценочный лист.
7) Защита группового проекта и презентация пособия по решению
рациональных уравнений.
8) Подведение итогов. Рефлексия.
Цель: обеспечить закрепление в памяти учащихся знаний, необходимых для успешного решения уравнений. Дать качественную оценку работы класса и каждого учащегося. (средний балл по оценочному листу)
9) Постановка домашнего задания.
Цель: Обеспечить понимание учащимися содержания и способов выполнения домашнего задания.
Домашнее задание: если вы получили оценку «5» или «4» :
При каком значении параметра p уравнение х2 + 6х + 8 = p
Имеет один корень; два корня, не имеет корней?
Решите уравнения: а) (х2 + 3х – 10 )( 1 +
 ) = 0
) = 0
б) 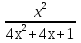 –
– 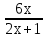 + 5 = 0
+ 5 = 0
в) 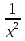 —
— 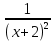 =
= 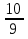
Если вы получили оценку «3» или «2» :
Решите графически: х2 + 2х – 3 = 0
Решите методом разложения на множители: х3 – 4х2 + 3х = 0
Решите способом подстановки: (2х + 1)2 — 4 (2х + 1) + 3 = 0
Приложение 1
Предварительное домашнее задание
Задание 1.
Решите уравнения 1-12 и проведите классификацию уравнений по виду.
Ответы:
(х – 5)2 + 9х =
 + 25 х = 3
+ 25 х = 3
0,5х2 + 0,7 = 0 нет действительных корней (Ø)
(х – 5)(х + 3) = 9 х = — 4 ; х = 6
 –
–  = 1 +
= 1 +  х = —
х = — 
(х – 5 )(х + 3 ) = 1 – 2х х = 4; 4
(х – 5)(х + 3) = 3(х – 5 ) х = 0; 5
2(х + 1) – 1 = 3 – (1 – 2х ) нет действительных корней (Ø)
1 – 2х + 4х2 = х2 – 2х + 1 х = 0
3(1 – х) +2 = 5 – 3х бесконечно много корней (х Є R)
2х2 + 3х + 4 = 0 нет действительных корней (Ø)
х2 + 6х + 4 = 0 х1 = — 3 +
 ; х2 = — 3 —
; х2 = — 3 — 
25х2 – 30х + 9 = 0 х1 = х2 = 0,6
Задание 2. Подготовьте одну физическую задачу, показывающую, что рациональные уравнения могут служить математическими моделями реальных ситуаций.
Приложение 2
Виды уравнений
Дробно-рациональные
(приводимые к виду P(х) = 0
Q(х)
где P(х) , Q(х) – многочлены и Q(х)≠0
№1
Целые рациональные
Линейные (приводимые к виду
ах = в)
(№4,7,9)
Квадратные
9приводимые к виду
ах2 + вх + с = 0
(а≠ 0)
Полные (а≠0, в≠0)
№3,10,11,12
Приведенные (а=1)
№3,11,12
Неприведенные
(а≠1)
№10
Неполные,
приводимые к виду
ах2 = вх = 0
(с = 0) №6
ах2 + с = 0
(в = 0) №2,5
ах2 = 0
(в = 0, с = 0) №8
Приложение 3
вариант 1
Вариант 2
Вариант3
1. (х – 3)(х + 4) = 0
1. (х – 8)(х +6) = 0
1. (х – 1)(х – 99) = 0
2. х2 – 14х + 49 = 0
2. х2 +18х + 81 = 0
2. х2 – 16х + 64 = 0
3. х2 – 12 = 0
3. х2 – 16 = 0
3. х2 – 5 = 0
4. 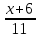 = 0
= 0
4. 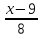 = 0
= 0
4. 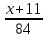 = 0
= 0
5. 0х = 24
5. 0х = 0
5. 5х = 5х
6. 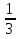 х = 4
х = 4
6. 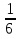 х = 21
х = 21
6. 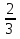 х = 4
х = 4
7. 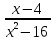 = 0
= 0
7. 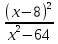 = 0
= 0
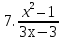 = 0
= 0
8. 6х2 = 0
8. 9х2 = 81
8. 8х2 = — 6
9. х2 – 5х – 6 = 0
9. х2 – 4х + 3 = 0
9. х2 – 113х + 112 = 0
10. (81 – х2) (2х – 1) = 0
10. (х2 – 16)(х – 5) = 0
10. (х – 1)(х2 – 121) = 0
11. 5х2 = х
11. х2 = х
11. 3х2 – х = 0
12. 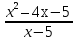 = 0
= 0
12. 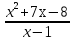 = 0
= 0
12. 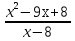 = 0
= 0
Приложение 5
х2 + ах + 12 = 0 а — параметр
ах2 — 2х + 4 = 0
2х2 = 4х + а = 0
Если коэффициент при х2 многочлена второй
степени содержит параметр, необходимо
разобрать случай, когда он обращается в 0!
Приложение 4
Квадратные уравнения, приводимые к виду
ах2 + вх + с = 0 ( а≠ 0)
D < 0
D = 0
D > 0
Два корня
х1 = х2 = — 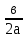
Корней нет
Два корня
х1 = х2 = 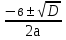
у
х0 х
а < 0
у
х1 х0 х2 х
а < 0
х1 <х2
у
х0 х
а < 0
у а > 0
х1 <х2
х0
х1 х2 х
у а > 0
х
0 х0
а > 0
у
х0 х
Приложение 6
Оценочный лист учащегося
Этапы урока
Задания
Баллы
1
Домашнее задание
2
Работа в группах
3
Работа в парах
4
Самостоятельная
работа
Итоговое кол-во
баллов
Оценка
infourok.ru
План-конспект урока по алгебре (9 класс) на тему: Урок по алгебре 9 класс » Дробные рациональные уравнения»
тема « Дробные рациональные уравнения»
Учебник «Алгебра-9» автор Ю.Н.Макарычев,
под редакцией С.А.Теляковского
тип урока: повторительно- обобщающий
Цели урока:
1.Образовательные цели урока:
— Повторение ранее изученного материала.
— Формирование умения решать дробно-рациональные уравнения, используя при этом различные приемы и методы.
2.Развивающие цели урока:
— Реализация принципов связи теории и практики.
— Развитие памяти, речи, любознательности, познавательного интереса
— Развитие аргументированной речи, доказательного воспроизведения в процессе деятельности.
— Развитие вычислительных навыков.
— Развитие коммуникативных навыков общения и умения слушать и слышать.
3.Воспитательные цели урока.
— Воспитание аккуратности, дисциплины.
— Воспитание настойчивости в достижении цели.
— Воспитание ответственного отношения к учёбе
Ход урока.
- Оргмомент (3мин)
— Здравствуйте, ребята! Садитесь. Сегодня на уроке мне хотелось бы вас пригласить в замечательный мир уравнений.
Наш урок я хочу начать с древней притчи. Шел мудрец, а навстречу ему три человека, которые несли под горячим солнцем тяжелые камни для строительства храма. Мудрец остановился и задал каждому вопрос: Что ты делал весь день?
Первый устало ответил: «Я целый день таскал тяжелые, ненавистные камни».
Второй спокойно ответил: -Я добросовестно выполнял свою работу.
А третий улыбнулся и ответил: -А я принимал участие в строительстве прекрасного храма.
Я хочу, чтобы вы, получая каждый день новые знания, не считали для себя тяжелой ношей, а наполняли и строили свой храм знаниями, умениями, навыками.
Девизом : Думать — коллективно! Решать — оперативно
2. Актуализация знаний, умений, навыков ( 4 мин)
Учитель: Посмотрите на доску. Какие виды уравнений вы видите?
Ученики: Целые и дробно-рациональные.
учитель : Как вы считаете, какое уравнение является « третьим лишним»?
ученик: Первое уравнение, т.к. оно – целое
Сформулируйте тему сегодняшнего урока .Тема : Решение дробных рациональных уравнений.
откройте тетрадь, запишите число и тему сегодняшнего урока.
Целью урока является : Отработать навыки решения дробно-рациональных уравнений, которые встречаются в ОГЭ.
3. Устно.
Учитель. Дайте определение дробно-рационального уравнения? (2мин)
Ученики:
а)Уравнение, в которых левая и правая части уравнения являются дробными выражениями, называются дробно-рациональными.
б) назовите алгоритм решения дробного рационального уравнения.
- Найти ОДЗ уравнения
- Найти общий знаменатель дробей, входящих в уравнение
- Умножить обе части уравнения на общий знаменатель
- Решить полученное целое уравнение
- Исключить из его корней те, которые обращают в нуль знаменатель.
в) назовите способы решения дробно- рациональных уравнений (1 мин)
(способ пропорции, равенство дроби нулю, умножение обеих частей уравнения на знаменатель, введение новой переменной)
слайд 2
г) Посмотрите внимательно на уравнение и определите, какие из чисел 4, 0, -2 не являются корнями уравнения. Ответы поясните. ( 2мин)
Учащиеся: 4 не может быть корнем, т.к. знаменатель обращает в нуль.
0 не является корнем, т.к. .
-2 является корнем, т.к.
Какой способ решения дробного рационального уравнения используется при решении? (основное свойство пропорции)
г) Перед вами решение уравнения. Но оно выполнено с ошибкою. Ваша задача: найти, какой шаг алгоритма нарушен, и назовите его правильное решение. Найди ошибку (слайд) (3мин)
— =0;
=0
ОДЗ : х-5
х2-х+6=0,
D = 1+24=25, D, 2-корня
х1 =3, х2 = -2. Ответ :-2; 3 Правильный ответ 2 ; -3.
Какой способ решения дробно- рационального уравнения вы использовали? (равенство дроби нулю)
(15 мин)
4. Основная часть. Решение заданий итоговой аттестации
Решить уравнение (5 мин)
а)
Один из учащихся работает у доски. По ходу решения ученик проговаривает алгоритм решения дробно — рационального уравнения.
ОДЗ : х;
7(х+3) -5(х-3) -18=0; 7х+21 -5х+15-18 =0, 2х=-18, х=-8 . Ответ -8.
б) Решить уравнение введением новой переменной № 298 (а) ( 8 мин)
( )2 +16()2 =17
ОДЗ : х 4, х-2
пусть ( )2 = у, у 0, тогда ()2= . получим уравнение у + 16-17 =0
=0, у2 — 17у + 16=0,
Д= 289 -64 =225, у1 = =1, у2 = =16
Вернемся к переменной
( )2 = 1 и ( )2 =16
= 1 = 4 ( -1 и – 4- посторонние корни)
=1, = 4 ,
х+ 2= х- 4 х+2 = 4(х-4), х+2 = 4х -16, -3х = -18, х= 6
нет решений
ответ : 6
5. Физкультминутка. ( 2 мин)
Упражнения для глаз с использованием геометрических фигур, расположенных на доске.
Задача. ( КИМ ОГЭ- 9) Из двух городов, расстояние между которыми 720 км, отправляются навстречу друг другу два поезда и встречаются на середине пути. Второй поезд вышел на 1 ч позднее первого со скоростью на 4 км/ч большей, чем скорость первого поезда. Найдите скорость каждого поезда. ( 6 мин)
х км/ч – скорость 1 поезда, х+4 км/ч – скорость 2 поезда.
ч- время первого, ч- время второго.
составим уравнение — =1.
ОДЗ : х 0, -4
360(х+4) – 360х – х2 — 4х =0, х2 + 4х -1440 = 0, Д= 16 +5760=5776,
х=36, 40 км/ч — второго
Ответ : 36 км/ч, 40 км/ч
6. Домашняя работа ( 1мин)
домашняя работа на партах у вас лежат листочки разного цвета:
зеленый — Уровень А, синий – Уровень В, желтый – уровень С. выберите каждый по своим силам листочек- это будет ваша домашняя работа
Уровень А
Уровень В
Уровень С
7. Рефлексия
- Доволен ли ты тем, как прошел урок?
- Было ли тебе интересно?
- Сумел ли ты получить новые знания?
- Ты был активен на уроке?
- Ты с удовольствием будешь выполнять домашнее задание?
- Ты сумел показать свои знания?
Подведение итога урока. (3 мин)
— Чем мы сегодня занимались на уроке?
— Какие уравнения мы решали?
— Какие способы решения уравнений мы повторили?
— Сегодня на уроке вы активно работали. И я желаю вам, чтобы каждый урок у вас зажигалась хотя бы одна звезда, звезда новых знаний.
А закончить наш урок хотелось бы словами великого ученого А.Эйнштейна: «Мне приходится делить свое время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно».
nsportal.ru
Урок алгебры на тему «Решение рациональных уравнений», 9 класс
Трофимова Светлана Николаевна
МБОУ «Гимназия №1» г. Ядрин Чувашской Республики
учитель математики и информатики
Конспект урока: Решение рациональных уравнений
Класс: 9
Время: 1 урок (45 минут)
Необходимое оборудование: доска, компьютер, проектор, раздаточные материалы
Цель урока: закрепить умения решать уравнения способом замены неизвестного.
Этапы урока
Оргмомент – 5 минут
Решение биквадратных уравнений – 7 минут
Презентация замены неизвестного при решении уравнений – 8 минут
Физкультминутка – 2 минуты
Работа в группах – 20 минут
Подведение итогов – 3 минуты
Ход урока
1) Уравнения с давних времен волновали умы человечества. У английского поэта средних веков Чосера есть замечательные строки, которые мы возьмем эпиграфом нашего урока:
Посредством уравнений, теорем
Я уйму разрешу проблем.
Бывают разные виды уравнений. Умения решать их очень важны не только для математики, но и для других наук. А сейчас мы повторим основной теоретический материал, который понадобится нам на уроке. Ответьте, пожалуйста, на следующие вопросы:
— Какие виды уравнений записаны на доске? (Линейное, квадратное, биквадратное)
— Как решить линейное уравнение? (Все слагаемые с неизвестным перенести в левую часть уравнения, все числа — в правую. Привести подобные слагаемые. Найти неизвестный множитель).
— Как решить квадратное уравнение? (Выделение полного квадрата, по формулам, используя теорему Виета и ее следствия.)
Ребята, сегодня мы будем решать целые и дробно-рациональные уравнения, которые входят в сборник заданий для подготовки к итоговой аттестации в 9 классе. При решении уравнений будем применять алгебраические преобразования, а также такой прием, как замена переменной. Ребята, приходилось ли вам применять замену неизвестного при решении уравнений? При решении каких уравнений? (биквадратных, возвратных).
2) Если надо решить биквадратное уравнение ах4 + bx2 + c=0, то вводим новую неизвестную, например, y=x2, получаем квадратное уравнение: ay2 + by + c=0. Решив это уравнение, найдем корни y1 и y2. Чтобы найти корни исходного уравнения, т.е. x1 и x2, надо решить два уравнения 1) x2 = y1 и 2) x2 = y2.
Решим биквадратное уравнение (задание на 2 балла)
x4 + 2×2 – 8 = 0 и 2×4 — 19×2 + 9 = 0 (Работа в группах по 4 человека)
3) Презентация замены неизвестного при решении уравнений (с помощью проектора на экране).
Пример 1. Решим уравнение
(x2 + x – 1) (2×2 +2x + 3) – 7(1 – x – x2) = 110 (1)
Раскрытие скобок приведет к уравнению четвертой степени, упростить решение помогает замена неизвестного.
Введем новое неизвестное t = x2 + x – 1, тогда 2×2 +2x + 3 = 2 (x2 + x – 1) +5,
1 – x – x2 = — ( x2 + x – 1) = -t. Поэтому уравнение (1) перепишется в виде:
t(2t + 5) + 7t = 110 или 2t2 + 12t – 110 = 0
Это уравнение имеет два корня t1 = 5, t2 = — 11
Поэтому корнями уравнения (1) являются корни двух уравнений:
1) x2 + x – 1 = 5 и 2) x2 + x – 1 = — 11
Решив каждое из уравнений 1) и 2), найдем все корни уравнения (1): x1 = -3, x2 = 2.
Ответ. -3; 2.
Пример 2. Решим уравнение
(x + 3) (x – 5) (x + 2) (x – 4) = 60 (2) [2, 18]
Раскрытие скобок приведет к уравнению четвертой степени, упростить решение помогает замена неизвестного. Но сначала в левой части уравнения умножим первый множитель на второй и третий на четвертый, потому что суммы свободных членов этих многочленов в каждой паре одинаковы: 3 + (- 5) = 2 + (-4), получим равносильное уравнение
(x2 — 2x – 15) (x2 — 2x – 8) = 60.
Введем новое неизвестное t = x2 — 2x – 15, тогда x2 — 2x — 8 =t + 7, поэтому уравнение перепишется в виде
t (t + 7) = 60 или t2 + 7t – 60 = 0
Это уравнение имеет два корня t1 = 5, t2 = — 12
Поэтому корнями уравнения (2) являются корни двух уравнений:
1) x2 — 2x – 15 = 5 и 2) x2 — 2x – 15 = — 12
Решив каждое из уравнений 1) и 2), найдем все корни уравнения (2): x1 = 1 — 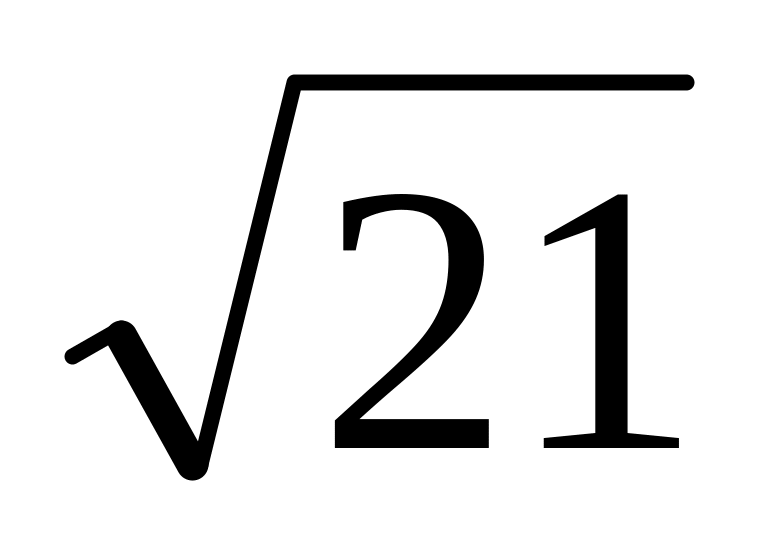 , x2 = 1 + , x3 = — 1, x4 = 3.
, x2 = 1 + , x3 = — 1, x4 = 3.
Ответ. x1 =1 — , x2 = 1 + , x3 = — 1, x4 = 3.
4) Физкультминутка
5) А теперь перейдем к решению более сложных задач (задания на 4 балла и 6 баллов). Двое работают у доски, остальные в группах по четыре человека.
Задания для работающих у доски:
1 задание. Решите уравнение x5 – 9×3 + 20x = 0. Указание: вынесите x за скобки.
2 задание. Решите уравнение (x2 – 5x) (x2 – 5x + 10) + 24 = 0. Указание: введите новое неизвестное x2 – 5x =t.
Задания для работы в группах:
1 задание. Решите уравнение (x – 2)2 (x2 – 4x + 3) = 12. Указание: выражение в первых скобках возведите в квадрат.
2 задание. Решите уравнение (x2 – 7x + 13)2 – (x – 3) (x – 4) = 1. Указание: перемножьте выражения в скобках (x – 3) (x – 4).
3 задание. Решите уравнение (x – 2) (x – 1) (x + 2) (x + 3) = 60 Указание: перемножьте нужные скобки.
4 задание. Решите уравнение 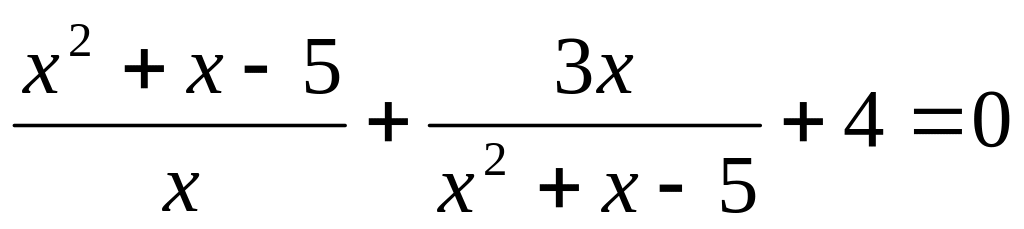 Указание: введите новое неизвестное
Указание: введите новое неизвестное 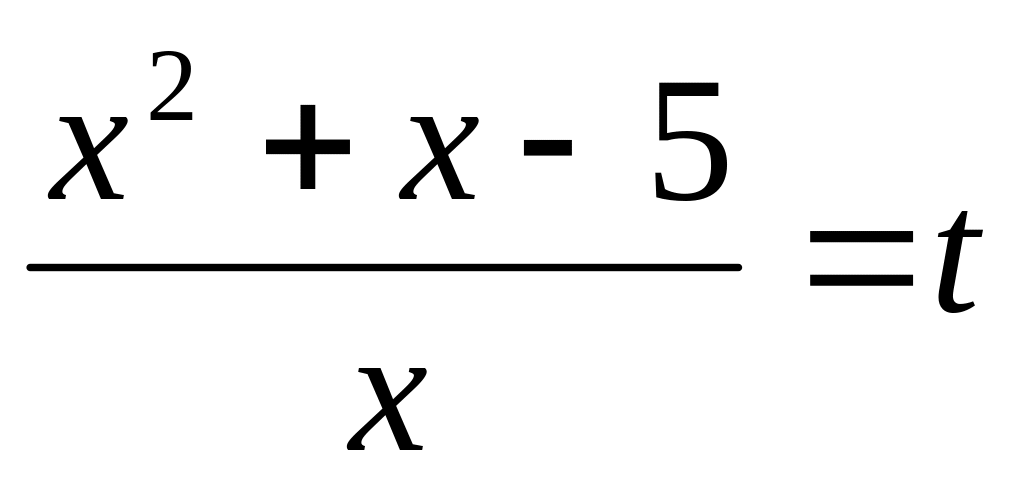
5 задание. Решите уравнение 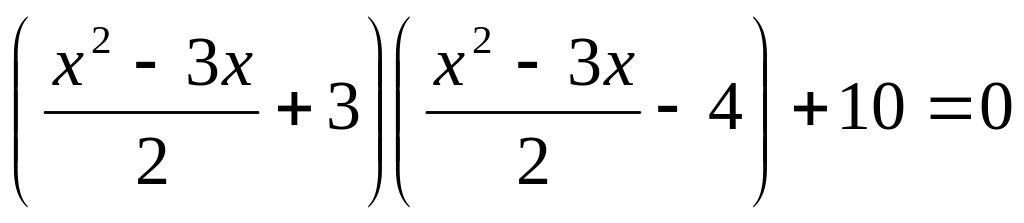 Указание: введите новое неизвестное
Указание: введите новое неизвестное 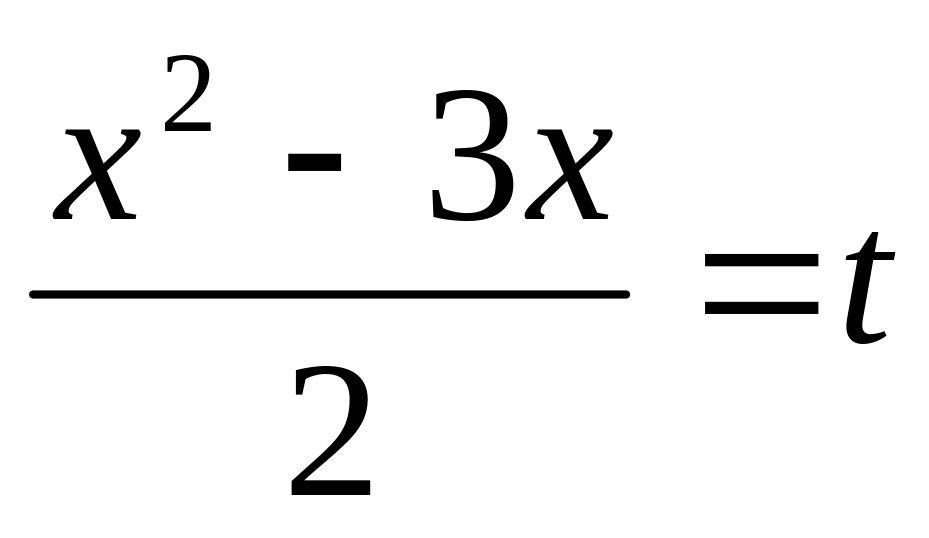
6 задание. Решите уравнение (x – 5)4 – 3 (x – 5)2 – 4 = 0. Указание: введите новое неизвестное (x – 5)2 = t.
6) Итак, сегодня на уроке мы с вами решали уравнения, используя метод замены неизвестного. Учебно-методическая газета “Математика” выходит под девизом: “Жизнь украшается двумя вещами: занятием математикой и ее преподаванием”, а вот для меня большая радость, если все, чему вы научились на уроках, можете использовать на экзаменах.
Список литературы:
Алгебра. Дидактические материалы. 8 класс / М.К. Потапов, А.В. Шевкин. – М.: Просвещение, 2014.
http://metodist.edu54.ru/node/47731
https://infourok.ru/individualnaya_rabota_na_urokah_matematiki-441415.htm
xn--j1ahfl.xn--p1ai
Конспект урока в 9 классе «Решение рациональных уравнений в ходе подготовки к ОГЭ»
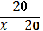
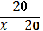
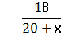
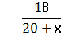


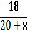
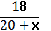
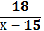
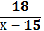
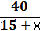
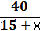
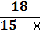
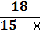
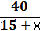
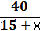


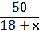

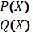









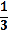
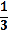
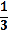

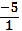
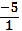


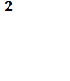
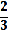
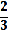
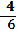
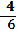
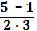
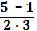
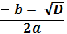
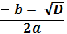
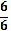
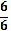
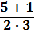
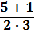
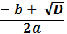
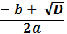
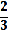
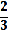


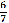
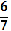
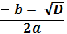
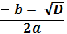
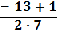
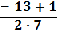
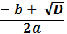
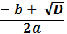
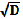
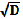
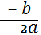
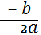
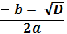
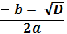
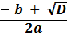
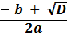
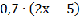
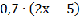






 Конспект урока математики в 9 классе
Конспект урока математики в 9 классе
Тема урока: Решение рациональных уравнений в ходе подготовки к ОГЭ.
Цели урока:
Образовательные • Обобщение и систематизация знаний учащихся;
• Формирование практических умений и навыков по осознанному применению полученных знаний.
Развивающие • Развитие математической речи;
• Развитие познавательной активности, умения анализировать и делать выводы;
• Развивать логическое мышление, сообразительность;
Воспитательные: • Воспитание культуры слушать своего одноклассника;
•Формирование аккуратности и внимания в письменной математической речи.
Оборудование: компьютер, мультимедийный проектор, тесты.
Ход урока:
Организационный момент (1 мин)
Сообщение темы и целей урока.
Слайд 1. Эпиграф урока «Ничего не делается само собой, без усилий и воли, без труда». А.И. Герцен
Систематизация знаний. (Фронтальный опрос, решение тестов)
Ребята, предлагаю вам перечень уравнений (Слайд 2) :
= +

2. 3х2 – 5х + 2 = 0
3. 0,7∙(2х-5) = 17 – 2∙ (0,3 + 7,25)
9х2 – 1 = 0
5. х2 + 7х + 12 = 0
6. 2х — 3 ∙ (х + 5) = -12
7. х2 + 4х – 5 = 0
8. х2 – 5х = 0
9. 7х2 + 13х + 6 = 0
10. х4 – 26 х2 + 25 = 0
11. 3х2 + 8х + 5 = 0
Все эти уравнения рациональные.
Какие уравнения называются рациональными ?
( уравнения, левая и правая часть которых явл. рациональными выражениями, называются рациональными.)
Мы рассмотрели три вида рациональных уравнений: линейные, квадратные и дробно-рациональные.
1. Линейные уравнения.
Какие из приведенных уравнений являются линейными ? (3 и 6)
Вспомним алгоритм решения линейного уравнения.
Слайд 3. Алгоритм решения линейного уравнения.
Алгоритм решения линейного уравнения
2х – 3(х + 5)=-12
1.Раскрыть скобки.
2. Перенести слагаемые с неизвестными в левую часть уравнения, а известные слагаемые в правую часть уравнения. Переносят слагаемые из одной части уравнения в другую с противоположным знаком.
3.Привести подобные слагаемые.
4.Найти неизвестный множитель.
5. Записать ответ.
2х – 3х – 15 = -12
2х – 3х = -12 + 15
-х = 3
х = 3 : (- 1)
х = -3
Ответ: -3
Решите уравнение №3 (на доске) b карточки на решение линейных уравнений
= 17 – 2∙(0,3 + 7,25) 1) 5х – 3 =4х – (2х + 1) Ответ: 2/3
1,4х — 3,5 = 17 — 0,6х — 14,5 2) 9х + 2 = 3∙(7 – 2х) – 4 Ответ: 1
1,4х + 0,6х = 17 – 14,5 + 3,5 3) 3х – 1 = 5∙(х – 2) – х Ответ: 3
2 х = 6
х=6 : 2
х=3 Ответ: 3
Найдем корни уравнения №6 (устно)
2.Квадратные уравнения.
1. Какие из предложенных уравнений являются квадратными ?
2.Общий вид квадратного уравнения. ах2 + вх + с = 0
3.Назовите полные квадратные уравнения.
4. Назовите коэффициенты в уравнении №11.
5.Какие квадратные уравнения называются приведенными ? (а = 1)
Назовите эти уравнения. (5, 7, 10)
6. От чего зависит количество корней квадратного уравнения. (от D = b²- 4ac)
Слайд 4. Алгоритм решения квадратного уравнения.
ax²+bx+c = 0
Вычислить дискриминант D = b²- 4ac.
Сравнить D с нулем: если D>0, то уравнение имеет два корня
x1 = и x2 = .
если D=0, то уравнение имеет единственный корень х =
если D<0, то уравнение не имеет корней.
Применяя алгоритм решения квадратного уравнения по вариантам выполнить тесты
№9 и №2.
к доске вызвать 2 учеников для контроля, решают молча и самостоятельно.
А) № 9 Найдите сумму корней уравнения 7х2 + 13х + 6 = 0.
D = b²- 4ac = 132 — 4∙7∙6 = 169 – 168 = 1, D>0, 2к., = 1
x1 = = = x2 = = =-1
x1 + x2 = — 1 Ответ: — 1
Проверить № 9,
Каким свойством обладают коэффициенты этого уравнения?
b = a + c, x1 = -1, x2 = -c/a.
Какое еще уравнение обладает этим свойством? ( № 11)
Слайд 5. Если b = a + c , то уравнение ax² + bx + c = 0 имеет корни x1 = -1, x2 = -c/a.
Используя свойство коэффициентов квадратного уравнения,
найдите наибольший корень уравнения № 11
3х2 + 8х + 5 = 0
устно по компьютеру рассказать решение.
b = a + c, 8 = 3 + 5 значит x1 = -1, x2 = = = — 1 x1 ∙ x2 = -1 ∙ (- 1 ) = 1
б) № 2. Найдите наибольший корень уравнения 3х2 – 5х + 2 = 0.
D = b²- 4ac = (-5)2 — 4∙3∙2 = 25 – 24 = 1, D>0, 2к., = 1
x1 = = = = 1 x2 = = = =
Ответ: 1
Проверить № 2, Обратите внимание на коэффициенты этого квадратного уравнения.
a + b + c = 0, x1 = 1, x2 = c/a.
Какое еще уравнение обладает этим свойством? ( № 7)
Слайд 6. Если a +b + c = 0, то уравнение ax² + bx + c = 0 имеет корни x1 = 1, x2 = c/a
Используя свойство коэффициентов квадратного уравнения,
Найдите наименьший корень уравнения х2 + 4х – 5 = 0
устно по компьютеру рассказать решение. a +b + c = 0, 1 + 4 – 5 = 0 значит x1 = 1, x2 = = = -5 Ответ: -5
в) Большой вклад в науку внес французский математик Франсуа Виет.
Сформулируйте теорему Виета: (Если приведенное квадратное уравнение имеет неотрицательный дискриминант, то сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.)
x2 + рх + q = 0 x1+ x2 = —p x1∙ x2 =q
При решении квадратных уравнений применяется теорема, обратная теореме Виета.
Слайд 7.
Тест №5 Найдите наибольший корень уравнения х2 + 7х + 12 = 0.
По теореме, обратная теореме Виета, x1+ x2 = -p= -7 и x1∙ x2 =q = 12.
Подбором найдем, что x1 = -4 x2 =- 3. Ответ: -3.
г) Назовите неполные квадратные уравнения. (№4 и №8)
Почему они так называются ? (b=о или c=0) №4 и №8 на доске самостоятельно 2 ученика.
№4 Найдите сумму корней уравнения 9х2 – 1 = 0.
Решение: 9х2 – 1 = 0, 9х2 = 1, х2 = 1/9, x1 = x2 = — , их сумма равна 0. Ответ: 0
Слайд 8 Если в уравнении ax² + bx + c = 0 коэффициент b = 0, то уравнение ax² + c = 0 имеет корни противоположные корни x=± (-c/a>0).
Определите при каком значении параметра n корни уравнения 2х2 – ( 5n -2)х – 1 =0 равны по модулю ? (отвечает устно) Решение: Корни уравнения 2х2 – ( 5n -2) – 1 = 0 равны по модулю, если b = 0.
5n -2 = 0, n = 0,4 Ответ: Корни уравнения 2х2 – ( 5n -2) – 1 = 0 равны по модулю при n = 0,4.
№8 Найдите произведение корней уравнения х2 – 5х = 0 .
Решение: х2 – 5х =0 , х∙( х — 5) = 0, х = 0 и х = 5. 0 ∙ 5 = 0 Ответ: 0
Слайд 9. Если в уравнении ax² + bx + c = 0 коэффициент с = 0, то уравнение ax² + bx = 0 имеет 2 корня x1 = 0 и x2 = — .
Определите при каком значении параметра n один из корней уравнения х2 + 8х + n2 – 6n + 5 = 0 равен нулю ?
(отвечает устно)
Решение: один из корней уравнения х2 + 8х + n2 – 6n + 5 = 0 равен нулю, когда с = 0
n2 – 6n + 5 = 0, a +b + c = 0, 1 + (-6) + 5 = 0, значит n = 1 и n = — = 5.
Ответ: Один из корней уравнения х2 + 8х + n2 – 6n + 5 = 0 равен нулю при n = 1 и n = 5.
д) Как называется уравнение №10 ? (биквадратное).
№ 10. Найдите наибольший корень уравнения х4 – 26 х2 + 25 = 0.
Решает у доски, отдельные учащиеся получают карточку
Ученик у доски объясняет решение уравнения х4 – 26 х2 + 25 = 0.
х2=t, t2 – 26t + 25 =0
D =b²-4ac=(-5)2 -4∙3∙2=25–24=1, D>0,2к.,
t1 =1, t2 =25
1) х2=1 x = ±1 2) х2=25 x = ±5 Ответ:5.
Решить уравнение самостоятельно:
1) х4 – 7 х2 – 18=0 Ответ: -3;3
2) х4 + 3 х2 — 4 = 0 Ответ: √7; -√7.
3) х4 – 7 х2 — 18 = 0 Ответ: -1; 1.
4) х4 — 14 х2 + 24 = 0 Ответ: √2; -√2,√12;-√12
Выполните тест №2. (3мин)
3.Дробно-рациональные уравнения
Среди предложенных уравнений мы не коснулись только № 1.
Как оно называется ? (дробно-рациональное)
Вспомним алгоритм его решения.
Слайд 10. Алгоритм решения дробно-рационального уравнения.
1.Привести уравнение к виду =0.
2.Найти О.Д.З., исключив значения х, при которых знаменатель дроби равен нулю.
3. Решить уравнение Р(х) = 0.
4.Определить корни уравнения, удовлетворяющие О.Д.З., записать ответ.
№1. Решаем на доске 18/(х2-9) = х/(х+3) + 4/(х-3)
18/(х2-9) — х/(х+3) — 4/(х-3) = 0
О.Д.З. (х+3)(х-3)≠0, х≠ -3, х≠3
18 – х(х-3) – 4(х+3) =0
-х2 –х + 6 =0
х2 + х- 6 =0 по т. Виета x1+ x2 = -p= -1 и x1∙ x2 =q = -6,
Подбором найдем, что x1 = 2 x2 =- 3 (не удовл) Ответ: 2.
С помощью дробно-рациональных уравнений решают задачи.
Слайд 10. (Устно) Катер, собственная скорость которого 18 км/ч прошел 50 км по течению реки и 8 км против течения за 3 часа. Найдите скорость течения реки.
Пусть скорость течения реки равна х км/ч.
Выберите уравнение для решения задачи 1) 50(х-3) — 8(Х+3) =18
2) 50/(18+х) +8/(18-х) =3
3) 50/(х+18) +8/(х-18)=3
3.Тест
Вариант 1
Вариант 2
1.Решите уравнение 3х+16=120-х Ответ:________
1.Решите уравнение 4-х=3х+96
Ответ:________
2.Соотнесите каждое квадратное уравнение А)х2-9=0 Б)2х -х2=0 В) х2-3х-4=0 и его корни
1)0 и 2 2)-3 и3 3)-1 и 4 4) -4 и 1
А
Б
В
2.Соотнесите каждое квадратное уравнение А)х2-4=0 Б)2х +х2=0 В) х2+9=0 и его корни
1)0 и -2 2)-2 и 2 3)-3 и 3 4) нет корней
А
Б
В
3. Катер, собственная скорость которого 15 км/ч прошел 40 км по течению реки и 18 км против течения за 4 часа. Найдите скорость течения реки.
Пусть скорость течения реки равна х км/ч.
15(х-4) — 18(х+4) =40
+ = 4
3) + = 4
3. Катер, собственная скорость которого 20 км/ч прошел 18 км по течению реки и 20 км против течения за 2 часа. Найдите скорость течения реки.
Пусть скорость течения реки равна х км/ч.
20(20+х) — 18(20-х) =2
+ = 2
+ = 2
4. Домашнее задание. № 272, № 285.
5. Подведение итогов урока. Рефлексия.
Объявить оценки за урок. Выслушать мнения учащихся о прошедшем уроке.
Слайд 11.
Продолжите предложения
“Сегодня на уроке
Я повторил … Мне понравилось… Я затруднялся… У меня получилось… Я могу… Я попробую… Меня удивило…
Используемая литература
1.Учебник «Алгебра 9 класс», Никольский С.М.
2.Учебник «Алгебра 8 класс», Никольский С.М.
3.ГИА9. Типовые тестовые задания, Ященко И.В.
4.ГИА. Математика, практикум. Лаппо Л.Д.
5.ГИА.Математика ( тренировочные тесты), Гришина И.В.
infourok.ru
Урок в 9-м классе «Решение рациональных уравнений»
Цель:
- Обобщить, углубить знания учащихся по решению рациональных уравнений.
- Способствовать формированию умений применять приемы сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию, развитию творческих способностей учеников путем решения заданий, содержащих модули, параметры.
- Побуждать учеников к самоконтролю, взаимоконтролю, самоанaлизу своей учебной деятельности.
Оборудование: экран, проектор, магнитная доска, плакаты.
Ход урока
1. Организационный момент.
2. Устный опрос
Проводится в виде фронтальной работы с классом. Ученики комментируют свои ответы.
Задания можно разделить на две части: в первой части проверяются теоретические знания, во второй – умения применять эти знания при решении уравнений.
Какие из чисел -2, 0, 2 являются корнями уравнений?
Уравнение |
х3-4х=0 |
х(х2-4х+4)=0 |
х3-2х=0 |
х3-4х+4=0 |
Чтобы решать уравнения, нужно совершать ряд преобразований, и делать это следует очень осмотрительно.
Например, решая уравнения, можно было рассуждать так:
Пример 1 |
Пример 2 |
х(х+3)=2х, |
|
На самом деле допущены ошибки. Какие?
— В результате неравносильных преобразований в уравнении 1 потерян корень х = 0, а в примере 2 появился « посторонний» корень х = 1.
— Как же избежать таких ситуаций??
— Прежде всего нужно четко понимать, какие действия нужно выполнить в ходе решения уравнения.
— Сегодня на уроке мы повторим, обобщим, приведем в систему изученные виды, методы и приемы решения рациональных уравнений.
3. Проверка домашнего задания.
На экране или на оборотной стороне доски заранее заготовлены ответы домашнего задания. Ученики отвечают по готовым записям. Работа ведется фронтально, но пары обмениваются тетрадями и проводят взаимопроверку.
Предварительное домашнее задание
Задание 1. Решить уравнения:
- (х-5)2+9х=
- х2+0,7=0.
- (х-5)(х+3)=9.
- — = 1 +
- (х-5)(х+3)= 1-2х.
- (х-5)(х+3)=3(х-5).
- 2( х+ 1) — 1=3 -(1 -2х).
- 1 — 2х+4х2=х2-2х+ 1.
- 3 (1 -х)+2=5-Зх.
- 2х2+Зх+4 =0.
- x2+6x+4=0.
- 25х2-30х+9=0.
Ответы:
- х=3
- Нет действительных корней..
- х = — 4, х = 6.
- х = —
- х1, 2 = ± 4.
- х=0, х=5.
- Нет действительных корней.
- 0.
- Бесконечное множество корней (х R).
- Нет действительных корней.
- х1,2 = -3±.
- х1=х2=
Провести классификацию уравнений, заданных в домашней работе по виду. В результате выполнения задания приходим к выводу (на экране проецируется через проектор).
Задание 2. Подготовить одну физическую задачу, показывающую, что рациональные уравнения могут служить математическими моделями реальных ситуаций.
В результате обсуждения и проверки домашнего задания выясняется сущность решения уравнений:
- Уравнения являются математическими моделями очень многих физических и иных явлений. Поэтому решение различных практических задач сводится к решению уравнений.
- Уравнением с одним неизвестным называется запись вида А(х) = В(х), в которой А(х) и В(х) — выражение от неизвестной х.
- Областью определения уравнения называется множество всех значений х, при которых определены обе части уравнения.
- Корнем или решением уравнения называется значение неизвестного, при подстановке которого в уравнение получается верное числовое равенство. Решить уравнение — значит найти все его корни или доказать, что их нет.
- Линейные и квадратные уравнения решаются по готовым формулам, они называются простейшими. Главная задача при решении любого уравнения — свести его к простейшему.
4. Работа по теме урока.
Этап I. Тест.
Цель : Проверить навыки решения простейших уравнений.
Работа проводится по карточкам в двух вариантах, состоящих из 20 уравнений, записанных в столбец. Для выполнения задания учащийся берет полоску бумаги и кладет ее справа от столбца, по которому собирается работать.
Решая, ученик записывает только ответы; напротив задания, вызвавшего затруднение, ставит прочерк; по истечении времени, отведенного на выполнение теста, по команде учителя листы подписываются и сдаются. Учитель открывает заранее записанный на доске список правильных ответов и критерии оценок. Проводится быстрая самопроверка решений. Для оценки работы надо: поставить знак «+» против верного ответа и знак «-» против неверного; подсчитать число плюсов.
Критерии оценок: «5» — за 20 плюсов; «4» — за 15-19 плюсов; «3» — за 10-14 плюсов; «2» — за 9 и менее плюсов.
Приложение 1
Этап 2.
Цель : установить связи между корнями квадратных, линейных уравнений и их коэффициентами.
№ |
Уравнение |
|
1 |
2(х+7)=2х+14 |
бесконечное множество корней |
2 |
3(х-1)-5(5+х)=7 |
решений не имеет |
3 |
(а2 -9)х=а2-5а+6 |
линейное уравнение с параметром; в зависимости от значения параметра а уравнение может иметь различное количество корней |
4 |
имеет один корень |
Решить уравнение с параметром а — это значит для каждого значения параметра найти значение неизвестной переменной, удовлетворяющее этому уравнению.
(а2 — 9)х = а2 — 5а + 6.
Решение.
Случай 1: а2-9=0.Тогда а=-3 или а=3.
Если а = — 3, то исходное уравнение примет вид 0х = 30 и корней не имеет.
Если а = 3, то получаем уравнение 0х = 0, для которого любое действительное число является корнем.
Случай 2: а2-90, т.е.а {-3;3}.
Выразим х через а:
х=
Ответ: если а = — 3, то корней нет;
если а = 3, то хR; если а {- 3; 3 } , то один корень .
Обобщая результаты решения уравнения, получаем связь числа корней линейного уравнения с его коэффициентами. На доске, можно собрать схему из заранее подготовленных карточек и прикрепит на доске магнитами или проецировать через экран.
Связь числа корней квадратногo уравнения ах2 + вх + с = 0 (а 0) с его дискриминантом Д = в2 — 4ас, и для каждого случая аналитического решения указать геометрическую модель.
Дальше:
Уравнения |
1. х2+ах+12=0 |
2. ах2-2х+4=0 |
3. 2х2+4х+а=0 |
х2+ах+12=0 и 2х2+4х+а=0 — квадратные уравнения с параметром. В этих уравнениях параметр а входит в состав второго коэффициента и свободного члена; ах2-2х+4=0 — это также уравнение с параметром, но параметр а входит в состав коэффициента при x2 многочлена второй степени. Это уравнение нельзя сразу решить по формулам для отыскания корней квадратного уравнения, т. к. о заданном уравнении мы не можем сказать, квадратное оно или линейное.
Если коэффициент при x2 многочлена второй степени содержит параметр, необходимо разбирать случай, когда он обращается в нуль.
Решим уравнение ах2 — 2х +4 = 0.
Решение. Рассмотрим два случая, когда а = 0 и когда а0.
1. при а=0 уравнение линейное -2х +4 = 0. Откуда х = 2.
2. При а уравнение квадратное, Д= 4- 1ба.
Если Д< 0, т. е. а> , уравнение решений не имеет.
Если Д= 0, т. е. а = , то уравнение имеет единственный корень х = 4.
Если Д> 0, т. е. а< , то уравнение имеет два корня .
О т в е т: если а>, то решений нет; если а =, то х = 4; если а<, а0, два корня ; если а = 0, то х=2.
Далее ученикам предлагается обобщить результаты домашнего задания, выполнив следующее. Задание проецируется на экран.
По окончании выполнения заданий открываются правильные ответы.
Этап 3.
1 задание. Установите связь между коэффициентами неполного квадратного уравнения и его корнями.
2 задание.
Установите связь между коэффициентами полного квадратного уравнения ax2 + вх + с= 0 (а 0) и его корнями.
3 задание. Решить уравнение несколькими способами: x2 -6х + 8= 0.
Далее открываются правильные решения (заранее заготовленные учителем). Учащиеся проводят взаимопроверку.
Вывод: уравнение можно решить разными приемами: способом группировки, вынесением общего множителя за скобки, использованием формул сокращенного умножения, способом выделения полного квадрата, разложением на множители квадратного трехчлена, графически. Все перечисленные приемы объединяет метод разложения на множители.
Этап 4. Показать использование методов разложения на множители и метода введения новых переменных .
Решить уравнение:
(х2 + х + 4)2 + 8х(х2 + х + 4) + 15х2 = 0
Решение 1. Разложим многочлен на множители способом выделения полного квадрата, предварительно представив слагаемое 15х2 =16х2-х2.
Имеем:
(х2+х+4)2+8х(х2+х+4)+15х2=(х2+х+4)2+2*4х(х2+х+4) +16х2-х2 = ((х2+х+4)+4х)2 –х2= (х2+х+4+4х-х)(х2+х+4+4х+х)=(х2+4х+4)(х2+6х+4)=0
| х2+4х+4=0 | х2+бх+4=0 |
| х=2 | х=-3 |
Все три найденных числа являются искомыми корнями.
Ответ:-3±;2.
Решение 2. Разложим многочлен на множители, используя способ группировки; предварительно представляя слагаемое
8х(х2+х+4)=3х(х2+х+4)+5х (х2+х+4).
Тогда (х2+х+4)2+8х(х2+х+ 4) + 15х2 = (х2+х + 4)2+3х(х2+х+4)+5х(х2+х+4)+15х2= (( х2+х+4)2+Зх(х2 х+4))+(5х(х2+х+4)+15х2) = (х2+х+4)(х2+х+4+3х)+5х(х2+х+4+Зх) = (х2+х+4+5х)(х2+х+4+Зх) = (х2+4х+4)(х2+6х+4) = (х2 +х +4)(х2+бх+4) = 0
Ответ:-3±;2.
Решение 3.
Ввести новую переменную у = х2+ х + 4, тогда уравнение примет вид у2 + 8ху + 15х2 = 0.
Учащиеся выбирают способ решения по желанию.
- способом группировки
- способом выделения полного квадрата
- относительно у, используя утверждение, обратное теореме Виета.
- как квадратное уравнение (относительно у) с четным вторым коэффициентом.
Вывод. Удачный выбор новый переменной делает решение уравнения более легкой.
Учитель вместе с учащимися формулирует суть метода введения новых переменных.
- Если уравнение f(х) = 0 удалось преобразовать к виду w(g(х)) = 0, то нужно ввести новую переменную у = g(х), решить уравнение w(у) = 0, а затем рассмотреть совокупность уравнений: g(х)=y1, g(х)=у2….где у1, у2…уп корни уравнения w(у) = 0.
На доске:
1 |
х4+8х2-9=0 |
4 |
х2-/х/=0 |
2 |
(х+2)2-2/х+2/-3=0 |
5 |
х(х-1)(х-2)(х-3)=24 |
3 |
(х2+1)2-6(х2+1)+5 =0 |
б |
— Какое из уравнений можно решить методом графическим, методом разложения на множители, методом введения новых переменных? (4)
— Что объединяет остальные уравнения?
Ответ: уравнение №1 — биквадратное, №2 -квадратное относительно модуля, №3 — квадратное относительно квадратного трехчлена, № 5-6 — рациональные уравнения.
Эти уравнения решаются методом замены переменной.
Решаем уравнение: х2 – 2 /х/ = 0
Метод разложения на множители.
Решение:
1) Если х 0, то / х /= х; х2 — 2х = 0; х = 0 или х = 2; оба значения удовлетворяют х .
2) Если х < 0, то /х /=- х; х2 + 2х = 0, х = 0 или х = -2;
Второе из найденных значений удовлетворяет условию х < 0 . Ответ: -2;0;2..
Графический метод.
Ответ: -2;0;2..
Метод введения новых переменных.
Решение:
Пусть /х/=t, тогда t2 -1 = 0, откуда получаем t = 0 или t =2.
Возвращаясь к исходной переменной, получаем х =2; х = -2; х = 0. Ответ: -2;0;2.
Новая переменная в уравнениях иногда действительно очевидна, но иногда ее трудно увидеть, а можно выявить лишь в процессе каких-либо преобразований.
Этап 5. Самостоятельная работа (уровень по выбору учащихся).
Решить уравнения:
urok.1sept.ru
Конспект урока по алгебре в 9 классе на тему «Дробные рациональные уравнения»
ПЛАН-КОНСПЕКТ УРОКА
Дробные рациональные уравнения
Учитель: Митяева Елена Владимировна
Предмет: алгебра
Класс: 9
Тема и номер урока в теме: Дробные рациональные уравнения, урок № 1
Цели урока
Обучающая: повторение алгоритма решения дробных рациональных уравнений, изученного в курсе 8 класса, отработка навыков решения дробных рациональных уравнений.
Развивающая: развитие познавательной и творческой активности, развитие логического мышления, памяти, внимания
Воспитывающая: воспитание ответственности, трудолюбия, математической культуры
Тип урока: урок — повторение
Материально-техническое оснащение: Компьютер, интернет, Skype, презентация к уроку «Дробные рациональные уравнения»
Время: 40 минут
СТРУКТУРА И ХОД УРОКА
Время( мин.)
Деятельность ученика
Деятельность учителя
Приемы, методы
Этап урока
№
1
Приветствие
Приветствие, проверка готовности учащегося
Организационный момент
1
2
Сдает тетрадь с домашней работой, отвечает на вопросы, анализирует ошибки
Проверяет выполненное домашнее задание, задает вопросы, анализирует ошибки
Диалог
Проверка домашнего задания
2
1
Записывает тему в тетрадь
Сообщает тему и цель урока
Сообщение темы и целей урока
3
10
Отвечает на вопросы
Задает вопросы, комментирует ответы
диалог
Актуализация знаний
4
13
Делает записи в тетради, задает вопросы.
Проговаривает алгоритм решения дробных рациональных уравнений; просматривает его на экране, принимает файл с алгоритмом
Формулирует определение дробного рационального уравнения, рассматривает один из способов решения дробных рациональных уравнений.
Предлагает ученику проговорить алгоритм решения дробных рациональный уравнений; демонстрирует алгоритм на экране, отсылает файл с алгоритмом ученику
Наглядно-иллюстративный;
диалог
Повторение изученного ранее материала
5
10
Выполняет задание в тетради, отвечает на вопросы учителя
Контролирует правильность выполнения задания учеником
Практическая работа
Отработка навыков
6
2
Отвечает на поставленные учителем вопросы
Задает учащемуся вопросы
Диалог
Подведение итогов урока
7
1
Запись задания в дневник
Формулирует задание, дает инструкции
Постановка домашнего задания
8
ОСНОВНОЙ УЧЕБНЫЙ МАТЕРИАЛ
Организационный момент. Начало урока.
Проверка домашнего задания.
Сообщение темы и целей урока.
В 8 классе ты уже учился решать дробные рациональные уравнения. Сегодня мы вспомним, какие уравнения называются дробными рациональными, повторим алгоритм их решения; улучшим навык решения таких уравнений.
Открывай учебник на стр. 13, записывай тему в тетрадь
Слайд 1.
Актуализация знаний.
Но сначала надо выполнить следующие задания.
1) Решить уравнение
Слайд 2
2) Найти общий знаменатель дробей
Слайд 3
3) Найти допустимые значения переменной выражения
Слайд 4
Повторение изученного ранее материала.
Рассмотрим уравнения. У них обе части являются из рациональными выражениями. Но хотя бы одна часть является дробным рациональным выражением.
Сформулируем определение: дробным рациональным уравнением называется уравнение, обе части которого являются рациональными выражениями, причем хотя бы одно из них — дробным выражением
Слайд 5
Решим уравнение
Слайд 6
Еще раз проговори алгоритм решения дробных рациональных уравнений.
Демонстрация алгоритма на экране
Слайд 7
Отработка навыков.
Решите уравнение, пользуясь алгоритмом
Слайд 8
Найти ОДЗ каждого уравнения
Слайд 9
Подведение итогов урока.
Слайд 10
Постановка домашнего задания.
Слайд 11
infourok.ru
«Использование различных приемов и методов при решении дробно-рациональных уравнений»
Конспект урока алгебры в 9 классе
Тема: «Использование различных приемов и методов
при решении дробно-рациональных уравнений»
Дата проведения: 23 ноября 2015 года
Цели: продолжить формирование умения решать дробно-рациональные уравнения, используя при этом различные приемы и методы.
Развивать логическое мышление, вычислительные навыки, умение пользоваться ранее изученным материалом.
Воспитывать аккуратность, взаимоуважение, дисциплинированность.
Ход урока
I. Организационный момент.
II. Устная работа.
Какие из чисел –1; 0; 2; 3 являются корнями уравнения:
а) = 0; б) = 0.
III. Объяснение нового материала.
1. Актуализация знаний учащихся: рассказать алгоритм решения дробно-рациональных уравнений и использовать этот алгоритм при решении уравнения.
Вывод: решение данного уравнения по алгоритму является громоздким, поэтому целесообразно применить ряд преобразований.
2. Рассмотреть пример 4 из учебника. Здесь возникает такая же ситуация: решение данного дробно-рационального уравнения приводит к целому уравнению четвертой степени, корни которого известными методами найти очень сложно. Зато после введения новой переменной полученное уравнение решается довольно просто.
3.На основании рассмотренных примеров делаются следующие
вывод ы:
1) Не всякое дробно-рациональное уравнение целесообразно решать по алгоритму.
2) Довольно эффективным методом решения дробно-рациональных уравнений является метод введения новой переменной.
IV. Формирование умений и навыков.
Упражнения:
1. № 293 (а), № 294 (а).
2. № 297 (а, б), № 298 (б).
3. № 299 (а).
.
Сделаем замену: , тогда
Получим уравнение:
;
;
2а2 – а – 3 = 0;
а1 = –1, а2 = .
Обратная замена:
; илих2 + х – 1 = 0;
D = 1 + 4 = 5;
х1, 2 = .
;
2х2 – 3х – 2 = 0;
D = 9 + 16 = 25;
х1 = = 2;
х2 = .
О т в е т: .
4. = –1,5.
Р е ш е н и е
Проверим, что х ≠ 0, и разделим числитель и знаменатель каждой дроби на х:
= –1,5.
Сделаем замену: . Получим:
;
8 (а – 5) + 10 (а + 1) + 3 (а + 1) (а – 5) = 0;
8а – 40 + 10а + 10 + 3а2 – 15а + 3а – 15 = 0;
3а2 + 6а – 45 = 0;
а2 + 2а – 15 = 0;
а1 = –5, а2 = 3.
Обратная замена:
; илих2 + 5х + 3 = 0;
D = 25 – 12 = 13;
х1, 2 = .
;
х2 – 3х + 3 = 0;
D = 9 – 12 = –3.
Решений нет.
О т в е т: .
5. = 3.
Решение
Вычтем и прибавим к выражению, стоящему в левой части уравнения, выражение , чтобы получить полный квадрат:
;
;
;
.
Сделаем замену: = t. Получим:
t2 + 2t – 3 = 0;
t1 = 1, t2 = –3.
Обратная замена:
= 1; илих2 – х – 1 = 0;
D = 1 + 4 = 5;
х1, 2 = .
= –3;
х2 + 3х + 3 = 0;
D = 9 – 12 = –3.
Решений нет.
О т в е т: .
V. Проверочная работа.
В а р и а н т 1
Решите уравнение:
а) ;
б) .
В а р и а н т 2
Решите уравнение:
а) ;
б) .
VI. Итоги урока.
Вопросы учащимся:
– Какими приемами и методами можно решать дробно-рациональные уравнения?
– Опишите решение дробно-рационального уравнения по алгоритму.
– В каких случаях при решении дробно-рациональных уравнений целесообразно использовать метод введения новой переменной?
Домашнее задание: № 296 (б), № 294 (б), № 297 (в), № 298 (б).
infourok.ru
 ) = 0
) = 0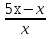 + 25 х = 3
+ 25 х = 3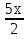 –
– 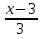 = 1 +
= 1 + 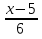 х = —
х = —