Тригонометрические уравнения. Простейшие тригонометрические уравнения Решить тригонометрическое уравнение sinx 1 2
Основными методами решения тригонометрических уравнений являются: сведение уравнений к простейшим (с использованием тригонометрических формул), введение новых переменных, разложение на множители. Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.
Необходимым условием успешного решения тригонометрических уравнений является знание тригонометрических формул (тема 13 работы 6).
Примеры.
1. Уравнения, сводящиеся к простейшим.
1) Решить уравнение
Решение:
Ответ:
2) Найти корни уравнения
(sinx + cosx) 2 = 1 – sinxcosx, принадлежащие отрезку .
Решение:
Ответ:
2. Уравнения, сводящиеся к квадратным.
1) Решить уравнение 2 sin 2 x – cosx –1 = 0.
Решение: Используя формулу sin 2 x = 1 – cos 2 x, получаем
Ответ:
2) Решить уравнение cos 2x = 1 + 4 cosx.
Ответ:
3) Решить уравнение tgx – 2ctgx + 1 = 0
Решение:
Ответ:
3. Однородные уравнения
1) Решить уравнение 2sinx – 3cosx = 0
Решение: Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1. Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим
Ответ:
2) Решить уравнение 1 + 7 cos 2 x = 3 sin 2x
Решение:
Используем формулы 1 = sin 2 x + cos 2 x и sin 2x = 2 sinxcosx, получим
sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0
Пусть cosx = 0, тогда sin 2 x = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1.
Значит cosx ≠ 0 и можно поделить уравнение на cos 2 x. Получим
tg 2 x – 6 tgx + 8 = 0
Обозначим tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y 2 = 2
а) tgx = 4, x= arctg4 + 2 k
б) tgx = 2, x= arctg2 + 2 k , k .
Ответ: arctg4 + 2 k , arctg2 + 2 k, k
4. Уравнения вида a sinx + b cosx = с, с ≠ 0.
1) Решить уравнение .
Решение:
Ответ:
5. Уравнения, решаемые разложением на множители.
1) Решить уравнение sin2x – sinx = 0.
Корнем уравнения f ( х ) = φ ( х ) может служить только число 0. Проверим это:
cos 0 = 0 + 1 – равенство верно.
Число 0 единственный корень данного уравнения.
Ответ: 0.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Простейшие тригонометрические уравнения решаются, как правило, по формулам. Напомню, что простейшими называются вот такие тригонометрические уравнения:
sinx = а
cosx = а
tgx = а
ctgx = а
х — угол, который нужно найти,
а — любое число.
А вот и формулы, с помощью которых можно сразу записать решения этих простейших уравнений.
Для синуса:
Для косинуса:
х = ± arccos a + 2π n, n ∈ Z
Для тангенса:
х = arctg a + π n, n ∈ Z
Для котангенса:
х = arcctg a + π n, n ∈ Z
Собственно, это и есть теоретическая часть решения простейших тригонометрических уравнений. Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона. Почему?
Да потому, что масса народу записывает эти буковки, не понимая их смысла совершенно! С опаской записывает, как бы чего не вышло…) С этим надо разобраться. Тригонометрия для людей, или люди для тригонометрии, в конце концов!?)
Разберёмся?
Один угол у нас будет равен arccos a, второй: -arccos a.
И так будет получаться всегда.
Если не верите, наведите курсор мышки на картинку, или коснитесь рисунка на планшете.) Я изменил число а на какое-то отрицательное. Всё равно, один угол у нас получился arccos a, второй: -arccos a.
Следовательно, ответ можно всегда записать в виде двух серий корней:
х 1 = arccos a + 2π n, n ∈ Z
х 2 = — arccos a + 2π n, n ∈ Z
Объединяем эти две серии в одну:
х= ± arccos а + 2π n, n ∈ Z
И все дела. Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом.
Если вы понимаете, что это не какая-то сверхнаучная мудрость, а просто сокращённая запись двух серий ответов, вам и задания «С» будут по плечу. С неравенствами, с отбором корней из заданного интервала… Там ответ с плюсом/минусом не катит. А если отнестись к ответу делово, да разбить его на два отдельных ответа, всё и решается.) Собственно, для этого и разбираемся. Что, как и откуда.
В простейшем тригонометрическом уравнении
sinx = а
тоже получается две серии корней.
Всегда. И эти две серии тоже можно записать одной строчкой. Только эта строчка похитрее будет:
х = (-1) n arcsin a + π n, n ∈ Z
Но суть остаётся прежней. Математики просто сконструировали формулу, чтобы вместо двух записей серий корней, сделать одну. И всё!
Проверим математиков? А то мало ли…)
В предыдущем уроке подробно разобрано решение (безо всяких формул) тригонометрического уравнения с синусом:
В ответе получились две серии корней:
х 1 = π /6 + 2π n, n ∈ Z
х 2 = 5π /6 + 2π n, n ∈ Z
Если мы будем решать это же уравнение по формуле, получим ответ:
х = (-1) n arcsin 0,5 + π n, n ∈ Z
Вообще-то, это недоделанный ответ.) Ученик обязан знать, что arcsin 0,5 = π /6. Полноценный ответ будет:
х = (-1) n π /6 + π n, n ∈ Z
Тут возникает интересный вопрос. Ответ через х 1 ; х 2 (это правильный ответ!) и через одинокий х (и это правильный ответ!) — одно и то же, или нет? Сейчас узнаем.)
Подставляем в ответ с х 1 значения n =0; 1; 2; и т.д., считаем, получаем серию корней:
х 1 = π/6; 13π/6; 25π/6 и так далее.
При такой же подстановке в ответ с х 2 , получаем:
х 2 = 5π/6; 17π/6; 29π/6 и так далее.
А теперь подставляем значения n (0; 1; 2; 3; 4…) в общую формулу для одинокого х . Т.е возводим минус один в нулевую степень, затем в первую, вторую, и т.д. Ну и, разумеется, во второе слагаемое подставляем 0; 1; 2 3; 4 и т.д. И считаем. Получаем серию:
х = π/6; 5π/6; 13π/6; 17π/6; 25π/6 и так далее.
Вот всё и видно.) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.
)
Формулы для решения тригонометрических уравнений с тангенсом и котангенсом тоже можно проверить. Но не будем.) Они и так простенькие.
Я расписал всю эту подстановку и проверку специально. Здесь важно понять одну простую вещь: формулы для решения элементарных тригонометрических уравнений есть, всего лишь, краткая запись ответов. Для этой краткости пришлось вставить плюс/минус в решение для косинуса и (-1) n в решение для синуса.
Эти вставки никак не мешают в заданиях, где нужно просто записать ответ элементарного уравнения. Но если надо решать неравенство, или далее нужно что-то делать с ответом: отбирать корни на интервале, проверять на ОДЗ и т.п, эти вставочки могут запросто выбить человека из колеи.
И что делать? Да либо расписать ответ через две серии, либо решать уравнение/неравенство по тригонометрическому кругу. Тогда исчезают эти вставочки и жизнь становится легче.)
Можно подвести итоги.
Для решения простейших тригонометрических уравнений существуют готовые формулы ответов. Четыре штуки. Они хороши для мгновенной записи решения уравнения. Например, надо решить уравнения:
sinx = 0,3
Легко: х = (-1) n arcsin 0,3 + π n, n ∈ Z
cosx = 0,2
Без проблем: х = ± arccos 0,2 + 2π n, n ∈ Z
tgx = 1,2
Запросто: х = arctg 1,2 + π n, n ∈ Z
ctgx = 3,7
Одной левой: x= arcctg3,7 + π n, n ∈ Z
cos x = 1,8
Если вы, блистая знаниями, мгновенно пишете ответ:
х= ± arccos 1,8 + 2π n, n ∈ Z
то блистаете вы уже, это… того… из лужи.) Правильный ответ: решений нет. Не понимаете, почему? Прочитайте, что такое арккосинус. Кроме того, если в правой части исходного уравнения стоят табличные значения синуса, косинуса, тангенса, котангенса, — 1; 0; √3; 1/2; √3/2 и т.п. — ответ через арки будет недоделанным.
Арки нужно обязательно перевести в радианы.
А если уж вам попалось неравенство, типа
то ответ в виде:
х πn, n ∈ Z
есть редкая ахинея, да…) Тут надо по тригонометрическому кругу решать. Чем мы и займёмся в соответствующей теме.
Для тех, кто героически дочитал до этих строк. Я просто не могу не оценить ваши титанические усилия. Вам бонус.)
Бонус:
При записи формул в тревожной боевой обстановке, даже закалённые учёбой ботаны частенько путаются, где πn, а где 2π n. Вот вам простой приёмчик. Во всех формулах стоит πn. Кроме единственной формулы с арккосинусом. Там стоит 2πn. Два пиэн. Ключевое слово — два. В этой же единственной формуле стоят два знака в начале. Плюс и минус. И там, и там — два.
Так что, если вы написали два знака перед арккосинусом, легче вспомнить, что в конце будет два пиэн. А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Когда-то я стал свидетелем разговора двух абитуриентов:
– Когда надо прибавить 2πn, а когда – πn? Никак не могу запомнить!
– И у меня такая же проблема.
Так и хотелось им сказать: «Не запоминать надо, а понимать!»
Данная статья адресована прежде всего старшеклассникам и, надеюсь, поможет им с «пониманием» решать простейшие тригонометрические уравнения:
Числовая окружность
Наряду с понятием числовой прямой есть еще и понятие числовой окружности.
Как мы знаем, в прямоугольной системе координат окружность,с центром в точке (0;0) и радиусом 1, называется единичной. Вообразим числовую прямую тонкой нитью и намотаем ее на эту окружность: начало отсчета (точку 0), приставим к «правой» точке единичной окружности, положительную полуось обмотаем против движения часовой стрелки, а отрицательную – по направлению (рис. 1). Такую единичную окружность называют числовой.
Свойства числовой окружности
- Каждое действительное число находится на одной точке числовой окружности.
- На каждой точке числовой окружности находятся бесконечно много действительных чисел. Так как длина единичной окружности равна 2π, то разность между любыми двумя числами на одной точке окружности равна одному из чисел ±2π ; ±4π ; ±6π ; …
Сделаем вывод: зная одно из чисел точки A, мы можем найти все числа точки A .
Проведем диаметр АС (рис. 2). Так как x_0 – одно из чисел точки А, то числа x_0±π ; x_0±3π; x_0±5π; … и только они будут числами точки C. Выберем одно из этих чисел, скажем, x_0+π, и запишем с его помощью все числа точки C: x_C=x_0+π+2πk ,k∈Z. Отметим, что числа на точках A и C можно объединить в одну формулу: x_(A ; C)=x_0+πk ,k∈Z (при k = 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки C).
Сделаем вывод: зная одно из чисел на одной из точек A или C диаметра АС, мы можем найти все числа на этих точках.
- Два противоположных числа находятся на симметричных относительно оси абсцисс точках окружности.
Проведем вертикальную хорду АВ (рис. 2). Так как точки A и B симметричны относительно оси Ox, то число -x_0 находится на точке B и, значит, все числа точки B задаются формулой: x_B=-x_0+2πk ,k∈Z. Числа на точках A и B запишем одной формулой: x_(A ; B)=±x_0+2πk ,k∈Z. Сделаем вывод: зная одно из чисел на одной из точек A или B вертикальной хорды АВ, мы можем найти все числа на этих точках. Рассмотрим горизонтальную хорду AD и найдем числа точки D (рис.
k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D).
Сделаем вывод: зная одно из чисел на одной из точек A или D горизонтальной хорды AD, мы можем найти все числа на этих точках.
Шестнадцать основных точек числовой окружности
На практике решение большинства простейших тригонометрических уравнений связано с шестнадцатью точками окружности (рис. 3). Что это за точки? Красные, синие и зеленые точки делят окружность на 12 равных частей. Так как длина полуокружности равна π, то длина дуги A1A2 равна π/2, длина дуги A1B1 равна π/6, а длина дуги A1C1 равна π/3.
Теперь можем указать по одному числу на точках:
π/3 на С1 и
Вершины оранжевого квадрата – середины дуг каждой четверти, следовательно, длина дуги A1D1 равна π/4 и, значит, π/4 – одно из чисел точки D1. Воспользовавшись свойствами числовой окружности, мы можем записать с помощью формул все числа на всех отмеченных точках нашей окружности. На рисунке отмечены также и координаты этих точек (опустим описание их получения).
Усвоив выше сказанное, мы имеем теперь достаточную подготовку для решения частных случаев (для девяти значений числа a) простейших уравнений.
Решить уравнения
1) sinx=1⁄(2) .
– Что от нас требуется?
– Найти все те числа x, синус которых равен 1/2 .
Вспомним определение синуса: sinx – ордината точки числовой окружности, на которой находится число x . На окружности имеем две точки, ордината которых равна 1/2 . Это концы горизонтальной хорды B1B2 . Значит, требование «решить уравнение sinx=1⁄2 » равнозначно требованию «найти все числа на точке B1 и все числа на точке B2».
2) sinx=-√3⁄2 .
Нам надо найти все числа на точках C4 и C3.
3) sinx=1 . На окружности имеем только одну точку с ординатой 1 – точка A2 и, значит, нам надо найти только все числа этой точки.
Ответ: x=π/2+2πk , k∈Z .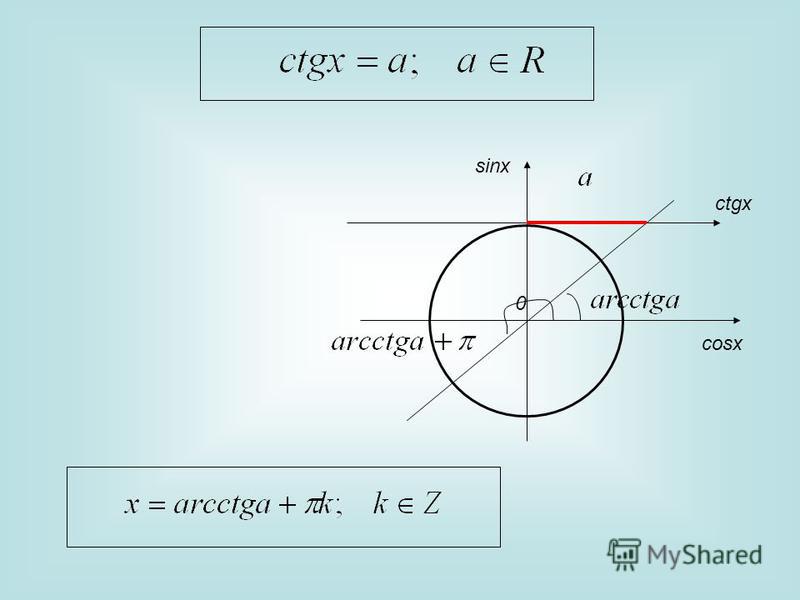
4) sinx=-1 .
Только точка A_4 имеет ординату -1. Все числа этой точки и будут конями уравнения.
Ответ: x=-π/2+2πk , k∈Z .
5) sinx=0 .
На окружности имеем две точки с ординатой 0 – точки A1 и A3 . Можно указать числа на каждой из точек по отдельности, но, учитывая, что эти точки диаметрально противоположные, лучше объединить их в одну формулу: x=πk ,k∈Z .
Ответ: x=πk ,k∈Z .
6) cosx=√2⁄2 .
Вспомним определение косинуса: cosx — абсцисса точки числовой окружности на которой находится число x. На окружности имеем две точки с абсциссой √2⁄2 – концы горизонтальной хорды D1D4 . Нам нужно найти все числа на этих точках. Запишем их, объединив в одну формулу.
Ответ: x=±π/4+2πk , k∈Z .
7) cosx=-1⁄2 .
Надо найти числа на точках C_2 и C_3 .
Ответ: x=±2π/3+2πk , k∈Z .
10) cosx=0 .
Только точки A2 и A4 имеют абсциссу 0, значит, все числа на каждой из этих точках и будут решениями уравнения.
.
Решениями уравнения системы являются числа на точках B_3 и B_4 .Неравенству cosxОтвет: x=-5π/6+2πk , k∈Z .
Заметим,что при любом допустимом значении x второй множитель положителен и, следовательно,уравнение равносильно системе
Решениями уравнения системы являются чила точек D_2 и D_3 . Числа точки D_2 не удовлетворяют неравенству sinx≤0,5 ,а числа точки D_3-удовлетворяют.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Решение уравнения sin x — cos x = 1. Урок-семинар
Цели урока:
Главная дидактическая цель: рассмотреть все возможные способы решения данного уравнения.
Обучающие: изучение новых приемов решения
тригонометрических уравнений на примере данного
в творческой ситуации урока-семинара.
Развивающие: формирование общих приемов решения тригонометрических уравнений; совершенствование мыслительных операций учащихся; развитие умений и навыков устной монологической математической речи при изложении решения тригонометрического уравнения.
Воспитывающие: развивать самостоятельность и творчество; способствовать выработке у школьников желания и потребности обобщения изучаемых фактов.
Вопросы для подготовки и дальнейшего обсуждения на семинаре.
- Приведение уравнения к однородному относительно синуса и косинуса.
- Разложение левой части уравнения на множители.
- Введение вспомогательного угла.
- Преобразование разности (или суммы) тригонометрических функций в произведение.
- Приведение к квадратному уравнению относительно одной из функций.
- Возведение обеих частей уравнения в квадрат.
- Выражение всех функций через tg x (универсальная подстановка).
- Графическое решения уравнения.
Все учащиеся разбиваются на группы (по 2-4 человека) в зависимости от общего количества учащихся и их индивидуальных способностей и желания. Самостоятельно определяют для себя тему для подготовки и выступления на уроке-семинаре. Выступает один человек от группы, а остальные учащиеся принимают участие в дополнениях и исправлениях ошибок, если в этом возникнет необходимость.
Организационный момент.
Учащимся сообщаются:
Тема урока:
“Различные способы решения тригонометрического уравнения sin x — cos x = 1
Форма проведения: урок – семинар.
Эпиграф к уроку:
“Крупное научное открытие дает решение
крупной проблемы, но и в решении любой задачи
присутствует крупица открытия.
Задача, которую
вы решаете, может быть скромной, но если она
бросает вызов вашей любознательности и
заставляет вас быть изобретательными и если вы
решаете ее собственными силами, то вы сможете
испытать ведущее к открытию напряжение ума и
насладиться радостью победы”
(Д. Пойа)
Задачи урока:
а) рассмотреть возможность решения одного и
того же уравнения различными способами;
б) познакомиться с различными общими приемами
решения тригонометрических уравнений;
в) изучение нового материала (введение
вспомогательного угла, универсальная
подстановка).
План семинара
- Приведение уравнения к однородному относительно синуса и косинуса.
- Разложение левой части уравнения на множители.
- Введение вспомогательного угла.
- Преобразование разности (или суммы) тригонометрических функций в произведение.
- Приведение к квадратному уравнению относительно одной из функций.
- Возведение обеих частей уравнения в квадрат.
- Выражение всех функций через tg x (универсальная подстановка).
- Графическое решения уравнения.
Содержание.
1. Слово предоставляется первому участнику.
Приведение уравнения sin x — cos x = 1 к
однородному относительно синуса и косинуса.
Разложим левую часть по формулам двойного
аргумента, а правую часть заменим
тригонометрической единицей, используя основное
тригонометрическое тождество:
2 sin cos — cos + sin = sin + cos ;
2 sin cos — cos =0 ;
cos = 0;
Произведение равно нулю, если хотя бы один из
множителей равен нулю, а другие при этом не
теряют смысла, поэтому следует
cos =0 ; =
= 0 -
однородное уравнение первой степени.
Делим обе
части уравнения на cos . (cos 0, так как если
cos = 0 , то sin — 0 = 0 sin = 0, а это противоречит
тригонометрическому тождеству sin + cos = 1).
Получим tg -1
= 0 ; tg = 1 ; =
Ответ:
2. Слово предоставляется второму участнику.
Разложение левой части уравнения sin x — cos x = 1 на множители.
sin x – (1+ cos x ) = 1; используем формулы 1+ cos x = 2 , получим ;
далее аналогично:
произведение равно нулю, если хотя бы один из
множителей равен нулю, а другие при этом не
теряют смысла, поэтому следует
cos =0 ; =
= 0 -
однородное уравнение первой степени. Делим обе
части уравнения на cos . (cos 0, так как если
cos = 0 , то sin — 0 = 0 sin = 0, а это противоречит
тригонометрическому тождеству sin + cos = 1)
Получим tg -1
= 0 ; tg = 1 ; =
Ответ:
3. Слово предоставляется третьему участнику.
Решение уравнения sin x — cos x = 1 введением вспомогательного угла.
Рассмотрим уравнение sin x — cos x = 1. Умножим и
разделим каждое слагаемое левой части
уравнения на .
Получим и
вынесем в левой части уравнения за скобку. Получим ; Разделим обе
части уравнения на и используем табличные значения
тригонометрических функций. Получим ; Применим
формулу синус разности.
;
Легко установить(с помощью тригонометрического
круга), что полученное решение распадается на два
случая:
;
Ответ:
4. Слово предоставляется четвертому участнику.
Решение уравнения sin x — cos x = 1 способом преобразования разности (или суммы) тригонометрических функций в произведение.
Запишем уравнение в виде , используя формулу приведения . Применяя формулу разности двух синусов, получим
;
и так далее, аналогично предыдущему способу.
Ответ:
5. Слово предоставляется пятому участнику.
Решение уравнения sin x — cos x = 1 способом приведения к квадратному уравнению относительно одной из функций.
Рассмотрим основное тригонометрическое
тождество ,
откуда следует
подставим
полученное выражение в данное уравнение.
sin x — cos x = 1 ,
Возведем обе части полученного уравнения в квадрат:
В процессе решения обе части уравнения возводились в квадрат, что могло привести к появлению посторонних решений, поэтому необходима проверка. Выполним ее.
Полученные решения эквивалентны объединению трех решений:
Первое и второе решения совпадают с ранее
полученными, поэтому не являются посторонними.
Остается проверить третье решение Подставим.
Левая часть:
Правая часть: 1.
Получили: , следовательно, – постороннее решение.
Ответ:
6. Слово предоставляется шестому участнику.
Возведение обеих частей уравнения sin x — cos x = 1 в квадрат.
Рассмотрим уравнение sin x — cos x = 1. Возведем обе части данного уравнения в квадрат.
;
;
Используя основное тригонометрическое тождество и формулу синуса двойного угла, получим ; sin 2x = 0 ; .
Полученное решение эквивалентно объединению четырех решений:
(эти решения можно нанести на единичную окружность). Проверка показывает, что первое и четвертое решения — посторонние.
Ответ:
7. Слово предоставляется седьмому участнику.
Использование универсальной подстановки в решении уравнения sin x — cos x = 1. Выражение всех функций через tg x по формулам:
Запишем данное уравнение с учетом приведенных
формул в виде .
,
получим
ОДЗ данного уравнения – все множество R.
При
переходе к
из рассмотрения выпали значения, при которых не имеет
смысла, т. е.
или .
Следует проверить, не являются ли решениями данного уравнения. Подставим в левую и правую часть уравнения эти решения.
Левая часть: .
Правая часть: 1.
Получили 1=1. Значит, — решение данного уравнения.
Ответ:
8. Слово предоставляется восьмому участнику.
Рассмотрим графическое решение уравнения sin x — cos x = 1.
Запишем рассматриваемое уравнение в виде sin x = 1 + cos x.
Построим в системе координат Оxy графики функций, соответствующих левой и правой частям уравнения. Абсциссы точек пересечения графиков являются решениями данного уравнения.
y = sin x – график: синусоида.
y = cos x +1 – график: косинусоида y = cos x, смещенная на 1
вверх по оси Oy. Абсциссы точек пересечения
являются решениями данного уравнения.
Ответ:
Итог урока.
- Учащиеся научились решать тригонометрические уравнения вида , освоили новый материал.
- На примере одного уравнения рассмотрели несколько способов решения.
- Учащиеся были непосредственными участниками урока, была задействована обратная связь в системе ученик-учитель.
- Учащиеся получили навыки самостоятельной работы с дополнительной литратурой.
Список использованной литературы:
- Татарченкова С.С. Урок как педагогический феномен – Санкт-Петербург: Каро, 2005
- Выгодский Н.В. Справочник по элементарной математике.-М.: Наука, 1975.
- Виленкин Н.Я. и др. За страницами учебника математики: Арифметика. Алгебра. Геометрия: Книга для учащихся 10-11 класса – М.: Просвещение, 1996.
- Гнеденко Б. {2}x \neq 0 и 1-\sin x \neq 0.
б) Решим неравенства:
1) -\frac{3\pi}{2} \leq \frac{\pi}{6}+2\pi m \leq -\frac{\pi}{2},
2) -\frac{3\pi}{2} \leq \frac{5\pi}{6}+2\pi n \leq — \frac{\pi}{2},
3) -\frac{3\pi}{2} \leq -\frac{\pi}{2}+2\pi k \leq -\frac{\pi}{2}.
при m, n, k \in \mathbb Z.
-\frac{3\pi}{2} \leq \frac{\pi}{6}+2\pi m \leq -\frac{\pi}{2},
-\frac{3}{2} \leq \frac{1}{6}+2\pi m \leq -\frac{1}{2},
-\frac{5}{3} \leq 2m \leq -\frac{2}{3},
-\frac{5}{6} \leq m \leq -\frac{1}{3}.
Нет целых чисел, принадлежащих промежутку \left [-\frac{5}{6}; -\frac{1}{3} \right ].
-\frac{3\pi}{2} \leq \frac {5\pi}{6}+2\pi n \leq — \frac{\pi}{2},
-\frac{3}{2} \leq \frac{5}{6}+2n \leq -\frac{1}{2},
-\frac{7}{3} \leq 2n \leq -\frac{4}{3},
-\frac{7}{6} \leq n \leq -\frac{2}{3}.
Единственное целое число, принадлежащее этому промежутку, n=-1. Тогда x=\frac{5\pi}{6}-2\pi=-\frac{7\pi}{6}.
-\frac{3\pi}{2} \leq -\frac{\pi}{2}+2\pi k \leq — \frac{\pi}{2},
-\frac{3}{2} \leq-\frac{1}{2} + 2k \leq-\frac{1}{2},
-1 \leq 2k \leq 0,
-\frac{1}{2} \leq k \leq 0.
Этому равенству удовлетворяет k=0, тогда x=-\frac{\pi}{2}.
Тетрадка в клеточку — Решение простейших тригонометрических уравнений
Рисунок 11. Решение уравнения sin
x = 0.Построим числовую окружность на координатной плоскости. Так как ось синусов соответствует оси OY, отметим на числовой окружности точки A0 (1; 0) и Aπ (-1; 0), у которых координата y равна 0 (рисунок 1). Корнями уравнения sinx = 0 является множество чисел, которым соответствуют эти точки. Очевидно, что все числа этого множества кратны π. Записать такой результат можно следующим образом:
x = πn, где n ∈ Z (дословно x = πn, где n принадлежит множеству целых чисел).
2. Решение уравнения sin
x = -1.На числовой окружности отметим точку (рисунок 1). Это единственная точка на окружности у которой координата y равна -1, поэтому множество чисел, которым соответствует эта точка числовой окружности и есть корни уравнения sinx = -1. Одно из чисел этого множества: . Все остальные корни уравнения отличаются от на значение кратное 2π, а значит ответ можно записать в виде:
, где n ∈ Z.
3. Решение уравнения sin
x = 1.На числовой окружности с координатой y равной 1 можно отметить только одну точку (рисунок 1). Она соответствует множеству чисел, одно из которых . Это множество является корнями уравнения sinx = 1. Все остальные корни уравнения отличаются от на значение кратное 2π, а значит ответ можно записать в виде:
, где n ∈ Z.
4. Решение уравнения cos
x = 0.Так как ось косинусов связывают с осью OX, корнями уравнения cosx = 0 является множество чисел, которым соответствуют точки числовой окружности и , у которых координата x равна 0 (рисунок 1). одно из чисел этого множества. Все остальные корни отличаются от на значение кратное π, поэтому корнями уравнения cosx = 0 являются:
, где n ∈ Z.
5. Решение уравнения cos
x = -1.Корнями уравнения cosx = -1 является множество чисел, которым соответствует точка числовой окружности Aπ (-1; 0), у которой координата x равна 1 (рисунок 1). π — одно из чисел множества. Все остальные корни отличаются от π на значение кратное 2π, поэтому корнями уравнения cosx = -1 являются
x = π + 2πn, где n ∈ Z.
6. Решение уравнения cos
x = 1.Корнями уравнения cosx = 1 является множество чисел, которым соответствует точка числовой окружности A0 (1; 0), у которой координата x равна 1 (рисунок 1).
0 — одно из чисел множества. Все остальные корни отличаются от 0 на значение кратное 2π, поэтому корнями уравнения cosx = 1 являются: x = 2πn, где n ∈ Z.
Рисунок 27. Решение уравнения .
Отметим на числовой окружности точки с координатой y равной . Это точки и (рисунок 2). Эти точки соответствуют числам и , а значит, всем числа видам и , где n ∈ Z. Ответ можно записать в виде:
, где n ∈ Z.
8. Решение уравнения .
Отметим на числовой окружности точки с координатой y равной . Это точки и (рисунок 2). Эти точки соответствуют числам и , а значит, всем числа видам и , где n ∈ Z. Ответ можно записать в виде:
, где n ∈ Z.
9. Решение уравнения .
Отметим на числовой окружности точки с координатой y равной . Это точки и (рисунок 2). Эти точки соответствуют числам и , а значит, всем числам вида и , где n ∈ Z. Ответ можно записать в виде:
, где n ∈ Z.
10. Решение уравнения .
Отметим на числовой окружности точки с координатой y равной . Это точки и (рисунок 2). Эти точки соответствуют числам и , а значит, всем числам вида и , где n ∈ Z. Ответ можно записать в виде:
, где n ∈ Z.
11. Решение уравнения .
Отметим на числовой окружности точки с координатой y равной . Это точки и (рисунок 2). Эти точки соответствуют числам и , а значит, всем числам вида и , где n ∈ Z. Ответ можно записать в виде:
, где n ∈ Z.
12. Решение уравнения .
Отметим на числовой окружности точки с координатой y равной . Это точки и (рисунок 2). Эти точки соответствуют числам и , а значит, всем числам вида и , где n ∈ Z. Ответ можно записать в виде:
, где n ∈ Z.
Рисунок 313. Решение уравнения .
На числовой окружности у точек и координата x равна (рисунок 3).
Эти точки соответствуют числам и , а значит, всем числам вида и , где n ∈ Z. Ответ можно записать в виде:, где n ∈ Z.
14. Решение уравнения .
На числовой окружности у точек и координата x равна (рисунок 3). Эти точки соответствуют числам и , а значит, всем числам вида и где n ∈ Z. Ответ можно записать в виде:
, где n ∈ Z.
15. Решение уравнения .
На числовой окружности у точек и координата x равна (рисунок 3). Эти точки соответствуют числам и , а значит, всем числам вида и , где n ∈ Z. Ответ можно записать в виде:
, где n ∈ Z.
16. Решение уравнения .
На числовой окружности у точек и координата x равна (рисунок 3). Эти точки соответствуют числам и , а значит, всем числам вида и , где n ∈ Z. Ответ можно записать в виде:
, где n ∈ Z.
17. Решение уравнения .
На числовой окружности у точек и координата x равна (рисунок 3). Эти точки соответствуют числам и , а значит, всем числам вида и , где n ∈ Z. Ответ можно записать в виде:
, где n ∈ Z.
18. Решение уравнения .
На числовой окружности у точек и координата x равна (рисунок 3). Эти точки соответствуют числам и , а значит, всем числам вида и , где n ∈ Z. Ответ можно записать в виде:
, где n ∈ Z.
Урок 42. уравнение sin x = a — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №42. Уравнение sin x = a.
Перечень вопросов, рассматриваемых в теме:
1) Понятие арксинус числа;
2) Тождества, связанные с арксинусом;
3) Решение тригонометрических уравнений;
Глоссарий по теме
Арксинусом числа m называется такое число α, что: и .
Арксинус числа m обозначают: .
Заметим, что такой промежуток для α берется потому, что синус на отрезке принимает все свои значения ровно по одному разу.
Из определения следует, что для
С другой стороны, если и , то
Таким образом, получаем два простейших тождества для арксинуса.
- для любого m:
- для любого α: .
Основная литература:
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни. – 4-е изд. – М.: Просвещение, 2011. – 368 с.: ил. – ISBN 978-5-09-025401-4, с. 310-314.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
- Так как является абсциссой точки М(α) координатной окружности, то для решения уравнения нужно сначала найти на этой окружности точки, имеющие абсциссу m, то есть точки пересечения окружности с прямой x=m. Если , то таких точек нет, если , то такая точка одна, если , то таких точек две.
После отыскания этих точек нужно найти все такие числа α, которые соответствуют этим точкам. Множество таких чисел и будет решением уравнения .
Примеры и разбор решения заданий тренировочного модуля
Рассмотрим пример на вычисление арксинуса.
Пример.
Вычислить
Решение:
Так как и то
Ответ: .
Задание.
Вычислить .
Ответ: .
На рисунке показано, как связаны друг с другом числа m и
Из рисунка видно, что
Запишем теперь с помощью арксинуса решение уравнения
Одним из решений уравнения является число . Так как , то число также является решением данного уравнения.
Точка соответствует всем числам вида
Точка соответствует всем числам вида
Таким образом, решением уравнения sinα=m являются все числа вида
(*)
Пример.
Решим уравнение
Решение:
Так как , то по формуле (*) получаем:
.
Задание
Решите уравнение
Ответ: .
Рассмотрим решение более сложных уравнений с синусом.
- Рассмотрим решение уравнения .
Решение:
, поэтому
Отсюда , или
Тогда
Ответ: .
- Рассмотрим решение уравнения
Решение:
, поэтому .
Отсюда получаем:
Мы получили два квадратных уравнения с параметром k.
Запишем их решения.
Для того чтобы число х было действительным, дискриминант должен быть неотрицательным. То есть:
(1) и (2)
Неравенство (1) выполняется при , так как k – целое, то .
Неравенство (2) выполняется при , так как k – целое, то .
Таким образом, получаем, что при целых значениях исходное уравнение имеет две серии решений:
При уравнение имеет два решения:
Ответ: а) при ,
б) при ,
в) нет решений при .
- Рассмотрим решение уравнения
Решение:
Так как синусы равны, то их аргументы связаны соотношением:
Отсюда:
Первое уравнение имеет решение при или при .
Второе уравнение имеет решение при или при .
Таким образом:
Ответ:
а) при ,
б) , при при ,
в) нет решений при .
- Рассмотрим решение уравнения
Решение:
Уравнение равносильно совокупности уравнений:
или:
Решение первого уравнения: .
Решение второго уравнения: .
Ответ:
- Рассмотрим решение уравнения
Решение:
Выразим синус:
Имеем две серии решений:
.
Изобразим эти множества на тригонометрической окружности:
Можно записать эти две серии в виде одного равенства:
.
Ответ: .
Заметим, что для краткости решение тригонометрического уравнения sin x=m можно записать в виде:
Пример 1.
Рассмотрим решение уравнения .
Прямая пересекает тригонометрическую окружность в двух точках:
M(π/3) и N(2π/3).
Точка M(π/3) соответствует всем числа вида .
Точка N(2π/3) соответствует всем числа вида .
Таким образом, решение уравнения можно записать так:
.
Ответ: .
Пример 2.
Рассмотрим решение уравнения .
Прямая y=1 имеет с тригонометрической окружностью одну общую точку: .
Этой точке соответствуют все числа вида . Поэтому решение уравнения имеет вид .
Ответ: .
Пример 3.
Рассмотрим решение уравнения .
Прямая y=0 имеет с тригонометрической окружностью две общие точки: С() и К(π).
Поэтому решение уравнения можно записать так: .
Ответ: .
Задание.
Решите уравнение .
Ответ: .
2. Мы можем записать решение уравнение для любых табличных значений m. В тех случаях, когда мы не знаем значения аргумента, соответствующее значению m, чтобы уметь решать уравнение для произвольных значений m, введем понятие арксинуса.
1 sin x
Вы искали 1 sin x? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 1 sinx, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «1 sin x».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 1 sin x,1 sinx,1 sinx x,1 sinx это,1 синус х,sin x 1,sinx 1,sinx 1 решение,sinx 1 это,sinx x 1,sinx чему равен,икс синус,решение sinx 1,решите уравнение sinx 1,решить уравнение sinx 1,син х 1,синус икс равен 1,чему равен sin x.
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 1 sin x. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 1 sinx x).Где можно решить любую задачу по математике, а так же 1 sin x Онлайн?
Решить задачу 1 sin x вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
заказ решений на аукционе за минимальную цену с максимальным качеством
Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:
- решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
- написание лабораторных, рефератов и курсовых
- выполнение заданий по литературе, русскому или иностранному языку.
Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.
Объединение сервисов в одну систему
Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:
- Форум, где посетители обмениваются идеями и помогают друг другу
- Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
- Аукцион, где цена за товар или услугу определяется в результате торгов
- Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Принцип работы
Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.
Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.
Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.
Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.
За счет чего будет развиваться сервис
Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения.
Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.Второе – удобный сервис для заказчиков и для желающих заработать на решениях.
Преимущества для заказчиков
Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.
Преимущества для решающих задания
Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.
Преимущества для владельца сервиса
Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.
Что необходимо для создания сервиса
- Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.
- Выбрать платежную систему.
- Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
- Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.
Тригонометрических уравнений — Учебный материал для IIT JEE
Уравнение, включающее одно или несколько тригонометрических отношений неизвестного угла, называется тригонометрическим уравнением, например cos 2 x — 4 sin x = 1
Следует отметить, что тригонометрическое тождество выполняется для каждого значения неизвестного угла, тогда как тригонометрическое уравнение выполняется только для некоторых значений (конечных или бесконечных) неизвестного угла.
например sec 2 x — tan 2 x = 1 является тригонометрическим тождеством, поскольку оно выполняется для любого значения x Î R.
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКОГО УРАВНЕНИЯ
Значение неизвестного угла, которое удовлетворяет данному уравнению, называется решением уравнения, например грех q = ½ Þq = p / 6.
Общее решение
Поскольку тригонометрические функции являются периодическими функциями, решения тригонометрических уравнений могут быть обобщены с помощью периодичности тригонометрических функций. Решение, состоящее из всевозможных решений тригонометрического уравнения, называется его общим решением.
Мы используем следующие формулы для решения тригонометрических уравнений:
· грех q = 0 Þ q = np,
· cos q = 0 Þq = (2n + 1),
· tan q = 0 Þ q = np,
· sin q = sin a Þq = np + (–1) n a, где aÎ [–p / 2, p / 2]
· cos q = cos aÞq = 2np ± a, где aÎ [0, p]
· tan q = tan a Þ q = np + a, где aÎ (–p / 2, p / 2)
· sin 2 q = sin 2 a, cos 2 q = cos 2 a, tan 2 q = tan 2 aÞq = np ± a,
· грех q = 1 Þq = (4n + 1),
· cos q = 1 Þ q = 2np,
· cos q = –1 Þ q = (2n + 1) p,
· sin q = sin a и cos q = cos aÞ q = 2np + a.
Примечание:
· Повсюду в этой главе n принимается как целое число, если не указано иное.
· Общее решение должно быть дано, если решение не требуется в указанном интервале.
За главное значение угла принимается· a. Численно наименьший угол называется главным значением.
Метод определения основного значения
Предположим, мы должны найти главное значение, удовлетворяющее уравнению sin = -.
Так как sin отрицателен, будет в 3-м или 4-м квадранте. Мы можем подойти к 3-му или 4-му квадранту с двух сторон. Если мы возьмем направление против часовой стрелки, числовое значение угла будет больше чем. Если подойти к нему по часовой стрелке, угол будет численно меньше, чем. За главное значение мы должны взять численно наименьший угол.
Итак, для основной суммы:
1. Если угол находится в 1-м или 2-м квадранте, мы должны выбрать направление против часовой стрелки, а если угол, если угол находится в 3-м или 4-м квадранте, мы должны выбрать направление по часовой стрелке.
2. Главное значение никогда не может быть численно больше чем.
3. Главное значение всегда находится в первом круге (т.е. в первом повороте)
По вышеперечисленным критериям будет или. Среди этих двух наименьшее числовое значение. Отсюда главное значение удовлетворения уравнения sin = -.
Алгоритм нахождения главного аргумента:
Шаг 1: Сначала нарисуйте тригонометрический круг и отметьте квадрант, в котором может лежать угол.
Шаг 2: Выберите направление против часовой стрелки для 1-го и 2-го квадрантов и выберите направление по часовой стрелке для 3-го и 4-го квадрантов.
Шаг 3: Найдите угол при первом повороте.
Шаг 4: Выберите численно наименьший угол среди этих двух значений. Найденный таким образом угол будет главной величиной.
Шаг 5: В случае, если два угла, один с положительным знаком, а другой с отрицательным знаком, соответствуют численно наименьшему углу, то принято выбирать угол с положительным знаком в качестве главного значения.
Пример 1: Iftan = — 1, то будет находиться во 2-м или 4-м квадранте.
Для 2-го квадранта мы выберем против часовой стрелки, а для 4-го квадранта. мы выберем направление по часовой стрелке.
В первом кружке получены два значения и.
Среди этих двух наименьший угол. Следовательно, главное значение.
Пример 2: Если cos =, то будет лежать в квадранте 1 или 4 .
Для 1-го квадранта мы выберем направление против часовой стрелки, а для 4-го квадранта мы выберем направление по часовой стрелке.
В первом круге при этом находятся два значения и.
Оба и — имеют одинаковое числовое значение. В таком случае будет выбрано главное значение.
Рисунок 17: Решить кроватку (sinx + 3) = 1.
Решение: sinx + 3 = Þ Þ n = 1 Þ sinx =
Þ x = или
Иллюстрация 18: Если sin 5x + sin 3x + sin x = 0, то найдите значение x, отличное от нуля, лежащее между 0 £ x £ .
Решение: sin 5x + sin 3x + sin x = 0 Þ (sin 5x + sin x) + sin 3x = 0
Þ 2 sin 3x cos 2x + sin 3x = 0 Þ sin 3x (2 cos 2x + 1) = 0
Þ sin 3x = 0; cos 2x = — Þ 3x = np, 2x = 2np ±
Требуемое значение x равно.
Рисунок 19: Найти все острые углы a такие, что cos a cos 2 a cos 4 a = .
Решение: Дано, что cosa cos2a cos4a =
2sina cosa cos2a cos4a = Þ 2sin2a cos2a cos4a =
Þ 2sin4a cos4a = sinaÞ sin8a — sina = 0
Þ 2sincos = 0
Либо sin = 0 Þ Þa =
Для n = 0 a = 0, что не является решением.
Þa = n = 1, т.е. a =
или cos Þ = (2n + 1) Þa = (2n + 1) Þa =
Следовательно, a =.
Рисунок 20: Решить для x: .
Решение:
Þ
Þ
Þ ÞÞ
sin2x = ± 1 Þ 2x = (2n + 1) Þ x = (2n + 1), n I
ЦЕЛЬ
1: Общее значение q, удовлетворяющее обоим требованиям, составляет:
.(А) 2нп (Б) 2нп + 7п / 6
(К) нп + п / 4 (Д) 2нп + п / 4
Решение: сначала выясним, что q лежит между 0 и 360 °.
Так как Þq = 210 ° или 330 °
и Þq = 30 ° или 210 °
Следовательно, q = 210 ° или значение, удовлетворяющее обоим требованиям.
\ Общая стоимость
Следовательно (B) — правильный ответ.
2: Ö3 сек 20 ° — сек 20 ° =
(А) 1 (В) 2
(К) 3 (Г) 4
Решение: Дано =
=
Следовательно (D) — правильный ответ.
3: загар A + 2 загар 2A + 4 загар 4A + 8 кроватка 8A =
(A) Детская кроватка A (B) желто-коричневый 6A
(C) детская кроватка 4A (D) Ни один из этих
Раствор: tan A + 2 tan 2A + 4 tan 4A + 8 cot 8A
= tanA + 2tan2A + 4tan4A + 8= детская кроватка
Следовательно (А) — правильный ответ.
4: Значение греха 12 °. sin48 ° .sin54 ° =
(А) 1/8 (В) 1/6
(C) 1/4 (D) 1/2
Решение: sin 12 °. sin48 ° .sin54 ° =
=
=
=
=
Альтернативный метод
Пусть q = 12 °
sin 12 °.
sin48 ° .sin54 ° ==
Следовательно (А) — правильный ответ.
5: Наименьшее положительное значение x (в градусах), для которогозагар (x + 100 °) = загар (x + 50 °) загар x загар (x — 50 °) составляет:
(А) 30 ° (В) 45 °
(С) 60 ° (Г) 90 °
Решение: Отношение можно записать как
Þ
Þ
Þ Þ cos50 ° + 2sin (2x + 50 °) cos (2x + 50 °) = 0
cos50 ° + sin (4x + 100 °) = 0 Þ cos50 ° + cos (4x + 10 °) = 0
cos (2x + 30 °) cos (2x — 20 °) = 0 Þ x = 30 °, 55 °
Þ Наименьшее значение x = 30 °
Следовательно (А) — правильный ответ.
6. Наиболее общее значение q, удовлетворяющее 3 — 2cosq –4sinq –cos2q + sin2q = 0:
(А) 2нп (Б) 2нп + п / 2
(К) 4нп (Д) 2нп + п / 4
Решение: 3 — 2cos q — 4 sin q — cos 2q + sin 2q = 0
Þ 3 — 2cos q — 4 sin q — 1 + 2sin 2 q + 2sin q cos q = 0
Þ 2sin 2 q — 2cosq — 4sin q + 2sin q cos q + 2 = 0
Þ (sin 2 q — 2sin q + 1) + cos q (sinq — 1) = 0
Þ (sin q — 1) [sin q — 1 + cos q] = 0
либо sin q = 1
Þq = 2np + p / 2, где n Î I
или, sin q + cos q = 1
cos (q — p / 4) = cos (p / 4) Þq — p / 4 = 2np ± p / 4
Þ q = 2np, 2np + p / 2, где n Î I
Следовательно, q = 2np, 2np + p / 2.
Следовательно (A, B) — правильный ответ.
7: Если sinq = 3sin (q + 2a), то значение tan (q + a) + 2tana равно:
(А) 0 (В) 2
(К) 4 (Г) 1
Решение: дан sin q = 3sin (q + 2a)
Þ грех (д + а-а) = 3 син (д + а + а)
Þ sin (q + a) cosa — cos (q + a) sina
= 3sin (q + a) cosa + 3cos (q + a) sina
Þ –2sin (q + a) cosa = 4cos (q + a) sina
Þ
Þ загар (д + а) + 2тана = 0
Следовательно (А) — правильный ответ.
8: Минимальное значение 3tan 2 q + 12 cot 2 q составляет:
(А) 6 (В) 8
(C) 10 (D) Ни один из этих
Решение: A.
M. ³ G.M Þ (3tan 2 q +12 детская кроватка 2 q) ³ 6Þ 3 tan 2 q + 12cot 2 q имеет минимальное значение 12.
Следовательно (D) — правильный ответ.
9: Если A + B + C =, то значение tanA + tanB + tanC равно:
(А) 3 (В) 2
(C)> 3 (D)> 2
Решение: tan (A + B) = tan (- C)
или, = tanC
или, tanA + tanB + tanC = tana tanB tanC
[с А.M. G.M.]
или, tanA tanB tanC
или, A B C 27 [в кубе с обеих сторон]
или tanA tanB tanC 3
tanA + tanB + tanC 3.
Следовательно (А) — правильный ответ.
{2}x \neq 0 и 1-\sin x \neq 0.
0 — одно из чисел множества. Все остальные корни отличаются от 0 на значение кратное 2π, поэтому корнями уравнения cosx = 1 являются: 
Эти точки соответствуют числам и , а значит, всем числам вида и , где n ∈ Z. Ответ можно записать в виде: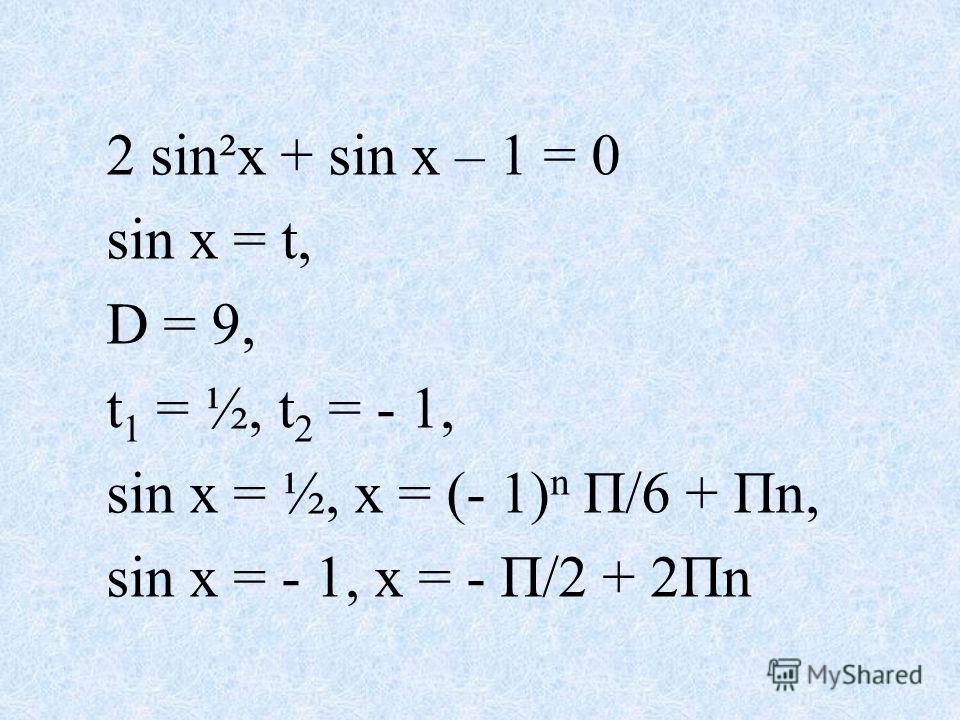
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 1 sin x. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 1 sinx x).
Причем, чем больше рейтинг пользователя, тем более значимым становится его голос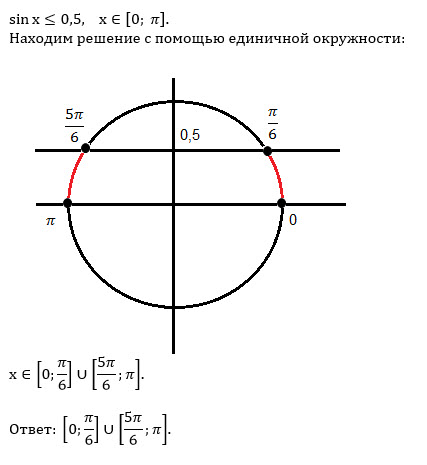
Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.
Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
sin48 ° .sin54 ° =
M. ³ G.M Þ (3tan 2 q +12 детская кроватка 2 q) ³ 6
уютный + sinx.siny.
tan 2q = 1 составляет:
2} x}
\ end {array} \ right.2} x}}}}
= {\ frac {1} {2} \ ln \ left | {\ frac {{1 + \ sin x}} {{1 — \ sin x}}} \ right | + {A_2}.}
\]
f (x) frac sqrt x 6 sqrt x 4
{2} -x-6} 🎉 Объявлен номер выигрышного билета Study-to-Win! Зайдите на панель управления билетами, чтобы узнать, выиграли ли вы! 🎉 Просмотр обозначения интервалов выигрышных билетов. Обозначение для представления интервала в виде пары чисел. Цифры — это конечные точки интервала. Скобки и / или квадратные скобки используются, чтобы показать, включены ли конечные точки. Например, [3, 8) — это интервал действительных чисел от 3 до 8, включая 3 и исключая 8. Вы также можете использовать различные математические функции: sin, cos, tan, sec, cot, csc, arcsin, arccos, arctan. , exp, ln, log2, log10, abs, sqrt и cubert.Когда функция y = f (x) имеет точку перегиба (изменяется от вогнутой вверх до вогнутой вниз), график ее производной y = f ‘(x) имеет максимум или … Список функций. Data Studio предоставляет ряд мощных функций, которые можно использовать в формулах вычисляемых полей. Более подробная информация о каждой функции, включая примеры, доступна в редакторе формул. Эта справка появится, когда вы начнете вводить формулу. Функция sqrt () определена в заголовочном файле math.h. Чтобы найти квадратный корень из типов данных int, float или long double, вы можете явно преобразовать тип в double с помощью оператора приведения.Вы также можете использовать функцию sqrtf () для работы с float и sqrtl () для работы с типом long double. Состав двух функций часто бывает трудно понять. Мы будем использовать пример задачи, включающей две функции, чтобы продемонстрировать, как легко найти композицию этих двух функций. непрерывная функция: если график f (x) имеет угол в точке x = a, то f (x) не дифференцируема в точке x = a. Другой способ, которым функция может иметь недифференцируемые точки, заключается в следующем: возьмите вашу любимую непрерывную функцию f (x) и ограничьте ее область определения некоторым отрезком [c; d].Ограничивая область значений
Калькулятор постарается максимально упростить результат. Обозначение функций. На предыдущем уроке вы узнали, как идентифицировать функцию, анализируя область и диапазон и используя тест вертикальной линии. Теперь мы собираемся взглянуть на обозначение функций и то, как они используются в алгебре. Типичное обозначение функции — f (x).Это читается как «f из x». Это НЕ означает, что f умножить на x. `f (x) = sqrt (x)` и `A = {1,4,16,36}`. Мы обнаружили, что вы используете AdBlock Plus или другое программное обеспечение для блокировки рекламы, которое препятствует полной загрузке страницы. После разблокировки веб-сайта обновите страницу и снова нажмите кнопку «Найти». Список функций. Data Studio предоставляет ряд мощных функций, которые можно использовать в формулах вычисляемых полей. Более подробная информация о каждой функции, включая примеры, доступна в редакторе формул.Эта справка появится, когда вы начнете вводить формулу. Начните изучение Графики Назначение радикальных функций. Изучите словарный запас, термины и многое другое с помощью What is the domain of y = sqrt x + 7 +5. (C) x> -7 x больше или равно. Опишите, как преобразуется график родительской функции y = sqrt x при построении графика y = -3sqrt x-6 График переводится на 6 единиц. Найдите область определения функции, определяемой уравнением. Граф кусочно-определенные функции. В разделе «Функции и обозначение функций» мы познакомились с концепциями домена и диапазона.2-3x \ text {.} \) Сформулируйте набор решений, используя интервальную нотацию, и при необходимости приблизьте. Область определения функции — это полный набор возможных значений независимой переменной. На простом английском языке это определение означает, что давайте вернемся к приведенному выше примеру, `y = sqrt (x + 4)`. Мы замечаем, что кривая находится либо на горизонтальной оси, либо над ней. Независимо от того, какое значение x мы попробуем, мы всегда получим …