Способы решения систем уравнений с двумя неизвестными

Линейные системы уравнений

Системы линейных уравнений. Метод подстановки 

+ показать

• Выражаем одну переменную через другую.

• Выраженную из одного уравнения переменную подставляем во второе уравнение. Получаем уравнение относительно одной переменной, которое и решаем.

• Опираясь на найденное значение одной переменной, находим значение второй, подставляя в оставшееся уравнение.

Решить систему уравнений: 

Решение: + показать

Системы линейных уравнений. Метод сложения 

+ показать

• Добиваемся, путем равносильных преобразований, наличия равных (или противоположных) коэффициентов при одной из неизвестных переменных в уравнениях.

• Вычитаем (или складываем) полученные уравнения с целью выхода на уравнение с одной неизвестной. 

• Решаем  полученное уравнение с одной неизвестной.

• Найденное значение одной переменной подставляем в любое из уравнений системы, находим значение второй.

1. Решить систему уравнений: 

Решение: + показать

Складываем уравнения системы, заменяя результатом одно из уравнений, оставляя другое.

Ответ:  

2. Решить систему уравнений: 

Решение: + показать

Нелинейные системы уравнений

Системы уравнений, сводящихся к линейным

1. Решить систему уравнений: 

Решение: + показать

Можно сделать замену и Тогда выходим на систему линейных уравнений:

Систему можно решить методом сложения, например.

Но приведем решение без замены.

Умножим первое уравнение системы на

, второе – на и произведем сложение полученных уравнений, оставим при этом в системе, например, первое уравнение исходной системы.

Ответ:  

2. Решить систему уравнений: 

Решение: + показать

Можно сделать замену и выйти на систему линейных уравнений:

Приведем решение без замены.

Выражаем из второго уравнения системы и подставляем в первое.

Ответ:  

Нелинейные системы уравнений. Метод подстановки

Решить систему уравнений: 

Решение: + показать

Выражаем из первого уравнения системы и подставляем во второе.

Ответ:  

Нелинейные системы уравнений. Метод сложения

Решить систему уравнений: 

Решение: + показать

Складываем уравнения системы, заменяя результатом одно из уравнений, оставляя другое.

Ответ:  

Нелинейные системы уравнений. Метод почленного умножения (деления)

1. Решить систему уравнений: 

Решение: + показать

Производим деление первой строки на вторую, оставляем в системе вторую строку без изменений.

Ответ:  

Симметрические системы. Метод введения переменной

Симметрическая система – система, все уравнения которой симметрические. Симметрическое уравнение от двух переменных и – уравнение, которое не изменяется при замене на и на .

Для таких систем удобно использовать замену  

Решить систему уравнений: 

Решение: + показать

При замене  приходим к следующей системе

 которую будем решать способом подстановки:

Производим обратную замену:

Ответ:

Системы однородных уравнений и приводящиеся к ним системы

Однородным уравнением с двумя неизвестными  будем называть уравнение вида

1. Решить систему уравнений: 

Решение: + показать

2. Решить систему уравнений: 

Решение: + показать

Применим прежде к системе метод сложения. После чего выйдем на однородное уравнение.

Ответ:

Графический метод решения систем уравнений

1. Решите графически систему уравнений: 

Решение: + показать

Выразим в обеих строках системы через :

Первое уравнение системы задает прямую, второе – гиперболу. Строим графики в одной системе координат, находим координаты точек пересечения графиков.

Ответ: 

2. Решите графически систему уравнений: 

Решение: + показать

3. Решите графически систему уравнений: 

Решение: + показать

---

Задания для самостоятельной работы

+ показать

Решите системы уравнений:

1.

Ответ:

2. 

Ответ:

3. 

Ответ:

4. 

Ответ:

5. 

Ответ:

6. 

Ответ:

7. 

Ответ:

8. 

Ответ:

Решите графически системы уравнений:

9. 

Ответ:

10. 

Ответ:

egemaximum.ru

Основные методы решения систем повышенной сложности. Видеоурок. Алгебра 9 Класс

На этом уроке мы продолжим изучение всех трех основных методов решения систем уравнений и их комбинаций на примере решения систем повышенной сложности. А также рассмотрим некоторые специфические приемы для упрощения различных типов систем.

Выбор метода решения системы зависит от её специфики. Основными являются стандартные методы – метод подстановки, метод алгебраического сложения, метод введения новых переменных. Возможны иные методы и их комбинации. Рассмотрим их на примерах.

Пример 1. Решить систему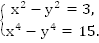

Решение: Специфика данной системы в том, что второе уравнение раскладывается на множители

 

Мы получили систему, линейную относительно 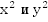. Исходную систему упростили методом подстановки. Полученную систему решаем методом алгебраического сложения.

 

 

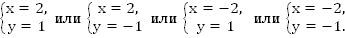
Мы решили систему комбинацией методов подстановки и алгебраического сложения.

Ответ: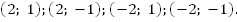

Пример 2. Решить систему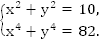

Решение: Можно сделать замену переменной и тем самым понизить степень уравнения. Но мы применим метод подстановки, выразим

 

 

 

 

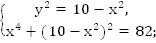
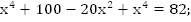
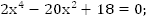
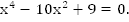
Получили биквадратное уравнение. По теореме Виета 

 

 

 

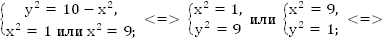
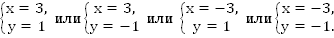
Ответ: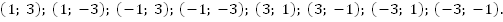

Пример 3. Решить систему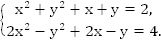

interneturok.ru

Как решается система уравнений? Методы решения систем уравнения.

Методы решения систем уравнения.

Разберем два вида решения систем уравнения:

1. Решение системы методом подстановки.
2. Решение системы методом почленного сложения (вычитания) уравнений системы.

Для того чтобы решить систему уравнений методом подстановки нужно следовать простому алгоритму:
1. Выражаем. Из любого уравнения выражаем одну переменную.
2. Подставляем. Подставляем в другое уравнение вместо выраженной переменной, полученное значение.
3. Решаем полученное уравнение с одной переменной. Находим решение системы.

Чтобы решить систему методом почленного сложения (вычитания) нужно:
1.Выбрать переменную у которой будем делать одинаковые коэффициенты.
2.Складываем или вычитаем уравнения, в итоге получаем уравнение с одной переменной.
3. Решаем полученное линейное уравнение. Находим решение системы.

Решением системы являются точки пересечения графиков функции.

Рассмотрим подробно на примерах решение систем.

Пример №1:

Решим методом подстановки

Решение системы уравнений методом подстановки

2x+5y=1 (1 уравнение)
x-10y=3 (2 уравнение)

1. Выражаем
Видно что во втором уравнении имеется переменная x с коэффициентом 1,отсюда получается что легче всего выразить переменную x из второго уравнения.
x=3+10y

2.После того как выразили подставляем в первое уравнение 3+10y вместо переменной x.
2(3+10y)+5y=1

3.Решаем полученное уравнение с одной переменной.
2(3+10y)+5y=1 (раскрываем скобки )
6+20y+5y=1
25y=1-6
25y=-5 |: (25)
y=-5:25
y=-0,2

Решением системы уравнения является точки пересечений графиков, следовательно нам нужно найти x и у, потому что точка пересечения состоит их x и y.Найдем x, в первом пункте где мы выражали туда подставляем y.
x=3+10y
x=3+10*(-0,2)=1

Точки принято записывать на первом месте пишем переменную x, а на втором переменную y.
Ответ: (1; -0,2)

Пример №2:

Решим методом почленного сложения (вычитания).

Решение системы уравнений методом сложения

3x-2y=1 (1 уравнение)
2x-3y=-10 (2 уравнение)

1.Выбираем переменную, допустим, выбираем x. В первом уравнении у переменной x коэффициент 3, во втором 2. Нужно сделать коэффициенты одинаковыми, для этого мы имеем право домножить уравнения или поделить на любое число. Первое уравнение домножаем на 2, а второе на 3 и получим общий коэффициент 6.

3x-2y=1 |*2
6x-4y=2

2x-3y=-10 |*3
6x-9y=-30

2.Из первого уравнения вычтем второе, чтобы избавиться от переменной x.Решаем линейное уравнение.
__6x-4y=2
   6x-9y=-30
-4y+9y=2+30

5y=32 | :5
y=6,4

3.Находим x. Подставляем в любое из уравнений найденный y, допустим в первое уравнение.
3x-2y=1
3x-2*6,4=1
3x-12,8=1
3x=1+12,8
3x=13,8 |:3
x=4,6

Точкой пересечения будет x=4,6; y=6,4
Ответ: (4,6; 6,4)

Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно. Без шуток. ЗДЕСЬ

tutomath.ru

Системы линейных уравнений с двумя переменными (Г.Г.Гаицгори)

Мы уже умеем решать линейные уравнения. Займёмся решением систем линейных уравнений, а именно таких систем, в которых есть две переменные, например:

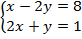
Есть два основных метода решения любых систем уравнений:

1. Метод подстановки.
2. Метод домножения и сложения.

Идея этого метода в следующем: пусть мы знаем значение одной из переменных. Тогда, чтобы найти вторую переменную, нужно подставить значение первой переменной в любое из уравнений. В результате получается обычное линейное уравнение, которое мы уже умеем решать.

Пример 1.

Рассмотрим в качестве примера систему уравнений:

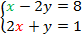
Если нам скажут, что , то найти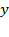

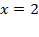 не составит труда – подставим значение , например, во второе уравнение: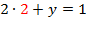

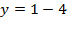
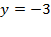
Такой же результат получится, если подставить известное значение 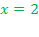 в первое уравнение:

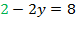
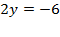
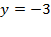
Т. е. мы подставляем известное значение переменной, получаем линейное уравнение с одной переменной, которое мы уже умеем решать.

Но что делать, если ни одно из значений переменных нам не известно?

Предположим, что мы уже знаем значение переменной 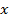. Тогда из первого уравнения мы бы получили такое значение второй переменной:

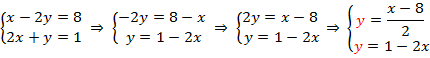
Но значение переменной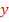

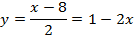
 в обоих уравнениях должно получиться одинаковым:

Или:

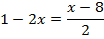
Решим это линейное уравнение – домножим обе части уравнения на 2:

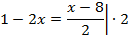
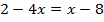
Перенесем все слагаемые с переменной в одну часть уравнения, а без неё – в другую:

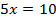
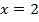
Получим решение системы:

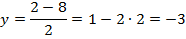
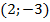
Ответ: .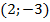

Каждый раз выражать переменную из двух уравнений необязательно.

Из первого уравнения мы получили:

Перепишем систему в эквивалентном виде: 

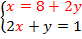
Говорят: «мы выразили переменную  из первого уравнения».

Как мы уже говорили, раз уравнения объединены в систему, то в каждом из этих уравнений речь идёт об одних и тех же 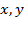. Значит, информацию об  из первого уравнения можно использовать во втором.

Именно поэтому метод называется «методом подстановки»: информацию из одного уравнения подставляем в другое. 

Заменим во втором уравнении  на эквивалентное выражение из первого уравнения. 

Получим:

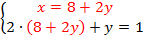
Дальше всё то же самое: получили линейное уравнение с одной переменной 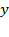, которое мы уже умеем решать:

---

 

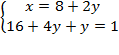
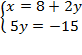
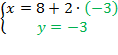
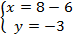
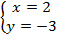
Как записывать ответ

 Рассмотрим систему уравнений:

Её решением будет пара чисел: 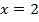 и .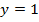

Записать этот ответ можно по-разному:

Ответ: .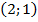

Ответ: .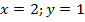

Ответ: .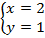

Во всех случаях понятно, о чем идет речь. Но все же запись 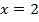 является уравнением (так как содержит знак равенства).

Решением системы является пара чисел, а не два уравнения (как во второй и третьей записях).

Так что формально верная запись ответа здесь только одна – в виде пары чисел .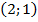

---

Метод подстановки, когда одно условие подставляется в другое, мы часто используем в жизни. При желании можно изучить пример использования этого принципа при поиске человека в социальных сетях.

---

 

Поиск в социальных сетях

Пример 1.

Представьте такую ситуацию. Вы в гостях у своего друга Пети познакомились с девочкой Женей и, уже вернувшись домой, решили найти её в социальной сети.

Вот что вы знаете:

1. Она подруга Пети.
2. Она тоже учится в 7 классе, хоть и в другой школе.
3. Её зовут Женя.
4. Она тоже живёт в Москве.

Каждое из этих условий в отдельности имеет очень много «решений». Друзей у Пети много, 7-классниц огромное количество, как и девочек с именем Женя.

Но так как все эти условия относятся к одному человеку, то это система условий:

Решением системы является такой человек, который соответствует сразу всем условиям. И решаем эту систему мы методом подстановки. Выбираем одно условие, затем в него подставляем другое (из всех решений, удовлетворяющих первому условию, выбираем только те, которые также удовлетворяют второму) и т. д.

Итак:

Открываете страничку Пети и выбираете список всех его друзей. Это решения первого условия. Предположим, их 256 (см. рис. 1):

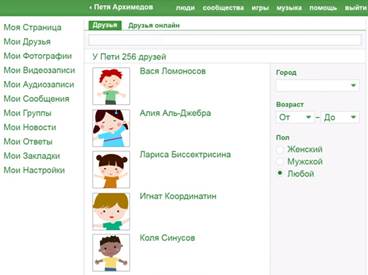
Рис. 1. Друзья Пети

Подставляем сюда второе условие. Раз она учится в 7 классе, то её возраст от 12 до 14 лет. Количество решений уменьшилось до 132. (см. рис. 2):

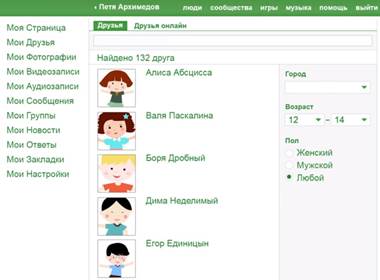
Рис. 2. Друзья Пети в возрасте от 12 до 14 лет

Добавляем условие, которое мы изначально забыли, но нам его подсказала сеть, – пол. Женский. Осталось 54. (см. рис. 3):

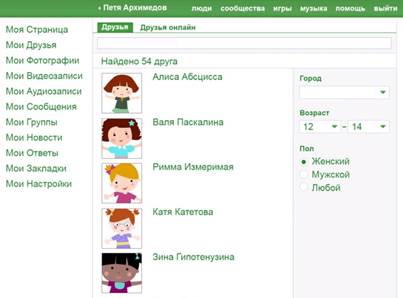
Рис. 3. Девочки – подруги Пети в возрасте от 12 до 14 лет

Ещё одно условие – город проживания Москва. Осталось 37 человек (см. рис. 4):

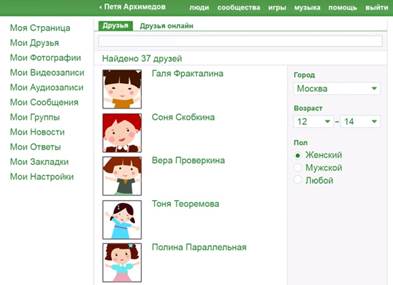
Рис. 4. Девочки – подруги Пети в возрасте от 12 до 14 лет, живущие в Москве

Наконец, вводим имя девочки – Женя. Осталось 2 человека (см. рис. 5):

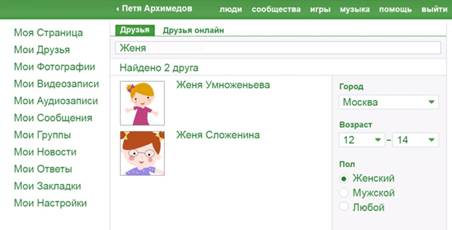
Рис. 5. Подруги Пети по имени Женя в возрасте от 12 до 14 лет, живущие в Москве

Итак, система имеет два решения, из них несложно выбрать нужного нам человека.

Мы последовательно в одно условие подставляли другое, и так 4 раза, т. е. решали задачу методом подстановки.

---

Сформулируем алгоритм решения системы уравнений методом подстановки:

1. Выразить одну (любую) переменную из любого уравнения через другую переменную.
2. Подставить полученное выражение в другое уравнение.
3. Решить уравнение с одной переменной.
4. Найденное значение переменной подставить в первое уравнение и найти значение второй переменной.

---

 

Практика. Метод подстановки

Пример 1. Решить систему уравнений:

Решение:

Выразим  из первого уравнения: 

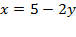
И подставим во второе уравнение:

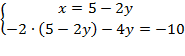
Решим второе уравнение – для начала раскроем скобки:

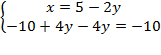
Таким образом, получим следующую систему:

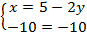
Во втором уравнении получили очевидный факт – верное равенство. Эта запись не несёт никакой полезной информации для нас, мы её можем исключить. Тогда останется только первое уравнение.

Система эквивалентна одному уравнению: 

,

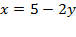а её решение – это решение данного уравнения, которых бесконечно много.

Итак, если после подстановки мы получили верное числовое равенство, то система имеет бесконечно много решений.

Ответ: бесконечно много решений.

 

Пример 2. Решить систему уравнений:

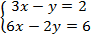
Решение:

Выразим 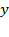 из первого уравнения:

Подставим выражение во второе уравнение:

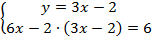
Решим полученное уравнение с одной переменной – раскроем скобки, используя распределительный закон, и получим:

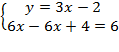
Таким образом, получим следующую систему:

Получили неверное числовое равенство. Т. е. уравнение, полученное после подстановки, не имеет решения. Задаем себе вопрос: при каких значениях переменных  и : ?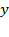

Не существует таких значений. Делаем вывод: система не имеет решений.

Таким образом, если после подстановки мы получили неверное числовое равенство, то решений у системы нет.

Ответ: нет решений.

 

Пример 3. Решить систему уравнений:

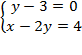
Решение:

Одно из уравнений содержит только одну переменную. Задача становится только проще. Выражаем 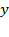 и подставляем во второе уравнение:

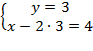
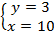
Получаем решение: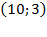

Ответ: .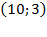

---

 

Пусть у нас есть двое уравновешенных весов. Если мы пересыпаем все с левых чаш на одну чашу других весов, а с правых – на вторую, то весы также будут уравновешены. Т. е. если сложить правые и левые части верных равенств, мы также получим верное равенство.

Как мы можем использовать это для решения систем линейных уравнений? Можно сложить уравнения системы. Зачем нам это делать? Если мы в результате избавимся от одной переменной, то получим линейное уравнение с одной переменной, которое мы умеем решать.

Пример 2. Решить систему уравнений:

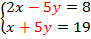
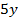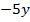Мы видим, что уравнения содержат слагаемые  и , которые взаимно уничтожатся при сложении.

Сложим отдельно левые и правые части уравнений системы:

Получаем:

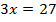
Мы получили линейное уравнение с одной переменной, решим его:

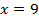
Теперь подставим найденное значение 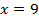 в любое из уравнений системы, например в первое, и найдем :

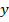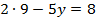
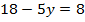
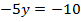
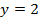
Получаем решение:

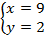
Ответ: .

 

В этом и состоит идея метода – исключить сложением одну из переменных.

Конечно, мы рассмотрели простой пример. Редко бывает, чтобы в двух уравнениях были слагаемые с одинаковыми (по модулю) коэффициентами. Поэтому нужно научиться приводить любую систему уравнений к эквивалентному виду, содержащему такие слагаемые. Как это сделать?

Вспомним, что при умножении и делении обеих частей уравнения на одно и то же ненулевое число получается эквивалентное уравнение, содержащее ту же информацию (с теми же корнями).

Пример 3. Решить систему уравнений:

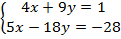
Умножим обе части первого уравнения на :

Получим:

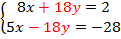
Заметим, что уравнения содержат слагаемые 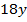 и 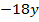. Теперь уже можно воспользоваться методом сложения:

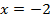
Подставим найденное значение 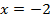 в первое уравнение:

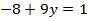
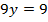
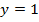
Получаем решение:

Ответ: .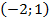

Сформулируем алгоритм решения систему уравнений методом домножения и сложения:

1. Преобразовать уравнения системы так, чтобы в результате сложения получилось уравнение с одной переменной (если необходимо).
2. Сложить отдельно левые и правые части уравнений системы.
3. Решить уравнение с одной переменной.
4. Найденное значение переменной подставить в любое уравнение и найти значение второй переменной.

---

 

Практика. Метод домножения и сложения 

interneturok.ru

Метод сложения в системе уравнений

23 октября 2015

Этим видео я начинаю цикл уроков, посвящённых системам уравнений. Сегодня мы поговорим о решении систем линейных уравнений методом сложения — это один из самых простых способов, но одновременно и один из самых эффективных.

Способ сложения состоит из трёх простых шагов:

1. Посмотреть на систему и выбрать переменную, у которой в каждом уравнении стоят одинаковые (либо противоположные) коэффициенты;
2. Выполнить алгебраическое вычитание (для противоположных чисел — сложение) уравнений друг из друга, после чего привести подобные слагаемые;
3. Решить новое уравнение, получившееся после второго шага.

Если всё сделать правильно, то на выходе мы получим одно-единственное уравнение с одной переменной — решить его не составит труда. Затем останется лишь подставить найденный корень в исходную система и получить окончательный ответ.

Однако на практике всё не так просто. Причин тому несколько:

• Решение уравнений способом сложения подразумевает, что во всех строчках должны присутствовать переменные с одинаковыми/противоположными коэффициентами. А что делать, если это требование не выполняется?
• Далеко не всегда после сложения/вычитания уравнений указанным способом мы получим красивую конструкцию, которая легко решается. Возможно ли как-то упростить выкладки и ускорить вычисления?

Чтобы получить ответ на эти вопросы, а заодно разобраться с несколькими дополнительными тонкостями, на которых «заваливаются» многие ученики, смотрите мой видеоурок:

Этим уроком мы начинаем цикл лекций, посвященный системам уравнений. А начнем мы из самых простых из них, а именно из те, которые содержат два уравнения и две переменных. Каждое из них будет являться линейным.

Системы — это материал 7-го класса, но этот урок также будет полезен старшеклассникам, которые хотят освежить свои знания в этой теме.

Вообще, существует два метода решения подобных систем:

1. Метод сложения;
2. Метод выражения одной переменной через другую.

Сегодня мы займемся именно первым методом — будем применять способ вычитания и сложения. Но для этого нужно понимать следующий факт: как только у вас есть два или более уравнений, вы вправе взять любые два из них и сложить друг с другом. Складываются они почленно, т.е. «иксы» складываются с «иксами» и приводятся подобные, «игреки» с «игреками» — вновь приводятся подобные, а то, что стоит справа от знака равенства, также складывается друг с другом, и там тоже приводятся подобные.

Результатами подобных махинаций будет новое уравнение, которое, если и имеет корни, то они обязательно будут находиться среди корней исходного уравнения. Поэтому наша задача — сделать вычитание или сложение таким образом, чтобы или $x$, или $y$ исчез.

Как этого добиться и каким инструментом для этого пользоваться — об этом мы сейчас и поговорим.

Решение легких задач с применением способа сложения

Итак, учимся применять метод сложения на примере двух простейших выражений.

Задача № 1

\[\left\{ \begin{align}& 5x-4y=22 \\& 7x+4y=2 \\\end{align} \right.\]

Заметим, что у $y$ коэффициент в первом уравнении $-4$, а во втором — $+4$. Они взаимно противоположны, поэтому логично предположить, что если мы их сложим, то в полученной сумме «игреки» взаимно уничтожатся. Складываем и получаем:

\[12x=24\]

Решаем простейшую конструкцию:

\[x=2\]

Прекрасно, мы нашли «икс». Что теперь с ним делать? Мы вправе подставить его в любое из уравнений. Подставим в первое:

\[5\cdot 2-4y=22\]

\[10-4y=22\]

Решаем:

\[-4y=22-10\]

\[-4y=12\left| :\left( -4 \right) \right.\]

\[y=-3\]

Ответ: $\left( 2;-3 \right)$.

Задача № 2

\[\left\{ \begin{align}& -6x+y=21 \\& 6x-11y=-51 \\\end{align} \right.\]

Здесь полностью аналогичная ситуация, только уже с «иксами». Сложим их:

\[0-10y=-30\]

Мы получили простейшее линейное уравнение, давайте решим его:

\[y=3\]

Теперь давайте найдем $x$:

\[6x-11\cdot 3=-5\]

\[6x=-51+33\]

\[6x=-18\]

\[x=-3\]

Ответ: $\left( -3;3 \right)$.

Важные моменты

Итак, только что мы решили две простейших системы линейных уравнений методом сложения. Еще раз ключевые моменты:

1. Если есть противоположные коэффициенты при одной из переменных, то необходимо сложить все переменные в уравнении. В этом случае одна из них уничтожится.
2. Найденную переменную подставляем в любое из уравнений системы, чтобы найти вторую.
3. Окончательную запись ответа можно представить по-разному. Например, так — $x=…,y=…$, или в виде координаты точек — $\left( …;… \right)$. Второй вариант предпочтительней. Главное помнить, что первой координатой идет $x$, а второй — $y$.
4. Правило записывать ответ в виде координат точки применимо не всегда. Например, его нельзя использовать, когда в роли переменных выступают не $x$ и $y$, а, к примеру, $a$ и $b$.

В следующих задачах мы рассмотрим прием вычитания, когда коэффициенты не противоположны.

Решение легких задач с применением метода вычитания

Задача № 1

\[\left\{ \begin{align}& 10x-3y=5 \\& -6x-3y=-27 \\\end{align} \right.\]

Заметим, что противоположных коэффициентов здесь нет, однако есть одинаковые. Поэтому вычитаем из первого уравнения второе:

\[10x-\left( -6x \right)-3y-\left( -3y \right)=5-\left( -27 \right)\]

\[10x+6x-3y+3y=5+27\]

\[16x=32\left| :16 \right.\]

\[x=2\]

Теперь подставляем значение $x$ в любое из уравнений системы. Давайте в первое:

\[10\cdot 2-3y=5\]

\[20-5=3y\]

\[15=3y\]

\[y=5\]

Ответ: $\left( 2;5 \right)$.

Задача № 2

\[\left\{ \begin{align}& 5x+4y=-22 \\& 5x-2y=-4 \\\end{align} \right.\]

Мы снова видим одинаковый коэффициент $5$ при $x$ в первом и во втором уравнении. Поэтому логично предположить, что нужно из первого уравнения вычесть второе:

\[0+6y=-22+4\]

\[6y=-18\left| :6 \right.\]

\[y=-3\]

Одну переменную мы вычислили. Теперь давайте найдем вторую, например, подставив значение $y$ во вторую конструкцию:

\[5x-2\cdot \left( -3 \right)=-4\]

\[5x+6=-4\]

\[5x=-4-6\]

\[5x=-10\left| :5 \right.\]

\[x=-2\]

Ответ: $\left( -3;-2 \right)$.

Нюансы решения

Итак, что мы видим? По существу, схема ничем не отличается от решения предыдущих систем. Отличие только в том, что мы уравнения не складываем, а вычитаем. Мы проводим алгебраическое вычитание.

Другими словами, как только вы видите систему, состоящую из двух уравнений с двумя неизвестными, первое, на что вам необходимо посмотреть — это на коэффициенты. Если они где-либо одинаковые, уравнения вычитаются, а если они противоположные — применяется метод сложения. Всегда это делается для того, чтобы одна из них исчезла, и в итогом уравнении, которая осталась после вычитания, осталась бы только одна переменная.

Разумеется, это еще не все. Сейчас мы рассмотрим системы, в которых уравнения вообще несогласованны. Т.е. нет в них таких переменных, которые были бы либо одинаковые, либо противоположные. В этом случае для решения таких систем применяется дополнительный прием, а именно домножение каждого из уравнений на специальный коэффициент. Как найти его и как решать вообще такие системы, сейчас мы об этом и поговорим.

Решение задач методом домножения на коэффициент

Пример № 1

\[\left\{ \begin{align}& 5x-9y=38 \\& 3x+2y=8 \\\end{align} \right.\]

Мы видим, что ни при $x$, ни при $y$ коэффициенты не только не взаимно противоположны, но и вообще никак не соотносятся с другим уравнением. Эти коэффициенты никак не исчезнут, даже если мы сложим или вычтем уравнения друг из друга. Поэтому необходимо применить домножение. Давайте попытаемся избавиться от переменной $y$. Для этого мы домножим первое уравнение на коэффициент при $y$ из второго уравнения, а второе уравнение — при $y$ из первого уравнения, при этом не трогая знак. Умножаем и получаем новую систему:

\[\left\{ \begin{align}& 10x-18y=76 \\& 27x+18y=72 \\\end{align} \right.\]

Смотрим на нее: при $y$ противоположные коэффициенты. В такой ситуации необходимо применять метод сложения. Сложим:

\[37x=148\]

\[x=4\]

Теперь необходимо найти $y$. Для этого подставим $x$ в первое выражение:

\[5\cdot 4-9y=38\]

\[20-9y=38\]

\[-9y=18\left| :\left( -9 \right) \right.\]

\[y=-2\]

Ответ: $\left( 4;-2 \right)$.

Пример № 2

\[\left\{ \begin{align}& 11x+4y=-18 \\& 13x-6y=-32 \\\end{align} \right.\]

Вновь коэффициенты ни при одной из переменных не согласованы. Домножим на коэффициенты при $y$:

\[\left\{ \begin{align}& 11x+4y=-18\left| 6 \right. \\& 13x-6y=-32\left| 4 \right. \\\end{align} \right.\]

\[\left\{ \begin{align}& 66x+24y=-108 \\& 52x-24y=-128 \\\end{align} \right.\]

Наша новая система равносильна предыдущей, однако коэффициенты при $y$ являются взаимно противоположными, и поэтому здесь легко применить метод сложения:

\[118x=-136\]

\[x=-2\]

Теперь найдем $y$, подставив $x$ в первое уравнение:

\[11\cdot \left( -2 \right)+4y=-18\]

\[-22+4y=-18\]

\[4y=4\]

\[y=1\]

Ответ: $\left( -2;1 \right)$.

Нюансы решения

Ключевое правило здесь следующее: всегда умножаем лишь на положительные числа — это избавит вас от глупых и обидных ошибок, связанных с изменением знаков. А вообще, схема решения довольно проста:

1. Смотрим на систему и анализируем каждое уравнение.
2. Если мы видим, что ни при $y$, ни при $x$ коэффициенты не согласованы, т.е. они не являются ни равными, ни противоположными, то делаем следующее: выбираем переменную, от которой нужно избавиться, а затем смотрим на коэффициенты при этих уравнениях. Если первое уравнение домножим на коэффициент из второго, а второе, соответственное, домножим на коэффициент из первого, то в итоге мы получим систему, которая полностью равносильна предыдущей, и коэффициенты при $y$ будут согласованы. Все наши действия или преобразования направлены лишь на то, чтобы получить одну переменную в одном уравнении.
3. Находим одну переменную.
4. Подставляем найденную переменную в одно из двух уравнений системы и находим вторую.
5. Записываем ответ в виде координаты точек, если у нас переменные $x$ и $y$.

Но даже в таком нехитром алгоритме есть свои тонкости, например, коэффициенты при $x$ или $y$ могут быть дробями и прочими «некрасивыми» числами. Эти случаи мы сейчас рассмотрим отдельно, потому что в них можно действовать несколько иначе, чем по стандартному алгоритму.

Решение задач с дробными числами

Пример № 1

\[\left\{ \begin{align}& 4m-3n=32 \\& 0,8m+2,5n=-6 \\\end{align} \right.\]

Для начала заметим, что во втором уравнении присутствуют дроби. Но заметим, что можно разделить $4$ на $0,8$. Получим $5$. Давайте второе уравнение домножим на $5$:

\[\left\{ \begin{align}& 4m-3n=32 \\& 4m+12,5m=-30 \\\end{align} \right.\]

Вычитаем уравнения друг из друга:

\[0-15,5n=62\]

\[n=\frac{65}{-15,5}=-\frac{124}{31}=-4\]

$n$ мы нашли, теперь посчитаем $m$:

\[4m-3\cdot \left( -4 \right)=32\]

\[4m+12=32\]

\[4m=20\]

\[m=5\]

Ответ: $n=-4;m=5$

Пример № 2

\[\left\{ \begin{align}& 2,5p+1,5k=-13\left| 4 \right. \\& 2p-5k=2\left| 5 \right. \\\end{align} \right.\]

Здесь, как и в предыдущей системе, присутствуют дробные коэффициенты, однако ни при одной из переменных коэффициенты в целое число раз друг в друга не укладываются. Поэтому используем стандартный алгоритм. Избавится от $p$:

\[\left\{ \begin{align}& 5p+3k=-26 \\& 5p-12,5k=5 \\\end{align} \right.\]

Применяем метод вычитания:

\[15,5k=-31\]

\[k=-\frac{31}{15,5}=-\frac{62}{31}=-2\]

Давайте найдем $p$, подставив $k$ во вторую конструкцию:

\[2p-5\cdot \left( -2 \right)=2\]

\[2p-5\cdot \left( -2 \right)=2\]

\[2p+10=2\]

\[2p=-8\]

\[p=-4\]

Ответ: $p=-4;k=-2$.

Нюансы решения

Вот и вся оптимизация. В первом уравнении мы не стали домножать вообще ни на что, а второе уравнение домножили на $5$. В итоге мы получили согласованное и даже одинаковое уравнение при первой переменной. Во второй системе мы действовали по стандартному алгоритму.

Но как найти числа, на которые необходимо домножать уравнения? Ведь если домножать на дробные числа, мы получим новые дроби. Поэтому дроби необходимо домножить на число, которое бы дало новое целое число, а уже после этого домножать переменные на коэффициенты, следуя стандартному алгоритму.

В заключение хотел бы обратить ваше внимание на формат записи ответа. Как я уже и говорил, поскольку здесь у нас тут не $x$ и $y$, а другие значения, мы пользуемся нестандартной записью вида:

\[n=-4\]

\[m=5\]

Решение сложных систем уравнений

В качестве заключительного аккорда к сегодняшнему видеоуроку давайте рассмотрим пару действительно сложных систем. Их сложность будет состоять в том, что в них и слева, и справа будут стоять переменные. Поэтому для их решения нам придется применять предварительную обработку.

Система № 1

\[\left\{ \begin{align}& 3\left( 2x-y \right)+5=-2\left( x+3y \right)+4 \\& 6\left( y+1 \right)-1=5\left( 2x-1 \right)+8 \\\end{align} \right.\]

Каждое уравнение несет в себе определенную сложность. Поэтому с каждым выражением давайте поступим как с обычной линейной конструкцией.

Первая:

\[3\left( 2x-y \right)+5=-2\left( x+3y \right)+4\]

\[6x-3y+5=-2x-6y+4\]

\[6x-3y+2x+6y=4-5\]

\[8x+3y=-1\]

Вторая:

\[6\left( y+1 \right)-1=5\left( 2x-1 \right)+8\]

\[6y+6-1=10x-5+8\]

\[6y-10x=-5+8-6+1\]

\[-10x+6y=-2\]

Итого мы получим окончательную систему, которая равносильна исходной:

\[\left\{ \begin{align}& 8x+3y=-1 \\& -10x+6y=-2 \\\end{align} \right.\]

Посмотрим на коэффициенты при $y$: $3$ укладывается в $6$ два раза, поэтому домножим первое уравнение на $2$:

\[\left\{ \begin{align}& 16x+6y=-2 \\& -10+6y=-2 \\\end{align} \right.\]

Коэффициенты при $y$ теперь равны, поэтому вычитаем из первого уравнения второе: $$

\[26x=0\]

\[x=0\]

Теперь найдем $y$:

\[3y=-1\]

\[y=-\frac{1}{3}\]

Ответ: $\left( 0;-\frac{1}{3} \right)$

Система № 2

\[\left\{ \begin{align}& 4\left( a-3b \right)-2a=3\left( b+4 \right)-11 \\& -3\left( b-2a \right)-12=2\left( a-5 \right)+b \\\end{align} \right.\]

Преобразуем первое выражение:

\[4\left( a-3b \right)-2a=3\left( b+4 \right)-11\]

\[4a-12b-2a=3b+12-11\]

\[4a-12b-2a-3b=12-11\]

\[2a-15b=1\]

Разбираемся со вторым:

\[-3\left( b-2a \right)-12=2\left( a-5 \right)+b\]

\[-3b+6a-12=2a-10+b\]

\[-3b+6a-2a-b=-10+12\]

\[4a-4b=2\]

Итого, наша первоначальная система примет такой вид:

\[\left\{ \begin{align}& 2a-15b=1 \\& 4a-4b=2 \\\end{align} \right.\]

Посмотрев на коэффициенты при $a$, мы видим, что первое уравнение нужно домножить на $2$:

\[\left\{ \begin{align}& 4a-30b=2 \\& 4a-4b=2 \\\end{align} \right.\]

Вычитаем из первой конструкции вторую:

\[0-26b=0\]

\[-26b=0\]

\[b=0\]

Теперь найдем $a$:

\[2a-0=1\]

\[a=\frac{1}{2}\]

Ответ: $\left( a=\frac{1}{2};b=0 \right)$.

Вот и все. Надеюсь, этот видеоурок поможет вам разобраться в этой нелегкой теме, а именно в решении систем простых линейных уравнений. Дальше еще будет много уроков, посвященных этой теме: мы разберем более сложные примеры, где переменных будет больше, а сами уравнения уже будут нелинейными. До новых встреч!

Смотрите также:

1. Пробный ЕГЭ-2011 по математике, вариант №5
2. Решение ЕГЭ-2011: вариант 1, часть B
3. Пробный ЕГЭ 2012. Вариант 10 (без логарифмов)
4. Как решать задачи про смеси и сплавы
5. Задача B5: площадь фигуры без клеток

www.berdov.com

Системы линейных уравнений с двумя переменными. Часть 2. Метод домножения и сложения

Пусть у нас есть двое уравновешенных весов. Если мы пересыпаем все с левых чаш на одну чашу других весов, а с правых – на вторую, то весы также будут уравновешены. Т. е. если сложить правые и левые части верных равенств, мы также получим верное равенство.

Как мы можем использовать это для решения систем линейных уравнений? Можно сложить уравнения системы. Зачем нам это делать? Если мы в результате избавимся от одной переменной, то получим линейное уравнение с одной переменной, которое мы умеем решать.

Пример 2. Решить систему уравнений:

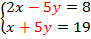
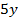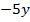Мы видим, что уравнения содержат слагаемые  и , которые взаимно уничтожатся при сложении.

Сложим отдельно левые и правые части уравнений системы:

Получаем:

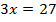
Мы получили линейное уравнение с одной переменной, решим его:

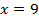
Теперь подставим найденное значение 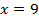 в любое из уравнений системы, например в первое, и найдем :

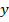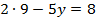
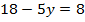
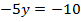
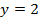
Получаем решение:

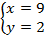
Ответ: .

 

В этом и состоит идея метода – исключить сложением одну из переменных.

Конечно, мы рассмотрели простой пример. Редко бывает, чтобы в двух уравнениях были слагаемые с одинаковыми (по модулю) коэффициентами. Поэтому нужно научиться приводить любую систему уравнений к эквивалентному виду, содержащему такие слагаемые. Как это сделать?

Вспомним, что при умножении и делении обеих частей уравнения на одно и то же ненулевое число получается эквивалентное уравнение, содержащее ту же информацию (с теми же корнями).

Пример 3. Решить систему уравнений:

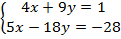
Умножим обе части первого уравнения на :

Получим:

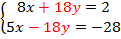
Заметим, что уравнения содержат слагаемые 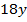 и 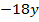. Теперь уже можно воспользоваться методом сложения:

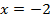
Подставим найденное значение 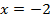 в первое уравнение:

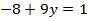
interneturok.ru

Графический метод решения системы уравнений. Видеоурок. Алгебра 9 Класс

Тема: Системы уравнений

Урок: Графический метод решения системы уравнений

Рассмотрим систему

Пару чисел 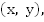 которая одновременно является решением и первого и второго уравнения системы, называют решением системы уравнений.

Решить систему  уравнений – это значит найти все её решения, или установить, что решений нет. Мы рассмотрели графики основных уравнений, перейдем к рассмотрению систем.

Пример 1. Решить систему

Решение:   

Это линейные уравнения, графиком каждого из них является прямая. График первого уравнения проходит через точки (0; 1) и (-1; 0). График второго уравнения проходит через точки (0; -1) и (-1; 0). Прямые пересекаются в точке (-1; 0), это и есть решение системы уравнений (Рис. 1).

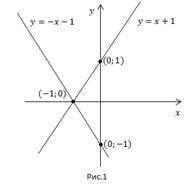
Решением системы является пара чисел  Подставив эту пару чисел в каждое уравнение, получим верное равенство.

Мы получили единственное решение линейной системы.

Ответ: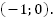

Вспомним, что при решении линейной системы возможны следующие случаи:

cистема имеет единственное решение – прямые пересекаются,

система не имеет решений – прямые параллельны,

система имеет бесчисленное множество решений – прямые совпадают.

Мы рассмотрели частный случай системы, когда p(x; y) и q(x; y) – линейные выражения от x и y.

Пример 2. Решить систему уравнений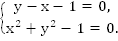

Решение:  

График первого уравнения – прямая, график второго уравнения – окружность. Построим первый график по точкам (Рис. 2).

x	0	-1
y	1	0

Центр окружности в точке О(0; 0), радиус равен 1.

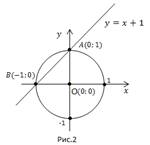
Графики пересекаются в т. А(0; 1) и т. В(-1; 0).

Ответ: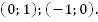

Пример 3. Решить систему графически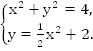

Решение: Построим график первого уравнения – это окружность с центром в т.О(0; 0) и радиусом 2. График второго уравнения – парабола. Она сдвинута относительно начала координат на 2 вверх, т.е. ее вершина – точка (0; 2) (Рис. 3).

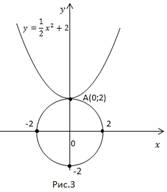
Графики имеют одну общую точку – т. А(0; 2). Она и является решением системы. Подставим пару чисел в уравнение, чтобы проверить правильность.

Ответ:

Пример 4. Решить систему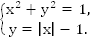

Решение: Построим график первого уравнения – это окружность с центром в т.О(0; 0) и радиусом 1 (Рис. 4).

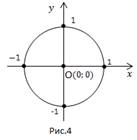
Построим график функции 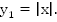 Это ломаная (Рис. 5).

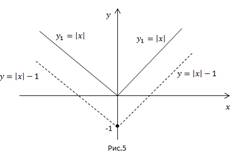
Теперь сдвинем ее на 1 вниз по оси oy. Это и будет график функции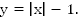

Поместим оба графика в одну систему координат (Рис. 6).

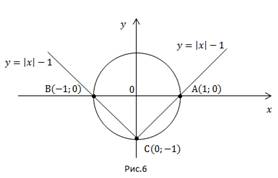
Получаем три точки пересечения – т. А(1; 0), т. В(-1; 0), т. С(0; -1).

Ответ: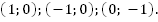

Мы рассмотрели графический метод решения систем. Если можно построить график каждого уравнения и найти координаты точек пересечения, то этого метода вполне достаточно.

Но часто графический метод даёт возможность найти только приближенное решение системы или ответить на вопрос о количестве решений. Поэтому нужны и другие методы, более точные, и ими мы займемся на следующих уроках.

 

Список рекомендованной литературы

1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.

2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.

3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.

4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.

5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.

6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.

 

Рекомендованные ссылки на интернет-ресурсы

1. Раздел College.ru по математике (Источник).

2. Интернет-проект «Задачи» (Источник).

3. Образовательный портал «РЕШУ ЕГЭ» (Источник).

 

Рекомендованное домашнее задание

1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 105, 107, 114, 115.

interneturok.ru