Технологическая карта урока геометрия 8 класс на тему » Решение задач на тему параллелограмм»

Технологическая карта урока геометрии 8 класс

Составила : учитель математики 1 квалификационной категории Хлопова Е.А. МОУ СОШ 36 г. Комсомольска на Амуре, Хабаровского края

Тема урока «Решение задач по теме: «Параллелограмм»

Тип урока Урок обобщения и систематизации

Цели Предметные: систематизировать знания о параллелограмме.

Личностные: развивать навыки самостоятельной работы, эмоциональной сферы,

анализа своей работы.

Метапредметные: умение самостоятельно определять цели своего обучения,

ставить и формулировать для себя новые задачи в учёбе и

познавательной деятельности.

Планируемые результаты учащийся научится решать задачи разного уровня сложности на

применение свойств и признаков параллелограмма из материалов ГИА.

Основные понятия Параллелограмм, его определение, свойства и признаки.

Организационная структура урока

Этапы проведения урока

Форма организации УД

Задания для учащихся, выполнение которых приведёт к достижению запланированных результатов

Презентация

Приложения

Учебник

1.Организационный этап

Учитель напоминает учащимся как работать с листами оценивания ( лист оценивании см приложение 1)

2.Постановка цели и задач урока. Мотивация учебной деятельности учащихся

3.Актуализация знаний

а) выберите на рисунке параллелограммы, ответ запишите в тетради

Ответ: 2,5,7

б)Найдите неизвестные элементы параллелограмма. А 10 см

В С <А =60⁰ В 7 см Найдите ВД, СД

Найдите остальные углы С

А Д Д

М N МК=?, ЕN=?

5 4

E К

в)Найдите параллелограмм. a||b, c||d

5 120⁰ а b

6 120

0 c d

3. Контроль и коррекция знаний

Тест (см. приложение 2)

4. Тренировочные задания

Задача 1. Устный опрос.

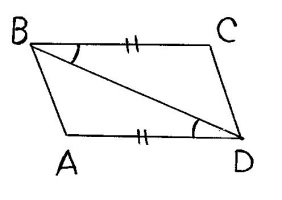
Докажите, что ABCD- параллелограмм.

Задача 2. Работа у доски.

Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне ВС. Найти ВС, если АВ = 40 см.

Задачи для работы в группах.

1 группа. Найдите стороны параллелограмма, если одна сторона в 3 раза меньше другой, а периметр параллелограмма равен 40 см.

2 группа. Найдите величину большего угла параллелограмма ABCD, если биссектриса угла А образует со стороной ВС угол, равный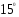 

. Ответ дайте в градусах.

3 группа. Стороны параллелограмма равны 8 см и 3 см. Биссектрисы двух углов, прилежащих к большей стороне, делят противоположную сторону на три части. Найдите длины этих отрезков.

7.Рефлексия учебной деятельности на уроке

Я сегодня научился решать задачи на применение свойств и признаков параллелограмма

8.информация о домашнем задании п42-43, №378(устно, уметь доказать), №380

Приложение1

Оценочный лист__________________________

Настроение

Приложение 2

Вариант 1.

1. Укажите верное утверждение:

А) Параллелограмм – это четырёхугольник, у которого сумма углов равна .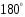

Б) Параллелограмм – это четырёхугольник, у которого противоположные стороны параллельны.

В) Параллелограмм – это четырёхугольник, у которого диагонали являются биссектрисами.

2. Укажите верное утверждение:

В параллелограмме ABCD:

А) AB > CD; Б) AB < CD; В) AB = CD.

3. Какое утверждение неверно?

А) Диагонали в параллелограмме равны.

Б) Диагонали в параллелограмме пересекаются.

В) Диагонали в параллелограмме точкой пересечения делятся пополам.

4. Какое утверждение не является свойством параллелограмма?

А) В параллелограмме все углы прямые.

Б) В параллелограмме противоположные углы равны.

В) В параллелограмме диагонали точкой пересечения делятся пополам.

5. Какое утверждение не является признаком параллелограмма?

А) Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник –параллелограмм.

Б) Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.

В) Если в четырёхугольнике два угла прямые, то этот четырехугольник – параллелограмм.

6. Найдите углы параллелограмма ABCD, если _.

7. Найдите периметр параллелограмма ABCD, если его смежные стороны равны 3 см и 45 мм.

Вариант 2.

1. Укажите верное утверждение:

А) Параллелограмм – это четырёхугольник, у которого противоположные стороны параллельны.

Б) Параллелограмм – это четырёхугольник, у которого диагонали равны.

В) Параллелограмм – это четырёхугольник, у которого сумма углов равна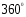

2. Укажите верное утверждение:

В параллелограмме ABCD:

А) BC < AD; Б) BC = AD; В) BC > AD.

3. Какое утверждение неверно?

А) Диагонали в параллелограмме точкой пересечения делятся пополам.

Б) Диагонали в параллелограмме пересекаются.

В) Диагонали в параллелограмме являются биссектрисами.

4. Какое утверждение не является свойством параллелограмма?

А) В параллелограмме диагонали перпендикулярны.

Б) В параллелограмме противоположные стороны равны.

В) Диагональ параллелограмма делит его на два равных треугольника.

5. Какое утверждение не является признаком параллелограмма?

А) Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.

Б) Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.

В) Если в четырёхугольнике две стороны параллельны, то этот четырехугольник – параллелограмм.

6. Найдите углы параллелограмма ABCD, если _.

7. Найдите периметр параллелограмма ABCD, если его смежные стороны равны 5 см и 35 мм.

.

ОТВЕТЫ К ТЕСТУ

Вариант 1. Вариант 2.

1. Б 1. А

2. В 2. Б

3. А 3. В

4. А 4. А

5. В 5. В

6. 60, 120 6. 70, 110

7. 15 см. 7. 17 см.

Решение задач по теме «Параллелограмм и трапеция». Видеоурок. Геометрия 8 Класс

На этом уроке мы рассмотрим комплекс задач на параллелограмм и трапецию. Для этого мы сначала повторим основные связанные с ними факты. Сначала мы вспомним свойства параллелограмма, а затем его признаки, потом уделим внимание свойствам равнобедренной трапеции. Основная часть урока будет посвящена рассмотрению примеров.

Тема: Четырехугольники

Урок: Решение задач по теме «Параллелограмм и трапеция»

Очевидно, что для решения задач на тему «Параллелограмм и трапеция», необходимо повторить основные понятия, связанные с этими фигурами. Вспомним их свойства и признаки.

Рассмотрим сначала параллелограмм.

Определение. Параллелограмм – четырехугольник, у которого каждые две противоположные стороны параллельны (см. Рис. 1).

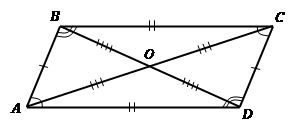
Рис. 1. Параллелограмм

Основные свойства параллелограмма:

Чтобы иметь возможность при решении задач пользоваться указанными свойствами, нам необходимо понимать, является ли указанный четырехугольник параллелограммом или нет. Для этого необходимо знать признаки параллелограмма.

Теорема. Первый признак параллелограмма. Если в четырехугольнике две противоположные стороны равны и параллельны (см. Рис. 2), то этот четырехугольник – параллелограмм. 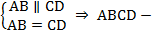 параллелограмм.

Рис. 2. Первый признак параллелограмма

Теорема. Второй признак параллелограмма. Если в четырехугольнике каждые две противоположные стороны равны (см. Рис. 3), то этот четырехугольник – параллелограмм.

 параллелограмм.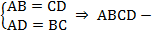

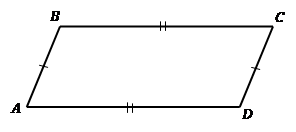
Рис. 3. Второй признак параллелограмма

Теорема. Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам (см. Рис. 4), то этот четырехугольник – параллелограмм. 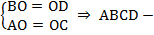 параллелограмм.

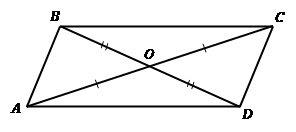
Рис. 4. Третий признак параллелограмма

Теперь рассмотрим такую фигуру, как трапеция. Отдельным ее видом является равнобедренная трапеция, имеющая важные свойства.

Определение. Равнобедренная трапеция

– это трапеция, в которой боковые стороны равны (см. Рис. 5).

 

Рис. 5. Равнобедренная трапеция

Теперь сформули

Материал для подготовки к ЕГЭ (ГИА, 8 класс): Зачет №1 Параллелограмм, ромб, трапеция 8 класс

По теме: методические разработки, презентации и конспекты

Презентация Площадь параллелограмма, треугольника, трапеции

Презентация подготовлена к уроку геометрии в 8 классе по теме «Площади четырёхугольников». Урок проводился в математическом классе и успели разобрать весь материал, представленный в презентации. После…

Презентация к уроку геометрии в 8 классе по теме: «Параллелограмм и трапеция»

На готовых чертежах можно показать прилежащие и противолежащие стороны и углы; найти их величину, используя свойства фигур. Можно использовать презентацию как при объяснении, так и при повторении мате…

Обобщающий урок по теме«ПРЯМОУГОЛЬНИК, ПАРАЛЛЕЛОГРАММ, РОМБ, КВАДРАТ»

систематизировать знания при изучении четырех фигур – параллелограмма, прямоугольника, ромба, квадрата.ПЛАН УРОКА:Знакомство со словами из «словаря».Устная работа по готовым чертежам.Сообщения четырех…

Занятие элективного курса по математике 9 класса подготовки к ГИА. Модуль «Геометрия». Решение задач по теме «Площадь параллелограмма, треугольника, трапеции»

Материал содержит план-конспект занятия по теме:»Площадь параллелограмма, треугольника, трапеции», презентации, тесты….

с.р по геометрии 8 кл Параллелограмм, ромб, квадрат, прямоугольник

с.р по геометрии 8 кл Параллелограмм, ромб, квадрат, прямоугольник. к учебнику Атаносян по теоретической части…

Зачет №6 Ромб 9 класс

Тренировочные задания по геометрии для подготовки обучающихся к ОГЭ…

Зачетная работа по геометрии по тем «Прямоугольник, параллелограмм, ромб, квадрат»

Зачетная работа проводится по билетам. В билете  три вопроса из устной части (на определение, на свойства, на построение чертежа к задаче) и три задачи, аналогичных представленным в практической …

Методическая разработка по геометрии (8 класс) по теме: Параллелограмм — урок геометрии в 8 классе

Урок  геометрии

Тема урока: Параллелограмм

ФИО автора: Логинова Татьяна Витальевна

МБОУ «Ильинская основная школа» Городецкий муниципальный район Нижегородская область

Область применения:  первый  урок по теме «Четырехугольники», третий урок курса геометрии 8класса (учебник Л.С. Атанасяна и др., М., «Просвещение», 2015г)

Тип урока: урок новых знаний.

Цель урока: создать условия для формирования и усвоения понятия параллелограмма и его свойств.

Задачи урока:

образовательная – конструктивное введение  понятия параллелограмма, на основе частично-поискового метода, вывод и доказательство свойств параллелограмма, формирование навыка применения теорем на базе первичного запоминания и усвоения;

развивающая – способствовать развитию умения доказывать, применяя новые понятия и теоремы;

воспитательная – умение вести диалог, вступать в многостороннее сотрудничество, умение сосредоточиться для достижения поставленной цели.

Планируемые УУД

• личностные: развитие  навыка сотрудничества и самостоятельности в работе, трудолюбия, аккуратности, развитие навыков самоанализа  и самоконтроля при оценке результата и процесса своей деятельности;
• метапредметные

• познавательные: анализ объектов с целью выделения общих признаков, выбор оснований и критериев для сравнения, выдвижение гипотез и их обоснование, подведение под понятие;
• коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли, владение монологической и диалогической речью, определение способов общения с одноклассниками, с учителем, сотрудничество в анализе информации;
• регулятивные: планирование своих действий для достижения поставленной цели; анализ собственной работы, оценка степени ее успешности, постановка учебной задачи, оценка результата учебной деятельности;

• предметные: владение базовым понятийным аппаратом, установление причинно-следственных связей и построение логической цепи рассуждений, владение способами доказательства.

Ход урока.

I.  Мотивация учебной деятельности. (2 мин)

— На прошлых уроках мы дали определение многоугольника. Сформулируйте  определение многоугольника. Приведите примеры многоугольников. Какой многоугольник мы изучили достаточно подробно?(треугольник, в 7 классе) Как вы думаете, можно ли так же подробно изучить четырехугольники? Наверно, да. Как вы думаете, чем мы займемся сегодня на уроке?(изучением четырехугольников). Конечно, не всех сразу. Но с одним особым мы познакомимся поближе. Посмотрите на экран, попробуйте разделить фигуры на какие-либо группы.

Из  всех предложенных вариантов выбираю тот, где выделены фигуры 2,4,5,8,9,11,12. На ИД их можно сдвинуть ближе.

— Сформулируем цель урока. (Изучить особый вид четырехугольника.)

II.  Актуализация (2 мин)

-Нам сегодня потребуются факты, хорошо нам знакомые. На рисунке найдите градусную меру углов.

-Как называются эти углы?

-Сформулировать свойства параллельных прямых.

-Сформулировать признаки параллельных прямых.

III. Конструктивное введение определения (2 мин)

-Построить две параллельные прямые а и в.

-Построить секущую с.

-Построить прямую d, параллельную прямой с.

-Обозначить точки пересечения последовательно A, B, C, D.

-Полученный четырехугольник назвали «Параллелограмм». Попробуйте дать определение параллелограмма.

IV. Отработка определения (3 мин)

1. Выбрать на рисунке (тот же рисунок 1) параллелограмм (на ИД)

2. Выбрать определение параллелограмма из предложенных (на листочках каждому):

V. Исследовательская работа в группах (5-7 мин)

Пересадить ребят по группам, заранее сформированным, (во время пересадки происходит эмоциональная и физическая разрядка; когда ученики сели по группам, они берутся за руки и поднимают их вверх в знак готовности физической и эмоциональной) раздать набор четырехугольников, дается задание группам:

— Представьте, что это — страна четырехугольников; как она устроена? какие взаимоотношения между ее жителями, кто с кем в родственных отношениях, кто только в соседских? произведите некоторые измерения, построения, это может помочь вам.; проанализируйте их; что общего у четырехугольников, чем они отличаются?  

Учитель контролирует процесс исследования, корректирует наводящими вопросами, предлагает доказать выдвинутые гипотезы.

VI. Физкультминутка.(1 мин)

-Встаньте из-за парт, обведите руками в воздухе все фигуры, которые вы исследовали. Фигуры должны быть большими и понятными. (включаем музыкальное сопровождение)

VII. Выдвижение гипотез, подтверждение или опровержение. (15-17 мин)

Выступления каждой группы, начиная с самой слабой. В результате должны быть выдвинуты гипотезы:

I.    Четырехугольники могут делиться на 3 группы:

• 4-угольники, у которых никакие стороны не параллельны;
• 4-угольники, у которых две противоположные стороны параллельны
• 4-угольники, у которых  противоположные стороны попарно параллельны, т.е. параллелограммы.

II.   В параллелограмме противоположные стороны равны и противоположные углы равны (первое свойство). Диагонали точкой пересечения делятся пополам (второе свойство).

По первой гипотезе можно составить начало таблицы, классифицирующей четырехугольники (см. приложение).  В целях экономии времени я «рисую» на интерактивной доске начало схемы, детям предлагаю составить схему дома на листе А4, оставляя место для продолжения. Потом она пригодится для шпаргалки по вычислению площадей. Составление схемы позволяет «открыть» детям тот факт, что прямоугольник и квадрат – тоже параллелограммы.

По второй гипотезе,  как правило, все группы приходят к нужному выводу. Попробуем доказать.

Фронтальная работа по доказательству первого свойства параллелограмма. Учитель записывает на доске, ученики записывают в тетради. (Обычно записываю это свойство как две разные теоремы. Это удобно в дальнейшем для формирования обратных теорем – признаков параллелограмма)

До второго свойства дети самостоятельно догадываются редко. Учитель предлагает построить диагонали, выполнить измерения, сравнить отрезки. Формулируется вывод (второе свойство параллелограмма): диагонали параллелограмма  делятся точкой пересечения пополам.

Аналогичная работа со вторым свойством.

Неверные гипотезы необходимо опровергнуть контрпримерами, лучше, если это сделают другие дети.

-Командиры групп, оцените работу каждого сотоварища. Кто шевелил мозгами(М), кто шевелил ушами(ШУ), кто слышал только краем уха (КУ), кто хлопал ушами(У).

VIII. Применение новых знаний (9-12 мин)

Задачи на готовых чертежах: (на ИД). Задачи  предлагаются для обсуждения в группах. Через 2 мин проверка ответов в задаче №1. Вслух обосновывается решение. По задаче №2 выслушиваются предложения от групп. Далее фронтально обсуждается ход решения (с помощью уравнения), задача оформляется в тетрадях с полным решением.

                   №1.                                                      №2.

IX. Формулировка домашнего задания для себя. (1 мин)

-Что мы делаем дома? (учим определение параллелограмма, свойства параллелограмма и их доказательства, и какую-то задачу)

-Задачу посложнее или попроще? (попроще, аналогичную той, что решали сейчас)

-Я тоже так думаю, значит, добавляем №372(в).

-А схему забыли? Составить начало схемы «Четырехугольники».

X.       Рефлексия (1-2 мин)

 –Вспомните весь урок. Кто сегодня М, ШУ, КУ, а кто У?

-Мне понравилось, как сегодня работал ……………………

-За урок я ставлю оценки …………………………………………

  -Продолжите фразу: (фразы приготовлены на ИД, дети продолжают их систематически)

-Я сегодня узнал….

-Я сегодня научился…

-Мне на уроке понравилось…

-Мне не понравилось….

-Я не понял…..

-После этого урока я смогу…

XI. Приложение.

Схема по теме «Четырехугольники»

Презентация к уроку по геометрии (8 класс) по теме: задачи на готовых чертежах по теме «Параллелограмм»

Слайд 1

Подготовила: Наседкина О.А., учитель математики 1 кв. категории МКОУ Квитокская СОШ№1 п.Квиток, Тайшетского района, Иркутской области Задачи на готовых чертежах

Слайд 2

Параллелограмм D С В А O Свойства: Диагонали в точке пересечения делятся пополам Противолежащие стороны равны Противолежащие углы равны 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

Слайд 3

Задача 1 D С В А Доказать, что ABCD — параллелограмм

Слайд 4

Задача 2 Доказать, что ABCD — параллелограмм D С В А

Слайд 5

Задача 3 O D C B А Дано: ∆ AOB = ∆ COD Доказать, что ABCD — параллелограмм

Слайд 6

Задача 4 D E M С В А P K Доказать, что ABCD — параллелограмм

Слайд 7

Задача 5 В D C A Доказать, что ABCD — параллелограмм

Слайд 8

Задача 6 O C B A D Доказать, что ABCD — параллелограмм

Слайд 9

Задача 7 B A O D C Доказать, что ABCD — параллелограмм

Слайд 10

Задача 8 A D C B Дано: ∆ ABC = ∆ CDA Доказать, что ABCD — параллелограмм

Слайд 11

Задача 9 K E D B A C Дано: AKCE -параллелограмм Доказать, что ABCD — параллелограмм

Слайд 12

Задача 10 B E F D C A Дано: AECF -параллелограмм Доказать, что ABCD — параллелограмм

Слайд 13

Задача 1 1 N F C B D A Дано: NBFD -параллелограмм Доказать, что ABCD — параллелограмм

Слайд 14

Задача 12 D C E B A M Дано: MBED -параллелограмм Доказать, что ABCD — параллелограмм

Слайд 15

Задача 1 3 40 ° 35 ° D C B A Дано: ABCD -параллелограмм Найти углы параллелограмма ABCD

Слайд 16

Задача 14 F E D O C A B Дано: ABCD -параллелограмм Доказать: OE = OF .

Слайд 17

Задача 14 O D C A B Дано: ABCD -параллелограмм Доказать:

Слайд 18

Задача 1 5 A E P D C B Дано: ABCD -параллелограмм Доказать: AP = CE .

Слайд 19

Задача 1 6 B P 4 1 D C A Дано: ABCD -параллелограмм Найти

Слайд 20

Задача 1 7 5 E D A B C Дано: ABCD -параллелограмм Найти

Слайд 21

Задача 1 8 K A D C B Дано: ABCD -параллелограмм Найти углы параллелограмма ABCD

Слайд 22

1.Саврасова С.М.,Ястребинецкий Г.А. Упражнения по планиметрии на готовых чертежах.- М.: просвещение, 1987.-112 с.: ил. 2. Зив Б.Г. и др. Задачи по геометрии: Пособие для учащихся 7-11 кл . Общеобразоват . учреждений. — М .: Просвещение , 2000.-271 с.: ил . 3. Рабинович Е.М. Сборник задач на готовых чертежах.-К.:1996.-56с. 4. Гаврилова Н.Ф. Поурочные разработки по геометрии: 8 класс.-2-е изд., перераб . и доп.-М.: ВАКО,2008.-368 с. Список литературы

Материал для подготовки к ЕГЭ (ГИА) по геометрии (8 класс) по теме: параллелограмм, задачи по геометрии готовым чертежам

По теме: методические разработки, презентации и конспекты

Сборник УСТНЫЕ ЗАДАЧИ НА ГОТОВЫХ ЧЕРТЕЖАХ Параллельные прямые.

Сборника УСТНЫЕ ЗАДАЧИ НА ГОТОВЫХ ЧЕРТЕЖАХ «Параллельные прямые» содержит 58 задач по теме. Задания пособия предназначены, прежде всего, для обучения школьников решению задач по только  что изученному…

Сборник УСТНЫЕ ЗАДАЧИ НА ГОТОВЫХ ЧЕРТЕЖАХ Смежные и вертикальные углы

Задания по теме «Смежные и вертикальные углы» предназначены, прежде всего, для обучения школьников решению задач по только что изученному материалу, а также при повторении  курса геометрии 7 класс, пр…

Сборник УСТНЫЕ ЗАДАЧИ НА ГОТОВЫХ ЧЕРТЕЖАХ Признаки равенства треугольников

Задания по теме «Признаки равенства прямоугольников» предназначены, прежде всего, для обучения школьников решению задач по только что изученному материалу, а также при повторении  курса геометрии 7 кл…

Сборник УСТНЫЕ ЗАДАЧИ НА ГОТОВЫХ ЧЕРТЕЖАХ «Признаки равенства прямоугольных треугольников»

 Сборник УСТНЫЕ ЗАДАЧИ НА ГОТОВЫХ ЧЕРТЕЖАХ «Признаки равенства прямоугольных треугольников»  содержит 28 задач по теме. Материал можно использовать при организации самостоятельной и индивидуальной раб…

Презентация «Задачи на готовых чертежах: Теорема о трёх перпендикулярах»

Одним из видов работы на уроке геометрии является решение задач по готовым чертежам. В презентации представлены задачи с чертежами по теме: «Теорема о трёх перпендикулярах»….

задачи на готовых чертежах по теме «Параллелограмм»

презентацию можно использовать при организации устной работы на уроке, при повторении, при закреплении изученного материала….

Параллелограмм (задачи)

Задачи из Открытого банка ЕГЭ по теме Параллелограмм…

План-конспект урока по геометрии (8 класс) по теме: Урок геометрии в 8 классе по теме «Параллелограмм»

МБОУ «Богатищевская СОШ»

Урок геометрии в 8 классе

«Параллелограмм»

(по учебнику А. В. Погорелова)

Учитель математики

высшей категории

Артамонова А.Е.

п. Богатищево

2013

Тема урока  «Параллелограмм»

Цели урока:

— образовательная: изучить определение и признак параллелограмма, научиться строить параллелограмм;

— развивающая: развитие логического мышления, творческого мышления, умения анализировать, развитие пространственных представлений, математической речи;

— воспитательная:  воспитание чувства прекрасного, интереса к предмету, коллективизма, взаимопомощи.

Тип урока: изучение нового

Методы работы:

• Исследование –  анализ, сравнение, наблюдение, сопоставление, обобщение, умение делать выводы, доказательство.

Формы урока:

• классно-урочная.
• работа в парах.
• работа в малых группах.

Ход урока:

1.Организационный момент. Постановка целей урока.

Сегодня мы познакомимся с новой геометрической фигурой. Научимся его построению. Новый материал вы будете отражать в тетрадях в виде опорных конспектов. Сюда же мы включим ключевые задачи, которые выделим с вами.

Три   пути    ведут   к знаниям:

путь размышления —  это путь самый   благородный,    

  путь подражания — это  путь самый легкий  

и  путь   опыта  —  это путь самый горький.

  Какой путь выберите вы?

II. Актуализация знаний .

Фронтальный опрос (в форме игры «Казино»):

1. Какая фигура называется четырехугольником?
2. Что такое диагонали четырехугольника?
3. Сформулируйте первый признак равенства треугольников.
4. Сформулируйте второй признак равенства треугольников.
5.  Сформулируйте третий признак равенства треугольников.
6. Сформулируйте свойство вертикальных углов.
7. Сформулируйте свойство внутренних накрест лежащих углов при параллельных прямых.
8. Сформулируйте свойство внутренних односторонних углов при параллельных прямых.
9. Сформулируйте признак параллельности прямых.
10.  Какая фигура называется треугольником?
11. Чему равна сумма углов четырехугольника? 
12. Существует ли четырехугольник со сторонами 4 см, 5 см, 9см и 10см?
13. Какие вершины четырехугольника называются соседними? 
14. Какие вершины четырехугольника называются противолежащими? 
15. Какие стороны четырехугольника называются противолежащими? 
16. Какие стороны четырехугольника называются  соседними? 

III. Открытие нового.

1. Сегодня мы  познакомимся с одним из видов четырехугольников. Посмотрите на фигуры  и разбейте их на две группы. (Необходимо добиться, чтобы учащиеся разбили фигуры на параллелограммы и другие фигуры.)

1 группа	2 группа
2,4,5,8	1,3,6,7,9,10,11

Учитель:  Что объединяет фигуры первой группы?

Решив ребус, определите тему урока.  

Учитель: Попробуйте дать определение параллелограмма.

Ученики совместно с учителем формулируют определение параллелограмма и

записывают схему определения понятия параллелограмм.

Параллелограмм: четырехугольник АВСD ;                              В                               С АВ II СD; И ВС II АD                                                                А                             D Обозначение:  АВСD.

2. Работа в группах по 2-3 человека (или индивидуально) по желанию учеников.

Докажите, что АВСD  — параллелограмм.

             

3. Выполним практическую работу.

Проведем две прямые,  пересекающие в точке О. Отложим от точки О на одной прямой отрезки АО=ОС, на другой – ВО=ОD. Соединим точки А,В,С, D.  Какую фигуру получили?  Давайте сформулируем утверждение, которое является признаком параллелограмма, и докажем его.

Теорема: Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.

Дано: ABCD — четырехугольник,         AC и BD пересекаются в 0, AO=OC, BO=OD. Доказать: ABCD-параллелограмм

                            Схема поиска доказательства теоремы

                          АBCD, О — точка пересечения диагоналей,  

OD=OB и ОА=ОС

                                                AOD= COB

                                     ∆AOD= ∆СОВ

                                    OBC=ODA             внутренними накрест лежащие

                                             AD||BC

Аналогично : АВ||CD

                                             ABCD  -параллелограмм

Доказательство:

ABCD — четырехугольник, точка О — точка пересечения его диагоналей.

1) т.к. AOD= COB (вертикальные), OD=OB (по условию теоремы),

 ОА=ОС (по условию теоремы), то  ∆AOD= ∆СОВ(1 признак)

2) OBC=ODA (соответствующие)

3) OBC иODA внутренние накрест лежащие для прямых AD и ВС и секущей BD,

Из 2) и  3) следует, что AD||BC (по признаку параллельности прямых).

4) Аналогично доказывается : АВ || CD  

Т.к. АВ || CD  и AD||BC, то ABCD  -параллелограмм (по определению)

                                                            Чтд.                        

IY. Физминутка для глаз.

-Не поворачивая головы, обведите взглядом стену класса по периметру по часовой стрелке;

классную доску по периметру против часовой стрелки;

четырехугольник, изображенный на доске по часовой стрелке и равный ему треугольник против часовой стрелки.

Поверните голову налево и посмотрите на линию горизонта, а теперь на кончик своего носа. Закройте глаза, сосчитайте до 5, откройте глаза и …

V. Закрепление изученного материала. (учащиеся самостоятельно выбирают задачи для решения с последующим разбором)

Задание:  используя рисунок, докажите, что АВСD  — параллелограмм.

1 уровень	2 уровень

Из истории

Параллелогра́мм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — линия) .

Термин «параллелограмм» согласно Проклу, был введен Евклидом. Понятие параллелограмма и некоторые его свойства были известны еще пифагорейцам.

В «Началах» Евклида доказывается некоторые свойства параллелограмма, например: диагональ разделяет его пополам. Евклид не упоминает о том, что точка пересечения диагоналей параллелограмма делит их пополам.

Полная теория параллелограммов была разработана к концу средних веков и появилась в учебниках лишь в XVII веке.

VI. Рефлексия.

• Что узнали для себя нового?
• Что заинтересовало? Почему?
• Проанализируйте свою работу на каждом этапе.
• Что показалось интересным?
• Что самое главное и что надо запомнить?

VIII. Домашнее задание.
 1.вопросы 6,7; № 3,4.

2.Найти второй способ доказательства  задач 1 и 2 уровней.

3. Составить рассказ о параллелограмме.

Творческая часть.

1.Свойство движимости параллелограмма. (  http://repetitor-problem.net/svoystva-parallelogramma-v-zhizni)

2.  Параллелограммы  в архитектуре, орнаментах.