Решение задач на дроби и проценты

В последние годы понятие «проценты» все чаще встречается в повседневной жизни. Повышение и снижение тарифов на услуги, инфляция, проценты по кредитам, сезонные распродажи- все эти словосочетания, а главное то, что стоит за ними, должны быть понятны каждому, начиная с детского возраста. Очевидно, отвечая требованиям времени, составители вариантов ГИА и ЕГЭ по математике включили задачи на проценты в основную часть заданий. Между тем тема «Проценты. Задачи на проценты» изучается в 6-м классе, а во всех последующих классах проценты появляются периодически в текстовых задачах, вызывая явно отрицательные эмоции у большинства учеников. Большая часть учащихся помнит, что для нахождения процента от числа нужно составить пропорцию и решить ее. Но как составить пропорцию, если в задаче сказано, что во второй день туристы прошли на 20 % меньший путь, чем в первый день, а сколько прошли в первый тоже неизвестно? Для того чтобы справиться с заданием типа В9

в демоверсии ЕГЭ 2009 года, нужно достаточно глубоко разобраться в теме «Задачи на проценты». Как научить детей решать задачи на проценты различного уровня сложности и когда?

На основании собственной практики работы авторам представляется, что использование метода решения задач на дроби и проценты, предложенного в учебнике Г.В.Дорофеева и Л.Г.Петерсон, при определенном изложении материала дает оптимальный результат. О нашем подходе к изучению темы «Задачи на дроби и проценты» и будет рассказано ниже.

На первом уроке темы «Задачи на дроби» в пятом или шестом классе (в зависимости от программы) говорится, что все задачи на дроби делятся на три типа:

1. Задачи на нахождение части от числа, выраженной дробью
2. Задачи на нахождение числа по его части, выраженной дробью
3. Задачи на нахождение дроби, которую одно число составляет от другого.

Затем каждый тип задач отрабатывается в течение одного-двух уроков по одинаковой схеме. Покажем ее на примере задач первого типа.

Учитель: Мы с вами уже умеем решать задачи, в которых нужно найти какую-то часть от числа. Давайте решим такую: В классе 20 человек. Из них 2\5 девочки. Сколько девочек в классе?

Учeники предлагают 20 разделить на 5 и затем результат умножить на 2 .Такие задачи они решали еще в начальной школе. Учитель соглашается, но предлагает записать решение в виде выражения, а затем преобразовать его следующим образом:

При этом два действия — деление на знаменатель дроби, а затем умножение на ее числитель заменим одним действием – умножением на дробь.

Приходим к правилу: Чтобы найти часть от числа, выраженную дробью, надо это число умножить на дробь.

К задаче составляется схема, по которой ясно видно, какая величина принимается за единицу («целое») и что является ее частью.

Затем каждая следующая задача решается аналогично: составляется схема, вслух проговаривается правило, по нему составляется выражение. Нужно пресекать попытки учащихся решать задачи так, как они решали раньше, т.е. сначала разделить на знаменатель дроби, а затем умножить на числитель. Мы объясняем, что «новый» способ легче для решения более сложных задач. Кроме того, показываем детям аналогию действия по нахождению дробной части числа с действием по нахождению числа в n раз больше данного. Пример: В классе 20 человек. Сколько человек в двух таких классах? 20 умножить на 2. А в трех? 20 умножить на 3. А в 2\5 класса? 20 умножить на 2\5.

Два других типа задач разбираются аналогично. В учебнике Г.В. Дорофеева, Л.Г. Петерсон «Математика 5,часть 2» даны формулировки соответствующих правил и схем к задачам. Затем проводится обобщающий урок по теме. На нем еще раз разбираются все типы задач на примере одной прямой и двух обратных к ней задач. Учитель просит какого-нибудь ученика придумать несложную задачу на нахождение части от числа, выраженной дробью.

Простой пример: В корзине лежало 16 грибов, Из них 3\4 белые. Сколько белых грибов было в корзине? На доске чертится схема, а затем записывается решение в соответствии с нужным правилом.

Теперь учитель предлагает составить задачу другого типа по тем же данным. В случае затруднения он сам произносит текст этой задачи. В корзине лежало 12 белых, что составляет 3\4 всех грибов, лежащих в корзине. Сколько всего грибов было в корзине?  Опять составляется схема и записывается решение.

С составлением задачи третьего типа дети обычно уже справляются самостоятельно. В корзине лежало 16 грибов, из них 12 белых. Какую часть всех грибов составляют белые?

На дом задается творческая работа. Каждому ученику нужно самому придумать, записать и красиво оформить 3 задачи: прямую и 2 обратные. Обязательные условия оформления работы:

• Назван тип и записано правило, по которому решается каждая из задач
• Начерчена схема к каждой задаче
• Записаны решения и ответы
• Числа и дроби выбраны достаточно простые
• Все работы вывешиваются на стенде и дети голосованием выбирают три лучшие, на их взгляд.

О чем только не придумываются задачи: часть красных роз в саду и часть «Мерседесов» на автосалоне, часть гнилых помидоров среди купленных и часть золотых монет среди найденного старинного клада. Детская фантазия безгранична. Но практика показала, что дети на годы запоминают придуманные задачи, а заодно и их решения.

В последующем при решении более сложных комбинированных задач на дроби учитель постоянно акцентирует внимание на том, что нужно найти в каждом промежуточном действии, т.е. какой тип задачи и по какому правилу действуем. Правила каждый раз проговариваются вслух. Вспомогательные схемы уже можно не чертить. Постепенно даже слабые ученики усваивают решение задач на дроби, ошибок становится все меньше.

Когда начинается тема: «Проценты. Задачи на проценты», учащимся достаточно четко разъяснить, что проценты – это те же дроби со знаменателем 100.

Снова вспоминаем три типа задач и теперь формулируем правила, как считать:

1. Процент от числа (т.е. часть, зная целое)
2. Целое по его проценту (т.е. части)
3. Процентное отношение (т.е. какую часть в процентах одно число составляет от другого)

Формулировка правил, формулы и схемы даны в учебнике «Математика 6, часть 1» тех же авторов.

Задачи всех трех типов опять последовательно отрабатываются на уроках. Снова проводится обобщающий урок по теме «Задачи на проценты», на котором дети вспоминают свои задачи на дроби. Те же три задачи формулируем иначе. В корзине лежало 16 грибов. Из них 75% составляли белые. Сколько белых грибов было в корзине? В корзине лежало 12 белых, что составляло 75% всех грибов, лежащих в корзине. Сколько всего грибов в корзине?

И наконец: В корзине из 16 грибов было 12 белых. Какой процент составляют белые от всех грибов в корзине? На дом учащимся опять задается творческая работа. Предлагается переделать свои задачи в задачи на проценты, сохранив по возможности не только условия, но и все числа, переведя дроби в соответствующие проценты. Задачи оформляются по прежним правилам, только без красивых картинок.

В качестве заключительного урока хорошо провести устный зачет. На нем каждый ученик должен ответить одно из правил (кому какое достанется), рассказать условие своей задачи, которую нужно решать, действуя по этому правилу, начертить схему и записать решение.

Далее можно переходить к решению более сложных, комбинированных задач.

Следует обратить внимание на задачи типа: «На сколько процентов 72 меньше, чем 18?». Мы советуем, особенно на первых порах, решать их только со схемами. Кроме того, учащиеся должны твердо усвоить и запомнить, что

то, с чем сравнивается, принимается за 100%. Поэтому решение любой задачи нужно начинать с вопроса: «Что мы принимаем за 100%?». Далее чертится схема:

По ней ясно видно, что задачу можно решать двумя способами. Первый способ:

1. Найти, на сколько 72 больше, чем 18? –на 54
2. Сколько % 54 составляет от 18 ?–(54:18)*100% (действуем по правилу- Как найти процентное отношение двух чисел? –Первое число разделить на второе и умножить на 100%)

Второй способ:

1. Сколько % 72 составляет от 18?- (та же цепочка рассуждений, что и во 2-м действии предыдущего решения, приводит нас к ответу 400%)
2. На сколько % это число больше 100%? -400%-100%=300%

При решении сложных задач на дроби и проценты, на наш взгляд, очень полезно (особенно для сильных учащихся) пытаться решать задачу несколькими способами. Если дети видят эти способы, это значит, что они действуют не автоматически, по заученному правилу, а разбираются в сути задачи.

Большая часть класса, в конце концов, усваивает алгоритмы решения задач различных типов. Поэтому, когда через некоторое время в теме: «Пропорции» начинаем разбирать решение задач на проценты методом пропорции, ученики часто говорят, что им легче «считать по правилам». Но мы объясняем учащимся, что это – еще один способ решения таких задач, который им очень пригодится в будущем на уроках химии.

Практика показала, что благодаря тщательному разбору тем в 5-6 классах: многократному вычерчиванию схем и проговариванию вслух правил, выполнению творческих заданий по составлению прямых и обратных задач разного типа – принципы решения задач на дроби и проценты не только хорошо усваиваются, но и не забываются с годами.

В 7-8 классах при решении текстовых задач достаточно большая часть учащихся может составить математическую модель ситуации, описанной в начале статьи. Если в первый день туристы прошли x км, а во второй на 20% меньше, чем в первый, то x- это 100%- (то с чем сравнивают). А путь во второй день составляет 80% от пути в первый день, т.е. от x, что можно вычислить по правилу нахождения процента от числа и получить 0,8x км.

На факультативных занятиях теми же методами решаются задачи на сплавы и растворы. В 9 классе при подготовке к экзамену по сборнику С.А.Шестакова мы снова вспоминаем три типа задач, схемы и правила их решения, которые теперь записываются в общем виде.

Первая параллель, с которой тема «Задачи на дроби и проценты» разбиралась по описанной выше методике, сейчас — 10 класс. Надеемся, что усвоенные алгоритмы при соответствующем повторении и тренинге помогут им успешно справиться с задачами типа В9 при решении ЕГЭ по математике в следующем году.

В заключение хочется отметить, что выбранная нами методика вовсе не предп

urok.1sept.ru

«Нахождение числа по его дроби». 6-й класс

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Современные требования к качеству обучения заставляют учителей искать пути совершенствования урока с использованием современных приемов педагогической техники, проявлять изобретательность и смекалку при построении процесса обучения в целом и при подготовке каждого конкретного урока в частности. Необходимость применять мультимедиа-технологию на уроках обусловлена тем, что в последнее время (и это не секрет) резко упало качество домашней подготовки учащихся, их самоподготовки. Этому есть объективные причины: слабая мотивация к учению, недостаточный контроль со стороны родителей, наличие всевозможных «решебников», мнение «и так «3» поставят». В этих условиях основная нагрузка по получению качественных знаний падает на учебный урок, на котором необходимо узнать, понять, закрепить, а теперь еще и выучить материал. В этих условиях урок должен быть мобилен, компактен, содержать максимум информации, доступной для восприятия учащимися, интересен. Что и заставляет меня применять на уроках мультимедиа–технологию, которая обеспечивает такое представление информации, при котором ученик воспринимает её одновременно и параллельно несколькими органами чувств. Ведь в реальной жизни человек более 90% информации получает от совместной деятельности органов зрения и слуха.

Здесь представлен урок «Основные задачи на дроби: нахождение числа по его дроби». Урок закрепления изученного материала. На данном уроке применяется информационно-коммуникационная технология. В течение урока проводится мультимедийное сопровождение, позволяющее сократить время, отводимое на повторение, эффективно провести фронтальный опрос учащихся, повысить интерес к предмету. Мультимедийное сопровождение позволяет многократно повторять содержание, тем самым добиваться полного понимания на разных этапах изучения нового материала. Сочетание современных технологий с традиционными повышает эффективность урока.

Цели:

• Повторить понятие процента, нахождения части от числа, числа по его части.
• Формировать навыки устного счета.
• Формировать умения и навыки решения основных задач на дроби.
• Развивать интересс к предмету, память, внимание;
• Воспитывать дисциплинированность, аккуратность.

Оборудование: Мультимедийный проектор, экран, компьютер.

Ход урока

I. Организационный момент. Сегодня у нас необычный урок, мы с вами совершим путешествие в «Страну задач». Во время путешествия мы посетим Городок «Устный счет», проедем станцию «Повторения», заглянем в «Домик умников» и остановимся в «Саду задач». (Слайд 2)

II. Повторение материала. (Внимание! Городок «Устный счет»)

1. Вычислите устно (слайд 3)

2. Переведите проценты в дробь (слайд 4). (Станция «Повторения»)

8% = 0,08; 100% = 1; 531%=5,31; 60% = 0,6; 41,7% = 0,417

3. Найдите часть от числа (слайд 5).

а)  от 14;

б)  от 39;

в)  от 100.

4. Найдите число (слайд 6).

а)  которого равны 14;

б)  которого равны 6;

в)  которого равны .

5. Выбери задачу (слайды 7–12). (Мы прибыли в «Сад задач»)

1) Бочонок вмещает 40 кружек кваса. Гномы выпили  части бочонка. Сколько кружек кваса они выпили? (24 кружки).

2) Белоснежка собрала 21 гриб, что составило  части от всех грибов, собранных гномами. Сколько грибов собрали гномы? (28 грибов).

3) Инопланетяне подарили Незнайке 6 волшебных карандашей, что составило 0,3 части от всех карандашей, привезённых ими на Землю. Сколько у них карандашей? (20 штук)

4) До избушки на курьих ножках 84 км. Ведьма пролетела  этого пути. Сколько километров ей осталось пролететь? (36 км).

5) Турист проплыл на байдарке 504 км, что составило 36% всего пути. Найдите длину всего пути.(1400 км)

III. Задание на дом: п.18 стр. 104,№ 681,№ 684,№ 679(1),№ 678(3,4) (слайд 13).

IV. Рефлексия. (Слайд 14)

У каждого ученика на парте лежит образец смайлика. Они поднимают и показывают тот смайлик, который выражает их отношение к умению решать задачи.

urok.1sept.ru

Конспект по математике «Решение задач на дроби»

Решение задач на дроби

Ключевые слова конспекта: решение задач на дроби, решения задач в 5-6 классе, ответы на задачи, нахождение части целого, восстановление целого по известной его части, нахождение отношения величин, увеличение (уменьшение) на часть целого, часть от части целого, нахождение целого по его части, выражение остатка через часть целого, выражение величины частью целого, часть от части целого, оставшаяся часть целого.

---

---

Решение основных и типовых задач на дроби для учащихся 5-6 классов, включая углубленный уровень изучения математики.

Задача № 1.   Нахождение части целого.

Андрей вышел из дома к озеру, до которого 900 м. Пройдя 3/5 пути, он встретил друга. На каком расстоянии от дома Андрей встретил друга?

РЕШЕНИЕ:

Целое задано числом 900. Чтобы ответить на вопрос задачи, надо найти 3/5 от 900.

Способ 1.
Найдем 1/5 от 900 и результат умножим на 3; получим 900 : 5 • 3 = 180 • 3 = 540.

Способ 2.
Умножим число 900 на дробь 3/5 и получим 540.

Ответ: 540 м.

Задача № 2.   Восстановление целого по известной его части.

Андрей вышел из дома к озеру и, пройдя 3/5 расстояния до озера, он встретил друга. Расстояние от дома до встречи с другом составило 540 м. Каково расстояние от дома Андрея до озера?

РЕШЕНИЕ:

Известна часть целого – число 540. Этой части соответствует дробь 3/5. Чтобы ответить на вопрос задачи, надо найти по дроби – неизвестное целое.

Способ 1.
Так как 540 – это три пятых целого, то одна пятая – это 540 : 3 = 180. А все целое – это пять пятых и оно равно 180 • 5 = 900.

Способ 2.
Разделим число 540 на дробь 3/5, получим 900.

Ответ: 900 м.

Задача № 3.   Нахождение отношения величин.

В школе 630 учащихся. В спартакиаде приняло участие 345 учащихся школы. Какая часть всех учащихся школы приняла участие в спартакиаде?

РЕШЕНИЕ:

Один учащийся школы – это 1/630 часть всех учащихся школы. Поэтому 345 учащихся составляют 345/630 всех учащихся школы. Сократив полученную дробь, запишем 23/42 всех учащихся школы.

Ответ: 23/42 всех учащихся школы.

Задача № 4.   Увеличение (уменьшение) на часть целого.

Цена упаковки составляет 3/50 цены игрушки. Какова стоимость игрушки с упаковкой, если цена игрушки 650 р.?

РЕШЕНИЕ:

Способ 1.
Сначала найдем цену упаковки: 650 : 50 • 3 = 39 (р.). Теперь, увеличив цену, найдем стоимость игрушки е упаковкой: 650 + 39 = 689 (р.).

Способ 2.
Если целое 1 и его часть ³/₅₀, то будем искать 1³/₅₀ от 650 р.
Имеем 650 • 53/50 = 689 (р.).

Ответ: 689 р.

Задача № 5.   Часть от части целого.

Из 550 учащихся школы в референдуме по вопросу о введении Ученического совета участвовали 22/25 числа всех учащихся. На вопрос референдума 3/4 числа учащихся, принявших участие в голосовании, ответили «да». Какую часть числа всех учащихся школы составили те учащиеся, которые ответили положительно?

РЕШЕНИЕ:

Вычислим число учащихся, утвердительно ответивших на вопрос референдума. Имеем 550 • 22/25 • 3/4 = 363 (уч.). Теперь найдем ответ на вопрос задачи: 363 : 550 = 33/50.

Ответ: 33/50 или 0,66.

Дополнительный вопрос: можно ли ответить на вопрос задачи, не зная числа учащихся школы?

Ответ: да, надо перемножить дроби, т.е найти 3/4 от 22/25.

Задача № 6.   Нахождение целого по его части.

В сборнике фантастики две повести. Первая занимает 35 страниц, а вторая – 2/7 книги. Сколько всего страниц в книге?

РЕШЕНИЕ:

Сначала найдем, какую часть рукописи занимает первая повесть: 1 – 2/7 = 5/7, а потом – целое по его части: 35 : 5/7 = 49.

Ответ: 49 страниц.

Задача № 7.   Выражение остатка через часть целого.

На пошив детской одежды ушел весь рулон ткани. Из 3/8 рулона сшили куртки, из четверти рулона – юбки, из оставшихся 24 м сшили несколько брюк. Сколько всего метров ткани было в рулоне?

РЕШЕНИЕ:

Найдем, из какой части всего рулона сшили куртки и юбки: 3/8 + 1/4 = 5/8. Теперь понятно, что на пошив брюк осталась часть, равная 1 – 5/8 = 3/8 рулона, которая составляет 24 м. Значит, во всем рулоне было 24 : 3/8 = 64 (м).

Ответ: 64 м.

Задача № 8. Выражение величины частью целого.

Оля истратила треть имевшейся у нее суммы денег, а потом еще 100 р. В итоге она истратила половину суммы. Сколько денег было у Оли первоначально?

РЕШЕНИЕ:

Чтобы разобраться в условии задачи, обратимся к рисунку.

Сначала узнаем, какую часть всей суммы составляют 100 р.: 1/2 – 1/3 = 1/6. Теперь мы знаем, что 100 р. – это 1/6 всей суммы. Чтобы ответить на вопрос задачи, нужно найти целое по его части. В данном случае можно попросту 100 р. умножить на 6. Получим, что у Оли было 600 р.

Ответ: 600 р.

Задача № 9.   Часть от части целого.

Перед поездкой бак автомобиля был заполнен на 4/5. Во время поездки была истрачена четверть имевшегося запаса бензина. Какая часть бака заполнена бензином к концу поездки?

РЕШЕНИЕ:

Если истрачена четверть от 4/5 бака, то это значит, что осталось 3/4 от 4/5 бака, т.е. всего наполнено бензином 3/5 бака.

Ответ: 3/5 бака.

Задача № 10.   Оставшаяся часть целого.

Ученик закрасил 3/8 круга синим цветом и 3/10 оставшейся части – желтым цветом. Какая часть круга осталась незакрашенной?

РЕШЕНИЕ:

Способ 1.
После закрашивания синим цветом остались незакрашенными 1 – 3/8 = 5/8 круга. Найдем 3/10 от 5/8 – получим 3/16. Сложим закрашенные части и получим 9/16. Значит, незакрашенными остались – 7/16.

Способ 2.
После закрашивания синим цветом остались незакрашенными 5/8 круга. После закрашивания желтым цветом остались незакрашенными 1 – 3/10 = 7/10 оставшейся части. Найдем 7/10 от 5/8 – получим 7/16.

Ответ: 7/16. Проверьте ответ, сделав рисунок.

 

---

Это конспект по математике на тему «Решение задач на дроби». Выберите дальнейшие действия:

uchitel.pro

Решение задач на нахождение дроби от числа и числа по его дроби. 6-й класс

Тип урока: комплексное применение знаний.

Цели:

• систематизация знаний по темам: «Действия с дробями»,  «Нахождение дроби от числа», «Нахождение числа по его дроби»;
• отработка практических навыков выполнения действий с дробями;
• расширение кругозора учащихся;
• развитие  познавательной активности, внимания, памяти, интереса к предмету математики;
• воспитание здорового образа жизни, бережного отношения к животным.

ХОД УРОКА

1. Организационный момент

Стихотворение читает ребенок:

Нам радостно, нам весело!
Смеемся мы с утра.
Но вот пришло мгновенье,
Серьезным быть пора.
Влево, вправо повернулись,
Друг другу улыбнулись
И в работу окунулись .

Мотивация урока.

– Здравствуйте! Я рада видеть вас всех на уроке математики.
– Какое настроение вы принесли на урок, я узнаю по индикаторам настроения
(Ученики показывают картинку, соответствующую их настроению в начале урока)
– Начать работу по теме урока мне хотелось бы с высказывания древнегреческого философа Саади «Ученик, который учится без желания –  это птица без крыльев» . И мне хотелось бы, чтобы было у вас желание учиться, узнавать новое, неопознанное не только на сегодняшнем уроке, а всегда и только в этом случае своими «крыльями» будете взлетать все выше и выше.

2. Актуализация знаний учащихся

– Тема нашего урока: Решение задач на нахождение дроби от числа и числа по его дроби.
– Как вы думаете, чем мы сегодня будем заниматься на уроке? (ответы учащихся)
– Правильно, сегодня на уроке мы повторим и закрепим навыки решения задач по данной теме.
– А результатом работы послужит выполнение теста в конце урока.
– Открываем тетради и записываем тему урока
Тогда – в путь! И пусть  девизом урока будут слова:

Думать – коллективно!
Решать – оперативно!
Отвечать – доказательно!
Бороться – старательно!
И открытия нас ждут обязательно!

– Наш урок пройдет в форме электронного журнала «Дроби вокруг нас». Любой журнал имеет страницы, так и мы рассмотрим следующие страницы  

Содержание

1. Историческая страница
2. Страница устной работы
3. Страница «Вмире животных»
4. Страница «Путешествия»
5. Страница «Здоровье»

– Итак, открываем  первую страницу  журнала это – «Историческая». Вы уже многое знаете из истории возникновения дробей, а сегодня мы продолжим знакомство с возникновением дробей и  ученик приготовил разные виды записи дробей 

Выступление ученика и плакат ученика

Первой дробь была дробь 1/2?. Посмотрите, как изображали дроби в Древнем Египте.

Первым дробную черту ввел  итальянский ученый  Фибоначчи.

1) – Спасибо. Молодцы. А сейчас мы посмотрим кто внимательно слушал и сможет ответить на мой вопрос: Кто первым изобрел черту дроби?
– Правильно, Фибоначчи, молодцы.
2) – А сейчас возьмите фломастеры и листочки на парте и запишите дробь как Древние Египтяне – 1 вариант, как Древние Китайцы – 2 вариант.

– Покажите теперь друг друг, у кого получилось?
– Оказывается приемы записи дробей в древности нам известны и мы даже можем их использовать, но конечно,  же традиционная запись нам удобнее и привычнее для выполнения различных заданий, поэтому мы продолжаем работу с дробями в их привычноим виде.
Переходим к следующей странице  Страница устной работы

3. Устная работа

На доске записаны дроби (Презентация, слайд 8)

Вопросы:

– Назовите правильные дроби. Как определяли?
– Назовите неправильные дроби. Как определяли?
– Выделите целую часть у неправильных дробей.
– Найдите произведение 1 и 3 дробей. Каким правилом пользовались?
– Разделите третью дробь на пятую. Какое правило применяли?
– Назовите равные дроби.

– Как найти число по заданной дроби?

Найти число, если:

1/6  его  составляют   360
5/6 его  составляют  60
0,5  его составляют 100

– Как найти дробь от числа?

Найти:

1/2 от 60
8/9 от 18.

– На этой странице мы повторили правила  нахождения дроби от числа и числа по его дроби. Я вижу, что вы хорошо справились с  заданиями, знаете правила.
– Посмотрите мы повторили 2 правила. Сколько типов задач по данной теме существует? (Два)
– Скажите, а когда задачу становиться легко решить? (Когда известен тип задачи)
– Правильно, значит самое главное уметь определять тип задачи.
– Поэтому сейчас я вам предлагаю 2 типа задач, они очень похожи и  мы будем определять тип каждой задачи.

4. Комплексное  применение  знаний

– Итак, я приготовила для вас на парте таблицы – посмотрите.
Задание таково: по условиям двух задач заполнить таблицу, т.е. определить все число, дробь от числа и соответственно определить тип задачи, и  решить её. Время работы 4 минуты

Тип задачи	Всё число	Дробь от числа	Значение дроби от числа	Решение задачи
1. Нахождение дроби от числа			?
2. Нахождение числа по его дроби	?

Вопросы к задаче1:

– Что есть всё число в задаче? (Всего учащихся)
– Известно ли оно? (50)
– О какой дроби от числа говорится в задаче? (2/5)
– Известно ли значение этой дроби? (Нет, его надо найти)
– О каком типе задач идёт речь? (Нахождение дроби от числа)

Решаем задачу 2
Проверяем решение

Сделаем проверку таблицы:

Тип задачи	Всё число	Дробь от числа	Значение дроби от числа	Решение задачи
1. Нахождение дроби от числа	50		?	50 · = 20
2. Нахождение числа по его дроби	?		20	20 : = 50

– Мы рассмотрели два типа задач, ответьте на мой вопрос: чтобы не допускать ошибок при решении как нам нужно читать условие? (внимательно)

5. Тренировочные упражнения

Следующая страница «В мире животных»

Мама-слониха имеет массу 600 кг.
Найдите массу слонёнка, если известно, что она составляет 1/5 часть от массы большого слона.

Два ученика решают на оборотах доски, а остальные в тетради, затем проверяем решение – 2 оценки.

При проверке проговорить тип задачи.

Решение: 600*1/5 =120 кг

Задача про тигренка.

Маленькому тигренку на обед положено 3 кг мяса, а он съел только ? от куска мяса. Сколько  килограммов мяса съел тигренок? (Все ученики решают в тетради. Затем проверка решения.)

Решение: 3 * 3/4 = 21/4 кг мяса

– Каким правилом мы пользовались,  решая эти задачи? (Нахождением дроби от числа)
– Ребята, а вы видели маленького тигренка и маленького слоненка? Где? А как вы думаете в неволе животным живется хорошо?
– А вот то место, где и тигренку и слоненку было бы комфортно…

6. Физминутка

Уголок природы (музыкальное сопровождение)

– Ребята! Что вы видите на слайде? Да, это любимое место отдыха каждого из нас – замечательный уголок природы. Воздух здесь чистый и свежий. Выполним дыхательную зарядку.

Дышим носом глубоко
Дышим носом глубоко –
Поднимаемся легко.
Я дышу,
Дышу свободно,
Глубоко и тихо –
Как угодно.
Выполню задание,
Задержу дыхание.
Раз, два, три, четыре –
Снова дышим:
Глубже, шире…

– Мы отдохнули, побывали в теплом, уютном месте, а теперь продолжим работу. Перелистывая страницы журнала, мы переходим к Странице «Путешествия». На этой странице нам представлена задача на вычисление длины пути между Москвой и Санкт-Петербургом, а это современный скоростной поезд Сапсан.

Поезд проехал 600 км, что составило 2/3 пути. Сколько километров составляет весь путь?

Два ученика решают на оборотах доски, а остальные в тетради, затем проверяем решение – 2 оценки.

Решаем: 600 : 2/3 = 900 км

– Как вы думаете, должен чувствовать себя человек, отправляющийся в путешествие?
– Правильно, он должен быть здоровым!

Ну а следующая страница в журнале  – страница «Здоровья»

Задача: Минимальный объем молочных продуктов, необходимый 12-летнему школьнику, составляет  3/20 от всей выпиваемой за день  жидкости, что составляет 300 грамм. Какой объем жидкости в среднем употребляет 12-летний школьник?

Решение самостоятельно, затем проверка

Решение: 300 :  = 2000г

ВОСПИТАНИЕ ЗОЖ

– Скажите ребята, а зачем 12-летнему учащемуся потреблять молочные продукты?
– А вы употребляете молочные продукты? Какие?
– А какие продукты еще полезны ученикам?
– Ребята, скажите а последние две задачи мы решали, используя какое правило?
– Большую часть журнала мы рассмотрели, и следующим заданием является выполнение теста по вариантам (раздаются задания).

7. Самостоятельная работа по вариантам (Приложение)

Затем проверка правильности решения

1 вариант

1 – в, 2 – а, 3 – б, 4 – 24%

2 вариант

1 – а, 2 – а, 3 – а, 4 – 42%

8. Рефлексия

– Ребята, вам понравилось на уроке, а какое настроение у вас сейчас? Покажите мне индикаторы вашего настроения на уроке.
Уходя из класса, прикрепите на доску одну из них.

9. Подведение итогов
– Выставление оценок 4 учащихся за решение задач на доске, отметить самых активных учеников, а остальные получат оценки за тест.
– Ребята, а какие цели мы ставили сегодня на уроке?
– Удалось ли нам их достигнуть?
– Какие типы задач сегодня на уроке мы решали?
– Сформулируйте правила нахождение дроби от числа и числа по его дроби.
– Чем отличаются и что общего в условиях этих задач?
– А какие вам понравились больше всего? были интересны? По

urok.1sept.ru

Задачи на дроби для 6 класса

Просмотр содержимого документа
«Задачи на дроби для 6 класса»

В столовую

На рынок

№ 528.С бахчи собрали 27 т арбузов.

В столовую направили этих

арбузов, а остатка отвезли

на рынок. Сколько тонн арбузов

отвезли на рынок ?

отвезли на рынок ?

Математика 6 класс. Н.Я.Виленкин. № 512.

РЕШЕНИЕ:

ВЕРНОЕ РЕШЕНИЕ:

За три дня на элеватор доставили 651 т зерна.

В первый день было доставлено

всего зерна .

Во второй 0,9 того, что было доставлено в первый день.

№ 514 . Математика 6 класс. Н.Я.Виленкин.

?

Сколько тонн зерна было доставлено на элеватор в третий день?

РЕШЕНИЕ:

ВЕРНОЕ РЕШЕНИЕ:

ЗАДАЧА

ДРОБЬ

УМНОЖЕНИЕ

ЧИСЛО

• ЗАДАЧА
• ДРОБЬ
• ЧИСЛО
• УМНОЖЕНИЕ

ЦЕЛЬ УРОКА:

• упражняться в нахождении числа от дроби, умножении и сокращении дробей

Куплено 15 кг яблок на приготовление варенья

израсходовали купленных яблок.

Сколько килограммов яблок было израсходовано на

варенье?

Сколько килограммов яблок осталось?

Математика 6 класс. Н.Я.Виленкин. № 543.

В баке автомобиля 60 л бензина. За день

было израсходовано 25 % этого бензина.

Сколько бензина израсходовали?

Сколько бензина осталось в баке?

Математика 6 класс. Н.Я.Виленкин. № 544.

60л

18

Сварили уху

поджарили

После удачной рыбалки Костя принес домой 1,4 кг рыбы.

Из этой рыбы сварили уху, а 80 % оставшейся –

поджарили.

Сколько рыбы поджарили?

1,4 кг

Математика 6 класс. Н.Я.Виленкин. № 557.

18

ФИЗКУЛЬТМИНУТКА

Съели в 1 раз

Съели на обед

Мама купила 800 г сыра. За столом съели всего сыра,

за обедом – , а остальной сыр съели за

ужином.

Сколько сыра

съели за ужином?

800 г

Математика 5 класс (часть 2). Г.В. Дорофеев, Л.Г. Петерсон. № 677.

21

multiurok.ru

Тренажёр по математике (6 класс) на тему: Задачи на тему: «Нахождение дроби от числа и числа по его дроби»

Задачи на тему: «Нахождение дроби от числа и числа по его дроби»

Решите задачи

1. В школьную столовую привезли 120 кг картофеля. В первый день  израсходовали   всего привезенного картофеля. Сколько килограммов картофеля израсходовали в первый день?                                                                                          

2. Длина  прямоугольника  56 см.  Ширина  составляет    длины.  Найти  ширину  прямоугольника.

3. Пришкольный  участок занимает площадь 600 м2.  Ученики шестого класса в первый день вскопали  0,3  всего участка. Какую площадь вскопали ученики в первый день?

 4.  В  драматическом  кружке  занимаются  25   человек.  Девочки  составляют  60 %  всех  участников  кружка.  Сколько  девочек  занимается  в  кружке?

5. Площадь огорода     га. Картофелем  засажено   огорода. Сколько гектаров засажено картофелем?

6. В один пакет насыпали  2   кг пшена, а в другой  –     этого количества.

    На сколько меньше пшена насыпали во второй пакет, чем в первый?

7. С одного участка собрали  2,7   т моркови, а с другого  –     этого       количества. Сколько всего собрали овощей с двух участков?

8. Пекарня выпекает в день 450 кг хлеба. 40 % всего хлеба идет в торговую сеть,    оставшегося – в столовые. Сколько кг хлеба каждый день идет в столовые?

9. В овощехранилище привезли 320 т овощей. 75 % привезенных овощей составлял картофель, а    остатка – капуста. Сколько тонн капусты привезли в овощехранилище?

10. Глубина горного озера к началу лета была  60м. За июнь его уровень понизился на 15%, а в июле оно обмелело на 12% от уровня июня. Какова стала глубина озера к началу августа?

11.  До обеда путник прошел 0,75 намеченного пути, а после обеда он прошел  пути,  пройденного до обеда. Прошел ли путник за день весь намеченный путь?  

12. На ремонт тракторов в зимнее время было затрачено 39 дней, а на ремонт комбайнов  — на 7 дней меньше. Время ремонта прицепного инвентаря составило  того времени, которое ушло на ремонт комбайнов. На сколько дней больше  длился ремонт тракторов, чем ремонт прицепного инвентаря?

13. В первую неделю бригадой было выполнено 30% месячной нормы, во    вторую – 0,8 того, что было выполнено в первую неделю, а в третью неделю —   того, что выполнили во вторую неделю. Сколько процентов месячной нормы осталось выполнить бригаде в четвертую неделю?

nsportal.ru

Урок математики для 6 класса по теме «Решение текстовых задач на сложение и вычитание дробей»

План-конспект урока математики 6 класc

Цели урока:

Образовательная – Моделировать сложение и вычитание дробей с помощью реальных объектов, рисунков, схем.

Выполнять сложение и вычитание дробей с одинаковыми и с разными знаменателями, используя навыки преобразования дробей; Решать текстовые задачи, содержащие дробные данные,

Развивающая – обучать приемам и методам рассуждения, развивать логическое мышление учащихся, математическую речь (устную и письменную), внимание.

Воспитательная — развивать интеллектуальные и творческие способности учащихся, познавательную активность, интерес к математике; поощрять самостоятельность учащихся при поиске способов решения задачи.

интерактивная доска (ИД), презентация, рабочие тетради

Формы работы учащихся: фронтальная работа, групповая технология, ИКТ.

План проведения урока:

Этапы урока

Формируемые учебные действия учащихся

1.Организационный момент (1 мин.)

Саморегуляция

2.Актуализация знаний (8 мин.)

Построение речевых конструкций, рационализация, применение алгоритма, выдвижение и проверка гипотез, умение анализировать и реагировать на поступающие ответы. Умение слушать других, контроль, самоконтроль.

3. Целеполагание и мотивация (2 мин.)

Оценка и прогнозирование, сравнение и анализ, наблюдение и исправление неверных решений

4. Усвоение новых знаний (7 мин.)

Анализирование и осмысливание текста задания, построение логической цепочки рассуждений. Коммуникативные способности, эстетическое сознание, анализ и осмысление

5. Физминутка (1 мин)

Эстетическое восприятие, здоровьесбережение

6. Закрепление изученного материала

(12 мин)

Выделение в условии задачи данных, необходимые для решения задачи, построение логической цепочки рассуждений, сравнивание разных точек зрения, перед принятием решения; аргументирование своей точки зрения; оценивание ответа, коммуникативность,

7. Самостоятельная работа( 7 мин)

самостоятельность , самоконтроль,

8. Подведение итогов урока, рефлексия

(2 мин.)

Предметная рефлексия, осознание актуальности изученного материала

Ход урока:

Развитие эрудиции, знакомство с профессией архитектора, дизайнера, строителя.

Развитие внимания, эстетического вкуса.

Учащиеся проверяют домашнее задание с помощью документ – камеры, приводят дроби к новому знаменателю, сравнивают дроби, решают 2 примера на смекалку

Цель урока

Сегодня на уроке мы продолжим работать с обыкновенными дробями. Что мы уже научились выполнять? А кто отгадает ребус? Ну. а теперь попробуйте сформулировать тему урока.

Дети рассуждают, анализируют, решают задачу

1) 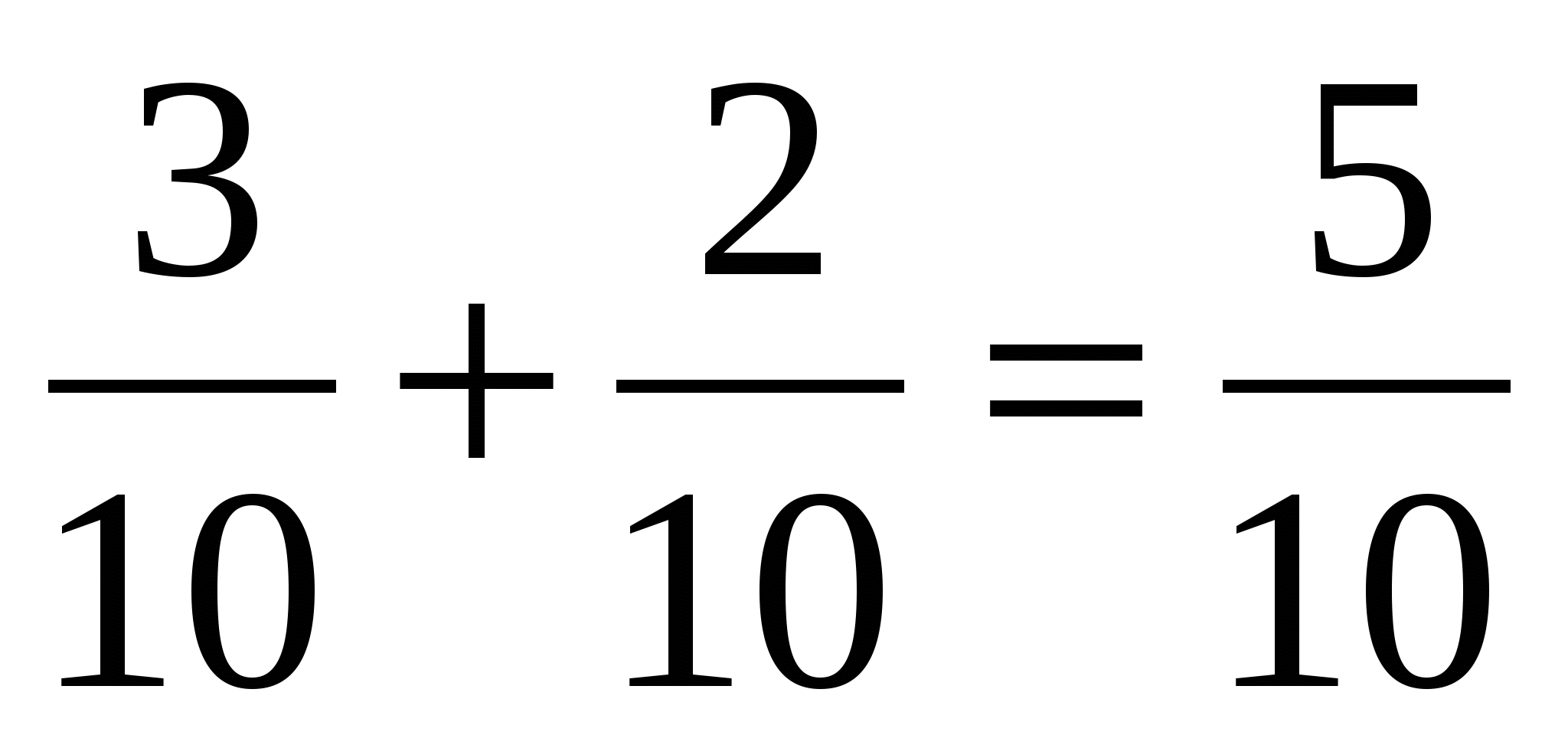(кг) яблок во 2 пакете

2) 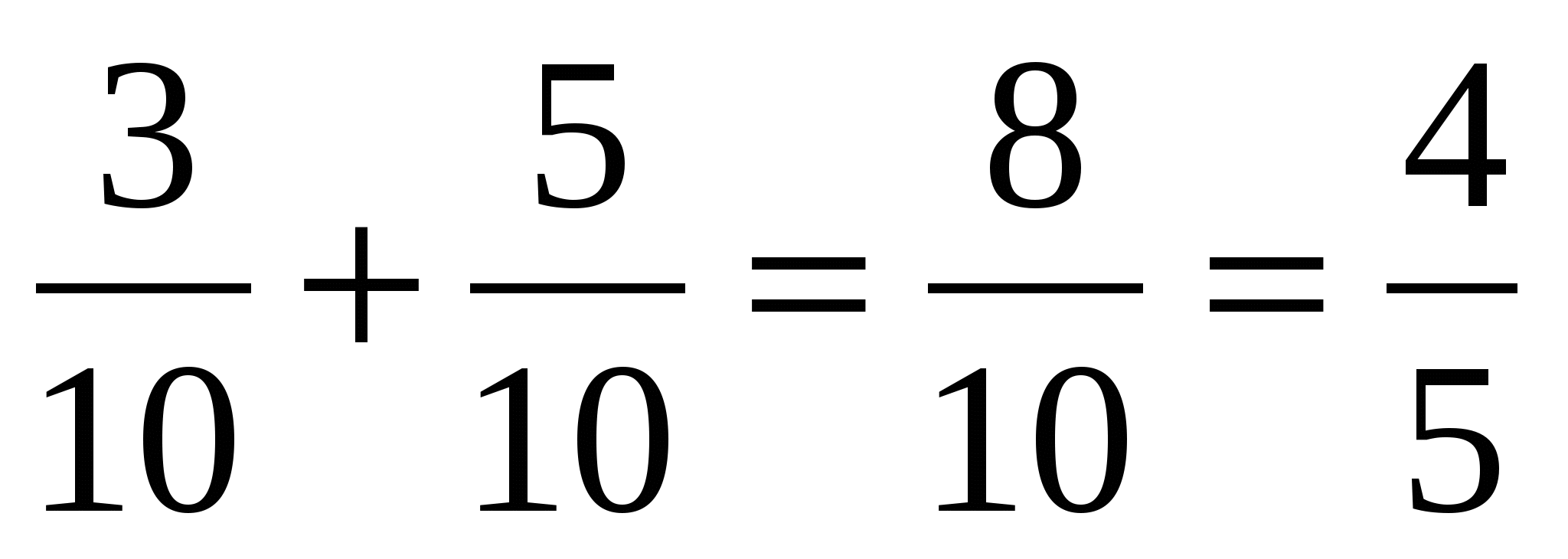(кг) яблок в двух пакетах

3) 1 — 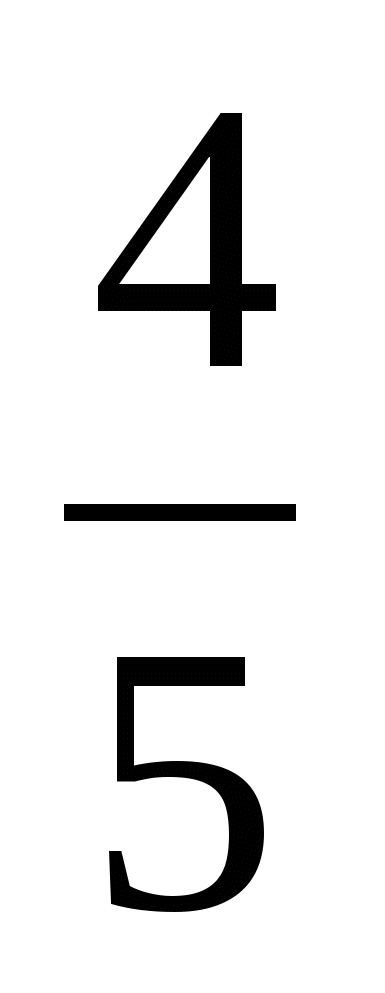= (кг) меньше чем 1 кг

4) (кг) = 1000:5 · 1 = 200(г)

Познавательные : работа с определениями понятий

Развитие эрудиции, познавательного интереса.

Ориентирование в электронном учебнике

Понимание информации, представленной в виде текста.

Формирование метапредметных связей, опора на жизненный опыт учащихся

Анализ речевых конструкций

Работа с алгоритмом

Читательские : понимание, осмысливание изучаемого материала

Коммуникативные:

Оформление своих мыслей с использованием символикой.

Учащиеся выполняют зарядку для глаз

Дидактические материалы:

№343 а) 1 — 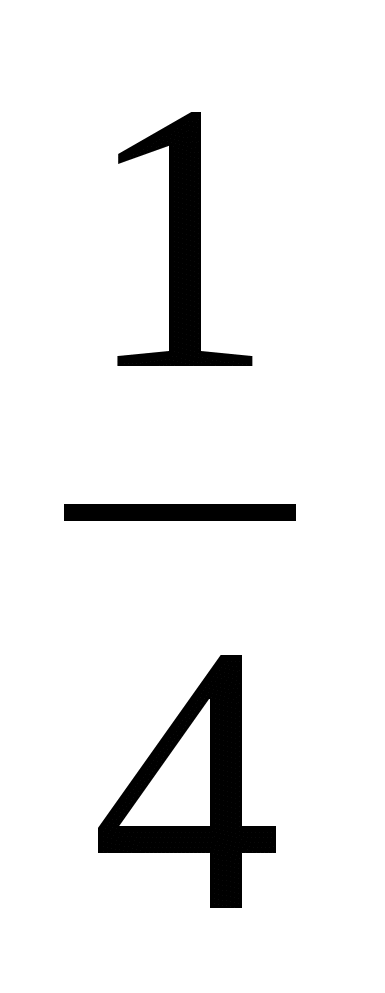(кг)

2 — ?, на (кг) больше

Всего — ? кг

Решение

1) 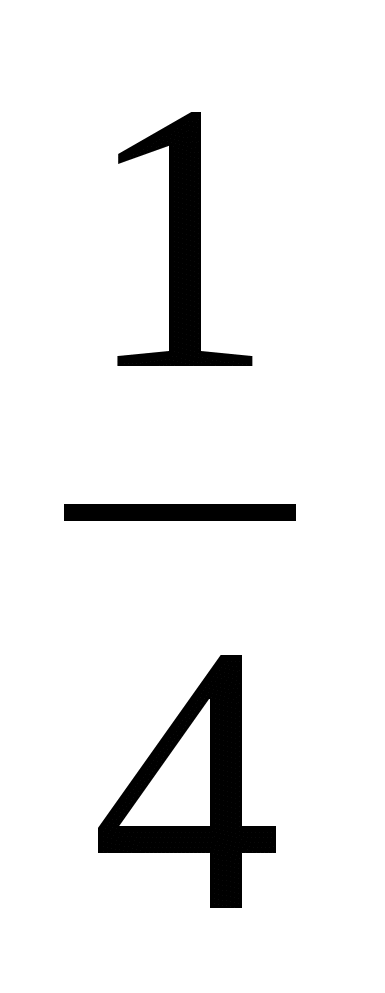+ = 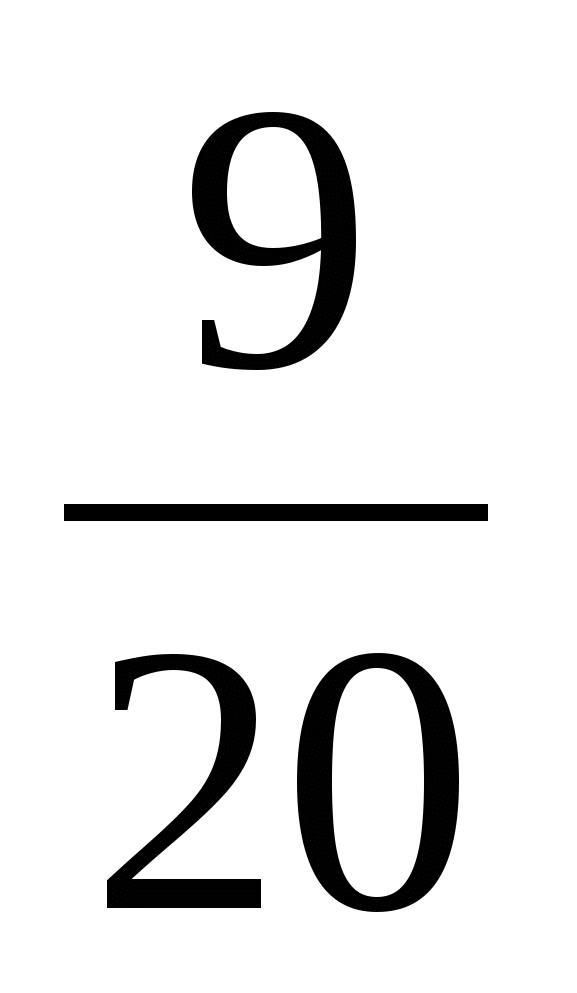(кг) –во 2 коробке

2) 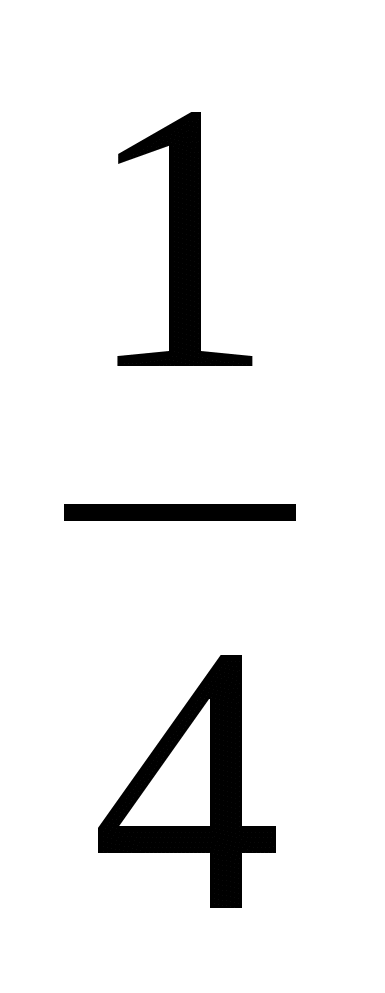+ 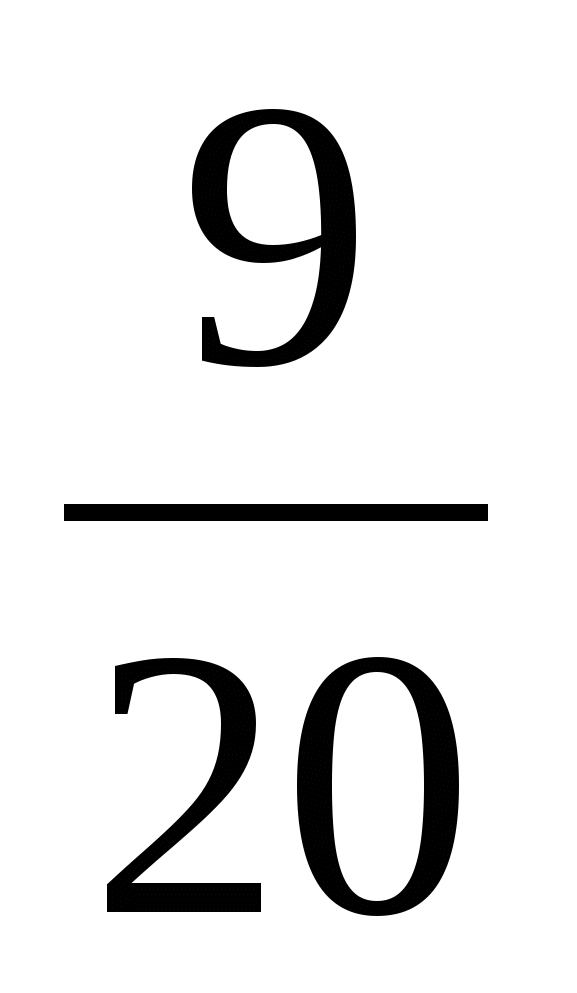= = 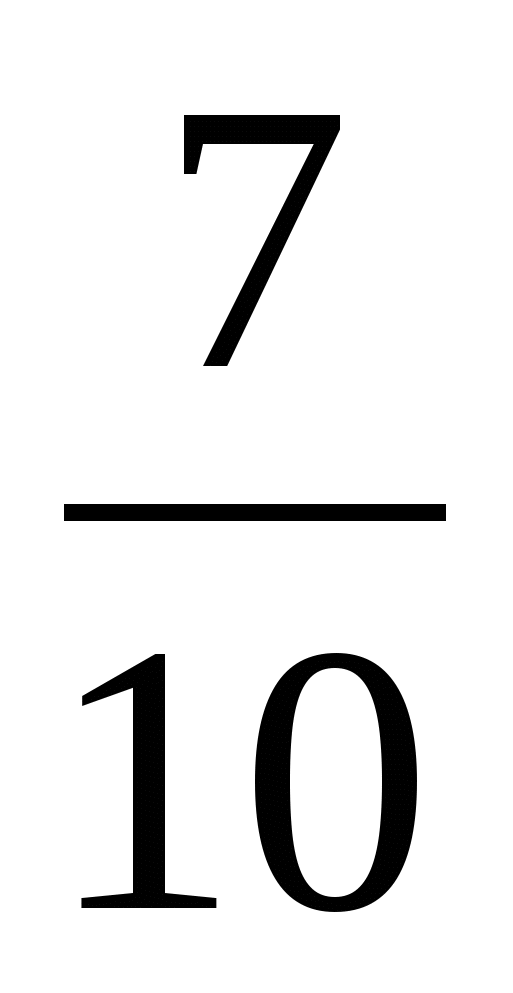(кг) = 1000:10 · 7 = 700(г)– в двух коробках

Ответ: 700 гр

б)До привала — 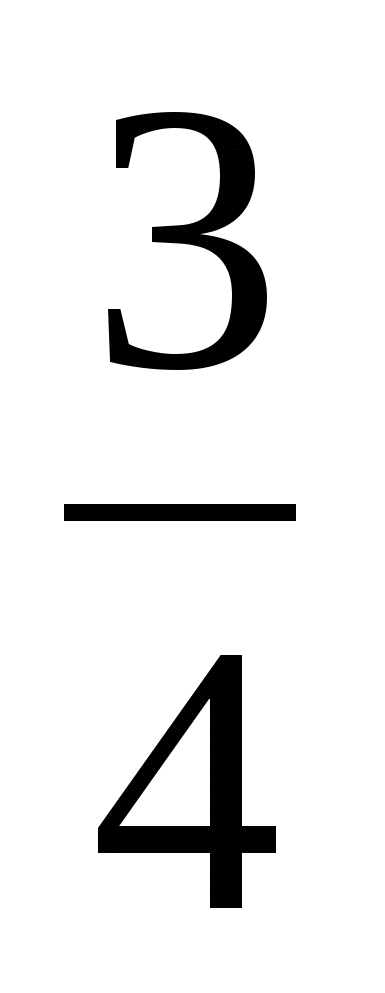ч,

Обратно — ? ч, на 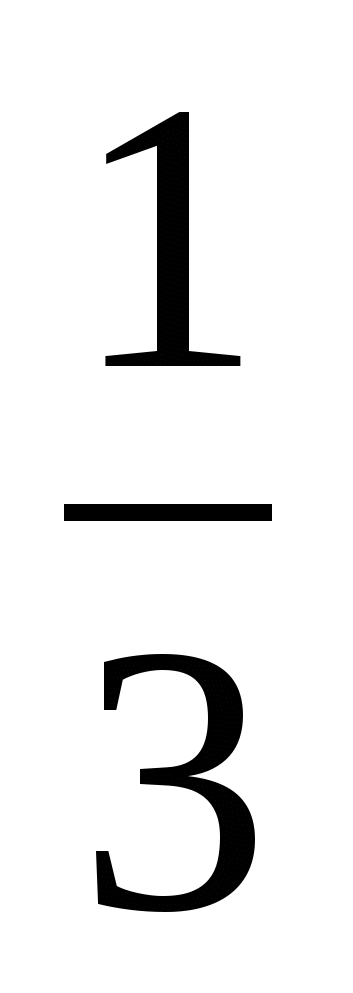больше

Привал — 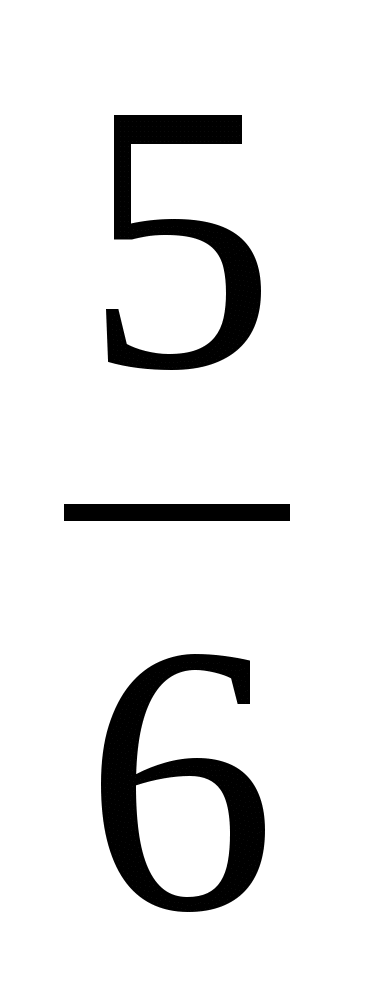(ч)

Всего — ? ч, мин

Решение

1) 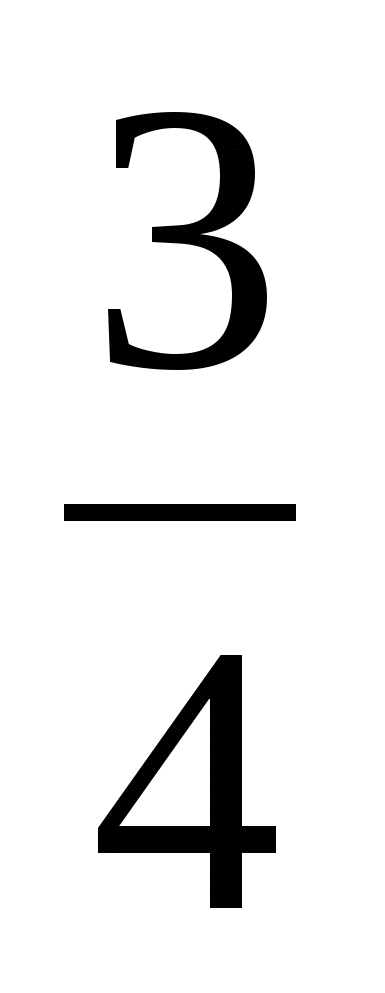+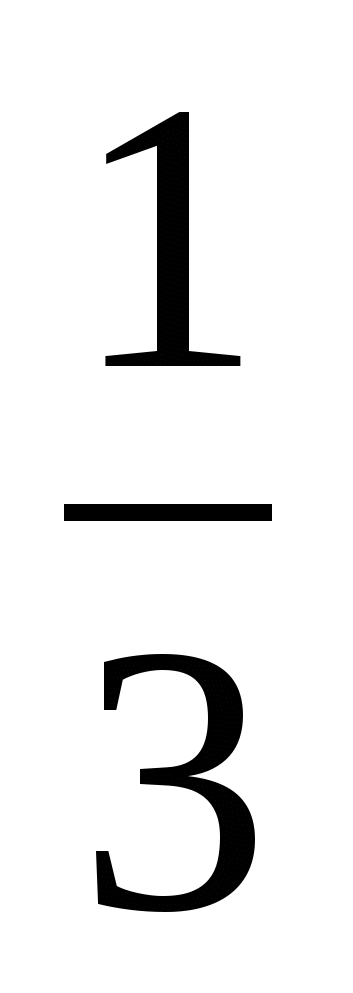= (ч) – обратный путь

2) + + 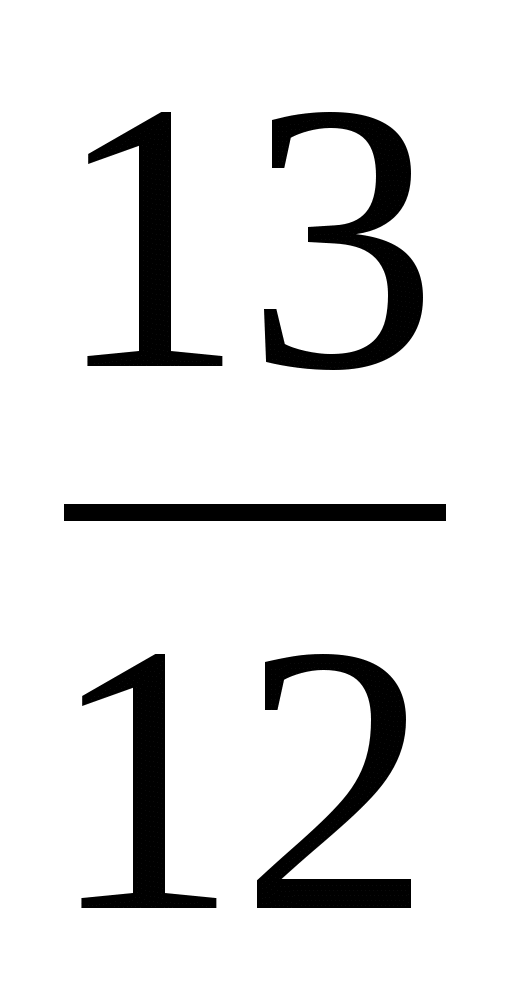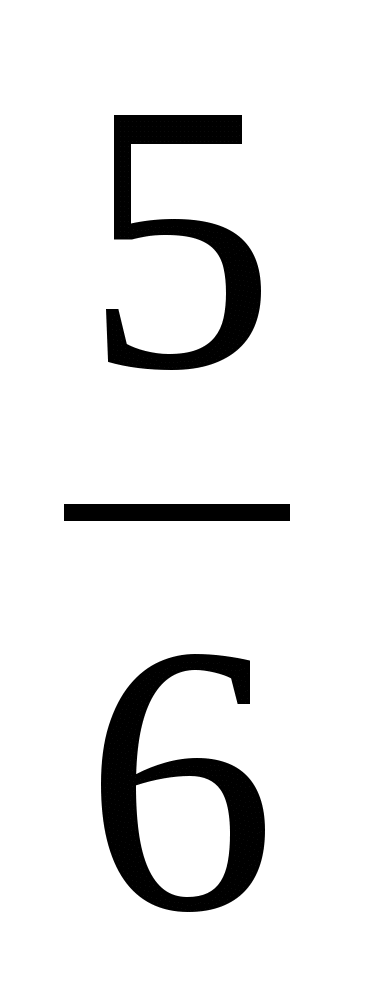= = 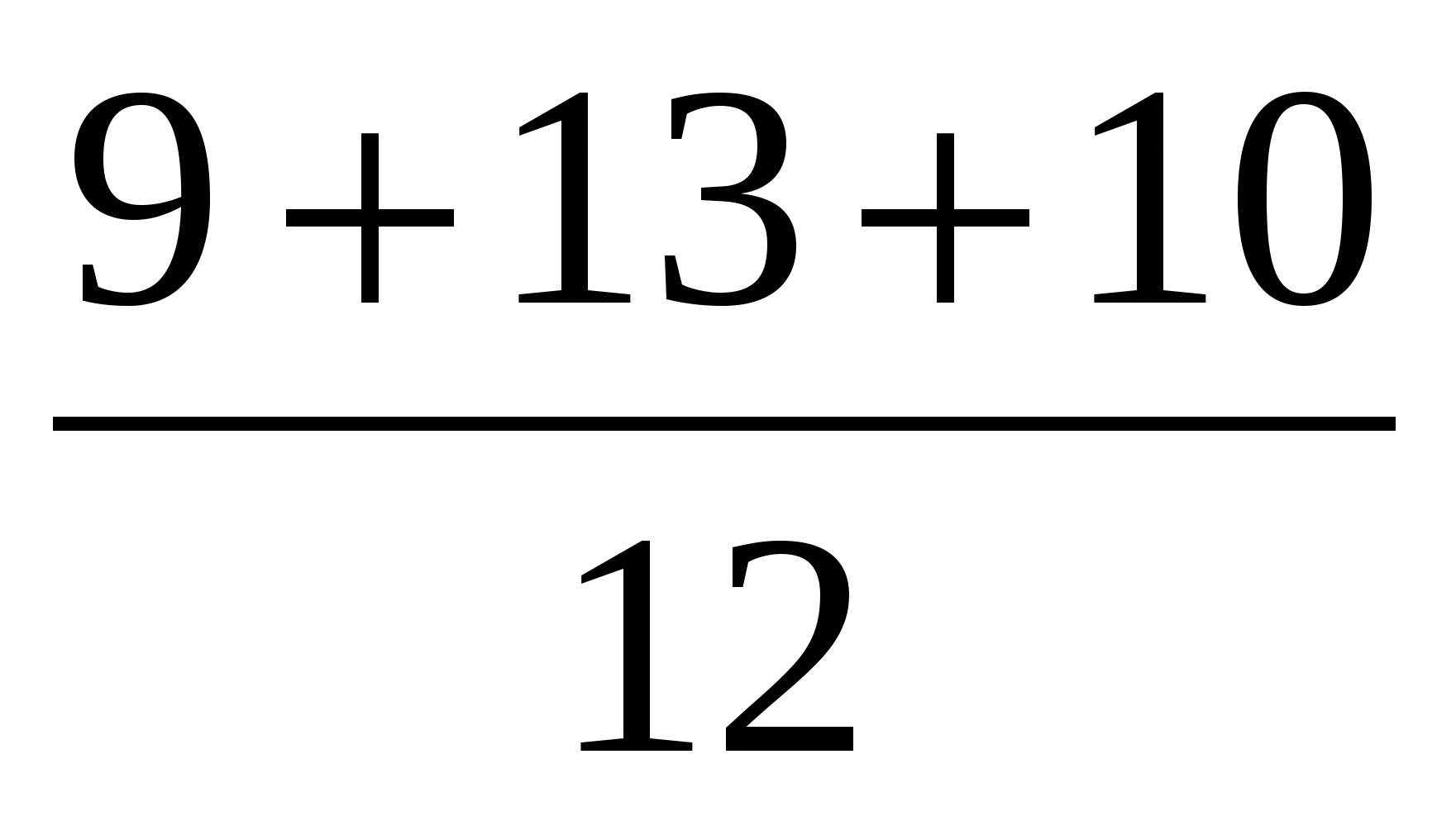=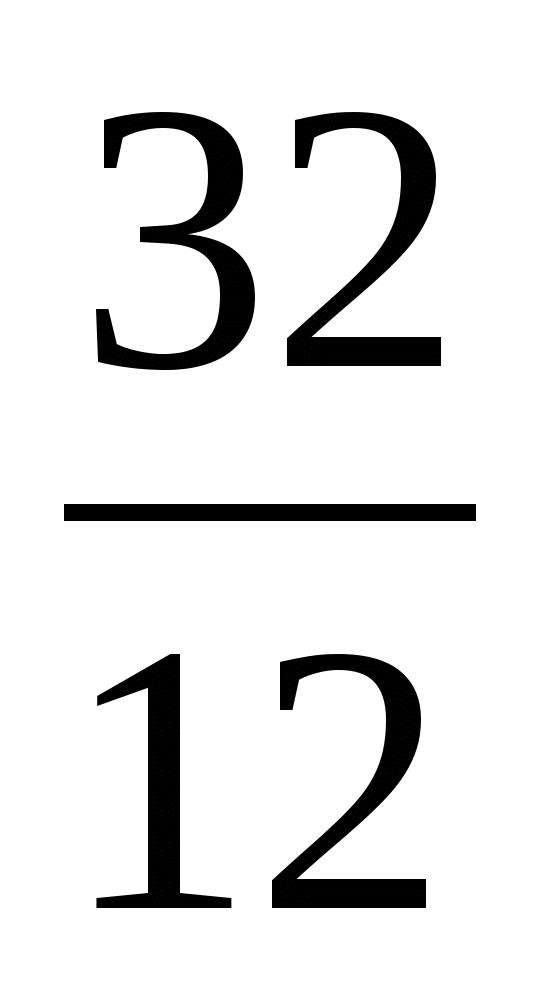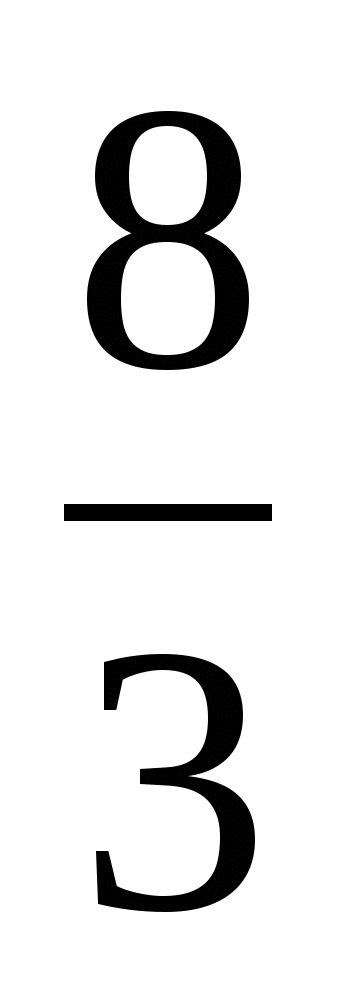(ч) – весь путь

3) 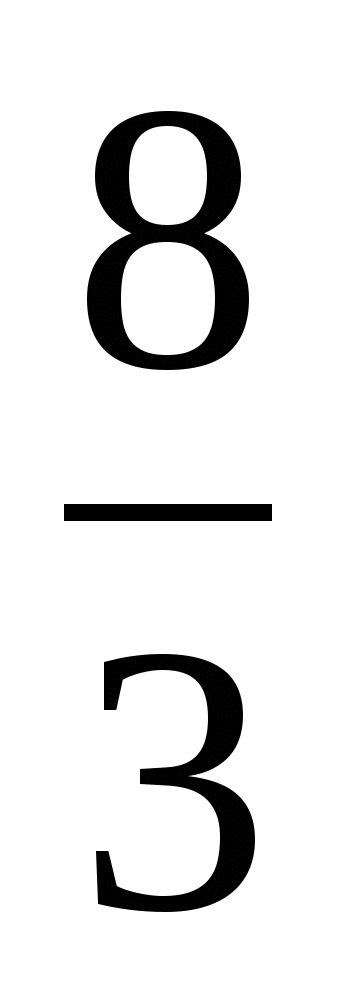ч = 60:3 · 8 = 160 (мин)

Ответ: 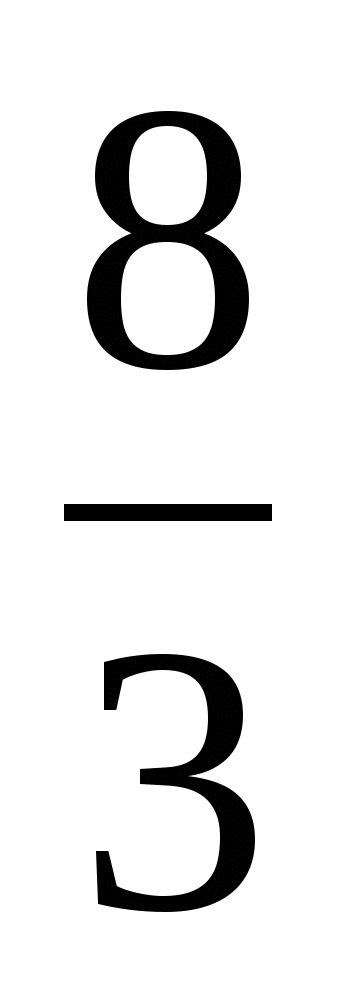ч = 160 (мин)

№ 554 Урок – 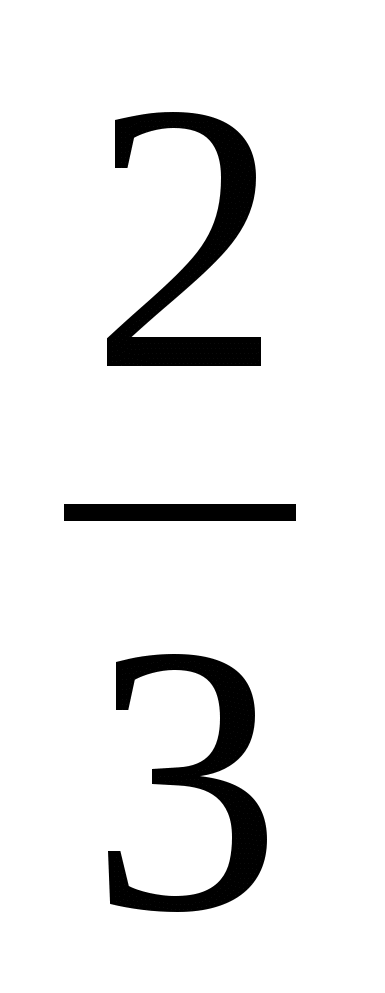ч

Перемена – ч

Всего — ? ч

Решение

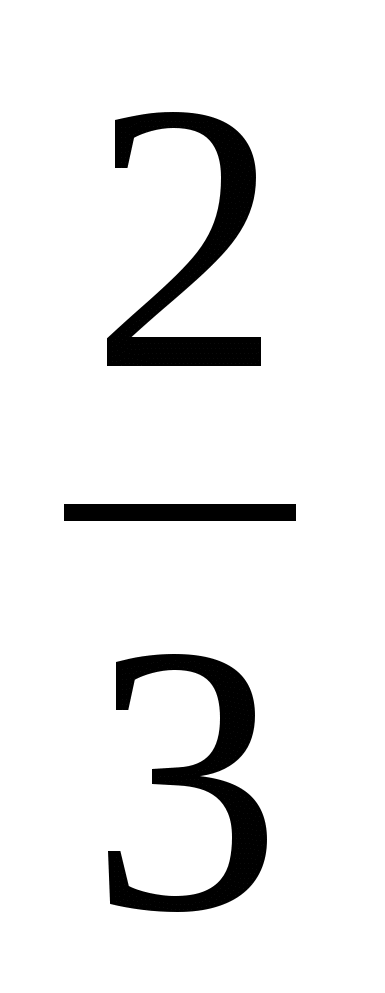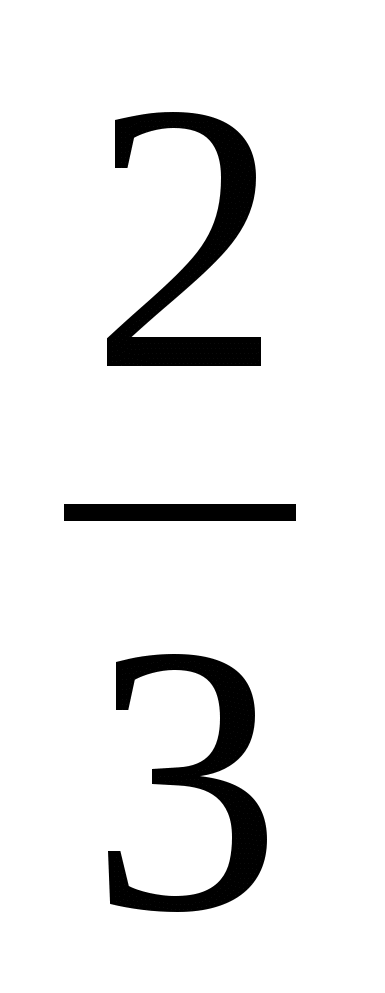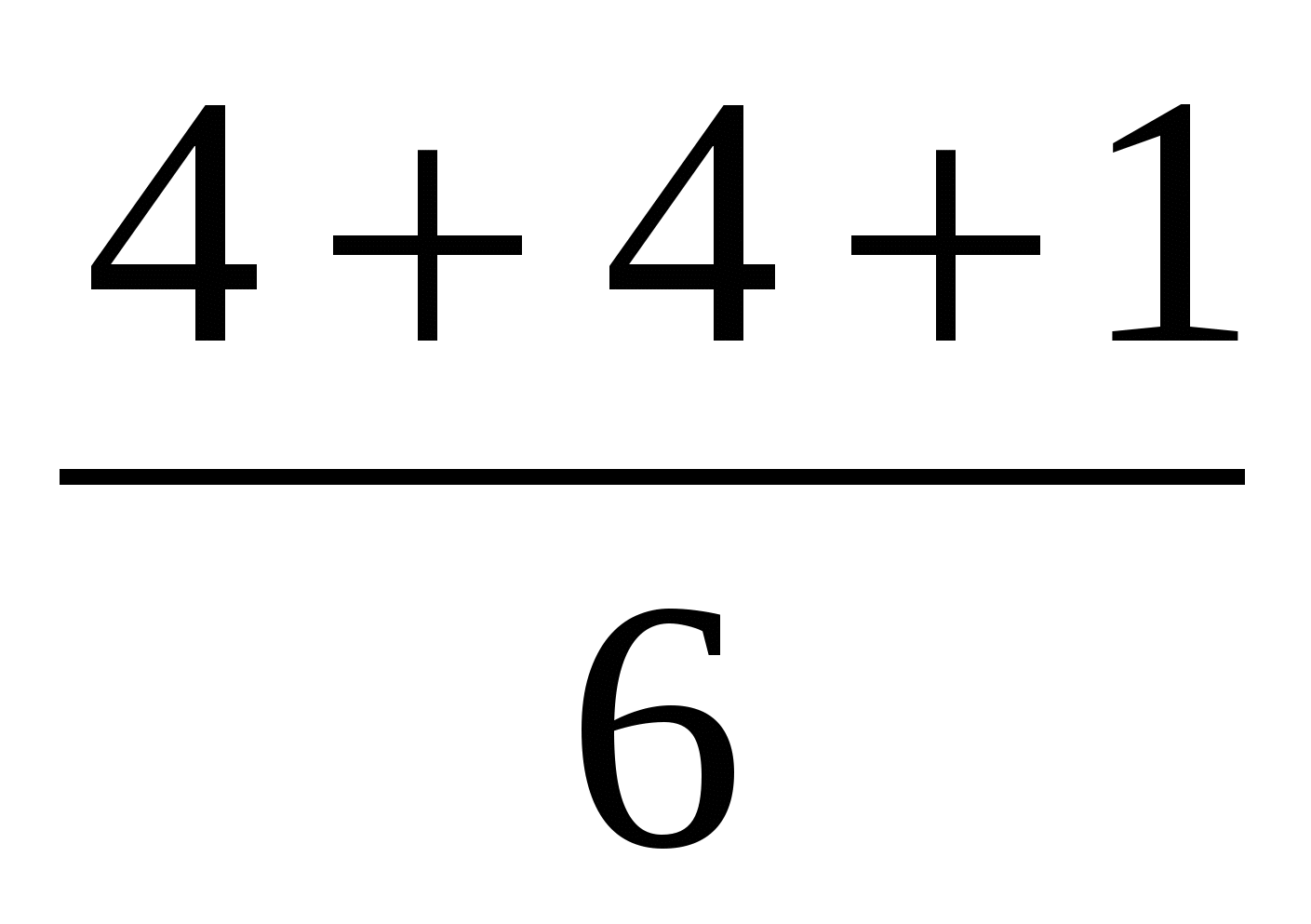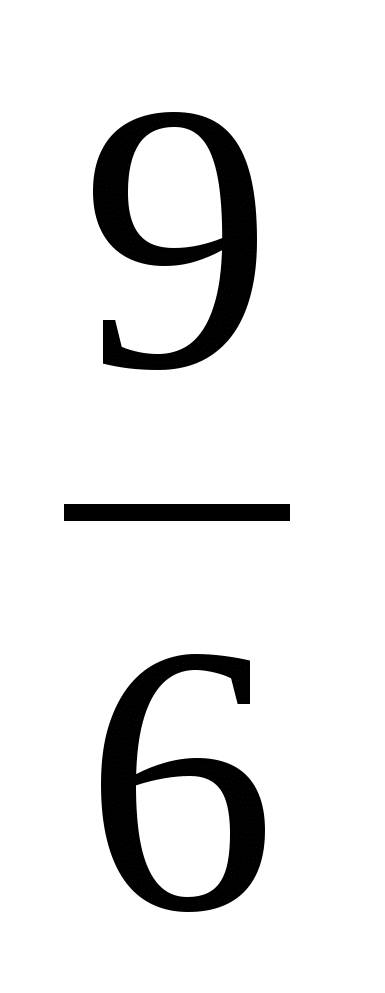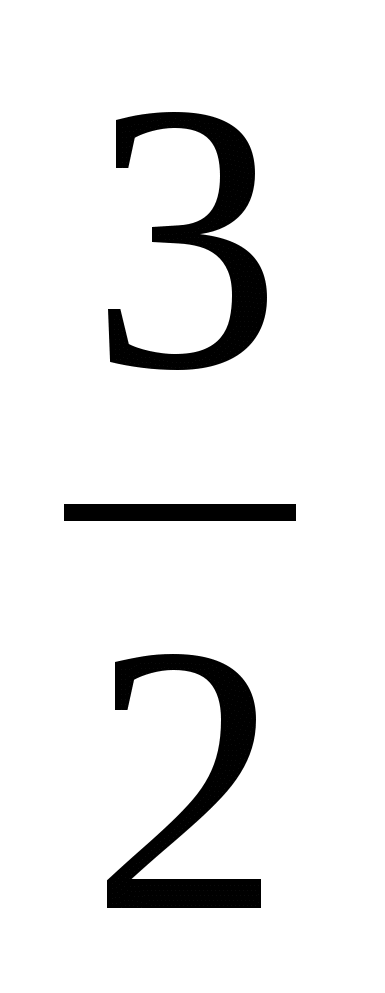+ ( + ) = = = (ч) = 60:2 · 3 = 90 (мин) – всего

Ответ: 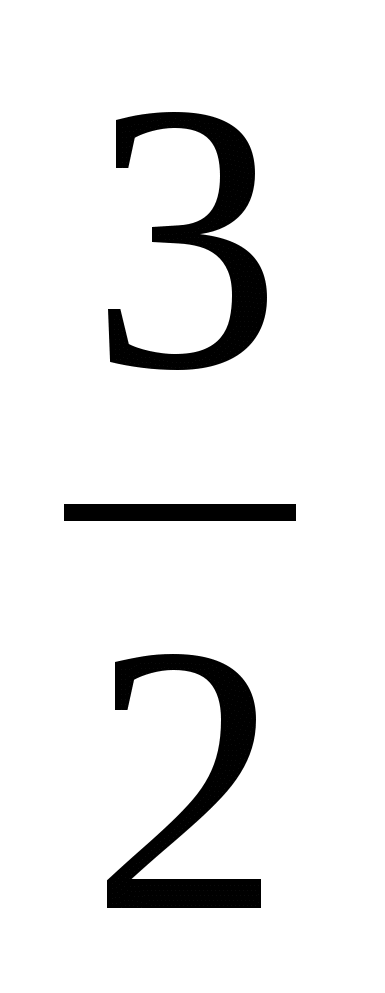(ч) = 90 (мин)

Реципация

Коммуникативные:

Оформление своих мыслей в устной форме, умение взаимодействовать с соседом при выполнении учебной задачи

Коммуникативные:

Обмен знаниями для принятия эффективных совместных решений

Личностные:

Умение делать умозаключения, аргументировать свою точку зрения.

Умение работать по алгоритму.

Самостоятельная работа Задачник на стр. 51

Вариант 1

Лит — 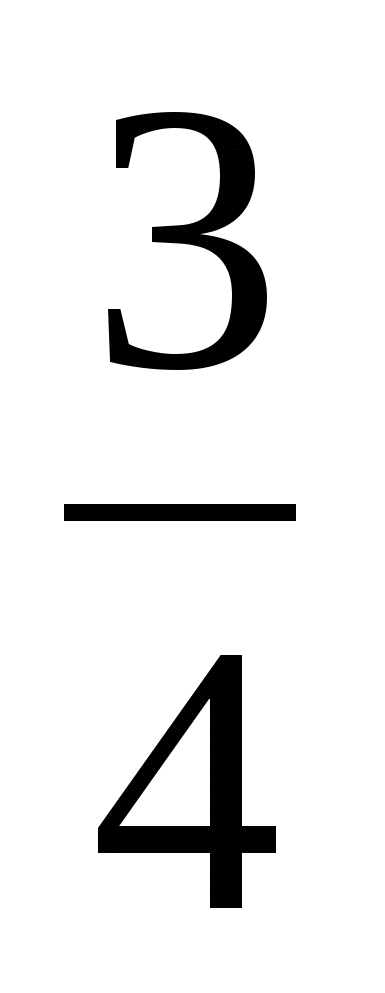(ч)

Биол — ? ч, на ч меньше

Всего? ч

Решение

1) 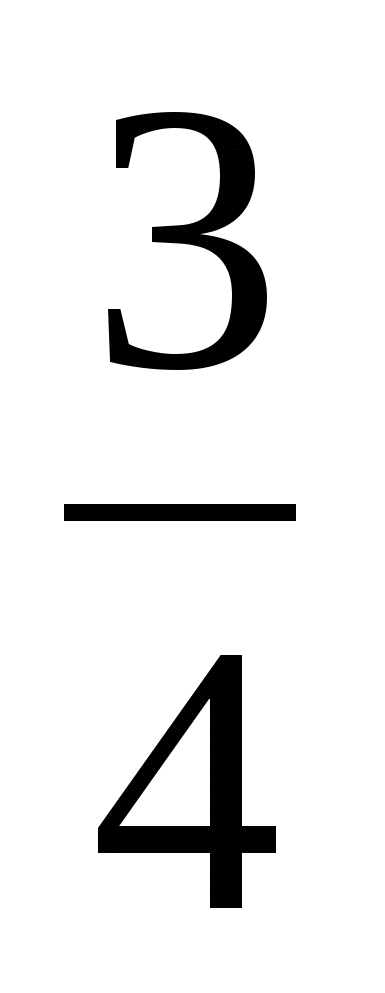+ = =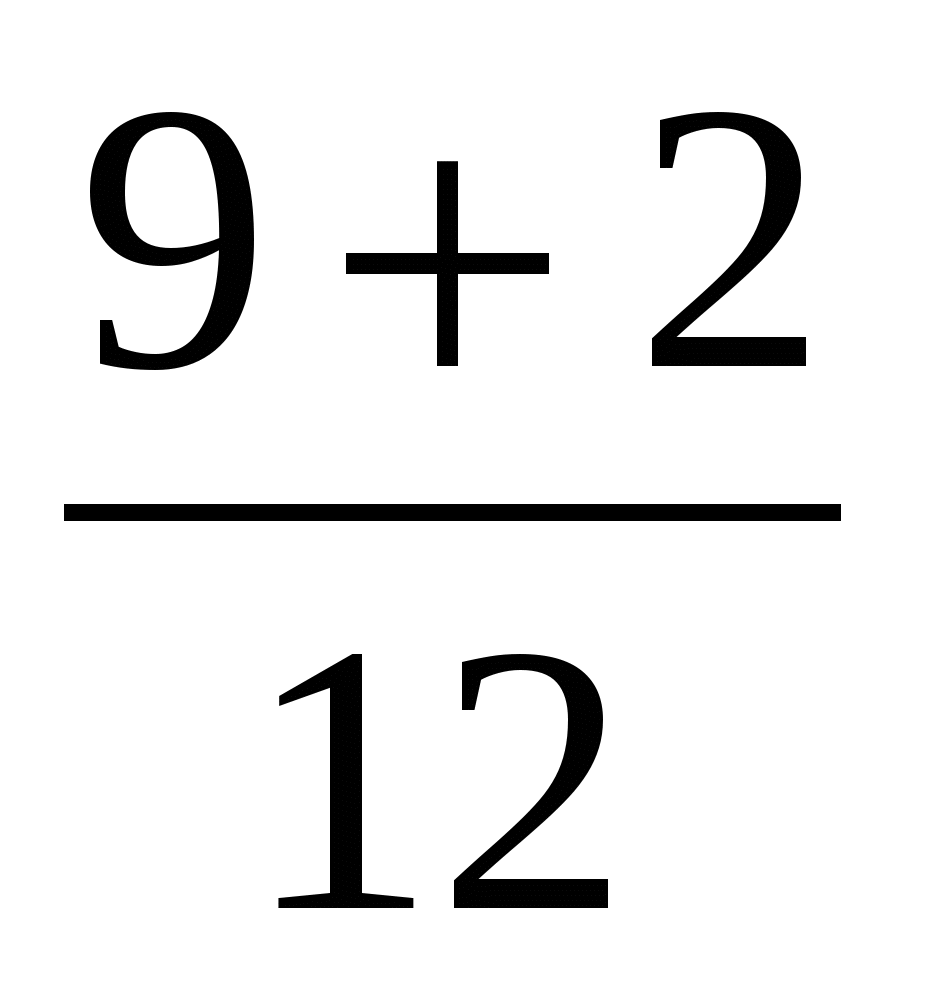 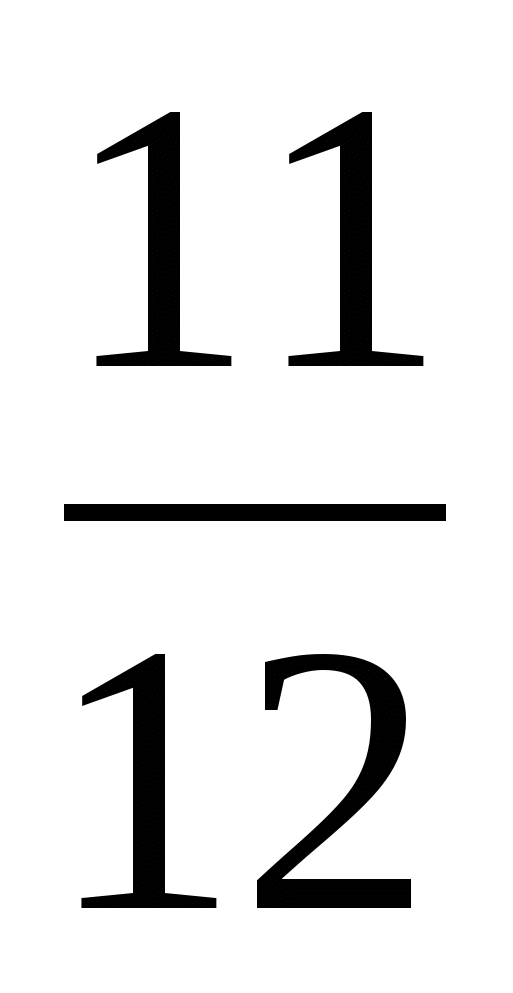(ч) всего

2) 1 — 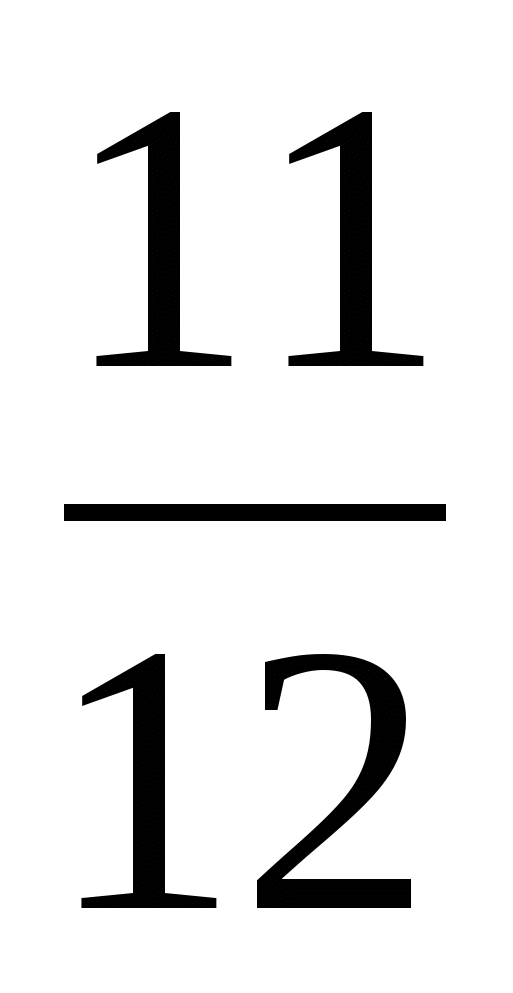=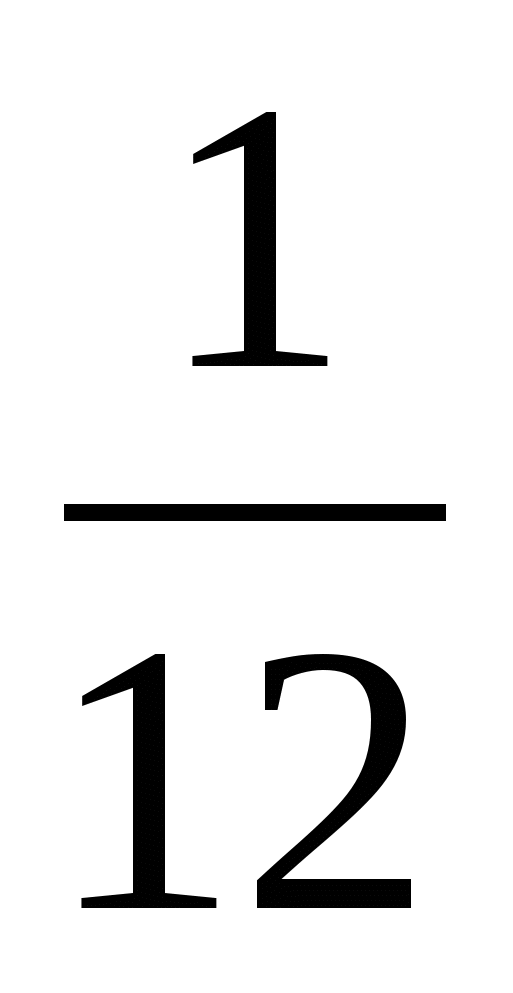(ч) = 60 :12 · 1 = 5 (мин)- меньше 1 ч

Ответ: всего — 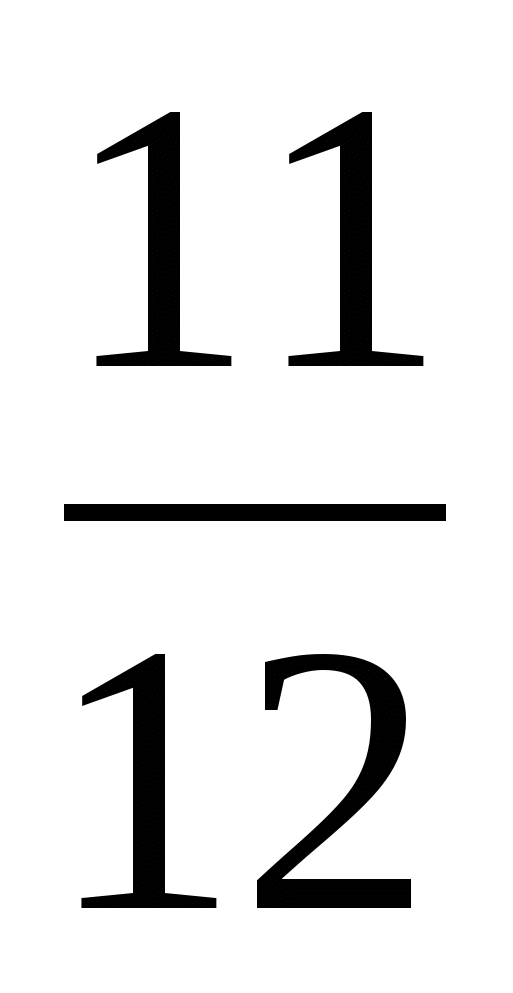(ч), больше 1 ч на 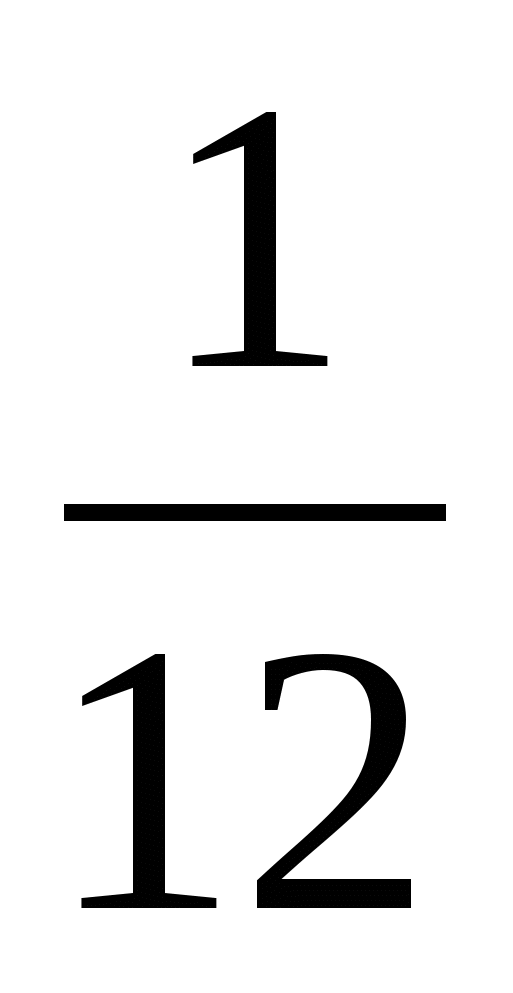(ч) = 5 (мин)

Вариант 2

Геог — 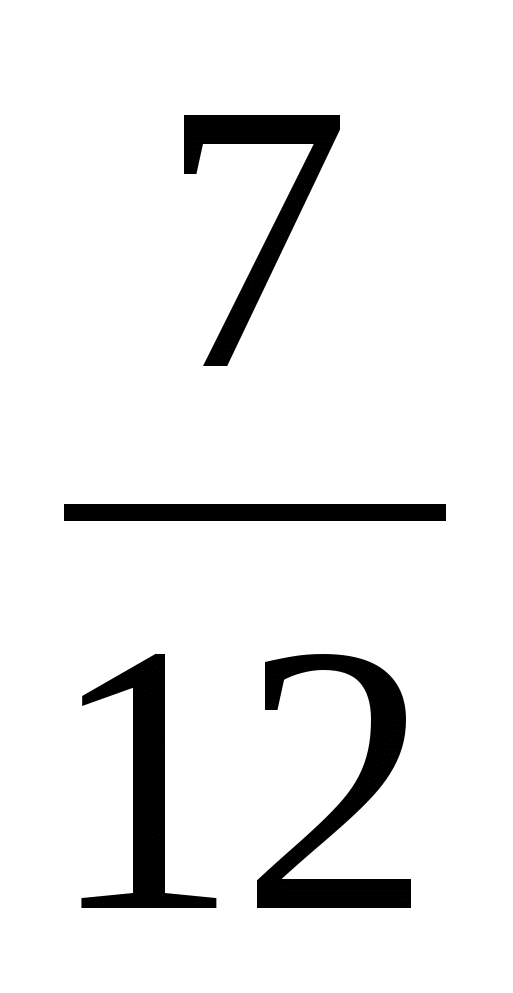(ч)

Истор — ? ч, на 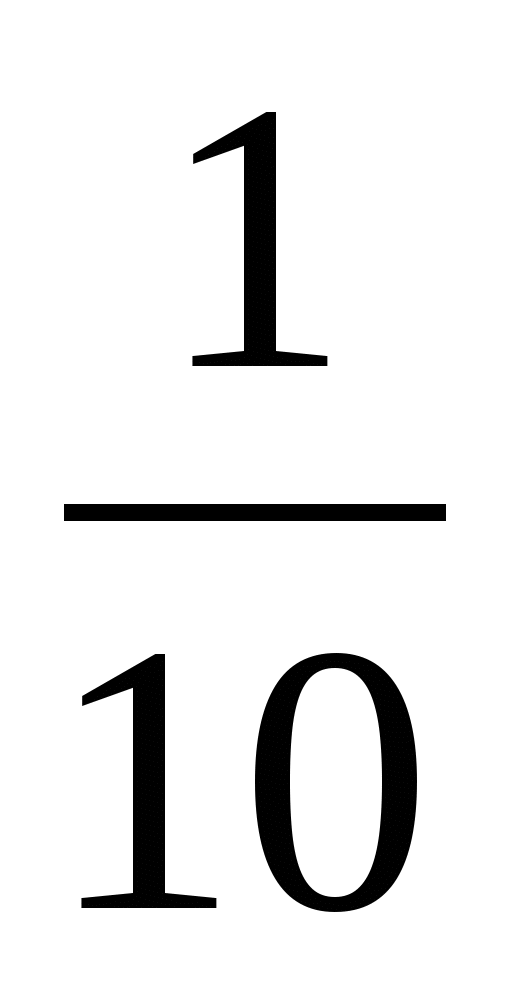ч меньше

Всего? ч

Решение

1) 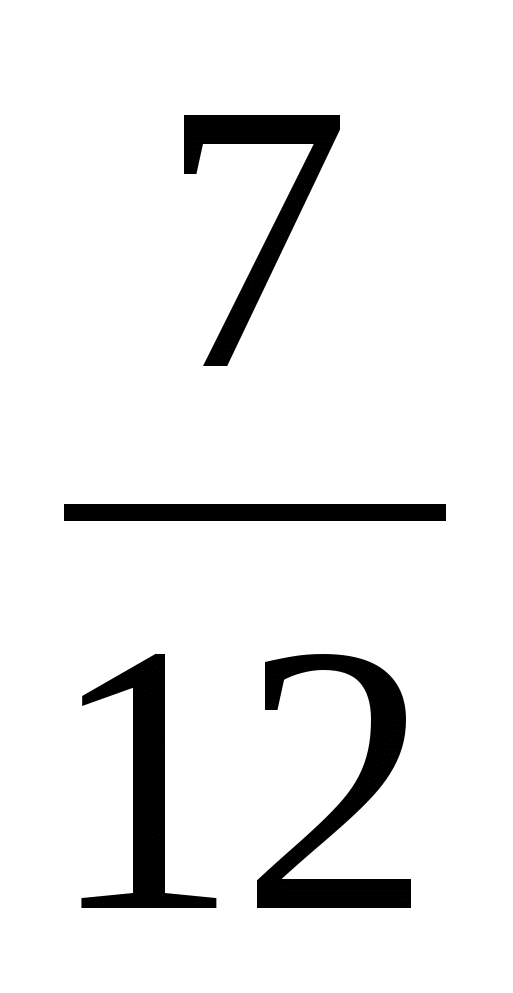+ 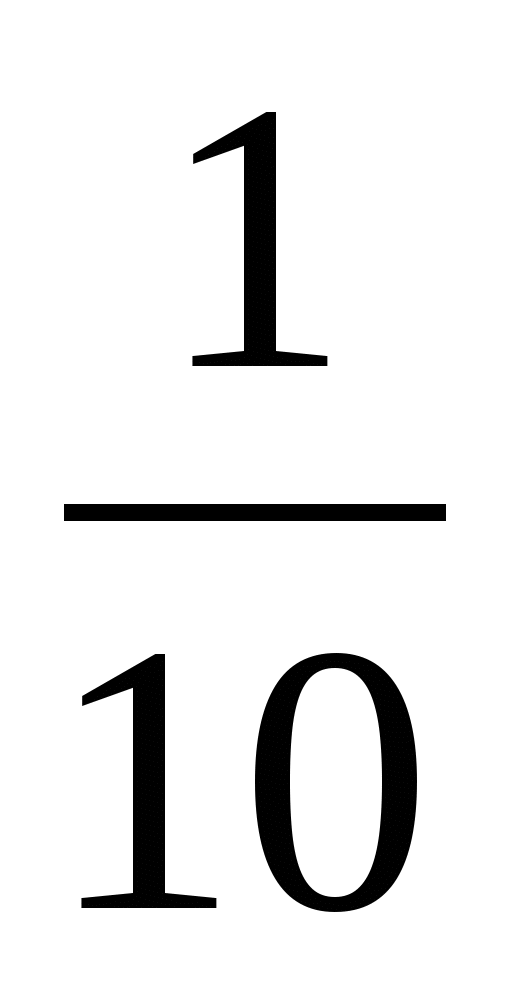= = 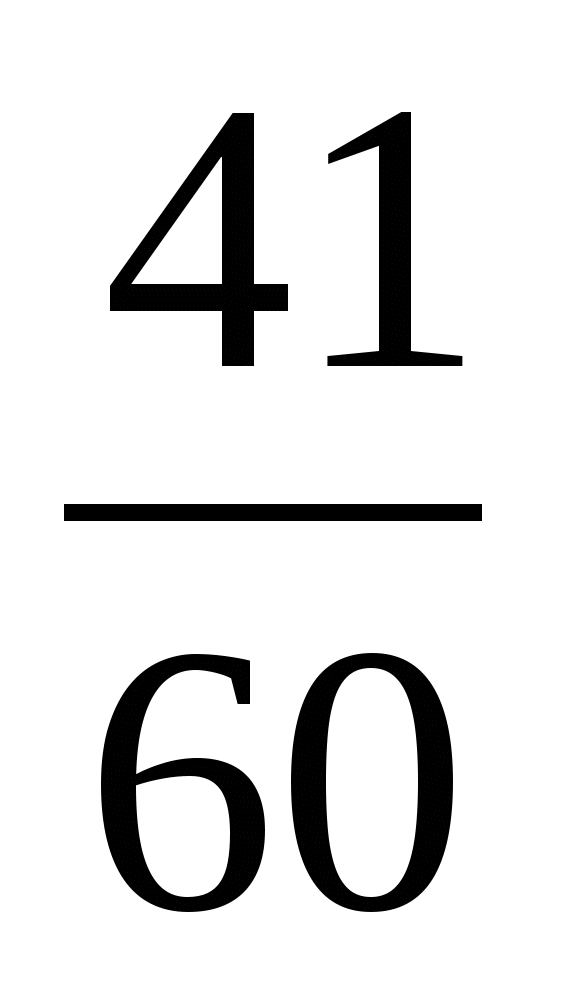(ч) всего

2) 1 — 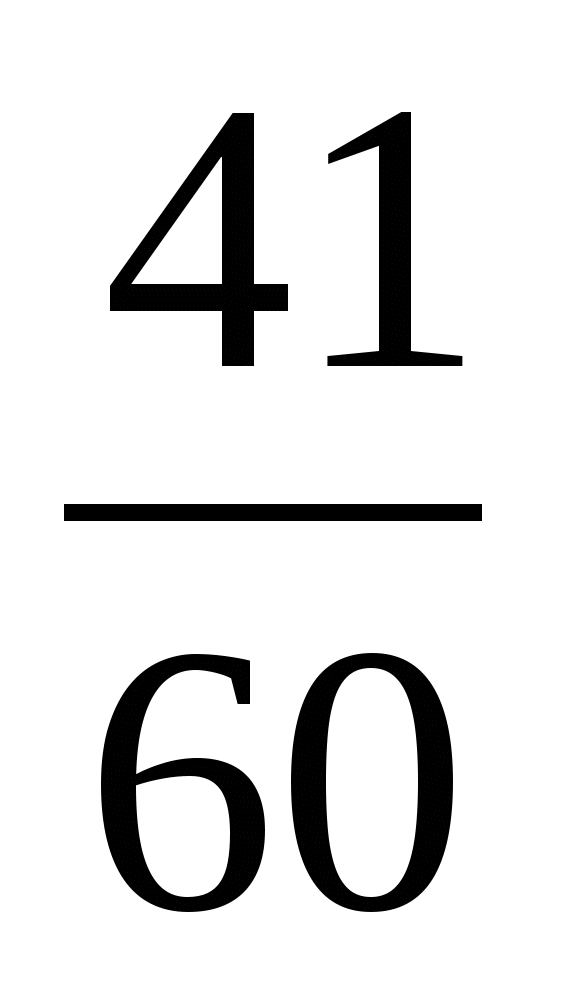=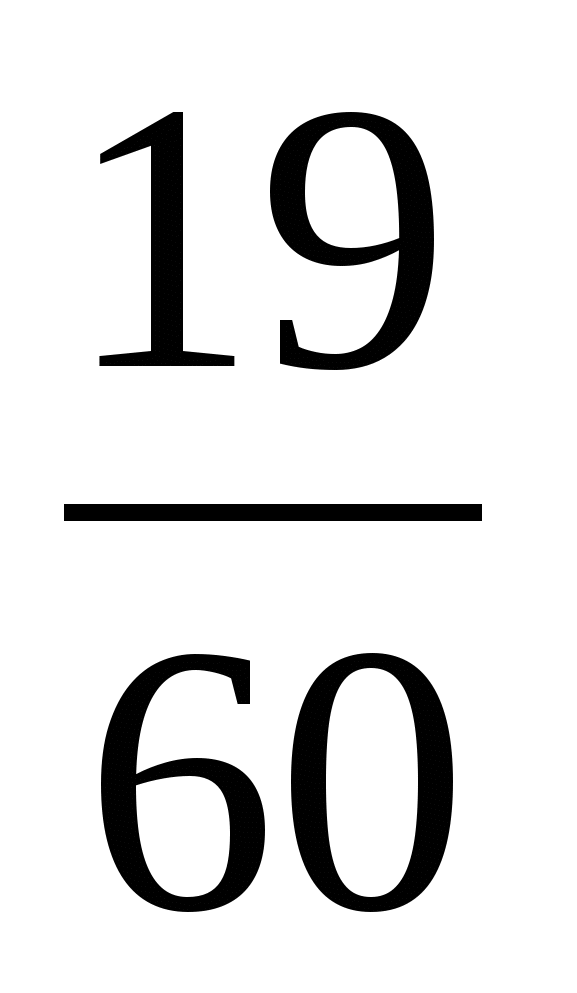(ч) = 60 :60 · 19 = 19 (мин)- меньше 1 ч

Ответ: всего — 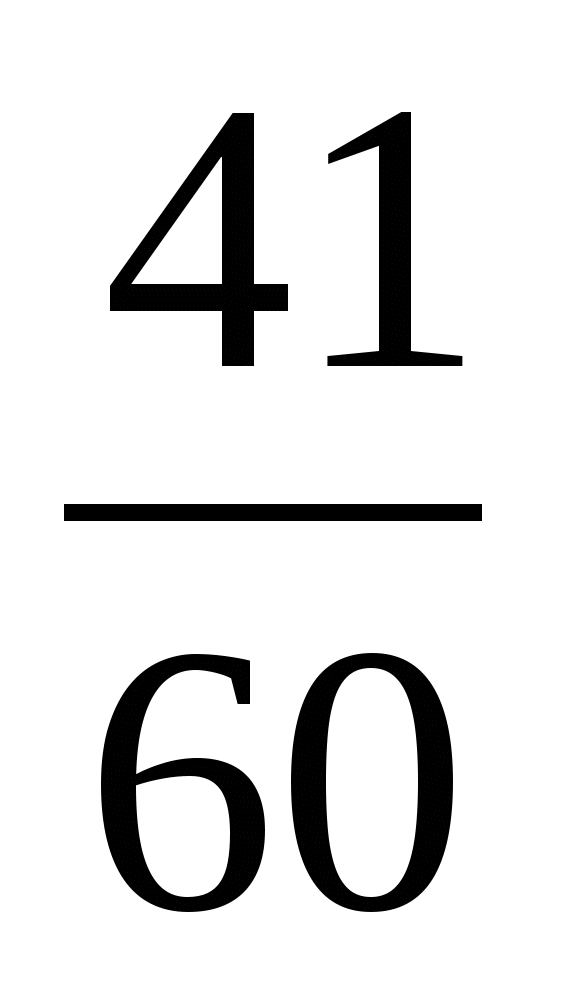(ч), больше 1 ч на 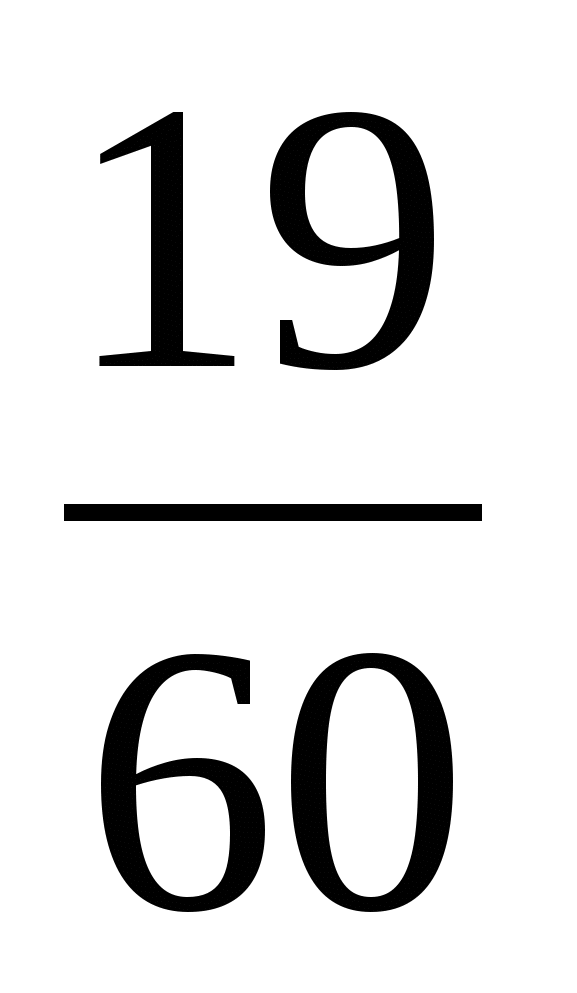(ч) = 19 (мин)

Подведение итогов урока

Дать качественную оценку работы класса и отдельных обучаемых

Подводит итог урока, оценивает работу учащихся

Развитие внимания, эстетического вкуса.

сообщает домашнее задание на следующий урок: Учебник: № 555 — 556

— Оцените свое состояние на сегодняшнем уроке. Насколько комфортно вы себя чувствовали, работая на уроке. Все ли было вам понятно.

— Изобразите, в зависимости от вашей самооценки, в своих тетрадях один из вариантов «смайлика». Спасибо за урок.

Учащиеся отвечают на вопросы, подводят итог урока

записывают домашнее задание в дневники.

infourok.ru