Выступление по математике на тему «Методика решения задач с помощью уравнений»
МЕТОДИКА РЕШЕНИЯ ЗАДАЧ С ПОМОЩЬЮ УРАВНЕНИЯ
(СОСТАВЛЕНИЕ МОДЕЛИ РЕШЕНИЯ)
Ларюточкина Е.Н.,
учитель математики
МБОУ «ИСОШ №1 им.Н.П.Наумова»
При решении задачи методом уравнений необходимо проанализировать условие с целью выбора основного неизвестного и выявления зависимости между величинами. Значительно облегчает этот этап решения краткая запись условия в виде схемы, таблицы и т.п. (если это, конечно, целесообразно, т.е. решение задачи сразу не очевидно).
Формировать понятие «величина» следует, начиная с начальной школы. Прочитав условие задачи, выясним о какой величине (или величинах) идёт речь в условии.
Задачи стараемся разделять по типам. Рассмотрим этот вопрос на конкретных примерах.
5 класс. Задачи на сравнение «в» и «вместе».
В двух карманах 84 ореха. В одном из них в 3 раза больше, чем в другом. Сколько орехов в каждом кармане?
Условие записываем ручкой, в виде схемы,
I карман ? 3 раза
84 ор.
II карман ?
а затем вписываем решение карандашом. Окончательно, схема выглядит следующим образом:
3х ор.
I карман ? 3 раза (3х+х) ор.
84 ор.
II карман ? х ор.
Решив уравнение, находим знаки вопроса в схеме. Что написано карандашом рядом со знаком вопроса? Ответили мы на вопрос?
5 класс. Задачи на сравнение «в» и «на»
Площадь физкультурного зала в 6 раз больше площади классной комнаты. Найдите площадь зала, если она больше площади классной комнаты на 250 м2.
Условие «в» Условие «на»
6х м2
Ф. зал ? 6 раз 250м2
Классная ком. ? х м2
6х>х на 250
Подчёркивается, что меньшую из неизвестных удобнее принимать за х.
5 класс.
Задача «было, изменения, стало»
В одной бочке было в 3 раза больше бензина, чем в другой. Когда в первую налили ещё 46 л, а во вторую – 18л, то в двух бочках стало 184 л бензина. Сколько литров бензина было в каждой бочке первоначально?
Величина одна, но она изменяется во времени. В таком случае краткую запись условия делаем в виде таблицы:
БЫЛОИЗМЕНЕНИЯ
СТАЛО
I б.
? 3 раза
+ 46
184 л
II б.
?
+18
После работы с таблицей по тексту задачи с помощью карандаша, она принимает вид:
БЫЛОИЗМЕНЕНИЯ
СТАЛО
I б.
? 3 раза
3х л
+ 46
(3х+46)л
3х+46+х+18
184 л
II б.
?
х л
+18
После записи условия задаю вопрос: сколько свободных мест (клеток) в таблице? (4). Значит, мы должны сформулировать 4 предложения и пятое – «на составление уравнения».
В дальнейшем схемы и таблицы будут предложены в окончательном виде, после того, как учащиеся поработают с ними карандашом.
5 класс. Задача «на части».
Для приготовления вишнёвого варенья на 2 части вишни берут 3 части сахара (по массе). Сколько вишни и сколько сахара пошло на варенье, если сахара пошло на 7 кг 600г больше, чем вишни?
Вишня ? 2ч. 2х г
Сахар ? 3ч. 3х г 7600 г 3х > 2х на 7600
Подчёркивается, что в задачах на части за х принимаем 1 часть. Здесь: пусть х г – масса одной части.
6 класс. Задача «было, изменения, стало»
В двух бригадах было поровну рабочих. Когда в первую бригаду поступило 8 человек, а из второй ушли 2 человека, в первой бригаде стало в 3 раза больше рабочих, чем во второй. Сколько рабочих было в каждой бригаде?
БЫЛОИЗМЕНЕНИЯ
СТАЛО
I б.
? х чел
+ 8 чел
(х+8) чел
3 раза
II б.
? х чел
— 2 чел
(х-2) чел
х+8>х-2 в 3 раза
6 класс. Задача «на движение» (по воде)
Теплоход проходит за 15 ч против течения реки столько же, сколько за 13 ч по течению. Найдите скорость течения, если собственная скорость теплохода 70 км/ч.
Vc =70 км/ч, Vтеч =х км/ч
vt
s
Против течения
(70 –х) км/ч
15 ч
15(70-х) км
По течению
(70+х) км/ч
13 ч
13(70+х) км
Уравнение, приводящее к решению задачи: 15(70-х)= 13(70+х)
6 класс. Задача «на движение»
Из аэропорта вылетел самолёт со скоростью 600км/ч. Через 0,5 часа вслед за ним вылетел другой самолёт со скоростью 750 км/ч. Через сколько часов второй самолёт после своего вылета будет впереди на 225 км?
vt
s
I сам-т
600км/ч
(х+0,5) ч
600(х+0,5) км
II сам-т
750 км/ч
х ч
0,5 ч
750х км
225 км
750х>600(х+0,5) на 225.
Данное условие равносильно уравнению:
750х — 600(х+0,5) = 225, решение которого является решением задачи.
6 класс. В I день туристы прошли намеченного пути, а во второй день 0,8 того, что прошли в I день. Как велик намеченный путь, если во второй день туристы прошли 24 км?
Подчёркивается, что в таких задачах, как правило, целое принимаем за х. Что здесь играет роль целого? Намеченный путь.
I д.
0,8**х км
II д. 0,8 от — это 24 км.
7 класс. Задача «на работу»
Чтобы сделать вовремя заказ, артель стеклодувов должна была изготовлять в день по 40 изделий. Однако она изготовляла ежедневно на 20 изделий больше и выполнила заказ на 3 дня раньше срока. Каков был срок выполнения заказа?
?(х+3) дня
40 (х+3) изд.
фактически
40+20 =60 (изд)
20 изд.
х дн.
3 дня
60х изд.
Уравнение для решения: 40 (х+3) =60х
8 класс. Задача на «совместную работу»
За 4 дня совместной работы двумя тракторами было вспахано поля. За сколько дней можно вспахать всё поле каждым трактором, если первым его можно вспахать на 5 дней быстрее, чем вторым?
4= вспах.п/д? х д.
5д.
4д
1 поле
2 тр-р
всего поля/день
? (х+5)д.
1 поле
В итоге работы над текстом задачи по таблице получаем уравнение:
+ = .
8 класс. Задача на движение
Мотоциклист проехал расстояние от пункта М до пункта N за 5 ч. На обратном пути он первые 36 км ехал с той же скоростью, а остальную часть пути – со скоростью на 3 км/ч большей. С какой скоростью ехал мотоциклист первоначально, если на обратный путь он затратил на 15 мин больше, чем на путь из М в N ?
15 мин = ч = ч
vt
s
Из М в N
? х км/ч
5 ч
5х км
Из N в М
х км/ч
3км/ч
(х+3) км/ч
ч ч
ч 5-
36 км
5х км
(5х-36) км
В итоге, получаем уравнение: + =
9 класс. Решение задачи с помощью системы уравнений
Рационализаторы цеха разработали и внедрили в производство усовершенствованный тип детали. Определите массу детали нового и старого типов, если известно, что деталь нового типа на 0, 2 кг легче детали старого типа, причём из 22 кг металла стали делать деталей нового типа на две больше, чем делали деталей старого типа из 24 кг металла.
д.24 кг
Старый тип
y кг
0,2 кг
д. 2 дет
22 кг
Нетрудно заметить, что в учебниках 5-9 кл. имеется много текстовых задач, которые аналогичны друг другу по связям между данными и по структуре решения. Такие задачи учат видеть общее.
И, если в 5 классе мы научим решать их, в последующих классах особых трудностей не возникает.
Схематизация позволяет высветить скрытые связи между величинами и, несомненно, помогает в решении задач.
Конспект урока на тему » Решение задач с помощью уравнений»
Урок № /1
ТЕМА: Решение задач с помощью уравнений
Тип урока: изучения нового материала
Задачи. создать условия для развития умений применять свойства
линейного уравнения с одной переменной при решении задач.
Планируемые результаты:
Предметные: познакомиться с математической моделью для решения задачи; научатся составлять математическую модель.
Метапредметные: познавательные- уметь использовать компьютерные и коммуникационные технологии как инструмент для достижения своих целей;
регулятивные- самостоятельно осознавать причины своего успеха или неуспеха и находить способы выхода из ситуации неуспеха;
коммуникативные— учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве
личностные: формировать интерес к изучению темы и желание применять приобретенные знания
Ход урока
I. Организационный момент.
Анализ контрольной работы. Работа над ошибками.
II. Объяснение нового материала.
1. Объяснение начать с решения конкретной (приведенной в учебнике) задачи № 1.
Можно воспользоваться таблицей:
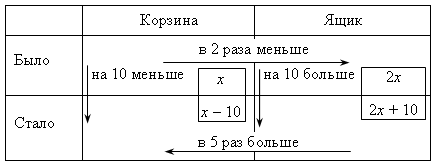
Сперва в таблице стрелками обозначаем и подписываем все зависимости, затем видим, что неизвестны все четыре клеточки, значит, обозначить переменной удобно главный вопрос задачи, например, количество яблок в корзине первоначально. Затем, по стрелкам, заполняем все клеточки. Последняя стрелка даст уравнение: 5(
Аналогичную таблицу можно составить для задачи № 2:
х + 2х + (х + 12) = 78.
При решении второй задачи особое внимание уделяется последнему этапу – интерпретации полученного результата.
III. Формирование умений и навыков.
1. № 143.
Решение:
Пусть в одной кассе было х билетов, тогда во второй – (х + 36) билетов. Зная, что всего было продано 392 билета, составим уравнение:
х + (х + 36) = 392;
х + х + 36 = 392;
2х = 356;
х = 178.
Следовательно, в первой кассе было продано 178 билетов.
Так как х + 36 = 178 + 36 = 214, то во второй кассе было продано 214 билетов.
Ответ: 178 и 214 билетов.
2. № 146.
Решение:
Анализ условия:
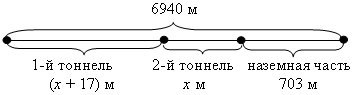
Пусть х м – длина одного тоннеля, тогда (х + 17) м – длина другого. Так как наземная часть составляет 703 м, а вся трасса – 6940 м, то длина тоннелей в сумме составляет (6940 – 703) м. Зная, что длина тоннелей равна х + (х + 17) м, составим уравнение:
х + (х + 17) = 6940 – 703;
х + х + 17 = 6237;
х + х = 6237 – 17;
2х = 6220;
х = 3110.
Значит, длина одного тоннеля равна 3110 м. Так как х + 17 = = 3110 + 17 = 3127, то длина другого тоннеля равна 3127 м.
Ответ: 3110 м и 3127 м.
3. № 147.
Анализ условия:
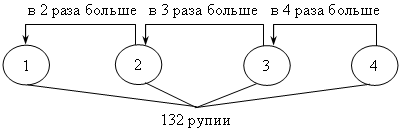
Пусть первый жертвователь дал х рупий, тогда второй дал 2х рупий, третий – 3 · 2х рупий, четвертый – 4 · (3 · 2х) рупий. Зная, что все вместе они дали 132 рупии, составим уравнение:
х + 2х + 3 · 2х + 4 · (3 · 2х) = 132;
х + 2х + 6х + 24х = 132;
33х = 132;
х = 132 : 33;
х = 4.
Значит, первый жертвователь дал 4 рупии. Так как 2х = 2 · 4 = 8, то второй дал 8 рупий. Так как 3 · 2х = 3 · 8 = 24, то третий дал 24 рупии. Так как 4 · (3 · 2х) = 4 · 24 = 96, то четвертый дал 96 рупий.
Ответ: 4; 8; 24 и 96 рупий.
4. № 148.
Анализ условия:
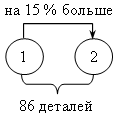
Пусть х деталей изготовил второй рабочий, тогда первый изготовил (х + 0,15х) деталей. Зная, что вместе они изготовили 86 деталей, составим уравнение:
х + (х + 0,15х) = 86;
х + х + 0,15х = 86;
2,15х = 86;
х = 86 : 2,15;
х = 40.
Значит, второй рабочий изготовил 40 деталей. Так как х + 0,15х = 40 +
+ 0,15 · 40 = 40 + 6 = 46, то первый рабочий изготовил 46 деталей.
Ответ: 46 деталей и 40 деталей.
IV. Итоги урока.
Домашнее задание: № 144; № 145; № 149; № 165.
Конспект урока по теме «Повторение. Решение задач с помощью уравнений»
Итак, сегодня мы займемся решением задач с помощью уравнений. Запишите в тетради тему урока: Решение задач с помощью уравнений.Что же такое уравнение? (Равенство, содержащее букву, значение которой нужно найти.)
Что такое корень уравнения? (Значение буквы, при котором из уравнения получается верное числовое равенство.)
Что значит решить уравнение? (Найти все его корни или убедиться в том, что корней нет.)
Как называются уравнения, имеющие одинаковые корни? (Равносильные)
Какие правила помогают нам при решении уравнений?
(Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное 0.)
(Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом знак.)
Молодцы! А теперь поработаем над составлением уравнений к конкретным ситуациям.
Закрепление пройденного материала (30мин).
№1 а) Используя данные рисунка, запишите алгебраические выражения, с помощью которых можно узнать количество открыток у каждого из детей:
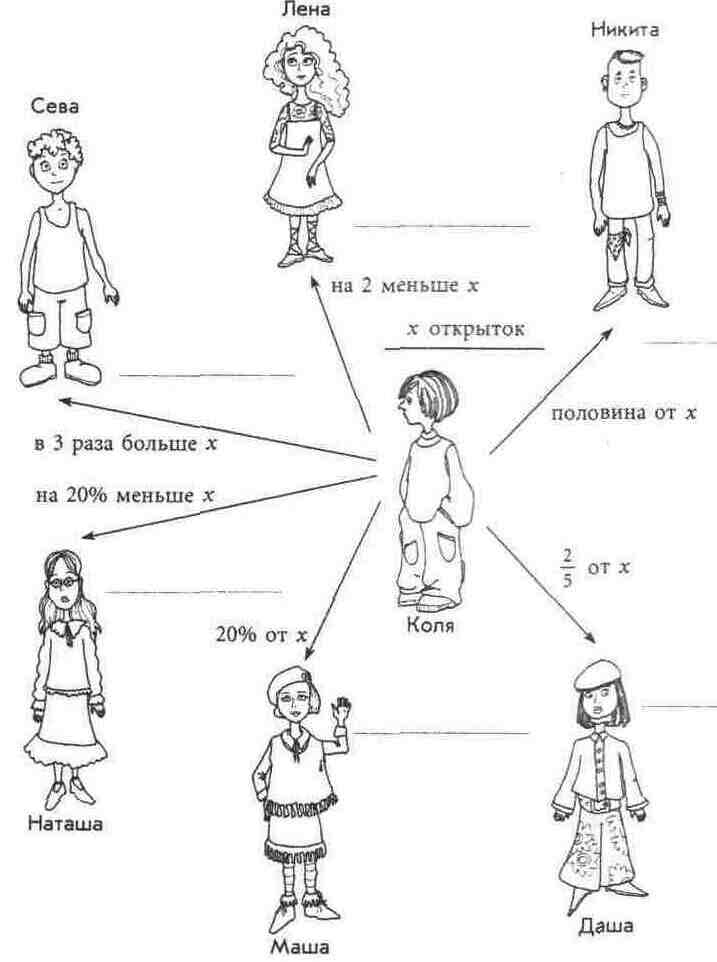
б) Запишите равенство по тексту, используя ответы к пункту а):
1) У Севы открыток больше, чем у Коли, на 40;
2) Если Коля отдаст Никите 5 открыток, то у них открыток станет поровну;
3) Если Маша возьмет у Коли 4 открытки, то у нее будет в 2 раза меньше открыток, чем у него.
в) Сколько открыток у Коли?
Сначала запишите выражения, которые показывают число открыток у каждого ребенка.
Коля х
Сева 3х
Лена (х – 2)
Никита 0,5 х
Даша 2:5 х (как найти дробь от числа?)
Маша 0,2 х (20% = 0,2)
Наташа 0,8 х (100% — 20%= 80%, 80% = 0,8)
А теперь составим уравнения к условиям пункта б).
1) У Севы открыток больше, чем у Коли, на 40
3х – х = 40 (3х – 40 =х; 3х =х + 40).
2) Если Коля отдаст Никите 5 открыток, то у них открыток станет поровну;
х – 5 =0,5х + 5.
3) Если Маша возьмет у Коли 4 открытки, то у нее будет в 2 раза меньше открыток, чем у него.
(0,2х + 4) *2 = х — 4
Сколько же открыток у Коли? Решим составленные уравнения и узнаем значение х, то есть узнаем количество открыток у Коли.
1 ряд 3х – х = 40
2 ряд х – 5 =0,5х + 5
3 ряд (0,2х + 4) *2 = х — 4
Ответ: 20 открыток.
Вспомним, какие этапы мы выделяем при решении задач.
I. Составление математической модели. (Анализ условия задачи и составление уравнения)
II. Работа с математической моделью. (Решение составленного уравнения)
III. Ответ на вопрос задачи.
№2 В одном бидоне молока в 3 раза больше, чем в другом. Когда из одного бидона перелили в другой 5 литров, молока в бидонах стало поровну. Сколько литров молока было в каждом бидоне первоначально?
Решение:
Сначала введём переменную, с помощью которой обозначим неизвестную нам величину, которую необходимо найти по условию задачи.
Пусть x л — количество молока, которое было до переливания во втором бидоне.
Тогда в первом бидоне его было 3x л.
После переливания в первом бидоне осталось (3x–5) л молока, а во втором стало (x+5) л.
По условию задачи известно, что после переливания в обоих бидонах молока стало поровну. Составим уравнение: 3x–5=x+5
3x−5=x+5
3x−x=5+5
2x=10
x=5 Ответ: в одном бидоне было 5 л молока, а в другом бидоне было 15 л молока.
№3 Человек на вопрос, сколько он заплатил за часы, ответил: «Если умножить цену на 4, и к результату прибавить 70, а из этой суммы вычесть 50, то остаток будет равен 220 долларов». Сколько он заплатил за часы?
Пусть цена часов равна x
Эта цена была умножена на 4, то есть получаем 4x
К произведению прибавили 70, то есть 4x+70
Из этого вычли 50, то есть 4x+70−50
Таким образом, мы записали условие задачи с помощью чисел в алгебраической форме, но у нас еще нет уравнения. Однако, согласно последнему условию задачи, все предыдущие действия в итоге привели к результату, который равен 220.
Поэтому, это уравнение выглядит так: 4x+70−50=220
После проведения операций с уравнением, получаем, что x=50.
То есть, значение x равно 50 долларов, что и есть искомой ценой часов.
№4 Со склада в магазины было вывезено 1234 швейных машин. На складе осталось 5 рядов швейных машин по 352 машин в каждом ряду. Сколько всего швейных машин было на складе?
х-1234=352∙5
х-1234=1760
х=1234+1760
х=2994
№5 Для того, чтобы поровну разлить 102 л молока, привезли сначала 30 бутылок, затем еще 4 таких же бутылки. Сколько литров составляет вместимость каждой бутылки?
(30+4)∙х=102
34∙х=102
х=102:34
х=3
№6 Андрей старше Олега на 4 года, а Олег старше Бориса в 1,5 раза. Вместе им 36 лет. Сколько лет каждому из них?
Ответ: 16 лет, 12 лет, 8 лет
№7 От турбазы до станции турист доехал на велосипеде за 3 часа. Пешком он смог бы пройти это расстояние за 7 часов. Известно, что пешком он идет со скоростью на 8 км/ч меньшей, чем едет на велосипеде. С какой скоростью ехал турист и чему равно расстояние от турбазы до станции?
Ответ: 14 км/ч, 42км
№8 Бригада должна была изготовить определенное количество стульев за 10 дней. Однако она ежедневно изготавливала на 20 стульев больше, чем планировалось первоначально, поэтому за 3 дня до срока ей осталось изготовить 58 стульев. Сколько стульев должна была изготовить бригада? Ответ: 660 стульев.
№9 В растворе содержится 40% соли. Если добавить 120 г соли, то в растворе будет содержаться 70% соли. Сколько граммов соли было в растворе первоначально?
Пусть х г соли было в растворе, тогда масса всего раствора : х:0,4=2,5х г. После того как в р-р добавили 120г соли в р-ре стало х+120 г соли, а масса р-ра: 2,5х+120г. В р-ре стало содержаться 0,7г соли. С.У. : 0,7(2,5х+120)=х+120
1,75х + 84=х+120
0,75х=36
х=48
Ответ 48гр
Домашнее задание (2 мин).
№1 Одно число больше другого в 4,5 раза. Если от большего числа отнять 54, а к меньшему прибавить 72, то получатся равные результаты. Чему равны эти числа?
№2 У Миши и Коли в коллекциях было одинаковое число марок. Когда Миша подарил часть своих марок младшему брату, а Коля в 1,4 раза меньшее число своих марок отдал на выставку, у Миши осталось 20 марок, а у Коли — 40 марок. Сколько марок было у каждого мальчика первоначально, сколько марок Коли на выставке и сколько марок Миша подарил брату?
Итог урока (2мин).
Учимся решать задачи с помощью уравнений
Тема: Учимся решать задачи с помощью уравнений.
Тип урока: Изучение нового материала
Цели урока: закреплять умение решать задачи с помощью уравнения; совершенствовать умение составлять задачу по данной диаграмме; развивать умение анализировать и рассуждать.
Задачи урока:
развивающая: закреплять у обучающихся навыки решения задачи, развивать умение работать самостоятельно; речь, память, внимание
воспитательная: воспитывать у обучающихся интерес к предмету, самостоятельность.
Планируемые результаты:
Личностные: развивать речь, мышление, наблюдательность; уметь строить речевые высказывания; развивать интерес к различным видам деятельности
Предметные: уметь письменно умножать многозначные числа на однозначное; совершенствовать вычислительные навыки;
Метапредметные: развивать творческое мышление, внимание, память; формировать умение работать в парах и группах; учить устанавливать причинно — следственные связи
Оборудование: учебник, учебная презентация, рабочая тетрадь
Математика, друзья,
Абсолютно всем нужна.
На уроке работай старательно
И успех придет обязательно!
-Ребята, вы все настроились на работу? Все будете стараться?
(ответы детей)
Приветствуют учителя
Коммуникативные: планирование учебного сотрудничества
Актуализация знаний
Устный счет.
1. Восстановите знаки действий и скобки так, чтобы равенства стали верными:
728 * 72 * 8 = 152 728 * 72 * 8 = 100
728 * 72 * 8 = 719 728 * 72 * 8 = 737
2. Задача.
В велогонке Дима, Саша, Андрей и Вася заняли со второго по пятое место. Саша обогнал Диму на 39 с, но отстал от Васи на 41 с. Андрей был впереди Васи на 12 с, но отстал от победителя на 13 с.
В каком порядке финишировали мальчики и с каким отставанием от победителя?
3. Математические ребусы.
Выполняют устный счет вместе с учителем по цепочке
Регулятивные: принимают и сохраняют уч задачу
Коммуникативные: участвуют в учебном диалоге
Познавательные: осознанно строят речевое высказывание
Сообщение темы урока
– Сегодня на уроке будем учиться решать задачи с помощью уравнений.
Коммуникативные: учитывают мнение одноклассников
Познавательные: осознанно строят речевое высказывание
Работа над темой урока
Работа по теме урока.
1. Задание 79.
– Прочитайте задачу.
– Что известно?
– Что требуется узнать?
– Для данной задачи составьте краткую запись, заполнив таблицу. Искомое обозначьте буквой х.
(Как х.)– Что получится, если число фломастеров в одной коробке умножить на число коробок? (Число фломастеров в 9 коробках.)
– Запишите соответствующее равенство, используя обозначение числа фломастеров в одной коробке через х.
х · 9 = 54.
– Это равенство будет являться уравнением, позволяющим решить данную задачу.
2. Задание 80.
– Составьте задачу, решить которую можно с помощью уравнения 9 · х = 36.
Запись:
1 коробка – 9 кг яблок.
х коробок – 36 кг яблок.
Решение:
9 · х = 36
х = 36 : 9
х = 4 (к.) – потребуется.
Ответ: 4 коробки.
3. Задание 81.
– Прочитайте задачу.
– Что известно?
– Что требуется узнать?
– Запишите уравнение с неизвестным делителем, являющееся решением данной задачи.
Запись:
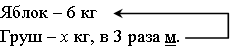
Решение:
6 : х = 3
х = 6 : 3
х = 2 (кг) – купили груш.
Ответ: 2 кг.
Находят значение выражения у доски
Рассуждают с учителем
Работают у доски и самостоятельно
Коммуникативные: учитывают мнение одноклассников
Познавательные: осознанно строят речевое высказывание
Физминутка
-Выполните столько наклонов вперед, во сколько раз 15 больше 3?
-Выполните по столько наклонов влево и вправо, во сколько раз 9 меньше 3?
— Присели столько раз, во сколько 12 больше 3?
— Подпрыгните столько раз, во сколько2 меньше 8?
Физминутка
Личностные: смена вида деятельности
Первичное закрепление
1. Задание 83.
– Рассмотрите диаграмму.
– Чему равна белая полоска? (15.)
– Чему равна синяя полоска? (90.)
– По данной диаграмме составили уравнение с неизвестным делителем 90 : х = 15.
– Сформулируйте задачу, решить которую можно с помощью данного уравнения.
Задача. На первой полке стояло 90 книг, а на второй – в 15 раз меньше. Сколько книг на второй полке?
– Найдите корень уравнения с помощью данной диаграммы. Запишите ответ составленной задачи.
Запись:
90 : х = 15
х = 90 : 15
х = 6 (кн.) – на второй полке.
Ответ: 6 книг.
2. Задание 84.
– Прочитайте задачу.
– Что известно?
– Что требуется узнать?
– Какое из уравнений является решением данной задачи? (х : 15 = 6)
– Начертите диаграмму, используя условие задачи.
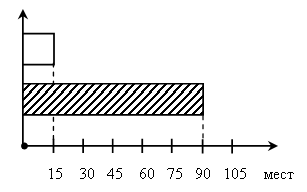
– С помощью диаграммы найдите ответ задачи.
– Будет ли это число являться корнем уравнения? (Будет.)
– Вычислите корень данного уравнения, выполнив умножение столбиком.
Запись:
х : 15 = 6
х = 15 · 6
х = 90 (мест) – занято.
Ответ: 72.
– Для выбранной задачи сформулируйте обратную задачу.
Задача. Число 72 уменьшили в несколько раз и получили число 9. Во сколько раз уменьшили 72?
– Запишите уравнение, с помощью которого можно решить обратную задачу.
Запись:
72 : х = 9
х = 72 : 9
х = 8
Ответ: уменьшили в 8 раз.
Анализируют условие задачи
Отвечают на поставленные вопросы
Коммуникативные: участвуют в учебном диалоге, работа в парах
Коммуникативные: учитывают мнение одноклассников
Рефлексия
– Что нового узнали на уроке?
– Как найти неизвестный множитель?
– Как найти неизвестное делимое?
– Как найти неизвестный делитель?
– Как можно записать решение задачи?
Подводят итоги вместе с учителем
Регулятивные: контроль своих действий на уроке
Домашнее задание
карточка
Открытый урок «Решение задач с помощью уравнений» 6 кл.
Конспект урока по математике 6 кл.
Тема урока: Решение задач с помощью уравнений
Цели:
Образовательная: вырабатывать навыки в решении задач с помощью уравнений;
Развивающая: развивать логическое мышление, умение анализировать ситуацию.
Воспитательная: воспитывать уверенность при принятии решений, интерес к математике, культуру математических записей.
Тип урока: усвоение новых знаний.
Оборудование: мультимедийное оборудование, презентация, роздаточный материал «Алгоритм решения задач с помощью уравнений»
Ход урока
1.Организационный момент. Эпиграф урока:
«Через математические знания, полученные в школе,
лежит широкая дорога к огромным,
почти необозримым областям труда и открытий»
Маркушевич А.И
2.Устный счет Диктант:
1.Равенство содержащее переменную, называется ….
2. Корнем уравнения называется значение переменной, при котором уравнение обращается в верное …
3. Решить уравнение, это значит найти все его …
4. Корни уравнения не изменяются, если обе части уравнения умножить на одно и то же число. (да)
5. Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак. (да)
3.Актуализация знаний. Решить уравнение (трое учеников решают у доски)
3х=4-х 34+х=2(11+х) 6х+12=7х-14
4.Создание проблемной ситуации. Решение задачи.
В книге 60 страниц.
Прочитали в 2 раза больше
страниц, чем осталось прочитать.
Сколько страниц осталось прочитать?
5. Мотивация учебной деятельности. Сообщение темы и целей урока
Вы уже знаете, что такое уравнение, что означает требование «решить уравнение». А задумывались ли вы над тем, зачем нам нужно уметь решать уравнения?
Дело в том, что очень много разнообразных задач проще решаются, если составить и решить уравнение, опираясь на их условия.
Сегодня на уроке мы будем решать задачи с помощью уравнений, анализировать ситуацию, подключая логическое мышление, при этом вы должны быть уверены в своих действиях, придерживаться правил оформления математических записей, и возможно, кто-то из вас сегодня заинтересуется математикой.
6.Формирование умений и навыков
Задача 1.
На автостоянке стоит 24 автомобиля, причем легковых автомобилей в 3 раза больше, чем грузовых. Сколько грузовых автомобилей стоит на автостоянке?
Решение задачи с помощью уравнений будет происходить по плану:
1.Проанализировать условие и определиться, какую величину обозначим переменной .
2.Через выбранную переменную выразить другие неизвестные величины, записать соответствующие математические выражения.
3.Составить уравнение, опираясь на данные, имеющиеся в условии задачи
4.Решить полученное уравнение.
5.Найти другие неизвестные величины.
6.Записать ответ.
Ученики получают карточки с алгоритмом решения задач с помощью уравнений.
Алгоритм решения задачи с помощью уравнений:
1.Проанализировать условие и определиться, какую величину обозначим переменной .
2.Через выбранную переменную выразить другие неизвестные величины, записать соответствующие математические выражения.
3.Составить уравнение, опираясь на данные, имеющиеся в условии задачи
4.Решить полученное уравнение.
5.Записать ответ.
Решение.
Пусть грузовых автомобилей х, тогда легковых будет 3х. По условию всего 24 автомобиля. х+3х=24
4х=24
х=24/4, х=6 . Ответ: 6 грузовых автомобилей.
7.Физкультминутка
Задача 2. Ученик решает у доски.
Задача 3. Самостоятельно
Желающие решают у доски Задача 4 и Задача 5.
8.Итог урока.
Что нового узнали на уроке?
Было ли вам интересно на уроке?
Все ли было вам понятно?
Понравился урок или нет?
9.Оценки, домашнее задание:(п.3.10, выучить алгоритм, №618,№619)
Презентация по математике на тему «Решение задач с помощью уравнений»
Описание презентации по отдельным слайдам:
1 слайд
Описание слайда:МБОУ «Восяховская СОШ «ОЦ» Урок математики 3 класс УМК «Перспективная начальная школа» Тема урока: «Решение задач с помощью уравнений» Учитель: Свалова И.А. 1 квалификационная категория Организационный момент.
2 слайд
Описание слайда:Начинается урок. Он пойдет ребятам впрок. Постарайтесь все понять, Учитесь тайны открывать, Ответы полные давайте И на уроке не зевайте.
3 слайд
Описание слайда:Что знаем и умеем? Составим постер со словом «Уравнение», находя правильные ответы на вопросы: Что такое уравнение? Что такое корень уравнения? Что значит найти корень уравнения? Где человек применяет уравнения? Актуализация знаний. Что знаем и умеем.
4 слайд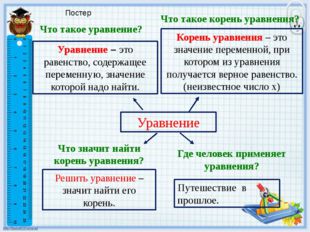
Описание слайда:Уравнение Уравнение – это равенство, содержащее переменную, значение которой надо найти. Что такое уравнение? Корень уравнения – это значение переменной, при котором из уравнения получается верное равенство. (неизвестное число х) Что такое корень уравнения? Решить уравнение – значит найти его корень. Что значит найти корень уравнения? Где человек применяет уравнения? Путешествие в прошлое. Постер
5 слайд
Описание слайда:Ребята, а вы знаете, когда люди начали решать уравнения? Тогда заглянем в прошлое? Уже 4000 лет назад вавилоняне и египтяне решали разные задачи землемерия, строительства и военного дела с помощью уравнений. Уравнения умели решать в древности также китайские и индийские ученые. В музее изобразительных искусств в Москве хранится папирус, изготовленный из растений, на котором сделаны записи около 3500 тысяч лет назад.
6 слайд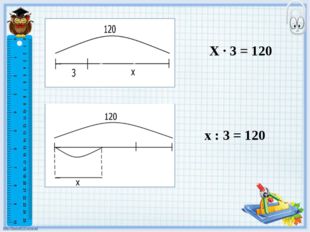
Описание слайда:Х · 3 = 120 х : 3 = 120
7 слайд
Описание слайда:Тема урока: Решение задач с помощью уравнений.
8 слайд
Описание слайда:Цель урока: Научиться решать задачи с помощью уравнений. Вспомним, что такое задача. Задача – это текст, в котором есть условие и требование. Какие действия нужно совершить, чтобы решить задачу? Алгоритм: 1. Прочитать задачу. 2. Составить краткую запись, схему или таблицу. 3. Составить план решения задачи. 4. Записать решение задачи. 5. Записать ответ. Постановка цели урока. Что знаем, что ещё можем узнать? Чему научимся.
9 слайд
Описание слайда:Задачи решать — нелегкое дело, Но за него возьмемся мы смело. А чтобы ошибок не допускать, Будем думать, смекать, вычислять. Открытие нового.
10 слайд
Описание слайда:Многие трудные арифметические задачи легко решаются с помощью уравнений. Если вы освоите искусство составлять уравнение по условию задачи и научитесь их безошибочно решать, то эти задачи будут вам по плечу.
11 слайд
Описание слайда:« Чтобы решить вопрос , относящийся к числам или величинам, нужно перевести задачу с родного языка на алгебраический (математический) » — писал великий английский учёный Исаак Ньютон. ( 1643-1727г.р.)
12 слайд
Описание слайда:Задача, которую можно решить уравнением: В нескольких тарелках 32 пирожка, по 8 пирожков на каждой тарелке. Сколько было тарелок?
13 слайд
Описание слайда:Как перевести задачу с русского языка на язык математики? На русском языке На языке математики В одной тарелке 8 пирожков Несколько тарелок Сколько было тарелок? Х тарелок Всего пирожков 32 пирожка Уравнение 8 · х = 32
14 слайд
Описание слайда:В корзине было несколько яблок. Их разложили в 4 пакета по 8 штук в каждом. Сколько яблок было в корзине. Задача Х : 8 = 4 Всего яблок Числояблок в 1 пакете Число пакетов Х 8 4
15 слайд
Описание слайда:Самостоятельная работа На поле привезли саженцы. Все привезенные саженцы рассадили в 15 рядов. В каждом ряду оказалось по 7 саженцев. Сколько всего саженцев привезли на поле? Реши задачу с помощью уравнения. Найди корень этого уравнения. Запиши ответ задачи. 1-вариант На базу приехали туристы. Всех приехавших туристов расселили в 32 домика. В каждом домике оказалось по 4 человека. Сколько туристов приехало на базу? Реши задачу с помощью уравнения. Найди корень этого уравнения. Запиши ответ задачи. 2-вариант Решение: Х : 15 = 7 Х = 7 · 15 Х = 105 Ответ: 105 саженцев. Решение: Х : 32 = 4 Х = 4 · 32 Х = 128 Ответ: 128 туристов.
16 слайд
Описание слайда:Рефлексия: Какую цель мы ставили перед собой? Мы достигли цели? Что особенно заинтересовало на уроке? Какая работа понравилась на уроке? Какая работа вызвала затруднение? Рефлексия. Оценка деятельности на уроке.
17 слайд
Описание слайда:Ребята, наклейте стикер на ту часть круга, которая соответствует вашему впечатлению от урока.
Курс профессиональной переподготовки
Учитель начальных классов
Курс повышения квалификации
Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:
Общая информация
Номер материала: ДВ-456752
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий| № п/п | Структурные элементы урока | Дидактическая задача | Деятельность учителя | Деятельность учащихся | Показатели реальных результатов | ||
|---|---|---|---|---|---|---|---|
| 1 | Организация начала урока | Подготовка учащихся к работе | Создаёт настрой на самоорганизацию деятельности ученика | Настраиваются на урок, получают информацию о содержании урока | Полная готовность класса и оборудования, быстрое включение учащихся в деловой ритм | ||
| 2 | Актуализация знаний и способов деятельности | Обеспечение мотивации, принятие учащимися цели УПД, актуализация комплекса знаний | Формулирует цели и задачи урока, организует дискуссию | Выполняют задания, участвуют в дискуссии | Готовность учащихся к активной УПД, на основе опорных знаний | ||
| 3 | Закрепление знаний и способов деятельности | Обеспечение усвоения знаний и способов деятельности на уровне применения в измененной ситуации | Предлагает выполнить разноуровневую самостоятельную работу | Выполняют самостоятельную работу, осуществляют самоконтроль и взаимоконтроль | Самостоятельное выполнение задания, получение достоверной информации о достижении всеми учащимися планируемых результатов обучения | ||
| 4 | Обобщение и систематизация знаний и способов деятельности | Создание условий для систематизации изученного материала, выявление уровня овладения системой знаний и умений, опытом творческой деятельности | Информация учителя о системе работы по теме и её перспективах в курсе основной школы | Работают с таблицами, составляют задачи по готовому уравнению | Умение составлять текстовые задачи, видеть рациональные способы составления уравнений | ||
| 5 | Подведение итогов занятия. Рефлексия. | Дать анализ и оценку успешности достижения цели. Мобилизация учащихся на рефлексию | Предлагает учащимся вернуться к цели урока | Осмысливают деятельность на уроке | Адекватность самооценки учащихся оценке учителя | ||
| 6 | Информация о домашнем задании | Обеспечение понимания цели, содержания и способов выполнения домашнего задания | Предлагает разноуровневые задания на выбор ученика | Выбирают задания, записывают | Реализация условий успешного выполнения заданий учащимися в соответствии с уровнем их развития | ||
| Этап урока | Деятельность учителя и ученика (содержание урока) | ||||||
| 1 | «Приветствие. Мотивация» | ||||||
| 2 | «Актуализация знаний и способов деятельности» Беседа: — Каков алгоритм решения задач с помощью уравнений? Ответ ученика:
— Подробно пояснить п. 2 Ответ ученика: По условию задачи можно разбить на 4 группы:
Работа с таблицей-опорой: |
||||||
| 3 | «Закрепление знаний и способов деятельности» — Применить данный теоретический материал при выполнении разноуровневой самостоятельной работы «Поле чудес». Цель: разгадать зашифрованное слово, установить закономерность его образования, определить тип каждой задачи по условию. Время выполнения работы — 15 мин. За каждую решенную задачу получаете жетон определенного цвета: «I уровень» — желтый жетон |
||||||
| 1 вариант | 2 вариант | ||||||
| «I уровень» | «I уровень» | ||||||
| Андрей старше Олега на 4 года, а Олег старше Бориса в 1,5 раза. Вместе им 36 лет. Сколько лет каждому из них? Ответ: 16 лет, 12 лет, 8 лет Задача 4 типа |
На первой полке было в 1,6 раза больше книг, чем на второй. Когда с первой полки взяли 4 книги, а на вторую положили 8 книг, то на обеих полках книг стало поровну. Сколько книг было на каждой полке первоначально? Ответ: 32 и 20 книг Задача 1 типа |
||||||
| «Х» | «О» | ||||||
| «II уровень» | «II уровень» | ||||||
| От турбазы до станции турист доехал на велосипеде за 3 часа. Пешком он смог бы пройти это расстояние за 7 часов. Известно, что пешком он идет со скоростью на 8 км/ч меньшей, чем едет на велосипеде. С какой скоростью ехал турист и чему равно расстояние от турбазы до станции? Ответ: 14 км/ч, 42км Задача 1 типа |
Кофейник и две чашки вмещают 740 г воды. В кофейник входит на 380 г воды больше, чем в чашку. Сколько граммов воды вмещает кофейник? Ответ: 500 г Задача 4 типа |
||||||
| «Р» | «Д» | ||||||
| «III уровень» | «III уровень» | ||||||
| На турбазе имеются палатки и домики. Всего их 25. В каждом домике живут 4 человека, а в каждой палатке 2 человека. Сколько на турбазе палаток и сколько домиков, если на турбазе отдыхают 70 человек? (решить задачу разными способами, обсудить решение в парах) Ответ: 15 палаток, 10 домиков Задача 4 типа |
|||||||
| «А» | |||||||
На доске ответы:
|
|||||||
Итог самостоятельной работы разгаданное слово «хорда»: Учитель дает определение, достает модель из «черного ящика». Каждый ученик получает оценку за самостоятельную работу, подняв жетоны. Задачу III-го уровня подробно разобрать, обсудить все способы её решения [см. Приложение 1]. Во время выполнения с/р двое сильных учеников выполняют индивидуальные задания на дополнительных досках (задачи 1 и 2). |
|||||||
Задача 1 Бригада должна была изготовить определенное количество стульев за 10 дней. Однако она ежедневно изготавливала на 20 стульев больше, чем планировалось первоначально, поэтому за 3 дня до срока ей осталось изготовить 58 стульев. Сколько стульев должна была изготовить бригада? Ответ: 660 стульев. Более подробное решение в Приложении 2. Задача 2 В классе 38 человек. Из них 16 играют в баскетбол, 17- в хоккей, 18 – в волейбол. Увлекаются двумя видами спорта: баскетболом и хоккеем – 4, баскетболом и волейболом – 3, волейболом и хоккеем – 5. Трое не увлекаются ни баскетболом, ни волейболом, ни хоккеем. Класс оценивает ответы работающих у доски. Справившиеся раньше с с/р получают дополнительные задания: составить задачи по уравнению, указать тип по условию [см. Приложение 3].
|
|||||||
| 4 | «Обобщение и систематизация знаний и способов деятельности» Информация учителя о системе работы по данной теме, начиная с 5-го класса, и перспективах в курсе основной школы. Ответ: 7 плюшек Беседа учителя: Рассмотреть другие способы составления уравнения, выбрать наиболее рациональный [см. Приложение 4]. |
||||||
| 5 | «Подведение итогов занятия» Выставление оценок, рефлексия (заполнение листа контроля). Для выставления итоговой оценки в журнал сдать тетради на проверку учителю. |
||||||
6 |
«Информация о домашнем задании» 1) Придумать по одной задаче и решить её всеми возможными способами, указать самый рациональный. 2) Задание на выбор по учебнику: Выбрали на «4» — 6 человек |
||||||