Приближенные методы вычисления определенных интегралов
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Брянская государственная инженерно-технологическая академия»
Кафедра математики
Приближенные методы вычисления определенных интегралов
Методические указания и задания к расчетно-графической работе
для студентов всех направлений подготовки бакалавров очной формы обучения
Составители: Баранова И.М., зав. кафедрой математики БГИТА,
Гущин Г.В., доцент кафедры математики БГИТА,
Еловиков А.Б., доцент кафедры Высшей математики ЗФЭИ,
Рецензент: Евтюхов К.Н. – к., ф.- м.н., профессор кафедры физики
Брянск 2012
Введение
При решении ряда физических и технических задач встречаются определенные интегралы, которые не могут быть вычислены в элементарных функциях. Кроме того, в некоторых важных задачах возникает необходимость вычисления определенных интегралов, подынтегральные функции которых не являются элементарными.
Наиболее употребляемыми приближенными методами вычисления определенных интегралов являются: метод прямоугольников, метод трапеций и метод парабол (Симпсона).
Основная
идея этих методов заключается в замене
подынтегральной функции 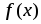 функцией более простой природы –
многочленом
функцией более простой природы –
многочленом 
 (0, 2, 3, …).
(0, 2, 3, …). 
Приближенные методы вычисления определенных интегралов
1. Метод прямоугольников
Разобьем
отрезок  на
на 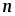 равных частей при помощи точек:
равных частей при помощи точек:
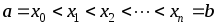 ,
,  ,
, 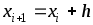 ,
, 
Метод прямоугольников заключается в замене интеграла суммой:
 .
.
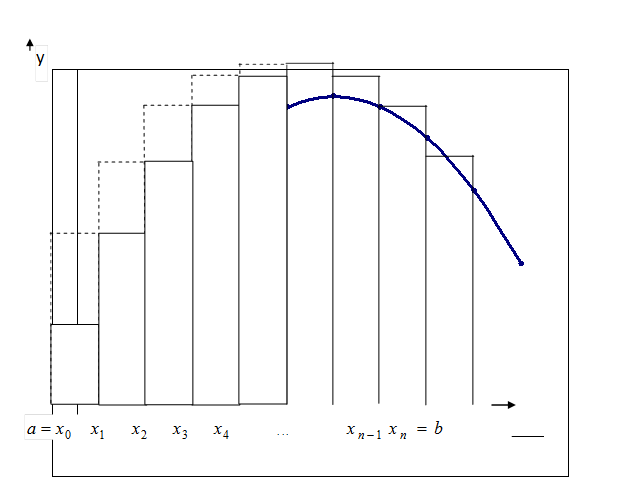
Для приближенных практических расчетов применяется формулы:
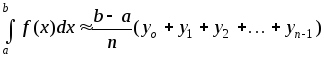 ,
(1)
,
(1)
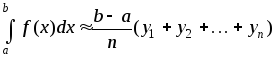 .
(2)
.
(2)
Из
рисунка ясно, что если  – положительная и возрастающая функция,
то формула (1) выражает площадь ступенчатой
фигуры, составленной из «входящих»
прямоугольников, а формула (2) – площадь
ступенчатой фигуры, состоящей из
«выходящих» прямоугольников.
– положительная и возрастающая функция,
то формула (1) выражает площадь ступенчатой
фигуры, составленной из «входящих»
прямоугольников, а формула (2) – площадь
ступенчатой фигуры, состоящей из
«выходящих» прямоугольников.
Абсолютная
погрешность приближенных равенств (1)
и (2) оценивается с помощью следующей
формулы: 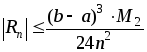 ,
где
,
где  – наибольшее значение
– наибольшее значение  на отрезке
на отрезке 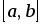 .
.
2. Метод трапеций
Разобьем
отрезок  на
на 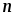 равных частей при помощи точек:
равных частей при помощи точек:

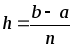 ,
, 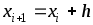 ,
, 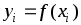 .
.Метод трапеций заключается в замене интеграла суммой:
 .
.
Для приближенных практических расчетов применяется формула:
 .
(3)
.
(3)
Абсолютная
погрешность приближения, полученного
по формуле трапеций, оценивается с
помощью формулы 
 .
.3. Метод парабол (метод Симпсона)
а)
Через любые три точки с координатами 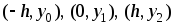 проходит только одна парабола
проходит только одна парабола  .
.


б)
Выразим площадь под параболой 
 через
через 
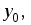
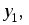
 :
: 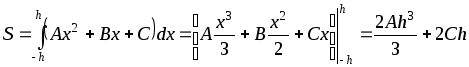 .
.
Учитывая
значения  и
и  из пункта а) следует:
из пункта а) следует:
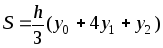
в)
Разобьем отрезок 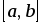 на
на 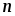 равных частей при помощи точек:
равных частей при помощи точек:
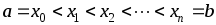 ,
,  ,
, 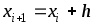 ,
,  .
.
Метод
парабол заключается в замене интеграла
суммой: 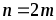
 .
.

Для
приближенных практических расчетов
применяется формула: 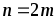
 .
(4)
.
(4)
Абсолютная
погрешность вычисления по формуле (4)
оценивается соотношением  ,
где
,
где  .
.
4. Оценка точности вычисления «неберущихся» интегралов
В
данной работе вычисление абсолютной и
относительной погрешности проводится
при условии, что известно точное значение
определенного интеграла. Однако не
всякая первообразная, даже тогда, когда
она существует, выражается в конечном
виде через элементарные функции. Таковы
первообразные, выраженные интегралами 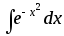
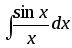 ,
, 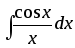 ,
, 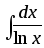 и т.д. Во всех подобных случаях первообразная
представляет собой некоторую новую
функцию, которая не сводится к комбинации
конечного числа элементарных функций.
и т.д. Во всех подобных случаях первообразная
представляет собой некоторую новую
функцию, которая не сводится к комбинации
конечного числа элементарных функций. Определенные
интегралы от таких функций можно
вычислить только приближенно. Для оценки
точности вычисления в таких случаях
используют, например, правило Рунге. В
данном случае интеграл вычисляется по
выбранной формуле (прямоугольников,
трапеций, парабол Симпсона) при числе
шагов, равном n, а затем при числе шагов,
равном 
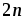 ,
вычисляется по формуле Рунге:
,
вычисляется по формуле Рунге: ,
для формул прямоугольников и трапеций
,
для формул прямоугольников и трапеций  ,
а для формулы Сипсона
,
а для формулы Сипсона 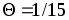 .
Таким образом, интеграл вычисляется
для последовательных значений числа
шагов
.
Таким образом, интеграл вычисляется
для последовательных значений числа
шагов 
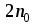 ,
,  ,
…, где
,
…, где  – начальное число шагов. Процесс
вычислений заканчивается, когда для
очередного значения
– начальное число шагов. Процесс
вычислений заканчивается, когда для
очередного значения 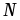 будет выполнено условие
будет выполнено условие 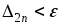 ,
где
,
где 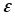 – заданная точность.
– заданная точность.Для того чтобы не вычислять один и тот же интеграл по нескольку раз для разных разбиений отрезка интегрирования, можно вычислить шаг интегрирования заранее.
Пример.
Выбрать шаг интегрирования для вычисления
интеграла  с точностью 0,01 пользуясь квадратурными
формулами прямоугольников, трапеций,
Симпсона.
с точностью 0,01 пользуясь квадратурными
формулами прямоугольников, трапеций,
Симпсона.
Квадратурная формула прямоугольников.
Вычислим,
при каком шаге 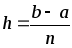 погрешность будет составлять 0,01:
погрешность будет составлять 0,01:
подынтегральный трапеция парабола неберущийся
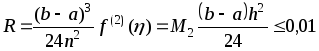 .
.
Поскольку  ,
то
,
то  .
.
При
шаге  отрезок
отрезок 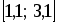 разбивается на
разбивается на 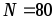 равностоящих узлов.
равностоящих узлов.
Квадратурная формула трапеций.
Вычислим,
при каком шаге  погрешность составит 0,01:
погрешность составит 0,01:
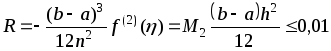 .
.
Поскольку 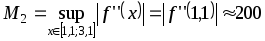 ,
,  .
.
При
шаге  ,отрезок
,отрезок 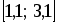 разбивается на
разбивается на 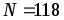 равностоящих узлов.
равностоящих узлов.
Квадратурная формула Симпсона.
Вычислим,
при каком шаге  погрешность составит 0,01:
погрешность составит 0,01:
 ,
,
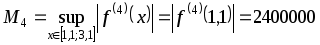 ,
, 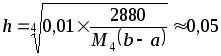 .
.
При
шаге 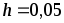 ,
отрезок
,
отрезок 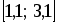 разбивается на
разбивается на  равностоящих узлов.
равностоящих узлов.
Как
и следовало ожидать, наименьшее количество
равностоящих узлов  получается при вычислении интеграла
по квадратурной формуле Симпсона.
получается при вычислении интеграла
по квадратурной формуле Симпсона.
Содержание РГР «Приближенные методы вычисления определенных интегралов»
Студенту предлагается работа, состоящая из четырех этапов:
1 этап – точное вычисление определенного интеграла.
2 этап – приближенное вычисление определенного интеграла одним из методов: прямоугольников или трапеций.
3 этап – приближенное вычисление определенного интеграла методом парабол.
4
этап – расчет и сравнение абсолютной
и относительной ошибок приближенных
методов: 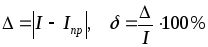 ,
где
,
где 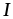 – точное решение интеграла,
– точное решение интеграла,  – значение интеграла, полученное с
помощью приближенных методов.
– значение интеграла, полученное с
помощью приближенных методов.
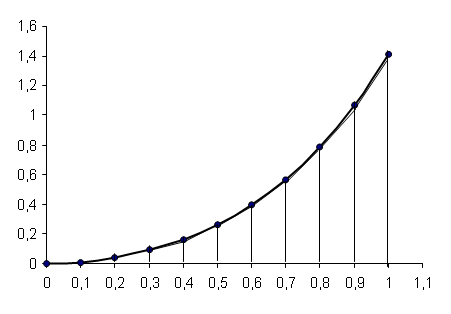
Построение графика подынтегральной функции.
Варианты и образец выполнения РГР приведены ниже.
Варианты
№ варианта | f(x) | a | b | Шаг h |
1 |
| 0 | 1 | 0,1 |
2 |
| 0 | 1 | 0,1 |
3 |
| 0 | 1 | 0,1 |
4 |
| 0 | 1 | 0,1 |
5 |
| 0 | π | 0,1π |
6 |
| 0 | 1 | 0,1 |
7 |
| 0 | 1 | 0,1 |
8 |
| 0 | 1 | 0,1 |
9 |
| 0 | 1 | 0,1 |
10 |
| 0 | π/2 | 0,05π |
11 |
| 0 | 1 | 0,1 |
12 |
| 0 | 1 | 0,1 |
13 |
| 0 | 1 | 0,1 |
14 |
| 1 | 2 | 0,1 |
15 |
| 0 | π | 0,1π |
16 |
| 1 | 2 | 0,1 |
17 |
| 0 | 1 | 0,1 |
18 |
| 0 | π/2 | 0,05π |
19 |
| 0 | 1 | 0,1 |
20 |
| 0 | π/2 | 0,05π |
21 |
| 0 | 1 | 0,1 |
22 |
| 0 | 1 | 0,1 |
23 |
| 0 | π/2 | 0,05π |
24 |
| 0 | π/2 | 0,05π |
25 |
| 0 | π/2 | 0,05π |
26 |
| 0 | π/2 | 0,05π |
27 |
| 0 | 1 | 0,1 |
28 |
| 0 | 1 | 0,1 |
29 |
| 0 | π/2 | 0,05π |
30 |
| 0 | 1 | 0,1 |
Образец выполнения РГР
Задание.
Вычислить интеграл 
1. Точное вычисление:

= 0,40631714.
2. Приближенное вычисление с помощью формул прямоугольников:
 ,
,
 ,
,  .
.
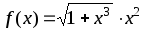 ,
,  .
.
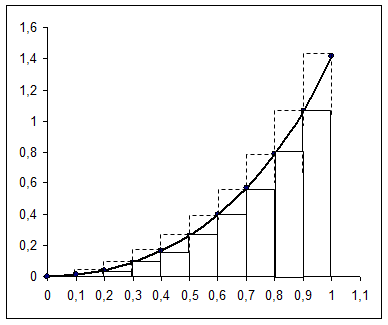
Составим таблицу:
№ | xi | yi = f (xi) |
0 | 0 | 0 |
1 | 0,1 | 0,010005 |
2 | 0,2 | 0,04016 |
3 | 0,3 | 0,091207 |
4 | 0,4 | 0,165041 |
5 | 0,5 | 0,265165 |
6 | 0,6 | 0,396981 |
7 | 0,7 | 0,567851 |
8 | 0,8 | 0,786966 |
9 | 0,9 | 1,065081 |
10 | 1 | 1,414214 |
По первой формуле прямоугольников получаем:
 ≈ 0,1
≈ 0,1 = 0,1·3,062514 = 0,306251.
= 0,1·3,062514 = 0,306251.
По второй формуле прямоугольников получаем:
 ≈ 0,1
≈ 0,1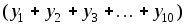 = 0,1· 4,802669 = 0,480267.
= 0,1· 4,802669 = 0,480267.
В данном случае первая формула дает значение интеграла с недостатком, вторая – с избытком.
Вычислим относительную и абсолютную погрешности.
I
= 0,40631714, 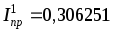 ,
, 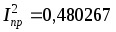
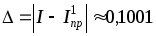 ,
, 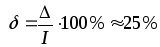 .
.
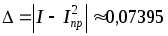 ,
,  .
.
3. Приближенное вычисление по формуле трапеций:
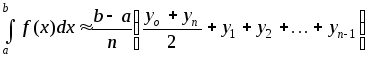
В нашем случае получаем:
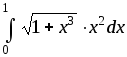 ≈ 0,1
≈ 0,1 = =0,1
= =0,1 = 0,1·4,095562 = =0,409556.
= 0,1·4,095562 = =0,409556.
Вычислим относительную и абсолютную погрешности.
I
= 0,40631714, 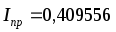
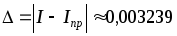 ,
,  .
.
4. Приближенное вычисление по формуле Симпсона:
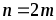

В нашем случае получаем:
 ≈
≈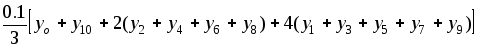 =
=
=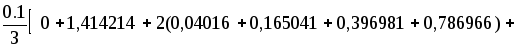
 = 0,406325.
= 0,406325.

Вычислим относительную и абсолютную погрешности.
I
= 0,40631714 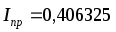
 ,
, 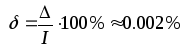 .
.
В
действительности, 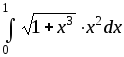 = 0,40631714.
= 0,40631714.
Таким
образом, при разбиении отрезка  на 10 частей по формуле Симпсона мы
получили 5 верных знаков; по формуле
трапеций – три верных знака; по формуле
прямоугольников мы можем ручаться
только за первый знак.
на 10 частей по формуле Симпсона мы
получили 5 верных знаков; по формуле
трапеций – три верных знака; по формуле
прямоугольников мы можем ручаться
только за первый знак.
Литература
Задачи и упражнения по математическому анализу для втузов: учеб. пособие для втузов / Г. С. Бараненков [и др.]; под ред. Б.П. Демидовича. — М.; Владимир: Астрель: Изд-во АСТ: ВКТ, 2010. — 495 с.
Кудрявцев, Л.Д. Краткий курс математического анализа: учеб. для вузов. Т. 1: Дифференциальное и интегральное исчисления функций одной переменной. Ряды / Л. Д. Кудрявцев. — 3-е изд., перераб. — М.: ФИЗМАТЛИТ, 2009. — 399 с.
Пискунов, Н.С. Дифференциальное и интегральное исчисления: учеб. пособие для втузов. В 2 т. Т. 1 / Н. С. Пискунов. — Изд. стер. — М.: Интеграл-Пресс, 2004. — 415 с.
Шипачев В.С. Высшая математика : учеб. для вузов / В. С. Шипачев. — 7-е изд., стер. — М.: Высш. шк., 2005. — 479 с.
studfile.net
Приближенные вычисления с помощью рядов
Степенные ряды широко используются в приближенных вычислениях. С их помощью с заданной точностью можно вычислять значения корней, тригонометрических функций, логарифмов чисел, определенных интегралов. Ряды применяются также при интегрировании дифференциальных уравнений.
1. Приближенное вычисление значений функций
Рассмотрим разложение функции в степенной ряд:
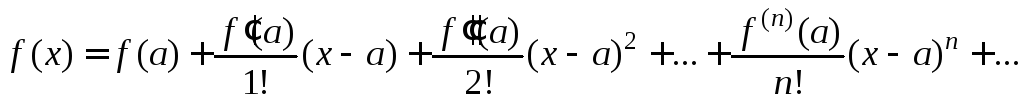 .
.
Для того, чтобы вычислить приближенное значение функции в заданной точке х, принадлежащей области сходимости указанного ряда, в ее разложении оставляют первые n членов (n – конечное число), а остальные слагаемые отбрасывают:
 .
.
Для оценки погрешности полученного приближенного значения необходимо оценить отброшенный остаток rn(x). Для этого применяют следующие приемы:
если полученный ряд является знакочередующимся, то используется следующее свойство: для знакочередующегося ряда, удовлетворяющего условиям Лейбница, остаток ряда по абсолютной величине не превосходит первого отброшенного члена.
если данный ряд знакопостоянный, то ряд, составленный из отброшенных членов, сравнивают с бесконечно убывающей геометрической прогрессией.
в общем случае для оценки остатка ряда Тейлора можно воспользоваться формулой Лагранжа:
 (илиx<c<a).
(илиx<c<a).
Пример 1. Пользуясь разложением в ряд sinx, вычислить sin20o с точностью до 0,0001.
Решение.
Чтобы можно было пользоваться формулой
(2), необходимо выразить значение аргумента
в радианной мере. Получаем 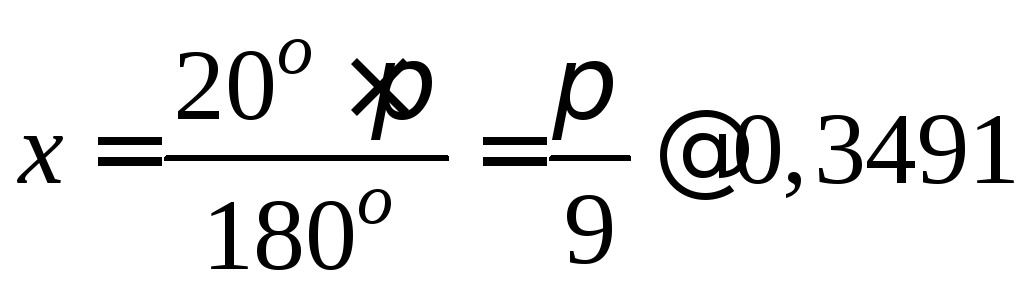 .
Подставляя это значение в формулу,
получаем
.
Подставляя это значение в формулу,
получаем
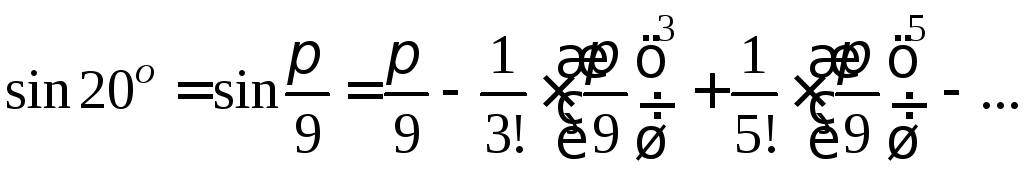
Полученный
ряд является знакочередующимся и
удовлетворяет условиям Лейбница. Так
как  ,
то этот и все последующие члены ряда
можно отбросить, ограничиваясь первыми
двумя членами. Таким образом,
,
то этот и все последующие члены ряда
можно отбросить, ограничиваясь первыми
двумя членами. Таким образом,
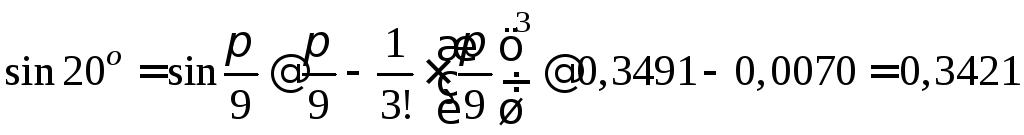 .
.
Пример
2. Вычислить 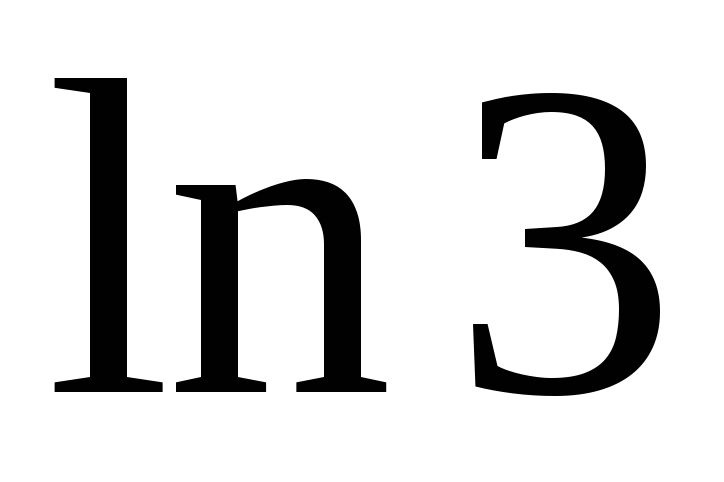 с точностью до 0,01.
с точностью до 0,01.
Решение.
Воспользуемся разложением 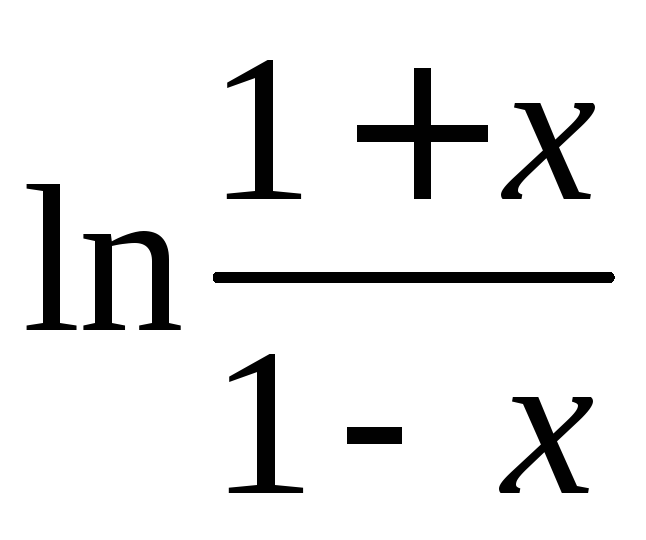 ,
где
,
где (см. пример 5 в предыдущей теме):
(см. пример 5 в предыдущей теме):
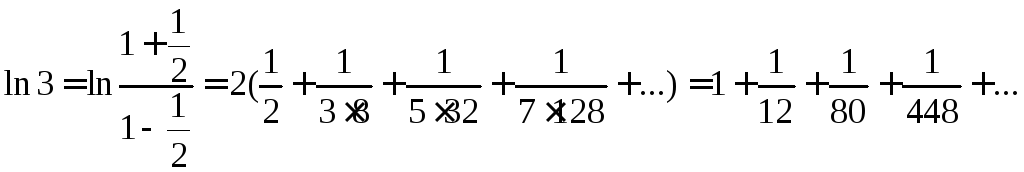
Проверим, можем ли мы отбросить остаток после первых трех членов разложения, для этого оценим его с помощью суммы бесконечно убывающей геометрической прогрессии:
 .
.
Таким образом, мы можем отбросить этот остаток и получаем
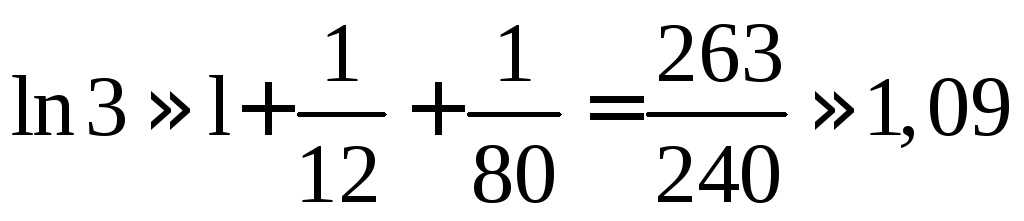 .
.
Пример
3. Вычислить 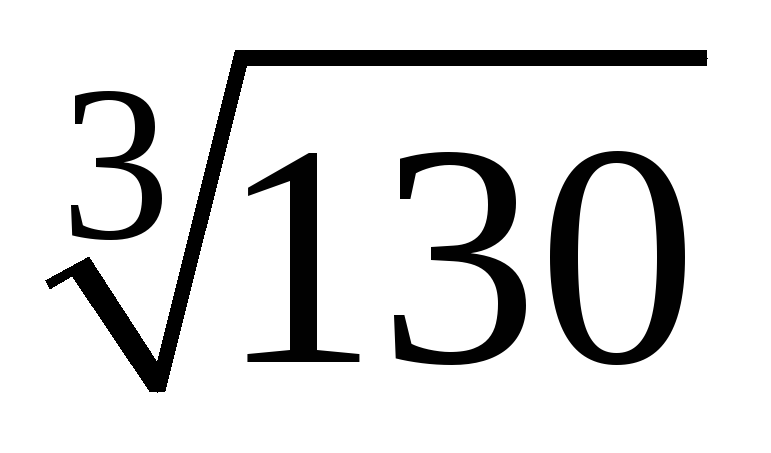 с точностью до 0,0001.
с точностью до 0,0001.
Решение. Воспользуемся биномиальным рядом. Так как 53 является ближайшим к 130 кубом целого числа, то целесообразно число 130 представить в виде 130=53+5.

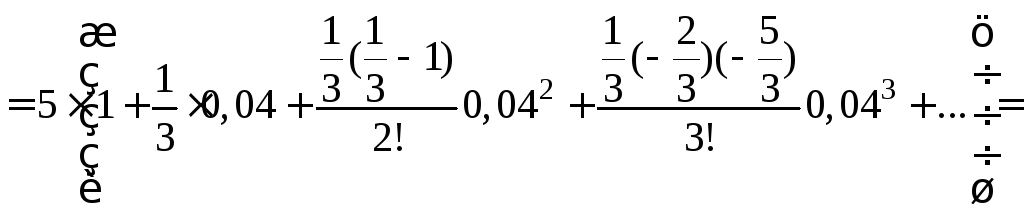
 ,
,
так как уже четвертый член полученного знакочередующегося ряда, удовлетворяющего признаку Лейбница, меньше требуемой точности:
 ,
поэтому его и следующие за ним члены
можно отбросить.
,
поэтому его и следующие за ним члены
можно отбросить.
2. Приближенное вычисление определенных интегралов
Многие практически нужные определенные или несобственные интегралы не могут быть вычислены с помощью формулы Ньютона-Лейбница, ибо ее применение связано с нахождением первообразной, часто не имеющей выражения в элементарных функциях. Бывает также, что нахождение первообразной возможно, но излишне трудоемко. Однако если подинтегральная функция раскладывается в степенной ряд, а пределы интегрирования принадлежат интервалу сходимости этого ряда, то возможно приближенное вычисление интеграла с наперед заданной точностью.
Пример
4: Вычислить
интеграл  с точностью до 0,00001.
с точностью до 0,00001.
Решение.
Соответствующий неопределенный интеграл 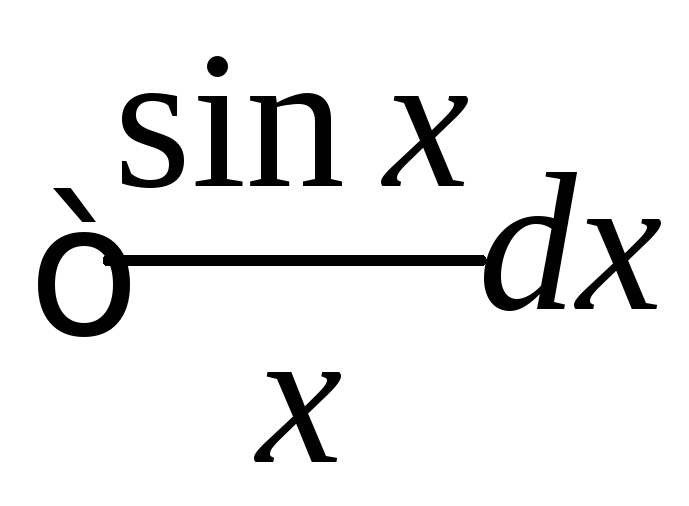 не может быть выражен в элементарных
функциях, т.е. представляет собой
«неберущийся интеграл». Применить
формулу Ньютона-Лейбница здесь нельзя.
Вычислим интеграл приближенно.
не может быть выражен в элементарных
функциях, т.е. представляет собой
«неберущийся интеграл». Применить
формулу Ньютона-Лейбница здесь нельзя.
Вычислим интеграл приближенно.
Разделив почленно ряд для sinx на x , получим:

Интегрируя этот ряд почленно (это возможно, так как пределы интегрирования принадлежат интервалу сходимости данного ряда), получаем:

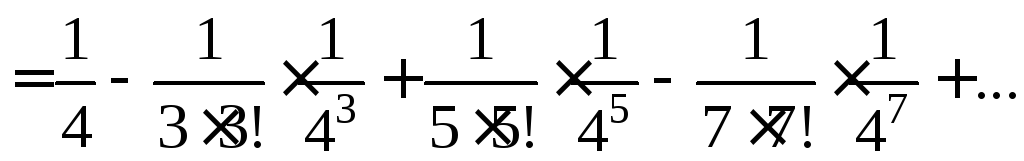
Так
как полученный ряд удовлетворяет
условиям Лейбница и  достаточно взять сумму первых двух
членов, чтобы получить искомое значение
с заданной точностью.
достаточно взять сумму первых двух
членов, чтобы получить искомое значение
с заданной точностью.
Таким образом, находим
 .
.
Пример
5. Вычислить
интеграл 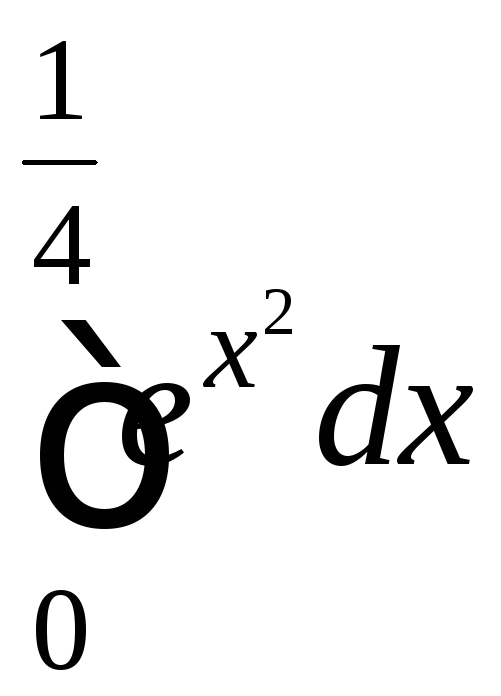 с точностью до 0,001.
с точностью до 0,001.
Решение.
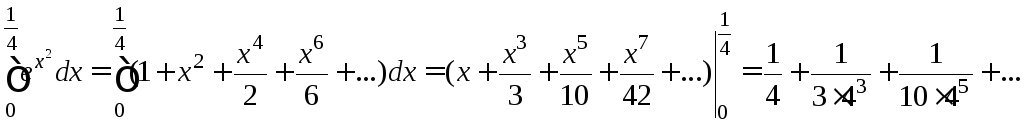
Проверим, можем ли мы отбросить остаток после второго члена полученного ряда.
 .
.
Следовательно,  .
.
studfile.net
Приближенное вычисление определенного интеграла, дифференциальных уравнений и вычисление значений функций
ТАШКЕНТСКИЙ УНИВЕРСИТЕТ
ИНФОРМАЦИОННЫХ ТЕХНАЛОГИЙ
УРГЕНЧСКИЙ ФИЛИАЛ
САМОСТОЯТЕЛЬНАЯ РАБОТА
По высшей математике
На тему
Приближенное вычисление определенного интеграла, приближенное решение дифференциальных уравнений, приближенное вычисление значений функций
Подготовил студент 914-14 группы
Джуманиязова Мардона
Приближенное вычисление определенного интеграла
Пусть требуется найти определенный интеграл от непрерывной функции ƒ(х). Если можно найти первообразную F(x) функции ƒ(х), то интеграл вычисляется по формуле Ньютона-Лейбница:

Но отыскание первообразной функции иногда весьма сложно; кроме того, как известно, не для всякой непрерывной функции ее первообразная выражается через элементарные функции. В этих и других случаях (например, функция
у = ƒ(х)
задана графически или табличнo) прибегают к приближенным формулам, с помощью которых определенный интеграл находится с любой степенью точности.
Рассмотрим три наиболее употребительные формулы приближенного вычисления определенного интеграла — формулу прямоугольников, формулу трапеций, формулу парабол (Симпсона), основанные на геометрическом смысле определенного интеграла.
Формула прямоугольников
Пусть на отрезке [а; b], а < b, задана непрерывная функция ƒ(х). Требуется вычислить интеграл численно равный площади соответствующей криволинейной трапеции.

Разобьем основание этой трапеции, т. е. отрезок [а; b], на n равных частей (отрезков) длины

(шаг разбиения) с помощью точек х0= а, x1, х2,…, хn = b. Можно записать, что
хi= х0+h• i,
где i = 1,2,…, n (см. рис. 200).
В середине
каждого такого отрезка построим ординату
ŷi =ƒ(сi)
графика функции у = ƒ(х).
Приняв эту ординату за высоту, построим прямоугольник с площадью h • ŷi.
Тогда сумма площадей всех n прямоугольников дает площадь ступенчатой фигуры, представляющую собой приближенное значение искомого определенного интеграла
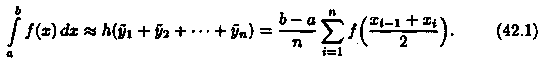
Формула (42.1) называется формулой средних прямоугольников.
Абсолютная погрешность приближенного равенства (42.1) оценивается с помощью следующей формулы:
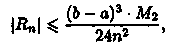
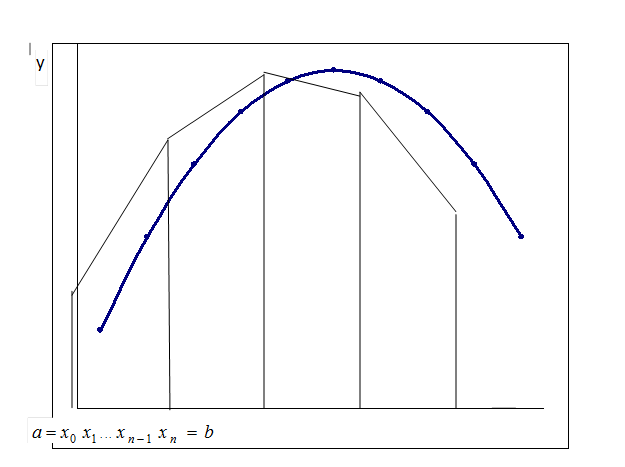
где М2 — наибольшее значение |ƒ»(х)| на отрезке [а; b],

Отметим, что для линейной функции
ƒ(х)=kх+b
формула (42.1) дает точный ответ, поскольку в этом случае
ƒ»(х)=0.
Формула трапеций
Формулу трапеций получают аналогично формуле прямоугольников: на каждом частичном отрезке криволинейная трапеция заменяется обычной.
Разобьем отрезок [а; b] на n равных частей длины
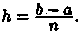
Абсциссы точек деления а = х0, x1,х2,…,b = хn (рис. 201). Пусть у0,у1…,уn соответствующие им ординаты графика функции. Тогда расчетные формулы для этих значений примут вид
хi= a+h*i, уi=ƒ(xi), i= 0,1,2,…, n;

Заменим кривую у=ƒ(х) ломаной линией, звенья которой соединяют концы ординат yiи yi+1 (i = 0,1,2,.. .,n). Тогда площадь криволинейной трапеции приближенно равна сумме площадей обычных трапеций с основаниями уi, yi+1 и высотой

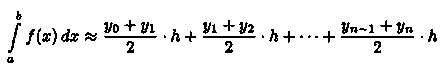
Или
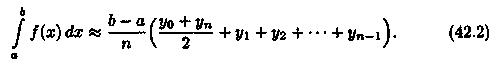
Формула (42.2) называется формулой трапеций.
Абсолютная погрешность Rn приближения, полученного по формуле трапеций, оценивается с помощью формулы
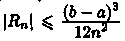 •
М2,
•
М2,
Где

Снова для линейной функции
у=kх +b
формула (42.2) — точная.
Формула парабол (Симпсона)
Если
заменить график функции у=ƒ(х) на каждом
отрезке [xi-1;xi]
разбиения не отрезками прямых, как в
методах трапеций и прямоугольников, а
дугами парабол, то получим более точную
формулу приближенного вычисления
интеграла 
Предварительно найдем площадь S криволинейной трапеции, ограниченной сверху графиком параболы
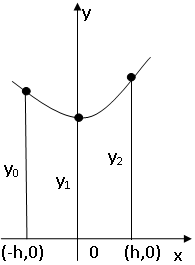
у = ах2+ bх + с,
сбоку — прямыми х = —h, х = h и снизу — Отрезком [-h; h].

Пусть парабола проходит через три точки M1(-h;у0), М2(0; y1), М3(h; у2), где
у0 = ah2 -bh + c
— ордината параболы в точке х = -h; y1 = с — ордината параболы в точке х = 0;
у2 = аh2 + bh+c
ордината параболы в точке х = h (см. рис 202). Площадь S равна

Выразим эту площадь через h, у0, y1, у2. Из равенств для ординат у (находим, что с=y1,

Подставляя эти значения с и а в равенство (42.3), получаем

Получим
теперь формулу парабол для вычисления
интеграла 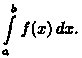
Для этого отрезок [а; b] разобьем на 2n равных частей (отрезков) длиной
Точками
xi=х0 + ih (i= 0,1,2,…, 2n).
В точках деления а = х0, x1, x2,…, x2n-2 ,x2n-1, x2n = b вычисляем значения подынтегральной функции ƒ(х): у0, у1,у2,…, у2n-2, у2n-1, у2n, где
уi=ƒ(хi)
(см. рис. 203).

Заменяем каждую пару соседних элементарных криволинейных трапеций с основаниями, равными h, одной элементарной параболической трапецией с основанием, равным 2h. На отрезке [х0;х2] парабола проходит через три точки (х0;у0), (x1;y1), (x2;y2). Используя формулу (42.4), находим
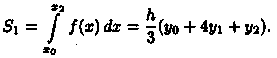
Аналогично находим
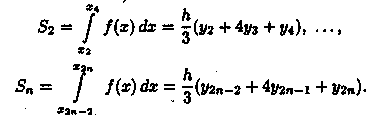
Сложив полученные равенства, имеем

Или

Формула (42.5) называется формулой парабол (или Симпсона).
Абсолютная погрешность вычисления по формуле (42.5) оценивается соотношением

Отметим, что формула (42.5) дает точное значение интеграла во всех случаях, когда ƒ(х) — многочлен, степень которого меньше или равна трем (тогда fIV = 0).
Пример 42.1. Вычислить, разбив отрезок интегрирования [0; 2] на 4 части.
Решение: Имеем:

ƒ(х) = х3,

(см.рис. 204)
а) по формуле прямоугольников:

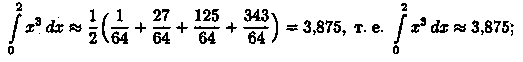
б) по формуле трапеции:

в) по формуле парабол:
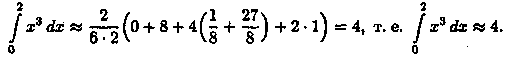
Приближенное решение дифференциальных уравнений
Если решение дифференциального уравнения не выражается через элементарные функции в конечном виде или способ его решения слишком сложен, то для приближенного решения можно воспользоваться рядом Тейлора.
Рассмотрим два способа решения дифференциальных уравнений с помощью степенных рядов.
Способ последовательного дифференцирования
При решении задачи Коши
 ,
,
используется ряд Тейлора
 ,
,
Где
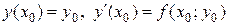 ,
,
а
остальные производные 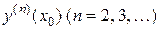 находятся путем последовательного
дифференцирования уравнения
находятся путем последовательного
дифференцирования уравнения
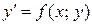
и подстановки начальных данных в выражения для этих производных.
Надо отметить, что способ последовательного дифференцирования применим для решения дифференциальных уравнений любого порядка.
Пример 3.12. Найти пять первых членов (отличных от нуля) разложения в степенной ряд решения дифференциального уравнения
 ,
,
Если
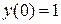 .
.
Решение. Находим решение дифференциального
уравнения (при  )
в виде
)
в виде
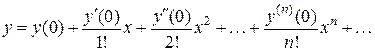 .
.
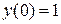 .
.
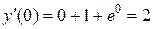 .
.
Далее
находим производные высших порядков и
значения производных при 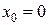 .
.
 .
.
Тогда
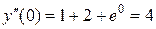 .
.
 .
.
Тогда
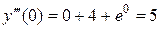 .
.
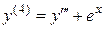 .
.
Тогда
 .
.
Подставляя найденные значения производных в искомый ряд, получаем:
 .
.
Способ неопределенных коэффициентов
Этот способ приближенного решения наиболее удобен для линейных дифференциальных уравнений с переменными коэффициентами.
Пусть, например, требуется решить уравнение
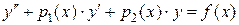
с начальными условиями
 .
.
Предполагая,
что коэффициенты 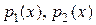 и свободный член
и свободный член  разлагаются в ряды по степеням
разлагаются в ряды по степеням 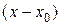 ,
сходящиеся в некотором интервале
,
сходящиеся в некотором интервале 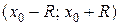 ,
искомое решение
,
искомое решение
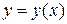
находится в виде степенного ряда

с неопределенными коэффициентами.
При
помощи начальных условий находим
коэффициенты  и
и 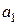 .
Для нахождения последующих коэффициентов
степенной ряд дифференцируем два раза
(каков порядок уравнения) и подставляем
выражения для функции
.
Для нахождения последующих коэффициентов
степенной ряд дифференцируем два раза
(каков порядок уравнения) и подставляем
выражения для функции 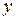 и ее производных в исходное уравнение,
заменив в нем
и ее производных в исходное уравнение,
заменив в нем 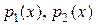 ,
, 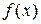 их разложениями. В результате получаем
тождество, из которого методом
неопределенных коэффициентов находим
недостающие коэффициенты.
их разложениями. В результате получаем
тождество, из которого методом
неопределенных коэффициентов находим
недостающие коэффициенты.
Построенный
степенной ряд сходится в том же интервале 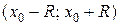 и является решением исходного уравнения.
и является решением исходного уравнения.
Пример 3.13. Найти решение уравнения
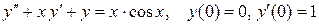 .
.
используя метод неопределенных коэффициентов.
Решение. Разложим коэффициенты уравнения 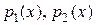 и
и 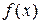 при
при 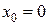 в степенные ряды
в степенные ряды
 ,
,
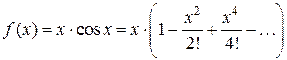 .
.
Решение исходного дифференциального уравнения находим в виде степенного ряда
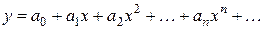 .
.
Тогда
,
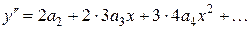 .
.
Из
начальных условий находим: 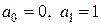 .
Подставляем полученные ряды в
дифференциальное уравнение:
.
Подставляем полученные ряды в
дифференциальное уравнение:

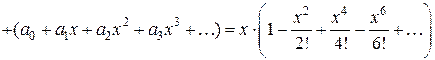 .
.
Приравнивая
коэффициенты при одинаковых степенях 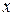 .
.
Приближенное вычисление значений функций
Абсолютная и условная сходимость числовых рядов
Знакопеременный ряд называют абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится. Знакопеременный ряд называют условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
Среди знакопеременных рядов абсолютно сходящиеся ряды занимают особое место: на такие ряды переносятся основные свойства конечных сумм (переместительность, сочетательность, распределительность).
Т.е. абсолютно сходящиеся ряды суммируются, вычитаются как обычные ряды. Суммы таких рядов не зависят от порядка записи членов. В случае условно сходящихся рядов, такие свойства, вообще говоря, не имеют места.
Ряд,
членами которого являются функции от  ,
называется функциональным.
,
называется функциональным.
 .
.
приближенный интеграл дифференциальный степенной
Придавая  определенное
значение х0 мы получаем числовой ряд
определенное
значение х0 мы получаем числовой ряд  ,
который может быть как сходящимся, так
и расходящимся.
,
который может быть как сходящимся, так
и расходящимся.
Если
полученный числовой ряд сходится, то
точка  называется
точкой сходимости ряда, если ряд
расходится – точкой расходимости.
Совокупность числовых значений аргумента
называется
точкой сходимости ряда, если ряд
расходится – точкой расходимости.
Совокупность числовых значений аргумента  ,
при которых функциональный ряд сходится,
называется его областью сходимости. В
области сходимости функционального
ряда его сумма является некоторой суммой
от
,
при которых функциональный ряд сходится,
называется его областью сходимости. В
области сходимости функционального
ряда его сумма является некоторой суммой
от  :
:
 .
.
Определяется она в области сходимости ряда равенством
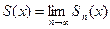 ,
,
Где

—
частичная сумма ряда. Среди функциональных
рядов в математике и ее приложениях
особая роль принадлежит рядам, членами
которых являются степенные функции
аргумента  ,
т.е. так называемые степенные ряды.
,
т.е. так называемые степенные ряды.
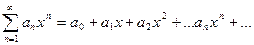
Действительные
или комплексные числа 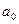 ,
, 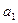 ,
…,
,
…, 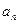 …
называются коэффициентами ряда, а
…
называются коэффициентами ряда, а  —
действительной переменной. Ряд расположен
по степеням
—
действительной переменной. Ряд расположен
по степеням  .
Рассматривают такие степенные ряды,
расположенные по степеням
.
Рассматривают такие степенные ряды,
расположенные по степеням 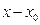 ,
т.е. ряд вида
,
т.е. ряд вида
 ,
,
где  —
некоторое постоянное число. Этот ряд
легко приводится к первому, если положить
—
некоторое постоянное число. Этот ряд
легко приводится к первому, если положить
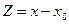 .
.
Сходимость степенных рядов
Область
сходимости степенного ряда содержит,
по крайней мере, одну точку: 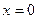 ,
в которой ряд сходится.
,
в которой ряд сходится.
Теорема Абеля. Если степенной ряд сходится при
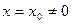 ,
,
то
он абсолютно сходится при всех значениях 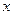 ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
 .
.
Доказательство. По условию ряд

сходится. Следовательно, по необходимому признаку сходимости
 .
.
Отсюда
следует, что величина  ограничена,
т.е. найдется такое число
ограничена,
т.е. найдется такое число 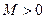 ,
что для всех
,
что для всех 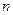 выполняется
неравенство
выполняется
неравенство
 ,
, 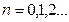 .
.
Пусть
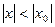 ,
,
тогда величина
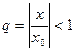
и следовательно,
 ,
,  ,
,
т.е.
модуль каждого члена ряда не превосходит
соответствующего члена сходящегося
ряда 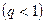 геометрической
прогрессии. Поэтому по признаку сравнения
при
геометрической
прогрессии. Поэтому по признаку сравнения
при  степенной ряд абсолютно сходящийся.
степенной ряд абсолютно сходящийся.
Следствие. Если
ряд (степенной) расходится при  ,
то он расходится и при всех
,
то он расходится и при всех 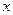 ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
|x|>|x0|.
Интервал и радиус сходимости степенного ряда
Из
теоремы Абеля следует, что если 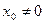 есть
точка сходимости степенного ряда, то
интервал
есть
точка сходимости степенного ряда, то
интервал 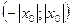 весь
состоит из точек сходимости данного
ряда при всех значениях
весь
состоит из точек сходимости данного
ряда при всех значениях  вне
этого интервала ряд расходится.
вне
этого интервала ряд расходится.
Интервал  называют
интервалом сходимости степенного ряда.
Положив
называют
интервалом сходимости степенного ряда.
Положив
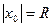 ,
,
интервал
сходимости можно записать в виде 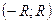 .
Число
.
Число 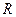 называется
радиусом сходимости степенного ряда,
т.е.
называется
радиусом сходимости степенного ряда,
т.е.  —
это такое число, что при всех
—
это такое число, что при всех 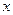 ,
для которых
,
для которых 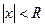 ,
ряд абсолютно сходится, а при
,
ряд абсолютно сходится, а при  ряд
расходится. В частности, когда степенной
ряд сходится лишь в одной точке
ряд
расходится. В частности, когда степенной
ряд сходится лишь в одной точке 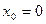 ,
то считаем, что
,
то считаем, что  .
Если же степенной ряд сходится при всех
значениях
.
Если же степенной ряд сходится при всех
значениях 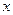 ,
то
,
то 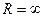 .
.
Отметим,
что на концах интервала сходимости (при 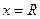 и
и 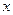 =-R)
сходимость ряда проверяется отдельно.
=-R)
сходимость ряда проверяется отдельно.
Для
нахождения радиуса сходимости степенного
ряда можно поступить следующим образом.
Составим ряд из модулей членов данного
степенного ряда 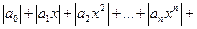 и
применим к нему признак Даламбера.
Допустим, что существует предел
и
применим к нему признак Даламбера.
Допустим, что существует предел
 ,
,  .
.
studfile.net




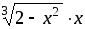
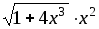




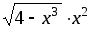

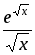
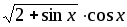

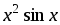
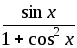
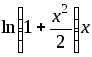
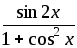

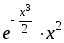
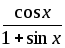




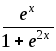

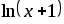
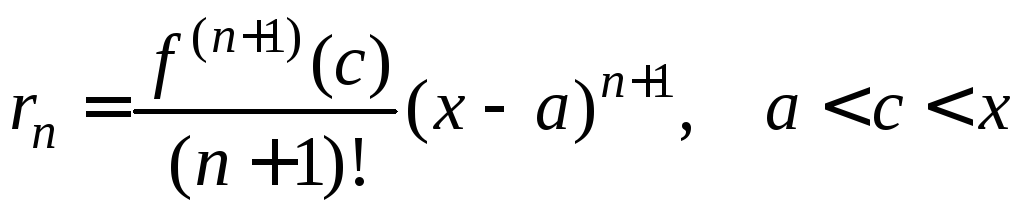 (илиx<c<a).
(илиx<c<a).